Abstract
Chromophoric biomolecules are exploited as reporters of a diverse set of phenomena, acting as internal distance monitors, environment and redox sensors, and endogenous imaging probes. The extent to which they can be exploited is dependent on an accurate knowledge of their fundamental electronic properties. Arguably of greatest importance is a precise knowledge of the direction(s) of the absorption transition dipole moment(s) (TDMs) in the molecular frame of reference. Such is the case for flavins, fluorescent redox cofactors utilized for ground and excited-state redox and photochemical processes. The directions of the TDMs in oxidized and semiquinone flavins were characterized decades ago, and the details of charge redistribution in these forms have also been studied by Stark spectroscopy. The electronic structure of the fully reduced hydroquinone anionic state, FlH−, however, has been the subject of unfounded assumptions and estimates about the number and direction of TDMs in FlH−, as well the electronic structure changes that occur upon light absorption. Here we have used Stark spectroscopy to measure the magnitude and direction of charge redistribution in FlH− upon optical excitation. These data were analyzed using TD-DFT calculations. The results show unequivocally that not one but two nearly orientation-degenerate electronic transitions are required to explain the 340–500 nm absorption spectral range, demolishing the commonly held assumption of a single transition. The difference dipole moments for these states show that electron density shifts toward the xylene ring for both transitions. These measurements force a reappraisal of previous studies that have used erroneous assumptions and unsubstantiated estimates of these quantities. The results put future optical studies of reduced flavins/flavoproteins on a firm photophysical footing.
Graphical Abstract
INTRODUCTION
Flavins (Fl) are redox cofactors whose excited-state electronic properties are exploited by both Nature and scientists. These vitamin B2 derivatives exist in three physiologically relevant oxidation (and two protonation) states, flavoquinone FlOX, flavosemiquinone FlH• (Fl•−), and flavohydroquinone FlH2 (FlH−), all of which play photobiological roles involving light from 300 to 500 nm. (See Figure 1 for the numbering scheme. FlH− is shown along with its transition dipole moments,1 vide infra.)
Figure 1.
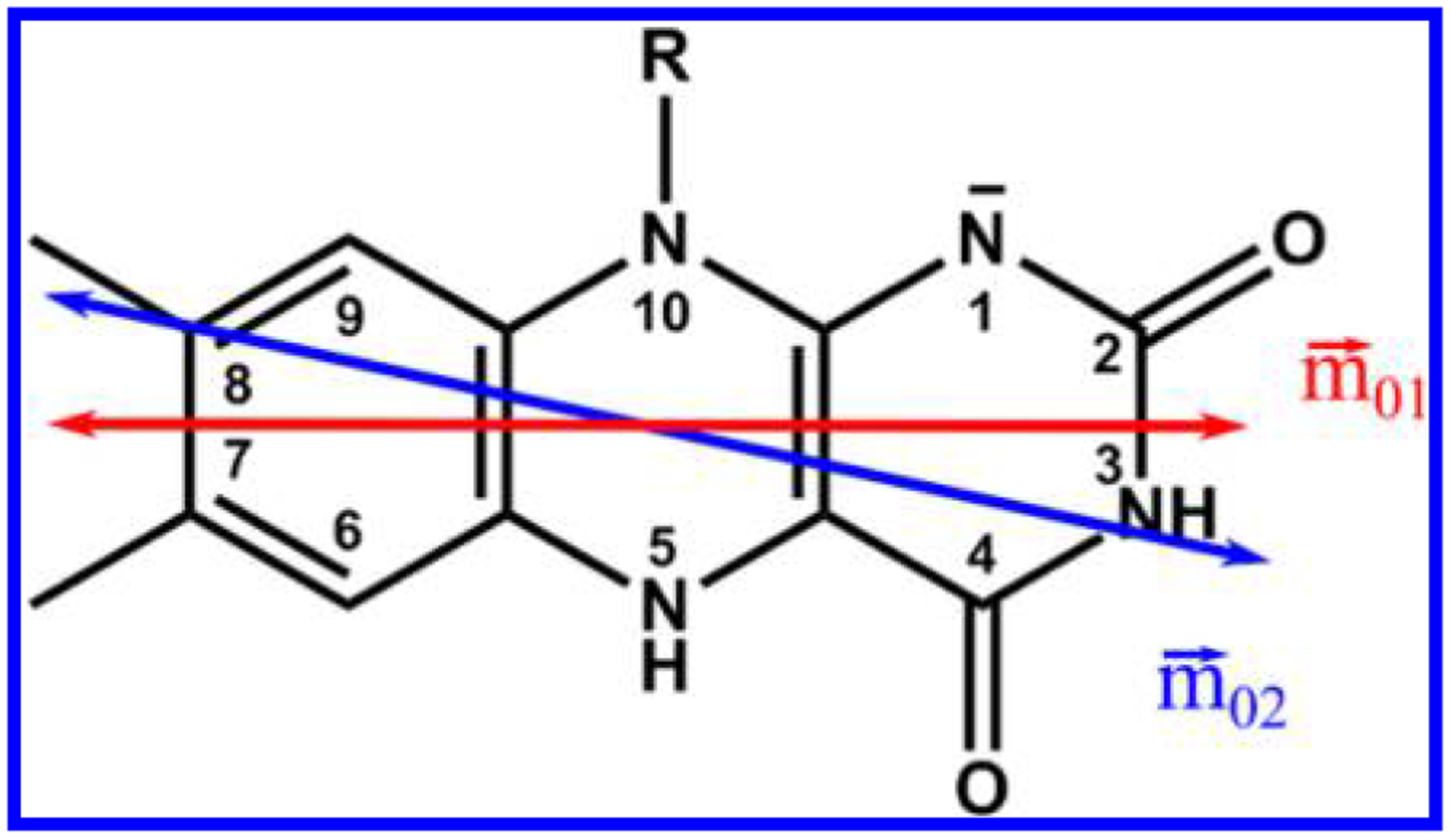
Structure and ring numbering of reduced flavin anion, FlH− (R = isobutyl). Experimentally determined transition dipole moments for the S0→S1 (red) and S0 →S2 (blue) transitions are shown1.
The excited-state electronic properties of molecules dictate their photodynamics and interactions with their surroundings. In the case of photobiology, accurate transition dipole moments (TDMs) and excitation-driven charge redistribution (difference dipole and polarizability moments) are required to properly interpret kinetics due to electron transfer, solvation, changes in hydrogen-bonding (HB) patterns, etc. They are also a critical test for electronic structure calculations. Flavin chromophores are used for biosensing,2–4 imaging,5–7 and molecular electronics,8–12 but they can only be fully exploited if their detailed electronic structure is understood.
The structure of the near-UV electronic transitions of FlOX and FlH• has been unambiguously assigned by Eaton et al. using optical linear dichroism of FMN-containing flavodoxin single crystals.13 The directions of the TDMs (, where 0 and n are the ground and final states) of FlOX and FlH• in the molecular frame have served as the “gold standard” against which a multitude of experimental and computational studies have been compared.
Charge redistribution upon photoexcitation affects electron transfer and solvation dynamics. The accompanying charge redistribution in *FlOX and *FlH• has been extensively characterized by our group using Stark spectroscopy.14–17 Stark spectroscopy affords a parsing of the excited-state charge distribution into difference dipole moments, , and difference mean polarizabilities, . These experiments are often complemented by electronic structure calculations. The resulting difference electron density maps have considerable analytical and predictive power.17
Comparatively, much less is known about the spectrum and excited-state electronic structure of the flavohydroquinone anion, FlH− (see Figure 2). In the mid-1970s, Ghisla et al. gathered 77 K absorption and emission spectra from reduced flavins and flavoproteins which suggested that there were three distinct transitions in the 300–500 nm range for FlH−.18 Although the paper has been highly cited, their seminal conclusion has been ignored by most people working in the field. Time-resolved emission studies on flavins and flavoproteins by Visser et al. in 1979 supported this assignment.19 Electronic structure calculations often substantiated the separation of the 340–500 nm band into two separate transitions, but many of these studies gave negligible oscillator strength (fosc < 0.01) to the S01 transition. Consequently, experimental studies in the ~30 years that followed have implicitly assumed that the shoulder at 425 nm is part of a vibronic progression that reaches a maximum at 360 nm.
Figure 2.
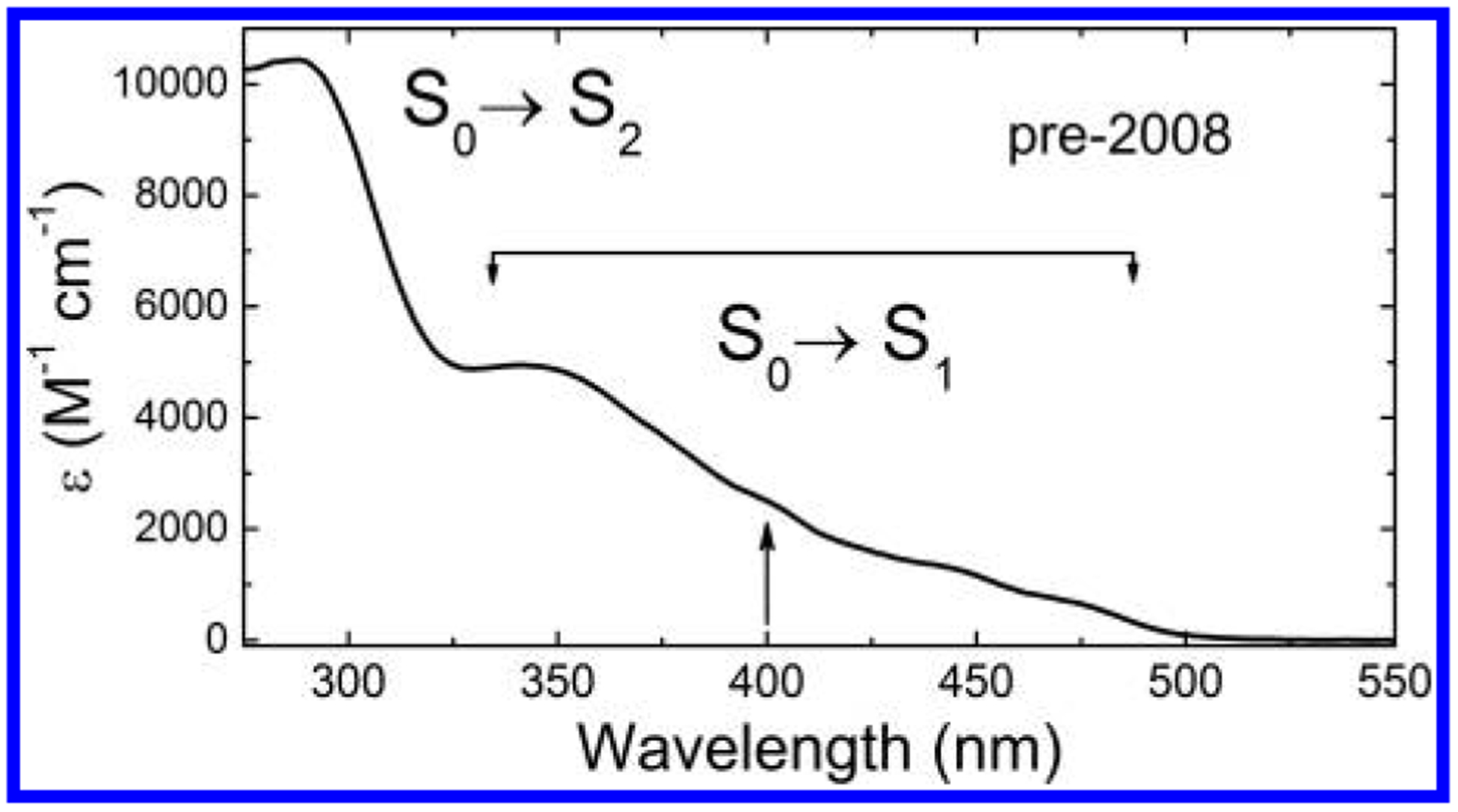
298 K absorption spectrum of FlH− in EtOH. S0→Sn assignments reflect pre-2008 assumptions about putative vibronic structure of the S0→S1 band between 350 and 500 nm, with the assumed S0→S2 band maximum at about 290 nm. The arrow at 400 nm indicates a commonly used Ti:sapphire laser wavelength for flavin studies.
Faced with the need to interpret ultrafast kinetic data for DNA photolyase (PL),20,21 a FADH−-dependent protein that repairs UV-damaged DNA, we analyzed the absorption spectrum of the reduced flavohydroquinone anion from flavin mononucleotide oriented in stretched PVA films using linear dichroism (LD, Figure 2, see ref 1). The broad absorption band from 340 to 500 nm was split into two nearly parallel transitions, centered at 425 nm and at 360 nm, vindicating the pioneering work of Ghisla and Visser. These TDMs are within 11° of each other and have a 3:1 ratio of oscillator strengths (f360/f425). Despite this report,1 researchers exploring the biomolecular spectroscopy of reduced flavins and flavoproteins “sidestepped” this two-state electronic structure confirmation. Many peer-reviewed studies have appeared in which the one TDM model is assumed or explicitly invoked.22–25 Some of these will be discussed below.
Here we show, using Stark spectroscopy and time-dependent density functional theory (TDDFT) calculations, that the LD study is indeed correct, and that charge redistribution accompanying the S01 and S02 transitions are significantly different in both magnitude and direction. This two-state spectral resolution requires a re-analysis of excited-state FlH− phenomena based on the one-band assumption, from photo-induced electron transfer (PET), to ultrafast solvation, to HB strength modulation. It also promises to expand our optical toolbox in affording sensical polarization measurements to be made, whether they focus on proteins26 or optogenetic/biosensor devices27,28 based on reduced flavin spectroscopy. Finally, these measurements provide a new standard to be met by theory.
MATERIALS AND METHODS
Sample Preparation.
N(10)-Isobutyl-7,8-dimethylisoalloxazine (Fl) was a generous gift from Prof. Vincent Rotello of the University of Massachusetts (Amherst) and was prepared as described in the Supporting Information (SI). Reduced anionic flavin was dissolved in 2-methyltetrahydrofuran (MeTHF). Photoreduction was performed in the presence of triethylamine (TEA) to deprotonate the reduced flavin18 at N(1) (pKa = 6.7). One μL of TEA was added to 600 μL of a 650 μM Fl solution in a 2 mm path length sealable quartz cuvette. The sample was placed in an anaerobic glovebox (MACS) and allowed to stir for 30–50 min while illuminated with blue light from a hand-held LED (Phillips GoLite, λ ≈ 468 nm). Reduction was monitored visually by the loss of bright yellow color of the solution. Low-temperature emission spectra of the frozen samples were measured to ensure full reduction of the flavin was achieved, as oxidized flavin has characteristic and bright red-shifted emission (~520 nm) compared with the emission from FlH− (~510 nm). Alternatively, photo-reduction of flavin was performed in the presence of NaBH4 and TEA in ethanol (see SI). Photodegradation products, mostly lumichrome,29 were assessed using HPLC (see SI).
Low-Temperature Absorption and Stark Spectroscopy.
The experimental setup of the Stark spectrometer has been discussed in detail previously (see SI).30 The 50 μm path length sample cuvette was loaded with 30–50 μL of FlH− by capillary action into the cuvette in an anoxic environment. The loaded sample was exposed to white light for <1 s to reduce any flavin that may have oxidized in the sample loading process and immediately plunged into liquid nitrogen. The presence of any oxidized flavin was checked at low temperature by its characteristic emission. Samples which contained no structured emission at 520 nm and greater were deemed suitable for data collection.
Low-temperature absorption spectra were recorded on the same instrumental setup, with an optical chopper operating at ~4 kHz to modulate the probe beam. In order to achieve sufficient signal to noise, a thicker 220 μm Teflon spacer was used to increase the path length for these measurements. Sample and reference intensities were recorded under identical conditions, and the absorption spectrum was calculated according to the Beer–Lambert law. Absorption and Stark data were corrected for solvent contraction (~20%).
Data Analysis.
Stark spectra were analyzed according to the procedure of Liptay,31 in which the Stark spectrum of an isotropic sample is described by
| (1) |
where is the magnitude of the applied electric field in V/m, h is Planck’s constant, and c is the speed of light. fc is the local field factor due to the enhancement of the applied electric field by the solvent cavity, and has been calculated previously as 1.56 for Fl in MeTHF.15 The energy-weighted extinction coefficient of the unperturbed chromophore as a function of wavenumber, , and its derivatives are weighted by the coefficients Aχ, Bχ, and Cχ.
The Aχ coefficient, which represents the transition polarizability and higher order terms, is generally negligible for an immobilized sample. The Bχ coefficient is related to the difference polarizability tensor, , of the molecule,
| (2) |
where is the TDM for S0→Sn0. is the trace (mean) of the difference polarizability tensor and is the projection of this tensor along the TDM.
The Cχ term is related to the difference dipole and , the angle between and :
| (3) |
The angle χ between the polarization of the incident light and the applied electric field is varied by rotating the sample with respect to the incident light. Spectra taken with a minimum of two values of χ are needed in order to solve for the Aχ, Bχ, and Cχ coefficients.
As a starting point for the fit, the low-temperature absorption spectrum (LTAS) was fitted to a sum of Gaussian functions that can be grouped together if multiple transitions are evident.15,17 The Stark spectra were then fitted simultaneously with the LTAS and its derivatives to eq 1. We have found that supplying initial guesses for the , , and ζA parameters for the nonlinear least-squares fitting program constrains the parameters to physically reasonable values rather than supplying the Aχ, Bχ, and Cχ coefficients independently. These parameters are used to calculate the values of Bχ and Cχ for each angle χ within the fitting algorithm. The initial guesses for Aχ must be introduced directly for each spectrum. While these terms are small, they are often necessary to achieve an adequate fit to the data. Excessively large Aχ values are often an indication of an artifactual fit. The uncertainties of the fitted parameters were estimated by a Monte Carlo simulation of 200 iterations in which the initial parameters are varied by 50% from the starting conditions and fit to the data. Parameters and errors are reported as the mean results of this simulation and the standard deviations, respectively.
TD-DFT and Finite Field Calculations.
Calculations were carried out similarly to the method employed previously.17,32 Reduced anionic 7,8,10-trimethylisoalloxazine (lumiflavin, LfH−) was used as a model system. The coordinates of FADH• from the crystal structure of Anacystis nidulans DNA photolyase (PDB ID 1TEZ)33 were used as a starting geometry and modified to LfH− by replacing the ribose and adenosine moieties with a methyl group, making lumiflavin, and adding a negative charge and hydrogens where necessary. The geometry was optimized using the 6–311+G(d,p) level of theory. This optimized geometry was used for all further calculations. The optimized geometry does not seem to correlate strongly with reasonable starting geometries, even those that are planar (cf. Choe et al.34).
The excitation energies, TDMs, and ground-state dipole moment were determined at the TD-DFT/6–311+G(d,p) level of theory using the B3LYP functional.35 Difference dipole moments were calculated using the finite-field method.32,36 Calculations were performed in Gaussian0337 for vacuum and with a polarizable continuum model (PCM)38 using a dielectric constant of 4.9 to simulate the MeTHF solvent.
The coordinate origin was based on the center of mass and was the same for both ground and excited states. The negative charge in the ground state is not centered on one atom but delocalized around N1. Excited-state static dipoles are calculated from a one-particle rho-CI density matrix for corresponding states (not from atomic charges) and do not include any electron correlation. These calculations often overestimate CT and are not accurate enough for quantitative purposes.39 However, this information was used to generate difference density maps to qualitatively demonstrate how the electron density is changing upon optical excitation.
As mentioned above, the finite-field method was used to calculate the difference dipole moments, as this method is very good in reproducing experimental results independent of the theory used.32 Finite-field calculations return the energy shifts for a transition due to a weak external electric field. The field is directed along the +x, −x, +y, −y, +z, and −z axes with respect to center of mass, and the resulting Stark shifts due to the interaction of the field with the difference dipoles are in the same molecular reference frame.
RESULTS
Absorption Spectra of FlH−.
The 77 K absorption spectrum of 650 μM FlH− in MeTHF is shown in Figure 3a. All bands sharpen upon cooling. In addition to the narrowing of the absorption bands, cooling leads to a red-shift of all of the peaks corresponding to apparent maxima at 435, 358, and 305 nm for the S0→S1, S0→S2, and S0→S3 transitions, respectively.
Figure 3.
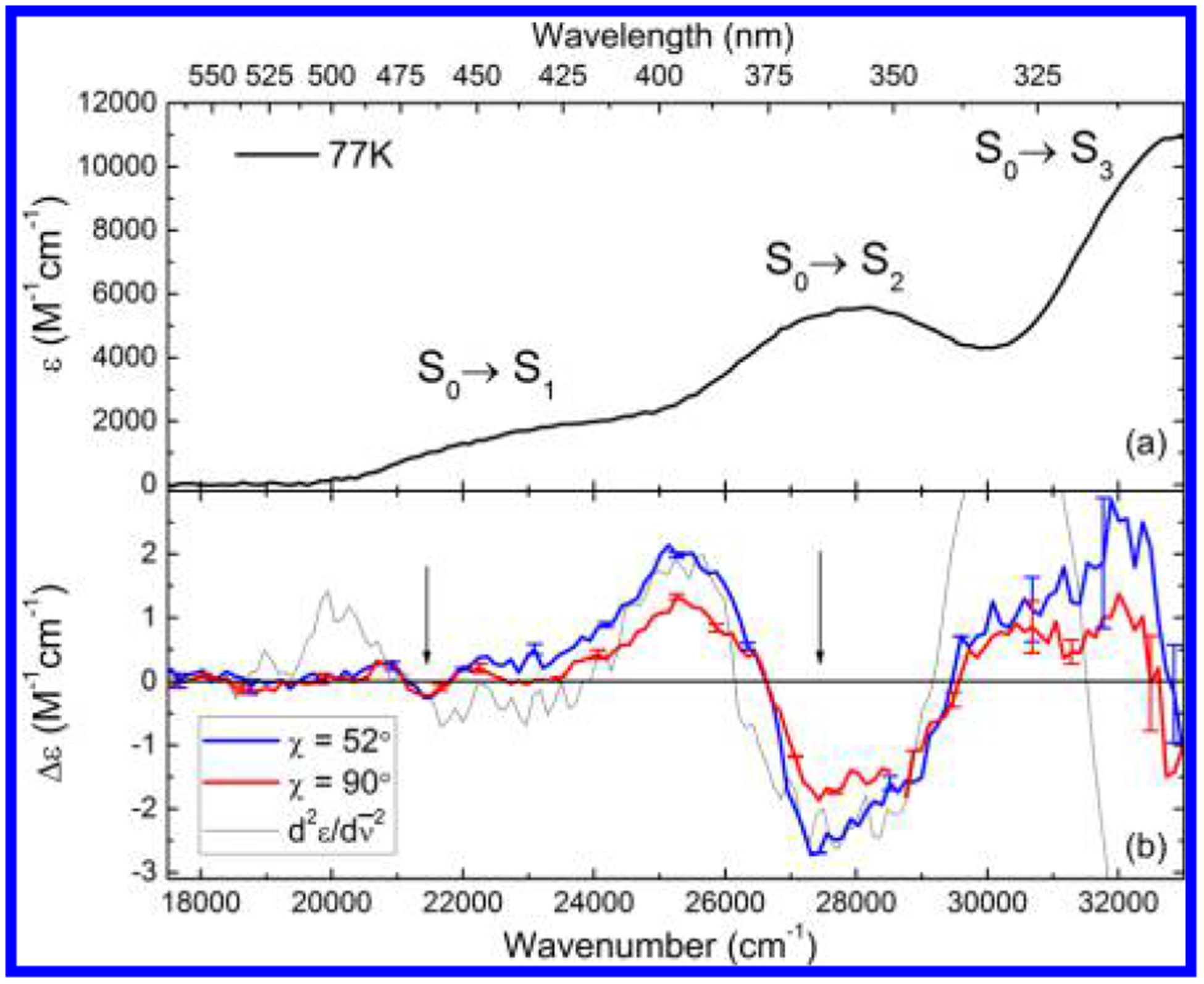
(a) Low-temperature absorption spectrum of FlH− in MeTHF. (b) Stark spectra of FlH− at two polarizations of the probe beam, as indicated by color. The second derivative of the LTAS (dotted line) is shown for comparison. The two spectral regions are indicated by arrows. Representative error bars are also shown.
Calculated Absorption Spectrum of FlH−.
The transition energies calculated by TD-DFT agree roughly with these experimental results. These calculations were performed on reduced anionic lumiflavin (LfH−), where the isobutyl group at N(10) has been replaced by a methyl group. In agreement with experimental data33,40 and previous computational studies,34,41–43 the optimized ground-state geometry is not planar but shows an approximately 21° “butterfly bend” about the N(5)–N(10) axis. Previous computational work has suggested that the spectral properties of the S0→S1 band are sensitive to this bend angle.44
The two lowest optically active calculated transitions for LfH− in a vacuum are found at 411 (24 331 cm−1) and 311 nm (32 154 cm−1), blue-shifted from the experimental values. The transitions of LfH− in the PCM are red-shifted compared to vacuum to 412 (−59 cm−1) and 367 nm (−4906 cm−1), in much closer agreement with experiment. The larger shift observed between vacuum and nonpolar solvent of the S0→S2 transition compared to S0→S1 suggests that .
The computed TDMs calculated at the TD-DFT/B3LYP/6–311+G(d,p) level of theory are shown in Figure 4 and tabulated in Table S1. points to the C(4) carbonyl, while is parallel with the long axis of the molecule. These results are similar to those obtained from our previous calculations at the TD-DFT/B3LYP/6–31G* level of theory (Figure 1).1 The calculated values for both basis sets are coincident and are rotated by about 9° from the experimentally determined TDM (Figure 4).
Figure 4.
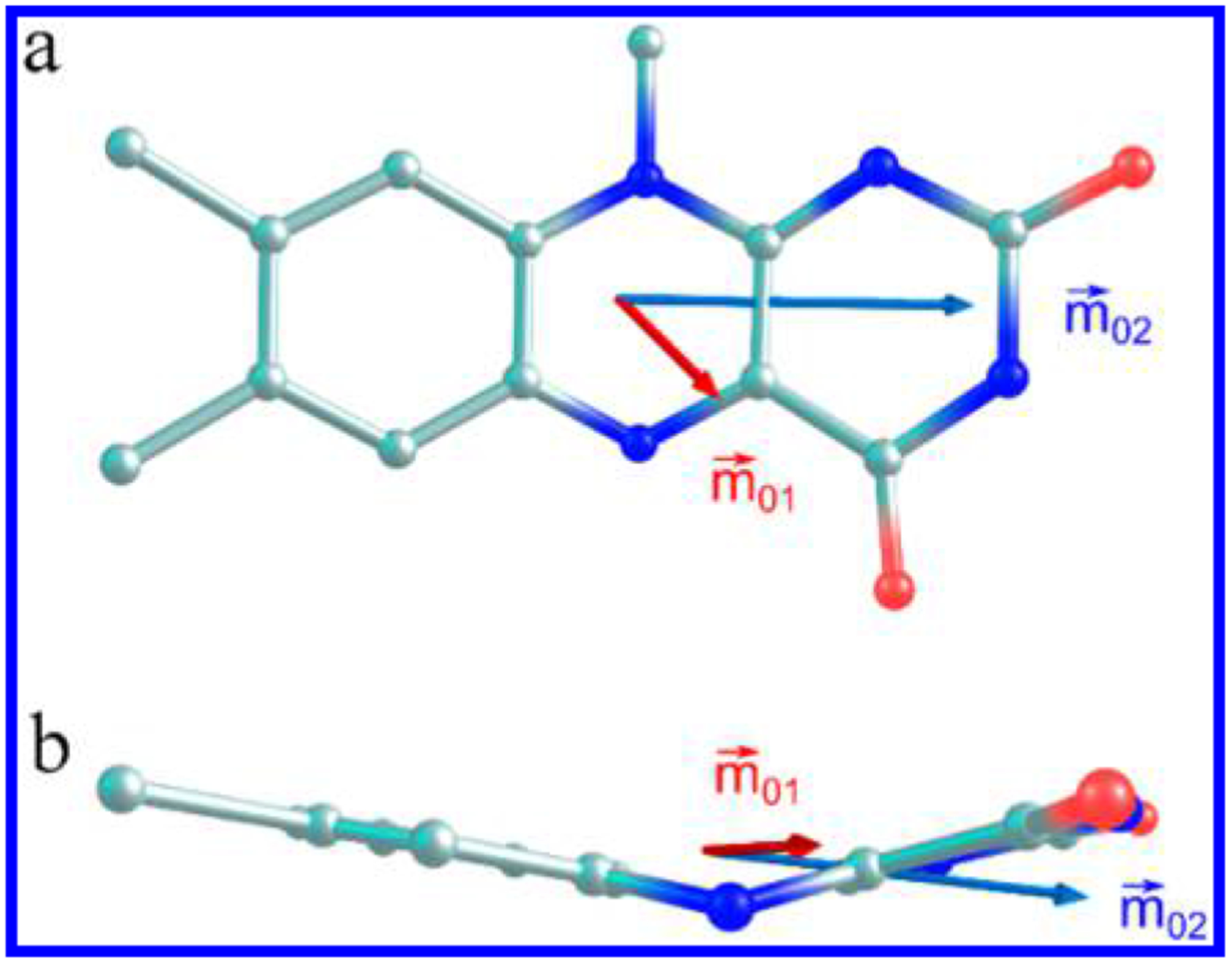
Transition dipole moments of the two lowest energy transitions of LfH− calculated at the TD-DFT/B3LYP/6–311+G(d,p) level of theory, shown from the top view (a) and side view (b) of the flavin ring.
Due to the bend along the N(5)–N(10) axis, these vectors do not necessarily lie within a plane, as was the case for the planar oxidized form of flavin. Figure 4b shows a side view of the flavin ring. has a small z-component and lies approximately parallel to the xylene “wing” of the flavin, while has almost no z-component, bisecting both “wings” of the molecule (see Table S1).
Fitting the Absorption and Stark Spectra.
The Stark spectrum, taken at two polarizations (horizontal, χ ≈ 52° ± 2°, and vertical, χ = 90° ± 2°, Figure 3b), was simultaneously fitted with the absorption spectrum. However, as pointed out earlier, a simple inspection of these Stark spectra leads to the basic conclusions of this study. The electric field-induced dichroism exhibited by the spectra confirms the existence of not one but two different transitions from 340 to 500 nm.
The initial fit of the experimental absorption spectrum was performed with two sets of Gaussian functions. The fitted parameters were used as inputs for the simultaneous fitting of absorption and Stark spectra. Representative fits and residuals are shown in Figure 5. This simultaneous fit required the inclusion of two transitions; a single transitions produced a very poor fit. The two transitions overlap strongly in the region between ~380 and 420 nm, with roughly equal extinction at ~400 nm. While this Gaussian fit of the absorption spectrum is not a true spectral deconvolution (the use of Gaussians is oversimplified), the electro-dichroic Stark spectra (Figure 3b) absolutely require this spectral decomposition, validating our LD result: there are indeed two nearly overlapping transitions where only one has been commonly assumed in the past.
Figure 5.
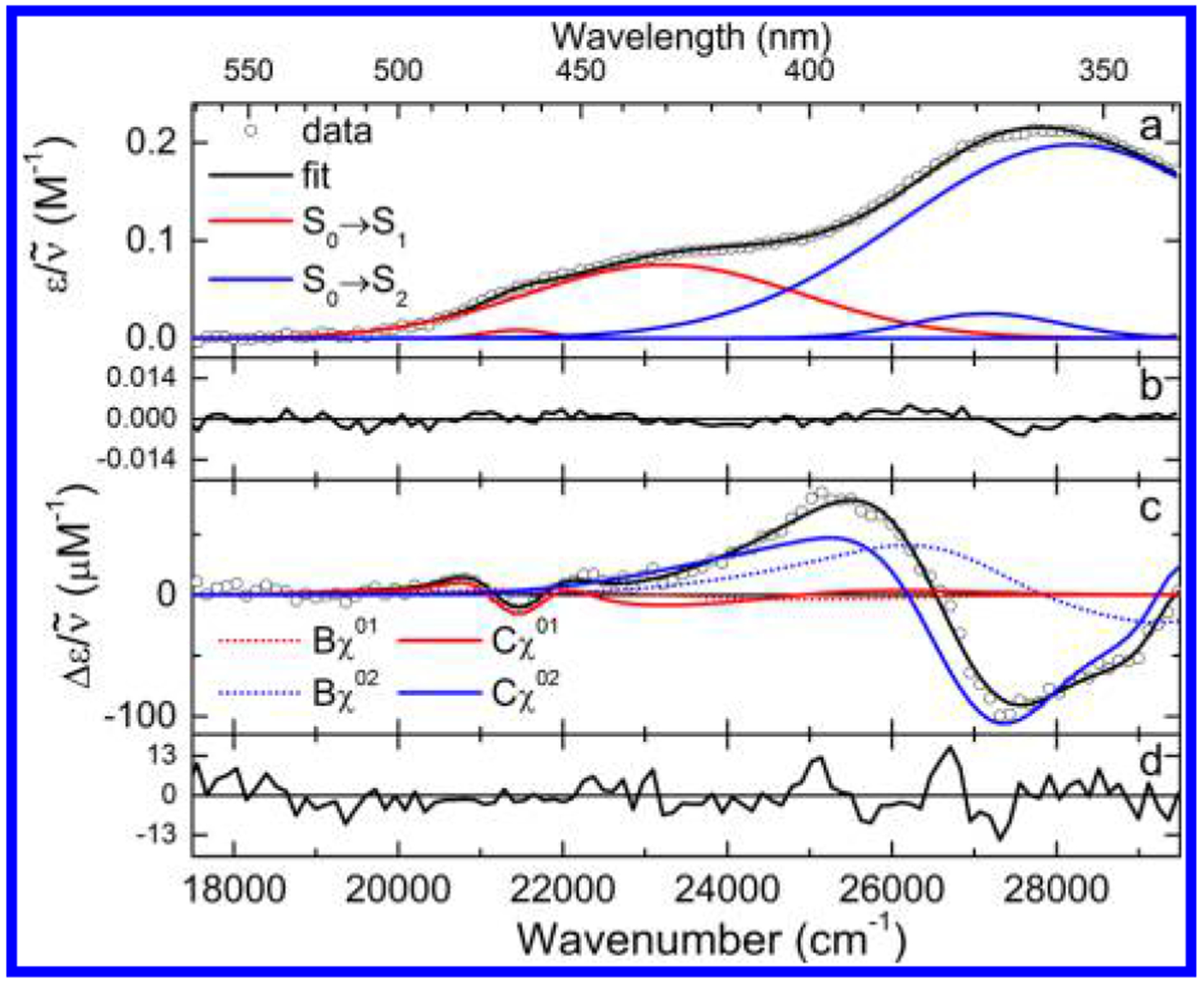
(a) Fit to the low-temperature absorption spectrum of FlH− in MeTHF with residuals (b). (c) Representative fit to the Stark spectrum at χ = 52° with residuals (d).
In the low-energy region (~22 000 cm−1), the spectra taken at horizontal and vertical polarizations are identical within experimental error. This requires that the angle be close to the magic angle, 54.7°. However, in the near-UV, the vertically polarized spectrum is clearly lower in amplitude than the horizontally polarized spectrum, requiring that be less than the magic angle. These observations are again strong evidence for the existence of two distinct electronic transitions in the 300–500 nm spectral range.
The dipolar (Cχ) term dominates the spectrum, as can be seen by the similarity of the band-shape of the experimental spectra with the second derivative of the LTAS (Figure 3b, dotted line). However, the features in the red region of the spectrum (~22 000 cm−1), while similar in shape to the second derivative, are only about half the amplitude that would be expected if the spectrum was due to a single electronic transition. This strongly suggests that .
The results of the quantitative analysis of the Stark spectra are shown in Table 1. These are the first experimentally determined values for the difference dipole moments of a reduced anionic flavin. The minimum number of Gaussians needed to obtain a satisfactory fit to the data was found to be two and three for the lowest two transitions, respectively. The fits are in agreement with the qualitative observations listed above; a satisfactory fit can only be achieved by modeling two distinct electronic transitions. The values for the two lowest transitions were found to be 1.5 and 3.6 D, respectively, using fc = 1.56.15,32,45 Also included in Table 1 are the difference dipole moments from the finite-field calculations.
Table 1.
Experimental and Computed Electronic Structure Parameters of FlH− in MeTHFa
| S0n | , Å3 | , D | , deg | , D | , deg |
|---|---|---|---|---|---|
| S01 | 6(2) | 1.5(0.2) | 52(12) | 1.53 | 52(12) |
| S02 | 29(7) | 3.6(0.3) | 4(4) | 8.37 | 4(4) |
Error estimates are given in parentheses. FF indicates finite-field calculations.
The ratio of , in agreement with the qualitative analysis. This ratio differs slightly from the value of ~3 found for flavins in the oxidized and semiquinone states.14,15,17 This is consistent with larger charge displacement for the planar, more aromatic FlOX and FlSQ compared to the bent FlH− state. In the bent geometry there is a loss of aromaticity that could reduce the degree of charge displacement.34
The ζA for the two bands follows the pattern in , close to the magic angle, and . This echoes the observations for FlOX in simple solvents14,15 and FAD and FADH• in DNA photolyase,17 where the S0→S1 transition shows almost no dichroism but S0→S2 exhibits a significant change in amplitude with respect to polarization. The small value for indicates that charge redistribution upon excitation from S0→S2 occurs primarily along the direction of . Given that charge-transfer (CT) bands generally have charge displacement along the CT TDM,46 the nature of the S02 transition is one of CT as well.
The derivative components of the fitted spectra are shown in Figure 5b. As expected, the second-derivative terms (Cχ, solid lines) dominate the fit. The low-energy transition is almost completely fit by this term, while the high-energy transition shows a substantial first-derivative component (Bχ, dotted line). This results in approximately a ratio of . This trend was found in the other redox states as well, but the magnitude of the for FlH− is significantly smaller than for either FlOX or FlSQ. We interpret this to be a consequence of the lower aromaticity in the bent form, inhibiting delocalization.
The high-energy transition gives a small zeroth derivative (Aχ) term, which is required to obtain a good fit to the experimental data. This was also true for oxidized flavins. The Aχ term is related to the hyperpolarizability and transition polarizability; however, the individual tensor components cannot be extracted from the Aχ coefficient in this type of analysis. Suffice it to say that the small magnitude of this term (~1 × 10−21) indicates that the fit is not artifactual.
Assignment of the exact direction, in the molecular frame, of the experimentally determined difference dipole moments from Stark spectroscopic data is facilitated by ab initio calculations. The angle between S0→Sn0 and gives information on the direction of charge redistribution upon excitation. For any particular experimental value of , there exist an infinite number of possible orientations which lie along two cones around the TDM that satisfy this condition. For flavins in the oxidized form, the isoalloxazine ring is planar, and charge redistribution is most likely to occur in the plane of the molecule. In this case, the number of orientations collapses to four, i.e., the vectors at the intersection of the cones with the molecular plane. While FlH− is bent in the optimized ground-state geometry, the small bend angle indicates that the difference dipole moment should lie primarily in the plane of the molecule.
The TD-DFT/PCM vector components of the permanent dipole moments of the ground and first two excited states of LfH− are shown in Figure 6, and tabulated in Table S1. The ground-state dipole and nearly parallel to the x-axis, with a minor component along the z-axis (out of plane). The first excited state is decreased relative to by ~1.5 D, relatively in the same direction, with a −1.27 D out-of-plane component. The second excited state is almost 10 D less than , with an out-of-plane component of 1.13 D, parallel to the left wing of the butterfly.
Figure 6.
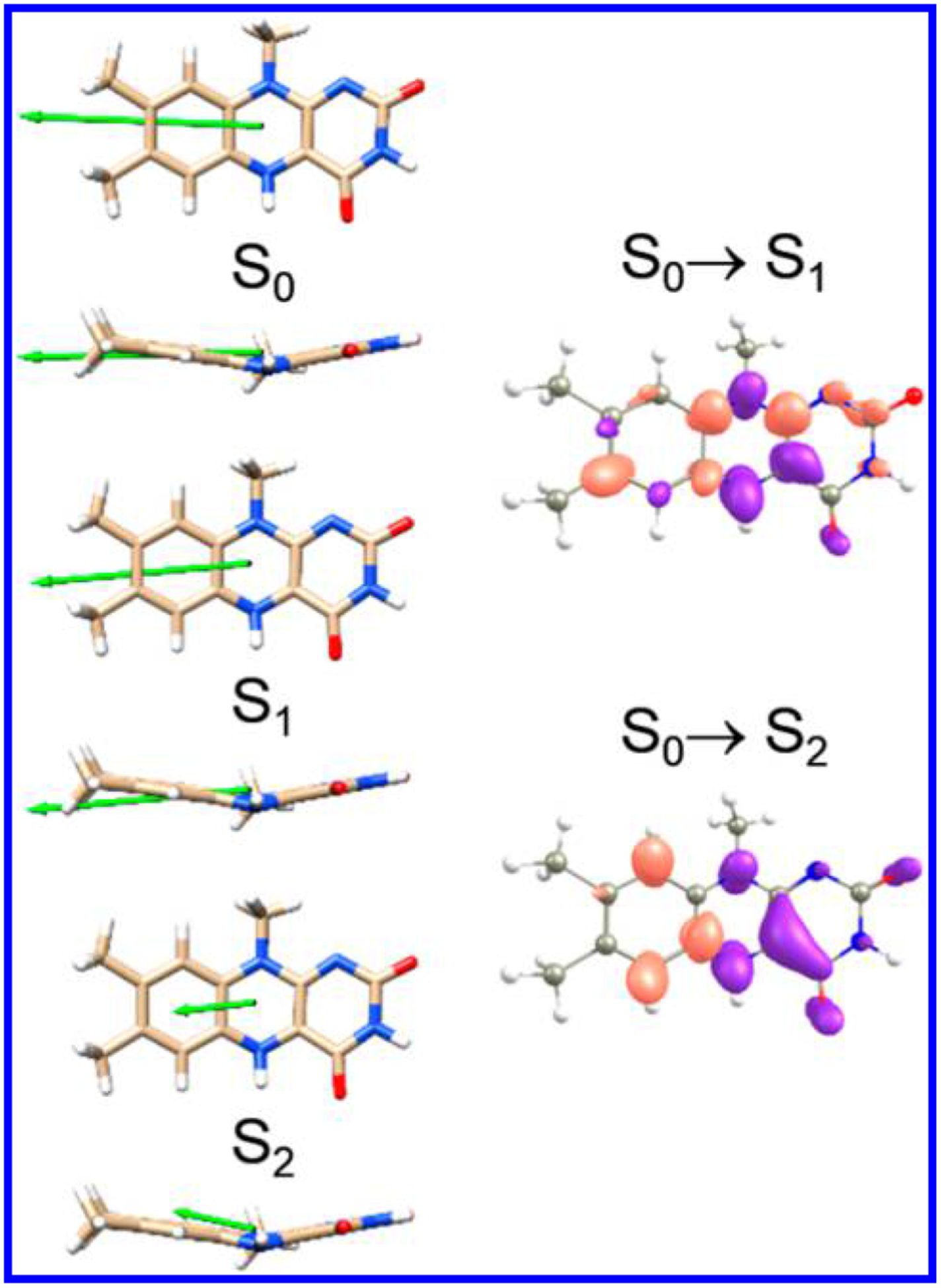
Directions of the calculated permanent dipole moments of the three lowest electronic states of LfH−, S0, S1, and S2, using a PCM (ε = 4.9) shown from the side and top of the molecule. The green arrows reflect the relative magnitudes of the dipole moments. Shown to the right are corresponding difference electron density maps of the S0→S1 and S0→S2 transitions with isosurfaces at the e/au3. Purple indicates increased positive charge, while red indicates increased negative charge.
The magnitudes of the computed difference dipole moments were 2.57 and 10.27 D for S0→S1 and S0→S2, respectively. is almost twice the experimentally determined value of 1.5 D, while is about 3 times larger than the experimental value. This result may be due to the well-known overestimation of CT character in TD-DFT calculations.47
The difference density maps show that C(7), C(9), C(9a), C(5a), N(1), C(2) N(3), and C(10a) acquire more electron density while C(5), C(4), and C(4a) lose electron density upon optical excitation to the S1 or S2 states (Figure 6, right). Overall, the molecule loses electron density on the middle pyrazine moiety and gains electron density on either side. For the S0→S2 transition the xylene ring becomes more electron rich while the rest of the molecule becomes electron deficient. Specifically C(5a), C(6), and C(9) lose electron density and N(5), N(10), C(4a), C(10a), and C(4) gain electron density.
The best picture of the orientation of the in the molecular frame is obtained by comparing the experimental against the finite-field as shown in Figure 7. points toward the C(4) carbonyl, while points toward N(3). Of the four possible directions for the experimental difference dipoles calculated using the fitted values of and experimental directions of , only one set closely matches the result from the finite-field calculations and is therefore assigned as the true direction of (solid arrows). agrees within 3° of , but is rotated 17° counterclockwise from . As noted, due to the bend of the flavin ring, the calculated difference dipole moments have minor z-components, causing the vectors to lie along the wings of the molecule (Figure S1). This result is expected for the experimental case also but cannot be refined further using the randomly oriented sample here. Even so, charge redistribution upon excitation is expected to occur primarily in the x−y plane of the molecule. For both transitions, the experimentally determined difference dipole moments indicate that electron density increases at C(9) in either the S1 or S2 excited state.
Figure 7.
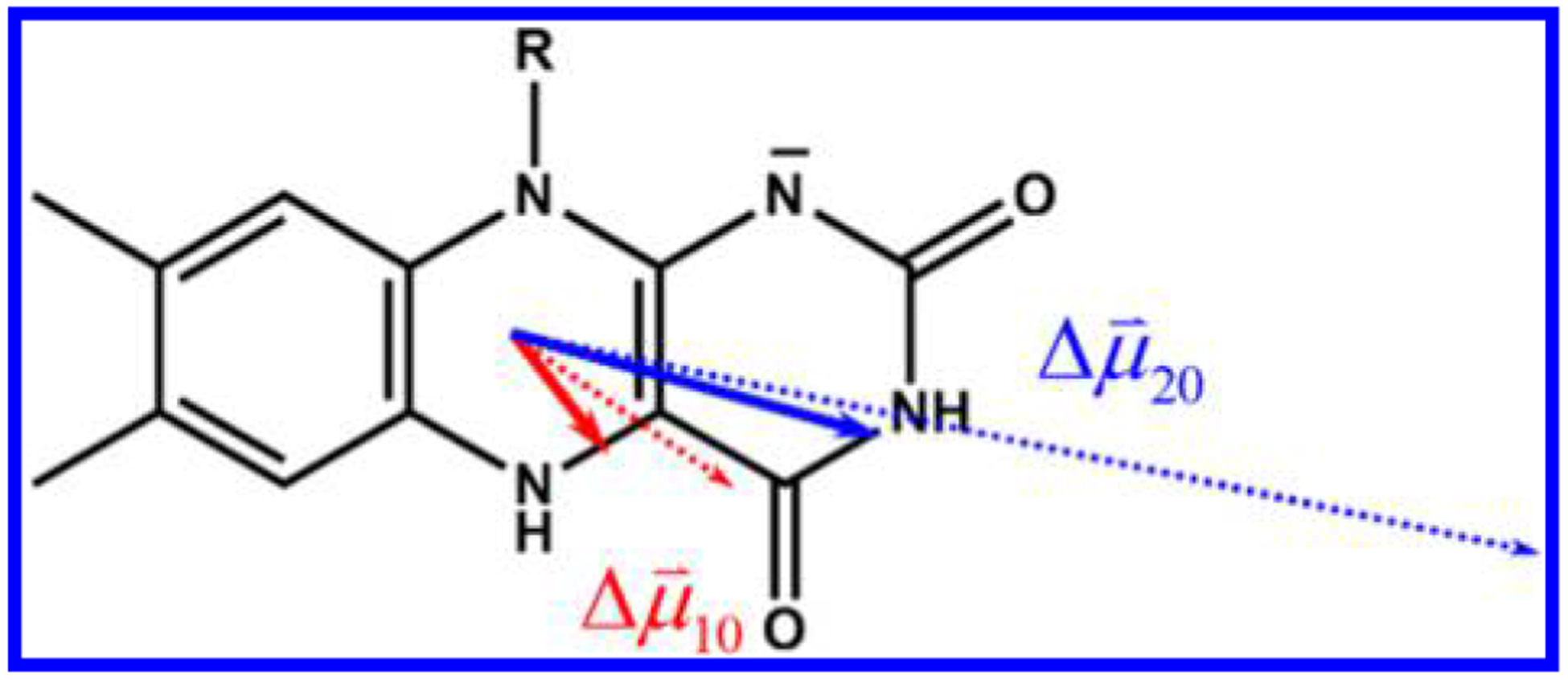
Orientation of the difference dipole moments of the two lowest energy transitions of FlH− in the molecular frame. Experimental vectors are shown as solid arrows, and vectors from finite-field calculations are shown as dashed arrows.
While the magnitude of charge redistribution is overestimated in the TD-DFT calculations, the direction of the difference dipoles is in agreement with our LD results. For both excitations into S1 and S2, it was found that electron density localizes on the xylene moiety of the flavin in the excited state. This result is opposite to that found for flavins in both the oxidized and semiquinone states, in which the pyrimidine ring of the flavin becomes electron rich upon excitation.17 The specific direction of charge redistribution has implications especially for flavins as catalytic cofactors in structured protein environments, such as DNA photolyase,17 where the xylene ring is proximal to the substrate. Placing the electron-rich region closest to the electron-accepting substrate should optimize the yield of the PET reaction compared with competing (deactivation) channels.48,49
There is, however, some difficulty in assigning the direction of charge displacement in the molecular frame due to the assumption of flavin planarity. These TD-DFT results, the INDO/S50 and ZINDO/S CIS51 calculations, and various experimental results suggest that reduced anionic flavins show a “butterfly bend” about the N(5)–N(10) axis of the isoalloxazine ring. The angle of this bend ranges from 16° to 32° over several computational studies, depending on the method used.34,41,43,48,51,52 Here, TD-DFT calculations gave a 21° bend in the ground-state optimized geometry. Interestingly, the geometry of the ground-state structure of FlH− from the crystal structure of A. nidulans PL (used here as the starting point) is more planar, with a bend of only 9°,33 presumably due to specific interactions with the chromophore binding site. It should be noted, however, that the flavin in the X-irradiated crystal may be in a mixture of oxidation states. Stuchebrukhov and co-workers suggest that the spectral position of the lowest band would be sensitive to this bend.51 The computed from our finite-field calculations show a z-component which causes the dipoles to fall along the “butterfly wings” of the flavin. Since these components are relatively small, the error in projecting the vectors to lie in a planar flavin should introduce only a small uncertainty as to the direction, if not magnitude, of charge displacement.
DISCUSSION
Low-temperature absorption and Stark spectra of anionic hydroquinone N(10)-isobutylflavin in MeTHF and ethanol were obtained and analyzed. TD-DFT and finite-field calculations were used to assign the direction of the difference dipole moments and difference electron densities in the molecular frame. Taken together, the results show that negative charge is transferred to the xylene moiety of the isoalloxazine upon optical excitation to either S1 (~425 nm) or S2 (~360 nm), verifying and extending our earlier LD study. The ratio of difference dipole moments . Polarizability changes are relatively small. We now discuss the ramifications of accepting the two-state model of *FlH− in the interpretation of spectroscopic experiments on reduced flavins/flavoproteins in the visible and near-UV.
Two States vs One State.
The results of this study require a re-examination of the interpretation and conclusions of many spectroscopic and computational studies in which excitation occurs at a point where the absorption bands of the two lowest transitions strongly overlap. The situation is reminiscent of the discovery of the degeneracy of the 1La and 1Lb bands of tryptophan.53 This confusion was ultimately resolved in 1960 by Gregorio Weber using low-temperature fluorescence polarization spectroscopy.54,55 The differing excited-state charge redistributions of these overlapping states were ultimately supplied by Pierce and Boxer using Stark spectroscopy.56
The current situation has arisen in part due to the widespread use of mode-locked doubled Ti:sapphire lasers. Doubled Ti:sapphire has its most stable output at 400 nm, shown here as a wavelength that leads to an equal degree of excitation into S1 and S2 (see arrow, Figure 2). Conclusions drawn from sub-picosecond experiments at or near this excitation wavelength are therefore vulnerable to effects such as internal conversion (IC) or complex solvation dynamics. A mixture of excited electronic states with different degrees of charge separation would be overlooked or convolved under a one-state assumption. Other studies involving steady-state excitation of FlH− must also be re-examined, particularly those that use emission anisotropy as an observable. Finally, future computational studies of *FlH− need to be performed that include these measurements as benchmarks. We now discuss a few studies perhaps most affected by the confirmation of the two-state picture of *FlH− electronic structure.
Experimental Studies.
We start with our own analysis of the repair of cyclobutane pyrimidine dimers (CPDs) by the DNA photolyase (PL) from 2003.20 When reduced folated-depleted PL absorbs blue light, only the FADH− cofactor is excited, resulting in PET to the CPD followed by scission of the cyclobutane bonds. By using 400 nm excitation with 267 nm probe pulses, we monitored the picosecond re-formation of the 5–6 C=C bonds in the CPD following PET. Probing just off the isosbestic point of the FADH–/FADH• redox couple (267 nm, see also the later more expansive work of Liu et al.57) also afforded an estimate of the PET lifetime. We modeled these data using a sum of exponentials, admittedly an over-simplification even in the one-state case. A lifetime of 32 ps was fitted to the initial PET event for a pentameric CPD substrate bound to A. nidulans PL. In the context of two TDMs (two-state) with picosecond IC, the 32 ps lifetime represents a convolution of a fast IC step with the slower PET step. This assumes that PET occurs exclusively from S1 and that excitation into S2 results in IC to S1 only. We discuss this assumption shortly.
The Zhong group has published many papers on the kinetics and mechanism of DNA photolyases (and cryptochromes)24,57–60 using 400 nm excitation in which the initial PET step in PL was modeled by a stretched exponential, , with τ = 170 ps and β = 0.71 for a T◇T cyclobutane thymidine dinucleotide dimer. This fitting function is useful when there is a distribution of ET rate constants due to environmental heterogeneity.61 However, a stretched exponential is incorrect when initial excitation resides in not one but two (S1 and S2) states. Their data should be re-analyzed in this context to see whether heterogeneity needs to be invoked when the fast S2→S 1 IC step is included in their kinetic model. As in our 2003 work, the possibility that S2 could result in PET-mediated repair without IC is not considered.
In a recent evaluation of a multiple pathways model for PET in PL, Lee et al.48 used state-of-the-art ab initio computations that suggest that PET from S2 to a CT state involving the FAD adenine may not be negligible in the overall repair process. If PET from S2→CPD through this CT state is kinetically competitive with IC, then a weighted parallel model may be more legitimate than a stretched exponential one. Lee et al. found that both the S1 and S2 states are significantly coupled with CT states involving both the flavin and CPD for high-efficiency electron transfer.48 We describe these calculations next.
In brief, QM/MM runs were performed using the A. nidulans PL-CPD structure reported by Mees et al.33 Molecular mechanics was used to obtain different conformations of the complex in time (2 fs steps, TIP3P water shell of 48 Å). After a suitable period, a frame was analyzed using the ADC(2)/def-SVP (algebraic diagrammatic construction through second order) method for the FADH−/CPD complex to obtain vertical excitation energies and oscillator strengths. In addition, generalized Mulliken–Hush62 coupling matrix elements (HAB) were computed between the 1ππ* (S1), 2ππ* (S2), CT(A) (charge transfer involving flavin and adenine), and CT(C) (charge transfer involving flavin and CPD) diabatic states. The relevant pathways are the IC pathway, 2ππ*→1ππ*, and PET via the CT(A) state, 2ππ*→CT(A). Both of these pathways result in electron transfer to the CPD and repair.
Here we use their couplings to compute a branching ratio, R, for 2ππ*→1ππ*, where H21 = 0.092 eV, and 2ππ*→CT(A), where H2CT(A) = 0.025 eV: R = (H2CT(A)/H21)2 = 0.074. Though small, R is not negligible, especially given the high signal to noise obtained by the Zhong group.23,63 In fact, it may be that the couplings are larger than calculated. This has to be decided through carefully executed ultrafast experiments or the re-evaluation of previous studies based on the multiple pathways picture.
The interpretation of solvation dynamics is also dependent on the two-state model. In 2010, Zhong’s group examined the solvation dynamics of *FMNH− in flavodoxin protein and simple solvent using the one-state assumption. Here the initial excited-state decay after 400 nm excitation was attributed to solvation dynamics due to a . The sources cited for this value were the LD and two of our Stark spectroscopy papers.1,14,15 However, all of them deal with oxidized flavin. From our work here, we now know that S1 and S2 in FlH− are excited at this wavelength and have different values. In a subsequent paper in 2010, discussing solvation in reduced photolyases, Chang et al.22 wrote, “we estimated that (the dipole-moment change between ground and excited states) should be around 1–2 D.” No justification or reference for this estimate was given. In a more recent paper from the same group,24 a one-state value appears, but this time citing our 2008 LD spectroscopy paper, in which we made no mention of but, rather ironically, the two-state TDM result was ignored.
Other cases can be cited where the two-state model could clarify complex kinetics. The study by Brazard et al. using 388 nm excitation shows that the early dynamics of *FADH− decay has sub-picosecond dynamics that appear to fit our model.25 The transient absorption spectrum at less than 1 ps shows a loss of absorption on the blue edge of the 520 nm excited-state absorption (ESA) band but no change on the red edge. This seems consistent with our two-state model, where the diminution of the red edge of the ESA corresponds to S2→S1 ultrafast relaxation.
BLUF proteins (Blue Light Using FAD) are light-activated regulators of gene expression.3,64–66 Using transient visible/IR spectroscopy, Tonge and Meech found evidence of an inverse H/D kinetic isotope effect (KIE) at the hydroquinone anion N(1) site which they ascribed to ground-state conformational heterogeneity.67–70 A regular KIE is obtained when the X–H bond is weakened in the excited state, while the reverse KIE occurs when HBs are strengthened. However, the two-state model calculations show that S1 has higher difference electron density than S2 (Figure 6). Higher density should strengthen the HB (λex > 410 nm). We predict that changing excitation from λ = 360 to 425 nm should cause the KIE to reverse. Based on the rho-CI density maps in Figure 6, N5–H should become a better HB donor and C4=O a better HB acceptor in both states. This prediction can be tested using their experimental approach.
Computational Studies.
There are too many studies of the electronic structure of reduced flavin to include all of them here.71 We focus mostly on those that deal with DNA photolyase. Computations by Stuchebrukhov et al.51 predicted a two-state model. However, the oscillator strength of the S01 transition was judged to be too small to promote direct excitation of S1. They found that the energies of S1 and S2 were sensitive to the protein environment and especially to the bend angle at the N(5)–N(10) axis of the flavin.
Both semiempirical and ab initio calculations executed by Prytkova et al.50 of *FADH− in DNA photolyase predicted that the lowest energy singlet excited state has electron density localized on the xylene ring of the flavin, in good agreement with our results. A difference dipole moment of ~13 D was calculated, with negative charge shifting from the pyrazine to the xylene ring. They too suggested, because of the negligible oscillator strength of the S01 transition, that the S1 state is populated only through IC from higher states, but that ET occurs from S1 because of the localization of electrons on the xylene ring proximal to the substrate, also supported by this work. They reasoned that PET was mediated by superexchange using the adenine as a bridge. Their computed difference dipole moment is ,50 which is about 3 times higher than our experimental result, but agrees with our TD-DFT result. While specific interactions with FADH− within the protein core will certainly affect excited-state charge redistribution, previous experimental studies of oxidized flavin indicated that the difference dipoles are not significantly modulated by incorporation into photolyase17 or other flavoproteins.16
Two recent computational studies deserve attention. Choe et al. in 2007 published a *FlH2 electronic structure study34 using the TD-DFT/PCM(water) method, B3LYP/aug-cc-pVDZ(-d) functional/basis, and a planar starting geometry. They explicitly confirmed the two-state model of Ghisla18 and Visser.19 The energies and oscillator strengths agree well with our results, even though the starting geometries are very different. The author suggests that the deprotonated molecule (FlH−) would have a similar electronic structure (Y. Choe, private communication).
Finally, the very high level computational work of Lee et al. presents a nuanced picture where PET in photolyase/CPD complexes occurs through several pathways involving more than the flavin S1 state.48 In particular, they focused on the role of CT states on both the FADH− and the CPD. To recap, their calculations were performed using the ADC(2) method,72,73 coupled with molecular mechanics to capture the varying ET coupling matrix elements due to different conformations. The conclusions of the calculations were supported by 77 K emission spectra of reduced EcPL that verify their prediction that the S1 state has a higher quantum yield than the S2 state. The two-state structure of *FADH− described herein was well reproduced.
The Lee study is reminiscent of how the picture of electron transfer in bacterial photosynthetic reaction centers evolved over time, going from a “direct vs superexchange” dialogue74–76 to one where distributions of electron-transfer rate constants77 and temperature-dependent transitions from one PET mechanism to another61 demonstrate the richness, complexity, and rather chaotic redundancy that evolution has conferred upon biological systems.
CONCLUSIONS
Stark spectroscopy was used to determine unequivocally that the near-UV/visible spectral region of the flavohydroquinone anion is composed of two optically accessible transitions, not one as has been previously assumed. Both S0→ S1 and S0→S2 transitions result in excited-state electron density localizing on the xylene moiety of the flavin. However, the extent of charge redistribution in these states is different by more than a factor of 2. The measured difference dipole moments of reduced anionic flavin are and for S0→S1 and S0→S2, respectively. The directions of the dipole vectors in the molecular frame were assigned with the aid of ab initio calculations. Both vectors lie principally along the long axis of the molecule, with pointing toward the carbonyl at C(4) while points toward N(3). This direct determination of charge redistribution in reduced anionic flavin requires a reconsideration of the dynamics and mechanism of the functional state for PET in PL and all other systems invoking the photochemistry or photophysics of reduced flavin. This can be the case even for processes taking place on the picosecond time scale.
Supplementary Material
ACKNOWLEDGMENTS
R.F.P. and R.J.S. were supported in part by NSF grant CHE-0847855 and by NASA Exobiology grant NNX13AH33G. G.K. acknowledges support from Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant TG-CHE130088 and TGCHE140112. The authors thank Prof. Vincent Rotello of the University of Massachusetts, Amherst, for providing the flavin used in this study. The authors also thank Drs. S. Matsika and W.Lee for stimulating conversations about their work.
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b06449.
Calculated TDMs of LfH—, an example of photo-degradation as analyzed by HPLC, and the Stark spectrum and room-temperature absorption spectra of reduced anionic flavin obtained using light, TEA, and NaBH4, including Figures S1–S3 and Tables S1 and S2 (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Siddiqui MSU; Kodali G; Stanley RJ J. Phys. Chem. B 2008, 112 (1), 119–126. [DOI] [PubMed] [Google Scholar]
- (2).Gomelsky M; Kaplan S J. Biol. Chem 1998, 273 (52), 35319–35325. [DOI] [PubMed] [Google Scholar]
- (3).Gomelsky M; Klug G Trends Biochem. Sci 2002, 27 (10), 497–500. [DOI] [PubMed] [Google Scholar]
- (4).Losi A Photochem. Photobiol 2007, 83 (6), 1283–1300. [DOI] [PubMed] [Google Scholar]
- (5).Chapman S; Faulkner C; Kaiserli E; Garcia-Mata C; Savenkov EI; Roberts AG; Oparka KJ; Christie JM Proc. Natl. Acad. Sci. U. S. A 2008, 105 (50), 20038–20043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Mukherjee A; Walker J; Weyant KB; Schroeder CM PLoS One 2013, 8 (5), e64753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Huang S; Heikal AA; Webb WW Biophys. J 2002, 82 (5), 2811–2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Pauszek RF; Kodali G; Caldwell ST; Fitzpatrick B; Zainalabdeen NY; Cooke G; Rotello VM; Stanley RJ J. Phys. Chem. B 2013, 117 (49), 15684–15694. [DOI] [PubMed] [Google Scholar]
- (9).Yu X; Eymur S; Singh V; Yang BQ; Tonga M; Bheemaraju A; Cooke G; Subramani C; Venkataraman D; Stanley RJ; Rotello VM Phys. Chem. Chem. Phys 2012, 14 (19), 6749–6754. [DOI] [PubMed] [Google Scholar]
- (10).Jordan BJ; Ofir Y; Patra D; Caldwell ST; Kennedy A; Joubanian S; Rabani G; Cooke G; Rotello VM Small 2008, 4(11), 2074–2078. [DOI] [PubMed] [Google Scholar]
- (11).Carroll JB; Cooke G; Garety JF; Jordan BJ; Mabruk S; Rotello VM Chem. Commun 2005, 30, 3838–3840. [DOI] [PubMed] [Google Scholar]
- (12).Rotello VM Curr. Org. Chem 2001, 5 (11), 1079–1090. [Google Scholar]
- (13).Eaton WA; Hofrichter J; Makinen MW; Andersen RD; Ludwig ML Biochemistry 1975, 14 (10), 2146–2151. [DOI] [PubMed] [Google Scholar]
- (14).Stanley RJ; Jang H J. Phys. Chem. A 1999, 103 (45), 8976–8984. [Google Scholar]
- (15).Stanley RJ; Siddiqui MS J. Phys. Chem. A 2001, 105 (49), 11001–11008. [Google Scholar]
- (16).Hopkins N; Stanley RJ Biochemistry 2003, 42 (4), 991–999. [DOI] [PubMed] [Google Scholar]
- (17).Kodali G; Siddiqui SU; Stanley RJ J. Am. Chem. Soc 2009, 131 (13), 4795–4807. [DOI] [PubMed] [Google Scholar]
- (18).Ghisla S; Massey V; Lhoste J-M; Mayhew SG Biochemistry 1974, 13 (3), 589–597. [DOI] [PubMed] [Google Scholar]
- (19).Visser A; Ghisla S; Massey V; Muller F; Veeger C Eur. J. Biochem 1979, 101 (1), 13–21. [DOI] [PubMed] [Google Scholar]
- (20).MacFarlane AW IV; Stanley RJ Biochemistry 2003, 42 (28), 8558–8568. [DOI] [PubMed] [Google Scholar]
- (21).Stanley RJ ACS Symp. Ser 2006, 935, 137–144. [Google Scholar]
- (22).Chang C-W; Guo L; Kao Y-T; Li J; Tan C; Li T; Saxena C; Liu Z; Wang L; Sancar A; Zhong D Proc. Natl. Acad. Sci. U. S.A 2010, 107 (7), 2914–2919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Liu Z; Wang L; Zhong D Phys. Chem. Chem. Phys 2015, 17(18), 11933–11949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Liu ZY; Guo XM; Tan C; Li J; Kao YT; Wang LJ; Sancar A; Zhong DP J. Am. Chem. Soc 2012, 134 (19), 8104–8114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Brazard J; Usman A; Lacombat F; Ley C; Martin MM; Plaza P J. Phys. Chem. A 2011, 115 (15), 3251–3262. [DOI] [PubMed] [Google Scholar]
- (26).Leenders R; Kooijman M; Van Hoek A; Veeger C; Visser AJWG Eur. J. Biochem 1993, 211 (1–2), 37–45. [DOI] [PubMed] [Google Scholar]
- (27).Yotter RA; Lee LA; Wilson DM IEEE Sens. J 2004, 4 (4), 395–411. [Google Scholar]
- (28).Bruggeman YE; Boogert A; vanHoek A; Jones PT; Winter G; Schots A; Hilhorst R FEBS Lett. 1996, 388 (2–3), 242–244. [DOI] [PubMed] [Google Scholar]
- (29).Holzer W; Shirdel J; Zirak P; Penzkofer A; Hegemann P; Deutzmann R; Hochmuth E Chem. Phys 2005, 308 (1–2), 69–78. [Google Scholar]
- (30).Pauszek RF; Stanley RJ, A “How-To” Guide to the Stark Spectroscopy of Flavins and Flavoproteins In Flavins and Flavoproteins: Methods and Protocols; Weber S, Schleicher E, Eds.; Springer: Berlin, 2014; Vol. 1146, pp 443–466. [DOI] [PubMed] [Google Scholar]
- (31).Liptay W, Dipole Moments and Polarizabilities of Molecules in Excited Electronic States In Excited States; Lim EC, Ed.; Academic Press, Inc.: New York, 1974; Vol. 1, pp 129–229. [Google Scholar]
- (32).Locknar SA; Peteanu LA; Shuai Z J. Phys. Chem. A 1999, 103 (14), 2197–2201. [Google Scholar]
- (33).Mees A; Klar T; Gnau P; Hennecke U; Eker APM; Carell T; Essen L-O Science 2004, 306 (5702), 1789–1793. [DOI] [PubMed] [Google Scholar]
- (34).Choe Y-K; Nagase S; Nishimoto K J. Comput. Chem 2007, 28 (4), 727–739. [DOI] [PubMed] [Google Scholar]
- (35).Lee CT; Yang WT; Parr RG Phys. Rev. B: Condens. Matter Mater. Phys 1988, 37 (2), 785–789. [DOI] [PubMed] [Google Scholar]
- (36).Kodali G; Narayanan M; Stanley RJ J. Phys. Chem. B 2012, 116 (9), 2981–2989. [DOI] [PubMed] [Google Scholar]
- (37).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Montgomery JA Jr.; Vreven T; Kudin KN; Burant JC; Millam JM; Iyengar SS; Tomasi J; Barone V; Mennucci B; Cossi M; Scalmani G; Rega N; Petersson GA; Nakatsuji H; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Klene M; Li X; Knox JE; Hratchian HP; Cross JB; Bakken V; Adamo C; Jaramillo J; Gomperts R; Stratmann RE; Yazyev O; Austin AJ; Cammi R; Pomelli C; Ochterski JW; Ayala PY; Morokuma K; Voth GA; Salvador P; Dannenberg JJ; Zakrzewski VG; Dapprich S; Daniels AD; Strain MC; Farkas O; Malick DK; Rabuck AD; Raghavachari K; Foresman JB; Ortiz JV; Cui Q; Baboul AG; Clifford S; Cioslowski J; Stefanov BB; Liu G; Liashenko A; Piskorz P; Komaromi I; Martin RL; Fox DJ; Keith T; Al-Laham MA; Peng CY; Nanayakkara A; Challacombe M; Gill PMW; Johnson B; Chen W; Wong MW; Gonzalez C; Pople JA Gaussian03; Gaussian Inc.: Greenwich, CT, 2004. [Google Scholar]
- (38).Mennucci B; Tomasi J J. Chem. Phys 1997, 106 (12), 5151–5158. [Google Scholar]
- (39).Foresman JB; Headgordon M; Pople JA; Frisch MJ J. Phys. Chem 1992, 96 (1), 135–149. [Google Scholar]
- (40).Park H-W; Kim S-T; Sancar A; Deisenhofer J Science 1995, 268 (5219), 1866–72. [DOI] [PubMed] [Google Scholar]
- (41).Walsh JD; Miller AF J. Mol. Struct.: THEOCHEM 2003, 623, 185–195. [Google Scholar]
- (42).Hasford JJ; Kemnitzer W; Rizzo CJ J. Org. Chem 1997, 62, 5244–5245. [Google Scholar]
- (43).Rizzo CJ Antioxid. Redox Signaling 2001, 3 (5), 737–746. [DOI] [PubMed] [Google Scholar]
- (44).Medvedev D; Stuchebrukhov AA J. Theor. Biol 2001, 210 (2), 237–248. [DOI] [PubMed] [Google Scholar]
- (45).Premvardhan L; Peteanu L Chem. Phys. Lett 1998, 296, 521–529. [Google Scholar]
- (46).Mulliken RS; Person WB Molecular Complexes; Wiley-Interscience: New York, 1969. [Google Scholar]
- (47).Dreuw A; Head-Gordon M Chem. Rev 2005, 105 (11), 4009–4037. [DOI] [PubMed] [Google Scholar]
- (48).Lee W; Kodali G; Stanley RJ; Matsika S Chem. - Eur. J 2016, 22, 11371. [DOI] [PubMed] [Google Scholar]
- (49).Pauszek R; Kodali G; Siddiqui MS; Stanley RJ Excited State Charge Redistribution in Reduced Flavins Obtained by Stark Spectroscopy: One Lump or Two? Proceedings of the 17th International Symposium on Flavins and Flavoproteins, Berkeley, CA, 2011. [Google Scholar]
- (50).Prytkova TR; Beratan DN; Skourtis SS Proc. Natl. Acad. Sci. U. S. A 2007, 104 (3), 802–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Zheng XH; Garcia J; Stuchebrukhov AA J. Phys. Chem. B 2008, 112 (29), 8724–8729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Boyd ASF; Carroll JB; Cooke G; Garety JF; Jordan BJ; Mabruk S; Rosair G; Rotello VM Chem. Commun 2005, 19, 2468–2470. [DOI] [PubMed] [Google Scholar]
- (53).Callis PR Methods Enzymol. 1997, 278, 113–150. [DOI] [PubMed] [Google Scholar]
- (54).Weber G Biochem. J 1960, 75, 335–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Valeur B; Weber G Photochem. Photobiol 1977, 25 (5), 441–444. [DOI] [PubMed] [Google Scholar]
- (56).Pierce DW; Boxer SG Biophys. J 1995, 68 (4), 1583–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Liu ZY; Tan C; Guo XM; Kao YT; Li J; Wang LJ; Sancar A; Zhong DP Proc. Natl. Acad. Sci. U. S. A 2011, 108 (36), 14831–14836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Kao YT; Saxena C; Wang LJ; Sancar A; Zhong DP Proc. Natl. Acad. Sci. U. S. A 2005, 102 (45), 16128–16132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Liu ZY; Zhang M; Guo XM; Tan C; Li J; Wang LJ; Sancar A; Zhong DP Proc. Natl. Acad. Sci. U. S. A 2013, 110 (32), 12972–12977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Tan C; Liu Z; Li J; Guo X; Wang L; Sancar A; Zhong D Nat. Commun 2015, 6, 7302. [DOI] [PubMed] [Google Scholar]
- (61).Chan CK; Dimagno TJ; Chen LXQ; Norris JR; Fleming GR Proc. Natl. Acad. Sci. U. S. A 1991, 88, 11202–11206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Cave RJ; Newton MD J. Chem. Phys 1997, 106 (22), 9213–9226. [Google Scholar]
- (63).Zhong D; Johnson MA; Martinez TJ Annu. Rev. Phys. Chem 2015, 66, 691–715. [DOI] [PubMed] [Google Scholar]
- (64).Gauden M; Yeremenko S; Laan W; van Stokkum IHM; Ihalainen JA; Van Grondelle R; Hellingwerf KJ; Kennis JTM Biochemistry 2005, 44 (10), 3653–3662. [DOI] [PubMed] [Google Scholar]
- (65).Jung A; Domratcheva T; Tarutina M; Wu Q; Ko W.-h.; Shoeman RL; Gomelsky M; Gardner KH; Schlichting I Proc. Natl. Acad. Sci. U. S. A 2005, 102 (35), 12350–12355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Kita A; Okajima K; Morimoto Y; Ikeuchi M; Miki K J. Mol. Biol 2005, 349 (1), 1–9. [DOI] [PubMed] [Google Scholar]
- (67).Brust R; Lukacs A; Haigney A; Addison K; Gil A; Towrie M; Clark IP; Greetham GM; Tonge PJ; Meech SR J. Am. Chem. Soc 2013, 135 (43), 16168–16174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Lukacs A; Zhao RK; Haigney A; Brust R; Greetham GM; Towrie M; Tonge PJ; Meech SR J. Phys. Chem. B 2012, 116 (20), 5810–5818. [DOI] [PubMed] [Google Scholar]
- (69).Lukacs A; Haigney A; Brust R; Zhao RK; Stelling AL; Clark IP; Towrie M; Greetham GM; Meech SR; Tonge PJ J. Am. Chem. Soc 2011, 133 (42), 16893–16900. [DOI] [PubMed] [Google Scholar]
- (70).Zhao RK; Lukacs A; Haigney A; Brust R; Greetham GM; Towrie M; Tonge PJ; Meech SR Phys. Chem. Chem. Phys 2011, 13 (39), 17642–17648. [DOI] [PubMed] [Google Scholar]
- (71).Kodali G; Stanley RJ Excited state electronic structure of flavins and flavoproteins from theory and experiment In Handbook of Flavins and Flavoproteins; Hille R, Miller S, Palfey B, Eds.; de Gruyter: Berlin, 2012. [Google Scholar]
- (72).Schirmer J Phys. Rev. A: At., Mol., Opt. Phys 1982, 26 (5), 2395–2416. [Google Scholar]
- (73).Trofimov AB; Schirmer J J. Phys. B: At., Mol. Opt. Phys 1995, 28 (12), 2299–2324. [Google Scholar]
- (74).Boxer SG; Goldstein RA; Lockhart D; Middendorf TR; Takiff L J. Phys. Chem 1989, 93 (26), 8280–8294. [Google Scholar]
- (75).Lauterwasser C; Finkele U; Scheer H; Zinth W Chem. Phys. Lett 1991, 183 (6), 471–477. [Google Scholar]
- (76).Stanley RJ; King B; Boxer SG J. Phys. Chem 1996, 100 (29), 12052–12059. [Google Scholar]
- (77).Wang ZY; Pearlstein RM; Jia YW; Fleming GR; Norris JR Chem. Phys 1993, 176 (2–3), 421–425. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


