Abstract
Determining the optimal targets of genomic subsampling for phylogenomics, phylogeography, and population genomics remains a challenge for evolutionary biologists. Of the available methods for subsampling the genome, hybrid enrichment (sequence capture) has become one of the primary means of data collection for systematics, due to the flexibility and cost efficiency of this approach. Despite the utility of this method, information is lacking as to what genomic targets are most appropriate for addressing questions at different evolutionary scales. In this study, first, we compare the benefits of target loci developed for deep- and shallow scales by comparing these loci at each of three taxonomic levels: within a genus (phylogenetics), within a species (phylogeography), and within a hybrid zone (population genomics). Specifically, we target evolutionarily conserved loci that are appropriate for deeper phylogenetic scales and more rapidly evolving loci that are informative for phylogeographic and population genomic scales. Second, we assess the efficacy of targeting multiple-locus sets for different taxonomic levels in the same hybrid enrichment reaction, an approach we term hierarchical hybrid enrichment. Third, we apply this approach to the North American chorus frog genus Pseudacris to answer key evolutionary questions across taxonomic and temporal scales. We demonstrate that in this system the type of genomic target that produces the most resolved gene trees differs depending on the taxonomic level, although the potential for error is substantially lower for the deep-scale loci at all levels. We successfully recover data for the two different locus sets with high efficiency. Using hierarchical data targeting deep and shallow levels: we 1) resolve the phylogeny of the genus Pseudacris and introduce a novel visual and hypothesis testing method that uses nodal heat maps to examine the robustness of branch support values to the removal of sites and loci; 2) estimate the phylogeographic history of Pseudacris feriarum, which reveals up to five independent invasions leading to sympatry with congener Pseudacris nigrita to form replicated reinforcement contact zones with ongoing gene flow into sympatry; and 3) quantify with high confidence the frequency of hybridization in one of these zones between P. feriarum and P. nigrita, which is lower than microsatellite-based estimates. We find that the hierarchical hybrid enrichment approach offers an efficient, multitiered data collection method for simultaneously addressing questions spanning multiple evolutionary scales. [Anchored hybrid enrichment; heat map; hybridization; phylogenetics; phylogeography; population genomics; reinforcement; reproductive character displacement.]
In the past decade, systematics has been transformed from a data-poor field, in which researchers were limited to a small handful of target loci, to a data-rich field in which we now have the ability to choose among thousands of potential target loci. The opportunity for data selection is now evident due to the development of a diversity of methods for genome subsampling (Lemmon and Lemmon 2013; McCormack et al. 2013; Jennings 2016). Although whole genomes will become available for an increasing number of study systems as sequencing costs decrease, computational constraints will likely require researchers to select from the sequenced genomes the target loci best suited for their questions of interest. Therefore, a fundamental question that needs to be addressed is: What types of target loci are best suited for answering questions at different evolutionary scales? As realized when the field of molecular phylogenetics was still in its infancy (Hillis and Huelsenbeck 1992), two important criteria to guide selection of the best targets are: 1) the target loci should have maximum phylogenetic signal (e.g., resulting in maximum gene tree resolution) and (2) the data associated with these target loci should contain a minimal amount of misleading signal (i.e., stochastic and systematic error). For population genomics studies, minimizing misleading signal (e.g., sequencing error and paralogy) is also an important criterion, although the preferred type of signal (e.g., diagnostic, random, genomically dispersed) can vary from study to study.
Since its first application to phylogenetics, hybrid enrichment (sequence capture) has provided researchers with the unprecedented ability to select target regions from hundreds to thousands of loci for answering questions in systematics and population genomics (Bi et al. 2012; Faircloth et al. 2012; Lemmon et al. 2012). The utility of this approach is so broad that hybrid enrichment has become one of the four primary means of data collection for genetic studies in evolutionary biology, along with RAD-seq (restriction enzyme associated DNA sequencing), transcriptome sequencing, and whole genome sequencing (Andrews et al. 2016; Jennings 2016; Hahn 2018). Hybrid enrichment has been used to target anchored loci (AHE; Lemmon et al. 2012), ultraconserved elements (UCE; Faircloth et al. 2012), exons with function unknown (Ng et al. 2009; Bi et al. 2012) and known (Margres et al. 2017a,b), and shallow-scale anonymous loci (Margres et al. 2017a,b). Although not commonly employed for shallow-scale studies, hybrid enrichment could also be used to obtain data from rapidly evolving anonymous intergenic regions of the genome, corresponding to those currently obtained through RAD-based approaches (reviewed by Lemmon and Lemmon 2013; McCormack et al. 2013; Margres et al. 2017a,b).
In this study, we compare the utility of two general classes of hybrid enrichment targets: 1) deep-scale loci developed for broad application across many studies and (2) shallow-scale loci developed for specific studies. We define deep-scale loci as those developed using a top-down approach with an emphasis on homology across deep timescales (e.g., a phylum or class). Top-down approaches often utilize existing genomic resources from phylogenetically disparate model systems. Conducting marker development from a top-down approach allows identification of deep-scale loci that can immediately be applied to nonmodel species within the broader group, without the costly and time-consuming effort needed to identify suitable targets for a particular system. This type of locus is often comprised of coding regions or other conserved regions of the genome. Here, we utilized one type of top-down approach, AHE, initially developed by Lemmon et al. (2012) to identify deep-scale loci in vertebrates. Subsequent work further refined for the target set for amphibians (Barrow et al. 2018; Heinicke et al. 2018). AHE loci have since been developed for diverse branches of the Tree of Life and successfully applied across deep to shallow phylogenetic scales (e.g., Margres et al. 2017a,b; Breinholt et al. 2018; Léveillé-Bourret et al. 2018; Haddad et al. 2018; Winterton et al. 2018).
We define shallow-scale loci as those developed using a bottom-up approach with an emphasis on efficient use in a shallow-level clade of interest (e.g., species). Bottom-up targets, typically developed using one or more closely related species, often contain more variable sites that provide greater resolution at shallow evolutionary scales (Karl and Avise 1993). Shallow-scale loci are useful for obtaining large numbers of SNPs for population genetic studies. Here, we use low-coverage WGS reads to identify suitable loci, while acknowledging that other approaches may also be suitable for developing this type of marker in new systems (e.g., Ali et al. 2016).
One goal of this study is to evaluate the relative merits of deep- and shallow-scale loci for addressing questions across taxonomic levels that span evolutionary scales. The most useful loci will both maximize phylogenetic signal and minimize error. With respect to maximizing signal, we measure gene tree resolution, the number of nucleotide variants, and the number of diagnostic SNPs. In terms of minimizing error, we measure the degree of gene tree discordance, the amount of alignment error, the quantity of missing and ambiguous data, and the presence of gene duplicates. We address which set of target loci is most useful for shallower and deeper-scale evolutionary studies. We also study the consequences of utilizing only one SNP per locus, an approach that is often necessary to satisfy the common assumption that SNPs are unlinked.
A second goal of this study is to determine whether loci developed using different approaches can be captured simultaneously in the same hybrid enrichment reaction. Rationale for this approach, which we term hierarchical hybrid enrichment, stems from the practical reason that researchers would benefit from being able to collect data for different project goals, from phylogenetics to population genomics, through the same laboratory protocol. By carefully planning the locus sets included in the hybrid enrichment design, researchers could sample sets of loci appropriate for different questions, thereby enhancing the long-term utility of their data sets for diverse evolutionary studies. Furthermore, since often it is unknown in advance which loci will be most informative for a particular question, including loci with diverse sequence characteristics could ensure that the data can be subsampled to include loci with sufficient resolution power to resolve clades important for a diversity of studies.
A third goal of this study is to address longstanding questions regarding the evolutionary history of chorus frogs (Pseudacris), using the most suitable sets of loci for each question. The genus Pseudacris is a widespread North American frog group consisting of 18 species (Powell et al. 2016). Despite much early taxonomic confusion based on morphological diagnoses, molecular studies have identified cryptic species, located contact zones among species, and elucidated most relationships among members of the genus (Moriarty and Cannatella 2004; Lemmon et al. 2007a,b; Lemmon and Lemmon 2008, Lemmon et al. 2008; Barrow et al. 2014). Several key relationships remain unresolved, however, due to conflict among studies (Lemmon et al. 2007a,b; Barrow et al. 2014; Duellman et al. 2016). We aim to 1) resolve these difficult relationships, assess the robustness of each node to data inclusion/exclusion using a heat map-based approach developed here, and apply this approach for testing alternative phylogenetic hypotheses. Chorus frogs are a well-documented system for studying reinforcement in contact zones between species (Fouquette 1975; Gerhardt and Huber 2002; Futuyma 2013). In different areas of sympatry between two species, Pseudacris feriarum and Pseudacris nigrita, one or the other species has diverged with respect to male acoustic signals and female mating preferences, due to selection against hybridization (Lemmon 2009; Lemmon and Lemmon 2010). What remains unclear is how many phylogenetically independent invasions into sympatry have occurred across the geographic distributions of the two species. Here, we aim to 2) determine how many times a reinforcement contact zone has formed independently across the range of the two species and determine the direction of gene flow within the contact zone. Finally, within sympatric regions, there is evidence for extensive ongoing and historical hybridization between P. feriarum and P. nigrita, but confidence intervals on microsatellite-based estimates are broad (Lemmon and Juenger 2017), pointing to uncertainty in hybridization frequency estimates. By adding population genomic data from many loci, we aim to 3) improve the precision of hybridization estimates and identify the classes of hybrids being formed.
Materials and Methods
Target Locus Data Generation and Assembly
Locus selection and probe design.
We identified two distinct types of target loci, deep scale and shallow scale. Deep-scale target loci were identified using the anchored hybrid enrichment approach initially developed by Lemmon et al. (2012), and refined for use in vertebrates (e.g., Ruane et al. 2015; Stout et al. 2016), arthropods (e.g., Young et al. 2016; Dietrich et al. 2017), and plants (e.g., Mitchell et al. 2017; Wanke et al. 2017). To ensure maximum enrichment efficiency in the target genus Pseudacris, we utilized the probes developed by Barrow et al. (2018), which were derived from two of our focal species, P. feriarum and P. nigrita. This AHE probe set targets 366 anchored loci averaging 1205 bp in length (details in Supplementary Methods available on Dryad at http://dx.doi.org/10.5061/dryad.0sf2hm8). Enrichment efficiency for these deep-scale loci was expected to be fairly robust across the entire genus (Lemmon et al. 2012).
Shallow-scale target loci were identified following the approach of Margres et al. (2017a,b). High-quality whole genome sequence reads of suitable length, GC content, and copy number were extended into flanking regions then compared across two species of Pseudacris to produce candidate target alignments (details in Supplementary Methods available on Dryad). After inspection of these candidates in Geneious v.7 (Kearse et al. 2012), we identified four criteria by which to select 1250 targets suitable for hybrid enrichment: 1) no poorly aligned regions, 2) no obvious paralogy, 3) minimal insertions/deletions, and 4) pairwise sequence similarity  70%. The script used to evaluate the loci by these criteria, as well as the summary tables, are provided through Dryad. Note that the enrichment efficiency for these shallow-scale loci is not expected to be very robust outside of the clade containing the references P. feriarum and P. nigrita.
70%. The script used to evaluate the loci by these criteria, as well as the summary tables, are provided through Dryad. Note that the enrichment efficiency for these shallow-scale loci is not expected to be very robust outside of the clade containing the references P. feriarum and P. nigrita.
The preliminary deep- and shallow-scale alignments were evaluated in a final step to remove repetitive regions and overlapping loci following Hamilton et al. (2016). To prevent competition for binding to DNA targets, locus overlap was evaluated and avoided. Enrichment probes 120 bp in length were tiled across P. feriarum and P. nigrita sequences for the 366 deep-scale and 1250 shallow-scale loci. Tiling probes uniformly at a density of 3.6 per species produced 57,557 probes. The kit comprised of these probes is hereafter referred to as Pseudacris v.1.
per species produced 57,557 probes. The kit comprised of these probes is hereafter referred to as Pseudacris v.1.
Sample selection and data collection.
A total of 227 chorus frog specimens representing 18 species were collected from 147 localities across the United States (Supplementary Fig. S1 and Table S1 available on Dryad). Appropriate state scientific collecting permits and ACUC protocol approvals were obtained prior to specimen collection. Tissues were frozen in liquid nitrogen or preserved in tissue buffer or 95% ethanol and stored at  80°C. Voucher specimens were deposited into the Texas Natural History Collection or the University of Florida Museum of Natural History (Supplementary Table S1 available on Dryad). Genomic DNA was extracted from tissue samples using the OMEGA Bio-tek E.Z.N.A. Tissue DNA kit.
80°C. Voucher specimens were deposited into the Texas Natural History Collection or the University of Florida Museum of Natural History (Supplementary Table S1 available on Dryad). Genomic DNA was extracted from tissue samples using the OMEGA Bio-tek E.Z.N.A. Tissue DNA kit.
Samples were processed at the Center for Anchored Phylogenomics at Florida State University (www.anchoredphylogeny.com) following the methods described in Lemmon et al. (2012) and the Supplementary Methods available on Dryad. Sequencing was performed in the Translational Science Lab in the College of Medicine at Florida State University. After quality filtering and demultiplexing, paired reads were merged following Rokyta et al. (2012), then assembled using the quasi-de novo assembly approach typically used for AHE data (described in Prum et al. (2015) and Hamilton et al. (2016); Supplementary Methods available on Dryad). The pipeline produced consensus sequences from which SNP, genotype, and haplotype data were obtained downstream (see below).
Locus Suitability Analysis
Taxon selection.
One of the primary goals of this study is to evaluate the relative merits of deep- and shallow-scale loci for addressing questions across taxonomic levels that span evolutionary scales. To this end, three taxon sets were selected to evaluate the suitability of the deep- and shallow-scale locus sets at different taxonomic scales (six locus-suitability data sets total). The phylogenetic taxon set (PHY), included 46 taxa (42 Pseudacris and two each of Hyla cinerea and Acris gryllus for outgroups). Each of the 18 Pseudacris species was represented by at least two individuals selected from different parts of the species’ range. For taxa that potentially included cryptic species based on mitochondrial DNA evidence, such as P. feriarum and the Pseudacris regilla complex (Lemmon et al. 2007a,b; Recuero et al. 2006a,b), additional individuals were also sequenced. Samples were chosen from localities where interspecific gene flow was unlikely (Supplementary Fig. S1 and Table S1 available on Dryad; Lemmon et al. 2007a,b).
The phylogeographic taxon set (GEO) included 80 individuals sampled across the range of P. feriarum (79 from the focal species and one outgroup sample from the type locality of the sister species, Pseudacris triseriata). Of these, 38 were sampled from areas of sympatry with respect to P. nigrita and 41 were sampled from allopatry (Supplementary Fig. S1c available on Dryad; Lemmon et al. 2007a,b; Lemmon 2009). Samples were included from all river systems in the Coastal Plain of the southeastern U.S. in which P. feriarum is known to occur (Supplementary Table S1 available on Dryad).
The population genomics taxon set (POP) included 102 individuals from the hybrid zone between P. feriarum and P. nigrita, which was previously studied by Lemmon and Juenger (2017) using 12 microsatellite loci. In the present study, these samples were genotyped again for the 1616 loci targeted by the Pseudacris v.1 kit. Individuals from the hybrid zone originated from the Apalachicola River floodplain in Liberty Co., Florida (Supplementary Fig. S1d available on Dryad); allopatric references for P. nigrita were sampled from Walton, Dixie, Holmes, Brevard, and Jefferson Counties, FL, USA; and allopatric references for P. feriarum were taken from Macon County, AL, USA and Davie and Nash Counties, NC, USA (Supplementary Fig. S1b,c and Table S1 available on Dryad).
Alignment generation.
Following Hamilton et al. (2016), data sets were constructed from the PHY, GEO, and POP taxon sets in an identical manner as follows: 1) orthology among consensus sequences at each target locus was determined using pairwise sequence divergence, 2) orthologous sets with at least 50% taxon presence were retained, 3) orthologous sequences were aligned using MAFFT (v7.023b; Katoh and Standley 2013), 4) alignments were refined using an automated trimmer/masker, then manually inspected in Geneious to identify and mask misaligned regions that remained (see Supplementary Methods available on Dryad). Lastly, we estimated a gene tree with 100 bootstrap replicates using the refined alignment for each locus in RAxML under the GTRGAMMA substitution model (version 8.1.21, Stamatakis 2006, 2014).
Locus suitability assessment.
For each of the six locus suitability data sets, we evaluated nine metrics of signal and error. These metrics include: 1) gene tree resolution, 2) gene tree discordance, 3) number of variants, 4) number of diagnostic SNPs, 5) mapping efficiency, 6) alignment error, 7) amount of missing data, 8) quantity of ambiguous characters, and 9) copy number (details in Supplementary Methods available on Dryad). At each taxonomic level, the value for each metric was compared between the shallow and deep data sets. The locus set producing the metric with the larger value was identified as being the more appropriate data set by that metric.
Phylogenetic Analyses
Data set generation.
Preliminary analyses indicated that levels of missing data were high in the shallow-scale loci at the phylogenetic scale (Supplementary Fig. S2 available on Dryad). This was especially true for outgroup and other taxa divergent from the focal species (P. feriarum); up to 70% of shallow-scale loci were missing at least one of the outgroup taxa. This pattern was not observed for the deep-scale loci ( 5% of loci were missing at least one outgroup taxon). Because nonrandom distributions of missing data have been shown to increase phylogenetic bias (Lemmon et al. 2009), we chose to include only the deep-scale loci in the final phylogenetic analyses. Beginning with the assemblies of deep-scale loci for individuals in the PHY taxon set, we phased diploid alleles following Pyron et al. (2016). Sets of haplotype sequences were then constructed based on the orthology determined during the generation of the preliminary PHY data set (but requiring 80% of individuals to be present to avoid the potential effects of missing data; Lemmon et al. 2009). After aligning sequences for each locus using MAFFT v7.023b (Katoh and Standley 2013), alignments were automatically trimmed and masked following Hamilton et al. (2016) then manually inspected in Geneious v.7 (Kearse et al. 2012), to ensure that no misaligned regions remained (see Supplementary Methods available on Dryad). At the end of the bioinformatics pipeline, 325 deep-scale loci were retained.
5% of loci were missing at least one outgroup taxon). Because nonrandom distributions of missing data have been shown to increase phylogenetic bias (Lemmon et al. 2009), we chose to include only the deep-scale loci in the final phylogenetic analyses. Beginning with the assemblies of deep-scale loci for individuals in the PHY taxon set, we phased diploid alleles following Pyron et al. (2016). Sets of haplotype sequences were then constructed based on the orthology determined during the generation of the preliminary PHY data set (but requiring 80% of individuals to be present to avoid the potential effects of missing data; Lemmon et al. 2009). After aligning sequences for each locus using MAFFT v7.023b (Katoh and Standley 2013), alignments were automatically trimmed and masked following Hamilton et al. (2016) then manually inspected in Geneious v.7 (Kearse et al. 2012), to ensure that no misaligned regions remained (see Supplementary Methods available on Dryad). At the end of the bioinformatics pipeline, 325 deep-scale loci were retained.
Estimating phylogenetic history.
The phylogeny of Pseudacris was estimated under both maximum likelihood (ML) and pseudocoalescent species tree approaches. The ML phylogeny was estimated with 100 bootstrap replicates in RAxML (version 8.1.21, Stamatakis 2006, 2014) under default settings, assuming a GTRGAMMA substitution model partitioned by locus. Individual gene trees with 100 bootstrap replicates were also estimated in RAxML under the GTRGAMMA substitution model. Nodes with low support were resolved to maximize the likelihood of the data, rather than being collapsed. This allowed the possibility of weak support being utilized (combined) across loci in the species tree analyses. However, note that completely unsupported nodes are randomly resolved, which is expected to result in more conservative estimates of species trees support. These bootstrap trees were used to estimate coalescent species tree with ASTRAL II (version 4.9.7, Mirarab et al. 2014; Mirarab and Warnow 2015).
Assessing phylogenetic data sensitivity.
Previous work has shown that disagreement among phylogenetic studies can be driven by a small number of the total genes included in a data set (Shen et al. 2017). To assess the effect of data selection, phylogenies were re-estimated after subsampling sites using 12 site-specific rate criteria and loci using 12 outlier loci criteria (144 combinations; Fig. 1; see Supplementary Methods available on Dryad for details). The robustness of each clade recovered in the full-data phylogenies was summarized as a matrix of bootstrap support values corresponding to the trees derived from the 144 data subsampling combinations. Overall representation of support was represented as a matrix averaged across nodes. Finally, the matrices were represented as a heat map in which the color of each cell indicates the support value derived from a particular subsampled data set (example given in Fig. 1c). We also computed both site and gene concordance factors using IQ-tree (Minh et al. 2013, 2018; Kalyaanamoorthy et al. 2017); for each of these cells and represent the effect of data subsampling on these concordance factors using heat maps similar to those described above.
Figure 1.
The effect of site and locus filtering on overall phylogenetic support. Sites were ranked by rate, then subsampled in 12 nested strategies (a), with an increasing number of the most variable sites being excluded in each successive strategy. For each site-removal strategy, gene trees were estimated from the resulting subsampled alignments and compared in order to compute the Euclidian distance from each tree to the center of multidimensional tree distance space (b). Trees were subsampled in 12 nested strategies with an increasing number of the loci with the largest tree distance being excluded in each successive strategy. Phylogenetic trees were estimated using each of the 144 resulting subsampled data sets (12 site-filtered  12 locus-filtered) and the average support value (averaged across the tree) are shown as a heat map, in which black indicates very strong support and white indicates moderate support (bootstrap support values from concatenated RAxML analyses are shown here). Overall support remains strong, except when a large portion of the sites or loci are removed, suggesting that the quantity of data available for analysis is more than sufficient to resolve the majority of the clades in the tree.
12 locus-filtered) and the average support value (averaged across the tree) are shown as a heat map, in which black indicates very strong support and white indicates moderate support (bootstrap support values from concatenated RAxML analyses are shown here). Overall support remains strong, except when a large portion of the sites or loci are removed, suggesting that the quantity of data available for analysis is more than sufficient to resolve the majority of the clades in the tree.
Testing alternative phylogenetic hypotheses.
To demonstrate the utility of the support matrices described above, alternative hypotheses concerning the unresolved relationships of two sets of species were tested. The first clade includes P. feriarum, P. triseriata, and Pseudacris kalmi, whereas the second clade includes P. nigrita, Pseudacris fouquettei, and Pseudacris maculata. For each clade, the support matrix was generated for all three possible species arrangements and the differences among the hypotheses were tested in a pairwise fashion using randomization tests. To compare two hypotheses, A and B, for example, a test statistic was computed as the difference between the support values under hypotheses A and B (averaged across the matrix representing the 144 analysis conditions). After the test statistic was computed, the support values were randomly shuffled across the two matrices being compared, while maintaining the matrix position. The difference between the average support value in each (randomized) matrix was then computed as a sample from the null distribution. The process was repeated until 10,000 samples from the null distribution were generated. The test statistic was compared to this distribution to produce a  -value. This test provides a statistically rigorous way to test alternative phylogenetic hypotheses while accounting for uncertainty that may be due to the particular data set chosen, which can sometimes have large effect on estimated relationships (Shen et al. 2017).
-value. This test provides a statistically rigorous way to test alternative phylogenetic hypotheses while accounting for uncertainty that may be due to the particular data set chosen, which can sometimes have large effect on estimated relationships (Shen et al. 2017).
Phylogeographic and Population Genomic Analyses
Data set generation.
The locus suitability analyses indicated that both deep- and shallow-scale loci are appropriate at the phylogeographic and population genetic scales (e.g., both types of loci showed low levels of missing data) and thus both types of loci were utilized in the analyses. Three data sets were constructed to study different aspects of the history of P. feriarum. The first data set (FER-SEQ) consisted of an alignment of haplotype sequences of 80 P. feriarum individuals sampled across the species’ range. The second data set (FER-SNP) consisted of SNPs sampled from the FER-SEQ data set after reducing the number of individuals to include just 55 individuals from ten populations representing the five river drainages along which P. feriarum forms a contact zone with P. nigrita. The third data set (HYB-SNP) consisted of 102 individuals from individuals found in one of these river drainages in which hybridization between P. feriarum and P. nigrita has been shown to occur. Details regarding the construction and composition of these three data sets are provided in the Supplementary Methods available on Dryad.
Estimating phylogeographic history.
The history of P. feriarum was estimated using the final 556-locus, 80 sample FER-SEQ data set under both ML and coalescent species tree approaches. Prior to phylogeny estimation, the best fit substitution model was estimated for each gene and the best locus-partitioning scheme were estimated using IQ-TREE with the following flags enabled: -m MFP+MERGE -rcluster 10 (Kalyaanamoorthy et al. 2017). IQ-TREE was then used to estimate the ML phylogeny (Nguyen et al. 2015) and support values (based on 1000 ultrafast bootstrap replicates; Minh et al. 2013) under the best-fit model and partitioning scheme (Chernomor et al. 2016). Individual gene trees estimated by IQ-TREE under the optimal substitution model were then used to estimate a coalescent species tree and support values in ASTRAL II (version 4.9.7, Mirarab et al. 2014; Mirarab and Warnow 2015).
Testing the number of invasions into sympatry using phylogeny constraints.
Each of the five river drainages is represented by individuals forming a monophyletic clade in both the ML and species tree. Although this monophyly suggests that each river drainage was invaded (from a neighboring allopatric area) during separate historical events, it is possible that one or more of the river drainages was invaded by a neighboring river drainage (suggesting that the invasions were not independent). If serial invasion of river drainages were the case, we would expect individuals from those neighboring river drainages to form a monophyletic clade. In order to determine whether the data sufficiently reject this alternative hypothesis, we used approximately unbiased (AU) tests (Shimodaira 2002), in which we compare the likelihood under a model constraining all individuals from the two adjacent river systems to be in one monophyletic clade (representing the single invasion hypothesis) with the likelihood under an unconstrained model (representing the multiple invasion hypothesis). In this test, if the data are significantly less likely under the constrained model, we can reject the single-invasion hypothesis in favor of the multiple-invasion hypothesis. By performing tests on all adjacent pairs of river drainages, which introduces a coarse spatial component, we can rule out the more complex scenarios containing more than two adjacent river drainages (the two river drainage constraint is a subset of the three river drainage constraint). These scores were compared, and significance of the difference was evaluated via likelihood ratio tests after a sequential Bonferroni correction (Rice 1989). AU tests were performed in IQ-TREE (Nguyen et al. 2015) using the “-au” option with 10,000 bootstrap replicates. Future studies containing more intense geographic sampling and more complex spatial components are underway.
Testing the number of invasions into sympatry by estimating dispersal history.
A single invasion of sympatry implies that an single ancestral P. feriarum population was founded by dispersal from allopatry to sympatry and that all sympatric individuals are derived from that ancestral population. This hypothesis can be tested by evaluating whether all ancestors of the sampled sympatric individuals existed in sympatry, or if one or more of these ancestors existed in allopatry. We performed this test using the continuous dispersal framework (PhyloMapper) developed by Lemmon and Lemmon (2008), which can be used to estimate the geographic locations of ancestors represented by internal nodes on a phylogeny describing the population history. Using the population history estimated for P. feriarum (described above) and the locations (GPS coordinates) corresponding to each of the populations at the tips of the phylogeny, we first estimated, in a ML framework, the locations of all of the populations represented by internal nodes on the phylogeny (hereafter referred to as the unconstrained analysis). To test the null hypothesis of one invasion (that all ancestors of the sympatric populations were located in sympatry), we repeated the analysis after imposing a constraint forcing each of the ancestral locations to be inside of the sympatry (the constrained analysis), as defined by the overlap of P. feriarum and P. nigrita in Supplementary Figure S1c available on Dryad. To test for significance, we compared the likelihood scores resulting from the constrained and unconstrained analyses using a likelihood ratio test. The test was repeated in a similar fashion for each geographically adjacent pair of sympatric regions (river drainages).
Assessing genetic structure and its distribution in geographic space.
We sampled SNPs from the GEO taxon set (excluding the P. triseriata outgroup) to investigate the genetic structure within P. feriarum across its distribution range. We used the algorithm implemented in conStruct (Bradburd et al. 2018) to visualize continuous genetic structure. The method differs from traditional genetic clustering methods by accounting for the decay in genetic relatedness resulting from geographic distance. We pooled individuals originating from the same localities and estimated allele frequencies for each SNP. In QGIS v3.4 (QGIS Development Team 2017), we computed pairwise geographic distances among the localities using GRASS GIS’ v.distance function (GRASS Development Team 2017). The allele frequency and geographic distance matrices were used as input for conStruct as implemented in R (R Core Team 2016), running duplicates of two chains from  = 1 to
= 1 to 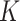 = 8 with 1
= 8 with 1 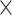 10
10 MCMC steps.
MCMC steps.
Testing alternative models of gene flow across a contact zone.
We constructed population-migration models to test alternative hypotheses for the direction of intraspecific gene flow in P. feriarum along each of the five river drainages. These models were tested using the 55-sample FER-SNP data set described above. Since preliminary analyses of an overall model containing all five river drainages (10 populations) proved to be computationally intractable, we instead constructed four-population demographic component models consisting of two allopatric and two sympatric populations from geographically adjacent river drainages (Supplementary Fig. S3 available on Dryad). These models included: 1) two-way gene flow between allopatry and sympatry, 2) one-way gene flow from allopatry to sympatry, and 3) one-way gene flow from sympatry to allopatry. In all models, two-way gene flow was also assumed to occur between the adjacent allopatric populations. For each of these models, we estimated demographic parameters (migration rates and effective population sizes) using Fastsimcoal2 (Excoffier et al. 2013), using frequency spectra (SFS) generated by Arlequin v3.5 (Excoffier and Lischer 2010), with .input arp files prepared with PGDSpider v2.1.(Lischer and Excoffier 2012). An unfolded SFS was used with a sequence from the sister taxon (P. triseriata) being used to determine ancestral states. Estimation of demographic parameters was conducted independently 100 times using different seeds during 40 optimization cycles (Excoffier et al. 2013), and estimation of likelihoods was obtained by using 10,000 iterations per cycle. The parameters estimated with the highest observed composite likelihood were used as priors to simulate 100 bootstrapped SFSs. To obtain confidence intervals for each parameter, bootstrapped SFSs were used to re-estimate parameters after initializing the Fastsimcoal2 algorithm from the values obtained in the initial highest composite likelihood (Excoffier et al. 2013). Selection of the most likely model was carried out by computing Akaike’s weight of evidence in favor of the model replicate with the highest composite likelihood (Johnson and Omland 2004).
Assessing the utility of deep- and shallow-scale loci.
We evaluated the population-migration model parameter estimates from Fastsimcoal2 to answer three questions: 1) Which type of loci (deep- or shallow scale) produced the most precise estimates of population size and migration rate? (2) Does subsampling one SNP per locus affect the precision of parameter estimates? (3) Do different locus types (deep- or shallow scale) produce different estimates of population size and migration rate? To answer these three questions, we conducted pairwise randomization tests using parameter estimates from the four Fastsimcoal2 analyses involving the best supported model (one-way gene flow from allopatry to sympatry, see Results section). The precision of each estimate was measured as width of the confidence interval for that estimate, with smaller values indicating higher precision. Each test statistic was compared to 10,000 values drawn from a null distribution to test for significance (see Supplementary Methods available on Dryad).
Quantifying hybridization in a sympatric population.
The distribution of hybrid indices in the Apalachicola River sympatric zone between P. feriarum and P. nigrita was estimated for 55 sympatric individuals (from the HYB-SNP data set described above using GenoDive v. 2.0b25 (Meirmans and Van Tienderen 2004). Allopatric P. feriarum (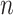 = 25) and P. nigrita (
= 25) and P. nigrita ( = 22) were used as reference groups in the analysis (Supplementary Table S1 available on Dryad). Note that the SNP-HYB data set included SNPs from both deep- and shallow-scale loci. Three SNP data sets were analyzed: a subsampled data set of 12 diagnostic SNPs between species, a subsampled data set of only one randomly-selected SNP per locus (to increase independence among SNPs), and the full set of SNPs across these two classes of loci. Point estimates of hybrid index were compared directly via linear regression to the same individuals analyzed for 12 microsatellite loci from Lemmon et al. (2011) and Lemmon and Juenger (2017) using JMP Pro11 (SAS Institute, Inc.).
= 22) were used as reference groups in the analysis (Supplementary Table S1 available on Dryad). Note that the SNP-HYB data set included SNPs from both deep- and shallow-scale loci. Three SNP data sets were analyzed: a subsampled data set of 12 diagnostic SNPs between species, a subsampled data set of only one randomly-selected SNP per locus (to increase independence among SNPs), and the full set of SNPs across these two classes of loci. Point estimates of hybrid index were compared directly via linear regression to the same individuals analyzed for 12 microsatellite loci from Lemmon et al. (2011) and Lemmon and Juenger (2017) using JMP Pro11 (SAS Institute, Inc.).
The range of hybrid classes within the contact zone was quantified with NewHybrids, using default parameters (Anderson and Thompson 2002). Analyses were conducted on the 12-diagnostic loci data set above and on a data set of 100 randomly drawn diagnostic SNPs. Both the 12- and 100-loci data sets were replicated four times by randomly choosing diagnostic SNPs and analyzing these data sets in NewHybrids. Analyses were attempted on greater than 100 loci, but these runs failed to converge for the larger data sets.
Results
Target Locus Recovery
Hierarchical hybrid enrichment provided an efficient way to obtain sequence data for loci designed for both deep- and shallow-scale use. Owing in part to a sufficient sequencing effort (mean coverage = 250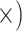 , we were able to recover a large portion of the target loci (mean = 87%, SD = 10%; Supplementary Tables S1–S4 available on Dryad). The success of this approach decreased with evolutionary distance from the reference species, especially for the shallow-scale loci (e.g., only half as many loci were recovered for the outgroup individuals; Lemmon et al. 2012). Likewise, the enrichment efficiency was good in general (44.5% of reads mapped on target; SD = 14%), but substantially lower for outgroups (15–25%).
, we were able to recover a large portion of the target loci (mean = 87%, SD = 10%; Supplementary Tables S1–S4 available on Dryad). The success of this approach decreased with evolutionary distance from the reference species, especially for the shallow-scale loci (e.g., only half as many loci were recovered for the outgroup individuals; Lemmon et al. 2012). Likewise, the enrichment efficiency was good in general (44.5% of reads mapped on target; SD = 14%), but substantially lower for outgroups (15–25%).
Locus Suitability
The type of target loci producing the greatest gene tree resolution varied by taxonomic level, following the expected pattern. Overall, deep-scale loci produced the best-resolved gene trees at the phylogenetic level, and shallow-scale loci produced the best-resolved gene trees at the phylogeographic and population genomic levels (Table 1; Fig. 2; Supplementary Table S5 available on Dryad). Note, however, that the level of resolution, although substantial at the phylogenetic level ( 50% of branches were well-resolved), was quite modest at both the phylogeographic and population genomic levels (
50% of branches were well-resolved), was quite modest at both the phylogeographic and population genomic levels (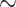 5% of branches were well-resolved), suggesting that gene trees estimated from these loci may not be appropriate for coalescent-based approaches that assume gene trees are resolved without error. The degree of gene tree discordance (Table 1; Supplementary Table S6 available on Dryad) was lower for shallow scale than for the deep-scale loci, regardless of the taxon set.
5% of branches were well-resolved), suggesting that gene trees estimated from these loci may not be appropriate for coalescent-based approaches that assume gene trees are resolved without error. The degree of gene tree discordance (Table 1; Supplementary Table S6 available on Dryad) was lower for shallow scale than for the deep-scale loci, regardless of the taxon set.
Table 1.
Relative utility of deep- and shallow-scale loci at three taxonomic levels (population genomic: POP, phylogeography: GEO, and phylogenetic: PHY) with respect to nine metrics
| Metric | POP | GEO | PHY | |
|---|---|---|---|---|
| Phylogenetic signal | Maximize gene tree resolution | Shallow (1.2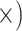
|
Shallow (1.2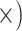
|
Deep (1.1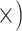
|
| Maximize variants per sequence | Deep (4.3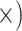
|
Deep (3.4
|
Deep (7.6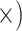
|
|
| Maximize diagnostic SNPs per sequencing effort | Shallow (8.5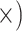
|
NA | NA | |
| Misleading signal | Clean mapping | Deep (1.1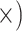
|
||
| Minimize gene tree discordance | Shallow (1.6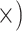
|
Shallow (1.6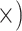
|
Shallow (1.6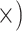
|
|
| Minimal alignment error | Deep (5.9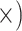
|
Deep (8.9
|
Deep (5.7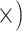
|
|
| Minimize % ambiguous characters | Deep (4.9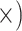
|
Deep (4.7
|
Deep (8.1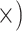
|
|
| Minimize missing data | Deep (4.8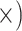
|
Deep (4.3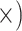
|
Deep (4.6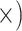
|
|
| Maximize single copy | Deep (3.9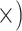
|
Deep (4.1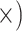
|
Deep (4.7
|
|
Notes: Details regarding how the metrics were computed, as well as values of the metrics, test statistics and  -values are given in Supplementary Methods and Tables available on Dryad. The preferred locus set for each criterion is listed in each cell with the ratio of improvement over the alternative locus type in parentheses. Note that for the gene tree resolution metric, the result assumes a bootstrap support threshold of 80%. Figure 4 provides results given other thresholds. Note that the general results were robust to level of trimming. Additional details are given in Supplementary Tables S5–S13 available on Dryad.
-values are given in Supplementary Methods and Tables available on Dryad. The preferred locus set for each criterion is listed in each cell with the ratio of improvement over the alternative locus type in parentheses. Note that for the gene tree resolution metric, the result assumes a bootstrap support threshold of 80%. Figure 4 provides results given other thresholds. Note that the general results were robust to level of trimming. Additional details are given in Supplementary Tables S5–S13 available on Dryad.
Figure 2.
Degree of gene tree resolution for six combinations of hybrid enrichment locus type and taxonomic scale. For each combination, the proportion of gene tree branches with support greater than a specified value (varied on the  -axis) was computed. Note that the locus type producing the most resolved gene trees depends on the taxonomic scale. Also note that the
-axis) was computed. Note that the locus type producing the most resolved gene trees depends on the taxonomic scale. Also note that the 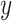 -axis scaling is not the same for the three graphs.
-axis scaling is not the same for the three graphs.
The occurrence of nucleotide variants differed greatly across target type, but not as expected: the deep-scale loci contained 3.4–7.6 times more variants than the shallow-scale loci (Table 1; Supplementary Table S7 available on Dryad). The difference in average lengths of the trimmed alignments for the PHY taxon set (deep scale: 2491 bp; shallow scale: 446 bp; Supplementary Table S2 available on Dryad) may contribute to this pattern. Nonetheless, the shallow-scale loci contained 8.5 times more diagnostic SNPs for the POP taxon set, when sequencing effort was considered (Table 1; Supplementary Table S8 available on Dryad).
By multiple metrics, the deep-scale loci were consistently less prone to error than shallow-scale loci (Table 1, Supplementary Tables S9–S13 available on Dryad). Of particular note is the high dropout level of the shallow-scale loci at the phylogenetic level; whereas usable alignments were obtained for 90% of deep-scale loci, useable alignments were obtained for only 42% of the shallow-scale loci (Supplementary Table S2 available on Dryad). Moreover, the remaining deep-scale loci were much more complete; only 5–7% of the characters in the deep-scale alignments were missing, while 25–33% of the characters in the shallow-scale loci were missing (Supplementary Table S13 available on Dryad). Finally, the deep-scale loci had substantially lower copy number than the shallow-scale loci; the average number of assembly clusters per locus was 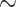 1.1 for the deep-scale loci compared to 4.3 to 5.2 for the shallow-scale loci (Supplementary Table S10 available on Dryad).
1.1 for the deep-scale loci compared to 4.3 to 5.2 for the shallow-scale loci (Supplementary Table S10 available on Dryad).
Phylogeny of the Genus Pseudacris
All nodes of the Pseudacris phylogeny were successfully resolved, with the exception of two within-species nodes. The final phylogenetic data set included 325 anchored loci for 46 taxa (92 alleles) and a total number of aligned base pairs = 493,889, after excluding loci with excessive missing data or possible paralogs. The tolerated missing data level was 5.6%. Very little topological discordance was found between the nuclear concatenated RAxML (Supplementary Fig. S4 available on Dryad) and ASTRAL trees (Fig. 3). The only difference identified were the relationships among P. regilla, Pseudacris hypochondriaca, and Pseudacris sierra, which include nonmonophyletic taxa, suggesting that the splitting of this complex into three species based on mitochondrial data (Recuero et al. 2006a,b) may have been premature. Our estimate of the rest of the Pseudacris phylogeny was consistent with one of the four trees presented in Barrow et al. (2014) that was derived from a 26-nuclear loci, single-allele *BEAST (v. 2.0; Heled and Drummond 2010) analysis. The other three Barrow et al. (2014) trees resulting from concatenated RAxML, multiple-allele *BEAST, and BUCKy analyses (v 1.4.0; Ané et al. 2007; Larget et al. 2010) conflicted with our results at one or more nodes.
Figure 3.
ASTRAL tree (a) and phylogeny with branch lengths (b, inset) of the genus Pseudacris showing phylogenetic sensitivity heat maps on nodes. Taxon numbers correspond to Supplementary Table S1 available on Dryad. On the heat maps, the color scale is the same as in Figure 1. Numbers to the lower left of a heat map indicate the support value when all data were included in the analysis (corresponds to lower left pixel of heat map), if that value was less than 100. The two nodes on which further hypothesis testing was performed (Fig. 4) are indicated by yellow circles around the heat map. The analogous concatenated maximum likelihood tree is presented in Supplementary Figure S2 available on Dryad.
The nodal heat maps derived from the support matrices described above indicated that most nodes are insensitive to data inclusion or exclusion across a broad range of conditions (Fig. 3). Although concordance factors varied substantially across nodes, the degree of data subsampling had comparatively little effect on concordance for a particular node (Supplementary Fig. S5 available on Dryad). Several key nodes that previously showed disagreement across studies varied in average bootstrap support depending on the quantity of loci and/or sites excluded (e.g., the P. regilla/hypochondriaca/sierra clade). Within the trilling frog clade, which includes Pseudacris brimleyi/Pseudacris brachyphona and its sister clade (Fig. 3), two of these ambiguous nodes were tested for robustness to alternative resolutions of the clade through randomization tests (Fig. 4; P. triseriata/P. kalmi/P. feriarum node and P. nigrita, P. fouquettei, P. maculata node). For both nodes, all alternative resolutions were strongly rejected (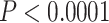 ) in favor of the relationships presented in Figure 3. We reserve resolution of the P. regilla complex for future work.
) in favor of the relationships presented in Figure 3. We reserve resolution of the P. regilla complex for future work.
Figure 4.
Hypothesis testing framework for comparing heat maps. The heat maps of three alternative resolutions were compared for each of two different clades (a and b) through randomization tests. Previous studies supporting each alternative resolution are indicated as follows: “Barrow” is Barrow et al. (2014), “Lemmon” is Lemmon et al. (2007a,b), and “Duellman” is Duellman et al. (2016). For both clades, the leftmost resolution was strongly favored ( ) as shown in Figure 3.
) as shown in Figure 3.
Phylogeography and Population Genomics of Pseudacris feriarum
Parallel invasions into sympatry.
Strong evidence was found for P. feriarum shifting up to five times from allopatry into sympatry with P. nigrita by following along the floodplains of multiple river systems (Fig. 5). The final phylogeographic data set included 556 loci from 80 individuals and a total number of base pairs = 683,138 (missing data = 4.1%). Both the concatenated ML and ASTRAL analyses indicated five geographically associated monophyletic clades in sympatry, corresponding to the five separate river systems bisecting the Coastal Plain of the southeastern U.S. ( ; Fig. 5c;). Results of AU tests supported five separate invasions: when samples from pairs of neighboring river systems were constrained to form a monophyletic clade, tree scores were significantly worse (Table 2). Results from the spatially continuous estimates of ancestral locations (using PhyloMapper) rejected the null model of one invasion in favor of a model with at least two invasions (
; Fig. 5c;). Results of AU tests supported five separate invasions: when samples from pairs of neighboring river systems were constrained to form a monophyletic clade, tree scores were significantly worse (Table 2). Results from the spatially continuous estimates of ancestral locations (using PhyloMapper) rejected the null model of one invasion in favor of a model with at least two invasions (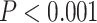 ; details provided in Table 2). Lastly, results from the analysis of genetic structure in geographic space (the conStruct analyses) show that the genomic composition of individuals varies substantially across the river five systems (see Supplementary Fig. S6 available on Dryad).
; details provided in Table 2). Lastly, results from the analysis of genetic structure in geographic space (the conStruct analyses) show that the genomic composition of individuals varies substantially across the river five systems (see Supplementary Fig. S6 available on Dryad).
Figure 5.
Phylogeography of P. feriarum, showing the geographic extent of the sampling (a), the intraspecific nuclear tree (b), and estimated routes of dispersal across the range and into the five river systems (c). Independent invasions of P. feriarum from allopatry into sympatry with P. nigrita are indicated by different colors on the tree (sympatric samples are colored, allopatric samples are not). Colors of clades match sample colors on map and correspond to colors of the arrows (numbering matches transects in Supplementary Fig. S3 available on Dryad). Bootstrap support is shown by grayscale dots on nodes.
Table 2.
Evaluation of multiple hypotheses of geographic expansion by P. feriarum into sympatry with P. nigrita along different river systems via the phylogenetic constraint test (AU) and the ancestral location test
| AU-test results | Ancestor location test results | |||||||
|---|---|---|---|---|---|---|---|---|
| Signif. worse | Signif. worse | |||||||
| Phylogeographic hypotheses | lnL score |
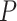 -value -value |
than ML tree? | Nodes constr. | DF | lnL score |
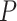 -value -value |
than ML tree? |
| Maximum likelihood tree |
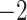 ,815,516.39 ,815,516.39 |
— | — | — | — |
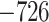 .165 .165 |
— | — |
| A. All shifts represent a single invasion |
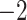 ,836,568.58 ,836,568.58 |
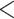 0.0001* 0.0001* |
Yes | 14 | 28 |
 .416 .416 |
5.62E-07* | Yes |
| B. Escambia and Apalachicola shifts represent a single invasion |
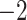 ,815,858.048 ,815,858.048 |
0.0042* | Yes | 3 | 6 |
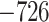 .699 .699 |
0.983971 | No |
| C. Apalachicola and Altamaha shifts represent a single invasion |
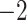 ,818,144.397 ,818,144.397 |
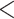 0.0001* 0.0001* |
Yes | 4 | 8 |
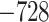 .6 .6 |
0.7714 | No |
| D. Altamaha and Edisto/Santee shifts represent a single invasion |
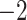 ,816,797.367 ,816,797.367 |
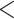 0.0001* 0.0001* |
Yes | 2 | 4 |
 .856 .856 |
0.499026 | No |
| E. Edisto/Santee and James/Anna shifts represent a single invasion |
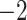 ,818,412.314 ,818,412.314 |
0.0001* | Yes | 8 | 16 |
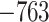 .348 .348 |
1.70E-09* | Yes |
Notes: River systems are represented in Figure 4. Maximum likelihood (lnL) scores of the best tree and different constraint trees (A–E) are shown in addition to the results from the two tests. Asterisks indicate significant tests.
Gene flow into the contact zone.
All four 4-population analyses consistently favored unidirectional gene flow from allopatry into sympatry over bidirectional gene flow based on Akaike’s weights (Supplementary Tables S14–S17 available on Dryad). The model assuming gene flow from sympatry to allopatry was deemed to be unsupported by the data after several attempts at analysis failed to converge after over 3400 CPU hours. Estimates of migration rates and effective populations sizes under the alternative models can be found in Supplementary Tables S18–S21 available on Dryad.
The utility of deep- and shallow-scale loci.
In general, shallow-scale loci produced more precise estimates of both population sizes and migration rates than deep-scale loci (Supplementary Figs. S7–S10 and Table S22 available on Dryad). This result was consistent between the full-SNP and one SNP per locus data sets. Reducing data sets to include only one SNP per locus did not significantly reduce precision of parameter estimates. Lastly, estimates of migration rates based on deep-scale loci were significantly higher than the analogous estimates based on shallow-scale loci (estimates of effective population size were not significantly different).
Hybridization in a sympatric population.
Hybrid index and hybrid class were estimated with high confidence, greatly exceeding previous microsatellite-based results. The final population genomic data set included 14,675 SNPs extracted from 564 shallow-scale and 281 deep-scale loci (845 total) for 102 taxa after removing loci showing evidence of recent duplication or  20% missing data. The total number of aligned bases equaled 738,000, after excluding missing data (7.6%). A total of 2786 sites were diagnostic between P. feriarum and P. nigrita (Supplementary Fig. S11 and Tables S23–S25 available on Dryad). For the three SNP data sets analyzed, the first included 12 randomly selected SNPs that were diagnostic between species (to compare to the 12-microsatellite data set), the second consisted of 768 randomly selected SNPs (one per locus—to study the effect of increasing independence among loci) from the 768 loci that included a variable site, and the third included all 14,765 SNPs extracted from the 845 deep- and shallow-scale loci (Supplementary Table S15 available on Dryad).
20% missing data. The total number of aligned bases equaled 738,000, after excluding missing data (7.6%). A total of 2786 sites were diagnostic between P. feriarum and P. nigrita (Supplementary Fig. S11 and Tables S23–S25 available on Dryad). For the three SNP data sets analyzed, the first included 12 randomly selected SNPs that were diagnostic between species (to compare to the 12-microsatellite data set), the second consisted of 768 randomly selected SNPs (one per locus—to study the effect of increasing independence among loci) from the 768 loci that included a variable site, and the third included all 14,765 SNPs extracted from the 845 deep- and shallow-scale loci (Supplementary Table S15 available on Dryad).
Precision of hybrid index was substantially improved through use of population genomic data for all three SNP data sets relative to estimates from 12 microsatellites (Lemmon and Juenger 2017). 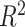 values varied from 0.746 (12-loci data set), to 0.752 (all SNPs data set), to 0.754 (one SNP/locus data set) when hybrid indices were compared to estimates from microsatellite data (
values varied from 0.746 (12-loci data set), to 0.752 (all SNPs data set), to 0.754 (one SNP/locus data set) when hybrid indices were compared to estimates from microsatellite data ( for all; Supplementary Table S1 available on Dryad). For comparison,
for all; Supplementary Table S1 available on Dryad). For comparison, 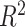 = 0.995 for 12-loci versus one SNP/locus;
= 0.995 for 12-loci versus one SNP/locus;  = 0.996 for 12-loci versus all SNPs; and
= 0.996 for 12-loci versus all SNPs; and  = 0.999 for one SNP/locus versus all SNPs (
= 0.999 for one SNP/locus versus all SNPs (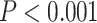 for all). Error estimates for hybrid indices decreased from the microsatellite (Supplementary Fig. S12a available on Dryad) to the SNP 12-loci data sets (Supplementary Fig. S12b available on Dryad) and most dramatically from the 12-loci to the 768 one SNP/locus (Supplementary Fig. S12c available on Dryad) data set. This improved precision revealed two putative F1 or F2 hybrids and one putative backcross to P. nigrita. Analysis of the all SNP data set (Supplementary Fig. S12d available on Dryad), which included 14,765 SNPs, provided similar values of hybrid index to the one SNP/locus data set (Supplementary Fig. S12c available on Dryad), but with very high precision.
for all). Error estimates for hybrid indices decreased from the microsatellite (Supplementary Fig. S12a available on Dryad) to the SNP 12-loci data sets (Supplementary Fig. S12b available on Dryad) and most dramatically from the 12-loci to the 768 one SNP/locus (Supplementary Fig. S12c available on Dryad) data set. This improved precision revealed two putative F1 or F2 hybrids and one putative backcross to P. nigrita. Analysis of the all SNP data set (Supplementary Fig. S12d available on Dryad), which included 14,765 SNPs, provided similar values of hybrid index to the one SNP/locus data set (Supplementary Fig. S12c available on Dryad), but with very high precision.
Consistent with hybrid index analyses, hybrid class analyses of the replicate 12-SNP and 100-SNP data sets identified the same three hybrid individuals. The placement of these hybrids varied across replicates in their identification as either an F2 hybrid or a F1 backcross to P. nigrita (Supplementary Table S26 available on Dryad). The placement of hybrids between these two classes varied less across the four 100-SNP replicates. Overall, most hybrid class analyses showed evidence of two F2 hybrids and one F1 P. nigrita backcross within the Apalachicola River hybrid zone (Supplementary Table S17 available on Dryad). These results are not directly comparable to the Lemmon and Juenger (2017) microsatellite data set due to the prohibitively low power in the latter study’s data set to estimate hybrid class.
Discussion
Our study demonstrates that deep- and shallow-scale genetic markers can be collected simultaneously and used to address questions at a variety of taxonomic scales. This approach alleviates some of the shortcomings of other data collection approaches. Methods such as RAD-seq are limited because missing data increases rapidly with increased taxonomic scale, whereas exon-capture and related approaches are limited because they often target conserved regions containing insufficient variation at shallow taxonomic scales. Hybrid enrichment allows researchers to collect markers derived from both top-down and bottom-up approaches and therefore circumvent these shortcomings by producing a more flexible data set. By subsampling different loci from this data set, we resolve a genus-level phylogeny of chorus frogs, uncover evidence for the independent and repeated formation of contact zones with one-way migration into sympatry, and estimate precisely the hybridization frequency in one sympatric population.
Locus Suitability
Top-down approaches can generate loci with substantial sequence variation at all but the shallowest taxonomic levels. Efficient collection of data from these targets relies on the presence of either UCE, the development of a probe set that represents diverse sequences (AHE), or the development of targets that span a modest time scale (exon-capture). Nonetheless, these loci can be screened for copy number and levels of variation, thus allowing high-quality data with minimal misleading signal to be collected efficiently. One additional advantage of this approach is that the data can be used more easily in future studies.
Bottom-up approaches can generate loci with substantial sequence variation at the shallowest taxonomic levels but are limited in their application to deeper levels. Even though the potential for error is elevated relative to loci obtained from top-down approaches, we found that of the target sets we tested, shallow-scale loci are the most cost-effective set for obtaining diagnostic SNPs. An advantage of this approach is that a larger number of loci can be targeted.
Data selection can significantly influence estimates of population genetic parameters. In our population models of a contact zone, estimates of both population size and migration rate were more precise when derived from loci developed specifically for shallow-scale use (i.e., using a bottom-up approach). It is unclear whether properties of the loci or the number of loci from these two sets were responsible for the difference (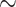 2 times more shallow-scale loci were utilized). The accuracy of estimates derived from these two locus types may also be different: migration rate estimates based on the deep-scale markers were significantly inflated relative to estimates based on shallow-scale markers. Since the true migration rates are unknown, it is unclear which locus set produced more accurate estimates. Surprisingly, precision in the estimates was not significantly reduced when SNPs were subsampled to one per locus to improve marker independence.
2 times more shallow-scale loci were utilized). The accuracy of estimates derived from these two locus types may also be different: migration rate estimates based on the deep-scale markers were significantly inflated relative to estimates based on shallow-scale markers. Since the true migration rates are unknown, it is unclear which locus set produced more accurate estimates. Surprisingly, precision in the estimates was not significantly reduced when SNPs were subsampled to one per locus to improve marker independence.
RAD-seq Versus Hybrid Enrichment for Data Collection
RAD-seq and hybrid enrichment offer different approaches to data collection, each with some notable advantages (Leaché et al. 2015; Harvey et al. 2016; Manthey et al. 2016). RAD-seq and related methods can be an efficient way to collect large numbers of loci across large numbers of individuals. One reason for the efficiency of this approach is the fact that sequence reads are aligned with respect to genomic position, reducing the coverage and effort required during the read assembly process. The method can also be applied without comparing genomic resources across deeper taxonomic scales. Hybrid enrichment, on the other hand, tends to lead to more complete alignments at deeper taxonomic scales where RAD-based approaches may suffer from allelic dropout (Arnold et al. 2013). The reason hybrid enrichment is more robust in this respect is that long (120 bp) probes used in hybrid enrichment can enrich regions containing up to 30% mismatches to the probe sequence. RAD-type approaches, conversely, require exact matches (of short kmers) for restriction enzymes to make the cuts consistently across individuals. A second advantage of hybrid enrichment is its flexibility with respect to the composition of target loci; probes can be designed to target well behaved anonymous loci (e.g., diagnostic and/or low copy), and/or specific functional loci (Margres et al. 2017a,b). We should note here that although we identified target regions from low-coverage whole genome data, the regions could also be identified from assembled genomes. The latter approach may be preferred because a more careful analysis of copy number may be possible using an assembled genome. One promising approach is to identify target regions from initial RAD-sequencing, then to use hybrid enrichment to recover those target regions across deeper time scales with less missing data (Ali et al. 2016).
Phylogenetic Resolution of the Genus Pseudacris
Despite genomic discordance at some nodes, we uncovered the first fully resolved phylogeny of Pseudacris. The nodal heat maps we present indicate that 90% of estimated relationships are not sensitive to the particular subset of the data that was analyzed, as long as at least 150 loci were used. For example, strong support for the placement of Pseudacris clarkii internal to the P. brachyphona/P. brimleyi clade but sister to the other trilling chorus frogs was found under a broad range of conditions (numbers of loci and sites; Figs. 1 and 3). This result indicates that the ancestral acoustic signal in the trilling frog clade was characterized by a fast pulse rate (P. brimleyi, P. brachyphona, and P. clarkii), which gave rise to the slow (P. nigrita and P. fouquettei) and intermediate (all other trilling frogs) pulse rate calls found in the remainder of the clade (Fig. 3; Lemmon et al. 2007a; Lemmon et al. 2007a,b). Although some workers have advocated the recognition of three species within the P. regilla complex (Recuero et al. 2006a,b), the paraphyly we found among these putative taxa suggests that more work is needed to determine whether P. regilla includes multiple species.
The heat map approach we developed represents a robust means of testing alternative phylogenetic hypotheses. The primary advantage of this test is that it accommodates variation due to data subsampling strategies. For one of the two clades for which alternative hypotheses were tested, resolution of P. kalmi–P. triseriata as the sister clade of P. feriarum differed from mitochondrial-based results (Lemmon et al. 2007a, Fig. 4b). Consistent with Barrow et al. (2014), the results here instead strongly support the biogeographic expansion hypothesis proposed by Smith (1957) concerning the origin of P. kalmi. Alternative resolutions of these three species were strongly rejected through the heat map-based tests (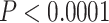 ; Figs. 3 and 4). In the second clade, resolution of P. fouquettei–P. nigrita as the sister clade of P. maculata also differed from mitochondrial-based results (Moriarty and Cannatella 2004; Lemmon et al. 2007a,b; Fig. 4a). In accord with one analysis of Barrow et al. (2014; only their 26-gene nuclear data set), our results clarify the position of P. maculata, which was previously obscured in mitochondrial data sets due to hybridization with P. clarkii (Moriarty and Cannatella 2004; Lemmon et al. 2007a,b). Alternative relationships of these taxa were strongly rejected through the heat map-based tests (
; Figs. 3 and 4). In the second clade, resolution of P. fouquettei–P. nigrita as the sister clade of P. maculata also differed from mitochondrial-based results (Moriarty and Cannatella 2004; Lemmon et al. 2007a,b; Fig. 4a). In accord with one analysis of Barrow et al. (2014; only their 26-gene nuclear data set), our results clarify the position of P. maculata, which was previously obscured in mitochondrial data sets due to hybridization with P. clarkii (Moriarty and Cannatella 2004; Lemmon et al. 2007a,b). Alternative relationships of these taxa were strongly rejected through the heat map-based tests ( ; Figs. 3 and 4).
; Figs. 3 and 4).
The resolved phylogeny of Pseudacris indicates that this genus should remain a single, stable taxon. Using previously published data, Duellman et al. (2016) suggested splitting the monophyletic genus Pseudacris into two genera with the sole justification that the two clades were geographically separated into a western (P. regilla complex) and an eastern (all other Pseudacris) clade. We reject this taxonomic change because: 1) our results indicate that Pseudacris remains a monophyletic clade, which is sister to the genus Acris, within the family Hylidae and 2) we contend that geographic separation is an insufficient criterion for splitting long-recognized monophyletic clades and leads to unnecessary taxonomic instability. For these reasons, we reject the splitting of Pseudacris into two genera and maintain the longstanding usage of this genus name.
Replicated Reinforcement in Independent Contact Zones
We have demonstrated that P. feriarum has invaded five different river systems through two to five different historical events (Fig. 5). Although this pattern is consistent with previous studies based on mitochondrial data (Lemmon et al. 2007a,b; Lemmon and Lemmon 2008), our study is the first to demonstrate statistical support for multiple independent invasions into sympatry. An important implication is that populations from each river system represent independent contact zones where reinforcement appears to be driving the evolution of premating reproductive isolation (Lemmon 2009; Lemmon and Lemmon 2010; Malone et al. 2014; Lemmon and Juenger 2017). In the most well-studied of these contact zones (Apalachicola River, FL), both natural and sexual selection against hybrids contributed to a 44% fitness cost to hybridization (Lemmon and Lemmon 2010). This cost has led to the evolution of strong female preferences in sympatry for conspecific and local male signals. Furthermore, evolution of the female preference has promoted a significant increase in the pulse rate and pulse number within male acoustic signals, causing these acoustic signals to diverge from P. nigrita. Male acoustic data from two other replicate contact zones have been studied to date (Edisto/Santee R., SC and James/Anna R., VA) and also show a strong pattern character displacement in one or the other of the two species (Lemmon 2009). Our study indicates that by utilizing the power of genome-wide locus sampling in phylogeographic studies, the number and location of independent contact zones can be uncovered, enabling researchers to exploit the power of phylogenetically replicated systems at the intraspecific level.
We found that gene flow of P. feriarum in each river system is unidirectional from allopatry to sympatry with P. nigrita (Supplementary Figs. 3 and 5 and Tables S18–S25 available on Dryad). This result matches the theoretical expectation that gene flow is expected to occur from the center to the edges of a species range, due to reduced habitat suitability at the edges (Kirkpatrick and Barton 1997). Evidence for gene flow into sympatry is also concordant with our finding that each river system was independently invaded by P. feriarum during the formation of the contact zone. Despite the homogenizing effect of allopatric alleles moving into sympatry, natural and sexual selection against hybridization with P. nigrita is strong enough to counteract the effects of gene flow, since male signals and female preferences of P. feriarum show strong divergence across the different sympatric areas (Lemmon 2009; Lemmon and Lemmon 2010). Future work with increased sampling could confirm this pattern using spatial clinal analyses (e.g., Derryberry et al. 2014; Engebretsen et al. 2016).
We find that hybrid index and hybrid class can be estimated more efficiently and precisely with SNP-based data compared to microsatellites. In contrast with the laborious effort required to develop a handful of microsatellites that amplify across species, the relative ease with which SNPs can be obtained through hybrid enrichment or other methods (e.g., RAD-seq, Andrews et al. 2016), indicates that SNP-based data are the more desirable option. Our results demonstrate that the previous microsatellite-based estimates of hybrid frequency by Lemmon and Juenger (2017) were incorrect, showing poor correspondence of hybrid index and lower precision. Lemmon and Juenger (2017) estimated that only three of 55 individuals sampled showed no evidence of introgression between species, whereas our results based on the same number of diagnostic SNPs indicate that 50 of 54 are not hybrids, revealing that microsatellite-based estimates of hybrid index are likely to be both inaccurate and imprecise (Supplementary Fig. S12 available on Dryad). The greatest improvement in precision was obtained by increasing the number of diagnostic SNPs from 12 to 768 (one SNP/locus). Although increasing to all 14,765 SNPs reduced error in hybrid index estimates for putative hybrids even further, the precision of the estimates are artificially low, due to nonindependence of SNPs within each locus.
Summary
We developed a hierarchical hybrid enrichment approach to target two discrete sets of genomic loci designed to simultaneously address questions spanning different evolutionary scales. Overall, the deep-scale loci were less prone to error and better suited to answering phylogenetic questions. The shallow-scale loci, however, produced a greater number of SNPs and more precise parameter estimates for population genetic analyses. At the phylogenetic level, we resolved with high confidence the remaining contested nodes across the genus Pseudacris and tested alternative resolutions of particular nodes using a novel heat map-based approach developed for this study. At the phylogeographic and population genomic levels, we determined that P. feriarum has formed up to five naturally replicated, independent reinforcement contact zones with P. nigrita along different Coastal Plain river systems of the southeastern U.S. with ongoing gene flow into the contact zone. Moreover, we obtained precise estimates of hybrid index in one of these five contact zones, thus significantly revising published estimates of hybridization frequency and hybrid indices in this region. Our results demonstrate how careful consideration of hybrid enrichment design can provide an invaluable resource for answering a broad array of biological questions across temporal and taxonomic scales.
Acknowledgments
For helpful discussions, we thank Craig Moritz, Ian Brennan, and Leonardo Tedeschi. For assistance locating or collecting samples, we thank Tim Andrus, Lisa Barrow, David Beamer, James Bettaso, Alvin Braswell, R. Bruce Bury, Carlos Camp, Sue Christopher, Joseph T. Collins, Don Forester, Aubrey Heupel, Wayne Hildebrand, Chris Hobson, Kelly Irwin, Lisa Irwin, Jay Kirk, Trip Lamb, Zack Lange, Joseph Lewis, Hannah Lucas, John MacGregor, John Malone, Malcolm McCallum, Bruce Means, Moses Michelsohn, Carolyn Moriarty, Brad Nissen, Chris Philips, Alex Pyron, Cameron Siler, Norman Scott, Samuel Sweet, Beckie Symula, Francis Thoennes, John Tucker, John Vanek, Lynea Witczak, and Josh Young.
We are grateful for tissue loans from Curtis Schmidt and Joseph T. Collins of the Sternberg Museum of Natural History, Fort Hays State University, and from David Cannatella and Travis LaDuc of the Texas Natural History Collection, University of Texas, Austin. Thanks to the Research Computing Center at Florida State University for computation support.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.0sf2hm8.
Funding
This work was supported by the National Science Foundation (DEB#1120516, DEB#1214325, DEB#1314449, DEB#1415545, and DEB#1416134).
References
- Ali O.A., O’Rourke S.M., Amish S.J., Meek M.H., Luikart G., Jeffres C., Miller M.R.. 2016. RAD capture (Rapture): flexible and efficient sequence-based genotyping. Genetics. 202:389–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson E.C., Thompson E.A.. 2002. A model-based method for identifying species hybrids using multilocus genetic data. Genetics. 160:1217–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews K.R., Good, J.M., Miller, M.R., Luikart G., Hohenlohe P.A.. 2016. Harnessing the power of RADseq for ecological and evolutionary genomics. Nat. Rev. Genet. 17:81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ané C., Larget B., Baum D.A., Smith S.D., Rokas A.. 2007. Bayesian estimation of concordance among gene trees. Mol. Biol. Evol. 24:412–426. [DOI] [PubMed] [Google Scholar]
- Arnold B., Corbett-Detig R.B., Hartl D., Bomblies K.. 2013. RADseq underestimates diversity and introduces genealogical biases due to nonrandom haplotype sampling. Mol. Ecol. 22:3179–3190. [DOI] [PubMed] [Google Scholar]
- Barrow L.N., Lemmon A.R., Lemmon E.M.. 2018. Targeted sampling and target capture: Assessing phylogeographic concordance with genome-wide data. Syst. Biol. 67:979–996. [DOI] [PubMed] [Google Scholar]
- Barrow L.N., Ralicki H.F., Emme S.A., Lemmon E.M.. 2014. Species tree estimation of North American chorus frogs (Hylidae: Pseudacris) with parallel tagged amplicon sequencing. Mol. Phylogenet. Evol. 75:78–90. [DOI] [PubMed] [Google Scholar]
- Bi K., Vanderpool D., Singhal S., Linderoth T., Moritz C., Good J.M.. 2012. Transcriptome-based exon capture enables highly cost-effective comparative genomic data collection at moderate evolutionary scales. BMC Genomics. 13:403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradburd G.S., Coop G.M., Ralph P.L.. 2018. Inferring continuous and discrete population genetic structure across space. Genetics. 210:33–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breinholt J.W., Lemmon A.R., Lemmon E.M., Xiao L., Kawahara A.Y.. 2018. Resolving relationships among the megadiverse butterflies and moths with a novel pipeline for anchored phylogenomics. Syst. Biol. 67:78–93. [DOI] [PubMed] [Google Scholar]
- Chernomor O., von Haeseler A., Minh B.Q.. 2016. Terrace aware data structure for phylogenomic inference from supermatrices. Syst. Biol. 65:997–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derryberry E. P., Derryberry G. E., Maley J. M., Brumfield R.T.. 2014. Hzar: hybrid zone analysis using an R software package. Mol. Ecol. Res. 14:652–663. [DOI] [PubMed] [Google Scholar]
- Dietrich C.H., Allen J.M., Lemmon A.R., Lemmon E.M., Takiya D.M., Evangelista O., Johnson K.P.. 2017. Leafhopper and treehopper (Hemiptera: Cicadomorpha: Membracoidea) phylogeny: the limits of phylogenomics? Insect Syst. Diversity. 1:57–72. [Google Scholar]
- Duellman W.E., Marion A.B., Hedges S.B.. 2016. Phylogenetics, classification, and biogeography of the treefrogs (Amphibia: Anura: Arboranae). Zootaxa. 4104:001–109. [DOI] [PubMed] [Google Scholar]
- Engebretsen K.N., Barrow L.N., Rittmeyer E.N., Brown J.M., Lemmon E.M.. 2016. Quantifying the spatiotemporal dynamics in a chorus frog (Pseudacris) hybrid zone over 30 years. Ecol. Evol. 6:5013–5031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L., Dupanloup I., Huerta-Sánchez E., Sousa V.C., Foll M.. 2013. Robust demographic inference from genomic and SNP data. PLoS Genet. 9:e1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L., Lischer H.E.L.. 2010. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol. Ecol. Resour. 10:564–567. [DOI] [PubMed] [Google Scholar]
- Faircloth B.C., McCormack J.E., Crawford N.G., Harvey M.G., Brumfield R.T., Glenn T.C.. 2012. Ultraconserved elements anchor thousands of genetic markers spanning multiple evolutionary timescales. Syst. Biol. 61:717–726. [DOI] [PubMed] [Google Scholar]
- Fouquette M.J. 1975. Speciation in chorus frogs. I. Reproductive character displacement in the Pseudacris nigrita complex. Syst. Zool. 24:16–23. [Google Scholar]
- Futuyma D.J. 2013. Evolution. 3rd ed Sunderland (MA): Sinauer Associates Inc; p. 656. [Google Scholar]
- Gerhardt H.C., Huber F.. 2002. Acoustic communication in frogs and insects. Chicago (IL): University of Chicago Press; p. 542. [Google Scholar]
- GRASS Development Team. 2017. Geographic resources analysis support system (GRASS GIS) Software, Version 7.2.
- Haddad S., Shin S., Lemmon A.R., Lemmon E.M., Svacha P., Farrell B., Sìlipinìski A., Windsor D., McKenna D.D.. 2018. Anchored hybrid enrichment provides new insights into the phylogeny and evolution of longhorned beetles (Cerambycidae). Syst. Entomol. 43:68–89. [Google Scholar]
- Hahn M.W. 2018. Molecular population genetics. Sunderland (MA): Sinauer Associates Inc., Oxford University Press; p. 352. [Google Scholar]
- Hamilton C.A., Lemmon A.R., Lemmon E.M., Bond J.E.. 2016. Expanding Anchored Hybrid Enrichment to resolve both deep and shallow relationships within the spider Tree of Life. BMC Evol. Biol. 16:212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey M.G., Smith B.T., Glenn T.C., Faircloth B.C., Brumfield R.T.. 2016. Sequence capture versus restriction site associated DNA sequencing for shallow systematics. Syst. Biol. 65:910–924. [DOI] [PubMed] [Google Scholar]
- Heinicke M., Lemmon A.R., Lemmon E.M., McGrath K., Hedges S.B.. 2018. Phylogenomic support for evolutionary relationships of New World direct-developing frogs (Anura: Terraranae). Mol. Phylogenet. Evol. 118:145–155. [DOI] [PubMed] [Google Scholar]
- Heled J., Drummond A.J.. 2010. Bayesian inference of species trees from multilocus data. Mol. Biol. Evol. 27:570–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillis D.M., Huelsenbeck J.P.. 1992. Signal, noise, and reliability in molecular phylogenetic analysis. J. Heredity 83:189–195. [DOI] [PubMed] [Google Scholar]
- Jennings B. 2016. Phylogenomic data acquisition: principles and practice. 1st ed Boca Raton (FL): CRC Press; p. 244. [Google Scholar]
- Johnson J.B., Omland K.S.. 2004. Model selection in ecology and evolution. Trends Ecol. Evol. 19:101–108. [DOI] [PubMed] [Google Scholar]
- Kalyaanamoorthy S., Minh B.Q., Wong T.K.F., von Haeseler A., Jermiin L.S.. 2017. ModelFinder: Fast model selection for accurate phylogenetic estimates. Nat. Methods. 14:587–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karl S.A., Avise J.C.. 1993. PCR-based assays of Mendelian polymorphisms from anonymous single-copy nuclear DNA: techniques and applications for population genetics. Mol. Biol. Evol. 10:342-361. [DOI] [PubMed] [Google Scholar]
- Katoh K., Standley D.M.. 2013. MAFFT multiple sequence alignment software version 7: improvements in performance and usability. Mol. Biol. Evol. 30:772–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kearse M., Moir R., Wilson A., Stones-Havas S., Cheung M., Sturrock S., Buxton S., Cooper A., Markowitz S., Duran C.. 2012. Geneious Basic: an integrated and extendable desktop software platform for the organization and analysis of sequence data. Bioinformatics. 28:1647–1649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M., Barton N.H.. 1997. Evolution of a species’ range. Am. Nat. 150:1–23. [DOI] [PubMed] [Google Scholar]
- Larget B.R., Kotha S.K., Dewey C.N., Ané C.. 2010. BUCKy: gene tree/species tree reconciliation with Bayesian concordance analysis. Bioinformatics. 26:2910–2911. [DOI] [PubMed] [Google Scholar]
- Leaché A.D., Chavez A.S., Jones L.N., Grummer J.A., Gottscho A.D., Linkem C.W.. 2015. Phylogenomics of phrynosomatid lizards: conflicting signals from sequence capture versus restriction site associated DNA sequencing. Genome Biol. Evol. 7:706–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon A.R., Brown J.M., Stanger-Hall K., and Lemmon E.M.. 2009. The effect of ambiguous data on phylogenetic estimates obtained by obtained by maximum-likelihood and Bayesian inference. Syst. Biol. 58:130–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon A.R., Emme S.A., Lemmon E.M., 2012. Anchored hybrid enrichment for massively high-throughput phylogenomics. Syst. Biol. 61:727–744. [DOI] [PubMed] [Google Scholar]
- Lemmon A.R., Lemmon E.M.. 2008. A likelihood framework for estimating phylogeographic history on a continuous landscape. Syst. Biol. 57:544–561. [DOI] [PubMed] [Google Scholar]
- Lemmon E.M. 2007. Patterns and processes of speciation in North American chorus frogs (Pseudacris) [Ph.D. Dissertation]. [Austin (TX)]: University of Texas, Austin. [Google Scholar]
- Lemmon E.M. 2009. Diversification of conspecific signals in sympatry: geographic overlap drives multidimensional reproductive character displacement in frogs. Evolution. 63:1155–1170. [DOI] [PubMed] [Google Scholar]
- Lemmon E.M., Juenger T.E.. 2017. Geographic variation in hybridization across a reinforcement contact zone of chorus frogs (Pseudacris). Ecol. Evol. 7:9485–9502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon E.M., Lemmon A.R.. 2010. Reinforcement in chorus frogs: lifetime fitness estimates including intrinsic natural selection and sexual selection against hybrids. Evolution. 64:1748–1761. [DOI] [PubMed] [Google Scholar]
- Lemmon E.M., Lemmon A.R.. 2013. High-throughput genomic data in systematics and phylogenetics. Ann. Rev. Ecol. Evol. Syst. 44:99–121. [Google Scholar]
- Lemmon E.M., Lemmon A.R., Cannatella, D.C.. 2007b. Geological and climatic forces driving speciation in the continentally distributed trilling chorus frogs (Pseudacris). Evolution. 61:2086–2103. [DOI] [PubMed] [Google Scholar]
- Lemmon E.M., Lemmon A.R., Collins J.T., Cannatella, D.C.. 2008. A new North American chorus frog species (Amphibia: Hylidae: Pseudacris) from the south-central United States. Zootaxa. 1675:1–30. [Google Scholar]
- Lemmon E.M. Lemmon A.R., Collins, J.T., Lee-Yaw J.A., Cannatella, D.C.. 2007a. Phylogeny-based delimitation of species boundaries and contact zones in the trilling chorus frogs (Pseudacris). Mol. Phylogenet. Evol. 44:1068–1082. [DOI] [PubMed] [Google Scholar]
- Lemmon E.M., Murphy M., Juenger T.E.. 2011. Identification and characterization of nuclear microsatellite loci for multiple species of chorus frogs (Pseudacris) for population genetic analyses. Conserv. Genet. Resour. 3:233-237. [Google Scholar]
- Léveillé-Bourret, E., Starr J.R., Ford B.A., Lemmon E.M., Lemmon A.R.. 2018. Resolving a rapid radiation using universal enrichment probes for hundreds of nuclear genes in non-model plants (CDS clade, Cyperaceae). Syst. Biol. 67:94–112. [DOI] [PubMed] [Google Scholar]
- Lischer H.E.L., Excoffier L.. 2012. PGDSpider: an automated data conversion tool for connecting population genetics and genomics programs. Bioinformatics. 28:298–299. [DOI] [PubMed] [Google Scholar]
- Malone J.H., Ribado J., Lemmon, E. Moriarty. 2014. Sensory drive does not explain reproductive character displacement of male acoustic signals in the upland chorus frog (Pseudacris feriarum). Evolution. 68:1306–1319. [DOI] [PubMed] [Google Scholar]
- Manthey J.D., Campillo L.C., Burns K.J., Moyle R.G.. 2016. Comparison of target-capture and restriction-site associated DNA sequencing for phylogenomics: a test case in cardinalid tanagers (Aves, Genus: Piranga). Syst. Biol. 65:640–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margres M.J., Bigelow A.B., Lemmon E.M., Lemmon A.R., Rokyta D.R.. 2017a. Selection to increase expression, not sequence diversity, precedes gene family origin and expansion in rattlesnake venom. Genetics. 206:1569–1580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margres M.J., Wray K.P., Hassinger A.T.B., Ward M., McGivern J.J., Lemmon E.M., Lemmon A.R., Rokyta D.R.. 2017b. Quantity, not quality: rapid adaptation in a polygenic trait proceeded exclusively through expression differentiation. Mol. Biol. Evol. 34:3099–3110. [DOI] [PubMed] [Google Scholar]
- McCormack J.E., Hird S.M., Zellmer A.J., Carstens B.C., Brumfield R.T.. 2013. Applications of next-generation sequencing to phylogeography and phylogenetics. Mol. Phylogenet. Evol. 66:526–538. [DOI] [PubMed] [Google Scholar]
- Meirmans P.G., Van Tienderen P.H.. 2004. GENOTYPE and GENODIVE: two programs for the analysis of genetic diversity of asexual organisms. Mol. Ecol. Notes. 4:792–794. [Google Scholar]
- Minh B.Q., Nygen M.A., von Haeseler A.. 2013. Ultrafast approximation for phylogenetic bootstrap. Mol. Biol. Evol. 30:1188–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minh B.Q., Hahn M.W., Lanfear R.. 2018. New methods to calculate concordance factors for phylogenomic datasets. bioRxiv. 487801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirarab S., Reaz R., Bayzid M.S., Zimmermann T., Swenson M.S., Warnow T.. 2014. ASTRAL: genome-scale coalescent-based species tree estimation. Bioinformatics. 30:i541–i548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirarab S., Warnow T.. 2015. ASTRAL-II: coalescent-based species tree estimation with many hundreds of taxa and thousands of genes. Bioinformatics. 31:i44–i52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell N., Lewis P.O., Lemmon E.M., Lemmon A.R., Holsinger K.E.. 2017. Anchored phylogenomics resolves the evolutionary relationships in the rapid radiation of Protea L. (Proteaceae). Am. J. Bot. 104:102–115. [DOI] [PubMed] [Google Scholar]
- Moriarty E.C., Cannatella D.C.. 2004. Phylogenetic relationships of the North American chorus frogs (Pseudacris: Hylidae). Mol. Phylogenet. Evol. 30:409–420. [DOI] [PubMed] [Google Scholar]
- Ng S.B., Turner E.H., Robertson P.D., Flygare S.D., Bigham A.W., Lee C., Shaffer T., Wong M., Bhattacharjee A., Eichler E.E., Bamshad M.. 2009. Targeted capture and massively parallel sequencing of 12 human exomes. Nature. 461:272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen L.-T., Schmidt H.A., von Haeseler A., Minh B.Q.. 2015. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol. Biol. Evol. 32:268–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell R., Conant R., Collins J.T.. 2016. Peterson field guide to North American Amphibians and reptiles. 4th Ed Boston (MA): Houghton Mifflin Harcourt; p. 512. [Google Scholar]
- Prum R.O, Berv J.S., Dornburg A., Field D.J., Townsend J.P., Lemmon E.M., and Lemmon A.R.. 2015. A fully resolved, comprehensive phylogeny of birds (Aves) using targeted next generation DNA sequencing. Nature. 526:569–573. [DOI] [PubMed] [Google Scholar]
- Pyron R.A., Hendry C.R., Hsieh F., Lemmon A.R., Lemmon E.M.. 2016. Integrating phylogenomic and morphological data to assess candidate species-delimitation models in Brown and Red-bellied snakes (Storeria). Zool. J. Linn. Soc. 177:937–949. [Google Scholar]
- QGIS Development Team. 2017. QGIS-Open source geographic information system (Version 2.14.19) [Software].
- R Core Team. 2016. R: A language and environment for statistical computing (Version 3.4) [Software].
- Recuero E., Martínez-Solano Í., Parra-Olea G., García-París M., 2006a. Phylogeography of Pseudacris regilla (Anura: Hylidae) in western North America, with a proposal for a new taxonomic rearrangement. Mol. Phylogenet. Evol. 39:293–304. [DOI] [PubMed] [Google Scholar]
- Recuero E., Martínez-Solano Í., Parra-Olea G., García-París M., 2006b. Corrigendum to “Phylogeography of Pseudacris regilla (Anura: Hylidae) in western North America, with a proposal for a new taxonomic rearrangement” [Mol. Phylogenet. Evol. 39 (2006) 293–304]. Mol. Phylogenet. Evol. 41:511. [DOI] [PubMed] [Google Scholar]
- Rice W.R. 1989. Analyzing tables of statistical tests. Evolution. 43:223–225. [DOI] [PubMed] [Google Scholar]
- Rokyta D.R., Lemmon A.R., Margres M.J., Arnow K.. 2012. The venom-gland transcriptome of the eastern diamondback rattlesnake (Crotalus adamanteus). BMC Genomics. 13:312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruane S., Raxworthy C.J., Lemmon A.R., Lemmon E.M., Burbrink F.T.. 2015. Comparing large anchored phylogenomic and small molecular datasets for species tree estimation: An empirical example using Malagasy pseudoxyrhophiine snakes. BMC Evol. Biol. 15:221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X.X., Hittinger C.T., Rokas A.. 2017. Contentious relationships in phylogenomic studies can be driven by a handful of genes. Nat. Ecol. Evol. 1:0216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimodaira H. 2002. An approximately unbiased test of phylogenetic tree selection. Syst. Biol. 51:492–508. [DOI] [PubMed] [Google Scholar]
- Smith P.W. 1957. An analysis of post-Wisconsin biogeography of the Prairie Peninsula region based on distributional phenomena among terrestrial vertebrate populations. Ecology. 38:205–218. [Google Scholar]
- Stamatakis A. 2006. RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics. 22:2688–2690. [DOI] [PubMed] [Google Scholar]
- Stamatakis A. 2014. RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics. 30:1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stout C.C., Tan M., Lemmon A.R., Lemmon E.M., Armbruster J.W.. 2016. Resolving Cypriniformes relationships using an anchored enrichment approach. BMC Evol. Biol. 16:244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wanke S., Mendoza C.G., Müeller S., Paizanni A., Neinhuis C., Lemmon A.R., Lemmon E.M., Samain M.-S.. 2017. Recalcitrant deep and shallow nodes in Aristolochia (Aristolochiaceae) illuminated using anchored hybrid enrichment. Mol. Phylogenet. Evol. 117:111–123. [DOI] [PubMed] [Google Scholar]
- Winterton S.L., Lemmon A.R., Gillung J.P., Garzon I.J., Badano D., Bakkes D.K., Breitkreuz L.C.V., Engel M.S., Lemmon E.M., Liu X., Machado R.J.P., Skevington J.H., Oswald J.D.. 2018. Evolution of lacewings and allied orders using anchored phylogenomics (Neuroptera, Magaloptera, Raphidioptera). Syst. Entomol. 43:330–354. [Google Scholar]
- Young A.D., Lemmon A.R., Skevington J.H., Mengual X., Stahls G., Reemer M., Jordaens K., Kelso S., Lemmon E.M., Hauser M., De Meyer M., Misof B., Wiegmann B.. 2016. The first anchored enrichment dataset producted for true flies (order Diptera) reveals insights into the phylogeny of flower flies (family Syrphidae) and sets the stage for future large-scale phylogenetic analyses. BMC Evol. Biol. 16:143. [DOI] [PMC free article] [PubMed] [Google Scholar]







