Inferring Tumor Proliferative Organization from Phylogenetic Tree Measures in a Computational Model

Abstract

We use a computational modeling approach to explore whether it is possible to infer a solid tumor’s cellular proliferative hierarchy under the assumptions of the cancer stem cell hypothesis and neutral evolution. We work towards inferring the symmetric division probability for cancer stem cells, since this is believed to be a key driver of progression and therapeutic response. Motivated by the advent of multiregion sampling and resulting opportunities to infer tumor evolutionary history, we focus on a suite of statistical measures of the phylogenetic trees resulting from the tumor’s evolution in different regions of parameter space and through time. We find strikingly different patterns in these measures for changing symmetric division probability which hinge on the inclusion of spatial constraints. These results give us a starting point to begin stratifying tumors by this biological parameter and also generate a number of actionable clinical and biological hypotheses regarding changes during therapy, and through tumor evolutionary time. [Cancer; evolution; phylogenetics.]

The cancer stem cell hypothesis (CSCH) posits that tumors are composed of a hierarchy of cells with varying proliferative capacities. Under this hypothesis, a subpopulation of “cancer stem cells,” also termed tumor-initiating cells (TICs), are able to self-renew through symmetric division and also to differentiate into tumor cells resembling transit-amplifying cells (TACs) through asymmetric division (Fig. 1a), giving rise to the entire diversity of cells within a tumor (Fialkow et al. 1967). The CSCH provides a conceptual framework by which to understand many different aspects of cancer progression, including: the occurrence of functional heterogeneity despite genetically identical states (Sottoriva et al. 2010; Vlashi et al. 2011; Magee et al. 2012); resistance to chemotherapy (Chen et al. 2012; Werner et al. 2016) and radiotherapy (Bao et al. 2006; Diehn et al. 2009; Dhawan et al. 2014); recurrence (Dingli and Michor 2006); and metastasis (Pang et al. 2010). Despite its popularity, the CSCH has been the subject of continual debate and modification in order to maintain compatibility with experimental observations (Gilbertson and Graham 2012; O’Connor et al. 2014; Scott et al. 2019).

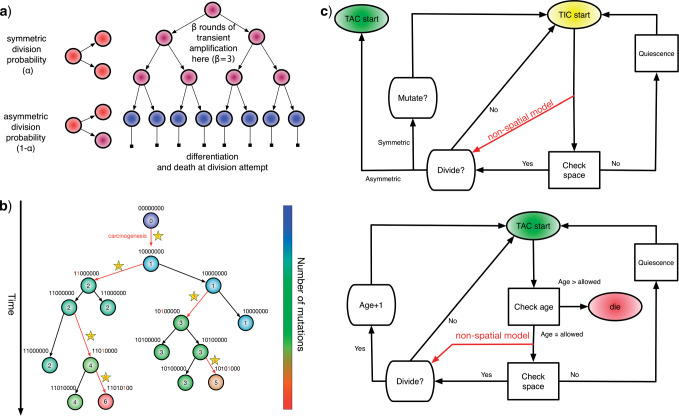
Figure 1.

Spatial stochastic model schematic with neutral mutation schema. a) The proliferative hierarchy. Each TIC can divide symmetrically with probability 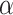to make two identical TIC progeny, or asymmetrically with probability 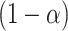to make one TIC and one TAC. TACs divide symmetrically until they reach a specific divisional age ( 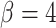for this work), after which they die upon division attempt. b) At each division event (branching) after the first (carcinogenesis, labeled with a 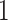), a random number of mutations drawn from a Poisson distribution with expectation 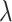is conferred on each daughter (subsequent starred events). Each mutation event is given a unique flag, which is inherited by its offspring unless they too mutate. Each unique mutation can then be considered as a novel mutant allele (red) appearing in the population. c) Flowchart outlining CA rules governing TIC and TAC growth, including spatial inhibition of growth and TAC age.

While the specifics of the CSCH are still a matter of debate, the clinical relevance of those cells with traits ascribed to TICs is clear. However, our ability to measure their dynamics in a clinical setting remains lacking. In vivo measurement efforts are limited to carefully conducted live imaging in genetically engineered mice (Ritsma et al. 2014), or genetic labeling and subsequent lineage tracing (Driessens et al. 2012). Although in vitro systems are better suited to the extraction of these parameters, to date little has been done to quantify them, as technically demanding single-cell lineage tracing (Lathia et al. 2011) is required. These experimental difficulties speak to the need for more theoretical work in this area, especially to propose metrics for quantifying proliferative parameters such as TIC symmetric division probability (Fig. 1a) from clinical data. This is of particular importance as there is mounting evidence for the effect of proliferative hierarchy on response to radiotherapy (Tamura et al. 2010) and chemotherapy (Chen et al. 2012), and microenvironmental factors such as hypoxia (Conley et al. 2012; Dhawan et al. 2016b), acidosis (Hjelmeland et al. 2011), growth factors (Doetsch et al. 2002), and even stromal cell co-operation or co-option (Vermeulen et al. 2010; Liu et al. 2011) have been shown to perturb this system. In summary, TIC symmetric division rate and somatic mutation rate are both specific parameters of interest in cancer biology, and these form the focus of the present modeling.

Several published mathematical models, using different formalisms and considering different aspects of heterogeneity, have predicted that the evolution of a solid tumor should depend strongly on whether or not it exhibits a proliferative hierarchy, and on the parameters of such a hierarchy. These models have included spatial proliferation constraints, microenvironmental heterogeneity, and selective pressures, and the noted differences include shape, clonal heterogeneity, rate of evolution, and growth dynamics. Werner et al. (2011) specifically studied the differences in bulk tumor behavior between tumors arising from mutant TICs and TACs in a nonspatial context. In a spatial context, the work of Sottoriva et al. (2010), Sottoriva and Tavaré (2011), Enderling et al. (2009), and Morton et al. (2011) represent the first papers where it was shown that the parameters governing TAC dynamics can constrain tumor growth, and also that TIC-driven tumors have significantly different spatial growth patterns: specifically, that they exhibit “patchy” growth. In none of these models, except Sprouffske et al. (2013), in which the main question centered on TAC numbers, were these differences studied across TIC symmetric division probabilities, which is a key parameter governing the hierarchy, and one that is exceedingly difficult to measure or perturb in vitro or in vivo.

To describe the evolutionary relationship between cells in a multicellular tissue, we require a phylogenetic approach. While the use of objective, genetic information to infer phylogenetic trees has a long history in evolutionary biology, its application to cancer evolution is much more recent, giving rise in the last decade to a subfield recently dubbed “PhyloOncology” by Somarelli et al. (2016). Using phylogenies reconstructed from spatially separated biopsies and informatic algorithms, many aspects of tumor evolution have begun to be elucidated (Gerlinger et al. 2014), including the genetic heterogeneity present within a primary tumor (Sottoriva et al. 2013), the origin of individual metastatic tumors within the primary site (Gerlinger et al. 2012; Naxerova and Jain 2015), the earliest events driving progression and metastasis (Zhao et al. 2016), and the effect of chemotherapy on primary and metastatic sites (Murugaesu et al. 2015; Faltas et al. 2016).

In addition to these sorts of questions, there are precedents in other fields for using phylogenetic information, integrated with population dynamics to infer other underlying biological processes—a technique termed phylodynamics (Grenfell et al. 2004). For example, Leventhal et al. (2012) proposed that the phylogenetic tree contains a “fingerprint” that can be used to determine the evolutionary process driving the population in question. Modeling the spread of HIV within a contact network, the authors investigated whether the network structure could be inferred from the resulting disease phylogenies. To address this question, the authors simulated a range of epidemics on several families of random graphs and measured the resulting phylogenetic trees, finding that certain tree-based measures could discriminate between the qualitatively different families of random graph structures considered.

We may expect cancer cell phylogenies to look quite different from viral phylogenies. Nevertheless, these precedents motivate us to ask whether a similar approach could be used to discriminate between in silico tumors with different symmetric division rates. To test this hypothesis, we study the effect of TIC symmetric division probability on tumor evolution using a computational modeling approach. We focus on observed patterns in reconstructed phylogenetic trees across a range of symmetric division probabilities. The estimation of this proliferative parameter from clinical data could help improve our understanding of the effect of therapies on tumor growth dynamics, and our ability to stratify tumors for consideration of different therapies. In this way, we seek to provide translatable measures to aid in understanding tumor biology: to use mathematical modeling to “see the invisible.”

The remainder of this article is structured as follows. We first present a spatial stochastic model of tumor growth under a proliferative hierarchy with neutral mutations, which we embed on a 2D lattice to enable the study of the effect of spatial constraints. Next, we develop an algorithm to reconstruct the branched phylogenetic structure from each realization of our tumor growth model. We apply a range of statistical measures of phylogenetic tree shape to simulation outputs for comparison. We explore the temporal dynamics of these measures over the course of tumor growth to assess whether they are robust to tumor size changes, and then to changes in mutation frequency. Finally, we discuss the possible clinical utility of these measures.

Materials and Methods

Model Development

Here, we describe the development of a 2D, lattice-embedded cellular automaton (CA) model of tumor growth with contact inhibition growing under neutral evolution and a proliferative hierarchy. We also develop a nonspatial companion model in order to assess the role of spatial constraints on the evolutionary process.

Proliferative hierarchy

For both models, we consider a proliferative hierarchy comprising two cell types, TICs and TACs. We assume that each TIC divides symmetrically with probability 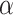, creating two TICs, and asymmetrically with probability , creating one TIC and one TAC. For simplicity, we assume that 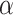takes a constant value for all cells in a given simulation, and is not dependent on the mutation rate (see below). Note that in practice, microenvironmental parameters such as nutrient deprivation (Flavahan et al. 2013), acidity (Hjelmeland et al. 2011), and hypoxia (Heddleston et al. 2009; Li et al. 2009), as well as accumulated mutations such as those commonly observed in colorectal cancers (Baker et al. 2014), are all known to be capable of affecting symmetric division probability among cells in a tumor. As it has been shown theoretically that the overall population dynamics of TIC-driven tumors is equivalent with or without TIC symmetric differentiation (Rodriguez-Brenes et al. 2011) (when a TIC divides to create two TACs), and as the lineage extinction possible in this case would significantly complicate our phylogenetic analysis, we make the simplifying assumption that there is no symmetric differentiation. We do not rule out that the addition of symmetric differentiation could affect phylodynamics, but leave that question for further study.

We assume that every TAC division is symmetric, creating two TACs, but only allow this to progress for 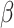rounds of division, after which the TAC will die if chosen to divide again. Here 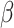represents the replicative potential of TACs, and is posited to represent telomere length (Poleszczuk et al. 2014). Previous theoretical work has shown that tumor growth kinetics in spatially constrained geometries are strongly affected by the value of 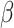(Morton et al. 2011). In particular, if 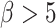, then simulated tumors experience unrealistically lengthy growth delays. Therefore, we follow a previously used assumption (Sottoriva et al. 2010; Sprouffske et al. 2013) and fix 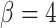. This mode of growth and differentiation is illustrated in Figure 1a. For simplicity, we neglect cell death, which could disrupt growth patterns. Indeed, Williams et al. (2016) have shown that the overall patterns of mutations, as measured by variant allele frequencies, is changed. The addition of cell death in this model is therefore a natural avenue for future work.

Neutral evolution

To understand the effects of neutral evolution on tumors with differing proliferative hierarchies, we extend our model of tumor growth under a proliferative hierarchy to include random mutations. At each cell division, there is a possibility that one or more mutations occur. To determine the number of mutations accumulated by a given daughter cell, we independently draw a random number from a Poisson distribution with expectation 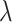. We assume for simplicity that every mutation arising in our model is unique. This “infinite sites” assumption is usually ascribed to Kimura (1969).

For simplicity, we assume that mutations confer no advantage, disadvantage or any other phenotypic change and therefore serve only as a method by which to track clonal lineages (i.e., they are neutral; Williams et al., 2016). This assumption could in principle be loosened to allow for positive selection (Bignell et al. 2010), or a balance of positive and negative selection (McFarland et al. 2013). A schematic of this model of evolution, and labeling scheme, is shown in Figure 1b.

For computational efficiency, instead of storing a genome of length 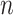(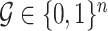), we record a unique integer flag only for the most recent mutation accumulated within a cell, which is passed down to its progeny, unless a mutation occurs, in which case a new flag (the next integer) is assigned. We also record each mutation event in the form of an ordered pair 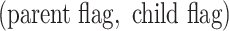, so that the complete genome, 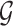, can be reconstructed for future use, and the length will be only as long as is needed to represent the changes which occurred during the simulation. As they are the only cells capable of forming tumors on their own, and infinite replication, we follow previous works in considering new mutations to accrue only in TICs (Sottoriva et al. 2010; Sottoriva and Tavaré 2011; Sprouffske et al. 2013; Poleszczuk et al. 2015). A natural extension for human cancer would be to consider instead sequences formed of DNA characters ATCG.

Nonspatial Model Implementation

To implement a first version of our hierarchical model with neutral evolution, we consider the case in which there are no spatial constraints—which could be a sensible model for liquid tumors like leukemias which are well mixed in the blood. We initialize our simulation with a single TIC. We then implement discrete updates, which we will term “time steps.” As we are not studying temporal dynamics here, we do not prescribe any proper dimension to this time. At each discrete time step, we choose a cell uniformly at random from the population to either divide and possibly mutate, or die. Our simulation is considered complete when the total population of cells reaches a prescribed number.

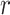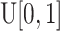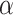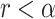If the cell is a TIC, then we first draw a random number, , from and compare it to the probability of symmetric division, . If , then the cell divides symmetrically, and we draw the number of new mutations accumulated in each daughter independently from a Poisson random distribution with expectation value 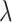. A new TIC daughter is then generated and given a mutational “identity” which is the mathematical sum of the parent cell’s identity and the number of new mutations. The parental cell is also updated by changing its identity based on the number of new mutations it accrues, if any. If the cell is not determined to divide symmetrically, then it divides asymmetrically and a TAC daughter is created with age 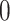and the parental TIC is updated for new mutations as above, see Figure 1.

If the chosen cell is instead a TAC, then we first check that its age is less than the allowed TAC age, 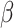. If the age is equal to the allowed TAC age, then the cell dies. If the age is less than the allowed TAC age, then the cell ages and divides, and a new daughter with the same identification is created, whereupon the loop continues (see Fig. 1 for schematic).

Spatial Model Implementation

As we are interested in the effect of the proliferative hierarchy on the neutral evolutionary process in solid, spatially constrained tumors, we embed our cell-based model in a 2D square lattice. While recent work has shown some qualitative differences in vascularized CA models between two and three dimensions, using a 2D lattice for unvascularized tissue is a common simplification (Anderson and Chaplain 1998; Alarcón et al. 2006; Gerlee and Anderson 2008; Scott et al. 2016) that allows spatial constraints to be studied in a computationally tractable manner. In addition to the above description of cell proliferation, we consider cell proliferation to be modulated by contact inhibition (Anderson 2005). A cell is allowed to divide only if at least one of the eight adjacent lattice sites (north, south, east, west, and diagonal neighbors) is unoccupied; if this is not the case, then we consider the cell to be in a quiescent state that may be exited when space becomes available. At each time step, each “cell” has an opportunity to divide given that it has space to do so. Cells are chosen uniformly at random for updates from the entire population to avoid order bias. Apart from these spatial effects, the model is otherwise identical to the nonspatial model presented earlier.

Cell-type specific rules

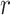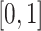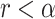If space is available, and the cell is a TIC, then the type of division is determined by choosing a uniform random number, , from . If , then the TIC divides symmetrically, creating another TIC that is placed uniformly at random in one of the free neighboring lattice sites. The parent and daughter TICs will independently acquire a random number of new mutations, as described above. If 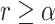, then the TIC divides asymmetrically, creating a TAC that is placed uniformly at random in one of the free neighboring lattice sites. The daughter TAC is created with the same mutation identity (ID) as the parent, and age 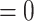, while the parent TIC will independently acquire a random number of new mutations, as described above.

If the chosen cell is instead a TAC, then the check after available space is a check of the cell’s proliferative age, which is the number of divisions as a TAC. If the TAC age is equal to the replicative potential, 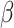, then the TAC dies, at which point it is removed from the simulation. If the TAC age is less than 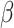, then we create a new TAC daughter and place it uniformly at random in one of the free neighboring lattice sites. The parent and daughter TACs share the same mutation ID and their age is updated to be one more than the age of the originally chosen TAC.

Full Implementation

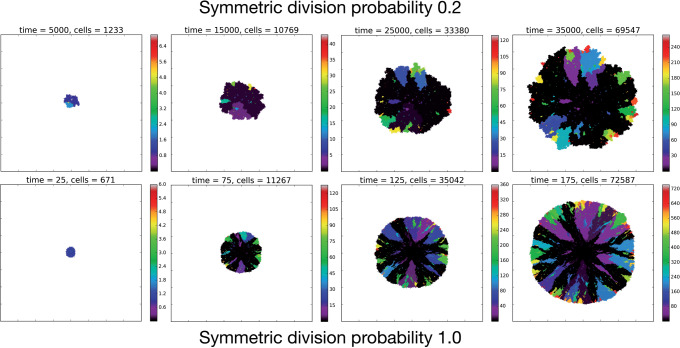
The full CA flowchart, represented in Figure 1c, schematizes the entire process of cell fate decisions that each cell undergoes at each time step in the spatial model. In the top panel, the rule set followed by the TICs is represented to include differentiation and mutation. In the bottom panel, the TAC rule set is defined to include death by terminal differentiation and TAC aging. An example simulation of tumor growth over time is shown in Figure 2, where the effect of lowering 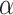can be seen on overall tumor growth kinetics, where the color-bar represents the current clonal state (mutation ID) of a given clone.

Figure 2.

Temporal evolution of the spatial model reveals observable morphologic differences between TIC-driven and non-TIC-driven tumors, as observed by others. We plot representative results of simulations of two tumors, each simulated on a square lattice of size 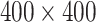. Top: a tumor simulated with 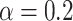and 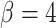. We notice, as have Enderling et al. (2009) and Sottoriva et al. (2010), a “patchy” clonal architecture, and nonuniform edge. Bottom: a tumor simulated with 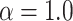, that is, no proliferative hierarchy. We note smooth edges, radial patterns of clonal architecture, and relatively faster population growth, reaching 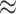70,000 cells in less than 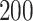time steps. To reach a similar size, the tumor with symmetric division probability of 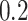took 35,000 time steps. Color bars denote number of mutations present in a given clone, note that the top scale is about 1/3 of bottom scale.

Recovering Phylogenetic Trees from Simulation

While experimentalists and clinicians can only infer phylogenies from incomplete data, reconstruction of the “true” phylogeny is possible in our model as we can record the entire life history of the simulated tumor. Thus, we can test whether phylogenetic tree-based measures are able to discriminate TIC symmetric division probability in the case where the “ground truth” is known. At each time step, we record the spatial location of each individual cell with its mutation ID, which is our CA state vector. Additionally, we record the evolutionary “life history” as a list of ordered pairs of every mutation event (parent mutational ID, child mutational ID). We then recursively construct the phylogenetic tree from this life history.

Phylogenetic tree reconstruction algorithm

To create the complete tree data structure required for our quantitative analyses, we use the information encoding the mutation events from our stochastic simulation. To this end, we create a list of unique parent–child pairs using the life history of mutation events. We then apply an iterative process in which each child is added as a subnode below the parent (from the unique parent–child pair). This process is continued until all parent–child pairs are added to the structure, and the tree is complete. The simulation code and functions to create these trees and calculate the metrics are freely available at https://github.com/cancerconnector/clonal_evolution.

Qualitative comparison of reconstructed trees

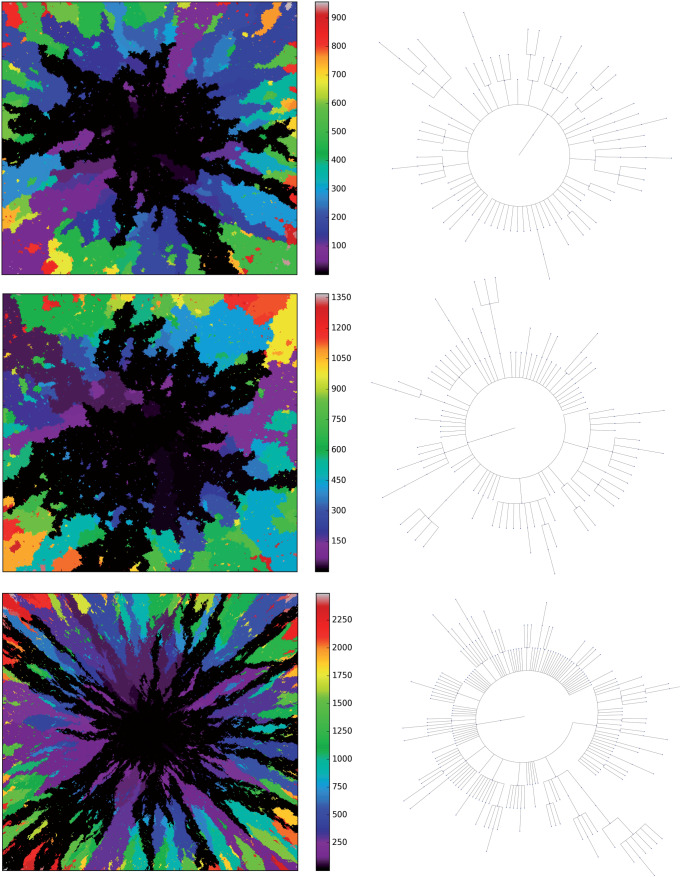
To compare phylogenies from simulations with different underlying parameter values, we first construct and visualize the phylogenies constructed from three example simulations with differing TIC symmetric division probabilities in Figure 3. It is clear by inspection that the number of mutations increases with symmetric division probability (more branches). However, the tree structure is not as easy to parse visually. For ease of visualization, the trees depicted in Figure 3 have been pruned of all terminal nodes (also called leaves) with no children of their own. While this transformation does affect the quantitative results, it does not qualitatively affect the resultant phylogenetic tree statistic ranks (see Figure 8 of Supplementary material freely available at https://github.com/cancerconnector/clonal_evolution). All analyses shown will utilize the full trees.

Figure 3.

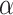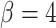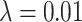Three example simulations with increasing symmetric division probability, (0.2, 0.6, and 1.0 from top to bottom) and their associated phylogenetic trees. Each example plot is the result of a single stochastic simulation of our spatial CA model. Each simulation is initiated with a single TIC and complete when the domain is full, in this case 250,000 cells. Parameter values are and . Visualized trees (right) have been pruned of all leaves for ease of visualization, which does not qualitatively affect measure rank (see Fig. 8).

Candidate Tree-Based Measures for Model Comparison

Visual inspection of Figure 3 suggests that simulations with different TIC symmetric division probabilities generate distinct phylogenetic trees. However, to draw meaningful conclusions we must perform a quantitative comparison. Here, we present several measures useful in summarizing and comparing phylogenetic trees. The most commonly studied property of a phylogenetic tree’s shape is its balance, defined as the degree to which internal nodes (branch points) have the same number of children as one another. Balance (or imbalance) indices depend only on the branching topology of trees, and not on other factors like branch length or other features of the terminal branches (leaves). Since the first balance index by Sackin (1972), many others have been proposed with slightly differing properties (Mir et al. 2013). One of the first papers to present a systematic comparison of a suite of balance indices (often denoted with the letter “B”) and indices of imbalance (denoted with “I”) was by Shao and Sokal (1990), who reported striking differences between the studies’ measures. Their central message was that different measures on trees can give insight into different aspects of the underlying processes governing the interactions, and one should thus consider several measures for any given tree or family of trees. In this study, we will consider several tree topology-based measures.

Before describing the measures, it is worthwhile to briefly define the terms which are used to describe trees, and the two basic underlying stochastic models which have been proposed to describe neutral evolution and the resulting topologies. Phylogenetic trees describe the evolutionary relationship between individuals with different traits from one another, or in the case of our model, different mutational combinations (genotypes). In our model, each simulation begins with a cell with mutation flag 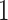, or a genotype with the first allele mutated (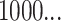), termed the “root,” and evolution progresses stochastically, by adding individual mutations at subsequent alleles and increasing the mutation flag, as described in Figure 1b. At each mutation event, an evolutionary branch point is created, which is termed a node in phylogenetic tree terminology. If this node gives rise to no other children during the simulation, it is termed a terminal node, or leaf. There are two common, classically referenced models, which bear mention here as well, since many tree topology-measures are normalized against them. The first, described by Yule (1925) and sometimes termed the “equal rate Markov” model, begins with a single root and proceeds by replacing, uniformly at random, a given leaf with a node with two children of its own. The process continues until the desired number of leaves exist. The other main model, termed the “Proportional to Distinguishable Arrangements” (PDA) or uniform model, was described by Rosen (1978). This model, which is truly a model of tree growth rather than an explicitly evolutionary process, begins as does the Yule model (and indeed ours) with a single node labeled 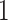. At each update step, a new leaf is added to the tree at any point, either internal node or leaf. These models will serve as normalization factors in several of the measures we present below, which are summarized graphically in Figure 4.

Figure 4.

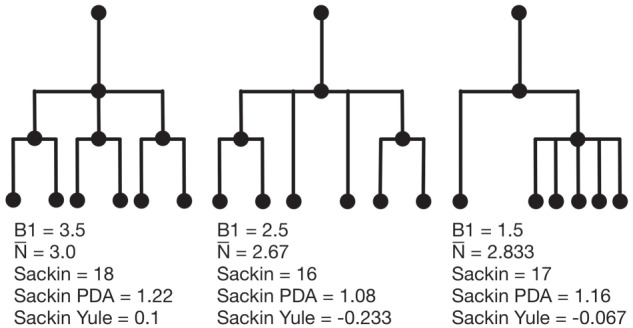
Example phylogenetic trees and their measures. From left to right the trees contain , 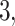and 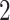internal nodes (dots) respectively, but the same number (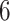) of terminal nodes.

Sackin index

The Sackin index was the first statistic used to understand the balance of a phylogenetic tree (Sackin 1972; Shao and Sokal 1990). To compute this statistic, one sums the number of ancestors (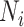) for each of the 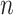terminal nodes of the tree:

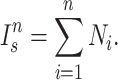(1)

This index increases with tree size: under the Yule growth model, its expectation 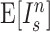grows as 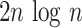(Yule 1925). One can therefore only perform a meaningful comparison of Sackin indices of trees generated from tumors if they are the same size.

Normalized Sackin index

To address this dependence on tree size, several normalizations to the Sackin index have been proposed, two of which we explore here. In particular, one can normalize the Sackin index of a phylogenetic tree to the expectation value of a similarly sized tree, under the Yule growth model:

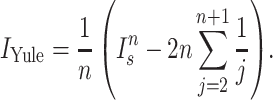(2)

One can alternatively normalize using the PDA model (Rosen 1978; Aldous 1996,2001) which is simply the Sackin index scaled by .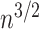

The B1 statistic

The B1 statistic, originally described by Shao and Sokal (1990), considers the balance of a tree. To calculate the measure, one uses all 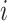internal nodes of the tree with the exception of the root (the founding cell). For each nonroot internal node 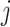, the maximum number of nodes traversed along the longest possible path to a terminal node, , is counted. The B1 statistic is then defined as

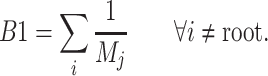(3)

The 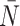statistic reports the average number of nodes above a terminal node. To compute this, we sum the path from each terminal node to the root, and divide by the number of terminal nodes. An alternative definition is the Sackin index “normalized” by the number of terminal nodes. We define this as

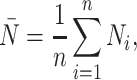(4)

where 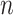is the number of tips and 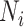is the number of internal nodes between tip 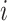and the root of the tree. For a more complete review and comparison of the measures presented here, and others, see Blum and François (2005) and Shao and Sokal (1990).

Examples of how these measures change on several example trees with equal numbers of leaves (but different numbers of internal nodes) are presented in Figure 4. (Note that in contrast with these polytomous trees, our tumor growth model does not exhibit polytomies, since all cell divisions are dichotomous and each node in the phylogenetic tree is defined by a unique mutation in an infinite sites model.) In these examples, we compute each of the presented measures for comparison. From left to right, the trees contain 4, 3, and 2 internal nodes, respectively, but the same number (6) of leaves. We note that the measures do not all follow the same pattern. For an exhaustive description of all possible trees with 6 leaves, and the correlation of a larger family of associated measures, see Shao and Sokal (1990).

Results

Measuring Trees from Simulation

As our primary goal is to identify whether tree-based measures allow discrimination of simulated tumors with different TIC symmetric division probabilities, we focus on changes in tree measures as we vary comparable simulations changing only this parameter. To compare the model tree measures, we first perform 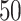stochastic simulations of both our nonspatial and spatial CA using a range of TIC symmetric division probabilities ( 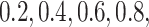and 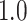), holding mutation rate and TAC lifetime constant ( 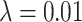and 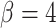). For each simulation, we construct the resulting phylogenetic tree at tumor size 250,000 cells, as described in the Materials and Methods section. We then measure the value of each summary index defined earlier for all 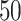simulations at the final time point and plot the distribution in a box-whisker plot, which is shown in Figure 5 with each data point overlaid in a swarm. Differences between distributions were determined using the Wilcoxon rank sum test. While these statistics were performed post hoc, we should note that standard statistics can be misleading for simulation based studies with arbitrarily large sample sizes (White et al. 2014) (see Figure 9 of Supplementary material freely available at https://github.com/cancerconnector/clonal_evolution for effect size).

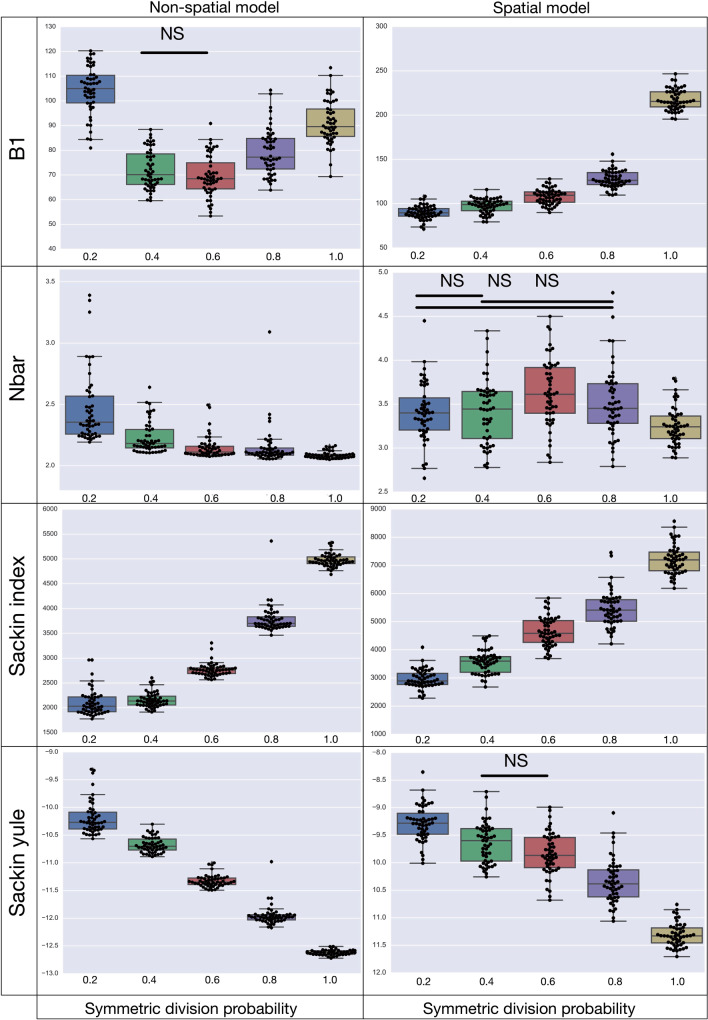
Figure 5.

A summary of four tree indices measured over a range of symmetric division probability. We plot the distribution of each of four measures of tree balance for the final resultant trees from 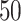simulations against symmetric division probability. All simulations were run with 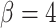and 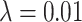until a tumor size of 250,000 cells was reached. In each plot, we display a box-whisker plot as well as the individual results as points. NS = nonsignificant by the Wilcoxon rank sum test.

Variation of Tree-Based Measures with Symmetric Division Probability

The results of the model are presented in Figure 5. We find that all of the indices have monotone relationships with symmetric division probabilities except for 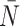in the spatial model, and B1 in the nonspatial model. Of note also, is that only in the Sackin index do we see qualitative agreement for the spatial and nonspatial models (monotone up/down) for both in the standard (normalized) Sackin model. This difference in utility of the different measures for the spatial and non-spatial models are not unexpected, as Shao and Sokal (1990) have previously shown that even for similar questions, different models of tree topology will have different uses. As our primary purpose is to understand the spatial cancer model, we will leave a deeper investigation into the dynamics of the nonspatial model for future work, and concentrate our analysis from here forward on the spatial model.

In terms of discernibility for the spatial model, of the normalized indices, the B1 statistic has the least overlap in error between symmetric division probabilities (i.e., comparing the cases 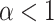with the case 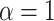). All measure distributions are significantly different by the Wilcoxon rank sum test (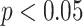) except 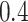and 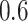in the Sackin index normalized by the Yule model (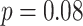). While we recognize the dangers in reporting p-values in simulation-based studies (White et al. 2014), we report them here for comparison, and report effect size as well, with full statistics for both the spatial and nonspatial model reported in Figure 9 of Supplementary material freely available at https://github.com/cancerconnector/clonal_evolution. The strongest effect for the spatial model is seen in the Sackin index (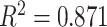), followed by the Yule normalized Sackin index ().

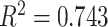Dynamics of Tree-Based Measures During Tumor Growth

As discussed in Materials and Methods, the measures considered here are strongly dependent on the total number of nodes in the tree. With all other parameters held constant, simply allowing a tumor to grow larger would increase the number of total mutations, and therefore the number of total nodes, subsequently altering the value of the measure. To ensure that the differences we have noted are robust to changing tumor size, we next consider how these measures evolve during the growth of a tumor.

To determine how these measures vary over the lifetime of a growing tumor, we measure each index over the course of multiple simulations. To accomplish this, we use the life history to reconstruct the phylogenetic tree at 20 equally spaced time points during the course of 50 simulations for each value of the symmetric division probability. Note that since the time taken for each simulated tumor to fill the spatial domain depends strongly on the symmetric division probability (see Figure 2), to compare “like for like” we break each life history into equally spaced time intervals, which act as surrogates for tumor size. Comparing across tumor size is of greater utility, clinically, since while the age of a given tumor is rarely known, size can be readily estimated.

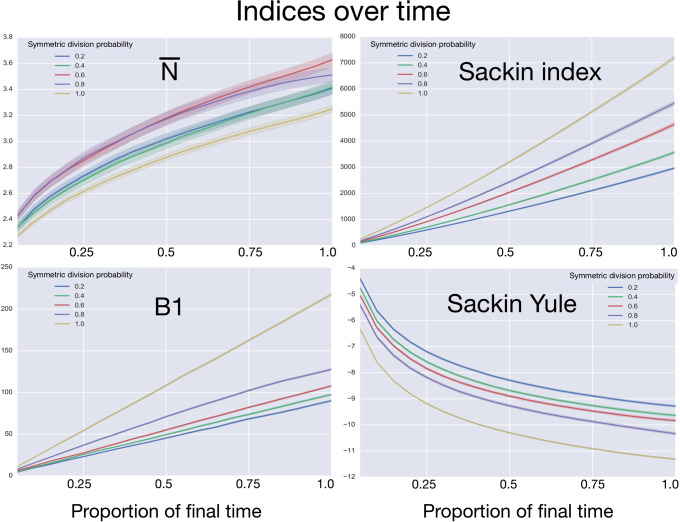
After reconstruction, we then create a “time” trace for each statistic. We plot these statistics over “time” in Figure 6, where each family of 50 simulations (for a given symmetric division probability) is represented by a single trace with the standard deviation represented by the colored error bars. We find that for each of the statistics, except 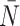, the relationships between the symmetric division probabilities are maintained over time, suggesting that, if we know the tumor size, and true phylogeny, we can estimate the relative symmetric division probability between two samples from these measures. This statement must be somewhat qualified by the fact that mutation probability was also held constant for these simulations. While estimating mutation probability is not trivial, significant advances have been made in measuring the speed of the “evolutionary clock” of tumors: essentially a proxy for mutation probability (Curtius et al. 2016). Further, we found that the rank order of each discriminatory measure holds throughout tumor growth, indeed becoming more discriminatory as the tumors grow larger (with the exception of 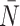). As the tumors simulated in this study are unrealistically small given the computational constraints, this information gives us hope that in tumors of realistic size, these measures would be even more useful. This becomes particularly important as the statistics that we have calculated come from the “true trees,” that is, trees comprised of all mutation events. In reality, trees would be inferred from the imperfect information gleaned from biopsies.

Figure 6.

Comparing phylogenetic tree measures across symmetric division probability through tumor growth. We plot the average and standard deviation (error bars) of four phylogenetic tree measures for each of the 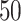simulations for a range of symmetric division probabilities over the course of tumor growth. Rank is maintained across symmetric division probabilities for each of the 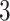tree measures with which we could discriminate between symmetric division probabilities. As before, 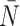is not predictive and changes rank throughout tumor growth. All tumors are grown to eventual confluence at 250,000 cells. In all simulations 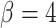and .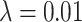

Dependence of Tree-Based Measures on Mutation Probability

As the tree measures depend heavily on the number of mutations within a given tumor, and therefore the number of branches within a given tree, we next ask how these measures behave when we vary mutation probability (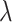) and symmetric division probability simultaneously. To answer this, we perform 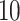stochastic simulations for each combination of the symmetric division probabilities considered previously and 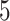different values for 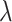varying over two orders of magnitude (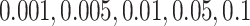), which spans most of the range (per cell per division) as noted by Alexandrov et al. (2013). We then use the previously described method to reconstruct the resulting phylogenies and calculate the measures previously discussed. In particular, we ask how the Sackin index, the B1 statistic and the normalized Sackin index perform over this range of 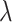to better understand the applicability of these measures in determining differences in symmetric division probability.

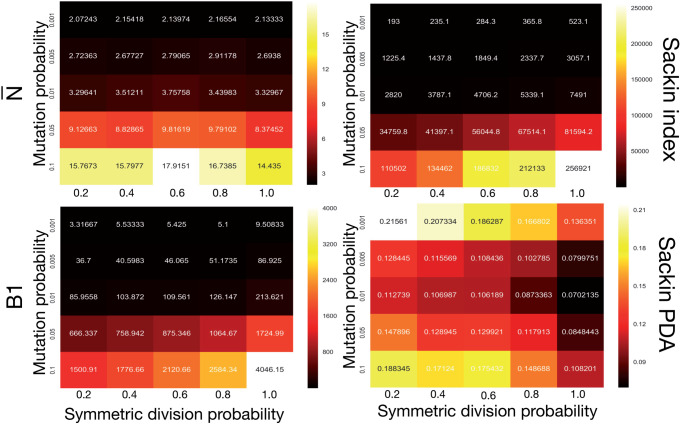
We plot the results of this parameter investigation in Figure 7. In each heat map, we plot the mean of the simulations for each parameter combination with symmetric division probability varied along the horizontal axis and mutation probability along the vertical axis. The indices which are not normalized by branch number, namely the Sackin index and B1 statistic, increase monotonically with mutation probability and symmetric division probability in all cases. The Sackin index normalized by the PDA model, however, varies somewhat unexpectedly and has a global minimum at symmetric division probability of 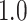and mutation probability 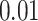. This measure is monotonic in symmetric division probability except at the highest mutation probability where it becomes somewhat more difficult to determine the differences. As before, the B1 statistic appears to be the most stable, and only breaks down slightly in its ability to distinguish between the families of simulations at the lowest mutation probability (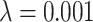) and the middle range of symmetric division probability (symmetric division probabilities 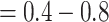), as can be seen in Figure 7. In these ranges of the parameter space, our model may not provide useful predictive power.

Figure 7.

Comparing phylogenetic tree measures across symmetric division probability and mutation probability. We plot the average of each of four phylogenetic tree measures at the end of each of 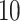simulations for a range of symmetric division probabilities and mutation probabilities. We vary mutational probability over two orders of magnitude (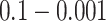), and simulate all tested symmetric division probabilities. Rank is maintained across symmetric division probabilities for each of the three of the four measures with which we could discriminate between symmetric division probabilities with changing mutation probability, allowing for differentiation between parameters. As before, the 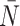statistic is not predictive. As expected, for the nonnormalized indices, Sackin, and B1, the measures change monotonically with both symmetric division and mutation probability. For the PDA normalized Sackin index, however, there is a global minimum for 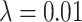and .

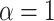Discussion

While the use of phylogenetic trees is increasing in translational oncology laboratories, there has yet to be a method found by which we can utilize the information clinically. To address this shortcoming, we worked to leverage the growing interest in biomarker derivation from spatially distinct tumor biopsies (Dhawan et al. 2016a), and the recent success of Leventhal et al. (2012) and others in teasing apart complex biological rules from phylogenetic information. We developed an individual-based model of tumor growth under a TIC-driven proliferative heterogeneity which undergoes neutral evolution. We then developed an algorithm to construct phylogenetic trees from simulated tumors. The resultant trees were then analyzed and compared using a suite of statistical measures of tree (im)balance. Through this method, we have generated a large data set that includes the observed statistical measures of the “true” phylogeny for tumors spanning the full range possible of symmetric division probabilities, which we feel is appropriate as symmetric division probabilities as low as 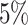have been reported in glioblastoma (Lathia et al. 2011) and as high as 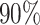have been reported in colorectal cancer (Baker et al. 2014). It is worth noting that, as our phylogenies are exact, some of the conclusions one may draw in the future from empirically inferred trees would have to be tempered by the inherent uncertainty in the inference process. Further, we are by no means the first group to seek to utilize simulation to study tree topology, with notable recent examples being INDELible, a flexible platform to simulation insertions and deletions (Fletcher and Yang 2009), as well earlier models of simulating neutral Wright–Fisher models (Hudson 2002).

In particular, we compared the classical measures of tree topology—the Sackin index and the B1 statistic—as well as normalized versions of each across several parameters of our spatial and nonspatial models as well as through the process of tumor growth. Not surprisingly, we found that the Sackin index was able to discriminate between the families of simulations as it is directly correlated with branch number (in this case correlating with total number of mutations in the TICs, which also is increased with increasing symmetric division probability). Encouragingly, we also found that the normalized version of this metric was able to discriminate between the different symmetric division probabilities, suggesting a more meaningful (and measurable) topological difference between the underlying phylogenetic trees resulting from these parameter changes (representing diverse biological traits).

While we have shown that these measures differ significantly from one another, we have not yet provided a method by which we can use the metric of a given tree to directly predict the symmetric division probability of an unknown tumor. However, the present work at least allows us to understand the rank order of symmetric division rate for two tumors given their measured indices. This could be particularly useful in certain clinical settings. For example, this could allow us to determine how a given therapy affects symmetric division probability by using our calculated measures over serial biopsies, and subsequent phylogenetic reconstruction. This could prove particularly useful in the treatment of leukemias, where the target cell is known to be the TIC, eradication of which is a requirement for cure (Roeder et al. 2006). In this case, after phylogenetic reconstruction using any of several methods available for single sample whole-genome sequencing (Carter et al. 2012; Roth et al. 2014; Deshwar et al. 2015), the tree topologies could be compared before and after therapy, giving a measure of relative change. Our metric (derived in this case from our nonspatial model results) could therefore prove a useful adjunct to existing methods of predicting TIC fraction (Werner et al. 2016) to determine therapeutic efficacy, and guide therapy breaks or switching.

Even with state-of-the-art multiregion sequencing approaches, most reconstructed cancer phylogenies are relatively small (Gerlinger et al. 2014; Zhao et al. 2016) with very few leaves, preventing the application of our statistical method in its current form. With continued advances in single-cell sequencing, and more examples of higher spatial sampling from larger tumors, like in the most recent TRACERx Renal study (Turajlic et al. 2018), the situation may change, but it is worth reiterating that this theory has not yet been shown to be quantitatively accurate in real tumor samples. Even in the case that it does not become effective in the near future, however, we assert that beginning to use metrics of tree topology to compare tumors before and after therapy, or across grade or survival, could prove useful to enhance our understanding of tumor evolution and treatment response in the near term.

Aiming towards a translatable method by which to infer the symmetric division probability in solid tumors, we have identified several phylogenetic tree-based measures that correlate with TIC symmetric division probability. We have found several measures which are able to discern differences in simulated tumors between symmetric division probabilities. These results are robust to changes in tumor size, specifically maintaining their rank throughout tumor growth. The rate of mutation does affect these results to some degree, but rank is maintained permitting comparison through time, or between tumors of similar size.

While there is some overlap amongst the measures when more than one parameter is varied, with information on mutation probability and tumor size, relative symmetric division probability can be estimated. We have restricted our focus to measures of (im)balance, a basic property of phylogenetic trees based only on their branching topology. With more information, such as evolutionary branch lengths (Kirkpatrick and Slatkin 1993; Mooers and Heard 1997) which are linked to the “speed” of a tumor’s molecular clock (Curtius et al. 2016), some of these limitations could be obviated. Further, we have only considered neutral evolution. While most tumor evolution is likely neutral (Williams et al. 2016), there is certainly evidence for nonneutrality in the form of driver and passenger mutations (McFarland et al. 2013,2017), which would drastically affect the resulting phylogenetic trees (Grenfell et al. 2004)—especially with intervening treatment regimens. How nonneutral evolution and treatment affect our measures remain avenues for future work.

Funding

This work was supported by a Vice-Chancellor’s Fellowship from the University of Sheffield to A.G.F. J.G.S. would like to thank the NIH Loan Repayment Program and the Paul Calabresi Career Development Award for Clinical Oncology (NIH K12CA076917) for their generous support. A.R.A.A. gratefully acknowledges funding from both the Cancer Systems Biology Consortium and the Physical Sciences Oncology Network at the National Cancer Institute, through grant nos. U01CA232382 and U54CA193489 as well as support from the Moffitt Center of Excellence for Evolutionary Therapy.