Hybrid Modeling of Ebola Propagation

Abstract

The Ebola virus disease (EVD) epidemic that occurred in West Africa between 2014–16 resulted in over 28,000 cases and 11,000 deaths - one of the deadliest to date. A generalized model of the spatiotemporal progression of EVD for Liberia, Guinea, and Sierra Leone in 2014–16 remains elusive. There is also a disconnect in the literature on which interventions are most effective in curbing disease progression. To solve these two key issues, we designed a hybrid agent-based and compartmental model that switches from one paradigm to the other on a stochastic threshold. We modeled disease progression with promising accuracy using WHO datasets.

I. INTRODUCTION

The Ebola virus disease (EVD) epidemic in the Western African nations of Sierra Leone, Liberia, and Guinea was the deadliest EVD epidemic to date. Between December 2013 and April 2016, the World Health Organization (WHO) reported more than 28,000 cases and 11,000 deaths. The time-scale from symptom onset to death is an average of 10 days in 50–90% of cases [1]. EVD can be transmitted through physical contact with bodily secretions, consuming infected meat, and touching contaminated objects [2]. Fruit bats are regarded as the reservoir host, which could directly infect humans or indirectly infect humans via primates [3]. One of the biggest gaps in research during an epidemic outbreak is to assess which interventions are most effective. For example, although the WHO now emphasizes safe and dignified burial practices as an essential component of good outbreak control, this was only well understood as the epidemic progressed [4], [5].

State-of-the-art network models are very realistic to reality, but are very computationally demanding and country specific, limiting generalizability [6]–[8]. Efforts to integrate network and compartmental models typically use a static threshold and the parameters of the compartmental model are usually over-fitted to the country of interest [9]–[11]. Further, there are existing hybrid models for molecular modeling, but these models have not been applied to model EVD [12]. We propose a novel hybrid model that addresses these issues by switching from an agent-based model to a compartmental model through the same stochastic threshold for Liberia, Guinea, and Sierra Leone. By doing so, we can generalize the model and identify which interventions can affect EVD propagation the most.

II. METHODS

A. Outbreak Data

A time series of cumulative reported EVD cases was collected from the WHO [5]. These patient data sets combine laboratory confirmed, suspected, and probable cases. There were 255 days recorded for a span of 3 years, roughly amounting to a reporting frequency of 1 in 4 days.

B. Threshold Determination

We created a simple stochastic threshold to switch between the agent-based model and compartmental model. In agreement with the gold standard [13] - switching when a certain number of individuals have been infected - we switched between the models when there were 9–20 cumulative cases. We found this range to be the most generalizable a posteriori to all three countries (mean=13.0, σ=3.2).

C. Agent-based Model Design

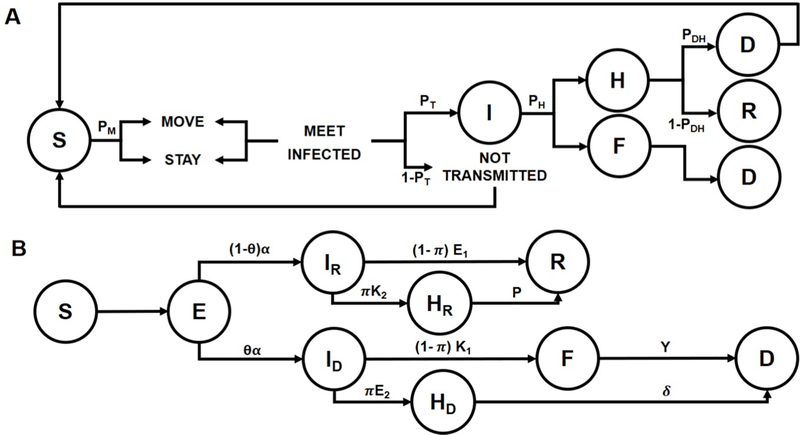
Our agent-based model (Fig. 1A) included six categorizations: Susceptible, Infected, Dead, Funeral, Hospital, and Recovered. The model was placed in a square bounded area, with a unitless width and height.

Fig. 1.

Hybrid agent-based model that combines an agent-based model and a compartmental model. A. The agent-based model consists of 6 compartments: Susceptible (S), Infected (I), Hospitalized (H), Recovered (R), Funeral (F), and Dead (D). Agents move based on probability thresholds to the 6 possible compartments. B. The compartmental model consists of 7 compartments, with Exposed (E) as the additional compartment. Individuals move through the different compartments based on a set of rates obtained from the literature or fitted on WHO data.

A single agent was assigned to be sick at t=0. They were assigned an incubation period on a log-normal distribution between 3–21 days [11] (a posteriori incubation period: mean=12.1; σ=5.8). At every time-step, representing a day, each agent in the system had a random value between 0 and 1 assigned to it. This value was compared against the likelihood of movement (PM ) to determine if the agent was to move, probability of transmission (PT ), probability of death without hospitalization (PDU ) or death with hospitalization (PDH ), and probability of seeking hospitalization(PH ). The values were obtained from compartmental EVD models in the literature: PDH and PH from Rivers et al. [14] and the rest from Hasenöhrl [15].

Researchers from the Bruno Kessler Foundation developed the agent-based model for the 2014 Liberia EVD outbreak that is most often regarded as the gold standard [16]. The foundations of their model is similar to ours, but the main difference is that they placed heavy emphasis on group exposure and transmission. Conversely, we only considered individual agents and focused more on modeling hospitalization and funeral transmissions. However, the gold standard agent-based model assumes that the death rate reduction from household protection kits would be the same as from safe funeral transmission, which seems unlikely given the abundant differences in these intervention approaches. We overcame this limitation by using different death rates from the literature [14] for those that die as a result of funeral transmission, die in a hospital, or die without hospitalization. Although the model we created is much simpler than the gold standard, we are only using the model for the beginning phases of the epidemic to obtain initial conditions for the compartmental model. On the other hand, the gold standard only uses an agent-based model for the entire simulation.

The following assumptions were made in our model:

• The scaling factor for the number of infected agents to the actual number of infected in each country is uniform.

• The mortality rates from the literature is assumed to be the same as in the beginning of the epidemic.

• Household transmission occurs at the same rate as community transmission.

D. Compartmental Model Design

We developed a compartmental model that is based on Hasenöhrl’s SEIHRFD model [15]. The model has seven compartments: (S)usceptible, (E)xposed, (I)nfected, (H)ospitalized, (F)uneral, (R)ecovered, and (D)ead. Susceptible and exposed individuals may transition to the infected compartment if they come into account with an infected individual. Our model separates the infected compartment into one that is destined to recover and one that is destined to die based on the a posteriori probability of survival. In reality, individuals may survive without hospitalization and individuals may also die without hospitalization. The model takes this into account by allowing individuals to transition straight to the recovered or to the funeral compartment respectively. Our model is different from Hasenöhrl’s because of our parameter inference strategy and the initial conditions used. A full schematic of the SEIHRFD model can be found in Fig. 1B.

The following assumptions were made in the model:

• The case fatality ratio is assumed to be equivalent to a mortality rate uniformly around 50%, even if they are hospitalized [14].

• The rate of infection and hospitalization between infected individuals who will recover or die is the same.

• The hospital compartment is infinitely big - there are no spatial restrictions.

• Every non-hospital deceased individual is buried following unsafe traditional practices.

• Those that recover are removed from the system, thereby implying no possibility of re-infection.

This is the system of ordinary differential equations that characterize our model:

$$\begin{array}{l}\frac{\text{d}S}{\text{d}t}=-\frac{1}{N}\left[{\beta }_{I_R}S{I}_R+{\beta }_{I_D}S{I}_D+{\beta }_{H_R}S{H}_R+{\beta }_{H_D}S{H}_D+{\beta }_{F}SF\right],\\ \frac{\text{d}E}{\text{d}t}=\frac{1}{N}\left[{\beta }_{I_R}S{I}_R+{\beta }_{I_D}S{I}_D+{\beta }_{H_R}S{H}_R+{\beta }_{H_D}S{H}_D+{\beta }_{F}SF\right]-\alpha E,\\ \frac{\text{d}{I}_R}{\text{d}t}=(1-\theta )\alpha E-(1-\pi ){ϵ}_1{I}_R-\pi {ϵ}_2{I}_R,\\ \frac{\text{d}{I}_D}{\text{d}t}=\theta \alpha E-(1-\pi ){\kappa }_1{I}_D-\pi {\kappa }_2{I}_D,\\ \frac{\text{d}{H}_R}{\text{d}t}=\pi {ϵ}_2{I}_R-\rho H_R,\\ \frac{\text{d}{H}_D}{\text{d}t}=\pi {\kappa }_2{I}_D-\delta H_D,\\ \frac{\text{d}R}{\text{d}t}=(1-\pi ){ϵ}_1{I}_R+\rho H_R,\\ \frac{dF}{dt}=(1-\pi ){\kappa }_1{I}_D-\gamma F,\\ \frac{dD}{dt}=\gamma F+\delta H_D.\end{array}$$

The SEIHRFD model was also decomposed into SEIHRD, SEIHR, SEIRD, and SEIR models. The different models will be compared to each other using the same parameters to examine the usefulness of adding certain compartments, in particular the hospitalized and funeral compartment as they are highly specific to the EVD outbreak of 2014–16.

E. Hybrid Model Parameter Optimization

1). Agent-based Model

Two parameters were varied when fitting the agent based model to the real data. The parameters modulated were the area of the model and the probability of movement for each agent. The accuracy of the model was calculated in each step and the best set of parameters were averaged between the set of 10 trials. We defined the best set of parameters as the global optima as opposed to steep cliffs - an indication of over-fitting. The averaging of 10 trials was done due to the high stochasticity of the agent-based model.

The final parameters are summarized in Table I.

TABLE I.

FINAL PARAMETERS FOR THE AGENT-BASED MODEL

Parameter	Guinea	Sierra L.	Liberia
Width/Height (w/h)	287	104	301
Prob. of Movement (PM)	0.67	0.60	0.41
Prob. of Transmission (PT)	0.70	0.70	0.70
Prob. of Death (No Hospital) (PDU)	0.70	0.70	0.70
Prob. of Death (Hospital) (PDH)	0.45	0.45	0.45
Prob. of Hospitalization (PH)	0.20	0.20	0.20

2). Compartmental Model

All the parameters that characterize the SEIHRFD model were simultaneously optimized by finding the minimum of the multivariate function. We performed the optimization for each model run for Sierra Leone (Table II) because of having the most number of cases to avoid over-fitting and finding local optima instead of global optima. The optimized parameters for Sierra Leone will serve to be our global optima. Subsequently, we used the optimized parameters from Sierra Leone and applied it to Liberia and Guinea to assess the performance of the model, and most importantly how generalizable our model is. Due to the stochasticity of the agent-based model, we ran 1000 runs of the model for each country in a Monte Carlo simulation.

TABLE II.

OPTIMIZED PARAMETERS FOR THE COMPARTMENTAL MODEL AND COMPARISON TO THE LITERATURE

Parameter	Symbol	Literaturea	Hybrid model (μ±σ)	Units
Population Size	N	4570	5454 ± 1026	People
Community Contact Rate - Infected to Recovered	βIR	0.128	0.158 ± 0.011	People−1 Days−1
Community Contact Rate - Infected to Dead	βID	0.128	0.159 ± 0.010	People−1 Days−1
Hospital Contact Rate - Hospitalized to Recovered	βHR	0.080	0.068 ± 0.004	People−1 Days−1
Hospital Contact Rate - Hospitalized to Dead	βHD	0.080	0.065 ± 0.005	People−1 Days−1
Funeral Contact Rate	βF	0.111	0.497 ± 0.051	People−1 Days−1
P. of Survival	1-ϑ	0.549	0.470 ± 0.038	N/A
Incubation Period	α−1	12.7	12.3 ± 2.1	Days
Infection to Recovery Duration	ε1−1	20.0	16.5 ± 1.4	Days
Duration until Hospitalization - Destined to Recover	χ2−1	4.12	3.66 ± 0.34	Days
Duration until Hospitalization - Destined to Die	ε2−1	4.12	3.51 ± 0.37	Days
Infection to Death Duration	χ1−1	10.4	14.3 ± 1.5	Days
P. of Seeking Hospitals	π	0.197	0.148 ± 0.025	N/A
Hospitalization to Recovery Duration	ρ−1	15.9	14.9 ± 1.1	Days
Hospitalization to Death Duration	δ−1	6.26	9.46 ± 0.60	Days
Duration of Traditional Burial	γ−1	4.50	1.88 ± 0.11	Days

^aLiterature values were obtained from compartmental EVD models [14], [15].

F. Performance Metric

The performance metric used for both the agent-based model and the compartmental model is based on the root-mean-squared error (RMSE).

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^n{\left(P_i-O_i\right)}^2}{n}}$$ (1)

$$Accuracy=100\mathrm{\%}\left(1-\frac{RMSE}{N}\right)$$ (2)

P is the predicted value from the model, O is the observed data from WHO datasets, and n is the number of data points. However, RMSE must be normalized to the total population N to be able to compare performance between the different countries. Hence, we will be using percentage accuracy as the population-independent performance metric. This metric is used because we can compare between the different models and with WHO data.

G. Intervention Effectiveness Analysis

After finding the median global optima (Table II) for each parameter through Monte Carlo simulations, several parameters were varied in 10% increments of their original values up to a total change of 70%. Only one parameter was modified at a time, while the others were kept the same with the median optimized parameters. Depending on what would be deemed as an intervention, some parameters were decreased in 10% increments (i.e. community contact rate) while some others were increased in 10% increments (i.e. probability of seeking hospitalization). Community contact rate and probability of movement were adjusted in order to simulate quarantine. Probability of transmission was modulated in order to simulate the introduction of a vaccine.

Probability of seeking hospitalization was modulated in order the simulate the setup of triage centers, either by local health care providers or by foreign aid. All of these modulations were done individually in both the compartmental and agent-based models. Additionally, funeral contact rates was also perturbed in the compartmental model. The number of infected at the end of each of these simulations were compared to the number of infected without any intervention to evaluate the effectiveness of the intervention strategy.

III. RESULTS

A. Model Validation

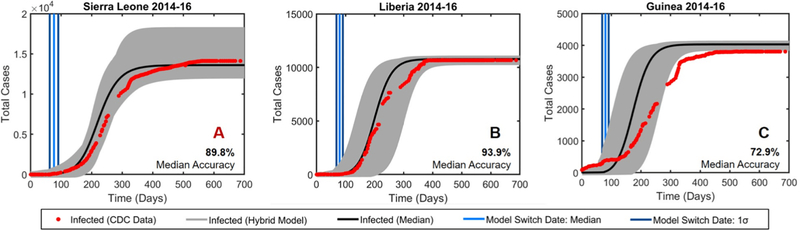
We ran a Monte Carlo simulation with 1000 runs using the final parameters from Table I for the agent-based part. The parameters for Sierra Leone in the compartmental model were optimized at each run to find global optima, whereas the parameters for Liberia and Guinea were taken from the median optimized parameters of Sierra Leone (Table II). The total population was assumed to be linearly scalable (N is 5454 and 2041 for Liberia and Guinea respectively).

Although the parameters were optimized for Sierra Leone, the hybrid model performed better for Liberia (Fig. 2B) than Sierra Leone (Fig. 2A) with an accuracy of 93.9% and 89.8% respectively. Liberia’s superior performance is most likely because the total number of infected reaches a steady state earlier in Liberia than in Sierra Leone, which would match the characteristics of the hybrid model more. However, Guinea (Fig. 2C) performed relatively poorly because the hybrid model is meant to start at t=0, but the WHO dataset for Guinea started when the cumulative number of cases was at 86.

Fig. 2.

Monte Carlo simulation (1000 runs) of the hybrid model. The grey region represents 100% of the simulations and the black line is the median output. The accuracy for each country was determined by comparing the median simulation outputs to WHO data. A. EVD propagation in Sierra Leone with parameter optimization to find global optima at every run. EVD propagation in Liberia (B.) and Guinea (C.) using the optimized parameters from Sierra Leone.

B. Comparison of Compartmental Models

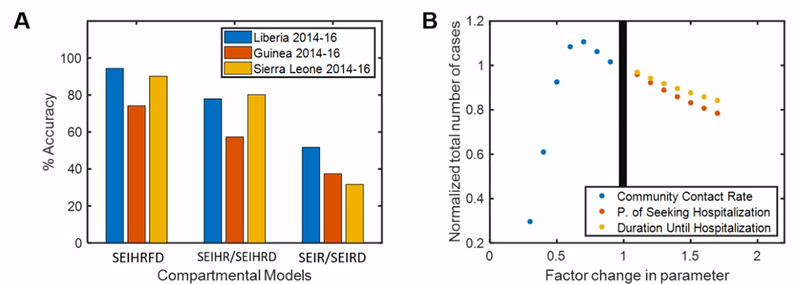
Our models suggest that adding more compartments improves performance (Fig. 3A). This study was done by using the median global optima parameters for each country. The average performance of the SEIHRFD model itself is around 87% across the three countries, which is better than the accuracy of 72% for the SEIHR/SEIHRD model and 35% for the SEIR/SEIRD model. Adding the funeral and hospitalized compartments improved the accuracy of the model by around 15% and 37% respectively. However, adding the dead compartment did not result in any significant changes to the model’s outputs, which is why we decided to group the SEIHR and SEIHRD models as well as the SEIR and SEIRD models. The agent-based model increases the overall accuracy by 4.6%.

Fig. 3.

A. Comparison of the different compartmental models using the median global optimized parameters. The models were compared to 2014–16 WHO data to evaluate the accuracy. B. Modifying the community contact rate, probability of seeking hospitalization, and time until hospitalization in 10% intervals shows that these parameters affect the total number of cases the most.

C. Intervention Effectiveness Analysis

Modifying the global optimized parameters of the compartmental model revealed which parameters affected the total number of cases the most (Fig. 3B). Against our expectations, decreasing the community contact rate initially resulted in a 10% increase in the total number of cases. After this initial peak, the total number of cases decreased by 70%, as expected. At a 70% increase in the probability of seeking hospitalization, the total number of cases decreased by 20%. The total number of cases decreased by 12% at a 70% increase in the rate of hospitalization. Therefore, our model suggests that improving quarantine (community contact rate) and access to hospitals (probability of seeking hospitalization and rate of hospitalization) could be the most effective interventions.

D. Parameter Sensitivity Analysis

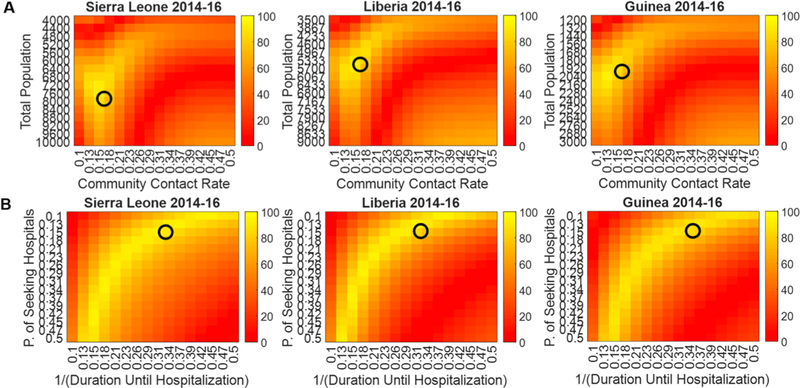
We used an inverse approach for the parameter sensitivity analysis. To demonstrate the generalizability of the hybrid model, we optimized the parameters for Sierra Leone in a Monte Carlo simulation to find the global optima, and then visualized the median global optimized parameters for all three countries in their respective heatmaps. The main purpose of this parameter sensitivity analysis is to demonstrate that our parameters are not over-fitted. We generated two sets of heatmaps: total population versus community contact rate (Fig. 4A) and probability of seeking hospitalization versus duration until hospitalization (Fig. 4B). We specifically chose these parameters because the community contact rate, probability of seeking hospitalization, and duration until hospitalization affected the total number of cases the most as shown in our intervention effectiveness analysis. Moreover, we assumed that the total population is linearly scalable. The heatmaps demonstrate that all four parameters are within the region of highest performance. As they are all not located in steep cliffs or isolated regions of high performance, the parameters are not local optima, but rather global optima. Hence, the heatmaps demonstrate that the parameters may be generalizable.

Fig. 4.

Heatmaps showing the generalizability of the hybrid model with the median global optimized parameters from Sierra Leone(black circle). The performance metric is accuracy (0–100%). The median global optimized parameters from Sierra Leone is shown to also be within the region of highest accuracy in Liberia and Guinea. There are no steep cliffs visible in any of the heatmaps, which suggests that our parameters are not over-fitted. A. Heatmaps varying the total population and community contact rate. B. Heatmaps varying the probability of seeking hospitalization and duration until hospitalization.

IV. DISCUSSION

We developed a novel hybrid model for the 2014–16 EVD outbreak that is generalizable to Sierra Leone, Liberia, and Guinea. Our solution resolves a large modeling gap in the literature, in that existing models have country-specific parameters and therefore of limited scalability. Although this is a good feature, in which there are some epidemiological parameters that are country independent (i.e. length of incubation period), there are also others that are related to cultural practices and therefore specific to a country (i.e. probability of hospitalization, duration until hospitalization). We wanted to demonstrate that a general model is possible, albeit with probably some compromises in accuracy over a country-specific model. With our model, we demonstrated that optimizing our parameters in a Monte Carlo simulation of 1000 runs for the country with the highest number of cases resulted in parameters that were generalizable to other countries as well. This was demonstrated when modeling Liberia, achieving an accuracy of 93.9%. One of the major limitations is that the WHO dataset did not start at t=0 for Guinea, and as a result the performance of the hybrid model when applied to Guinea cannot be fairly considered. One clear improvement is to run the hybrid model on other countries with more complete datasets. We also met our second endpoint: identifying the most effective interventions to curb disease progression. Firstly, it was clear that adding hospitalization and funeral compartments have a large impact on the effectiveness of a model, so improving data collection methods for hospitalization and funeral data on the ground should be a priority of community health workers in future epidemics. Secondly, it was found that reducing the community contact rate and increasing access to hospitalization had a large impact on disease propagation. As quarantine is the physical equivalent through which the community contact rate could be reduced, our model therefore suggests that a viable method for curbing disease progression is by improving quarantine practices. However, considering the impact of contact tracing and population engagement are not easily accounted for in our model. In accordance with our modeling findings, an epidemiological study [17] underscores that the lack of access to hospitalization in both urban and rural areas was a major proponent of EVD propagation. Hospitals readily closed down after admitting EVD patients for decontamination, but in the process restricted susceptible individuals from the most basic of healthcare needs, and this in turn may have caused even more deaths than if access to healthcare was maintained [17].

Perhaps the biggest limitation in the methodology is that our optimized parameters do not match the literature values closely. This is because our model is under-constrained due to data availability. Parameters such as mortality rate and the population could be fixed, and we could have rather focused on more of the sociological parameters (i.e. community contact rate). The literature values could have also deviated from our parameters because the models were based on Liberia 2014, whereas our model is optimized for Sierra Leone between 2014–16. The easiest way to rectify this issue is to optimize our model for Liberia 2014 data, but performing this optimization is incongruent with the purposes of this study. Assuming that all of the out-of-hospital deaths are unsafe funerals may have overestimated the rate of burials, as not all families necessarily practice the same religious practices.

An inherent limitation of the WHO dataset we used is that situation reports document cases when reported or confirmed, but not when an individual is originally infected. Albeit a minor one, there is an intrinsic phase delay in the hybrid model because we want to model the cases from the day of symptom onset. This limitation does not affect our results significantly. Two strategies for further exploration would be important to prioritize. Firstly, there is room for improvement in refining the simulation. Although we were limited by the ability of the computers the team had access to, usage of a computer able to process a greater amount of information would allow the team to increase the size of the model in a variety of metrics, which could help improve its accuracy. Due to computational limitations, we only ran Monte Carlo simulations for the overall hybrid model, but it would have also been useful to do so when modifying the different parameters of the compartmental model. The agent-based simulation could also be refined by implementing more complex network dynamics, such as household transmissions. In addition, the stochasticity of the agent-based model prevented us from using the overall hybrid model for the intervention effectiveness analysis, but only the compartmental model. A potential solution could be reducing the range for the random number generator, or adding weights to certain potential options for the random generator, as this generator is what creates the stochasticity in the parameters used in this model. Additionally, improvements could be made in the threshold selection process, which dictates when the model switches from agent-based to compartmental modeling. The current method switches over on the same stochastic threshold for all three countries, but we cannot justify that the chosen threshold maximizes the accuracy of the model. Ideally, we should also perform a threshold sensitivity analysis for all three countries to choose one common threshold.

Although the model has been shown to be accurate for the total number of cases of EVD in all three countries, we did not examine if this was also the case for the total number of deaths. An immediate point for further exploration is to ensure that the hybrid model performs equally well for modeling the total number of deaths over time. Furthermore, the hybrid model is somewhat limited in the spatial aspect. There are currently no parameters in the model that allow us to also investigate how human mobility patterns between the countries affect disease propagation. As a single infected airline passenger traveling from Liberia to Nigeria was linked to 894 contacts and 20 EVD cases in Nigeria, it can be inferred that disease transmission of EVD and other epidemics through airports would be very dangerous due to the high relative disease transmission in airports relative to the overall disease transmission in a country [18], [19]. Therefore, it would be useful to have an airport subsystem as part of the larger hybrid model and allow exchange between the two.