OpenGraphGym: A Parallel Reinforcement Learning Framework for Graph Optimization Problems

Abstract

This paper presents an open-source, parallel AI environment (named OpenGraphGym) to facilitate the application of reinforcement learning (RL) algorithms to address combinatorial graph optimization problems. This environment incorporates a basic deep reinforcement learning method, and several graph embeddings to capture graph features, it also allows users to rapidly plug in and test new RL algorithms and graph embeddings for graph optimization problems. This new open-source RL framework is targeted at achieving both high performance and high quality of the computed graph solutions. This RL framework forms the foundation of several ongoing research directions, including 1) benchmark works on different RL algorithms and embedding methods for classic graph problems; 2) advanced parallel strategies for extreme-scale graph computations, as well as 3) performance evaluation on real-world graph solutions.

Introduction

Solving graph optimization problems effectively is critical in many important domains, including social networks, telecommunications, marketing, security, transportation, power grid, bioinformatics, traffic planning, scheduling, and emergency preparedness. However, many of the graph optimization problems are in the class of NP-hard problems, and require exponential time algorithms to search for optimal solutions. Due to the exact graph algorithms’ exponential time complexity, practical approaches most often use either approximation algorithms or heuristic algorithms to tackle big graphs. The approximation algorithms are of polynomial time (if they do exist), but in theory can be several times worse than the optimal solutions. The heuristic algorithms are fast, but do not have the same guaranteed solution quality as that of approximation algorithms. Also, heuristic algorithms typically require experts’ knowledge, insights, and repeated redesigns to create efficient heuristics.

Instead of devising different heuristics for different graph problems and distinct graph datasets, we aim to utilize machine learning techniques to “learn” effective heuristics automatically. Since 2016, a few researchers have started to design reinforcement learning and deep learning methods to solve combinatorial optimization problems [4, 11–14, 16, 22]. The rational behind it is that graphs from the same application domain or similar types are not totally different from each other; they may have similar structures and are often solved repeatedly. Hence, it can be beneficial to use machine learning to generalize the methods or heuristics to find near optimal solutions.

To investigate different deep reinforcement learning methods, and design new domain-specific graph embeddings to capture graph features, we design and implement an open source AI environment to allow users to rapidly plug in and test new RL algorithms and graph embeddings for graph optimization problems. The new open source RL framework, named OpenGraphGym, is targeted at achieving both high performance and high quality of the computed graph solutions. Our work has the following contributions. 1) We design and create an extensible framework for generic graph problems. A suit of NP-hard graph problems and graph embedding methods can be added into our framework conveniently. Our framework can also be used to benchmark several RL algorithms for graph optimization problems. 2) Our distributed RL framework can utilize multiple GPUs. 3) Case study shows that our framework can help to provide better solutions for Minimum Vertex Cover problems (a classic NP-hard graph problems).

In the remainder of the paper, we will first introduce the related work, then describe how to convert (or map) conventional graph problems to RL problems in Sect. 3. In Sect. 4, we will present the OpenGraphGym framework design and implementation details. A case study of using OpenGraphGym to solve the Minimum Vertex Cover problem with different types of graphs will be shown in Sect. 5. Finally, Sect. 6 will present our conclusions and future work.

Related Work

Reinforcement learning (RL) was commonly used in the field of playing games [17, 20, 21]. Recently, researchers started to investigate if RL can be used to help solve NP-hard graph problems. Based on the observation that knowledge learned from some problem instances can be applied to a similar type of problem instances, Dai et al. [11] created an end-to-end RL model that combines graph embedding and the objective Q function to tackle NP-hard graph problems. In their work, the solution is built by incrementally adding vertices. They studied the Minimum Vertex Cover, the Maximum Cut, and the Traveling Salesman problems by applying the Q-learning algorithm. Meanwhile, their results also proved that the strategy learned by the smaller size of graphs could be applied to the larger size of graphs. Bello et al. [4] also applied RL to graph optimization problems. However, they focused on euclidean Travelling Salesman Problems (TSP), and their methods cannot be applied to other graph problems conveniently.

Besides RL methods, researchers have also employed supervised machine learning methods to solve graph problems. Li et al. [12, 14] applied the Graph Convolution Network (GCN) to find multiple solutions in one step, then used a tree search model to select the best solution. The labeled SATLIB dataset [10] was used to train their GCN model. Another similar work was done by Mittal et al., who also used GCN to generate multiple solutions [16]. However, instead of using tree search, they took advantage of RL to select the best solution. In addition, Vinyals et al. applied a neural network architecture called pointer network to address graph combinatorial optimization problems [22]. The following study by Kool et al. modified the pointer network by introducing an attention-based encoder-decoder model and applied it to the TSP problem [13].

Compared to the existing work, our project targets creating an open AI framework that is optimized for solving big graph optimization problems. The major differences are as follows. First, our OpenGraphGym framework is an open environment, in which additional graph embedding methods, different RL algorithms, and new graph problems can be plugged in and tested rapidly. Second, OpenGraphGym is designed to be a high performance computing solution that can support distributed GPU systems. By contrast, the existing work is either constrained to a very small subset of graph problems, or works on shared-memory systems only. Third, the end-to-end learning approach realized in OpenGraphGym follows the line of research done by Dai et al. [11], but we extend it with new parallel GPU computing algorithms and a distinct software design and implementation using Tensorflow [1] and Horovod [19].

Methodology

In this section, we describe how to apply RL to solve graph optimization problems, which involves processing input graphs, reducing graph problems to RL problems, and executing RL training and testing.

Graph Processing for Reinforcement Learning

In conventional RL applications such as Atari games [17], input data are typically represented as matrices. For instance, pixel images may be taken as input to train deep neural network (DNN) models.

To handle graphs, an intuitive way is to feed a graph’s corresponding adjacency matrix to DNN models. It is feasible. However, there are two major issues: 1) It requires a lot of memory space to train a DNN model due to graphs’ large dimensions; 2) The successfully trained model only works for the graphs that have the same number of vertices as that of the training graph. To solve the issues, we use the technique of graph embedding, which is currently an active research area [5]. In brief, graph embedding can take a graph or vertex as input, then produce a p dimension vector that represents the useful information of the graph or vertex. Here, the dimension of p is predefined by users.

In our current implementation, we support two graph embedding of structure2vec [6] and node2vec [8]. Other graph embedding methods can be added to OpenGraphGym by extending certain classes. In Sect. 4.3, we explain how to add a new graph embedding method to OpenGraphGym.

Reinforcement Learning Formulation

In reinforcement learning, an agent and an environment interact with each other repeatedly in every step. For each step, the agent will take an action, then the environment will provide the agent with a reward and the old and new states. Eventually, the RL process will stop at a special “finished” state, which is called the 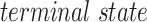. The above sequence of steps until terminal state is called an episode.

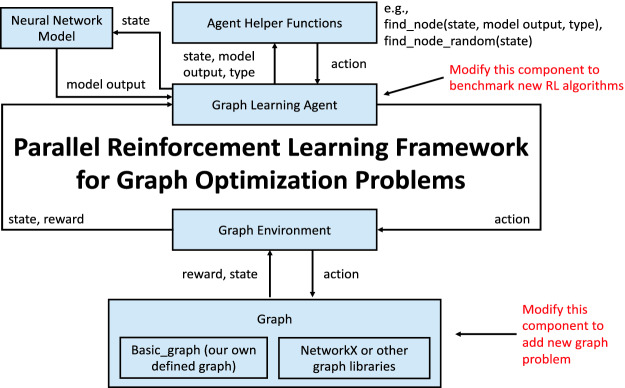
Figure 1 shows the architecture of our OpenGraphGym framework. In the framework, the Graph Learning Agent takes an action by selecting and adding the “best” node to the graph problem’s partial solution. Then, the Graph Environment returns the reward. The reward is used to justify the quality of a solution. It varies for different graph problems. More details of the framework will be introduced in Sect. 4.1.

Fig. 1.

The OpenGraphGym framework architecture.

For different types of graph problems, there are different formulations for the graph problem’s RL algorithm. For instance, an RL algorithm for a distinct graph problem may have a new representation of state, a problem-specific action, and a redefined reward.

As an example, Table 1 shows two graph problems’ states, actions, termination states, and rewards. The graph problems of the Minimum Vertex Cover (MVC) and the Maximum Cut (MAX) are defined briefly as follows:

• Minimum Vertex Cover (MVC): Given an undirected graph, find the smallest subset of nodes to cover all the edges.

• Maximum Cut (MAX): Given an undirected graph, a subset of nodes S, assume the cut set is the set of edges that only has one end in S, find S with the largest weight of the cut set.

Table 1.

Examples of NP-hard graph problems that are defined in RL algorithms

Problem	State	Action	Reward	Termination
MVC	Subset of nodes selected as the partial solution	Add a new node to the partial solution	Number of nodes used to cover all edges at the end of the episode	All edges are covered
MAX	Subset of nodes selected as the partial solution	Add a new node to the partial solution	Cut set weight at the end of the episode	Cut set weight cannot be improved

In Table 1, we can observe that the state and the action for MVC and MAX are same. However, the reward and the termination varies. As to MVC, the reward and the termination are related to the number of edges. As to MAX, the reward and termination are related to the cut set weight. Note that although we pick two NP-hard graph problems, our framework can be extended to solve more graph optimization problems.

Graph-RL Training and Testing Algorithms

In the previous Sect. 3.2, we have introduced how to formulate a graph RL algorithm. The next step is to train and test the model. In this section, we will summarize the algorithm of training and testing.

As shown in Algorithm 1, we will first initialize the experience replay memory buffer and the objective Q function (lines 2–4). Then, for each episode, we will select a random graph from the distribution D (line 6). One distribution of graphs include graphs generated using the same model and parameters. Next, we will initialize three sets of vertices (lines 8 and 9). Two of them (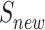 and 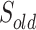) are for the solution. 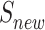is a set of vertices that includes all the nodes which have been selected as the solution in the current step. 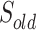is a set of vertices that includes all the nodes which have been selected as the solution in the previous step. Another one (C) is for the candidate nodes. A temporary replay buffer is also initialized (line 10). At each step, the agent will either randomly or according to a policy to select a node 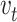from the candidate nodes set C (line 12). Then, we will update the solution sets 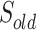and 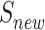(lines 13–16). Meanwhile, 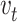will also be removed from the candidate nodes set C. 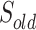, 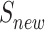and the selected node 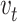will be combined and be added to the temporary replay buffer 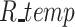. Tuples in the temporary buffer will be pushed to the replay buffer R when we finish one episode (lines 19–20). At each step, we will also update the objective function Q by sampling a batch of tuples from the replay buffer R.

After we have trained an RL agent successfully, we can utilize the trained agent to find solutions to a set of new unseen graphs afterwards. Such an algorithm is called an RL Testing algorithm. The RL Testing algorithm is nearly the same as the training algorithm Algorithm 1 except for two differences: 1) Only the best candidate node will be selected every step (in line 12), and 2) the RL agent will not update the objective function (in line 17).

Design and Implementation of OpenGraphGym

This section presents 1) the main components of our framework, 2) how we design the framework to support parallel computing on multiple GPUs, and 3) how to extend the framework to support new graph optimization problems and graph embedding methods. Our code can be found at https://github.com/zwj3652011/OpenGraphGym.git.

Main Software Components

As shown in Fig. 1, OpenGraphGym has five main components, which are described as follows:

• Graph Learning Agent: It is the agent that is responsible for reinforcement learning for graph problems. It constantly receives input from three other components: the Neural Network Model, the Agent Helper Functions, and the Graph Environment. The Neural Network Model provides DNN model output (e.g., Q values), the Agent Helper Functions provides actions, and the Graph Environment provides states and rewards. On the other hand, the Graph Learning Agent also sends information to the three components constantly.

• Neural Network Model: It defines the graph embedding function and the RL agent’s DNN model. During RL training, the Neural Network Model takes a graph state as input and produces a Q value. The Q value will be sent to the Agent for making decisions. In the current implementation of OpenGraphGym, we use the deep network Q-learning (DQN) method. Our next work will add the support of other RL methods such as A2C and A3C.

• Agent Helper Functions: It is a set of functions that are used by the RL agent to compute its appropriate action. By receiving the parameters of states, models outputs and graph problem types, the helper functions computes the action needs to be taken by checking the model output and the graph problem type. Please note that the Agent Helper Functions varies for different graph problems. In our framework, we include the Agent Helper Functions for some graph problems.

• Graph Environment: The Graph Environment is the interface between the Graph and the Graph Learning Agent. Action, reward and state will be transferred through it. For example, when the action is received from the Graph Learning Agent, the Graph Environment will call the function step to send the action to the component Graph. Then, it will receive the state and the reward from the component Graph. Finally, it will push the state and the reward to the Graph Learning Agent.

• Graph: It is a graph object implemented by our framework. Each graph object stores a set of graph-related information (e.g., number of nodes, number of vertices). Currently, our framework supports two types of graph objects. In the Basic Graph, we store the node lists, edge lists, number of nodes, and other basic information of a graph. Another one is defined by the networkX graph library [9]. NetworkX will read graph objects from edgelist files. The Basic Graph object is more flexible and can be extended by the user. If users cannot find a metric of graphs in networkX or other graph libraries, they can define and add their metrics to the Basic Graph object.

In general, the above components can be classified into two categories. The first category is designed to support for the agent part in RL, which includes the first three components. The Graph Learning Agent works as the interface between them. The second category is designed to support the environment part, for which the Graph Environment is the interface of them.

Furthermore, our framework is designed to be modular. By modifying a couple of components, it can be extended to support new graph embedding methods, RL algorithms, and graph optimization problems. For example, if a user desires to study another graph problem, the user needs to modify the Graph component to do it. In Sect. 4.3, we will show more details about it.

Parallel Implementation Using Multiple GPUs

The OpenGraphGym framework is able to support RL training on multiple GPUs. The following content describes how we distribute the workload and compute the graph RL in parallel among multiple GPUs.

• Parallel Setup and Initialization: Our framework will launch n processes given a number of n available GPUs. One CPU and one GPU will be mapped to one process. Inside each process, we create an instance of Graph Learning Agent and an instance of Graph Environment. Each Graph Learning Agent has its own copy of the global DNN model (i.e., a single model but duplicated multiple times on multiple GPUs), as well as a private RL replay buffer. At the beginning of the parallel execution, we use the distributed deep learning framework Horovod [19] to ensure each agent’s DNN model will be initialized with the same weights.

• Exploring Graphs in Parallel: We use an asynchronous algorithm to let each process explore training on different graphs in parallel. At the start of each episode, every process will select a random graph from all the training graphs based on their unique random seeds. At the end of the episode, each process will then push its experience tuples to its own replay buffer. Note that all the training graphs are generated automatically by our framework.

• Computing Gradients: In the previous step, each process has started to explore graphs asynchronously. Then, at the end of every step, as shown in Algorithm 1, line 16, each process needs to sample some tuples from their replay memory buffer and compute the gradients. Assume the batch size is b and we have n processes, each process will sample b/n tuples and compute the averaged gradients of b/n tuples. Thus, each process will have one gradient. Finally, all processes’ gradients will be averaged. We use the distributed deep learning framework Horovod [19] to finish the gradient computing. Horovod will accomplish two major tasks in this step: 1) add a barrier to wait for all processes to finish the gradient computing, and 2) average all processes’ gradients and broadcasts it to them.

• Updating Model: In the previous step, all processes have received the averaged gradients. Then, each process needs to update their DNN model using the new gradient, as shown in Algorithm 1, line 17. Please note that all processes’ DNN models are still the same after updating for the following two reasons: 1) DNN models are initialized to be the same, and 2) the gradients used to update the DNN models are identical for all processes.

Please note that the above operations are not executed in the same frequency. As shown in the Algorithm 1, the agent’s DNN model will be updated in each step. Hence, the operations of Computing Gradients and Updating Model will be called every step. Moreover, in each episode, a new graph will be explored. Therefore, the operation of Exploring Graphs will be called every episode.

Framework Extensibility

In this section, we demonstrate the extensibility of our framework from two perspectives: 1) how to support other graph optimization problems, and 2) how to add new graph embedding methods.

Now, we use an example to show to extend OpenGraphGym to support other graph optimization problems. In the case of adding the Max Cut problem (MAX), we need to modify the Graph component as shown in Fig. 1. More specifically, two functions will be modified, which are: 1) the environment constructor (function __init__ in graph.py), and 2) the step function (function update_state in graph.py). In the environment constructor, we need to add a new local variable to represent the cut set weight inside the environment initialization function. In the step function, we then calculate the MAX-specific cut set weight to decide the termination state and the corresponding reward. Table 1 shows the definitions of the reward and termination state for the MAX graph problem.

To demonstrate how to add the new graph embedding method, we will use an example of adding the node2vec embedding method. Node2vec is a graph embedding method aiming at preserving each node’s neighborhood information [8]. We use the open-source node2vec library Node2Vec in our framework [18]. Two functions needs to be modified in the Graph component are 1) the environment constructor (function __init__ in graph.py), and 2) the step function (function update_state in graph.py). As to the environment constructor, we need to set up the node2vec model using the APIs provided by the Node2Vec library. As to the step function, we need to reset and update the node2vec model when the graph is modified.

A Case Study on Minimum Vertex Cover (MVC)

To evaluate the performance and accuracy of the OpenGraphGym framework, we compare the solution found by our RL framework with that of other classical solvers on the MVC problem. In addition, we did experiments to show the improved convergence rate by utilizing multiple GPUs.

Experimental Setting

The software and hardware configurations for all our experiments are provided as follows.

Software: To implement OpenGraphGym, we use Horovod version 0.16.4 to compute DNN gradients in a distributed setting, as mentioned in Sect. 4.2. Horovod can help with our distributed training by doing the following three tasks: 1) initialize each agent’s DNN models to be the same, 2) add a barrier for multiple processes gradient computing, and 3) average the gradients from all processes and broadcast it to them. We also use Tensorflow version 1.12.0 [1], graph library networkX version 2.4 [9], and the HPC environment toolkit Docker version 18.09.2 [15]. Tensorflow is responsible for the agent’s neural network training and inference. As for networkX, we use it to generate, manipulate, and evaluate different graphs. As to Docker, we create an environment using Docker and install all required libraries of our framework. Then, we can deploy the environment conveniently to a new HPC system. Docker helps us to manage the software and libraries used in our framework.

Graph Datasets Used: Our graph datasets contain two types of graphs, which are generated by two different distributions or random graph generation models. In the following content, we will present how graphs are generated using them. We will also present the parameter values we set for each model.

• Erdős-Rényi (ER) Graphs: The Erdős-Rényi model will generate a random graph with the graph size m and the edge possibility r [7]. We use the function erdos_renyi_graph in networkX to generate different sizes of ER graphs. The edge probability is set to 0.15, which means every possible edge has the possibility of 0.15 to exist.

• Barabási-Albert (BA) Graphs: The Barabási-Albert model generate the random graph based on the graph size m and the edge density d [2]. Edge density d is equal to the number of edges from a new node to the existing nodes. We use the function barabasi_albert_graph in networkX with the edge density of 4 to generate BA graphs.

Computer System: We use an Nvidia DGX workstation to do all experiments, which consists of 40 CPU cores and 4 Volta V100 GPUs. More details of the system is provided in Table 2.

Table 2.

An Nvidia DGX System.

CPU	Intel Xeon CPU E5-2698 v4 2.20 GHz
GPU	Nvidia Volta V100
Number of CPU Cores	40
Number of GPUs	4
Memory per GPU	16 GB
Operating System	Ubuntu
OS Version	16.04.6

Others: In addition, we use the learning rate 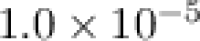and batch size 128 to train our DNN model. The RL parameter exploration rate 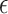is set to 0.1. The size of the RL replay buffer is set to store up to 50,000 experience tuples.

Quality of Graph Problem Solutions

To evaluate the quality of our graph solutions, we compare the results generated by five different MVC solvers:

• Graph-RL: This is our RL framework of OpenGraphGym.

• Random: The Random solver finds a solution by randomly taking a node from the graph in each step.

• 2-OPT: The 2-OPT approximation algorithm takes both endpoints of an edge from the graph in each step. Its solution is guaranteed to be less than twice of the optimal solution [3].

• Greedy: The Greedy algorithm builds the solution by simply adding the node with the largest degree in each step.

• Exhaustive Search: For the verification purpose, we also implement a “brute-force” random search MVC solver. We let this program continuously search for large numbers of solutions until no better solution could be found in one hour.

In our validation experiment, we use 40 graphs to train the RL agent, and use 10 graphs to test the agent. The 10 test graphs has never been seen by the agent during training. Note that the training graphs and test graphs belong to the same type of graphs: either ER or BA type.

Table 3 shows four different datasets used in our experiments (one dataset per row), each with different average number of nodes and edges in the ER or BA type. In the table, the graph type, average number of vertices and edges are shown in the first three columns. The best two solutions are also highlighted in a bold font.

Table 3.

Experiments with MVC on both ER and BA graphs. All MVC solutions shown here are averaged over 10 testing graphs. Five solvers (Graph-RL, Random, 2-OPT, Greedy, Exhaustive Search) are compared. The best two solutions are highlighted in bold for each dataset. Graph-RL is the solution obtained by our OpenGraphGym framework.

Graphs	Avg#nodes	Avg#edges	Graph-RL	Random	2-OPT	Greedy	Exhaustive search
ER	20	30.1	10.1	17.8	15.2	16.3	9.4
BA	20	64	11.4	18	16.2	16	12
ER	50	190.4	33.2	48	45	47.4	36.4
BA	50	184	28.8	48	41.8	46	34.3

As to the ER graph dataset with 20 nodes, the exhaustive search algorithm obtains the best solution with 9.4. Our Graph-RL algorithm is the second-best with 10.1. As to the BA graph dataset with 20 nodes, our solver is the best one with MVC size 11.4. The second-best is the exhaustive search algorithm with the best MVC size 12. For the rest of the solvers, the 2-OPT and the Greedy are similar, whose solutions are around 15 and 16. Finally, the random method produces the worst solutions for both ER and BA graphs.

We also use ER and BA graph datasets that have 50 nodes for training and testing. As shown in the two rows at the bottom of Table 3, our Graph-RL solver always found the best MVC solutions.

Based on the above comparison, we can say that our Graph-RL solver and the exhaustive search solver are constantly better than the other three solvers. In addition, the quality of the Graph-RL solutions is comparable to that of the long-time exhaustive searching algorithm.

Deploying an Agent Trained by Small Graphs to Test Bigger Graphs

The DNN model implemented by our framework can support graphs with various sizes. This feature enables us to train and test graphs with distinct sizes. To test the generalization performance of our model, we train the model on smaller size of graphs first. Then, we test the learned model using larger size of graphs.

The new experimental results are shown in Fig. 2. For this experiment, we use a dataset with 40 ER graphs that have an average number of 20 nodes for training. However, we use a dataset of 10 ER graphs that have a number of 50 nodes for testing. For every 20 episodes of training, we use the 50-node testing dataset to test the model’s solution quality. From Fig. 2, we can observe that after around 75 episodes, the average number of nodes to cover the test graph dataset reaches 34.8, which is close to the exhaustive search algorithm’s solution. This result demonstrates that an RL agent trained from small graphs can be generalized to solve larger size graphs.

Fig. 2.

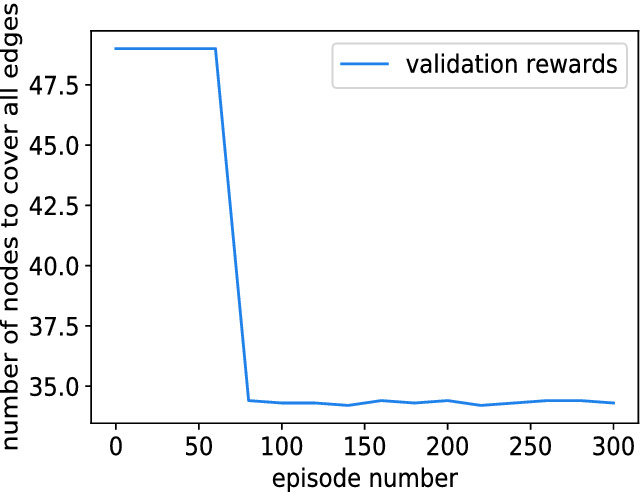
Generalization ability test. 40 graphs with 20 nodes are used to train the model. At every 20 episodes, the model will be tested using 10 graphs with 50 nodes.

Effect of Using Multiple GPUs

Finally, we use multiple GPUs to accelerate the RL training process with our OpenGraphGym framework. In the experiment, the training dataset has 40 ER graphs and the test dataset has 10 ER graphs. All the training and testing graphs have an average number of 20 nodes. Also, we evaluate the trained RL model’s solution with the test graph dataset in every episode.

As shown in Fig. 3, the blue line represents the MVC solutions computed by a single GPU. The orange line represents the solutions computed by four GPUs. From the figure, we can observe that when we use one GPU, our framework can find the best solutions after 80 episodes. By contrast, the framework takes only 62 episodes to find the best solutions when using four GPUs. This experiment shows that our RL framework is able to find the best solution of a problem by taking fewer episodes (i.e., converging faster) when more GPUs are used.

Fig. 3.

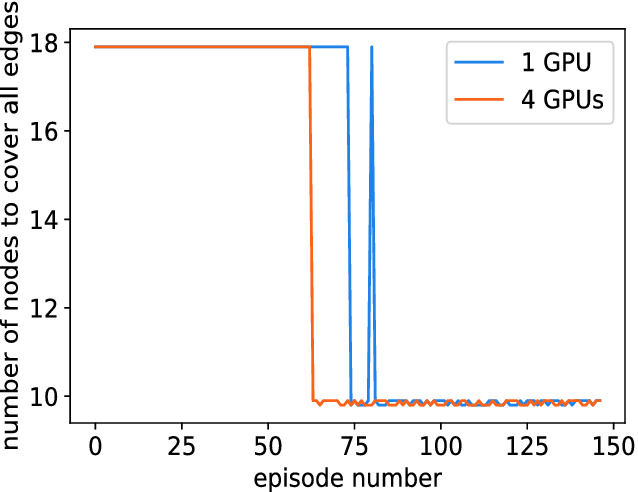
In this set of experiments, we use multiple GPUs for training on ER graphs with 20 nodes. The orange line is for the testing results with four GPUs. The blue line is for the results with one GPU. (Color figure online)

Conclusion

In this work, we design and implement a parallel reinforcement learning framework OpenGraphGym for graph optimization problems. Then, we use the MVC as the test case to demonstrate that the solution provided by our framework is better than some classical MVC solvers. This work focuses on three research directions: 1) We aim to use the open framework to benchmark various new RL algorithms and embedding methods. 2) Many real-world graphs are extreme-scales. We will add the support of extreme-scale graphs to our framework. 3) Currently, we only support a few basic parallel strategies. To better utilize the high performance computing resources, we will extend the OpenGraphGym framework to design more advanced and efficient parallel strategies.