Abstract
After mating, female mosquitoes need animal blood to develop their eggs. In the process of acquiring blood, they may acquire pathogens, which may cause different diseases in humans such as malaria, zika, dengue, and chikungunya. Therefore, knowing the parity status of mosquitoes is useful in control and evaluation of infectious diseases transmitted by mosquitoes, where parous mosquitoes are assumed to be potentially infectious. Ovary dissections, which are currently used to determine the parity status of mosquitoes, are very tedious and limited to few experts. An alternative to ovary dissections is near-infrared spectroscopy (NIRS), which can estimate the age in days and the infectious state of laboratory and semi-field reared mosquitoes with accuracies between 80 and 99%. No study has tested the accuracy of NIRS for estimating the parity status of wild mosquitoes. In this study, we train an artificial neural network (ANN) models on NIR spectra to estimate the parity status of wild mosquitoes. We use four different datasets: An. arabiensis collected from Minepa, Tanzania (Minepa-ARA); An. gambiae s.s collected from Muleba, Tanzania (Muleba-GA); An. gambiae s.s collected from Burkina Faso (Burkina-GA); and An.gambiae s.s from Muleba and Burkina Faso combined (Muleba-Burkina-GA). We train ANN models on datasets with spectra preprocessed according to previous protocols. We then use autoencoders to reduce the spectra feature dimensions from 1851 to 10 and re-train the ANN models. Before the autoencoder was applied, ANN models estimated parity status of mosquitoes in Minepa-ARA, Muleba-GA, Burkina-GA and Muleba-Burkina-GA with out-of-sample accuracies of 81.9±2.8 (N = 274), 68.7±4.8 (N = 43), 80.3±2.0 (N = 48), and 75.7±2.5 (N = 91), respectively. With the autoencoder, ANN models tested on out-of-sample data achieved 97.1±2.2% (N = 274), 89.8 ± 1.7% (N = 43), 93.3±1.2% (N = 48), and 92.7±1.8% (N = 91) accuracies for Minepa-ARA, Muleba-GA, Burkina-GA, and Muleba-Burkina-GA, respectively. These results show that a combination of an autoencoder and an ANN trained on NIR spectra to estimate the parity status of wild mosquitoes yields models that can be used as an alternative tool to estimate parity status of wild mosquitoes, especially since NIRS is a high-throughput, reagent-free, and simple-to-use technique compared to ovary dissections.
Introduction
Evaluation of existing malaria control interventions such as insecticide-treated nets (ITNs) and indoor residual spraying (IRS) relies upon, among other factors, the assessment of the changes occurring in the mosquito parity structure prior to and after implementation of an intervention [1–3]. The parity status of mosquitoes corresponds with their capability to transmit Plasmodium parasites, with an assumption that parous mosquitoes are more highly capable than nulliparous mosquitoes, as they may have accessed parasite-infected blood. A shift in the parity structure towards a population with more nulliparous mosquitoes signifies a reduction in the risk of disease transmission [2, 4, 5], as the chances that mosquitoes carry the malaria parasite declines [6].
The current standard technique for estimating the parity status of female mosquitoes involves dissection of their ovaries to separate mosquitoes into those that have previously laid eggs, known as the parous group (assumed to be old and potentially infectious), and those that do not have a gonotrophic history, known as the nulliparous group (assumed to be young and non-infectious) [7]. Another standard technique also based on the dissection of ovaries determines the number of times a female mosquito has laid eggs [8]. However, both techniques are laborious, time consuming, and require skilled technicians. These technical difficulties lead to analysis of small sample sizes that often fail to capture the heterogeneity of a mosquito population.
Near infrared spectroscopy (NIRS) complimented by techniques from machine learning, have been demonstrated to be alternative tools for predicting age, species, and infectious status of laboratory and semi-field raised mosquitoes [9–20]. NIRS is a rapid, non-invasive, reagent-free technique that requires minimal skills to operate, allowing hundreds of samples to be analyzed in a day. However, the accuracy of NIRS techniques for predicting the parity status of wild mosquitoes has not been tested. Moreover, recently, it has been reported that models trained on NIR spectra using an artificial neural network (ANN) estimate the age of laboratory-reared An. arabiensis, An.gambiae, Aedes aegypti, and Aedes albopictus with accuracies higher than models trained on NIR spectra using partial least squares (PLS) [20].
In this study, we train ANN models on NIR spectra preprocessed according to an existing protocol [9] to estimate the parity status of wild An. gambiae s.s. and An. arabiensis. We then apply autoencoders to reduce the spectra feature space from 1851 to 10 and re-train ANN models. The ANN model achieved an average accuracy of 72% and 93% before and after applying the autoencoder, respectively. These results suggest ANN models trained on autoencoded NIR spectra as an alternative tool to estimate the parity status of wild An. gambiae and An. arabiensis. High-throughput, non-invasive, reagent free, and simple to use NIRS analyses compliment the limitations of ovary dissections.
Materials and methods
Ethics approvals
Ethics approvals for collecting mosquitoes in Minepa-ARA, Burkina-GA and Muleba-GA datasets from residents’ homes were obtained from Ethics Review Boards of the Ifakara Health Institute (IHI-IRB/No. 17–2015), the Colorado State University (approval No. 09-1148H), and the Kilimanjaro Christian Medical College (Certificate No. 781), respectively.
Data
We use data from wild An. arabiensis (Minepa-ARA) collected from Minepa, a village in southeastern Tanzania (published in [21] and publicly available for reuse), from wild An. gambiae s.s (Muleba-GA) collected from Muleba, northwestern Tanzania (mosquitoes published in [22], permission to reuse was obtained from the senior author) and from wild An. gambiae s.s collected from Bougouriba and Diarkadou-gou villages in Burkina Faso (Burkina-GA) (published in [12] and publicly available for reuse).
Mosquitoes in the Minepa-ARA and Muleba-GA datasets were captured using CDC light traps placed inside residential homes. Mosquitoes that were morphologically identified as members of the Anopheles gambiae complex were processed further. Prior to scanning, wild mosquitoes collected in Minepa were killed by freezing them for 20 minutes in a freezer that is calibrated to -20º C. After freezing the mosquitoes were re-equilibrated to room temperature for 30 minutes. Wild mosquitoes collected in Muleba were killed using 75% ethanol, dissected according to the technique described by Detinova [23] to determine their parity status, and preserved in silica gel. Mosquitoes in Minepa-ARA were dissected after scanning. Following a previous published protocol to collect spectra [9], mosquitoes in both Minepa-ARA and Muleba-GA were scanned using a LabSpec 5000 near-infrared spectrometer with an integrated light source (ASD Inc., Malvern, UK). After spectra collection, mosquitoes in Minepa-ARA were dissected to score their parity status. Then polymerase chain reaction (PCR) was conducted on DNA extracted from mosquito legs (in both Minepa-ARA and Muleba-GA) to identify species type as previously described [24]. Each mosquito was labeled with a unique identifier code linking each NIR spectrum to parity dissection and PCR information.
Data from wild An. gambiae s.s from Burkina Faso were published in [12] and publicly available for reuse. These mosquitoes are referred to as independent test sets 2 and 3 (ITS 2 and ITS 3) in [12]. ITS 2 has 40 nulliparous and 40 parous mosquitoes, and ITS 3 has 40 nulliparous and 38 parous mosquitoes. In this study, we combine these two datasets into one dataset and refer it as Burkina-GA. Mosquitoes in Burkina-GA (N = 158) were collected in 2013 in Burkina Faso from Bougouriba and Diarkadou-gou villages using either indoor aspiration or a human baited tent trap, and their ovaries were dissected according to the Detinova method [23]. Mosquitoes were preserved in silica gel before their spectra were collected using a LabSpec4i spectrometer (ASD Inc., Boulder, CO, USA).
Model training and testing
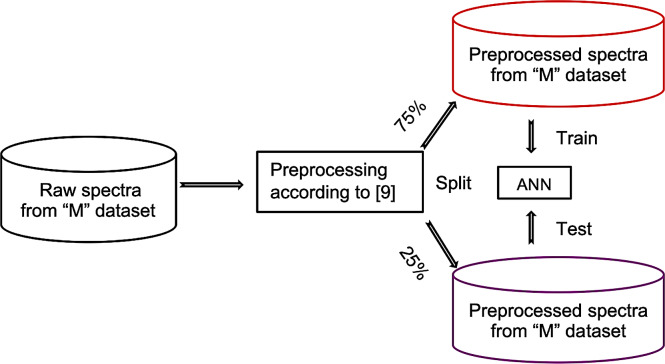
We trained models on four datasets, namely Minepa-ARA, Muleba-GA, Burkina-GA, and Muleba-Burkina-GA (Muleba-GA and Burkina-GA combined). Before training models, spectra in all datasets were pre-processed according to the previously published protocol [9] and divided into two groups (nulliparous and parous). Spectra in the nulliparous and parous groups were labeled zero and one, respectively. The two groups were then merged, randomized, and divided into a training set (75%; N = 927 for Minepa-ARA, N = 140 for the Muleba-GA, N = 158 for Burkina-GA and N = 298 for Muleba-Burkina-GA) and a test set (the remaining 25% in each dataset). On each dataset, using ten Monte-Carlo cross validations [20, 25] and Levenberg-Marquardt optimization, a one hidden layer, ten-neuron feed-forward ANN model with logistic regression as a transfer function was trained and tested in MATLAB (Fig 1).
Fig 1. Training and testing ANN model on spectra preprocessed according to Mayagaya et al. [9].
“M” is either Minepa-ARA, Muleba-GA, Burkina-GA, or Muleba-Burkina-GA.
Based on the accuracy of the model presented in Table 1 in the Results and Discussion section, we explored how to improve the model accuracy. Normally a parous class, unlike a nulliparous class, often is represented by a limited number of samples, posing a problem of data imbalance during model training. In this case, a large amount of data is required to obtain enough samples in a parous class for a model to learn and characterize it accurately. Obtaining enough data for model training is always challenging. The most common ways of dealing with the data imbalance are either to discard samples from a nulliparous class to equal the number of samples in a parous class or to bootstrap samples in a parous class [26]. However, discarding data to equalize the data distribution in two classes in the training set leaves an imbalanced test set. Also, it is this imbalanced scenario to which the model will be applied in real cases. In addition, throwing away samples, especially from data sets with a high dimension feature space, can lead to over-fitting the model. Alternatively, for datasets with a high dimension feature space, instead of discarding data from a class with a large number of samples, feature reduction techniques are employed [26]. Feature reduction reduces the size of the hypothesis space initially presented in the original data, thereby reducing the size of data required to adequately train the model. Principal component analysis (PCA) and partial least squares (PLS) are the commonly used unsupervised and supervised feature reduction methods, respectively, especially for cases whose features are linearly related [27, 28]. Autoencoders recently are used as an alternative to PCA in cases involving both linear and non-linear relationships [29–32].
Table 1. Accuracies of reconstructing original feature spaces from encoded feature spaces.
MSE = mean square error.
| Metric | Steps | Encoded-Minepa-ARA | Encoded-Muleba-GA | Encoded-Burkina-GA |
|---|---|---|---|---|
| MSE | Step 1 | 0.0046 | 0.0029 | 0.0031 |
| Step 2 | 0.00005 | 0.0027 | 0.0022 | |
| Step 3 | 0.00008 | 0.0029 | 0.0011 |
An autoencoder is an unsupervised ANN that learns both linear and non-linear relationships present in data and represents them in a new reduced dimension data space (which also can be used to regenerate the original data space) without losing important information [33–35]. The autoencoder has two parts, the encoder part, where an original dataset is encoded to a desired reduced feature space (encoded dataset) and the decoder part where the encoded dataset is decoded to an original dataset to determine how accurately the encoded dataset represents the original dataset. Fig 2 illustrates an example of an autoencoder in which an 1850-feature dataset is stepwise encoded to a 10-feature dataset. There is no formula for the number and size of steps to take to get to a desired feature size. However, taking several steps results on losing very little information, compared with taking a single step.
Fig 2. Autoencoder reducing feature space dimension.
Once an encoded feature space can reconstruct the original feature space with an acceptable accuracy, the decoder is detached, and a desired model (in our case an ANN binary classifier) is trained on the encoded feature space as shown in Fig 3.
Fig 3. ANN model trained on a dataset with an encoded feature space.
Egg laying appears to be affected by both linear and non-linear relationships. Hence, we separately train autoencoders on the Minepa-ARA, Muleba-GA, Burkina-GA, and Muleba-Burkina-GA datasets to reduce spectra feature dimensions from 1851 to 10 (Fig 4).
Fig 4. Reducing spectra feature space using an autoencoder and re-constructing original feature spaces from their respective encoded feature spaces (reconstruction accuracies presented in Table 1).
Figures generated from MATLAB.
Table 1 presents accuracies of reconstructing original feature spaces from their respective encoded feature spaces. We refer to the autoencoded Minepa-ARA, Muleba-GA, Burkina-GA, and Muleba-Burkina-GA datasets as Encoded-Minepa-ARA, Encoded-Muleba-GA, Encoded-Burkina-GA, and Encoded-Muleba-Burkina-GA, respectively. We then train ANN models on Encoded-Minepa-ARA, Encoded-Muleba-GA, Encoded-Burkina-GA, and Encoded-Muleba-Burkina-GA (Fig 5).
Fig 5. Training and testing of ANN model on autoencoded spectra.
M is either Minepa-ARA, Muleba-GA, Burkina-GA, or Muleba-Burkina-GA dataset.
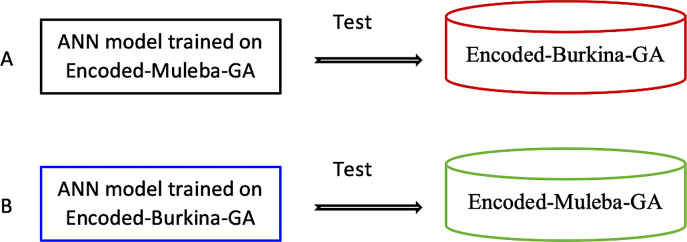
Finally, we used the Encoded-Burkina-GA and the Encoded-Muleba-GA datasets as independent test sets to test accuracies of ANN models trained on the Encoded-Muleba-GA dataset and on the Encoded-Burkina-GA dataset, respectively (Fig 6A and 6B).
Fig 6. Independent testing of ANN model trained on encoded datasets.
A) Applying an ANN model trained on the Encoded-Muleba-GA dataset to estimate the parity status of mosquitoes in the autoencoded Burkina-GA dataset. B) Applying the ANN model trained on the Encoded-Burkina-GA dataset to estimate the parity status of mosquitoes in the Encoded-Muleba-GA dataset.
Results and discussion
In this study, we demonstrated that near-infrared spectroscopy (NIRS) can estimate accurately the parity status of wild collected An. arabiensis and An. gambiae s.s. Referring to the published results in [11] (ANN models achieve higher accuracies than PLS models), we trained and tested an ANN model on NIRS spectra in four different datasets, pre-processed according to a previously published protocol [9]. The model achieved accuracies between 68.7 and 81.9% (Table 2, Figs 7 and 8). Table 2 further presents various metrics to score the performance of our classifiers, namely sensitivity, specificity, precision, and area under the receiver operating characteristic (ROC) curve (AUC). We calculated sensitivity, specificity, precision and accuracy of the model using Equs 1, 2, 3, and 4, respectively [36–39]. Sensitivity (also known as recall) is the percentage of correctly predicted parous mosquitoes, specificity is the percentage of correctly predicted nulliparous mosquitoes [20], and precision is the proportion of true parous mosquitoes out of all mosquitoes estimated by the model as parous [39]. We presented both sensitivity and precision because different scholars prefer one metric to another especially for cases with imbalanced data [39].
Table 2. Performance of an ANN model trained on 75% of mosquito spectra with 1851 features (before autoencoder) and tested on the remaining 25% spectra (out of the sample testing).
AUC values are the area of the ROC curves in Fig 8. Minepa-ARA (Nulliparous = 656, Parous = 271), Muleba-GA (Nulliparous = 119, Parous = 21) Burkina-GA (Nulliparous = 80, Parous = 78).
| Minepa-ARA (N = 927) | Muleba-GA (N = 140) | Burkina-GA (N = 158) | Muleba-Burkina-GA (N = 298) | |
|---|---|---|---|---|
| Accuracy (%) | 81.9 ± 2.8 | 68.7 ± 4.8 | 80.3 ± 2.0 | 75.7 ± 2.5 |
| Sensitivity (%) | 79.7 ± 3.2 | 37.8 ± 6.6 | 76.5 ± 2.1 | 70.2 ± 3.1 |
| Specificity (%) | 86.0 ± 1.6 | 80.1 ± 2.7 | 88.3 ± 2.3 | 77.6 ± 2.9 |
| Precision (%) | 74.3 ± 3.4 | 31.3 ± 5.2 | 77.8 ± 1.8 | 68.8 ± 3.2 |
| AUC (%) | 77.2 | 55.9 | 83.6 | 76.4 |
Fig 7. Box plots of parity estimation score when ANN models trained on 75% of spectra before the autoencoder was applied and tested on the remaining spectra (25%) (out of the sample testing).
A, B, C, and D represent results for the Minepa-ARA, Muleba-GA, Burkina-GA, and Muleba-Burkina-GA (mosquitoes in Muleba-GA and Burkina-GA datasets combined) datasets, respectively.
Fig 8. ROC curves (AUCs presented in the last row of Table 2) showing results when ANN models trained on 75% of spectra before the autoencoder was applied and tested on the remaining spectra (25%) (out of the sample testing).
A, B, C, and D represent results for the Minepa-ARA, Muleba-GA, Burkina-GA, and Muleba-Burkina-GA (mosquitoes in Muleba-GA and Burkina-GA datasets combined) datasets, respectively. In each ROC curve, a threshold of 0.5 was used to compute true positive rate and false positive rate.
Let
True Positive (TP) = Number of mosquitoes correctly classified by the model as parous,
False Positive (FP) = Number of mosquitoes wrongly classified by the model as parous,
True Negative (TN) = Number of mosquitoes correctly classified by the model as nulliparous,
Positive (P) = Total number of mosquitoes in test set that are parous, and
Negative (N) = Total number of mosquitoes in test set that are nulliparous.
Then
| (1) |
| (2) |
| (3) |
| (4) |
AUC was computed from the receiver operating characteristic (ROC) curve shown in Fig 8 generated by plotting the true parous rate against the false parous rate at different threshold settings. A higher AUC is interpreted as higher predictivity performance of the model [40, 41]. The ROC curve normally presents the performance of the model at different thresholds (cut off points), providing more information on the accuracy of the classifier [40, 41]. Table 3 provides confusion matrices from the last (tenth) Monte-Carlo cross validation showing model accuracy in absolute values.
Table 3. Confusion matrices showing accuracies of the models in absolute values when the models were trained on spectra before feature reduction by autoencoder.
A) Minepa-ARA, B) Muleba-GA, C) Burkina-GA and D) Muleba-Burkina-GA. Results from the last Monte-Carlo cross validation.
| Actual Parity | ||||
|---|---|---|---|---|
| Estimates | Nulliparous | Parous | Total | |
| Nulliparous | 165 | 17 | 182 | |
| A | Parous | 31 | 61 | 92 |
| Total | 196 | 78 | 274 | |
| Nulliparous | 28 | 4 | 32 | |
| B | Parous | 8 | 3 | 11 |
| Total | 36 | 7 | 43 | |
| Nulliparous | 20 | 6 | 26 | |
| C | Parous | 4 | 18 | 22 |
| Total | 24 | 24 | 48 | |
| Nulliparous | 46 | 9 | 55 | |
| D | Parous | 14 | 22 | 36 |
| Total | 60 | 31 | 91 | |
We hypothesized that results presented in Tables 2 and 3, and in Figs 7 and 8 were influenced by the size of a dataset used to train the model. The model that was trained on a dataset with a relatively larger number of mosquitoes, especially in the parous class, performed better than the model trained on the dataset with fewer mosquitoes.
The current standard preprocessing technique [9] leaves a mosquito spectrum with an 1851- dimensional feature space. Mathematically, binary inputs with a 1851-dimensional feature space present hypothesis space dimensions for the model to learn [42–44]. Successful learning of such hypothesis space dimensions requires many data points (mosquitoes in our case). Finding enough wild mosquitoes, especially parous mosquitoes, for a model to learn such a hypothesis space is expensive and time consuming. Feature reduction is an alternative to overcome this, as it reduces the hypothesis space dimension initially presented by the original data, hence lowering the number of data required to train the model efficiently. Techniques such as principal component analysis (PCA) [27, 28], partial least squares (PLS) [27, 45, 46], singular value decomposition (SVD) [30, 46, 47], and autoencoders can reduce a feature space to a size that can be learned by the available data without losing important information. PCA, PLS, and SVD are commonly used when features are linearly dependent [27, 28], otherwise, an autoencoder, which can be thought as a nonlinear version of PCA, is used [29–32].
Therefore, we applied an autoencoder as illustrated in Figs 2 and 4 to reduce the spectra feature space from 1851 features to 10 features (Table 1 presents the accuracies of reconstructing original feature spaces from the encoded (reduced) feature spaces), cutting down the hypothesis space dimensions from to , and re-trained ANN models (Figs 3 and 5). As presented in Tables 4 and 5, and in Figs 9 and 10, the accuracy of the model improved from an average of 72% to 93%, suggesting an ANN model trained on autoencoded NIR spectra as an appropriate tool to estimate the parity status of wild mosquitoes.
Table 4. Performance of an ANN model trained on 75% of the encoded mosquito spectra (10 features) and tested on the remaining 25% of the encoded mosquito spectra.
AUC values are the area of the ROC curves in Fig 10. Minepa-ARA (Nulliparous = 656, Parous = 271), Muleba-GA (Nulliparous = 119, Parous = 21), Burkina-GA (Nulliparous = 80, Parous = 78).
| Minepa-ARA (N = 927) | Muleba-GA (N = 140) | Burkina-GA (N = 158) | Muleba-Burkina-GA (N = 298) | |
|---|---|---|---|---|
| Accuracy (%) | 97.1 ± 2.2 | 89.8 ± 1.7 | 93.3 ± 1.2 | 92.7 ± 1.8 |
| Sensitivity (%) | 94.9 ± 1.6 | 70.1 ± 2.3 | 91.7 ± 1.9 | 88.2 ± 2.9 |
| Specificity (%) | 98.6 ± 1.3 | 96.9 ± 1.2 | 96.4 ± 1.6 | 94.7 ± 2.1 |
| Precision (%) | 93.7 ± 2.4 | 62.5 ± 3.2 | 91.3 ± 1.4 | 93.1 ± 2.5 |
| AUC (%) | 96.7 | 91.5 | 93.1 | 94.9 |
Table 5. Confusion matrices showing accuracies of the models in absolute values when the models were trained on spectra after feature reduction by autoencoder.
A) Minepa-ARA, B) Muleba-GA, C) Burkina-GA, and D) Muleba-Burkina-GA. Results from the last Monte-Carlo cross validation.
| Actual Parity | ||||
|---|---|---|---|---|
| Estimates | Nulliparous | Parous | Total | |
| Nulliparous | 192 | 7 | 199 | |
| A | Parous | 4 | 71 | 95 |
| Total | 196 | 78 | 274 | |
| Nulliparous | 33 | 2 | 35 | |
| B | Parous | 3 | 5 | 8 |
| Total | 36 | 7 | 43 | |
| Nulliparous | 22 | 3 | 25 | |
| C | Parous | 2 | 21 | 23 |
| Total | 24 | 24 | 48 | |
| Nulliparous | 58 | 4 | 62 | |
| D | Parous | 2 | 27 | 29 |
| Total | 60 | 31 | 91 | |
Fig 9. Box plots showing results when ANN models trained on 75% of encoded spectra in datasets were tested on the remaining encoded spectra (25%).
A, B, C, and D represent results for the Encoded-Minepa-ARA, Encoded-Muleba-GA, Encoded-Burkina-GA, and Encoded-Muleba & Burkina-GA (mosquitoes in Encoded-Muleba-GA and Encoded-Burkina-GA datasets combined) datasets, respectively.
Fig 10. ROC curves (AUCs presented in the last row of Table 4) showing results when ANN models trained on 75% of encoded spectra were tested on the remaining encoded spectra (25%).
A, B, C, and D represent results for the Encoded-Minepa-ARA, Encoded-Muleba-GA, Encoded-Burkina-GA, and Encoded-Muleba-Burkina-GA (mosquitoes in Encoded-Muleba-GA and Encoded-Burkina-GA datasets combined) datasets, respectively. In all ROC curves, a 0.5 threshold was used to calculate false positive rate and true positive rate.
We further applied a model trained on encoded Muleba-GA dataset to estimate the parity status of mosquitoes in the encoded Burkina-GA dataset and a model trained on encoded Burkina-GA dataset to estimate the parity status of mosquitoes in encoded Muleba-GA. Here we wanted to test how the model performs on mosquitoes from different cohorts. As presented in Table 6, the model performed with accuracies of 68.6% and 88.3%, respectively, showing a model trained on encoded Burkina-GA dataset extrapolates well to mosquitoes from a different cohort than a model trained on the encoded Muleba-GA dataset.
Table 6. Independent testing of ANN models trained on Muleba-GA and Burkina-GA encoded datasets.
| ANN model trained on Encoded-Muleba-GA, tested on Encoded-Burkina-GA | ANN model trained on Encoded-Burkina-GA, tested on Encoded-Muleba-GA | |
|---|---|---|
| Accuracy (%) | 68.6 | 88.3 |
| Sensitivity (%) | 26.5 | 86.1 |
| Specificity (%) | 94.4 | 92.2 |
A possible explanation of the results shown in Table 6 could be that, unlike for the Burkina-GA dataset, the number of parous mosquitoes (N = 21) in the Muleba-GA dataset was not representative enough for a model to learn important characteristics that extrapolate to mosquitoes in a cohort other than the one used to train the model. Although the Muleba-GA model had the poor sensitivity as presented in Table 6, the Burkina-GA model results still suggest that ANN model trained on acceptable number of both encoded parous and nulliparous can be applied to estimate parity status of mosquitoes from different cohorts other than the one used to train the model.
Conclusion
These results suggest that applying autoencoders and artificial neural networks to NIRS spectra as an appropriate complementary method to ovary dissections to estimate parity status of wild mosquitoes. The high-throughput nature of near-infrared spectroscopy provides a statistically acceptable sample size to draw conclusions on parity status of a particular wild mosquito population. Before this method can be used as a stand-alone method to estimate the parity status of wild mosquitoes, we suggest repeating of the analysis on different datasets with much larger mosquito sample sizes to test the reproducibility of the results. Hence, with the results presented in this manuscript, we recommend complementing ovary dissection with ANN models trained on NIRS spectra with their feature reduced by an autoencoder to estimate parity status of wild mosquito population.
Supporting information
Column header, wavelengths in ‘nm’.
(ZIP)
Acknowledgments
We extend our gratitude to Benjamin Krajacich for allowing us to use his already-published datasets (Burkina-GA dataset) in our analyses; the USDA, Agricultural Research Service, Center for Grain and Animal Health Research, USA for loaning us the near-infrared spectrometer used to scan the mosquitoes; and Gustav Mkandawile who worked tirelessly to make sure we obtained mosquitoes in the Minepa-ARA and Muleba-GA datasets.
Mention of trade names or commercial products in this publication is solely for the purpose of providing specific information and does not imply recommendation or endorsement by the U.S. Department of Agriculture. USDA is an equal opportunity provider and employer.
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
Data collection was funded by: Grand Challenges Canada Stars for Global Health funded by the government of Canada grant 043901 awarded to MTSL; DFID/MRC/Wellcome Trust through the Joint Health Trials Scheme awarded to JDC (Award Number MR/L004437/1); National Institute of Allergy and Infectious Diseases grant R01-AI094349-01A1; and Marquette University Graduate School, for studentship awarded to MPM.
References
- 1.Robert V, Carnevale P. Influence of Deltamethrin Treatment of Bed Nets on Malaria Transmission in the Kou valley, Burkina Faso. Bull World Health Organ. 1991;69(6):735 [PMC free article] [PubMed] [Google Scholar]
- 2.Coleman S, Dadzie SK, Seyoum A, Yihdego Y, Mumba P, Dengela D, et al. A Reduction in Malaria Transmission Intensity in Northern Ghana After 7 Years of Indoor Residual Spraying. Malaria Journal. 2017;16(1):324 10.1186/s12936-017-1971-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Magesa SM, Wilkes TJ, Mnzava A, Njunwa KJ, Myamba J, Kivuyo M, et al. Trial of Pyrethroid Impregnated Bednets in An Area of Tanzania Holoendemic for Malaria Part 2. Effects on the Malaria Vector Population. Acta Trop. 1991;49(2):97–108. 10.1016/0001-706x(91)90057-q [DOI] [PubMed] [Google Scholar]
- 4.Dye C. The Analysis of Parasite Transmission by Bloodsucking Insects. Annu Rev Entomol. 1992;37(1):1–19. [DOI] [PubMed] [Google Scholar]
- 5.Garrett-Jones C. Prognosis for Interruption of Malaria Transmission Through Assessment of the Mosquito's Vectorial Capacity. Nature. 1964;204(4964):1173–5. [DOI] [PubMed] [Google Scholar]
- 6.Beier JC. Malaria Parasite Development in Mosquitoes. Annu Rev Entomol. 1998;43(1):519–43. [DOI] [PubMed] [Google Scholar]
- 7.Detinova TS. Age Grouping Methods in Diptera of Medical Importance With Special Reference to Some Vectors of Malaria. Monogr Ser World Health Organization. 1962; 47:13–108 [PubMed] [Google Scholar]
- 8.Polovodova VP. Age Changes in Ovaries of Anopheles and Methods of Determination of Age Composition in Mosquito Populations. Med Parazit (Mosk). 1941;10:387. [Google Scholar]
- 9.Mayagaya VS, Michel K, Benedict MQ, Killeen GF, Wirtz RA, Ferguson HM, et al. Non-destructive Determination of Age and Species of Anopheles gambiae sl Using Near-infrared Spectroscopy. American Journal of Tropical Medicine and Hygiene. 2009;81(4):622–30. 10.4269/ajtmh.2009.09-0192 [DOI] [PubMed] [Google Scholar]
- 10.Sikulu M, Killeen GF, Hugo LE, Ryan PA, Dowell KM, Wirtz RA, et al. Near-infrared Spectroscopy as a Complementary Age Grading and Species Identification Tool for African Malaria Vectors. Parasites & Vectors. 2010;3(1):1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Milali MP, Sikulu-Lord MT, Kiware SS, Dowell FE, Corliss GF, Povinelli RJ. Age Grading An. gambiae and An. Arabiensis Using Near-infrared Spectra and Artificial Neural Networks. BioRxiv. 2018:490326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Krajacich B. J., Meyers J. I., Alout H., Dabire R. K., Dowell F. E., Foy B. D. Analysis of Near-infrared Spectra for Age-grading of Wild Populations of Anopheles gambiae. Parasites & Vectors. 2017. January 1,;10(1):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sikulu MT, Majambere S, Khatib BO, Ali AS, Hugo LE, Dowell FE. Using a Near-infrared Spectrometer to Estimate the Age of Anopheles Mosquitoes Exposed to Pyrethroids. PloS One. 2014;9(3):e90657 10.1371/journal.pone.0090657 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mayagaya VS, Ntamatungiro AJ, Moore SJ, Wirtz RA, Dowell FE, Maia MF. Evaluating Preservation Methods for Identifying Anopheles gambiae s.s and Anopheles arabiensis Complex Mosquitoes Species Using Near-infrared Spectroscopy. Parasites & Vectors. 2015;8(1):60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dowell FE, Noutcha AE, Michel K. The Effect of Preservation Methods on Predicting Mosquito Age by Near-infrared Spectroscopy. American Journal of Tropical Medicine and Hygiene. 2011;85(6):1093–6. 10.4269/ajtmh.2011.11-0438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ntamatungiro AJ, Mayagaya VS, Rieben S, Moore SJ, Dowell FE, Maia MF. The Influence of Physiological Status on Age Prediction of Anopheles arabiensis Using Near-infrared Spectroscopy. Parasites & Vectors. 2013;6(1):1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sikulu-Lord MT, Milali MP, Henry M, Wirtz RA, Hugo LE, Dowell FE, et al. Near-infrared Spectroscopy, a Rapid Method for Predicting the Age of Male and Female Wild-Type and Wolbachia Infected Aedes aegypti. PLoS Negl Trop Dis. 2016;10(10):e0005040 10.1371/journal.pntd.0005040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sikulu-Lord MT, Maia MF, Milali MP, Henry M, Mkandawile G, Kho EA, et al. Rapid and Non-destructive Detection and Identification of Two Strains of Wolbachia in Aedes aegypti by Near-infrared Spectroscopy. PLoS Negl Trop Dis. 2016;10(6):e0004759 10.1371/journal.pntd.0004759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Maia MF, Kapulu M, Muthui M, Wagah MG, Ferguson HM, Dowell FE, et al. Detection of Plasmodium falciparum Infected Anopheles gambiae Using Near-infrared Spectroscopy. Malaria Journal. 2019;18(1):85 10.1186/s12936-019-2719-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Milali MP, Sikulu-Lord MT, Kiware SS, Dowell FE, Corliss GF, Povinelli RJ. Age Grading An. gambiae and An. arabiensis Using Near-infrared Spectra and Artificial Neural Networks. PloS One. 2019;14(8):e0209451 10.1371/journal.pone.0209451 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Milali MP, Sikulu-Lord MT, Kiware SS, Dowell FE, Povinelli RJ, Corliss GF. Do NIR Spectra Collected from Laboratory-reared Mosquitoes Differ from Those Collected from Wild Mosquitoes? PloS One. 2018;13(5):e0198245 10.1371/journal.pone.0198245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.LeClair C, Cronery J, Kessy E, Tomás EV, Kulwa Y, Mosha FW, et al. ‘Repel All Biters’: An Enhanced Collection of Endophilic Anopheles gambiae and Anopheles arabiensis in CDC light-traps, from the Kagera Region of Tanzania, in the Presence of a Combination Mosquito Net Impregnated with Piperonyl Butoxide and Permethrin. Malaria Journal. 2017;16(1):336 10.1186/s12936-017-1972-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Detinova TS. Determination of the Physiological Age of the Females of Anopheles by the Changes in the Tracheal System of the Ovaries. Medical Parasitology. 1945;14(2):45–49. [PubMed] [Google Scholar]
- 24.Paskewitz SM, Collins FH. Use of the Polymerase Chain Reaction to Identify Mosquito Species of the Anopheles gambiae Complex. Med Vet Entomol. 1990;4(4):367–73. 10.1111/j.1365-2915.1990.tb00453.x [DOI] [PubMed] [Google Scholar]
- 25.Xu Q, Liang Y, Du Y. Monte Carlo Cross‐validation for Selecting a Model and Estimating the Prediction Error in Multivariate Calibration. A Journal of the Chemometrics Society. 2004;18(2):112–20. [Google Scholar]
- 26.Storkey A. When Training and Test Sets are Different: Characterizing Learning Transfer. Dataset Shift in Machine Learning. 2009:3–28. [Google Scholar]
- 27.Mouazen AM, Kuang B, De Baerdemaeker J, Ramon H. Comparison Among Principal Component, Partial Least Squares and Back Propagation Neural Network Analyses for Accuracy of Measurement of Selected Soil Properties with Visible and Near-infrared Spectroscopy. Geoderma. 2010;158(1):23–31. [Google Scholar]
- 28.Shlens J. A Tutorial on Principal Component Analysis. ArXiv Preprint ArXiv:1404.1100. 2014.
- 29.Chicco D, Sadowski P, Baldi P. Deep Autoencoder Neural Networks for Gene Ontology Annotation Predictions. Proceedings of the 5th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics; ACM; 2014.
- 30.Bourlard H. Auto-association by Multilayer Perceptrons and Singular Value Decomposition. 2000. [DOI] [PubMed] [Google Scholar]
- 31.Kingma DP, Welling M. Auto-encoding Variational Bayes. ArXiv Preprint ArXiv:1312.6114. 2013.
- 32.Liu Y, Wu L. High Performance Geological Disaster Recognition Using Deep Learning. Procedia Computer Science. 2018;139:529–36. [Google Scholar]
- 33.Baldi P. Autoencoders, Unsupervised Learning, and Deep Architectures. Proceedings of ICML Workshop on Unsupervised and Transfer Learning; 2012.
- 34.Liou C, Huang J, Yang W. Modeling Word Perception Using the Elman Network. Neurocomputing. 2008;71(16–18):3150–7. [Google Scholar]
- 35.Liou C., Cheng W., Liou J., and Liou D. Autoencoder for Words. Neurocomputing. 2014;139:84–96. [Google Scholar]
- 36.Altman DG, Bland JM. Statistics Notes: Diagnostic Tests 1: Sensitivity and Specificity. BMJ. 1994. June 11;308(6943):1552 10.1136/bmj.308.6943.1552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Smith C. Diagnostic Tests (1)–Sensitivity and Specificity. Phlebology. 2012. August;27(5):250–1. 10.1258/phleb.2012.012J05 [DOI] [PubMed] [Google Scholar]
- 38.Lalkhen AG, McCluskey A. Clinical Tests: Sensitivity and Specificity. Continuing Education in Anaesthesia, Critical Care & Pain. 2008. December;8(6):221–3. [Google Scholar]
- 39.Saito T, Rehmsmeier M. The Precision-recall Plot is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PloS One. 2015;10(3):e0118432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Powers DM. Evaluation From Precision, Recall and F-measure to ROC, Informedness, Markedness and Correlation. 2011. [Google Scholar]
- 41.Fawcett T. An Introduction to ROC Analysis. Pattern Recog Lett. 2006;27(8):861–74. [Google Scholar]
- 42.Stone P, Veloso M. Layered Learning. European Conference on Machine Learning; Springer; 2000.
- 43.Dietterich TG. Machine-learning Research. AI Magazine. 1997;18(4):97. [Google Scholar]
- 44.Domingos PM. A Few Useful Things to Know About Machine Learning. Commun ACM. 2012;55(10):78–87. [Google Scholar]
- 45.Abdi H. Partial Least Square Regression (PLS Regression). Encyclopedia for Research Methods for the Social Sciences. 2003;6(4):792–5. [Google Scholar]
- 46.Golub GH, Reinsch C. Singular Value Decomposition and Least Squares Solutions In Linear Algebra. Springer; 1971. p. 134–51. [Google Scholar]
- 47.De Lathauwer L, De Moor B, Vandewalle J. A Multilinear Singular Value Decomposition. SIAM Journal on Matrix Analysis and Applications. 2000;21(4):1253–78. [Google Scholar]