Toward Task Connectomics: Examining Whole-Brain Task Modulated Connectivity in Different Task Domains

Abstract

Human brain anatomical and resting-state functional connectivity have been comprehensively portrayed using MRI, which are termed anatomical and functional connectomes. A systematic examination of tasks modulated whole brain functional connectivity, which we term as task connectome, is still lacking. We analyzed 6 block-designed and 1 event-related designed functional MRI data, and examined whole-brain task modulated connectivity in various task domains, including emotion, reward, language, relation, social cognition, working memory, and inhibition. By using psychophysiological interaction between pairs of regions from the whole brain, we identified statistically significant task modulated connectivity in 4 tasks between their experimental and respective control conditions. Task modulated connectivity was found not only between regions that were activated during the task but also regions that were not activated or deactivated, suggesting a broader involvement of brain regions in a task than indicated by simple regional activations. Decreased functional connectivity was observed in all the 4 tasks and sometimes reduced connectivity was even between regions that were both activated during the task. This suggests that brain regions that are activated together do not necessarily work together. The current study demonstrates the comprehensive task connectomes of 4 tasks, and suggested complex relationships between regional activations and connectivity changes.

Introduction

The concept of the human connectome has been proposed as the comprehensively mapping of structural connections among neurons or brain regions at different scales (Sporns et al. 2005). The human connectome on the macroscale refers to white matter connection matrices among brain regions (Hagmann et al. 2008). The functional connectome, on the other hand has typically based on resting-state functional MRI (fMRI) (Biswal et al. 1995) to examine functional connectivity matrices among brain regions (Biswal et al. 2010). Both approaches have significantly advanced our understandings of brain organizations (Salvador et al. 2005; van den Heuvel and Sporns 2011; Yeo et al. 2011). Recently, there is an increasing awareness on the importance of the dynamics of functional connectivity (Hutchison et al. 2013), which may be an important component toward an understanding of brain functions in different cognitive and affective processes (Bullmore and Sporns 2012; Park and Friston 2013). Even though the dynamics of functional connectivity can be observed in resting-state, different task demands may be critical factors that modulate the fluctuations of functional connectivity. Therefore, examining comprehensive matrices of task modulated functional connectivity in different task contexts may provide critical information on brain functional integration. Using the terminology of connectome, we have termed such comprehensive mapping as “task connectome” (Di et al. 2017).

Several methods have been developed to study task modulated functional connectivity on fMRI data, most importantly psychophysiological interaction (PPI) (Friston et al. 1997) and beta series correlations (BSC) (Rissman et al. 2004). Earlier implementation of these methods typically adopted a seed-based approach with predefined regions of interest (ROIs), which limits a study to only focus on specific regions and tasks. Recently, several meta-analyses have been performed to pool studies with different seed regions and task domains to examine how different tasks may modulate connectivity between different brain systems (Smith et al. 2016; Di et al. 2017). Alternatively, studies could adopt a ROI-based approach to study pair-wise connectivity among ROIs (Fornito et al. 2011, 2012; Gerchen et al. 2014; Di et al. 2017). This approach can avoid a priori hypothesis on the involvement of certain brain regions, but most of the studies so far have focused on one or 2 specific tasks. Until recently, researchers have started to examine whole brain task connectivity in different task conditions either using a continuous task design (Krienen et al. 2014) or concatenated task conditions from block-designed tasks (Cole et al. 2014). An important finding from this line of studies is that whole brain connectivity patterns during different task conditions are very similar to what have been observed in resting-state (Cole et al. 2014; Krienen et al. 2014). Though, these prior studies did not contrast between well-controlled experimental conditions, and therefore not possible to infer involvements of specific connections in certain cognitive or affective processes.

In the current study, we sought to portray the task modulated connectivity matrices across ROIs that sampled the whole brain during different task domains. To achieve this, we leveraged large-scale open-access fMRI datasets of the Human Connectome Project (HCP) (Barch et al. 2013) and UCLA Consortium for Neuropsychiatric Phenomics LA5c Study (Poldrack et al. 2016). For each of the 7 tasks analyzed, there are an experimental and a corresponding control condition, which enabled us to examine task modulated connectivity between 2 well-controlled conditions. We applied whole brain PPI analysis (Di et al. 2017) to obtain task modulated connectivity matrices across ROIs for each task. This enabled us to examine the relationships between task modulated connectivity and their regional activation levels. One straightforward prediction is that increased connectivity in a task will usually take place between regions that are (co)activated during the task. Alternatively, it is possible that there are broader involvements of brain regions that communicate with each other at different levels, even though they do not show altered regional activations. This predicts that there might be regions that are not activated during a task that will show task modulated connectivity with other brain regions.

Materials and Methods

Experimental Design

The current analysis included fMRI data from 7 separate tasks, which were designed in either blocked or event-related fashion. For each task, there was 1 experimental condition, 1 corresponding control condition, and a baseline condition. We are interested in the differences between the experimental and corresponding control conditions, both in terms of local activations and connectivity. The 6 of the 7 tasks were derived from the HCP project (Barch et al. 2013), including the emotion processing, gambling, language, relation processing, social cognition, and working memory tasks, all of which were blocked designed. These tasks were designed to activate different parts of the brain, and therefore were ideal for the purpose of the current study to map task modulated connectivity in different brain systems. The motor task was not included, because it contrasts finger movement versus toe movement, which is not expected to modulate whole brain level connectivity. The experimental and control conditions of the 6 tasks are outlined in Table 1. For the language task, the stimuli of language understanding and arithmetic problems were both delivered auditorily. While for all the other tasks, the stimuli were delivered visually. All the tasks required some sorts of responses from the subjects. For the emotion, gambling, and relational tasks, the subjects were required to make response for each trial in both the experimental and control conditions. The subjects were only required to response to the target trials (either 2-back or 0-back) in the working memory task. And for the language and social cognition task, the subjects have to only respond to a simple question at the end of each block for both conditions. More information about the task designs can be found in (Barch et al. 2013).

Table 1.

Summary of task conditions in the 7 tasks included in the current study. The first 6 tasks were derived from Human Connectome Project (HCP), while the last stop signal task was derived from UCLA Consortium for Neuropsychiatric Phenomics LA5c Study. Please note that the repetition time (RT) is 720 ms for the HCP data, and 2000 ms for the UCLA data

Task	n	# of images	Design	Experimental condition	Total length	Control condition	Total length	Stimuli modality
Emotion	94	176 × 2	Blocked	Emotional face judgment	108 s	Shape judgment	108 s	Visual
Gambling	94	253 × 2	Blocked	Mostly reward	112 s	Mostly loss	112 s	Visual
Language	97	316 × 2	Blocked	Language understanding	206 s	Arithmetic task	236 s	Auditory
Relational	94	232 × 2	Blocked	Relational judgment	96 s	Matching judgment	96 s	Visual
Social cognition	93	274 × 2	Blocked	Social interaction	115 s	Random movement	115 s	Visual
Working memory	94	405 × 2	Blocked	2 back	220 s	0 back	220 s	Visual
Stop signal	114	184	Event-related	Stop trial	32 trials	Go trial	96 trials	Visual/Auditory

An event-related designed stop signal task from the UCLA Consortium for Neuropsychiatric Phenomics LA5c Study (Poldrack et al. 2016) was also used for this study. We included this dataset to add an event-related designed task, which is complementary to the HCP data. During the task, the subjects were asked to indicate the direction of an arrow (left or right) presented in the screen. For one-fourth of the trials, there was a 500 Hz tone, that is, the stop signal, being presented shortly after the arrow, where the subjects have to withdraw their motor response. There were 128 trials in total, with 96 Go trials and 32 Stop trials. The trials were designed in a fast event-related fashion, with mean intertrial interval of 2.5 s (range from 2 to 5.5 s). More information about the task designs can be found in (Poldrack et al. 2016).

Subjects and MRI Acquisition Parameters

Data From HCP

We analyzed a sample of 100 unrelated subjects (54 females) from HCP dataset. Overall, 17 subjects fell within the age range between 22 and 25 years, 40 subjects fell between 26 and 30 years, 42 subjects fell between 31 and 35 years, and one subject was older than 36 years. All the subjects were scanned for the 6 tasks. After eliminating subjects with large head motions during each task, there were 93–97 subjects remaining for different tasks (Table 1). We calculated framewise displacement for translation and rotation separately (Di and Biswal 2015), and large head motion for a task was defined as maximum framewise displacement greater than 2 mm or 2° in either the translation or rotation direction or in either of the 2 runs of each task. The MRI data were scanned using Siemen’s standard 32-channel head coil. Each task was scanned for 2 fMRI runs, with variable lengths for different tasks. For each task, one run was acquired with right-to-left phase encoding, and the other run with left-to-right phase encoding. The scanning parameters for the fMRI were: repetition time (TR) = 720 ms; echo time (TE) = 33.1 ms; flip angle (FA) = 52°; field of view (FOV) = 208 × 180 mm²; slice number = 72; voxel size = 2.0 mm isotropic; multiband factor = 8. The scanning parameters for the T1 weighted MRI were: TR = 2400 ms; TE = 2.14 ms; FA = 8°; FOV = 224 × 224; voxel size = 0.7 isotropic.

Data From UCLA Consortium for Neuropsychiatric Phenomics LA5c Study

The stop signal task dataset was obtained from the OpenfMRI database, with accession number ds000030. After removing subjects with missing files and large head motions (see above), fMRI data from a total of 114 healthy subjects were included (52 females). The mean age of the subjects was 31.1 years (range from 21 to 50 years). The MRI data were scanned using 1 of 2 Siemens scanners with 32-channel head coils. The task was scanned in a single run. The fMRI data were collected using a T2*-weighted echoplanar imaging (EPI) sequence with the following parameters: TR = 2000 ms, TE = 30 ms, FA = 90°, matrix 64 × 64, FOV = 192 mm; slice thickness = 4 mm, slice number = 34. 184 fMRI images were acquired for each subject. The parameters for the T1 weighted structural image were the following: TR = 1900 ms, TE = 2.26 ms, FOV = 250 mm, matrix = 256 × 256, sagittal plane, slice thickness = 1 mm, slice number = 176.

FMRI Data Preprocessing

For the HCP data, we adopted the minimally preprocessed data (Glasser et al. 2013) for our analysis. The data have gone through spatial artifact/distortion correction, cross-modal registration, and spatial normalization to MNI (Montreal Neurological Institute) space. Therefore, we did not perform further preprocessing on the HCP data. We note that the preprocessed data were not spatially smoothed, which was not a necessary step in this study because the primary analyses were ROI-based.

The fMRI data preprocessing for the UCLA data were performed using SPM 12 (v6685; http://www.fil.ion.ucl.ac.uk/spm/) in MATLAB 8.2 environment (https://www.mathworks.com/). The T1 weighted anatomical image for each subject was firstly segmented into gray matter, white matter, cerebrospinal fluid, and other tissues with reference to tissue probabilistic maps in MNI space, and the deformation field maps were obtained. The first 2 fMRI images of each subject were discarded. The remaining 182 images were realigned to adjust head motion, and coregistered to the anatomical image. Then the deformation field maps were used to normalize all the functional images into MNI space. During the normalization the images were resampled with a voxel resolution of 3 × 3 × 3 mm³, and spatially smoothed by using a Gaussian kernel of 8 mm full width at half maximum.

Regions of Interest

The choice of ROIs needs to consider the tradeoff between spatial coverage, spatial resolution, and the problem of multiple comparisons. We chose the Dosenbach’s 160 ROIs, which are functionally representative to sample the whole brain (Dosenbach et al. 2010). The 160 ROIs were assigned into 6 functional modules: (1) cerebellar, (2) cingulo-opercular, (3) default mode, (4) frontoparietal, (5) occipital, and (6) sensorimotor modules. Because this ROI system does not include critical subcortical structures that are involved in emotional processing, we additionally included 4 ROIs of the bilateral amygdala and parahippocampus in our analysis (Di et al. 2013). As a result, 164 ROIs were used in the whole brain analysis. The ROIs were defined as spheres, with a radius of 8 mm.

Task Activation Analysis and Time Series Extraction

All fMRI data analyses were also performed using SPM 12 (v6685) in MATLAB 8.2 environment. We first performed voxel-wise general linear model (GLM) analysis to examine task activations and extract ROI time series for each task. For all the HCP tasks excepting the language task, there were 2 regressors representing the experimental and control conditions in the GLM, leaving the fixation condition as an implicit baseline. For the language task, however, there is no implicit baseline. We therefore only modeled the language condition as a regressor in the GLM. The task regressors were calculated by convolving a box-car function of the task design with the canonical hemodynamic response function (HRF) in SPM. After model estimation, a contrast was defined for each task to obtain task related activations for the experimental condition compared with the respective control condition. For the language task, a simple contrast of 1 for the language regressor was used. For each task and each of the 164 ROIs, the first eigenvariate was extracted for each task run using SPM’s volume of interest function. When extracting time series, effects of no interest, for example, low frequency drifts and constant baseline were adjusted. We additionally regress out 24 head motion regressors (6 rigid-body transformations, their one time-point lag, and all their correspondent squared time series) to minimize the effects of head motion on subsequent analyses (Friston et al. 1996).

For the stop signal task, similar GLM model was built for each subject to obtain task activations. Two separate regressors were defined to reflect the effects of the Go and Stop trials, respectively. The trial variables were convolved with HRF to form blood-oxygen-level dependent (BOLD) level regressors. A total of 24 head motion regressors were also included in the GLM model of the stop signal task. After model estimation, the contrast between the Stop and Go conditions was defined for each subject. The first eigenvariate of each of the 164 ROIs was extracted after adjusting for head motion effects, low frequency drifts, and constant baseline.

In addition to the voxel-wise analysis, we also performed ROI-wise analysis to compare the regional activation results with later PPI results. Similar GLMs as in the voxel-wise analysis but without effects of no-interest were applied to the ROI time series, because the effects of no-interest have already been removed during the time series extraction. The beta estimates of modeled effects and contrasts of interest were then calculated. Group level one sample t test on the contrast values of each task was performed for each ROI. There were 164 comparisons (ROIs) for each task. So that we adopted false discovery rate (FDR) of P < 0.05 to correct for the total 164 comparisons. The ROIs were labeled as significantly activated, significantly deactivated, or not activated based on the FDR corrected P value for each task.

PPI Analysis

There are 2 ways to calculate the PPI terms. The conventional way is to directly multiply the BOLD level psychological variable (a task design variable convolves with the HRF) with the time series of a region (Friston et al. 1997). Alternatively, the time series of a region is first deconvolved with the HRF to represent the time series at the neuronal level, and the PPI term is calculated by multiplication of the deconvolved time series with the task design variable. The PPI term is then convolved back with the HRF to represent a prediction variable at the BOLD level (Gitelman et al. 2003). The later approach is better for properly dealing with the asynchrony of task design and observed BOLD response. However, the deconvolution may not work well due to intersubject and inter-regional variability of hemodynamic responses, and PPI results in block-designed data were very similar when using the 2 methods (Di and Biswal 2017). Therefore, for the block-designed HCP tasks, we used the direct way to calculate PPI term by performing a point-by-point multiplication between box-car convolved psychological function and the time series of a ROI. For each task and each ROI, PPI terms were calculated for the experimental and control conditions, separately. New GLM models were then built, with one regressor of the time series of a ROI, 2 regressors of task conditions, 2 regressors of PPIs, and 1 constant term. The contrasts of interest were the differences in PPI effects between the 2 conditions.

For the event-related designed task, however, deconvolution is necessary. The time series of a ROI was first deconvolved with the HRF, and point-by-point multiplied with the psychological design variable. The PPI terms of the Go and Stop trials were calculated separately with the corresponding psychological variables. The neuronal level PPI terms were convolved with the HRF to represent the BOLD level predictors of PPI effects. Similar GLM models were built to examine PPI effects, with 1 regressor of the time series of a ROI, 2 regressors of task conditions, 2 regressors of PPIs, and 1 constant term. The contrasts of interest were the differences in PPI effects between the Stop and Go conditions.

The PPI effects were calculated between each pair of the 164 ROIs, which resulted in a 164 × 164 matrix for each task and each subject. The contrast matrix for each subject was symmetrized (Supplementary material in Di et al. 2017), and one sample t-test across subjects were performed at each pair of ROIs. For each task, there are in total 13 366 connections to be tested (164 × 163/2). FDR correction was used for each task at P < 0.05 to deal with the multiple comparison problem.

The thresholded matrices of positive or negative PPI effects can be treated as network graphs, where the 164 ROIs represent the nodes and PPI effects represent the edges of a graph. From the graph-theory point of view, we can calculate degree of a node as the number of significant PPI effects this node has. We defined increased or decreased hubs of a task as the nodes with increased or decreased degree higher than the averaged degree plus one standard deviation of degree across all the 164 nodes, respectively. We also identified the giant component of each graph, which represents the largest connected subnetwork of a graph. The network layout of the giant component of increased graph of each task was visualized using Gephi (https://gephi.org/), Yifan Hu’s algorithm was used for the layout, which combines a force-directed model to spatialize the nodes and reduce edge crossing and uses a multilevel algorithm to reduce the complexity (Hu 2005).

Crossmethod Validation of PPI Results

In addition to PPI analysis, we performed other similar methods to cross validate the task modulated connectivity results. For the block-designed tasks from the HCP dataset, we calculated Spearman’s rank correlation coefficients of concatenated time series of each condition across the 164 ROIs after removing the first 6 s of data from each block to account for transient hemodynamic effects (Di et al. 2017). The correlation matrices were transformed into Fisher’s z matrices, and then compared between the 2 task conditions in each task. This resulted in a 164 × 164 matrix of correlation differences for each task. The same FDR correction was used at P < 0.05 to account for multiple comparisons.

For the event-related stop signal task, we obtained an activation map for each trial (beta map), and calculate the correlations of trial-by-trial variabilities among the 164 ROIs for the Go and Stop conditions, and then compared the differences of the BSCs between the conditions (Rissman et al. 2004). We used the single-trial versus all-other-trials approach (Mumford et al. 2012). To define the GLM model of a trial, 2 regressors were included in the model, one representing the trial of interest and the other representing all other trials. With additional 24 head motion regressors and constant, there were in total 27 regressors in the model (Supplementary Fig. S1). One GLM model was used to obtain one beta image for a specific trial. After estimating beta maps for different trials, mean beta values of each ROI were extracted to form beta series for each subject. The beta series from all the 164 ROIs were grouped into 2 sets representing the Go and Stop conditions, and Spearman’s rank correlation coefficients were calculated among the 164 ROIs. The 2 correlation matrices from the 2 conditions were transformed into Fisher’s z matrices. At each element of the matrix, a paired t-test was performed between the 2 conditions across subjects. The same FDR correction was used at P < 0.05. All the codes for the data analysis in the current analysis are available from osf.io/dka6g.

Results

Task Activations

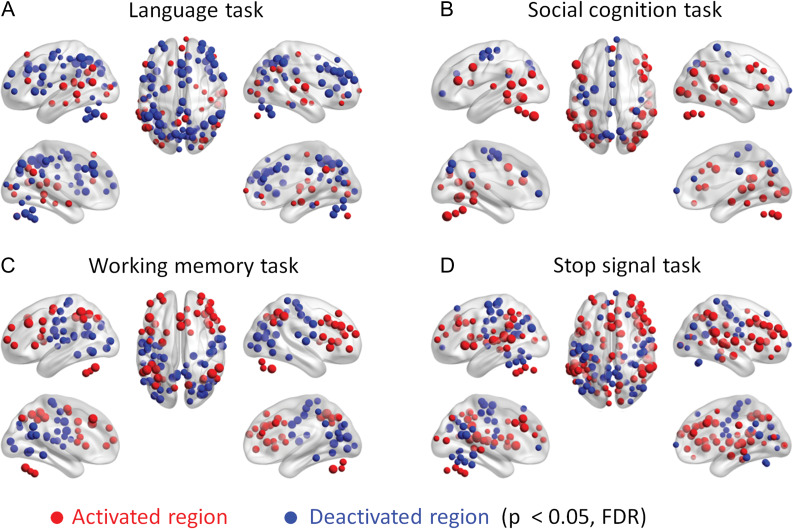
We first performed activation analysis for each task to identify ROIs that showed task activations and deactivations during the task condition compared with their respective control condition. Figure 1 outlines task activations of the 4 tasks that later showed significant PPI effects. The activations of the language, social cognition, and working memory tasks basically replicated the results of Barch et al. (2013). For the stop signal task, the Stop condition showed increased activations compared with the Go condition in inhibition related regions such as the anterior cingulate cortex, bilateral insula, and bilateral dorsolateral prefrontal cortex (Schall et al. 2017). The superior temporal lobe was also activated, which is reasonable because the stop signal was delivered auditorily. In contrast, decreased activations were observed in many regions including the sensorimotor cortex, probably because apparent motor response was withdrawn in the Stop condition. The ROI-based activation results for all the 7 tasks are reported in Supplementary Figure S2.

Figure 1.

ROI-wise (region of interest) activations in the 4 tasks that later showed significant psychophysiological interactions (PPI) effects. Red and blue regions indicate increased and decreased activations during the task condition compared with the respective control condition at P < 0.05 of FDR (false discovery rate) correction.

Psychophysiological Interactions

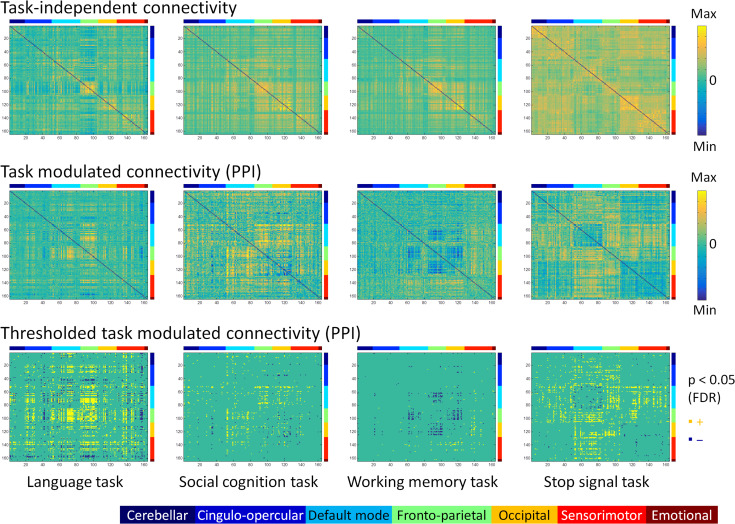
The PPI analysis revealed that 4 tasks, including the language, social cognition, working memory, and stop signal tasks, showed statistically significant task modulated connectivity at P < 0.05 of FDR correction. Figure 2 illustrates the raw and thresholded matrices of the PPI effects across the 164 ROIs for the 4 tasks. For reference to the baseline functional connectivity, we also show the main effects of the seed time series in the PPI models on the top row of Figure 2. For each task, both increased and decreased connectivity in the task condition compared with its respective control condition were found. The ROIs in the matrices are organized into 7 functional modules. Therefore, it can be seen that there are rectangle like effects in the matrices which represent similar effects within a functional module or between 2 modules. The task modulated connectivity of the language task seemed to involve in many different brain systems. While the other 3 tasks showed task related connectivity in specific brain systems. Increased connectivity in the social cognition task mainly took place between the default mode module and other modules, including the cingulo-opercular, frontoparietal, occipital, and sensorimotor modules. Increased connectivity in the working memory task mainly took place between the sensorimotor module to both the frontoparietal and occipital modules. In contrast, decreased connectivity in the working memory task mainly took place between the default mode and frontoparietal modules, and between the frontoparietal and occipital modules. Lastly, increased connectivity in the stop signal task mainly took place between the default mode module and other modules including the cingulo-opercular, frontoparietal, occipital, and sensorimotor modules, and between the frontoparietal module and other modules such as the cingulo-opercular and occipital modules.

Figure 2.

Whole brain task-independent connectivity (top row) and task modulated connectivity (middle and bottom rows) matrices for the language, social cognition, working memory, and stop signal tasks across 164 regions of interest. The upper 2 rows showed unthresholded matrices. The displayed range for each matrix was adjusted for each matrix, and was assured to be positive and negative symmetrical. The bottom row showed thresholded matrices of task modulated connectivity at P < 0.05 of FDR (false discovery rate) correction. Yellow and blue elements in the matrices indicate increased and decreased connectivity between each task and its corresponding control conditions. The color bars on the top and right side of each matrix represent 7 functional brain modules: (1) cerebellar, (2) cingulo-opercular, (3) default mode, (4) frontoparietal, (5) occipital, (6), sensorimotor, and (7) emotional modules.

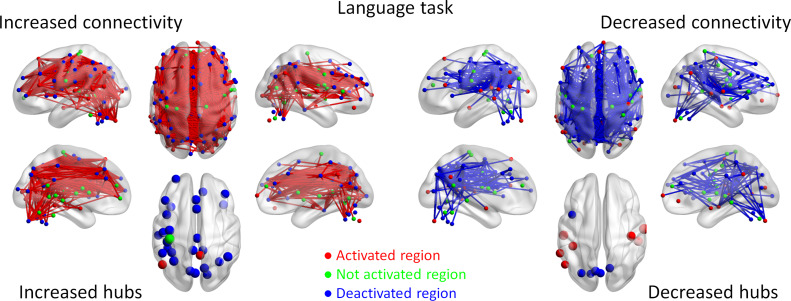
To better illustrate the spatial distributions of task modulated connectivity, we plotted the connections with increased or decreased connectivity on a brain model using BrainNet Viewer (Xia et al. 2013). For the language task, widespread connections have been observed showing increased or decreased functional connectivity during the language condition compared with the math condition (Fig. 3). There were in total 1 323 significant positive effects. Except for 2 effects, all other effects formed a giant component covering 141 ROIs. Although we can observe increased connectivity between task activated regions that are directly related to language processing, for example, the left inferior frontal regions and superior temporal regions, the majority of increased connectivity actually took place between task deactivated regions. The hubs of increased connectivity were also mostly deactivated during the language condition (Supplementary Table S1 for a full list of the hub regions). Conversely, there were in total 460 significant negative PPI effects. Except for 2 effects, all other effects formed a giant component covering 120 ROIs. It is noteworthy that many task positive regions, for example, the bilateral temporal lobe regions, showed reduced connectivity with task negative regions.

Figure 3.

Increased (red lines) and decreased (blue lines) functional connectivity in the language task (story comprehension vs. arithmetic operation). Significant connectivity was identified at P < 0.05 with false discovery rate (FDR) correction. The lower left and right panels show the hubs of the increased and decreased connectivity networks, respectively. Region colors represent activated (red), deactivated (blue), and no significant activations (green) during the task compared with control conditions.

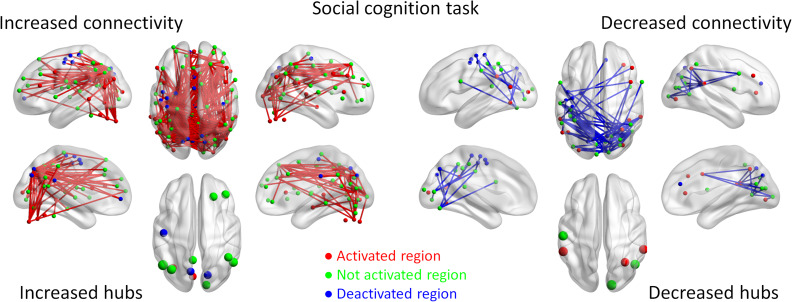
For the social cognition task, we observed widespread connections (325) that showed increased connectivity (Fig. 4). Except for 2 effects, all other effects formed a giant component covering 108 ROIs. Increased connectivity mainly occurred between posterior brain regions, for example, between the visual and parietal regions, and between anterior and posterior brain regions, for example, between the parietal and frontal regions. It is noteworthy that a number of regions that are not activated during the task (green regions), especially the prefrontal cortex regions, showed increased connectivity with the parietal and visual regions, suggesting a broad involvement of the prefrontal cortex in the theory of mind task even though their activation level did change. Many of the frontal and parietal regions that were not activated during the social interaction condition were the hubs of increased connectivity (see also Supplementary Table S2). In contrast, 69 connections showed decreased connectivity. Except for 2 effects, all other effects formed a giant component covering 37 ROIs. A majority of reduced connectivity were taken place between bilateral occipital or temporal regions and between occipital and sensorimotor regions, many of which were activated during the social interaction condition (red regions).

Figure 4.

Increased (red lines) and decreased (blue lines) functional connectivity in the social cognition task (social interaction vs. random movement). Significant connectivity was identified at P < 0.05 with false discovery rate (FDR) correction. The lower left and right panels show the hubs of the increased and decreased connectivity networks, respectively. Region colors represent activated (red), deactivated (blue), and no significant activations (green) during the task compared with control conditions.

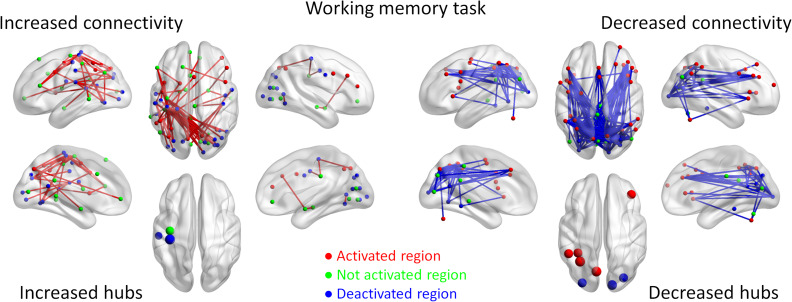
For the working memory task, we observed 66 connections that showed increased connectivity (Fig. 5). Except for 9 effects, the others formed a giant component covering 44 ROIs. Again, although there were a small number of task positive regions that showed increased connectivity, the majority of increased connectivity was between task negative regions or no activation regions. The hubs of decreased connectivity were in the sensorimotor regions which were deactivated or not activated during the 2-back condition (Supplementary Table S3). In contrast, 179 connections showed decreased connectivity. Except for 2 effects, the remaining effects formed a giant component covering 51 regions. Reduced connectivity was mainly between visual regions to frontal or parietal regions. It is noteworthy that a large number of reduced connectivity also occurred between the frontal and parietal regions that were activated during the 2-back condition and have strong implications in supporting working memory (Owen et al. 2005).

Figure 5.

Increased (red lines) and decreased (blue lines) functional connectivity in the working memory task (2-back vs. 0-back). Significant connectivity was identified at P < 0.05 with false discovery rate (FDR) correction. The lower left and right panels show the hubs of the increased and decreased connectivity networks, respectively. Region colors represent activated (red), deactivated (blue), and no significant activations (green) during the task compared with control conditions.

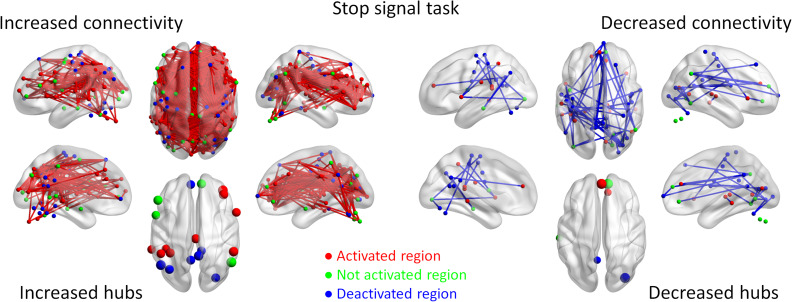
Lastly for the stop signal task, we observed widespread connections (899) that showed increased connectivity, which formed a single giant component covering 142 ROIs (Fig. 6). Increased connectivity involved not only task positive regions such as the bilateral temporal regions, bilateral dorsolateral frontal regions, and anterior cingulate regions, but also task negative and no activation regions. In contrast, 71 connections showed decreased connectivity, which were mainly between task negative regions. The hub regions of decreased connectivity were mainly from the default mode network (Supplementary Table S4).

Figure 6.

Increased (red lines) and decreased (blue lines) functional connectivity in the stop signal task (Stop trial vs. Go trial). Significant connectivity was identified at P < 0.05 with false discovery rate (FDR) correction. The lower left and right panels show the hubs of the increased and decreased connectivity networks, respectively. Region colors represent activated (red), deactivated (blue), and no significant activations (green) during the task compared with control conditions.

Connectivity Differences and Local Activations

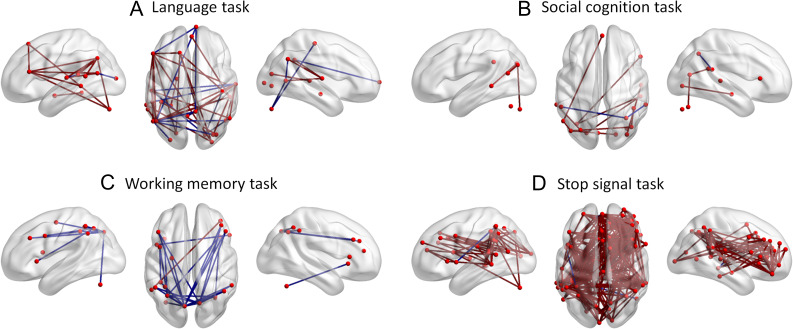
We have shown widespread connectivity modulations which go beyond task activated regions in most of the tasks. But task modulated connectivity between only the regions that are activated during a task is more relevant to existing theories of different cognitive functions. Therefore, we displayed task modulated connectivity between only the task activated regions for each task (Fig. 7). It does show some effects that are consistent with current views of brain functions. For example, the language task increased functional connectivity between the left lateral frontal region to the left parietal and superior temporal regions (Fig. 7A). However, in some cases, there is even reduced connectivity between the task activated regions. For example, although bilateral frontoparietal regions were activated during the working memory task, functional connectivity between these frontal and parietal regions were mainly reduced (Fig. 7C).

Figure 7.

Increased (red lines) and decreased (blue lines) connectivity only among the task activated regions in each task.

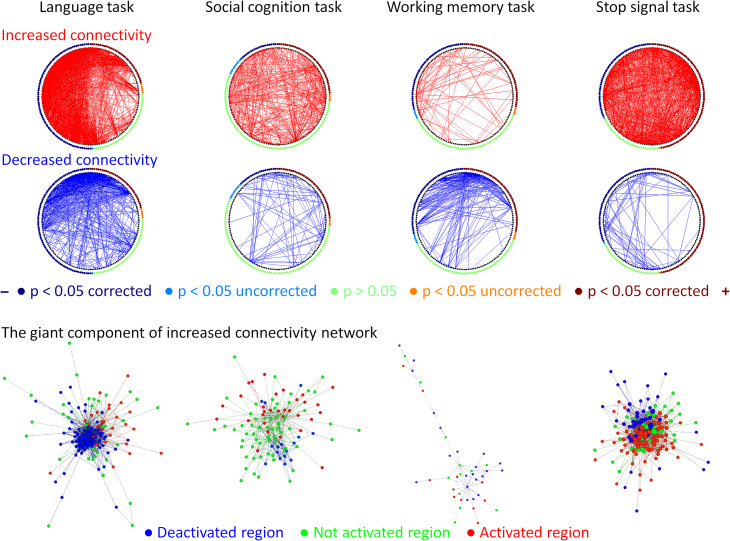
To better illustrate the relationship between regional activations and task modulated connectivity, we used circular plots to display the task modulated connections with the ROIs sorted based on their levels of activations (Fig. 8, upper rows). The increased and decreased connectivity did not show clear patterns that are associated with regional task activations, especially for the increased connectivity. It was particularly true for the language, social cognition, and stop signal tasks. For the reduce connectivity, there was a pattern that many connectivity were between one task activated region and one task deactivated region. However, there were also reductions in connectivity that was between one region that was not activated by the task and the other region that was either activated or deactivated during the same task. We next plotted the giant components of the task increased connectivity graphs of the 4 tasks in the bottom row of Figure 8. For all the tasks, we observed intermixed connectivity between task positive, task negative, and no activation regions. The task positive regions along did not show clear community structures. Instead, they seemed to show increased connectivity to all the 3 types of regions.

Figure 8.

Relationships between the task modulated connectivity and regional activation levels. The upper 2 rows show circular plots of increased (red) and decreased (blue) connectivity in different tasks. The regions along the circle were ordered based on their activations in each task, and were colored based on their statistical significance levels. The bottom row illustrates the network layouts of the first giant component of increased connectivity network using Yifan Hu’s algorithm. Node colors in the network layout represent the activation levels in each task.

Validations of the PPI Results

Direct comparisons of correlation differences for the 3 block-designed tasks with significant PPI results demonstrate similar patterns of task modulated connectivity (Supplementary Fig. S3). The correlations of task modulated connectivity matrices between PPI and correlation differences ranged from 0.64 to 0.87, suggesting cross methods consistency of task modulated connectivity effects.

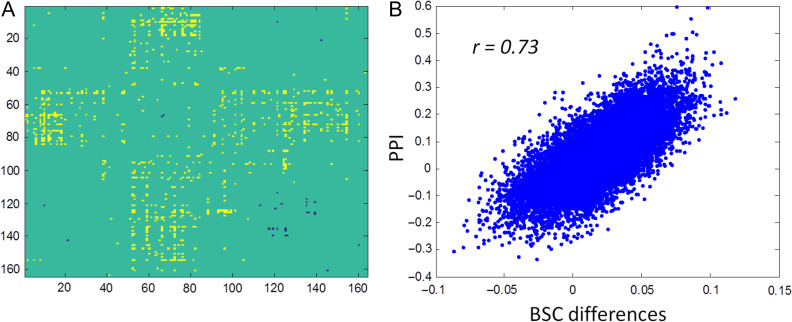
To validate the PPI results of the event-related designed stop signal task, we performed BSC analysis on the same data. Significant BSC differences between the Stop and Go conditions could be observed when using the single-trial versus all-other-trials method (Fig. 9A). The matrix was similar to those obtained in the PPI analysis (Fig. 2). However, the number of significant effects reduced. The correlation between the PPI matrix and BSC differential matrix yielded a correlation of 0.73 (Fig. 9B), which also suggested cross methods consistency of task modulated connectivity effects.

Figure 9.

Beta series correlation (BSC) differences using the single-trial versus all-other-trials method (A) in the stop signal task, and the relationship between the results from psychophysiological interaction (PPI) and BSC differences (B).

Discussion

By leveraging large-scale task fMRI datasets from HCP and UCLA projects, the current analysis demonstrated that it is possible to derive whole brain task-modulated connectomes between 2 well-controlled task conditions during both block-designed and event-related designed tasks. The patterns of task modulated connectivity in different tasks shed new lights to large-scale functional integrations of the brain. First, task modulated connectivity was widespread, far beyond the regions that were typically activated during the tasks. There was no clear relationship between the level of activations of regions and increased or decreased functional connectivity between them. Second, reduced connectivity could be observed between 2 task activated regions, challenging the notion that task coactivations represent task modulated connectivity.

Existing models of brain functional integration in a certain task typically focus on the regions that are activated during the task. However, the current data suggest that for some tasks there were regions that were not activated during the task contrast showed increased connectivity with other brain regions. One typical example is the social cognition task, where its brain theories usually focus on the bilateral temporoparietal junction and medial prefrontal cortex (Castelli et al. 2000; Schurz et al. 2014). Although the bilateral frontal regions have been activated during the social vs. random contrast, the activations tuned out to be restricted (Fig. 1B). The PPI analysis demonstrated widespread prefrontal regions that were not activated during the task showed significant functional connectivity increase with posterior brain regions (Fig. 4). Further examinations confirmed that the baseline task-free connectivity was mainly positive between the prefrontal regions with posterior regions, suggesting increased positive functional integration in the social interaction condition compared with the random movement condition. One explanation may be that the activations of these prefrontal regions keep at a high level in both the social interaction and random movement conditions, so that the direct comparisons of activations could not show differences. On the other hand, information integration between the prefrontal regions and posterior regions did increase during the social interaction condition compared with the random movement condition. Because of the nature of the regression-based analysis, it is difficult to infer the direction of the information integration. It is plausible that the prefrontal regions serve as a top-down modulator to posterior regions such as the superior temporal sulcus (STS) and temporoparietal junction (TPJ) which are directly involved in mentalizing (Frith and Frith 2006). Alternatively, it is also possible that the prefrontal regions receive information from posterior regions, but do not actively modulate the posterior regions. Studies using both brain lesion (Shamay-Tsoory and Aharon-Peretz 2007) and transcranial magnetic stimulation (TMS) (Kalbe et al. 2010) methods have suggested that the dorsolateral prefrontal cortex is responsible for cognitive theory of mind. The current data provide a connectivity based model that could explain the involvement of dorsolateral prefrontal cortex in theory of mind processing.

Another interesting observation of the current results is that coactivated regions do not necessarily imply an increased connectivity between them. There may be decreased functional connectivity between 2 positively activated regions. A clear example is the working memory task, where the bilateral frontoparietal regions have been strongly linked to the working memory process (Owen et al. 2005). There was, however, mainly decreased connectivity among the frontoparietal regions in the current working memory task (Fig. 7C). It is noteworthy that the baseline connectivity among the frontoparietal regions were positive, confirming that there were reduced functional integration in the 2-back condition than the 0-back condition. This suggests that even though these regions are activated together, they are not working more together during the 2-back condition than during the 0-back condition. The decreased connectivity may suggest inhibitory process between the frontal and parietal regions. An alternative explanation may be that the increased and decreased functional connectivity may relate to different oscillation mechanisms at different frequency band. For example, an electroencephalogram study has suggested that increased working memory load is associated with increased functional connectivity in theta band and reduced connectivity in alpha band. Therefore, different frequency oscillations may give rise to different functional connectivity modulations, so that may result in either increased or decreased connectivity as measured from BOLD signals. A broader implication of the reduced connectivity is that coactivations of 2 regions in a task do not necessarily imply an increased connectivity between these 2 regions. This is consistent with our previous observations of reduced connectivity between visual areas in a visual checkerboard task (Di et al. 2015). Although coactivation patters were highly correlated with functional networks and resting-state connectivity (Toro et al. 2008; Smith et al. 2009; Di et al. 2013), the associations between coactivation and task related connectivity differences are rather loose. Practically, the coactivations pattern has been widely used as meta-analytic connectivity modeling (Robinson et al. 2009) to study task related functional connectivity and networks. But one should be cautious about the interpretation of coactivation based results, because it cannot imply task modulated connectivity.

The current results demonstrated that reduced connectivity is ubiquitous in different task conditions. It is reasonable, because maintaining functional connectivity, especially long range connectivity, is expensive in terms of energy consumption (Bullmore and Sporns 2012). In addition, reduced connectivity may reflect less interference from task unrelated regions, ensuring more efficient communications among task related regions. Consistent with this, whole brain level modulatory interactions (interactions among 3 brain regions) are mainly negative, which may serve as functional segregation between different functional modules (Di and Biswal 2015). Of course, the connectivity differences reported in the current study are relative changes of connectivity between conditions, such that an alternative explanation of decreased connectivity could be the increased connectivity in the control task. For example, for the language task, there are more regions that showed higher activation during the arithmetic task condition than the language task condition. Reduced functional connectivity in the language task may be explained as increased connectivity during the arithmetic task, especially between the regions that involve arithmetic calculation, that is, bilateral frontoparietal regions.

When considering task modulated connectivity between known brain systems, we found that the default mode network and frontoparietal network were more likely to show task modulated connectivity in all the 4 tasks (Fig. 2). The involvement of the frontoparietal connectivity with other brain systems is not surprising, and is consistent with the role of these regions in flexible task controls (Cole et al. 2013). The task modulated connectivity between the default mode network regions and other brain systems is also consistent with a previous study showing task-positive functional connectivity of the default mode network in different task domains (Elton and Gao 2015). This line of results suggests that the default mode network may be actively involved in external-oriented tasks through interacting with other brain systems.

The current analysis demonstrates the feasibility of using the PPI framework to study whole-brain level task related connectivity, or task connectome. The results suggest limitations of the typically used PPI analysis strategy, that is, seed-based analysis, because task modulated connectivity can occur beyond task activated regions. This highlights the importance of the task connectomics approach, that is, examining whole brain task modulated connectivity to obtain a more complete picture of brain connectivity modulations. A caveat of whole brain approach is that the number of ROI pairs increases exponentially as the number of ROI increases, therefore there will be severe multiple-comparison problem as the number of ROIs increases. In addition, the effect sizes for PPI are in general smaller than the main effects of task activations (Di and Biswal 2017). Large sample size and enough scan duration are needed for reliable whole brain level analysis. In a recent study, we have shown very limited test–retest reliability of task modulated connectivity in a simple checkerboard task (Di and Biswal 2017). The scan durations of different task conditions in the current analysis are also limited (Table 1), which prevents us to explore the behavioral correlations of the PPI effects (Vul et al. 2009; Dubois and Adolphs 2016). Lastly, the current analysis examined PPI effects between each pair of ROIs. As a consequence, the possibility that an observed PPI effect between 2 regions is mediated by a third region cannot be ruled out. The task connectome matrix across all ROIs could be estimated at the same time with some computational techniques such as regularization (Smith et al. 2011; Di et al. 2017), which might be helpful to minimize confounding influences of other regions.

Estimating task related connectivity in an event-related designed task, especially fast event-related designed task, is still challenging. The current analysis estimated task modulated connectivity on the stop signal task by using both PPI and BSC approaches, and found consistent task related connectivity between the 2 methods. Of course, properly modeling of single trial activation (Mumford et al. 2012) is critical for the BSC method. And for the current data, only the single-trial versus all-other-trials method could yield similar results to the PPI analysis. However, in contrast to Cisler et al. (2014), we showed that there were more statistical significant effects using PPI analysis than using BSC analysis, suggesting the advantage of PPI over BSC in terms of statistical sensitivity. This may be due to the short intertrial interval in the current task, so that reliable single-trial beta maps were difficult to obtain. Anyway, the notion of the advantage of BSC over PPI on event-related data (Cisler et al. 2014) is still not clear, and warrants further investigations.

Conclusion

The current study demonstrated task connectomes across whole brain ROIs in 4 of 7 tasks. These task connectomes suggest broader involvement of brain regions than simple regional task activations, confirming the importance of studying whole brain task connectomes. The increased and decreased functional connectivity can take place between activated, deactivated, or not activated regions. There were no clear relationships between the task modulated connectivity and regional task activations. These results may shed new light to brain models of these cognitive or affective functions.

Funding

U.S. National Institutes of Health (NIH) grants (R01 AG032088 and R01 DA038895).