Working Memory Load Modulates Neuronal Coupling

Abstract

There is a severe limitation in the number of items that can be held in working memory. However, the neurophysiological limits remain unknown. We asked whether the capacity limit might be explained by differences in neuronal coupling. We developed a theoretical model based on Predictive Coding and used it to analyze Cross Spectral Density data from the prefrontal cortex (PFC), frontal eye fields (FEF), and lateral intraparietal area (LIP). Monkeys performed a change detection task. The number of objects that had to be remembered (memory load) was varied (1–3 objects in the same visual hemifield). Changes in memory load changed the connectivity in the PFC–FEF–LIP network. Feedback (top-down) coupling broke down when the number of objects exceeded cognitive capacity. Thus, impaired behavioral performance coincided with a break-down of Prediction signals. This provides new insights into the neuronal underpinnings of cognitive capacity and how coupling in a distributed working memory network is affected by memory load.

Introduction

The number of objects that can be held in working memory (cognitive capacity) is limited (Vogel and Machizawa 2004). Cognitive capacity is directly related to cognitive ability (Conway et al. 2003; Alloway and Alloway 2010; Fukuda et al. 2010; Unsworth et al. 2014) and is lowered in neurological diseases and psychiatric disorders (Luck and Vogel 2013). Therefore, studying how working memory load affects neural processing can inform our understanding of why there is a capacity limit and how cognitive function breaks down in various neurological and psychiatric diseases and disorders.

Studies of working memory load and its limits have focused on coordinated activity in frontoparietal networks known to play a major role in working memory (Gray 1994; Klingberg et al. 2002; Todd and Marois 2005; Palva et al. 2010; Dotson et al. 2014; Awh et al. 2006). These studies predicted capacity limits using measures of network integration (how different parts of these networks are connected together) and synchrony (Roux et al. 2012; Stevens et al. 2012). In light of recent observations that visual working memory is independent for the 2 visual hemifields (Buschman et al. 2011; Kornblith et al. 2016) and that changes in load have different effects on oscillatory dynamics of different frequencies (Kornblith et al. 2016), we aimed for a further understanding of working memory load on network dynamics in the frontoparietal cortex.

To that end, we re-examined LFP data from a change detection task in which working memory load was varied between 1 and 3 objects in each hemifield (Buschman et al. 2011). We previously reported (Kornblith et al. 2016) that load affected low (8–50 Hz) and high (50–100 Hz) power differently depending on time during the trial. We found a dissociation between the effects of load on lower- versus higher-frequency power and their relationship to behavior. Notably, independence between the visual hemifields was apparent in high, but not low, frequencies. Independence means that increases in stimulus load in one hemifield have no effect on the animal’s ability to remember stimuli in the opposite hemifield (Buschman et al. 2011). Likewise, increasing stimulus load only effects neural activity related to stimuli in the same hemifield, not neural activity related to stimuli in the opposite hemifield (Buschman et al. 2011; Kornblith et al. 2016). Also, load effects on power were similar below and above the cognitive capacity. This cannot explain abrupt decrease in behavioral performance above capacity. Further, earlier power and synchrony analyses did not describe the directionality of interactions between brain areas.

Here, we aim to provide a mechanistic explanation of load effects by focusing on changes in the strength and directionality of neuronal coupling. We develop a large-scale cortical network model comprising the prefrontal cortex (PFC), frontal eye fields (FEF), and the lateral intraparietal area (LIP). This is an extension of our earlier model (Pinotsis et al. 2014; Bastos and Litvak et al. 2015) based on Predictive Coding and uses Cross Spectral Density (CSD) responses to infer changes in neuronal coupling that underlie the changes in spectral power at different frequencies. Our model addresses how load-dependent dynamics effects directed functional connectivity. It also suggests abrupt changes in neuronal coupling above capacity and a break-down of Prediction signals. Finally, it shows that functional hierarchies in large cortical networks do not necessarily change when neuronal coupling changes.

Results

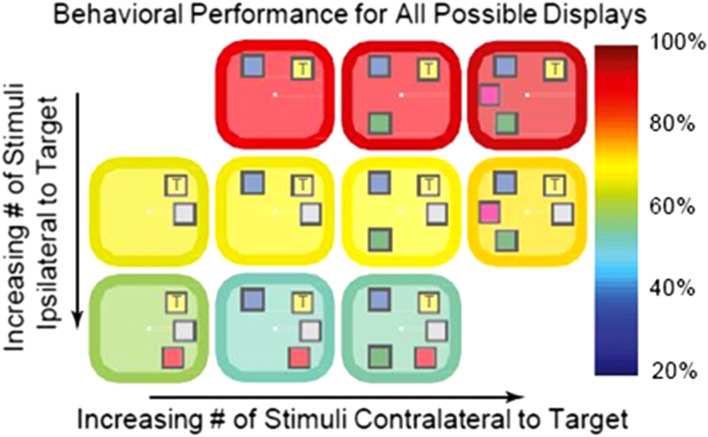
Our change detection task and behavioral results have been described in detail (Buschman et al. 2011), see also Figure 1. Two monkeys were presented with a sample array of 2–5 colored squares for 800 ms. This was followed by a delay period (800- to 1000-ms). After that, a test array was presented. This differed from the sample array in that one of the squares had changed color (target). Monkeys were trained to make a saccade to the target. We analyzed LFP data from the memory delay period. During this delay, there was no sensory stimulation or motor responses that might affect neuronal dynamics. We examined the relationship between dynamics and functional connectivity.

Figure 1.

Behavioral performance (indicated by the color of the border/background) for all possible stimulus displays. Adding objects to the same side (ipsilateral) as the target (marked with a “T”) impaired performance (rows), whereas adding objects to the other side (contralateral) had no effect. This result argues for separate capacities in each hemisphere.

In our earlier work (Buschman et al. 2011; Kornblith et al. 2016), we found separate, independent capacities in the right versus left visual hemifields. Early in the memory delay, lower frequency power decreased with both ipsilateral and contralateral load but high frequency power increased only with contralateral load. By contrast, late in the memory delay, low-frequency power continued to decrease with ipsilateral load but increased with contralateral load. Also, ipsilateral load effects on high frequency power were weak and there was no effect of contralateral load. To sum up, there were different effects on power in the LIP–FEF–PFC network depending on whether load was presented in the ipsilateral or contralateral visual hemifield. This motivated a separate analysis of load effects for the 2 hemifields. This was also supported by (1) different processing of contralateral and ipsilateral stimuli found in visual perception studies (Tootell et al. 1998) and (2) anatomical differences in frontoparietal connectivity for ipsilateral and contralateral connections (Barbas et al. 2005). (3) Our own prior results using these same data. Behaviorally and neurophysiologically, the 2 hemifields seem separate and independent. Increasing stimulus load only affected behavioral performance to stimuli on the same side, not those in the opposite hemifield (Buschman et al. 2011). Neurophysiologically, we see the same thing. Stimulus information in spiking is only degraded by increases in stimulus load in the same hemifield (Buschman et al. 2011) and, likewise, effects on LFP power are hemifield dependent.

In short, we assumed that power changes found in (Kornblith et al. 2016) reflect coupling changes and analyzed the effects of ipsilateral and contralateral load separately. The idea that changes in phenomenological measures, like power, reflect coupling changes is common; for example, pathological oscillations are thought to be the signature of aberrant neuronal coupling in psychiatric diseases (Uhlhaas and Singer 2012), such as autism (Dickinson et al. 2015) or schizophrenia (Gonzalez-Burgos and Lewis 2008). Further, in previous work (Miller and Cohen 2001) we suggested that FB signals from PFC to lower areas support successful execution of working memory and decision making tasks. In this task, the animal successfully performed the task below but not above the cognitive capacity limit. We therefore expected PFC coupling to change below and above the capacity limit.

We focused on changes between (1) early versus late delay and (2) different load values (1–3 items per hemifield). We expected differences in coupling for early and late delay because our prior work using these data showed differences in power and synchrony between the early and late delay that depended on load and laterality (Kornblith et al. 2016). We therefore asked if there were any differences in PFC signals between early and late delay. We also tested different loads because performance degrades with increased load (Buschman et al. 2011).

To sum up, both electrophysiological and behavioral data suggest that coupling may change in the PFC–FEF–LIP network. Our analysis comprised 3 parts. First, we found the coupling pattern in the PFC–FEF–LIP network during the memory delay in order to determine their basic functional connectivity. Second, we asked whether the strength of connections changed with changes in contralateral and ipsilateral load and between the early versus late memory delay. Third, we examined how changes in load below versus above the animal’s behavioral capacity limit affected network connectivity.

Functional Hierarchy in the PFC–FEF–LIP Network

We first examined the functional hierarchy between the PFC, FEF, and LIP. To find this hierarchy, we adapted our earlier canonical microcircuit (CMC) model (Pinotsis et al. 2014; Bastos et al. 2015) to describe activity in the PFC–FEF–LIP network (Figure 2).

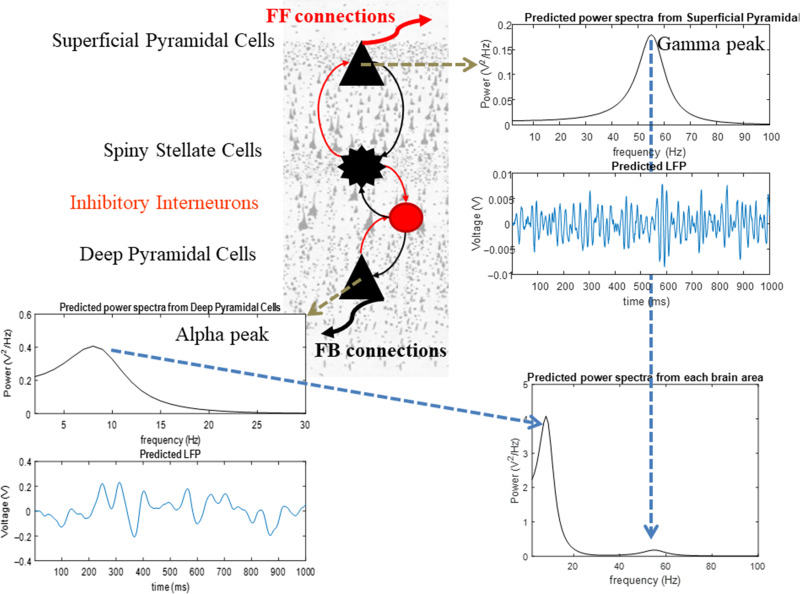
Figure 2.

The canonical microcircuit model (CMC). The model suggests a canonical cortical architecture for the primate cortex. There are 4 populations of neurons (spiny stellate cells, superficial and deep pyramidal cells and inhibitory interneurons). These are connected together with excitatory (red) and inhibitory (black) intrinsic connections (thin lines). This set of populations and connections is motivated by anatomical and theoretical considerations supporting a canonical cortical microcircuitry (Douglas and Martin 2007; Bastos et al. 2012; Pinotsis et al. 2013). Power spectra and LFPs produced by these cells are shown in the top right and bottom left plots, respectively. Power spectra from each brain area are shown in the bottom right plot. Model parameters are chosen so that superficial and deep pyramidal cells oscillate at the gamma and alpha bands. These different laminar responses result from assuming different time constants (depending on GABAergic vs. glutamatergic neuromodulation) and intrinsic delay parameters for the different neuronal populations.

The CMC model is based on the Predictive Coding Model (Bastos et al. 2012) and experimental (Buffalo et al. 2011) and theoretical observations (Bauer et al. 2014; Friston et al. 2015). It builds on experimental observations that superficial and deep pyramidal cells oscillate at the gamma and alpha band, respectively (Bastos and Vezoli et al. 2015; Michalareas et al. 2016) and that superficial and deep pyramidal cells are the main origins of feedforward (FF) and feedback (FB) connections (Hilgetag et al. 1996; Vezoli et al. 2004). These spectral asymmetries across cortical layers (i.e., gamma power predominant in superficial and alpha power predominant in deep layers) follow from Predictive Coding where FB connections convey Prediction signals at slower time scales (alpha) compared with bottom-up connections that convey Prediction Error signals at faster time scales (gamma). Following these observations, the parameters of the CMC model were chosen so that superficial and deep pyramidal cells oscillate at the gamma and alpha band, respectively (Fig. 2).

We extended the CMC model to construct a large-scale model that could describe the activity in the PFC–FEF–LIP network (the “large-scale CMC model”; Fig. 3). It is an extension of the single area CMC model shown in Figure 2 and comprises FF and FB connections between PFC, FEF and LIP (red and black thick lines in Fig. 3). These connections define an anatomical hierarchy (see also Supplementary Experimental Procedures and Methods section). Lower areas send signal to higher areas via FF connections and receive top down input from them via FB connections. FF (respectively FB) connections are assumed to be excitatory (respectively inhibitory). FF (respectively FB) input from area A to area B results in an increase (respectively decrease) of activity in area B that is proportional to the activity in area A. The constant of proportionality is the FF (respectively FB) coupling strength. In Predictive Coding, FF and FB signals form the basis of how the brain understands the world: according to this theory, the brain’s goal is to predict sensory inputs. Brain areas interact recurrently so that Predictions (FB signals) are compared with sensory inputs and updated according to how much they deviate from them (FF signals). The theory suggests that this iterative process is repeated until deviations are minimized. Thus, FF (sensory) input excites higher cortical areas. FB signals inhibit FF inputs and allow only FF signals that were not predicted to be passed forward.

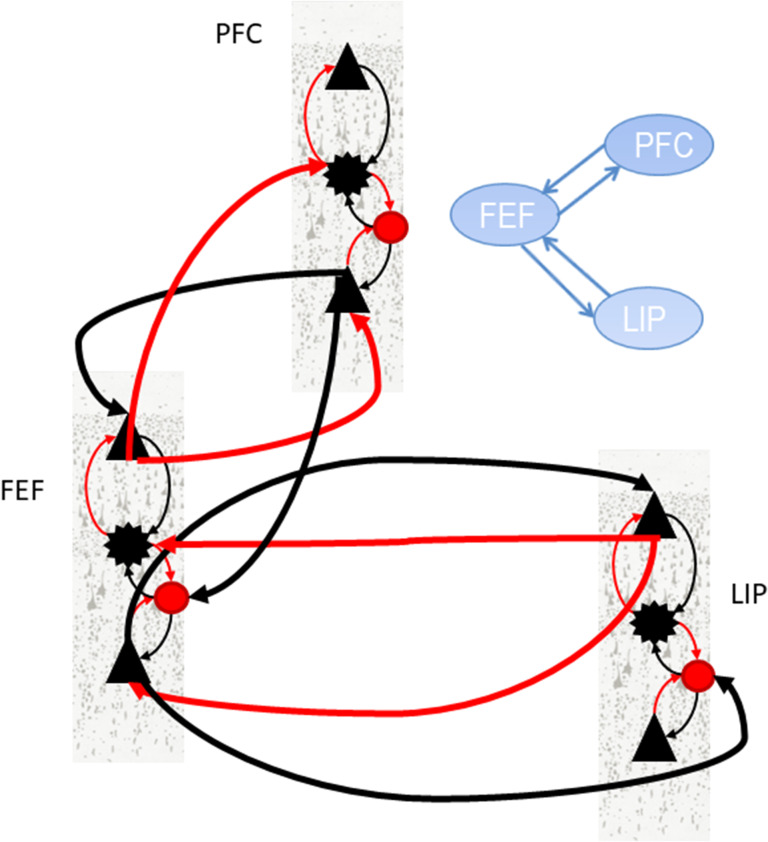
Figure 3.

Large-scale CMC model. The model describes the large-scale structure of the primate cortex. Different brain areas are connected with extrinsic connections (thick lines). Intrinsic connections are as described in Figure 2. Extrinsic connections are as follows: Feedforward (FF) connections are assumed to originate in superficial layers and target input spiny stellate cells and deep pyramidal cells. Feedback (FB) connections are assumed to originate from deep layers and target superficial pyramidal cells and inhibitory interneurons. This pattern of extrinsic and intrinsic coupling has been shown to explain activity in parietal and frontal areas (Heinzle et al. 2007; Ma et al. 2012; Phillips et al. 2015; Ranlund et al. 2016; Díez et al. 2017). We have omitted extrinsic connections between PFC and LIP in the figure and depicted 1 out of 4 possible connection patterns that correspond to results from anatomical studies (Hilgetag et al. 2016). This is variant “FEF” of the large-scale CMC model (see main text for details).

To sum so far, our large-scale CMC model predicts oscillatory interactions and hierarchical relations in the PFC–FEF–LIP network based on FF and FB coupling between brain areas and local oscillatory dynamics within each area. It also assumes that FF and FB signals propagate at different frequencies and convey Prediction Errors and Predictions, respectively. Thus, it allows us to test whether changes in phenomenological measures, like power, reflect coupling changes. It also allows us to link coupling changes due to memory load to Predictive Coding. Increasing FB (respectively FF) signals with increasing load would correspond to stronger Predictions (respectively Prediction Errors). In this context, failure to perform the task when the number of stimuli exceeds cognitive capacity, implies a failure in Prediction signals. Thus, we expected FB from PFC to break down above the capacity limit.

The anatomical hierarchy shown in Figure 3 follows recent studies that exploit differential laminar source and termination patterns and tract tracing experiments to obtain the hierarchical distribution of brain areas (Hilgetag et al. 2016; Markov et al. 2014; Medalla and Barbas 2006). However, whether the functional hierarchy will follow the anatomical hierarchy is not clear. Functional hierarchies are not as robust as anatomical hierarchies and are often task-dependent (Buschman and Miller 2007; Bastos and Vezoli et al. 2015).

To find the functional hierarchy in the PFC–FEF–LIP network, we fitted the large-scale CMC model to CSD data from trials with the same memory load. This data contained information about oscillatory interactions in different frequency bands (Kornblith et al. 2016). For model fitting, we used Dynamic Causal Modeling (DCM) (David et al. 2006; Pinotsis and Friston 2014; Moran et al. 2015; Pinotsis et al. 2016; Garrido et al. 2009; Kiebel et al. 2009). DCM is a standard approach for model fitting. It has been widely used to determine the directionality of information flow and functional hierarchy in brain networks (Gluth et al. 2015; Hare et al. 2011; Hillebrandt et al. 2014; Li et al. 2014; Smith et al. 2006). Specifically, DCM has been applied to the analysis of neuronal activity in frontal and parietal areas and during functions ranging from attention to memory, decision making, and psychiatric diseases, similarly to the frontoparietal network and working memory task considered here (Mechelli et al. 2004; Garrido et al. 2009; Wang et al. 2010; Jacques et al. 2011; Vossel et al. 2012; FitzGerald et al. 2015).

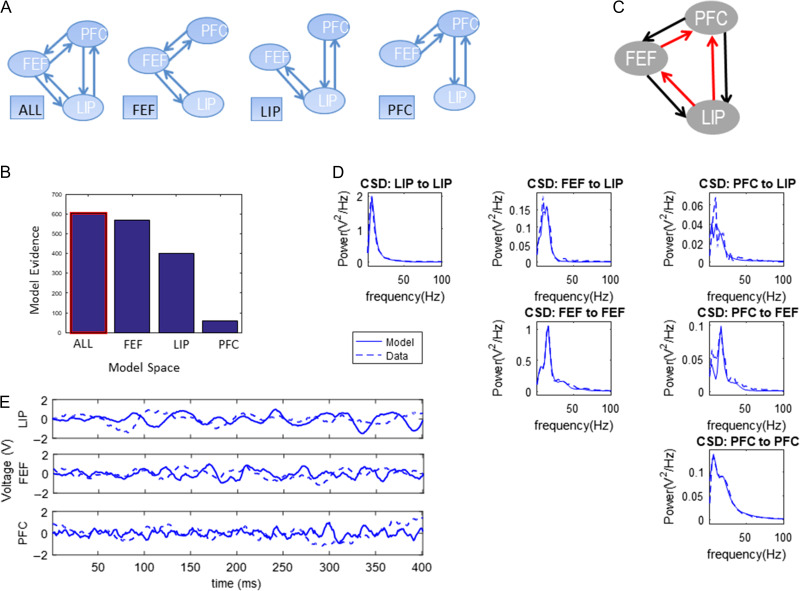
To find the functional hierarchy, we used Bayesian model comparison (BMC) (Friston et al. 2007). BMC is a process comprising (1) model fitting and (2) computation of model evidence. Model evidence is a mathematical quantity that expresses how likely each a model is for a given dataset. Usually one considers a set of models (model space) and finds the model with highest evidence. We first fitted different variants of the large-scale CMC model (Fig. 3) to our data. These model variants differed in the connections between PFC, FEF and LIP. They are shown in Fig. 4A and describe all possible functional hierarchies. They are called “ALL,” “FEF,” “LIP,” and “PFC,” respectively. Model “FEF” is the model where FEF is connected to PFC and LIP and there are no direct connections between PFC and LIP. This was the coupling of the model shown in Figure 3 and is what one would expect from anatomical studies (Hilgetag et al. 2016). Alternatives are described by the other 3 models. These are similar to model “FEF,” where FEF is replaced by PFC and LIP. Model “ALL” assumed that all areas were connected and information flows in FF and FB directions between all areas. When 2 areas are connected with both FF and FB connections, we say that they are connected with reciprocal (R) connections.

Figure 4.

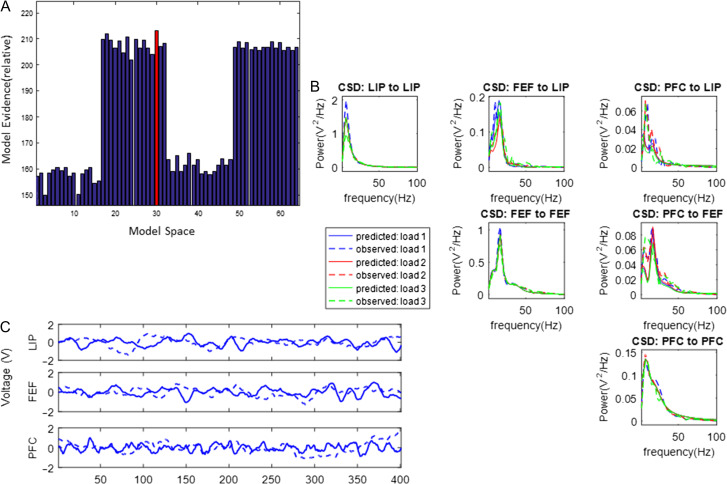
(A) Possible functional hierarchies in the PFC–FEF–LIP network. (B) Bayesian model comparison (BMC) results after fitting variants of the large-scale CMC model to trials with one contralateral object during the early delay period. (C) The model with highest evidence was model “ALL.” All brain areas occupy the same hierarchical level. (D) Model fits to CSD data. (E) Using posterior parameter estimates, we simulated LFPs. In all plots, dashed lines depict model predictions and solid lines depict observed data (CSD or LFPs).

To find the model evidence, BMC uses an approximation called Free Energy. Conceptually, BMC can be thought of as a generalization of classical model comparison approaches, for example, Bayesian Information Criterion (BIC). The difference is in the cost function used. BMC uses Free Energy that also includes a complexity term in addition to an accuracy term. For a model to have the highest evidence both terms should be maximized: the accuracy term is maximized when the model fits the data best (i.e., it has the smallest error). The complexity term is maximized when all model parameters are necessary for fitting the data. If a model has parameters that are not necessary, this term will not be maximum and therefore the evidence for that model will be lower. The reason is that unnecessary parameters will have large posterior correlations between them. Each parameter does not explain the data in a unique way (similarly to coefficients of determination in classical statistics, posterior correlations quantify the explanatory power of model parameters in Bayesian statistics). These correlations will enter into the complexity term and make it smaller (for more details, see Friston et al. 2007). Even if the model with the highest number of parameters fits the data best (has the maximum accuracy) this model will not have the highest evidence if some parameters are unnecessary (the complexity term will not be maximum).

We performed BMC between variants of the large-scale CMC model. This allowed us to find the model that best fit the data and whose parameters were necessary for fitting the data (i.e., the model that did not “over-fit” the data). We fitted the 4 models of Figure 4A to 4 different datasets. The first 2 datasets included CSD data from trials with 1 contralateral object, from the early (500–900 ms after sample onset) or late (1100–1500 ms after sample onset) delay period. The last 2 datasets included CSD data from trials with one ipsilateral object (and the same delay periods). The winning model had the highest evidence among all models considered. In general, the difference in model evidence between (winning) model A and its runner up B is useful because it immediately yields the probability that model A is more likely than model B (this is called exceedance probability of model A vs. B) (To obtain the exceedance probability from the difference in model evidence one has to apply a sigmoid function (Kass and Raftery 1995).). It can be shown mathematically, that if this difference is bigger than 3, the exceedance probability is equal to 1, that is the winning model is 100% more likely than its runner up and any other model that was considered. A summary of the fitting process is included in section “Dynamic Causal Modeling” of Supplementary Material. This process has also been described in detail in several earlier publications (Friston et al. 2012; Pinotsis et al. 2014).

We first fitted CSD data from trials with one contralateral object during the early delay period (different memory loads are presented below). The results of our analysis are shown in Figure 4. Model fits are shown in Figure 4D. Plots show alpha and gamma power model fits: in most cases model predictions (solid lines) fully overlapped with experimental data (dashed lines). This is not surprising as priors have been carefully chosen to accurately reproduce alpha and gamma activity (Bastos et al. 2012; Friston et al. 2015). Small discrepancies between data and model fits occurred only when CSD power was weak (~0.05 V²/Hz, top right panel in Fig. 4D). Model fitting yielded posterior parameter estimates. Including these estimates in our model, we obtained simulated LFPs. These are shown with solid lines in Figure 4E. Observed LFPs are shown with dashed lines.

Figure 4B shows the model evidence for the 4 models tested (corresponding to possible hierarchies shown in Fig. 4A). The winning model was model “ALL”: all areas were connected with reciprocal connections (highlighted with a red frame in Fig. 4B, shown in Fig. 4C). Model fits and simulated LFPs show a good fit to experimentally observed data (Fig. 4D,E, respectively).

Supplementary Figures S1–S3 show the corresponding results for contralateral load and late delay and ipsilateral load and early and late delay, respectively. These are very similar to Figure 4. Although load effects on power were different between early and late delay and for contralateral and ipsilateral load (see Fig. 5 in Kornblith et al. 2016), we found that the functional hierarchy did not change between the early and late delay periods and was also the same for contralateral and ipsilateral objects. Model fits and LFPs are also shown in Supplementary Figures S1B–S3B and S1C–S3C and are very similar to Figure 4D,E.

For a contralateral object, the difference in model evidence between model “ALL” and its runner up was $\mathrm{\Delta }F=29$ for early delay and $\mathrm{\Delta }F=111$ for late delay (Fig. 4B and Supplementary Fig. S1A). For ipsilateral object, the difference in model evidence of the winning model “ALL” with respect to the runner up was $\mathrm{\Delta }F=60$ during early delay and $\mathrm{\Delta }F=21$ during late delay (Supplementary Figs S2A and S3A). Because $\mathrm{\Delta }F$ was bigger than 3, model “ALL” had exceedance probability equal to 1 for all 4 datasets considered. These results were robust to using trials with different memory loads (see Supplementary Fig. S4). In all cases, model “ALL” had the highest evidence. This means that the functional hierarchy in the PFC–FEF–LIP network did not change when changing memory load and for different parts of the delay period despite the different load effects on spectral power (A careful reader might question if finding model “ALL” (the model with most parameters) as the winning model might be the result of overfitting. Above, we laid out technical arguments about how the particular cost function (Free Energy) used for model comparison prevents this. We also noted that we obtained the same result using 12 different datasets (Fig. 4B and Supplementary Figs S1A–S3A and S4). On top of these arguments, we note that we found a different model as the winning model using the same datasets but changing the threshold of high pass filtering. During our preliminary investigations (not shown), we had found winning model “FEF” by using trials where ipsilateral load was varied and focusing on low frequency responses only (2–50 Hz).).

To sum so far, we found that all 3 brain areas in the PFC–FEF–LIP network had reciprocal functional connections. In other words, all 3 areas were on the same hierarchical level. The pattern of FF and FB connections (functional hierarchy) did not change with memory load and for early versus late delay. Next, we compared alternative variants of the winning model of the first part of our analysis (model “ALL”) where we allowed a different subset of FF and FB connections to change with load (and the rest of the connections were left unaffected). This revealed changes in the strength of functional connections with changes in memory load (Note that in the analysis above we fitted the large-scale CMC model to data from trials with the same memory load. Our goal was to test whether certain connections were present or not. In the analysis below, we fitted the model to data from trials with different memory load simultaneously. This allowed us to focus on changes of model parameters with increasing load.).

Feedforward and Feedback Coupling Strengths Changed With Load and Time

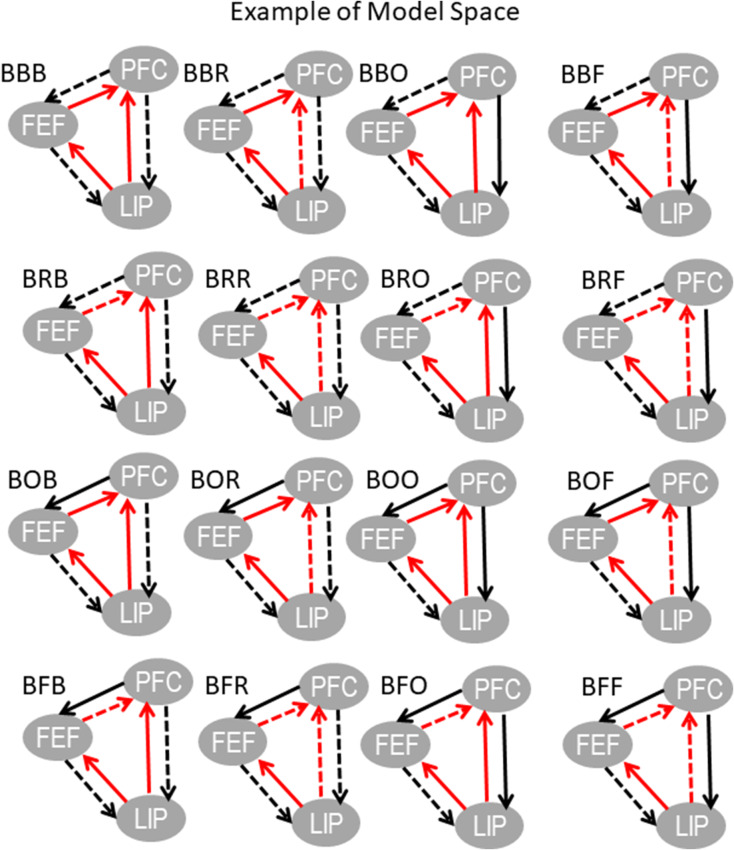
Above, we saw that the model “ALL” best captured the functional hierarchy between PFC, FEF, and LIP (i.e., they all had reciprocal, R, connections with each other). Here, we test whether FF, FB, or R coupling in the early versus late memory delay was affected by working memory load. We did so using BMC to compare variants of model “ALL”. In these model variants, different FF, FB, or R connections were allowed to change for different load conditions. These model variants are described by an acronym shown in the entries of Table 1. They corresponded to all possible connections that could change with increasing object load and included models where connections did not change. There were 64 such variants. The first 16 variants (first 2 lines of Table 1) are also depicted in Figure 5. The same variant was fitted to CSD data for all contralateral and ipsilateral load conditions and from data from early or late memory delay. Coupling parameters were allowed to change progressively between the lowest and highest load conditions. Coupling changes between different load conditions were assumed to be linear increments (increases or decreases) to coupling corresponding to lowest load. In other words, load changes were assumed to have modulatory effects on cortical coupling and are called trial specific effects in DCM. This is similar to trial specific effects in fMRI literature (Coderre and van Heuven 2013; Den Ouden et al. 2008; Gordon et al. 2015).

Table 1.

Model space including all possible variants of model “ALL”

1: BBB	2: BBR	3: BBO	4: BBF	5: BRB	6: BRR	7: BRO	8: BRF
9: BOB	10: BOR	11: BOO	12: BOF	13: BFB	14: BFR	15: BFO	16: BFF
17: RBB	18: RBR	19: RBO	20: RBF	21: RRB	22: RRR	23: RRO	24: RRF
25: ROB	26: ROR	27: ROO	28: ROF	29: RFB	30: RFR	31: RFO	32: RFF
33: OBB	34: OBR	35: OBO	36: OBF	37: ORB	38: ORR	39: ORO	40: ORF
41: OOB	42: OOR	43: OOO	44: OOF	45: OFB	46: OFR	47: OFO	48: OFF
49: FBB	50: FBR	51: FBO	52: FBF	53: FRB	54: FRR	55: FRO	56: FRF
57: FOB	58: FOR	59: FOO	60: FOF	61: FFB	62: FFR	63: FFO	64: FFF

Note: Each variant had an acronym. The first letter in this acronym corresponds to the connections that were allowed to change with load between LIP and FEF. The second letter corresponds to the connections that were allowed to change between FEF and PFC. The third letter corresponds to the connections that were allowed to change between PFC and LIP. The letters F, B, and R correspond to feedforward, feedback, and reciprocal connections, respectively. The letter O corresponds to connections that were not allowed to change.

Figure 5.

Plots showing variants of model “ALL.” These correspond to the 16 variants included in first 2 lines of Table 1. Each variant had an acronym. The letters in the acronym correspond to connections that were allowed to change for different load conditions. These are also shown with dashed lines. Solid lines depict connections that were not allowed to change.

Each variant had an acronym (Table 1). For example, in variant BBF, the feedback connections between LIP and FEF and FEF and PFC and the feedforward connections between LIP and PFC were allowed to change with load. Connections that were not allowed to change with increasing memory load were depicted with solid lines. Connections that were allowed to change were depicted with dashed lines. Using BMC, we identified the most likely model (i.e., the set of connections affected by contralateral and ipsilateral load and in the early vs. late delay) among the 64 alternatives (see Fig. 6A for contralateral load and early delay and Supplementary Figures S5A–S7A for contralateral load and late delay and ipsilateral load and early and late delay, respectively). These Figures include bar plots of model evidence. We call the space of all possible variants “model space”. This is shown in the horizontal axis and is the same as in Table 1. Figure 6B,C and Supplementary Figures S5B–S7B and S5C–S7C show model fits to CSD data and simulated and observed LFPs, respectively. These are similar to results in Figure 4D,E and Supplementary Figures S1B–S3B and S1C–S3C.

Figure 6.

Contralateral WM Load Effects on FF and FB coupling in the PFC–FEF–LIP network during early delay. Plots follow the format of Figure 3. (A) Bayesian model comparison (BMC) results after fitting the 64 variants of model “ALL” included in Table 1. (B) Model fits to CSD data. (C) Simulated and observed LFPs. In all plots, dashed lines depict model predictions and solid lines depict observed data (CSD or LFPs).

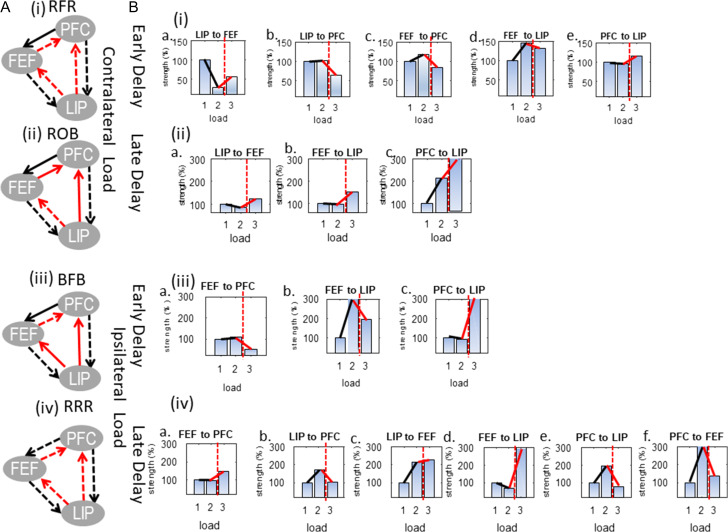
The winning models are shown in Figure 7A(i)–(iv): RFR and ROB were the winning models for contralateral load during early and late delay and BFB and RRR were the winning models for ipsilateral load during early and late delay. Model evidence of winning models is shown with red bars. The difference in model evidence between them and their runner ups was $\mathrm{\Delta }F=1$ and $\mathrm{\Delta }F=24$ for contralateral load during early and late delay and $\mathrm{\Delta }F=0.7$ and $\mathrm{\Delta }F=4$ for ipsilateral load, respectively. The corresponding model exceedance probabilities were 74% and 100% for variants RFR and ROB and 65% and 100% for variants BFB and RRR, respectively.

Figure 7.

(A) Models that had the highest evidence for each experimental condition. Dashed lines denote connections that were modulated by load. RFR and ROB were the winning models for contralateral load during (i) early and (ii) late delay and BFB and RRR were the winning models for ipsilateral load during (iii) early and (iv) late delay. (B) Changes in neuronal coupling strengths due to changes in (i) contralateral load during early delay; (ii) contralateral load during late delay; (iii) ipsilateral load during early delay; and (iv) ipsilateral load during late delay. Coupling strengths corresponding to the lowest load are shown with blue bars. The cognitive capacity limit is shown with a vertical red dashed line. Strength changes below (respectively above) the capacity limit are shown with black (respectively red) lines.

What these models showed was that changing contralateral load affected R coupling between LIP and FEF and FB coupling between PFC and LIP throughout the delay period (Fig. 7A(i, ii)). However, FF input to PFC from the other 2 brain areas was affected by contralateral load only during early delay (Fig. 7A(i)). Also, changing ipsilateral load affected FB coupling between LIP and the other 2 areas and FF coupling between FEF and PFC throughout the delay period (Supplementary Fig. S7A(iii, iv)). During late delay, on the other hand, all connections in the network were affected by changing load: on top of the above connections, FF coupling between LIP and the other 2 areas and FB coupling between FEF and PFC changed with ipsilateral load (Supplementary Fig. S7A(iv)) (The results of Fig. 7A show that models with R of FF connections between LIP and FEF are favored in the corresponding model comparisons. These are the models 17–32 and 49–64, see also rows 3–4 and 7–8 in Table 1. These results can also be useful for family-wise inference which we will consider in future work.).

To sum this analysis, we identified different sets of connections that were affected by increasing memory contralateral and ipsilateral load during different parts of the delay period. Having established load-specific changes in connection strengths, we can now proceed to our last analysis. In this last set of analyses we examine in greater detail how coupling changed with changes in load below and above the animal’s working memory capacity.

Increases and Decreases in Feedforward and Feedback Coupling Strengths Below and Above Capacity

Here, we explore the changes in coupling between areas as a result of changes in load. To organize this discussion, we distinguish changes below (from load 1 to load 2) and above (from load 2 to load 3) the animal’s behavioral capacity. There were as many coupling parameters in our model as thick lines in winning model “ALL” (Fig. 4C).

The results below were obtained from the same model fits as in the previous section. We used model fits of the winning model only (winning models are shown in Fig. 7A). In the previous section, the winning model (and the other 63 alternatives of Table 1) was fitted to CSD data for all load conditions simultaneously. Coupling strengths were allowed to change progressively between the lowest and highest contralateral and ipsilateral load. We also used CSD data obtained during early and late delay. The set of coupling strengths that changed with load determined the winning model in each case. Below, we discuss these strengths and their progressive changes (Fig. 7B).

Coupling strengths corresponding to the lowest load (one contralateral or ipsilateral object) were rescaled so that they were equal to 100%. The 3 blue bars in each panel show coupling strength for loads 1, 2, and 3 (from left to right). This reveals progressive changes in the same coupling strength as load increases. Strengths were normalized with respect to the lowest load condition. Besides the blue bars, each panel includes 3 additional lines connecting adjacent bars: black (shows coupling changes below the capacity limit), solid red (shows coupling change above the capacity limit) and dashed red (separates coupling below and above the capacity limit). Recall that FB connections were inhibitory while FF connections were excitatory (these are shown with black and red arrows connecting brain areas in Fig. 4C). In Figure 7B(i) (respectively B(ii)), we show changes in coupling strengths during the early (respectively late) delay period when contralateral load changes. In Figs 7B(iii) (respectively 7B(iv)), we show the corresponding changes when ipsilateral load changes.

Almost all parameters (15/17) were significantly modulated above the capacity limit: they showed marked increases or decreases of at least 25% or more. We will call these changes “strong” as opposed to other changes that we will call “weak.” Below the capacity limit fewer parameters were strongly modulated (9/17). We first focused on changes in coupling strength below the capacity limit. These changes can be readily seen by focusing on the slope of black lines in Figure 7B(i, ii): almost horizontal (respectively oblique) lines correspond to weak (respectively strong) changes. Changes in connections involving PFC followed a consistent spatiotemporal pattern regardless of whether load change was contralateral or ipsilateral: they were weak during early delay and strong during late delay signaling bigger PFC involvement closer to the decision time (i.e., during late delay) (This general trend had one exception: the FF connection from FEF to PFC which was weakly modulated when increasing ipsilateral load during late delay, see Fig. 7B(iv)a.). Conversely, changes in the other FF and FB connections (between LIP and FEF) followed the opposite pattern: they were strong during early delay and weak during late delay but for contralateral load only (for ipsilateral load they were strong throughout the delay period).

Specifically, for contralateral load during early delay, we observed strong changes in the FF and FB connections between LIP and FEF but not PFC, compare black lines in Figure 7B(i)a, (i)d with black lines in Figure 7B(i)b, (i)c, (i)e. Similarly, for ipsilateral load, compare black line in Figure 7B(iii)b with black lines in Figure 7B(iii)a, (iii)c. This also means that excitatory input to PFC did not increase due to higher load (black lines in Fig. 7B(i)b, (i)c, (iii)a). At the same time, FEF input from LIP decreased with increasing load (black line in Fig. 7B(i)a) and input from FEF to LIP increased (black lines in Fig. 7B(i)d, (iii)b).

For contralateral load during late delay, the above pattern of connection changes was reversed: connections between LIP and FEF showed weak modulations with load (black lines in Fig. 7B(ii)a, (ii)b). At the same time, FB input from PFC to LIP showed a strong increase with increasing load (black line in Fig. 7B(ii)c). Similarly, for ipsilateral load FF and FB PFC connections also showed a strong increase with load (black lines in Fig. 7B(iv)b, (iv)e, (iv)f). However, in contrast to what we observed for contralateral load, connections between LIP and FEF continued to show strong modulations (as in the early delay period, see black lines in Fig. 7B(iv)c, (iv)d).

Interestingly, above the cognitive capacity limit (when going from load 2 to load 3), changes in connections in the PFC–FEF–LIP network were strong. The only exception was the LIP–FEF connections during early delay for contralateral load and late delay for ipsilateral (red lines in Fig. 7B(i)d, (iv)c). We will see below that connections between LIP and FEF showed the opposite pattern of changes above capacity in comparison to their pattern below capacity. Also, signals to and from PFC were affected by load during both early and late delay (below capacity they were affected by load only during late delay). Most importantly, FB signals from PFC and FEF were modulated differently for contralateral and ipsilateral load.

During early delay, FF input to PFC from the other 2 brain areas was strongly reduced above the capacity limit, see red lines in Figure 7B(i)b, (i)c, (iii)a. Similarly, FB input from PFC to LIP increased above capacity during early delay (red lines in Fig. 7B(i)e, (iii)c). This was also the case for contralateral load during late delay (red line in Fig. 7B(ii)c). However, for ipsilateral objects and late delay FB signals from PFC broke down: they showed a strong reduction (as opposed to increase in all other cases) when exceeding the capacity limit (red lines in Fig. 7B(iv), (iv)f). This was accompanied by a strong reduction (break down) in FF input from LIP to PFC (red line in Fig. 7B(iv)b). These were the only cases where coupling above the capacity limit was very similar to coupling for lowest load. FF input from FEF on the other hand showed an increase (red line in Fig. 7B(iv)a). FF input from LIP to FEF also increased above capacity regardless of object hemifield and delay period (red lines in Fig. 7B(i)a, (ii)a, (iv)c). FB input from FEF reduced for early (red lines in Fig. 7B(i)d, (iii)b) and increased for late delay above capacity for both contralateral and ipsilateral objects (red lines in Fig. 7B(ii)b, (iv)d).

Above we described coupling changes with increasing load. To quantify how likely these changes were we used posterior probabilities (coupling estimates were found using DCM which is a Bayesian approach for model fitting). These are shown in Supplementary Figures S8 and S9. They are the probabilities of a significant nonzero change with respect to the coupling strength for the lowest load. Because all parameters were normalized to the lowest load condition, we included posterior probabilities only for load 2 and load 3. These are shown in matrix form. Columns correspond to the brain areas from which connections originated and rows to areas where they terminated. The number of these matrices is one less than the number of possible loads (there are no probabilities for the lowest load). The posterior probability of changes in coupling strengths for contralateral load ranged between 53% and 100% (respectively 62–100%) for early (respectively late) delay, see Supplementary Figure S8. The posterior probabilities for coupling parameters for ipsilateral load ranged between 71% and 100% (respectively 54–100%) for early (respectively late) delay, see Supplementary Figure S9.

Discussion

We studied the effects of changing working memory load on neuronal dynamics during a change detection task. We analyzed CSD data obtained using LFPs from frontal and parietal areas, namely, PFC, FEF, and LIP. Activity in this frontoparietal network has been found to consistently change with training (Goldman-Rakic 1995; Li et al. 1999) and has been associated with cognitive capacity (Rottschy et al. 2012).

We followed up on earlier work (Buschman et al. 2011; Kornblith et al. 2016), where we had found that neuronal activity in high, but not low, frequencies reflects independent processing of ipsilateral and contralateral objects and changes substantially between early and late delay period. Independent processing of objects in different hemifields has also been confirmed by (Matsushima and Tanaka 2014) and is supported by early anatomical studies (Goldman-Rakic and Schwartz 1982). In (Kornblith et al. 2016), neuronal activity changes with load were captured as spectral power effects. However, these effects were similar below and above the cognitive capacity, which appears at odd with a reduction in behavioral performance observed when capacity is exceeded. Further, earlier power and synchrony analyses did not describe the directionality of neuronal interactions. Here, we aimed at a mechanistic explanation of load effects by focusing on changes in the strength and directionality of neuronal coupling. We extended our earlier model based on Predictive Coding (CMC model; Pinotsis et al. 2014; Bastos and Litvak et al. 2015) and used it to analyze CSD data. The CMC model can predict oscillatory interactions and hierarchical relations in the PFC–FEF–LIP network based on FF and FB coupling between brain areas and local oscillatory dynamics within each area. It has been validated pharmacologically (Muthukumaraswamy et al. 2015), using data from single-gene mutation channelopathy (Gilbert et al. 2016) and aging studies (Cooray et al. 2014; Moran et al. 2014). The model has also explained the manipulation of sensory expectation and attention engaging frontoparietal networks in healthy subjects and patients (Auksztulewicz and Friston 2015; Cooray et al. 2014; Díez et al. 2017; Phillips et al. 2015; Ranlund et al. 2016). A very similar model was recently used to explain context-dependent dynamics in hierarchical brain networks (Mejias et al. 2016).

We first studied the basic functional hierarchy in the PFC–FEF–LIP network. We determined its form and asked whether this changed with memory load and time during the delay period. Anatomical connections provide the substrate for functional connections but functional hierarchies can be different than anatomical hierarchies. They can be task-dependent and even change during a task (Buschman and Miller 2007; Bastos and Vezoli et al. 2015) as a result of goal-directed behavior (Miller 1999; Miller and Cohen 2001) and of processing abstract information (Koechlin et al. 2003). Also, there are reciprocal anatomical connections between frontal areas are other frontal and parietal areas (Medalla and Barbas 2006; Hilgetag et al. 2016). Some studies have placed PFC at the top and parietal areas at the bottom of functional hierarchies in visual perception tasks (Bastos and Vezoli et al. 2015; Michalareas et al. 2016). However, the functional hierarchy in the change detection task we studied here was unknown.

To find the functional hierarchy, we compared variants of our model corresponding to different hierarchical relations between PFC, FEF, and LIP using BMC (Friston et al. 2007). We found that PFC, FEF, and LIP had reciprocal functional connections (they were at the same hierarchical level). This result was the same regardless of memory load and time during the delay period. However, load effects on power were different of low for contralateral and ipsilateral objects and early versus late delay (Kornblith et al. 2016). Therefore, it might well be that although the functional hierarchy remained the same across trials with different load and throughout the delay period, the amount of signal transmitted through FF and FB connections, that is, the strength of FF and FB connections, changed with load and time.

Thus, we then identified different subsets of FF and FB connections whose strength changed with load during different parts of the delay period. We used BMC to compare different models corresponding to all possible combinations of connections that might be affected by load. After finding the most likely model, we focused on the corresponding changes in coupling strengths. These explain the weak load effects on power (1–2% power change per added object) found in Kornblith et al. (2016) without changing the functional hierarchy.

We found that below the capacity limit connections involving PFC were affected later than connections involving other frontal and parietal areas for contralateral and ipsilateral load. During early delay, connections between LIP and FEF were strongly affected by load while connections involving PFC did not change much. FF input from LIP decreased with increasing load while FB input to LIP increased. This could be related to the fact that receptive fields observed in LIP are unilateral and have a narrow spatial tuning (Platt and Glimcher 1998). During late delay, connections involving PFC were strongly modulated for contralateral and ipsilateral load but connections between LIP and FEF were not affected for contralateral load. However, when ipsilateral load changed, changes in connections between LIP and FEF remained strong during late delay (similarly to early delay). This could be related to the widespread and more dense patterns of ipsilateral as opposed to contralateral connections to frontal areas (Barbas et al. 2005). Based on the above results, our model predicts that, below the capacity limit, PFC engages strongly in network activity only close to the decision time (above capacity, PFC engages throughout the delay period, see below). Further, as load increased, we observed increases in both FF input to PFC and FB signals from PFC to other frontal and parietal areas. These reflected increased FF drive due to higher load and increasing FB stabilizing signals from PFC to counteract increased in cognitive demands (load) due to increased FF drive in earlier areas. They are similar to earlier modeling results (Macoveanu et al. 2006; Edin et al. 2009; Wei et al. 2012).

Above the cognitive capacity limit, connections that we had previously identified to be affected by load changes showed strong modulations. Connections involving PFC were affected by load throughout the delay period. Importantly, FB connections were modulated differently by contralateral and ipsilateral load. FB stabilizing signals from PFC increased above capacity for contralateral load but were significantly reduced (broke down) for ipsilateral load. This could explain reduced behavioral performance when the total number of objects in the same (but not the opposite) hemifield as the target object exceeded the capacity limit found by (Buschman et al. 2011). This also provides an interesting link to Predictive Coding. Break-down of Prediction signals coincided with impaired behavioral performance. This difference in coupling changes while changing contralateral versus ipsilateral load supports earlier findings about independent capacities of the 2 hemifields (Buffalo et al. 2011; Matsushima and Tanaka 2014). Stabilizing signals from FEF to LIP also broke down above capacity for ipsilateral, but not contralateral load. This supports an important role of FB from frontal areas in successful performance. Interestingly, FB signals from FEF broke down earlier than PFC FB signals (these broke down closer to decision time). This might be related to the fact that loss of information about object identity in PFC occurs later than other frontal areas (Buschman et al. 2011).

To sum up, we found that neuronal coupling changes as a result of changing the number of objects maintained in working memory. These changes are dynamic and evolve as the time for behavioral response (decision) approaches. We also found that FB coupling breaks down when the number of ipsilateral objects is above the cognitive capacity limit and that this occurs first in parietal and then frontal areas. These results shed new light in coupling changes that might underlie reduced cognitive capacity and behavioral performance. They also suggest network-specific pathological changes in neuronal coupling that might occur in various neurological and psychiatric diseases and disorders (Luck and Vogel 2013).

Funding

National Institutes of Mental Health (NIMH R37MH087027, NIMH R01MH091174) and the Picower Institute Innovation Fund.