1. Shaping the strengths of biomolecular NMR within a rapidly evolving landscape
Structural biology is witnessing exciting times as new technical developments change the way how biomolecules are studied. The spectacular leap that cryo-electron microscopy has made over the last years, enabled by combining better detectors, better analysis tools and improved samples, is much discussed [1]. In the X-ray diffraction (XRD) field, the introduction of groundbreaking new instrumentation, in particular X-ray free-electron lasers which enable entirely new applications [2,3], as well as arguably less spectacular but highly useful continued developments of automated beamlines, nano-focused beams or serial crystallography [4], also continue to maintain X-ray crystallography’s role as the workhorse of structure determination, with higher throughput and better data from smaller crystals. The capacity of biomolecular NMR to determine structures has also continuously improved. Higher field strengths, cryogenic probes and optimal isotope labeling have boosted sensitivity and resolution. More efficient and automated data treatment facilitates and accelerates structure determination [5]. Magic-angle spinning solid-state NMR (MAS NMR) has continued improving its capacity to determine structures, in particular due to faster spinning and proton detection. NMR stays an important technique also for determining structures of nucleic acids and their complexes.
Nonetheless, structure determination by NMR a is not expanding; in contrast to XRD and EM, the number of NMR structures deposited in the Protein Data Bank per year has in fact been slightly decreasing over the last decade to about 400, compared to about 10,000 by XRD and >800 by EM. In terms of the size of the protein structures, NMR lags behind other techniques: the vast majority of the ca. 12,000 structures solved to date by NMR are from proteins less than 20 kDa in size, suggesting that NMR has a rather limited window when it comes to structure determination.
Do these numbers mean that the role of NMR for understanding biomolecular function at the atomic level decreases? I argue that biomolecular NMR is rather focusing on its real strength, namely its ability to link static 3D structures to the function of the molecules by probing structural heterogeneity, dynamics and interactions. The rapid development of solid-state NMR for increasingly complex and large biomolecules, as well as the widespread application of specific isotope-labeling schemes in liquids and solids have largely removed inherent physical boundaries to the size and complexity of samples for which NMR can provide atomic-level insights into function. New developments, both in terms of hardware and pulse sequences, keep increasing the level of detail and accuracy at which (bio)molecular dynamics can be probed.
In this perspective I want to outline some of the exciting new developments and sketch some ideas we will likely see arising over the next years. I selectively pick some of the developments in terms of methods. Necessarily, the snapshot I provide here is subjective and its brevity excludes the possibility to extensively discuss and cite many other great developments, such as RDCs and PREs, and applications, and I apologize for the certainly biased glimpse of a very active field. Thorough reviews on the topic are available [6–13].
2. Principles and limits of NMR dynamics studies – And how to surpass them
Biomolecules are inherently flexible entities, performing their actions by dynamically sampling many conformations and by interacting with other molecules in a complex cellular environment. Ultimately, a complete description of a protein’s behavior at the molecular level should include not a single set of coordinates, but a wide ensemble of structures each with its free energy and the energy barriers that separate these states. No single technique is able to provide such a complete description of multiple structures – many of which are only very transient and low-populated – but NMR has capabilities which bring to light many aspects of these dynamic ensembles. The unique ability of NMR to probe dynamics comes from the combination of two factors, (i) the possibility to probe simultaneously hundreds to thousands of individual spins, no matter whether the biomolecule is folded, unfolded, inside a cell, in a crystal or part of a large assembly, and (ii) the multitude of parameters that one can, in principle, measure which carry information about motion. Spins are sensitive to their environment and thus to fluctuations of their environment, i.e., dynamics. Whenever one of its interactions within its environment fluctuates, namely the isotropic chemical shift, the chemical-shift anisotropy or quadrupolar coupling (for spins I > 1/2), or its dipolar/scalar couplings (including couplings to electron spins), these fluctuations may give rise to spin relaxation and an averaging of the given interaction.
In a nutshell, according to the time scale of the motion and the involved interactions we can find different cases:
-
(i)
If the motion occurs on a time scale that is very short compared to the strength of the interaction – e.g. the difference in the isotropic chemical shifts of the involved states or the bond-vector orientation in the magnetic field and thus the dipolar coupling – then this interaction is averaged. The observed quantity reflects the population-weighted average over all sampled states. In solids, the averaged anisotropic quantities (dipolar/quadrupolar/CSA) directly reflect the amplitude of motion. In isotropic solution the average of these quantities is zero, such that they become uninformative, but the averaged isotropic chemical shift nonetheless remains a useful probe of motion.
-
(ii)
If the exchange is slow on the time scale of the considered interaction, one observes the “rigid limit”, i.e. individual signatures from the individual contributing states. Exchange-type experiments, of isotropic [14] or anisotropic quantities [15], allow visualizing the interconversion between states in this slow exchange regime.
-
(iii)
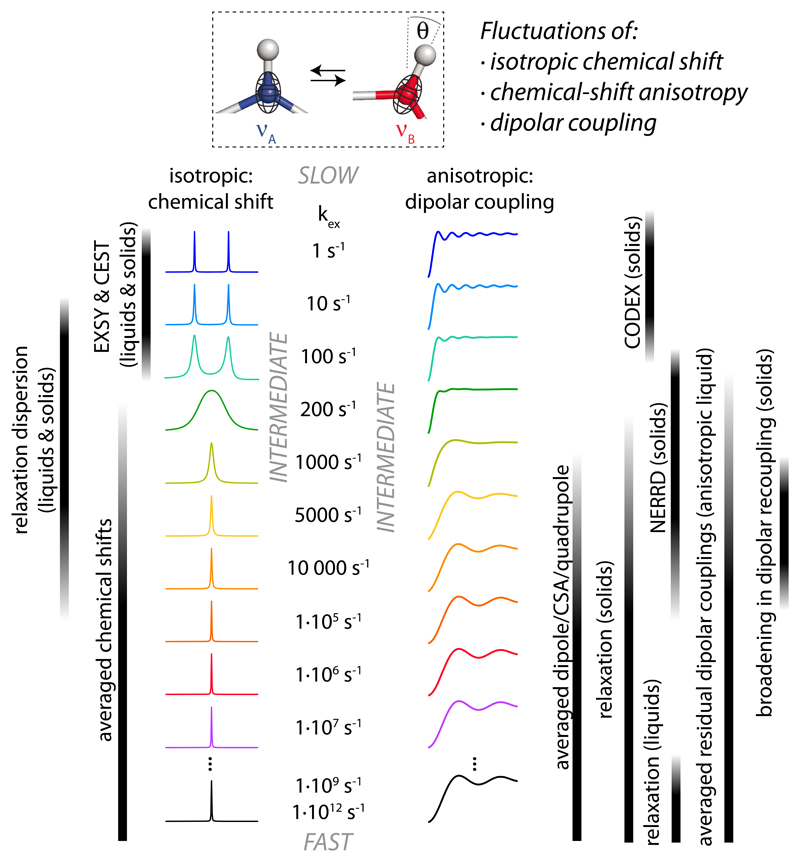
The frontier between the ‘fast exchange’ and ‘slow exchange’ regimes depends on the interaction strength, as illustrated in Fig. 1 for the case of isotropic chemical-shift fluctuation (typically a few hundred Hz at most) and a bond-vector/dipolar-coupling fluctuation (typically tens of kHz). In this ‘intermediate regime’ spectral features, i.e. chemical-shift lines or recoupling curves, are broadened (Fig. 1). This broadening can be quantified to obtain information about the relative populations of the exchanging states, their difference in interaction strength (e.g. chemical shift) and the exchange kinetics. This kind of approaches have turned out to be particularly powerful for isotropic chemical-shift exchange, in particular CEST or relaxation-dispersion techniques, and, although to much lesser extent for studying motions associated with dipolar couplings [16,17].
-
(iv)
Lastly, the fluctuations of anisotropic interactions lead to spin relaxation. Measuring rate constants of relaxation depend on both amplitudes and time scales of the fluctuations.
Fig. 1. Averaging of NMR interactions and NMR approaches to measure dynamics.
(Top) Schematic representation of a XAH bond undergoing fluctuations of its bond orientation and the isotropic chemical shift(s). (Center) Averaging of isotropic chemical shifts from two states, separated by 60 Hz and populated to equal amounts, as a function of the exchange rate constant is shown on the left. This averaging occurs in solids and liquids alike. The right side illustrates averaging of dipolar couplings under 40 kHz MAS and a recoupling sequence (REDOR), illustrated here for a 3-site exchange (axially symmetric) with a rigid-limit dipolar coupling of 10 kHz. The techniques that allow determining dynamics, based on fluctuations of the isotropic chemical-shift and the anisotropic (dipolar coupling) interaction are shown to the left and right, respectively. Abbreviations: CEST. Chemical-exchange saturation transfer. EXSY. Exchange spectroscopy. CODEX. Centerband-only detection of exchange. NERRD. Near-rotary resonance relaxation dispersion.
In practice, the NMR spectroscopist faces both practical and theoretical challenges on the way from NMR data to a full dynamic picture of the molecule. Possibly the most important challenge comes the fact that the conformational space of a biomacro-molecule is vast and the number of measurable parameters is always insufficient to describe this space extensively. Attempts to determine the structures of all the exchanging conformations and the thermodynamics and kinetics of interconversion essentially always deal with an experimentally underdetermined problem, necessitating models for data interpretation. The experimentalist furthermore needs to carefully design the experiments keeping in mind many considerations. Which parameters are best suited to probe which aspects of motion? To which time scales and amplitudes of motions is a given experimental observable sensitive? What are possible artefactual contributions to the observed experimental parameter which are not to be interpreted in terms of dynamics? Given that the observables are generally local from individual spins, how can the observed parameters be linked to a structural view of the protein’s motion? And in this context, given that motion often implies a large number of atoms, what can one learn about their correlated motions?
3. Spin relaxation: New hardware and analysis approaches
Nuclear spin relaxation experiments are routinely used in solution-state NMR studies, and in an increasing number of studies also in solids, most commonly 13C or 15N auto-relaxation (R1, R1ρ, R2) or heteronuclear NOE effects. From my perspective, the popularity of detailed spin-relaxation measurements in liquids, en vogue 10 or 20 years ago, is declining; in more and more cases the experimentally measured order parameters are only estimated from chemical-shift based procedures, which suffices for many questions [18,19]. Even with lengthy measurements it is not easy to gain much more insight than “loops are more flexible than secondary structures”, which often does not answer mechanistic questions.
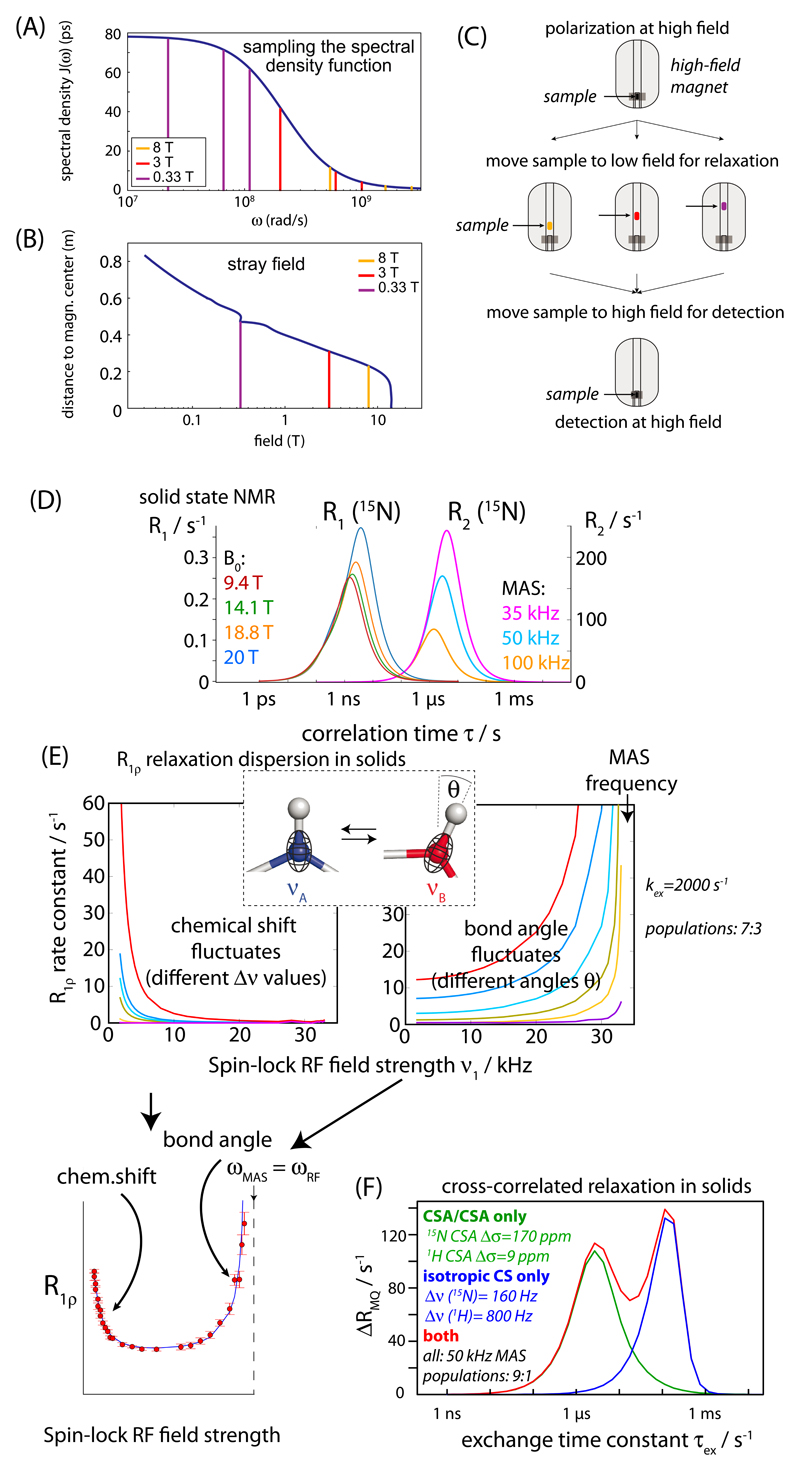
There are two fundamental challenges for gaining more information. The first one is related to the fact that relaxation rate constants sample the underlying spectral density function – which describes the motion of the considered moiety – only at a fairly small set of frequencies, namely zero frequency and (combinations of) the Larmor frequencies of the involved nuclei at the given static magnetic field and possibly the spin-lock RF field strength in case of R1ρ (Fig. 2A). In other words, while with the knowledge of the motion of a given bond, e.g. from an MD trajectory, one can calculate relaxation parameters in a straightforward manner, the inverse is generally not possible because too little information about the spectral density is available. The solution to this ill-posed problem is to measure relaxation rate constants at as many B0 magnetic field strengths as possible (and possibly complement by multi-temperature measurements). Sensitivity and spectral resolution considerations, however, dictate the lowest acceptable B0 field strengths; technical and budget considerations limit the highest available field strength. In practice, relaxation experiments are thus performed over ca. 500 to 1000 MHz 1H Larmor frequency at best. Multiple relaxation data within this range certainly help augment the accuracy of motional parameters, but the sampling of the spectral density function remains limited within this factor-of-two range of fields.
Fig. 2. Relaxation approaches in liquids and solids.
(A) Spectral density function, and the frequencies sampled by 13C relaxation experiments in three different static magnetic field strength, indicated with colors/vertical lines. (B)-(C) Principle of high-resolution relaxometry; (B) the magnetic field as a function of the vertical distance from the magnetic center of the magnet. (C) Schematic overview of the experiment design. The Boltzmann polarization at high field is excited, and for the relaxation delay the sample is shuttled to different locations in the low-field region of the magnet. For high-resolution detection of the signal the sample is shuttled back to the magnetic center. (D) Longitudinal and transverse 15N relaxation rate constants in a spinning solid, induced by the 1H-15N dipolar coupling and the 15N CSA tensor. As revealed by these data, each relaxation parameter has a range of correlation times to which it is sensitive, while it is insensitive outside. Therefore, motions on time scales outside these sensitive “windows” are difficult to probe. In all simulations the NH order parameter was assumed to be S2 = 0.9. For the R2 data, the magnetic field strength was 14.1 T. The MAS frequency is important for all transverse relaxation experiments, but it is negligible for R1 experiments. (E) R1ρ relaxation dispersion experiments in solids. Isotropic chemical-shift fluctuations (left) and angular fluctuations both contribute to different regimes of the relaxation dispersion profile. Both effects are relevant, and therefore the experimentalist can choose to probe chemical-shift or angular fluctuations, depending on the MAS and spin-lock frequencies. Details are reported in reference [57]. (F) Differential relaxation of ZQ and DQ coherences due to fluctuations of anisotropic and isotropic chemical shifts in a 1H-15N spin pair. While the differential relaxation due to cross-correlated modulation of the two isotropic chemical shifts is present in liquids and solids, the CSA/CSA CCR is present only in solids. Details and more simulations are reported in reference [56]. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
A very interesting approach is to physically transfer the sample to different locations in the stray-field of a high-resolution NMR magnet during the relaxation period, thus varying the field from about 15 or 20 T down to 0.1 T [20–23]. In first applications, the Ferrage group has used a “blow-gun-like” system to shuttle protein samples to B0 fields down to ca. 0.3 T, thus providing almost a factor of 100 in the range of measured field strengths (Fig. 2B,C). These exciting studies have provided insights into backbone and side chain motions on ps-ns time scales in a much more detailed manner than classical high-field NMR relaxation measurements [23,24].
As more experimental observables become available, the question of refined models for data analysis becomes important. While standard high-field relaxation data are most often interpreted in the framework of simple models, comprising one amplitude of motion for a given moiety, and one associated time scale, now one needs to consider multiple motions on different time scales and possibly distributions of correlation times [25]. I am convinced that molecular dynamics (MD) simulations will become an increasingly important part of such data analyses [24].
Even with enhanced sampling of the motion by multi-field relaxation, an inherent limitation remains: the overall tumbling of molecules in solution causes all correlation functions to decay to zero, typically on a nanosecond time scale, and any internal dynamics on longer time scales are thereby rendered invisible, no matter whether one has a fancy sample-shuttle at hand. Magic-angle spinning solid-state NMR may help out, because molecules do not undergo overall isotropic motion in solids, such that relaxation is, in principle, only induced by internal motion, and relaxation in solids thus reports on this motion, a priori irrespective of its time scale. Experimental challenges towards obtaining “clean” relaxation data in solids, free from contributions that are not related to dynamics, have largely been overcome over the last decade by specific labeling/deuteration and increasingly high MAS frequencies. I am convinced that these developments will further help making more relaxation parameters quantitatively exploitable, including the notoriously difficult 1H relaxation parameters [26,27].
An increasing number of studies have shown that it is indeed possible to probe motions across many time scales by MAS NMR relaxation measurements. Several studies have exploited this potential to propose models of motion with contributions on several time scales [27–29]. However, also relaxation measurements in solids have inherent pitfalls, again related to the fact that relaxation rate constants probe the spectral density function only at a small set of frequencies. As a consequence, relaxation rate constants have their specific “windows” of time scales to which they are most sensitive (Fig. 2D). Smith et al. have pointed out that the view of motion we obtain from experimental MAS NMR data is biased by the sensitivity of the relaxation parameters [30], and proposed an alternative approach in which ‘detectors’ estimate the amplitude of motion for specific ranges of motional correlation times [31].
I foresee as a next important development the implementation of sample shuttles in MAS NMR. The realization of such MAS-relaxometry requires overcoming technical challenges, related to displacing along the bore of the magnet an object that spins along the magic angle, possibly within hundreds of milliseconds. Furthermore, one will need to think again about effects occurring at low B0 field, such as accelerated spin diffusion, which may make relaxation parameters unreliable. Nonetheless, MAS-relaxometry bears great potential: unlike solution-NMR relaxometry described above, probing relaxation over B0 fields spanning 2 orders of magnitude would provide insight into internal motions from ps to ms essentially without any inherent “blind spot”. Such data sets, possibly combined with MD simulations, may bring us into a situation where we can truly visualize how different backbone and side chain dihedral angles fluctuate, rather than approximating motion by the very rough models we use now.
The sample-shuttle systems can also help in situations where the exchange is in the intermediate regime at the magnetic center of the magnet, but in the fast exchange at the low-field position, which may make invisible peaks detectable [32]. As an additional advantage, being able to bring the sample rapidly to a location with low field will also open possibilities for more efficient correlation spectroscopy for resonance assignment or structure determination. One may design experiments where coherence transfer takes place at low field, where the small chemical-shift differences may be advantageous for coherence transfer, and detecting signals at the field providing best-possible resolution. Such ideas have been realized in solution-NMR [22].
A different and very promising development over the last years is the use of NOEs for determining structures in a highly accurate manner, and thereby also simultaneously determining several co-existing conformations precisely. The high precision required for such attempts to reliably determine multiple conformational states is generally challenged by spin diffusion, which makes distances only an approximate measure. The use of ‘exact NOEs’ overcomes this limitation, and several cases of interesting multi-state structure determinations have provided a glimpse of certainly many more future applications [33]. This approach brings NMR yet a step closer to the goal of visualizing the conformational space sampled by a protein.
4. Visualizing functionally relevant conformational states with μs-ms life times
The characterization of exchange processes on the μs-ms time scale has arguably been the most exciting field in NMR over the last decade. It turns out that this time scale is often particularly relevant for biomolecular function, as it coincides with turnover rate constants of many enzymes and protein folding processes. The states that are in exchange are often only sparsely populated, to a few percent or less, making their detection with, e.g. crystallographic methods difficult. From an NMR perspective the μs-ms time scale generally corresponds to the regime where the fluctuations of the NMR interactions are ‘slow-to-intermediate’ (cf.Fig. 1), where they induce broadening of spectral features. In particular for isotropic chemical-shift fluctuations a large arsenal of techniques exists that exploit the associated line broadening or the magnetization transfer in distinct peaks corresponding to the exchanging states.
The past and on-going developments aim at “seeing” these transient states, sometimes called “invisible” states due to their elusive nature, in all their detail. What are their structures? How dynamic are these states on shorter time scales? What are the energy barriers that separate these states from the more readily accessible ground state ensembles? How are these states related to enzyme turnover or the onset of amyloid formation?
So far most approaches to probe μs-ms motions have exploited the isotropic chemical-shift fluctuations. Relaxation-dispersion techniques exploit the effect of conformational exchange on transverse magnetization [12,34], and EXSY and CEST approaches monitor longitudinal-magnetization transfer upon exchange [35,36]. The foundations for these techniques have been laid many decades ago [14,37,38]. The successful implementation of these techniques to complex biomolecules required first that one has the sensitivity and resolution to study large biomolecules, which was not possible in the days of the first EXSY/CEST/relaxation-dispersion ideas. Furthermore, it has been critical to separate “artefactual” effects from, e.g., J-coupling evolution [39,40], from dynamics-induced effects and thus be able to quantify these experiments. Through continuous refinement and development, nowadays a large arsenal of methods is available to probe exchange for virtually every type of backbone and side chain spin (1H, 13C, 15N), including CPMG, R1ρ and adiabatic R2ρ [41,42] type of methods, and methods allowing to derive structures [43,44] and probe fast-timescale dynamics of these excited states [45]. New hardware has allowed the application of strong RF fields and thus expanded the range of time scales that can be observed, down to a few microseconds [46].
All these methods rely on a difference in chemical shifts of a given nucleus in the exchanging states. What if the exchanging states happen to have similar or even identical chemical shifts? In some cases one may “blow up” the exchange effects by multiple-quantum experiments [47,48], thus allowing to reliably detect and quantify conformational exchange over a wider range of cases. But what if the exchanging states have identical chemical shifts, such that chemical-shift based relaxation dispersion experiments necessarily fail? Even in such cases, one may detect the exchange process, as long as the exchanging states differ in their intrinsic relaxation properties [49,50].
Exchanging conformations generally differ not only by their chemical shifts but also by the orientations of the bond vectors. Being able to detect exchange via these bond-orientation change would make it possible to sense even exchange without chemical-shift change. Even more importantly, knowing bond-vector orientations in the excited state provide very useful information to actually determine structures of these elusive conformers.
In isotropic solution, however, the overall tumbling averages the dipolar couplings and CSAs, with are associated to the bond vectors, to zero, and thus these attempts are bound to fail. It is only when partially aligning the sample in anisotropic solution, that one can reintroduce these tensorial quantities. This idea has been exploited in elegant studies, in which conformational exchange has indeed been measured via residual dipolar couplings [51,52]. These approaches have allowed determining three-dimensional structures of ‘invisible’ states.
In the solid state, these anisotropic interactions are not averaged to zero by stochastic Brownian motion, but rather periodically modulated by coherent sample spinning under the experimentalist’s control. One can interfere with this averaging by irradiating the spins with radio-frequency (RF) fields. Interference between MAS, RF and dynamics can be exploited to detect and quantify dynamics. Fig. 2E illustrates how one can quantitatively access bond-vector fluctuations through R1ρ experiments with spin-lock RF fields approaching rotary-resonance conditions (ωRF ~ n· ωMAS, n = 1/2, 1, 2,…). In principle, this type of “near-rotary-resonance relaxation dispersion” (NERRD) approach should be applicable to many sites. I believe that continued methods development [26] will provide information about the amplitudes of motion at many 1H, 13C and 15N sites, both through the bond-vector fluctuation and isotropic chemical-shift fluctuation. Ultimately, this information will allow determining structures of transient states in solids, thus opening many applications to very large proteins, membrane proteins and insoluble assemblies.
5. Seeing correlated motions
Dynamics of proteins, and in particular slow (μs-ms) exchange dynamics, involve relatively high transition barriers (several kcal/mol), and imply concerted motion of many atoms. The approaches described above probe dynamics only locally, atom by atom. The concerted nature of conformational exchange is generally deduced from the observation of similar exchange parameters for a group of atoms, and statistical tests of this assumption.
Can one gain direct insight into concerted motion? A promising route towards direct visualization of correlated motion is the use of differential multiple-quantum relaxation involving distant spins (reviewed in ref. [53]). Cross-correlated fluctuations of the isotropic chemical shifts of two nuclei lead to differential relaxation of zero- and double-quantum terms, thus providing a direct handle on motion sensed by different atoms. These experiments require the generation of MQ terms involving two spins. For directly bonded spin, such terms are readily generated. However, to observe correlated motions involving distant atoms one needs to generate MQ terms for two remote spins, which is technically difficult and associated with low efficiency. Using scalar-based coherence transfer steps, the relaxation of MQ terms involving e.g. neighboring Cαi- Cαi+1 [54] spins could be monitored, revealing concerted motion of adjacent residues.
Obviously, it would be more interesting to observe correlated motion involving bonds which are not connected by bonds, across longer distances in space. Here again, MAS NMR may offer interesting routes, because coherent transfer through dipolar couplings can be achieved: for example, double-quantum 1H–1H transfer between methyls and amides has been reported over ca. 6 Å [55], thus making it straightforward to connect spins across β-strands or through the densely packed protein core. Although not yet explored, such approaches could be used to generate MQ terms involving distant nuclei and exploit these to detect correlated motions of sites that may be separated by many residues along the sequence. To the best of my knowledge, this route has not been exploited yet.
In solids, not only the correlated motion of two isotropic chemical shifts leads to differential MQ relaxation, but also the correlated fluctuations of the two involved CSA tensors (Fig. 2F). This effect provides another route to probing correlated motions, possibly over long distances. Using MAS NMR differential MQ relaxation techniques for 1H-15N pairs it has been shown that μs-ms dynamics can be reliably detected [56], inviting for further developments of long-range MQ relaxation experiments.
6. NMR dynamics for the next decades of JMR
NMR spectroscopy disposes of a large toolbox of methods that bring us closer to the ultimate goal of describing the free-energy landscape of protein at its full structural, thermodynamic and kinetic detail of which I have highlighted here only a few routes. The future developments will, in my view, be along two lines. (i) Experimentally, both hardware and pulse sequence developments will extend the number of parameters we can measure, and thus the information we can extract. I see particularly the continued development of faster magic-angle spinning, making “clean” relaxation parameters available for more spins, paralleled with new pulse sequences, e.g. multiple-quantum relaxation or relaxation-dispersion in solids. The sample-shuttle systems, possibly combined with MAS, will finally allow to meaningfully use realistic physical models of protein dynamics. The integration of complementary data, such as single-molecule FRET, SAXS, EPR or (room-temperature) X-ray diffraction will complement NMR data particularly with long-range information, which are notoriously difficult to get by NMR. (ii) With more data available increases the level of detail, and in view the combination with MD simulations will further gain in importance and bridge experimental data and molecular mechanisms. These details can in many cases be crucial to link 3D structures, from XRD or EM, to function. Just like the much-cited “revolution” in EM, progress will not come from a single advance but from the joint improvement of hardware, pulse sequences, samples and analysis approaches. Much to do for JMR’s next half-century.
Acknowledgements
I thank Fabien Ferrage for providing graphical material used in part of Fig. 2. I acknowledge support of my group from the European Research Council (StG-2012-311318-ProtDyn2Function).
References
- [1].Cheng Y. Single-particle Cryo-EM—how did it get here and where will it go. Science. 2018;361(6405):876–880. doi: 10.1126/science.aat4346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Chapman HN, Fromme P, Barty A, White TA, Kirian RA, Aquila A, Hunter MS, Schulz J, DePonte DP, Weierstall U, et al. Femtosecond X-ray protein nanocrystallography. Nature. 2011;469(7332):73–77. doi: 10.1038/nature09750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Coquelle N, Sliwa M, Woodhouse J, Schirò G, Adam V, Aquila A, Barends TRM, Boutet S, Byrdin M, Carbajo S, et al. Chromophore twisting in the excited state of a photoswitchable fluorescent protein captured by time-resolved serial femtosecond crystallography. Nat Chem. 2018;10(1):31–37. doi: 10.1038/nchem.2853. [DOI] [PubMed] [Google Scholar]
- [4].Coquelle N, Brewster AS, Kapp U, Shilova A, Weinhausen B, Burghammer M, Colletier J-P. Raster-scanning serial protein crystallography using micro- and nano-focused synchrotron beams. Acta Crystallogr Sect D Biol Crystallogr. 2015;71(5):1184–1196. doi: 10.1107/S1399004715004514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Würz JM, Kazemi S, Schmidt E, Bagaria A, Güntert P. NMR-based automated protein structure determination. Arch Biochem Biophys. 2017;628:24–32. doi: 10.1016/j.abb.2017.02.011. [DOI] [PubMed] [Google Scholar]
- [6].Charlier C, Cousin SF, Ferrage F. Protein dynamics from nuclear magnetic relaxation. Chem Soc Rev. 2016;45(9):2410–2422. doi: 10.1039/c5cs00832h. [DOI] [PubMed] [Google Scholar]
- [7].Schanda P, Ernst M. Studying dynamics by magic-angle spinning solid-state NMR spectroscopy: principles and applications to biomolecules. Prog Nucl Magn Reson Spectr. 2016;96:1–46. doi: 10.1016/j.pnmrs.2016.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Krushelnitsky A, Reichert D. Solid-state NMR and protein dynamics. Prog Nucl Magn Reson Spectrosc. 2005;47(1–2):1–25. [Google Scholar]
- [9].Lewandowski JR. Advances in solid-state relaxation methodology for probing site-specific protein dynamics. Acc Chem Res. 2013;46(9):2018–2027. doi: 10.1021/ar300334g. [DOI] [PubMed] [Google Scholar]
- [10].Salvi N. Theoretical tools for the design of NMR relaxation dispersion pulse sequences. Prog Nucl Magn Reson Spectrosc. 2015;88–89:105–115. doi: 10.1016/j.pnmrs.2015.06.002. [DOI] [PubMed] [Google Scholar]
- [11].Milles S, Salvi N, Blackledge M, Jensen MR. Characterization of intrinsically disordered proteins and their dynamic complexes: from in vitro to cell-like environments. Prog Nucl Magn Reson Spectrosc. 2018;109:79–100. doi: 10.1016/j.pnmrs.2018.07.001. [DOI] [PubMed] [Google Scholar]
- [12].Mittermaier AK, Kay LE. Observing biological dynamics at atomic resolution using NMR. Trends Biochem Sci. 2009;34(12):601–611. doi: 10.1016/j.tibs.2009.07.004. [DOI] [PubMed] [Google Scholar]
- [13].Kleckner IR, Foster MP. An introduction to NMR-based approaches for measuring protein dynamics. BBA – Proteins Proteomics. 2011;1814(8):942–968. doi: 10.1016/j.bbapap.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Jeener J, Meier BH, Bachmann P, Ernst RR. Investigation of exchange processes by two-dimensional NMR spectroscopy. J Chem Phys. 1979;71(11):4546–4553. [Google Scholar]
- [15].deAzevedo ER, Hu WG, Bonagamba TJ, Schmidt-Rohr K. Centerband-only detection of exchange: efficient analysis of dynamics in solids by NMR. J Am Chem Soc. 1999;121(36):8411–8412. [Google Scholar]
- [16].DeAzevedo ER, Saalwachter K, Pascui O, De Souza Aa, Bonagamba TJ, Reicher D. Intermediate motions as studied by solid-state separated local field NMR experiments. J Chem Phys. 2008;128(10):1–12. doi: 10.1063/1.2831798. [DOI] [PubMed] [Google Scholar]
- [17].Rothwell WP, Waugh JS. Transverse relaxation of dipolar coupled spin systems under Rf irradiation: detecting motions in solids. J Chem Phys. 1981;74(5):2721–2732. [Google Scholar]
- [18].Berjanskii MV, Wishart DS. A simple method to predict protein flexibility using secondary chemical shifts. J Am Chem Soc. 2005 doi: 10.1021/ja054842f. [DOI] [PubMed] [Google Scholar]
- [19].Shen Y, Bax A. Protein backbone and sidechain torsion angles predicted from NMR chemical shifts using artificial neural networks. J Biomol NMR. 2013;56(3):227–241. doi: 10.1007/s10858-013-9741-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Redfield AG. Shuttling device for high-resolution measurements of relaxation and related phenomena in solution at low field, using a shared commercial 500 MHz NMR instrument. Magn Reson Chem. 2003;41(10):753–768. [Google Scholar]
- [21].Redfield AG. High-resolution NMR field-cycling device for full-range relaxation and structural studies of biopolymers on a shared commercial instrument. J Biomol NMR. 2012;52(2):159–177. doi: 10.1007/s10858-011-9594-1. [DOI] [PubMed] [Google Scholar]
- [22].Cousin SF, Charlier C, Kadeřávek P, Marquardsen T, Tyburn J-M, Bovier P-A, Ulzega S, Speck T, Wilhelm D, Engelke F, et al. High-resolution two-field nuclear magnetic resonance spectroscopy. Phys Chem Chem Phys. 2016;18(48) doi: 10.1039/c6cp05422f. [DOI] [PubMed] [Google Scholar]
- [23].Charlier C, Khan SN, Marquardsen T, Pelupessy P, Reiss V, Sakellariou D, Bodenhausen G, Engelke F, Ferrage F. Nanosecond time scale motions in proteins revealed by high-resolution NMR relaxometry. J Am Chem Soc. 2013;135(49):18665–18672. doi: 10.1021/ja409820g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Cousin SF, Kadeřávek P, Bolik-Coulon N, Gu Y, Charlier C, Carlier L, Bruschweiler-Li L, Marquardsen T, Tyburn J-M, Brüschweiler R, et al. Time-resolved protein side-chain motions unraveled by high-resolution relaxometry and molecular dynamics simulations. J Am Chem Soc. 2018;140(41):13456–13465. doi: 10.1021/jacs.8b09107. [DOI] [PubMed] [Google Scholar]
- [25].Smith AA, Ernst M, Meier BH, Ferrage F. Reducing bias in the analysis of solution-state NMR data with dynamics detectors. arXiv. 2018 doi: 10.1063/1.5111081. 1812.01890. [DOI] [PubMed] [Google Scholar]
- [26].Gauto DF, Hessel A, Rovó P, Kurauskas V, Linser R, Schanda P. Protein conformational dynamics studied by 15N and 1H R1ρ relaxation dispersion: application to wild-type and G53A ubiquitin crystals. Solid State Nucl Magn Reson. 2017;87:86–95. doi: 10.1016/j.ssnmr.2017.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Rovo P, Smith CA, Gauto D, De Groot BL, Schanda P, Linser R. Mechanistic insights into microsecond time-scale motion of solid proteins using complementary 15N and 1H relaxation dispersion techniques. J Am Chem Soc. 2019;141(2):858–869. doi: 10.1021/jacs.8b09258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Smith AA, Testori E, Cadalbert R, Meier BH, Ernst M. Characterization of fibril dynamics on three timescales by solid-state NMR. J Biomol NMR. 2016;65(3–4):171–191. doi: 10.1007/s10858-016-0047-8. [DOI] [PubMed] [Google Scholar]
- [29].Zinkevich T, Chevelkov V, Reif B, Saalwächter K, Krushelnitsky A. Internal protein dynamics on Ps to Ms timescales as studied by multi-frequency 15N solid-state NMR relaxation. J Biomol NMR. 2013;57(3):219–235. doi: 10.1007/s10858-013-9782-2. [DOI] [PubMed] [Google Scholar]
- [30].Smith AA, Ernst M, Meier BH. Because the light is better here: correlation-time analysis by NMR spectroscopy. Angew Chemie Int Ed. 2017;56(44):13590–13595. doi: 10.1002/anie.201707316. [DOI] [PubMed] [Google Scholar]
- [31].Smith AA, Ernst M, Meier BH. Optimized, “detectors” for dynamics analysis in solid-state NMR. J Chem Phys. 2018;148(4) doi: 10.1063/1.5013316. 045104. [DOI] [PubMed] [Google Scholar]
- [32].Cousin SF, Kadeřávek P, Haddou B, Charlier C, Marquardsen T, Tyburn J-M, Bovier P-A, Engelke F, Maas W, Bodenhausen G, et al. Recovering invisible signals by two-field NMR spectroscopy. Angew Chemie Int Ed. 2016:9886–9889. doi: 10.1002/anie.201602978. [DOI] [PubMed] [Google Scholar]
- [33].Vögeli B, Orts J, Strotz D, Chi C, Minges M, Wälti MA, Güntert P, Riek R. Towards a true protein movie: a perspective on the potential impact of the ensemble-based structure determination using exact NOEs. J Magn Reson. 2014;241:53–59. doi: 10.1016/j.jmr.2013.11.016. [DOI] [PubMed] [Google Scholar]
- [34].Palmer AG, Massi F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem Rev. 2006;106(5):1700–1719. doi: 10.1021/cr0404287. [DOI] [PubMed] [Google Scholar]
- [35].Fawzi NL, Ying J, Ghirlando R, Torchia DA, Clore GM. Atomic resolution dynamics on the surface of amyloid protofibrils probed by solution NMR. Nature. 2011;480(7376):268–272. doi: 10.1038/nature10577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Vallurupalli P, Bouvignies G, Kay LE. Studying, “invisible” excited protein states in slow exchange with a major state conformation. J Am Chem Soc. 2012;134(19):8148–8161. doi: 10.1021/ja3001419. [DOI] [PubMed] [Google Scholar]
- [37].Forsén S, Hoffman RA. Study of moderately rapid chemical exchange reactions by means of nuclear magnetic double resonance. J Chem Phys. 1963;39(11):2892–2901. [Google Scholar]
- [38].McConnell HM. Reaction rates by nuclear magnetic resonance. J Chem Phys. 1958;28(3):430. [Google Scholar]
- [39].Loria JP, Rance M, Palmer AG. A relaxation-compensated carr-purcell-meiboom-gill sequence for characterizing chemical exchange by NMR spectroscopy. J Am Chem Soc. 1999;121(10):31–2332. [Google Scholar]
- [40].Hansen DF, Vallurupalli P, Kay LE. An improved 15 N relaxation dispersion experiment for the measurement of millisecond time-scale dynamics in proteins. J Phys Chem B. 2008;112(19):5898–5904. doi: 10.1021/jp074793o. [DOI] [PubMed] [Google Scholar]
- [41].Chao FA, Byrd RA. Geometric approximation: a new computational approach to characterize protein dynamics from NMR adiabatic relaxation dispersion experiments. J Am Chem Soc. 2016;138(23):7337–7345. doi: 10.1021/jacs.6b02786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Mangia S, Traaseth NJ, Veglia G, Garwood M, Michaeli S. Probing slow protein dynamics by adiabatic R1ρ and R2ρ NMR experiments. J Am Chem Soc. 2010;132(29):9979–9981. doi: 10.1021/ja1038787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Vallurupalli P, Hansen DF, Kay LE. Structures of invisible, excited protein states by relaxation dispersion NMR spectroscopy. Proc Natl Acad Sci USA. 2008;105(33):11766–11771. doi: 10.1073/pnas.0804221105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Neudecker P, Robustelli P, Cavalli A, Walsh P, Lundstrom P, Zarrine-Afsar A, Sharpe S, Vendruscolo M, Kay LE. Structure of an intermediate state in protein folding and aggregation. Science. 2012;336(6079):362–366. doi: 10.1126/science.1214203. [DOI] [PubMed] [Google Scholar]
- [45].Hansen DF, Vallurupalli P, Kay LE. Measurement of methyl group motional parameters of invisible, excited protein states by NMR spectroscopy. J Am Chem Soc. 2009;131(35):12745–12754. doi: 10.1021/ja903897e. [DOI] [PubMed] [Google Scholar]
- [46].Ban D, Gossert AD, Giller K, Becker S, Griesinger C, Lee D. Exceeding the limit of dynamics studies on biomolecules using high spin-lock field strengths with a cryogenically cooled probehead. J Magn Reson. 2012;221:1–4. doi: 10.1016/j.jmr.2012.05.005. [DOI] [PubMed] [Google Scholar]
- [47].Yuwen T, Vallurupalli P, Kay LE. Enhancing the sensitivity of CPMG relaxation dispersion to conformational exchange processes by multiple-quantum spectroscopy. Angew Chemie Int Ed. 2016;55(38):11490–11494. doi: 10.1002/anie.201605843. [DOI] [PubMed] [Google Scholar]
- [48].Gopalan AB, Yuwen T, Kay LE, Vallurupalli P. A methyl 1H double quantum CPMG experiment to study protein conformational exchange. J Biomol NMR. 2018;72(1-2):79–91. doi: 10.1007/s10858-018-0208-z. [DOI] [PubMed] [Google Scholar]
- [49].Yuwen T, Brady JP, Kay LE. Probing conformational exchange in weakly interacting, slowly exchanging protein systems via off-resonance R 1ρ experiments: application to studies of protein phase separation. J Am Chem Soc. 2018;140(6):2115–2126. doi: 10.1021/jacs.7b09576. [DOI] [PubMed] [Google Scholar]
- [50].Fawzi NL, Ying J, Torchia DA, Clore GM. Probing exchange kinetics and atomic resolution dynamics in high-molecular-weight complexes using dark-state exchange saturation transfer NMR spectroscopy. Nat Protoc. 2012;7(8):1523–1533. doi: 10.1038/nprot.2012.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Vallurupalli P, Hansen DF, Stollar E, Meirovitch E, Kay LE. Measurement of bond vector orientations in invisible excited states of proteins. Proc Natl Acad Sci USA. 2007;104(47):18473–18477. doi: 10.1073/pnas.0708296104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Igumenova TI, Brath U, Akke M, Palmer AG. Characterization of chemical exchange using residual dipolar coupling. J Am Chem Soc. 2007;129(44):13396–13397. doi: 10.1021/ja0761636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Vögeli B, Vugmeyster L. Distance-independent cross-correlated relaxation and isotropic chemical shift modulation in protein dynamics studies. ChemPhysChem. 2019;20(2):178–196. doi: 10.1002/cphc.201800602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Lundström P, Mulder FAA, Akke M. Correlated dynamics of consecutive residues reveal transient and cooperative unfolding of secondary structure in proteins. Proc Natl Acad Sci USA. 2005;102(47):16984–16989. doi: 10.1073/pnas.0504361102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Huber M, Hiller S, Schanda P, Ernst M, Böckmann A, Verel R, Meier BH. A proton-detected 4D solid-state NMR experiment for protein structure determination. ChemPhysChem. 2011;12(5):915–918. doi: 10.1002/cphc.201100062. [DOI] [PubMed] [Google Scholar]
- [56].Tollinger M, Sivertsen AC, Meier BH, Ernst M, Schanda P. Site-resolved measurement of microsecond-to-millisecond conformational-exchange processes in proteins by solid-state NMR spectroscopy. J Am Chem Soc. 2012;134(36):14800–14807. doi: 10.1021/ja303591y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Marion D, Gauto DF, Ayala I, Giandoreggio-Barranco K, Schanda P. Microsecond protein dynamics from combined bloch-mcconnell and nearrotary-resonance R1ρ relaxation-dispersion MAS NMR. ChemPhysChem. 2019;20(2):276–284. doi: 10.1002/cphc.201800935. [DOI] [PMC free article] [PubMed] [Google Scholar]