Influence of single-stranded DNA Coatings on the Interaction Between Graphene Nanoflakes and Lipid Bilayers

Abstract

Using molecular dynamics simulations, it is demonstrated that a partial coating of single-stranded DNA (ssDNA) reduces the penetration depth of a graphene nanoflake (GNF) into a phospholipid bilayer by attenuating the hydrophobic force that drives the penetration. As the GNF penetrates the bilayer, the ssDNA remains adsorbed to the GNF outside of the bilayer, where it shields the graphene from the surrounding water. The penetration depth is found to be controlled by the amount of ssDNA coating the GNF, with a sparser coating resulting in a deeper penetration since the ssDNA shields less of the GNF surface. As the coating density is increased, the likelihood of the GNF entering the bilayer is reduced, where it instead tends to lie flat on the bilayer surface with the sugar phosphate backbone of ssDNA interacting with the hydrophilic lipid headgroups. While no bilayer disruption is observed for a partially inserted ssDNA-coated GNF, a larger, bare, partially inserted GNF is found to preferentially extract phospholipids from the bilayer, offering further evidence of lipid extraction as a main cytotoxicity mechanism of GNFs. Therefore, a coating of ssDNA may reduce the cytotoxicity of GNFs by shielding the unfavorable graphene-water interaction, thus preventing graphene penetration and lipid extraction.

Graphical Abstract

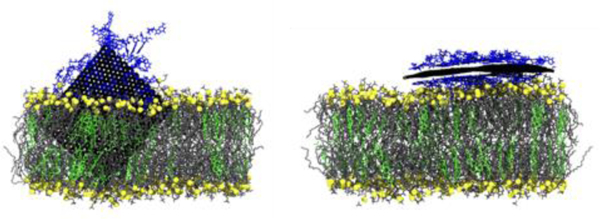
Introduction

Since its discovery,¹ graphene and other related materials (e.g., carbon nanotubes, fullerenes) have received considerable attention due to their physical and electronic properties,² and have shown promise for use in biomedical applications,^3–5 such as drug delivery,^6,7 tissue engineering,^8,9 gene delivery,¹⁰ and biosensing.¹¹ In particular, one promising application is the use of graphene-based electrodes to measure membrane potential changes and detect electrical activity in neuronal networks. However, the efficiency of these graphene-based sensors falls off exponentially with the distance from the cell or tissue; as such, maximizing the efficiency of these devices requires graphene be placed close to the cell or tissue surface.¹² Bringing graphene in close contact to cell membranes may be problematic since graphene is reportedly cytotoxic¹³ due to its ability to induce oxidative stress¹⁴ and disturb cell membranes.^15,16 Furthermore, interactions between graphene and membranes could complicate their utility as sensors. For example, in experiments by Kitko et al., cholesterol (CHOL) content increased and lipid packing enhanced when cells resided directly on single-layer graphene film,¹⁷ which resulted in neurotransmission changes and activation of G protein-coupled receptors.¹²

The literature, in particular aided by molecular dynamics (MD) simulation, has established that the hydrophobicity of graphitic materials is a significant driving force in terms of their interactions with lipid membranes. For example, MD simulation calculations of the free energy of C60 buckyballs penetrating phospholipid membranes revealed a strong energetic driving force (~20 kcal/mol) for insertion into the membrane;¹⁸ this hydrophobic driving force was seen to increase by a factor ~2 as the C60 adopts a more planar geometry (e.g., an open-shell buckyball, intermediate between a sphere and a flat sheet).¹⁹ This strong hydrophobic interaction has been directly related to membrane disruption in other studies. For example, atomistic simulation studies have shown that bare, partially inserted graphene nanoflakes (GNFs) extract lipids from pure phospholipid bilayers,²⁰ in order to shield the portion of the GNF exposed to water.^16,21 In other simulations, Santiago et al., using a coarse-grained approach, observed graphene insertion and lipid rearrangement in liposomes, in addition to graphene-facilitated-lipid-extraction during vesicle fusion.²² Using a mesoscale model, Zhang et al. reported that GNFs selectively remove cholesterol from phospholipid-cholesterol membranes,²¹ which was hypothesized to be related to the strong ring stacking that occurs between cholesterol and graphene. In other work, simulations of smaller GNFs that could fully insert into the membranes, and thus shield the hydrophobic surface of the GNF from water, did not demonstrate significant membrane disruption or lipid extraction.²³ To this end, biomolecular coatings⁴ hold promise as a means of mitigating the effects of the hydrophobicity of graphitic materials, reducing membrane insertion and disruption. DNA is an attractive choice for coating GNFs, as it has been shown that the nucleobases can readily adsorb onto the hydrophobic surface of graphitic materials due to dispersion and π-π stacking interactions.^24–30 Such coatings have been shown to increase the dispersibility of graphene in solution, which suggests that the absorbed DNA is indeed effective at reducing the hydrophobic interaction of graphene with the environment.³¹ Additionally, similar materials, such as DNA coated single-walled carbon nanotubes, have seen success in areas such as gene delivery, providing a strong basis for their use.³² However, it is currently unknown how the presence of a DNA coating affects the interaction between GNFs and lipid bilayers and how it changes GNF’s penetration and disruption of cell membranes.

In this work, the interactions between lipid membranes and both bare GNFs and GNFs coated with single stranded DNA (ssDNA) are investigated via MD simulations with atomistically-detailed molecular models using the CHARMM forcefield.^33–39 Bilayers are modeled as a mixture of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and CHOL. Bare GNF simulations are conducted to provide a baseline for comparison to coated GNFs and to compare, using atomistically detailed models, to the results of Zhang et al., who found that CHOL is selectively removed from membranes.²¹ The effect of ssDNA coating the GNFs is examined as a function of the ssDNA coating density, focusing on the impact of the coating on the penetration behavior of the GNF into the bilayer membrane. The effect of proteins and other molecules that naturally occur in biological systems are not considered in order to isolate the interactions between membranes, GNFs and ssDNA. Steered MD simulations, whereby GNFs are directed into the membrane, are also performed to further probe the molecular interactions and insertion of the bare and coated GNFs. To the best of our knowledge, this is the first computational study of the interaction between graphene-ssDNA complexes and lipid bilayers.

Simulation Methods and Models

Bilayer construction:

Preassembled DOPC-CHOL bilayers containing 200 lipids per leaflet were generated via the CHARMM-GUI.^33,40–44 The mixed DOPC-CHOL bilayer contained 44 CHOL molecules per leaflet, randomly dispersed throughout the bilayer leaflets with an equal amount of CHOL molecules in either leaflet. The bilayers were immersed in water, such that there was approximately a 5 nm layer of water on each side when considering small GNFs (5 nm 2 5nm) (i.e., 10 nm separation between the bilayer and its periodic image); simulations of larger GNFs (5 nm × 10 nm ) double this separation between the bilayer and its periodic image. The configurations generated by the CHARMM-GUI are representative of equilibrated liquid-crystalline bilayers.^42,43 A steepest decent energy minimization was performed on the hydrated bilayers generated by the CHARMM-GUI, followed by a short isobaric simulation (i.e., simulated in the NPT ensemble) of 375 ps to ensure relaxation prior to the addition of GNF and/or DNA. It was confirmed that the bilayer properties (i.e., area-per-lipid and bilayer height) were stable during this short simulation.

GNF construction:

GNFs were created with the VMD carbon nanostructure builder.⁴⁵ Two GNFs with dimensions 5 nm × 5 nm and 5 nm × 10 nm were constructed. While in practice GNFs are generally on the order of hundreds of nm in lateral dimensions and can have more complex shapes,^46,47 the model GNFs in this study enable us to investigate how the edges and sharp corners that can be present on realistic GNFs interact with phospholipid bilayers. Additionally, these sizes allow us to examine: (1) a GNF that can fully insert in the bilayer and (2) a GNF that is large enough that the GNF does not fit completely within the hydrophobic core of the bilayer, yet allows for a system size (i.e., size of bilayer and water layer) small enough that it can be simulated with atomistic models without computational expense being a limiting factor.

ssDNA coating:

ssDNA strands were initialized with the make-na server,⁴⁸ which uses the nucleic acid builder module of AmberTools to construct geometrically accurate DNA molecules.⁴⁹ Sequences of single-stranded poly-G₁₀ were initialized with a type-B helix. The ssDNA coils were approximately 3.5 nm long with a radius of 2 nm. The ssDNA chains were placed on each side of a 5×5 nm GNF. The chains were initially placed with their long axis parallel to the GNF, approximately 5 Å from the surface. The system was then solvated and neutralized with Na⁺ ions. 50 ns of simulated tempering⁵⁰ was performed with a temperature range 300 ≤ T ≤ 700 K, to allow the DNA molecules to adopt low-energy configurations on the GNF. The upper temperature limit of 700 K was chosen to induce large conformational changes in the ssDNA.²⁹ Since ring-ring stacking interactions are expected to drive the ssDNA-GNF complex towards configurations with the nucleobases lying flat on the GNF surface,³¹ the ssDNA molecule that had the most (eight out of ten) bases lying flat on the surface was used to build the coated GNF systems. The flat ssDNA chain is approximately 6 nm × 2 nm in size. These chains were replicated to generate sparsely, moderately, and densely coated GNFs by placing one, two, and three ssDNA molecules, respectively, on each side of the GNF (referred to as 2 ssDNA, 4 ssDNA, and 6 ssDNA, respectively, throughout the paper.

Simulation details:

All simulations were performed in GROMACS 5.1^51–56 using a timestep of 1 fs. The non-bonded interaction potential was smoothly switched off between 10 and 12 Å, beyond which Coulombic interactions were treated with the particle-mesh Ewald method.⁵⁷ A temperature of 300 K was maintained via the Nosé-Hoover thermostat.^58,59 The simulation system was coupled semi-isotropically to the Parrinello-Rahman barostat to maintain a pressure of 1 atm independently in the bilayer normal and lateral directions.⁶⁰ The atomistic CHARMM36 force field was used to model DOPC and CHOL,³⁷ and TIP3P was used to model water.⁶¹ Similar to a recent study,⁶² the atoms in the graphene sheet were treated as aromatic ring carbons, i.e., type CG2R61 in the CHARMM General Force Field (CGenFF),⁶³ with the appropriate bond-stretching and angle-bending interactions also from CGenFF. Note, dihedral interactions were not included in the graphene model, consistent with previous studies.³¹ CHARMM27^34,35 was used to model the ssDNA.

GNF insertion simulations:

In all cases, the GNF (coated or uncoated) was positioned with a corner pointing toward the bilayer surface approximately 0.5 nm from the bilayer surface. This orientation was chosen to increase the likelihood of insertion, based on preliminary tests and prior work that suggests GNFs typically insert into the bilayers in a corner-first fashion.²⁰ With the exception of the steered simulations discussed later, the position/orientation of the GNF was not constrained prior to insertion, and was allowed to freely move throughout the system in all directions; since periodic boundary conditions are used, the GNF is able to interact with either side of the membrane further increasing the likelihood of insertion. For systems with ssDNA molecules, overlapping water molecules were removed and neutralizing Na⁺ ions were added; these systems each contained approximately 170,000 atoms. The complete process of constructing the system is graphically shown in Fig. S1 of the Supporting Information. A steepest decent energy minimization was performed to remove high-energy atomic overlaps, after which the systems were simulated in the NPT ensemble. For simulations with ssDNA coatings, simulation times ranged from 60 to 508 ns, depending on the time required for penetration/steady state behavior to occur, where, in general, simulation time increase with coating density. Four independent simulations were performed for the insertion of bare GNF and six for each of the three ssDNA coating densities studied. The individual simulation times for the coated GNF simulations are reported in Table 1.

Table 1:

Summary of simulations performed with an ssDNA coating. Center-of-mass separation, D, is calculated from the last 10 ns of simulation data, representing the mean and standard deviation. The time for the GNF to insert a depth less than 3.5 nm, Time (D < 3.5), and total simulation time are both truncated to the nearest nanosecond. The area occupied by the ssDNA at the 1 ns (initial) and the final snapshot are also reported.

ssDNA coating	trial	D (nm)	Time (D < 3.5 nm) (ns)	Total Simulation Time (ns)	ssDNA area initial : final (nm2)	Insert/Flat
2-chains	run1	0.58 ± 0.07	6	100	15.6 : 13.9	Insert
2-chains	run2	0.91 ± 0.08	43	133	21.1 : 19.9	Insert
2-chains	run3	0.95 ± 0.07	13	168	17.4 : 15.9	Flat, Insert at ~100 ns
2-chains	run4	0.68 ± 0.06	10	100	20.3 : 13.5	Insert
2-chains	run5	0.75 ± 0.11	19	168	18.6 : 11.0	Insert
2-chains	run6	0.53 ± 0.10	12	100	24.7 : 14.2	Insert
4-chains	run1	2.20 ± 0.08	90	182	39.6 : 38.4	Insert
4-chains	run2	2.85 ± 0.10	30	318	49.6 : 47.2	Flat
4-chains	run3	1.95 ± 0.14	56	250	53.6 : 36.7	Flat, Insert at ~ 160 ns
4-chains	run4	3.20 ± 0.07	36	269	43.3 : 44.8	Flat
4-chains	run5	1.93 ± 0.08	30	134	57.4 : 23.1	Insert
4-chains	run6	1.36 ± 0.09	10	134	46.1 : 23.9	Insert
6-chains	run1	3.11 ± 0.08	49	180	60.9 : 59.2	Flat
6-chains	run2	2.70 ± 0.07	313	400	70.2 : 46.1	Insert
6-chains	run3	3.21 ± 0.06	68	492	58.0 : 57.1	Flat
6-chains	run4	3.06 ± 0.09	276	508	73.7 : 57.4	Flat
6-chains	run5	3.01 ± 0.09	127	493	68.8 : 62.3	Flat
6-chains	run6	2.44 ± 0.08	179	303	59.1 : 52.4	Insert

Steered MD procedure:

Steered MD simulations were conducted by attaching harmonic springs to the corner atom of the GNF and then pulling the GNF into the bilayer midplane over the course of a 5 ns simulation for the 5 nm × 5 nm GNF as a function of ssDNA coating. The bilayer was not held fixed, but no noticeable drift was observed over the course of the short simulation. As described in the results, a spring constant (k) of 50 kJ mol⁻¹ nm⁻² was chosen for these calculations as it provided the closest match to the free (i.e., non-steered) simulations in terms of penetration depth. The force of the harmonic spring and the distance traveled by the GNF is recorded during the course of these simulations and the work computed by integrating the force over the distance traveled.

Results and Discussion

Bare GNF insertion

The prototypical insertion of a small (5 nm × 5 nm) unrestrained, bare GNF into a phospholipid-cholesterol bilayer is shown in Fig. 1a–f. From visual inspection of the simulation trajectory, the penetration occurs corner first with the sheet oriented roughly perpendicular to the bilayer surface, in agreement with the preferred orientation from other work.²⁰ To quantify the insertion process beyond visual inspection, three metrics are considered: (1) the distance, D, between the center-of-mass of the GNF and the center-of-mass of the bilayer, projected in the direction normal to the bilayer (Fig. 1g); (2) the magnitude of the dot-product between the two diagonals of the GNF and the bilayer normal, where a value of unity for one of the two measures indicates a corner first orientation when the GNF is aligned with the bilayer normal (labeled as “Corner” in Fig 1h); (3) and the angle between GNF and bilayer normal (see Fig 1i), where a value of 0 degrees indicates perpendicular alignment with the bilayer interface. These measures confirm a rapid (< 5 ns) insertion of the GNF into the bilayer after it initially comes into close contact, where insertion is indeed corner first and with the GNF slightly tilted with respect to the bilayer normal (~10 degrees). The corner first orientation of the GNF, whereby part of the GNF is exposed to water, results in a small number of DOPC molecules partially extracted from the bilayer to shield the hydrophobic surface as shown in Figs. 1c, d. This corner first orientation persists until ~ 30 ns (Fig 1e), at which point the GNF reorients slightly to adopt a more edge-first configuration, as evidenced visually by the final simulation snapshot (Fig. 1f) and by the change in the value of the corner orientation metric (Fig. 1h); this reorientation allows the GNF to be more effectively shielded by the membrane. At the end of the simulation the GNF has further aligned with the bilayer normal (i.e., tilt angle ~ 0 degrees, in Fig. 1i). This alignment with the bilayer normal is not unexpected since the lipids in the fluid-state bilayer do not adopt a uniform tilt angle that might otherwise influence GNF orientation. A small amount of disruption around the GNF is observed at the bilayer-water interface at the end of the simulation (e.g., see Fig 1f), where a small number of DOPC molecules nearest the GNF have risen up slightly from the membrane to provide additional shielding, since the GNF is slightly larger than the height of the membrane tail-region. We note that there does not appear to be any significant disruption of the membrane itself aside from the small region around the GNF at the end of the simulation. These results are consistent with Chen et al. who also considered a GNF whose dimensions closely match that of the bilayer height, and did not observe any significant bilayer disruption.²³

Figure 1:

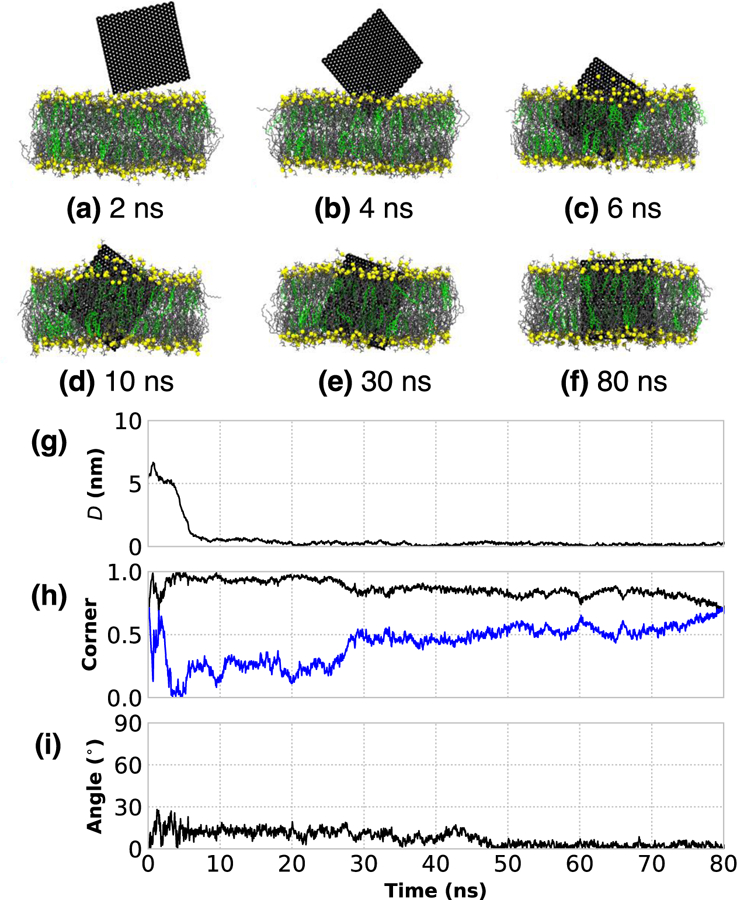
The rapid corner first, insertion of a bare 5 nm × 5 nm GNF into a bilayer. (a–f) Simulation renderings of the insertion process as function of time; water is not shown for clarity, phosphorous atoms of DOPC are shown as yellow to highlight boundary, DOPC tails are shown as gray, and CHOL colored green. (g) Distance between the centers-of-mass of the GNF and bilayer, projected along the bilayer normal, shows the rapid insertion at ~8 ns. (h) The value of unity for normalized dot product calculated between the vectors describing the GNF diagonals (blue and black) and the bilayer normal indicates corner first insertion. (i) The angle between the GNF and bilayer normal, where GNF inserts at ~10 degrees from normal; after ~50 ns, the value is close to 0 degrees, closely aligned with the bilayer normal.

Fig. 2a–f presents a second prototypical example of GNF insertion. In contrast to Fig. 1, the insertion process is slower after the GNF first comes into close contact with the membrane, because the GNF initially lies flat upon the bilayer surface. This is shown visually in Figs. 2b,c and can also be evidenced in Fig. 2g by the plateau of the separation measurement at D~2.5 nm (i.e., half of the approximate bilayer height), a value of ~0 for the corner first metric in Fig. 2h, and a value of ~90 degrees for the GNF angle in Fig. 2i, between 20 and 50 ns. While this flat configuration is certainly less favorable than an inserted configuration, coarse-grained studies of graphene and bilayer liposomes identified a similar configuration where lipids ultimately rearrange to coat the flat graphene configuration.²² At ~55 ns of simulation time, the GNF begins to extract a small number of phospholipids onto the GNF surface nearest the corner, as it begins to slowly increase its tilt and start a corner first insertion into the bilayer (Figs. 2d,e); the corner orientation metric (Fig. 2h) increase towards unity during this stage from 55–100 ns. Note, in this case, the GNF is not perpendicular to the bilayer interface when insertion occurs at ~60 ns, but instead at ~60 degrees with the GNF gradually transitioning to a more perpendicular alignment by the end of the simulation, as shown in Fig. 2i. As in Fig. 1, the edge first configuration of the GNF results in part of the GNF exposed to water, where again partial extraction of a small number of phospholipids is observed to coat the portion of GNF exposed to water (Fig. 2e). Visually, near the end of the simulation time considered (150 ns, Fig. 2f), the GNF maintains a configuration intermediate between a corner-first and edge-first orientations, with a small amount of DOPC partially extracted to coat the surface; increased simulation time would likely result in an edge first orientation, similar to Fig. 1, as this maximizes shielding of the GNF. A third independent trial (see Fig. S2 in the SI) demonstrates behavior intermediate between the cases shown in Figs. 1 and 2, where the GNF contacts the membrane at an unfavorable orientation (~70 degrees from the bilayer normal) and reorients during insertion, but does not lie flat upon the bilayer surface.

Figure 2:

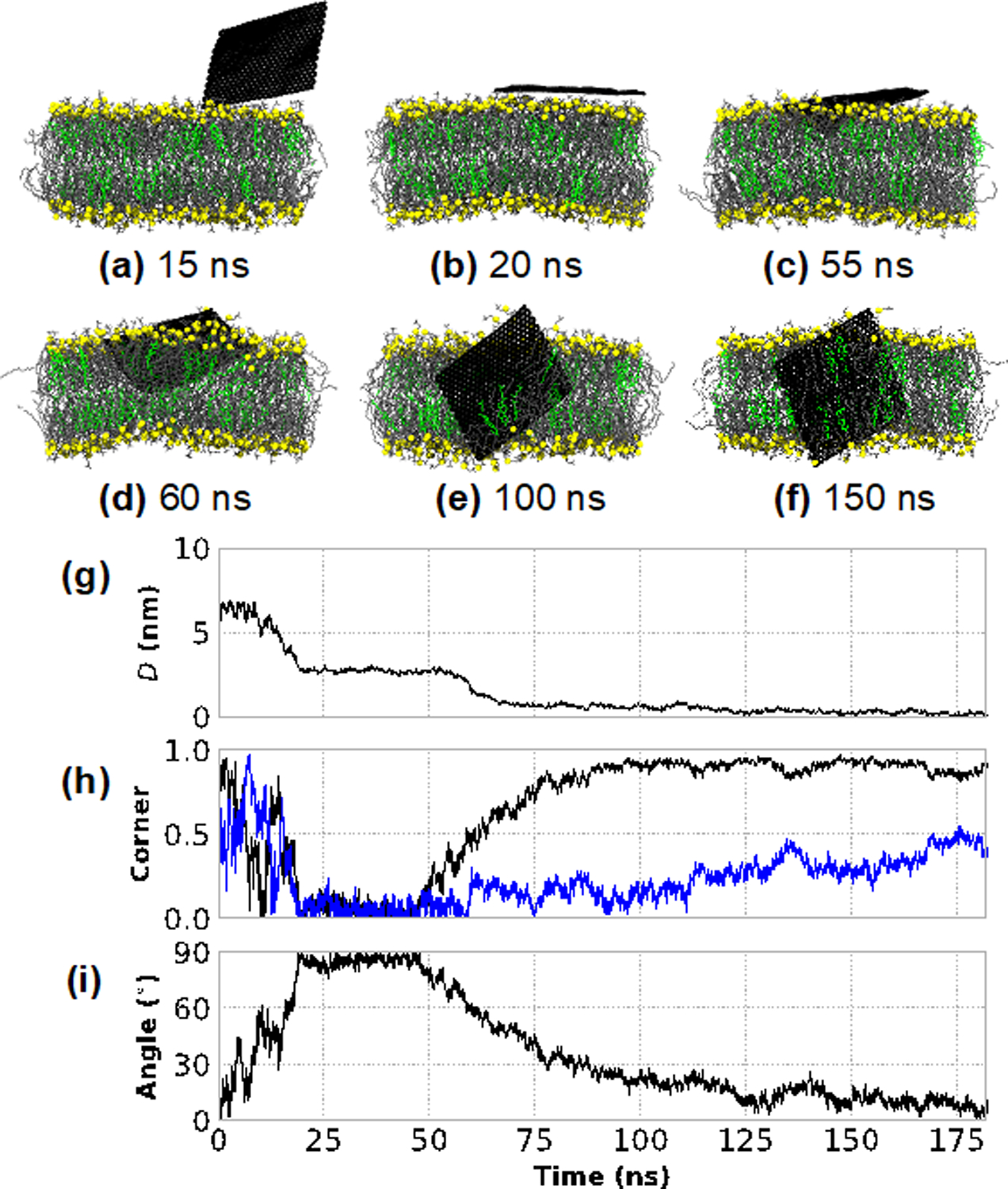
Insertion of a bare 5 nm × 5 nm GNF into the bilayer, whereby the GNF first adopts a “flat” configuration perpendicular to the bilayer normal. (a–f) Simulation renderings of the insertion process as a function of time; the same color scheme as Figure 1 is used. (g) The distance between the centers-of-mass of the GNF and bilayer, projected along the bilayer normal, capturing the flat configuration between ~20–60 ns, and the eventual insertion at ~60ns. (h) The normalized dot product calculated between the vectors describing the GNF diagonals (blue and black) and the bilayer normal, capturing the corner first insertion as shown by the gradual increase towards unity of one of the vectors starting at ~50ns. (i) The value of ~90 degrees between ~20 and 50 ns for the angle between the GNF and bilayer normal indicates the regime where the GNF adopts a flat configuration; the gradual increase towards 0 degrees after ~60 ns demonstrates that the GNF does not insert perpendicularly, but rather gradually aligns with the bilayer normal after insertion.

GNF-induced lipid extraction

Experimentally, GNFs are typically much larger (10–1,000 μm) than the bilayer thickness (~5 nm) and thus insertion would require the GNF to protrude from the bilayer, with a significant portion of the hydrophobic surface exposed to water. To mimic a situation in which a large GNF penetrates a cell membrane and a portion of the GNF is still exposed to the extracellular fluid, simulations of an uncoated 5 nm x10 nm GNF are considered. This configuration was realized by allowing an unrestrained GNF to freely penetrate into the bilayer and then, after insertion, restraining the motion of the GNF atoms in the direction normal to the bilayer using a harmonic potential with a force constant of 1000 kJ mol⁻¹ nm⁻². The restraints were used to prevent the GNF from completely sinking into the bilayer, thus mimicking the more realistic case where the GNF is much larger than the bilayer thickness. Note, the insertion behavior of this larger GNF closely resembles that of the prototypical insertion shown in Fig. 1 of the smaller 5 nm × 5 nm GNF. After insertion, lipids are extracted from the bilayer to coat the hydrophobic GNF surface as shown in Fig. 3a, consistent with prior simulation studies.¹⁶ This is also consistent with the partial extraction of lipids seen in Figs. 1 and 2 for the corner first configuration of the smaller GNF. Visually, the lipids leave the bilayer in the direction roughly perpendicular to the bilayer plane, without large rotational motion or dragging surrounding lipids along. The extracted lipids on the GNF align with the GNF surface to form an efficient packing and coat the GNF surface, where the hydrophilic phosphatidylcholine headgroups of DOPC protrude from the GNF edge or perpendicular to its surface to maximize their exposure to water. Lipid extraction onto the exposed GNF surface is quantified in Fig. 3b by identifying lipids that are close to the surface of the GNF and 2.5 nm above/below the bilayer center-of-mass (roughly approximating the bilayer-water interface). A simple distance cutoff of 0.5 nm between a GNF carbon atom and the first carbon atom in the DOPC chain and the first carbon in the CHOL ring structure was used to identify molecules on the GNF surface. Fig. 3b quantifies that the number of lipids increases until approximately 15 ns, consistent with visual inspection (see Fig. 3a), at which point the values appear roughly constant (~20 total lipids). Fig. 3c plots the surface accessible solvent area (SASA) of the GNF calculated using VMD⁶⁴ with a probe of 2.75 Å (roughly the diameter of water). The SASA measurement rapidly decreases and becomes roughly constant at 15 ns, consistent with visual inspection and quantification of lipid extraction, and clearly demonstrates the role of lipid extraction as a means to shield the GNF from the water solvent. As the simulation time progresses, we visually observed that additional lipids are extracted from the bilayer (see Fig. 3a), however these do not directly lie upon the GNF itself. These additional lipids coat the existing layer of lipids and act to further shield the hydrophobic lipid tails on the lipids GNF surface from water. Significant bilayer disruption is observed at the end of the 75 ns simulation time, as shown in Fig. 3a.

Figure 3:

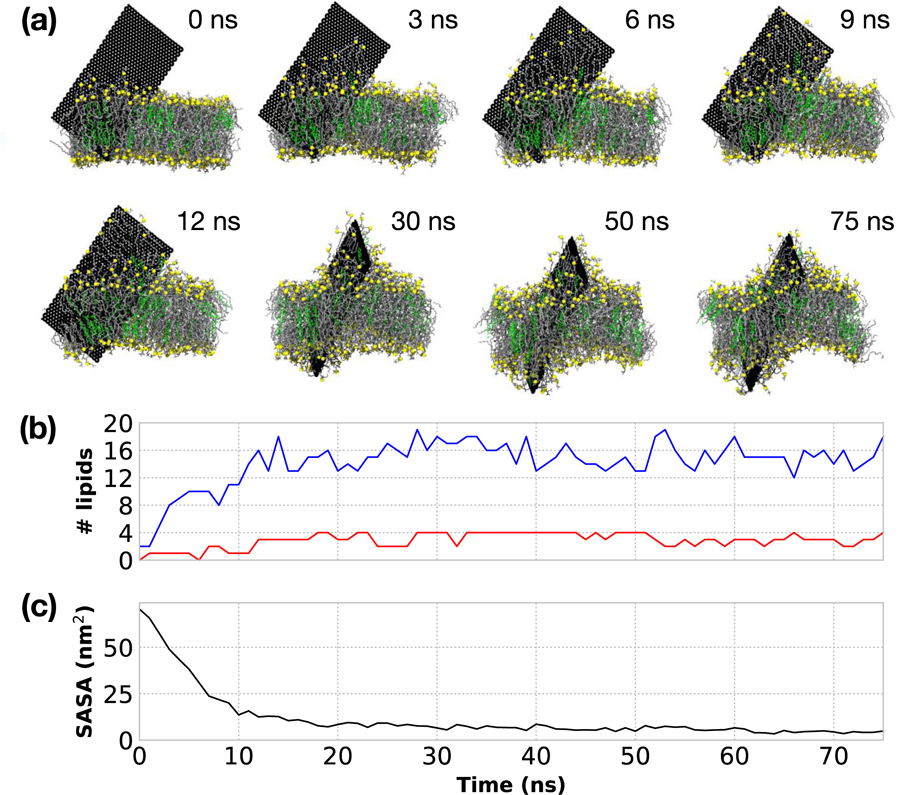
(a) Simulation snapshots of the extraction of lipids for a 5 nm ×10 nm GNF. The GNF surface is fully coated by a single layer of lipids ~15 ns. After which additional lipids are extracted to further coat the lipids already on the surface of the GNF, providing additional shielding of the lipid tails, resulting in significant membrane disruption by the end of the simulation time considered (75 ns). Phosphorus shown in yellow, DOPC tails in grey, CHOL colored green. Water is not shown for clarity. The camera location is changed (i.e., rotated) for the final three snapshots to highlight the further extraction and disruption of the bilayer; the position of GNF itself does not change during the course of the simulation due to the applied restraints. (b) Quantification of the number of lipids extracted from the bilayer. DOPC shown in blue and CHOL shown in red. (c) Calculation of the surface accessible solvent area of the GNF as a function of time.

As previously discussed, prior simulations have demonstrated that an uncoated GNF can disrupt bilayers by extracting lipids to cover the hydrophobic graphene surface.^13,16 Our simulations are consistent with these results and clearly demonstrate that the GNF must be larger than the dimensions of the bilayer height for such significant extraction to occur, i.e., the difference between the work of Tu et al.¹⁶ where significant extraction was observed, and Chen et al.²³ where no extraction was observed, can be associated with the GNF size and not necessarily dependent on any other methodological differences. It is worth noting that Tu et al. performed simulations with very large GNFs, where there was an apparent, continual extraction of lipids due to the large availability of exposed sites on GNF surface. For the simulations reported herein, a termination of lipid extraction directly onto the GNF is observed once there is no more available space on the surface of the GNF, although additional lipid extraction occurs to further envelope the lipids that lie directly on the GNF surface.

Upon examination of the extraction by lipid type, we find phospholipids are primarily extracted, with only a few CHOL molecules removed from the bilayer; this can be observed visually in Fig. 3a and is quantified in Fig. 3b. Specifically, at 12 ns, there are 16 DOPC molecules and 3 CHOL on the GNF (in the region outside the membrane) and these values remain roughly consistent throughout the remainder of the simulation. As such, the CHOL concentration on the GNF is approximately 16%, slightly lower than 22% concentration of CHOL in the membrane. The slight preference to DOPC extraction could be related to the hydrophilic phosphatidylcholine headgroup attenuating the cost of the DOPC molecules to be near water, given that CHOL lacks a similarly large, flexible hydrophilic headgroup. While ring stacking of CHOL on the honeycomb surface of the GNF may result in a stronger binding, the results herein suggest that there is not a stronger driving force to extract CHOL from the bilayer compared to extracting DOPC. At best, the tendency for lipid extraction is equal between the two species and largely dictated by the lipid concentration in the membrane. This finding contradicts the results of Zhang et al.,²¹ who found that CHOL molecules fully coated the GNF, while no phospholipids were extracted from the bilayer. We note that such drastic differences in behavior likely arise as a result of the different models used; whereas the present work uses the fully atomistic CHARMM force field, the work presented in Zhang et al.²¹ used a mesoscale dissipative particle dynamics (DPD) model. DPD relies on treating all interactions as repulsive, soft spheres, where spatial organization (e.g., such as a phase separation) are driven by the relative scale of the repulsion between beads. The findings of Zhang et al. are consistent with the fact that, in their DPD model, the repulsive force between graphene and phospholipid head or tail beads was set to much higher values than the repulsion between graphene and cholesterol beads in their simulations; modification of these strengths would likely result in a different behavior. Based on the atomistic simulations presented here, the interactions used by Zhang et al. do not accurately model the underlying behavior. Although no complete bilayer destruction occurred over the timescale considered for the 5 nm × 10 nm GNF system, a larger sheet would likely extract more lipids and thus have a larger influence on the bilayer structure. Furthermore, if DOPC is selectively removed, the relative concentration of CHOL must increase within the membrane, which could potentially alter the structure and behavior of the membrane (e.g., the creation of CHOL rich microdomains). While our results strongly suggest CHOL is not preferentially extracted from the bilayer onto the GNF portion that is exposed to water, larger simulations and longer timescales would be required to investigate whether there is preferential CHOL organization around the GNF within the bilayer membrane.

Influence of ssDNA coating on the Insertion of GNFs

Since the hydrophobic shielding provided by a bilayer drives the insertion of a GNF, the question arises whether a coating on the GNF, in this case ssDNA, can provide the same level of shielding and thus reduce or eliminate insertion. This question is explored by examining the insertion behavior of GNFs with different levels of ssDNA coating. Here, the insertion of small GNFs (5 nm × 5 nm) with differing levels of ssDNA on the surface (2, 4, and 6 ssDNA per GNF, distributed evenly on each side) into DOPC-CHOL bilayers are considered. We calculate the surface accessible solvent area (SASA) of the GNFs with a test particle of diameter 2.75 Å (approximate diameter of water) for each coating density at 1 ns (i.e., prior to insertion) using VMD.⁶⁴ For each of the six replicates an average GNF SASA of 49.8 ± 4.3, 33.8 ± 1.4, and 17.3 ± 0.5 nm² is found for the 2, 4, and 6 ssDNA per GNF systems, respectively. As expected, the ssDNA provides increased shielding of the GNF as the number of strands increases. The total GNF area occupied by ssDNA using SASA was also calculated and areas of 19.6 ± 3.2, 48.3 ± 6.6, and 65.1 ± 6.6 nm² were obtained for the 2, 4, and 6 ssDNA per GNF systems, respectively; these values are reported in Table 1 for each replicate and simulation snapshots of representative coated GNFs are included in Fig. 4. For reference, the GNF itself (ignoring the lipids and ssDNA) has an average SASA of 77.7 ± 8.6 nm², calculated from the initial (at 1 ns) and final configuration of the GNF in the 18 replicates presented in Table 1 (note, this is higher than a simple area estimate of 50 nm² based on nominal dimensions of the GNF as the SASA calculation considers edge effects and does not treat the surface as perfectly smooth). The GNF SASA and area-occupied by the ssDNA do not scale linearly with the number of ssDNA, likely due to the fact that a larger number of ssDNA conformations/GNF binding locations are accessible for lower surface coverages of ssDNA than higher.

Figure 4:

Visualization of a representative initial configuration of the ssDNA coated GNF and the final simulation snapshot for each of the 18 independent simulations; the color scheme is consistent with prior figures (see Fig. 1) with ssDNA uniformly colored blue. Water is not shown for clarity; simulations are rendered such that the GNF is positioned in the center of the simulation cell.

Table 1 reports the behavior as a function of ssDNA coating density for each of the 6 independent simulations performed for each coating density. Fig. 4 provides a visualization of the final configuration of each of the 18 simulations presented in Table 1. Analysis of the center-of-mass separation and the orientation metrics as a function of time are presented in Figs. S3–5 in the Supporting information for each simulation. In general, as the ssDNA coating density increases, the likelihood of a GNF inserting into the bilayer is reduced (over the simulation timescales considered). For the lowest density, the GNF inserted in all six simulations, whereas only two simulations showed GNF insertion for the highest density. Similarly, as the ssDNA coating density increases, the center-of-mass separation (D) between the GNF and bilayer also increases, i.e., reduced insertion. This is because the ssDNA is not removed from the GNF surface after insertion and the ssDNA does not enter the bilayer, thus it prevents the GNF from fully penetrating into the bilayer. As such, while the hydrophobic driving force for insertion is significant, it is likely weaker than the ssDNA-GNF interaction, since the ssDNA remains largely adsorbed (note, this is discussed in more detail in the context of the steered simulations below). The number of ssDNA per side of the GNF remains constant during the simulations. We note that, as can be seen in the visualizations in Fig. 4, there are several cases where parts of the ssDNA strand dangle from the edge of the GNF, although there are no cases where the ssDNA fully desorbed from the GNF over the course of the simulation times considered. This behavior can also be quantified by comparing the initial to final area occupied by the ssDNA on the GNF presented in Table 1, where significant drops in the area occupied by the ssDNA are observed for systems with dangling strands; in almost all cases, the area occupied by the ssDNA is reduced by the end of the simulation, related to the compaction of the ssDNA to a smaller portion of the GNF as a result of the penetration process. The simulation time taken for the GNF to reach a center-of-mass separation of less than 3.5 nm, labeled as Time (D< 3.5 nm), is also reported in Table 1, rounded to the nearest nanosecond. This distance of 3.5 nm reasonably captures when the GNF starts strongly interacting with the bilayer, as the GNF at this distance has either begun to insert in the bilayer or is lying flat upon the bilayer surface. Table 1 demonstrates that, despite all simulations starting from the same basic configuration, the time it takes for a GNF to start strongly interacting with the bilayer increases with ssDNA density; this further supports the idea of reduced GNF-ssDNA hydrophobicity as ssDNA density increases (i.e., SASA of the GNF decreases), since the GNF, on average, spends more time dispersed in the water. In general, there is no significant extraction of lipids at the end of the simulation runs, although for systems that first adopt a flat configuration before insertion, a small amount of lipid extraction occurs during the intermediate configurations prior to insertion (as shown in Fig. 2 for a bare GNF).

More specifically, considering the case of the lowest ssDNA coating (2 ssDNA, 1 per side) where the GNF inserts into the bilayer in all six independent simulations, the general insertion behavior closely matches that of the bare, uncoated GNFs, discussed above. Five of the six independent simulations conducted directly insert into the bilayer, corner first, where the GNF is roughly parallel to the bilayer normal (similar to Fig. 1). A single case initially adopts a flat configuration (run 3), before eventually inserting after ~100 ns, with a mechanism that appears the same as in Fig. 2 (i.e., temporary extraction of a small number of lipids, followed by the GNF increasing its tilt and inserting corner first). The center-of-mass separation, D, varies from 0.53 nm to 0.95 nm between runs, which appears related to the location of the ssDNA on the GNF and the orientation of the GNF (e.g., corner vs. edge conformations, see Fig. 4). Increasing the coating density (4 ssDNA), the GNF inserted into the bilayer in four of six independent simulations. In three cases the GNF inserts directly, corner first and roughly normal to the bilayer, similar to Fig. 1. A single case (run 3) first adopts a flat configuration before reorienting and inserting into the bilayer, similar to Fig. 2. The increased ssDNA density further reduces the insertion, where center-of-mass separation, D, ranges from 1.36 to 2.20 nm for inserted GNFs, where again, variability between runs appears to be associated with the arrangement of the ssDNA on the GNF and GNF orientations (see Fig. 4). In the remaining two simulations, GNFs adopt flat configurations and do not insert over the timescale of the simulations considered (318 ns and 269 ns for runs 2 and 4, respectively). It is possible that insertion may occur in these two cases if the simulation time were extended, given that run 3 was also seen to insert from a flat configuration. However, the shielding of the water-GNF interactions by the ssDNA likely mitigates some of the driving force associated with the lipid extraction, which appears to precede the start of the GNF insertion.

Further increasing the ssDNA density (6 ssDNA) results in different behavior being observed. Four of the six cases adopt flat configurations and do not insert over the simulation times considered (180, 492, 508, and 493 ns for runs 1, 3, 4, and 5, respectively), suggesting the ssDNA at this density strongly shields the GNF, removing much of the driving force for insertion and lipid extraction that appears to precede insertion for flat configurations. The other two cases (runs 2 and 6) do insert into the bilayer; however, the process appears much slower than for the lower density cases and follows a slightly different mechanism. Specifically, Fig. 5g plots the insertion of the GNF into the bilayer (run 2 in table 1); the GNF first interacts with the bilayer sheet in a corner-first configuration, with the corner residing within the headgroup region without any appreciable insertion for nearly 200 ns (between ~75 to 275 ns), after which the GNF begins to insert (Fig. 5a–f). At the end of the simulation (400 ns, see Fig. 5f), portions of the ssDNA appear to dangle off the side of the GNF as a result of the insertion (area occupied by the ssDNA is reduced from 70.2 to 46.1 nm²), since the amount of free space on the GNF for which the ssDNA can be compressed is comparatively lower due to the increased number of ssDNA, thus requiring some amount of shedding to enable this insertion amount; note, since parts of the ssDNA are hydrophilic, this would not necessarily be an unfavorable configuration for the system, assuming the GNF itself remains fully shielded from the water, as discussed in more detail below. Similarly, for run 6, insertion of the GNF only begins after ~100 ns of simulation time, requiring an additional ~125 ns for the GNF to reach its final depth (see Fig. S5).

Figure 5.

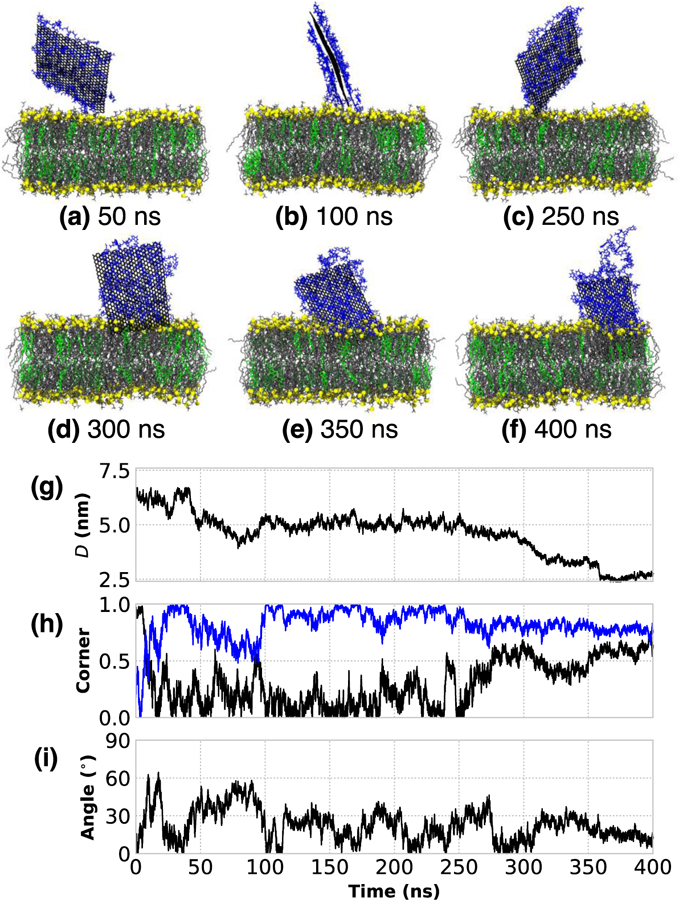
(a–f) Visualization of the insertion process of “run2” (see Table 1) for a GNF coated with 6 ssDNA. (g) The distance between the centers-of-mass of the GNF and bilayer, projected along the bilayer normal, where the GNF sits at the interface for ~75–275 ns, and the eventual insertion at ~300ns. (h) The normalized dot product calculated between the vectors describing the GNF diagonals (black and blue) and the bilayer normal, capturing the corner first orientation of the GNF during the time it sits at the interface (~75–275 ns), and the transition to a more edge first configuration after insertion at ~300 ns (i.e., the convergence of the value of the two diagonals) (i) The angle between the GNF and bilayer normal.

The trends as a function of coating density can be rationalized by considering the driving force for bilayer penetration. The ssDNA coating provides a hydrophobic shielding similar to lipid shielding following GNFs’ membrane insertion or lipid extraction, since the π-π stacking allows the hydrophobic bases of ssDNA to lie flat on the GNF surface, while the sugar-phosphate backbone favorably interacts with water. As such, instead of ssDNA desorption from the GNF, in general, the ssDNA is compacted on the sheet during insertion, owing to the ability of ssDNA to freely rotate and translate on the GNF surface. The adsorbed DNA prevents the GNF from inserting into the bilayer until the ssDNA moves away from the bilayer interface and locally rearranges into a denser packing on the GNF. This process appears to occur on a longer timescale than bare GNF entry into the bilayer, hence the increased timescales as coating density increases. As such, ssDNA translation appears to be the rate determining step after insertion starts, since more ssDNA must translate and compress in the more densely coated systems and must do so in a concerted manner, slowing the dynamics of the process.

Steered simulations

To further examine the insertion behavior, steered MD simulations are performed in which the GNF is pulled from the solution into the middle of the bilayer using a harmonic spring. Note, in all cases, the GNF is oriented “corner first” and perpendicular to the bilayer interface (insertion angle of 0 degrees), consistent with the preferred insertion of the free (i.e., non-steered) simulations previously performed and the observations made in prior studies.^16,21,23 To further support the use of a 0 degree insertion angle, the relative work required to insert a bare GNF as a function of insertion angle is reported in Table 2, where an angle of 0 degrees was observed to require the least amount of work. Table 3 summarizes the center-of-mass separation, D, average D, area occupied by the ssDNA (using the same procedure used for the free simulations), and relative work to insert the GNF to the final penetration depth (i.e., relative to the work to insert a bare GNF to its final penetration depth). The center-of-mass separations are seen to increase as the ssDNA coating increases (i.e., reduced penetration), consistent with the free simulations discussed above (see Table 1). The average D for the GNFs in the steered simulations closely matches the average value of the GNFs that insert in the free simulations, as reported in Table 3. The area on the GNF occupied by the ssDNA is also reported in Table 3, where good agreement is observed between free and steered simulations (note, the average values of the area occupied by the ssDNA for the free simulations only includes systems where insertion was observed); for the 6 ssDNA case, the steered simulations, on average, have a slightly higher occupied area, likely because the steered simulations insert less (i.e., larger value of D); longer timescales that allow the ssDNA to translate/compact on the GNF would likely be required to increase insertion. As shown in Table 3, the relative work of insertion increases with ssDNA coating density, resulting from compaction of the ssDNA on the surface, although the relative work increase does not appear to scale linearly with the ssDNA density. The increased work to insert as ssDNA density increases is consistent with the increased timescales and reduced likelihood of insertion seen in the free simulations as coating density increases. Since the GNFs that first lie flat at the bilayer interface enter the bilayer at an angle much greater than 0°, for the cases where insertion is observed (e.g., the insertion of the bare GNF in Fig. 2 starts when the GNF is ~60°), we could expect the relative work required for the insertion of coated GNFs that first lie flat to be further increased beyond the values in Table 3. This may explain why, for example, we did not observe insertion in any of the cases where the GNFs adopted a flat configuration for the 6 ssDNA systems (i.e., runs 1 and 3 – 5). Note, the above work uses a spring constant of 50 kJ mol⁻¹ nm⁻². Stronger spring constants to steer the GNF were also considered (specifically, 125, 250, and 500 kJ mol⁻¹ nm⁻²), however these resulted in increased penetration and the gradual shedding of some of the ssDNA from the GNF, and thus were not consistent with the free simulations; simulation snapshots for each of the coating densities as a function of spring constant are included in the Supporting Information in Fig. S6 and penetration depths reported in Fig. S7. However, we note that the increased insertion and shedding observed as the spring constant was increased (i.e., additional work applied to insert the GNF) further supports the prior observation that the ssDNA-GNF interactions are stronger than the hydrophobic driving force for insertion; significant ssDNA shedding is only observed when additional work is applied to the system.

Table 2.

Relative work to insert a bare, corner GNF as a function of the angle of insertion; the relative work is the ratio of the work between a given angle and a corner-first insertion at 0 degrees.

Angle (deg)	Relative work
0	1
15	1.11 ± 0.16
30	1.15 ± 0.12
45	1.47 ± 0.10

Table 3:

Summary of steered simulations performed with ssDNA coating compared to steered MD. Center-of-mass separation, D, for the free simulations is calculated from the last 10 ns of simulation data for runs that insert, representing the mean and standard deviation. For the steered MD simulations, D, is calculated after 5ns of simulation time. Area of the GNF occupied by ssDNA at the end of the simulation is also presented for the free and steered simulations. The relative work is calculated from the steered MD simulations, where the work required for a coated GNFs to reach its final insertion depth is scaled by the work of a bare GNF to reach its final penetration depth

ssDNA coating	Free, D (nm)	Steered, D (nm)	Free, final ssDNA SASA (nm2)	Steered, final ssDNA SASA (nm2)	Relative work increase
2-chains	0.73 ± 0.20	0.65 ± 0.17	14.7 ± 3.0	18.6 ± 2.3	1.73 ± 0.26
4-chains	1.86 ± 0.20	1.80 ± 0.26	30.5 ± 8.1	36.4 ± 4.8	2.95 ± 0.24
6-chains	2.57 ± 0.11	2.81 ± 0.18	54.2 ± 11.4	69.0 ± 4.5	3.28 ± 0.25

The consistency between the free and steered simulations (with a spring constant of 50 kJ mol⁻¹ nm⁻²) suggests that steered simulations can serve as a means of rapidly screening different GNF coatings, as each of the steered simulations required only 5 ns of simulation time, as compared to the upwards of 500 ns for some of the free simulations. Based on the results presented herein, steered simulations that result in high values of D (i.e., reduced insertion) would be less likely to insert into the membranes. Similarly, given that the 6 ssDNA systems show a significantly reduced likelihood of membrane insertion, identifying coatings where the relative work exceeds the work associated 6 ssDNA (~3, see Table 3) could additionally identify biological coatings that could potentially prevent membrane insertion and disruption.

Conclusions

The interactions between bare and coated graphene nanoflakes (GNFs) and membranes have been examined, demonstrating how the surface adsorption of single-stranded DNA (ssDNA) molecules modulates GNF’s interaction with a lipid membrane. Specifically, MD simulations show that small GNFs penetrate phospholipid/cholesterol bilayers, typically with a corner of the sheet first entering the bilayer, while the sheet surface is oriented approximately perpendicular to the bilayer plane. Examination of small, bare GNFs of the same dimensions as the bilayer height showed no significant disruption of the bilayer. Examination of a larger GNF that protrudes from the bilayer showed lipids almost immediately migrate to coat the exposed hydrophobic graphene surface and shield it from the water. Disproportionately more phospholipids left the bilayer than cholesterol molecules, likely due to cholesterol’s less hydrophilic lipid headgroup and deeper position within the bilayer. Coating the GNF with short ssDNA chains (10 repeat units) was shown to attenuate the hydrophobic interaction of the GNF with water. In general, the hydrophobic interaction driving the GNF into the bilayer was insufficient to expel the ssDNA from the surface due to strong non-covalent binding (hydrophobic and π-π stacking) of nucleobases to the honeycomb lattice of the graphene surface. As the sheet sinks into the bilayer, the ssDNA molecules are pushed closer together on the protruded portion of the GNF. The surface area occupied by the compressed ssDNA molecules was found to dictate the final penetration depth of the GNF. As the ssDNA coating density increased, the timescale of GNF insertion into the lipid bilayer increased and the likelihood of insertion decreased. The steered MD simulations reaffirmed that the ssDNA coating reduces the GNF’s ability to penetrate the bilayer by increasing the work required for membrane insertion.

Together, these results demonstrate a possible biocompatibility mechanism of biomolecular coatings on GNFs. By providing hydrophobic screening, the coating acts as a surfactant and reduces the driving force for penetration of the cell membrane by GNFs, which is a source of cytotoxicity of graphene.^15,16 However, one must keep in mind that the relative interaction strengths of the coating and cell membrane with the GNF are important, and that coating chemistry will play a large role in these interactions. Here, we have shown that 10-mer oligonucleotides composed of strictly guanosine repeat units provide an adequate coverage to minimize de-coating. The coating strength may change with different nucleotides and length as different nucleobases have different interaction strengths with graphene.^24–27 Moreover, the coating density on a GNF should be expected to play an important role in the relative interactions of the coating and cell membrane with graphene. As shown for the most densely coated GNF here, it is possible to prevent GNF penetration into a lipid bilayer via a dense ssDNA coating in some cases. It has been reported that pristine graphene can lie flat on a cell membrane and cut off large areas of the membrane surface, causing complete loss of membrane integrity.¹⁶ Notably, however, for the most densely coated GNF, which lies flat on the bilayer surface, our studies indicate no lipids were extracted from the bilayer in simulations in excess of 500 ns, and thus the effect of this interaction on a cell membrane is unknown. In fact, generally no lipids were extracted from the bilayer in any of the coated simulations, likely because minimal amounts of bare graphene protruded into the aqueous phase in any of the systems.