Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 2;59(12):8514–8521. doi: 10.1021/acs.inorgchem.0c00958

Structural Evolution of Ferroelectric and Ferroelastic Barium Sodium Niobate Tungsten Bronze

Solveig Stubmo Aamlid 1, Sverre Magnus Selbach 1, Tor Grande 1,*
PMCID: PMC7303971  PMID: 32484688

Abstract

graphic file with name ic0c00958_0007.jpg

The crystal structure of the ferroelastic and ferroelectric tungsten bronze Ba2NaNb5O15 (BNN) has been debated. Here, we re-examine the crystal structure of BNN by ambient powder X-ray diffraction combined with density functional theory calculations. We demonstrate that the room temperature space group is Cmm2 with significant cation disorder on the Ba and Na cation sublattices. Density functional theory calculations reveal a relatively flat energy landscape between structures of different symmetries, including the energetics of cation disorder. We also study the structural evolution and the ferroelectric and ferroelastic phase transitions by high-temperature X-ray diffraction and dilatometry. The ferroelectric phase transition at 570 °C is of first order and cause the cell to expand in the c direction, while the ferroelastic distortion starting at 270 °C takes place in the ab plane and does not affect the polarization. The phase transitions are not coupled, which means that BNN is a ferroic material with two primary and uncoupled order parameters.

Short abstract

The space group of the tetragonal tungsten bronze Ba2NaNb5O15 was confirmed experimentally to be Cmm2 with partly Na and Ba cation disorder, while the most energetically favorable ordered structure was identified as Bbm2 by first-principles calculations. The thermal evolution of the crystal structure was determined, including a ferroelectric phase transition with contraction in the c direction at 570 °C and a ferroelastic transition at 270 °C, which is decoupled from the polarization and takes place in the ab plane.

Introduction

The tetragonal tungsten bronze (TTB) structure is comprised of corner-sharing octahedra that are linked in such a way that triangular, square, and pentagonal sites are formed. The structure is referred to as filled TTB if all the square and pentagonal sites are filled; a classical example of this is Ba2NaNb5O15 (BNN), where the octahedra are filled with Nb, the square sites with Na, and the pentagonal sites with Ba. BNN is a uniaxial and proper ferroelectric material with a remarkably high Curie temperature (585 °C), which also goes through a second ferroelastic phase transition at 260 °C.1−3 The Curie temperature of BNN is dependent on the thermal history, which was described already in 1969.4 This effect is well studied in another tungsten bronze, SrxBa1–xNb2O6 (SBN), and has been attributed to cation ordering from density functional theory (DFT) calculations as well as experiments.5−8 The tetragonal tungsten bronze structure of BNN, first published by Jamieson,1 has an aristotype phase with P4/mbm symmetry, as it is for all tetragonal tungsten bronzes. The polar paraelastic space group is P4bm, meaning that the polarization is along the c direction. The ferroelastic structure has been a matter of discussion; it was determined to be Cmm2 by Jamieson and Niizeki et al.,1,9Ccm21 by Toledano,10Bbm2 by Labbe et al. in 1990,11 and finally Ferriol concluded in 2001 that Pba2 was the room temperature symmetry.12 The difference between these structures is whether the ferroelastic distortion comes along the [1 1 0] or [1 0 0] directions of the aristotype tetragonal cell, and whether octahedral tilts cause a larger unit cell. The structure is also affected by incommensurate modulations, a characteristic feature of a whole range of tungsten bronzes.11,13

In previous DFT calculations on BNN, Yamachi et al. used the Cmm2 space group and calculated a polarization of 34.8 μC/cm2, concluding that the d0-ness of the Nb causes the second-order Jahn–Teller type mechanism displacing the Nb cations.14 This mechanism is similar to what was shown for SBN.15 The octahedral tilts and rotations possible in the hexagonal and tetragonal tungsten bronzes were thoroughly investigated recently, showing what kinds of tilts are possible in these structures while keeping rigid units.16−18

Here, we re-examine the crystal structure of BNN by powder X-ray diffraction combined with DFT calculations, to determine the correct structure at ambient temperature. Moreover, we explore the thermal evolution of the crystal structure by high temperature X-ray diffraction and thermal analysis (dilatometry), and the coupling between the ferroelastic and ferroelectric transitions. Finally, the possible influence of cation disorder in BNN on the structural and functional properties is investigated.

Experimental and Computational Methods

Synthesis

The BNN ceramics were synthesized using dried NaCO3 (>99.999%), BaCO3 (>99.98%), and Nb2O5 (>99.99%) as precursors (Sigma-Aldrich). Because of the high volatility of Na at high temperatures, NaNbO3 was first formed by mixing in ethanol, drying, pressing at 30 MPa, and calcination for 4 h at 700 °C. Stoichiometric amounts of NaNbO3, BaCO3, and Nb2O5 were then mixed in ethanol, dried, uniaxially pressed at 30 MPa, and calcined at 1200 °C. The calcined powders were mixed by ball milling, sieved, uniaxially pressed at 90 MPa, further compressed with a cold isostatic press at 200 MPa, and sintered at 1300 °C for 2 h (referred to as sintered). Two pellets were quenched from the sintering temperature at 1300 °C (referred to as quenched), and one of these was annealed at 800 °C for 30 min and then quenched (referred to as annealed). Heating/cooling rates were 300 °C/h, except for the quenched and annealed samples, where the door to the furnace was opened to allow for faster cooling rates. The pellets were polished to remove any excessive grain growth on the surface.

Characterization

X-ray diffraction (XRD) was performed on powder samples from crushed sintered pellets. A room-temperature variable counting time (VCT) measurement was done using a SIMENS D5000 instrument with monochromatic Cu Kα1 radiation for 24 h. A Pawley-fit was performed for the Cmm2 and Pba2 space groups, while a full Rietveld refinement was performed for the Cmm2 structure. A modified Thompson-Cox-Hastings pseudo-Voigt (TCHZ) model19,20 was used for the peak shape; all symmetry inequivalent ion positions, nine thermal parameters, and the stoichiometrically restricted occupancies of Na and Ba were refined as described in Table S1.

Powders from crushed quenched and annealed samples were measured with a Bruker DaVinci1 diffractometer with Cu Kα radiation. Full Rietveld refinements were performed as for the previous refinement, but with peak shapes described with a fundamental parameter model.

High-temperature XRD (HT-XRD) was performed using a Bruker D8 Advance with Cu Kα radiation, våntec-1 SuperSpeed detector and measured after equilibration at set temperatures every 25 °C from 100 to 225 °C, every 10 °C from 235 to 725 °C, and every 25 °C from 750 to 800 °C. The real temperatures were found by calibration by similar measurements using corundum (Al2O3), and the real maximum temperature found to be 672 °C (set-point 800 °C). Pawley fits were performed to find the unit cell parameter evolution, refining also sample displacement and peak broadening by using a fundamental parameter model. A high-resolution, high-temperature scan was performed at the highest temperature over the course of 10 h. The high temperature refinement was performed using the P4/mbm model applying the same approach as for the quenched and annealed samples.

A 5 mm diameter rod sintered at 1300 °C was measured by dilatometry (Netzsch DIL402C) in air up to 800 °C, using heating and cooling rates of 2 °C per minute. The cooling cycle was used for the analysis.

There are no unexpected, new, or significant hazards or risks associated with the experimental work.

Computational Details

Density functional theory calculations were performed using the Vienna Ab initio Simulation Package (VASP)21−24 software with the projector augmented wave (PAW) method.25 The PBEsol exchange correlation functional was applied26 along with PBE pseudopotentials Ba_sv (5s2 5p6 6s2), Na pv (2p6 3s1), Nb_sv (4s2 4p6 4d3 5s2), and O (2s2 2p4). An energy cutoff for the wave functions of 650 eV, a 2 × 2 × 6 Monckhorst-Pack k-point grid (for the 46-atom unit cell), an electronic convergence threshold of 10–8 eV, and force on all ions below 10–4 eV/Å were used. The convergence criteria for the energy cutoff and k-point grid were an energy change of less than 1 meV/atom. An SBN P4/mbm cell was used as a starting point.

Phonon calculations were done using the finite displacement method implemented in the phonopy package.27 Starting with the 46-atom unit cell, the ferroelectric phonon mode that led to the experimentally observed P4bm was frozen in. The Pba2 and Cmm2 cells were created by manually distorting the crystal to the experimental magnitude of the strain with subsequent relaxation. To describe any tilt modulations, a 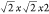Inline graphic supercell was used, which makes the phonons in A and Z high-symmetry points of the Brillouin zone accessible. In order to access the R point, a 2 × 2 × 2 unit cell is needed, which is too memory intensive. Because of the change in cell size, a 2 × 2 × 4 Monckhorst-Pack grid was used for the larger cells. The polarization was calculated with the Berry phase method.28,29 In order to access the Bbm2 structure, we used the monoclinic description in the Ama2 setting as used by Materials Project mp-119962430 and a 4 × 2 × 2 Monckhorst-Pack grid. Symmetry analyses were done using the ISOSUBGROUP tool.31

The cation disorder in BNN is expected to consist of Ba and Na atoms switching lattice sites. We used a 1 × 1 × 2 supercell of the polar P4bm structure to assess the possible configurations. The ground state is a 1 × 1 × 2 supercell with Na on the A1 sites and Ba on the A2 (Figure 1). If we let one pair of Na and Ba switch positions, we place the Ba on the A1 first (only one option since the sites are symmetry equivalent), and then there are two symmetry inequivalent sites where Na can be placed on A2 (Figure 1). The Na can be placed in such a way that the Na are in the Same Plane in the double unit cell (NaSP), or so that the Na are in Alternating Planes (NaAP) These two configurations are the ones included in this work. If we interchange 2 cations, it is 19 possible configurations (SI, Note S1). The fully inverted structure has five options, and the structures with three and four cations interchanged were not explored.

Figure 1.

Figure 1

Open in a new tab

(a) Ordered ground state configuration of Ba2NaNb5O15, (b) cation disordered BNN labeled NASP corresponding to swapping of Na cations in the same ab plane (c) cation disordered BNN labeled NaAP corresponding to swapping of cations in alternating ab planes. Only Na and Ba are shown for clarity.

Thermodynamic Model

A thermodynamic model for cation disorder in tungsten bronzes6 can be derived for the disorder in BNN by starting from the chemical equation describing the cation interchange:

graphic file with name ic0c00958_m002.jpg 1

Assuming the Gibbs energy of the cation interchange to be

graphic file with name ic0c00958_m003.jpg 2

the final expression for equilibrium becomes

graphic file with name ic0c00958_m004.jpg 3

The α and β parameters in eq 3 can be calculated from 0 K enthalpies derived from density functional theory calculations.

Results

Experiments

The room temperature diffractogram and the Rietveld refinement with space group Cmm2 are shown in Figure 2, and the refined parameters can be found in Table 1. The room temperature refinements of the two space groups demonstrate that the Pba2 symmetry can be excluded by a simple Pawley fit. The difference between the two space groups is in which direction the ferroelastic distortion takes place. Even though the reflection conditions are the same for the two space groups, only the Cmm2 can capture the ferroelastic distortion because of the strain direction. Some of the Bragg reflections fitted with the Pba2 and Cmm2 space groups are shown in the insets in Figure 2. To get a satisfactory fit, cation disorder on the square and pentagonal sites was also required. Using a completely cation-ordered structure caused the thermal parameters on the A1 site to become negative, indicating too low electron density.

Figure 2.

Figure 2

Open in a new tab

Rietveld refinement of room temperature X-ray (Cu Kα1 radiation) diffractogram of Ba2NaNb5O15 using the Cmm2 structure. The inset shows selected reflections and refinements with the Pba2 and Cmm2 space groups, demonstrating strain along [110] due to the observed double reflection. The background intensity increases at higher angles because of variable count time (VCT).

Table 1. Refined Cmm2 Crystal Structure of Ba2NaNb5O15a.

site Wyckoff position atom x y z occupancy Biso (Å2)
A2_1 4d Ba 0.17264(15) 0.5 0.5 0.943(2) 3.76(8)
    Na 0.17264(15) 0.5 0.5 0.057(2) 3.76(8)
A2_2 4e Ba 0.5 0.67202(15) 0.5 0.943(2) 3.76(8)
    Na 0.5 0.67202(15) 0.5 0.057(2) 3.76(8)
A1 4c Na 0.75 0.25 0.485(9) 0.886(5) 5.8(2)
    Ba 0.75 0.25 0.485(9) 0.114(5) 5.8(2)
Nb1_1 2a Nb 0 0 0.974(5) 1 2.12(7)
Nb1_2 2b Nb 0 0.5 0.976(5) 1 2.12(7)
Nb2_1 8f Nb 0.89182(11) 0.31861(12) 0.992(4) 1 2.54(7)
Nb2_2 8f Nb 0.68152(12) 0.39139(11) 0.990(4) 1 2.54(7)
O1_1 4d O 0.2888(11) 0.5 –0.00(3) 1 2.6(3)
O1_2 4e O 0.5 0.7711(11) 0.01(2) 1 2.6(3)
O2_1 8f O 0.8486(10) 0.2142(10) –0.00(3) 1 4.7(3)
O2_2 8f O 0.7913(11) 0.3593(10) 0.01(3) 1 4.7(3)
O3_1 8f O 0.9257(10) 0.0824(11) –0.008(19) 1 4.1(3)
O3_2 8f O 0.9153(11) 0.4280(10) 0.023(12) 1 4.1(3)
O4_1 8f O 0.1076(12) 0.3120(12) 0.545(14) 1 5.1(3)
O4_2 8f O 0.6810(13) 0.6100(11) 0.549(14) 1 5.1(3)
O5_1 2b O 0 0.5 0.52(3) 1 4.1(5)
O5_2 2a O 0.5 0.5 0.51(5) 1 4.1(5)
Open in a new tab
a

A total of 92 independent parameters were refined. The unit cell parameters are a = 17.58881(10) Å, b = 17.62308(9) Å, and c = 3.992668(17) Å. The refinement converged with an Rwp value of 7.02 and a GOF of 1.48.

Rietveld refinements of diffraction patterns of the quenched and annealed samples are summarized in Figure S1 and Table S2. The structural models for both these samples require cation disorder to be included to give a satisfactory fit. The Na occupation of A2 (0.060 and 0.063 for the quenched and annealed sample respectively), and hence the degree of disorder is, surprisingly, slightly higher in the annealed sample. However, this difference is small and within the experimental uncertainty. Hence, thermal annealing at 800 °C did not influence the cation occupancy of Na and Ba in the BNN sample used in this work.

Selected diffractograms from HT-XRD are shown in Figure 3. The evolution of the diffractograms demonstrates that both the unit cell parameters and the symmetry change due to the ferroelastic and ferroelectric phase transitions. The changes in the lattice parameters around the ferroelectric transition is highlighted with the red lines in Figure 3a, the (040) reflection only show expansion of the a parameter, while the (021) reveals the contraction in the c parameter at high temperature. The ferroelectric transition also gives rise to a splitting of the of the (221) and (330) reflections, highlighted in Figure 3b. Finally, the weaker splitting that occurred over a wider temperature region in the same reflection on the ferroelastic transition is shown in Figure 3c.

Figure 3.

Figure 3

Open in a new tab

High-temperature X-ray diffractograms of Ba2NaNb5O15 measured with Cu Kα radiation. (a) Selected diffractograms highlighting the anisotropic thermal expansion of the lattice parameters. The (hkl) labels are given for the aristotype structure with space group P4/mbm. (b) A detailed view of a reflection with a fingerprint of the ferroelectric transition with 10 °C set step length. (c) A detailed view of the same reflection showing the ferroelastic transition with 25 °C set step length for the first five scans and then 10 °C set step length from 196 to 318 °C.

Phase transition temperatures and unit cell parameters as a function of temperature were determined from the HT-XRD data, and these are plotted as a function of temperature in Figure 4. The ferroelectric distortion is clearly visible in the expansion of the c parameter, as the polarization direction is along c, while the a parameter contracts on cooling. The c parameter continues to expand well below the phase transition temperature before the thermal contraction resumes, indicating that the magnitude of the polar distortion that causes this expansion is still evolving. The ferroelastic transition is not visible in the c parameter but causes a gradual splitting of the a and b parameters. The dashed lines at 276 and 586 °C mark the phase transition temperatures, determined by the temperature evolution of the Rwp values. The coefficient of volumetric thermal expansion was calculated from the diffraction data to be αV,FE = 34 × 10–6 K–1 in the ferroelastic region between 83 and 266 °C, and αV,PE = 21 × 10–6 K–1 in the paraelectric region between 590 and 672 °C.

Figure 4.

Figure 4

Open in a new tab

Lattice parameters a, b, and c of Ba2NaNb5O15 as a function of temperature. Phase transition temperatures are marked with vertical dashed lines at 276 and 586 °C.

The refinement of the X-ray diffraction pattern for the longer scan at 672 °C is shown in Figure S2. The P4/mbm structure gives a satisfactory fit if cation disorder is allowed, or else the thermal parameters for the A1 sites become negative.

The dilatometry data upon cooling of the sintered BNN rod is given in Figure 5 together with the first temperature derivative. The dashed lines denote the phase transitions at 270.5 and 570 °C respectively. The figure clearly demonstrates the thermal expansion of BNN and the abrupt contraction of the volume across ferroelectric transition. The ferroelastic transition is only visible in the first derivate, where the added tangent lines indicate that the second derivative of the volume with respect to temperature is discontinuous. It is thus concluded from the XRD and the dilatometry measurements that the ferroelectric transition must be of first order, while the ferroelastic has more second-order characteristics. Finally, the linear thermal expansion in the ferroelastic region between 100 and 200 °C was determined to αL,FE = 13 × 10–6 K–1, and in the paraelectric region between 640 and 740 °C to αL,PE = 4.8 × 10–6 K–1.

Figure 5.

Figure 5

Open in a new tab

(Top) Dilatometry curve of Ba2NaNb5O15 collected upon cooling and (bottom) the numeric temperature derivative of the curve. The numeric derivative was calculated with a moving-average filer with window size 5. The dashed lines indicate the phase transition temperatures at 270.5 and 570 °C.

DFT Calculations

The starting point for the DFT calculations was a well converged aristotype P4/mbm structure. Frozen phonon calculations from this cell yielded strong instabilities and energy gain in going to the ferroelectric P4bm phase, as expected. The Pba2 and Cmm2 structures were realized by manually distorting the unit cell parameters to experimental values and subsequent relaxation, but the energy lowering from P4bm to the two orthorhombic space groups is negligible as seen in Table 2. The polarization in the c direction is shown in the same table. The polarization is in good agreement with experimental values and previous DFT calculations.2,14 The ferroelastic distortion does not affect the polarization.

Table 2. Calculated Space Group, Relative Energies, Boltzmann Probability and Polarization of Some Select Crystal Structures of Ba2NaNb5O15.

type space group relative energyb (eV/u.c.) Boltzmann probability at 500 °C polarization (μC/cm2)
aristotype P4/mbm 0 (def.)   0
ferroelectric P4bm –0.41 0.86 42.7
ferroelastic Cmm2 –0.41   42.7
ferroelastic Pba2 –0.41   42.8
disordereda P1 (NaSP) –0.22 0.09 42.0
disordereda P1 (NaAP) –0.26 0.05 41.6
ferroelastic with tilts Ima2 –0.53   43.7
ferroelastic with tilts Ccm21 –0.48   39.9
ferroelastic with tilts Bbm2 –0.54   40.6
experimental       40c
Open in a new tab
a

Disordered means cation disordered structures.

b

The convergence criteria for the energy cutoff and k-point grid were an energy change of less than 1 meV/atom.

c

Experimental value from Wemple et al.2

A visualization of the two relaxed cation disordered structures can be found in SI, Figure S3. The main changes are a rattling in the ab plane for the Na and Ba, especially for Na on A2, and some octahedral tilting. The space group, energy lowering, and Boltzmann probabilities of the disordered structures as described in the computational details are shown in Table 2. The niobium oxide octahedra network exhibit tilting of the octahedra, which is allowed because of the reduced symmetry from the cation disordering. The strongest effect is on the sodium atoms in the A2 sites, which move away from the center of the A2 sites to be able to optimize the oxygen coordination. Cation disorder weakly affects the polarization, and the lower polarization is in accordance with the lower TC of the samples quenched from higher temperatures,4 albeit not enough to explain the lower TC alone. An attempt was made to fit the cation disordered structures to the experimental data. However, the double unit cell and artificial cation ordering cause the simulated diffractograms to have extra reflections that are not observed experimentally (Figure S4).

The phonon calculations on the 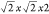Inline graphicP4bm cell reveal 21 phonon modes with negative frequencies in the G, A, and Z points in the Brillouin zone. The phonon dispersion is flat, indicating that the phonons might be able to freeze in at points that are not in the zone boundary, and that the structures might be close in energy. Upon further investigation of the instabilities, it is noted that some are degenerate, most are ferroelastic tilt modes, and some contribute to energy lowering. The two modes with the lowest frequency and largest energy lowering, shown in Table 2, are Ima2 and Ccm21, which are found in the A and Z points respectively. They are both allowed to be continuous and improper ferroelastic transitions from symmetry analysis in the ISOSUBGROUP framework in the ISOTROPY Software Suite.31 These two tilt modulated structures are visually comparable to the ones in the Supplementary Information in ref (17).

Fits to selected parts of the diffractogram with the Ima2 and Ccm21 structures that lower the energy the most are shown in Figure S4. The double unit cell with tilt modes allows for correlated cation on-site disorder on the A2 sites, which cause reflections in the diffractogram that are not observed. Our XRD data are not sufficient to refine the oxygen positions in the tilt modulated structure due to the many degrees of freedom and low scattering power of oxygen compared to the heavy cations. The Bbm2 cell was also relaxed with DFT, and the relative energies for all the investigated tilt modulated structures can be found in Table 2. The tilt modes provide some energy lowering but are close in energy, and some are doubly degenerate in order parameter space, meaning that the order parameter direction can fluctuate. Rietveld refinement to selected parts of the diffractogram for the Bbm2 structure is also shown in Figure S4, which similarly to the other tilt modulated and disordered structures display reflections that are not observed with XRD. Finally, a fit to the Bbm2 structure with the cations constrained to their higher-symmetry Cmm2 sites showed that the extra reflections (mostly) disappear. Similar results could be achieved for the other tilt modulated structures. To conclude on the symmetry of the oxygen sublattice data obtained by neutron diffraction is required. Although the Bbm2 structure is the most stable from DFT calculations at 0 K, we cannot easily predict if there will be tilt modulations at room temperature. The Berry phase calculations for the Ima2, Ccm21, and Bbm2 tilt modulated structures can be found in Table 2, showing that the first slightly increase the polarization, while the two latter slightly lower it.

Discussion

The BNN crystal structure is polar along the c direction, ferroelastic in the ab plane with a variety of possible tilt modulations, and significant cation disorder at room temperature is evident in BNN. We have investigated this by combining DFT calculations and Rietveld refinements of XRD data. We have also investigated the ferroelectric and particularly the ferroelastic phase transition more closely.

The ferroelectric phase transition takes place at very a high temperature compared to prototype ferroelectric materials with perovskite structure. A conventional Jahn–Teller mechanism is proposed14,15 as the symmetry goes from the aristotype P4/mbm to P4bm when the mirror plane perpendicular to the c axis is lost, and polarization arises along the c direction. This phase transformation is associated with a large volume expansion caused by the large increase in c lattice parameter and small decrease in a lattice parameter, but no ferroelastic domains are formed as BNN is a uniaxial ferroelectric.

The ferroelastic transition happens several hundred degrees below the ferroelectric and is much more subtle in terms of volume and energy, the letter inferred from 0 K enthalpies obtained by DFT. These two transitions seem not to be coupled to each other, which means that BNN has two primary and uncoupled order parameters. This can be seen purely from the symmetry changes32 and is further supported by the fact that Berry phase-calculated polarization is not affected by the ferroelastic distortions and that they occur far apart in temperature.

The energy differences for the cation disorder are in a similar range as the enthalpy of the ferroelectric phase transition, inferring that a significant cation disorder is probable. When we calculate Boltzmann probabilities at 500 °C only including the P4bm and the disordered structures, the result is that 86% of the cells will be ordered. Our disordered unit cells are only 1/4 disordered, and with our Rietveld refinements we show that this simple model does not capture the full scale of the observed cation disorder. There are more possible cation configurations with higher entropy that could be included, but this is computationally costly, but which would not change the overall picture of the likelihood of cation disorder. 500 °C is a conservative estimate for a temperature below the ferroelectric transition where the cation mobility is expected to be extremely low. In turn, this means that the cation mobility will be small and the cation ordering practically frozen in when the ferroelectric transition is reached.

The influence of cation disorder on the ferroelectric properties in the tungsten bronzes is well described for SBN,8 but there are some major differences in how BNN behaves compared to SBN. In this work, we were not able to influence the cation order by heat treatment. Our hypothesis is that cation disorder is kinetically much easier in SBN due to the intrinsic cation vacancies in SBN. In BNN, the kinetics of cation ordering will be dominated by the concentration of vacancies on the A sites caused by cation nonstoichiometry and thermal excitations, which will inevitably be sensitive to sample preparation details. An effort was made to refine the Ba and Na occupancies without constricting the cation stoichiometry or allowing for cation disorder, which gave a small overstoichiometry. Similarly, when refining the occupancies without constricting the overall cation stoichiometry but allowed for cation disorder (which makes the refinement uncertain due to correlation effects), the occupancies indicated A site deficiency. However, the lack of influence of the thermal annealing on the cation disorder is a strong indication that the A site vacancy concentration is not substantial. Another notable difference in the disorder-polarization interactions in BNN compared to SBN is that the behavior of the Curie temperature with quenching temperature is the opposite. This can be explained by the size-difference effect proposed by Zhu et al.,13 suggesting that a large difference in size makes for a higher Curie temperature. When Ba and Na swap lattice sites, the average cation size on the two sublattices approach each other and the Curie temperature decrease. With increasing cation disorder in SBN, the vacancy goes to the A1 site, while the A2 site is filled with more Sr, reducing the effective size difference.7,8 It is thus expected that filled tungsten bronzes behave like BNN while unfilled behave like SBN. A final comment on cation disorder-polarization interactions in BNN is that the polarization is only weakly affected by disorder, analogous to what was observed in the unfilled tungsten bronze lead niobate PbNb2O6 (PN)33 and unlike what was observed in SBN. The reason is that the cation disorder in SBN includes a vacancy, which makes the structural changes upon disordering more pronounced, and especially the tilt modes are strongly affected. These tilt modes are coupled to the ferroelectric polarization in SBN, unlike the uncoupled tilt modes in BNN.

When looking at the acoustic phonons in the P4bm phonon spectra, we can see that there are several instabilities at different k-points with similar frequencies. A true proper ferroelastic phase transition has to be associated with the softening of an acoustic phonon and also has to have the spontaneous strain as its order parameter.34 It is likely that the ferroelastic transition should be accompanied by tilt modes, as the energy is not lowered for the ferroelastic space group without tilts (Cmm2 and P4bm), while it is lowered for the ones with tilts (Ima2, Ccm21, and Bbm2). The small enthalpy differences between the ferroelastic space groups in combination with the flat phonon landscape indicates that phonon modes can freeze in at various places in the Brillouin zone without affecting the energy significantly. This means that small perturbations in the crystal lattice could determine the final structure and be a source for the inconsistent space group determination and the (in)commensurate modulations observed in this material. Such a small perturbation can be for instance thermal stresses during cooling or cation disorder on the A1/A2 cation sublattice. One possible consequence of this is that the local and the global structures can differ from each other.

A Landau fit, shown in Figure 6, was made to the spontaneous strain to determine the critical exponent of the ferroelastic phase transition, as defined by

graphic file with name ic0c00958_m006.jpg 4

where the aorth and borth denote the observed orthorhombic a and b lattice parameters respectively, and a0,T is the extrapolated a lattice parameter from the tetragonal phase. The εs,T, as it is the order parameter of the phase transformation, is proportional to the reduced temperature to the power of the critical exponent β. Doing a mean square fit results in a in a value of exponent β of 0.32(9) ± 0.01, which lies within the expectation for a system with order parameter dimensionality N = 1 and system dimensionality d = 3, which is the 3D Ising model.35 This is as expected for a 3D system with two states, which is reasonable considering that we will get two ferroelastic twin domains. The uncertainty was found by extracting the Jacobian from the least-squares fit and computing a 95% confidence interval with a set TC.

Figure 6.

Figure 6

Open in a new tab

A Landau fit of the experimental strain from HT-XRD data of Ba2NaNb5O15 using eq 4 gives a critical exponent β of 0.32(9) ± 0.01.

The strain direction in ferroelastic BNN is the tetragonal [110] direction. However, there is no energy lowering with the Cmm2 structure relative to the P4bm. Our DFT calculations show that tilt modes lower the energy, although the exact space group has not been experimentally verified. Following Ascher’s rule,36 supported by the smooth evolution of the Landau strain, and the fact that we get energy lowering from the tilt modes, we suggest that the ferroelastic transition goes to either Ima2 or Ccm21 symmetry. Any incommensurate modulations or commensurate modulation to Bbm2 do not contribute significantly to the ferroelasticity, although their onset might be close to the ferroelastic transition. It is also known that the tilt modes in BNN can be incommensurate or commensurate dependent on temperature. However, the tilt modulated structures do not fit the XRD pattern as well as the higher-symmetry space group Cmm2. This is because the structures made with periodic boundary conditions in DFT get artificial symmetries because the cations are ordered in a corrugated manner along the channels. It is known that positional disorder in the ab plane for the cations in the A2 channel is common in the tungsten bronzes, and the signal from the oxygen anions is comparatively low. In short, the NbO6-octahedral network experiences, possibly (in)commensurate, tilt modulations, while the cations stay in their disordered state (Cmm2) also below the ferroelastic transition. The tilts do not affect the polarization significantly.

Conclusion

The structural consequences of the ferroelectric and ferroelastic phase transitions in BNN were studied using a combination of XRD, dilatometry, and DFT. The ferroelectric transition is at 570 °C between the aristotype P4/mbm and the polar P4bm, and the ferroelastic transition takes place at 270 °C. The global average ferroelastic room temperature space group is found to be Cmm2 by XRD, but the most energetically favorable structure at 0 K as calculated by DFT is Bbm2, closely followed by the previously not suggested Ima2. Configurational cation disorder was demonstrated by Rietveld refinement of the XRD data and rationalized by the energy landscape for cation disorder inferred from DFT calculations. We observe two primary and uncoupled ferroic order parameters. We suggest that the small enthalpy differences and the flat phonon landscapes in combination with local perturbations such as cation disorder are the cause for the (in)commensurate tilt modulations commonly reported for tetragonal tungsten bronzes.

Acknowledgments

The authors acknowledge financial support from NTNU, The Norwegian University of Science and Technology, and from Ivar Lykkes fond, DKNVS. Computational resources were provided by Sigma2 Uninett through the Project NN9264K. We thank Ulrich Aschauer and Gerhard Henning Olsen for helpful discussions and input, and for scripts that implement the frozen phonon method.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c00958.

  • Note S1: Explanation of the symmetry inequivalent cation configurations with two Ba on A1 and two Na on A2. Table S1: The Rietveld refinement details for the BNN powder sample. Table S2: The Rietveld refinement results and R-values of quenched and annealed samples. Figure S1: Rietveld refinements of the quenched and annealed samples of BNN. Figure S2: Refined high temperature XRD data using the P4/mbm aristotype as the structure model. Figure S3: The disordered (NaSP and NaAP) structures after relaxation. Figure S4: Selected space groups and the disordered structures fitted to the XRD data (PDF)

The authors declare no competing financial interest.

Supplementary Material

ic0c00958_si_001.pdf (819KB, pdf)

References

  1. Jamieson P. B.; Abrahams S. C.; Bernstein J. L. Ferroelectric Tungsten Bronze-Type Crystal Structures. II. Barium Sodium Niobate Ba(4+x)Na(2–2x)Nb10O30. J. Chem. Phys. 1969, 50 (10), 4352–4363. 10.1063/1.1670903. [DOI] [Google Scholar]
  2. Wemple S. H.; DiDomenico M.; Camlibel I. Relationship between linear and quadratic electro-optic coefficients in LiNbO3, LiTaO3, and other oxygen-octahedra ferroelectrics based on direct measurement of spontaneous polarization. Appl. Phys. Lett. 1968, 12 (6), 209–211. 10.1063/1.1651955. [DOI] [Google Scholar]
  3. Scott J. F. Ferroelectrics go bananas. J. Phys.: Condens. Matter 2008, 20 (2), 021001 10.1088/0953-8984/20/02/021001. [DOI] [Google Scholar]
  4. Burns G.; O’Kane D. F. Transition temperature variations in sodium barium niobate and related compositions. Phys. Lett. A 1969, 28A (11), 776–777. 10.1016/0375-9601(69)90617-3. [DOI] [Google Scholar]
  5. Guo R.; Bhalla A. S.; Burns G.; Dacol F. H. Studies on annealing and quenching of strontium barium niobate (SBN) single crystals: A-site cation ordering-disordering effect. Ferroelectrics 1989, 93 (1), 397–405. 10.1080/00150198908017376. [DOI] [Google Scholar]
  6. Olsen G. H.; Selbach S. M.; Grande T. On the energetics of cation ordering in tungsten-bronze-type oxides. Phys. Chem. Chem. Phys. 2015, 17 (45), 30343–30351. 10.1039/C5CP05119C. [DOI] [PubMed] [Google Scholar]
  7. Graetsch H. A. Structural changes of relaxor ferroelectric Sr0.52Ba0.48Nb2O6 (SBN52) on quenching and reheating. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2017, 73 (5), 820–826. 10.1107/S2052520617007880. [DOI] [PubMed] [Google Scholar]
  8. Aamlid S. S.; Selbach S. M.; Grande T. The effect of cation disorder on ferroelectric properties of SrxBa1-xNb2O6 (SBN) tungsten bronzes. Materials 2019, 12 (7), 1156–1167. 10.3390/ma12071156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Yamada T.; Iwasaki H.; Niizeki N. Elastic Anomaly of Ba2NaNb5O15. J. Appl. Phys. 1970, 41 (10), 4141–4147. 10.1063/1.1658426. [DOI] [Google Scholar]
  10. Toledano J. C. Theory of the ferroelastic transition in barium sodium niobate. Phys. Rev. B 1975, 12 (3), 943–950. 10.1103/PhysRevB.12.943. [DOI] [Google Scholar]
  11. Labbe P.; Leligny H.; Raveau B.; Schneck J.; Toledano J. C. X-ray structural determination of the quasicommensurate phase of barium sodium niobate. J. Phys.: Condens. Matter 1990, 2, 25–43. 10.1088/0953-8984/2/1/002. [DOI] [Google Scholar]
  12. Ferriol M. Crystal growth and structure of pure and rare-earth doped barium sodium niobate (BNN). Prog. Cryst. Growth Charact. Mater. 2001, 43, 221–244. 10.1016/S0960-8974(01)00007-9. [DOI] [Google Scholar]
  13. Zhu X.; Fu M.; Stennett M. C.; Vilarinho P. M.; Levin I.; Randall C. A.; Gardner J.; Morrison F. D.; Reaney I. M. A Crystal-Chemical Framework for Relaxor versus Normal Ferroelectric Behavior in Tetragonal Tungsten Bronzes. Chem. Mater. 2015, 27 (9), 3250–3261. 10.1021/acs.chemmater.5b00072. [DOI] [Google Scholar]
  14. Yamauchi K.; Picozzi S. Interplay between charge order, ferroelectricity, and ferroelasticity: tungsten bronze structures as a playground for multiferroicity. Phys. Rev. Lett. 2010, 105 (10), 107202-1–107202-4. 10.1103/PhysRevLett.105.107202. [DOI] [PubMed] [Google Scholar]
  15. Olsen G. H.; Aschauer U.; Spaldin N. A.; Selbach S. M.; Grande T. Origin of ferroelectric polarization in tetragonal tungsten-bronze-type oxides. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93 (18), 180101-1–180101-5. 10.1103/PhysRevB.93.180101. [DOI] [Google Scholar]
  16. Whittle T. A.; Schmid S.; Howard C. J. Octahedral tilting in the tungsten bronzes. Addendum. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2018, 74 (6), 742–744. 10.1107/S2052520618015263. [DOI] [PubMed] [Google Scholar]
  17. Whittle T. A.; Schmid S.; Howard C. J. Octahedral tilting in the tungsten bronzes. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2015, 71 (3), 342–348. 10.1107/S2052520615008252. [DOI] [PubMed] [Google Scholar]
  18. Campbell B.; Howard C. J.; Averett T. B.; Whittle T. A.; Schmid S.; Machlus S.; Yost C.; Stokes H. T. An algebraic approach to cooperative rotations in networks of interconnected rigid units. Acta Crystallogr., Sect. A: Found. Adv. 2018, 74 (5), 408–424. 10.1107/S2053273318009713. [DOI] [PubMed] [Google Scholar]
  19. Young R. A.The Rietveld Method; Oxford University Press: Oxford, 1993; Vol. 5. [Google Scholar]
  20. Thompson P.; Cox D. E.; Hastings J. B. Rietveld Refinement of Debye-Scherrer Synchrotron X-ray Data from Al2O3. J. Appl. Crystallogr. 1987, 20, 79–83. 10.1107/S0021889887087090. [DOI] [Google Scholar]
  21. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  22. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  23. Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49 (20), 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
  24. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47 (1), 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  25. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59 (3), 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  26. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100 (13), 136406-1–136406-4. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  27. Togo A.; Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  28. Spaldin N. A. A beginner’s guide to the modern theory of polarization. J. Solid State Chem. 2012, 195, 2–10. 10.1016/j.jssc.2012.05.010. [DOI] [Google Scholar]
  29. Resta R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 1994, 66 (3), 899–915. 10.1103/RevModPhys.66.899. [DOI] [Google Scholar]
  30. Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. A. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
  31. Stokes H. T.; van Orden S.; Campbell B. J. ISOSUBGROUP: an internet tool for generating isotropy subgroups of crystallographic space groups. J. Appl. Crystallogr. 2016, 49 (5), 1849–1853. 10.1107/S160057671601311X. [DOI] [Google Scholar]
  32. Hlinka J.; Privratska J.; Ondrejkovic P.; Janovec V. Symmetry Guide to Ferroaxial Transitions. Phys. Rev. Lett. 2016, 116 (17), 177602. 10.1103/PhysRevLett.116.177602. [DOI] [PubMed] [Google Scholar]
  33. Olsen G. H.; Sørby M. H.; Selbach S. M.; Grande T. Role of Lone Pair Cations in Ferroelectric Tungsten Bronzes. Chem. Mater. 2017, 29 (15), 6414–6424. 10.1021/acs.chemmater.7b01817. [DOI] [Google Scholar]
  34. Salje E. K.; Hayward S. A.; Lee W. T. Ferroelastic phase transitions: structure and microstructure. Acta Crystallogr., Sect. A: Found. Crystallogr. 2005, 61 (1), 3–18. 10.1107/S0108767304020318. [DOI] [PubMed] [Google Scholar]
  35. Guida R.; Zinn-Justin J. 3D Ising model: the scaling equation of state. Nucl. Phys. B 1997, 489, 626–652. 10.1016/S0550-3213(96)00704-3. [DOI] [Google Scholar]
  36. Ascher E. Role of Particular Maximal Subgroups in Continous Phase Transitions. Phys. Lett. 1966, 20 (4), 352–354. 10.1016/0031-9163(66)90735-9. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic0c00958_si_001.pdf (819KB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES