Genetic consequences of being a dwarf: do evolutionary changes in life-history traits influence gene flow patterns in populations of the world’s smallest goldenrod?

Abstract

Background and Aims

Contrasting life-history traits can evolve through generations of dwarf plant ecotypes, yet such phenotypic changes often involve decreased plant size and reproductive allocation, which can configure seed dispersal patterns and, subsequently, population demography. Therefore, evolutionary transitions to dwarfism can represent good study systems to test the roles of life-history traits in population demography by comparing genetic structure between related but phenotypically divergent ecotypes.

Methods

In this study, we examined an ecotypic taxon pair of the world’s smallest goldenrod (stem height 2.6 cm) in alpine habitats and its closely related lowland taxon (30–40 cm) found on Yakushima Island, Japan. Genetic variation in chloroplast DNA sequences, nuclear microsatellites and genome-wide single-nucleotide polymorphisms were used to investigate 197 samples from 16 populations, to infer the population genetic demography and compare local genetic structure of the ecotypes.

Key Results

We found a pronounced level of genetic differentiation among alpine dwarf populations, which were much less geographically isolated than their lowland counterparts. In particular, several neighbouring dwarf populations (located ~500 m apart) harboured completely different sets of chloroplast haplotypes and nuclear genetic clusters. Demographic modelling revealed that the dwarf populations have not exchanged genes at significant levels after population divergence.

Conclusions

These lines of evidence suggest that substantial effects of genetic drift have operated on these dwarf populations. The low-growing stature and reduced fecundity (only 3.1 heads per plant) of the dwarf plants may have reduced gene flow and rare long-distance seed dispersal among habitat patches, although the effects of life-history traits require further evaluation using ecological approaches.

INTRODUCTION

Understanding the factors and processes that shape early population divergence is one of the major objectives of evolutionary biology. Although large-scale spatial genetic structure often reflects historical isolation (e.g. climate change, geological evolution and land bridge configurations) (Magri et al., 2006; Qiu et al., 2011; Sork et al., 2016), for local genetic structure the roles of gene flow and ecological differentiation become more influential. The pattern of gene flow often depends on landscape heterogeneity more than geographical distance, which configures the connectivity of suitable habitats and thus individual dispersal patterns (Manel et al., 2003; Holderegger et al., 2010). Life-history traits (e.g. dispersal mode, growth form and size), which are inherent to each population/species, can also influence gene exchanges between populations (Vekemans and Hardy, 2004; Hardy et al., 2006). Meta-analyses of population genetic statistics over a range of plant lineages have revealed the phenotypic trait sets of significance for predicting genetic structure (Hamrick 1996; Nybom and Bartish, 2000; Aguinagalde et al., 2005; Duminil et al., 2007, 2009). Among these, the way in which seeds are dispersed can be an important determinant in shaping population genetic structure when it is a good representation of the realized dispersal distance (Takeuchi et al., 2004; Aguinagalde et al., 2005; Duminil et al., 2007). Hence, for non-zoochorous plants seed dispersal distance can be formulated as a function of release height (Tamme et al., 2014), with seed dispersal distance increasing with increasing release height (De Frenne et al., 2011). However, the effects of release height (or plant height) on genetic structure are not always straightforward, partly because life-history traits affect genetic structure in ways that depend on context (e.g. historical, ecological and especially taxonomic context) (Duminil et al., 2007).

To isolate the effect of life-history traits, studies can benefit from comparison of the genetic structure of phylogenetically related species that differ in particular traits but share most evolutionary contexts. Contrasting life-history traits can evolve through the generation of compact or dwarf plant ecotypes, which are repeatedly selected in various evolutionary contexts, including coastal habitats (Lowry, 2012), alpine environments (Billings and Mooney, 1968), and under grazing pressure by mammals (McNaughton, 1984; Suzuki et al., 2009). Such phenotypic changes are thought to be a local adaptation to harsh environments by avoiding abiotic or biotic stress, and are sometimes accompanied by life-history trait changes, including a markedly decreased number of inflorescences and lower reproductive allocation (Suzuki, 2008; Hirano et al., 2017). Therefore, evolutionary transitions to dwarf ecotypes can offer opportunities to test the roles of changes in life-history traits by comparing genetic structure between related but phenotypically divergent ecotypes.

A hotspot of dwarf plants is located in the alpine area of Yakushima Island, a continental island of the Japanese archipelago in East Asia. More than 80 taxa with miniaturized plant body size have been identified on the island (Hatsushima, 1991). Comparative analyses of the dwarf taxa on the island and their counterpart species with larger body size have revealed evidence for the recent emergence of parallel dwarfism (Huziwara, 1965; Fujishima et al., 1990; Yokoyama et al., 2003; Tsukaya, 2005; Ishikawa et al., 2006; Shinohara and Murakami, 2006; Yano et al., 2007; Kokubugata et al., 2010; Higashi et al., 2013; Okuyama, 2016; Sun et al., 2016; Kakezawa et al., 2017). Similarly, the Eurasian goldenrod (Solidago virgaurea L. complex) evolved into an extremely dwarf taxon [Solidago minutissima (Makino) Kitamura] in the central alpine area of Yakushima Island, which includes populations with an average stem height of 2.6 cm (Fig. 1). In lowlands of the island, larger Solidago populations, which are genetically very close to the dwarf type, are parapatrically distributed (Sakaguchi et al., 2018). Stem height and reproductive efforts as represented by the number of flower heads differ considerably between the Solidago ecotypes (Fig. 1).

Fig. 1.

(A) Location of Yakushima Island in the southernmost area of the main islands of the Japanese Archipelago and the border of the Ryukyu Archipelago. (B) Geographical map of Yakushima Island. The altitudinal zonation and topography of the island are shown. The localities of lowland populations (L1–L5) and alpine dwarf populations (R1–R7, W1–W4) are shown as black circles. Two other known localities for lowland populations are indicated by open circles. (C) Stature of a flowering plant from the lowland population (KYO 00071707). (D) Scanned images of living plants from four alpine populations. (E) Alpine dwarf plants in divergent habitats: (E1) W3 population in wetland habitat; (E2) R1 population in rock habitat.

In general, plant height has been shown to be one of the most influential factors for predicting dispersal distance (Thomson et al., 2011). Also, reduced fecundity or number of seeds of dwarf plants can have negative effects on the number of seeds being uplifted and dispersed across long distances (Nathan et al., 2002), which could reduce gene flow between populations. In this study, according to these predictions we investigated gene flow in divergent ecotypic populations of Solidago on Yakushima Island to test the hypothesis of whether the reduced probability of propagule dispersal in dwarf populations decreases gene flow among local populations. Under this scenario, genetic drift is expected to have larger roles in isolating dwarf populations, resulting in a stronger genetic structure than that of larger populations. The hypothesized evolutionary process represents an important feedback effect of being a dwarf on population demography, and testing this hypothesis using molecular markers can provide insights into the genetic consequences of life-history trait evolution in plants.

MATERIALS AND METHODS

Distribution of Solidago populations on Yakushima Island

Since the dwarf taxon Solidago minutissima has long been of evolutionary interest to botanists, the localities are well represented by specimens, which show that dwarf populations occur in the high-elevation area of 1700–1930 m a.s.l. and rarely around 1300 m (KYO 00071694) (Fig. 1). In August 2014, we visited 11 alpine populations to collect leaf material along a route from Yodo-go River to Mt Nagata (1886 m) via the major peaks of Mt Kuromi (1831 m), Mt Kurio (1867 m) and Mt Miyanoura (1936 m). Because alpine dwarf populations were found in both wetlands and crevasses in rock surfaces, we recorded the habitat type for each population. The lowland populations are known to inhabit the southern slopes of the mountain ranges (Fig. 1). Although there are relatively few localities of the lowland populations, most occur in sunny places along the main rivers or around waterfalls, indicative of a fragmented distribution. We collected lowland population samples from five localities in November 2013 and August 2014.

Molecular experiments

The collected leaf samples were dried immediately using silica gel and kept in the dark at room temperature before DNA extraction. Plant DNA was extracted using a slightly modified cetyltrimethylammonium bromide method (Murray and Thompson, 1980).

Chloroplast fragment sequencing.

The population samples (197 samples from 16 populations; Table 1) were sequenced in one intergenic region (trnH-psbA) of the chloroplast genome using universal primers (Shaw et al., 2005). The PCR was performed in a 10-µL volume containing 20 ng of template DNA, 1 µL of 10× PCR buffer, 0.8 µL of 2.5 mm dNTP, 0.05 µL of 50 µm each primer, and 0.25 units of TaKaRa Ex Taq (TaKaRa, Otsu, Japan). The PCR cycle was as follows: template denaturation at 94 °C for 3 min, followed by 30 cycles of denaturation at 94 °C for 1 min, annealing at 52 °C for 1 min, and extension at 72 °C for 1 min, followed by a final extension at 72 °C for 7 min. The PCR products were sequenced using the ABI Prism BigDye Terminator Cycle Sequencing Ready Reaction Kit v3.1 (Applied Biosystems, Foster City, CA, USA), and electrophoresed on an ABI Prism 3100 Genetic Analyzer (Applied Biosystems).

Table 1.

Information and genetic variation of the Solidago populations analysed in this study. For the haplotype frequency of chloroplast DNA (cpDNA), the number of each haplotype within the population is shown in parentheses. Abbreviations: n, number of samples analysed; Na, number of alleles averaged over loci for nuclear SSR and double-digest restriction-site-associated DNA sequencing (ddRAD-seq) SNP markers; AR, allelic richness, H_E, expected heterozygosity; H_O, observed heterozygosity. Asterisks indicate populations with significant deviation from Hardy–Weinberg equilibrium (P < 0.01)

Population code	Population no.	Habitat type	Flowering time	Altitude (m)	cpDNA		Nuclear SSR					ddRAD-seq
					N	Haplotype frequency	n	Na	AR	H E	H O	n	Na	Ar	H E
R1	POP_163	Rock	Late July to early September	1828	24	H1 (1), H3 (23)	24	3.3	1.8	0.391	0.328 *	17	1.7	1.1	0.217
R2	POP_164	Rock	Late July to early September	1747	3	H3 (3)	3	1.8	1.6	0.238	0.304	3	1.2	1.0	0.263
R3	POP_165	Rock	Late July to early September	1927	2	H3 (2)	2	1.8	1.8	0.287	0.382	2	1.1	0.9	0.314
R4	POP_166	Rock	Late July to early September	1864	4	H3 (4)	4	1.9	1.6	0.263	0.279	2	1.0	0.9	0.329
R5	POP_167	Rock	Late July to early September	1856	11	H3 (11)	11	2.6	1.7	0.328	0.327	10	1.6	1.0	0.203
R6	POP_168	Rock	Late July to early September	1823	17	H3 (17)	17	3.2	1.6	0.286	0.266	12	1.7	1.1	0.212
R7	POP_169	Rock	Late July to early September	1695	3	H3 (3)	3	1.8	1.6	0.271	0.294	3	1.2	0.9	0.269
W1	POP_170	Wetland	Late July to early September	1753	19	H2 (14), H3 (5)	19	3.4	1.8	0.368	0.331	17	1.7	1.1	0.218
W2	POP_171	Wetland	Late July to early September	1784	19	H3 (19)	19	3.2	1.6	0.292	0.241	12	1.6	1.0	0.206
W3	POP_172	Wetland	Late July to early September	1781	21	H3 (21)	21	3.2	1.7	0.328	0.294	10	1.6	1.1	0.205
W4	POP_173	Wetland	Late July to early September	1729	21	H3 (21)	21	3.3	1.7	0.311	0.265	14	1.6	1.0	0.210
L1	POP_160	Rock	Late October to November	410	14	H4 (1), H5 (13)	14	3.4	2.0	0.454	0.408	8	1.5	1.0	0.211
L2	POP_161	Riverside	Late October to November	31	14	H4 (14)	14	3.1	1.9	0.398	0.401	9	1.5	1.0	0.215
L3	POP_159	Riverside	Late October to November	62	14	H4 (14)	14	3.0	1.9	0.398	0.408	10	1.6	1.0	0.215
L4	POP_162	Riverside	Late October to November	21	6	H4 (6)	6	2.1	1.6	0.276	0.225	3	1.1	0.8	0.278
L5	POP_099	Riverside	Late October to November	337	5	H4 (5)	5	2.2	1.9	0.342	0.353	0	-	-	-
Mean (alpine)					13		13.1	2.7	1.7	0.306	0.301	9.3	1.5	1.0	0.241
Mean (lowland)					10		9.8	2.6	1.8	0.354	0.359	5.5	1.4	1.0	0.236
Mean (all)					12.3		12.3	2.7	1.7	0.327	0.319	8.3	1.4	1.0	0.238

Nuclear microsatellite genotyping.

The population samples (197 samples from 16 populations; Table 1) were genotyped using 17 microsatellite markers, consisting of expressed sequence tag simple sequence repeat (SSR) markers developed for this complex (Sakaguchi and Ito, 2014) and three genomic SSR markers (Salt1, Salt3 and Salt17) of Solidago altissima (Sakata et al., 2013). For all loci, the forward primer was synthesized with one of three different M13 sequences (5′-CACGACGTTGTAAAACGAC-3′/5′-TGTGGAA TTGTGAGCGG-3′/5′- CTATAGGGCACGCGTGGT-3′), and the reverse primer was tagged with a pig-tail sequence (5′-GTTTCTT-3′) to promote full adenylation (Brownstein et al., 1996). The PCR reaction was performed following the methods of Sakaguchi and Ito (2014). The PCR products were loaded onto an autosequencer (GenomeLab GeXP; Beckman Coulter, Brea, CA, USA) to assess the fragment lengths using Fragment Analysis Software v. 8.0 (Beckman Coulter).

Double digest restriction-site-associated DNA sequencing

A double digest restriction-site associated DNA (ddRAD) library was prepared for the population genetic samples (132 samples from 15 populations; Table 1) using the protocol by Peterson et al. (2012) with minor modifications. Briefly, 10 ng of genomic DNA was digested with EcoRI and BglII (New England Biolabs, Ipswich, MA, USA) and adapters were ligated at 37 °C overnight in a 10-µL volume containing 1 µL of 10× NEBuffer 2, 0.1 µL of 100× BSA (New England Biolabs), 0.4 µL of 5 µm EcoRI adapter and BglII adapter, 0.1 µL of 100 mm ATP and 0.5 µL of T4 DNA ligase (Enzymatics, Beverly, MA, USA). The reaction solution was purified with AMPure XP (Beckman Coulter). Next, 3 µL of purified DNA was used in the PCR amplifications in a 10-µL volume containing 1 µL of each 10 µm index and TruSeq universal primer, 0.3 µL of KOD-Plus-Neo enzyme, 1 µL of 10× PCR buffer (Toyobo, Osaka, Japan), 0.6 µL of 25 mm MgSO₄ and 1 µL of 10 mm dNTP. For several of the DNA samples used in the phylogenetic analysis, the PCR amplification included 1 µL of each 10 µm index and TruSeq universal primer and 5 µL of 2× KAPA HiFi HotStart ReadyMix (Kapa Biosystems, Wilmington, MA, USA). Thermal cycling was initiated with a 94 °C step for 2 min, which was followed by 20 cycles of 98 °C for 10 s, 65 °C for 30 s and 68 °C for 30 s. The PCR products were pooled and purified again with AMPure XP. The purified DNA was loaded onto 2.0 % agarose gel and fragments of around 320 bp were retrieved using E-Gel SizeSelect (Life Technologies, Carlsbad, CA, USA). After quality assessment using an Agilent 2100 Bioanalyzer (Agilent Technologies, Santa Clara, CA, USA), the library was sequenced with 51-bp single-end reads in one lane of an Illumina HiSeq2000 (Illumina, San Diego, CA, USA). The primer sequences used in this study are described in Sakaguchi et al. (2015).

Data analysis of chloroplast sequences and nuclear microsatellite genotypes

The chloroplast sequence data were edited and aligned using BioEdit v. 7.0.8.0 software (Hall, 1999). The alignment file was imported into GENALEX 6.3 software (Peakall and Smouse, 2006) to recover the chloroplast haplotypes. The relationships among the haplotypes were inferred based on a median-joining network using Network v. 5 software (Bandelt et al., 1999).

The microsatellite genotype data were used to characterize genetic diversity and infer the genetic structure of the Solidago populations. Number of alleles per locus (Na), allelic richness (AR) (El Mousadik and Petit, 1996) and expected and observed heterozygosity (H_E and H_O) (Nei, 1987) were calculated for each population using FSTAT 2.9.3 software (Goudet, 1995). FSTAT 2.9.3 was also used to test significant deviation from Hardy–Weinberg equilibrium for populations with a sufficient number of samples (n > 15) and compare genetic differentiation F_ST between the alpine and lowland groups, including 1000 permutations to obtain a two-tailed P value. To explore the population genetic structure, a population genetic model implemented in the STRUCTURE software (Pritchard et al., 2000) was applied, which assumed Hardy–Weinberg disequilibrium within genetic clusters, because the species complex has self-incompatibility (Kühn et al., 2004) and inbreeding is uncommon (Sakaguchi and Ito, 2014). It was also assumed that each individual had admixed ancestral origins, that different gene pools that had retained their allele frequency were correlated (Falush et al., 2003), and that the sampling locations were designated as prior information to obtain improved parameter estimates (Hubisz et al., 2009). Then, 20 independent STRUCTURE simulations were run for each K (K = 1–15), with 100 000 burn-in steps followed by 100 000 Markov chain Monte Carlo steps. To complement the model-based STRUCTURE analysis, a neighbour-joining phylogenetic tree (Saitou and Nei, 1987) was constructed using the ape R package (Paradis et al., 2004) based on a distance matrix calculated using the stats R package (R Development Core Team, 2018) in R v. 3.2.2 (R Development Core Team, 2015).

Demographic inference of population divergence of alpine and lowland groups

To infer the past demography of the alpine and lowland populations, approximate Bayesian computation (ABC) was applied to simulate genetic polymorphism data of the microsatellite loci for the two population groups. ABC is a flexible computational algorithm designed to perform complex model-based inferences, and can bypass exact likelihood calculations using summary statistics and large computer simulations (Cornuet et al., 2008; Csillery et al., 2010). In this study, we assumed five alternative demographic models, in which population size was assumed to change from the ancestral population (N_ANC) to the current sizes (N_ALP and N_LOW) during time T_DIV, with different combinations of migration parameters: (1) full isolation with migration (IM) model (N_ANC, N_ALP, N_LOW, T_DIV, M_LOW>ALP and M_LOW<ALP); (2) a bidirectional migration model with the same migration rate (N_ANC, N_ALP, N_LOW, T_DIV and M); (3) directional migration model 1, in which post-divergence migration occurred in only one direction from the alpine to the lowland population (N_ANC, N_ALP, N_LOW, T_DIV and M_LOW<ALP); (4) directional migration model 2, in which migration occurred from the lowland to the alpine population (N_ANC, N_ALP, N_LOW, T_DIV and M_LOW>ALP); and (5) a divergence model, where the diverged populations were isolated without migration (N_ANC, N_ALP, N_LOW and T_DIV). The prior distributions employed were as follows: population size parameters (N_ANC, N_ALP and N_LOW) in log scales were uniform [2, 5] with no constraints among the size parameters; the time parameter T_DIV was uniform [100, 10 000] among generations; the mutation rate per generation in log scale was uniform [–6, –4]. The prior information for the migration parameters was set as uniform [0.001, 2] for each complexed parameter of (N × M). The prior distribution for the time parameter was set so that the divergence would have taken place in a relatively recent timeframe, since the population divergence on Yakushima Island has been suggested to have followed the divergence of regional lineages of Japan in the late Pleistocene era (Sakaguchi et al., 2018). Each one million data simulations for the 144 alpine and 53 lowland individuals genotyped at 17 unlinked microsatellite loci was performed by drawing parameter values from the prior distribution combinations using fastsimcoal2 v. 2.5.2.21 software (Excoffier et al., 2013) and ABCtoolbox v. 2 (Wegmann et al., 2010). Seven summary statistics [mean number of alleles and heterozygosity over loci for each of the alpine and lowland populations, and the modified M ratio (Garza and Williamson, 2001) over the loci for each of the alpine and lowland populations, and F_ST between populations] of the genetic data were calculated with the arlsumstat v. 3.5.2 software (Excoffier and Lischer, 2010). The summary statistics were used for the model selection procedure based on the posterior probability of the models using the abc R package (Csilléry et al., 2012) in R v. 3.2.2. Model selection was performed with a tolerance value (i.e. percentage of accepted simulations) of 0.0001, and non-linear regression correction based on the neuralnet method was applied to correct imperfect matches between the observed and simulated summary statistics. The goodness of fit of a selected model was assessed by checking that the observed data were surrounded by simulated data, which were displayed as principle component analysis (PCA) envelopes containing a specific percentage of simulations (here, three percentages were tested, 10, 20 and 30 %), using the abc R package. In addition, the rejection algorithm implemented in the gfit function of the abc package was performed to obtain a value of the goodness-of-fit statistic for 100 pseudo-observed datasets with a tolerance value of 0.01 as the default. Then, the posterior distribution of the demographic parameters was estimated for each demographic scenario based on 0.01 % of the simulated data closest to the observed data with the neuralnet corrections using the abc R package.

Data analysis of ddRAD-seq-derived short reads

After read-trimming using Trimmomatic v. 0.32 software (Bolger et al., 2014) following the methods of Sakaguchi et al. (2017), Stacks 1.08 (Catchen et al., 2011) was used to de novo assemble the ddRAD-seq reads, as no genome reference of Solidago virgaurea complex is currently available. The assembly was performed with the following parameter settings: minimum number of identical reads required to create a stack, m = 3; nucleotide mismatches between loci within a single individual, M = 2; and mismatches between loci when building the catalogue, n = 1. The single nucleotide polymorphism (SNP) genotype for each individual was exported with a minimum read depth of 6 using the ‘populations’ command (Catchen et al., 2011). The exported genotype data were processed using PLINK v. 1.07 software (Purcell et al., 2007); markers with minor allele frequency <0.03, missing individual rate >0.6, missing locus rate >0.6 and significant deviation from Hardy–Weinberg equilibrium (P < 0.01) were filtered out (Sakaguchi et al., 2017). The SNPs were then analysed using BayeScan v2.0 software (Foll and Gaggiotti, 2008) (Supplementary Data Fig. S1), and the markers with a log-transformed posterior probability exceeding a threshold of 1.5 were considered to be candidate outliers. The outliers were removed from the dataset to generate the SNP datasets consisting of candidate neutral markers. For the filtered SNP data, we performed STRUCTURE and neighbour-joining phylogenetic tree analyses, as was done for the nuclear microsatellite genotype data.

Landscape genetics of the alpine populations

To examine the association between individual genetic variation and geography and habitat type, PCA was applied to the microsatellite and SNP data of the alpine populations. For the SNP dataset, BayeScan v2.0 was used to detect outlier markers displaying allele frequencies unusually diverged between the different habitat types (‘rock’ or ‘wetland’) in alpine areas (Table 1). The candidate outliers were removed from the subsequent landscape genetic analysis, because we were interested in estimating the neural population dynamics in the alpine area. The R package adegenet (Jombart, 2012) was used to perform the PCA analysis in R v. 3.1.0 to extract synthetic variables in which genetic variation between individuals was maximized. The resultant axis scores of the first 20 PCA axes were used to find the multivariate redundancy analysis (RDA) axes explicitly in association with the habitat difference, while the effect of geography was partialled out. RDA is a multivariate regression method based on constrained ordination. In brief, RDA summarizes the generic variation matrix, which can be constrained by a matrix of explanatory variables (e.g. environmental factors in the case of landscape genetics). Then, the remaining genetic variance, which was not constrained by explanatory variables, was analysed with a standard PCA. Accordingly, the total variance in the genetic matrix can be partitioned into constrained and unconstrained variances. Furthermore, it can deal with individual metrics without transforming distances, which could reduce the power of distance-based analyses to detect associations, and can incorporate multiple variables simultaneously and is relatively robust to collinearity between predictors (Wagner and Fortin, 2016). Using RDA for individual-based landscape genetics can provide high accuracy in detecting environmental associations and offer robust performance when applied to various landscapes (Kierepka and Latch, 2015). The RDA and subsequent model selection based on Akaike’s information criterion values were performed using the vegan package in R v. 3.1.0.

Correlation analysis

The pairwise genetic distance between individuals was calculated following the method of Kosman and Lenard (2005) using the popgenreport R package. Euclidean distance matrices were calculated for the variables for correlation with genetic distance, including geographical distance and habitat type difference (0 or 1), using the R packages stats and geosphere (Hijmans, 2016). The statistical correlation between the genetic matrix and four distance matrices was analysed using Mantel tests and partial Mantel tests to control for the effect of geography. The correlation analyses were performed for both the alpine and the lowland population. An estimation of the parameters with 999 permutations was conducted using the vegan R package (Oksanen et al., 2012).

Demographic analysis of alpine populations

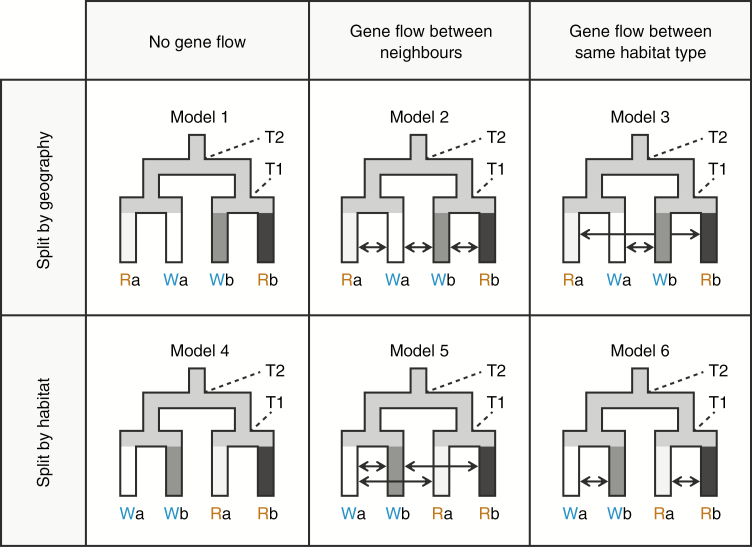
We compared population demographic models for alpine Solidago populations, in which geography, habitat type and gene flow were considered to have shaped the observed genetic polymorphisms (Fig. 4). For this analysis, alpine populations were grouped into four populations [Ra (consisting of R1 and R2 populations; n = 27), Wa (W1 and W2; n = 38), Wb (W3 and W4; n = 42) and Rb (R4–R7; n = 35)], based on their geographical positions, habitat types and genetic structure (see Results section). The R3 population was excluded from this analysis because of its small sample size (n = 2) and difficulty in group assignment. The common ancestral population (size N_ANC) was assumed to branch consecutively at T₂ and T₁, to generate the four current populations (sizes N_Ra, N_Rb, N_Wa, N_Wb). Models 1–3 represented a branching pattern in which populations split according to geography, while models 4–6 assumed that first divergence took place according to habitat type (i.e. rock versus wetland divergence). In models 2 and 5, bidirectional gene flow was considered only between adjacent populations (Ra ⟷ Wa, Wa ⟷ Wb and Wb ⟷ Rb), while gene flow was assumed to occur between the same habitat types (Ra ⟷ Rb and Wa ⟷ Wb) in models 3 and 6. The prior distributions were set as in the modelling for alpine and lowland populations, except that the time parameters T₁ and T₂ followed uniform [10, 3000] and uniform [10, 5000], respectively. Each million of the data simulations was performed using fastsimcoal2 v. 2.5.2.21 software (Excoffier et al., 2013) and ABCtoolbox v. 2 (Wegmann et al., 2010). In addition to the within-population summary statistics used in alpine–lowland analysis, pairwise F_ST between populations was calculated with arlsumstat v. 3.5.2 software (Excoffier and Lischer, 2010). The 18 summary statistics were used for the model selection procedure and parameter inference using the abc R package (Csilléry et al., 2012) in R v. 3.2.2.

Fig. 4.

Graphic representation of alternative demographic models for alpine Solidago populations in Yakushima Island. Four population groups were defined based on geographic proximity and habitat type (R, rock; W, wetland). Different colours in population trees indicate different population sizes, and arrows represent bidirectional gene flow.

Predicting seed dispersal distance

To compare the influences of stem height difference between alpine dwarf and lowland populations, the mean seed dispersal distance was predicted based on the model proposed by Tamme et al. (2014). Here, dispersal distance is expressed as a function of four fixed terms:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}:\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{a}\mathrm{l}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}=\mathrm{D}\mathrm{S}+\mathrm{G}\mathrm{F}+\mathrm{S}\mathrm{M}+\mathrm{R}\mathrm{H}}\end{array}}$$

where DS is dispersal syndrome, GF is growth form, SM is seed mass and RH is release height.

DS and GF were set to ‘wind.special’ and ‘herb’, considering the traits of S. virgaurea. For the SM variable, seed mass was obtained based on 30 mature seeds from individuals of S. minutissima under cultivation in Kyoto University, to obtain an estimate of single-seed mass of 0.4 mg. In this study, release height was assumed to be stem height when the Solidago plants were in bloom. We measured the stem height of natural Solidago populations in alpine wetland habitats in August 2014. The stem height data for the lowland populations were collected from voucher specimens deposited in the Kyoto University herbarium (KYO). The average stem height values were used to represent the values for the alpine and lowland populations. We used the R package dispeRsal (Tamme et al., 2014) in R v. 3.4.0 (R Development Core Team, 2017) to predict the mean dispersal distances, with a linear mixed model with the family [‘Compositae’ (= Asteraceae)] and order (‘Asterales’) as nested random variables. More information on this package can be found in the supplementary material of Tamme et al. (2014). In addition, we counted the number of flower heads per stem on the alpine and lowland plants used to measure the stem heights.

RESULTS

Divergence between alpine dwarf and lowland populations

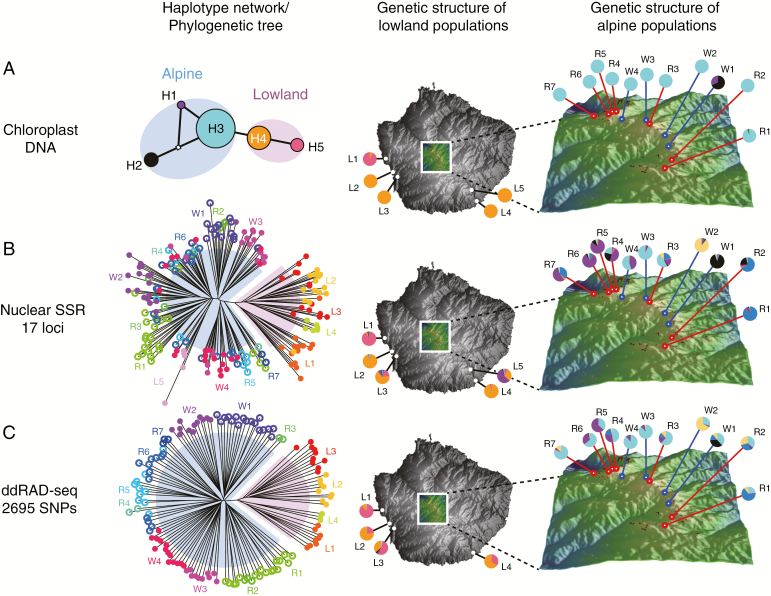
Chloroplast DNA sequencing detected five haplotypes, which were distinguished by the length of polymorphisms of SSRs (GenBank accession numbers LC318477–LC318481). The alpine and lowland populations showed complete differentiation in haplotype frequency, where H1–H3 were specific to alpine plants and H4–H5 to lowland plants (Fig. 2). The two closely related haplotypes H3 and H4, separated by only one mutational step, were the most frequent within each group, indicating they may represent more ancestral states (see haplotype network in Fig. 2A), while the remaining haplotypes were detected in particular populations (W1 and L1).

Fig. 2.

Population genetic structure of Solidago populations inferred by (A) chloroplast DNA sequencing, (B) nuclear SSRs and (C) ddRAD-seq of SNP markers. The haplotype network based on chloroplast DNA variations and phylogenetic trees based on nuclear markers are shown, where the pale blue and pink blobs indicate the population assignment based on altitudinal difference (blue, alpine; pink, lowland). To illustrate the spatial genetic structure, (A) the haplotype frequency of each population and (B, C) the portion of genetic clusters inferred by the STRUCTURE analysis (Pritchard et al., 2000) for each population are shown. Note that the colours used for the population origins in phylogenetic trees and the STRUCTURE clusters are not comparable (B, C).

Nuclear markers of microsatellites (127 alleles detected over 197 samples genotyped at a rate of 0.998) and genome-wide SNPs from ddRAD-seq (2695 SNPs over 132 samples genotyped at a rate of 0.646) revealed clear lineage divergence patterns between the alpine and lowland populations (F_ST = 0.207 for microsatellites and G_ST = 0.041 for SNPs), which was consistent between the different marker types and clustering methods (Fig. 2B, C). When the degree of population differentiation was compared between the alpine and lowland population groups, no significant group difference in F_ST values (alpine group, F_ST = 0.134; lowland, F_ST = 0.168; P = 0.634) was detected. The phylogenetic tree based on SNPs clustered the individual samples well according to population origin, while the tree based on microsatellites failed to do so, due to a lack of genetic polymorphisms for each sample. However, at the population level, the microsatellite data revealed clearer clustering patterns in the STRUCTURE analysis compared with SNP data, from which more ‘admixture-like’ assignment probabilities were inferred for each population. The clustering patterns at K = 7 are shown in Fig. 2B and C, because the log-likelihood of the data in STRUCTURE runs reached a plateau around K = 7 and no further meaningful clusters appeared after K = 7 (see more clustering patterns for K = 1–10 in Supplementary Data Fig. S2). The population genetic structure in the alpine area was complex; the two wetland populations (W1 and W2) were assigned to unique genetic clusters (black and pale yellow colours in Fig. 2B, C), while some clusters (e.g. light blue and purple) were shared among geographically close populations. Compared with the alpine area, the lowland populations were far more geographically isolated, but we detected a genetic cluster (orange colour in Fig. 2B, C) shared by the L2–L4 populations. Population L1 was genetically diverged from the remaining populations in terms of the dominance of the H5 chloroplast haplotype and pink genetic clusters in the nuclear marker analysis (Fig. 2).

Population demographic inference

The nuclear microsatellite data were used to model the lineage divergence pattern of the alpine and lowland populations based on the ABC approach. While acknowledging that scenario selection based on the ABC method should be considered with caution owing to its approximation error in the posterior probabilities (Robert et al., 2011), the simple divergence model received overwhelming support over the alternative models. The posterior probability of the divergence model was 0.981 versus full isolation with the migration model (0.006), bidirectional migration model (0.002) and directional migration models (0.001 and 0.016, respectively). The Bayes factors were 1.000 for the divergence model, 0.001 for the full model, 0.002 for the bidirectional migration model, and 0.007 and 0.134 for the alternative directional migration models. The model fit was evaluated based on PCA visualization, which confirmed that the observed data were well surrounded by envelopes of simulated data (Supplementary Data Fig. S3). The goodness-of-fit test for the divergence model yielded a P value of 0.446, which indicated that the mean distance between the observations and accepted simulations did not differ significantly. The posterior distributions of demographic parameters of the selected model had unimodal peaks, distinct from the uniform prior distributions (Supplementary Data Fig. S4). The population sizes of the two populations were estimated to have decreased from their common ancestral population after divergence (Table 2). The absolute time estimate of population divergence was calculated as 22 628 (15 099–29 596) years before present, an event during the last glacial maximum, by converting the posterior estimate of T_DIV of 6465 (4314–8456) generations (Table 2) with an assumed generation time of 3.5 years (Kawano, 1988).

Table 2.

Prior and posterior distributions of demographic parameters for the simple split model, which was selected based on the posterior probability of models for the Solidago population in alpine and lowland areas of Yakushima Island

Statistics		Log(NALP)	Log(NLOW)	Log(NANC)	T DIV	Log(mutation rate)
Prior		Uniform [2, 5]	Uniform [2, 5]	Uniform [2, 5]	Uniform [10, 10 000]	Uniform [−6, −4]
Posterior	2.5 % percentile	1.90	2.30	3.64	4314	−5.22
	Median	2.65	2.64	4.42	6465	−4.55
	Mean	2.75	2.70	4.40	6502	−4.62
	Mode	2.47	2.56	4.59	6364	−4.48
	97.5 % percentile	4.39	3.15	5.05	8456	−4.15

Landscape factors associated with population divergence

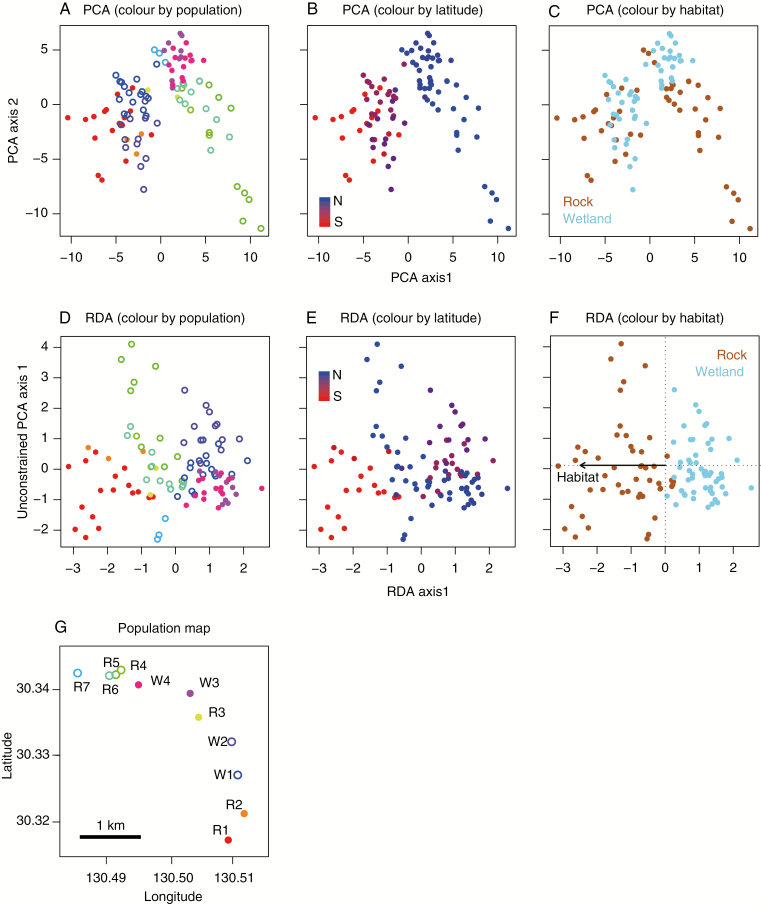
The alpine dwarf populations were distributed across open habitats in rock crevasses or wetlands along mountain ridges (Figs 2 and 3G). PCA was applied to summarize the genome-wide SNP data to estimate individual genetic structure in the dwarf populations (Fig. 3). Along the first two PCA axes, the individuals were scored in the order of the geographical position of the populations (Fig. 3A, B) and not with habitat type (Fig. 3C). The first 20 PCA axis scores were then correlated with geography and habitat variables using the RDA method. The model selection result suggested that most of the genetic variation in alpine dwarf populations was explained by a combination of the two explanatory variables (geography and habitat), which was consistent with the analyses based on genome-wide SNPs and nuclear SSRs (nSSRs) (selected full models’ Akaike weights: 0.842 and 0.920 for SNPs and SSRs, respectively; Table 3). The RDA first-axis score and the constraining variable (habitat type) showed strong correlations for both genetic markers [SNPs, r = −0.991; nSSRs, r = −0.944] (Fig. 3F). Individual correlations using Mantel tests revealed significant correlations between genetics and geography and habitat type in the alpine populations, and the correlation between genetics and habitat was still significant when the effect of geography was partialled out (Table 4, Supplementary Data Fig. 5). The geographic dependency of genetic divergence was also detected in the lowland populations, which was significant in both the SNP and nSSR datasets (Table 4).

Fig. 3.

Genetic structure of alpine Solidago individuals as inferred by (A–C) PCA and (D–F) RDA based on ddRAD-seq of SNP markers. The different colours represent (A, D, G) population origins, (B, E) spatial arrangement of populations and (C, F) habitat differences (rock or wetland type).

Table 3.

Model selection results for the RDAs of the PCA scores of alpine Solidago populations for the ddRAD-seq of SNP and nSSR markers. The analysis is constrained by habitat variables and conditioned with a geographical term. AIC, Akaike information criterion; con, conditioned; wi, Akaike weight

Marker	Model	AIC	ΔAIC	wi
SNPs	Habitat + con(Geography)	531.7	0	0.842
	con(Geography)	535.6	3.89	0.120
	Habitat	538.3	6.58	0.031
	Null	541.6	9.93	0.006
nSSR	Habitat + con(Geography)	362.9	0	0.920
	Habitat	368.6	5.69	0.053
	con(Geography)	370.2	7.30	0.024
	Null	374.7	11.75	0.003

Table 4.

Mantel test results of the correlation between genetic distance and spatial and environmental isolation factors in alpine Solidago populations. Partial Mantel tests were performed to detect the correlation with the habitat factor by controlling for a partial effect of geography. The results are shown for the datasets of the ddRAD-seq of SNP and nSSR markers

Populations	Marker	Model	r	P value
Alpine	SNPs	Genetic ~ Geography	0.440	< 0.001
		Genetic ~ Habitat	0.176	< 0.001
		Genetic ~ Habitat | Geography	0.106	< 0.001
Lowland	SNPs	Genetic ~ Geography	0.438	< 0.001
Alpine	nSSR	Genetic ~ Geography	0.245	< 0.001
		Genetic ~ Habitat	0.136	< 0.001
		Genetic ~ Habitat | Geography	0.084	< 0.001
Lowland	nSSR	Genetic ~ Geography	0.354	< 0.001

Population demography of alpine dwarf populations

The posterior probability for model 1 and model 4 was 0.469 and 0.385, respectively, and these two demographic models without gene flow terms attained higher support than the other models (Table 5). This indicates that gene flow between adjacent (assumed in models 2 and 4) or same-habitat (models 3 and 6) populations is at non-significant levels (Fig. 4). At the same time, the comparable levels of support for models 1 and 4 suggest that our genetic data may not have enough information to distinguish the branching patterns, or that hierarchical population divergence may have occurred in short periods of time (T₁ and T₂ posterior distributions overlapped largely in both models; Table 5). The posteriors of population size parameters showed similar distributions in these two models (medians of current sizes ranging from 3.92 to 4.24 for model 1 and from 3.79 to 4.61 for model 4; ancestral size of 2.42 for model 1 and 2.44 for model 4) (Table 5). Population divergence was inferred to have occurred 2701 (1289–4333) and 2745 (850–4609) generations ago for models 1 and 4, respectively. The goodness-of-fit test yielded P values of 0.826 for model 1 and 0.551 for model 4, and the observed data were well surrounded by envelopes of simulated data in PCA plots (Supplementary Data Fig. S6).

Table 5.

Summary of population demographic analysis of alpine Solidago populations in Yakushima Island. Posterior probabilities (PP) and Bayes factors (BF) of models, prior and posterior distributions of the demographic parameters for five alternative models are shown [median (2.5 %, 95 % percentiles) are reported for each parameter]. NM, effective number of migrants

Model	PP	Demographic parameter
	BF	log(NRa)	log(NRb)	log(NWa)	log(NWb)	log(NANC)	T 1	T 2	log (NM)	log (mutation rate)
		unif [2, 5]	unif [2, 5]	unif [2, 5]	unif [2, 5]	unif [2, 5]	unif [10, 3000]	unif [10, 5000]	unif [0.001, 2]	unif [-6, -4]
Model 1	0.469	4.07	3.92	4.11	4.24	2.42	1483	2701	–	-4.89
	1.000	(2.63, 4.96)	(2.76, 4.31)	(3.52, 4.81)	(4.04, 5.13)	(2.02, 3.56)	(1202, 1813)	(1289, 4333)	–	(-5.20, -4.85)
Model 2	0.002	3.97	3.04	3.26	4.15	2.02	1871	2796	1.065	-5.38
	0.003	(3.96, 4.98)	(3.29, 4.51)	(3.59, 4.42)	(3.94, 4.87)	(2.06, 3.20)	(590, 2747)	(834, 4339)	(0.183, 1.972)	(-5.45, -4.64)
Model 3	0.102	4.07	3.92	4.11	4.24	2.42	1084	2178	0.527	-4.89
	0.218	(3.39, 4.32)	(3.04, 4.34)	(3.55, 4.39)	(3.66, 4.60)	(2.12, 3.05)	(717, 1651)	(−41, 5812)	(0.851, 1.163)	(-5.04, -4.77)
Model 4	0.385	4.55	3.79	3.94	4.61	2.44	1138	2745	–	-5.00
	0.820	(3.97, 4.95)	(3.04, 4.27)	(3.26, 4.38)	(4.15, 4.86)	(2.02, 3.14)	(399, 2724)	(850, 4609)	–	(-5.38, -4.50)
Model 5	0.022	3.76	3.90	3.81	4.10	2.30	1045	3229	−0.182	-4.93
	0.046	(2.62, 4.43)	(2.75, 4.45)	(3.27, 4.11)	(3.68, 4.24)	(2.00, 3.15)	(−159, 2289)	(1964, 4337)	(0.775, 1.901)	(-5.23, -4.49)
Model 6	0.021	3.95	3.52	3.92	4.40	2.46	1523	2543	0.354	-5.05
	0.044	(3.44, 4.17)	(3.11, 3.73)	(3.36, 4.42)	(3.10, 5.17)	(1.85, 3.38)	(744, 2395)	(725, 4448)	(0.665, 1.177)	(-5.79, -4.13)

Simulated seed dispersal distance and flower head production

The average stem length of alpine wetland Solidago plants was 2.6 cm (s.d. = 1.6 cm) (see flowering plant images in Fig. 1), which was much shorter than that of the lowland plants [38.6 cm (s.d. = 16.0 cm)]. Based on the linear mixed effect model as a function of life-history traits, the mean seed dispersal distances were predicted to be 4.8 m for alpine plants and 14.8 m for lowland plants. The average number of flower heads produced per stem was 3.1 (s.d. = 2.7) for the alpine wetland populations and 17.0 (s.d. = 9.1) for the lowland populations.

DISCUSSION

Historical divergence of the alpine dwarf and lowland populations

The genetic analyses based on three types of molecular markers consistently revealed a clear divergence between the alpine dwarf and lowland Solidago populations. No chloroplast haplotypes were shared between the population groups (Fig. 2A), and the individuals were clustered separately for each of the alpine and lowland populations based on nuclear microsatellite and SNP analyses, except for one population, L5, showing an ‘admixed’ origin based on nuclear microsatellites (Fig. 2B, C). The population demographic analysis offered further insights into their lineage divergence history, suggesting that the alpine populations evolved independently of the lowland without extensive genetic exchange (Table 2).

This finding is in contrast to the previously reported population dynamics of alpine S. virgaurea populations in other mountain ranges, which repeatedly revealed little genetic differentiation from lowland populations (Nakamura et al., 1997; Hirano et al., 2017; Sakaguchi et al., 2017). The S. virgaurea complex generally occupies a wide range of elevations in other temperate regions (Nishizawa et al., 2001; Bergstern, 2009; Kiełtyk and Mirek, 2014; Takahashi and Matsuki, 2017), and active gene flow along elevational gradients has been suggested to link local populations, resulting in low population differentiation (e.g. F_ST = 0.000–0.027) (Hirano et al., 2017). However, on Yakushima Island, under a humid climate with an annual mean precipitation reaching 7400 mm in the inland mountains (Takahara and Matsumoto, 2002), dense cloud forests develop along the middle elevation range, under which light-demanding Solidago plants cannot survive. Hence, the populations are distributed only in alpine open habitats or lowland areas with sparse canopies maintained by natural disturbances such as waterfalls or droughts on rock tops. In addition, temporal isolation likely contributed to the limited gene flow, as there is a difference in flowering time of nearly 2 months between the alpine and lowland populations (Table 1), serving as a prezygotic reproductive isolation mechanism. These altitudinal and temporal isolation factors, and probably also ecological local adaptation, would have reduced the probability of gene flow between the two population groups.

Pronounced genetic structuring in the alpine dwarf populations

The group comparison of genetic differentiation showed that the dwarf populations differentiated from each other at levels comparable to those of the lowland populations (P = 0.634 in permutation test). The STRUCTURE analysis showed that the allelic constitutions of several dwarf populations, particularly the wetland populations, drifted away even from neighbouring populations (Fig. 2, Supplementary Data Fig. S1). Also, demographic modelling revealed that gene flow after the divergence of dwarf populations was not at significant levels (Table 5). These findings are noteworthy because the dwarf populations included relatively large numbers of plants (at least several hundreds of ramets) and are less geographically isolated than the lowland populations. These characteristics of dwarf populations are suggestive that they may be less prone to drifts/bottlenecks than the lowland populations. In fact, the population genetic diversity of the dwarf populations was comparable to and sometimes higher than that of the lowland populations (Table 1), which occupy a much broader range and are far more isolated due to dense evergreen forests (Fig. 1). Hence, the pronounced population divergence in the alpine area would have been caused by factors specific to the dwarf populations.

Life-history traits of the dwarf populations may have affected the levels of gene flow between local populations. Stem length of dwarf Solidago plants was only 2.6 cm on average, from which the seed dispersal distance was predicted to be 4.8 m, a much shorter distance than the geographical distances between isolated populations. In addition, the decreased number of propagules due to dwarfism (3.1 heads for alpine plants versus 17.0 for lowland plants) could further reduce the probability of dwarf populations exchanging genes via rare long-distance dispersal (Tackenberg et al., 2003; Nathan, 2006). However, it should be noted that expected seed dispersal distance may not fully predict the realized gene flow pattern; unpredictable long-distance dispersal, variations in weather conditions and variation in recruitment of dispersed seeds under natural habitat conditions [e.g. topographic effects in complex alpine environments (Hirao and Kudo, 2004; Cortés et al., 2014)] may be equally important factors. Further research is needed to assess these possibilities, for example by assessing fine-scale gene dispersal (Hardy et al., 2004) and by simulating the seed dispersal probability under various weather conditions in alpine and lowland populations (Tackenberg et al., 2003).

Factors shaping genetic structure within dwarf populations

In landscape genetics theory, one ultimate driver of spatial genetic structure is the effect of landscape heterogeneity on gene flow and the resulting local populations (Manel et al., 2003; Wagner and Fortin, 2016). The alpine landscape is characterized by dynamic changes of topography, which generate diverse microhabitats for alpine plants (e.g. dry and windy ridges, rock outcrops, snowbeds in topographic depressions, and scattered wetland). Across the environmental matrix, light and water conditions (Körner, 2003), nutrient availability (Little et al., 2016), plant–soil interactions (Sedlacek et al., 2014) and community interactions (Wheeler et al., 2015) are key factors affecting seedling establishment and subsequent growth, and therefore gene flow between microhabitats in alpine complex environments. The apparent association between genetic variation and habitat type in the dwarf Solidago populations (Fig. 3, Tables 3 and 4) may be explained by a scenario in which gene flow predominantly links the populations in similar environments via selection against maladapted individuals that have migrated from alternative habitats (Rundle and Nosil, 2005; Nosil et al., 2009). In fact, however, we found strong population isolation even between neighbouring wetland habitats, as evidenced by complete fixation to different chloroplast haplotypes and a predominance of different genetic clusters in similar habitat types (e.g. W1 and W2) (Fig. 2). Also, habitat-specific gene flow models (models 3 and 6) were not preferred in demographic model analysis for the dwarf populations (Table 5). These lines of evidence suggest that the apparent association would be brought about by a non-adaptive process of genetic drift in these dwarf populations leading to substantial genetic differentiation (Fig. 3D). This explanation, in turn, highlights the importance of reduced gene flow in isolated dwarf populations, shaping strong population genetic structure (Wright, 1931; Pannell and Fields, 2014; Sexton et al., 2014).

Although the genome-wide genetic differentiation in alpine populations would be largely caused by neutral population dynamics, this does not preclude the possibility that the populations showed adaptive responses to their native habitats, as often seen in the S. virgaurea complex (Kawano, 1988; Bergstern, 2009; Hirano et al., 2017; Sakaguchi et al., 2019). Given local adaptations to either habitat, the introduction of locally maladapted genes and phenotypes due to strong and asymmetrical gene flow can affect local populations via hybrid inviability (Edmands, 1999). Hence, the reduced gene flow among the alpine dwarf populations is hypothesized to have contributed to the population divergence by promoting local adaptation to alternative habitats, serving as divergent substrates for growth. Transplants (Sedlacek et al., 2015) and other approaches, such as common garden experiments (e.g. Sambatti and Rice, 2007; Hirst et al., 2017) and the space-by-time substitution (Sedlacek et al., 2016; Wheeler et al., 2016), and genomic screening of adaptive genes (e.g. Turner et al., 2010; Kubota et al., 2015) are desirable in future studies to understand the respective roles of neutral processes (i.e. the balance of gene flow and drifts) and natural selection in population isolation in these dwarf populations.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Figure S1: results of the BayeScan analysis of genome-wide SNP markers obtained in Solidago populations. Figure S2: results of the STRUCTURE analysis of genome-wide SNP markers in Solidago populations. The log-likelihood of the data [LnP(D)] and delta K values are plotted against the number of genetic clusters (K = 1–15) for nuclear microsatellite and genome-wide SNP markers. The clustering patterns for each dataset are shown from K = 1 to K = 10. Figure S3: principal component analysis representing the goodness of fit of the approximate Bayesian computation for the population demographic analysis. The colour blobs indicate the density distribution of the simulated data, while the observed data are shown as black crosses. Figure S4: posterior (solid lines) and prior (dotted lines) distribution of each demographic parameter inferred from the selected divergent model. Figure S5: isolation by distance (IBD) and isolation by habitat plots for lowland and alpine populations based on (a–c) nSSRs and (d–f) ddRAD-seq of SNP markers. The solid lines are based on predictions from linear regression models. Figure S6: PCA representing the goodness of fit of the approximate Bayesian computation for the demographic analysis of alpine dwarf populations. The colour blobs indicate the density distribution of the simulated data, while the observed data are shown as black crosses. Results are shown for the two models with high posterior support.

FUNDING

This research was supported by the Japan Society for the Promotion of Science (KAKENHI 16H04827, 18K14778 and 25291085) and by the Japan Science and Technology Agency ‘Strategic International Collaborative Research Program’ (grant 4-1403).