Non-rigid Event-by-event Continuous Respiratory Motion Compensated List-mode Reconstruction for PET

Abstract

Respiratory motion during PET/CT imaging can cause significant image blurring and underestimation of tracer concentration for both static and dynamic studies. In this study, with the aim to eliminate both intra-cycle and inter-cycle motions, and apply to dynamic imaging, we developed a non-rigid event-by-event (NR-EBE) respiratory motion compensated list-mode reconstruction algorithm. The proposed method consists of 2 components, the first component estimates a continuous non-rigid motion field of the internal organs using the internal-external motion correlation (NR-INTEX). This continuous motion field is then incorporated into the second component, non-rigid MOLAR (NR-MOLAR) reconstruction algorithm, to deform the system matrix to the reference location where the attenuation CT is acquired. The point spread function (PSF) and time-of-flight (TOF) kernels in NR-MOLAR are incorporated in the system matrix calculation and therefore are also deformed according to motion. We first validated NR-MOLAR using a XCAT phantom with a simulated respiratory motion. Non-rigid EBE motion compensated image reconstruction using both components were then validated on three human studies injected with ¹⁸F-FPDTBZ and one with ¹⁸F-FDG tracers. The human results were compared to conventional non-rigid motion correction using discrete motion field (NR-Discrete, one motion field per gate) and a previously proposed rigid EBE motion compensated image reconstruction (R-EBE) that was designed to correct for rigid motion on a target lesion/organ. The XCAT results demonstrated that NR-MOLAR incorporating both PSF and TOF kernels effectively corrected for non-rigid motion. The ¹⁸F-FPDTBZ studies showed that NR-EBE out-performed NR-Discrete, and yielded comparable results with R-EBE on target organs while yielding superior image quality in other regions. The FDG study showed that NR-EBE clearly improved the visibility of multiple moving lesions in the liver where some of them could not be discerned in other reconstructions, in addition to improving quantification. These results show that NR-EBE motion compensated image reconstruction appears to be a promising tool for lesion detection and quantification when imaging thoracic and abdominal regions using PET.

I. INTRODUCTION

POSITRON emission tomography (PET) imaging in thoracic and abdominal regions is often degraded by respiratory motion. The average respiration-induced displacement of organs is in the range of 10 – 25 mm in the superior-inferior (SI) direction, and 5 – 10 mm in the anterior-posterior (AP) direction [1, 2]. This magnitude of movement can cause substantial blurring and reduction of signal to background contrast in tumors and organs, leading to hampered disease detection and radiotracer quantification in both static [3–7] and dynamic studies [8].

Many approaches have been proposed to correct for respiratory motion. Respiratory gating that divides the list-mode data into different gates, based on either temporal phase or respiratory displacement information [9, 10], can be reconstructed into multiple image volumes. Each image corresponds to a particular respiratory phase. However, albeit easy to implement, this method yields poor signal-to-noise ratio (SNR) as only a portion of the coincidence events are used in reconstruction. To maintain the count statistics in the reconstructed image while compensating for motion, approaches have been proposed to transform each gated image stack to a reference gate using non-rigid image registration followed by averaging [11]. The transformation field can be estimated based on 4D CT, simultaneously acquired MRI [4, 12] , joint PET/MR estimation [13], or gated PET images. Alternatively, the transformation field can also be incorporated into the iterative image reconstruction framework, which is often referred to as motion compensated image reconstruction (MCIR) [4–7, 14–20]. Several studies have shown that MCIR could yield better quantitative and qualitative performance than post-reconstruction registration approach for both rigid [21] and non-rigid motion compensation [6, 22].

Non-rigid MCIR can be implemented in two ways: 1) Image deformation – this can be done by warping the reconstructed image from a reference respiratory geometry to other respiratory gates (i.e., target gates) prior to the forward projection. After back projection, the updating image is warped back to the reference gate position [14, 19, 23]; 2) System matrix deformation – this is done by deforming the system matrix from a target respiratory geometry to a reference respiratory gate for each respiratory phase [4, 17, 18, 24], allowing both the emission image and attenuation map not to move. Both approaches have been demonstrated to compensate for respiratory motion effectively and yield comparable performance [25]. The major difference between these two approaches is that the first approach requires two sets of motion fields, i.e., the forward transformation from the reference to the target gates, and the transpose of the transformation [26] or the inverse of the motion field [12, 14, 19] for back warping the updating image and the sensitivity map to the reference gate. Care must be taken to ensure that spatial mismatch after a full transformation cycle (target to reference, then reference to target) is minimal. Such inconsistency could lead to degradation of resolution and quantitative accuracy [19]. In contrast, the latter approach only requires one set of motion field between each pair of target and reference gates and does not need the transpose/inverse motion field.

Existing non-rigid MCIR methods incorporate discrete motion fields that assume each respiratory gate is motion free. However, there can be a large amount of intra-gate motion present, especially during inspiration gates, as shown in our previous study [5]. In addition, inter-cycle motion variation can also cause motion blur that is not properly corrected by existing methods [27]. Furthermore, none of these methods are applicable to dynamic studies that require the non-rigid motion field at each time point for list-mode reconstruction. We have previously proposed the Internal-External Motion Correlation (INTEX) method that estimates continuous rigid internal organ motion based on the respiratory trace acquired on an external device [5, 28]. This motion information is then incorporated into a motion-compensation OSEM list-mode algorithm for resolution-recovery reconstruction (MOLAR) framework [29] to perform Rigid Event-by-Event (R-EBE) respiratory motion correction during reconstruction. This approach has been shown to correct for both inter- and intra-gate respiratory motions effectively [5], and has been applied to dynamic data [8]. However, as this method can only correct for rigid motion, the target organ may have remaining motion blur caused by non-rigid motion. In addition, for patients with multiple lesions, multiple reconstructions with rigid INTEX (R-INTEX) may be required for each target lesion, which might be impractical.

In this study, with the aim to correct for non-rigid respiratory motion on an event-by-event basis in the reconstruction for both static and dynamic PET data, we developed a solution that consists of two components: 1). Non-rigid INTEX (NR-INTEX) estimates a continuous deformation field for each voxel at a timing resolution that matches an external respiratory trace, e.g. 40 Hz or 50 Hz as in this study; 2). Non-Rigid MOLAR (NR-MOLAR) compensates for non-rigid motion by deforming the system matrix according to the deformation field to perform non-rigid motion correction for each coincidence event. The point spread function (PSF) and time-of-flight (TOF) kernels were also deformed according to the motion field in our implementation. We first validated NR-MOLAR using simulated XCAT phantom data, which provided known motion fields. The application of both NR-INTEX and NR-MOLAR for non-rigid EBE (NR-EBE) MCIR was then compared to: 1). single gated reconstruction at end-expiration phase; 2). A conventional non-rigid MCIR using discrete motion field (NR-Discrete, one motion field per gate); 3). and the previously developed R-EBE [5] on three healthy human studies with ¹⁸F-FPDTBZ (pancreas tracer [30]) and a ¹⁸F-FDG study of a liver cancer patient who had multiple lesions in the abdominal region. In section II, we describe NR-INTEX and NR-MOLAR in detail. Section III presents the experiments and the quantitative evaluation methods. Section IV presents the results of the simulations and human studies. The findings are discussed in Section V, and the conclusion of the study is given in Section VI.

II. Material and Methods

In this study, all data were acquired on Siemens Biograph mCT scanners. The respiratory traces in patient studies were acquired using Anzai belt system (Anzai Medical, Tokyo, Japan), which was attached to the human subjects’ lower abdomen to record the respiratory motion in the AP direction. An overview of the data generation and the steps of the proposed approaches is shown in Fig. 1. The dashed line denotes the reconstruction without motion information that is equivalent to conventional MOLAR; the solid lines denote the workflow of the proposed non-rigid EBE motion compensation method. The NR-INTEX component is presented in section II B, and NR-MOLAR is given in II C.

Fig. 1.

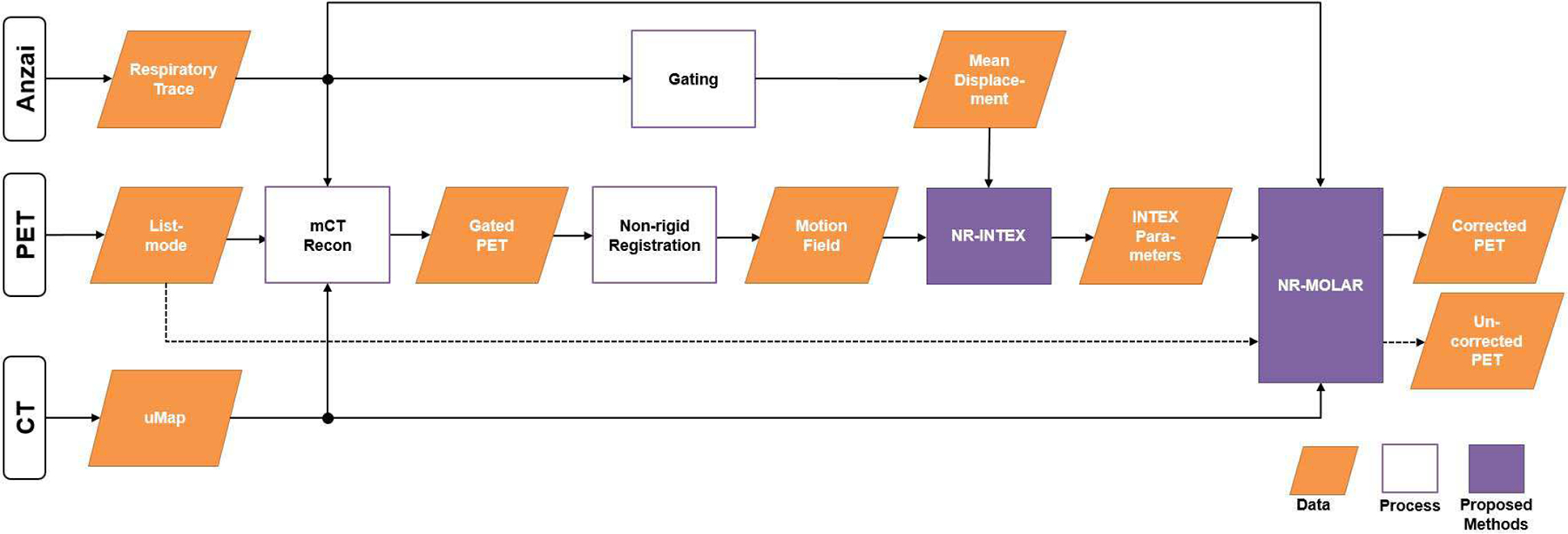
Overview of the proposed motion compensation framework. The dashed line denotes the reconstruction without motion information which equivalents to conventional MOLAR; the solid lines denote the workflow of the proposed motion compensation method.

A. Estimation of Motion field and Motion Model

To generate motion fields, each PET list-mode dataset is first binned into eight phase gates followed by OSEM reconstruction with 3 iterations, 21 subsets using the manufacturer’s software, which includes PSF and TOF information. We denote the gated PET reconstruction as ${\lambda }^g=\left({\lambda }_j^g,g=1,\dots ,G,j=1,\dots ,J\right)$ where g is the g^th image in the sequence of G respiratory gates, and J is the total number of voxels in the image. The motion fields between each respiratory gate and a single reference gate (RG) image λ^RG are then estimated using non-rigid registration.

In general, non-rigid registration seeks to estimate the transformation $T^{g\to \mathit{R}\mathit{G}}:{ℝ}^3\mapsto {ℝ}^3$, which is a spatial mapping of all points in the target image λ^g to their corresponding points in the reference image λ^RG, where the arrow notation g → RG indicates non-rigid deformation from image space g to space RG. We seek the transformation estimate ${\widehat{T}}^g{}^{\to \mathit{R}\mathit{G}}$ that maximizes a similarity metric Γ between the two images λ^g and λ^RG :

$${\widehat{T}}^{g\to RG}=\text{arg\hspace{0.17em}max}\left[\Gamma \left({\lambda }^{RG},{\lambda }^g\circ T^{g\to RG}\right)+\gamma R(T)\right]$$ (1)

where ○ is the transformation operator that denotes application of the transformation to the image, R is a regularization term, which is a function of the transformation T , and γ is the regularization parameter. In this work, we set Γ to be the normalized mutual information metric (NMI) [31]. We parameterize our deformation model using a free-form deformation (FFD) [32], which uses the displacements of an isotropic grid of B-spline control points to define the transformation, and R is taken to be a measure of the linear elastic bending energy that enforces smoothness of the transformation deformation field. We implement the above equation using a multi-resolution approach with 3 levels, with a final B-spline control point spacing of 15 mm, and optimize the similarity metric using the conjugate gradient method. This algorithm is implemented as part of the BioImage Suite software package [33]. For motion-compensated reconstruction, given $x_j^g=\left(x_j^g,y_j^g,z_j^g\right)$ as the center location of the j^th voxel at gate g, the voxel based displacement/motion fields in each (x, y, z) direction can then be generated from the transformation:

$$x_j^g+\Delta x_j^{g\to RG}=x_j^{g\to RG}$$ (2)

where $\Delta x_j^{g\to RG}$ denotes the displacement of voxel j from gate g to RG in x : Left-Right (LR), y: AP, and z: SI directions, respectively. These non-rigid displacement fields will be used to estimate continuous displacement fields and be incorporated into MOLAR for event-by-event motion correction.

Assuming the change of radiotracer distribution between gates is solely caused by motion, the following equivalence holds:

$${\lambda }_j^{g\to RG}\lambda \left(x_j^{g\to RG}\right)=\lambda \left(x_j^g+\Delta x_j^{g\to RG}\right)=\lambda \left(x_j^g\right){\lambda }_j^g$$ (3)

This is illustrated in Fig. 2, where the transformed voxel j centered at location ($x_j^{g\to RG}$, $y_j^{g\to RG}$, $z_j^{g\to RG}$) may not align with the image grid and overlap with neighboring voxels. A tri-linear interpolation is therefore applied to combine all possible contributions of ${\lambda }_l^{g\to RG}$ (here we substitute index j with index l to avoid confusion) to ${\lambda }_i^{RG}$ in the image grid corresponding to RG as used in previous studies [15, 17]:

$${\lambda }_j^{RG}=\sum _{l\in N_{j,g}}{w}_{l,j}^{g\to RG}{\lambda }_l^{g\to RG}$$ (4)

where ${\lambda }_i^{RG}$ denotes the mean intensity value in voxel j at RG after applying both transformation and interpolation, Nj,g represents all neighborhood voxels of the reference gate voxel j based on its position in gate g, $w_{l,j}^{g\to RG}$ is a weighting factor that determines the portion of the overlapping volume between voxel l (of gate g) and its neighboring voxel j (in gate RG).

Fig. 2.

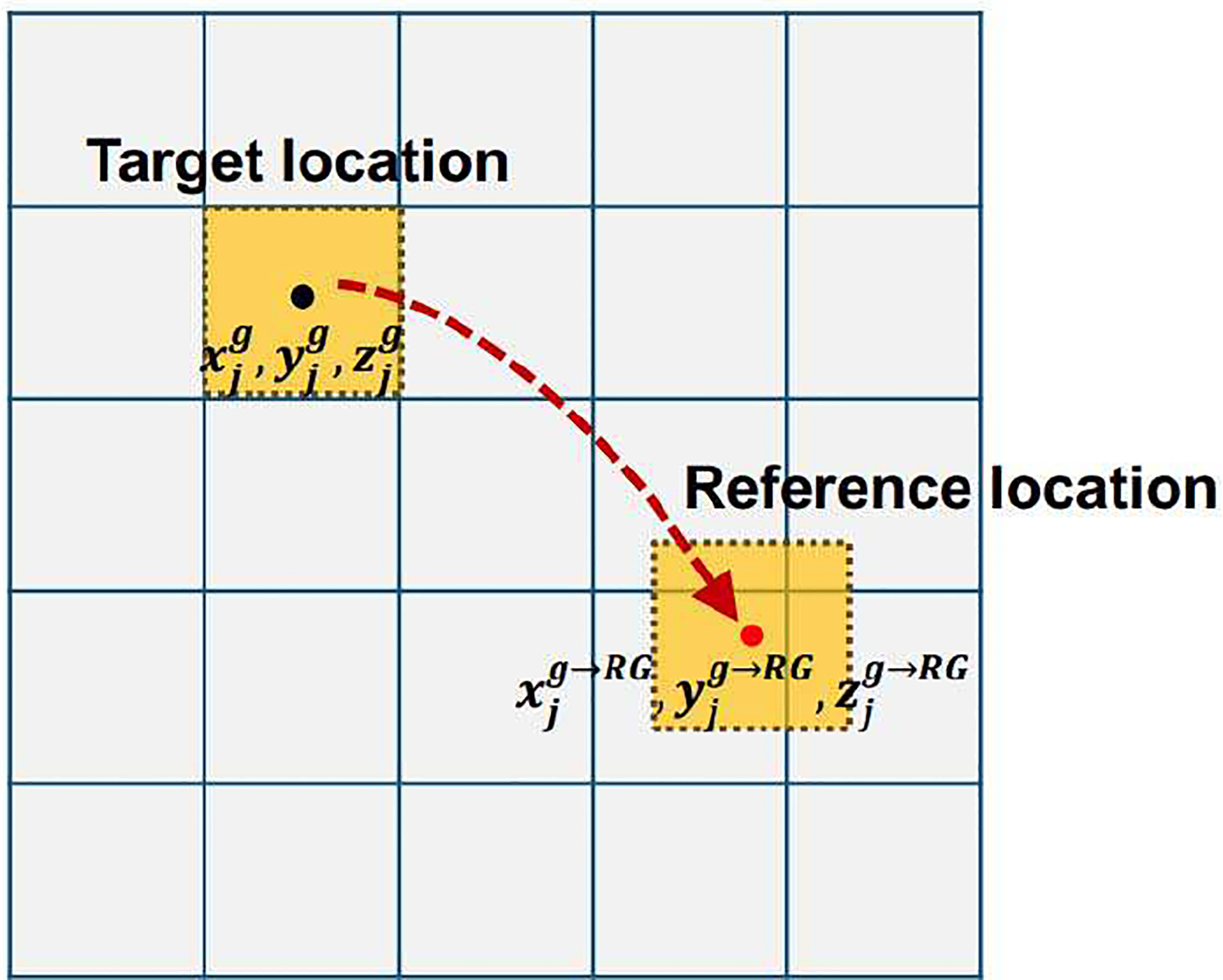
Illustration of the transformation from the target location to the reference location on a single image grid.

In this study, we choose the end-expiration phase, where the attenuation correction CT is acquired, as the RG, and the other respiratory gates are denoted as target gates (TG). Rather than directly registering all TG images to the RG, we instead take advantage of the fact that the image sequence is temporally smooth such that images λ^g and λ^g+1 have relatively less deformation than the deformation between images λ^g and λ^g+2. Here, we register each image only to its immediate temporal neighbor toward the RG. For example, by choosing gate 5 as the reference, for g < 5, we calculate the transformations T ^1→2, T ^2→3, T ^3→4, and T ^4→5, and for the images g > 5, we calculate the transformations T ^6→5, T ^7→6, and T ^8→7. We then concatenate these transformations to form an overall transformation, e.g., T ^1→5.

B. NR-INTEX: Estimation of a continuous motion field

To perform non-rigid respiratory motion correction on an event-by-event basis, we must estimate the continuous motion field of the internal organs. We have previously developed INTEX to convert a respiratory trace acquired externally into rigid internal organ displacement for a single organ [5, 28]. The external trace is recorded by the Anzai belt in the format of relative displacement (unitless) denoted as D(t), where t is time, which is recorded at 40Hz or 50Hz (depending on the version of the Anzai software). The internal organ motion is obtained by measuring the displacement of the center of mass (in mm) ${\overline{\Delta x}}_{com}^g$, of a target organ for each respiratory gate g with respect to the reference gate. By performing phase gating on the respiratory trace in the same way as the list-mode data, we compute the mean displacement ${\overline{D}}^g$ of the trace corresponding to each gate. Based on the internal displacement ${\overline{\Delta x}}_{com}=\left({\overline{\Delta x}}_{com}^1,\dots ,{\overline{\Delta x}}_{com}^G\right)$ and external motion information $\overline{D}=\left({\overline{D}}^1,\dots ,{\overline{D}}^g\right)$, linear correlations can be established for each direction:

$${\overline{\Delta x}}_{com}=P_{1x}\overline{D}+P_{2x}$$ (5)

where P_1x, P_2x, are the slope and intercept estimated from linear fitting in each direction x=(x, y, z). A 3D displacement vector x_com (t) that models the rigid motion of the target organ can therefore be obtained at each time point t by converting the continuous respiratory trace D (t) as follows:

$$\Delta x_{com}(t)=P_{1x}D(t)+P_{2x}$$ (6)

In this study, we extend the INTEX correlation to continuous non-rigid displacement fields that will be used to deform the system matrix in NR-MOLAR. We first establish INTEX correlation between the displacement fields $\Delta x_j=\left(\Delta x_j^{1\to RG},\dots ,\Delta x_j^{G\to RG}\right)$ and the mean displacement of the respiratory trace $\overline{D}$ for each voxel j:

$$\Delta x_j=P_{1x,j}\overline{D}+P_{2x,j}$$ (7)

where P_{1x, j} , P_{2x, j} are the slope and intercept for each voxel j. A total of 6 parameter matrices (3 slopes and 3 intercepts) were generated as the inputs for NR-MOLAR. With this linear correlation for each voxel, the continuous time-dependent displacement field $\Delta x_j^{t\to RG}$ representing the point-to-point transformation between the respiratory displacement at time t and RG for each direction can be obtained:

$$\Delta x_j^{t\to RG}=P_{1x,j}D(t)+P_{2x,j}$$ (8)

The displacement fields are generated at the temporal frequency of the Anzai acquisition during reconstruction. We also compute R² of the linear fitting (Eq 7) in each direction to assess the goodness of linear fitting at the voxel level; this metric will be used for evaluation for all studies.

C. NR-MOLAR: Deforming the System Matrix

In NR-MOLAR, we define ${\overline{y}}^t=\left({\overline{y}}_i^t,i=1,\mathrm{..},I\right)$ as the expected value of the prompt coincidences along LOR i at time t, where I is the total number of LORs. Let λ^t = (λ^t_j , j = 1, … , J) denotes the time-varying radioactivity map (time varying solely due to motion), its element λ^t_j represents the average radioactivity concentration within voxel j at time t. Without motion compensation, the coincidence events acquired at time t can then be written as:

$${\overline{y}}^t=C{\lambda }^t+r+s$$ (9)

where C is a simplified system matrix with dimension of I×J, and each element c_i,j c_i(xj ) denotes the probability of an annihilation originating from voxel j being detected on LOR i accounting for geometry, resolution, attenuation, and solid angle effects; r and s represent the expectations of random and scattered events. For motion compensation, our aim is to reconstruct a single image λ at the reference gate using all the coincidence events. This can be achieved by either deforming the image from the reference respiratory phase to a target phase at time t to obtain λ^RG→t, or the system matrix at each time t to a reference phase to obtain $c_{i,j}^{t\to RG}$. We adopted the latter approach in this study. Following Eq 3 and 4, $c_{i,j}^{t\to RG}$ can be derived and Eq 9 can be rewritten as:

$${\overline{y}}^t=C^{t\to RG}\lambda +r+s$$ (10)

Deforming the system matrix can be seen as “bending” the LORs into curves of response (CORs), where both forward and back-projections are traced along the CORs. Therefore, both emission and attenuation images can be kept at the reference position where the attenuation CT is acquired to achieve matched attenuation correction in the reconstruction. In list-mode notation, for event k occurring on LOR i(k) at time t(k), we replace indexes i by k, and substitute c_k,j, in the conventional TOF MOLAR [29] by $c_{k,j,{\tau }_k}^{t\to RG}$, the updating equation for list-mode NR-MOLAR can then be derived as:

$${\lambda }_j^{n+1}=\frac{{\lambda }_j^n}{Q_j}\sum _{k=1}^K\frac{c_{k,j,i_k}^{t\to RG}{L}_k{A}_k{N}_k}{T\left(\sum _j^{\prime }{c}_{k,j^{\prime },{\tau }_k}^{t\to RG}{L}_k{A}_k{N}_k{\lambda }_{j^{\prime }}^n+R_{k,{\tau }_k}+S_{k,{\tau }_k}\right)}{Q}_j=\frac{1}{n_T}\sum _{t_t^{\prime }=1}^{n_T}\sum _{i=1}^I\sum _{\tau =1}^{n_{\tau }}{c}_{i,j,t^{\prime },\tau }^{t\to RG}{L}_{i,t^{\prime }}{A}_{i,t^{\prime }}{N}_i$$ (11)

where n is the iteration number, k represents the index of each detected event, $c_{k,j,{\tau }_k}^{t\to RG}$ is the deformed system matrix element including TOF kernel after applying Eq. 3 and 4 to $c_{k,j,{\tau }_k}^{t(k)}$, i.e.,

$$c_{k,j,{\tau }_k}^{t(k)}=c_{k,j}^{t(k)}{\zeta }_{k,j,{\tau }_k}^{t(k)}$$ (12)

where τ_k represents the TOF bin for event k, and ${\zeta }_{k,j,{\tau }_k}^{t(k)}$ is the TOF kernel indicating the contribution of image voxel j to time bin τ_k for event k. Since the LOR becomes curved, both the PSF and TOF kernels are deformed to match. L_k is the decay factor, A_k is the attenuation factor. N_k is the sensitivity (normalization) term, $R_{k,{\tau }_k}$ is the randoms rate estimate and $S_{k,{\tau }_k}$ is the scatter rate estimate in counts per second in TOF bin τ_k. Scatter events are estimated using the TOF SSS as proposed in [29]. Since respiratory motion is spatially smooth, for computational savings, scatter is considered as motion independent in this study. The random events are estimated from the product of the singles rates of the two detectors for each LOR, and then uniformly distributed across all TOF bins. Q is the sensitivity image that is calculated by back-projecting randomly sampled single events along the CORs to account for the effects of motion on voxel sensitivity. In the calculation of Q, each time frame of duration T (seconds) is divided into n_T short time bins denoted t′ in seconds. n_τ represents the total number of TOF bins (n_τ =13 for the mCT).

D. PSF Modeling

In MOLAR, the PSF resolution modeling is approximated as the product of two line spread functions (LSF), one for radial ( f_r(Δr)) and one for axial ( f_z(Δz)) resolution, indexed by the perpendicular radial distance Δr and perpendicular axial distance Δz from voxel j to LOR i(k)of event k such as:

$$c_{k,j}^{t(k)}=c_0{f}_k^r\left(r_{k,j}^{t(k)}\right)f_k^z\left(z_{k,j}^{t(k)}\right){\Omega }_{k,j}^{t(k)}$$ (13)

where c₀ is a scaling term that gives c its correct units of mm, Ωis the factor compensating for the solid angle of the voxel with respect to the LOR, and f (.) is the Gaussian resolution function determined by the full-width-at-half-maximum (FWHM) of the system resolution [34]. The Gaussian resolution function is truncated such that the resolution contribution of the edge voxels is no more than 5% of the total. Each $c_{k,j}^{t(k)}$ of the PSF kernel is computed at the target location $x_j^t$ and then deformed by applying Eq. 3 and 4. Since the motion compensation is non-rigid and the neighboring voxels contributing to the PSF kernel can move differently, the shape of the kernel in the reference image can therefore appear as deformed depending on the displacement fields.

III. Experiments

A. XCAT Simulations

To validate the quantitative performance of NR-MOLAR, we generated a XCAT phantom simulating a ¹⁸F-FDG scan of a lung cancer patient at end-inspiration and end-expiration phases. A lung tumor with 16 mm diameter was inserted in the lower lobe of the right lung. The tumor to lung contrast was set to 8:1. Respiratory motion was simulated with a maximum magnitude of 20 mm in the superior-inferior direction, and 12 mm in the anterior-posterior direction using the XCAT’s internal respiratory trace. To isolate the effect of motion correction without confounding factors due to motion estimation, we used the ground truth motion vectors (TG −> RG) generated by XCAT simulator in the motion compensated reconstruction.

Both TG and RG list-mode datasets were generated using the forward-projector of MOLAR simulating a 10-min acquisition based on the Siemens mCT scanner. Attenuation was incorporated in the simulation. Randoms, scatter and TOF were not simulated. About 300M events were generated per respiratory gate to simulate a high-count study to reduce the confounding factors of noise on image quality. To assess the performance of NR-MOLAR, we reconstructed the TG list-mode data without and with system matrix deformation, and compared to the reconstruction of the RG list-mode data. The reconstruction from TG list-mode data motion deformed to the RG position is denoted as TG-NR-MOLAR hereafter. An ideal reconstruction should yield similar results for RG and TG-NR-MOLAR. All the images were reconstructed with 3 iterations and 21 subsets using 2 × 2 × 2 mm voxels. A 4-mm FWHM Gaussian PSF kernel was modeled in the reconstruction. For the reconstructions of TG and RG, phase-matched attenuation maps were used. For the TG-NR-MOLAR, the RG attenuation map was used. All the reconstructions were then post-filtered with a 4 mm FWHM Gaussian filter.

B. Human Studies

We applied the proposed NR-EBE (NR-INTEX combined with NR-MOLAR) to the scans from three healthy human subjects (S1, S2, and S3) injected with ¹⁸F-FP-DTBZ [30] and one liver cancer patient injected with ¹⁸F-FDG. All human studies were acquired on the Siemens mCT scanner. An Anzai belt was attached to each subject’s lower abdomen to record respiratory traces.

In the ¹⁸F-FPDTBZ studies, an average of 248 MBq was injected and the first 10 min of a 2-h scan was evaluated. The liver cancer patient was injected with 225 MBq FDG followed by a 3-min scan, 60 min post-injection. The FPDTBZ and FDG list-mode data were first reconstructed into 8 respiratory phases, and 5 respiratory phases, respectively, based on phase gating using the vendor’s default reconstruction. Fewer respiratory gates were used for the FDG study since the count level was low. The motion fields between each respiratory gate and the reference gate at end-expiration were obtained using the freeform deformation registration as discussed in section IIA. The CT images were acquired at end-expiratory phase by coaching the subjects to hold their breath at end-expiration. The single-phase attenuation maps were used in all PET reconstructions. Scatter, randoms and decay were corrected in the reconstruction. TOF and 4-mm FWHM Gaussian PSF kernel were modeled in the reconstruction. For the FDG study, a 3D Gaussian filter with 5 mm FWHM was applied to the reconstructed images to reduce noise.

We evaluated NR-EBE against four other reconstructions: 1). no motion correction (NMC); 2). single gated reconstruction at end-expiration phase (Gated); 3). NR-Discrete, which uses the same inter-gate motion fields, $\Delta x_j=\left(\Delta x_j^{1\to RG},\dots ,\Delta x_j^{G\to RG}\right)$, as used to build continuous NRINTEX. The difference is that NR-Discrete uses one motion field per gate to deform the system matrix in NR-MOLAR; 4). R-EBE (R-INTEX+MOLAR) as previously described [5]. For R-EBE, the pancreas of the FPDTBZ study and a medium sized lesion (~ 15 mm diameter) located at the center of the liver of the FDG study were selected as the target organ to calculate R-INTEX.

C. Performance Evaluations

To evaluate the performance of NR-MOLAR with the XCAT data, we first computed the difference images between the reconstructions of TG, TG-NR-MOLAR and the ground truth RG. Effective MCIR would produce minimal structural differences between the ground truth RG and TG-NR-MOLAR reconstructions, which was assessed visually.

The quantitative evaluations were performed by measuring the relative bias of the mean activity in the lesion and myocardium between the ground truth RG and TG-NR-MOLAR.

$$\mathit{\text{Rel}}.\mathit{\text{Bias}}=\frac{m_{\text{ROI}}^{TG-NR-MOLAR}-m_{\text{ROI}}^{RG}}{m_{\text{ROI}}^{RG}}\times 100\%$$ (14)

where m is the mean intensity value in the selected ROI, and the superscript denotes the corresponding reconstruction. The lesion ROI was selected as the entire lesion defined on the phantom, and the ROI on the myocardium was defined on three central slices in the coronal view.

In the human studies, to evaluate the quality of linear correlation between the respiratory trace and the motion field at a voxel level, we first assessed the goodness of fit (R²) for each voxel for each human study visually. We further used scatter plots of R² versus motion amplitude of each voxel to reveal the relationship between the correlation and motion amplitude.

The quantitative evaluations for the human FP-DTBZ studies were performed by measuring the mean activity concentrations (Bq/mL) in pancreas and kidney, and the target (pancreas and kidneys) to background contrast (TBC). The ROIs were drawn on 3 consecutive slices in the coronal view (Supplementary Fig. S1¹). For the FDG study, we computed the mean SUV values of 26 small-to-medium metastatic lesions (< 15 mm diameter). All the ROIs (as shown in Supplementary Fig. S1) were defined on the Gated image at end-expiration phase and applied to NMC, Gated, NR-Discrete, R-EBE and NR-EBE corrected reconstruction.

IV. Results

A. XCAT Simulations

The reconstructed images of the XCAT simulations at one coronal slice are shown in Fig. 3. Comparing the reconstructions of TG (Fig. 3a) and RG (Fig. 3b) list-mode data, it can be seen the locations of the liver dome, heart and the lesion are different due to respiratory motion. The lung volume is also smaller in the TG than in the RG. The reconstruction of the TG list-mode data with NR-MOLAR (Fig. 3c) using the ground truth motion field (∇x^TG→RG) generated by the XCAT simulator yielded similar images as the RG reconstruction. The difference images between the reconstructions and the ground truth phantom RG are shown in Fig. 3(d) – (f), respectively, which also confirms that NR-MOLAR can effectively account for respiratory motion displacement by deforming system matrix. For quantification, the relative differences of the mean activity between RG and TG-NR-MOLAR (Eq. 14) were 2.7% and 4.1% in the lung lesion and the myocardium ROIs, respectively.

Fig. 3.

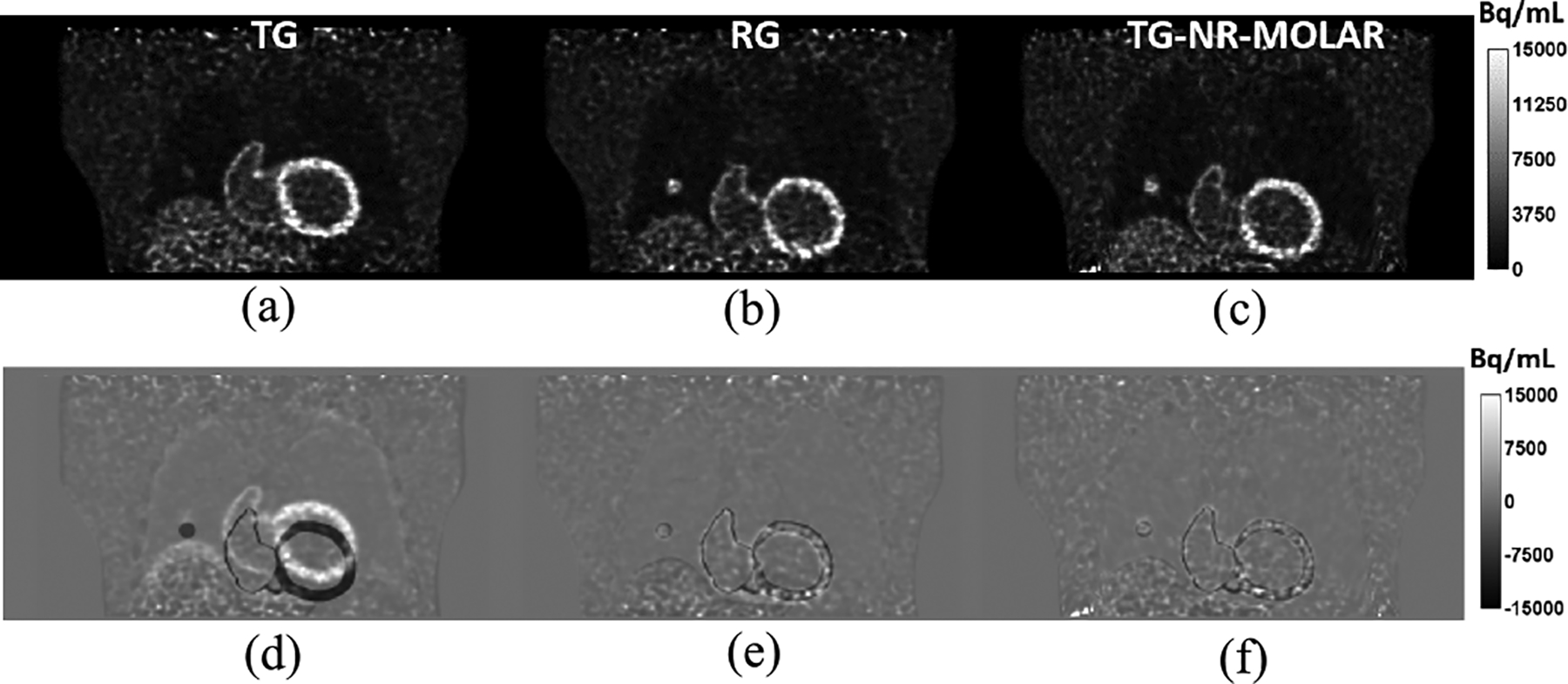
Results of the XCAT phantom simulation. (a) NMC reconstruction of target gate (TG). (b) NMC reconstruction of reference gate (RG). (c) NR-MOLAR reconstruction of TG with the ground truth motion field. (d) The difference image between the reconstructed TG and the ground truth phantom RG. (e) The difference image between the reconstructed RG and the ground truth phantom RG. (f) The difference image between TG-NR-MOLAR and the ground truth phantom RG.

B. Human Studies

Figure 4 shows the estimated motion field (end-inspiration to end-expiration) overlaid on trans-axial, coronal and sagittal views of a sample ¹⁸F-FP-DTBZ human study (subject S2). The motion amplitudes in the SI direction measured from the centroid of the pancreas was 17.4 mm, 8.3 mm and 7.4 mm, for S1, S2 and S3, respectively. For a sample voxel located in the renal cortex (denoted by the red dot in Fig. 4a), its correlation with the external Anzai trace is shown in Fig. 5. For this voxel, high correlations (R²≈0.9) were observed in both SI and AP directions, and no correlation was found in the LR direction. However, it can be seen that the motion amplitude in the LR direction was negligible. To assess the goodness of fit for all the voxels, we generated images of R² in each direction (SI, AP, and LR), allowing us to assess the quality of fitting in relation to anatomical location. The R² distributions from the same subject in Figs 4 and 5 in the same coronal slice is shown in Fig. 6(b–d) overlaid by the contours of the liver, pancreas and spleen (Fig. 6a). It can be seen that the R² value was generally uniform and high (>0.7) in the SI direction. The distribution in the AP direction had more local variations in the middle of the image, but the correlation was larger than 0.5 in most of the regions. In contrast, the distribution was patchy in the LR direction with very low correlation in the center of the image, and relatively higher correlation in the left and right regions.

Fig. 4.

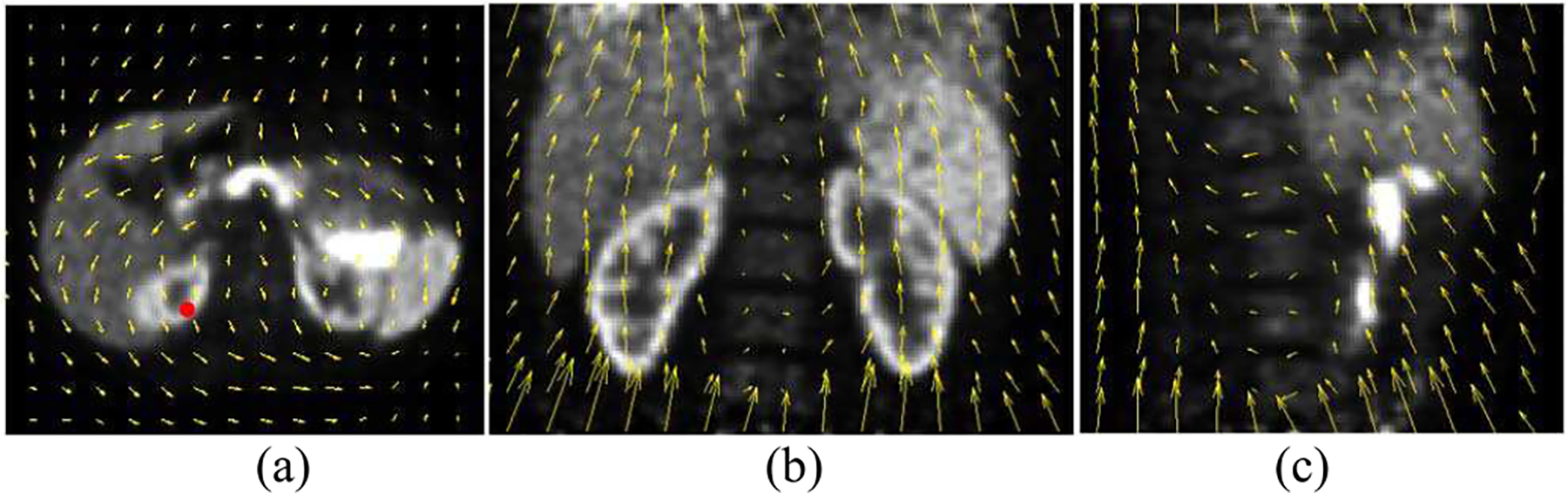
Estimated motion fields (yellow arrows) from a human FP-DTBZ scan (subject S2) in (a) trans-axial (b) coronal, and (c) sagittal directions point from end-inspiration phase to end-expiration phase overlaid on gated PET reconstructions post-filtered with a Gaussian filter (5 mm FWHM).

Fig. 5.

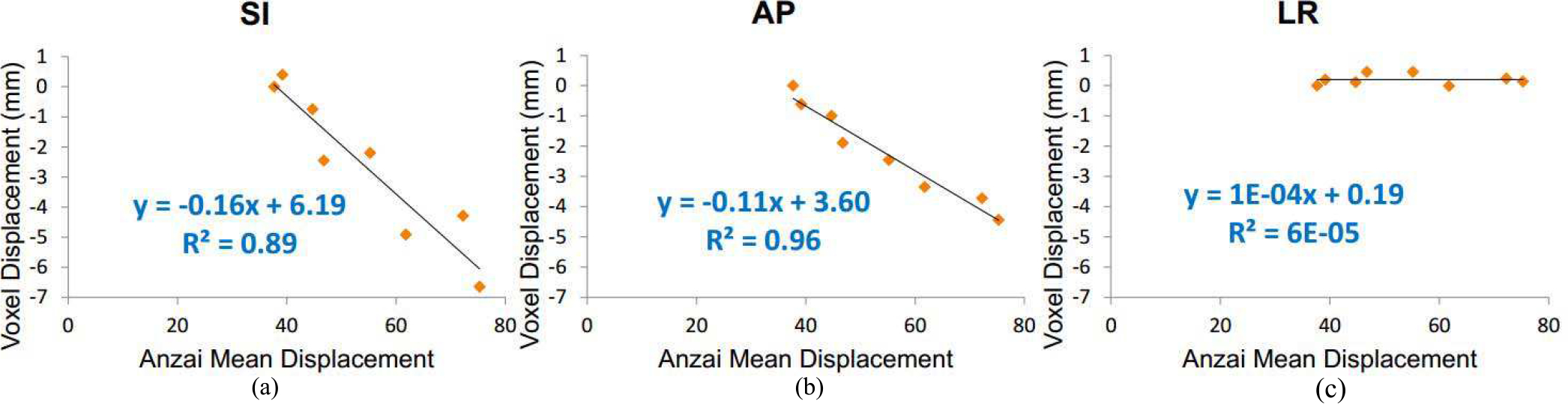
Correlations between the external Anzai displacement and the motion vector in 3 directions of a sample voxel located in the renal cortex (denoted by the red dot) as shown in Fig. 4.

Fig. 6.

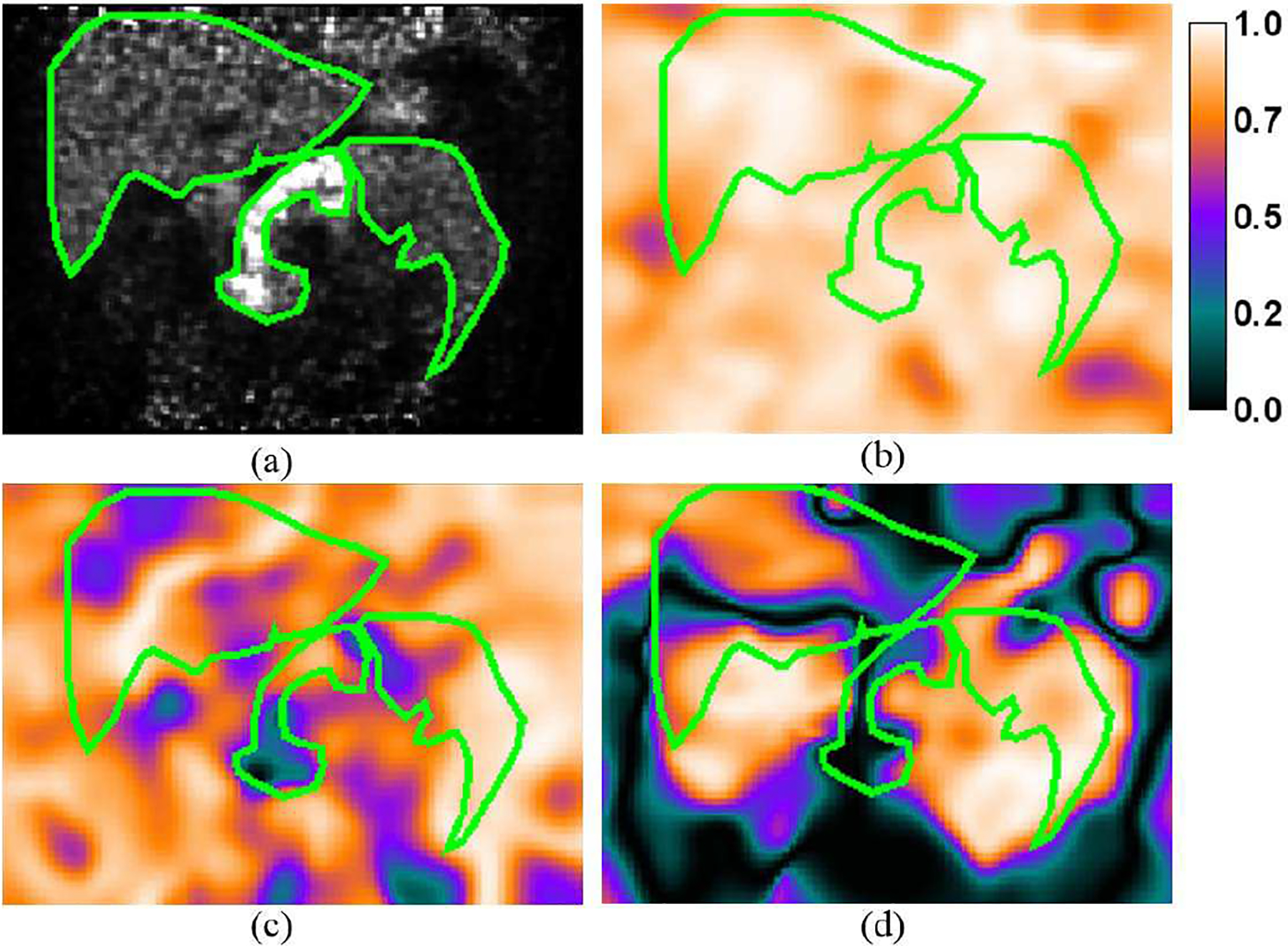
(a) A sample coronal slice of the gated reconstruction of a ¹⁸F-FP-DTBZ study showing elevated radiotracer uptake in the pancreas. The contours of the liver, pancreas and spleen are highlighted in green color. Maps of R² (goodness of fit) in the (b) SI, (c) AP, and (d) LR directions overlaid by the contours of the organs.

To investigate the potential impact of voxels with low correlation with the Anzai data on motion correction, we generated scatter plots of the displacement of each voxel versus their R² values in each direction and the results are shown in Fig. 7. The orange rectangular boxes highlight the voxels that have motion displacements smaller than 4 mm with R² values below 0.6. For voxels with low correlation, their absolute displacements were mostly smaller than 4 mm, which was the FWHM of the PSF kernel used in NR-MOLAR. Similar trends were also observed in the other human studies (results not shown). This analysis illustrated that while some voxels have low correlation with the external trace in certain directions, most of them had small motion amplitudes, and therefore, we did not expect those voxels to have substantial impact on the motion correction results.

Fig. 7.

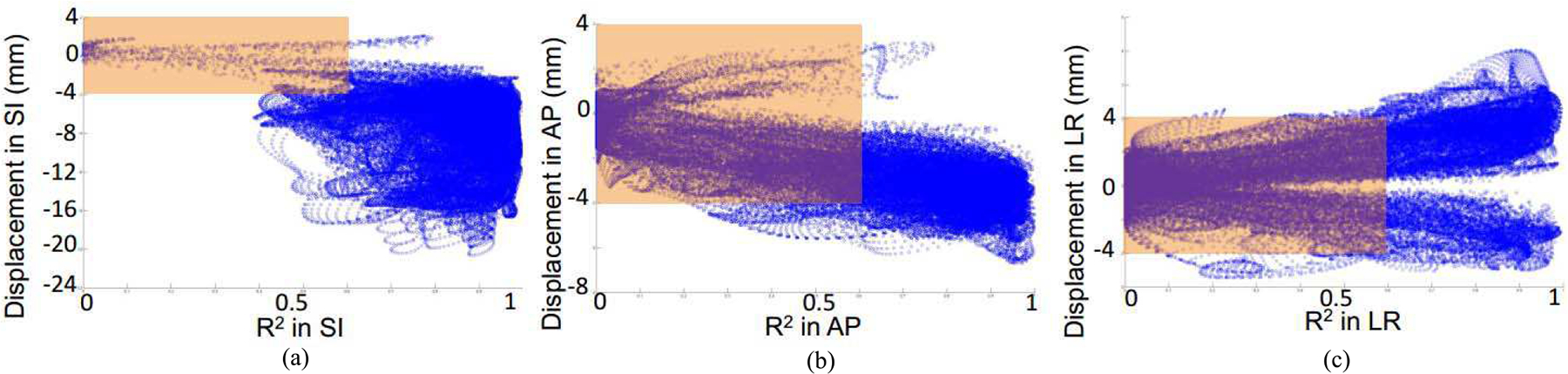
Scatter plots of the voxel displacements in the motion field versus R² in each direction of the same human study as shown in Fig. 4.

Fig. 8 presents sample reconstructed images in the coronal view of a ¹⁸F-FP-DTBZ study (one study is shown here and the other two studies can be found in the supplementary materials Fig. S2). It can be seen in the NMC images that the fine structures of the renal cortex (denoted by the solid arrows) were blurred due to respiratory motion. The Gated reconstruction at end-expiration phase yielded sharper fine structures in the renal cortex at the cost of substantially increased image noise as only 1/8 of the counts were used. NR-EBE yielded sharper and thinner fine structures of renal cortex, and recovered a higher contrast of the cold spot in spleen than NR-Discrete (denoted by the dotted arrow), which is likely attributed to the reduced intra-gate motion with NR-EBE. Although R-EBE yielded similar image quality as NR-EBE in the renal cortex, NR-EBE yielded noticeably sharper rental cortex in the right kidney, and higher contrast of the cold spot in the spleen. In addition, since R-EBE transformed the LORs in the entire FOV rigidly based on the motion information estimated from a single organ, for the organs that do not move in accordance and have non-rigid movement components, R-EBE can yield artifactual blurring. This situation is demonstrated in Fig. 9 with zoomed-in images showing the uptake in the bone marrow. It can be seen that R-EBE blurred the gaps in the bone marrow (denoted by the arrows) compared with other reconstructions.

Fig. 8.

Sample reconstructed images of one ¹⁸F-FP-DTBZ subject (S2). The solid arrows denote the fine structures of the renal cortex that are noticeably sharper in R-EBE and NR-EBE reconstructions where both of which corrected for intra-gate respiratory motion. The dotted arrows denote a cold spot in spleen that has higher contrast in NR-EBE reconstruction than other reconstructions.

Fig. 9.

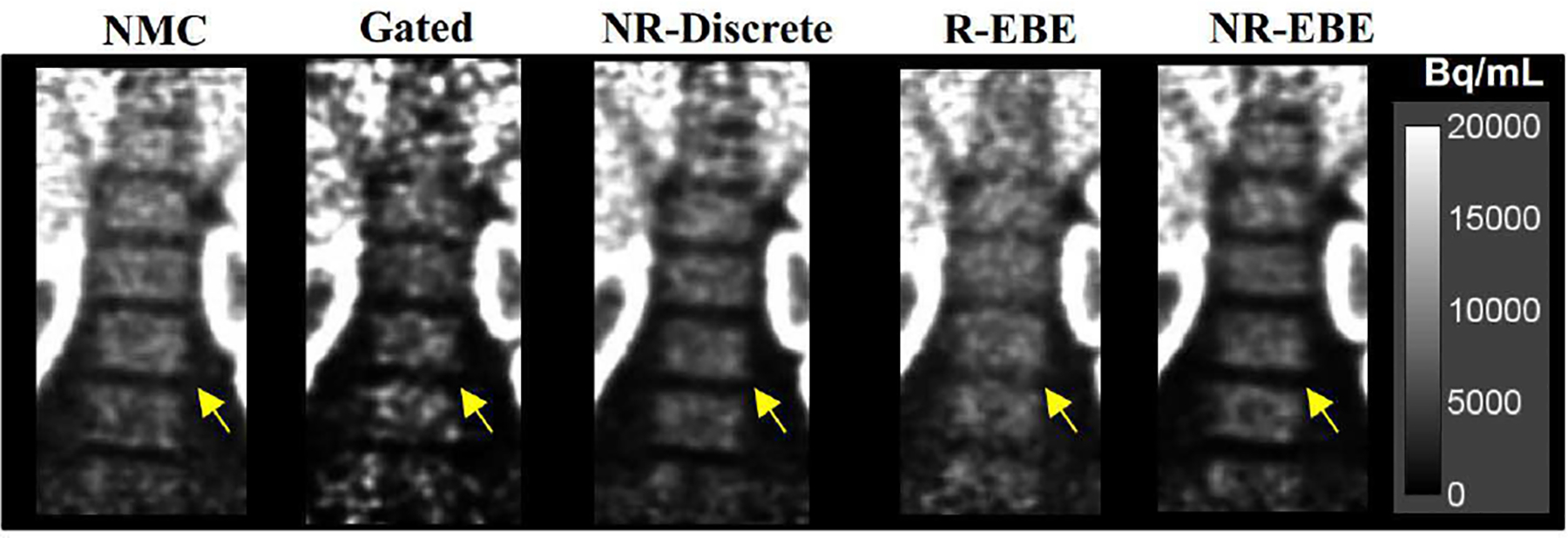
Zoomed-in images showing the bone marrow of the same subject as shown in Fig. 8. The arrows denote the gaps where R-EBE yielded artificial blurring due to the rigid transformation of the LORs in the FOV. Non-rigid motion corrections, i.e. NR-Discrete and NR-EBE yielded similar results as NMC reconstruction in these motionless structures.

Tables 1 and 2 show the quantitative analysis of the mean radioactivity concentration and the TBC in different organs, respectively. The results are summarized as percentage increase compared to NMC images. It can be seen that NR-Discrete achieved an average of ~8% increase across 3 human subjects in 3 regions, while R-EBE and NR-EBE achieved an average increase of ~10% in the same measurement. Gated reconstruction yielded a larger increase from 12.4% to 17.5% in those regions likely because the ROIs were defined on the Gated reconstructions, which matches the best with Gated reconstruction but might have a slight mismatch around the boundaries in other reconstructions. Regarding TBC, NR-EBE yielded higher contrast than NR-Discrete, where both were substantially better than R-EBE. The higher TBC achieved by NR-Discrete and NR-EBE was mainly due to the reduced activity in the background (supplementary materials Table S1). This could be attributed to the more accurate motion estimation based on the non-rigid registration, which reduced the spill-over of the activity from renal cortex and pancreas into the background regions and led to higher contrast.

Table I.

Mean Activity increases (%) of different Motion Corrections compared to NMC reconstruction in different organs of the ¹⁸F-FPDTBZ studies.

Subject	Right kidney				Left Kidney				Pancreas
	Gated	NR-Discrete	R-EBE	NR-EBE	Gated	NR-Discrete	R-EBE	NR-EBE	Gated	NR-Discrete	R-EBE	NR-EBE
1	22.2	8.8	13.2	11.7	22.8	7.6	13.6	12.8	17.9	5.3	15.1	9.7
2	11.4	5.9	8.3	6.1	16.9	7.0	10.4	9.5	7.7	5.5	6.3	6.2
3	8.3	8.6	7.5	10.0	12.6	6.9	5.7	9.3	11.5	13.3	9.6	13.1
Mean	13.9	7.8	9.6	9.3	17.5	7.2	9.9	10.5	12.4	8.0	10.3	9.7

Table II.

Target to background contrast (TBC) increases (%) achieved by different Motion Corrections compared to NMC reconstruction in different organs of the ¹⁸F-FPDTBZ studies.

Subject	Right kidney				Left Kidney				Pancreas
	Gated	NR-Discrete	R-EBE	NR-EBE	Gated	NR-Discrete	R-EBE	NR-EBE	Gated	NR-Discrete	R-EBE	NR-EBE
1	47.4	36.9	35.6	51.2	43.2	45.3	25.6	67.7	30.3	41.9	22.2	58.9
2	26.9	31.9	25.3	33.7	37.1	29.0	15.9	33.4	24.2	38.3	13.6	49.2
3	18.8	30.1	22.8	31.9	9.1	8.1	4.0	14.9	72.7	52.7	21.7	54.1
Mean	31.0	32.9	27.9	38.9	29.8	27.5	15.2	38.7	42.4	44.3	19.2	54.0

For the ¹⁸F-FDG study, two sample coronal slices that include multiple metastatic lesions are shown in Fig. 10. The lesion denoted by the red solid arrow is the target lesion for computing rigid INTEX in R-EBE. The red dashed arrows denote 7 sample lesions that were subject to respiratory motion blurring. Gated reconstruction led to higher contrast on some of the lesions. However, the significantly increased background noise prohibited the detection of lesions 1 and 5. Although NR-Discrete increased the lesion contrast, some of the lesions, e.g. lesion 6, still appeared as motion blurred. This is likely due to the intra-gate motion. R-EBE yielded increased contrast and more rounded shape on the target lesion and its neighboring lesions (1 – 3). However, lesions 4 – 7 located in a different part of the liver and the lesions denoted by the green solid arrows were even more blurred than the NMC reconstruction. Among all the reconstructions, NR-EBE yielded the highest contrast and rounder shape of the lesions. Lesions 4 and 5 have also become clearly discerned.

Fig. 10.

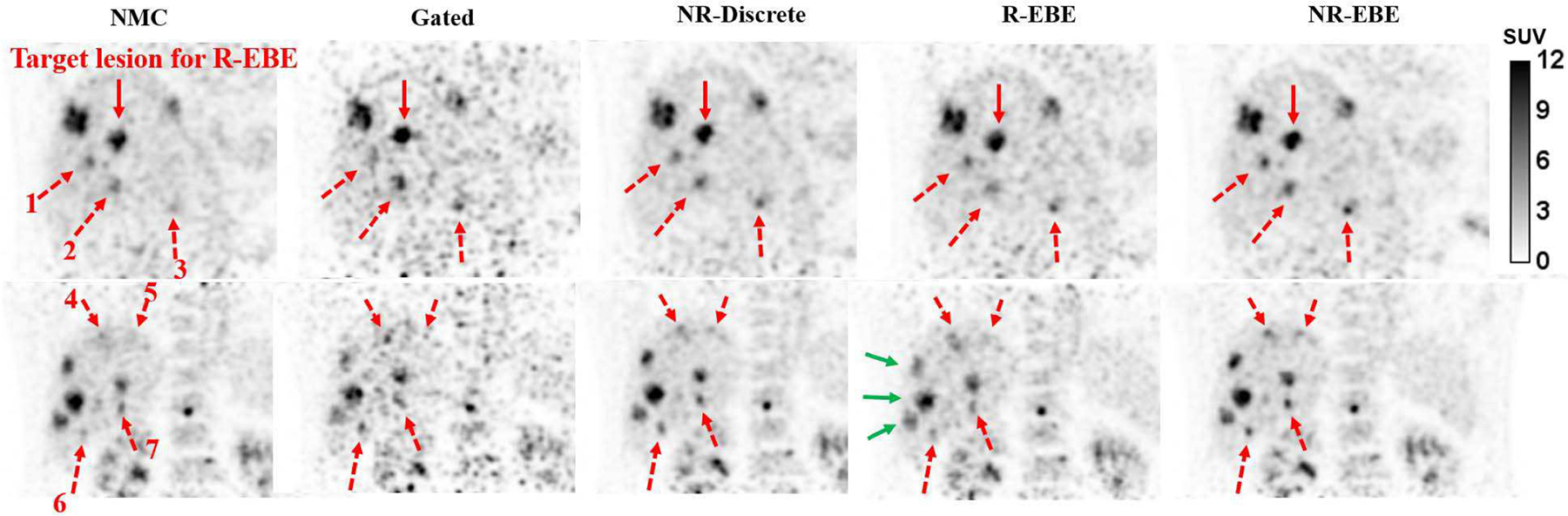
Two sample coronal slices of the ¹⁸F-FDG study. The red solid arrows denote the target lesion for estimating rigid motion in R-EBE. The red dotted arrows denote 7 sample lesions on which NR-EBE yielded substantial improvements in terms of contrast and shape compared to other reconstructions. The green solid arrows denote the lesions that are more blurred after R-EBE motion correction. This could be due to their movements were different to the target lesion.

The relative difference of lesion SUV mean of all the reconstructions compared to NMC were computed for 25 lesions (the full result is shown in the supplementary materials Fig. S3). The mean and standard deviation of the percentage improvements over all the lesions for Gated, NR-Discrete, R-EBE and NR-EBE are 35% ± 37%, 25% ± 23%, −5% ± 19%, and 34% ± 26%, respectively. Gated reconstruction yielded reduced SUV on 5 lesions (range: −3% - −13%) , which might be attributed to noise. R-EBE, NR-Discrete and NR-EBE all yielded 26% increase in SUV on lesion 1 as it was the target lesion. However, R-EBE yielded reduced SUV on 15 other lesions as those did not move in coherent with the target lesion. NR-EBE yielded superior performance than NR-Discrete on 19 out of 25 lesions and similar performance on the rest. All the motion corrected reconstructions yielded a small SUV reduction on lesion 25 (Gated: −13%, NR-Discrete: −3%, R: −12%, NR-EBE: −6%), which is the one located in the bone marrow.

V. Discussion

In this study, we have proposed a novel approach to compensate for non-rigid respiratory motion on an event-by-event basis in the reconstruction. This approach consists of two components, NR-INTEX and NR-MOLAR. NR-INTEX estimates the non-rigid internal organ motion for each voxel in high temporal resolution by using the linear correlation between an external respiratory trace and the motion fields estimated from gated reconstructions. NR-MOLAR uses the motion field to deform the system matrix that consists of LOR based PSF kernel to compensate for motion in the reconstruction.

In NR-MOLAR, we adopted a system matrix deformation approach that involves transformation followed by a tri-linear interpolation as proposed in [17, 18, 35]. Lamere et al. [17, 36] reported that this approach could potentially lead to artifacts in areas such as in the diaphragm where large elastic deformation occurred. This might be attributed to the fact that when two neighboring voxels are “pulled apart” due to large motion displacement, the voxels between them might not be “filled in” with tri-linear interpolation. These “void” voxels will not be intersected by the CORs in the forward/back projections and will not get updated. This is particularly the case when Siddon ray-tracing was used as the forward/back projector, and the PSF kernel was not modeled in their studies. The resolution model implemented in MOLAR is a wide-band projection operator which could potentially remedy this problem as the PSF consists of more neighboring voxels in addition to the tri-linear interpolation. Therefore, such “void” voxels are less likely to be created. Indeed, we did not observe any artifact in the liver dome in our XCAT study that was simulated with 20 mm maximum motion magnitude in the SI direction. Another solution that might completely eliminate the possibility of “void” voxels could be reconstructing the images using unorganized point clouds [37]. In addition, the transformation implementation did not preserve mass. Previous studies have reported using different approaches to achieve mass preservation such as multiplying the Jacobian determinant after interpolation [12, 38] or activity preserving interpolation [26]. However, all these studies aimed to correct for cardiac motion, where the motion field can change abruptly locally. In contrast, the gradient of respiratory motion field is locally smooth. Therefore, we do not expect preserving mass will have a big impact on our results. That being said, comparisons between mass-preserving and non-mass preserving techniques on respiratory motion correction with different gradient and magnitude, and their impacts on transforming image versus transforming system matrix warrant comprehensive further investigations, which are beyond the scope of this study.

To obtain motion fields at high temporal resolution for event-by-event non-rigid motion correction, we extended the previously proposed R-INTEX [5], which was designed to correct for rigid motion, to NR-INTEX. This was achieved by establishing linear correlations between the external respiratory trace and each voxel in the motion field. However, as poor correlation may affect the accuracy of motion compensation as demonstrated in our previous study [5], it is therefore, important to examine the quality of the correlation for each voxel, and its relationship with the motion magnitude. The distributions of R² in Fig. 6 showed that the correlation was high and relative uniform in the SI and AP directions in general. A heterogeneous correlation distribution was seen in the LR direction with very low correlation in the center of the body, which was in line with our expectation as the organs along the midline should have minimal motion in the LR direction. We further explored the correlation between R² and their motion magnitude for each voxel. The scatter plot results in Fig. 7 reveal that the majority of the voxels with low correlations (<0.6) also had motion magnitudes smaller than 4 mm. As this small estimated motion magnitude was smaller than the intrinsic system resolution, we do not expect the voxels with low correlation would impact the resulting image quality substantially. Nonetheless, for those voxels that do not actually move, minor motion displacements introduced by the non-rigid B-spline warping operator and tri-linear interpolation in the reconstruction could introduce blurring effects. Although it did not seem to affect the quantification substantially, we expect this quantification bias might be further reduced for static lesions if a threshold is used in NR-INTEX, such that the effective motion displacement is set to zero if the motion magnitude or correlation is smaller than certain levels.

Comparing to NR-Discrete for the human studies, NR-EBE further reduced motion blurring and yielded higher mean activity in the organs/lesions. NR-Discrete applied one motion field to all the events in the same respiratory phase. However, as large intra-gate motion could occur within an inspiration phase [5], a single motion field may not be most accurate for these events, and therefore residual motion remained in the results. In contrast, NR-EBE used NR-INTEX to interpolate the motion field according to the respiratory trace, which adapts to the respiratory motion variation down to millisecond, thus generating a more accurate motion field at each time point for each event. On the other hand, R-EBE applied rigid-motion displacement obtained from a target organ (i.e., pancreas in the FPDTBZ studies or a single lesion in the FDG study) to the entire FOV, whereas other organs (i.e., spleen or the other lesions) might not move consistently with the target organs/lesion. We observed that NR-EBE and REBE performed similarly for the target organs/lesion, while R-EBE introduced artefactual blurring to bone marrow and reduced SUV for the rest of the lesions. Indeed, previous studies have demonstrated that liver, pancreas, spleen and kidneys all have different magnitudes of movement during breathing [1]. Therefore, if a single known lesion/organ is the target for motion correction, R-EBE would be desired due to its simplicity on the estimation of the motion displacement. However, if multiple targets are present in the FOV or if there are no known targets, NR-EBE is a more practical and accurate approach.

Further investigation should be performed to compare NR-EBE results with gated reconstruction at matched count statistics acquired from prolonged scans, and the commercial optimal gating approaches [39] on more patient studies. We expect that for patient with regular breathing patterns and no baseline shift of the respiratory trace, the optimal gating or quiescent period gating [40] approaches could yield comparable quantification, albeit with moderately increased image noise. However, these motion correction approaches will become less effective if the breathing pattern is more irregular or in count-limited studies such as ⁹⁰Y-PET/CT [41]. In addition, while we focused on motion correction for static PET in this study, the NR-EBE can be directly applied to dynamic PET studies, similar to our previous implementation of R-EBE for dynamic PET [8].

A preset number of gates (8 gates for the FPDTBZ studies, and 5 gates for the FDG study) were used to generate gated PET images and derive continuous displacement fields. The optimal number of gates depends on multiple factors such as the total number of coincidence events and the patient’s breathing pattern. For high-count studies with irregular breathing pattern, a moderate increase of the number of gates, e.g., from 5 to 8, would reduce intra-gate motion blurring, which might lead to more accurate motion estimation and higher correlation with the external trace. However, for studies with lower counts, such as the FDG study, the increased noise associated with more gates could lead to less accurate motion estimation. In addition, since we perform registration on adjacent gated images, the increased number of gates could lead to very small displacements between adjacent gates, which might not be captured by the registration algorithm. We also do not expect that more than 8 gates would substantially improve the already high linear correlation. Therefore, based on our data to date, 5 – 8 respiratory gates are suggested depending on the factors discussed above.

One of the factors that could impact the performance of motion correction is the optimization of the registration. In the current study, the FFD B-spline control point spacing was set to 15 mm to provide a balanced tradeoff between the smoothness of the motion fields and the accuracy of the registration result on individual organs, such as the kidneys. This parameter was applied in all the human studies, and the registration results were assessed visually for each individual dataset prior to reconstruction. Since PET images are noisy, a smaller control point space (e.g., 5 mm) caused registration of noise and the cost function optimization was trapped at local minima. The algorithm eventually returned erroneous registrations such that the organs in the deformed target image appeared distorted. On the other hand, a larger control point space (e.g., 30 mm) did not yield satisfactory registration for individual organs like kidneys. In addition, we set the regularization term to be γ =0.001. In reality, respiratory motion in the abdomen results in discontinuous motion fields, e.g., at the boundaries between soft tissue and rigid anatomical structures, such as the bone. Our transformation model, on the other hand, is smooth and continuous. We therefore chose a small regularization value to allow for large, local deformations in the transformations while maintaining smoothness. Larger γ values resulted in displacement fields that were overly smooth (e.g., we observed false spine motion where there was in fact none). Finally, our registration method used a hierarchical approach that proceeded in a coarse to fine manner. Using a multi-resolution sampling factor of 2, we adjusted both the transformation model B-spline control point spacing and the image resolution at each level. For registration using three levels, we thus started the registration procedure using a 60-mm isotropic B-spline control point grid, and progressed to 30-mm and 15-mm control point spacing. During the hierarchical registration procedure, the images were also down-sampled using the same factor. By registering the images using this hierarchical approach, the initial registration level first aligned large soft tissue structures with large displacements, and then the motion was subsequently refined at later registration levels. Using a greater number of registration levels showed no improvement to the registration results.

We also took the advantage of the temporally smooth nature of the image sequence to register images to their immediate temporal neighbor (adjacent gate in the direction towards the reference gate (RG)). Adjacent transformations were then concatenated together to form a registration chain back to the RG image. We performed this approach because adjacent images have less deformation in the anatomy than when using non-adjacent images. Therefore, the registration algorithm will more easily converge to a satisfactory transformation estimate between adjacent gates. On the other hand, if the deformations between corresponding anatomical structures are too large, as observed in non-adjacent images, e.g. between gate 1 and gate 5 (the RG) in the sequence, then the registration algorithm might have to optimize a transformation with large displacements that can more likely become trapped in suboptimal local minima due to the low SNR in noisy PET images. The advantage of this sequential registration versus direct registration is further demonstrated in Fig. S4 in the supplementary material.

A more objective assessment of the registration result would require segmentation of the VOIs in each frame, and then computing the overlap measures between TG and RG after registration [42]. This objective assessment would also allow the registration parameter to be optimized for each dataset. We anticipate that an optimized registration for each individual dataset could further improve the image quality and quantitative accuracy. In future work, it is worthwhile to investigate the impact of the registration on NR-EBE, and at what extent the registration errors could corrupt the reconstruction results.

A caveat of the human studies presented in this study is the use of single phase attenuation CT to reconstruct the gated PET images followed by registrations. The motion estimation might be affected by attenuation artifacts that could be present in the gated reconstructions, particularly near the liver dome. Nonetheless, no obvious artifacts were observed in the reconstruction results. Further investigation should be conducted on estimating the motion fields based on non-attenuation corrected PET images in non-rigid registration and compare to ground truth motion fields or by using a joint reconstruction and motion estimation approach [43, 44].

Another limitation of the proposed method could be the computation time for reconstruction. For a list-mode data with ~38M true events (the ¹⁸F-FDG study) and running the reconstruction on a cluster with 32 CPUs, the conventional MOLAR [29] (3 iter, 21 subsets) completed the reconstruction in 80 min, while the NR-INTEX NR-MOLAR reconstruction took 187 min. The longer reconstruction time might hinder its use for routine reconstruction. However, it has also been shown that GPU-accelerated MOLAR can perform 40x faster than the CPU only code [45]. Therefore, we anticipate that NR-INTEX can be vastly accelerated using the GPU based version, which will be investigated in the future.

VI. Conclusions

In this study, we have proposed a novel approach to correct for non-rigid respiratory motion on a continuous event-by-event basis for list-mode PET reconstruction. The proposed method demonstrated improved visibility of moving lesions and radiotracer uptake quantification in comparison to discrete non-rigid motion correction, and continuous rigid motion correction on multiple human studies, which appears to be a promising tool for compensating respiratory motion in both static and dynamic PET studies.