Abstract
We study distributions of a general reduced-order dependence measure and apply the results to conditional independence testing and feature selection. Experiments with Bayesian Networks indicate that using the introduced test in the Grow and Shrink algorithm instead of Conditional Mutual Information yields promising results for Markov Blanket discovery in terms of F measure.
Keywords: Conditional Mutual Information, Asymptotic distribution, Feature selection, Markov Blanket, Reduced-order dependence measure
Introduction
Consider a problem of selecting a subset of all potential predictors 
to predict an outcome Y, which consists of all predictors significantly influencing it. Selection of active predictors leads to dimension reduction and is instrumental for many machine learning and statistical procedures, in particular in structure learning of dependence networks. Commonly for this task, such methods incorporate a sequence of conditional independence tests, among which the test based on Conditional Mutual Information (CMI) is the most frequent. In the paper we consider properties of a general information-based dependence measure 
introduced in [2] in a context of constructing approximations to CMI. This is a reduced-order approximation which disregards approximations of order higher than 3. It can also be considered as a measure of predictive power of X for Y when variables 
have been already chosen for this task. Special cases include Mutual Information Minimization (MIM), Minimum Redundancy Maximum Relevance (MrMR) [11], Mutual Information Feature Selection (MIFS) [1], Conditional Information Feature Extraction (CIFE) [7] and Joint Mutual Information (JMI) [14] criteria. They are routinely used in nonparametric approaches to feature selection, variable importance ranking and causal discovery (see e.g. [4, 13]). However, theoretical properties of such criteria remain largely unknown hindering study of associated selection methods. Here we show that 
exhibits dichotomous behaviour meaning that its distribution can be either normal or coincides with a distribution of a certain quadratic form in normal variables. The second case is studied in detail for binary Y. In particular for two popular criteria CIFE and JMI, conditions under which their distributions converge to distributions of quadratic form are made explicit. As two cases of dichotomy differ in behaviour of the variance of 
, its order of convergence is used to detect which case is actually valid. Then a parametric permutation test (i.e. a test based on permutations to estimate parameters of the chosen distribution) is used to check whether candidate variable X is independent of Y given 
.
Preliminaries
Entropy and Mutual Information
We denote by 
, 
a probability mass function corresponding to X, where 
is a domain of X and 
is its cardinality. Joint probability will be denoted by 
. Entropy for discrete random variable X is defined as
 |
1 |
Entropy quantifies the uncertainty of observing random values of X. In case of discrete X, H(X) is non-negative and equals 0 when the probability mass is concentrated at one point. The above definition naturally extends to the case of random vectors (i.e. X can be multivariate random variable) by using multivariate probability instead of univariate probability. In the following we will frequently consider subvectors of 
which is a vector of all potential predictors of class index Y. The conditional entropy of X given Y is written as
 |
2 |
and the mutual information (MI) between X and Y is
 |
3 |
This can be interpreted as the amount of uncertainty in X which is removed when Y is known which is consistent with an intuitive meaning of mutual information as the amount of information that one variable provides about another. MI equals zero if and only if X and Y are independent and thus it is able to discover non-linear relationships. It is easily seen that 
. A natural extension of MI is conditional mutual information (CMI) defined as
 |
4 |
which measures the conditional dependence between X and Y given Z. An important property is chain rule for MI which connects 
to 
:
 |
5 |
For more properties of the basic measures described above we refer to [3]. A quantity, used in next sections, is interaction information (II) [9]. The 3-way interaction information is defined as
 |
6 |
which is consistent with an intuitive meaning of existence of interaction as a situation in which the effect of one variable on the class variable depends on the value of another variable.
Approximations of Conditional Mutual Information
We consider a discrete class variable Y and p discrete features 
. Let 
denote a subset of features indexed by a subset 
We employ here greedy search for active features based on forward selection. Assume that S is a set of already chosen features, 
its complement and 
a candidate feature. In each step we add a feature whose inclusion gives the most significant improvement of the mutual information, i.e. we find
 |
7 |
The equality in (7) follows from (5). Observe that (7) indicates that we select a feature that achieves the maximum association with the class given the already chosen features. For example, first-order approximation yields 
, which is a simple univariate filter MIM, frequently used as a pre-processing step in high-dimensional data analysis. However, this method suffers from many drawbacks as it does not take into account possible interactions between features and redundancy of some features. When the second order approximation is used, the dependence score for candidate feature is
 |
8 |
The second equality uses (6). In literature (8) is known as CIFE (Conditional Infomax Feature Extraction) [7] criterion. Observe that in (8) we take into account not only relevance of the candidate feature, but also its possible interactions with the already selected features. However, frequently it is useful to scale down the corresponding term [2]. Among such modifications the most popular is JMI
 |
where the second equality follows from (5). JMI was also proved to be an approximation of CMI under certain dependence assumptions [13]. Data-adaptive version of JMI will be considered in Sect. 4. In [2] it is proposed to consider a general information-theoretic dependence measure
 |
9 |
where 
are some positive constants usually depending in decreasing manner on the size 
of set S. Several frequently used selection criteria are special cases of (9). MrMR criterion [11] corresponds to 
whereas more general MIFS (Mutual Information Feature Selection) criterion [1] corresponds to pair 
. Obviously, the simplest criterion MIM corresponds to (0, 0) pair. CIFE defined above in (8) is obtained for (1, 1) pair, whereas 
leads to JMI. In the following we consider asymptotic distributions of the sample version of 
, namely
 |
10 |
and show how the distribution depends on underlying parameters. In this way we gain a more clear idea what is an influence of 
and 
on the behaviour of 
. Sample version in (10) is obtained by plugging in fractions of observations instead of probabilities in (3) and (4).
Distributions of a General Dependence Measure
In the following we will state our theoretical results which study asymptotic distributions of 
where 
is possible multivariate discrete vector and then we apply it to previously introduced framework by putting 
and 
. We will show that its distribution is either approximately normal or, if the asymptotic variance vanishes, is approximately equal to distribution of quadratic form of normal variables. Let 
be a vector of probabilities for (X, Y, Z) and we assume whence forth that 
for any triple of (x, y, z) values in the range of (X, Y, Z). Moreover, f(p) equals 
treated as a function of p, Df denotes a derivative of function f and 
convergence in distribution. The special case of the result below for CIFE criterion has been proved in [6].
Theorem 1
(i) We have
 |
11 |
where 
and 
(ii) If 
then
 |
12 |
where V follows 
distribution, 
and 
is a Hessian of f.
Proof
Note that 
equals
 |
After some calculations one obtains that 
equals for 
 |
13 |
Let 
, 
. Then 
. The remaining part of the proof relies on Taylor’s formula for 
. Details are given in supplemental material [5].
We characterize the case when 
in more detail for binary Y and 
which encompasses CIFE and JMI criteria. Note that binary Y case covers an important situation of distinguishing between cases (
) and control (
). We define two scenarios:
Scenario 1 (S1):
for any 
and 
(
denotes conditional independence of X and Y given Z).Scenario 2 (S2):
such that 
and for 
, 
and for 
we have 
.
Define W as
 |
14 |
We will study in detail the case when 
and either 
or at least one of the parameters 
equal 0. We note that all cases of used information-based criteria fall in one of these categories [2]. We have
Theorem 2
Assume that 
and 
. Then we have:
-
(i)
If
and 
then one of the above scenarios holds with W defined in (14). -
(ii)
If
or 
then Scenario 1 is valid.
The analogous result can be stated for the case when at least one of the parameters 
or 
equals 0 (details are given in supplement [5]).
Special Case: JMI
We state below corollary for criterion JMI. Note that in view of Theorem 2 Scenario 2 holds for JMI. Let
 |
15 |
Corollary 1
Let Y be binary. (i) If 
then
 |
(ii) If 
then 
and
 |
where V and H are defined in Theorem 1. Moreover in this case Scenario 1 holds.
Note that 
implies 
as in this case Scenario 1 holds. The result for CIFE is analogous (see supplemental material [5]).
In both cases we can infer the type of limiting distribution if the corresponding theoretical value of the statistic is nonzero. Namely, if 
(
) then 
(respectively, 
) and the limiting distribution is normal. Checking that 
is simpler than 
as it is implied by 
for at least one 
. Actually, 
is equivalent to conditional independence of X and Y given 
for any 
which in its turn is equivalent to 
. In the next section we will use a behaviour of the variance to decide which distribution to use as a benchmark for testing conditional independence. In a nutshell, the corresponding switch which is constructed in data-adaptive way and is based on different order of convergence of the variance to 0 in both cases. This is exemplified in the Fig. 1 which shows boxplots of the empirical variance of JMI multiplied by sample size in two cases, when the theoretical variance is 0 (model M2 discussed below) or not (model M1). The Figure clearly indicates that the switch can be based on the behaviour of the variance.
Fig. 1.
Behaviour of the empirical variance multiplied by n in the case when corresponding value of 
is zero (yellow) or not (blue). Models: M1, M2 (see text), 
, 
, 
, 
. (Color figure online)
JMI-Based Conditional Independence Test and Its Behaviour
JMI-Based Conditional Independence Test
In the following we use 
as a test statistic for testing conditional independence hypothesis
 |
16 |
where 
denotes set of 
with 
. A standard way of testing it is to use Conditional Mutual Information (CMI) as a test statistic and its asymptotic distribution to construct the rejection region. However, it is widely known that such test loses power when the size of conditioning set grows due to inadequate estimation of 
for all strata 
. Here we use as a test statistic 
which does not suffer from this drawback as it involves conditional probabilities given univariate strata 
for 
. As behaviour of 
is dichotomous on (16) we consider a data-dependent way of determining which of the two distributions: normal or distribution of quadratic form (abbreviated to d.q.f. further on) is closer to distribution of 
. Here we propose a switch based on the connection between distribution of the statistics and its variance (see Theorem 1). We consider the test based on JMI as in this case 
is equivalent to 
. Namely, it is seen from Theorem 1 that normality of asymptotic distribution corresponds to the case when the asymptotic variance calculated for samples of size n and n/2 should be approximately the same and should be strictly smaller for a larger sample otherwise. For each strata 
we permute corresponding 
values of X
B times and for each permutation we obtain value of 
as well as an estimator of its asymptotic variance 
. The permutation scheme is repeated for randomly chosen subsamples of original sample of size n/2 and B values of 
are calculated. We than compare the mean of 
with the mean of 
using t-test. If the equality of the means is not rejected we bet on normality of asymptotic distribution, in the opposite case d.q.f. is chosen. Note that permuting samples for a given value 
we generate data 
which follows null hypothesis (16) while keeping the distribution 
unchanged. In Fig. 2 we show that when conditional independence hypothesis is satisfied then distribution of estimated variance 
based on permuted samples follows closely distribution of 
based on independent samples. Thus indeed using permutation scheme described above we can approximate the distribution of the variance of JMI under 
for a fixed conditional distribution 
.
Fig. 2.
Comparison of variances’ distributions under conditional independence hypothesis. SIM corresponds to distribution of 
based on 
simulated samples. PERM is based on 
simulated samples. For each of them X was permuted on strata (
) and 
was calculated. Models: M1, M2 (see text), 
, 
, 
, 
Now we approximate sample distribution of 
by 
when normal distribution has been picked or when d.q.f. has been picked approximation is 
(with 
being the empirical mean of 
) or scaled chi square 
where parameters are based on three first empirical moments of the permuted samples [15]. Then the observed value 
is compared to quantile of the above benchmark distribution and conditional independence is rejected when this quantile is exceeded. Note that as parametric permutation test is employed we need much smaller B than in the case of non-parametric permutation test and we use 
. Algorithm will be denoted by JMI(norm/chi) or JMI(norm/chi_scale) depending on whether chi square or scaled chi square is considered in the switch. The pseudocode of the algorithm is given below in Algorithm 1 and the code itself is available in [5]. For comparison we consider two tests: asymptotic test for CMI (called CMI) and semi-parametric permutation test (called CMI(sp)) proposed in [12]. In CMI(sp) the permutation test is used to estimate the number of degrees of freedom of reference chi square distribution.
Numerical Experiments
We investigate the behaviour of the proposed test in two generative tree models shown in the left and the right panel of Fig. 3 which will be called M1 and M2. Note that in model M1 
whereas for model M2 the stronger condition 
holds. We consider the performance of JMI based test for testing hypothesis 
when the sample size and parameters of the model vary. As 
is satisfied in both models this contributes to the analysis of the size of the test.
Fig. 3.
Models under consideration in an experiment I. The models in the left and right panel will be called M1 and M2.
Observations in M1 are generated as follows: first, Y is chosen from Bernoulli distribution with success probability 
. Then 
are generated from 
given 
and 
given 
, where elements of 
are equal 
and 
with 
and 
some chosen values. Then Z values are discretised to two values (0 and 1) to obtain 
. In the next step 
is generated from conditional distribution 
given 
and then 
is discretised to 
. We note that such method of generation yields that 
and Y are conditionally independent given 
and the same is true for 
. Observations in M2 are generated similarly, the only difference being that 
is now generated independently of 
.
We will also check the power of the tests in M1 for testing hypotheses 
and 
as neither of them is satisfied in M1. Note however, that since information 
and 
decreases when k (or 
, 
) increases the task becomes more challenging for larger k (or 
, 
, respectively) which will result in a loss of power for large k when sample size is fixed.
Estimated tests sizes and powers are based on 
times repeated simulations.
We first check how the switch behaves for JMI test while testing 
(see Fig. 4). In M1 for 
as 
given 
and 
asymptotic distribution is d.q.f. and we expect switching to d.q.f. which indeed happens in almost 100
. For 
, 
asymptotic distribution is normal which is reflected by the fact that the normal distribution is chosen with large probability. Note that this probability increases with n as summands 
of 
for 
converge to normal distributions due to Central Limit Theorem. The situation is even more clear-cut for M2 where 
for all k and the switch should choose d.q.f.
Fig. 4.
The behaviour of the switch for testing 
in M1 and M2 models (
, 
, 
).
Figure 5 shows the empirical sizes of the test when theoretical size has been fixed at 
and 
and 
. We see that empirical size is controlled fairly well for CMI(sp) and for the proposed methods, with the switch (norm/chi_scale) working better than the switch (norm/chi). A superiority of the former is even more pronounced for 
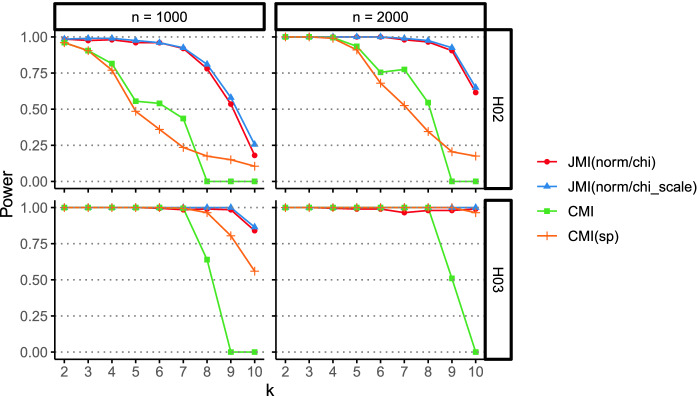
and when 
are dependent (not shown). Note erratic behaviour of size for CMI, which significantly exceeds 0.1 for certain k and then drops to 0. Figures 6 and 7 show the power of the considered methods for hypotheses 
and 
. It is seen that for 
, 
the expected decrease of power with respect to k is much more moderate for the proposed methods than for CMI and CMI(sp). JMI (norm/chi_scale) works in most cases slightly better than JMI (norm/chi). For 
power of CMI(sp) is similar to that of CMI but it exceeds it for large k, however, it is significantly smaller than the power of both proposed methods. For 
superiority of JMI-based tests is visible only for large k when n is moderate (
), whereas for 
it is also evident for small k. With changing 
and 
superiority of the proposed methods is still evident (see Fig. 7). Note that for fixed 
the power of all methods decreases when 
increases.
Fig. 5.
Test sizes for testing 
in M1 and M2 models (
, 
) for fixed 
.
Fig. 6.
Power for testing 
and 
in M1 model (
, 
).
Fig. 7.
Power for testing 
in M1 model (
, 
).
Application to Feature Selection
Finally, we illustrate how the proposed test can be applied for Markov Blanket (MB, see e.g. [10]) discovery of Bayesian Networks (BN). MB for a target Y is defined as the minimal set of predictors given which Y and remaining predictors are conditionally independent [2]. We have used the JMI test (with normal/scaled chi square switch) in the Grow and Shrink (GS, see e.g. [8]) algorithm for MB discovery and compared it with GS using CMI and CMi(sp). GS algorithm finds a large set of potentially active features in the Grow phase and then whittles it down in the Shrink phase. In the real data experiments we used another estimator of 
equal to the empirical variance of JMIs calculated for permuted samples which behaved more robustly. The results were evaluated by F measure (the harmonic mean of precision and recall). We have considered several benchmark BNs from BN repository https://www.bnlearn.com/bnrepository (asia, cancer, child, earthquake, sachs, survey). For each of them Y has been chosen as the variable having the largest MB. The results are given in Table 1. It is seen that with respect to F in the majority of cases GS-JMI method is the winner and ties with one of the other methods and the more detailed analysis indicates that this is due to its largest recall in comparison with GS-CMI and GS-CMI(sp) (see supplement [5]). This agrees with our initial motivation of considering such method which was the lack of power (i.e. missing important variables) by CMI-based tests.
Table 1.
Values of F measure for GS algorithm using JMI, CMI and CMIsp tests. The winner is in bold.
| Dataset | Y | MB size | JMI | CMI(sp) | CMI |
|---|---|---|---|---|---|
| Asia | Either | 5 | 0.58 | 0.57 | 0.58 |
| Cancer | Cancer | 4 | 0.78 | 0.65 | 0.56 |
| Child | Disease | 8 | 0.55 | 0.74 | 0.55 |
| Earthquake | Alarm | 4 | 0.87 | 0.87 | 0.76 |
| Sachs | PKA | 7 | 0.83 | 0.88 | 0.59 |
| Survey | E | 4 | 0.81 | 0.52 | 0.54 |
Conclusions
We have proposed a new test of conditional independence based on approximation JMI of the conditional mutual information CMI and its asymptotic distributions. We have shown using synthetic data that the introduced test is more powerful than tests based on asymptotic or permutation distributions of CMI when a conditioning set is large. In our analysis of real data sets we have indicated that the proposed test used in GS algorithm yields promising results in MB discovery problem. Drawback of such a test is that it disregards interactions between predictors and target variables of order higher than 3. Further research topics include systematic study of 
and especially how its parameters influence the power of the associated tests and feature selection procedures. Moreover, studying tests based on extended JMI including higher order terms is worthwhile.
Contributor Information
Valeria V. Krzhizhanovskaya, Email: V.Krzhizhanovskaya@uva.nl
Gábor Závodszky, Email: G.Zavodszky@uva.nl.
Michael H. Lees, Email: m.h.lees@uva.nl
Jack J. Dongarra, Email: dongarra@icl.utk.edu
Peter M. A. Sloot, Email: p.m.a.sloot@uva.nl
Sérgio Brissos, Email: sergio.brissos@intellegibilis.com.
João Teixeira, Email: joao.teixeira@intellegibilis.com.
Mariusz Kubkowski, Email: m.kubkowski@ipipan.waw.pl.
Małgorzata Łazȩcka, Email: malgorzata.lazecka@ipipan.waw.pl.
Jan Mielniczuk, Email: miel@ipipan.waw.pl.
References
- 1.Battiti R. Using mutual information for selecting features in supervised neural-net learning. IEEE Trans. Neural Netw. 1994;5(4):537–550. doi: 10.1109/72.298224. [DOI] [PubMed] [Google Scholar]
- 2.Brown G, Pocock A, Zhao M, Luján M. Conditional likelihood maximisation: a unifying framework for information theoretic feature selection. J. Mach. Learn. Res. 2012;13(1):27–66. [Google Scholar]
- 3.Cover TM, Thomas JA. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing) New York: Wiley-Interscience; 2006. [Google Scholar]
- 4.Guyon I, Elyseeff A. An introduction to feature extraction. In: Guyon I, Nikravesh M, Gunn S, Zadeh LA, editors. Feature Extraction. Heidelberg: Springer; 2006. pp. 1–25. [Google Scholar]
- 5.Kubkowski, M., Łazȩcka, M., Mielniczuk, J.: Distributions of a general reduced-order dependence measure and conditional independence testing: supplemental material (2020). http://github.com/lazeckam/JMI_CondIndTest
- 6.Kubkowski, M., Mielniczuk, J., Teisseyre, P.: How to gain on power: novel conditional independence tests based on short expansion of conditional mutual information (2019, submitted)
- 7.Lin D, Tang X. Conditional infomax learning: an integrated framework for feature extraction and fusion. In: Leonardis A, Bischof H, Pinz A, editors. Computer Vision – ECCV 2006; Heidelberg: Springer; 2006. pp. 68–82. [Google Scholar]
- 8.Margaritis, D., Thrun, S.: Bayesian network induction via local neighborhoods. In: Proceedings of the 12th International Conference on Neural Information Processing Systems, NIPS 1999, pp. 505–511 (1999)
- 9.McGill WJ. Multivariate information transmission. Psychometrika. 1954;19(2):97–116. doi: 10.1007/BF02289159. [DOI] [Google Scholar]
- 10.Pena JM, Nilsson R, Bjoerkegren J, Tegner J. Towards scalable and data efficient learning of Markov boundaries. Int. J. Approximate Reasoning. 2007;45(2):211–232. doi: 10.1016/j.ijar.2006.06.008. [DOI] [Google Scholar]
- 11.Peng H, Long F, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005;27(1):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- 12.Tsamardinos I, Borboudakis G. Permutation testing improves bayesian network learning. In: Balcázar JL, Bonchi F, Gionis A, Sebag M, editors. Machine Learning and Knowledge Discovery in Databases; Heidelberg: Springer; 2010. pp. 322–337. [Google Scholar]
- 13.Vergara JR, Estévez PA. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2013;24(1):175–186. doi: 10.1007/s00521-013-1368-0. [DOI] [Google Scholar]
- 14.Yang, H.H., Moody, J.: Data visualization and feature selection: new algorithms for nongaussian data. In: Advances in Neural Information Processing Systems, vol. 12, pp. 687–693 (1999)
- 15.Zhang JT. Approximate and asymptotic distributions of chi-squared type mixtures with applications. J. Am. Stat. Assoc. 2005;100:273–285. doi: 10.1198/016214504000000575. [DOI] [Google Scholar]