Abstract
We introduce new hybrid algorithms, DBSCAN Solver and Solution Partitioning Solver, which use quantum annealing for solving Vehicle Routing Problem (VRP) and its practical variant: Capacitated Vehicle Routing Problem (CVRP). Both algorithms contain important classical components, but we also present two other algorithms, Full QUBO Solver and Average Partitioning Solver, which can be run only on a quantum processing unit (without CPU) and were prototypes which helped us develop better hybrid approaches. In order to validate our methods, we run comprehensive tests using D-Wave’s Leap framework on well-established benchmark test cases as well as on our own test scenarios built based on realistic road networks. We also compared our new quantum and hybrid methods with classical algorithms - well-known metaheuristics for solving VRP and CVRP. The experiments indicate that our hybrid methods give promising results and are able to find solutions of similar or even better quality than the tested classical algorithms.
Keywords: VRP, Vehicle Routing Problem, Quantum annealing
Introduction
Vehicle Routing Problem (VRP) is an important combinatorial optimization problem in which the goal is to find the optimal setting of routes for a fleet of vehicles which should deliver some goods from a given origin (depot) to a given set of destinations (customers) [1]. It is a generalization of the Travelling Salesman Problem (TSP) (introduced first as the Truck Dispatching Problem [1]) in which one vehicle has to visit some number of destinations in the optimal way [2]. Both problems are proven to be NP-hard [3]. There exist the exact algorithms able to find optimal solutions in a reasonable time for relatively small instances, but generally, those problems are computationally difficult and the state-of-the-art approaches applied in practice are based on heuristics (constructive, improvement and composite) and metaheuristics [4, 5].
Recently, we can observe a noticeable progress in the development of quantum computing algorithms and it turned out that they may be particularly successful in solving combinatorial optimization problems, such as TSP and VRP [6]. The first quantum algorithms for TSP and VRP already exist and in the scientific literature we can find algorithms which can be run on gate-based quantum computers [7–17] as well as quantum annealing algorithms which can be run on adiabatic quantum computers [18–24].
In this paper, we present new methods for solving VRP and its more practical variant, CVRP (Capacitated Vehicle Routing Problem), in which all vehicles have a limited capacity. The algorithms introduced in this paper are based on quantum annealing, because due to the number of available qubits, those algorithms have currently a greater chance to give any practical improvement over classical algorithms.
We developed and present four algorithms: Full QUBO Solver (FQS), Average Partition Solver (AVS), DBSCAN Solver (DBSS) and Solution Partitioning Solver (SPS). The first and second one are designed only for solving VRP, DBSCAN solver can also solve CVRP if capacities of all vehicles are equal, SPS is able to solve CVRP with arbitrary capacities. It is also important to add that the last two methods are hybrid algorithms and they contain important components which should be run on classical processors.
In order to evaluate different algorithms for solving VRP using quantum annealing, we carried out series of experiments using D-Wave’s Leap framework [25] which contains implementations of built-in solvers and allows to implement new solvers. We used QBSolv [26] run on quantum processing unit (QPU) and simulating quantum annealing on classical processors (CPU), as well as hybrid solver [27] run on both, QPU and CPU.
Beside quantum algorithms, we also wanted to test and compare several well-known classical algorithms which gave good results in previous studies. Based on a comprehensive literature review [5] and further analysis, we selected 4 metaheuristics: based on simulated annealing [28], bee algorithm [29], evolutionary annealing [30] and recursive DBSCAN with simulated annealing [31], respectively.
In order to reliably compare different algorithms, we conducted experiments on well-established benchmark datasets [32, 33], as well as on datasets created by us, with realistic road networks (taken from the OpenStreetMap service) and artificially generated orders.
The rest of the paper is organized as follows: in Sect. 2, we describe in details all the quantum annealing solvers which we used in our experiments. Sections 3 and 4 present the design and results of our experiments, respectively. Section 5 outlines possible future research directions and concludes the paper.
CVRP Solvers Based on Quantum Annealing
In this section, we describe QUBO formulations and solvers which we developed for different variants of VRP: general VRP, CVRP with equal capacities and CVRP with arbitrary capacities. Before that, we introduce our notation and assumptions.
Notation and Assumptions
We assume that in each instance of VRP (or CVRP) we have a road network represented as a directed connected graph with vertices and edges. We also assume that the depots and destinations to which the orders of customers should be delivered are always located in vertices of the road network (in the case of benchmark instances and artificial networks, it may be even assumed that the road network is defined by locations of orders, while in the case of realistic road networks, real locations of orders are usually close enough to vertices determining the road network graph).
Let M be the number of available vehicles and N the number of orders. Let’s denote the vehicles as 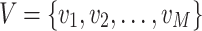 and the orders as
and the orders as 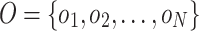 . We assume that there is always a depot located in one of the vertices (we also assume that destinations of orders are not located in the depot - such orders can be just served immediately so are not interesting) and all vehicles are initially located in the depot and should finish all routes back in the depot. Therefore, we have in total
. We assume that there is always a depot located in one of the vertices (we also assume that destinations of orders are not located in the depot - such orders can be just served immediately so are not interesting) and all vehicles are initially located in the depot and should finish all routes back in the depot. Therefore, we have in total 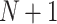 significant vertices and without any loss of generality, we can assume that our graph has exactly
significant vertices and without any loss of generality, we can assume that our graph has exactly 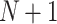 vertices and
vertices and  directed edges (we can just consider edges built based on the shortest paths between every pair of vertices in the original graph), destination of the order
directed edges (we can just consider edges built based on the shortest paths between every pair of vertices in the original graph), destination of the order 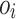 is located in the vertex i and the depot is located in the vertex
is located in the vertex i and the depot is located in the vertex 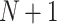 . We can also denote the cost of the direct travel from the vertex i (destination of the order
. We can also denote the cost of the direct travel from the vertex i (destination of the order  ) to the vertex j (destination of the order
) to the vertex j (destination of the order 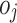 ) as
) as 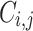 . We can also define
. We can also define  and
and  for
for 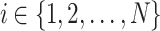 as the costs of direct travels from the depot to the destinations of orders and from the destinations of orders to the depot, respectively.
as the costs of direct travels from the depot to the destinations of orders and from the destinations of orders to the depot, respectively.
Let’s assume that  if in a given setting the vehicle number i visits the vertex number j as k-th location on its route (for
if in a given setting the vehicle number i visits the vertex number j as k-th location on its route (for  and
and 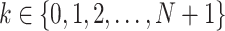 ), otherwise
), otherwise  . We always have
. We always have 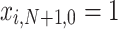 and
and 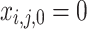 for
for  (the depot is always the first location), and if
(the depot is always the first location), and if  for some K then for
for some K then for 
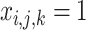 (each vehicle stays in the depot after reaching it).
(each vehicle stays in the depot after reaching it).
Full QUBO Solver
First, we defined a basic QUBO formulation used for solving VRP instances. The formulation is based on a similar formulation for TSP in [20].
Let’s define the binary function
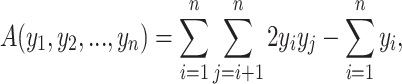 |
where 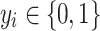 for
for  . It is easy to prove that the minimum value of
. It is easy to prove that the minimum value of  is equal to
is equal to  and this value can be achieved only if exactly one of
and this value can be achieved only if exactly one of  is equal to 1.
is equal to 1.
By definition of VRP, the problem of minimizing the total cost can be defined as minimizing the function:
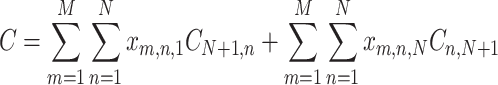 |
1 |
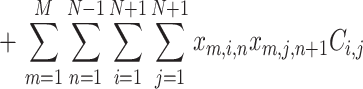 |
2 |
The first component of the sum C is a sum of all costs of travels from the depot - the first section of each cars’ route. The second is a cost of the last section of a route (to depot) in a special case when a single car serves all N orders (only in such a case the component can be greater than 0). The last part is the cost of all other sections of routes.
To assure that each delivery is served by exactly one vehicle and exactly once, and that each vehicle is in exactly one place at a given time, the following term (in which all A components are equal to  only for such desired cases) should be included in our QUBO formulation:
only for such desired cases) should be included in our QUBO formulation:
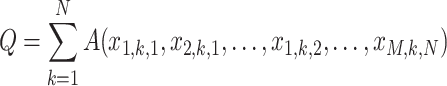 |
3 |
 |
4 |
By definition of VRP, QUBO representation of this optimization problem is
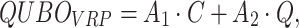 |
5 |
for some constants  and
and 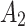 , which should be set to ensure that the solution found by quantum annealer minimizes Q (which should be
, which should be set to ensure that the solution found by quantum annealer minimizes Q (which should be  ) to ensure satisfiability of the aforementioned constraints (after running initial tests we set
) to ensure satisfiability of the aforementioned constraints (after running initial tests we set 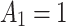 ,
, 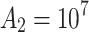 ).
).
Average Partition Solver (APS)
APS is a variation of Full QUBO Solver for which we decrease the number of variables for each vehicle by assuming that every vehicle serves approximately the same number of orders. This means, every vehicle can serve up to  deliveries, where A is the total number of orders divided by the number of vehicles and L is a parameter (called “limit radius”), which controls the number of orders. The QUBO formulation is the same as in case of Full QUBO Solver but the number of variables
deliveries, where A is the total number of orders divided by the number of vehicles and L is a parameter (called “limit radius”), which controls the number of orders. The QUBO formulation is the same as in case of Full QUBO Solver but the number of variables 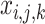 is lower (
is lower ( ), which simplifies computations.
), which simplifies computations.
DBSCAN Solver (DBSS)
DBSS allows us to use quantum approach combined with a classical algorithm. This particular algorithm is inspired by recursive DBSCAN [31]. DBSS uses recursive DBSCAN as a clustering algorithm with limited size of clusters. Then, TSP is solved for each cluster separately by FQS (just by assuming in the QUBO formulation that the number of vehicles equals 1). If the number of clusters is equal to the number of vehicles, the answer is known immediately. Otherwise, the solver runs recursively considering clusters as deliveries, so that each cluster contains orders which in the final result are served one after another without leaving the cluster. What is more, we concluded that by limit the total sum of weights of deliveries in clusters, this algorithm can solve CVRP if all capacities of vehicles are equal.
Solution Partitioning Solver (SPS)
While adding capacity constraints is not simple, we were looking for the solution that can use results generated by DBSS. Therefore, we developed SPS. It is a simple algorithm which divides TSP solution found by another algorithm (e.g., DBSS) into consecutive intervals, which are the solution for CVRP. The idea is as follows:
Let  be the TSP solution for N orders, let
be the TSP solution for N orders, let  be a capacity of the vehicle v, let
be a capacity of the vehicle v, let  be the sum of weights of orders
be the sum of weights of orders 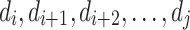 (in the order corresponding to TSP solution) and let
(in the order corresponding to TSP solution) and let 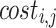 be the total cost of serving only orders
be the total cost of serving only orders  . Also, let
. Also, let 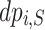 be the cost of the best solution for orders
be the cost of the best solution for orders 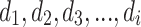 and for the set of vehicles S. Now, the dynamic programming formula for solving CVRP is given by:
and for the set of vehicles S. Now, the dynamic programming formula for solving CVRP is given by:
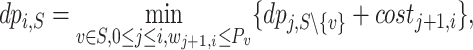 |
6 |
where 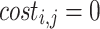 and
and 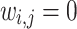 for
for 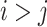 . Formula (6) returns a plenty of possible routes, but it also finds the optimal solution. We can speed it up by noticing that if two vehicles have the same capacity, it doesn’t matter which one of them we choose, but pessimistically, capacities can be pairwise distinct. We propose the following heuristic to optimize this solution:
. Formula (6) returns a plenty of possible routes, but it also finds the optimal solution. We can speed it up by noticing that if two vehicles have the same capacity, it doesn’t matter which one of them we choose, but pessimistically, capacities can be pairwise distinct. We propose the following heuristic to optimize this solution:
Instead of set S of vehicles, consider a sequence
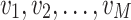 of vehicles and assume that we attach them to deliveries in such an order.
of vehicles and assume that we attach them to deliveries in such an order.- Now, our dynamic programming formula is given by:

7 - To count this dynamic effectively, we can observe that:
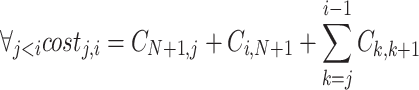
8 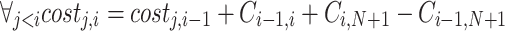
9 
10
So if we have counted dp for fixed k, then for counting dp for
11 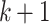 we can store all dp values for k and increase them, one by one (starting from
we can store all dp values for k and increase them, one by one (starting from 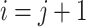 ), by a right side of Eq. 10. Using monotonic queue, we can get minimum in O(1) time.
), by a right side of Eq. 10. Using monotonic queue, we can get minimum in O(1) time.
We can now select some random permutations of vehicles and perform dynamic programming for each of them. The number of permutations can be regulated by additional parameter. With optimization of dynamic programming, the complexity of this algorithm is O(NMR), where R is the number of permutations.
The greatest limitation of SPS is that it considers only one TSP solution. Nonetheless, we observed that DBSS for more than one vehicle works in a similar way.
Design of Experiments
The goal of our experiments was to test and compare different formulations of QUBO (solving different variants of VRP) on different datasets and with different solvers and settings (number of qubits and quota of time on quantum processor). We ran them using D-Wave’s Leap platform [25] and its 2 solvers: qbsolv [26] and hybrid solver [27]. To run comprehensive and comparable experiments, we prepared several datasets:
Christofides1979 - a standard benchmark dataset for CVRP, well-known and frequently investigated by the scientific community [32, 33],
A dataset built by us based on a realistic road network of Belgium, acquired from the OpenStreetMap service.
Christofides1979 consists of 14 tests, where each test instance is described by three files. The first one provides the number of vehicles and their capacity (the same for all vehicles). The second file describes the orders, i.e. their coordinates in  dimensional plane and the demand. The last file reports the time matrix (times of travel between various vertices in a graph). For a purpose of running our experiments and compare the results, we selected only 9 out of 14 tests because in case of other tests some hybrid or classical algorithms were not able to find any good solutions. All the important parameters describing Christofides1979 instances are given in Table 1.
dimensional plane and the demand. The last file reports the time matrix (times of travel between various vertices in a graph). For a purpose of running our experiments and compare the results, we selected only 9 out of 14 tests because in case of other tests some hybrid or classical algorithms were not able to find any good solutions. All the important parameters describing Christofides1979 instances are given in Table 1.
Table 1.
Parameters of instances of Christofides1979 used in our experiments.
| Test name | Nr of vehicles | Capacity | Nr of orders |
|---|---|---|---|
| CMT11 | 7 | 200 | 120 |
| CMT12 | 10 | 200 | 100 |
| CMT13 | 11 | 200 | 120 |
| CMT14 | 11 | 200 | 100 |
| CMT3 | 8 | 200 | 100 |
| CMT6 | 6 | 160 | 50 |
| CMT7 | 11 | 140 | 75 |
| CMT8 | 9 | 200 | 100 |
| CMT9 | 14 | 200 | 150 |
In the case of the second dataset, we generated in total 51 tests. Each test was characterized by the number of orders. Table 2 presents a description of this dataset. Basically, it consists of 4 groups of test cases: small test (small number of orders), medium tests (medium number of orders), big tests (large number of order), mixed tests (various number of orders with some additional conditions).
Table 2.
Parameters and descriptions of tests
| Test | Number of orders | Description |
|---|---|---|
| small-0 | 2 | No further conditions |
| small-1 | 2 | |
| small-2 | 2 | |
| small-3 | 1 | |
| small-4 | 2 | |
| small-5 | 5 | |
| small-6 | 6 | |
| small-7 | 5 | |
| small-8 | 4 | |
| small-9 | 6 | |
| medium-0 | 20 | No further conditions |
| medium-1 | 26 | |
| medium-2 | 27 | |
| medium-3 | 24 | |
| medium-4 | 25 | |
| medium-5 | 25 | |
| medium-6 | 20 | |
| medium-7 | 14 | |
| medium-8 | 17 | |
| medium-9 | 15 | |
| big-0 | 52 | No further conditions |
| big-1 | 42 | |
| big-2 | 48 | |
| big-3 | 48 | |
| big-4 | 50 | |
| group1-1 | 42 | No further conditions |
| group1-2 | 54 | |
| range-6-1 | 47 | Magazines are at most 6 km from city center |
| range-6-2 | 50 | |
| range-8-12-1 | 50 | Magazines are at least 8 km and at most 12 km from city center |
| range-8-12-2 | 50 | |
| range-8-12-3 | 46 | |
| range-8-12-4 | 51 | |
| range-8-12-5 | 50 | |
| range-8-12-6 | 50 | |
| range-5-1 | 50 | Orders are at most 5 km from city center. Vehicles have capacity greater than total demand |
| range-5-1 | 50 | |
| range-3-1 | 37 | Orders are within 3 km from city center |
| range-3-2 | 29 | |
| range-4-1 | 9 | Orders are within 4 km from city center |
| range-4-2 | 7 | |
| range-4-75-1 | 75 | Orders are within 4 km from city center. We have 75 orders |
| range-4-75-2 | 75 | |
| range-4-100-1 | 100 | Orders are within 4 km from city center. We have 100 orders |
| range-4-100-2 | 100 | |
| range-4-150-1 | 150 | Orders are within 4 km from city center. We have 150 orders |
| range-4-150-2 | 150 | |
| range-4-200-1 | 200 | Magazines and orders are within 4 km from city center. We have 200 orders |
| range-4-200-2 | 200 | |
| clustered1-1 | 57 | In each one of four 1-km circles spread across the map, there is between 6 and 20 orders |
| clustered1-2 | 55 |
In every experiment, our programs computed the minimal cost of serving all orders. D-Wave’s quantum annealing machine is naturally nondeterministic, so are the returned results, so for every algorithm and on every test case we ran 5 experiments. The code of programs used in our experiments is publicly available at [34].
Results of Experiments
In this section, we present results of experiments conducted using QBSolv and hybrid solver built-in D-Wave’s Leap framework and using algorithms described in Sect. 3.
Full QUBO Solver (FQS)
First, we investigated Full QUBO Solver (FQS) on test cases small-0 - small-9. On every test except small-0, we ran experiments for 3 different numbers of vehicles (1, 2, 3) on quantum processor (FQS QPU [26]), its classical simulator (FQS CPU) and using a hybrid solver (FQS Hybrid [27]). On small-0 there were only 2 orders so we tested only 1, 2 vehicles.
As we can see in Table 3, QBSolv (FQS CPU and FQS QPU) exacerbates final results in test cases with more vehicles. For more vehicles, it can potentially generate the same solution as for less vehicles, because some vehicles can be just ignored. Solutions generated with hybrid solver (FQS Hybrid) confirm that. However, the size of QUBO makes the solutions with more vehicles unavailable for QBSolv. In hybrid solver, we have such a problem in only one case (small-9). However, in only 1 test case (small-3) QBSolv was able to improve the solution returned for smaller number of vehicles. In addition, in most cases QBSolv was not able to find a solution on QPU, the size of the instance and the number of the required variables and qubits was just too large. Also the required time of computations on QPU was worse than in case of CPU or hybrid approach. Therefore, we concluded that it doesn’t make sense to run more experiments on QPU for larger test cases (with more cars and more orders) and we conducted next tests only using QBSolv on CPU and using a hybrid solver.
Table 3.
Results on small and medium datasets
| Test | Vehicles | FQS CPU | FQS QPU | FQS Hybrid | APS CPU | APS Hybrid | DBSS CPU |
|---|---|---|---|---|---|---|---|
| small-0 | 1, 2 | 11286 | 11286 | 11286 | 11286 | 11286 | – |
| small-1 | 1 | 10643 | 10643 | 10643 | 10643 | 10643 | – |
| 2 | 10643 | 10643 | 10643 | 12379 | 12379 | – | |
| 3 | 10643 | – | 10643 | – | – | – | |
| small-2 | 1 | 21311 | 21311 | 21311 | 21311 | 21311 | – |
| 2 | 21311 | – | 21311 | 24508 | 24508 | – | |
| 3 | 22192 | – | 21311 | – | – | – | |
| small-3 | 1 | 18044 | 18044 | 18044 | 18044 | 18044 | – |
| 2 | 20819 | – | 18033 | 22193 | 22193 | – | |
| 3 | 22843 | – | 18033 | – | – | – | |
| small-4 | 1 | 15424 | 15424 | 15424 | 15424 | 15424 | – |
| 2 | 17364 | – | 15424 | 19472 | 19472 | – | |
| 3 | 17364 | – | 15424 | – | – | – | |
| small-5 | 1 | 10906 | 10906 | 10906 | 10906 | 10906 | – |
| 2 | 11676 | – | 10906 | 13480 | 13480 | – | |
| 3 | 11754 | – | 10906 | – | – | – | |
| small-6 | 1 | 20859 | 20859 | 20859 | 20859 | 20859 | – |
| 2 | 26735 | – | 20859 | 26735 | 26735 | – | |
| 3 | 27110 | – | 20859 | – | – | – | |
| small-7 | 1 | 18117 | 18117 | 18117 | 18117 | 18117 | – |
| 2 | 18710 | – | 18117 | 23114 | 23114 | – | |
| 3 | 21666 | – | 18117 | – | – | – | |
| small-8 | 1 | 12198 | 12198 | 12198 | 12198 | 12198 | – |
| 2 | 12494 | – | 12198 | 13282 | 13282 | – | |
| 3 | 13282 | – | 12198 | – | – | – | |
| small-9 | 1 | 19184 | 19184 | 19184 | 19184 | 19184 | – |
| 2 | 19848 | – | 19184 | 21438 | 21438 | – | |
| 3 | 21438 | – | 19848 | – | – | – | |
| medium-0 | 1 | 20774 | – | 21775 | 20774 | 21775 | 24583 |
| 2 | 36966 | – | 29879 | 25737 | 25217 | 27994 | |
| 3 | 28226 | 27237 | 34185 | ||||
| medium-1 | 1 | 29868 | – | 29423 | 29868 | 29423 | 27606 |
| 2 | 50639 | – | 39485 | 30820 | 31129 | 31346 | |
| 3 | – | – | – | 33376 | 32018 | 32588 | |
| medium-2 | 1 | 37045 | – | 35208 | 37045 | 35208 | 29442 |
| 2 | 55579 | – | 36511 | 33235 | 33163 | 32947 | |
| 3 | – | – | – | 36600 | 32569 | 34480 | |
| medium-3 | 1 | 30206 | – | 29422 | 30206 | 29422 | 31092 |
| 2 | 51787 | – | 35774 | 31428 | 30273 | 33790 | |
| 3 | – | – | – | 35994 | 33627 | 33712 | |
| medium-4 | 1 | 21257 | – | 20762 | 21257 | 20762 | 21435 |
| 2 | 34379 | – | 25470 | 22410 | 22722 | 22885 | |
| 3 | – | – | – | 23599 | 22176 | 25446 | |
| medium-5 | 1 | 23013 | – | 21642 | 23013 | 21462 | 21737 |
| 2 | 36149 | – | 22041 | 22775 | 23076 | 23403 | |
| 3 | – | – | – | 24899 | 22386 | 24336 | |
| medium-6 | 1 | 23804 | – | 24664 | 23804 | 23804 | 23926 |
| 2 | 35826 | – | 24490 | 24265 | 25178 | 25510 | |
| 3 | – | – | – | 27032 | 23364 | 25122 | |
| medium-7 | 1 | 22847 | – | 22847 | 22847 | 22847 | 28308 |
| 2 | 33441 | – | 26550 | 24331 | 24460 | 30482 | |
| 3 | – | – | – | 27156 | 27156 | 34064 | |
| medium-8 | 1 | 23843 | – | 14566 | 23843 | 14566 | 15575 |
| 2 | 20804 | – | 15931 | 14256 | 14808 | 15829 | |
| 3 | – | – | – | 15815 | 15466 | 16930 | |
| medium-9 | 1 | 12228 | – | 12395 | 12228 | 12395 | 12842 |
| 2 | 16606 | – | 13950 | 12321 | 12830 | 14926 | |
| 3 | – | – | – | 13221 | 13178 | 14619 |
For larger VRP instances (medium-0 - medium-9), we observed that the transition from one vehicle to two vehicles is difficult. QBSolv usually returns much worse results (there is only 1 exception, test case medium-8). For the hybrid solver, in only one case the result for two vehicles is better (medium-6) but the results are usually still better than in case of QBSolv. We also noticed that the order of deliveries in tests with one vehicle was not optimal for majority of test cases. Only the least instances - with up to 15 orders - seem to be solved optimally. An interesting thing is that differences between results for two vehicles and one vehicle are very discrepant and it is not caused by the number of orders. By analyzing full results, we concluded that for 2 vehicles the solvers divided deliveries evenhandedly and for some tests it is a good way to build the optimal solution. We came up with an idea that since solvers found only these solutions, we can ask them to optimize only that kind of solutions, so we implemented Average Partition Solver, which demands less qubits.
Average Partition Solver (APS)
We extended Full QUBO Solver with an option of changing the maximum difference between the number of deliveries attached to the vehicles, i.e., a deflection from the average number of deliveries per one vehicle. We found out experimentally that it should be 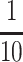 of the number of deliveries, which gives maximum difference in our test cases equal to 5. Having 1 vehicle, APS works exactly the same as Full QUBO Solver, so we ran experiments only for more vehicles (but we also included the results for 1 vehicle in Table 3, just for comparison).
of the number of deliveries, which gives maximum difference in our test cases equal to 5. Having 1 vehicle, APS works exactly the same as Full QUBO Solver, so we ran experiments only for more vehicles (but we also included the results for 1 vehicle in Table 3, just for comparison).
In most test cases, the results found using APS were better than results found by FQS. We can also notice that differences between results for 3 vehicles and results for 2 vehicles generated by APS are lower than the differences between results for 2 vehicles and 1 vehicle generated by FQS. However, in case of 3 vehicles, QBSolv on CPU still can’t find better solutions with only 2 vehicles. The hybrid solver can find better solutions in cases with 3 vehicles than in cases with only 2 vehicles in 4 (out of 10) test cases.
DBSCAN Solver (DBSS)
We can see in Table 3 that DBSS usually gives worse results than the APS, but we expected that it may change in case of tests with more orders thanks to utilizing the power of recursive DBSCAN.
Indeed, on big test cases with a larger number of orders, DBSS gives much better results than APS (Table 4). Additionally, DBSS can be run on larger instances and don’t need assumption that every vehicle serves approximately the same number of deliveries (as it is in case of APS).
Table 4.
Comparison of results for Average Partition Solver and DBSCAN Solver on big test cases.
| Vehicles | APS CPU | DBSS CPU | |
|---|---|---|---|
| big-0 | 1 | 80084 | 71594 |
| 2 | 97286 | 71051 | |
| big-1 | 1 | 157660 | 146828 |
| 2 | 206782 | 149200 | |
| big-2 | 1 | 168646 | 154105 |
| big-3 | 1 | 85873 | 62236 |
| big-4 | 1 | 156411 | 129279 |
Solution Partitioning Solver (SPS)
At the beginning, we tested SPS on test cases where all capacities are equal, in order to compare results with DBSS which can solve this problem. The results are presented in Table 5. In some cases, our solvers were not able to find the proper solutions (we mark such cases as “Not valid”) but in general, SPS outperformed DBSS.
Table 5.
Comparison of DBSCAN Solver and Solution Partitioning Solver (SPS) run on CPU on big test cases with various capacities.
| Vehicles | Capacity | SPS (CPU) | DBSS (CPU) | |
|---|---|---|---|---|
| big-0 | 2 | 100 | 70928 | 73508 |
| 2 | 85 | 72295 | 73189 | |
| 2 | 80 | 75150 | Not valid | |
| 3 | 100 | 71320 | 76717 | |
| 3 | 70 | 71251 | 78012 | |
| 3 | 55 | Not valid | 76807 | |
| 5 | 100 | 71740 | Not valid | |
| 5 | 50 | 78726 | 91066 | |
| 5 | 40 | 85976 | Not valid | |
| big-1 | 2 | 100 | 150608 | 158631 |
| 2 | 80 | 150608 | 152946 | |
| 2 | 65 | 150804 | 156188 | |
| 3 | 100 | 151525 | 153673 | |
| 3 | 60 | 153190 | 152854 | |
| 3 | 45 | 164055 | Not valid | |
| 5 | 100 | 151930 | 168789 | |
| 5 | 40 | 156242 | 165271 | |
| 5 | 30 | 174519 | 176935 |
Based on those experiments, we decided to test further only SPS and compare it with 4 classical algorithms - simulated annealing (SA), bee algorithm (BEE), evolutionary annealing (EA) and recursive DBSCAN with simulated annealing (DBSA). We ran next experiments with even more orders on mixed test cases generated by us (Table 2) and on benchmark datasets Christofides1979 (Table 1). The results are presented in Table 6 and Table 7.
Table 6.
Comparison of results achieved by Solution Partitioning Solver (SPS) and classical algorithms (SA - simulated annealing, BEE - Bee algorithm, EA - evolutionary annealing, DBSA - DBSCAN with simulated annealing) on a benchmark dataset Christofides79.
| Test name | SPS | SA | BEE | EA | DBSA |
|---|---|---|---|---|---|
| CMT11 | 25.54 | 23.62 | 36.18 | 16.52 | 19.94 |
| CMT12 | 26.84 | 53.06 | 20.24 | 20.68 | 21.37 |
| CMT13 | 25.97 | 86.72 | 34.66 | 35.05 | 19.44 |
| CMT14 | 26.83 | 52.52 | 20.23 | 20.23 | 22.8 |
| CMT3 | 25.13 | 48.3 | 28.38 | 28.82 | – |
| CMT6 | 17.58 | 48.3 | 15.42 | 28.82 | 15.82 |
| CMT7 | 29.42 | 41.4 | 27.89 | 31.68 | 23.18 |
| CMT8 | 26.5 | 51.16 | 26.67 | 28.09 | 19.4 |
| CMT9 | 34.14 | 76.34 | 44.25 | 42.81 | – |
Table 7.
Results of Solution Partitioning Solver compared with results for classical algorithms run on artificially generated test cases.
| Type | Deliveries | SPS | Simul. Ann. | Bee | Evolution | |
|---|---|---|---|---|---|---|
| clustered1-1 | Average | 57 | 69850 | 66379 | 60876 | 48923 |
| Best | 57 | 69080 | 52119 | 56358 | 48152 | |
| clustered1-2 | Average | 55 | 77173 | 74341 | 81438 | 54719 |
| Best | 55 | 75530 | 59947 | 68772 | 53490 | |
| group1-1 | Average | 42 | 158919 | 156217 | 153495 | 137989 |
| Best | 42 | 155388 | 146526 | 142774 | 135593 | |
| group1-2 | Average | 54 | 171732 | 145380 | 145325 | 137626 |
| Best | 54 | 165043 | 141065 | 140947 | 136307 | |
| range-6-1 | Average | 47 | 71670 | 68003 | 67234 | 59937 |
| Best | 47 | 68459 | 62312 | 64404 | 59827 | |
| range-6-2 | Average | 50 | 80490 | 84380 | 83915 | 73651 |
| Best | 50 | 79640 | 79574 | 85917 | 73051 | |
| range-8-12-1 | Average | 50 | 142008 | 146553 | 142835 | 129069 |
| Best | 50 | 140170 | 136369 | 127372 | 126555 | |
| range-8-12-2 | Average | 50 | 146798 | 137628 | 145332 | 129048 |
| Best | 50 | 143598 | 135493 | 136776 | 128803 | |
| range-8-12-3 | Average | 46 | 105544 | 105051 | 98366 | 92792 |
| Best | 46 | 101577 | 99004 | 94423 | 91921 | |
| range-8-12-4 | Average | 51 | 147993 | 143309 | 148900 | 128316 |
| Best | 51 | 145559 | 140088 | 128575 | 124405 | |
| range-8-12-5 | Average | 50 | 146719 | 143516 | 145685 | 134162 |
| Best | 50 | 143993 | 139784 | 139796 | 133245 | |
| range-8-12-6 | Average | 50 | 146984 | 148194 | 150121 | 136326 |
| Best | 50 | 141467 | 138781 | 139400 | 134692 | |
| range-5-1 | Average | 50 | 81728 | 68900 | 69052 | 67896 |
| Best | 50 | 72527 | 67984 | 68022 | 67691 | |
| range-5-2 | Average | 50 | 81759 | 69342 | 68564 | 67981 |
| Best | 50 | 76868 | 67958 | 67780 | 67716 | |
| range-3-1 | Average | 37 | 39790 | 37268 | 36260 | 29326 |
| Best | 50 | 36851 | 32877 | 35650 | 29180 | |
| range-3-2 | Average | 29 | 34361 | 39336 | 34068 | 30497 |
| Best | 50 | 33548 | 35340 | 32908 | 30466 | |
| range-4-1 | Average | 50 | 21559 | 21604 | 21604 | 21604 |
| Best | 50 | 21317 | 21604 | 21604 | 21604 | |
| range-4-2 | Average | 50 | 18044 | 18498 | 18640 | 18498 |
| Best | 50 | 18044 | 18498 | 18497 | 18498 | |
| range-4-100-1 | Average | 100 | 84916 | 106625 | 118550 | 85346 |
| Best | 50 | 81303 | 98522 | 112389 | 84514 | |
| range-4-100-2 | Average | 100 | 91527 | 105538 | 127744 | 86538 |
| Best | 50 | 88566 | 97312 | 111513 | 84750 | |
| range-4-150-1 | Average | 150 | 90394 | 98711 | 119547 | 101126 |
| Best | 50 | 88040 | 91972 | 108442 | 100195 | |
| range-4-150-2 | Average | 150 | 112539 | 118351 | 171620 | 125444 |
| Best | 50 | 110104 | 110401 | 170164 | 121462 | |
| range-4-200-1 | Average | 200 | 112618 | 124269 | 179239 | 139991 |
| Best | 50 | 111259 | 120510 | 171530 | 137684 | |
| range-4-200-2 | Average | 200 | 135243 | 158634 | 223262 | 202373 |
| Best | 50 | 131349 | 135931 | 203352 | 194707 | |
| range-4-75-1 | Average | 75 | 62439 | 60423 | 65381 | 52701 |
| Best | 50 | 60283 | 56337 | 62051 | 51846 | |
| range-4-75-2 | Average | 75 | 72077 | 76964 | 85849 | 60753 |
| Best | 50 | 70403 | 71164 | 84140 | 60168 |
Conclusion and Future Research Directions
We introduced new hybrid algorithms for solving VRP and CVRP and ran tests using D-Wave’s Leap framework on well-established benchmark test cases and on our own test scenarios built based on realistic road networks. We also compared our new quantum and hybrid methods with classical algorithms - well-known metaheuristics for solving VRP and CVRP. The results indicate that our hybrid methods give promising results and are able to find solutions of a similar quality to the tested classical algorithms.
Our primary future research direction is extending QUBO formulations to solve even more realistic variant of VRP - the Vehicle Routing Problem with Time Windows (VRPTW). Also, we are planning to compare our hybrid algorithms with even more classical algorithms for solving VRP and its variants.
Acknowledgment
The presented research was carried out within the frame of the project “Green LAst-mile Delivery” (GLAD) realized at the University of Warsaw with the project partners: Colruyt Group, University of Cambridge and Technion. The project is supported by EIT Food, which is a Knowledge and Innovation Community (KIC) established by the European Institute for Innovation & Technology (EIT), an independent EU body set up in 2008 to drive innovation and entrepreneurship across Europe.
Contributor Information
Valeria V. Krzhizhanovskaya, Email: V.Krzhizhanovskaya@uva.nl
Gábor Závodszky, Email: G.Zavodszky@uva.nl.
Michael H. Lees, Email: m.h.lees@uva.nl
Jack J. Dongarra, Email: dongarra@icl.utk.edu
Peter M. A. Sloot, Email: p.m.a.sloot@uva.nl
Sérgio Brissos, Email: sergio.brissos@intellegibilis.com.
João Teixeira, Email: joao.teixeira@intellegibilis.com.
Michał Borowski, Email: m.borowski@mimuw.edu.pl.
Paweł Gora, Email: p.gora@mimuw.edu.pl.
Katarzyna Karnas, Email: k.karnas@mimuw.edu.pl.
Mateusz Błajda, Email: m.blajda@mimuw.edu.pl.
Krystian Król, Email: k.krol@mimuw.edu.pl.
Artur Matyjasek, Email: a.matyjasek@mimuw.edu.pl.
Damian Burczyk, Email: d.burczyk@mimuw.edu.pl.
Miron Szewczyk, Email: m.szewczyk@mimuw.edu.pl.
Michał Kutwin, Email: m.kutwin@mimuw.edu.pl.
References
- 1.Dantzig GB, Ramser JH. The truck dispatching problem. Manage. Sci. 1959;6(1):80–91. doi: 10.1287/mnsc.6.1.80. [DOI] [Google Scholar]
- 2.Kirkman T. XVIII. On the representation of polyedra. Philos. Trans. R. Soc. Lond. 1856;146:413–418. [Google Scholar]
- 3.Karp RM. Reducibility among combinatorial problems. In: Miller RE, Thatcher JW, Bohlinger JD, editors. Complexity of Computer Computations. Boston: Springer; 1972. pp. 85–103. [Google Scholar]
- 4.Laporte G, Toth P, Vigo D. Vehicle routing: historical perspective and recent contributions. EURO J. Transp. Logist. 2013;2:1–4. doi: 10.1007/s13676-013-0020-6. [DOI] [Google Scholar]
- 5.Gora, P., et al.: On a road to optimal fleet routing algorithms: a gentle introduction to the state-of-the-art. In: Smart Delivery Systems, Solving Complex Vehicle Routing Problems, Intelligent Data-Centric Systems, pp. 37–92 (2020)
- 6.Zahedinejad, E., Zaribafiyan, A.: Combinatorial optimization on gate model quantum computers: a survey (2017). https://arxiv.org/abs/1708.05294
- 7.Feng X, Wang Y, Ge H, Zhou C, Liang Y. Quantum-inspired evolutionary algorithm for travelling salesman problem. In: Liu G, Tan V, Han X, editors. Computational Methods. Dordrecht: Springer; 2006. pp. 1363–1367. [Google Scholar]
- 8.Beheshti AK, Hejazi SR. A novel hybrid column generation-metaheuristic approach for the vehicle routing problem with general soft time window. Inf. Sci. 2015;316:598–615. doi: 10.1016/j.ins.2014.11.037. [DOI] [Google Scholar]
- 9.Beheshti AK, Hejazi SR. A quantum evolutionary algorithm for the vehicle routing problem with delivery time cost. Int. J. Ind. Eng. Prod. Res. 2014;25(4):287–295. [Google Scholar]
- 10.Greenwood, G.W.: Finding solutions to NP problems: philosophical differences between quantum and evolutionary search algorithms. In: Proceedings of the 2001 Congress on Evolutionary Computation (2001)
- 11.Zeng K, Peng G, Cai Z, Huang Z, Yang X. A hybrid natural computing approach for the VRP problem based on PSO, GA and quantum computation. In: Yeo SS, Pan Y, Lee Y, Chang H, editors. Computer Science and its Applications. Dordrecht: Springer; 2012. pp. 23–28. [Google Scholar]
- 12.Srinivasan, K., Satyajit, S., Behera, B.K., Panigrahi, P.K.: Efficient quantum algorithm for solving travelling salesman problem: an IBM quantum experience (2018). https://arxiv.org/abs/1805.10928
- 13.Cui, L., Wang, L., Deng, J., Zhang, J.: A new improved quantum evolution algorithm with local search procedure for capacitated vehicle routing problem. Math. Probl. Eng. (2013). 10.1155/2013/159495. Article ID 159495
- 14.Zhang, J., Wang, W., Zhao, Y., Cattani, C.: Multiobjective quantum evolutionary algorithm for the vehicle routing problem with customer satisfaction. Math. Probl. Eng. (2012). 10.1155/2012/879614. https://www.hindawi.com/journals/mpe/2012/879614, Article ID 879614
- 15.Dai H, Yang Y, Li H, Li C. Bi-direction quantum crossover-based clonal selection algorithm and its applications. Expert Syst. Appl. 2014;41(16):7248–7258. doi: 10.1016/j.eswa.2014.05.053. [DOI] [Google Scholar]
- 16.You, X., Miao, X., Liu S.: Quantum computing-based Ant Colony Optimization algorithm for TSP. In: 2nd International Conference on Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, 2009, pp. 359–362 (2009). 10.1109/PEITS.2009.5406879
- 17.Wang Y, et al. A novel quantum swarm evolutionary algorithm and its applications. Neurocomputing. 2007;70:633–640. doi: 10.1016/j.neucom.2006.10.001. [DOI] [Google Scholar]
- 18.Martonák R, Santoro GE, Tosatti E. Quantum annealing of the traveling-salesman problem. Phys. Rev. E. 2004;70:057701. doi: 10.1103/PhysRevE.70.057701. [DOI] [PubMed] [Google Scholar]
- 19.Santoro GE, Tosatti E. Optimization using quantum mechanics: quantum annealing through adiabatic evolution. J. Phys. A Math. Gen. 2006;39(36):R393. doi: 10.1088/0305-4470/39/36/R01. [DOI] [Google Scholar]
- 20.Lucas A. Ising formulations of many NP problems. Front. Phys. 2014;2:5. doi: 10.3389/fphy.2014.00005. [DOI] [Google Scholar]
- 21.Smelyanskiy, V.N., et al.: A Near-Term Quantum Computing Approach for Hard Computational Problems in Space Exploration (2012)
- 22.Kieu, T.D.: Quantum adiabatic computation and the travelling salesman problem (2006). https://arxiv.org/abs/quant-ph/0601151
- 23.Feld, S., et al.: A hybrid solution method for the capacitated vehicle routing problem using a quantum annealer. In: Frontiers in ICT, vol. 6 (2019). https://www.frontiersin.org/articles/10.3389/fict.2019.00013/full
- 24.Feld, S., et al.: A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer (2019)
- 25.D-Wave’s Leap project. https://www.dwavesys.com/take-leap. Accessed 7 Feb 2020
- 26.https://docs.ocean.dwavesys.com/projects/qbsolv/en/latest. Accessed 7 Feb 2020
- 27.https://docs.ocean.dwavesys.com/projects/hybrid/en/latest. Accessed 7 Feb 2020
- 28.Tavakkoli-Moghaddam R, Safae N, Kah MMO, Rabbani M. A new capacitated vehicle routing problem with split service for minimizing fleet cost by simulated annealing. J. Franklin Inst. 2007;344(5):406–425. doi: 10.1016/j.jfranklin.2005.12.002. [DOI] [Google Scholar]
- 29.Szeto WY, Yongzhong WY, Ho SC. An artificial bee colony algorithm for the capacitated vehicle routing problem. Eur. J. Oper. Res. 2011;215(1):126–135. doi: 10.1016/j.ejor.2011.06.006. [DOI] [Google Scholar]
- 30.Bañosa R, Ortega J, Gil C, Márquez AL, Toroc F. A hybrid meta-heuristic for multi-objective vehicle routing problems with time windows. Comput. Ind. Eng. 2013;65(2):286–296. doi: 10.1016/j.cie.2013.01.007. [DOI] [Google Scholar]
- 31.Bujel, K., Lai, F., Szczecinski, M., So, W., Fernandez, M.: Solving high volume capacitated vehicle routing problem with time windows using recursive-DBSCAN clustering algorithm. arXiv:1812.02300v2
- 32.http://www.vrp-rep.org/datasets/item/2014-0002.html. Accessed 7 Feb 2020
- 33.Christofides N, Mingozzi A, Toth P. The vehicle routing problem. In: Christofides N, Mingozzi A, Toth P, Sandi C, editors. Combinatorial Optimization. Chichester: Wiley; 1979. pp. 315–338. [Google Scholar]
- 34.Code used in our experiments. https://github.com/xBorox1/D-Wave-Leap---CVRP/tree/master/vrp. Accessed 7 Feb 2020


