Amino Acid and Oligopeptide Effects on Calcium Carbonate Solutions

Abstract

Biological organisms display sophisticated control of nucleation and crystallization of minerals. In order to mimic living systems, deciphering the mechanisms by which organic molecules control the formation of mineral phases from solution is a key step. We have used computer simulations to investigate the effects of the amino acids arginine, aspartic acid, and glycine on species that form in solutions of calcium carbonate (CaCO₃) at lower and higher levels of supersaturation. This provides net positive, negative, and neutral additives. In addition, we have prepared simulations containing hexapeptides of the amino acids to consider the effect of additive size on the solution species. We find that additives have limited impact on the formation of extended, liquid-like CaCO₃ networks in supersaturated solutions. Additives control the amount of (bi)carbonate in solution, but more importantly, they are able to stabilize these networks on the time scales of the simulations. This is achieved by coordinating the networks and assembled additive clusters in solutions. The association leads to subtle changes in the coordination of CaCO₃ and reduced mobility of the cations. We find that the number of solute association sites and the size and topology of the additives are more important than their net charge. Our results help to understand why polymer additives are so effective at stabilizing dense liquid CaCO₃ phases.

Short abstract

Simulations reveal the mechanisms by which organic additives stabilize calcium (bi)carbonate liquid phases.

Introduction

While there have been major advances in the production of synthetic, bioinspired materials in recent years,¹⁻³ the degree of control that biological organisms can exercise in engineering hard, mineralized tissues with distinct functionalities and morphologies far surpasses anything available using current technologies. Three crystalline polymorphs of calcium carbonate are found in biology: calcite, aragonite and vaterite, in order of decreasing thermodynamic stability.⁴⁻⁶ These ordered materials are often formed after the initial deposition of amorphous calcium carbonate (ACC)^7,8 (which was suggested in ref (9) to exhibit short-range coordination geometries reminiscent of aragonite or calcite). Experiments examining the growth of sea urchin spicules^10,11 and corals¹² have shown that calcite and aragonite formation is preceded by hydrated ACC phases, which dehydrate before crystallization.

Organic molecules are found in mineralized tissues throughout biology, usually in the form of an organic matrix or as inclusions.⁴ For example, ∼5 wt % of nacre is made from proteins and polysaccharides that glue hexagonal aragonite tablets together and give the material increased toughness and impact resistance.¹³ In calcitic materials, the organic matter can inhibit crack propagation.¹⁴ However, the organic material is not present simply to improve the mechanical function of biominerals. Proteins and peptides can control nucleation and crystal growth processes.^9,15 Certain proteins, such as the sea urchin matrix protein LSM34, are essential for the formation of calcite spicules.¹⁵⁻¹⁷ Simulations have shown that the avian egg-shell protein, Ovocleidin-17, hastens the formation of calcite from initially amorphous nanoparticles.¹⁸ Proteins and peptides adsorbed onto a β-chitin matrix are thought to selectively nucleate nacreous aragonite in mollusk shells.^19,20 Intrinsically disordered proteins (IDPs), which are present in nacre, self-assemble during mineralization and selectively precipitate vaterite or aragonite.^21,22 The inherent conformational freedom associated with IDPs appears to modulate the mechanisms associated with both mineralization and the resulting mineral phases.²³⁻²⁶ Protein control of the amount of impurities, such as Mg(II), in amorphous phases may be an important step in aragonite polymorph selection.²⁷ Inspired by these examples in nature, synthetic additives have been designed and applied to control the morphology and rate of crystal growth.^28,29 Other synthetic additives appear to inhibit crystallization. Polyaspartic acid (Poly(ASP)) in solution, for example, retarded the transformation of amorphous liquid and solid phases of calcium carbonate into crystalline ones.³⁰⁻³² Although a wealth of research has been dedicated to understanding how organic additives control the nucleation and growth of calcium carbonate, these mechanisms remain surprisingly unclear.

De Yoreo et al.³³ presented possible pathways to crystals from initially free ions in solution that may involve stable or metastable particles. In the case of calcium carbonate, nanometer-sized clusters,^34,35 liquids,^30,36−38 solid amorphous^10−12,39 and crystalline^40,41 particles have all been presented in pathways to the formation of macroscopic crystalline materials. The initial formation of a CaCO₃ phase from ions in solution has been intensely investigated. Several studies^37,42,43 support the notion that, at mild supersaturation, the solution speciation is consistent with a classical picture of nucleation. The solution contains free Ca²⁺ and CO₃^2– ions, ion pairs, and occasionally larger ion clusters, which form stochastically but are ultimately transient, unstable species. Alternatively, prenucleation clusters (PNCs) of ions were suggested^30,34,44 as the thermodynamically stable solute species. Simulations revealed^35,45,46 that these clusters have a dynamic size distribution and that their constituent ions have a high degree of translational and rotational freedom. The prenucleation cluster pathway proposes that, on increasing supersaturation, the internal mobility of ions within PNCs decreases and an interface is formed with the solution. The resulting species aggregate to minimize surface tension and form a macroscopic amorphous phase.³²

We can study the control exerted by proteins and peptides on nucleation and crystallization by investigating the activities of their fundamental building blocks: amino acids. Picker et al.⁴⁷ performed a complete survey of the effect of the 20 protein-forming amino acids on various aspects of calcium carbonate nucleation in titration experiments at pH 9.75. Aspartic acid (ASP) influences all stages of nucleation by increasing the amount of bound calcium before nucleation, increasing the induction time for nucleation, and favoring the growth of calcite by inducing a less-stable intermediate phase. Glutamic acid affected the amount of free calcium in solution before nucleation the most, while serine and ASP were best at delaying nucleation. Glycine (GLY) and ASP were the only amino acids that significantly affected the solubility of nucleated phases.⁴⁷ Simulations performed on ASP suggest that this amino acid stabilizes amorphous CaCO₃ nanoparticles.^45,46 Both citrate and ASP delay nucleation, but not necessarily by complexation to cations.⁴⁶ Simulations suggest that the binding of ASP (in the protonation state adopted here) to ACC is through the amine group rather than the carboxylate group as might be expected.⁴⁸ Indeed, other advanced sampling simulations suggest that the binding energies of calcium carbonate ion pairs to guanidinium and carboxylate groups are approximately equal.⁴⁹ Experiments confirmed that both ASP and GLY extend the lifetime of amorphous precursors.⁵⁰ Adsorption of amino acids to growing crystalline surfaces can influence both the morphology and phase of the crystalline calcium carbonate produced.^51,52

The chemical activity of additives may be key to controlling the nucleation and growth of calcium carbonate. However, particularly for templated growth, we might also expect the size and topology of any organic matrix to be as important for nucleation and growth control. This has been shown for calcium oxalate growth, where oligopeptide chain lengths from 5 to 20 monomers of glutamic acid clearly affected the stabilities and morphologies of the resulting crystalline phases.⁵³ Simulations showed that oligo-glutamates organized cations in solution before nucleation. This may be the cause of the dependence of crystal morphologies on oligomer chain length.⁵⁴ Experimental studies of artificial peptide additives suggest that the peptide’s charge and folding properties in solution control crystallization.^55,56 Molecular simulations revealed that the strength of adsorption of the peptide/polymer to calcite is influenced by the flexibility of the molecule backbone. This may have consequences for crystal templating.⁵⁷

Computer simulations have provided much insight into the early stages of phase separation in a range of systems.⁵⁸⁻⁶¹ Here, we report molecular dynamics (MD) simulations that investigate the effect of three amino acids (AAs) on calcium carbonate aqueous solutions. These were arginine (ARG), ASP, and GLY, the chemical structures for which are provided in Figure 1. The protonation state for each molecule was chosen for a solution where the pH was ∼9. This provided molecules that were positively charged (ARG), negatively charged (ASP), and neutral (GLY) overall. In addition, we explored the effect of additive size by simulating oligomers of the three AAs containing six monomers bonded through peptide links, i.e., hexapeptides of ARG, ASP, and GLY which we label 6ARG, 6ASP, and 6GLY, respectively.

Figure 1.

Amino acid molecules in the speciation state adopted in this work.

Computational Methods

Typically, experiments studying CaCO₃ nucleation are performed under basic conditions and at millimolar ion concentrations. Limited simulation times mean that we are unlikely to observe the full effect of additives on CaCO₃ species during nucleation under these conditions. Therefore, we have simulated ion concentrations that approach the experimental supersaturations and also higher supersaturations where earlier simulations^35,36 showed that liquid-like ionic networks are maintained in the steady state. Simulations will be referred to as low salinity or high salinity and indicated by a subscript “LS” and “HS”, respectively, in system labels.

Table 1 provides the initial composition for all systems. The number of carbonate and bicarbonate ions were chosen to neutralize the total calcium charge, setting c(CO₃^2–)/c(HCO₃^–) to give a pH of 10.3, according to the Henderson–Hasselbalch equation. At this pH, the NH₃⁺ groups of AAs become susceptible to deprotonation. Our earlier simulations initiated with a fixed number of ions showed consistent reductions in pH (cf. the initial configurations) because of preferential binding of carbonate to calcium. The simulations reported here indicate that the steady-state pH of solutions at low salinity was 9.4–9.8; hence, the adopted speciation states for the AAs are sensible. Oligopeptides were formed as a peptide chain of six AAs and the concentration of oligopeptides was a fraction of the AA concentration to ensure that we retained the same numbers of end-chain organic functional groups. Na and Cl ion concentrations were chosen to ensure that the ionic strength (I) in all simulations was 0.11 M (low salinity) and 2.2 M (high salinity) at t = 0, and that the total charge in simulation cells was zero. Ions were initially dispersed in solution by randomly populating cubic cells before adding water.

Table 1. System Composition for Low and High Salinity Simulations^a.

system	n(Na+)	n(Cl–)	n(add)	n(Ca2+)	n(CO32–)	n(HCO3–)	n(H2O)	c(Ca2+) [mM]	c(C) [mM]	c(add) [mM]
CONLS	23	23	0	47	30	34	100 000	26	36	0
ARGLS	5	23	18	47	30	34	100 000	26	36	10
ASPLS	23	5	18	47	30	34	100 000	26	36	10
GLYLS	23	23	18	47	30	34	100 000	26	36	10
CONHS	23	23	0	100	64	72	10 000	560	760	0
ARGHS	5	23	18	100	64	72	10 000	560	760	100
ASPHS	23	5	18	100	64	72	10 000	560	760	100
GLYHS	23	23	18	100	64	72	10 000	560	760	100
6ARGHS	5	23	3	100	64	72	10 000	560	760	17
6ASPHS	23	5	3	100	64	72	10 000	560	760	17
6GLYHS	23	23	3	100	64	72	10 000	560	760	17

^an(X) and c(X) indicate the number and concentration, respectively, of ion X.

The force field of Demichelis et al.³⁵ was employed in the current work. This accurately captures the energetics of ion solvation and uses flexible SPC/Fw water.⁶² The intramolecular interactions for l-amino acids and l-oligopeptides were modeled using the (ff14SB) AMBER force field.⁶³ Accurately capturing the physical interactions between atoms at the organic/inorganic interface when combining existing force fields is not straightforward. Simple mixing rules (e.g., Lorentz–Berthelot mixing) offer an inexpensive route to generating intermolecular potentials but often lead to incorrect forces between atoms.^64,65 These rules rely on the balance of short-range van der Waals/Pauli repulsion and long-range electrostatic force contributions being approximately the same in both the adopted inorganic and organic force fields. This is rarely the case for mineral-organic systems. Fitting classical potentials to data from ab initio calculations is preferable but is computationally demanding enough to render a study of multicomponent systems intractable over reasonable time scales. Here, we used a generic procedure to fit the intermolecular terms between the Demichelis and AMBER force fields that has been shown to reproduce, for example, the correct adsorption energies for the binding of organic molecules to mineral surfaces, when compared to ab initio calculations. Intermolecular potentials between the organic atoms and all other solute atoms were fitted using this “Schröder method”, as described by Freeman et al.,⁶⁶ while the organic–water interaction parameters were calculated using the standard Lorentz–Berthelot rules. Example force field input files are included in the Supporting Information (SI).

The DL_POLY 4.03 MD simulation package^67,68 was used throughout. Simulations were run with the velocity Verlet algorithm and a time step of 1 fs (configurations were stored every 1 ps). Simulations were performed at 298 K and 1 atm using a Nosé–Hoover⁶⁹ thermostat and barostat with 0.1 and 1.0 ps relaxation times, respectively. The number of atoms and chemical bonds were fixed in the simulations. Electrostatic energies were calculated using the smooth particle mesh Ewald method,⁷⁰ and three-dimensional periodic boundaries were implemented. A 200 ps MD simulation was performed with all solute atoms frozen to equilibrate the box volume. The final configuration was used to initiate MD simulations where all atoms were mobile. The solute cluster sizes, free ion concentrations, and coordination numbers were monitored in order to identify when a steady state had been achieved. A total of 20 and 60 ns trajectories—with the final 2 or 10 ns used to calculate equilibrium averages—were generated for low- and high-salinity systems, respectively.

The potential of mean force (PMF) for monomer–monomer association in solution was measured using umbrella sampling⁷¹ (US) with the PLUMED plugin.⁷² Approximately 50 US windows were used to sample a monomer separation reaction coordinate from 1.5–24 Å in 0.5 Å steps, and extra windows were added to sample high-energy regions of the reaction coordinate accurately. A simple harmonic potential, with a force constant of at least 12 k_BN_AT (where k_B is the Boltzmann constant, N_A is Avogadro’s constant, and T is temperature), was applied to restrain the distance between monomers. Simulations in each US window were performed for at least 1 ns and the WHAM program⁷³ was used to calculate free-energy changes in the reaction coordinate space. Probability distributions were monitored to ensure proper sampling of the reaction coordinate between adjacent US windows. These simulations were performed at 298 K and 1 atm and monomer concentrations were 10 mM. Na and Cl ions (also at 10 mM) were added to maintain a background electrolyte concentration. Coordination numbers between specific atom types were monitored using the function defined in PLUMED, which goes smoothly from one to zero over a range of atom separation distances. This was set using the region of the first and second minima in radial pair distribution functions to define the switching function parameters.

Clusters were defined as collections of solute ions or molecules where interatomic distances were within 3.5 Å. The position of the first peak in the Ca–O(H₂) radial distribution functions (RDFs) for free ions and ions in liquidlike amorphous calcium carbonate is less than this distance (at ∼2.5 Å). The cutoff adopted ensures that fluctuations in the number and size of clusters are minimized. Clusters were defined in terms of the number of ions or molecules (N) and cluster size probability distributions (f (N)) were calculated. In addition, the average number of clusters where N = 1 allowed the calculation of free ion/molecule concentrations, ionic strengths, and pH at equilibrium. This approach provides a liberal estimate for the number of “free” ions or molecules in solution, given that solvent-separated and solvent-shared coordinated ions are considered to be free. Self-diffusion coefficients (D) were calculated using Einstein’s relation:

1

where N is the total number of atoms of interest in a cluster and r(t) are the Cartesian coordinates as a function of time t. We calculated the value of D for the center of mass of clusters and subtracted this from the diffusion rate of ions to measure the diffusion of ions and molecules within clusters. The free-energy changes for ion pairing in low-salinity simulations were estimated using the activity of the ions once a steady state was reached. The activity coefficient (γ) values were obtained using the extended Debye–Hückel equation:

2

This model for ion activities was chosen because the I values at the steady state were of the order of tens of millimoles. Here, A = 1.82 × 10⁶(εT)^−3/2 and B = 50.3(εT)^−1/2, where ε is the relative permittivity of SPC/Fw water (79.63) and T is the temperature (298 K) of the simulations. z is the magnitude of the ionic charge, and a is a measure of the radii of solvated ions.

Results and Discussion

Low Salinity

Approximately 10 ns of simulation time were required to reach a steady state in systems at low salinity. The concentrations of free ions at the steady state (see Table S1 in the SI) decreased in all systems, because of ion binding in solution. This was reflected in a change of ionic strength, which decreased to 25%–30% of the initial value. The concentration of calcium ions, c(Ca²⁺), in CON_LS (i.e., the control system; see Table S1) was slightly higher (5–9 mM) than recent estimates for the limit of solution stability (3–5 mM) in pure calcium carbonate solutions,³⁹ where the free-energy barrier to phase separation goes to zero. However, the free-energy landscape for this process in microscopic, thermodynamically closed systems is a function of both the size and composition of the initial state;⁷⁴ therefore, it is not surprising that concentrations beyond the limit of solution stability in the macroscopic case are found. Approximately 50% of the total (bi)carbonate was bound in CON_LS at the steady state, but this was higher in the AA systems, most notably in ARG_LS, where only ∼17% of the total (bi)carbonate was free in solution by the end of the simulation. [Note: both here and hereafter, the term “(bi)carbonate” refers to both carbonate and bicarbonate ions.]

The fraction of bound species at low salinity are presented in Figure 2. By the end of the simulation, 60%–80% of the calcium was bound, which is consistent with typical experiments^35,47 and simulation studies.³⁵ Carbonate ions were preferentially bound to calcium over bicarbonate anions, and Na and Cl ions remained dispersed (using the definition of free ions adopted here) in solution. The preferential binding of carbonate over bicarbonate led to a reduction of the pH to ∼9.5 in all systems except for ARG_LS, where the pH was slightly higher (9.8 ± 0.1). ARG and GLY did lead to some reduction in the fraction of bound calcium, compared to the reference CON_LS state. However, analysis of cluster species indicated that this was not due to calcium binding directly to AAs. Indeed, given the system size limitations, it could be argued that, in the model used here, the presence of AAs has a limited effect on the amount of calcium carbonate binding before nucleation. Using another force field, Raiteri et al. measured the free energies of binding Ca²⁺ and CaCO₃⁰ to ASP as −12 kJ mol^–1 and approximately −2 kJ mol^–1, respectively, with a larger barrier for ASP coordination to the ion pair than to the free cation.⁴² Our simulations indicated that the association of carbonate ions to calcium to form ion pairs was relatively fast (the thermodynamic driving force to forming CaCO₃ ion pairs is large,⁷⁵ ∼20 kJ mol^–1). Since most Ca²⁺ ions are bound in these species (and occasionally in larger clusters), it is not surprising that even the additive with no net charge, GLY, had only a small effect on the number of dispersed Ca²⁺ ions in solution. However, the general trend was that the amount of calcium binding was greater for ASP than for positively charged (ARG) or neutral (GLY) AAs in solution. The trend in our simulations is less obvious than in the experiments of Picker et al.,⁴⁷ where ASP had a stronger effect on the amount of free calcium in solution than ARG and GLY. This could be an effect of limited system sizes in the simulations and/or the model adopted here.

Figure 2.

Average fraction of bound ions, f_bound, in the steady state taken from the final 2 ns of total simulation time. Error bars show uncertainties in the data of one standard deviation in the trajectory window sampled. The shaded regions indicate the fraction of bound Ca²⁺, CO₃^2– and HCO₃^– in CON_LS for ease of comparison to systems containing amino acids.

It is clear from Figure 2 that, while the binding of carbonate was not affected by the presence of AAs, there were significant differences between the systems simulated in the fractions of bicarbonate binding. These followed the sequence ARG_LS > GLY_LS > ASP_LS > CON_LS. The binding trend is consistent with the opposing charges of amino acids and bicarbonate, with the most positively charged AA binding the largest fraction of the negatively charged bicarbonate anion. Indeed, upon close inspection of cluster species, it was clear that a large number of clusters that contained AAs also contained bicarbonate (see Figure S1 in the SI), where the anion was bound to −NH_x functional groups. However, negatively charged additives (ASP) also showed increased bicarbonate binding, compared to the control state. The preference for calcium to bind to carbonates means that the solution is enriched with bicarbonate at early times, and bicarbonate can hydrogen-bond to AAs in solution.

The fractions of AAs bound at the steady state was high in all systems, and in the case of ARG_LS, no free ARG was found in solution by the end of the simulation. The fraction of bound AAs followed the sequence ARG_LS > GLY_LS > ASP_LS, following the fraction of bicarbonate binding. In addition, in GLY_LS and ASP_LS, a significant number of free Na ions were removed from solution, and the trend in sodium binding matched that for AA binding. Binding of sodium was through the negatively charged carboxylate AA groups (see Figure S1). While chloride remained free in solution, up to 30% of the sodium was bound at the steady state. The presence of spectator ions in experiments maintains a background electrolyte charge density. However, it is important to consider their potential role in nucleation mechanisms, since they can bind to AA residues. In some cases, this binding enables the transport of certain AA residues in the cells of living organisms.^76,77 Experimental data on the equilibrium binding of spectator ions to amino acids is limited, but data do suggest that Na⁺ binding to ASP, at least, is favorable at 298 K (log₁₀(K) = 0.42, where K is the equilibrium constant for association).⁷⁸

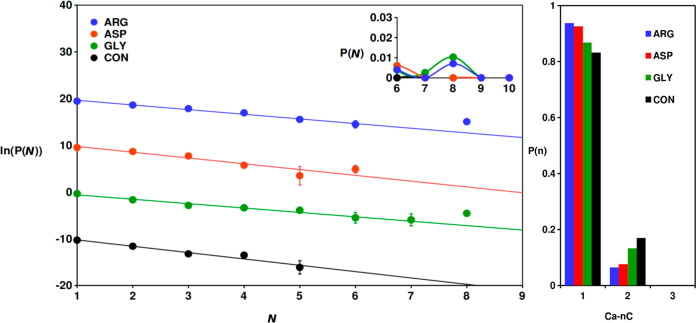
Figure 3 shows that the steady-state cluster size probability distribution, P(N), for clusters containing N molecules/ions (using the first-shell coordination criterion to determine clustering), was dominated by free ions and ion pairs for all systems in the low-salinity regime; the probability of larger species rapidly decayed. In CON_LS, the entire probability distribution could be fitted to an exponential function. In contrast, larger clusters, containing up to eight ions or molecules, were observed with a higher probability in GLY_LS and ARG_LS. In addition, the gradients of the linear fits of ln(P(N)) in Figure 3 for systems containing AAs were slightly perturbed, compared to the control system, particularly for GLY_LS and ARG_LS. These changes were caused by relatively large species that formed predominantly via the association of bicarbonate anions, Na⁺ cations, and AAs (see examples in Figure S1), e.g., [ARG(HCO₃)₂]⁻ and [ASP(Na)(HCO₃)₂]^2–. In ARG_LS, the largest complex that we observed did contain calcium carbonate with the formula, [ARG(Ca)₃(CO₃)₂(HCO₃)₂]⁺. Two bicarbonate ions were coordinated to the nitrogen-containing groups of the AA: one was bound to both the guanidinium and amine groups, while the other was more loosely bound to the amine group of the α-carbon. The calcium carbonate ions formed a cluster around the AA guanidinium group, with carbonates interacting with −NH_x groups and Ca ions coordinating to adjacent carbonate and bicarbonate O atoms. While there is obviously an electrostatic attraction between the oppositely charged ions, the geometries of the clusters indicated that hydrogen bonding was also present. We also observed a [GLY(Ca)₂(CO₃)₂]⁰ species where the binding of a (Ca)₂(CO₃)₂ ionic network was through carbonate oxygen groups binding to −NH_x groups and Ca ions interacting with carboxylate O atoms. While these associated species appear to be mechanically stable for reasonably long times in the simulations, their relative thermodynamic stability has not been established.

Figure 3.

(Left) Natural logarithm of cluster size (N) probability distributions measured in the final 2 ns of simulations at low salinity. N includes all solute ions and molecules within the clusters. The distributions were shifted as ln(P(N)) – 10, ln(P(N)), ln(P(N)) + 10, and ln(P(N)) + 20 for CON_LS, GLYS_LS, ASP_LS, and ARG_LS, respectively. The cluster size distribution for N = 6–10 is given in the inset. Lines are included as a visual reference, and error bars indicate one standard deviation in the data. (Right) Probabilities for calcium to coordinate to n (bi)carbonate ions in the first coordination sphere.

Where Ca and carbonate ions were present in the associated AA species, they had a tendency to exist as small ionic networks interacting with the adjacent AA stabilized by other ions, such as bicarbonate or sodium. The calcium carbonate networks were similar to the small clusters which occurred with low probability in CON_LS. AAs seemed to provide an environment within the solution onto which the liquidlike ionic networks could associate. Figure 3 also provides the coordination probabilities for Ca ions to bind to n (bi)carbonate ions in all solutions at low salinity. Whereas larger clusters of all molecule types were found in AA systems, the degree to which ionic calcium carbonate networks formed actually decreased, as indicated by the slight increase in the probability for calcium to bind to a single (bi)carbonate anion. The size of the calcium carbonate networks (in terms of the numbers of ions) in systems containing AAs was approximately the same as those in CON_LS, so the presence of AAs may produce ionic networks with reduced coordination, because of competing chemical interactions with the organic functional groups present in the additives.

The liquidlike calcium carbonate networks first identified in simulations³⁵ were initially thought to be the thermodynamically stable solute species which directly participated in the formation of post-nucleation phases (i.e., PNCs).³⁵ Wallace et al.³⁶ suggested that a population of small, dynamic clusters were stable in a statistical sense upon spontaneous liquid–liquid demixing. More recent experimental work suggests that these postulated PNCs transform to dense liquid calcium carbonate phases before the limit of solution stability is reached.³² However, the proposed thermodynamic stability of liquidlike clusters in solution before nucleation has been questioned.^37,43,79 Smeets et al.³⁷ showed that a dense liquid phase of calcium carbonate is the first product of nucleation from solution, which is consistent with other experiments.^30,32 Experimental analyses of the species in solution before nucleation did not detect the presence of PNCs. Furthermore, Henzler et al.⁴³ used Ca K-edge X-ray absorption near-edge structure spectroscopy to examine the speciation of Ca²⁺ in solution under a range of conditions and found this to be independent of concentration in the prenucleation regime. However, the interpretation of the data from the analyses in these works has also been questioned.⁸⁰

Here, we will limit our discussion of PNCs to computational work that examines the stability of liquidlike clusters in solution before nucleation. Demichelis et al.³⁵ used a speciation model to determine the free-energy change for ion association from cluster size probability distributions in MD simulations over a range of calcium carbonate concentrations and pH levels. They adopted the assumption—following, e.g., the work of Gebauer et al.³⁴ and Kellermeier et al.⁸¹—that the equilibrium constant for direct cation–anion coordination in clusters is independent of cluster size in the so-called “multiple binding model”. Fitting to all pH levels, the free-energy change for the reaction CaCO₃⁰ + (CaCO₃⁰)_n → (CaCO₃⁰)_n+1 is −21.7 kJ mol^–1 (and the equilibrium constant (K) is equal to 6355) for all n. At concentrations much closer to typical experiments, cluster size distributions over a range of pH levels show a rapid decay in cluster sizes with ion pairs dominating cluster populations (see Figure 3 and the work of Smeets et al.³⁷) These results appear to conflict with the predictions of the multiple binding model. Basing their estimate on species populations in the steady state, Smeets et al. suggested that the free-energy change for the above reaction where n = 1 is much less negative than the equivalent change for the reaction Ca²⁺ + CO₃^2– → CaCO₃⁰. The limitations of MD time scales were suggested as a possible reason for the smaller predicted equilibrium constants.⁸⁰

To address the apparent discrepancy between the simulation results, we have performed US simulations to calculate the potentials of mean force (PMF) and establish the equilibrium constants for the following equilibria:

3

4

PMFs were measured as a function of the separation distance between monomer units on the left-hand-side of the above equations. (Figure S2 in the SI shows the sampled probability densities for the reaction coordinate.) These can be used to obtain Gibbs free-energy changes (ΔG) for association, provided that we add an analytical correction to the resulting PMFs to account for the increasing phase space volume as a function of the monomer–monomer separation distance, r_AB:

5

In the above equation, r_c was the maximum distance sampled in the calculations. Therefore, we obtain one-dimensional free-energy profiles (see Figure 4) that asymptotically approach a limiting value of ΔG in the reaction coordinate sampled. The equilibrium constants for ion binding can then be calculated using the pair correlation function treatment that has been well-documented elsewhere:^54,75,80,82

6

In the above equation, r₀ is the minimum distance in the calculated free-energy profiles. Two corrections are made to the calculated equilibrium constant. The first accounts for the fact that K should be defined at standard concentrations, while the second makes use of activity coefficients, calculated using eq 2, to account for the effect of the background electrolyte in the simulations. Note that the measured K value in eq 6 will be affected by the choice of integral limits, which are not predetermined. The limits chosen here account for the formation of even weakly associated species with multiple solvation shells between monomer units.

Figure 4.

(Top) Potential of mean force energies (ΔG) for the association of AB monomers in water, as a function of monomer–monomer distance r_AB, calculated from US simulations. (Bottom) Representative atomic configurations for minima A, B, and C identified for the association of two ion pairs in water. Ca, C, O, and H atoms are shown as gold, cyan, red, and white spheres with lines showing molecular bonds and green lines highlighting Ca–C connections within 3.5 Å. Only atoms of water molecule atoms within 4.1 Å of ions are shown for the sake of clarity.

Figure 4 shows the resulting free energies. It is obvious that the free energies of binding a cation and anion in solution are much more negative than those calculated for bringing two ion pairs into direct contact. We calculate log(K₁) = 4.0 and log(K₂) = 1.9, giving ΔG₁ = −22.9 kJ mol^–1 and ΔG₂ = −10.8 kJ mol^–1. An uncertainty of k_BN_AT = 2.5 kJ mol^–1 applies to the data. ΔG₁ is equal to earlier results from advanced sampling calculations.⁷⁵ These measurements support the earlier suggestion that the equilibrium constant for binding two ion pairs in a single step is much smaller than that for the binding of a cation with an anion.³⁷ Consistent with earlier calculations using the same model,⁷⁵ solvent-separated (r_AB ≈ 0.7 nm) and solvent-shared ion pair states (r_AB = 0.5 nm) are visited as ions are brought close to each other before a CaCO₃⁰ contact ion pair is formed. The global minimum (r_AB = 0.34 nm) indicates a preference for monodentate carbonate binding. In the case of ion-pair–ion-pair association, only a bias potential applied to the distance between the centers of mass of the ion pairs was enforced. Therefore, it was important to ensure that, before and during association, the individual ion pairs remained intact (see Section S1 and Figure S3 in the SI). The representative atomic configurations in Figure 4 highlight that the first, relatively broad minimum in the energy landscape seen upon decreasing r_AB (∼0.6 nm) represents a solvent-separated state, where a cation and anion from adjacent ion pair monomers are coordinated via water molecules, which are oriented to maximize favorable interactions between the Ca²⁺ ion and the O of the carbonate. The remaining ions in each ion pair are surrounded by solvation shells, aside from the direct ion-pair coordination. A small energy barrier must be overcome to displace water molecules from these ions in order to form a state where all ions are associated within their first two coordination spheres when r_AB = 0.44 nm. This state is still a solvent-separated one and, while it appears as a distinct minimum, we are not biasing the sampling of different water coordination numbers surrounding each ion which could affect the topological features and relative free-energy barriers of the resulting energy landscapes.⁷⁵ The most stable state is observed when r_AB = 0.33 nm and, here, all of the ions are directly coordinated to adjacent ions in a liquidlike chain. Similar calculations have recently been conducted by Raiteri et al.,⁸³ using a rigid molecule version of the force field adopted here and a newly developed polarizable force field. The rigid force field model suggests that ΔG₂ = −6.0 kJ mol^–1, which was slightly less negative than the result from the polarizable force field (−6.8 kJ mol^–1). Our result suggests a more favorable binding energy; this could be due to the constraints imposed to maintain the ion pair monomers in the other work, and differences in the chosen integral limits for the calculation of equilibrium constants. Raiteri et al. extended their study to measure the free-energy changes for adding two more ion pairs into growing clusters. The binding energies were between −4.6 kJ mol^–1 and −10 kJ mol^–1, depending on the reaction step and force field used to add ion pairs into clusters. The authors highlight that the negative free energies indicate increased thermodynamic stability for the larger clusters in solution. We agree that equilibrium constants larger than unity should result in a population of larger clusters (than ion pairs) in solution, albeit the concentration of these species will be low at typical free-ion concentrations in the millimolar regime. However, it is also important to consider the different types of ion associates that will form in solution. As highlighted in this work, both ion pairs in direct contact and solvent-shared and solvent-separated clusters of ion pairs were observed in simulations. We can measure the equilibrium constant, K_CIPs, for the formation of (CaCO₃⁰)₂, where ions are directly coordinated or where ion pair monomers are separated by water molecules. This is done by calculating the ratio of line integrals for different regions in the free-energy profile that represent these states; i.e.,

7

Using the above equation, log(K_CIPs) = −0.16 and the free-energy change for the removal of water to form an ion cluster with ions in direct contact is 0.9 kJ mol^–1. Hence, while the association of two ion pairs is thermodynamically favorable, (CaCO₃⁰)₂ populations will be dominated by highly hydrated, weakly bound associates in the standard state. In future work, it will be necessary to explore the free energies for different solvation states in clusters containing more than a single ion pair to reduce the uncertainty in this estimate for the equilibrium between directly coordinated and solvent-separated ions in (CaCO₃⁰)_n states.

Both our results and those of Raiteri et al.⁸³ indicate that the equilibrium constant for Ca–CO₃ binding in clusters is larger than unity (and, therefore, association is favorable) but much smaller than for the formation of the ion pair from dispersed monomers, and Raiteri et al. also find different equilibrium constants for different steps in stepwise multiple binding, contrary to the underlying assumption in the multiple binding model. In light of these new results and interpretation, a re-evaluation of the cluster size probability distributions and the role of water in clusters that would emerge in pure calcium carbonate solutions before nucleation should be considered, and experimental efforts in this endeavor will be invaluable. A smaller population of prenucleation clusters does not have significant implications for the prenucleation cluster pathway. However, we cannot confirm the role of these clusters in nucleation from these calculations alone. We should also note that (i) the accuracy of the adopted force field has been questioned,⁴³ and (ii) a thermodynamic-kinetic growth model of calcium carbonate growth suggests that clusters may be present are merely spectators,⁷⁹ although the analyses in both these papers have also been criticized.⁸⁰

Our MD calculations suggest that the presence of AAs reduces the density of calcium carbonate ionic networks in solution. Not only did we see a reduction in the average coordination by calcium, we also found that slightly more free calcium was available in solution. However, in our simulations, there is no replenishment of the (bi)carbonate which associates with AAs and therefore a constant background concentration of the anion cannot be maintained. New methods, which allow for simulations at constant supersaturation may prove useful to circumvent these issues in future studies.⁸⁴⁻⁸⁶ If AAs sequestered bicarbonate in experiments, then the equilibrium distribution of carbonate/bicarbonate in the bulk solution would adjust to counter this change in bicarbonate concentrations. To further analyze the chemical interactions described above, approximations for the free-energy changes (provided in Table S2 in the SI), based on species populations, for the forward reactions in the following equilibria were calculated:

8

9

For the control system, the free-energy changes for the formation of the ion pairs in eqs 3 and 8 were −21 kJ mol^–1 and −12 kJ mol^–1, respectively, in good agreement with earlier simulations^35,75 and the free-energy calculations here. The frequencies for ion attachment/detachment events was ∼0.03 ps^–1, with 60% of events occurring in ion/molecule clusters containing at least two of the monomers. This is a good indication that the systems reached a steady state. Given the large changes in the amount of free bicarbonate in solution in the steady state, due to association with AA, we calculated the approximate free-energy changes for bicarbonate association reactions (i.e., eq 9). The forward reaction was slightly more favorable in GLY_LS than in ASP_LS (ΔG = −11 kJ mol^–1 (GLY_LS) and −10 kJ mol^–1 (ASP_LS)). This means that the driving force for bicarbonate association to calcium is comparable to binding with AAs. Because all of the arginine is involved in associated species, it is not possible to approximate the free energy of binding using the above approach. Instead, we performed US calculations of ARG binding to bicarbonate. The resulting ΔG profile showed a plateau at ∼10 Å, as shown in Figure S4 in the Supporting Information. No energy barrier inhibits the bicarbonate from binding to ARG through the guanidinium functional group to bicarbonate oxygens (ΔG ≈ −17 kJ mol^–1), where the (ARG)N–O(bicarb) coordination number was slightly greater than two. Guanidinium groups are known to bind strongly to carbonate from previous simulations.¹⁸ An energy barrier of ∼4 kJ mol^–1 separates this minimum from the most stable coordination state (with a negligible kink in the free-energy profile at ∼5 Å), where the conformational freedom available to ARG allows multiple NH_x groups to associate with bicarbonate (ΔG ≈ −19 kJ mol^–1 for additional binding). Here, the mean coordination number between (ARG)N and O(bicarb) was between three and four, with much higher coordination levels through both first and second coordination shell binding (see Figure S4). Conformational freedom and multiple hydrogen bonds to bicarbonate help explain why ARG binds most strongly to anions in solution.

Since bicarbonate binds so effectively to ARG, we might expect carbonate also to bind strongly, given that the charge density of this anion is larger. The free-energy profile for ARG associated with carbonate is provided in Figure S5 in the Supporting Information. ΔG increases as a function of r from the most stable state up to a maximum of ∼10 Å. An energy barrier of several kJ mol^–1 separates dispersed and coordinated states. Coordination geometries for ARG–carbonate are quite similar to the ones for the bicarbonate case with minima at similar positions in the reaction coordinate. However, the kink that appeared in Figure S4 at ∼4.8 Å is a defined minimum in the case of carbonate. The energy to remove carbonate from ARG is ∼7 kJ mol^–1 less positive than that for bicarbonate. Combining this with the observation of a barrier to ARG–carbonate binding and the preference for calcium to bind to carbonate over bicarbonate (where the binding is around twice as strong and with minimal energy barriers to association), it is not surprising that we see significant association of ARG with bicarbonate in solution.

High Salinity

At increasing levels of supersaturation, solution stability decreases and phase separation becomes increasingly likely until the limit of solution stability is reached, when phase separation is instantaneous. Demichelis et al.³⁵ observed the formation of extended clusters, which consumed the majority of ions in solution at high calcium carbonate concentrations and at high pH. Smeets et al.³⁷ presented these extended ionic networks as the dense liquid phases that were found in experiments^30,38 and predicted in simulations elsewhere.³⁶ Here, we examine the effect of additives during the formation of extended calcium carbonate networks in solution.

In the high salinity simulations, ion association was observed immediately. Figure 5 shows how the size of the largest clusters increased during the simulations. In the case of CON_HS, the largest clusters grew steadily up to around 40 ns after which a plateau in cluster size (N) against time is superimposed on significant noise. The large fluctuations in the cluster sizes indicate that the growth was not only by addition of dispersed ions and small clusters but also by the association of already large clusters of solute monomers, and that clusters occasionally dissociated into smaller species but were coordinated within a few solvation layers. It is possible that the largest clusters would further associate. However, because the concentration of these species decreases over time and because their mobility in solution decreases due to increased mass, long simulation times may be required. Over the final 10 ns of simulation, the average size of the largest cluster was 47 ± 12.

Figure 5.

(Left) Largest cluster size in simulations as a function of time t at high salinity, according to the total number of ions/molecules N. Points show measurements from trajectory data and lines show a running average over 50 ps. (Right) cluster size probability distributions averaged over the final 10 ns of simulation; data are shown on a logarithmic scale of probability.

Compared to CON_HS, there was an increase in the growth rate of clusters when AAs were included in the solution. This was most apparent in ARG_HS, where there was a rapid increase in the largest cluster up to N ≈ 50 in the first nanosecond, followed by a steadier rate of growth that was interspersed several times with jumps in the value of N as large associates combined up to N = 177 ± 10 at the steady state. A movie of the formation of clusters can be found in the SI. The growth of the largest assemblies in GLY_HS was not as rapid, but at the steady state beyond 40 ns, a large species emerged that was slightly smaller (N = 160 ± 17) than the assembly in ARG_HS. The average size of the largest cluster in ASP_HS fluctuates significantly after an initial rapid increase in N over the first 20 ns. This was due to dynamic first-shell coordination between two large regions of the cluster, which contained ∼100 and 200 solute monomers, respectively (the largest mean cluster size over the final 10 ns was 133 ± 46). Increasing the adopted truncation distance in the definition of associated monomers would attenuate these fluctuations, and we note that the dynamic first-shell coordination displayed here is not indicative of clusters dissociating (i.e., seemingly independent clusters were associated by ions separated by solvation shells). The size of the largest sampled clusters followed ASP_HS > ARG_HS > GLY_HS > CON_HS. Both the net charge and the size of the molecular additives were important for the formation of large assemblies. The simulations were repeated an additional two times from different starting configurations and the results were qualitatively the same.

Cluster size probability distributions over the final 10 ns of simulations are provided in Figure 5. In CON_HS, there was a rapid decrease in the cluster size probabilities. The probability of finding species where N = 1, 2, and 3, that is for free ions, ion pairs, and ion trimers, was 0.66, 0.16, and 0.08, respectively. Two additional broad peaks with low probabilities were observed centered around N = 35 and 65. Visual inspection (see Figure S6 in the Supporting Information) showed a handful of large, dynamically coordinated assemblies of ions that were mainly composed of calcium and carbonate. A wide distribution in Ca–C coordination probabilities was found with a maximum for calcium binding with two (bi)carbonates (see Figure S7A in the Supporting Information). Decomposing these into contributions from carbonate and bicarbonate highlight that the network is dominated by the divalent anion, with a maximum of just two bicarbonates binding to a single calcium (see Figures S7B and S7C in the Supporting Information). The average coordination number of Ca²⁺ to CO₃^2– and HCO₃^– was 1.5 ± 0.1 and 0.4 ± 0.1, respectively. The high mobility of ions in clusters is evident in the measured diffusion coefficients (D_Ca) for Ca ions. The mean D_Ca in CON_HS was 1.61 × 10^–6 cm² s^–1—an order of magnitude lower than the diffusion coefficient, D_H2O, for water (1.66 × 10^–5 cm² s^–1; D_H2O for pure SPC/Fw water was 2.34 × 10^–5 cm² s^–1). We measured D_Ca as a function of distance from the center of mass of the largest cluster (see Figure S8 in the Supporting Information), and for Ca ion closest to the core, D_Ca = 1.02 × 10^–7 cm² s^–1, while for a Ca ion at the periphery of the cluster, D_Ca = 1.27 × 10^–6 cm² s^–1 (when the diffusion of the cluster was subtracted). Even at the center of the cluster, ions diffuse faster than in solid ACC,⁸⁷ by ∼3 orders of magnitude. An order-of-magnitude change in the self-diffusion coefficient of ions in dense liquid carbonate phases was measured by Bewernitz et al., using NMR techniques.³⁰ The remaining solution contains the smaller associates and free ions, which were largely bicarbonate. This is reflected in the concentrations provided in Table 2. Approximately 37% of bicarbonate remained completely solvated in their first shells by the end of the simulation. In contrast, 98%–99% of calcium and carbonate ions were directly coordinated to other ions. The concentrations of these species are approximately the same as those obtained in simulations at low salinity. In addition, both Na and Cl ions remained dispersed in solution. This type of behavior can be expected from earlier predictions.³⁵ At higher pH values, Smeets et al.³⁷ observed the complete separation of large, single calcium carbonate liquidlike associates from a lean solution. However, simulations in this work, at pH ∼9 (see Table 2), contain bicarbonate ions that cannot convert to carbonate and are less likely to associate with calcium.

Table 2. Solute Concentrations, I, and pH over the Final 10 ns of Simulation of Initially High Salinity Simulations Containing Amino Acids^a.

system	c(Na+) [mM]	c(Cl–) [mM]	c(AA) [mM]	c(Ca2+) [mM]	c(CO32–) [mM]	c(HCO3–) [mM]	I [M]	pH
CONHS	119 ± 1	122 ± 1	0	13 ± 7	3 ± 1	150 ± 9	0.23 ± 0.02	8.7 ± 0.1
ARGHS	0	127 ± 1	0	11 ± 5	1 ± 1	50 ± 8	0.11 ± 0.01	8.8 ± 0.1
ASPHS	0	28 ± 0.2	0	15 ± 5	4 ± 2	69 ± 10	0.09 ± 0.01	9.1 ± 0.1
GLYHS	6 ± 1	127 ± 0.1	0	8 ± 4	4 ± 3	62 ± 10	0.12 ± 0.01	9.2 ± 0.1

^ac(X) indicate the concentration of ion X.

All of the simulations that included AAs showed multimodal probability distributions with a much clearer separation between dispersed ions, small associates, and large associates (see Figure 5), compared to CON_HS. While there was always a high probability to find free ions and small ion associates, peaks at large N were centered around the sizes of the largest clusters, as discussed above. We do find, generally, a separation of large, single solute-associated species from a population of much smaller species that are dominated by free ions and ion pairs. In contrast to CON_HS, the probabilities for finding clusters containing N = 1, 2, and 3 were 0.62, 0.14, and 0.12 in ARG_HS. However, in ASP_HS, as noted above, we observed a dynamic clustering (using the adopted truncation distance for association of 3.5 Å) between two large ASP-rich regions in this system; therefore, two peaks are observed in the cluster size probability distribution at N ≈ 100 and 200, with the smaller cluster being ∼4 times more probable (on average). All of the largest assemblies displayed some degree of dynamic ordering. The broad peak centered around N = 180 in ARG_HS highlights this (also see individual data points in the left of Figure 5). The size of this cluster, measured in terms of radius of gyration, was ∼1.7 nm.

As solute monomers associated rapidly into a small number of large assemblies, which appear to be in dynamic equilibrium with smaller associates in a solution where the ionic strength is ∼10% of the initial conditions (see Table 2), it is helpful to consider mechanisms and thermodynamic driving forces for the association. It is reasonable to assume that the solution is beyond its stability limit at t = 0, given the level of the initial supersaturation here. Indeed, this limit was predicted to be on the order of c(Ca) that we found at the steady state in low-salinity simulations.³⁹ Because the association of calcium with the divalent carbonate anion is thermodynamically more favorable, the initially homogeneous solution decomposes by forming CaCO₃ clusters, which are then in a dynamic equilibrium with the remaining ions in the surrounding solution. These dense liquids could subsequently dehydrate to form solid ACC.³⁶Figure S9 in the Supporting Information provides the RDFs for Ca–C, as a function of time. These do not indicate any increasing density of the ionic network over the final 10 ns, but there are fluctuations in the ratios of monodentate versus bidentate carbonate binding to calcium. Advanced sampling simulations have indicated that the transition from liquidlike calcium carbonate nanoparticles to solidlike ACC with stoichiometry CaCO₃·H₂O occurs in clusters containing 30–40 CaCO₃ ion pairs.⁸⁸ However, kinetic barriers to dehydration will limit the amount of water that can be removed from the liquidlike clusters in these simulations, and calculations sampling different hydration levels should be considered.

All of the AAs were associated in clusters by the end of the simulations. In ARG_HS and GLY_HS, the AAs were found in the single, large clusters that emerged, whereas, in ASP_HS, four of the AAs were in a cluster that was dynamically coordinated to another cluster containing the remaining 14 AAs. Table S3 in the Supporting Information shows that, in systems containing additives, the level of calcium and carbonate association was similar to that observed in CON_HS. However, there was greater association of bicarbonate, with 83%–88% bound in solution over the final 10 ns of simulation (at t = 0, c(HCO₃^–) ≈ 400 mM). The amount of bicarbonate binding ranked as follows: ARG_HS > GLY_HS > ASP_HS > CON_HS, with the trend being consistent with that observed at low salinities. The removal of these additional ions from the solution where additives were included led to a reduction in ionic strength to approximately half the levels of CON_HS and increases in the final pH (see Table 2). Cl ions remained dispersed in solution surrounded by water, yet Na ions were bound in associates in the final 10 ns of simulation, in stark contrast to the observations in CON_HS. While there was no correlation in the removal of sodium with additive charge, we note that the amount of sodium added was to control the initial ionic strength; therefore, where additives were positive, fewer Na ions were simulated.

Snapshots of the configurations for the AA simulations at high salinity at the end of 60 ns simulation are provided in Figure 6. The large cluster containing all of the AAs can be seen surrounded by a CaCO₃ ionic network, which adsorbs to the AA assembly. Other CaCO₃ ionic networks can be seen in the surrounding solution, along with free ions, ion pairs, and other small associates. These depictions are similar to what was seen in CON_HS. It appears that the large cluster assembly is facilitated by bicarbonate ions (see Figure 6 and the movie in the Supporting Information). A large number of bicarbonate ions is observed throughout the highlighted region and is stabilized through hydrogen bonding to ARG molecules, as found in US calculations at low salinity. Some carbonate ions are also observed at the periphery of the assemblies. Because the guanidinium functional groups of ARG have a tendency to be directed toward bicarbonates in the center of the assembly, carboxylate groups tend toward the periphery of the cluster and we observed coordination of these groups to sodium. The average coordination probabilities are 1.3 ± 0.03 and 0.5 ± 0.03 for Ca–carbonate and Ca–bicarbonate in clusters and the distribution of Ca–C binding shifts to smaller values (see Figure S7 in the Supporting Information). The decrease in carbonate coordination is due to the topology of the AA assembly limiting the mass density of the calcium carbonate network. A small amount of calcium is coordinated to the AAs through carboxylate groups (see Figure S7). From these data, we see that the ARG assembly provides an environment where calcium carbonate networks can adsorb. In doing so, the ionic network takes on coordination levels that are smaller than networks in the remaining solution, which indicates a decreasing ability to increase ionic density. In addition, the mobility of calcium decreases when adsorbed to the ARG assembly. Figure S8 shows that the diffusion coefficients for Ca ions in the largest cluster were 6.1 × 10^–8 cm² s^–1 and 3.1 × 10^–7 cm² s^–1 (when we subtract the diffusion of the cluster) for ions closest to the core and those at the interface between AAs and solution, respectively. There is approximately an order of magnitude difference in the diffusion of Ca ions in the largest clusters when the AAs are present, compared to CON_HS.

Figure 6.

Snapshots from the end of 60 ns of simulation of solutions containing calcium (bi)carbonate and AA additives at high salinity. A key to atom types is provided; water and chloride are not shown for the sake of clarity. Green lines show calcium–(bi)carbonate inner-sphere coordination. In ARG_HS, the entire simulation cell is shown. The AA assemblies are shown with smoothed surfaces created according to approximately twice the van der Waals radii of solute atoms. The AA assemblies are enlarged on the right with a solid surface, indicating the approximate boundary with surrounding ions and water. In ARG_HS, we also highlight the hydrogen bonding (shown by the dashed lines) between ARG molecules and bicarbonate in the core of the assembly.

The large AA assemblies that form in GLY_HS and ASP_HS were again facilitated by the coordination of AAs to bicarbonates through −NH₃ groups. However, here, we also observe a significant amount of sodium within the assemblies coordinated to the AAs through carboxylate functional groups. These Na ions had a tendency to be in the core of clusters, which is where maximum coordination can be achieved. This provides anions coordinated to AAs that can also bind to calcium. Again, we saw calcium carbonate networks adsorbing to the surfaces of assemblies and the networks themselves were quite substantial in size. The largest cluster contained 50% of the total calcium and carbonate available in the simulation, while 70% and 85% of the total bicarbonate and sodium were found in the cluster, respectively. For GLY_HS, the coordination probabilities (see Figure S7) were shifted to smaller values. In ASP_HS, the shape of the coordination distributions was closest to CON_HS. This can be explained by the composition of the clusters. As shown in Figure 6, two regions rich in ASP are connected by a CaCO₃ network. This liquidlike network undergoes dynamic ordering, producing the large fluctuations in the largest cluster size, as a function of time in Figure 5. The cluster comprises 65%, 70%, and 63% of the total calcium, carbonate, and bicarbonate in the system and a significant amount of these ions is found away from the surface of the AA assemblies. In both GLY_HS and ASP_HS, the smaller size of additives leads to different geometries for the adsorbed calcium carbonate networks, cf. ARG_HS. This affects the ionic coordination in the networks. In ASP_HS in particular, coordination levels larger than those observed in CON_HS are evident. In both cases, we again found a small amount of Ca binding directly through the AA carboxylate groups.

When supersaturations are high, the additives interact with the calcium carbonate liquidlike networks that are observed in control simulations. Only subtle changes in the coordination of the networks are seen. It is interesting to speculate about how additives would control nucleation if solute concentrations were lowered and system size limitations were not evident. In this case, it is reasonable to assume that several smaller additive assemblies could be stabilized by the presence of bicarbonate and so-called spectator ions. The CaCO₃ networks that form could adsorb to these assemblies and connect them in solution. In the presence of poly(ASP), experiments^30,89 have shown that a dense liquid phase of calcium carbonate is stabilized in solution. It was assumed that the mechanism of action was to remove Ca ions in solution; subsequent diffusion of carbonate eventually led to crystallization. Our results suggest that Ca depletion from the mother solution is not necessary to stabilize dense liquid calcium carbonate. However, the action of extended polymers may be different from assemblies of individual AA monomers.

Oligopeptides

We have also considered the effect of additive size on the formation of clusters in solution, again at high salinity. Here, we simulated oligopeptide chains of ARG, ASP, and GLY, where six monomer AAs were connected by peptide bonds. In forming the peptide bonds, NH₃⁺ and CO₂^– groups are replaced and so fewer functional groups are available for coordination to ions in solution. Nonetheless, the net charges of 6ARG, 6ASP, and 6GLY were +6e, −6e and zero in the simulation cells. Figure S10 in the Supporting Information provides the structures that were adopted in this work. Three oligopeptides were included in simulations, in order to retain the same total charge.

Rapid growth of large assemblies emerged in simulations of calcium (bi)carbonate in the presence of 6AA oligopeptides, just as when AAs were included. Large clusters were observed in equilibrium with a surrounding solution where the free ion concentrations at the steady state (see Table S4 in the Supporting Information) were generally consistent with simulations containing AAs. Again, all of the 6AAs formed clusters with other solute monomers. There were some subtle changes in solution compositions at the steady state. Most notably, there were slight increases in the pH of 6ARG_HS (9.1 ± 0.1), compared with ARG_HS (8.8 ± 0.1). In addition, the ionic strength of 6GLY_HS (0.17 ± 0.01 M) increased compared with GLY_HS (0.12 ± 0.01 M). Table S5 in the Supporting Information provides the fraction of bound solute species at the steady state. For ease of comparison, Figure 7 shows the differences between the binding fractions in these simulations and those containing AAs at high salinity. The formation of peptide chains from six AAs clearly does not have any impact on the level of Ca²⁺ and CO₃^2– association in solution. Both 6ASP_HS and 6GLY_HS show a reduction in the fraction of bicarbonate binding. While all 6AA simulations show a reduction in the fraction of sodium binding, this is most notable in 6ARG_HS and 6GLY_HS. These changes can be reconciled by considering the difference in chemistries of the AA additives on forming peptide bonds. In all cases, the ability for −NH_x and −CO₂ functional groups of AAs to bind to bicarbonate and sodium is reduced when those groups are replaced by the peptide bond. 6ARG_HS and 6ASP_HS retain these functional groups in their side chains; therefore, the changes are minimized in these systems.

Figure 7.

(Left) Differences between the fractions of bound solute (using a coordination distance cut-off criterion) between simulations containing AAs and 6AAs. (Right) Cluster size probability distributions in solutions containing 6AAs at high salinity, according to the total number, N, of ions/molecules in clusters. Data were averaged over the final 6 ns of simulation, and error bars show uncertainties of one standard deviation.

The reduction in the number of chemical functional groups able to bind to solute monomers is also evident in the cluster size probability distributions, shown in Figure 7. Again, we note that the choice of cutoff in determining clusters will affect the measured cluster size populations. The largest clusters were found for 6ARG_HS, where the cluster size distribution was shifted to slightly smaller values. In 6ASP_HS, all of the additive molecules were contained in a single cluster, shown in Figure 8, and the size of this cluster is smaller than the largest cluster in ASP_HS. We also note that, in the case of oligopeptides, there are more large clusters in the simulations. Figure 8 shows that 6AAs are stabilized by coordination to bicarbonate and sodium. The conformational freedom of the additives allows multiple binding of them to the same solute monomer. At high supersaturations, chelation of solute monomers in close proximity to the additives will be fast (assuming that the energy barriers for this process are accessible), while diffusion of the additive clusters will be relatively slow. In contrast, solute binding to smaller AA additives enables assembly of large clusters. Given sufficient time, there could be further association and restructuring of the 6AA clusters, but this may be beyond reasonable simulation time scales. We can see, particularly in the case of 6GLY_HS, that two 6GLY molecules have folded to coordinate to several cations; these then formed a larger cluster, facilitated by the calcium (bi)carbonate in solution.

Figure 8.

Snapshots from the end of 60 ns of simulation of solutions containing calcium (bi)carbonate and 6AA additives at high salinity. A key to atom types is provided; water and chloride are not shown for the sake of clarity. Green lines highlight calcium–(bi)carbonate inner-sphere coordination. The largest clusters containing 6AAs are shown with all atoms within 3 Å also shown. The plot shows the distributions of the total number of clusters (containing at least three solute monomers) versus the number of solute monomers (N) in the largest cluster from the final nanosecond of simulation. Data for CON_HS at the steady state are plotted for comparison.

Figure 8 shows the distribution of cluster sizes versus the total number of clusters in 6AA simulations, along with the results from CON_HS. The distribution for 6ARG_HS is relatively narrow. This large cluster was formed of ∼150 solute monomers, which consisted of ∼55Ca²⁺, ∼34CO₃^2–, and ∼56HCO₃^– ions and all of the additive molecules. Two groups are apparent for 6ASP_HS. Here, a 3(6ASP) cluster containing ∼20Ca²⁺, ∼8CO₃^2–, and ∼36HCO₃^– (for an average total of 85 monomers) formed separately to a single, liquid (CaCO₃)₂₂ ionic network, which dynamically associated with the additive assembly in the simulation. A much more disperse dataset was found for 6GLY_HS, but this was still very different from the control simulation at high salinity. Both the number of solute binding sites and additive size appear to be important to control the level of dynamic clustering in the liquid phase.

RDFs in Figure S11 in the Supporting Information show that the dominant monomer binding to 6ARG was bicarbonate, with also some carbonate binding. Calcium has a tendency to be found beyond the first coordination sphere of atoms in 6ARG. While 6ASP and 6GLY also coordinate to bicarbonate, Na ions are present at smaller coordination distances and there is a reduction in the amount of calcium coordination in the outer sphere of the atoms in these systems. In all of the large 6AA clusters, we find CaCO₃ ionic networks adsorbed. Therefore, these additives act in much the same way as AAs at high salinity. Figure S12 in the Supporting Information provides the coordination probabilities for Ca inner-sphere coordination in clusters. Very limited coordination is found between calcium and 6AAs. The coordination profiles for Ca binding to bicarbonate were much the same as for AA simulations (also see Figure S7). The differences between additives for high coordination levels of Ca–nCO₃ became more apparent when compared to AA simulations. For example, the probabilities of Ca–3CO₃ were 0.1, 0.14, and 0.19, respectively, for 6ARG_HS, 6ASP_HS, and 6GLY_HS, respectively. In terms of the average total coordination number of Ca to (bi)carbonate, we found an increase in the case of 6ARG_HS (n = 1.82 and 2.01 in ARG_HS and 6ARG_HS) and 6GLY_HS ((n = 1.93 and 2.22 in GLY_HS and 6GLY_HS) and a decrease for 6ASP_HS (n = 2.01 and 2.16 in ASP_HS and 6ASP_HS). These could be due to varying levels of bicarbonate available to coordinate to calcium, although the changes are relatively small.

The difference between AAs and 6AAs on calcium (bi)carbonate solutions is subtle. The crucial difference is that, in the oligopeptides, all the chemical functional groups available for solute association are present together in one molecule. At low salinity, we should expect to see relatively large species forming in solution, especially given the observations of AA effects at low salinity. This could be the reason why small molecule additives are less effective at stabilizing dense liquid CaCO₃ than polymers. No evidence is found that increasing the size of the additive had a significant effect on the formation of CaCO₃ ionic networks in water. However, as in simulations of assembled AAs, the additives provide environments where CaCO₃ can associate. Association, either through electrostatic interactions or by hydrogen bonding also liberates water from solute monomers, which will have a stabilizing effect for the system, particularly when initial solute concentrations are relatively high.

Conclusions

All of the AA additives slightly affected the speciation of calcium (bi)carbonate solutions at pH and concentration levels that targeted typical experimental conditions to study phase separation. AAs provided coordination sites for cations and anions to bind. Association of bicarbonate to −NH_x groups suggests that nucleation might be regulated not just by controlling c(Ca), but also c((H)CO₃). In addition, while AAs did not significantly affect the formation of liquidlike CaCO₃ networks, they do provide sites for the dynamic coordination of these entities. This was most apparent on solution decomposition at high salinity. CaCO₃ was found predominantly at the interface between extended AA assemblies and surrounding solution. The topologies of these assemblies appear to have some control on the coordination of calcium in the clusters. Furthermore, there was a clear decrease in the mobility of calcium when bound at the edge of these assemblies, even when compared to highly coordinated calcium (by carbonate) in the core of CaCO₃ ionic networks. Increasing the size of additives by forming oligopeptides did have some subtle effects on the activities of additives in solution. This was caused by the loss of chemical sites to bind to solute monomers in the formation of the peptide chain. However, generally, there was no significant difference, compared to AA simulations at high supersaturations. We do note that, at concentrations closer to experimental conditions, the high density of solute monomer binding sites in a peptide or polymer will be important and is likely to make these additives more effective than small amino acids, where some degree of assembly will be necessary to control the CaCO₃ networks that also form in solution.

The mechanisms for control of calcium (bi)carbonate association by additives presented here are consistent with experiments showing that poly(ASP) stabilizes a dense liquid phase of calcium carbonate before precipitation of an amorphous solid.^32,89 Ion self-diffusion coefficients in extended networks in this work compare favorably with those measured for dense liquid phases.³⁰ Sebastiani et al.³² suggested that the position of the liquid–liquid binodal for phase separation in calcium carbonate solutions is unaffected by the addition of poly(ASP), but the presence of the polymer delays the formation of amorphous calcium carbonate. Our work supports this and provides mechanistic insight into how the existence of liquidlike calcium carbonate networks may be prolonged. Bewernitz et al.³⁰ postulated that the negatively charged carboxylate groups sequester calcium from solution to inhibit the precipitation of a solid phase. Cantaert et al.⁹⁰ found that the positively charged additive, poly(allylamine hydrochloride), also stabilized thin films of liquidlike calcium carbonate. They suggested a similar mechanism of “microphase separation”, followed by coalescence of droplets driven by an influx of carbonate into a solution containing the polymer and calcium. Our work shows that calcium (bi)carbonate networks can associate with organic additives in solution. The association appears to be thermodynamically favorable and the resulting reduced mobility of ions means that the additives stabilize these networks, which would otherwise transform more quickly into solid calcium carbonate. The number of solute binding sites and their availability to associate with calcium carbonate networks (requiring some level of conformational flexibility) is likely to be important for stabilizing a dense liquid phase. The charge of the additive appears to be less important, but the charge distribution in additives might help to control the topology of the associating calcium carbonate networks and therefore inhibit solid precipitation.

Glossary

Abbreviations

MD

molecular dynamics

PMF

potential of mean force

PNC

prenucleation cluster

US

umbrella sampling

RDF

radial distribution function

ACC

amorphous calcium carbonate

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.cgd.9b01693.

• DL_POLY input force field files for the systems simulated in this work (ZIP)

• Movie showing the formation of clusters (MPG)

• Discussion of ion pair–ion pair association in umbrella sampling calculations; supplemental figures and tables (PDF)

Author Contributions

All authors designed the research. A.R.F. and R.I.M. performed the simulations and analyzed data. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Funding was provided by the Engineering and Physical Science Research Council. This work was supported by the EPSRC [EP/I001514/1], which funds the Materials Interface with Biology consortium, and the Materials Modeling consortium.

The authors declare no competing financial interest.