Restricted-Variance Molecular Geometry Optimization Based on Gradient-Enhanced Kriging

Abstract

Machine learning techniques, specifically gradient-enhanced Kriging (GEK), have been implemented for molecular geometry optimization. GEK-based optimization has many advantages compared to conventional—step-restricted second-order truncated expansion—molecular optimization methods. In particular, the surrogate model given by GEK can have multiple stationary points, will smoothly converge to the exact model as the number of sample points increases, and contains an explicit expression for the expected error of the model function at an arbitrary point. Machine learning is, however, associated with abundance of data, contrary to the situation desired for efficient geometry optimizations. In this paper, we demonstrate how the GEK procedure can be utilized in a fashion such that in the presence of few data points, the surrogate surface will in a robust way guide the optimization to a minimum of a potential energy surface. In this respect, the GEK procedure will be used to mimic the behavior of a conventional second-order scheme but retaining the flexibility of the superior machine learning approach. Moreover, the expected error will be used in the optimizations to facilitate restricted-variance optimizations. A procedure which relates the eigenvalues of the approximate guessed Hessian with the individual characteristic lengths, used in the GEK model, reduces the number of empirical parameters to optimize to two: the value of the trend function and the maximum allowed variance. These parameters are determined using the extended Baker (e-Baker) and part of the Baker transition-state (Baker-TS) test suites as a training set. The so-created optimization procedure is tested using the e-Baker, full Baker-TS, and S22 test suites, at the density functional theory and second-order Møller–Plesset levels of approximation. The results show that the new method is generally of similar or better performance than a state-of-the-art conventional method, even for cases where no significant improvement was expected.

1. Introduction

The optimization of molecular structures is instrumental for the computational chemistry procedure to establish the fundamental thermodynamics of a chemical process—the reaction enthalpy and the activation energy. The zeroth-order understanding of the dynamics of a chemical reaction is based on the optimization of equilibrium structures, transition states, reaction pathways, constrained optimization on the ground-state potential energy surface, and so forth. In photochemistry, the location of conical intersections along the reaction pathway plays a fundamental role in understanding the radiative and radiationless decay of excited molecular systems. In general, optimization, unconstrained or constrained, on ground- and excited-state potential energy surfaces is the essence in our extraction of a qualitative understanding and a quantitative prediction of the nature of a chemical process. For this reason, various efforts to make optimization procedures as robust and efficient as possible are of fundamental importance to computational chemistry. In this report, we will present an alternative to the usual approach in computational chemistry—the standard surrogate model of restricted-step second-order Taylor expansion approximations¹⁻³ in combination with approximative second derivatives⁴ and a Hessian-update method, for example, the BFGS⁵⁻¹¹ and MSP¹²⁻¹⁴ approaches used for minimum and transition-state optimizations, respectively.

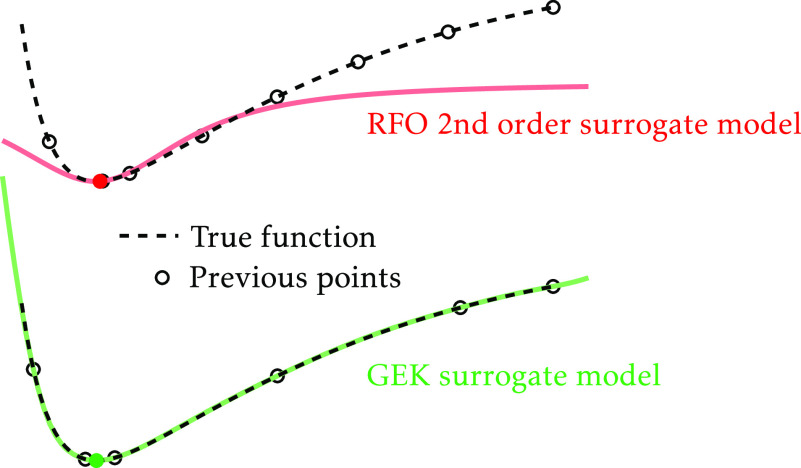
The standard surrogate model has several shortcomings. To mention a few, the method is not an exact interpolator, that is, it can in general only exactly reproduce the gradients of the last two molecular structures, this surrogate model will never converge to the exact ab initio model, the surrogate model cannot in general describe anharmonic characteristics, success is critically associated with the Hessian update method, it cannot simultaneously describe several stationary points, and it does not facilitate an explicit measure of the difference between the surrogate and the exact model. What will be described here is an approach that in its simplicity will actually address all these problems of standard optimization methods.

The Kriging model^15,16—a Gaussian process regression-like procedure—is an exact interpolation procedure to describe a multidimensional function. Adapted to molecular geometry optimization, the multidimensional function is the energy and the independent variables are the coordinates of the nuclei. The Kriging model exists in several forms—simple, ordinary, or universal Kriging. In its initial form, the interpolation approach is based on measured or computed energies for various molecular structures. However, molecular geometry optimizations are most efficient in a framework in which both energy and analytical gradients are computed at the same time. To take full advantage of the information provided by the gradients a special form of Kriging has been developed—the gradient-enhanced Kriging (GEK).¹⁷⁻¹⁹ Recently the GEK approach has been used for geometry optimizations for equilibrium and transition-state structures.²⁰⁻²³ These initial studies have demonstrated the potential of the Kriging procedure in association with molecular structure optimizations. However, these studies have also shown that in order to be competitive with commonly used algorithms, a GEK-based method should also be able to make use of the empirical and practical knowledge accumulated through decades of use and improvement of second-order methods. In particular, Meyer and Hauser²³ have proved that a good choice of internal coordinates is an essential part of a successful GEK-based optimization algorithm, as it is for conventional ones, and they have also suggested that the use of a heuristic estimate for the Hessian matrix would be of particular importance. The main differences between the present work, which addresses the previously mentioned points, and these recent similar approaches will be presented in Section 3.6. It is also worth to mention that Gaussian process regression has been used for the optimization of, for example, minimum energy reaction paths and in minimum mode saddle-point searches.²⁴⁻²⁷

It is the hypothesis of the current project that the GEK superior properties, as compared to standard second-order optimization procedures, do not require a large amount of data and also manifest themselves in situations with limited data. In this respect, it is suggested that GEK-guided molecular structure optimization for systems close to an equilibrium structure can outperform standard methods.

In this report, an implementation of GEK will be described, based as much as possible on standard procedures used in molecular geometry optimization. The most significant difference will be that the surrogate model is based on GEK rather than a second-order truncated Taylor expansion of the energy surface. Also, a standard restricted-step optimization procedure is used, with the simple but significant difference that the step restriction is subject to a cap on the expected variance (the uncertainty) of the surrogate model—a restricted-variance optimization. The optimization will be done in internal coordinates, thus eliminating translational and rotational variance from the surrogate model. The use of internal coordinates,^28,29 further, enables the implementation of different effective length scales for the various coordinates—the so-called l values. The GEK, as used in this report, uses the approximate Hessian to define l values and the appropriate internal coordinates for the coordinate space in which the Kriging data are expressed (but Hessian update methods are unnecessary). In this report, it will be described in detail how the hyperparameters—the l value and the baseline or trend function—can be defined such that the model for a single sample point completely includes all quantitative properties of a conventional approach with a Hessian model function (HMF).⁴ The use of additional sample points in the GEK takes on the role of the Hessian update procedure.

The rest of this report will be organized as follows. First, the design considerations of a GEK-based molecular structure optimizer are discussed. Second, a theory section is presented to highlight the essence of the required relations to attain the objectives for the implementation of the new optimization method. Subsequently, the computational details are presented, followed by a discussion of the results. Finally, summary and conclusions are presented.

2. Design

Machine learning methods are commonly associated with vast amount of data and data mining. Successful molecular structure optimizations, on the other hand, are manifested by limited data—the less data used, the more successful the optimization. To design a machine learning implementation for structure optimization requires an understanding of why standard methods work as well as they do. Following this insight, a GEK-guided optimizer should mimic these features as close as possible. Hence, we will very briefly address the recipe which is the key feature that makes ordinary structure optimization work.

Let us first start with the blunt statement that any optimization based on only analytical energies and gradients, as is commonly the case in ab initio implementations, is nothing more than a tweaked steepest descent method. The road to success is guided by several key features. First, the selection of coordinates to specify the molecular structure is of fundamental importance. The very first implementations of molecular structure optimizations typically used the Cartesian rectilinear coordinates. However, it is clear today that curvilinear coordinates are by far superior to rectilinear coordinates (see, e.g., refs (28) and (29)). One possible reason for this success is that in curvilinear coordinates the Hessian will be diagonally dominant. Second, the generation and use of an approximate Hessian (in the absence of the exact one) will provide the optimization procedure with crucial information of the shape of the energy landscape and will guide the optimization procedure in a firm way toward the stationary point. One of the most used such approximate Hessians is the one based on a HMF.⁴ The success of this approximate Hessian is argued to be its ability to provide a reasonable guess not only of the diagonal elements but also of the off-diagonal terms—the coupling between the internal coordinates. Third, the use of a Hessian update procedure which will modify the approximate Hessian to be semiconsistent with the acquired gradient information. It is worth noting that different types of update methods are suggested for different types of optimization cases (e.g., local minimum or transition state structure optimizations), and that the update is normally done for a limited set of gradients. Fourth and final, the optimization procedure itself. The consensus today is that a step-restricted second-order optimization scheme, such as the restricted-step rational-function optimization procedure, is the preferred approach.¹

In the proposed implementation of the GEK-guided molecular structure optimization all of these key features will be considered. That is, the procedure will use internal coordinates, as suggested under the first point. Internal coordinates will, additionally, be of benefit because this will result automatically in a surrogate model of the energy surface which is translationally and rotationally invariant. Moreover, the last point will be fully implemented, that is, microiterations will explore the surrogate model using state-of-the-art restricted-step second-order procedures. Note, however, that in association with a GEK procedure the step restriction can be modified and this will be described below. The second and third points—approximate Hessian and Hessian update—are very much related. We start by noting that in the conventional optimization procedure, the approximate Hessian is a seed for the Hessian update procedure. We propose to use the information provided by the approximate Hessian for defining the internal coordinates and the characteristic lengths used in the surrogate model. When the model is built with a single sample point, its second derivatives will be identical to the HMF approximate Hessian. The addition of further sample points—energies and gradients—will modify the surrogate model, and this will therefore take the place of a Hessian update method. By design the method is an exact interpolation and will always be consistent with all of the data that the Kriging is based on. Furthermore, not only will the energy and gradients be represented exactly at the sample points, the model can represent several stationary points at the same time. This last property will not be of particular importance when the only goal is to find a local minimum, as in the present work, but consider that, in the case of a chemical reaction, the surrogate model will be able to represent the minima of the reactants and the products, and the stationary point of the transition state at the same time, if appropriate data is supplied, providing a more realistic representation of the “true surface”.

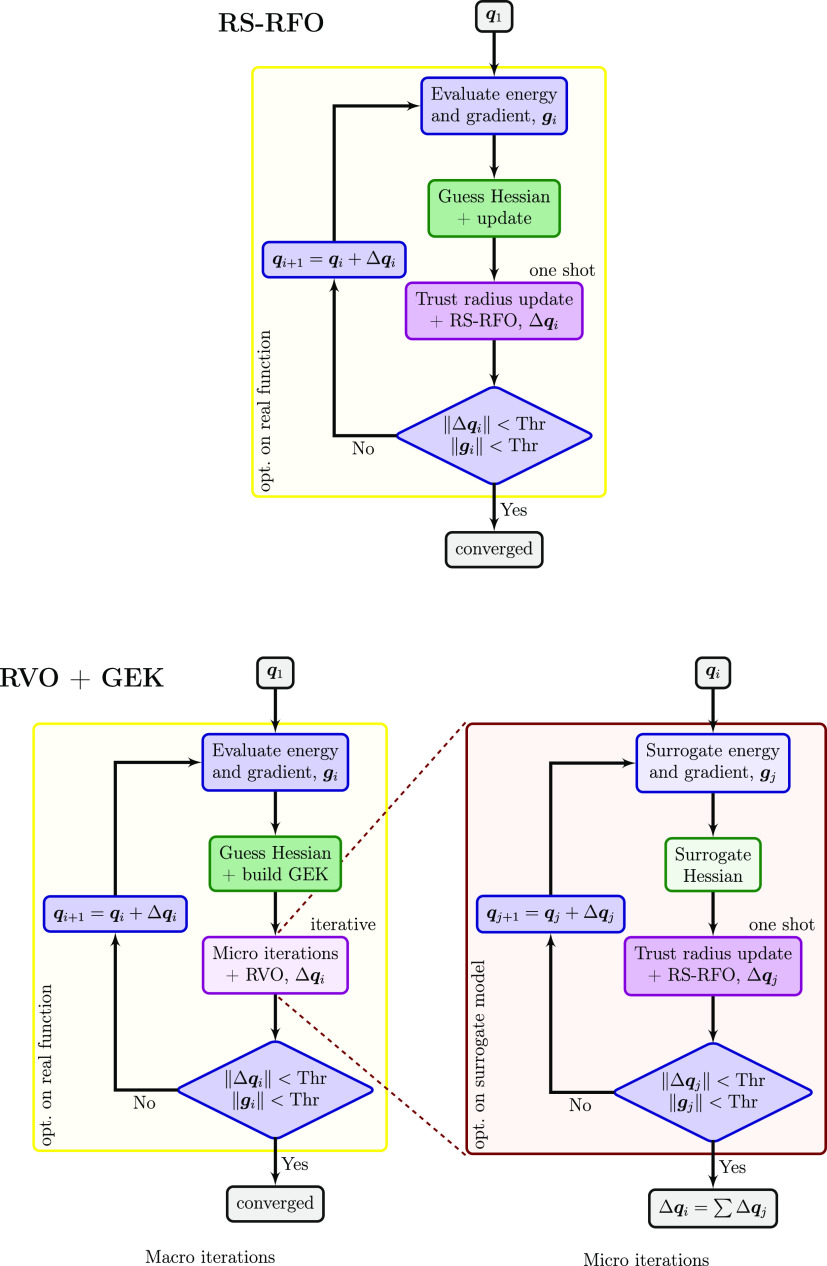
With this in mind, the conventional and GEK-supported optimizations are rather similar (see Figure 1). The major difference is that for GEK-supported optimizations, it becomes necessary to have two nested loops of macro and micro iterations, with the latter engaged to find a stationary point on the surrogate model. In the conventional optimization, the stationary point on the surrogate model is found analytically in one shot (although several tries may be needed to satisfy step restrictions). The outer (macro) loop resembles otherwise the conventional loop, with the difference that the guessed Hessian is used to build the GEK surrogate model and it is not subject to Hessian update methods. The inner (micro) loop, in turn, is identical to a conventional loop, except that energies, gradients, and analytical Hessians are obtained from the surrogate model. The variance restriction is implemented by ensuring that the microiterations remain within the variance threshold.

Figure 1.

Schematic comparison of the conventional RS-RFO optimization method (top) and the proposed RVO algorithm, based on a GEK surrogate model, and using RS-RFO in the micro iterations (bottom).

In the theory section to come, it will be demonstrated how the GEK can be parameterized and implemented such that it should be in all respects as good as, if not better than, the standard state-of-the-art quasi-Newton optimizers available today.

3. Theory

Initially, a presentation of the Kriging and GEK model is given. A brief discussion then proceeds to present the Matérn covariance function. This will be followed by a description of how the GEK model can be constructed using the information from the approximate Hessian. The section is concluded with a brief summary of the differences between the present GEK-supported optimization implementation method and other similar recently published ones. In what follows here bold lower- and uppercase symbols represent vectors and matrices, respectively.

3.1. Kriging

The Kriging approach is a method to design a mathematical basis for making predictions through inter- or extrapolation. In the case of molecular geometry optimizations, the energy predictor—the surrogate model, E*(q)—will predict the energy as a function of the coordinates (arbitrary coordinates, e.g., Cartesian, internal coordinates, etc.) of the molecular system, q. This predictor is based on the known energies at some n sets of coordinates of the molecular system—the source data or sample points, E(q_i) for i ∈ {1, ..., n}.

The Kriging model or, as it is also called, Gaussian process regression (GPR), is based on an equation containing two terms

1

the components of this equation will be explained in some details below. The first term, μ, is the trend function (in its simplest form, the mean or a constant), while the second term is the local deviation of the energy around μ.³⁰ First, the covariance vector v(q) contains the correlation between the coordinates of the prediction point q and each sample point q_i. Second, the covariance matrix M holds the correlation between the sample points. Finally, y is the column vector of function values from the source data, which in our case are the energies of the system, that is, y_i = E(q_i), and 1 is a vector of n elements with the value of one, where n again is the total number of sample points.

The correlation can be calculated in internal coordinates or Cartesian coordinates, and can be defined by various kernels or covariance functions, for example, Gaussian or Matérn covariance function³¹ (see below). The covariance matrix M is an n × n matrix defined as follows

2

where f is a covariance function and d_ij is a scalar generalized distance between the coordinates at sample points i and j, in our case expressed as

3

where K is the number of degrees of freedom of the molecular system (K = 3N – 6 for a nonlinear system with N nuclei and no external fields) and l_k is a scale parameter that influences the width of the covariance function—the characteristic length—in the kth dimension. The covariance vector v(q) is defined analogously, replacing one of the sample points with the desired arbitrary point q, that is

4

In particular, at the jth sample point, q = q_j, the covariance vector is identical to the jth column of the covariance matrix M.

The predictor is sometimes expressed in two alternate forms, highlighting its linear combination features. On the one hand, it can be viewed as a linear combination of basis functions (given by the covariance function f) centered at the sample points

5

where the vector w, the weights, is the solution of the linear system

6

The w vector depends only on the sample points (their coordinates and energies), and the only dependence on the prediction point q is through the basis functions (the covariance vector) v(q).

On the other hand, the predictor can also be viewed as a linear combination of the energies at the sample points

7

where now the dependence on q is included in the weights ω, which are however independent on the energies. The ω vector is similarly obtained as the solution of the linear system

8

The first form has the advantage that the same w vector can be used for prediction on any point q, while in the second case, the ω(q) vector can be obtained once the coordinates of the sample points are known, regardless of their energies. For the present application, we find the first form, eq 5, more convenient and efficient.

The trend function μ can in principle be chosen in a number of ways, giving rise to different Kriging variants. Its role is providing a base or default value in the absence of any data, or far from any sample point. In simple Kriging, μ is given a fixed constant value, as a parameter or determined by the problem to solve. In ordinary Kriging, it is also a constant, but its value is determined from the source data, to reflect the expectation value of the underlying random process. In universal Kriging, it is a general function of the coordinates, μ(q), with parameters that are to be determined as part of the Kriging procedure. In the rest of this work, we will refer only to simple Kriging, so the trend function μ is effectively an externally defined constant.

3.2. Gradient-Enhanced Kriging

In many optimization problems, it is usual that not only the value of the function but also its derivatives with respect to the coordinates are available. Molecular geometry optimizations are no different and in addition to the energy, at a particular sample point, E(q_i), one can often compute the gradient, g(q_i) = ∇E(q_i), efficiently.

The formulation of GEK has been presented in two different ways—the indirect and the direct versions—where the latter is a mathematically more strict extension, and this is the version we used in the present algorithm. In this approach, the gradient data are added explicitly to the equations, such that

9

where u is a new set of weights particular to the gradient information. The whole affair can be included in the original formalism by simple generalization of the covariance vector v, the covariance matrix M, the column vector of function values y, and the vector 1, such that the contribution from the gradient information is included in a consistent way (for details consult ref (18)). Note that now the basis functions for the surrogate model are not only the covariance functions centered at each sample point, v_i(q) but also the derivative of each with respect to every degree of freedom k, .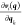

3.3. Details of the Covariance Function

The covariance function f plays a central role in the Kriging and GEK model, being used in the definition of M and v. It expresses the expected correlation between data point energies, based on the difference in their coordinates. Informally, basic requirements on f are that it should give 0 for points at infinite distance, and 1 for identical points; it should also be independent of the order of the points, f(x,y) = f(y,x); furthermore, it should produce an invertible M if eq 1 is to be used. A more rigorous description of covariance functions can be found, for example, in ref (32).

Common covariance functions are the exponential, squared exponential (Gaussian), and Matérn covariance functions. The latter is a family that can be tuned with a parameter p and includes the first two as special cases. For integer non-negative values of p, the Matérn covariance function can be written as the product of an exponential and a polynomial of order p

10

which simplifies to the exponential covariance function for p = 0

11

and to the squared exponential or Gaussian covariance function in the limit p → ∞

12

(Note that d_ij is a distance and always non-negative, eq 3.)

Because the predictor is expressed as a linear combination of basis functions, and the coefficients w,u are independent on the predicted coordinate q, obtaining analytical derivatives for the predictor is trivial as long as the corresponding derivatives for the covariance function are available. In the GEK formalism, the surrogate model includes first derivatives of the covariance function. Therefore, in order to compute analytical Hessians, we require that at least up to third derivatives of the covariance function be defined.

The derivative of f₀ is undefined at d_ij = 0, as it shows a cusp and will not even be appropriate for building a GEK model. The Gaussian covariance function, however, is infinitely differentiable. Other members of the Matérn family are differentiable up to order 2p, which sets a minimum value of p = 2 for our GEK-based optimization

13

this is also known as the Matérn-5/2 covariance function, due to a more general parameterization in terms of 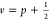. Following ref (20), we used f₂ as the covariance function for our model.

3.4. Restricted-Variance Optimization

Among the most successful second-order methods for molecular structure optimizations is the rational function approach.^33,34 In particular, the automatic restricted-step version of the method,¹ restricted-step rational-function optimization (RS-RFO), has proven to be a robust optimizer.³⁵ It is critical to the optimization procedure that no steps are taken such that the new structure is outside of the range in which the second-order approximation is valid. Hence, the step-restriction element of the procedure is instrumental for successful optimizations. This approach, however, has a shortcoming: the size of the step restriction has to be chosen. Here, ad hoc procedures and experimentation have led to reasonable rules for how large such restriction is and how this value can be modulated during the course of the optimization.

The GEK model, in difference to any second-order optimization procedure, contains an explicit measure of the quality of the surrogate model—the expected error or variance at any given structure. If the electronic structure calculations are reproducible, the corresponding energy at a sample point is known with certainty and the variance should be zero; however, for any other structure the predicted variance, s²(q), can be used as a measure of the reliability of the surrogate model. Hence, a restricted-variance optimization (RVO) scheme has been implemented in which the step restriction in the microiterations is not done with respect to the size of the displacement but according to whether the predicted variance at the new structure is below a tolerated threshold. If not, the step length is reduced until the value of the variance is below the threshold. Because the variance restriction will not limit the step size in absolute terms, it has a definite advantage in exploring large geometry displacements if this is supported by an acceptable variance.

For a positive definite M (which is guaranteed by a Matérn covariance function), the expected variance for the prediction is given by³⁶

14

where the first factor accounts for the variance of the sample points, while the second measures the distance of q to the sample points, and will give zero whenever q = q_i. Assuming a Gaussian variance, the actual energy can thus be estimated, with a 95% confidence, to lie in the interval .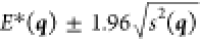

The variance restriction is enforced by making sure that every microiteration (see Figure 1, bottom right) produces a 95% confidence interval within the specified threshold, that is

15

If that is not the case, the step restriction is halved and the microiteration is recalculated. If the step restriction becomes very small, or the predicted variance is very close to the threshold, the microiterations are stopped. The microiterations are considered converged, and therefore stopped, when they satisfy the global convergence criteria and the predicted gradient is smaller than the gradient at the last macro iteration; this is to ensure improvement when the gradient is already converged, but not the step size. The micro iterations are also stopped when they reach a maximum iteration number.

3.5. Selection of Characteristic Lengths

The GEK model has a number of parameters that can be adjusted, namely the characteristic lengths—l_k values—and the trend function μ. A usual strategy is to adjust these l values to maximize the likelihood³⁷ and the trend function to make sure that the surrogate model is bound—that it has at least a minimum at a finite distance from the sample points. In practice optimizing the l values is a nontrivial task in itself and, especially with large number of dimensions, can be a computational bottleneck.

The role of the l values is to provide an individual length scale for each coordinate. The energy can be expected to be very sensitive to small changes in some coordinates (e.g., strong bonds), while large changes in other coordinates are needed to produce significant energy changes (e.g., weak dispersion interactions). To some extent, this same information is encoded in the approximate HMF Hessian, which assigns an estimated force constant to each degree of freedom. Thus, in this research project a completely different way to select the “optimal” l values is suggested. In line with the design considerations mentioned above, these parameters will be set such that the curvature of the surrogate model at the latest sample point, i, reproduces the HMF approximate Hessian if the model is built with only this sample point. This is implemented as follows.

First, we note that with a single sample point the surrogate model Hessian is diagonal, with elements given by

16

Therefore, we first diagonalize the approximate Hessian, yielding linear combinations of coordinates as eigenvectors. The subsequent optimization will be in the basis of these eigenvectors. In our approach, as in ref (20), the trend function μ is set as the maximum energy value among the sample points, E_max, plus a constant, to ensure a bound surrogate model; therefore, μ – E_max is a constant and equal to μ – E(q_i) when the model is built with this single sample point because E_max = E(q_i) in this case. It follows that the l values can be set, for a Matérn-5/2 kernel, eq 13, from the following expression

17

where l_k is the characteristic length of coordinate k and H_kk is the corresponding eigenvalue of the approximate Hessian (which is always positive definite⁴). In this way, the surrogate model Hessian exactly matches the HMF Hessian evaluated at the sample point q_i. It is prudent to point out that because every new structure has its own approximate Hessian, the l values are re-evaluated on each (macro) iteration. Hence, this procedure corresponds to a dynamic change of the l values during the course of the optimization. To avoid too large characteristic lengths, H_HMF(q_i)_kk is set to be no smaller than some threshold. It should also be emphasized that the surrogate model’s Hessian only matches the approximate Hessian if the model is built with a single point (something that will only be actually done on the first macro iteration), but this condition is used to define the l values. As further sample points are added to the model, the surrogate model’s Hessian at the latest point will be modified. Thus, including more sample points effectively replaces the Hessian update procedure of standard quasi-Newton methods.

3.6. GPR versus RVO

Before continuing, the key differences between the present implementation (RVO) and that by Denzel and Kästner (GPR)²⁰ are highlighted in some detail. In the GPR implementation, Cartesian coordinates were employed, an assortment of different thresholds for step restrictions (0.5 a₀ to 5 a₀) were applied for different optimization methods, the underlying optimization method was a L-BFGS algorithm with a “window” (number of steps in memory) equal to the number of dimensions of the molecular system, a special design is implemented to facilitate overshooting, a single l value of 20 a₀ is used, and, finally, a multilevel surrogate model is implemented. This is to be compared with the present implementation (RVO) which uses force-constant-weighted internal coordinates (the surrogate model is now translational and rotational invariant), a variance restriction is implemented, the underlying optimization method in the micro iterations is a RS-RFO procedure, the GEK-supported optimization uses the data of a limited set of structures (10, see below) to generate the surrogate model, no special features (e.g., overshooting) are implemented to accelerate the optimization, multiple l values are automatically selected based on the HMF approximate Hessian, and no multilevel procedure is engaged.

The implementation by Jacobsen and co-workers²² is in many aspects similar to the one of Denzel and Kästner,²⁰ in that it uses Cartesian coordinates and a single l value. However, the latter is dynamically updated maximizing the marginal likelihood during each optimization. Computational results are presented for seven molecular systems ranging from crystal structures and clusters to small molecules.

Compared with Meyer and Hauser’s implementation of GPR with internal coordinates,²³ the main differences are that they define the internal coordinates at the initial structure, do not employ force constant (Hessian) information to define the coordinates, use a single l value for all coordinates, which they optimize by minimizing the likelihood, and apply a cumulative step-length restriction on the micro iterations. In contrast, we redefine the internal coordinates at every macroiteration using a force-constant-weighted approach, the l values are defined from the HMF Hessian, and the micro iterations are limited by a maximum variance, not a maximum step length. Indeed, they write: “a slightly worse performance can be expected for longer trajectories, possibly requiring an occasional reconstruction of the active set of coordinates” and “future undertakings will have to encode this knowledge [force constants and couplings], e.g., via a pre-informed choice of hyperparameters in their machine learning models”. The present method addresses these two points exactly (without previous knowledge of their work, we may note).

4. Computational Details

The new optimization procedure has been implemented in the Slapaf module of the open-source OpenMolcas quantum chemistry program package.³⁸ The linear system of equations (eq 6, extended with gradients¹⁸) is solved using the standard LAPACK routine dposv.³⁹ Benchmark calculations are performed to test the hypothesis that GEK-supported geometry optimization does not need vast amount of data but is already superior to standard second-order methods with few sample points. Further goals of the benchmarks are to investigate and document the significance of restricted-variance optimizations when starting at a structure far from the final one and the ability of GEK-supported optimization to cope with anharmonic or very flat energy surfaces.

Below, the benchmarks are described in some detail, followed by a brief presentation on how the remaining hyperparameters of the GEK model and RVO procedure were optimized.

4.1. Benchmark Test Suites

For the benchmarking of the method the following test suites have been employed: (i) the Baker equilibrium structures, extended by including three additional molecules used as sample cases in the original paper (e-Baker),⁴⁰ (ii) the Baker transition state structures (Baker-TS),⁴¹ and (iii) the S22 suite designed by Hobza and coworkers.⁴² The first set is included for reference and to demonstrate that GEK-supported optimization has advantages already for cases where conventional methods converge fast. The second set of structures was initially designed for benchmarking transition state optimizations with initial starting structures close to the expected transition state structures. However, here, as in ref (20), the starting structures are employed to compute the equilibrium structures of the reactants or the products. In this sense, the test set provides starting structures that are not trivially close to a converged structure. It is expected that this would exhibit the superiority of the new approach as compared to conventional methods. However, the analysis will be possibly blurred by the selected restricted step, which ultimately could be the most significant contribution to slow convergence. Nevertheless, it will possibly expose the benefits of a restricted-variance optimization. Furthermore, the test set is included here so that a direct comparison can be made to the work of Denzel and Kästner.²⁰ The latter test suite—S22—will allow for an analysis of the significance of weak interactions. This suite contains 22 van der Waals complexes in which dispersion and/or hydrogen bonding dominate the interactions.

Initially, the e-Baker test suite is used as a training set for the hyperparameters (see below), in combination with the Hartree–Fock method and a 6-31G basis set. Benchmark calculations are then conducted for the e-Baker and Baker-TS test suites at the DFT level of approximation, using the B3LYP functional and def2-SVP basis set. For the S22 test suite, MP2 calculations were performed using the 6-31G** basis set. The RVO optimization procedure was benchmarked against the standard optimization procedure, as implemented in OpenMolcas using default options. This implementation is a RS-RFO procedure which uses a step restriction of 0.3 au, force-constant-weighted internal coordinates, the HMF approximate Hessian, and BFGS Hessian updates. No symmetry constraints were used, unless explicitly mentioned. The convergence criteria, used both for the RVO and standard optimizations, were the default values: gradient root-mean-square (rms) and maximum component below 3 × 10⁴E_ha₀^–1 and 4.5 × 10⁴E_ha₀^–1, respectively; displacement rms and maximum component below 1.2 × 10³a₀ and 1.8 × 10³a₀.

To reduce the influence of numerical noise in the comparisons and to ensure a proper description of the PES around equilibrium structures, especially in dispersion- or BSSE-bound complexes of the S22 and Baker-TS sets, the accuracy of the computed energies and gradients was increased 2–3 orders of magnitude from the default. We note, however, that the results for the e-Baker and Baker-TS sets do not change significantly due to the increased accuracy. In the Supporting Information, we include tables obtained with the default OpenMolcas accuracy, that can be compared with Tables 1 and 2.

Table 1. Number of Macroiterations to Converge the Molecular Geometry Optimization of the Molecular Structures of the e-Baker Test Suite Using Conventional RS-RFO and RVO Supported by GEK^a.

	HF/6-31Gb		DFT(B3LYP)/def2-SVP
molecule	RS-RFO	RVO	RS-RFO	RVO	rmsd
1: water	3	3	4	4	0.000
2: ammonia	4	4	3	4	0.000
3: ethane	5	4	4	4	0.000
4: acetylene	4	4	3	4	0.000
5: allene	4	3	4	4	0.000
6: hydroxysulphane	7	7	7	6	0.000
7: benzene	3	3	4	3	0.000
8: methylamine	5	5	3	3	0.000
9: ethanol	5	5	5	4	0.000
10: acetone	5	5	5	5	0.000
11: disilyl ether	14	11	15	12	0.000
12: 1,3,5-trisilacyclohexane	12	10	34	13	0.003
13: benzaldehyde	6	6	6	6	0.000
14: 1,3-difluorobenzene	5	4	5	4	0.000
15: 1,3,5-trifluorobenzene	5	4	8	4	0.000
16: neopentane	4	4	6	4	0.001
17: furan	5	5	5	5	0.000
18: naphthalene	5	4	5	5	0.000
19: 1,5-difluoronaphthalene	5	5	5	5	0.000
20: 2-hydroxybicyclopentane	15	13	12	13	0.001
21: ACHTAR10	10	9	29	16	0.002
22: ACANIL01	6	6	6	6	0.000
23: benzidine	10	9	11	8	0.000
24: pterin	7	7	7	6	0.000
25: difuropyrazine	6	5	6	5	0.000
26: mesityl oxide	7	6	7	6	0.000
27: histidine	29	24	33	28	0.003
28: 2,3-dimethylpentane	27	23	18	23	0.015
29: caffeine	7	6	7	6	0.000
30: menthone	32	21	25	25	0.004
31: ACTHCP	21	16	21	18	0.001
32: histamine–H+	17	14	18	14	0.000
33: hydrazobenzene	16	15	26	18	0.004

^aHighlighted in bold are cases where the difference between both methods is larger than 1 iteration. The last column shows the root mean square displacement (rmsd, in Å) between the final structures of the previous two columns.

^bStep and variance restrictions are disabled.

Table 2. Number of Macroiterations to Converge the Molecular Geometry Optimization of the Molecular Structures of the Baker-TS Test Suite Using Conventional RS-RFO and RVO Supported by GEK^a.

	this work			ref (20)b		RVO vs GPR
reaction	RS-RFO	RVO	rmsd	L-BFGS	GPR	rmsd
1: HCN ⇌ HNC	12	13	0.000	22	18	0.000
2: HCCH ⇌ CCH2	13	12	0.000	24	20	0.000
3: H2CO ⇌ H2 + CO*	32	36	0.985	59	103	0.557
4: CH3O ⇌ CH2OH	7	7	0.000	18	15	0.000
5: ring opening cyclopropyl*	24	11	0.842	42	37	0.842
6: ring opening bicyclo[1.1.0]butane (TS 1)	19	13	0.000	30	28	0.001
7: ring opening bicyclo[1.1.0]butane (TS 2)	23	13	0.000	54	48	0.001
8: 1,2-migration β-(formyloxy)ethyl	36	28	0.001	87	93	0.005
9: butadiene + ethylene ⇌ cyclohexenec*	116	75	0.009	89	122	1.005
10: s-tetrazine ⇌ 2HCN + N2	9	7	0.000	15	21	0.000
11: trans-butadiene ⇌ cis-butadiene	9	6	0.000	32	30	0.001
12: CH3CH3 ⇌ CH2CH2 + H2	11	9	0.000	24	16	0.000
13: CH3CH2F ⇌ CH2CH2 + HF	11	7	0.000	20	15	0.001
14: vinyl alcohol ⇌ acetaldehyde	15	13	0.000	19	26	0.001
15: HCOCl ⇌ HCl + CO	10	8	0.000	12	12	0.000
16: H2O + PO3– ⇌ H2PO4–	32	28	0.002	64	74	0.001
17: CH2CHCH2–O–CHCH2 ⇌ CH2CHCH2CH2CHO	26	21	0.002	98	73	0.008
18: SiH2 + CH3CH3 ⇌ SiH3CH2CH3	17	17	0.001	44	38	0.008
19: HNCCS ⇌ HNC + CS	17	13	0.000	25	19	0.001
20: HCONH3+ ⇌ NH4+ + CO	13	9	0.000	21	19	0.000
21: rotational TS in acrolein	21	12	0.000	49	47	0.001
22: HCONHOH ⇌ HCOHNHO	11	9	0.000	23	20	0.000
23: HNC + H2 ⇌ H2CNH	15	10	0.000	21	18	0.000
24: H2CNH ⇌ HCNH2	16	13	0.000	25	18	0.000
25: HCNH2 ⇌ HCN + H2*	48	42	0.482	254	30	1.197

^aThe root mean square displacement (rmsd, in Å) between the final structures is shown in the third numerical column. As a reference the GPR and L-BFGS results of Denzel and Kästner, using DFT, are listed. Finally, the rmsd between the RVO and GPR optimized structures is presented. Highlighted in bold are cases where the difference between the first two columns is larger than 1 iteration. An asterisk marks cases where RVO clearly converges to a different local minimum from RS-RFO and/or GPR.

^bSee Table S2 in ref (20).

^cRS-RFO and RVO optimizations performed with symmetry constrained to C_s.

4.2. GEK Hyperparameter Optimization

There are two hyperparameters affecting the GEK surrogate model: The characteristic lengths or l values, and the trend function μ. As mentioned above, it is possible to optimize the l values by maximizing a likelihood function, but we chose to set them derived from the HMF approximate Hessian (eq 17). This leaves the trend function as the only hyperparameter to optimize. We set it as some energy above all the sample points used to build the model, to guarantee that the surrogate model contains at least a minimum in the region close to the sample points. We note that our l values actually depend on the value of the trend function.

It was observed that in the optimizations of the e-Baker test suite, where initial structures are relatively close to the final minima, step restriction based on length or variance is not an important feature. Thus, step and variance restriction in RS-RFO and RVO were disabled for the HF e-Baker test suite, and the value of the trend function was coarsely optimized by minimizing the total iteration count in this set. The final value we arrived at was 10.0E_h above the highest energy of the sample points; this is, by the way, identical to the value used in ref (20). Note also that this value corresponds directly to (μ – E_max) in eq 17.

It can be argued that there are additional hyperparameters, which we set somewhat arbitrarily: the covariance function was chosen, as described above, to be the Matérn-5/2 covariance function, we did not test other possibilities. The minimum value for the HMF Hessian eigenvalues (affecting the maximum allowed l value) is 0.025E_ha₀^–2. The number of sample points (geometries, energies and gradients) selected to build the surrogate model was limited to 10, and these are simply the last 10 macro iteration points; this number is twice the default number of iterations used to update the Hessian matrix in the RS-RFO procedure. The limited number of sample points is sufficient to acquire accuracy around the stationary point which is the target of the optimization. A much larger number of sample points would, of course, have to be used if the purpose were to generate a global surrogate model. It is our experience, during this project, that the convergence rate is rather insensitive to the number of sample points once it exceeds 5. As a compromise between the additional CPU time of the RVO, as compared to RS-RFO, and superior convergence of the former, we have selected to use 10 sample points.

4.3. RVO Parameters

The main parameter affecting the RVO optimization, once the surrogate model has been defined, is the variance restriction or the maximum allowed uncertainty in the energy prediction, eq 15. The threshold is designed to be a factor (formally of length dimensions) times the largest Cartesian gradient component for the last iteration, and no lower than a minimal value. The minimal value was set very small, at 10^–10E_h, while the factor was optimized by minimizing the iteration count in some “difficult” cases (especially #21 in DFT e-Baker and #3, #8 and #25 in Baker-TS), while at the same time avoiding convergence problems related to transformation from internal coordinates to Cartesians, which can occur for large displacements. The final value was 0.3a₀.

The initial step restriction for the microiterations (Figure 1, bottom right) is set to the larger of the default value (0.3 au) and 10³ times the gradient norm (in atomic units). The microiterations are stopped if the predicted variance is within 0.1% of the threshold, or if the step size is below 10^–5 times the initial one. The maximum microiteration count (never reached in our final calculations) was set to 50.

5. Results and Discussion

In analyzing the character and robustness of the GEK-supported molecular geometry optimization, three different test suites were employed, the e-Baker, Baker-TS, and S22 test suites—results are listed in Tables 1, 2, and 3. These test suites will measure the performance for optimizations of covalently bonded systems, cases when starting structures are far from the equilibrium structures, and cases of dispersion- and hydrogen-bonded systems. The three different cases are discussed separately below.

Table 3. Number of Macroiterations to Converge the Molecular Geometry Optimization of the Dimers of the S22 Test Suite Using Conventional Restricted-Step Rational-Function (RS-RFO) and RVO Supported by GEK^a.

complex	RS-RFO	RVO	rmsd
Hydrogen-bonded Complexes
1: (NH3)2	5	6	0.000
2: (H2O)2	6	6	0.001
3: formic acid dimer	7	6	0.000
4: formamide dimer	7	6	0.000
5: uracil dimer HB	7	6	0.000
6: 2-pyridoxine·2-aminopyridine	15	16	0.001
7: adenine·thymine WC	18	14	0.001
Dispersion Dominated Complexes
8: (CH4)2	20	16	0.004
9: (C2H4)2	5	3	0.000
10: benzene·CH4	4	3	0.010
11: PD benzene dimer	7	15	0.000
12: pyrazine dimer	8	11	0.002
13: stacked uracil dimer	24	20	0.001
14: stacked indole·benzene	61	122	0.044
15: stacked adenine·thymine	29	23	0.002
Mixed Complexes
16: ethene·ethyne	6	6	0.000
17: benzene·H2O	35	29	0.002
18: benzene·NH3	33	29	0.002
19: benzene·HCN	31	7	0.027
20: T-shaped benzene dimer	5	7	0.000
21: T-shaped indole benzene	4	7	0.001
22: phenol dimer	21	17	0.003

^aHighlighted in bold are cases where the difference between the two methods is larger than 1 iteration.

However, before we commence with this, a brief statement on the additional timing accrued due to the use of GEK rather than RS-RFO is in order. It is our experience that with the limited number of sample points used in our test, 10, that additional CPU time is insignificant compared to the timing of computing energies and gradients. As an example, for the histamine–H⁺ molecule (#32 in the e-Baker set), performing a DFT calculation of the energy and gradient evaluation took little more than 6 min, whereas at the 10th iteration both the RVO and RS-RFO required less than 1 s of CPU time.

5.1. e-Baker Test Suite

In the HF/6-31G run, all systems converge smoothly with both RS-RFO and RVO methods. We remind that these calculations were done with no effective step restriction. The total number of iterations was reduced from 316 with RS-RFO to 270 with RVO (Table 1), a 15% reduction, mostly due to a better performance in the more difficult cases (#27 and later). Although the value of the trend function was optimized to the performance in this test suite, we did not find a great dependence on the exact value. Values from 1.0E_h to 100.0E_h above the maximum energy give results, with total number of iterations ranging from 290 to 275, respectively. This shows that the choice of the trend function value is not critical for a successful optimization, and setting the l values in a consistent manner as in eq 17 compensates for the scale changes. Nevertheless, we observe that the low end of trend function values results in too small l values, too small step sizes, and larger number of iterations (e.g., 386 iterations with 0.1E_h).

In the B3LYP/def2-SVP run, normal step restrictions are applied to both RS-RFO and RVO, although the only cases where they were effective for more than one step were #6, #20, and #33 with RS-RFO and #33 with RVO. The value of the trend function was not further optimized for this run, and we see a similar behavior, with RVO in general outperforming RS-RFO, especially for the cases with more iterations. The only case where RVO is significantly (more than 1 iteration) worse than RS-RFO is #28, which is also the case where the final geometries differ the most (rmsd 0.015 Å), and RVO reaches an energy 0.0017 kcal/mol lower. The gradient is converged after four iterations with both methods, and the rest of the iterations are spent in converging the step size, it could be argued that RS-RFO reaches a spurious early convergence. The total number of iterations is reduced from 357 with RS-RFO to 291 with RVO, almost a 20% reduction.

Our expectations for the e-Baker test suite were that GEK-supported optimization would be at best on par with standard methods—the latter having been developed over the last 40 years since Pulay suggested the direct use of analytic gradient to investigate molecular potential energy surfaces.⁴³ In particular, enormous progress on this matter was attributed to the development of the use of internal coordinates, Hessian-update methods, and restricted-step second-order optimization methods. Hence, it is a pleasant surprise that the GEK-supported optimization procedure in most cases equals or outperforms a state-of-the-art standard optimization method.

5.2. Baker-TS Test Suite

For the Baker-TS test suite, a more significant difference between conventional and GEK-supported optimization is expected. Indeed this is observed (see Table 2). However, the comparison with the results of Denzel and Kästner²⁰ offers first the following observation: while their GPR implementation outperforms the L-BFGS option, both are remarkably inferior to the conventional RS-RFO implementation in the OpenMolcas package. This is most likely a manifestation of the importance of using internal coordinates, as already shown in other works,^23,29,44,45 and a reasonable estimate for the initial approximate Hessian, but can also be affected by the differences in optimization method and convergence criteria. When comparing the results obtained for this work (RS-RFO vs RVO), it is seen that RVO in general excels over the conventional RS-RFO procedure. In particular, excluding #3, #5, and #25, which converge to different final geometries and should not be directly compared, the total number of iterations is reduced from 459 to 343, a 25% reduction. In practically all cases, the number of iterations is reduced by two or more.

Because the initial structures are close to a transition state, it should not be surprising that we find some cases where different methods converge to different structures. However, it is only in #5 that the differences are due to converging to different sides of a saddle point—RVO converges to cyclopropyl, RS-RFO, and GPR converge to allyl, and changing the step or variance restriction can change the outcome. In the other starred cases in Table 2 (#3, #9, #25), the final structures are weakly bound complexes and different local minima are found. In #3, RS-RFO converges to O–C···H–H, RVO converges to C–O···H–H, and GPR converges to a bent C–O···H–H structure. In #25, RS-RFO and RVO converge to H–C≡N···H–H but differ in the orientation of the H₂ molecule, whose H atoms are not equivalent in the initial structure; GPR converges to HCN + H₂ with no discernible intermolecular bonding pattern. In #9, RS-RFO and RVO converge to practically the same structure; the differences with GPR are displayed in Figure 2. The surface is very flat and the gradient for RS-RFO and RVO is already converged after around 20 iterations.

Figure 2.

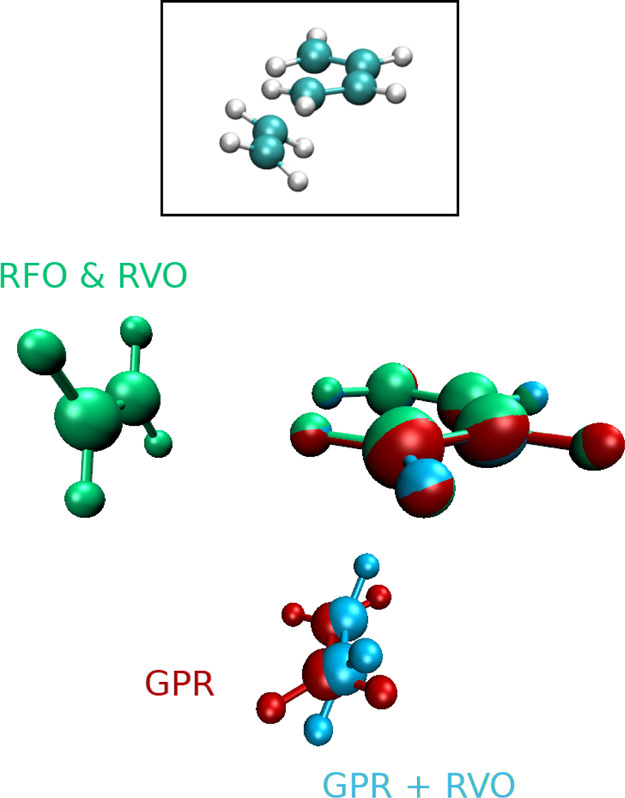
Structures of the butadiene + ethylene complex. Color coding: cyan & white (framed)—the starting structure in the Baker-TS test suite (#9) (ref (41)); green—the optimized structure with RS-RFO and with RVO; red—the GPR optimized structure (ref (20)); blue—the RVO optimized structure starting from the red one.

5.3. S22 Test Suite

The results for the S22 test suite are presented in Table 3. We expect this set to show differences due to the different ability of second-order and GEK surrogate models for describing anharmonicities. However, this effect is probably obscured by the fact that the initial structures are relatively close to the final minimum and that the PES is in most cases very flat.

This suite is divided in three sections according to the dominant character of the intramolecular interactions. The first section, dominated by hydrogen bonds, is characterized by relatively strong interactions and we see a similar behavior as in most of the e-Baker test suite: RS-RFO does good job and RVO is of about the same or slightly better quality. The second section contains cases where the interactions are mostly due to dispersion. Here the differences are larger, and more mixed; in cases #15, #11 and #14 RVO performs worse than RS-RFO. In the third section, mixed complexes, results are mixed too; in cases #20 and #21 RVO performs slightly worse, and in #19, the large difference in iteration count can be attributed to a spurious early convergence of RVO, to a structure 0.0066 kcal/mol higher in energy than RS-RFO. We notice that in the cases where RVO performs worse, and particularly in #14, the PES is extremely flat and RVO takes very many iterations (from iteration 50 to 122, the energy descends monotonously less than 0.01 kcal/mol). Overall, the total iteration count is 358 with RS-RFO and 375 with RVO or, excluding #14 and #19 (where the geometry differences are the largest), 266 and 246, respectively.

Although we did not see the expected improvement with RVO for the S22 suite, we believe these results are satisfactory, considering that these systems were in no way included in the optimization of the GEK parameters and RVO procedure, and that the observed deficiencies can probably be overcome either by a further improvement of the settings (e.g., the minimal force constant of 0.025E_ha₀^–2 could be too large for these systems, which would benefit from longer characteristic distances) or by implementing specific overshooting procedures as in ref (20).

5.4. Global Results

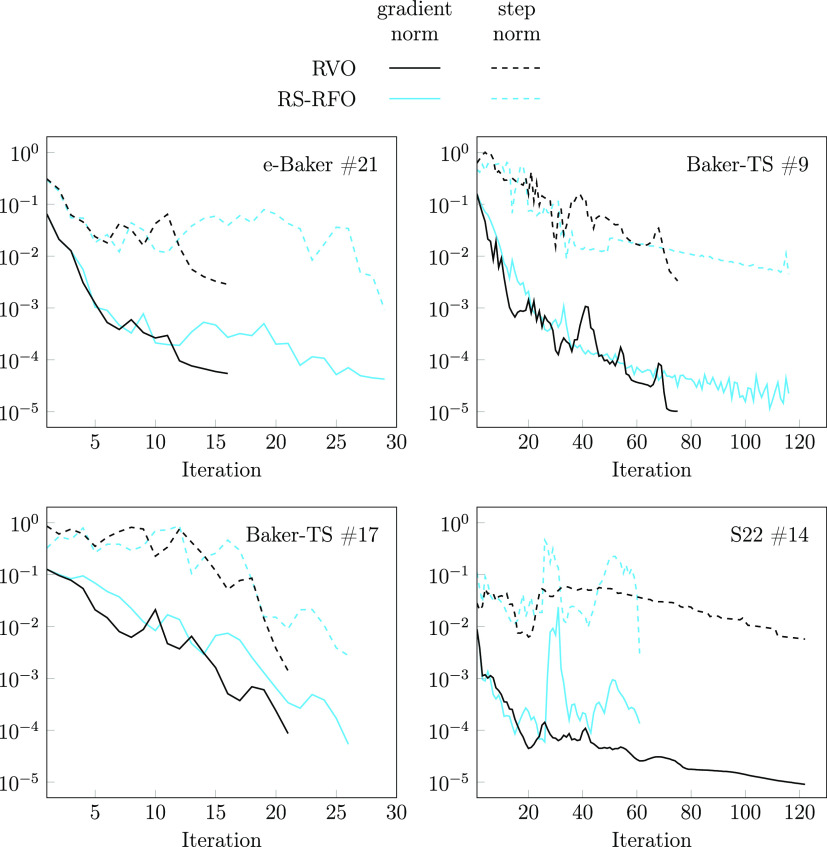
As examples, in Figure 3 we represent the convergence behavior of four selected cases, comparing the evolution of the gradient and the change in geometry with RS-RFO and RVO. The first case corresponds to #21 in the e-Baker suite (with DFT), for which RVO converges some 13 iterations earlier than RS-RFO. In the second half of the optimization, RS-RFO fails to significantly reduce the gradient, possibly due to taking too large steps (dashed blue line). The second example is #9 in the Baker-TS suite, which takes many iterations with both methods, with RVO again outperforming RS-RFO. After some 40 iterations, RS-RFO more or less consistently but slowly reduces the gradient and step size, while the rate of decrease of RVO is faster, and it shows some punctual increases in the gradient that are compensated after a few iterations. The third example is #17 in the Baker-TS suite, displaying a qualitatively similar behavior with both optimization methods, but again somewhat faster with RVO. Finally, the last plot corresponds to the worst case for RVO, #14 in the S22 suite. Here, RVO needs twice as many iterations as RS-RFO, and the roles are practically inverted with respect to Baker-TS #9. It is evident that the gradient is below the convergence threshold (compare with the RS-RFO gradient at the last iteration) since very early, and it is only the reduction of the step size that requires more iterations, which for RVO results in a painfully slow process. It is, in fact, a general observation that the gradient tends to converge faster than the step size.

Figure 3.

Evolution of the Euclidean norm of the gradient (solid lines) and step size (dashed lines), in Cartesian coordinates and atomic units, during the optimization for 4 selected cases. Data for RS-RFO in blue and for RVO in black.

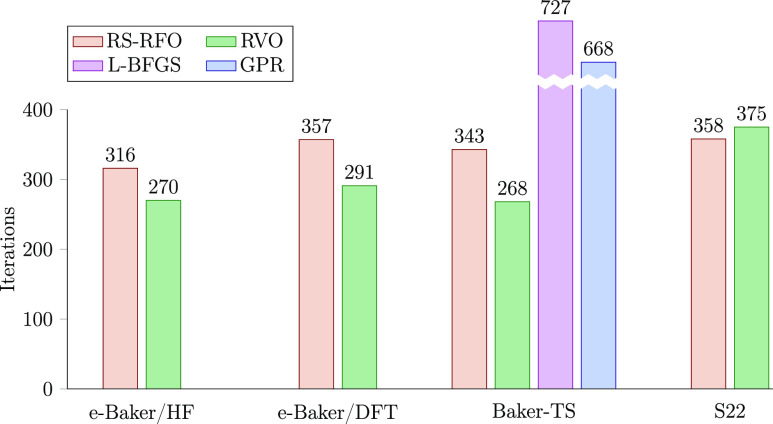
To summarize the results, we show in Figure 4 the total iteration count of the different test sets. The large difference between RS-RFO/RVO and L-BFGS/GPR can mostly be attributed to the use of internal coordinates in the former methods. It can nevertheless be noted that the improvement from RS-RFO to RVO is larger than from L-BFGS to GPR, both in absolute and relative terms, although it could be that the L-BFGS results include cases where it converges to a different structure from GPR.

Figure 4.

Total iteration counts in the different benchmark sets, obtained with the RS-RFO and RVO methods. For comparison, the results from ref (20) for the Baker-TS set are also provided (L-BFGS and GPR). In the Baker-TS results, cases #3, #5, #9, and #25 have been excluded for all methods.

6. Summary

In this paper we report a gradient-enhanced-Kriging-supported algorithm for molecular geometry optimizations. The implementation uses the standard tools that have marked the success of state-of-the-art molecular geometry optimizations, in particular the use of internal coordinates and approximate Hessian. The approximate Hessian provided by the HMF is first used to define a nonredundant set of internal coordinates to describe molecular geometries, and the surrogate model is therefore invariant to translations and rotations. In addition, the approximate Hessian’s eigenvalues are used to determine the characteristic lengths of the different dimensions, avoiding a costly hyperparameter optimization while including a discrimination between the different degrees of freedom. Once the surrogate model is built, the minimum is found via microiterations, with the constraint that the predicted variance or uncertainty must be below a dynamic threshold, proportional to the last computed gradient.

The proposed method has been tested on three different sets of systems, comparing in most cases favorably to a conventional optimization algorithm. In cases where the geometry changes are large (Baker-TS), the new method yields a significant reduction of iteration count, and even when the initial geometry is close to the converged structure (e-Baker, S22) the performance is usually at least on par with a standard second-order optimization. The only cases where we noticed a performance degradation are characterized by very weak forces and slow convergence, further optimization of the method or specific actions may be needed for these cases.

To conclude, a new method for geometry optimization has been presented. Although in its infancy it is robust and efficient. Besides its advantage in terms of number of iterations, the new method removes the need for ad hoc update procedures for trust radius or approximate Hessian, commonly found in conventional quasi-Newton methods.

To comment, finally, on another quote from Meyer and Hauser:²³ “The latter [well-established optimizer packages as they are implemented in most computational chemistry program packages] are still outperforming Gaussian process regression, even if formulated in internal coordinates, but take large advantage of hard-coded physical knowledge, which has been gathered through decades of research and continuous fine-tuning”. In this work we propose a simple way of incorporating this “hard-coded physical knowledge” into the GEK model, and our results confirm that this results in a method capable of competing with “well-established optimizer packages” (at least one, as implemented in one quantum chemistry program package).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00257.

• Results for e-Baker and Baker-TS suites with default accuracy for energies and gradients (PDF)

• Input file templates for the benchmark calculations and resulting Molden⁴⁶ files, including initial, intermediate, and final structures (ZIP)

The authors declare no competing financial interest.