Kernel-Based Machine Learning for Efficient Simulations of Molecular Liquids

Abstract

Current machine learning (ML) models aimed at learning force fields are plagued by their high computational cost at every integration time step. We describe a number of practical and computationally efficient strategies to parametrize traditional force fields for molecular liquids from ML: the particle decomposition ansatz to two- and three-body force fields, the use of kernel-based ML models that incorporate physical symmetries, the incorporation of switching functions close to the cutoff, and the use of covariant meshing to boost the training set size. Results are presented for model molecular liquids: pairwise Lennard-Jones, three-body Stillinger–Weber, and bottom-up coarse-graining of water. Here, covariant meshing proves to be an efficient strategy to learn canonically averaged instantaneous forces. We show that molecular dynamics simulations with tabulated two- and three-body ML potentials are computationally efficient and recover two- and three-body distribution functions. Many-body representations, decomposition, and kernel regression schemes are all implemented in the open-source software package VOTCA.

1. Introduction

Machine learning (ML) techniques have a long history of interpolating the high-dimensional potential energy surface (PES) of molecular systems.¹⁻⁴ Access to an accurate PES enables the simulation of the system’s dynamics. In comparison to standard molecular dynamics (MD),⁵ ML does not explicitly rely on fixed force field functions. This has recently resulted in impressive MD studies for various materials and molecular systems.⁶⁻¹²

To get there, it does not quite suffice to gather reference configurations and train a Gaussian process (GP) or neural network—the interpolation space is simply too large for all but the simplest of systems. Instead, incorporating physical symmetries in the ML model effectively reduces the interpolation space, thereby helping convergence. An early realization of this aspect was demonstrated by Behler and Parrinello, who relied on symmetry functions to incorporate translational and rotational invariance:¹³ If the physics of the problem does not depend on arbitrary translations, encode particle geometries by means of relative distances. A number of molecular representations have since built on these ideas to offer more efficient learning performance.^11,14−16 Other aspects that aim at incorporating physics include local dynamical symmetries found in molecules¹⁷ and the learning of tensorial properties.¹⁸⁻²⁰

Incorporating symmetries does not have to be done at the level of the representation: one can also build it in the ML architecture. When building kernel-based ML models for force fields, the GP aims at inferring a vector-valued function.²¹ The underlying vector field ought to remain curl-free—directly related to energy conservation in simple Hamiltonians—which can be implemented by learning the Hessian of the kernel.^22,23 Several variants of this strategy have by now been implemented to learn energy-conserving force fields.^6,10,24,25 In parallel, the learning of forces has sparked interest in building so-called covariant kernels, meaning that the prediction rotates with the sample in three-dimensional space. Glielmo et al. have derived an analytic expression for a covariant Gaussian kernel.²⁶ It effectively builds on the integration over all actions of the rotation group by means of a Haar measure.²⁷ Covariant ML models have more recently been developed for neural networks.^28,29

In addition to symmetries, physical intuition and approaches can be further implemented to help build better ML models. Rather than learning the full PES at once, it can prove easier to converge a series of ML models that follow a body decomposition of the interactions, akin to a cluster expansion or virial equation for a real gas.^6,11,30−32 Parametrizing ML models for each body term is not necessarily straightforward, because reference calculations typically contain all contributions at once. The contribution of each body is instead often inferred by means of a decomposition ansatz, which assumes the target property to be decomposable in terms of a linear combination of function values.^24,33

Once trained, an ML model is ready to be used as a force predictor coupled to an MD integrator. In the context of ab initio MD simulations based on quantum-mechanical calculations, an ML model leads to significant performance improvements: While the former scales with the number of electrons raised to some power (≥3), the ML model will typically scale almost linearly with the number of nuclei, albeit with a large prefactor. John and Csányi³⁰ pointed out that the situation is very different when running coarse-grained (CG) simulations^34,35—lumping together atoms into superparticles or beads. Since they are typically parametrized from classical atomistic simulations, the scaling will be similar, apart from a small reduction due to the reduced number of particles.³⁰ To remedy this situation and recover some computational efficiency, one can resolve to project the ML model onto standard tabulated potentials, as suggested by Glielmo et al.³¹ This is the objective of the present study.

The scope of this paper is to summarize key aspects of applying GP regression to parametrize force fields of molecular liquids in a computationally efficient setting. A decomposition of the PES to two- and three-body interactions is presented, ultimately projected onto tabulated potentials to avoid making ML predictions at each integration time step. We compare several kernels that encode various levels of physics. Further technical refinements are incorporated, such as a smooth decay close to the interaction cutoff.⁶ We also discuss performance during learning and structural accuracy in the condensed phase of a liquid. Results are presented for two example liquids: a two-body Lennard-Jones system and a three-body Stillinger–Weber system.

Finally, we extend our implementation to the coarse-graining of molecular liquids. CG is an appealing resolution in soft matter due to its ability to reach longer length and time scales.^35,36 We specifically focus on bottom-up strategies that systematically derive a CG model from higher-level microscopic information.³⁷ Consistency between the equilibrium probability densities of the two models leads to the many-body potential of mean force (MB-PMF), which effectively replaces the coveted PES.³⁸ One practical approach to building a CG model is force matching (FM) or multiscale coarse-graining (MS-CG),³⁸⁻⁴⁰ which projects the MB-PMF into the space of force fields defined by the CG basis set. Both kernel-based and neural-network approaches have recently been applied to solving the MS-CG problem.^30,41,42 Akin to the study of John and Csányi,³⁰ we solve the MS-CG problem using kernels on both two- and three-body interactions, but we project the resulting decompositions onto computationally efficient tabulated potentials. We discuss both parametrization strategies and structural accuracy of the resulting condensed phase of liquid water.

2. Kernel-Based Regression for Force Fields

We first recapitulate the terminology of a Gaussian process, keeping in mind physical quantities relevant to liquids. A sample i in our data set will represent particle i and its environment, which we will specify later. A particle can be an atom or a molecule.

We propose to learn a mapping Q → O between the representation of sample i, Q_i, and an observable, O_i = O(Q_i). The observable may correspond to the sample’s energy or force, for instance. Training a kernel model is then equivalent to solving the set of linear equations O = K̂α, where the kernel function K̂_ij = K(Q_i, Q_j) = Cov(O_i, O_j) measures the similarity between samples Q_i and Q_j, and α is the vector of weight coefficients. The latter is optimized by inverting the regularized problem

1

where λ implements Tikhonov regularization. Prediction of the observable for a configuration Q* is then given by an expansion of the kernel evaluations on the training set

2

summing over the N training points.

2.1. Particle-Decomposition Ansatz

The above-mentioned formulation can, in principle, be applied to learn local properties of a liquid, such as forces, F. Reference high-level simulations provide the force of a particle embedded in its environment, represented by Q. A kernel machine can then be set out to learn the mapping Q → F. Learning this mapping directly is in general challenging, due to the interpolation size of Q. Instead, we aim at breaking down the problem to ease convergence of the kernel and avoid extrapolation.

We first limit the size of our particle environments or configurations, Q, by setting a cutoff, r_cut. In other words, for a sample i only the neighbors j with r_ij ≤ r_cut are added to the environment Q_i. Note that this decomposition assumes that r_cut is large enough to account for the physical interaction range, which is not always possible, e.g., for unscreened long-range Coulomb interactions.

Q are further decomposed in body terms, q, which consist of interparticle interactions: from pairwise, to triplets, all the way to fully many-body. In the following we limit our approach to the first two terms, though the method generalizes in a straightforward manner.

The potential benefit of the body expansion is its reasonable convergence, which helps to reduce the size of Q. We denote the body decomposition using a superscript: q⁽²⁾ and q⁽³⁾ for vertices of pair and triplet interactions. These interparticle interactions can be associated with a set of local forces, f⁽²⁾ and f⁽³⁾, which are a priori unknown. The present framework thus motivates several mappings

3

where K̂ and k̂^(b) denote the global and local kernels and b runs over pairwise and triplet models.

While learning a local model is a more attractive option, we do not have direct access to the local forces f⁽²⁾ and f⁽³⁾. The particle-decomposition ansatz assumes that the force acting on a particle due to its environment can be approximated by a set of constitutive interparticle interactions

4

where p and t run over P_i pair and T_i triplet interactions. Each pair interaction is between a pair of particles, p = (ab), and each triplet is between three particles, t = (abc), where a, b, and c are the indices of particles in a pair or triplet; o is the index of the central particle of configuration i, in a pair p or triplet t. The body expansion and the indexing are illustrated in Figure 1. The total number of interparticle interactions for sample Q_i is thus M_i = P_i + T_i.

Figure 1.

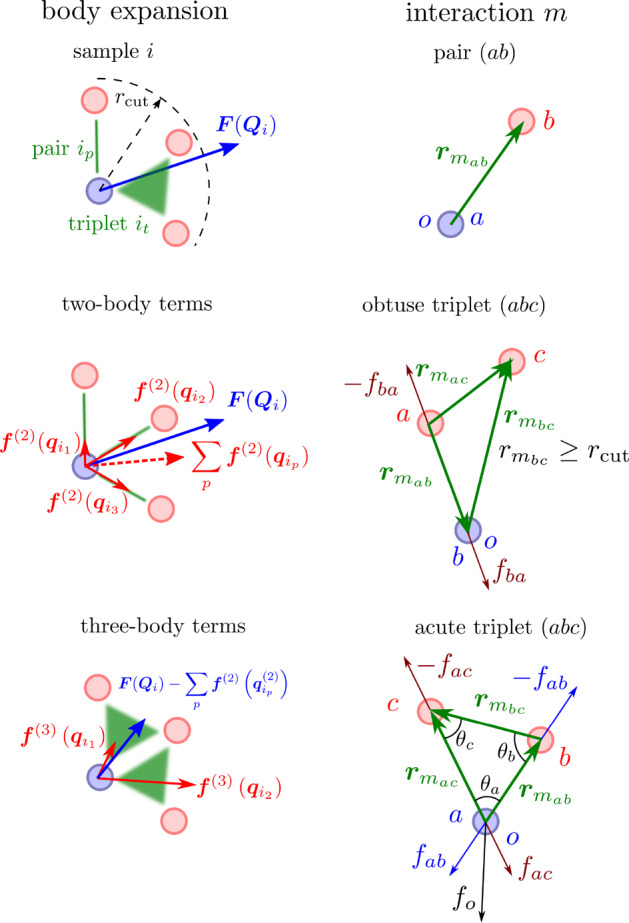
(left) Illustration of the body expansion of a configuration i on pairs and triplets, where the reference force F(Q_i) acts on the central particle. The two-body terms are shown by interparticle vectors (green lines) and result in total pairwise force ∑_p f⁽²⁾(q_ip⁽²⁾). A similar decomposition for triplets is used to fit the residual, i.e., total minus two-body, force. (right) Representations used for pairs and triplets. a, b, and c are the particles of the pair or triplet, and o is the central particle of the sample, which can be either a, b, or c. For triplets, two situations are possible: For obtuse triplets, with one edge larger than cutoff, the force on the central particle o = b is due to the reaction force on particle a. For acute triplets with all edges below the cutoff, the force on the central particle o = a, f_o, is a sum of two forces, f_ac and f_ab, which depend on all three angles, θ_a, θ_b, and θ_c. For vector differences, we use the standard convention, r_mab = r_mb – r_ma.

Equation 4 formally links the kernels K̂, k̂⁽²⁾, and k̂⁽³⁾. We will use the target properties available for the global kernel, K̂, in order to infer an ML model for the local interactions. To this end, we concatenate a set of N particle environments together with the corresponding set of M local interactions

5

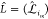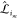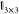where we introduce the mapping matrix . Its component, , is a 3 × 3 identity matrix, , if particle environment i contains the pair or triplet interaction m, and a 3 × 3 zero matrix, 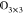, otherwise. L̂ is the bookkeeping matrix that connects the local interactions with the right particle environments. It has dimension 3N × 3M due to the three spatial dimensions.

We can now relate the particle-environment kernel K̂ to its local counterpart, k̂, by

6

leading to the relationship 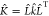. Similar to L̂, both K̂ and k̂ have a block matrix structure, 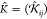and 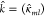, where elements and 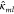are 3 × 3 matrices.

Training a model then corresponds to solving the equation F = K̂α and taking advantage of the relationship between global and local kernels

7

with a regularization term λ and a 3N-dimensional vector of weight coefficients α.

Once trained, the ML model can be used for predictions of the local interactions, f*. An analogous link between the covariance matrices of the global and local kernels for prediction only yields

8

where k̂* denotes the local kernel between training and test data.

Note that the prediction for entire particle environments yields a new mapping matrix L̂* for the test data,

9

2.2. Representations

It is useful to describe local interactions in terms of internal coordinates as they are invariant with respect to translations. For pairwise interactions we therefore use the interparticle vector of a pair m, r_mab = r_mb – r_ma to represent a pair of particles a and b. For triplet interactions we use the three interparticle vectors, r_mab, r_mac, and r_mbc.

When predicting a rotationally invariant property, such as energy, or when building a covariant kernel from a rotationally invariant one, it is sufficient to use a rotationally invariant representation. For a pair m with particles (a, b) we use the interparticle distance

10

while for a triplet m with particles (a, b, c) we use a vector of three interparticle distances

11

3. Covariant, Conservative Fields

If the target property is a vector, such as a force, we expect the kernel to behave like a second rank tensor upon rotations of coordinates. Formally, this can be expressed as²⁶

12

for any two rotation matrices 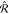and 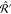. This condition imposes restrictions on the form of the kernel , forcing it to become covariant.

Apart from covariance, we are interested in conservative force fields, for which the total energy of a particle is conserved. Mathematically, the force field has to be curl-free or be a gradient of a scalar function (energy).

We now discuss three different approaches to construct a matrix-valued kernel, for which the target property rotates with the sample and is curl-free.

3.1. Explicit Rotations

We first propose to encode covariance in explicit rotations of individual local representations. To do this, we use the covariance of local kernels

13

where for every local interaction m we introduced a rotation matrix .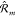

To relate all M pairs or triplets with their local counterparts, we introduce a block-diagonal matrix of rotation matrices

14

We can then link the 3N × 3N dimensional global kernel, K̂, with the 3M × 3M dimensional local kernels, k̂⁽²⁾ and k̂⁽³⁾

15

which is a variation of eq 6 that includes rotations of individual local interactions.

As such, training a kernel model amounts to a modification of eq 7

16

and prediction becomes

17

We now chose rotation matrices such that 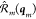becomes invariant with respect to sample rotations, by rotating the individual pairs or triplets into a fixed axis system. In practice, we align pairs along the z-axis, and triplets are aligned in the zy plane, as explained in the Supporting Information.

In the fixed frame interaction representations become rotationally invariant and we can use representations given by eqs 10 and 11 and a standard Gaussian kernel to compare them:

18

The covariance in this scheme is encoded into the explicit rotation matrix R̂. In practice, R̂ and L̂ can be combined by replacing unit 3 × 3 matrices in L̂ by corresponding rotation matrices.

Note that each local kernel element 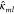is matrix-valued. We can assume that all three components are independent. However, since such kernel does not yield a conservative force, the ML model will have to learn it empirically. In the Supporting Information we derive an explicit expression for 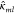that results in a conservative three-body kernel.

3.2. Integration over SO(3)

A covariant matrix-valued kernel can also be constructed by integrating a scalar kernel over all rotation matrices, effectively summing over all actions of the rotation group:^26,31

19

where 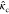is the covariant 3 × 3 matrix-valued kernel, while k_b represents a base scalar-valued kernel. Glielmo et al. derived an analytical solution for pairs, starting from a Gaussian kernel, k_b⁽²⁾(q_m, q_l) = exp(−(r_mab – r_lab)²/2σ²), yielding²⁶

20

where α_ml = r_mab² + r_lab²/4σ², γ_ml = r_mabr_lab/2σ², and r̂_mab = r_mab/r_mab. Note that covariance of 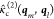is encoded in the tensor product between the two interparticle vectors, .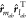

3.3. Hessian of the Scalar Kernel

An alternative statement consists in recognizing that the local forces are spatial derivatives of the potential energy of a respective pair or triplet, f = −∇E_m. As such, a kernel between two forces can be expressed through the energies involved, and that the spatial derivatives can be taken out of the scalar kernel function

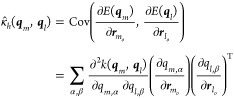21

where we neglected the second term that contains a first-order partial derivative of the kernel function, because they will be zero around training points. Here, α and β run over the different components of the representation vector; o is the central particle of the samples, as illustrated in Figure 1.

The Hessian-based kernel is proportional to the tensor product

and is therefore covariant, similar to the covariant kernel of section 3.2. In addition, it is energy conserving, since it ensures a curl-free force field.

We now choose a Gaussian kernel, eq 18, as scalar-valued kernel. For pairwise interactions, the representation (10) results in an energy-conserving force kernel:

22

where

r̂_mab = (δ_mo,mb – δ_mo,ma)r_mab/r_mab; the expression for r̂_lab can be obtained by exchanging m with l in r̂_mab. Note that the Kronecker deltas only change the sign of the kernel element, depending on whether the central particle of the sample, o, coincides with particle a or b. The tensor product, , is responsible for the covariance of the kernel, similar to the kernel obtained by integrating over SO(3). The scalar prefactor is, however, different.

For a three-body kernel, the representation (11) has three components, and the Hessian-based kernel becomes a sum over the three pair distances in a triplet:

23

with

Its covariance and conservativeness are now explicit: it is a sum of three tensor products and three radial fields. Generalization to any descriptor and scalar kernel is given in the Supporting Information.

We now compare the performance of three ML models for Lennard-Jones (two-body) and Stillinger–Weber (three-body) fluids.

4. Two-Body Lennard-Jones Fluid

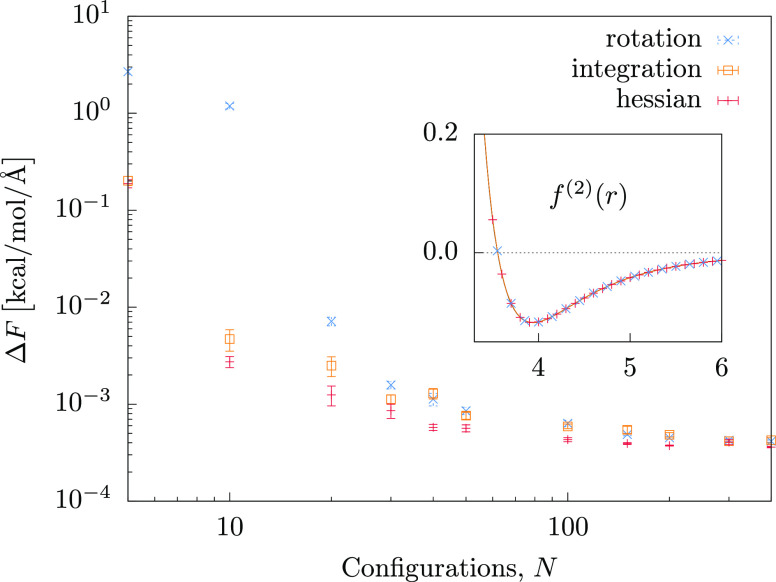
Simulation details of the Lennard-Jones (LJ) fluid are given in the Supporting Information. In Figure 2 we compare the learning curves of the integration, Hessian, and rotation kernels. The LJ force field is learned accurately and efficiently irrespectively of the kernel. The ML model saturates at around 100 particle environments or configurations in the training set, corresponding to roughly 2900 reference pairwise interactions, with an error of ΔF ≈ 4 × 10^–4 kcal/mol/Å per configuration. For r_cut = 6.0 Å the average number of pairs per particle environment is 29, implying a mean error per pair of 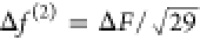≈ 8 × 10^–5 kcal/mol/Å. Here we assume that the M_i individual pair forces of each configuration i are independent and their errors have the same magnitude. A per-pair error is close to the output precision of the reference forces in the simulation trajectory, 10^–5 kcal/mol/Å. There is virtually no difference between the performances of the three different kernels, suggesting that they all encode the same amount of physics relevant to this system—they are covariant and curl-free—which is evident for radial fields.

Figure 2.

Learning curves of the pair-force kernels applied to the LJ fluid. ΔF is the force error per configuration; N is the number of training configurations. The average number of pairs per configuration is 29. (inset) Predicted force fields, f⁽²⁾(r), are virtually identical to the original LJ reference. Each ML prediction is based on 400 training configurations.

The prediction of the force field projected on the pairwise distance r leads to a quantitative recovery of the reference potential, as shown in the inset of Figure 2 for N = 400 configurations.

5. Three-Body Stillinger–Weber Fluid

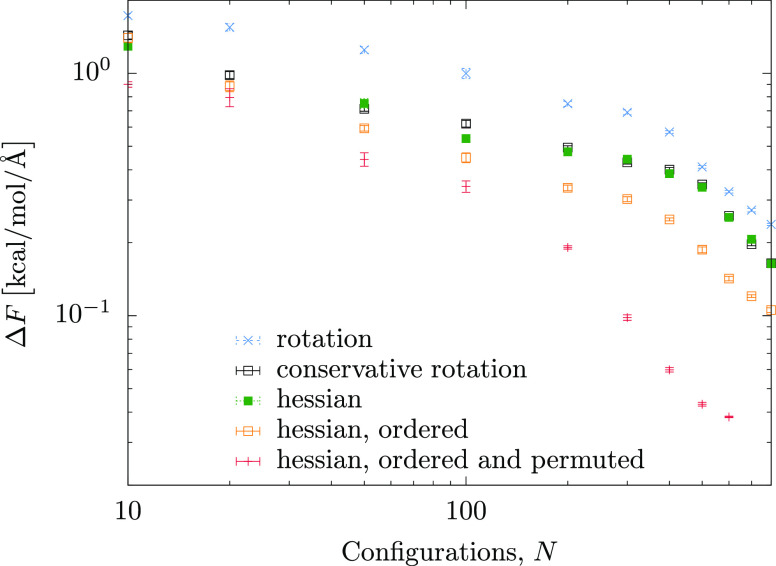
Next, we compare the learning of the three-body forces of the Stillinger–Weber (SW) fluid. Simulation details of the SW fluid are given in the Supporting Information. Note that we only compare the Hessian and the rotation kernels, since an analytic expression for the integration kernel exists only for the scalar case.³¹ In Figure 3 we compare the learning curves for the Hessian (green), rotation (blue), and conservative rotation (black) kernels. One can clearly see that the nonconservative kernel performs significantly worse than the Hessian kernel, but once we make it conservative, its performance becomes comparable to that of the Hessian kernel.

Figure 3.

Learning curves of the three-body force kernels applied to the SW fluid. ΔF is the force error per configuration; N is the number of training configurations. The average number of triplets per configuration is 43 in all cases except the last curve. The Hessian kernel with ordered representation and all permutations has on average 52 triplets per particle, due to a different decomposition of the configuration into three-body interactions.

In spite of the fact that the conservative rotation and Hessian kernels encode all physical symmetries of the force field, one can, however, further improve the ML model. To do this, we recall that the efficiency of the body decomposition relies, in part, on the interaction cutoffs: only those triangles which have two edges smaller than the cutoff contribute to the body expansion. If the central vertex of the triangle, o, is linked to an edge longer that the cutoff (e.g., bc in the obtuse triplet shown in Figure 1), the force on this particle is only due to the shorter edge. In other words, a representation that emphasizes the shorter edge would lead to a faster learning. One can enforce this asymmetry by sorting the triplet representation vector, eq 11, with respect to the edge lengths. Indeed, the corresponding learning curve, Figure 3, orange, learns faster than the model with a simple descriptor.

Similarly, for triangles with all three edges below the cutoff, the force on every vertex is a sum of two forces originating from the neighboring edges, as depicted for an acute triplet in Figure 1. Each force depends on the three angles of the triangle, and their “individual” representations differ only by permutations of elements of the representation vector, eq 11. Hence, the optimal representation for the total force on a particle should include three permutations of this representation. In fact, adding these permutations, in addition to ordering the descriptor, leads to an even better ML model, with the best learning curve shown in Figure 3, red symbols. In other words, this representation captures well the internal decomposition of the three-body force on three vertices of the triangle. This is the model we will be using in the remainder of this work, referring to it as a Hessian kernel model. For this model, 600 training configurations result in the average error of 0.04 kcal/mol/Å per configuration or of 0.006 kcal/mol/Å per triplet, given an average of 52 triplets per configuration.

6. Cutoffs and Switching Functions

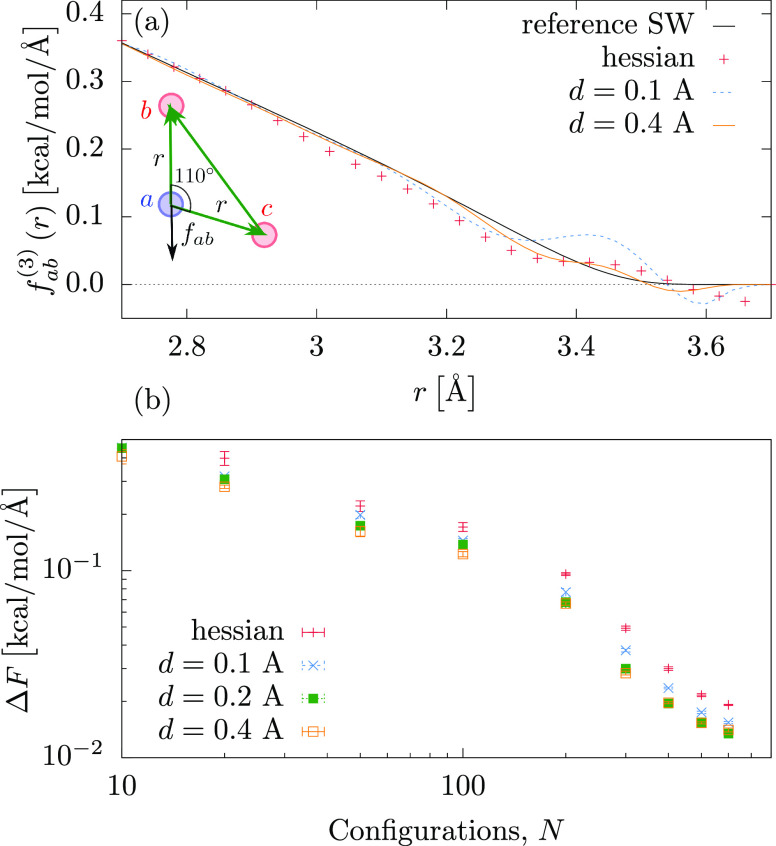
To avoid numerical instabilities and ensure energy conservation in an MD simulation, the short-range forces ought to smoothly decay to zero at the cutoff distance, r_cut. This is indeed the case for the LJ force field learned above; see the inset of Figure 2. If we, however, use the ML model for the SW fluid and predict forces for a triangle with fixed angles, the force shows some fluctuations at r_cut, as shown Figure 4a. This is due to the limited training set size.

Figure 4.

Comparison of the three-body Hessian kernel applied to the SW fluid, without and with switching function for d = 0.1 and d = 0.4 Å. In each case the ML models were based on 600 configurations. (a) Force scan of particle a along r_mab⁽³⁾. (b) Learning curves for the different ML models.

One way to correct for these artifacts is to enforce smoothness via a switching function⁶

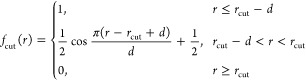24

which goes smoothly to zero in the transition region of r_cut – d < r < r_cut.

In case of a standard force field one would multiply the interparticle force with the cutoff function f_cut(r) with an appropriate transition region d. Applying f_cut(r) to the ML model means that each entry of the mapping matrix 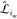is multiplied by f_cut(r_mab) for pairs and f_cut(r_mab) f_cut(r_mac) for triplets. The same distance-dependent weight has to be applied to the mapping matrix of the training, L̂, and prediction, L̂*. As such, pairs and triplets that are close to the cutoff distance contribute less to the GP regression, guaranteeing a smooth decay of the prediction to zero at r_cut.

In Figure 4a we show force cross sections of triplets trained on N = 600 configurations of the three-body SW fluid using the Hessian kernel for different smoothing functions. One can see that incorporating f_cut suppresses fluctuations around the cutoff. This is also reflected in the learning curves, shown in Figure 4b. The lowest test error per particle environment is about ΔF = 0.03 kcal/mol/Å for M = 600 configurations, obtained with d = 0.4 Å, corresponding to a mean test error per triplet of about 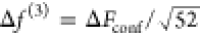≈ 0.004 kcal/mol/Å. Though the accuracy is not significantly improved for the SW liquid, using the switching function is essential for coarse-grained force fields, discussed in section 9, to ensure that the mean force decays to zero at the cutoff.

7. Covariant Meshing

The error of the three-body force kernel predictions could be further decreased by increasing the training set size. This, however, is not possible due to the size of the kernel matrix, which reaches the computer memory limits: While the maximum number of configurations N is relatively small (hundreds), they involve tens of thousands of triplet interactions M. To bound the size of the kernel, we propose to mesh the representation. To make meshing efficient, we make use of the kernel covariance: All samples that are only rotated with respect to each other are assigned to the same bin. In other words, we mesh the rotationally invariant representation and supplement it with the rotation matrices. Apart from reducing the size of the kernel, meshing averages over forces, which as we will see in section 9 results in smoother coarse-grained force fields.

In practice, we precompute the pair or triplet kernel k̂_bins on a fixed grid, limiting the number of kernel elements to M_bins × M_bins for training. Due to the covariance of the force kernels, one can choose an arbitrary reference orientation of the binned pair and triplet representations. For the two-body kernel, we use a linear binning with M_bins between r_min and r_max and an orientation of the pair vector along the z-axis. For the three-body kernel, we choose a uniform binning on a three-dimensional grid, as described in the Supporting Information.

The binned pairs and triplets are rotated to the pairs and triplets of each sample with the help of the mapping matrix 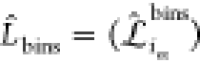. The index i denotes the N configurations and m denotes the M_bins pairs or triplets in the set of binned representations. Each matrix element 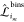is a 3 × 3 matrix:

25

where i_l denotes pairs or triplets of configuration i; is the rotation matrix that rotates pair or triplet i_l to the fixed orientation of the binned representation m.

We apply a Gaussian smearing, w_ilm, so that a pair or triplet i_l is related to several binned representations. For pairs

26

where r_il,ab and r_mab^bins are pair distances of the actual and binned pairs. For triplets the weights are a product of three Gaussians:

27

The learning and predicting can be readily derived from eqs 7–9 and are given in the Supporting Information.

In Figure 5 we compare the meshed MLs for the LJ (two-body) and SW (three-body) liquids. As expected, reducing the number of bins systematically saturates the error to higher values, since it lowers the resolution of the predicted force field. Covariant meshing does allow us to include another 2 orders of magnitude in training data, but the high-resolution 1000-bin (LJ) or 9900-bin kernels (SW) do not result in smaller errors than the original kernel. We also do not observe a faster rate of learning. We therefore conclude that the covariant meshing is not needed to reduce the error for ML models of simple systems. However, as stated above, machine learning of coarse-grained force fields requires much larger training set sizes. We will therefore see that meshing is unavoidable and is, in fact, the key for building an accurate coarse-graining model.

Figure 5.

(a) Learning curves of pair force kernels for the LJ fluid. Comparison of test errors for Hessian kernel with σ = 0.5 Å without and with binning with different number of bins from 200 to 1000. (b) Learning curves of three-body force kernels for the SW fluid. Comparison of test errors for Hessian kernel with switching function (eq 24) with d = 0.4 Å without and with binning with different number of bins from 3600 to 9900. The optimized hyperparameters are σ₁ = 0.7 Å, σ₂ = 0.7 Å, and σ₃ = 1.4 Å.

8. Tabulated Force Fields

We now use the ML force field to run MD simulations. To balance the flexibility of ML with the necessity for quick force evaluations,³¹ we project the ML model on tabulated two- and three-body potentials, as described in the Supporting Information.

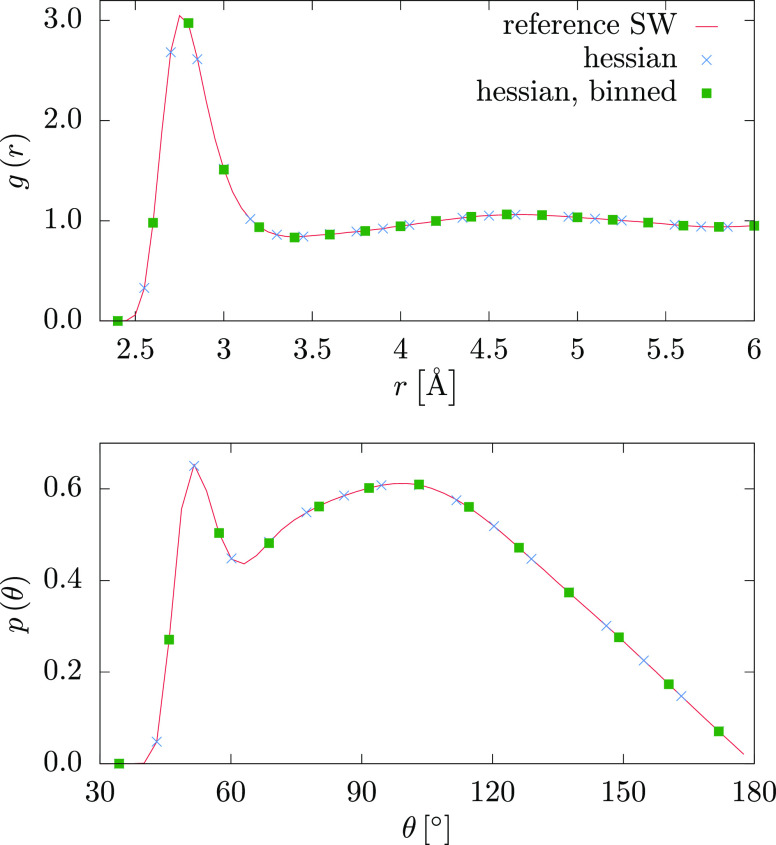
Figure 6 compares the distribution functions of the original SW model with the tabulated kernel predictions of the three-body forces. All curves are virtually identical, confirming that the kernel predictions projected on a tabulated potential lead to the correct sampling of the canonical ensemble. Note that the computational cost of these simulations is comparable to the original three-body SW potential, but there is no restriction on the functional form of the three-body potential, which in this case exactly matches the SW potential. The performance on a 20 core node with MPI paralellization is about 130 ns/day for the SW potential, about 140 ns/day for the tabulated kernel prediction with binning, and about 144 ns/day for the tabulated kernel prediction without binning. Evaluating the kernel prediction at each simulation time step would be more computationally expensive by orders of magnitude.⁴³ While a kernel prediction at each MD time step of an all-atom simulation is competitive with quantum-mechanical calculations, the benefit of a coarse-grained simulation with respect to its atomistic counterpart is not necessarily straightforward.

Figure 6.

Comparison of MD simulation of tabulated three-body kernel predictions with the reference SW simulation. g(r) is the pair; p(θ) is the angular distribution functions. p(θ) is calculated using a cutoff of 3.7 Å. We use a Hessian kernel with a switching function and d = 0.4 Å, 600 configurations without binning, and 10 000 configurations with 9900 bins.

9. Coarse-Graining

We move on to the challenging task of learning a coarse-grained (CG) force field for molecular liquids. The idea of coarse-graining is to reduce the number of degrees of freedom by combining several atoms into one CG particle. We assume that the position of the CG particle i, R_i, is its center of mass:

28

We focus on a one-bead CG model of liquid SPC/E water.⁴⁴ Water is a particularly interesting liquid, as it has a strong local orientational order and therefore has attracted significant attention also regarding CG modeling. It is well-known that especially for CG water models pair potentials alone fail to fully capture the structural correlations of the atomistic system. To do so, at least three-body interaction terms are required.⁴⁵⁻⁴⁸

Mapping the atomistic degrees of freedom to a CG representation leads to a degeneracy: many fine-grained configurations map to a single point in the conformational space of the CG model.³⁵ We will refer to the reference coarse-grained atomistic forces as instantaneous collective forces (ICFs):

29

where f_j are the atomistic forces of each atom j assigned to bead i.

We now introduce the 3N-dimensional block vector of the N instantaneous collective forces of the N CG particles, 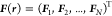. Noid and co-workers showed that the mean force, ⟨F⟩_R, gives the required canonical distribution of coarse-grained variables.³⁸ The subscript R denotes the canonical average over all fine-grained configurations r that map to a specific CG configuration 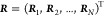. Hence, one wants to learn the mapping between R and the mean force (MF), not the ICF. In force matching, the ensemble averaging is performed implicitly when solving the linear regression problem.^39,49,50 Alternatively, the mean force can be obtained explicitly by performing additional atomistic simulations with constrained CG coordinates.³⁰

Here, we pursue a different approach, and average ICFs using covariant meshing, introduced in section 7. In fact, a representation which depends exclusively on the coarse-grained variables will automatically average the ICF into the MF. In practice, for the two-body kernel, we bin the center-of-mass distances. The resulting ML model should be identical to the two-body force matching (FM) results.^48,50

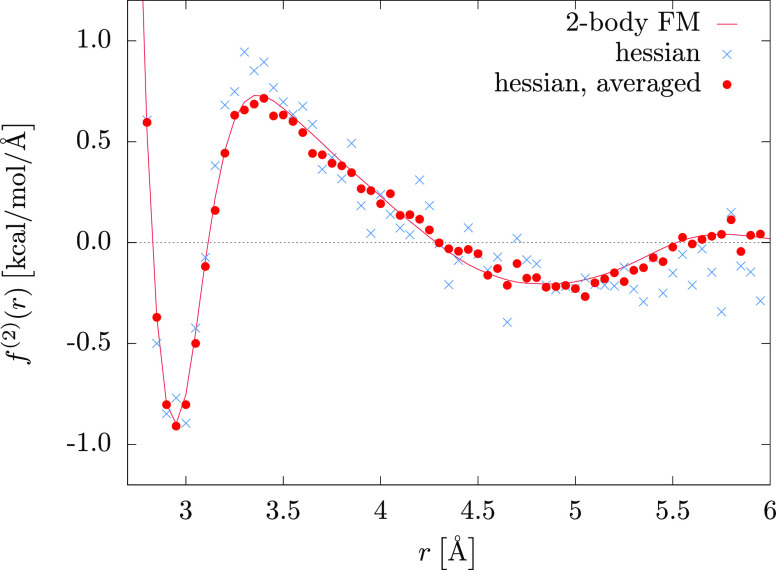
Figure 7 illustrates the CG two-body force kernel predictions for 10⁴ configurations with 1000 bins and a switching function, eq 24, with d = 0.4 Å. The use of switching is essential here: the MD simulations of ML models with and without switching are compared in the Supporting Information. We also show an average over 10 independent training sets, as it is often done in minibatch training in deep learning.⁵¹ In all cases the binned kernel predictions are close to the FM results. Averaging over the resulting output tables helps to reduce the error by smoothing the force curves, but is not critical for MD simulations, where stochastic integrators of thermostats compensate for small force fluctuations.

Figure 7.

CG SPC/E water. Two-body force matching is compared to a kernel prediction based on 10⁴ configurations with 1000 bins and an average over 10 independent kernel predictions. Optimized hyperparameter σ = 0.5 Å; output on a grid up to r_cut = 6 Å.

We now apply this averaging scheme to the three-body forces and train ML on the residual force between target and pairwise model:⁴⁸

30

where F_i is the ICF on CG particle i as given by eq 29 and F_i^2-body is the CG pairwise force.^48,50 We should make clear that F_i is the pairwise force from force matching as we want to compare learning the same residual forces with that in our previous FM parametrization. To learn these residual forces, we use the binned three-body Hessian kernel including all permutations and a switching function, eq 24, with d = 0.4 Å. We use 9900 bins and hyperparameters of σ₁ = 0.7 Å, σ₂ = 0.7 Å, and σ₃ = 1.4 Å. We then project the ML models onto tabulated force fields as described in section 8 with a total N_out = 27 900 table entries. Finally, we average over the 10 independent table predictions.

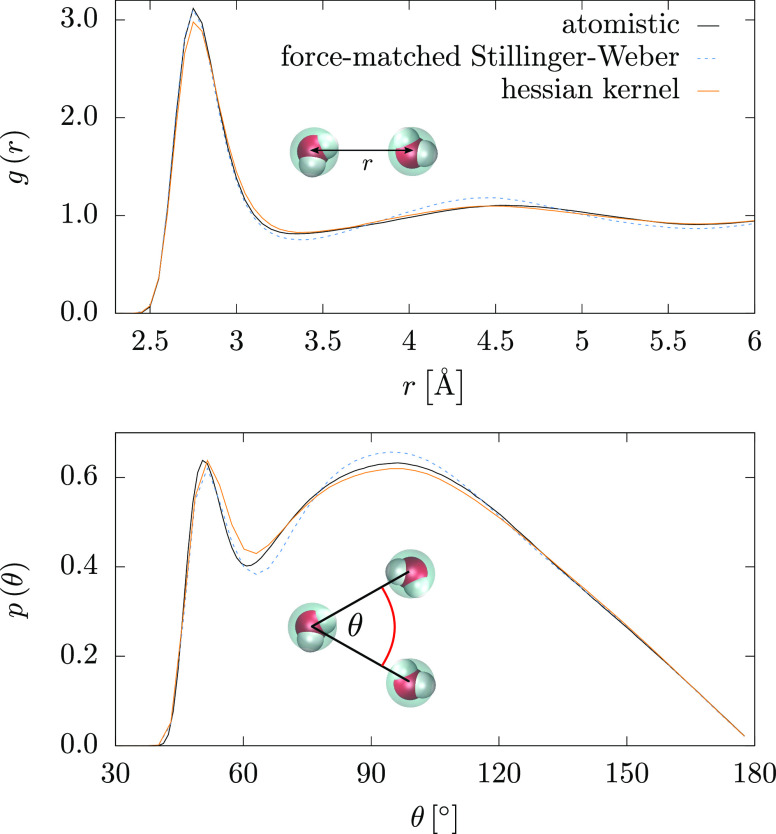
In Figure 8, we show the liquid water distribution functions for three different simulations: the original atomistic simulations, the force matching, and the Hessian kernel model. All schemes use a cutoff for the three-body forces of r_cut = 3.7 Å and employ the same FM two-body forces with a cutoff of r_cut = 12 Å.

Figure 8.

CG SPC/E water system. Comparison of MD simulations for the atomistic simulations, coarse-grained model using force matching to parametrize the SW model, and Hessian kernel averaged over 10 predictions with 9900 bins. Both pair, g(r), and angular, p(θ), distribution functions are shown.

The ML model is very close to the atomistic curve and reproduces the second peak of the RDF better than the FM parametrization of the SW potential. The angular distribution is also more accurate than the FM result. This stems from the additional flexibility of the fitting procedure: the FM fit imposes a fixed functional form on the radial dependence of the three-body force, while the ML model is fully flexible. The average pressure at the CG level is slightly too high at the atomistic density for both the ML and FM models, 4 and 3 kbar, respectively. We showed that one can correct for this by adding a small linear perturbation to the pair force without altering the structural properties.⁴⁸

10. Software

All simulations are performed with the LAMMPS package.⁵² A custom implementation of the features presented here can be found online.⁵³ It includes the pair styles sw/table and 3b/table as user packages. The coarse-graining procedure relies on the open-source software package VOTCA,⁵⁰ also available online.⁵⁴

11. Conclusions

We have described several practical ingredients of the kernel-based regression for classical simulations of liquids. Our approach is to first train a machine learning model by using body decomposition and then project this model onto tabulated potentials.

First, we explain in detail the general idea of the decomposition ansatz and use it to link the accessible particle-environment kernel with the local interaction kernels. We then concentrate on covariant and conservative kernels for pair and triplet interactions and compare three approaches: an analytic integration over the rotation group, the Hessian of a scalar kernel, and a kernel that makes predictions in a fixed axis system. The three kernels perform equally well on a two-body Lennard-Jones fluid, quickly converging to the precision of the reference data. Their limitations become evident when learning the three-body Stillinger–Weber (SW) fluid, where the lack of energy conservation is detrimental to the learning performance. Overall, we find that the best performing Hessian kernel is also the easiest to adapt and implement.

Several technical points help us to further improve the learning performance. The use of a switching function close to the interaction cutoff reduces noisy features and is a useful addition for coarse-grained interactions. A postaveraging procedure over multiple ML models smoothens the resulting force fields. Covariant meshing of training configurations helps to increase the training set size. We present and implement these linear models in the general framework provided by the decomposition ansatz, which also offers the potential to build hybrid models that would learn only parts of the local interaction.

Last, the extension to coarse-grained liquids has shown to be the most challenging. By switching from the potential energy surface to the many-body potential of mean force, coarse-graining introduces degeneracy in the reference configurations that map to a single point at the coarse-grained level. This introduces noise in the learning procedure. Rather than relying on extra simulations with constrained coarse-grained degrees of freedom, we propose to use covariant meshing to average the instantaneous force into a mean force. Using this approach we recover accurate two- and three-body structural distribution functions of the atomistic liquid water. The covariant meshing in combination with tabulation is a promising technique to construct computationally cheap and flexible two- and three-body models for a range of CG applications.

All machine learning models and coarse-graining procedures are integrated in the VOTCA⁵⁴ and LAMMPS⁵³ packages which are publicly available.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.9b01256.

• Derivation of the Hessian of the scalar kernel, explicit form of the conservative rotation kernel, details of two-body Lennard-Jones fluid and three-body Stillinger–Weber fluid, technical details for the cutoffs, covariant meshing, tabulated force field, and coarse-graining sections (PDF)

The authors declare no competing financial interest.