Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 22;20(5):3185–3191. doi: 10.1021/acs.nanolett.9b05232

Mechanical Tension of Biomembranes Can Be Measured by Super Resolution (STED) Microscopy of Force-Induced Nanotubes

Debjit Roy 1, Jan Steinkühler 1, Ziliang Zhao 1, Reinhard Lipowsky 1, Rumiana Dimova 1,*
PMCID: PMC7304919  PMID: 32320255

Abstract

graphic file with name nl9b05232_0004.jpg

Membrane tension modulates the morphology of plasma-membrane tubular protrusions in cells but is difficult to measure. Here, we propose to use microscopy imaging to assess the membrane tension. We report direct measurement of membrane nanotube diameters with unprecedented resolution using stimulated emission depletion (STED) microscopy. For this purpose, we integrated an optical tweezers setup in a commercial microscope equipped for STED imaging and established micropipette aspiration of giant vesicles. Membrane nanotubes were pulled from the vesicles at specific membrane tension imposed by the aspiration pipet. Tube diameters calculated from the applied tension using the membrane curvature elasticity model are in excellent agreement with data measured directly with STED. Our approach can be extended to cellular membranes and will then allow us to estimate the mechanical membrane tension within the force-induced nanotubes.

Keywords: giant vesicles, membrane nanotubes, STED microscopy, micropipette aspiration, membrane tension, optical tweezers

Introduction

Cellular membranes are found to attain a multitude of morphologies and often exhibit highly curved segments with certain functionality. In particular, highly curved membrane nanotubes are involved in several cellular functions such as cell migration,1 signaling,2 remote communication and motility,3 and cell spreading.4 Tunneling membrane nanotubes also play an important role in transfer of cellular content (small molecules, proteins, prions, viral particles, vesicles, and organelles) in a variety of cell types5−9 as well as electrical signals.10 During migration, tubular membrane protrusions (also referred to as retracting fibers) are formed behind the migrating cell and are responsible for releasing cellular content.11 In all of these examples, when not supported by the underlying substrate, membrane shape is modulated by membrane tension which affects the membrane surface area and morphology.12,13 Membrane tension thus provides a link between membrane mechanics, morphology, as well as mechanical transduction in the cell, for example, via tension-sensitive membrane channels. However, how cellular tension is regulated and mechanobiological cues are perceived by the cell is poorly understood.14

In principle, plasma membrane tension can be indirectly inferred from nanotube pulling experiments where the membrane diameter and force of pulling could be used to extract membrane mechanical parameters such as tension, bending rigidity, and spontaneous curvature.15−19 Tension-sensitive probes with fluorescence decay lifetimes depending on tension have also been recently introduced.20 However, it is unclear how curvature and local probe concentration increase due to sorting mechanisms affects the dye performance. Apart from providing the means to assess the membrane bending rigidity and tension, tube pulling experiments also allow the study of cellular processes that take place at highly curved membranes.21−26 In these experiments, the cell or vesicle is immobilized or more often aspirated by a micropipette setting the membrane tension, and a tube is typically pulled by means of optical-tweezer manipulation of a bead attached to the membrane. For a fixed bending rigidity of the membrane, the tube radius depends on membrane tension and thus measuring the radius allows assessing this mechanical parameter. However, membrane nanotube diameters are not directly accessible via diffraction-limited microscopy imaging and these limitations obstruct progress in the field.27

Here, we measure for the first time the diameter of membrane nanotubes directly using stimulated emission depletion (STED) nanoscopy as a function of membrane tension in a controlled reconstituted system. To form membrane nanotubes, we employ giant unilamellar lipid vesicles (GUVs).28 GUVs represent a popular model system of cellular membranes as their response to external factors as well as thermodynamic state can be visualized under the optical microscope.29,30 In addition, they are amenable to micromanipulation (see Chapters 11 and 16 of ref (28)). Pulling a membrane nanotube (also referred to as tether) provides such a micromanipulation protocol, in which  a cylindrical membrane segment with a diameter ranging between 20 nm to few hundreds nanometers is extruded from the GUV. Controlled membrane nanotubes can be generated by hydrodynamic flow31−34 (both inward and outward tubes with respect to the vesicle body can be pulled34), gravity,35 micromanipulation,31,36,37 and magnetic or optical tweezers15,38−40 (see also overview in ref (41)), whereby tube formation is enforced by a localized pulling force.

We use micropipettes to aspirate and hold the vesicle in place and to modulate the membrane tension by adjusting the aspiration pressure. The imposed tension mimics cellular conditions corresponding to the cortical tension.42 To pull the nanotube from the vesicle, a sticky microsphere, trapped by the optical tweezers, is used as a handle. For a GUV being aspirated at a suction pressure, at which the GUV tongue inside the micropipette is longer than the micropipette radius, the total membrane tension is given by41

graphic file with name nl9b05232_m001.jpg 1

where Rv and Rp are the respective radius of the vesicle and micropipette, ΔPasp is the aspiration pressure of the micropipette, m is the membrane spontaneous curvature, and κ is the bending rigidity of the membrane. The first term in eq 1 is the aspiration tension43 for which we will use the notation Σasp. The trapped bead, located at the terminal of an outward nanotube pulled from the aspirated GUV, experiences a force13,41

graphic file with name nl9b05232_m002.jpg 2

which contains two terms that depend on the spontaneous curvature m, because the total membrane tension Σ̂ depends on the spontaneous curvature as well, see eq 1. In our experiments, the spontaneous curvature is so small that we can ignore these two m-dependent terms; further below, we will justify this condition for the system we explore. As a consequence, the total membrane tension Σ̂ reduces to the first term in eq 1, which represents the aspiration tension Σasp. Furthermore, for negligible spontaneous curvature, the aspiration tension becomes equal to the mechanical tension which can now be deduced from the aspiration geometry and the aspiration pressure. In addition, the last term in eq 2 can be ignored because of the small mean curvature of the vesicle.

To perform tube pulling experiments, we switch between confocal fluorescence and bright-field imaging: the membrane nanotube is visualized in confocal mode and the force on the trapped object is obtained from bead position recorded in bright-field mode. At a fixed tube length, the force ft, acting on the trapped bead, can be estimated from the bead off-center displacement from the trap axis, Δx, as ft = κtrΔx, where κtr is the trap constant determined independently, see Experimental Section. From the dependence ft versus 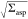Inline graphic, one can deduce the bending rigidity. Alternatively, this material property could be assessed from the membrane nanotube radius, if the latter could be measured: the radius of a cylindrical tube Rt depends on the aspiration tension through the relation41,44

graphic file with name nl9b05232_m004.jpg 3

In general, the tube radius is smaller than the resolution of the optical microscope (∼200 nm), which makes it impossible to measure it directly. AFM imaging could be used when the tubes adhere to a substrate45 but, as a result of this adhesion, the tube morphology will be deformed into a noncylindrical shape which can no longer be described by the tube radius alone. In other studies, the tube radius is estimated indirectly from correlating the fluorescence intensity count.46−48 However, it is unclear how curvature influences the dye performance. Moreover, dye sorting taking place in membrane nanotubes16,49 necessarily affects the tube fluorescence intensity and thus the measurement of the nanotube diameter. The radii of spontaneously formed tubes (not pulled by tweezers) can be also roughly inferred from spontaneous curvature measurements17,50,51 (see pages 9–11 in ref (52) for a review of approaches to measure the membrane spontaneous curvature), but an assumption has to be made for the shape of the tube (cylindrical or necklace-like).

With the advent of super resolution microscopy, the optical microscope resolution has been improved to a few tens of nanometers53,54 and thus, in principle, can be used to measure membrane nanotube diameters. Previously, STED microscopy has been used to study the membrane heterogeneity55−57 and to assess dimensions of endoplasmic reticulum structures using point spread function fitting.58 It has advantages over other super resolution microscopic techniques such as photoactivated localization microscopy (PALM)59 and stochastic optical reconstruction microscopy (STORM),60 which require the acquisition of a high number of images (typically a few thousand frames)61 and are thus slower imaging techniques. In this Letter, we report direct measurement of membrane nanotube diameters with unprecedented resolution using STED microscopy. For this purpose, we have integrated an optical tweezers setup in a microscope equipped for STED imaging.

Experimental Section

Vesicle Preparation and Characterization

GUVs were grown from 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC) doped with 0.1 mol % biotinyl cap phosphatidylethanolamine (PE) (both from Avanti Polar Lipids) and 0.5 mol % ATTO 647N dye (AttoTech) using electroformation in 100 mOsm/kg sucrose solution; for details see Section S1 in the Supporting Information (SI). Occasionally, we also explored vesicle membranes containing cholesterol (Chol), namely at POPC/Chol 9:1 molar ratio. An optically trapped streptavidin-coated bead of diameter ∼2 μm adhered to the vesicles due to biotin–streptavidin bonding. The vesicles were diluted in isotonic medium of 40 mM glucose and 30 mM sodium chloride solution. This external solution was chosen (i) to enhance the optical contrast of the vesicle in phase-contrast observation but avoid vesicle deformation by gravity, (ii) to ensure strong biotin–streptavidin binding, which requires the presence of sodium chloride,40 and (iii) to establish conditions of low asymmetry across the membrane so that the spontaneous curvature is negligible51 (at these conditions the spontaneous curvature is comparable to the mean curvature of the GUVs and the last two terms in eq 2 can be ignored). The bending rigidity of the membrane was measured from fluctuation analysis according to previously published protocol,62 see Section S2 in the Supporting Information. All experiments were performed at ∼22 °C. MATLAB (2014a) and Origin 2015 were used for the image and data analysis.

Experimental Setup

In our experiment, a membrane nanotube is extruded from an aspirated GUV using an optically trapped microsphere (Figure 1). The setup includes three parts (see Section 3 in the SI): micropipette system to hold and aspirate GUVs, optical tweezers to extract the membrane nanotube, and confocal and STED scanning for fluorescence imaging. The setup is based on an inverted microscope (IX83, Olympus Inc., Japan), which is a part of a commercial STED system (Abberior GmbH, Germany). For optical trapping, we have established home-built tweezers by introducing a continuous wave TEM00 mode 1064 nm laser beam (YLR-10-LP, IPG Photonics Corp.) from the microscope back port (SI Figure S1). The laser beam is tightly focused using a 1.2 numerical aperture (NA) water immersion objective (UPLSAPO60, Olympus Inc., Japan with a working distance of 0.28 mm) to form the optical trap. The objective is also used for the fluorescence imaging. Bright-field images were collected using a CCD camera positioned at the back port of the microscope (SI Figure S1). To quantify the trap stiffness, we employed the viscous drag method: the sample was displaced at a constant velocity while trapping a bead and monitoring its off-center displacement, see SI Section S3.1. To hold and aspirate the GUVs, a micropipette was inserted into the sample chamber using a three-dimensional micromanipulator system (Narishige Corp., Japan) clamped on the microscope (SI Section S.3.2). For fluorescence imaging, a 640 nm pulsed laser was used for excitation and another pulsed 775 nm laser beam was used for emission depletion. A spatial light modulator placed in the STED beam path enabled 3D STED; for comparison between 2D and 3D STED, see SI Section S3.3).

Figure 1.

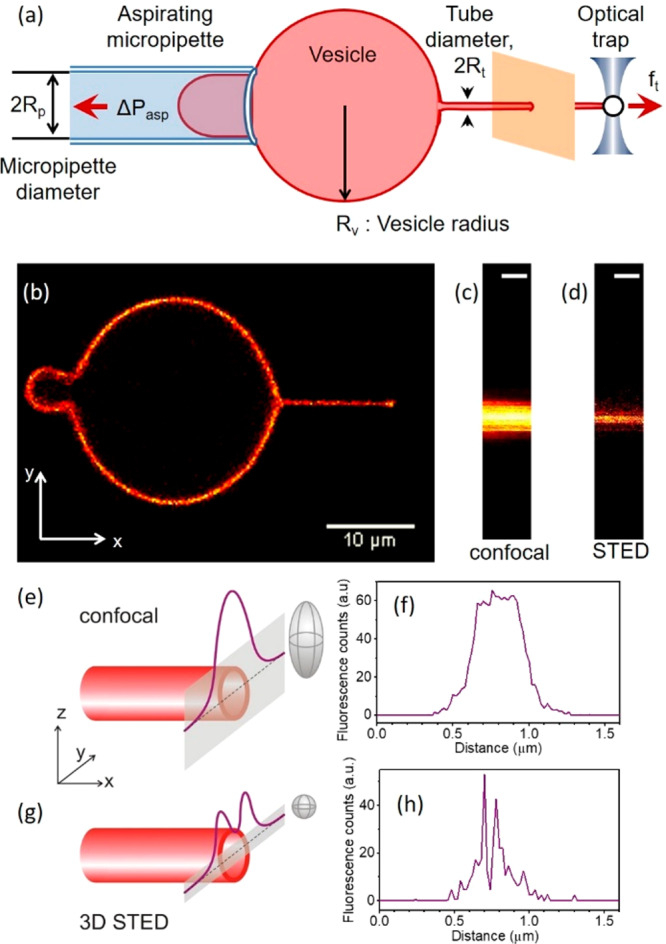
Figure 1

Open in a new tab

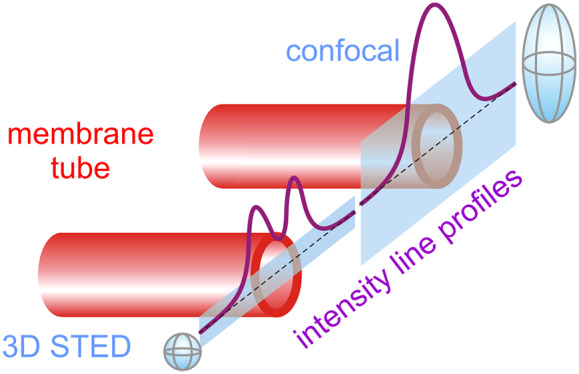
Scheme of the experimental approach of pulling membrane nanotubes and example line scans acquired with confocal and STED microscopy. (a) Schematic of the experiment. (b) Membrane nanotube extrusion as seen in confocal fluorescence imaging. (c) Confocal and (d) 3D STED image of a small portion of the extruded nanotube (scale bars correspond to 500 nm). (e, g) Schematic illustration and (f, h) experimentally acquired data from line scans (gray bands in panels e and g) across a membrane nanotube (red cylinder) when using confocal (e, f) and 3D STED (g, h) imaging; for lucidity, the rough dimensions of the scanning voxels are illustrated as gray ellipsoids in (e, g).

Results and Discussion

GUVs with diameters typically between ∼20 to 25 μm were aspirated via micropipettes with diameters of 3 to 5 μm. A floppy GUV was chosen (see Movie S1 for an example), aspirated by the micropipette at a low aspiration pressure and brought into the contact with streptavidin-coated bead trapped by the optical tweezers. The low vesicle tension allowed us to achieve a larger contact area of the bead with the membrane (occasionally the vesicle was displaced so that the position of the bead was well inside the GUV interior but still engulfed by the membrane). After waiting for few seconds, the aspirated GUV was moved away from the trapped bead and a membrane nanotube was extruded from the vesicle due to strong biotin–streptavidin noncovalent bonding. In all experiments, we kept the length of the enforced nanotube to be between 8 and 10 μm. By doing so, the hydrodynamic contribution arising from the vesicle wall is minimized.63 If the tube is shorter, not only the noncylindrical part of the vesicle and the fluorescence from it can affect the measurements but also the high power STED beam can destabilize the trapped bead and affect the trapping efficiency. Much longer tubes were also avoided as the whole GUV with its aspirated tongue would be out of the field of view. In addition, trapping potential in the outer region of the imaging field could be affected by spherical aberration of the microscope objective.

The membrane nanotube was visualized under the confocal microscope (Figure 1b). For the ease of the experiments, the center of the GUV spherical portion outside the pipet and the center of the trapped bead (and thus also the membrane nanotube) were kept in the same plane, which was fixed to 20 μm above of the cover glass surface; this condition ensured no hydrodynamic effects on the trapped bead and constant trapping efficiency.63 The micropipette and GUV diameters were measured from the confocal image.

To measure the tube diameter, we recorded a kymograph of a line scan perpendicular to the nanotube axis (y-axis in Figure 1b). Even though the signal-to-noise (S/N) ratio of 2D STED images was higher than those of 3D STED images (see Figure S5 in the Supporting Information), the out-of-focus signal arising from the nanotube practically reduces the resolution in the former images. This effect is even more pronounced when comparing confocal and 3D STED scans, see Figure 1c–h. The pixel dwell time was adjusted to 20 μs to obtain 3D STED images with significant S/N ratio and higher effective resolution compared to 2D STED imaging. The STED resolution was measured using 20 nm beads and found to be <40 nm in both x- and y-axes (SI Section S3.3 and Figures S3 and S4). Therefore, in a STED line scan across the tube, the two wall-crossings of a membrane nanotube with radius larger than 20 nm should be, in theory, resolvable under these system settings. However, due to the inherent vibrations of the micropipette (∼31 nm, over six measurements of the positional fluctuations of the micropipette tip), the thermal motion of trapped beads (∼15 nm, obtained from the trap stiffness, which was measured to be 74 ± 2 pN/μm, see SI Section S3.1), and the GUV itself, the membrane nanotubes are found to laterally fluctuate with an amplitude of the order of few hundred nanometers in the y-direction (see Figure 2a,b), which is in the range of the expected tube diameter. As a result, in a major fraction of the line scans in a kymograph, instead of two clearly defined peaks (as sketched in Figure 1g), we detect several noisy maxima. The appearance of multiple peaks was reduced to some extent by adjusting the pixel size to 20 nm (at lower pixel size, the scans were significantly noisier, see SI Figure S6). Larger pixel sizes were not explored as the resolution of the STED microscope was found to be <40 nm in both x- and y-axes while the pixel size is typically kept about half of STED resolution as a rule of oversampling.64−66 To reduce contributions from nanotube fluctuations, the line scans were aligned (Figure 2c, see also Section S4 in the Supporting Information). Subsequent averaging allowed identifying two clearly resolved fluorescence maxima arising from the two tube wall-crossing of the line scan; see Figure 2d. STED line scans that did not show two clear peaks after applying all of the above-mentioned steps were discarded from the analysis; these discarded line scans represented approximately 56% of all scans collected and result from out-of-focus displacement, micropipette vibration, and membrane fluctuations. We denote the tube diameter determined from this interpeak distance as 2Rt, STED and measured it for different aspiration pressures ranging between 15–140 × 10–6 N/m; see Figure S7 in the Supporting Information.

Figure 2.

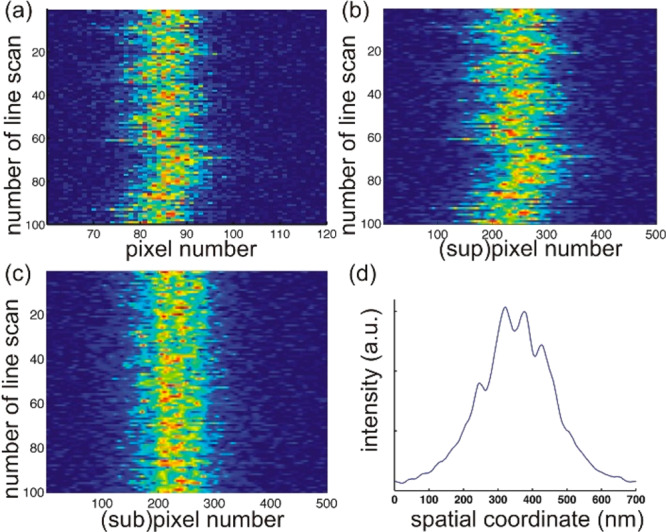
Figure 2

Open in a new tab

Tube line-scan kymograph, line-scans alignment and extraction of an averaged intensity profile. (a) A 3D STED kymograph consisting of 100 line scans of a single nanotube collected with 20 nm pixel size at 20 μs pixel dwell time (color code indicates intensity); the tube exhibits significant lateral fluctuations in the y-direction. (b) To obtain subpixel accuracy the individual line scans were linearly interpolated with 0.1 pixel resolution (see SI Section S4). (c) Same nanotube kymograph after alignment of the line scans according to maximal intensity overlap. (d) Averaged line scan along the y-axis of a single line-scan kymograph, which enables reliable detection of the nanotube diameter from the y-position position of the two highest maxima. This particular tube had a diameter of 72 ± 11 nm.

To avoid excessive photobleaching and decrease in fluorescence signal of the pulled nanotubes, each measurement at a given tension was performed only once. To estimate the precision of the image processing, we performed three repeat measurements on a single tube and found the standard deviation to be 11 nm.

We then aimed at comparing the tube diameter measured from the STED images, 2Rt, STED, with the tube diameter, 2Rt, indirectly assessed from the applied aspiration pressure following eq 3. For this, a precise knowledge of the membrane bending rigidity is required. The bending rigidity was measured with two independent methods. Analysis of the thermal fluctuations of free GUVs using a previously established protocol62 yielded for the bending rigidity 23 ± 2 kBT as assessed on five different vesicles (see Section S2 in the Supporting Information). We also measured this membrane elastic property from tube pulling experiments using eq 2 which gave a bending rigidity value of 23 ± 5 kBT as assessed from measurements on different vesicles (see Section S5 in the Supporting Information). The results from the two approaches are in excellent agreement and are consistent with previous data.67

Using the obtained value for the bending rigidity (κ = 23 kBT), we compared the diameters of tubes directly measured from the STED images, 2Rt, STED, with the respective tube diameters, 2Rt, independently assessed from the imposed membrane tension following eq 3. For the vesicles made of POPC/Chol we took κ = 32.5 kBT corresponding to the linearly proportional increase in the bending rigidity upon the incorporation of 10 mol % cholesterol in POPC membranes as reported in ref (68). The comparison shown in Figure 3 demonstrates that the experimental STED data and estimates from the elastic sheet model (with independently measured bending rigidity) are in excellent agreement. Presumably, for tube diameters approaching 50 nm and below, the accuracy of the STED measurements does not allow precise determination because the tube diameter reaches the size of a couple of pixels.

Figure 3.

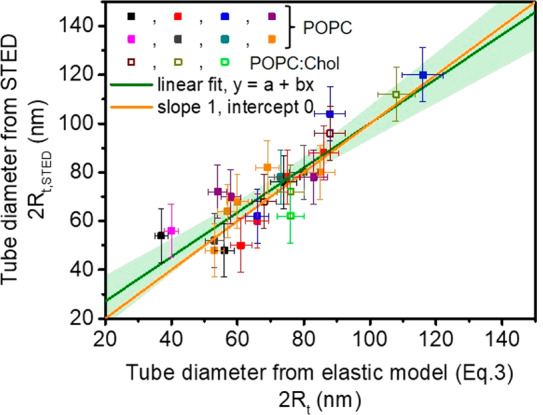
Figure 3

Open in a new tab

Plot of membrane nanotube diameters as directly measured using STED (Rt, STED) versus tube diameter estimated using eq 3 (Rt). Different colors correspond to measurements on different vesicles. Solid symbols represent data measured on POPC vesicles and open symbols are data collected on vesicles made of POPC/Chol 9:1 (molar ratio). The green line is a linear fit, y = a + bx, with a = 8.86 nm and b = 0.91, and the light green band represents a 95% confidence interval. The orange line with slope 1 is included for comparison.

Conclusions

We have shown for the first time that super-resolution microscopy like STED can be used to directly measure the membrane nanotube diameter. For membrane tubes pulled in a controlled fashion from GUVs aspirated in micropipettes, the tube diameter measured microscopically is in excellent agreement with estimates inferred from knowledge of the membrane tension and membrane rigidity. Thus, we provide the first direct evidence for the validity of the widely used curvature elasticity model for nanotubes down to tube diameters of 50 nm. STED imaging of tubes pulled from vesicles of known bending rigidity offers a means of assessing the membrane tension without the need of operating micromanipulation setups such as micropipette aspiration.

In the current paper, we were able to measure the three quantities that enter eq 3 independently: the tube radius by STED, the aspiration tension Σasp from the aspiration pressure, and the bending rigidity by tube pulling. In this way, we were able to confirm eq 3 directly, see Figure 3. As it stands, eq 3 is based on the implicit assumption that the mechanical membrane tension is laterally uniform and that the mechanical tension Σt within the tube is equal to the aspiration tension. The latter assumption is, however, unnecessary. In fact, the mechanical balance within the nanotube leads to a slightly modified and more general form of eq 3 for which the aspiration tension is replaced by the tube tension Σt. As a consequence, the tube tension is given by Σt = κ/(2Rt2). The latter relation can be used to obtain the mechanical tube tension from the measured values of the bending rigidity and the tube radius. It will be interesting to use this more general form of eq 3 to estimate the tube tension of plasma membranes, combining the previously obtained bending rigidity of these membranes69 with the tube radius as measured by STED.

Furthermore, assessing the tube tension from super-resolution imaging as introduced here could be applied, for example, to study (i) the dynamics of migratory cells leaving behind membrane nanotubes from which migratosomes with signaling material will be released,11 (ii) curvature coupling of proteins to highly bent membranes,46 as well as (iii) flows and tension propagation in cells48 (it has already been shown that under the right conditions, STED microscopy can be applied to live-cell imaging without inducing substantial photodamage70) The analysis described here was limited to symmetric membranes with zero spontaneous curvature. Comparing the minimal forces needed to pull out tubes and the second term in eq 2 suggests that our approach can be extended to asymmetric membranes for which the magnitude of the spontaneous curvature is comparable to or larger than 1/(240 nm). The imaging methodology developed here based on measuring tube diameters with STED offers access to direct measurements of material characteristics such as tension and rigidity of cell membranes.

Acknowledgments

This work is part of the MaxSynBio consortium which is jointly funded by the Federal Ministry of Education and Research of Germany and the Max Planck Society. D.R. acknowledges helpful input from M. Karimi regarding micropipette manipulation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.9b05232.

  • Vesicles preparation and observation; fluctuation spectroscopy; setup; optical trapping and calibration; micropipette manipulation; STED imaging and image analysis; bending rigidity data from tube pulling (PDF)

  • Fluctuating floppy vesicle suitable for micropipette aspiration (real time, 10 s at 24 frames per second) (AVI)

Author Present Address

† (D.R) Department of Biochemistry and Molecular Biophysics, Washington University School of Medicine, St. Louis, Missouri 63110, U.S.A.

Author Contributions

R.D. and D.R. designed the experiments. D.R., J.S., and Z.Z. performed the experiments and analyzed the data. R.L. developed the theory. All authors wrote the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nl9b05232_si_001.pdf (1MB, pdf)
nl9b05232_si_002.avi (7.5MB, avi)

References

  1. Diz-Munoz A.; Krieg M.; Bergert M.; Ibarlucea-Benitez I.; Muller D. J.; Paluch E.; Heisenberg C. P. Control of Directed Cell Migration In Vivo by Membrane-to-Cortex Attachment. PLoS Biol. 2010, 8 (11), e1000544. 10.1371/journal.pbio.1000544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Hanna S. J.; McCoy-Simandle K.; Miskolci V.; Guo P.; Cammer M.; Hodgson L.; Cox D. The Role of Rho-GTPases and actin polymerization during Macrophage Tunneling Nanotube Biogenesis. Sci. Rep. 2017, 7 (1), 8547–8547. 10.1038/s41598-017-08950-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chauveau A.; Aucher A.; Eissmann P.; Vivier E.; Davis D. M. Membrane nanotubes facilitate long-distance interactions between natural killer cells and target cells. Proc. Natl. Acad. Sci. U. S. A. 2010, 107 (12), 5545. 10.1073/pnas.0910074107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kumar A.; Kim J. H.; Ranjan P.; Metcalfe M. G.; Cao W.; Mishina M.; Gangappa S.; Guo Z.; Boyden E. S.; Zaki S.; York I.; García-Sastre A.; Shaw M.; Sambhara S. Influenza virus exploits tunneling nanotubes for cell-to-cell spread. Sci. Rep. 2017, 7, 40360. 10.1038/srep40360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Lou E.; Fujisawa S.; Morozov A.; Barlas A.; Romin Y.; Dogan Y.; Gholami S.; Moreira A. L.; Manova-Todorova K.; Moore M. A. S. Tunneling Nanotubes Provide a Unique Conduit for Intercellular Transfer of Cellular Contents in Human Malignant Pleural Mesothelioma. PLoS One 2012, 7 (3), e33093. 10.1371/journal.pone.0033093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rustom A.; Saffrich R.; Markovic I.; Walther P.; Gerdes H. H. Nanotubular highways for intercellular organelle transport. Science 2004, 303 (5660), 1007–1010. 10.1126/science.1093133. [DOI] [PubMed] [Google Scholar]
  7. Wang Z.-G.; Liu S.-L.; Tian Z.-Q.; Zhang Z.-L.; Tang H.-W.; Pang D.-W. Myosin-Driven Intercellular Transportation of Wheat Germ Agglutinin Mediated by Membrane Nanotubes between Human Lung Cancer Cells. ACS Nano 2012, 6 (11), 10033–10041. 10.1021/nn303729r. [DOI] [PubMed] [Google Scholar]
  8. Haimovich G.; Ecker C. M.; Dunagin M. C.; Eggan E.; Raj A.; Gerst J. E.; Singer R. H. Intercellular mRNA trafficking via membrane nanotube-like extensions in mammalian cells. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (46), E9873–E9882. 10.1073/pnas.1706365114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Shen J.; Zhang J.-H.; Xiao H.; Wu J.-M.; He K.-M.; Lv Z.-Z.; Li Z.-J.; Xu M.; Zhang Y.-Y. Mitochondria are transported along microtubules in membrane nanotubes to rescue distressed cardiomyocytes from apoptosis. Cell Death Dis. 2018, 9 (2), 81. 10.1038/s41419-017-0145-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Wang X.; Gerdes H.-H. Long-distance electrical coupling via tunneling nanotubes. Biochim. Biophys. Acta, Biomembr. 2012, 1818 (8), 2082–2086. 10.1016/j.bbamem.2011.09.002. [DOI] [PubMed] [Google Scholar]
  11. Ma L.; Li Y.; Peng J.; Wu D.; Zhao X.; Cui Y.; Chen L.; Yan X.; Du Y.; Yu L. Discovery of the migrasome, an organelle mediating release of cytoplasmic contents during cell migration. Cell Res. 2015, 25 (1), 24–38. 10.1038/cr.2014.135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lipowsky R. Remodeling of membrane compartments: some consequences of membrane fluidity. Biol. Chem. 2014, 395 (3), 253–74. 10.1515/hsz-2013-0244. [DOI] [PubMed] [Google Scholar]
  13. Lipowsky R. Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature. Faraday Discuss. 2013, 161, 305–331. 10.1039/C2FD20105D. [DOI] [PubMed] [Google Scholar]
  14. Sachs F. Mechanical Transduction and the Dark Energy of Biology. Biophys. J. 2018, 114 (1), 3–9. 10.1016/j.bpj.2017.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Heinrich V.; Waugh R. E. A piconewton force transducer and its application to measurement of the bending stiffness of phospholipid membranes. Ann. Biomed. Eng. 1996, 24 (5), 595–605. 10.1007/BF02684228. [DOI] [PubMed] [Google Scholar]
  16. Sorre B.; Callan-Jones A.; Manneville J. B.; Nassoy P.; Joanny J. F.; Prost J.; Goud B.; Bassereau P. Curvature-driven lipid sorting needs proximity to a demixing point and is aided by proteins. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (14), 5622–5626. 10.1073/pnas.0811243106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dasgupta R.; Miettinen M. S.; Fricke N.; Lipowsky R.; Dimova R. The glycolipid GM1 reshapes asymmetric biomembranes and giant vesicles by curvature generation. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 5756–5761. 10.1073/pnas.1722320115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Waugh R. E.; Evans E. A. Thermoelasticity of red blood cell membrane. Biophys. J. 1979, 26, 115–132. 10.1016/S0006-3495(79)85239-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hochmuth R. M.; Mohandas N.; Blackshear P. L. Measurement of Elastic-Modulus for Red-Cell Membrane Using a Fluid Mechanical Technique. Biophys. J. 1973, 13 (8), 747–762. 10.1016/S0006-3495(73)86021-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Colom A.; Derivery E.; Soleimanpour S.; Tomba C.; Molin M. D.; Sakai N.; González-Gaitán M.; Matile S.; Roux A. A fluorescent membrane tension probe. Nat. Chem. 2018, 10 (11), 1118–1125. 10.1038/s41557-018-0127-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Aimon S.; Callan-Jones A.; Berthaud A.; Pinot M.; Toombes G. E. S.; Bassereau P. Membrane Shape Modulates Transmembrane Protein Distribution. Dev. Dev. Cell 2014, 28 (2), 212–218. 10.1016/j.devcel.2013.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Simunovic M.; Evergren E.; Golushko I.; Prévost C.; Renard H.-F.; Johannes L.; McMahon H. T.; Lorman V.; Voth G. A.; Bassereau P. How curvature-generating proteins build scaffolds on membrane nanotubes. Proc. Natl. Acad. Sci. U. S. A. 2016, 113 (40), 11226. 10.1073/pnas.1606943113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ramakrishnan N.; Sreeja K. K.; Roychoudhury A.; Eckmann D. M.; Ayyaswamy P. S.; Baumgart T.; Pucadyil T.; Patil S.; Weaver V. M.; Radhakrishnan R. Excess area dependent scaling behavior of nano-sized membrane tethers. Phys. Biol. 2018, 15 (2), 026002 10.1088/1478-3975/aa9905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Stepanyants N.; Jeffries G. D. M.; Orwar O.; Jesorka A. Radial Sizing of Lipid Nanotubes Using Membrane Displacement Analysis. Nano Lett. 2012, 12 (3), 1372–1378. 10.1021/nl203983e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Barooji Y. F.; Rørvig-Lund A.; Semsey S.; Reihani S. N. S.; Bendix P. M. Dynamics of membrane nanotubes coated with I-BAR. Sci. Rep. 2016, 6, 30054. 10.1038/srep30054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Stachowiak J. C.; Schmid E. M.; Ryan C. J.; Ann H. S.; Sasaki D. Y.; Sherman M. B.; Geissler P. L.; Fletcher D. A.; Hayden C. C. Membrane bending by protein-protein crowding. Nat. Cell Biol. 2012, 14 (9), 944–949. 10.1038/ncb2561. [DOI] [PubMed] [Google Scholar]
  27. Pontes B.; Monzo P.; Gauthier N. C. Membrane tension: A challenging but universal physical parameter in cell biology. Semin. Cell Dev. Biol. 2017, 71, 30–41. 10.1016/j.semcdb.2017.08.030. [DOI] [PubMed] [Google Scholar]
  28. Dimova R.; Marques C.. The Giant Vesicle Book; Taylor & Francis Group, LLC: Boca Raton, 2019. [Google Scholar]
  29. Dimova R. Giant Vesicles and Their Use in Assays for Assessing Membrane Phase State, Curvature, Mechanics, and Electrical Properties. Annu. Rev. Biophys. 2019, 48 (1), 93–119. 10.1146/annurev-biophys-052118-115342. [DOI] [PubMed] [Google Scholar]
  30. Dimova R.; Aranda S.; Bezlyepkina N.; Nikolov V.; Riske K. A.; Lipowsky R. A practical guide to giant vesicles. Probing the membrane nanoregime via optical microscopy. J. Phys.: Condens. Matter 2006, 18 (28), S1151–S1176. 10.1088/0953-8984/18/28/S04. [DOI] [PubMed] [Google Scholar]
  31. Rossier O.; Cuvelier D.; Borghi N.; Puech P. H.; Derenyi I.; Buguin A.; Nassoy P.; Brochard-Wyart F. Giant vesicles under flows: Extrusion and retraction of tubes. Langmuir 2003, 19 (3), 575–584. 10.1021/la026236t. [DOI] [Google Scholar]
  32. Borghi N.; Rossier O.; Brochard-Wyart F. Hydrodynamic extrusion of tubes from giant vesicles. EPL (Europhysics Letters) 2003, 64 (6), 837. 10.1209/epl/i2003-00321-x. [DOI] [Google Scholar]
  33. Huang Z. H.; Abkarian M.; Viallat A. Sedimentation of vesicles: from pear-like shapes to microtether extrusion. New J. Phys. 2011, 13, 035026 10.1088/1367-2630/13/3/035026. [DOI] [Google Scholar]
  34. Dasgupta R.; Dimova R. Inward and outward membrane tubes pulled from giant vesicles. J. Phys. D: Appl. Phys. 2014, 47 (28), 282001. 10.1088/0022-3727/47/28/282001. [DOI] [Google Scholar]
  35. Bo L.; Waugh R. E. Determination of Bilayer-Membrane Bending Stiffness by Tether Formation from Giant, Thin-Walled Vesicles. Biophys. J. 1989, 55 (3), 509–517. 10.1016/S0006-3495(89)82844-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Cans A. S.; Wittenberg N.; Karlsson R.; Sombers L.; Karlsson M.; Orwar O.; Ewing A. Artificial cells: Unique insights into exocytosis using liposomes and lipid nanotubes. Proc. Natl. Acad. Sci. U. S. A. 2003, 100 (2), 400–404. 10.1073/pnas.232702599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Shnyrova A. V.; Bashkirov P. V.; Akimov S. A.; Pucadyil T. J.; Zimmerberg J.; Schmid S. L.; Frolov V. A. Geometric Catalysis of Membrane Fission Driven by Flexible Dynamin Rings. Science 2013, 339 (6126), 1433–1436. 10.1126/science.1233920. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Koster G.; Cacciuto A.; Derényi I.; Frenkel D.; Dogterom M. Force Barriers for Membrane Tube Formation. Phys. Rev. Lett. 2005, 94 (6), 068101 10.1103/PhysRevLett.94.068101. [DOI] [PubMed] [Google Scholar]
  39. Cuvelier D.; Derenyi I.; Bassereau P.; Nassoy P. Coalescence of membrane tethers: experiments, theory, and applications. Biophys. J. 2005, 88 (4), 2714–2726. 10.1529/biophysj.104.056473. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Prévost C.; Tsai F.-C.; Bassereau P.; Simunovic M. Pulling Membrane Nanotubes from Giant Unilamellar Vesicles. J. Visualized Exp. 2017, 130, e56086 10.3791/56086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Lipowsky R.Understanding Membranes and Vesicles: A Personal Recollection of the Last Two Decades. In Physics of Biological Membranes; Bassereau P., Sens P., Eds.; Springer International Publishing: Cham, 2018; pp 3–44. [Google Scholar]
  42. Tinevez J.-Y.; Schulze U.; Salbreux G.; Roensch J.; Joanny J.-F.; Paluch E. Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (44), 18581. 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Evans E. A.; Waugh R.; Melnik L. Elastic area compressibility modulus of red cell membrane. Biophys. J. 1976, 16 (6), 585–595. 10.1016/S0006-3495(76)85713-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Waugh R.; Hochmuth R. Mechanical equilibrium of thick, hollow, liquid membrane cylinders. Biophys. J. 1987, 52, 391–400. 10.1016/S0006-3495(87)83227-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Lamour G.; Allard A.; Pelta J.; Labdi S.; Lenz M.; Campillo C. Mapping and Modeling the Nanomechanics of Bare and Protein-Coated Lipid Nanotubes. Phys. Rev. X 2020, 10 (1), 011031 10.1103/PhysRevX.10.011031. [DOI] [Google Scholar]
  46. Sorre B.; Callan-Jones A.; Manzi J.; Goud B.; Prost J.; Bassereau P.; Roux A. Nature of curvature coupling of amphiphysin with membranes depends on its bound density. Proc. Natl. Acad. Sci. U. S. A. 2012, 109 (1), 173–178. 10.1073/pnas.1103594108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Bhatia T. An image-processing method to detect sub-optical features based on understanding noise in intensity measurements. Eur. Biophys. J. 2018, 47 (5), 531–538. 10.1007/s00249-017-1273-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Shi Z.; Graber Z. T.; Baumgart T.; Stone H. A.; Cohen A. E. Cell Membranes Resist Flow. Cell 2018, 175 (7), 1769–1779. 10.1016/j.cell.2018.09.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Tian A.; Baumgart T. Sorting of Lipids and Proteins in Membrane Curvature Gradients. Biophys. J. 2009, 96 (7), 2676–2688. 10.1016/j.bpj.2008.11.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Liu Y.; Agudo-Canalejo J.; Grafmüller A.; Dimova R.; Lipowsky R. Patterns of Flexible Nanotubes Formed by Liquid-Ordered and Liquid-Disordered Membranes. ACS Nano 2016, 10 (1), 463–474. 10.1021/acsnano.5b05377. [DOI] [PubMed] [Google Scholar]
  51. Karimi M.; Steinkühler J.; Roy D.; Dasgupta R.; Lipowsky R.; Dimova R. Asymmetric Ionic Conditions Generate Large Membrane Curvatures. Nano Lett. 2018, 18 (12), 7816–7821. 10.1021/acs.nanolett.8b03584. [DOI] [PubMed] [Google Scholar]
  52. Bassereau P.; Jin R.; Baumgart T.; Deserno M.; Dimova R.; Frolov V. A.; Bashkirov P. V.; Grubmüller H.; Jahn R.; Risselada H. J.; Johannes L.; Kozlov M. M.; Lipowsky R.; Pucadyil T. J.; Zeno W. F.; Stachowiak J. C.; Stamou D.; Breuer A.; Lauritsen L.; Simon C.; Sykes C.; Voth G. A.; Weikl T. R. The 2018 biomembrane curvature and remodeling roadmap. J. Phys. D: Appl. Phys. 2018, 51 (34), 343001. 10.1088/1361-6463/aacb98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Sahl S. J.; Hell S. W.; Jakobs S. Fluorescence nanoscopy in cell biology. Nat. Rev. Mol. Cell Biol. 2017, 18, 685. 10.1038/nrm.2017.71. [DOI] [PubMed] [Google Scholar]
  54. Hell S. W.; Sahl S. J.; Bates M.; Zhuang X.; Heintzmann R.; Booth M. J.; Bewersdorf J.; Shtengel G.; Hess H.; Tinnefeld P.; Honigmann A.; Jakobs S.; Testa I.; Cognet L.; Lounis B.; Ewers H.; Davis S. J.; Eggeling C.; Klenerman D.; Willig K. I.; Vicidomini G.; Castello M.; Diaspro A.; Cordes T. The 2015 super-resolution microscopy roadmap. J. Phys. D: Appl. Phys. 2015, 48 (44), 443001. 10.1088/0022-3727/48/44/443001. [DOI] [Google Scholar]
  55. Honigmann A.; Mueller V.; Hell S. W.; Eggeling C. STED microscopy detects and quantifies liquid phase separation in lipid membranes using a new far-red emitting fluorescent phosphoglycerolipid analogue. Faraday Discuss. 2013, 161 (0), 77–89. 10.1039/C2FD20107K. [DOI] [PubMed] [Google Scholar]
  56. Honigmann A.; Mueller V.; Ta H.; Schoenle A.; Sezgin E.; Hell S. W.; Eggeling C. Scanning STED-FCS reveals spatiotemporal heterogeneity of lipid interaction in the plasma membrane of living cells. Nat. Commun. 2014, 5, 5412. 10.1038/ncomms6412. [DOI] [PubMed] [Google Scholar]
  57. Sezgin E.; Schneider F.; Zilles V.; Urbančič I.; Garcia E.; Waithe D.; Klymchenko A. S.; Eggeling C. Polarity-Sensitive Probes for Superresolution Stimulated Emission Depletion Microscopy. Biophys. J. 2017, 113 (6), 1321–1330. 10.1016/j.bpj.2017.06.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Barentine A. E. S.; Schroeder L. K.; Graff M.; Baddeley D.; Bewersdorf J. Simultaneously Measuring Image Features and Resolution in Live-Cell STED Images. Biophys. J. 2018, 115 (6), 951–956. 10.1016/j.bpj.2018.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Betzig E.; Patterson G. H.; Sougrat R.; Lindwasser O. W.; Olenych S.; Bonifacino J. S.; Davidson M. W.; Lippincott-Schwartz J.; Hess H. F. Imaging Intracellular Fluorescent Proteins at Nanometer Resolution. Science 2006, 313 (5793), 1642. 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
  60. Huang B.; Bates M.; Zhuang X. Super-resolution fluorescence microscopy. Annu. Rev. Biochem. 2009, 78, 993–1016. 10.1146/annurev.biochem.77.061906.092014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Nienhaus K.; Nienhaus G. U. Where Do We Stand with Super-Resolution Optical Microscopy?. J. Mol. Biol. 2016, 428, 308–322. 10.1016/j.jmb.2015.12.020. [DOI] [PubMed] [Google Scholar]
  62. Gracià R. S.; Bezlyepkina N.; Knorr R. L.; Lipowsky R.; Dimova R. Effect of cholesterol on the rigidity of saturated and unsaturated membranes: fluctuation and electrodeformation analysis of giant vesicles. Soft Matter 2010, 6 (7), 1472–1482. 10.1039/b920629a. [DOI] [Google Scholar]
  63. Kraikivski P.; Pouligny B.; Dimova R. Implementing both short- and long-working-distance optical trappings into a commercial microscope. Rev. Sci. Instrum. 2006, 77 (11), 113703. 10.1063/1.2400023. [DOI] [Google Scholar]
  64. Punge A.; Rizzoli S. O.; Jahn R.; Wildanger J. D.; Meyer L.; Schönle A.; Kastrup L.; Hell S. W. 3D reconstruction of high-resolution STED microscope images. Microsc. Res. Tech. 2008, 71 (9), 644–650. 10.1002/jemt.20602. [DOI] [PubMed] [Google Scholar]
  65. Lauterbach M. A.; Keller J.; Schönle A.; Kamin D.; Westphal V.; Rizzoli S. O.; Hell S. W. Comparing video-rate STED nanoscopy and confocal microscopy of living neurons. J. Biophotonics 2010, 3 (7), 417–424. 10.1002/jbio.201000038. [DOI] [PubMed] [Google Scholar]
  66. Wildanger D.; Medda R.; Kastrup L.; Hell S. W. A compact STED microscope providing 3D nanoscale resolution. J. Microsc. 2009, 236 (1), 35–43. 10.1111/j.1365-2818.2009.03188.x. [DOI] [PubMed] [Google Scholar]
  67. Dimova R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 2014, 208 (0), 225–234. 10.1016/j.cis.2014.03.003. [DOI] [PubMed] [Google Scholar]
  68. Henriksen J.; Rowat A. C.; Brief E.; Hsueh Y. W.; Thewalt J. L.; Zuckermann M. J.; Ipsen J. H. Universal behavior of membranes with sterols. Biophys. J. 2006, 90 (5), 1639–1649. 10.1529/biophysj.105.067652. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Steinkühler J.; Sezgin E.; Urbančič I.; Eggeling C.; Dimova R. Mechanical properties of plasma membrane vesicles correlate with lipid order, viscosity and cell density. Communications Biology 2019, 2 (1), 337. 10.1038/s42003-019-0583-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Kilian N.; Goryaynov A.; Lessard M. D.; Hooker G.; Toomre D.; Rothman J. E.; Bewersdorf J. Assessing photodamage in live-cell STED microscopy. Nat. Methods 2018, 15 (10), 755–756. 10.1038/s41592-018-0145-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl9b05232_si_001.pdf (1MB, pdf)
nl9b05232_si_002.avi (7.5MB, avi)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES