Programming van der Waals interactions with complex symmetries into microparticles using liquid crystallinity

Using liquid crystals to program van der Waals interactions for bottom-up assembly.

Abstract

Asymmetric interactions such as entropic (e.g., encoded by nonspherical shapes) or surface forces (e.g., encoded by patterned surface chemistry or DNA hybridization) provide access to functional states of colloidal matter, but versatile approaches for engineering asymmetric van der Waals interactions have the potential to expand further the palette of materials that can be assembled through such bottom-up processes. We show that polymerization of liquid crystal (LC) emulsions leads to compositionally homogeneous and spherical microparticles that encode van der Waals interactions with complex symmetries (e.g., quadrupolar and dipolar) that reflect the internal organization of the LC. Experiments performed using kinetically controlled probe colloid adsorption and complementary calculations support our conclusion that LC ordering can program van der Waals interactions by ~20 k_BT across the surfaces of microparticles. Because diverse LC configurations can be engineered by confinement, these results provide fresh ideas for programming van der Waals interactions for assembly of soft matter.

INTRODUCTION

The assembly of particles into clusters and networks underlies the formation of diverse forms of soft matter, including foams, emulsions, and thin-film coatings (1, 2). Whereas most past studies have focused on materials formed via interparticle interactions that are spherically symmetric, recent studies have moved to design soft materials through the bottom-up assembly of particles that encode anisotropic interparticle interactions. One set of approaches has focused on the use of nonspherical particles (2–6) and explored how entropic (or excluded volume) interactions guide the self-assembly of colloids into a range of complex structures including colloidal quasi-crystals (7) and photonic materials with packings and properties not previously accessible (8, 9). Another set of promising approaches have focused on patterning of the surface chemistry of spherical or nonspherical microparticles and colloids (so-called patchy particles), including use of sequence-controlled interactions that can be programmed by hybridization of DNA (6).

Van der Waals interactions are ubiquitous in all particulate systems, and thus, general and versatile methods to manipulate the symmetry of van der Waals interactions acting between particles represent an additional promising approach to program assembly of soft matter (10). Here, we report exploration of an approach to control the symmetry of van der Waals interactions within particulate systems that is based on the synthesis of polymeric microparticles from liquid crystals (LCs). Specifically, we describe how compositionally homogeneous and spherical polymeric microparticles that have well-defined patterns of internal orientational order can encode van der Waals interactions with complex symmetries. We polymerize LC microdroplets, prepared as oil-in-water emulsions, and demonstrate that internal orientational order can be used to tune spatial variation of van der Waals interactions across the surfaces of the microparticles by ~20 k_BT [as probed by interaction with a micrometer-sized polystyrene (PS) colloid].

Van der Waals interactions include dipole-dipole (Keesom), dipole-induced dipole (Debye), and instantaneous dipole-induced dipole (London dispersion) interactions (1). These interactions can be calculated from Lifshitz theory using the low-frequency (Keesom and Debye forces) and high-frequency (i.e., refractive indices; London forces) components of the dielectric response function of constituent materials (1). A range of materials have anisotropic dielectric functions (11, 12), including LCs, a phase of matter that combines long-range orientational order and liquid-like mobility of its molecular constituents (13). When placed into contact with confining surfaces, past studies have demonstrated via both experiment and theory that LCs adopt orientations that maximize attractive van der Waals interactions between the LC and the confining medium (often described as the orientational anchoring of LCs on surfaces) (14–17). This phenomenon forms the basis of most electro-optical devices (13). In contrast, in this paper, we report the use of LCs to synthesize microparticles with desired internal orientational order, as evidenced by their anisotropic optical properties, and demonstrate that the internal configurations of these polymerized LC microparticles can be used to program complex yet predictable spatial patterns of van der Waals interactions. We experimentally characterize the magnitude of variation in and the spatial patterning of van der Waals interactions by quantifying the organization of probe colloids assembled through a kinetically controlled process on the surfaces of the LC microparticles. These results, when combined with calculations, support our conclusion that LCs provide the basis of a versatile approach that permits programming of van der Waals interactions with magnitudes that are relevant to bottom-up assembly processes in a range of materials-related contexts (18).

RESULTS

The ordering of LCs confined within micrometer-scale domains is controlled by interfacial interactions, the elastic energies of strained states of the LCs, and topological defects that occur in systems where continuous strain of the LCs cannot accommodate the boundary conditions (13, 19–21). A remarkably diverse array of organizations of LCs within microdroplets have been reported, spanning achiral and chiral LCs formed from organic and aqueous phases (19, 20). We began our study by examining achiral nematic LCs formed from mixtures of 4-cyano-4′-pentylbiphenyl (5CB), the reactive mesogen 1,4-bis[4-(3-acryloyloxypropyloxy)benzoyloxy]-2-methylbenzene (RM257) (22), and the photoinitiator 2-dimethoxy-2-phenylacetophenone (DMPA; the mass ratio of the mixture was 10:15:1 RM257:5CB:DMPA) (23, 24). Both nematic 5CB and RM257 have anisotropic dielectric response functions, with refractive indices and static dielectric constants of 5CB and RM257 being greatest along the LC director (as detailed in the Supplementary Materials).

We dispersed the LC mixture into glycerol to form micrometer-sized LC droplets having the so-called bipolar configuration, a configuration with quadrupolar symmetry and an LC director profile that converges at the north and south pole to surface defects (also known as boojums) (Fig. 1C). This configuration is consistent with a tangential orientation of the LC at the interface to glycerol (21). Following photopolymerization, bright-field (Fig. 1A) and polarized light micrographs (crossed polars; Fig. 1B) confirmed that the polymeric microparticles preserved the bipolar configuration of the LC droplets from which they were formed (illustrated in Fig. 1C). No asphericity in shape was measured in the polymeric microparticles, consistent with the interfacial energy of the LC droplets being large compared with elastic energies (23, 24).

Fig. 1. Bipolar LC microparticles, experiments, and theoretical predictions.

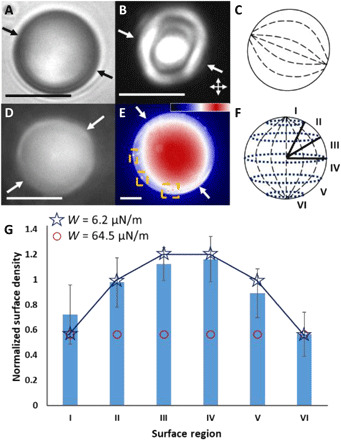
Representative (A) bright-field and (B) polarized light micrographs (double-headed arrows show orientations of polarizers) of a polymerized bipolar LC microparticle. (C) Illustration of the internal ordering of the microparticle in (A) and (B). (D) Fluorescence micrograph of a polymerized bipolar microparticle in the presence of probe PS colloids but no added NaCl and (E, colorized) in the presence of probe colloids and 10 mM aqueous NaCl. Orange boxes highlight the location of four in-focus adsorbed probe colloids. (E) Inset: Lookup table (LUT) for the colorized fluorescence micrograph (ImageJ, “UnionJack”). (F) Microparticle surface regions used to classify probe colloid locations on the surfaces of polymerized bipolar microparticles. (G) Blue bars: Normalized surface densities of probe colloids measured to adsorb onto the surfaces of polymerized bipolar microparticles. The bipolar microparticle data were calculated from 11 independent experiments, with 84 polymerized LC microparticles and 952 probe colloids adsorbed onto the surfaces of these microparticles. The error bars are 95% confidence intervals on the averages for the 84 microparticles. (stars and circles) Theoretical predictions of adsorbed colloid densities on the surfaces of bipolar microparticles, with indicated tangential anchoring strength. The white single-headed arrows on micrographs indicate the locations of the surface defects. Scale bars, 15 μm (λ_ex = 505 nm, λ_em = 515 nm).

We mapped spatial variation of the van der Waals interactions across the surfaces of the polymerized bipolar microparticles by irreversibly adsorbing small PS probe colloids (1 μm in diameter, impregnated with a hydrophobic boron dipyrromethene-based fluorophore; λ_ex = 505 nm, λ_em = 515 nm) onto the surfaces of the microparticles. Because the strength of van der Waals interactions between particles with radii r₁ and r₂ scales as r₁r₂/(r₁ + r₂) at small separations (1), by using LC microparticles with radii between 20 and 80 μm and probe PS colloids with radii of 500 nm, the strength of interaction of the probe colloid was designed to be independent of LC microparticle size. We measured the zeta potentials of the probe colloids and bipolar microparticles in water to be −56 ± 1 mV (n = 5) and −49 ± 6 mV (n = 12), respectively [error bars are the sample standard deviation (SD)]. Consistent with these measurements, in the absence of electrolyte added to water, fluorescence imaging (Fig. 1D) revealed that probe colloids did not adsorb onto the surfaces of the polymerized bipolar microparticles (additional discussion of LC microparticle fluorescence is presented in the Supplementary Materials). Charge screening achieved via addition of sodium chloride (NaCl) (final concentration, 10 mM) was observed to initiate irreversible heterocoagulation between probe colloids and LC microparticles, consistent with attractive van der Waals interactions exceeding the strength of the electrical double-layer repulsion (Fig. 1E).

Next, we quantified the spatial distribution of probe colloids adsorbed on the surfaces of the bipolar microparticles in the presence of 10 mM NaCl. The total number of probe colloids adsorbed onto the microparticles increased with time, consistent with a kinetically controlled aggregation process (see below). Accordingly, we fixed the adsorption time at 30 min to achieve at most 25 adsorbed colloids per microparticle (the low density of colloids minimized the influence of colloid-colloid interactions on the spatial distribution of colloids on each microparticle). We quantified the areal densities of adsorbed probe colloids σ_i within each of six regions defined on the surfaces of the LC microparticles (Fig. 1F; more than 900 probe colloids and 80 polymerized microparticles were used in these measurements; additional images shown in the Supplementary Materials) and normalized these densities by the total areal density of probe colloids, σ_t. Inspection of Fig. 1G reveals that the average areal densities of probe colloids (σ_i/σ_t) adsorbed over the surfaces of the bipolar microparticles are not uniform. Specifically, an adsorption profile that is symmetric about the equatorial plane was observed, with the normalized areal density of probe colloids being lowest near the surface defects that mark the north and south poles of the microparticles. The measured surface densities in the polar regions lie outside of the uniform distribution (normalized areal density of unity) at a 95% confidence level, indicating depletion of adsorbed colloid density near the poles relative to the uniform distribution. Conversely, adsorbed probe colloid density in the equatorial regions of the microparticles was measured to be nearly twice that of the polar regions. The symmetry (quadrupolar) of this probe colloid pattern is similar to symmetry of LC ordering within the bipolar microparticle.

As control experiments, we repeated the methods described above using either LC microparticles polymerized in the radial configuration or microparticles polymerized after heating the LC to form an isotropic phase. Figure 2 shows representative bright-field micrographs (Fig. 2, A and D), polarized light micrographs (crossed polars; Fig. 2, B and E), and schematic illustrations of the internal ordering of 5CB/RM257 within the microparticles (Fig. 2, C and F). The radial configuration of the microparticle is characterized by local perpendicular (homeotropic) surface alignment of the LC over the entire droplet interface, an orientation that was achieved by addition of sodium dodecyl sulfate (SDS) to the aqueous phase (final concentration of 2 mM) before polymerization. Isotropic microparticles, prepared by heating the LC mixture to above the nematic-isotropic transition temperature (~60°C) in glycerol before polymerization, were characterized by the absence of any optical birefringence upon cooling to room temperature (the random polymer network formed by RM257 frustrated the appearance of nematic order upon thermal quenching to room temperature; see the Supplementary Materials for additional detail). Both types of microparticles had zeta potentials that were indistinguishable from the bipolar microparticles [−51 ± 5 mV (n = 11) and −47 ± 3 mV (n = 8) for radial and isotropic microparticles, respectively; error is the sample SD]. In contrast to the polymerized bipolar microparticles, we measured no statistically significant variation (95% confidence intervals) in areal density of probe colloids adsorbed on the surfaces of the polymerized radial or isotropic microparticles (Fig. 2G).

Fig. 2. Radial LC and isotropic microparticles and their characterization.

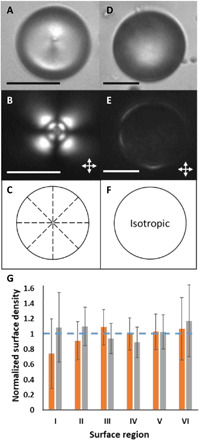
Representative (A and D) bright-field and (B and E) polarized light micrographs (double-headed arrows show orientations of polarizers) of a polymerized radial LC (A and B) and isotropic (D and E) microparticle. (C and F) Illustrations of the internal orderings of the microparticles in (A) and (B) and (D) and (E), respectively. (G) Bars: Normalized surface density of PS probe colloids adsorbed onto the surfaces of polymerized radial LC (orange) and isotropic (gray) microparticles. The radial microparticle data were calculated from 12 independent experiments, with 132 polymerized LC microparticles and 503 adsorbed probe colloids. The isotropic microparticle data were calculated from 20 independent experiments with 179 polymerized microparticles and 521 adsorbed probe colloids. The error bars are 95% confidence intervals on the averages for the 132 radial LC and 179 isotropic microparticles. The horizontal dashed line corresponds to a uniform adsorption density across all surface regions. Scale bars, 15 μm.

The results in Figs. 1 and 2, when combined, led us to hypothesize that the spatial patterning of probe colloids over the surfaces of the bipolar microparticles arose from van der Waals interactions that were encoded by the orientational ordering of molecules within the bipolar microparticles. Before developing a detailed model of the van der Waals interactions encoded by the LC microparticles, we estimated the order of magnitude of variation in energy of a probe colloid interacting with a bipolar microparticle by first calculating orientation-dependent Hamaker constants for the interaction of an LC slab (with the birefringence of 5CB) with an isotropic slab (with optical properties of PS) across water (eq. S1, see the Supplementary Materials for additional information). We calculated the Hamaker constants to change from 1.7 × 10⁻²⁰ J to 1.3 × 10⁻²⁰ J as the LC orientation within the LC slab changed from planar to homeotropic (i.e., perpendicular). When analyzed using the Derjaguin approximation (1), we calculated the van der Waals interaction energy between a 1-μm-diameter probe colloid and LC slab to change by 15 k_BT with the orientation of the LC [calculated at a surface separation corresponding to the Debye screening length of aqueous 10 mM NaCl (3 nm)]. The magnitude of this effect (i.e., >10 k_BT, verified below by experiment) provides initial support for our hypothesis that the orientations of LCs within microparticles can be used to encode variations in van der Waals interactions that are sufficiently large to direct bottom-up assembly of soft matter systems.

To develop a quantitative prediction of the spatial variation of the strength of van der Waals interactions across the surfaces of bipolar LC microparticles in water, we first calculated the LC director profiles by minimizing the elastic and surface contributions to the free energy of the LC droplets from which the polymeric microparticles were synthesized (see the Supplementary Materials). For these calculations, the orientation of the easy axis of the LC at the droplet surface (i.e., the lowest free energy orientation) was assumed to be tangential and the magnitude of the surface anchoring energy, W (the energetic penalty associated with deviations of the nematic director from the easy axis at a droplet interface), was varied in strength from 64.5 to 0.6 μN/m, corresponding to strong and weak anchoring, respectively (Fig. 3, A to C).

Fig. 3. Theoretical predictions of bipolar LC microparticle internal ordering and attractive interaction energies.

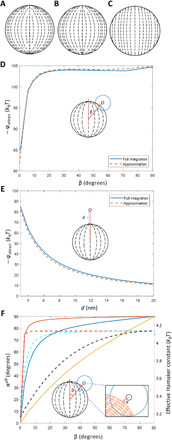
(A to C) Director profiles in the x-z plane of a bipolar LC microparticle calculated numerically for tangential surface anchoring energies of 64.5 μN/m (A), 6.2 μN/m (B), and 0.6 μN/m (C). (D and E) Attractive interaction energy calculated using Eq. 1 either by (solid lines) integrating over all volume elements of a bipolar microparticle with intermediate (W = 6.2 μN/m) tangential anchoring or by (dashed lines) approximating LC ordering at the surface nearest the probe colloid as representative of the entire volume, at various angles of incidence (β) at a surface-to-surface separation, d, of 3 nm (D) and at various surface-to-surface separations above the pole (β = 0°) (E). (D) Inset: Illustration showing the angle of incidence, β. (E) Inset: Illustration showing location of probe colloid as surface-to-surface separation is varied. (F) Calculated average director angle, α^eff, sampled by a probe colloid as a function of β and a separation of 10 nm from the surface of the bipolar microparticle. (Solid lines) Results are shown for surface anchoring energies of 64.5 μN/m (orange), 6.2 μN/m (blue), and 0.6 μN/m (gold). The corresponding effective Hamaker constant for interaction energies calculated according to Eq. 1 (dashed lines) for surface anchoring energies of 64.5 μN/m (red), 6.2 μN/m (cyan), and 0.6 μN/m (black) is also shown. (F) Inset: Illustration of LC ordering near a probe colloid and the angle, α, between a probe colloid and the local LC director.

The energy-minimized LC director profiles were used to calculate the van der Waals interaction energy as

$${\mathrm{\varphi }}_{\text{Attract}}={\int }_{{\mathrm{\Omega }}_1}\frac{{\mathrm{\varphi }}_b(x_1){\mathit{dV}}_1}{4\mathrm{\pi }{b}^3/3}=\frac{{-4r}_1^3}{3\mathrm{\pi }}{\int }_{{\mathrm{\Omega }}_1}\frac{[A_{\mathrm{o}}+(A_{\mathrm{m}}-A_{\mathrm{o}})\text{sin}(\mathrm{\alpha })]}{{(R{(x_1)}^2-r_1^2)}^3}d{V}_1$$ (1)

where Ω₁ defines the spherical volume of a LC microparticle of radius r₁ interacting with a probe PS colloid, x₁ is the position of the center of a LC microparticle volume element of radius b, φ_b is the interaction energy between a LC microparticle volume element and probe colloid, α is the angle between the nematic director of a LC microparticle volume element and the line joining the centers of the LC microparticle volume element and probe colloid, R(x₁) is the center-to-center distance between the probe colloid and the LC microparticle volume element, and A_o and A_m are the Hamaker constants calculated using the ordinary refractive index and dielectric constant of the LC, or the arithmetic means of the ordinary and extraordinary refractive indices and dielectric constants, when the LC is interacting with PS, respectively. We calculated this quantity using adaptive quadrature with relative and absolute error tolerances of 10⁻⁵ (Figure 3D, 3E, described in detail in Supplementary Materials). Inspection of Fig. 3D reveals that, for intermediate surface anchoring (W = 6.2 μN/m), the van der Waals interaction energy of the colloid-LC microparticle pair varies by approximately 20 k_BT as the colloid samples the surface of the bipolar microparticle (with a surface separation of 3 nm, corresponding to the Debye screening length). At the same surface separation, the absolute magnitude of the van der Waals interaction energy at the polar region is ~−85 k_BT (Fig. 3E).

To provide insight into the results shown in Fig. 3, D and E, we characterized the average orientation of LC near the probe colloid (α^eff; the local value of α is defined in the inset of Fig. 3F) for the different surface anchoring energies (Fig. 3F). Inspection of Fig. 3F reveals that for strong (solid orange line), intermediate (solid blue line), and weak (solid gold line) tangential anchoring of the LC at the surface of the microparticle, α^eff approaches 0° when the probe colloid nears each surface defect of the bipolar microparticle (β = 0°), indicating that the ordinary (minimum) refractive index of the LC dominates the van der Waals interactions in the polar regions. In contrast, near the equatorial regions of the microparticle, α^eff approaches 90°, indicating that the van der Waals interactions near the equator reflects an average of the ordinary and extraordinary refractive indices of the LC. Qualitatively, the higher effective refractive index, and correspondingly stronger van der Waals interactions, experienced by probe colloids in the equatorial region of the bipolar microparticle is consistent with our experimental observations of higher adsorbed probe colloid density near the equator (Fig. 1G). Figure 3F also reveals that the change in dielectric response function experienced by a probe colloid near a bipolar microparticle is a strong function of anchoring energy, with weak tangential surface anchoring providing a more gradual variation in local Hamaker constant across the bipolar microparticle surface than strong tangential surface anchoring. We also found that the van der Waals interaction energies calculated from Eq. 1 were well approximated by calculations based on the orientations of the LC nematogens at the surface of the bipolar microparticles (Fig. 3, D and E), consistent with our observation that the van der Waals interactions are particularly sensitive to the surface anchoring energy and thus surface orientation of the LC (see below).

Next, we evaluated the net interaction energy, φ_net, between a probe colloid and polymerized bipolar microparticle as the sum of attractive van der Waals and repulsive electrical double-layer interactions (1). We calculated the electrical double-layer interaction using continuum theories with a constant and uniform surface charge density at infinite separations (25, 26). These theories, which assume pairwise additivity of constituent volumes of condensed phases, break down for colloids with sizes of tens of nanometers (27) but are generally found to be good approximations for microparticles. We interpret the adsorbed colloid locations observed in our experiments with 10 mM aqueous NaCl to arise from primary aggregation events between the probe colloids and polymerized LC microparticles. When using an anchoring energy of W = 6.2 μN/m, we found that φ_net values calculated using surface potentials at infinite separation of −50 mV predicted the presence of this primary minimum with 10 mM salt but the absence of it in pure water (Fig. 4, A and B). This value of the surface potential at infinite separation is also in good agreement with measured zeta potentials (see above; additional details are given in the Supplementary Materials).

Fig. 4. Net interaction energies at assorted ionic strengths, and flux calculations.

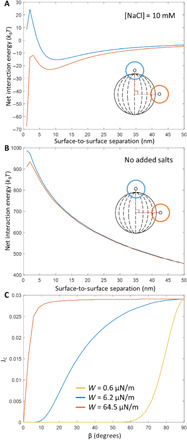
(A and B) Net interaction energy, φ_net (W = 6.2 μN/m), calculated as a function of surface-to-surface separation between a probe colloid and polymerized bipolar microparticle (A) in the presence of aqueous 10 mM NaCl (Debye screening length = 3.04 nm) and (B) in the absence of added salts. In the absence of added salt, we measured the water to have a resistivity of 0.056 μS/cm at 25°C, from which we calculated the Debye screening length to be 458 nm (equivalent to a 1:1 electrolyte at concentration of 440 nM). Orange corresponds to the probe colloid near the equator of the bipolar microparticle; blue represents an approach near the poles. (C) Flux of probe colloids onto the surfaces of bipolar microparticles, calculated using Eq. 2 with surface potentials of −50 mV and the indicated anchoring energies for different angles of incidence.

As noted above, our experimental observations of the spatial patterning of probe colloids on the surfaces of the LC microparticles are consistent with a kinetically controlled process (28, 29). Accordingly, we used φ_net to evaluate a particle flux, J_C, of probe colloids onto the surface of each microparticle as

$$J_C=\frac{F_C}{1+\raisebox{1ex}{$r_2$}\!\left/ \!\raisebox{-1ex}{$r_1$}\right.}{\int }_{(1+\raisebox{1ex}{$r_2$}\!\left/ \!\raisebox{-1ex}{$r_1$}\right.)}^{\infty }\frac{D_{12}^{\infty }}{D_{12}}(\mathrm{\rho })\exp \left(\frac{{\mathrm{\varphi }}_{\mathrm{net}}\left(\mathrm{\rho }\right)}{k_{B}T}\right)\frac{d\mathrm{\rho }}{{\mathrm{\rho }}^2}$$ (2)

where F_C is the probe colloid flux in the absence of intermolecular (van der Waals and electrical double layer) or hydrodynamic interactions between the probe colloid (radius, r₁) and the microparticle (radius, r₂), and φ_net is scaled by the thermal energy, k_BT, at a dimensionless center-to-center separation, ρ (scaled by r₁). Hydrodynamic interactions between the probe colloid and microparticle were incorporated by calculating changes in relative diffusion rates, D₁₂^∞/D₁₂, as a function of dimensionless separation (see the Supplementary Materials). Figure 4C shows that probe colloid fluxes, calculated for a microparticle surface potential at infinite separation of −50 mV and a range of tangential surface anchoring energies, are highest in the equatorial regions of the microparticle, and that spatial variation in probe colloid flux is greatest for W = 6.2 μN/m.

Next, we integrated the probe colloid fluxes in Fig. 4C over the surface regions of the microparticles defined in Fig. 1F, for surface potentials at infinite separation of −50 mV and strong (64.5 μN/m), intermediate (6.2 μN/m), and weak (0.6 μN/m) tangential LC surface anchoring (see the Supplementary Materials for results of this process applied to intermediate anchoring). Inspection of Fig. 1G reveals our predictions based on strong surface anchoring to yield an almost uniform surface density of probe colloids, in contradiction to our experiments. However, our predictions for the spatial variation in probe colloid adsorption density on the surfaces of microparticles with intermediate tangential surface anchoring yields close agreement (within 95% confidence intervals) with experiment (Fig. 1G). Specifically, the equatorial region of the surface of the bipolar microparticles is decorated with a density of probe colloids that is approximately twice that of the polar regions. In addition, the quadrupolar symmetry of the distribution of adsorbed probe colloids is consistent between experiment and calculation.

To provide an additional test of our hypothesis that van der Waals interactions can be encoded by the internal configurations of LC microparticles, we prepared LC microparticles with dipolar symmetry. The director profile of the LC droplet used in these experiments (called a pinned preradial configuration) was characterized by local homeotropic surface alignment of the LC and a pinned surface defect. This configuration was achieved by adsorbing a PS colloid onto the LC microdroplet surface before addition of SDS to the aqueous phase (final concentration of 2 mM; Fig. 5, A to D). After polymerization, pinned preradial microparticles were thoroughly rinsed with pure water to remove SDS from the surfaces of the microparticles. Zeta potential measurements of these microparticles [zeta potential of −47 ± 3 mV; error is the sample SD (n = 9)] yielded values similar to polymerized bipolar LC microparticles (see above). We note that the probe colloid used to pin the surface defect photo-bleaches during polymerization and thus does not affect adsorption statistics of the probe colloids. Inspection of Fig. 5E reveals that pinned preradial microparticles also encode van der Waals interactions that lead to a nonuniform distribution of adsorbed probe colloid density. Specifically, close to the surface defect, we observe an enhancement of adsorbed colloid density that lies outside of a 95% confidence interval. Elsewhere, a uniform distribution of colloid density is measured (within 95% confidence).

Fig. 5. Pinned preradial LC microparticles, their characterization, and theoretical predictions.

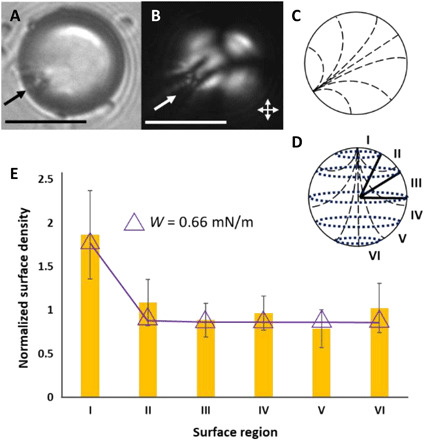
Representative (A) bright-field and (B) polarized light micrographs (double-headed arrows show orientations of polarizers) of a polymerized pinned preradial microparticle. (C) Illustration of the internal ordering of the microparticle in (A) and (B). (D) Coordinate system used to characterize the location of colloids adsorbed to the surfaces of the polymerized pinned preradial microparticles. (E) Bars: Normalized surface densities of PS probe colloids measured to adsorb onto the surfaces of polymerized pinned preradial microparticles. The pinned preradial microparticle data were calculated from 46 independent experiments with 121 polymerized LC microparticles and 493 adsorbed probe colloids. The error bars are 95% confidence intervals on the averages for the 121 LC microparticles. Triangles: Calculated colloid density on pinned preradial microparticles, evaluated using a strong homeotropic anchoring strength. The single-headed arrows on micrographs indicate the locations of the surface defects. Scale bars, 15 μm.

In the absence of a PS colloid adsorbed to the surface of the LC droplet, 2 mM SDS was observed to cause the LC droplets to adopt radial configurations. We interpret this result to indicate that the orientation of LC at the surface of the pinned preradial droplets before polymerization corresponds to strong homeotropic anchoring. We compared our experimental results obtained with pinned preradial microparticles (Fig. 5E) to colloid adsorption densities calculated using a variety of surface anchoring energies and surface potentials at infinite separation (see the Supplementary Materials). We found that predictions based on surface potentials of −50 mV and strong homeotropic anchoring (W = 0.66 mN/m) were unique in matching our experimental results (Fig. 5E). The high colloid adsorption density observed close to the surface defect is caused by van der Waals interactions generated by the near-tangential orientation of the LC just below the microparticle surface [in contrast to the bipolar microparticles (see Fig. 3, C and D, and associated text), calculations based on the surface orientation of the pinned preradial microparticle did not capture the experimental trends in Fig. 5E]. The dipolar symmetry of the predicted and measured colloid adsorption profiles shown in Fig. 5E contrasts with the quadrupolar symmetry of the profiles measured with the bipolar microparticles, providing additional support for our conclusion that manipulation of LC ordering within microparticles provides a versatile means to pattern van der Waals interactions across the surfaces of the microparticles.

DISCUSSION

In the study reported in this paper, we characterized anisotropic van der Waals interactions programmed into microparticles via control of internal LC ordering by quantifying kinetically controlled colloid adsorption over the surfaces of the LC microparticles. Our experiments and supporting calculations revealed that spatial variation of the van der Waals interactions across the surfaces of the LC microparticles was as large as 20 k_BT, a magnitude that is sufficiently large to be useful in engineering the bottom-up assembly of soft materials (18). We note that the LC microparticles used in our experiments were prepared by polymerization of RM257. The polymer network formed by the RM257 prevented lateral motion of probe colloids that adsorbed to the surfaces of the LC microparticles. In contrast, a number of past studies have reported adsorption of colloids onto the surfaces of LC microdroplets with mobile interfaces (23, 30). When the interfaces of the LC microdroplets are mobile, adsorbed colloids are able to migrate laterally across surfaces, driven by release of elastic energy in the strained LC. We emphasize that this lateral migration does not occur in our experimental system. In addition, whereas the experiments in this paper were designed to achieve irreversible adsorption of the probe colloids (under kinetic control), experiments in which repulsive electrical double-layer interactions prevent irreversible adsorption, and thus permit exploration of equilibrium spatial distributions governed by Boltzmann probability distribution functions, will lead to even higher levels of control over the placement of colloids for precision engineering of colloidal matter.

Our study also reveals that the near-surface orientation of LC mesogens has a strong effect on the spatial variation of van der Waals interactions. Past studies have established that the surface orientations of LCs in confined systems reflect a rich interplay between the elastic and surface anchoring energies of LCs, and that this balance can be tuned further through a variety of methods (e.g., external fields) (19–21). For example, a competition between surface anchoring and elastic energies as a function of the size of an LC droplet can lead to LC droplet assuming a so-called uniform internal configuration (absent of strain), in which the LC surface orientations change continuously across the surfaces of the droplets (24). We predict that such a surface variation in the LC orientation can program van der Waals interactions that cause the density of surface adsorbed colloids at the pole and equator to differ by a factor of ~10⁶ (see the Supplementary Materials for further information on this prediction).

We interpret our experimental observations in terms of van der Waals interactions between LC microparticles and probe colloids. Although LCs with splay and bend strain can generate flexoelectric effects (31, 32) in micrometer-sized droplets, as detailed in the Supplementary Materials, ionic species present in our experimental systems containing 10 mM NaCl will screen flexoelectric effects. Briefly, in the absence of added salts, we calculate that the mobile ion content of the LC used in our study (33, 34) will dominate the charge density associated with flexoelectric polarizations when the LC droplet radii are larger than ~3 μm. In addition, we add 10 mM NaCl to the aqueous phase used in our experiments, which will further increase the mobile ion content of the LC (33, 34) and decrease the critical radius below which flexoelectric effects become important to ~1 μm. In contrast, the diameters of the LC droplets used in our experiments range from 20 to 80 μm.

Overall, the results of this study establish the basis of a general and facile approach for programming van der Waals interactions into colloidal soft matter systems, as the ordering of LCs can be varied widely and manipulated predictably in a range of experimental geometries (20, 21). For example, in addition to the nematic LC director configurations reported above, so-called axial configurations of LC domains have been demonstrated in previous experiments (20, 21), as well as director configurations using other LC phases [e.g., smectic, cholesteric, and blue phases (13, 19, 20)]. The principles reported in this paper are also not limited to spherical polymeric particles, as LC ordering can be readily manipulated in membranes (35), slabs (36), microwells and grids (37), and capillaries (38). In addition, LCs are known to respond to weak external fields (e.g., electric or magnetic) and exhibit a range of temperature-dependent phases (13), thus opening up opportunities for dynamic control of van der Waals interactions in soft matter systems. Interfacial events that change surface anchoring of LCs [e.g., enzymatic processing of a lipid (37)] can also be used to manipulate the magnitude of the van der Waals interactions encoded by LCs.

We envisage the principles demonstrated in this paper to be applicable to a range of soft matter phenomena, such as adhesion and wetting at surfaces, and formation of colloidal assemblies, including crystals, glasses, and gels (1, 2). Our results also guide the design of systems in which changes in van der Waals interactions could be triggered by phenomena that alter LC ordering, including adsorbate-driven anchoring transitions (37) or thermally induced phase transitions (13). LC emulsions, for example, can be triggered to coalesce or coat a surface following a stimuli-induced change in LC orientation. Whereas the LC systems described in our paper are created at local equilibrium, orientational order induced in nonequilibrium states [e.g., shear-induced order (39) or actively driven processes (i.e., active nematics) (40)] provides additional opportunities to manipulate van der Waals interactions via the approach reported in this paper.

MATERIALS AND METHODS

Chemicals were used as received from the manufacturers without additional purification. 5CB (>99.5%) was obtained from Jiangsu Hecheng Advanced Materials Co. Ltd. (Nanjing, China). Reactive mesogen RM257 (>95%) was obtained from BOC Sciences (Shirley, NY). Photoinitiator, DMPA (>99%), NaCl (>99%), SDS (98%), toluene (anhydrous, 99.8%) and glycerol (≥99.5%) were obtained from Sigma-Aldrich (St. Louis, MO). Fluorescent PS microspheres [FluoSpheres; sulfate-functionalized, 1.0-μm-diameter, yellow-green fluorescent (λ_ex = 505 nm, λ_em = 515 nm), 2 weight % (wt%) solids in distilled water with 2 mM azides] were obtained from Thermo Fisher Scientific (Waltham, MA). Deionization of a distilled water source was performed with a Milli-Q system (Millipore, Bedford, MA).

Synthesis of LC microparticles

All emulsions were made using mixtures of 5CB, reactive mesogen RM257, and photoinitiator DMPA (40 wt% RM257/5CB). The mixture was prepared by combining 40 mg of RM257, 4 mg of DMPA, 60 μL of 5CB, and 60 μL of toluene in a glass vial by vortexing. Toluene was added as a cosolvent to aid in the mixing of RM257 and DMPA. After all solids were dissolved, the vial was left in a fume hood open to the atmosphere overnight to remove the toluene by evaporation. The vial was loosely covered with aluminum foil during this process to avoid exposure to light. The starting mixture was not degassed and was stored away from ambient light. We used procedures detailed elsewhere (23, 24) to obtain the desired LC microparticle configurations.

Bipolar LC microparticles

Bipolar microparticles were prepared by gently shearing, with a spatula, 6 μL of the 40 wt% RM257/5CB material (10:15:1 RM257:5CB:DMPA) at room temperature in 2-mL glycerol for 15 s. Polymerization was initiated by exposing the sample to long-wave ultraviolet light (365 nm; Spectroline E-Series, Spectronics Corporation, Westbury, NY) for 30 min (2.5 mW/m² at a distance of 5 cm). The vial was turned by hand at 8-min intervals to minimize creaming (density of glycerol = 1.26 g/mL, density of 5CB = 1.008 g/mL, density of RM257 = 1.22 g/mL). Following polymerization, 2 mL of deionized water was added to the vial and the sample was vortexed until the microparticles were well dispersed. The sample was allowed to sit for 10 min to enable the microparticles to cream. For imaging, microparticles from near the air-glycerol/water interface (comprising the largest microparticles of the cream) were withdrawn and added to an imaging well.

Radial LC microparticles

Radial microparticles were prepared by homogenizing 10 μL of the starting material in 2 mL of water for 10 s at 6500 rpm with a homogenizer [T 25 digital ULTRA-TURRAX equipped with an S25 N-10G dispersing element (IKA, Wilmington, NC)]. Following homogenization, 41 μL of 100 mM aqueous SDS was added to the vial (final concentration, 2 mM). Polymerization was initiated by exposing the sample to ultraviolet light for 30 min, turning the sample by hand at 8-min intervals. Following polymerization, 2 mL of deionized water was added to the vial and the sample was vortexed for 10 s. Next, an imaging well was prepared by combining 1 mL deionized water and 60 μL of the dispersion containing the polymerized LC microparticles withdrawn from near the bottom of the vial with a glass pipette (where the largest microparticles were located due to sedimentation, density of 5CB = 1.008 g/mL). The sample was allowed to settle for 30 min, after which the water/SDS mixture above the sample was decanted in 0.8 mL aliquots and subsequently replaced with 0.8 mL of pure deionized water. The addition and removal of the water was repeated 10 times to minimize SDS in the sample. After rinsing, 111 μL of 100 mM aqueous NaCl (final concentration, 10 mM) was added to the imaging well. Next, 1 μL of 1-μm-diameter fluorescent PS colloids was added to the imaging well and mixed with a glass pipette.

Isotropic microparticles

Isotropic polymeric microparticles were prepared as described above for bipolar LC microparticles except that the 2 mL of glycerol was heated to 60°C on a hot plate before adding the RM257/5CB mixture. In addition, during the polymerization step, the sample was kept at 60°C to ensure that the RM257/5CB material remained isotropic. The polymerized material was allowed to cool to room temperature before mixing with salts and/or fluorescent PS probe colloids. Not all microparticles produced by this procedure were isotropic. Upon cooling, it was observed that many particles were radial or bipolar or had polydomains of LC under polarized light microscopy (see the Supplementary Materials for an example of LC microparticle with polydomains). The isotropic microparticles prepared by this method represent less than 5% (by number) of the microparticles synthesized in each batch (given that they are a kinetically trapped state of the system).

Pinned preradial LC microparticles

Pinned preradial LC polymeric microparticles were prepared as described above for radial LC microparticles except that the LC was homogenized in 2 mL of water containing 2 μL of fluorescently labeled PS colloids and 222 μL of 100 mM aqueous NaCl. An important note is that the PS colloids used to pin the defects photobleach during polymerization and cannot be seen with fluorescence microscopy.

Imaging

An imaging well (Nunc Lab-Tek II Chamber Slide System, Thermo Fisher Scientific) was prepared by adding 1 mL deionized water and 111 μL of 100 mM aqueous NaCl to one of four chambers. Next, 60 μL of the dispersion containing the polymerized LC microparticles was added to the imaging well followed by 1 μL of 1-μm-diameter fluorescent PS colloids. The imaging well was then mixed with a glass pipette and covered with a coverslip to prevent evaporation of water. The dispersion was allowed to incubate for 30 min before imaging. Bright-field, polarized light, and fluorescence imaging was performed using an Olympus IX71 inverted epifluorescence microscope (Center Valley, PA) equipped with a 60× objective, crossed polarizers, mercury lamp, and Chroma filter (457 nm ≤ λ_exc ≤ 502 nm, and 510 nm ≤ λ_em ≤ 562 nm). Bright-field, polarized light, and fluorescence micrographs were collected with a Hamamatsu 1394 ORCA-ER charge-coupled device camera (Bridgewater, NJ) connected to a computer and controlled through SimplePCI imaging software (Compix Inc., Cranberry Township, NJ). Imaging of individual wells was performed for 30 min.

Zeta potentials of polymerized LC microparticles

Zeta potential measurements were performed using Malvern Instruments Zetasizer Nano ZSP (Worcestershire, UK) using aqueous dispersions of polymerized bipolar LC, radial LC, pinned preradial LC, and isotropic microparticles. The dispersions were prepared by diluting ~60 μL of the polymerized microparticles in 20 mL of deionized water (~1.5 × 10⁻² volume% particles).

Statistical analysis

The bipolar microparticle data were calculated from 11 independent experiments, with 84 polymerized LC microparticles and 952 probe colloids adsorbed onto the surfaces of these microparticles. The radial microparticle data were calculated from 12 independent experiments, with 132 polymerized LC microparticles and 503 adsorbed probe colloids. The isotropic microparticle data were calculated from 20 independent experiments with 179 polymerized microparticles and 521 adsorbed probe colloids. The pinned preradial microparticle data were calculated from 46 independent experiments with 121 polymerized LC microparticles and 493 adsorbed probe colloids. The error bars are 95% confidence intervals on the averages on the region values for the 84 bipolar LC, 132 radial LC, 179 isotropic, and 121 pinned preradial microparticles.

Two-tailed, paired, Student’s t-tests were used to determine whether the values yielding the averages of the surface regions in Figs. 1G, 2G, and 5E were distinguishable from one another. We used a probability of <5% to indicate that a region was distinguishable. This analysis revealed that for the bipolar LC microparticle dataset, the following pairs of regions were distinguishable: I and II, I and III, I and IV, I and V, II and VI, III and VI, IV and VI, and V and VI. This analysis also revealed that for the radial LC and isotropic microparticle datasets, the values for all regions were not distinguishable. In addition, this analysis revealed that for the pinned preradial LC microparticle dataset, the value of region I was distinguishable from all other regions, while all other regions were not distinguishable from one another.

Probe PS colloids, bipolar LC, radial LC, isotropic, and pinned preradial LC microparticles were measured to have zeta potentials in water of −56 ± 1 mV (n = 5), −49 ± 6 mV (n = 12), −51 ± 5 mV (n = 11), −47 ± 3 mV (n = 8), and −47 ± 3 mV (n = 9), respectively, where n is the number of measurements in the sample SD calculation for the error bars.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/25/eabb1327/DC1