SUMMARY
High-dimensional data, such as those generated by single-cell RNA sequencing (scRNA-seq), present challenges in interpretation and visualization. Numerical and computational methods for dimensionality reduction allow for low-dimensional representation of genome-scale expression data for downstream clustering, trajectory reconstruction, and biological interpretation. However, a comprehensive and quantitative evaluation of the performance of these techniques has not been established. We present an unbiased framework that defines metrics of global and local structure preservation in dimensionality reduction transformations. Using discrete and continuous real-world and synthetic scRNA-seq datasets, we show how input cell distribution and method parameters are largely determinant of global, local, and organizational data structure preservation by 11 common dimensionality reduction methods.
Graphical Abstract
In Brief
Dimensionality reduction tools are critical to visualization and interpretation of single-cell datasets. Heiser and Lau use unbiased, quantitative metrics to evaluate how common embedding techniques such as t-SNE and UMAP maintain native data structure. Datasets with discrete and continuous topologies indicate that input cell distribution is integral to algorithm performance.
INTRODUCTION
Single-cell RNA sequencing (scRNA-seq) offers parallel, genome-scale measurement of tens of thousands of transcripts for thousands of cells (Klein et al., 2015; Macosko et al., 2015). Data of this magnitude provide powerful insight toward cell identity and developmental trajectory—states and fates—that are used to interrogate tissue heterogeneity and characterize disease progression (Regev et al., 2017; Wagner et al., 2019). Yet, extracting meaningful information from such high-dimensional data presents a massive challenge. Numerical and computational methods for dimensionality reduction have been developed to reconstruct underlying distributions from native “gene space” and provide low-dimensional representations of single-cell data for more intuitive downstream interpretation. Basic linear transformations such as principal-component analysis (PCA) have proven to be valuable tools in this field (Sorzano, Vargas and Montano, 2014; Tsuyuzaki et al., 2020). However, given the distribution and sparsity of scRNA-seq data, complex nonlinear transformations are often required to capture and visualize expression patterns. Unsupervised machine learning techniques are being rapidly developed to assist researchers in single-cell transcriptomic analysis (Van der Maaten and Hinton, 2008; Pierson and Yau, 2015; Wang et al., 2017; Linderman et al., 2017; Becht et al., 2018; Ding, Condon and Shah, 2018; Lopez et al., 2018; Mcinnes and Healy, 2018; Risso et al., 2018; Eraslan et al., 2019; Townes et al., 2019). Because these techniques condense cell features in the native space to a small number of latent dimensions, lost information can result in exaggerated or dampened cell-cell similarity. Furthermore, depending on input data and user-defined parameters, the structure of resulting embeddings can vary greatly, potentially altering biological interpretation (Kobak and Berens, 2019).
With a deluge of computational techniques for dimension reduction, the field is lacking a comprehensive assessment of native organizational distortion consequential to such methods. We present an unbiased, quantitative framework for evaluation of data structure preservation by dimensionality reduction transformations. We propose metrics for broad characterization of these methods based on cell-cell distance in native, high-dimensional space. Initial benchmarking of 11 published software tools on discrete and continuous cell distributions shows global, local, and organizational data structure conservation under different parameter and input conditions. Applying our framework to additional data types underscores the modality- and dataset-specific nature of dimension reduction performance.
RESULTS
Cell Distance Distributions Describe Global Structure of High-Dimensional Data
In order to evaluate dimensionality reduction techniques, Euclidean cell-cell distance in native, high-dimensional space is used as a quantitative standard. In scRNA-seq, counts of unique molecular identifiers (UMIs) for each gene make up the features of the dataset, while every observation represents a single cell (Figure 1A). In this way, transcriptomic data is represented as an m × n matrix (observations × features).
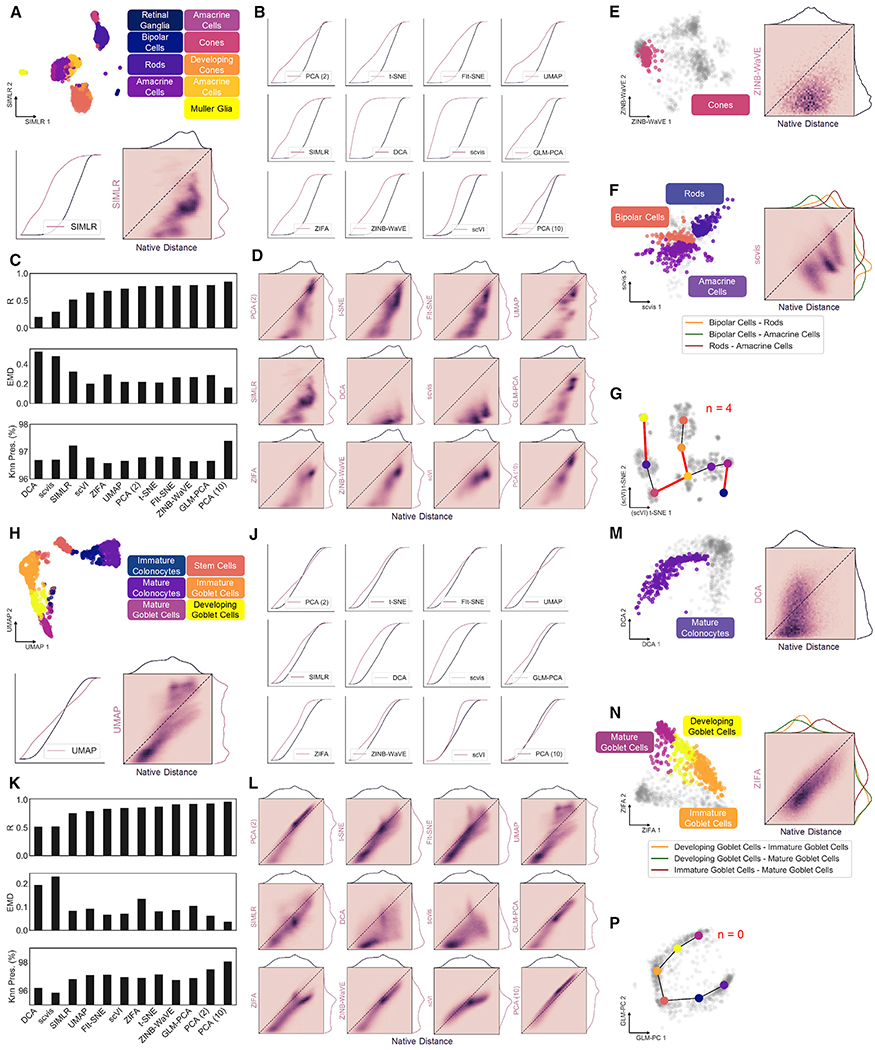
Figure 1. Cell Distance Distributions Describe Global Structure of High-Dimensional Data.
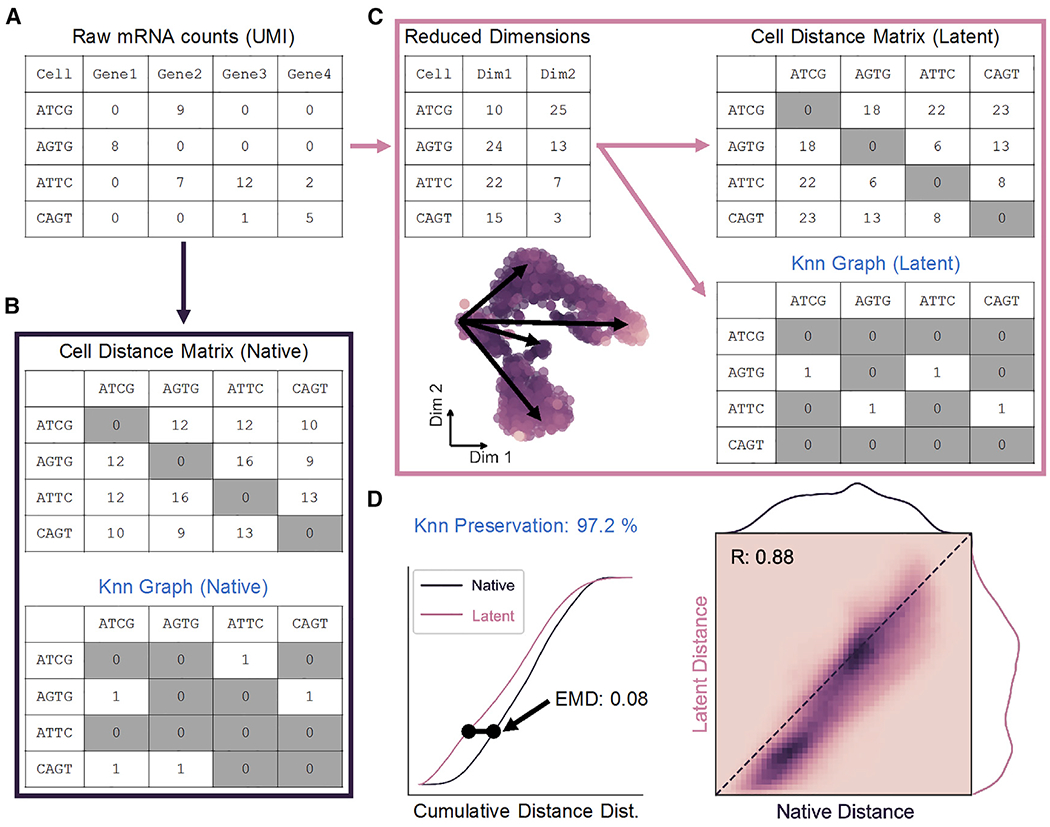
(A) Representation of scRNA-seq counts matrix.
(B) Cell-cell distances in native gene space are calculated to generate an m × m matrix, where m is the total number of cells. The K nearest-neighbor (Knn) graph is constructed from these distances as a binary m × m matrix.
(C) Upon transformation to low-dimensional space, a distance matrix and Knn graph can be calculated as in (B).
(D) Distance matrices from native (B) and latent (C) spaces are used to build cumulative probability density distributions, which can be compared to one another by Earth-Mover’s distance (EMD; left). Unique cell-cell distances are correlated (right), and Knn preservation represents element-wise comparison of nearest-neighbor graph matrices in each space.
See also Figure S1.
Global data structure in the native space can be constructed by first calculating an m × m matrix containing the pairwise distances between all observations in n dimensions (Figure 1B, top). The upper triangle of this symmetric distance matrix contains unique cell distances in the dataset, which can then be represented by a probability density distribution as in Figure 1D. From these distances, local “neighborhoods” can be defined in the form of a K nearest-neighbor (Knn) graph. The Knn graph is represented as a binary m × m matrix that defines the K cells with the shortest distances to each cell in the dataset (Figure 1B, bottom). Similarly, a distance distribution and Knn graph can be constructed from a low-dimensional latent space resulting from dimensionality reduction (Figure 1C).
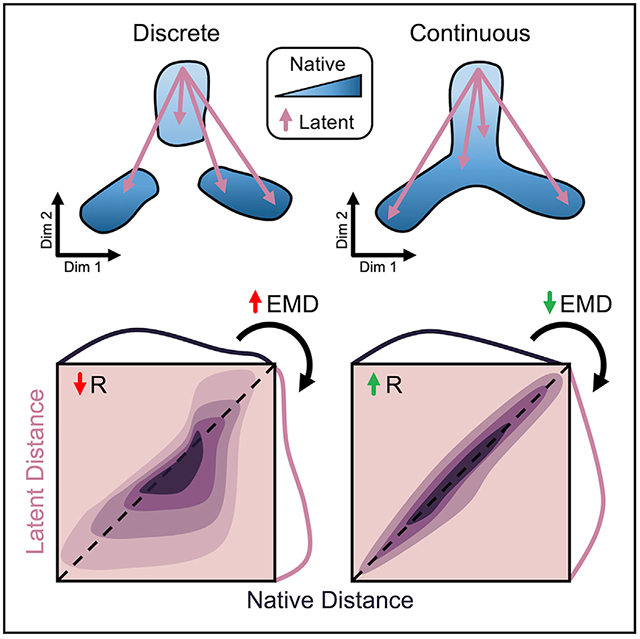
Preservation of unique distances following dimension reduction is measured by direct Pearson correlation, while structural alteration of the cell distance distribution is quantified by the Wasserstein metric or Earth-Mover’s distance (EMD; Figure 1D). Widely applied to image processing, EMD determines the energy cost associated with shifting one distribution to another (Werman, Peleg and Rosenfeld, 1985; Rubner, Tomasi and Guibas, 1998, 2000; Levina and Bickel, 2001). This metric is ideal for our application as it scales linearly with separation of the means of two continuous distributions, in contrast to similar Cramér-von Mises or Kolmogorov-Smirnov distances, and therefore captures maximum variability (Cramér, 1928; Kolmogorov, 1933). Finally, preservation of a Knn graph before and after low-dimensional embedding can also be quantified as the percentage of total matrix elements conserved in order to describe maintenance of local substructures in the data.
Discrete and Continuous Cell Distributions Exemplify Common Biological Patterns
A major consideration for testing dimensionality reduction techniques is the true structure of the input data in native, high-dimensional space. For the scope of our evaluation, we identify two overarching classes of scRNA-seq data for proof-of-principal: discrete and continuous. Discrete single-cell data are comprised of differentiated cell types with unique, highly discernable gene expression profiles. These data include classic PBMC experiments and neuronal datasets that can be easily clustered into distinct cell types (Zeisel et al., 2015; Rheaume et al., 2018). Conversely, continuous data contain multifaceted expression gradients present during cell development and differentiation and are commonly associated with dynamic systems such as erythropoiesis or embryonic development (Tusi et al., 2018; Wagner et al., 2019).
Mouse retina cells, analyzed using Drop-seq by Macosko and coworkers, provide a discrete cell distribution for our analysis (Macosko et al., 2015). Counts data from 20,478 genes for 1,326 cells were analyzed using Louvain clustering to determine cell clusters (Figure 2A; Levine et al., 2015). We performed relatively coarse clustering, ignoring subtype heterogeneity in favor of clusters reflecting principal cell identity amenable to our downstream analyses (see STAR Methods). A t-distributed stochastic neighbor embedding (t-SNE) projection primed with 100 principal components (PCs) of all transcript counts allows for visualization of the data structure and represented cell types (Figure 2B). As evident from the 2D embedding, these data are highly discrete, and constituent cell clusters are easily distinguished by expression of marker genes identified in Macosko et al. (2015) (Figures 2C and S2A).
Figure 2. Discrete and Continuous Cell Distributions Exemplify Common Biological Patterns.
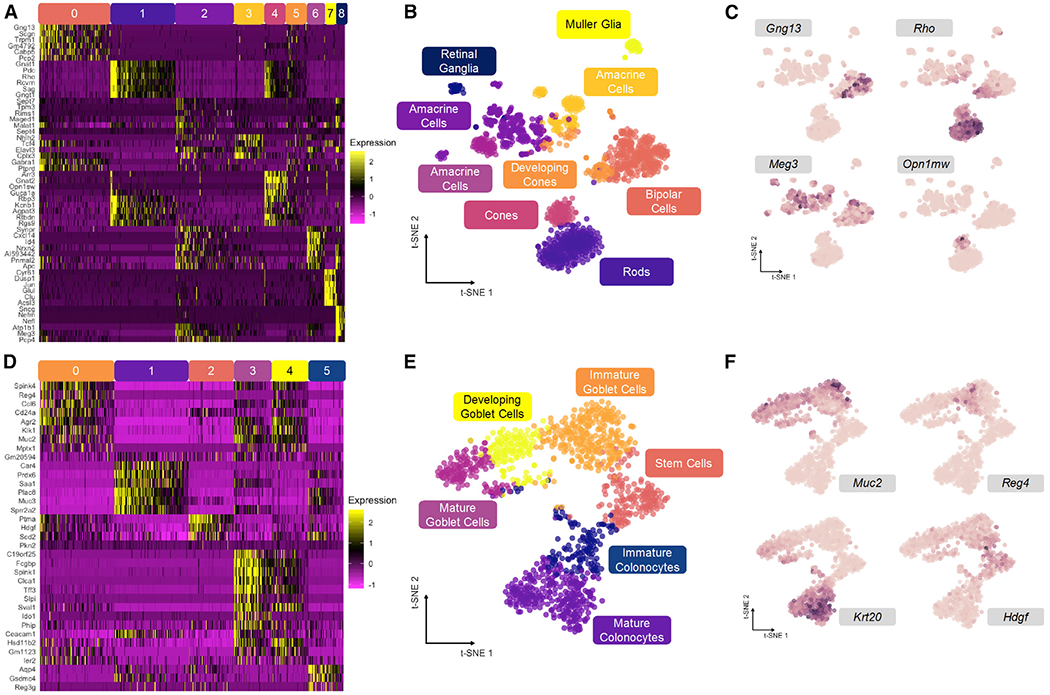
(A) Relative expression of top genes in each cluster for mouse retina dataset.
(B) t-SNE embedding primed with 100 principal components of retina dataset with overlay of consensus clusters.
(C) t-SNE projection from (B) with overlay of marker genes used to identify cell types in (A).
(D) Relative expression of top genes in each cluster for mouse colonic epithelium dataset.
(E) t-SNE embeding primed with 100 principal components of colon dataset with overlay of consensus clusters.
(F) t-SNE projection from (E) with overlay of marker genes used to identify cell types in (D).
See also Figure S2.
Mouse colon data, representing a continuous distribution of actively differentiating cells along the crypt axis of the colonic epithelium, were generated with indexing droplets (inDrop) scRNA-seq (Herring et al., 2018). Counts data from 25,504 genes for 1,117 cells were similarly clustered and embedded using t-SNE to visualize continuous data structure (Figures 2D and 2E). The six clusters form a branching continuum of cell states identified by expression markers (Figures 2F and S2B), resolving two major lineages in the colon: absorptive and secretory cells (Lepourcelet et al., 2005; Tamura et al., 2007; Larsson et al., 2012). These clusters are linked together by pseudotemporal trajectories, and thus, their arrangement is expected to be conserved upon low-dimensional embedding.
Input Cell Distribution Determines Performance of Global Structure Preservation
Using metrics outlined in Figure 1, we compared 11 dimensionality reduction techniques applied to continuous and discrete datasets. To allow for direct input to these tools and comparison with linear PCA in the following analyses, raw counts for both datasets were feature-selected to the 500 most variable genes. Alternatively, a common preprocessing approach is initial dimension reduction with PCA, and we compare 500 PCs to our 500 variable genes (VGs) to demonstrate how this may affect downstream structure preservation (Figure S3A). Though our framework measures structure preservation relative to the input cell distribution, performance of dimension reduction methods is expected to vary under different preprocessing conditions, and we encourage the use of our metrics to evaluate not only the tools themselves but also upstream handling of the data.
Calculating our metrics on all cells in the dataset, we first assess global structure preservation following transformation to a latent space. Representative examples of 2D projections and their corresponding distance distributions and correlations using single-cell interpretation via multikernel learning (SIMLR) for the retina dataset and uniform manifold approximation and projection (UMAP) for the colon dataset are shown in Figure 3A and Figure 3H, respectively. Notably, the largest discrepancy in structural preservation is between the two datasets, highlighting the significance of input cell distribution to overall method performance. For example, Knn preservation is intuitively higher for most methods when applied to the colon dataset (Table S1), reflecting the notion of continuous neighborhoods—a moving window of expression gradients—connecting all cells through developmental pseudotime (PT). Another important observation regarding the dimension-reduced spaces involves the directionality of the cell distance distribution shift. A compression of distances from native to latent space is indicated by a shift left in the cumulative distance distribution (Figures 3B, 3J, and S1A) or below the identity line in the unique distance correlation (Figures 3D, 3L, and S1B). Alternatively, a shift right in the cumulative distance distribution or above the identity line of the distance correlation signifies an exaggeration of native distances. These phenomena are important in the context of global versus local structure preservation. For example, UMAP appears to compress small, local distances to a greater extent than t-SNE, while both methods maintain relative global structure as indicated by a favorable correlation of large distances. Although this characteristic of UMAP embeddings causes greater information loss reflected in less favorable preservation metrics (Figures 3C and 3K; Table S1), clusters within the resulting projections tend to be visually condensed and perhaps more easily interpreted (Figures S3B and S3C).
Figure 3. Global and Local Structure Preservation Analysis of Dimension Reduction Methods on Discrete and Continuous scRNA-seq Datasets.
(A) Example 2D projection of mouse retina data using SIMLR with cluster overlay (top). Cumulative distance distributions for native and latent spaces (bottom left) and 2D histogram representing correlation between unique distances (bottom right).
(B) Cumulative distance distributions of evaluated projections of retina data.
(C) Summary of structure preservation metrics for retina data.
(D) 2D histograms of cell distance correlations for retina data.
(E) Example 2D projection of retina data using zero-inflated negative binomial-based wanted variation extraction (ZINB-WaVE) and overlay of cone cells (left) and 2D histogram representing correlation between the two sets of unique distances (right).
(F) Same as in (E) for distances between bipolar, amacrine, and rod cell clusters, using scvis projection.
(G) Example graph representation of cluster topology for retina dataset, using t-SNE projection primed with single-cell variational inference (scVI) latent space. Red edges represent those not present in minimum spanning tree of native graph.
(H) Same as in (A), with UMAP projection of mouse colon data.
(J) Cumulative distance distributions of evaluated projections for colon data.
(K) Summary of structure preservation metrics for colon data.
(L) 2D histograms of cell distance correlations for colon data.
(M) Same as in (E), with deep count autoencoder (DCA) projection of mature colonocytes.
(N) Same as in F for distances between immature, developing, and mature goblet cell clusters, using zero inflated factor analysis (ZIFA) projection.
(P) Same as in (G), but for the colon dataset, using generalized principal component analysis (GLM-PCA) projection.
These findings are particularly important when considering datasets and data types beyond scRNA-seq. For instance, other single-cell technologies such as assay for transposase-accessible chromatin (scATAC-seq) and mass cytometry (CyTOF) have expectedly diverse distributions of cell-cell distances due to technical differences in dynamic range, dropout rate, and noise. Applying our structural preservation framework to two datasets used to benchmark UMAP against t-SNE, fast Fourier transform-accelerated interpolation-based t-SNE (FIt-SNE) and scvis (Becht et al., 2018; Figure S4), we identify a clear distinction between these CyTOF and scRNA-seq datasets that is deterministic of method performance (see STAR Methods, Theoretical basis for difference in dimension reduction performance across single-cell techniques). Indeed, we assert that input data structure is highly variable across single-cell technologies and biological samples (Figure S3D), and we recommend evaluating dimensionality reduction tools in the context of their intended application.
Parameter Optimization Plays Key Role in Structural Preservation
User-defined parameters for unsupervised algorithms often present themselves as “black-box” knobs with unknown consequences. Tuning these parameters can be a daunting task for the single-cell analyst, but it is known to be crucial to algorithm performance (Belkina et al., 2019; Kobak and Berens, 2019; Tsuyuzaki et al., 2020). Using our proposed metrics, we evaluated global structure preservation across a range of perplexity (n_neighbors) values for t-SNE and UMAP applied to both discrete and continuous data. Through a balance of distance correlation, EMD, and Knn preservation, we can identify an initial range of optimal perplexity values between 3% and 10% of the total number of cells in the dataset (Figure S3E).
Additionally, as our framework is agnostic to the distance metric and neighborhood size (K) chosen for evaluation, we can perform cursory comparisons of possible alternatives to Euclidean distance (Figure S3F) and titrate the value of K to determine its effect on observed preservation values (Figure S3G). Here, we observe optimal K between 3% and 10% of the dataset size to reliably discriminate between methods, in accordance with the perplexity parameter.
Substructure Analysis Elucidates Contribution to Global Performance
To corroborate results of global structure preservation and dissect contribution of local (within cluster) and organizational (between cluster) distances to overall dimension reduction performance, clusters were isolated for targeted substructure quantification. Here, we can measure distance preservation of individual clusters as well as distances between clusters to emphasize local arrangement (Figures S1C and S1D).
Retinal cone cells (Figure 2A; cluster 4, n = 94) were used as an example of local distances in the discrete dataset, while mature colonocytes (Figure 2D; cluster 1, n = 273) were isolated in the colon dataset (Figures 3E and 3M). Local distance compression represents the overarching trend for the 11 evaluated tools, indicated by a correlation shift below the identity line (Figures S3H and S3J). The latent spaces from scVI and 10-component PCA are notable exceptions, yielding the two lowest EMD values for each dataset (Figure S3M). This most likely results from the 10dimensional latent spaces of these methods capturing more cellular variability than 2D projections, and these two embeddings should be considered with this caveat in the context of our larger analysis. Added noise in the SIMLR latent space of mouse retina cells indicates a disagreement with Louvain cluster membership, and may be attributed to the truncated, 500-feature input used for our analysis (Figure S3H). Moreover, this observation suggests that discrete, “on-off” expression patterns are less robust to dropouts that cause mis-assignment of cell type than continuous gradients of gene expression.
Besides maintenance of local structure, dimensionality reduction methods are also tasked with preserving cellular neighborhoods or relationships between clusters. By calculating the distribution of distances from cells in one cluster to those in another, we can evaluate these associations to investigate organization of data substructures (Figures S1C, 3F, and N). In the mouse retina dataset, distances between bipolar cells, rod cells, and amacrine cells (Figure 2A; clusters 0,1, and 2, n = 309,281, and 258) are marked largely by compression, with some tools altering the arrangement of the three clusters (Figure S3K, red boxes). For example, the bipolar and amacrine clusters are closest to one another in the native gene space, but bipolar cells are closer to rod cells in the UMAP embedding, indicated by the ordering of each distribution. Conversely, relative distances between three adjacent clusters along the goblet cell lineage (Figure 2D; clusters 0, 3, and 4, n = 274,140, and 135) are more highly conserved by all embeddings. These results confirm that related cells in continuous scRNA-seq data are tethered to their neighbors through intermediate expression states, resulting in improved structure preservation upon latent projection (Figures S3L and S3N).
To further capture substructure rearrangement in low-dimensional embeddings, we construct a coarse graphical representation of our native and latent spaces, with minimum spanning trees (MSTs) connecting nearest neighbor cluster centroids (Figures 3G and 3P). Comparing the edges of each graph allows us to evaluate latent cluster topology relative to the native space, as permuted edges indicate rearrangement of substructures following dimension reduction. Once again, we see a global increase in topological preservation of continuous versus discrete data, corroborating previous observations (Figures S3P–S3R).
Simulated Datasets with Defined Topology Validate Observations
Single-cell data with expected global topology were simulated using Splatter (Zappia et al., 2017). Three distinct lineages, equally separated in high dimensional space, originate from a common state. A discrete simulation was generated by removing the central shared state (Figure 4A), while the continuous dataset maintains complete connectivity between the three developmental paths (Figure 4F). Pseudotime (PT) values, assigned to each cell by the simulation, should correlate directly to distance in the embedding and can thus be used as an alternative ground-truth native structural distribution for our framework. Both simulations were processed by previously evaluated dimensionality reduction tools (Figures 4B, 4C, 4G, and 4H), and latent distances between cells from the three defined paths were correlated to pairwise sums of corresponding PT values (Figures 4D, 4E, 4J, and 4K). In this way, large PT sums between cells at the ends of each simulated path and small PT sums between cells near the shared central state should have the largest and smallest distances from one another in an ideal latent embedding, respectively. Again, dimension reduction of discrete data performs poorly compared to the entirely continuous simulation. All embeddings generally cluster each path properly (Figure 4B), but misorientation of these clusters from their shared center results in negative structural correlation for some embeddings including t-SNE and UMAP (Figures 4C and 4; Table S2).
Figure 4. Simulated Datasets with Defined Topology Validate Observations.
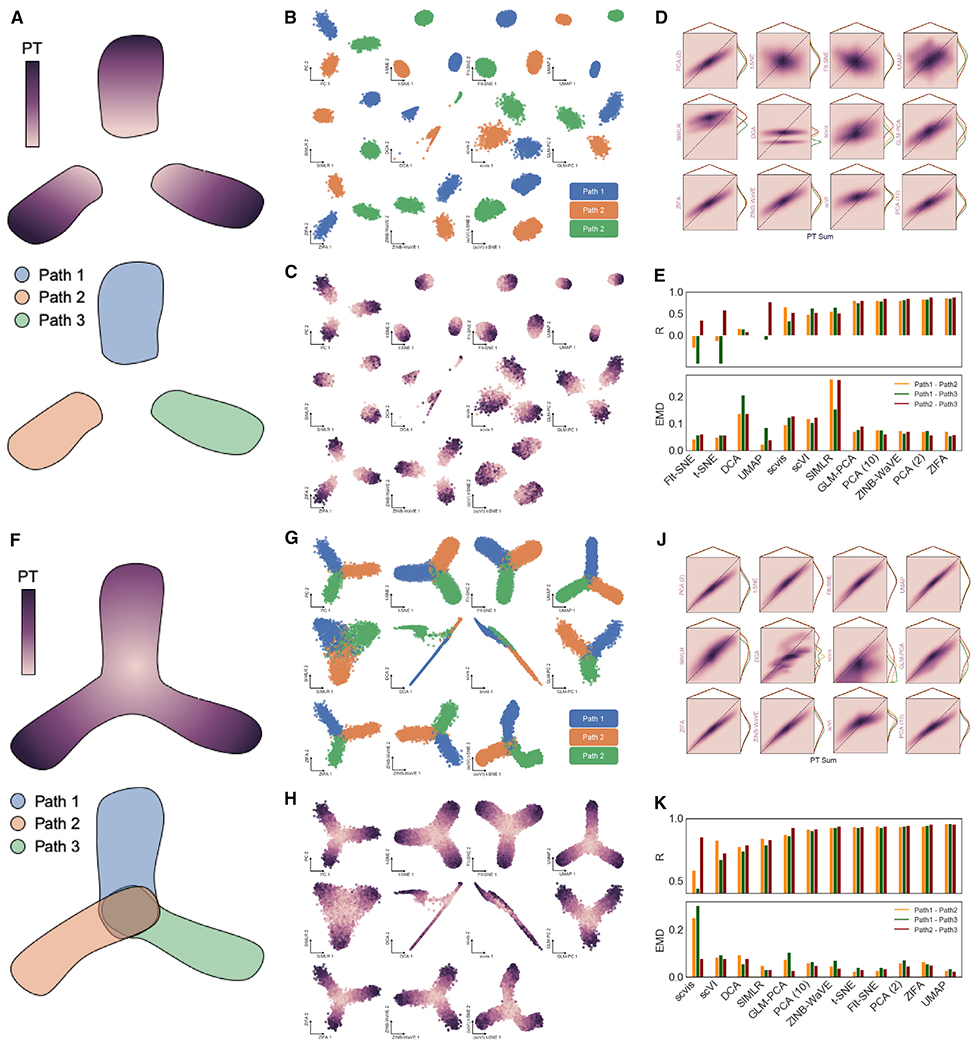
(A) Diagram of discrete synthetic data with ground-truth topology defined by three equally spaced developmental paths along directional pseudotime (PT) from a common source state (removed to discretize paths).
(B) 2D embeddings by 11 dimensionality reduction tools showing unique paths defined in discrete simulation.
(C) Same as in (B), with overlay of PT values for each cell as defined in simulation.
(D) 2D histograms showing correlation of pairwise distances between cells in each of the three developmental paths with the sum of PT values between each pair of cells as ground-truth topology.
(E) Summary of correlation and EMD values between cells in each path for all dimensionality reduction methods.
(F) Diagram of continuous synthetic data with ground-truth topology defined by three developmental paths along directional PT from a common source state.
(G) 2D embeddings by 11 dimensionality reduction tools showing unique paths defined in continuous simulation.
(H) Same as in (G), with overlay of PT values for each cell.
(J) 2D histograms showing correlation of pairwise distances between cells in each of the three developmental paths with the sum of PT values between each pair of cells as ground-truth topology.
(K) Summary of correlation and EMD values between cells in each path of continuous simulation for all dimensionality reduction methods.
DISCUSSION
As high-dimensional data become increasingly pervasive in systems biology, computational tools for reliable and reproducible analysis of these data are tremendous assets to discovery. Dimensionality reduction techniques allow for embedding cellular observations with tens of thousands of features into a low-dimensional space for visualization and downstream processing. We present an unbiased, quantitative framework based on native cell distance to evaluate data structure preservation by these tools.
We identified dispersion trends in local and global distance distributions that denote expansion and contraction of native cell distances. This allowed us to evaluate general performance of dimensionality reduction methods on entire single-cell datasets and take a deeper dive to examine how distances within or between clusters contribute to the global structure of a low-dimensional embedding (Figures 3 and S3). With a goal of grouping cells by their gene expression profiles, most dimension reduction tools evaluated herein compress local distances, embellishing cluster similarity, while maintaining or expanding global distances, exaggerating cluster distinction. These characteristics of dimensionality reduction methods are desirable for most applications. However, resolution of rare cell types and sub-cluster heterogeneity may be lost, stressing the importance of preprocessing, feature selection, and user-defined parameters (Figure S3).
Discrete scRNA-seq data are more susceptible to structural perturbation by downstream dimension reduction, as indicated by larger EMD values and lower distance correlations in the retina dataset than colonic epithelial data (Figure 3). We also observed cluster rearrangement within the retina dataset, suggesting that relative substructure organization is poorly defined for discrete datasets while continuous cell distributions are more robust to these effects (Figure S3). Cursory exploration of perplexity and K parameters in t-SNE and UMAP, as well as alternative preprocessing approaches, reveals a range of optimal values that yield favorable structure preservation metrics, endorsing the need for parameter and preprocessing optimization for dimensionality reduction of single-cell datasets (Figures S3E and S3G). The above observations were confirmed using simulated datasets with defined global topology that could be quantified in place of native cell distances (Figure 4).
Finally, a careful look at additional synthetic and real-world data confirms that behavior of dimensionality reduction methods is primarily driven by the input cell distance distribution that is modality and dataset specific (Figure S4). Our findings challenge the context in which dimensionality reduction methods are benchmarked and indicate that performance characterization is often not universally extensible. Consequently, we encourage evaluation of such tools on data types, datasets, and preprocessing approaches specific to the user’s intended application.
STAR★METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, KSL (ken.s.lau@vanderbilt.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
The code generated during this study is available at https://github.com/KenLauLab/DR-structure-preservation.
METHOD DETAILS
Cell Filtering
Raw counts expression matrices downloaded from GEO (accession IDs GSM1626793, GSM2743164) were filtered for high-quality cells prior to downstream analysis. The cumulative sum of total UMI counts for each cell was plotted along with the slope of the secant line to the curve as a function of rank-ordered cell. The distance between these two curves was used as a metric for determining the rate of diminishing cell quality. The cell number at which this distance was 50% of its maximum was chosen as a cutoff, with cells contributing less UMI counts were removed. Next, a 100-component PCA and UMAP with n_neighbors value of 0.5% of the total cells in the dataset were used to visualize cell populations and manually gate out clusters containing high mitochondrial counts, indicating dead cells. Analysis performed using scanpy (Wolf, Angerer and Theis, 2018).
Process shown in:
Clustering
PhenoGraph (Levine et al., 2015) was used to perform Louvain clustering on both datasets in Python. To create coarse, ground-truth clusters, the algorithm was run on 100 principal components of all genes in each dataset. For the retina data, 100 PCs of 20,478 genes explained 33.5% of the variance in the dataset. For the colon data, 100 PCs of 25,505 genes explained 54.0% of the variance. k values of 50 and 100 for generating the Knn graph to seed the Louvain algorithm for the retina and colon datasets, respectively, were chosen to provide coarse clustering of major cell types. Nine resulting clusters for the retina dataset and six resulting clusters in the colon dataset were analyzed by Seurat’s Find All Markers and Do Heatmap functions (Butler et al., 2018) to obtain visualizations of up- and down-regulated genes in each cluster (Figure 2A,D).
Process shown in:
Dimensionality Reduction
All dimensionality reduction was performed on feature-selected data containing the most variable genes in each dataset. Genes were rank-ordered by variance using the Pandas (version 0.22.0) (Mckinney, 2010) DataFrame.var function in Python, and the top 500 were chosen. Each dimensionality reduction technique was run “out-of-the-box” with default parameters on the feature-selected data. DCA, scvis, scVI, ZINB-WaVE and GLM-PCAtake raw, unnormalized counts as input. Developers of ZIFA recommend a log2 transformation of counts, which we first normalized to the maximum UMI count within each cell. Arcsinh-transformed counts normalized to the maximum UMI count in each cell were used for all other methods (t-SNE, FIt-SNE, UMAP, SIMLR, PCA).
Visualization
Cumulative cell distance distributions were plotted from the upper triangle of symmetrical cell distance matrices using triu_indices function from the numpy Python package (version 1.16.3) (Oliphant, 2006). The histogram and cumsum functions from numpy were used to plot cumulative distribution functions using n/100 bins, where n is the length of the flattened distance vector. Unique distance correlation was visualized using the JointGrid and kdeplot functions from the seaborn package (version 0.9.0) (Waskom et al., 2014), as well as the pyplot.hist2d function from the matplotlib package (version 3.0.3) (Hunter, 2007). Cluster topology graphs were plotted using the network function draw_networkx.
Functions used for above visualizations can be found in:
Splatter Simulation
Simulated single-cell datasets were generated using the Splatter package (1.8.0) (Zappia et al., 2017). Continuous dataset was generated with 500 features (nGenes) and 3,060 observations (batchCells), with a lib.loc value of 10 and lib.scale value of 0.05 to generate data close to observed counts distributions from scRNA-seq. The simulation defined three paths with equal group.prob values (0.3333333) originating at the same state (path.from = c(0,0,0)). Each path had path.nSteps value of 1,000 indicating as many possible continuous expression states emanating from the common origin state. These step values are used as pseudotime (PT) measures in our analysis. Discrete simulation data was generated by simply excluding all cells with PT values less than 400, eliminating the common central state. The resulting dataset had 1,873 observations for the 500 features of the continuous simulation. When evaluating embeddings of these simulated data, native cell-cell distance distributions were replaced with cell-cell PT sums normalized in the same fashion. These analyses were only performed pairwise between cells in each of the three developmental paths.
Functions used for above simulation can be found in:
Theoretical basis for difference in dimension reduction performance across single-cell techniques
Based on prior evidence and common practice in the field, we aim to validate our metrics and address the challenges our results pose to current conceptions about popular dimensionality reduction tools. UMAP was benchmarked against t-SNE, FIt-SNE and scvis on three datasets (Becht et al., 2018): two CyTOF – Samusik and Wong – and one scRNA-seq – Han mouse cell atlas. We applied our structural preservation framework to the Samusik and Han datasets (Weber and Robinson, 2016; Han et al., 2018), making interesting observations that both substantiate our metrics and emphasize a major takeaway from this study.
Figure S4A compares t-SNE to UMAP on the hematopoietic subset of the Han scRNA-seq dataset. Interestingly, the two methods perform very similarly, with UMAP slightly outperforming t-SNE as described in Becht et al. (2018). Figures S4B–S4D reflect a similar analysis of the Samusik CyTOF dataset, where there is a clear improvement in unique distance preservation by UMAP over t-SNE, indicated by a strong increase in cell-cell distance correlation. Again, this result agrees with Becht and coworkers, who also correlated cell distances to show vast improvement over t-SNE and other methods. Nonetheless, our framework identifies a marginal increase in EMD for UMAP overt-SNE, indicating a higher degree of global structural distortion, likely due to more compact clustering by UMAP (Figure S4B). We propose that improved performance of UMAP applied to CyTOF data is due to the input cell distribution.
Because mass cytometry measurements have a larger dynamic range and lower dropout rate than scRNA-seq, the overall variance of cell distance distributions from CyTOF is greater (Figure S3D). This allows for better discrimination between “large” (global) and “small” (local) distances in the native space. With this in mind, we can explore the mathematical basis for global distance preservation in UMAP versus t-SNE to help explain why these advantages may not always be clearly observed when applied to scRNA-seq data.
First, t-SNE models the conditional probability that any two points xi, xj would be neighbors if neighbors were chosen in proportion to a Gaussian probability density function at xi (Van der Maaten and Hinton, 2008). We can simplify this probability density function to Equation 1.1 under the right parameter conditions. Conditional probability for low-dimensional distances between points yi,yj, is modeled by the Student t-distribution, simplified in Equation 1.2.
| (1.1) |
| (1.2) |
UMAP models distance probabilities very similarly. Equations 2.1 and 2.3 show simplification of high-dimensional conditional probabilities given the defined symmetrization used by UMAP (Equation 2.2). Equation 2.4 shows UMAP’s low-dimensional distance probability model, which is not exactly the Student t-distribution, but approximates to it underthe right parameters a and b (Mcinnes and Healy, 2018).
| (2.1) |
| (2.2) |
| (2.3) |
| (2.4) |
The cost function for optimization of t-SNE coordinates is Kullback-Leibler divergence (DKL), defined in Equation 3.1 for X representing the set of cell-cell distances in the high-dimensional (native) space, and Y representing the set of corresponding distances in the low-dimensional (latent) space. We additionally notate pij and qij as P(X) and Q(Y) for all xi,xj∈X and yi,yj∈Y, respectively. The first term of this equation is close to 0 for both large and small X, so you can approximate DKL by the second term alone and substitute pij and qij from Equations 2.3 and 2.4 for P(X) and Q(Y) (Equation 3.2).
| (3.1) |
| (3.2) |
Evaluating the limits of DKL in Equation 3.2, there is a large penalty at small X and large Y, but for large X the penalty is marginal regardless of Y (Equations 3.3, 3.4).
| (3.3) |
| (3.4) |
On the other hand, UMAP uses cross entropy (CE) as its cost function (Equation 4.1). This function behaves the same as t-SNE for small X, shown in Equations 4.2 and 4.3. The difference arises at large X, where the penalty becomes very large for small Y (Equation 4.4).
| (4.1) |
| (4.2) |
| (4.3) |
| (4.4) |
Undoubtedly, the CE cost function has theoretical advantages over DKL, and strikes a balance between local and global distance preservation for more uniformly distributed samples. So why is performance seemingly equivalent on scRNA-seq data such as our colon and retina datasets, as well as the Han hematopoietic dataset evaluated by Becht, et al.? We propose that the negative binomial nature of scRNA-seq data causes the native set of cell distancesX to have a small variance (even following normalization and log or arcsinh transformation), resulting in a similar cost function profile in both t-SNE and UMAP. Conversely, CyTOF data with more variant cell distances are predisposed to favorable optimization by the CE cost function.
To further test this hypothesis with a simpler example, we generated a synthetic dataset consisting of two 1,000-point Gaussians in three-dimensional space (Figure S4J). The resulting cell distance distribution is bimodal, consisting of local distances between cells in each Gaussian and global distances from one point cloud to the other. UMAP outperformed t-SNE drastically in correlation and EMD values, with only a slight loss in Knn preservation (to be expected, as t-SNE favors small distances in its optimization) (Figures S4K and S4L). This result corroborates prior evidence that UMAP distinguishes itself greatly on datasets with clear “local” and “global” distance populations, owing to its cost function. Consequently, we assert that behavior of dimensionality reduction methods is predominantly governed by the input data itself, and we encourage evaluation of these techniques on data types, datasets, and normalization and preprocessing approaches specific to an intended application.
QUANTIFICATION AND STATISTICAL ANALYSIS
Distance Metric Calculations
Pearson correlation was performed for Euclidean cell-cell distance preservation analysis using the scipy.stats.pearsonr function from the scipy package (version 1.1.0) (Oliphant, 2007). The wasserstein_1d function from the POT package (version 0.6.0) (Flamary and Courty, 2017) was used to calculate the Earth Mover’s Distance between vectors containing unique distances between all cells in the dataset (upper triangle of distance matrix), except for local comparisons between clusters, where the entire flattened matrix was used as the cell-cell distance matrices are not symmetrical. K nearest neighbor graphs were constructed using the scikit-learn (version 0.20.0) (Pedregosa et al., 2011) function sklearn.neighbors.kneighbors_graph. Knn preservation was calculated as the percentage of elements in the Knn graph matrix that are conserved. Cluster centroid topology graphs and minimum spanning trees were generated using networkx (version 2.2) (Hagberg, Schult and Swart, 2008).
Functions used for above calculations can be found in:
Supplementary Material
KEY RESOURCES TABLE
Highlights.
Cell distance distributions define global data structure in native and latent space
Input cell distribution is determinant of dimensionality reduction performance
Modality-specific cell distributions influence degree of structural preservation
ACKNOWLEDGMENTS
The authors would like to acknowledge the Vanderbilt Epithelial Biology Center, Vanderbilt Quantitative Systems Biology Center, and Bob Chen from the Lau lab for helpful discussions. K.S.L. is funded by the NIH (grants R01DK103831, P50CA236733, U01CA215798, and U54CA217450), and C.N.H. is funded by NIH grant U2CCA233291.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.celrep.2020.107576.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Becht E, McInnes L, Healy J, Dutertre C-A, Kwok IWH, Ng LG, Ginhoux F, and Newell EW (2018). Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol 37, 38–44. [DOI] [PubMed] [Google Scholar]
- Belkina AC, Ciccolella CO, Anno R, Halpert R, Spidlen J, and Snyder-Cappione JE (2019). Automated optimal parameters for T-distributed stochastic neighbor-embedding improve visualization and allow analysis of large datasets. Nat. Commun 10, 5415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler A, Hoffman P, Smibert P, Papalexi E, and Satija R (2018). Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol 36, 411–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cramér H (1928). On the composition of elementary errors. Scand. Actuar. J 1928, 13–74. [Google Scholar]
- Ding J, Condon A, and Shah SP (2018). Interpretable dimensionality reduction of single cell transcriptome data with deep generative models. Nat. Commun 9, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eraslan G, Simon LM, Mircea M, Mueller NS, and Theis FJ (2019). Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun 10, 390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flamary R, and Courty N (2017). POT Python optimal transport library. https://github.com/rflamary/POT. [DOI] [PubMed] [Google Scholar]
- Hagberg AA, Schult DA, and Swart PJ (2008). Exploring network structure, dynamics, and function using Network. In Proceedings of the 7th Python in Science Conference, Varoquaux G, Vaught T, and Millman J, eds. (SciPy; ), pp. 11–15. [Google Scholar]
- Han X, Wang R, Zhou Y, Fei L, Sun H, Lai S, Saadatpour A, Zhou Z, Chen H, Ye F, et al. (2018). Mapping the mouse cell atlas by Microwell-Seq. Cell 772, 1091–1107.e17. [DOI] [PubMed] [Google Scholar]
- Herring CA, Banerjee A, McKinley ET, Simmons AJ, Ping J, Roland JT, Franklin JL, Liu Q, Gerdes MJ, Coffey RJ, and Lau KS (2018). Unsupervised trajectory analysis of single-cell RNA-seq and imaging data reveals alternative tuft cell origins in the gut. Cell Syst 6, 37–51.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter JD (2007). Matplotlib: a 2D graphics environment. Comput. Sci. Eng 9, 99–104. [Google Scholar]
- Klein AM, Mazutis L, Akartuna I, Tallapragada N, Veres A, Li V, Peshkin L, Weitz DA, and Kirschner MW (2015). Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 767, 1187–1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobak D, and Berens P (2019). The art of using t-SNE for single-cell transcriptomics. Nat. Commun 70, 5416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolmogorov A (1933). Sulla determinazione empirica di una legge di distribuzione. G. Ist. Ital. Attuari. 4, 83–91. [Google Scholar]
- Larsson E, Tremaroli V, Lee YS, Koren O, Nookaew I, Fricker A, Nielsen J, Ley RE, and Backhed F (2012). Analysis of gut microbial regulation of host gene expression along the length of the gut and regulation of gut microbial ecology through MyD88. Gut 67, 1124–1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lepourcelet M, Tou L, Cai L, Sawada J, Lazar AJ, Glickman JN, Williamson JA, Everett AD, Redston M, Fox EA, et al. (2005). Insights into developmental mechanisms and cancers in the mammalian intestine derived from serial analysis of gene expression and study of the hepatoma-derived growth factor (HDGF). Development 732, 415–27. [DOI] [PubMed] [Google Scholar]
- Levina E, and Bickel P (2001). The Earth Mover’s distance is the Mallows distance: some insights from statistics. In Proceedings Eighth IEEE International Conference on Computer Vision. ICCV 2001 (IEEE Computer Society), pp. 251–256. [Google Scholar]
- Levine JH, Simonds EF, Bendall SC, Davis KL, Amir AD, Tadmor MD, Litvin O, Fienberg HG, Jager A, Zunder ER, et al. (2015). Data-driven phenotypic dissection of AML reveals progenitor-like cells that correlate with prognosis. Cell 762, 184–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linderman GC, Rachh M, Hoskins JG, Steinerberger S, and Kluger Y (2017). Efficient algorithms for t-distributed stochastic neighborhood embedding. Nat. Methods 76, 243–245. [Google Scholar]
- Lopez R, Regier J, Cole MB, Jordan MI, and Yosef N (2018). Deep generative modeling for single-cell transcriptomics. Nat. Methods 75, 1053–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macosko EZ, Basu A, Satija R, Nemesh J, Shekhar K, Goldman M, Tirosh I, Bialas AR, Kamitaki N, Martersteck EM, et al. (2015). Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell 767, 1202–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mcinnes L, and Healy J (2018). UMAP: uniform manifold approximation and projection for dimension reduction. arXiv, 1802.03426. https://arxiv.org/pdf/1802.03426.pdf. [Google Scholar]
- Mckinney W (2010). Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference, van der Walt S and Millman J, eds. (SciPy; ), pp. 56–61. [Google Scholar]
- Oliphant T (2006). Guide to NumPy (Continuum Press; ). [Google Scholar]
- Oliphant TE (2007). Python for scientific computing. Comput. Sci. Eng 9, 10–20. [Google Scholar]
- Pedregosa F,Varoquaux G, Gramfort A, Michel V, Thirion B, et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res 72, 2825–2830. [Google Scholar]
- Pierson E, and Yau C (2015). ZIFA: dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biol. 76, 241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regev A, Teichmann SA, Lander ES, Amit I, Benoist C, Birney E, Bodenmiller B, Campbell P, Carninci P, Clatworthy M, et al. ; Human Cell Atlas Meeting Participants (2017). The Human Cell Atlas. eLife 6, e27041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rheaume BA, Jereen A, Bolisetty M, Sajid MS, Yang Y, Renna K, Sun L, Robson P, and Trakhtenberg EF (2018). Single cell transcriptome profiling of retinal ganglion cells identifies cellular subtypes. Nat. Commun 9, 2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risso D, Perraudeau F, Gribkova S, Dudoit S, and Vert JP (2018).A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun 9, 284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubner Y, Tomasi C, and Guibas LJ (1998). A metric for distributions with applications to image databases. In Sixth International Conference on Computer Vision (IEEE Cat. No. 98CH36271)(Narosa Publishing House; ), pp. 59–66. [Google Scholar]
- Rubner Y, Tomasi C, and Guibas LJ (2000). The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vision 40, 99–121. [Google Scholar]
- Sorzano COS, Vargas J, and Montano AP (2014).A survey of dimensionality reduction techniques. arXiv, 1403.2877. http://arxiv.org/abs/1403.2877. [Google Scholar]
- Tamura M, Tanaka S, Fujii T, Aoki A, Komiyama H, Ezawa K, Sumiyama K, Sagai T, and Shiroishi T (2007). Members of a novel gene family, Gsdm, are expressed exclusively in the epithelium of the skin and gastrointestinal tract in a highly tissue-specific manner. Genomics 89, 618–629. [DOI] [PubMed] [Google Scholar]
- Townes FW, Hicks SC,Aryee MJ, and Irizarry RA (2019). Feature selection and dimension reduction for single cell RNA-Seq based on a multinomial model. Genome Biol. 20, 295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuyuzaki K, Sato H, Sato K, and Nikaido I (2020). Benchmarking principal component analysis for large-scale single-cell RNA-sequencing. Genome Biol. 9, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tusi BK, Wolock SL, Weinreb C, Hwang Y, Hidalgo D, Zilionis R, Waisman A, Huh J, Klein AM, and Socolovsky M (2018). Population snapshots predict early haematopoietic and erythroid hierarchies. Nature 555, 54–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Maaten L, and Hinton G (2008). Visualizing data using t-SNE. J. Mach. Learn. Res 9, 2579–2605. [Google Scholar]
- Wagner Weinreb, D.E. C, Collins ZM, Briggs JA, Megason SG, and Klein AM (2019). Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 360, 981–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B, Zhu J, Pierson E, Ramazzotti D, and Batzoglou S (2017). Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nat. Methods 74, 414–416. [DOI] [PubMed] [Google Scholar]
- Waskom M, Botvinnik O, Hobson P, Cole JB, Halchenko Y, Hoyer S, Miles A, Augspurger T, Yarkoni T, Megies T, et al. (2014). seaborn: v0.5.0 (November 2014) (Zenodo; ). [Google Scholar]
- Weber LM, and Robinson MD (2016). Comparison of clustering methods for high-dimensional single-cell flow and mass cytometry data. Cytometry A 89, 1084–1096. [DOI] [PubMed] [Google Scholar]
- Werman M, Peleg S, and Rosenfeld A (1985). A distance metric for multi-dimensional histograms. Comput. Gr. Image Process. 32, 328–336. [Google Scholar]
- Wolf FA, Angerer P, and Theis FJ (2018). SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 79, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zappia L, Phipson B, and Oshlack A (2017). Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 78, 174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeisel A, Muñoz-Manchado AB, Codeluppi S, Lönnerberg P, La Manno G, Juréus A, Marques S, Munguba H, He L, Betsholtz C, et al. (2015). Brain structure. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347, 1138–1142. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code generated during this study is available at https://github.com/KenLauLab/DR-structure-preservation.