Highlights
-
•
The batch reactor dynamics is used to predict SARS-CoV-2 spreading.
-
•
The reactor model can phenomenologically explain the virus spreading.
-
•
The model predicts the peak (day and entity) and the infection extinction.
-
•
Initial Value Problem for ODE has been solved with an unknown initial condition.
-
•
Algorithm robustness and convergence have been tested.
Keywords: SARS-CoV-2, Infection dynamics, Batch chemical reactor, Predictive model, Non-linear regression, Pandemic mathematical model
Abstract
The pandemic infection of SARS-CoV-2 presents analogies with the behavior of chemical reactors. Susceptible population (A), active infected population (B), recovered cases (C) and deaths (D) can be assumed to be molecules of chemical compounds and their dynamics seem well aligned with those of composition and conversions in chemical syntheses. Thanks to these analogies, it is possible to generate pandemic predictive models based on chemical and physical considerations and regress their kinetic parameters, either globally or locally, to predict the peak time, entity and end of the infection with certain reliability. These predictions can strongly support the emergency plans decision making process. The model predictions have been validated with data from Chinese provinces that already underwent complete infection dynamics. For all the other countries, the evolution is re-regressed and re-predicted every day, updating a pandemic prediction database on Politecnico di Milano’s webpage based on the real-time available data.
Nomenclature
- Symbols/Acronyms
Meaning [UoM]
- A
Number of people susceptible to infection [Number of people]
- A0
Total amount of people that will be infected during pandemic elapsing [Number of people]
- AIPP
Active Infected Population at the Peak [Number of people]
- B
Active infected cases [Number of people]
- C
Recovered cases [Number of people]
- D
Deceased cases [Number of people]
- Cf
Recovered cases at pandemic extinction [Number of people]
- Df
Deceased cases at pandemic extinction [Number of people]
- fobj
Objective function [–]
- IED
Infection Extinction Day [day]
- IPT
Infection Peak Time [day]
- IVP
Initial Value Problem [–]
- JHU
John Hopkins University [–]
- k0i
Kinetic constant without sigmoidal modification [1/day]
- ki
i-th reaction kinetic constant with sigmoidal modification [1/day]
- Ri
i-th reaction [People/day]
- TIP
Total Infected Population [Number of people]
- UW
University of Washington [–]
Greek letters
- Α
Kinetic constant weight parameter [1/day]
- Β
Kinetic constant time-lag parameter [1]
1. Introduction
Data analytics and trend extrapolation for future predictions are often demanded in simplified models (Buzzi-Ferraris and Manenti, 2011). Linear, cubic or polynomials are the most widespread models for their easiness of implementation and clearness of result interpretation (Ryan, 2008). In the practice, an easy prediction is welcome when some general and macro trends are useful, as it happens in the global economy, energy markets and resource trading to quote a few. On the other hand, accuracy and robustness in the predictions assume more and more relevance when the phenomena to be predicted deal with primary needs, like health, surgical treatments or pandemic situations (Layne et al., 2020), and especially when such phenomena can be modeled in more robust and reliable ways (Wu et al., 2020a, Wu et al., 2020b).
Proposed models mainly deal with the domestic and international infection diffusion based on the number of flight passengers (Chinazzi et al., 2020), person-to-person transmissions (Chan et al., 2020) and transmission chain tracking (Grubaugh et al., 2019). Some models are also attributing a primary role to social interactions (Stevens, 2020), before and after governmental restrictions and considering how compliant the population is, but no one is trying to search analogies with chemical and physical phenomena where the process dynamics modeling experience has a long and consolidated history (CAPE Working Party, 2020, EFCE, 2020, Gani et al., 2020).
The impressive analogies between the behavior of SARS-CoV-2, infection diffusion (Chinazzi et al., 2020, Wu et al., 2020a, Wu et al., 2020b) and chemical reactor dynamics (Fogler, 2006, Froment et al., 2009, Levenspiel, 2004), batch reactors in particular, are the seminal idea to develop a generalized mathematical model for infection spread dynamics. Then, some relevant information, such as the infection peak, for both time and active infected population, the end of the pandemic and its origins, can be predicted to develop appropriate countermeasures.
2. Analogies
Chemical reactors are modeled with reactions and balances. Reactions identify chemical transformations of molecules through kinetic mechanisms and mass and energy balances identify the nature and morphology of the reactor where transformations take place.
Assuming that each person corresponds to a molecule of a specific chemical species, the susceptible, healthy, population can be considered as the reactant (component A). It is worth saying that A is not the total population of a region or a country, but, for the scope of the proposed model, it is the total population that will be infected at the end of the infection. Before the infection, we have only the susceptible population inside the reacting system. Infection outbreak starts generating a new component B (reaction intermediate) representing the active infected people. After picking up the infection, people have two feasible paths in terms of reaction transformation: recovering through reaction R2 (component C, cured, healthy immune people) or passing away through reaction R3 (component D, deceased people). The general kinetic mechanism for the infection appears as follows:
| (1) |
Each reaction step is governed by a kinetic parametric relationship in the Arrhenius form (Bodke et al., 1999). Kinetic mechanism (1) takes place in a hypothetical reactor. The active volume for the reaction is the susceptible population (A). If the population can move around, the chemical reactor is considered as continuous, since the chemical compounds can either enter or exit it during the operations. Inlet and outlet flowrates are properly simulated by transmission models which have already been proposed in the virology and transmission literature (Chinazzi et al., 2020, Grubaugh et al., 2019, Wu et al., 2020a, Wu et al., 2020b). Moreover, when the starting population is fixed, as it is the case during governmental lockdown, the chemical reactor mainly behaves as a batch process, where inlet and outlet flows are null. This latter case fits appropriately the current situation in many countries and regions and the batch reactor balances can reasonably predict the infection behavior. At the end of the infection, recovered people are supposed to be immunized. If future evidences will not confirm any immunization (Gretchen, n.d, Jiang, 2020), recovered people will have to be considered reintegrated as part of the healthy population again with the same original probability to be re-infected by the SARS-CoV-2. The kinetic mechanism will be then furtherly simplified to:
| (2) |
The proposed model is intentionally the easiest one to show the potential in applying chemical engineering principles to topics only apparently far away from them. Nevertheless, more sophisticated models will be ideated and implemented to progressively achieve more reliable predictions.
3. Materials and methods
3.1. Model description
The batch-type reactor model has been implemented in order to dynamically characterize the evolution of each specie involved in the kinetic scheme. Batch-type numerical simulation have already been proposed (Stevens, 2020), however, a stochastic system has been developed. In this work, the virus spreading is be modelled as a batch (i.e. an intrinsically dynamic chemical reactor) providing therefore a phenomenological interpretation of data in order to monitor and predict the time evolution of the spreading process. According to the proposed chemical engineering model, people are represented as molecules, while the batch reactor stands for the country where the infection is spreading. Following the kinetic scheme a portion of the whole population is susceptible of contagion (molecule A). The population is therefore progressively infected (molecule B). At this point, B can follow one of two parallel reaction paths: either they recover from the virus (molecule C) or pass away from it (molecule D). Hence, molecule B is the intermediate product of the reaction mechanism and it is expected to have a maximum peak during the infection evolution as well as to completely disappear at the infection extinction time. The described reactions and corresponding kinetic constants are reported in ((3), (4), (5))
| (3) |
| (4) |
| (5) |
Kinetic constants for the reactions are described according to a modified Arrhenius-type law where the temperature-dependence is considered negligible due to the isothermal nature of the infection outbreak. The general equation of the kinetic constant consists of a pre-exponential factor (ki 0) and the time-dependent sigmoid correction. This correction is tuned by parameters, weight (α) and time lag (β) to properly follow the dynamic evolution of the system.
The rationale behind the choice of a sigmoid-time correction lies in the shape of the sigmoidal function itself. Its focal properties are the sluggish initial response, followed by an exponential growth and a final asymptote approach (Stephanopoulos, 1984). These properties are shaped by additional tuning parameters: weight (α) and time lag (β). The former is responsible for dilating or shortening the dynamic response of the function in time while the latter shifts the response in time causing an anticipation or delay. This approach is applied with the same values of α and β to each reaction kinetic constants.
The choice of a kinetic constant as shown in (6) allows to have a sigmoid-like profile as seen in existing infection models (Akhtar et al., 2019, Stojanović et al., 2019, Wu et al., 2020c, Zeng et al., n.d):
| (6) |
The chemical reactions rates are considered as first-order in reactant concentration (in this case, concentration corresponds to the number of molecules which have a peculiar property):
| (7) |
| (8) |
| (9) |
Therefore, according to the kinetic scheme provided in (1) and the chemical reaction rates ((7), (8), (9)) in a batch reactor (Fogler, 2006, Froment et al., 2009, Levenspiel, 2004), the component balances at isothermal conditions are stated as follows:
| (10) |
At a first moment, the second order autocatalytic reaction:
representing the infection phenomenon related to contacting was taken into account as well. However, the same results are obtained and the computational time almost doubles. The associated reaction rate results indeed orders of magnitude lower than the reaction (3). This is due to the fact that the susceptible population is much higher than the currently infected people and the presence of B in the reaction rate expression substantially lowers the reaction rate final value.
Ordinary Differential Equation (ODE) system (10) stability has been largely analyzed (Li and Muldowney, 1995). Moreover, it requires initial conditions for each of the differential equations provided. Initial conditions for active infected cases (), recovered cases (), and death cases () are trivial since they are zero at the infection beginning. On the other hand, the initial susceptible population is unknown since its value can only be derived from the final value of the sum of the remaining species and , considering that, at the extinction of the epidemic, the infected species is no more available:
| (11) |
The integration of differential systems with initial unknown conditions is called Initial Value Problem (IVP) (Buzzi-Ferraris and Manenti, 2015). Since the initial condition highly affects not only the concentration profile of each species and the peak dynamics (i.e: time position and intensity) but also the final steady state condition, a robust numerical strategy should be adopted to solve the problem associated to system (10) with initial conditions (11) (Floudas, 1995, Floudas and Pardalos, 2014, Grossmann and Biegler, 2004).
3.2. Numerical method
ODE system (10) is adopted to analyze infection data provided by Johns Hopkins University (hereafter JHU) and Washington University (hereafter WU) websites (John Hopkins University, 2020, University of Washington, 2020). In equation (6) all kinetic parameters ( and infection parameters and , weight and time lag respectively) are unknows and they have to be estimated through data fitting as in typical regression problems involving model-based optimizations (Buzzi-Ferraris and Manenti, 2010). In regressions, an optimizer is aimed at minimizing a least-sum-of-squares objective function () to match infection data and model previsions:
| (12) |
The adopted numerical solution strategy is a global coupling between minimization and ODE solver blocks-structures implemented in MATLAB 2019b. This numerical problem is a typical nested optimization problem. The structure of this problem can be divided in two main different optimization layers: an outer one and an inner one. The former aims at finding the optimal initial condition (i.e. ). The latter evaluates the optimal regression parameters each time the outer optimization is called (Floudas, 1995, Floudas and Pardalos, 2014, Grossmann and Biegler, 2004). The problem is solved once a convergence criterion is met. Thus, the algorithm structure can be summarized as follows:
-
1.
Assignment of a wide range for variable;
-
2.
Domain discretization;
-
3.
Iterative search for optimal (outer optimization);
-
4.
For each search: model-based optimization for parameter estimation (inner optimization);
-
5.
Initialization of differential system;
-
6.
Numerical integration;
-
7.
Steps (2) to (5) repeated until convergence.
Main convergence criterion for the outer optimization can be stated as follows:
| (13) |
When , which is the Total Infected Population (TIP) at the Infection Extinction Day (IED) estimated at the iteration i, differs less than 0.5 infected people with respect to the estimation at the previous iteration , the procedure is concluded.
It has been observed that the model is able to reasonably predict the infection evolution only when the inflectional point of the sigmoidal function in time is overcome since, there, the concavity change, both in A and B component profiles. At that point, predictions of the nearing peak in terms of intensity and position become reliable.
4. Results
4.1. Regression and validation
The proposed mathematical model consists of four ordinary differential equations evolving along the time axis and providing the temporal evolution of: (i) total infected cases; (ii) active infected cases; (iii) recovered cases; and (iv) death cases. The key-step for data fitting and predictions deals with the estimation of 5 adaptive parameters, which concerned with the chemical reaction rates and the infection dynamics. Each of three chemical reactions have a specific reaction rate parameter and data collected for SARS-CoV-2 outbreak in online databases (Dong et al., 2020, John Hopkins University, 2020) supports their regression process. The remaining two parameters deal with the Kermack and McKendrick-like transmission models (Anderson, 1991) as well as microbial growth models (Lin et al., 2000) to identify the projection of total infected cases at the extinction date of the infection.
The calculation procedure merges two well-consolidated techniques in scientific community of Computer Aided Process Engineering (CAPE Working Party, 2020) and European Federation of Chemical Engineering (EFCE)’s Working Party: (i) the nested optimization approach (Duran and Grossmann, 1987, Varvarezos et al., 1992) to overcome model over-parametrization; and (ii) the robust model-based techniques to identify and correct the gross errors in measurement, communication and delay in collecting data.
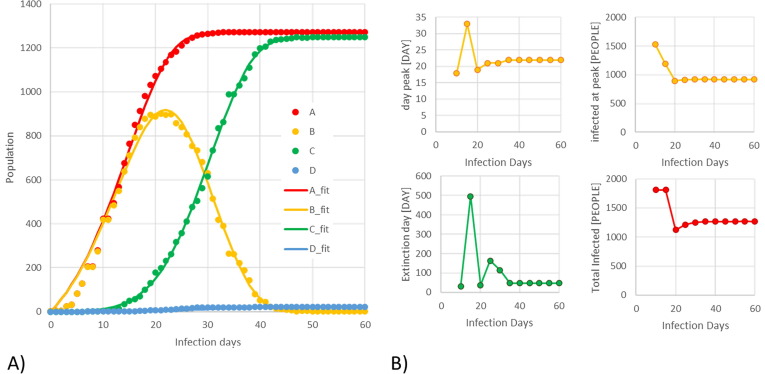
Data for model regression and validation are acquired from (University of Washington, 2020) and samples are provided in Fig. 1 . It illustrates the trends for Henan Chinese province, where the infection extinction day has been achieved. It can be noted that the proposed model properly interprets the whole dataset consisting of 60 observation days. In particular, relevant information like the Infection Peak Time (IPT), the Active Infected Population Peak (AIPP), the Infection Extinction Day (IED) and the Total Infected Population (TIP) are well predicted.
Fig. 1.
Model prediction (solid lines) and model validation using UW data (dots) for the Chinese province of Henan. A) On the left side, the trends of: TIP (red); active infections (orange); recovered cases (green); and death cases (blue). B) On the right side, the small trends report the convergence paths of predictions considering the subsequent re-regressions of new daily data: the IPT and AIPP (orange); IED (green) and TIP (red). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Nevertheless, the relevant use of the model is the prediction when the infection dynamics is not yet clearly developed. For the Henan province, Fig. 1 also shows 4 smaller trends on the right side, which represent the convergence paths of IPT, AIPP, IED, and TIP, while the dataset is progressively enlarging day after day. As it is possible to note, the relevant information can be predicted largely before the complete evolution of the infection and with reasonable robustness. After about 20 days since the beginning of data collection, the identification of the peak and extinction dates are very close to the real final data registered 40 days later.
According to numerical theories, the prediction can be considered reasonable when the TIP trend has already passed its maximum rate, which consists of its maximum derivative in mathematical terms. Before such a point, the predictions are considered unreliable for two correlated reasons: (i) the first infection cases are usually identified with uncertain delay time (COVID-19, the SARS-CoV-2 disease, incubation and identification) and the initial small amount of the infected is strongly affected by large errors; (ii) small datasets affected by gross errors cannot be considered as a good data sample (Buzzi-Ferraris and Manenti, 2011). For future developments, it would be therefore mandatory to regress the model not only forward, but backward as well to better predict the real starting point of the infection in a given population to overcome the initial lack of information and/or measures.
Model predictions can strongly support the decision-making process to predispose at the right time materials and logistics for hospitals, dedicated buildings, human resources, doctors, health materials, and medical machines.
4.2. Predictions
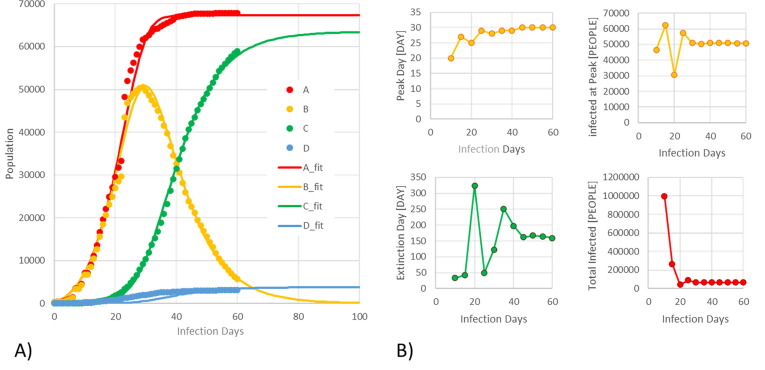
According to Johns Hopkins’ database (John Hopkins University, 2020) (updated to 23rd March), the 10 countries largely affected by COVID-19 are reported in Table 1 . In particular the Chinese province of Hubei is still the largest region worldwide for TIP and its predictions are reported in Fig. 2 . On the left side, the dynamics are almost completely evolved and the model is properly fitting the trends, converging to the TIP with less than 1% error and to the IPT with 1 day only of error at the day 20 of the infection (33% of total infection time for Hubei province).
Table 1.
Total infection cases at the 23rd March 01:00PM GMT. Source: JHU.
| Total infected cases (Component A) |
Country |
|---|---|
| 81.454 | China |
| 59.138 | Italy |
| 35.224 | US |
| 29.909 | Spain |
| 24.873 | Germany |
| 21.638 | Iran |
| 16.246 | France |
| 8.961 | Korea, South |
| 7.724 | Switzerland |
| 5.745 | United Kingdom |
Fig. 2.
Model prediction (solid lines) and model validation using UW data (dots) for the Chinese province of Hubei. A) TIP (red); active infections (orange); recovered cases (green); and death cases (blue). B) The small trends report the convergence paths of predictions considering the subsequent re-regressions of new daily data: the IPT [day] and AIPP [people] (orange); IED (green) and TIP (red). Chinese government changed the data collection methodology at the infection day 23: this motivates the discontinuity in the trends and the large oscillations in the converging paths in its neighborhoods. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
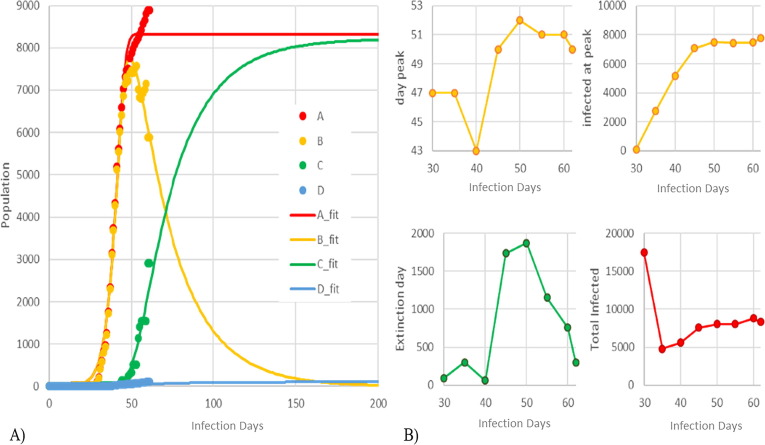
South Korea is the country with the longest historical database for SARS-CoV-2 infection out of China and predictions are reported in Fig. 3 . Collected data are showing a TIP trend that is still linearly increasing after the identified AIPP on day 30. It, unavoidably, means that South Korea is not really behaving like a total batch reactor: a small, but continuous, inlet flow of infections is still present in the country. The model is constantly underestimating the TIP by 7% in the last observations to better robustly fit the remaining relevant information, especially the IED, which is rapidly converging to a shorter time in the last days.
Fig. 3.
Model prediction (solid lines) and model validation using UW data (dots) for South Korea. A) On the left side of the trends of: TIP (red); active infections (orange); recovered cases (green); and death cases (blue). B) On the right side, the small trends report the convergence paths of predictions considering the subsequent re-regressions of new data: the IPT [day] and AIPP (orange); IED (green) and TIP (red). South Korea predictions currently underestimate the TIP by 7% to better fit the remaining relevant information. Such a gap on the IPT is expected to zero in few days since the converging paths are achieving a steady-state. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
It is worth remarking that the figures represent the profile of A as the sum of B, C and D. In addition, small charts on the right side in Fig. 2, Fig. 3 show the predicted main parameters (IPT, AIPP, IED and TIP) according to the number of days taken into account in the dataset.
5. Discussion
Thanks to this study, in reaction engineering terms, it is possible to distinguish four infection stages of epidemics/pandemics:
-
–
the starting stage (infection outbreak). It is the initial part of the infection from the case 0 to the inflectional point of the TIP. It is characterized by an increasing infection rate, but with a small amount of infected cases. Usually, it is affected by relevant errors in measures and wrong identification of infected cases. This stage has an explosion-like trend and cannot be modeled in mechanistic manner; moreover, small data affected by gross errors cannot be a base for model-based predictions;
-
–
the early stage (infection transmission). It is the stage where the infection is fast spreading and the TIP is enlarging dramatically. It is identified between the inflectional point and the AIPP. Model predictions become useful to quantify the pandemic entity. It is worth saying that the nature of this stage and the following ones differs from the nature of the starting stage: the starting stage is governed by the natural progression of the infection in a population, whereas the subsequent stages are governed by contingency measures adopted by the population and governments (forced behavior);
-
–
the mature stage (infection mitigation). It represents the days where the impact of the infection is decreasing in terms of active infected cases. It goes from the AIPP to the steady state of the TIP, which means that new active infections no longer occur. In this stage, conversion rate from active infection cases into recovered and death cases is the highest. It still involves a relatively large amount of active infected cases and usually expires when the incubation time has passed since the last new infection case;
-
–
and the final stage (infection extinction). It starts when the TIP achieves the steady state and it strongly depends on the hospital treatments and sickness activity. It is considered concluded when the last active infection case is either recovered or dead.
The Hubei province belongs to the final stage: South Korea is just entered the mature stage.
Once all the data and the related convergence paths will be collected, the kinetic parameters governing each phase will be properly estimated. They will serve as good guesses for numerical model-based predictions of the next potential pandemics.
The model is progressively improving the predictions every day and its potential could support all the countries affected by SARS-CoV-2 pandemic to make decisions and organize supplies and human resources. For this reason, the mathematical model proposed in this work will be extended and adapted to all the countries and related regions where available infection data are provided. A global platform has to be organized soon at the https://www.super.chem.polimi.it. The aim is to collect all the data for the SARS-CoV-2 infection dynamics and estimate local and global kinetic parameters.
6. Conclusions
Predictions not only based on stochastic approaches, but also on phenomenological theories, could provide an additional element for governments and associations to make decision processes stronger and more robust. The idea of comparing infection dynamics to batch reactor behavior and chemical kinetics seems to provide good information also in early stages, when the infection is progressing fast. By definition, decision-making robustness in emergencies means also to adopt more different tools for future predictions and more sophisticated models can be proposed to improve the prediction reliability. Platform and database for SARS-CoV-2 predictions and, in general, for pandemic predictions, has been launched at CMIC Dept. “Giulio Natta” Politecnico di Milano website with the aim of studying kinetic parameters for infection outbreak, transmission, mitigation and extinction.
CRediT authorship contribution statement
F. Manenti: Conceptualization, Methodology, Supervision, Writing - original draft. A. Galeazzi: Conceptualization, Software, Validation, Investigation, Writing - review & editing. F. Bisotti: Methodology, Software, Validation, Investigation, Writing - review & editing. K. Prifti: Validation, Investigation. A. Dell’Angelo: Validation, Investigation, Writing - review & editing. A. Di Pretoro: Validation, Investigation, Writing - review & editing. C. Ariatti: Software, Validation, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
Authors gratefully acknowledge the scientific discussions with elected delegates of CAPE, EFCE’s Working Party, and funding support MSJ0DIDA01 from the Centre for Sustainable Process Engineering Research (SuPER) at Politecnico di Milano.
References
- Akhtar M., Kraemer M.U.G., Gardner L.M. A dynamic neural network model for predicting risk of Zika in real time. BMC Med. 2019;17:1–16. doi: 10.1186/s12916-019-1389-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M. Discussion: The Kermack-McKendrick epidemic threshold theorem. Bull. Math. Biol. 1991;53:3–32. doi: 10.1016/S0092-8240(05)80039-4. [DOI] [PubMed] [Google Scholar]
- Bodke A.S., Olschki D.A., Schmidt L.D., Ranzi E. High selectivities to ethylene by partial oxidation of ethane. Science. 1999;285:712–715. doi: 10.1126/science.285.5428.712. [DOI] [PubMed] [Google Scholar]
- Buzzi-Ferraris G., Manenti F. Wiley-VCH; Weinheim, Germany: 2015. Differential and Differential-Algebraic Systems for Chemical Engineer: Solving Numerical Problems. [Google Scholar]
- Buzzi-Ferraris G., Manenti F. Data interpretation and correlation. Kirk-Othmer Encyclopedia. 2011 [Google Scholar]
- Buzzi-Ferraris G., Manenti F. Wiley-VCH; Weinheim, Germany: 2010. Interpolation and Regression Models for the Chemical Engineers: Solving Numerical Problem. [Google Scholar]
- CAPE Working Party, 2020. CAPE WP web page [WWW Document]. March, 2020. URL https://www.wp-cape.eu/.
- Chan J.F.W., Yuan S., Kok K.H., To K.K.W., Chu H., Yang J., Xing F., Liu J., Yip C.C.Y., Poon R.W.S., Tsoi H.W., Lo S.K.F., Chan K.H., Poon V.K.M., Chan W.M., Ip J.D., Cai J.P., Cheng V.C.C., Chen H., Hui C.K.M., Yuen K.Y. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395:514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chinazzi, M., Davis, J.T., Ajelli, M., Gioannini, C., Litvinova, M., Merler, S., Pastore Y Piontti, A., Mu, K., Rossi, L., Sun, K., Viboud, C., Xiong, X., Yu, H., Halloran, M.E., Longini, I.M., Vespignani, A., 2020. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science (New York, N.Y.) 9757, 1–12. https://doi.org/10.1126/science.aba9757. [DOI] [PMC free article] [PubMed]
- Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet. Infect. Dis. 2020;3099:19–20. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duran M.A., Grossmann I.E. An outer-approximation algorithm for a class of mixed-integer nonlinear programs. Math. Program. 1987;39:337. doi: 10.1007/BF02592081. [DOI] [Google Scholar]
- EFCE, 2020. European Federation of Chemical Enginnering Web Page [WWW Document]. URL https://efce.info/.
- Floudas C.A. first ed. Oxford University Press; 1995. Nonlinear and Mixed-Integer Optimization - Fundamentals and Applications. [Google Scholar]
- Floudas C.A., Pardalos P.M. Princeton Univerity Press; 2014. Recent Advances in Global Optimization. [Google Scholar]
- Fogler H.S. Prentice Hall; Prentice Hall: 2006. Elements of Chemical Reaction Engineering. [Google Scholar]
- Froment F.G., Bischoff K.B., De Wilde J. third ed. John Wiley & Sons; 2009. Chemical Reactor Analysis and Design. [Google Scholar]
- Gani R., Bałdyga J., Biscans B., Brunazzi E., Charpentier J.C., Drioli E., Feise H., Furlong A., Van Geem K.M., de Hemptinne J.C., ten Kate A.J.B., Kontogeorgis G.M., Manenti F., Marin G.B., Mansouri S.S., Piccione P.M., Povoa A., Rodrigo M.A., Sarup B., Sorensen E., Udugama I.A., Woodley J.M. A multi-layered view of chemical and biochemical engineering. Chem. Eng. Res. Des. 2020;155:133–145. doi: 10.1016/j.cherd.2020.01.008. [DOI] [Google Scholar]
- Gretchen, V., n.d. New blood tests for antibodies could show true scale of coronavirus pandemic. Science. https://doi.org/doi:10.1126/science.abb8028.
- Grossmann I.E., Biegler L.T. Part II. Future perspective on optimization. Comput. Chem. Eng. 2004;28:1193–1218. doi: 10.1016/j.compchemeng.2003.11.006. [DOI] [Google Scholar]
- Grubaugh N.D., Ladner J.T., Lemey P., Pybus O.G., Rambaut A., Holmes E.C., Andersen K.G. Tracking virus outbreaks in the twenty-first century. Nat. Microbiol. 2019;4:10–19. doi: 10.1038/s41564-018-0296-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang S. Don’t rush to deploy COVID-19 vaccines and drugs without sufficient safety guarantees. Nature. 2020;579 doi: 10.1038/d41586-020-00751-9. [DOI] [PubMed] [Google Scholar]
- John Hopkins University, 2020. Coronavirus COVID-19 Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) [WWW Document]. February 19. URL https://www.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6.
- Layne S.P., Hyman J.M., Morens D.M., Taubenberger J.K. New coronavirus outbreak: Framing questions for pandemic prevention. Sci. Transl. Med. 2020;12:1–3. doi: 10.1126/scitranslmed.abb1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levenspiel, O., 2004. Chemical reaction engineering, 3rd Ed. ed. Wiley, New York, USA. https://doi.org/10.1201/9781420014389.ch11.
- Li M.Y., Muldowney J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995;125:155–164. doi: 10.1016/0025-5564(95)92756-5. [DOI] [PubMed] [Google Scholar]
- Lin J., Lee S.M., Lee H.J., Koo Y.M. Modeling of typical microbial cell growth in batch culture. Biotechnol. Bioprocess Eng. 2000;5:382–385. doi: 10.1007/BF02942217. [DOI] [Google Scholar]
- Ryan, T.P., 2008. Modern Regression Methods. John Wiley & Sons. https://doi.org/10.1002/9780470382806.
- Stephanopoulos G. first ed. Prentice Hall; 1984. Chemical process control - An Introduction to Theory and Practice. [Google Scholar]
- Stevens, H., 2020. Why outbreaks like coronavirus spread exponentially, and, how to “flatten the curve” [WWW Document]. March 14. URL https://www.washingtonpost.com/graphics/2020/world/corona-simulator/.
- Stojanović O., Leugering J., Pipa G., Ghozzi S., Ullrich A. A Bayesian Monte Carlo approach for predicting the spread of infectious diseases. PLoS ONE. 2019;14 doi: 10.1371/journal.pone.0225838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- University of Washington, 2020. Novel Coronavirus (COVID-19) Infection Map [WWW Document]. January 21. URL https://hgis.uw.edu/virus/.
- Varvarezos D.K., Grossmann I.E., Biegler L.T. An outer-approximation method for multiperiod design optimization. Ind. Eng. Chem. Res. 1992;31:1466–1477. doi: 10.1021/ie00006a008. [DOI] [Google Scholar]
- Wu, Joseph T., Leung, K., Bushman, M., Kishore, N., Niehus, R., Salazar, P.M. De, Cowling, B.J., Lipsitch, M., Leung, G.M., 2020. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan , China. Nature Medicine. https://doi.org/10.1038/s41591-020-0822-7.
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, K., Darcet, D., Wang, Q., Sornette, D., 2020. Generalized logistic growth modeling of the COVID-19 outbreak in 29 provinces in China and in the rest of the world 1–42. https://doi.org/https://doi.org/10.1101/2020.03.11.20034363. [DOI] [PMC free article] [PubMed]
- Zeng, T., Zhang, Y., Li, Z., Liu, X., Qiu, B., n.d. Predictions of 2019-nCoV Transmission Ending via Comprehensive Methods.