Spatial modeling, risk mapping, change detection, and outbreak trend analysis of coronavirus (COVID-19) in Iran (days between February 19 and June 14, 2020)

Highlights

• •Comparison of Iranian coronavirus data with other countries.
• •Predicting the trends of deaths from COVID-19 using regression.
• •Spatial modeling, risk mapping, and change detection of COVID-19 using the random forest (RF) machine learning technique.
• •Validation of the modeled risk maps.

Abstract

Objectives

Coronavirus disease 2019 (COVID-19) represents a major pandemic threat that has spread to more than 212 countries with more than 432,902 recorded deaths and 7,898,442 confirmed cases worldwide so far (on June 14, 2020). It is crucial to investigate the spatial drivers to prevent and control the epidemic of COVID-19.

Methods

This is the first comprehensive study of COVID-19 in Iran; and it carries out spatial modeling, risk mapping, change detection, and outbreak trend analysis of the disease spread. Four main steps were taken: comparison of Iranian coronavirus data with the global trends, prediction of mortality trends using regression modeling, spatial modeling, risk mapping, and change detection using the random forest (RF) machine learning technique (MLT), and validation of the modeled risk map.

Results

The results show that from February 19 to June 14, 2020, the average growth rates (GR) of COVID-19 deaths and the total number of COVID-19 cases in Iran were 1.08 and 1.10, respectively. Based on the World Health Organisation (WHO) data, Iran’s fatality rate (deaths/0.1 M pop) is 10.53. Other countries’ fatality rates were, for comparison, Belgium – 83.32, UK – 61.39, Spain – 58.04, Italy – 56.73, Sweden – 48.28, France – 45.04, USA – 35.52, Canada – 21.49, Brazil – 20.10, Peru – 19.70, Chile – 16.20, Mexico– 12.80, and Germany – 10.58. The fatality rate for China is 0.32 (deaths/0.1 M pop). Over time, the heatmap of the infected areas identified two critical time intervals for the COVID-19 outbreak in Iran. The provinces were classified in terms of disease and death rates into a large primary group and three provinces that had critical outbreaks were separate from the others. The heatmap of countries of the world shows that China and Italy were distinguished from other countries in terms of nine viral infection-related parameters. The regression models for death cases showed an increasing trend but with some evidence of turning. A polynomial relationship was identified between the coronavirus infection rate and the province population density. Also, a third-degree polynomial regression model for deaths showed an increasing trend recently, indicating that subsequent measures taken to cope with the outbreak have been insufficient and ineffective. The general trend of deaths in Iran is similar to the world's, but Iran’s shows lower volatility. Change detection of COVID-19 risk maps with a random forest model for the period from March 11 to March 18 showed an increasing trend of COVID-19 in Iran’s provinces. It is worth noting that using the LASSO MLT to evaluate variables’ importance, indicated that the most important variables were the distance from bus stations, bakeries, hospitals, mosques, ATMs (automated teller machines), banks, and the minimum temperature of the coldest month.

Conclusions

We believe that this study's risk maps are the primary, fundamental step to take for managing and controlling COVID-19 in Iran and its provinces.

Introduction

Phylogenetic analysis suggested that coronaviruses (CoV) belong to the Coronavirinae subfamily, comprising Alphacoronavirus, Betacoronavirus, Gammacoronavirus and Deltacoronavirus genera (Zhong et al., 2003, Fouchier et al., 2003). Of the four genera, alpha and beta coronaviruses result in respiratory illness in humans and gastroenteritis in animals, and gamma and delta affect birds (Cui et al., 2019). The first report of the pathogenic behavior of alpha and beta coronaviruses was announced when the outbreak of severe acute respiratory syndrome (SARS) occurred in 2002 in Guangdong Province, China (Zhong et al., 2003, Fouchier et al., 2003). Prior to the 2002 outbreak, the coronaviruses showed mild infections among humans. A decade after SARS, the Middle East respiratory syndrome coronavirus (MERS-CoV) was identified as a highly pathogenic virus in Middle Eastern countries (Zaki et al., 2015). Swine Pandemic (pH1N1) Influenza – a virus that emerged in Mexico in 2009 – and the emergence of MERS-CoV in Saudi Arabia were reported in other countries (El Zowalaty and Järhult, 2020, Wu et al., 2020). SARS-CoV infected more than 8000 people and caused 774 deaths (Chang et al., 2020), but the MERS-CoV had higher infection rates and lower fatality rates (Wu et al., 2020). The pathogenic behavior of SARS- CoV, and MERS- CoV was not limited to human communities; severe respiratory syndrome was also reported in animals (Masters and Perlman, 2020). Analysis of coronaviruses' genetics demonstrated the receptor-binding motif of SARS- CoV has been mutated in humans and wild animals (bats and civets) (Hu et al., 2015). A recombinant SARS- CoV was detected in bats and transmitted to people through civets in Guangdong Province (Cui et al., 2019). A virus outbreak in 2012 showing a similar scenario might have occurred for MERS-CoV. In December 2019, a novel and alarmingly contagious primary atypical (viral) pneumonia named COVID-19 broke out in Wuhan, China, and aggressively spread over the world. COVID-19 reportedly shares an identical receptor, Angiotensin-converting enzyme 2 (ACE2), with the SARS-Cov (Wu et al., 2020, Zhao et al., 2020).

On February 11, 2020, the World Health Organization (WHO) named the novel viral pneumonia “Corona Virus Disease (COVID-19)” (Chang et al., 2020). Recently, the International Committee on Taxonomy of Viruses (ICTV) proposed this novel coronavirus be named “SARS-CoV-2” as a result of the phylogenetic and taxonomic analysis of this novel coronavirus (Gorbalenya et al., 2020). These three globally spreading emerging infectious diseases (SARS-CoV, MERS-CoV, and COVID-19) are caused by β-coronaviruses, mainly infecting bats, but also found in camels and rabbits (Chang et al., 2020). There is currently neither a vaccine against COVID-19 nor any specific, proven, antiviral medication (World Health Organization, 2020a, Coalition for Epidemic Preparedness Innovations, 2020), making it a severe global threat.

Coronaviruses are a continuing pandemic threat that has spread to more than 212 countries, with over 432,902 recorded deaths and 7,898,442 confirmed global infections (as of June 14, 2020); the number of new confirmed cases continues to rise. As of mid-June, 83,132 COVID-19 cases have been confirmed in mainland China of whom 4634 have died. There have been 187,427 confirmed cases of infection in Iran, and the death toll has reached 8837 (Anon., 2020a). The WHO’s decision (Velavan and Meyer, 2020) was partly based on the fact that most of the virus’s global spread can still be traced to countries that have experienced large outbreaks, such as the USA, Iran, India, and Brazil (Velavan and Meyer, 2020). Therefore, health boards, governments, and public services need to co-operate globally to prevent its further spread. Many publications have addressed the new coronavirus in terms of its clinical characteristics, immunological studies, and the international spread of COVID-19 (El Zowalaty and Järhult, 2020, Wu et al., 2020, Chang et al., 2020, Velavan and Meyer, 2020, Ahmed et al., 2020, Al-rabiaah et al., 2020, Chen et al., 2020, Gao et al., 2020, Lai et al., 2020a, Lai et al., 2020b, Level et al., 2019, Mallapaty, 2020, Xu et al., 2020, Zhang et al., 2020. A few studies investigating its spread have produced risk maps either for COVID-19 during an outbreak or for similar coronavirus respiratory syndromes (Wu et al., 2020, Chen et al., 2018), or even for risk assessments of other global viral diseases (Dom et al., 2016, Li et al., 2017, Sabir et al., 2015, Saito et al., 2015, Sarfraz et al., 2014, Tu et al., 2014. Given the clinical severity of COVID-19 infection, the extent of the outbreak, and public concern, it is important to establish accurate epidemiological limitations, thus solid information is essential for inputs into models. In general, there are too many factors on each pandemic disease, including environmental, agro-ecological, and meteorological variables. Each disease and the risk mapping related to it has some effective factors, and each disease can be connected to climate, water, animals, humans, and even soils (Brevik et al., 2019, Kumar et al., 2019, Yadav et al., 2020). So, it is important to select the most important effective factors for each pandemic disease. It is also vital to rapidly develop robust information using unbiased and reliable methods to provide situational awareness and to improve response to the pandemic (Wu et al., 2020). This study aims to conduct spatial modeling, risk mapping, change detection, and outbreak trend analysis of COVID-19 in Iran (Figure 1 ) to produce the first comprehensive investigation that may assist with the management and control of the COVID-19 crisis.

Figure 1.

Trend of COVID-19 outbreak in the provinces of Iran since February 19, 2020.

Methods

Study area

The country of Iran has an area of 1,648,195 square kilometers located between 25°3′50″ and 39°46′16″ N and between 44°2′19″ and 63°19′18″ E. Iran borders Armenia, Azerbaijan, and Turkmenistan on its north, Afghanistan, and Pakistan on its east, Turkey and Iraq on its west, and the Persian Gulf and Oman Sea to the south. Unfortunately, at various times, Iran has faced a number of serious infectious diseases, many of which have been successfully controlled. Plague, a pandemic disease that still occurs in some regions around the world, has affected Iran at different times from 1829 to 1966 with an estimated two million deaths (Hashemi Shahraki et al., 2016). Between January 2000 and September 2010, 738 cases of Crimean–Congo Haemorrhagic Fever (CCHF) with 108 deaths were described in Iran (Askarian et al., 2012). Tuberculosis has been well controlled in Iran; the incidence of tuberculosis was 17/100,000 population, and its spread was 23/100,000 population. Tuberculosis has a mortality ratio of 1.8/100,000 people (Askarian et al., 2012, World Health Organization, 2020b). The annual outbreak of malaria in Iran was predicted to be 0.14–8.74/1000 people in 2010. According to the WHO, there were nearly 70,000 confirmed malaria cases in Iran in 2010 (Askarian et al., 2012, World Health Organization, 2020c).

This study is composed of four steps:

• aComparing Iranian coronavirus data with other countries
• bPredicting the trends of deaths from COVID-19 using regression
• cSpatial modeling, risk mapping, and change detection of COVID-19 using the random forest (RF) machine learning technique (MLT)
• dValidation of the modeled risk maps (Figure 2 )

Figure 2.

The flowchart of methodologies for risk mapping coronavirus in Iran.

Comparing Iran’s COVID-19 trend with the global trend

First, we assess the growth rates (GRs) of active cases and deaths in Iran. The data were extracted from daily reports produced by Iran's Ministry of Health and Medical Education (IMHME). All active cases, deaths, and recoveries were compiled in Excel. An analysis of the correlation between the number of active cases and the number of deaths was conducted using Spearman’s Rho. Another analysis examined the relationships between ages and sexes of active cases and deaths. Following the IMHME approach, these age groups were used to produce nine classes: 1) < = 9, 2) 10–19, 3) 20–29, 4) 30–39, 5) 40–49, 6) 50–59, 7) 60–69, 8) 70–79, and 9) > = 80. All analyses were done using Excel, SPSS, SAS, and ArcGIS. The data for Iran were compared to data describing other countries' experiences, particularly the 24 countries with the highest COVID-19 confirmed death rates. The data for the other countries were collected from the “Worldometer” page (https://www.worldometers.info/coronavirus/) (Anon., 2020b). The coronavirus cases of six continents (Europe, North America, Asia, South America, Africa, and Oceania) were compared in total active cases, total number recovered, and total deaths (Anon., 2020b).

Heatmap and correlation analysis

Simple correlation coefficients for the number of the infected cases in Iran’s 31 provinces were calculated with SAS software. A heatmap was created using cluster analysis and shiny heatmap tools (Khomtchouk et al., 2017). The data used for heatmap construction were normalized based on Z-scores (Eq. 1)

$$z=\frac{X_i-\overline{X}}{\text{σ}}$$ (1)

where X_i, $\overline{X}$, and σ are raw data, mean, and standard deviation for each tested trait. The number of infected cases (y) and the number of days (x) after the first report of coronavirus in each province were subjected to regression to identify the best model parameters. The number of infected cases (y) was also regressed on the province population (x).

Prediction of death cases trend using a regression model

The trend of deaths was captured by a cubic or third-degree polynomial specification as:

$$Dailydeath\left(t\right)={\text{α}}_0+{\text{α}}_{1}t+{\text{α}}_2{t}^2+{\text{α}}_3{t}^3$$ (2)

where $Dailydeath\left(t\right)s$ represent the death cases in a day, and t denotes the number of days starting from February 19. This model was extracted from the equation applied to estimate total deaths as an accumulation of daily cases. Other specifications, including quadratic or fourth-degree polynomial forms, were examined, but it was determined that the cubic form produced the most accurate predictions (Aik et al., 2018). We also used an ARMA model to compare the processes used to generate the data for Iran and the rest of the world. This model includes two procedures: the autoregressive (AR) and moving-average (MA) processes. An ARMA model of order (p, q) can be written as (Enders, 2004):

$$y\left(t\right)={\text{β}}_0+\sum _{i=1}^p{\beta }_i{y}_{t-i}+\sum _{j=1}^q{\beta }_j{\epsilon }_{t-j}$$ (3)

where y is the dependent variable and $\epsilon$ is the white noise stochastic error term. In this model, y denotes the total number of deaths, and t is the number of days since the date on which the first death was reported. In the case of significant fluctuations in the numbers of deaths per day, a volatility model, the autoregressive conditional heteroskedasticity (ARCH) model, was applied so that p can be presented as:

$${\sigma }^2\left(t\right)={\text{θ}}_0+\sum _{i=1}^p{\theta }_i{\epsilon }_{t-i}$$ (4)

where ${\sigma }^2\left(t\right)$ is the one-period ahead forecast variance, it is obtained from past information.

Spatial modeling and risk mapping using RF MLT

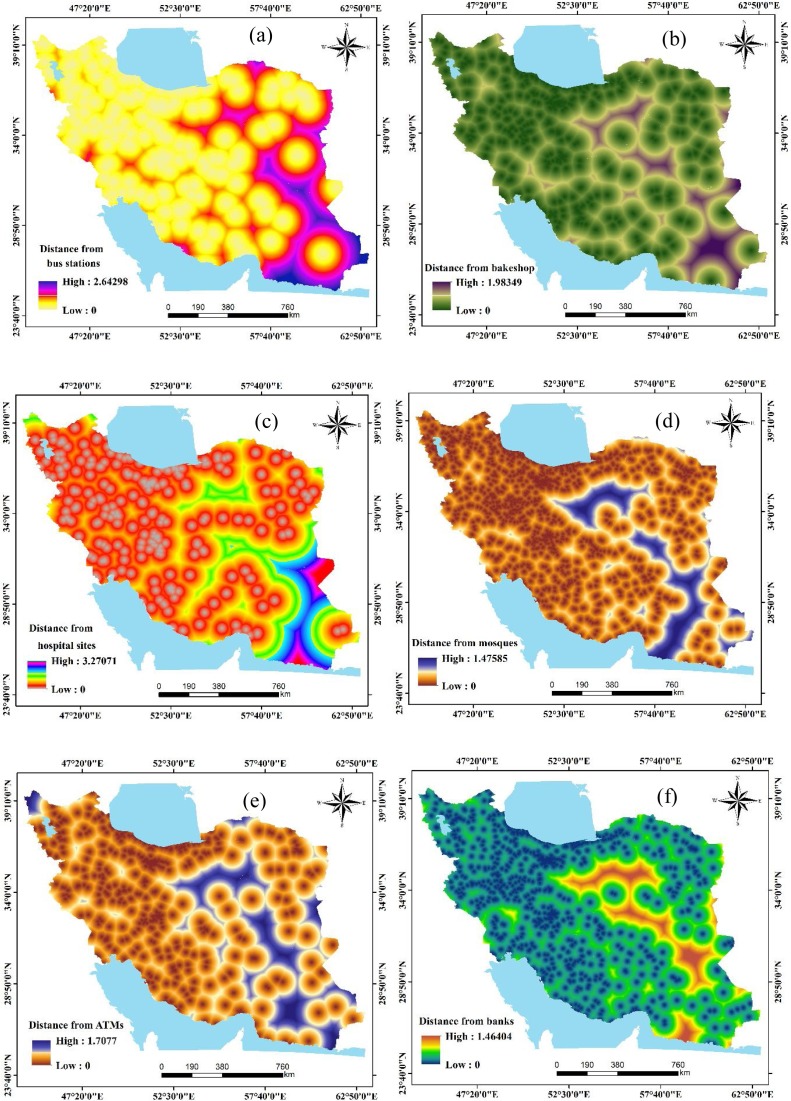
One of the most important spatial modeling and risk mapping steps is to prepare data matrices that include the dependent variables (the total number of cases) and sets of independent (or predictor) variables. In this study, data describing several anthropogenic and climatic factors were compiled and mapped. These variables included: distances from bus stations, bakeshop (bakeries), hospitals, mosques, automated teller machines (ATMs), banks, fuel stations, and attraction sites, the density of cities, human footprint, distance from roads, the density of villages, minimum temperature of the coldest month (MTCM), the maximum temperature of the warmest month (MTWM), precipitation of wettest month (PWM), and precipitation of driest month (PDM) (Figure 3 (a–p)).

Figure 3.

Predictor variables used for COVID-19 risk mapping in Iran.

Predictor variables

The 16 predictor variables were chosen based on a review of the literature and on expert knowledge. There is much debate on the impact of local climate coalitions on the outbreak of COVID-19. Previous studies have confirmed the effects of weather conditions on the survival and spread of droplet-mediated viral diseases (Shaman et al., 2011, Barreca and Shimshack, 2012), and the roles of temperature and humidity on rates of COVID-19 spread have been assessed in a few studies. One study (Luo et al., 2020) showed that changes in temperature and humidity alone do not necessarily lead to decreased transmission of COVID-19. More research into the effects of climatic variables on COVID-19 transmission is needed. MTCM, MTWM, PWM, and PDM were acquired at a spatial resolution of 30 s (∼1 km (Fouchier et al., 2003)) from WorldClim datasets (https://www.worldclim.org/data/index.html) (Hijmans et al., 2005, Anon., 2020c) to spatially model COVID-19. To account for anthropogenic factors that may increase infection risk through contact with contaminated surfaces or person-to-person contact, public spaces of primary importance were included in the modeling. These data were acquired from Open Street Map (https://www.openstreetmap.org/) (Anon., 2020d). The Euclidian distance to the most critical social concentration spaces and facilities, including banks, bakeries, ATMs, bus stations, fuel stations, hospitals, and mosques, were measured using ArcGIS Spatial Analyst Tools. To evaluate the effects of settlements and infrastructure on a broader scale, we calculated geographic distances to road networks and the densities of cities and towns. To factor in the effects of other human-features on the outbreak, the human footprint layer was integrated into the models. This layer is measured using variables related to human development (e.g., population, electric power) and combined into one seamless layer at a spatial resolution of ∼1 km (Venter et al., 2016). Because of the human footprint map's coarse precision, we also included the village density across the country using a kernel density function applied to village locality-layer obtained from a topographic map of the country at a scale of 1: 50,000.

Random forest (RF)

RF (Breiman, 2001) is an extensively employed robust MLT that applies numerous trees to attain superior classification precision because single trees produce feeble results due to greater adjustment and bias (Arabameri et al., 2018). RF is highly efficient for handling obscure and unknown data and functions well, even if a dataset is large and complex (Rahmati et al., 2019). RF has been used in many fields and has demonstrated very high forecast accuracy (Chen et al., 2018, Masetic and Subasi, 2018, Hong et al., 2016, Pham et al., 2017, Al-Quraishi et al., 2018, Heddam and Kisi, 2018, Pourghasemi and Rahmati, 2018, Kim et al., 2018, Patel et al., 2019, Hashimoto et al., 2019. It consists of two major internal phases: the algorithm constructs copious bootstrap trials, which are considered calibration sets, and builds categorization conditions for every tree. During the former process, a few datasets not used during bootstrapping are left behind; these are known as out-of-bag trials (OOB) and are used to evaluate the accuracy of categorization and to estimate precision. Afterward, several factors are selected arbitrarily from the entire set of factors to reduce interdependence among all sets of trees, thereby reducing the chances of miscalculation (Genuer et al., 2010). The advantages of the RF technique are: (a) elimination of overfitting, (b) minimizing preconception and inconsistency owing to the assimilation of outcomes of each tree, (c) less association due to the large number of trees and the restriction of the number of factors, (d) error measurements through OOB information, and (e) maximized forecast precision (Prasad et al., 2006, Wiesmeier et al., 2011). The execution of RF is expressed as follows:

• 1For c = 1 to C,
• (2)Drag a bootstrap trial X* of amount M from the calibration dataset.
• (3)Develop the RF tree Y_c to the bootstrapped dataset through iteration of the subsequent measures for all concluding tree nodes, until the least node extent of M_min is arrived at.
• (4)Choose d variables arbitrarily from the s variables.
• (5)Choose the best variable amongst the d.
• (6)Make two daughter nodes by rifting the node.
• 7Produce the ensemble of trees ${[Y_c]}_1^C$

For doing a forecast for an instance, y:

$$Regression:{\stackrel{\wedge }{f}}_{gj}(y)=\frac{1}{C}\sum _{c=1}^C{Y}_c(y)$$

Classification: ${\stackrel{\wedge }{L}}_c(y)$ is the forecast classification of the cth RF tree. Now, ${\stackrel{\wedge }{L}}_{gj}(y)$ = maximum opt for ${[{\stackrel{\wedge }{L}}_c(y)]}_1^C$.

The RF can be conducted using the ‘randomForest’ package (Breiman et al., 2018) in R software.

Variable importance using the least absolute shrinkage and selection operator (LASSO)

LASSO is based on ridge regression (Frank and Friedman, 1993) and non-negative Garrote (Breiman, 1995). It regularizes, manages collinearity, and performs feature selection (Frank and Friedman, 1993, Vasquez et al., 2016). In regularization, the model sets an upper limit to the sum of the absolute values of the selected variables of the regression model. If the sum exceeds the limit, the model shrinks the coefficients by penalizing (l₁ norms) with a shrinkage factor and making some coefficients equal to 0 (Li and Sillanpää, 2012). In particular, it reduces the residual sum of squares (RSS) subject to an l₁ penalty term:

$$\beta =\arg \min \parallel C-B\beta {\parallel }_2^2+\lambda \parallel \beta {\parallel }_{}1$$ (5)

where λ refers to the tuning parameter determined based on the crosscheck. However, the non-zero coefficients are also chosen in the variable-selection procedure to reduce the prediction-accuracy error. The model is suitable for several statistical problems and multi-dimensional problems due to its accurate predictions and ease of interpretability (Bühlmann and van de Geer, 2011).

Validation of COVID-19 risk maps

The receiver operating characteristics (ROC) curve was applied to the verification and validation of the model. The ROC curve and its AUC (area under the curve) values were sorted into five classes (Yesilnacar, 2005, Pourghasemi et al., 2019, Pourghasemi et al., 2020a, Pourghasemi et al., 2020b): poor (0.5−0.6), moderate (0.6−0.7), good (0.7−0.8), very good (0.8−0.9), and excellent (0.9–1.00). AUC values close to 1 indicate high accuracy; values closer to 0.5 indicate low accuracy.

Results and discussion

Data for the 24 countries with the highest confirmed total cases (more than 50,000), deaths, total recovered, active cases, serious/critical, and test rates per 0.1 M pop (as of June 13, 2020) were compiled (https://www.worldometers.info/coronavirus/)⁴⁰ and analyzed (Table 1 ). Results are Belgium – 83.32, UK – 61.39, Spain – 58.04, Italy – 56.73, Sweden – 48.28, France – 45.04, USA – 35.52, Canada – 21.49, Brazil – 20.10, Peru – 19.70, Chile – 16.20, Mexico– 12.80, Iran – 10.40, and Germany – 10.58. The lowest deaths/0.1 M pop among these top 24 countries were between 0.3 and 5.7 in China – 0.3, Bangladesh – 0.7, India – 0.7, Pakistan – 1.20, South Africa – 2.40, Qatar – 2.50, Saudi Arabia – 2.70, Russia – 4.70, and Turkey – 5.70. Iran’s portions of the world pandemic were 2.35% of all active cases, 2.02% of all deaths, 3.64% of all recovered, 0.87% of active cases, 5.09% of serious/critical cases, and 220.3 total cases per 0.1 M population. Also, Table 1 shows that countries with more than 200 cases per 0.1 M population are Qatar (2792.8), Chile (875.8), Peru (683.3), USA (647.4), Spain (621.7), Belarus (563.40), Belgium (517.10), UK (433.7), Brazil (400.4), Italy (391.4), Russia (356.4), Saudi Arabia (354.5), Canada (260.9), France (240.3), Germany (223.7), Iran (220.3), and Turkey (209.6), respectively. The active cases of > 100 people per 0.1 M population were found in Qatar, USA, Peru, Brazil, Russia, Chile, and Saudi Arabia, respectively, whereas the highest number of severe cases are in Chile (8.67), Qatar (8.26), Saudi Arabia (5.3), Canada (5.13) and USA (5.06). The coronavirus cases of six continents (Europe, North America, Asia, South America, Africa, and Oceania) were compared for total active cases, total recovered, and total deaths (Figure 4 ). Results show that the highest total deaths were observed in Europe (42.21%), North America (33.40%), South America (13.70%), Asia (9.20%), Africa (1.45%), and Oceania (.03%). The highest total active cases were found in North America (31.12%), Europe (27.86%), Asia (20.28%), South America (17.62%), Africa (2.99. %), Oceania (0.11%). Also, the highest total recovered cases are found in Europe (29.83%), North America (26.99%), Asia (25.07%), South America (15.10%), Africa (2.80. %), Oceania (0.22%), respectively (as of June 13, 2020).

Table 1.

Top 24 countries with high case rate per 0.1 M pop.

Country	Total Cases/0.1 M	Deaths/0.1 M	Total Recovered/ 0.1 M	Active Cases/0.1 M	Serious, Critical/0.1 M	Tests/0.1 M
Qatar	2792.80	2.50	1967.80	822.49	8.26	10215.50
Chile	875.80	16.20	718.50	141.08	8.67	4291.20
Peru	683.30	19.70	339.07	324.46	3.38	4062.20
USA	647.40	35.50	259.86	351.99	5.06	7340.90
Spain	621.70	58.00	–	–	1.32	9550.70
Belarus	563.40	3.20	308.07	252.15	0.97	7559.40
Belgium	517.10	83.30	142.80	291.01	0.76	8716.80
Sweden	515.00	48.30	–	–	2.69	3218.90
UK	433.70	61.40	–	–	0.72	9760.80
Brazil	400.40	20.10	201.24	179.02	3.91	694.60
Italy	391.40	56.70	289.20	45.46	0.36	7548.40
Russia	356.40	4.70	188.20	163.54	1.58	9986.90
Saudi Arabia	354.50	2.70	237.29	114.49	5.30	3124.80
Canada	260.80	21.50	157.32	82.03	5.13	5603.20
France	240.30	45.00	111.55	83.67	1.33	2121.50
Germany	223.70	10.60	205.20	7.95	0.53	5603.40
Iran	220.30	10.40	174.82	35.12	3.28	1452.70
Turkey	209.60	5.70	178.05	25.86	0.81	3068.90
South Africa	110.90	2.40	62.17	46.33	0.35	1835.40
Mexico	108.00	12.80	78.97	16.28	0.29	305.50
Pakistan	60.00	1.20	22.68	36.16	0.05	380.20
Bangladesh	51.30	0.70	10.83	39.74	0.00	297.60
India	23.30	0.70	11.77	10.88	0.65	399.20
China	5.80	0.30	5.44	0.01	0.00	0.00
World	100.8	5.54	51.64	43.62	0.69	–

Figure 4.

Coronavirus cases on six continents.

Distribution of the GR of total active cases in Iran is presented in Figure 5 . Results show that the two days with the lowest growth rates of cases in Iran were March 04 (GR = 0.67) and March 08 (GR = 0.69). The five days with the highest growth rates of Iranian cases occurred on February 21 (GR = 3.67), February 27 (GR = 2.41), February 25 (GR = 1.89), March 01 (GR = 1.88), and March 06 (1.85). The average GR during the 116 days was 1.10. It decreased from March 31 to June 14.

Figure 5.

Distribution of the GR of total active cases in Iran.

Of 187,427 people who were confirmed to have been infected by Covid-19 in Iran between February 19 and June 14, 2020, 8837 died (Figure 6 ). The days with the highest GR of deaths were February 22 (3.00), March 03 (2.50), March 07 (2.38), and February 26 (2.33). The days with the lowest death GR were February 21 (GR = 0.5), May 25 (GR = 0.59), May 15 (GR = 0.68), May 16 (GR = 0.73), Feb 25 (GR = 0.75), May 22 (GR = 0.77), May 22 and June 2 (GR = 0.79). We had a decreasing trend from March 25, but in our analyses, we observed some increasing trends on April 01 and April 04. The average death GR over the 116 days was 1.08. Also, the number of total active cases and deaths (Table 2 ) was highly correlated (0.921) at a confidence level of 99%.

Figure 6.

Distribution of the GR of total death cases in Iran.

Table 2.

Correlation of total cases and deaths using Spearman’s Rho calculator.

			Total cases	Total deaths
Spearman's Rho	Total cases	Correlation Coefficient	1.000	.921**
		Sig. (2-tailed)	.	.000
		N	39	39
	Total deaths	Correlation Coefficient	.921**	1.000
		Sig. (2-tailed)	.000	.
		N	39	39

The number of infected patients per 100,000 inhabitants and the cumulative curves for Iranian provinces (Figure 7 ) is relatively high, particularly for residents of Qom County. The rate of infection per 100,000 was highest in Semnan Province.

Figure 7.

COVID-19 infected patients per 100,000 population and the cumulative curve in Iran’s provinces.

In terms of the outbreak among age groups and by sex (Figure 8 ), the highest number of active cases was among 50−59-year-olds. In this cohort, the percentages of women (23.7%) and men (21.6%) were similar. The group with the second-highest risk was the 60−69-year-old cohort. The percentages of active cases in this class were 20.2% and 18.2% for women and men, respectively. The age cohort with the fewest cases was children younger than nine years old. There was no discernible difference between the sexes in this age group. Women have more risk than men, especially in age groups 10–19, 30–39, 40–49, 70–79, and >80 years old. Between the ages 40 and 69, men have a lower (58.2%) rate of infection than women (59.1%).

Figure 8.

Relationship between various age groups and sex in active cases.

The reports of deaths (Figure 9 ) indicate that the group with the largest percentage of deaths from COVID-19 was the 60 to 69-year-olds. Men constituted a greater proportion of the deaths in this cohort. The average percentage of deaths by sex for this age group was equal at 25.12%. The analysis indicated 70 to 79-year-olds had the second-highest death rate at 22.3% (men = 20.3% and women = 24.3%). People older than 50 are the most vulnerable category based on deaths (average = 84.15, men = 85.6, and women = 82.7%) (Figure 9). There are more deaths among the elderly than among youth. The age group with the greatest number of deaths among women was the younger-than-39 group, however, the number of men who died in this group exceeded the number of women.

Figure 9.

Relationship between various age groups and sex in death cases.

Virus infections in the provinces of Iran

The number of infections in Isfahan province was strongly correlated (above 0.80) with the number of infections in Semnan, Zanjan, and Yazd provinces (Table 3 ). Yazd borders Isfahan, demonstrating close communication between these provinces enables the spread of the virus. Alborz, also showing a high level of infection, was highly correlated with Qazvin. The centers of these provinces are relatively close to each other; a highway connecting them facilitated social contact and consequently, communication of the virus to Qazvin. East Azerbaijan was highly correlated with Tehran and West Azerbaijan. Although these provinces are not neighbors, there is air travel and ethnic affinity between the people of these provinces. Tehran was weakly correlated with neighboring Alborz province. One reason for this low correlation may be that there was a timely alert about the virus in the centers of these provinces, discouraging intercity traffic. Qom, the center of the coronavirus outbreak in the country, was strongly correlated with Golestan, Guilan, and Mazandaran. These three Northern provinces have good weather and many tourist attractions. The Ministry of Transportation reported that there was heavy traffic between Qom and the northern provinces during the first days of the COVID-19 outbreak in Qom. Sistan-o-Balouchistan, with low infection rates, was strongly correlated (r = 0.76) with its neighboring province, Kerman. In conclusion, correlation analysis suggests that distance, tourism attraction, and ethnic affinity might promote the inter-province spread of the virus; the role of other factors remains unclear.

Table 3.

Correlation coefficients of the number of coronavirus infection cases among Iran's 31 provinces (days between 19 February to 22 March 2020).

Province	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
1-Ardabil	1
2-Isfahan	0.50	1
3-Alborz	0.60	0.65	1
4-Ilam	0.40	0.20	0.25	1
5-East Azerbaijan	0.58	0.59	0.46	0.37	1
6-West Azerbaijan	0.69	0.66	0.49	0.42	0.72	1
7-Bushehr	0.67	0.51	0.65	0.62	0.40	0.55	1
8-Tehran	0.39	0.48	0.46	0.37	0.67	0.53	0.39	1
9-Charmahal-Bakhtiari	0.49	0.13	0.31	0.47	0.0008	0.21	0.51	0.17	1
10-South- Khorasan	0.23	0.50	0.41	0.30	0.34	0.38	0.48	0.44	0.40	1
11-Razavi-Khorasan	0.21	0.52	0.31	0.60	0.64	0.56	0.50	0.44	0.14	0.42	1
12-North-Khorasan	0.47	0.46	0.23	0.06	0.17	0.50	0.27	0.11	0.12	0.19	−0.007	1
13-Khuzestan	0.66	0.40	0.55	0.55	0.51	0.61	0.73	0.60	0.29	0.38	0.36	0.46	1
14-Zanjan	0.53	0.75	0.68	0.51	0.46	0.54	0.56	0.42	0.27	0.39	0.51	0.35	0.54	1
15-Semnan	0.54	0.81	0.70	0.46	0.58	0.61	0.65	0.59	0.47	0.69	0.51	0.33	0.59	0.77	1
16-Sistan-Baluchistan	0.34	0.40	0.40	0.33	0.30	0.58	0.56	0.36	0.33	0.27	0.40	0.49	0.57	0.22	0.47	1
17-Fars	0.73	0.51	0.42	0.45	0.63	0.79	0.43	0.54	0.5	0.33	0.44	0.59	0.62	0.46	0.57	0.64	1
18-Ghazvin	0.69	0.71	0.75	0.20	0.37	0.51	0.50	0.45	0.55	0.47	0.23	0.40	0.37	0.68	0.65	0.24	0.58	1
19-Qom	0.005	0.48	0.37	0.25	0.08	0.18	0.26	0.33	0.17	0.15	0.32	0.16	0.14	0.47	0.46	0.53	0.24	0.32	1
20-Kordistan	0.46	0.60	0.46	0.33	0.31	0.34	0.54	0.25	0.37	0.62	0.35	0.65	0.49	0.67	0.66	0.34	0.47	0.58	0.34	1
21-Kerman	0.18	0.52	0.35	0.18	0.50	0.63	0.18	0.43	0.03	0.33	0.42	0.44	0.41	0.32	0.54	0.76	0.63	0.19	0.53	0.29	1
22-Kermanshah	0.57	0.38	0.40	0.54	0.53	0.69	0.45	0.57	0.37	0.34	0.46	0.54	0.77	0.6	0.56	0.6	0.82	0.41	0.30	0.54	0.62	1
23-Kohgiluye-BoyerAhmad	0.30	0.01	0.31	0.12	−0.03	0.19	0.27	0.23	0.64	0.39	−0.003	0.23	0.37	0.3	0.38	0.25	0.41	0.41	0.10	0.42	0.14	0.55	1
24-Golestan	0.28	0.53	0.45	0.08	0.23	0.39	0.34	0.16	0.26	0.3	0.26	0.52	0.21	0.45	0.54	0.63	0.49	0.42	0.70	0.64	0.62	0.43	0.36	1
25-Guilan	0.47	0.55	0.69	0.10	0.40	0.42	0.42	0.52	0.26	0.07	0.38	0.02	0.31	0.57	0.47	0.33	0.41	0.66	0.56	0.22	0.26	0.37	0.28	0.44	1
26-Lorestan	0.22	0.52	0.51	0.46	0.40	0.34	0.53	0.34	0.43	0.68	0.65	0.07	0.21	0.55	0.68	0.41	0.36	0.44	0.58	0.64	0.42	0.37	0.31	0.66	0.39	1
27-Mazandaran	0.31	0.41	0.23	0.44	0.27	0.34	0.49	0.18	0.46	0.12	0.43	0.25	0.25	0.37	0.56	0.60	0.46	0.20	0.63	0.41	0.43	0.35	0.20	0.69	0.37	0.59	1
28-Markazi	0.64	0.48	0.60	0.21	0.51	0.54	0.45	0.69	0.42	0.37	0.22	0.005	0.4	0.47	0.58	0.16	0.48	0.60	0.23	0.19	0.16	0.37	0.39	0.23	0.69	0.35	0.23	1
29-Hormozgan	0.48	0.41	0.11	0.63	0.25	0.54	0.46	0.22	0.44	0.3	0.29	0.62	0.4	0.35	0.43	0.48	0.63	0.34	0.31	0.49	0.36	0.45	0.07	0.38	−0.006	0.34	0.56	0.14	1
30-Hamadan	0.41	0.49	0.35	0.40	0.47	0.42	0.62	0.53	0.57	0.8	0.49	0.12	0.4	0.34	0.74	0.41	0.44	0.41	0.27	0.57	0.31	0.36	0.38	0.41	0.24	0.74	0.54	0.55	0.41	1
31-Yazd	0.74	0.73	0.76	0.44	0.71	0.71	0.74	0.48	0.22	0.36	0.48	0.43	0.72	0.75	0.8	0.51	0.60	0.54	0.35	0.60	0.50	0.60	0.23	0.57	0.55	0.52	0.55	0.54	0.41	0.50	1

Heatmap for coronavirus spread in Iran and other countries

The heat map represents the provinces grouped by similarity using color intensity (= COVID-19 contamination rate) (Figure 10 ). The heatmap shows two critical time intervals for the COVID-19 outbreak in Iran. Similar color patterns from February 19–28 establish the first time-interval, which had low numbers of diagnosed cases in all provinces. The second interval was in March when infection aggressively spread to most provinces. The virus outbreak was critical in Tehran, Qom, Markazi, and East Azerbaijan in the third interval. The heatmap divided provinces into several groups concerning disease rate and days since February 19. Tehran, Isfahan, and Mazandaran were distinct from many of the other provinces. Qom, Alborz, and Markazi, three neighbors, were grouped. The color spectrum of the heatmap shows that March 6th, 10th, and 14th were critical infection days for all provinces.

Figure 10.

Heatmap of coronavirus outbreak and classification of Iran’s provinces.

Other countries with more than 100 infected coronavirus cases were clustered in the heat map based on nine parameters (Figure 11 ). The heat map suggested that there are two multiple-member groups, and that China and Italy are set off separately. France, Germany, Iran, Spain, and South Korea constituted a distinct group. Of the nine coronavirus related parameters, the total recovered and the number of cases of infection were detected to be separate from the rest of the parameters.

Figure 11.

Heatmap of coronavirus outbreak and classification of the world's countries.

Goodness-of-fit for the relationship between the number of diagnosed infections and the number of days after the first appearance of coronavirus

The results of regression models of the relationship between the number of infected cases and the number of days after the first virus outbreak in Iran are shown in Figure 12 . No single response curve was significant for all provinces, but the cubic model represented the highest coefficient of determination (R²) for most provinces. The number of diagnosed cases in Kohgiluye and Boyer-Ahmad provinces showed no significant relationship to the day since the outbreak began. The quadratic model was the best fit for Bushehr, North Khorasan, Golestan, and Yazd provinces. For the remaining provinces, cubic was the best model for the relationship between infections and elapsed time. The highest coefficients of determination (R²) were observed in the regression model fitted for West Azerbaijan (R²  = 79.3%), and then Semnan, Fars, and Yazd. In 14 of the 31 provinces, the number of infections slowed down after several days of outbreak and spread in Iran, but infections continued to rise in Yazd until March 17. The results showed that the infection rate was related to population densities in Iran's provinces. Apart from virus evolution and adaptation, the human factors of population growth, urbanization, movement and travel, and vector travel are the most important factors driving virus outbreaks (Enria et al., 1998, Hu, 2006). The number of people required for virus circulation in an area is at least 200,000. The results revealed that the coronavirus outbreak was critical in Tehran, the country’s most crowded city. Coronaviruses need to maintain themselves in the population, and larger populations facilitate the spread of the virus and incidence of disease in susceptible individuals (Hu, 2006). Infection with coronavirus was more critical in Iran’s more-populated provinces (i.e., Tehran and Isfahan). Isfahan is an industrial city with many factories, and heavy human traffic might assist higher rates of spread around the urban area. It has been shown that low-income citizens migrating from the countryside for work have driven disease-spread to high-density urban areas in African countries (Patel et al., 2019).

Figure 12.

Test for the best fit of regression models for the number of infected with coronavirus and days after the first day of infected cases in the 31 Iranian provinces.

The regression models suggested a cubic trend for the relationship between the province’s population and infections (Figure 13 ).

Figure 13.

Relation of the population of Iran’s provinces with the number of infected cases with coronavirus.

The trends of deaths in Iran

A regression model was used to determine trends in death rates in Iran (Table 4 ). The explanatory variables that are exponents of the lag of days after outbreak explain more than 99% of the variation in the patterns of deaths. The Ljung–Box Q-statistics (Table 4) indicated that the residuals are not significantly correlated. Also, the Jarque-Bera test of normality shows that residuals are normally distributed. Evaluation of prediction accuracy (Figure 14 ) determined that predicted values were, to a great extent, able to keep pace with the actual values.

Table 4.

Regression results for Covid-19 death cases in Iran.

Regressor	Coefficient	Standard error	t-statistics	probability
Constant	−69.762	124.662	−0.537	0.591
t	11.645	1.039	11.208	0.000
t2	−0.210	0.019	−10.952	0.000
t3	0.001	0.0001	10.150	0.000
Adjusted $R^2$	0.999
Q(1)a	1.014			0.314
Q(2)a	1.306			0.520
Jarque Berra	4.382			0.111

^a$Q(p)$ is the significance level of the Ljung–Box statistics in which the first p of the residual autocorrelations is equal to zero.

Figure 14.

Actual deaths cases versus estimated cases.

The main point is that the deaths are increasing over the prediction horizon; however, it shows two turning points. Around mid-April, a turning point is observed. In other words, based on the data applied to estimate the regression model, the death trend slowly reveals the turning point. Regarding the global context, for instance, for the incidence of SARS (Wong, 2008), HAV (Alberts et al., 2019), ARI (Leonenko et al., 2016), and A (H1N1) v (Flasche et al., 2011), a turning point is expected to occur, meaning that after passing the peak, the frequency of deaths should decease. An emerging, slowly increasing trend simply means that the Iranian government's measures might have been effective in coping with the outbreak at that time. However, the slowly increasing trend, on June 01, tends to reveal a rapidly increasing trend, which may be considered a second turning point. This fact simply means that the subsequent measures taken by the Iranian government have not yet been enough to cope with the outbreak and that there is a need for more restrictive measures, like widespread quarantine. Note that the model is more appropriate for investigating the effectiveness of the Iranian government's measures than predicting the future values of mortality rate. In general, we should see a decreasing trend; however, the current situation is far from that, indicating that there has been an inadequate impact of control measures, and there is a lot of room for improvement.

Comparing global and Iranian death rates

Both the global and Iranian models are presented with a fourth-degree polynomial specification (Figure 15 ). For both, deaths are increasing exponentially, but there is a steeper rate for Iran's increase of deaths in the beginning. This fact has been examined more deeply and in a quantitative way, using ARMA time-series estimation (Table 5 ).

Figure 15.

Comparing trends of deaths in Iran to the world.

Table 5.

The results of ARMA model for Covid-19 death cases of world and Iran.

	Regressor	Coefficient	Standard error	t-statistics	probability
World	Constant	221.902	25.073	8.85	0.000
	AR(1)	1.311	0.003	331.90	0.000
	AR(2)	−0.268	0.004	−60.67	0.000
	AR(8)	−0.128	0.002	−51.55	0.000
	Resid^2(-1)	2.812	0.261	10.761	0.000
	Adjusted $R^2$	0.918
	Q(1)a	1.803			0.179
	Q(2)a	2.511			0.285
	Jarque Berra	8.704			0.012
Iran	Constant	5427.451	3119.420	1.73	0.084
	AR(1)	1.999	0.018	109.53	0.000
	AR(2)	−0.999	0.018	−54.75	0.000
	MA(2)	−0.286	0.090	−3.15	0.002
	Adjusted $R^2$	0.996
	Q(1)a	1.200			0.273
	Q(2)a	1.359			0.507
	Jarque Berra	1.226			0.120

^a$Q(p)$ is the significance level of the Ljung–Box statistics in which the first p of the residual autocorrelations is equal to zero.

These models may show the activities of the variables in a specific time horizon. To ensure comparability, a 116-day time horizon was used for both. This is the period for which data are available for Iran (February 19 to June 14). The world model is generated by an AR (3_1,2,8) process (Table 5), while the Iranian modeling of the death trend was obtained with a moving average, resulting in an ARMA (2, 1). However, the absolute value of the AR terms for Iran is higher than that of the world model, indicating a faster increase. Also, the death trend is characterized by volatility since a moving average process (Iran), and autoregressive conditional heteroskedasticity (ARCH) (World) were calculated. These processes model volatility. Given the significant coefficients for these variables, the deaths in the world tend to fluctuate more than those occurring in Iran. This is not easily captured in the trends (Figure 15).

The diagnostic statistics indicate that the models are acceptable since Q-statistics indicate that the residuals are not significantly correlated. The Jarque Berra statistic supports the normality of residuals at a conventional significance level for Iran's specification. However, for World specifications, residuals are not normally distributed, thus, one needs to exercise caution. All coefficients are significant at 99 percent.

Relative importance of variables using LASSO MLT

As stated in the methods section, the LASSO MLT was used to determine the relative importance of the variables and to determine the impact of each factor on the COVID-19 outbreak in Iran (Figure 16 ). The most important variables were the distances from bus stations, bakeshop, hospitals, mosques, ATMs, and banks, and MTCM. On the other hand, the outbreak was least related to the village’s density, PWM, and PDM.

Figure 16.

Relative importance of variables in outbreak trend of using the LASSO MLT.

COVID-19 risk mapping using the RF MLT

In the current study, the RF MLT was used for spatial modeling and mapping COVID-19 in Iran twice, on March 11 and March 18. To run the RF, the tree and variables numbers were set on 1000 and 4, respectively. The results of the confusion matrix (Table 6 ) indicate the classification model’s performance. In total, 5263 active cases were predicted as classes of coronavirus. Among that set, almost 4940 cases were predicted in the correct class, whereas 323 cases were predicted in the wrong class. The value of OOB as an error rate was 21.14%, meaning that the accuracy of the training dataset (the modeling process) is 78.86%. Finally, the COVID-19 risk map (Figure 17 (a–b)) on March 11 was prepared and divided into four classes according to the natural break method. The visual interpretation shows that the provinces of Tehran, Qom, Alborz, Mazandaran, and Guilan, are classified as high risk of coronavirus (COVID-19). In contrast, Sistan-o-Balochistan, Hormozgan, Bushehr, Kerman, and South Khorasan are all low-risk provinces.

Table 6.

Confusion matrix of the random forest model (On March 11th, 2020).

	0 (No)	1 (Yes)	Class error
0 (No)	4312	951	0.181
1 (Yes)	1274	3989	0.242

Figure 17.

COVID-19 risk map of active cases in Iran ; a) On March 11, and b) On March 18.

The classification risk map on March 18 shows an increasing trend in the outbreak of COVID-19 in Iran after a week. Also, our analysis (Figure 16) indicates that, in addition to Tehran, Alborz, Qom, Mazandaran, and Guilan, the provinces of Qazvin, Markazi, Golestan, Ardabil, Isfahan, East Azerbaijan, and parts of provinces of Khorasan Razavi, Semnan, and Lorestan are also high-risk regions. This suggests that the COVID-19 outbreak is increasing every day, and therefore it is important to consider some different tactics, particularly quarantines, to control and manage the virus. At the moment (March 17), parts of southern and southwestern Iran are safer than other regions. So, risk mapping can be introduced as an important tool in assessing the speed of pandemic trends for each country. There are too many machine learning and expert-based techniques for this purpose, so we have suggested a model, namely the RF in this study. A boosted regression tree (BRT) was used for the spread mapping of Avian influenza A (H7N9) in China. For this aim, some environmental, agro-ecological, and meteorological factors are applied, and the model's ability to be measured using the ROC curve (Fang et al., 2013). In this line, spatial risk maps were prepared for monitoring and a trend analysis of influenza A H5N1 and H7N9 in China. For this research, a MaxEnt (Maximum Entropy) model was applied using several environmental factors and its results were validated by ROC curve (Bui et al., 2017). Currently a WEB GIS-based approach is a common tool for mapping various epidemic outbreaks. One of these applications was mapping dengue outbreaks in the tropical and sub-tropical areas including, the Lahore district. Results of mapping using climate, land use/ land cover, NDVI (Normalized Difference Vegetation Index), and population density showed that the most important factor for this disease was population density (Butt et al., 2020). Concerning COVID-19, John Hopkins University is pioneered mapping daily reports of active cases and deaths (https://coronavirus.jhu.edu/map.html). This site is known as a coronavirus resource center and can be effective for other countries to simulate and estimate COVID-19 outbreaks using various machine learning techniques by creating a risk mapping. This map is a robust information tool for managers, prime ministries, and governments to decrease socioeconomic effects, as well as deaths in each country, and it can provide situational awareness to improve responses to the pandemic.

Validation of the RF MLT

The validation of the COVID-19 risk maps (Figure 18 and Table 7 ) shows that the accuracy of these maps for March 11 and March 17 is 0.866 and 0.836, with standard errors of 0.005 and 0.004, respectively. Hence, according to the ROC-AUC categorization (Yesilnacar, 2005), the maps can be considered very good (0.8−0.9).

Figure 18.

The ROC curve of RF MLT for mapping risk of COVID-19; a) On March 11, and b) On March 18.

Table 7.

The AUC value of COVID-19 risk maps using RF MLT.

AUC values		Standard Error	Asymptotic Significant	Asymptotic 95% Confidence Interval
				Lower Bound	Upper Bound
March 11th	0.866	0.005	0.000	0.856	0.877
March 17th	0.836	0.004	0.000	0.829	0.844

Conclusions

Coronavirus disease 2019 (COVID-19) represents a continuing pandemic threat and has spread globally. It is crucial to investigate the spatial drivers to prevent and control this epidemic. An RF MLT with 16 independent variables was used to model and map the risk of COVID-19. The LASSO algorithm determined the relative importance of each of these 16 variables. The GR of active cases, deaths, and correlations between them, age cohorts, and sexes were considered. Some comparisons were made of the death rates in Iran with 18 other countries. Finally, a non-linear regression model was used to evaluate the general trend of daily deaths. The estimation equation shows how a variable would behave if the current management protocols are continued. Comparing the general trends of Iran and the world revealed that the death trends are similar, but the world's trend shows significant volatility. The greater volatility for the world suggests that some countries are experiencing coronavirus death volatility with a different severity than that experienced in Iran. The main policy implication is that deaths, to some extent, may be limited by using more effective management measures. These measures may be more important and more effective, particularly when the early-experiencing countries' measures are taken into consideration. We speculate that the risk map and analyses provided in this study imply that this analysis may be the first and most important step in the future management and control of COVID-19 in Iran and in its provinces.

Conflict of interests

We declare no competing interests.

Funding

Iran National Science Foundation (INSF), Grant No. 99007155.

Availability of data and materials

All data and materials used in this work are publicly available.

Ethics approval and consent to participate

The ethical approval or individual consent was not applicable

Contributors

HRP, SP, BH, ZF, SRFSh, SB, RKh, ME, GhGh, AF, RS, ZH, MHT, JPT, AZ, FS contributed to study design, the literature search, data collection, data analysis, software working, and writing of this article. All authors read and approved the final report.

Appendix A. Supplementary data

The following is Supplementary data to this article: