Identification of influential users on Twitter: A novel weighted correlated influence measure for Covid-19

Abstract

In the era of advanced mobile technology, freedom of expression over social media has become prevalent among online users. This generates a huge amount of communication that eventually forms a ground for extensive research and analysis. The social network analysis allows identifying the influential people in society over microblogging platforms. Twitter, being an evolving social media platform, has become increasingly vital for online dialogues, trends, and content virality. Applications of discovering influential users over Twitter are manifold. It includes viral marketing, brand analysis, news dissemination, health awareness spreading, propagating political movement, and opinion leaders for empowering governance. In our research, we have proposed a sustainable approach, namely Weighted Correlated Influence (WCI), which incorporates the relative impact of timeline-based and trend-specific features of online users. Our methodology considers merging the profile activity and underlying network topology to designate online users with an influence score, which represents the combined effect. To quantify the performance of our proposed method, the Twitter trend #CoronavirusPandemic is used. Also, the results are validated for another social media trend. The experimental outcomes depict enhanced performance of proposed WCI over existing methods that are based on precision, recall, and F1-measure for validation.

1. Introduction

Online social networks (OSNs) provide a platform where diverse people can interact, express, and share their ideas. Analyzing the content over social media has perceived a prodigious change to contour public thoughts in a society that gave birth to the task of discovering influential users. Identifying influential users have received attention towards cross-domain sustainable applications by serving the society across multiple dimensions, including political inclination, e-governance, social media influencers, financial risks estimation, viral marketing, career move prediction, smart healthcare, finding essential proteins, etc. [11], [13], [14], [16], [29]. Among other micro-blogging platforms, Twitter served as an emerging medium and de facto communication platform. Owing to the enhancements in Twitter science, along with the enriched network tools and techniques, the exploration of Twitter influencers has become strategically significant from a global and local perspective. The influence of user-profiles on Twitter can be determined by several factors, for instance, popularity, activity, friends, followers, and network structure. The main goal of our research is to build a novel sustainable approach to reveal the user influence in the real-world Twitter network. Our initiative is focussed on utilizing profile-centric attributes along with the underlying network topological connections.

1.1. Related research

In the last decade, lots of research is conducted towards identifying influential or powerful user profiles on Twitter. Influential users are often referred as authoritative actors [6], opinion leaders, innovators [9], prestigious individuals [15], and curators [31] by different researchers. Some influence measurement methods use graph theory integrated with structural parameters, while others are purely based upon individual profile parameters or interactions with other online users. Authors proposed activity-based influence measure which counts the total number of tweets or status messages by a particular user from his timeline namely, TweetRank [23]. Similarly, another measure is known as, Tweet Count Score was proposed, which aggregated the count of tweets and retweets [24]. In yet another study, authors provided a metric called Topical Strength [25] to identify authoritative users by taking the sum of original tweets, retweets, and replies posted by a user, about a specific topic or trend. Next, some popularity-based metrics are developed depending upon the number of followers and followings. Follower-Rank is another such influence metric proposed by [8], which is expressed as the number of followers of an individual and Follower-Followee ratio [2] in the Twitter network. Another measure based upon followers and followee ratio is a paradoxical discounted measure [15]. To diminish the effect of trade-offs between several followers and followee of the user, a new metric namely, popularity [1] was developed. Homophily and reciprocity are taken forward by another research for computing user influence that considered the follower-graph generated from trending topics on Twitter [21]. A comparative study was carried out over three metrics i.e. in-degree, retweets, and mentions [22], from which the authors concluded that in-degree alone encapsulates very less information about the influence of the user. In another study, attempts were made to identify the opinion leaders on Twitter on the basis of network size and tweets posting rate [26].

Some researchers have also explored the influence metrics, based upon structural properties of the Twitter relationship graph. In one of the studies, the out-degree of an online user and direct associations for its neighbors were used to compute the influence score of the user [17]. In another work, some benchmark centrality metrics were employed to discover the influential leaders in the network [3]. Later, a comparative study was made to find opinion leaders in the Higgs Boson Twitter network, by using some common centrality measures [27]. Moreover, the authors have also experimented with the information flow process triggered through nodes that were identified as influential profiles.

Several influence measures based upon PageRank and Eigenvector in context of Twitter are developed by taking mention and retweetssubgraphs [10], [18], [19], [21], [32]. A novel framework was developed based on diffusion probability and degree centrality to capture the influence maximization [20]). A comparison was drawn with degree-based influential users using Monte-Carlo simulations. In another research, random-walk based measure was developed to capture influence in the micro-blog network and compared with the TwitterRank method [33]. Another influencer metric, known as H-index has been explored in view of Twitter to uncover influential users [28]. In this study, the post forwarding behavior of a user is explored to rule out the influence as well as passivity. This led to the conclusion that highly influential users need not be always popular in the world of social media

From the above literature survey, it can be observed that the new measures are persistently emerging, and every measure can be distinguished based on the measurement criteria. The former research interest has been significantly based upon either single criteria or the sole values of the measure. This means that the existing methods are currently based upon only a single parameter either on a degree or retweet etc. but fails to embed the joint impact of multiple parameters in the form of a single score. However, our research would introduce a novel influence measure, which could incorporate the combined-weighted impact of correlated user-timeline features (profile attributes) and topic-based network structural features (interaction attributes).

1.2. Research highlights

The main contributions of the study is organized as follows:

• •Novel measure namely, Weighted Correlated Influence is proposed to compute the influence scores of each user in the micro-blog Twitter network.
• •Our efficient approach determines the topical influencers in global social networks fragmented into the topical network that is being generated in the content of a specific topic or keyword.
• •Two sets of features are embedded, which includes individual profile parameters in the entire timeline and inherent structural features by analyzing the user-user relationship graph.
• •Twitter subgraphs of tweets, retweets, mentions, replies, and mentions-in-retweets are considered to capture the user interactions, required for computing structural features.
• •The experiment is conducted on real-word Twitter networks, built on global trends exhibiting 18473 (#CoronavirusPandemic) and 15018 (#DelhiViolence), respectively.
• •Correlation matrix for all timeline and structural features is computed
• •The performance of the proposed measure is analyzed with the counterpart algorithms, and the comparative study reveals the effectiveness of our proposed algorithm in terms of precision, recall, and F1-measure.

The remaining work is organized in three succeeding sections. Section 2 outlines the overall proposed methodology, followed by the dataset description, experiments, and results in Section 3. Finally, the paper is concluded in Section 4 with a future scope and open research challenges.

2. Proposed methodology

In this section, the proposed methodology is explained with the set of symbols, assumptions, and definitions. Our study is significantly focussed on building a model to efficiently derive the influence of users in the Twitter social network.

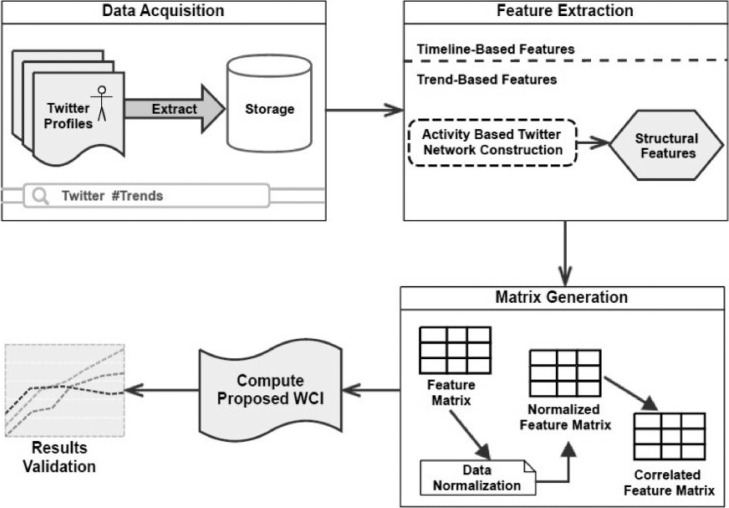
Social network can be mathematically defined as a graph with a set of nodes and edges. Similarly, the Twitter network can be defined as a directed graph ($\overrightarrow{G}=v,\overrightarrow{e}$), wherevis the set of vertices representing users, and the relationship between users can be defined by the interactions between them, hence, forming directed edges. Interaction between users on Twitter can be in the form of a tweet, retweet, mention, replies, follow-up, and followee. Fig. 1 depicts the steps and the framework for computing influence score by the proposed measure. The mathematical symbols are enlisted in Table 1 .

Fig. 1.

A proposed framework for computing novel Weighted Correlated Influence (WCI) measure. A sequence of steps includes data gathering phase, namely data acquisition followed by feature extraction step, which helps to yield a feature matrix that is required for building a correlated feature matrix. Finally, results validation and comparative analysis are performed.

Table 1.

Explanation of symbols used in the study for the proposed influence measure.

Symbol	Description
v	Number of vertices i.e. users in a directed graph $|\overrightarrow{G}|$
$\overrightarrow{e}$	Number of directed edges in $\overrightarrow{G}$
λ	Number of features
Fv, λ	Feature matrix
Cλ, λ	Correlated Feature matrix
FOi	Total number of followers of ith node
FLi	Total number of followers of ith node
Li	Total number of followers of ith node
Ti	Total number of followers of ith node
FVi	Total number of followers of ith node
IDi	In-degree centrality of ith node
ODi	Out-degree centrality of ith node
Bi	Betweenness centrality of ith node
Pi	PageRank centrality of ith node
Ei	Eigenvector centrality of ith node

In this research, a weighted Correlated Influence (WCI) measure is proposed to compute the influence score for each user in a network. This is initiated with the identification of profile features and building the interaction graph, required for feature set construction.

• AFeature extraction and data pre-processing

Data acquisition is performed using Twitter's REST API to build a feature set for each user based upon their trend-specific and timeline-specific activity. Two different types of Twitter relationships were considered; one is between users, and the other one is between users and tweets. List of profile-based and derived features are enumerated in Table 2 . To acquire profile attributes, timeline-based features are extracted including the count of followers(FO), following(FL), tweets(T), lists(L), favorites(FV), accountsage, and Twitter-verifiedstatus. Additionally, we have computed trend-specific features using user and tweets graph obtained from five different interactions, namely tweets, retweets, mentions, replies, and mentions-in-retweets. After capturing all the interactions, a Twitter subgraph is formed. Subsequently, the trend-specific subgraph is considered to calculate in-degree(ID), out-degree(OD), betweenness(B), PageRank(P), and Eigenvector(E)topological-based centrality scores [4], [5], [7], [12]. Among all, account age and verified status were eliminated to build feature set. From the features, each user is represented by 10 features. All selected features have a numerical value that could assist in deriving influential users. We commence our research by gleaning all the features and generate Feature Matrix (FM) as per our constructed dataset. Feature matrix F _v, λ of size v × λ is demarcated in Eq. (1), where v designates to unique users and λ represents the distinct timeline and trend-based features. Hence, $\lambda =10$ and v depends upon the dataset undertaken in our research.

$$F_{v,\lambda }={\left[\begin{array}{c}\begin{array}{ccc}{f}_{1,1}& f_{1,2}& .\\ f_{2,1}& f_{2,2}& .\\ .& .& .\end{array}\begin{array}{ccc}.& f_{1,\lambda -1}& f_{1,\lambda }\\ .& f_{2,\lambda -1}& f_{2,\lambda }\\ .& .& .\end{array}\\ \begin{array}{ccc}.& .& .\\ .& .& .\\ f_{v,1}& f_{v,2}& .\end{array}\begin{array}{ccc}.& .& .\\ .& .& .\\ .& f_{v,\lambda -1}& f_{v,\lambda }\end{array}\end{array}\right]}_{v\times \lambda }$$ (1)

Table 2.

List of features extracted per user. Features are extracted based on user-user and user-tweet relationship. Timeline and trend-specific features are listed under the category of Twitter relationship.

Twitter Relationship	User	Tweet
User	Timeline-Based Features	Trend-Specific Features
	Number of Followers/Fans	In-Degree
	Number of Following/Friends	Out-Degree
	Number of Tweets/Statuses	Betweenness
	Number of Lists	PageRank
	Number of Favorites/ Likes	Eigenvector
	Accounts Age
	Verified status

Moreover, each cell value f _{i, j}of matrix F _v, λ represents the particular feature value concerning a user where $iϵ\left\{1\dots v\right\}$and$jϵ\left\{1\dots \lambda \right\}$. For instance, we have built two datasets with 15018 and 18473 number of users. Hence, the size of the feature matrix will be denoted by F _15018, 10 and F _18473, 10 respectively. All the feature values were normalized in the range of [0, 1].

This process of normalizing the scores is known as data pre-processing. Normalized Feature Matrix (NFM) is obtained so that none of the feature values could enjoy a biased impact in further calculations. Additionally, for timeline-based features, Min-Max normalization is applied, whereas in the case of Trend based features directed graph centrality normalization is employed.

• AGenerating correlated feature matrix (CFM)

The NFM is used for the generation of symmetrical Correlated Feature Matrix (CFM), denoted as C _λ, λand is defined in Eq. (2). Each cell value c _{k, l} ∈ C _λ, λ in CFM matrix embodies the correlation score computed using Pearson's correlation coefficient [30] between two features. Though, it is an asymmetrical matrix, the cell values across left diagonal remains 1 as $\left[k,l\right]ϵ1\dots \lambda .$

$$C_{\lambda ,\lambda }={\left[\begin{array}{c}\begin{array}{ccc}{c}_{1,1}& c_{1,2}& .\\ c_{2,1}& c_{2,2}& .\\ .& .& .\end{array}\begin{array}{ccc}.& c_{1,\lambda -1}& c_{1,\lambda }\\ .& c_{2,\lambda -1}& c_{2,\lambda }\\ .& .& .\end{array}\\ \begin{array}{ccc}.& .& .\\ .& .& .\\ c_{\lambda ,1}& c_{\lambda ,2}& .\end{array}\begin{array}{ccc}.& .& .\\ .& .& .\\ .& c_{\lambda ,\lambda -1}& c_{\lambda ,\lambda }\end{array}\end{array}\right]}_{\lambda \times \lambda }$$ (2)

Moreover, the correlation score in CFM can range from $\left[-1,1\right]$ depending upon the association among distinct features. If the value is encountered as zero, it means that the features are uncorrelated otherwise positively or negatively correlated depending upon the direct or inverse relation. For instance, in our study, the value of λ i.e. feature count is 10, therefore; the size of C _λ, λis 10 × 10.

This is followed by using CFM as an input matrix to obtain a characteristic vector of the form represented in Eq. (3). The characteristic values are first computed by taking the characteristic equation as the base for all reckonings. The characteristic vector,$M=\left\{m_1,m_2,\dots ,m_{\lambda }\right\}$ is generated against ɛ number of characteristic values. Hence, for the square matrix CFM, with size λ × λ, a total of λ characteristic values are generated. Moreover, λ numbers of characteristic vectors are produced of size λ × 1 counter to λ number of characteristic values.

$${\left[\begin{array}{ccc}\begin{array}{cc}{c}_{1,1}-\epsilon & c_{1,2}\\ c_{2,1}& c_{2,2}-\epsilon \end{array}& \cdots & \begin{array}{cc}{c}_{1,\lambda -1}& c_{1,\lambda }\\ c_{2,\lambda -1}& c_{2,\lambda }\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{c}_{\lambda ,1}& c_{\lambda ,2}\end{array}& \cdots & \begin{array}{cc}{c}_{\lambda ,\lambda -1}& c_{\lambda ,\lambda }-\epsilon \end{array}\end{array}\right]}_{\lambda \times \lambda }{\left[\begin{array}{c}{m}_1\\ m_2\\ :\\ :\\ .\\ m_{\lambda }\end{array}\right]}_{\lambda \times 1}={\left[\begin{array}{c}0\\ 0\\ :\\ :\\ .\\ 0\end{array}\right]}_{\lambda \times 1}$$ (3)

• AComputing proposed weighted correlated influence (WCI) measure

Our proposed Weighted Correlated Influence (WCI) Measure for each user is computed by finding out the relative impact factors of each feature, which are used as the weights to integrate all the normalized feature scores by multiplying with their respective weights (Algorithm 1 ). The information encapsulated in individual features is now, encapsulated in a single score which reflects the combined effect of their interaction with other users along with their discrete profile activity. Therefore, the proposed WCI measure is mathematically defined using linear Eq. (4):

$$WC{I}_i=\sum _{j=1}^{\lambda }{\beta }_j{f}_{i,j}\forall i\in V$$ (4)

Algorithm 1.

Proposed Weighted Correlated Influence (WCI) algorithm for computation of user influence scores in social network.

Proposed Algorithm for Computation of WCI Measure

Input: Twitter Subgraph $\overrightarrow{G}$ ($v,\overrightarrow{e}$)

Procedure:

1:  Obtain feature matrix Fv,  λ

2:  Generate Normalize feature matrix Fv,  λ to assortment [0, 1]

3:  Compute Correlated Feature Matrix C λ,  λ

// Pearson's Correlation coefficient: $\mathit{Corr}(A,B)=\frac{n(\sum \mathit{AB})-(\sum A)(\sum B)}{\sqrt{[n\sum A^2{(\sum A)}^2][n\sum B^2{(\sum B)}^2]}}$

4:  Find the characteristic equation of matrix Cλ,  λ

5:  $\text{det}\left[C-\epsilon \mathrm{I}\right]=0$ // I is the identity matrix

6:  Generate characteristic vector M sorted in decreasing order

7:  Vector analogous to maximum characteristic value is elected to yield weights${\beta }_j\forall \mathrm{j}=1\dots \lambda .$

8:  Calculate score WCIi such that$i\in \left[1,v\right]:WC{I}_i=\sum _{j=1}^{\lambda }{\beta }_j{f}_{i,j}$

Output: WCIi∀ i ∈ v

Here, i ∈ [1, v] and β _j are the weights representing the relative correlated impact of each timeline and trend-based structural features. Moreover, β _j is the analogous vector to subsequent chief characteristic value i.e., ${\mathit{\beta }}_{\mathit{j}}={\mathit{m}}_{\mathit{j}}$, ɛ _j is maximum. The peak value is used to incorporate the highest variation encountered in the data. Therefore, higher is the value of WCI, more influential will the user and vice-versa. The time complexity of the proposed twitter-based influence measure is reliant upon individual features, which in our case accomplishes in $\mathit{O}\left(\mathit{en}+{\mathit{n}}^2\right)$.

Some pre-requites are associated with our work proposal. Our proposed method is applicable for online streaming data only i.e. instance of a subnetwork in the growing phase is captured for appropriate investigational outcomes. Secondly, a network instance is a prerequisite to continue with the reckoning of associated profile based and structural features. Besides, there is reliance above a Twitter search REST API to crawl the data and structural centralities to build the dataset and for designing our novel proposed Weighted Correlated Influence (WCI) Measure.

3. Experimentation and results

For experimentation purposes, we have selected two trend-specific real-time Twitter datasets to exemplify our proposed methodology. One of which is a Covid-19 trend, i.e. #CoronavirusPandemic, and the other is on #DelhiViolence. Table 3 describes distinct characteristics of Twitter networks considered for experimentation.

Table 3.

Dataset characteristics studied in this work. Structural properties and some statistics from crawled data. Two distinct types of the network formed with total nodes (v) and edges (), along with derived parameters, including the number of connected components, maximum in-degree, maximum out-degree, average geodesic distance, and tweets crawled time.

Network Name		Type	v	e	Number of Connected Components	Maximum Degree		Average Geodesic Distance	Tweets Crawled Time
Twitter	#DelhiViolence	$\overrightarrow{G}$	15018	21509	925	80(Out-Degree)	3860(In-degree)	4.41	24-02-2020 to 25-02-2020
	#CoronavirusPandemic	$\overrightarrow{G}$	18473	22833	3143	44(Out-Degree)	1621(In-degree)	5.79	11-03-2020 to 12-03-2020

For the real-time investigation, Twitter profile data and allied connections against the two most trending hashtag were extracted using JavaScript Object Notation (JSON) and Twitter search REST Application Programming Interface (API) to fetch the required data which in turn forms a directed social network. To verify the effectiveness of our proposed measure precision, recall, and F1-measure validation methods are used. For performance comparison, five Twitter influence methods to identify influential nodes are considered: TweetRank [23], Popularity [1], PageRank, Out-Degree, and Eigenvector. These validation methods are computed on a distinct top-k set of k influential nodes identified by each method. Firstly, the reference list or set of influential users is generated which contains a unique values for matching the top-k set retrieved by each measure. New reference list is generated each time for distinct k value and it is represented as R_k. For instance, the top-k influential users identified by proposed WCI measure is denoted by N_k(WCI). Similarly, for other methods it is defined separately as N_k(TR), N_k(P), N_k(PR), N_k(OD), and N_k(E). Therefore, for cross-validation reference list is mathematically defined in Eq. (5):

$$R_k=N_k\left(WCI\right)\cap N_k\left(TR\right)\cap N_k\left(P\right)\cap N_k\left(PR\right)\cap N_k\left(OD\right)\cap N_k\left(E\right)$$ (5)

The precision is defined as the ratio of correctly identified number of influential users when matched to the reference list to the total number of influential users in the top-k set. Likewise, recall is the ratio of the correctly identified number of influential users to the total number of users that occurred in a particular reference list. The F1-measure is referred to the weighted average of precision and recall. Thus, accustomed version of validation methods for proposed WCI measure defined in the context of discovering prominent users are presented in Eqs. (6-8):

$$Precisio{n}_k=\frac{N_k\left(WCI\right)\cap R_k}{N_k\left(WCI\right)}$$ (6)

$$Recal{l}_k=\frac{N_k\left(WCI\right)\cap R_k}{R_k}$$ (7)

$$F{1}_k=\frac{2\times Precisio{n}_k\times Recal{l}_k}{Precisio{n}_k+Recal{l}_k}$$ (8)

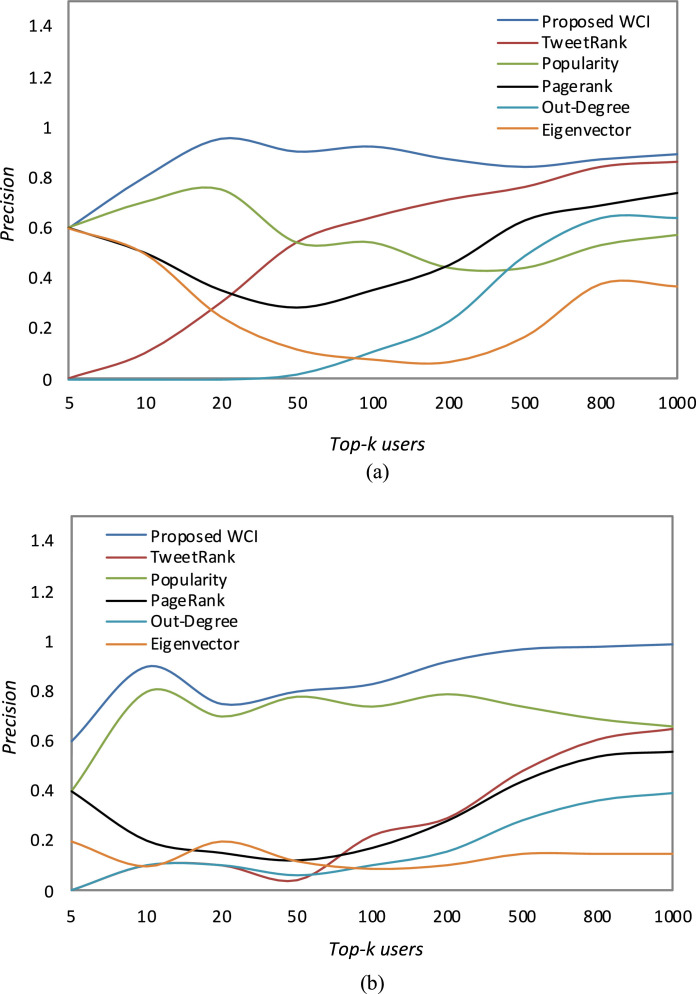
The experimental results for precision, recall, and F1 measure is accomplished for nine different k values $\left(k=5,10,20,50,100,200,500,800,1000\right)$ on both the datasets. Illustrations of experimental outcomes are shown in (Fig. 2, Fig. 3, Fig. 4 ). The highest precision value is obtained by our proposed WCI measure for both the datasets taken into consideration. Its value is mostly above 80% and also reaches between 92% to 99% when the value of k increases from 200 to 1000 in the case of Covid-19 trend, i.e. ${\overrightarrow{G}}_{\#CoronavirusPandemic}$. Next, we find that popularity measure achieves the second-best precision, and also its rank is uniform across both the datasets. Next, there is a flip case between TweetRank and PageRank measure i.e. their average precision is found out to be nearly the same. Moreover, TweetRank has the third rank in ${\overrightarrow{G}}_{\#CoronavirusPandemic}$and forth in ${\overrightarrow{G}}_{\#CoronavirusPandemic}$whereas, vice-versa is the case with PageRank. As k increases, TweetRank shows an upward trend, as in Fig. 2. (a). However, generally, in all the cases of measures, there is a somewhat upward-decline trend as the value of k increases. The lowest precision is of Eigenvector followed by the Out-Degree and vice-versa in both the datasets. The outcomes reveal that if only the trend-specific structural method is used alone it provides very little impact in discovering influential users. Furthermore, if only Tweet count is used to indicate influence score, it may not be that much viable. Moreover, the popularity measure which consumes only the followers i.e. fans count indicates important criteria for influencing. However, a combination of the impact of tweets, followers, following, lists, favorites along with trend-specific parameters has a greater ability to find out the influence score of a user over Twitter.

Fig. 2.

Performance comparison based upon precision for top-k computed by six influence measures including, proposed WCI, TweetRank, Popularity, PageRank, Out-Degree, and Eigenvector is shown for both Twitter (a) ${\overrightarrow{G}}_{\#DelhiViolence}$ & (b) ${\overrightarrow{G}}_{\#CoronavirusPandemic}$.

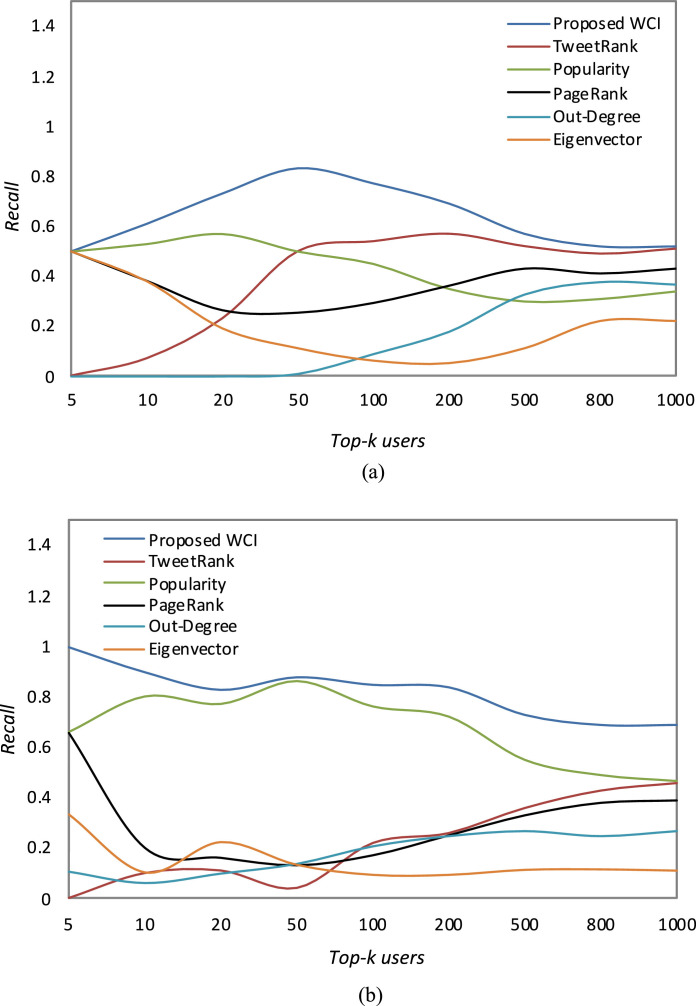
Fig. 3.

Performance comparison based upon recall for top-k computed by six influence measures including, proposed WCI, TweetRank, Popularity, PageRank, Out-Degree, and Eigenvector is shown for both Twitter (a) ${\overrightarrow{G}}_{\#DelhiViolence}$ & (b) ${\overrightarrow{G}}_{\#CoronavirusPandemic}$.

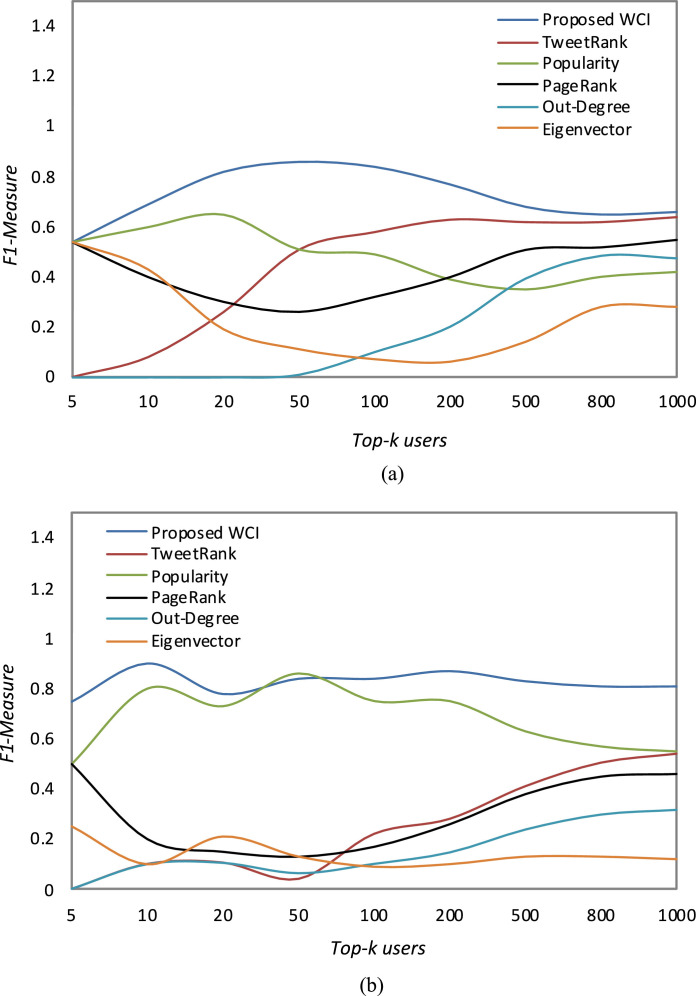
Fig. 4.

Performance comparison based upon F1 for top-k computed by six influence measures including, proposed WCI, TweetRank, Popularity, PageRank, Out-Degree, and Eigenvector is shown for both Twitter (a) ${\overrightarrow{G}}_{\#DelhiViolence}$ & (b) ${\overrightarrow{G}}_{\#CoronavirusPandemic}$.

The recall and F1 scores are also computed on the same parameters, like precision. Result illustrated in Fig. 3 (a-b) shows that the proposed WCI measure has the best recall value. Recall value is affected by the number of users in the reference list. So, as the value of k increases, there is a downwards trend seen in almost all the measures. A recall is increased if the top-k users identified by an algorithm matches maximum to the users occurred in the reference list i.e. R_k. Popularity gained the second rank uniformly followed by the TweetRank and PageRank respectively in case of ${\overrightarrow{G}}_{\#DelhiViolence}$. The lowest rank is achieved by Eigenvector trailed by Out-Degree. In case of Covid-19 dataset i.e. ${\overrightarrow{G}}_{\#CoronavirusPandemic}$, third rank though is of PageRank trailed by TweetRank but all remaining measures except popularity have very low recall value. When on average precision and recall are calculated, there is a huge difference between proposed WCI and popularity with TweetRank, Pagerank, Out-Degree, and Eigenvector. Next, the F1 measure is inclusive of both precision and recall. Experimental results for different values of k are demonstrated in Fig. 4 (a-b). From the outcomes, the proposed WCI measure outstrips all the other methods. Popularity gained the second rank among others whereas again there is a flip case for TweetRank and PageRank in both the datasets. The lowest performance is of Out-Degree and Eigenvector which concludes that influence is largely affected by timeline-based parameters but there is also an impact of a well-connected user in a trend activity subgraph. To reveal the influential user, we cannot rely only upon profile attributes; to unpick the social connections formed in the tweet-mention-retweet graph is having its own impact.

The influence score by our proposed WCI measure and the other measures considered in the grounds of comparison is computed for all the users lying in both the distinct datasets used for the study. Tables 4 and 5 highlights the rank outcome of the top 10 most influential users.

Table 4.

Twitter influence score statistics for ${\overrightarrow{G}}_{\#\mathit{Delh}\mathit{Viol}\mathit{ence}}$. Rank-wise order of top ten users with their node id is shown for six influence measures including proposed WCI measure, TweetRank, Popularity, PageRank, Out-Degree, and Eigenvector.

${\overrightarrow{G}}_{\#DelhiViolence}$
Influence Measures	Proposed WCI	TweetRank	Popularity	PageRank	Out-Degree	Eigenvector
Rank-wise User Id	1871	7758	2	1611	14857	1611
	14962	11887	14962	70	3105	9140
	2	4058	137	9140	3359	4635
	4059	13790	1871	149	3143	1296
	1873	10544	7071	4635	3146	7375
	6805	2583	6805	1296	3149	13200
	137	1178	27	7375	3140	14018
	1874	5817	55	2439	3147	9415
	7071	3384	1873	4	12478	12372
	7758	10075	1807	6126	2669	14627

Table 5.

Twitter influence score statistics for ${\overrightarrow{G}}_{\#CoronavirusPandemic}$. Rank-wise order of top ten users with their node id is shown for six Influence measures including proposed WCI measure, TweetRank, Popularity, PageRank, Out-Degree, and Eigenvector.

${\overrightarrow{G}}_{\#CoronavirusPandemic}$
Influence Measures	Proposed WCI	TweetRank	Popularity	PageRank	Out-Degree	Eigenvector
Rank-wise User Id	298	1700	298	7694	410	7694
	7694	11839	2225	797	10205	1171
	9	5216	1440	9	10952	454
	67	14145	9	801	4804	8172
	11214	13848	654	825	167	11213
	2225	7860	1450	891	18081	15062
	1440	8434	949	916	171	11381
	472	18081	11214	1064	17701	16372
	654	13230	21	930	9385	14213
	1450	6470	472	799	1796	10850

Correlation statistics of both the Twitter datasets are listed in Table 6 . Pearson's correlation score is computed among each distinct pair of six influence measures including proposed WCI. Therefore, 15 pairs are highlighted in the respective table. Statistics are computed by considering all the user's scores encountered in the underlying dataset. The highest correlation was found to be between proposed WCI and popularity measure i.e. 0.919 and 0.709 in the case of both the datasets. High positive value signifies that both the measures are positively correlated. Next, a pair of algorithms which are highly positively correlated are proposed WCI & TweetRank, and PageRank & Eigenvector. The results are varied for other pairs in both the datasets. Proposed WCI & PageRank are positively correlated to some extent in both the datasets but negative correlation with Out-degree in case of ${\overrightarrow{G}}_{\#\mathit{Coro}\mathit{navi}\mathit{rusP}\mathit{ande}\mathit{mic}}$ and with Eigenvector in case of ${\overrightarrow{G}}_{\#DelhiViolence}$. Interestingly, the PageRank influence measure is positively correlated with all the other five measures. In one and another case Out-Degree and Eigenvector seems to be negatively correlated with other methods except with PageRank. A negative correlation illustrates an inverse relationship among pairs to some extent.

Table 6.

Pearson's correlation statistics among six influence algorithms namely proposed WCI measure, TweetRank, Popularity, PageRank, Out-Degree, and Eigenvector for both the generated Twitter datasets is presented. A total of 15 potential pairs are shown.

Algorithms	${\overrightarrow{G}}_{\#\mathit{Delh}\mathit{Viol}\mathit{ence}}$	${\overrightarrow{G}}_{\#\mathit{Coro}\mathit{navi}\mathit{rusP}\mathit{ande}\mathit{mic}}$
Proposed WCI & TweetRank	0.686	0.257
Proposed WCI & Popularity	0.709	0.919
Proposed WCI & PageRank	0.017	0.358
Proposed WCI & Out-Degree	0.003	$-0.046$
Proposed WCI & Eigenvector	$-0.035$	0.184
TweetRank & Popularity	0.113	0.083
TweetRank & PageRank	0.113	0.017
TweetRank & Out-Degree	0.046	0.046
TweetRank & Eigenvector	$-0.031$	0.03
Popularity & PageRank	0.025	0.221
Popularity & Out-Degree	$-0.051$	$-0.07$
Popularity & Eigenvector	$-0.033$	0.09
PageRank & Out-Degree	0.012	0.029
PageRank & Eigenvector	0.525	0.511
Out-Degree & Eigenvector	$-0.021$	0.001

4. Conclusion

In this paper, a novel Twitter-based influence measure namely Weighted Correlated Influence (WCI) is proposed which generically combines the relative impact of ten different features categorized under two varied feature set i.e. Timeline and trend specific. Proposed work focuses on extracting the profile attributes along with the disclosure of hidden strength of the user buried under the social connections formed in the Twitter subgraph. The contribution of structural centrality measures is taken into account for computing the feature set. User influence score is calculated using five different measures and performance analysis is done by using three different validation methods namely precision, recall, and F1 score. Based upon the two datasets generated using globally trending hashtags, results shows that our proposed measure outperforms all other measures. It has been seen that the user who has many followers or has the highest tweet count does not necessarily be the most influential user. It has also been noted that if only the trend specific influence measures which consume dynamics of the graph i.e. mention, retweet and tweet subgraphs alone are not sufficient in uncovering the powerful users. Therefore, cumulating the impact of all these important parameters results in effectively addressing the problem of discovering influential users over Twitter. From a future perspective, more parameters can be explored and a better comprehensive list of features can be generated to compute the influence score. Moreover, the proposed approach can be redefined mathematically and reconnoitred over different micro-blogging platforms.

Declaration of Competing Interest

None.