Analysis of a mathematical model for COVID-19 population dynamics in Lagos, Nigeria

Abstract

This work examines the impact of various non-pharmaceutical control measures (government and personal) on the population dynamics of the novel coronavirus disease 2019 (COVID-19) in Lagos, Nigeria, using an appropriately formulated mathematical model. Using the available data, since its first reported case on 16 March 2020, we seek to develop a predicative tool for the cumulative number of reported cases and the number of active cases in Lagos; we also estimate the basic reproduction number of the disease outbreak in the aforementioned State in Nigeria. Using numerical simulations, we show the effect of control measures, specifically the common social distancing, use of face mask and case detection (via contact tracing and subsequent testings) on the dynamics of COVID-19. We also provide forecasts for the cumulative number of reported cases and active cases for different levels of the control measures being implemented. Numerical simulations of the model show that if at least 55% of the population comply with the social distancing regulation with about 55% of the population effectively making use of face masks while in public, the disease will eventually die out in the population and that, if we can step up the case detection rate for symptomatic individuals to about 0.8 per day, with about 55% of the population complying with the social distancing regulations, it will lead to a great decrease in the incidence (and prevalence) of COVID-19.

1. Introduction

The world is presently battling with ongoing outbreaks of a coronavirus disease, namely, coronavirus disease 2019 (COVID-19) caused by the novel coronavirus, SARS-COV2, a highly virulent virus that has caused COVID-19 to be a fatal disease, a disease which targets the human respiratory system. The pandemic started with a cluster of patients being admitted in late December 2019 to hospitals with an initial diagnosis of pneumonia and the patients were linked to a seafood and wet animal market in Wuhan, Hubei Province, China [32]. By January 2, 2020, 41 admitted hospital patients had been confirmed of being infected with COVID-19 [32]. By January 22, 2020, a total of 571 cases of COVID-19 were reported in 25 provinces in China [22], [32]. On January 30, 2020, about 7734 cases have been confirmed in China, with 90 cases reported in about 13 countries [4], [32] including the United States, India, Canada, France, Germany and the United Arab Emirates. As of May 27, 2020, 5,656,615 cases of COVID-19 have been reported worldwide, with about 355,355 deaths [12].

COVID-19 is transmitted from human-to-human via direct contact with contaminated surfaces and through the inhalation of respiratory droplets from infected individuals [3]. Presently, there is no vaccine or antiviral treatments approved for the prevention or management of COVID-19 [37]. To effectively reduce the spread of COVID-19, governments have been implementing different control meaures such as imposing strict, mandatory lockdowns, and encouraging (and in some cases strictly enforcing) other measures such as individuals maintaining a minimum distance between themselves (social distancing), avoiding crowded events, imposing a maximum number on individuals in any gathering (religious and social) and the use of face masks while in public [9]. To further help in mitigating the spread of COVID-19, contact tracing of suspected infected cases have been stepped up in several countries and detected cases (asymptomatic and symptomatic) are quickly placed on isolation for prompt treatment [9].

In Nigeria, the first (index) case of COVID-19 was announced on 27 February, 2020 [26]. As of May 27, 2020, Nigeria had reported 8733 cases of COVID-19, with 254 deaths, 5978 active cases (undergoing treatment) and 2501 discharged cases [26]. As of that same date, the city of Lagos, Nigeria (the epicenter of the disease in the country) had reported 4012 confirmed cases, with 47 deaths, 3220 active cases and 745 discharged cases [26]. However, it is imperative to clearly state that just 48,544 samples were tested that led to the detection of the cases in the country of Nigeria as a whole (a country of over 200 million persons), as of May 27, 2020 [26]. Hence, it is expected that, likely, several cases of COVID-19 remains undetected in the general population (whether in Nigeria or even in the city of Lagos, in particular), hereby rendering the announced figures as a gross underreporting of the actual burden of the disease in the country (Lagos, inclusive). Of course, it is expected that, with improved testing rates, more cases of COVID-19 will be detected and a clearer picture of the true state of the disease burden in Nigeria will become evident.

Mathematical models have long been used as tools in gaining insight into the dynamics of infectious diseases [11], [18], [27], [28], [30], [31], [33], [34], [35], [38]. Several mathematical models have already been formulated for the population dynamics of COVID-19 in several countries [1], [2], [13], [15], [17], [19], [20], [25], [36]. In this study, we will be presenting a mathematical model that investigates the impact of some control measures on the spread of covid-19 in a human population; the work will be looking critically at the situation in Lagos, Nigeria, hence we will be making use of data for the aforementioned city. The model, parameterized using the COVID-19 cumulative number of reported cases and the number of active cases for Lagos, will provide a realistic assessment of the burden of the disease for Lagos. Using the results from the quantitative study of the model, we will assess the impact of social distancing, use of face masks and case detection (via testing) on the disease burden in Lagos and make predictions for the cumulative number of reported cases and number of active cases as well as the likely peak time for the Lagos situation.

2. Model formulation

The total human population at time t, denoted by N_h(t), is split into a mutually exclusive sub-populations of susceptible humans (S(t)), exposed humans (E(t)), asymptomatic infectious humans (A(t)), symptomatic infectious humans (I(t)), detected infectious humans via testing (and are isolated and in some form of hospitalization for prompt treatment) (I_D(t)) and recovered humans (R(t)). Thus, $N_h\left(t\right)=S\left(t\right)+E\left(t\right)+A\left(t\right)+I\left(t\right)+I_D\left(t\right)+R\left(t\right)$. We assume that those in the I_D are completely isolated and do not come in contact with the general population.

The model for COVID-19 transmission dynamics in a population is given by the following system of deterministic non-linear differential equations in (2.1), with Table 1 describing the associated state variables and parameters in the model (2.1) while Fig. 1 gives the flow diagram of model (2.1).

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =& -\frac{{\beta }_c(\alpha A+I)}{N_h-I{}_D}S\hfill \\ \hfill \frac{dE}{dt}& =& \frac{{\beta }_c(\alpha A+I)}{N_h-I{}_D}S-\sigma E\hfill \\ \hfill \frac{dA}{dt}& =& \nu \sigma E-(\theta +{\gamma }_a)A\hfill \\ \hfill \frac{dI}{dt}& =& (1-\nu )\sigma E-(\psi +\gamma {}_O+d{}_O)I\hfill \\ \hfill \frac{dI{}_D}{dt}& =& \theta A+\psi I-({\gamma }_i+d{}_D)I{}_D\hfill \\ \hfill \frac{dR}{dt}& =& {\gamma }_{i}I{}_D+{\gamma }_{a}A+\gamma {}_{O}I.\hfill \end{array}$$ (2.1)

Mathemarical models without demographic parameters (that is, birth and natural death) of the form (2.1) have been used extensively in studying the dynamics of epidemics [6], [10], [18], [37], [41], [42]. Demographic parameters including births and natural deaths can be exluded when investigating the dynamics of an epidemic that is occuring within a few weeks or months [10], [16], [37], [41], [42]. If we introduce parameters that represents social distancing and the use of face masks into the force of infection of the basic model (2.1), whereby a new parameter δ represents the proportion of the population that maintains the minimum distance required to prevent an infection (at least 1 m apart), so that 0 ≤ δ ≤ 1, and another parameter ε represents the fraction of the entire population that effectively makes use of a face mask (where we assume that the face masks are with high efficacy), any time they are in public, so that 0 ≤ ε ≤ 1, the basic model (2.1) now becomes

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =\hfill & -\frac{{\beta }_c(1-\delta )(1-\epsilon )(\alpha A+I)}{N_h-I{}_D}S\hfill \\ \hfill \frac{dE}{dt}& =\hfill & \frac{{\beta }_c(1-\delta )(1-\epsilon )(\alpha A+I)}{N_h-I{}_D}S-\sigma E\hfill \\ \hfill \frac{dA}{dt}& =\hfill & \nu \sigma E-(\theta +{\gamma }_a)A\hfill \\ \hfill \frac{dI}{dt}& =\hfill & (1-\nu )\sigma E-(\psi +{\gamma }_o+d_o)I\hfill \\ \hfill \frac{dI{}_D}{dt}& =\hfill & \theta A+\psi I-({\gamma }_i+d_D)I{}_D\hfill \\ \hfill \frac{dR}{dt}& =\hfill & {\gamma }_{i}I{}_D+{\gamma }_{a}A+{\gamma }_{o}I.\hfill \end{array}$$ (2.2)

Table 1.

Description of variables and parameters in the model (2.1).

Variable	Interpretation
S	Susceptible humans
E	Exposed humans (infected but not infectious and show no sign of disease)
A	Asymptomatically-infectious humans (undetected)
I	Symptomatically-infectious humans (undetected)
ID	Detected infectious humans (asymptomatic and symptomatic) via testing
R	Recovered humans
Parameter	Interpretation
βc	Effective transmission rate
σ	Progression rate from exposed state to infectious state
ν	Fraction of new infectious humans that are asymptomatic
α	Modification parameter that accounts for the reduced infectiousness of humans
	in the A class when compared to humans in the I class
γa, γo, γi	Recovery rates for individuals in the A, I and ID classes, respectively
ψ	detection rate (via contact tracing and testing) for the I class
θ	detection rate (via contact tracing and testing) for the A class
d0, dD	Disease induced death rates for individuals in the I and $I{}_D$ classes, respectively

Fig. 1.

Schematic diagram of the model (2.1), where $\lambda =\frac{{\beta }_c(\alpha A+I)}{N_h-I{}_D}$.

It is imperative to state that, in the setting being considered in this work, the strict adoption of the use of face mask was being promoted well into the ongoing outbreaks in Nigeria, in particular the city of Lagos, after a five weeks total lockdown in the city was lifted.

3. Analysis of the model (2.2)

In this section, we seek to qualitatively study the dynamical properties of the COVID-19 model (2.2).

3.1. Basic properties of the model

3.1.1. Positivity and boundedness

For the model (2.2) to be epidemiologically meaningful, it is important to show that all its state variables are non-negative for all time (t) > 0 and that $\mathcal{D}$ is, indeed, bounded. We claim the following:

Theorem 3.1

Let the initial data for the model(2.2)be S(0) ≥ 0, E(0) ≥ 0, A(0) ≥ 0, I(0) ≥ 0, I_D(0) ≥ 0, R(0) ≥ 0

Then the solutions (S, E, A, I, I_D, R) of the model (2.2) are positive for all time t > 0.

Proof

Let $t_1=\sup \{t>0:S>0,E>0,A>0,I>0,I{}_D>0,R>0\in [0,t]\}$. Thus, t ₁ > 0.

We have, from the first equation of the system (2.2) that

$$\frac{dS}{dt}=-\lambda S,\text{where}\lambda =\frac{{\beta }_c(1-\delta )(1-\epsilon )(\alpha A+I)}{N_h-I{}_D}$$

which can be re-written as

$$\int \frac{dS}{dt}=-\int \lambda S$$

so that

$$S\left(t_1\right)=S\left(0\right)\exp [-\underset{0}{\overset{t_1}{\int }}\lambda \left(u\right)du]>0$$

Similarly, it can be shown that: $E>0,A>0,I>0,I{}_D>0,R>0.$

 □

Lemma 3.1

The region$\mathcal{D}=\{(S,E,A,I,I{}_D,R)\in {\mathfrak{R}}_{+}^6:N_h\le N_h\left(0\right)\}$is positively-invariant for the model(2.2)and attracts all positive solutions of the model.

Proof

Adding all the equations of the model (2.2) gives

$$\frac{d{N}_h}{dt}=-(d_{0}I+d_D{I}_D)$$

which can be re-written as

$$\frac{d{N}_h}{dt}\le -\delta N_h\text{with}\delta =min(d_0,d_D)$$

Thus:

$$\int \frac{d{N}_h}{N_h}\le \int -\delta dt$$

so that

$$N_h\left(t\right)\le N_h\left(0\right)e^{-\delta t}$$

N_h(t) approaches N_h(0) as t → ∞. Hence the region $\mathcal{D}$ attracts all solutions in ${\mathfrak{R}}_{+}^6$  □

3.2. Local asymptotic stability of the disease-free equilibrium (DFE) of the model (2.2)

The COVID-19 model (2.2) has a DFE, obtained by setting the right-hand sides of the equations in the model (2.2) to zero, given by

$$\begin{array}{cc}\xi {}_0=\hfill & (S^{*},E^{*},A^{*},I^{*},I_D^{*},R^{*})\hfill \\ =\hfill & (N_h\left(0\right),0,0,0,0,0)\hfill \end{array}$$ (3.1)

The linear stability of the disease free equilibrium, ξ ₀ can be established using the next generation operator method on the system (2.2). Using the notation in [39], the matrix F (of new infections) and the matrix V (of the transfer of individuals between compartments) are respectively, given by

$$F=\left(\begin{array}{cccc}0& \beta {}_C(1-\delta )(1-\epsilon )\alpha & \beta {}_C(1-\delta )(1-\epsilon )& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right),$$

$$V=\left(\begin{array}{cccc}\sigma & 0& 0& 0\\ -\nu \sigma & \theta +{\gamma }_a& 0& 0\\ -(1-\nu )\sigma & 0& \psi +\gamma {}_0+d{}_0& 0\\ 0& -\theta & -\psi & {\gamma }_i+d_D\end{array}\right)$$

Hence, it follows from [39] that the basic reproduction number of the model (2.2), denoted by ${\mathcal{R}}_c,$ is given by

$${\mathcal{R}}_C={\beta }_C(1-\delta )(1-\epsilon )[\frac{\nu \alpha }{\theta +{\gamma }_a}+\frac{1-\nu }{\psi +d_0+\gamma {}_0}].$$

We claim the following:

Theorem 3.2

The DFE,$\xi {}_0,$of the model(2.2)is locally asymptotically stable (LAS) if${\mathcal{R}}_c<1,$and unstable if${\mathcal{R}}_c>1$.

Proof

The local stability of the model (2.2) is analysed by the Jacobian matrix of the system (2.2) evaluated at the disease-free equilibrium $\xi {}_0,$ given by:

$$\left(\begin{array}{cccccc}0& 0& -{\beta }_c\alpha & -{\beta }_c& 0& 0\\ 0& -\sigma & {\beta }_c\alpha & {\beta }_c& 0& 0\\ 0& \nu \alpha & -(\theta +{\gamma }_a)& 0& 0& 0\\ 0& (1-\nu )\sigma & 0& -(\psi +{\gamma }_0+d_0)& 0& 0\\ 0& 0& \theta & \psi & -({\gamma }_i+d_D)& 0\\ 0& 0& {\gamma }_a& {\gamma }_0& {\gamma }_i& 0\end{array}\right)$$

The eigenvalues are given by ${\lambda }_1=-({\gamma }_i+d_D)$ and the solutions of the characteristic polynomial

$${\lambda }^3+{\Phi }_1{\lambda }^2+{\Phi }_2\lambda +{\Phi }_3=0,$$ (3.2)

where ${\Phi }_1=(\sigma +\theta +{\gamma }_a+\psi +{\gamma }_0+d_0),{\Phi }_2=\sigma (\theta +{\gamma }_a+\psi +{\gamma }_0+d_0)+(\theta +{\gamma }_a)(\psi +{\gamma }_0+d_0)-\nu \sigma {\beta }_c\alpha -(1-\nu )\sigma {\beta }_c,{\Phi }_3=\sigma (\theta +{\gamma }_a)(\psi +{\gamma }_0+d_0)(1-\mathcal{R}{}_C)$.

Applying the Routh-Hurwitz criterion, the cubic Eq. (3.2) will have roots with negative real parts if and only if Φ₁ > 0, Φ₃ > 0 and Φ₁Φ₂ > Φ₃. Clearly, Φ₁ > 0 and ϕ ₃ > 0 (if $\mathcal{R}{}_C<1$). As a result, the disease-free equilibrium, $\xi {}_0$ is locally asymptotically stable if $\mathcal{R}{}_C<1$. □

The threshold quantity ${\mathcal{R}}_c$ is the control reproduction number for the model (2.2). It represents the average number of secondary COVID-19 infections generated by a typical infectious individual (asymptomatic and symptomatic) in a completely susceptible population where control measures are present [39]. By Theorem 3.2, biologically speaking, COVID-19 can be eliminated from the population when ${\mathcal{R}}_c<1$ if the initial sizes of the population of the model are in the region of attraction of the DFE. The first term of ${\mathcal{R}}_c$ represents the average number of secondary infections generated by a typical asymptomatically infectious individual while the second term represents the average number of secondary infections generated by a typical symptomatically infectious individual.

3.3. Global asymptotic stability (GAS) of the disease free equilibrium (DFE) of the model (2.2)

Consider the Lyapunov function (the linear Lyapunov function has been widely used to prove the GAS of DFE [14], [29]):

$$\begin{array}{cc}\mathcal{L}\hfill & =\frac{(\psi +d{}_0+\gamma {}_0)\alpha \beta {}_C(1-\delta )(1-\epsilon )\nu +(\theta +{\gamma }_a)(1-\nu )\beta {}_C(1-\delta )(1-\epsilon )}{(\theta +{\gamma }_a)(\psi +d{}_0+\gamma {}_0)}E\hfill \\ & +\frac{\alpha \beta {}_C(1-\delta )(1-\epsilon )}{\theta +{\gamma }_a}A+\frac{\beta {}_C(1-\delta )(1-\epsilon )}{\psi +d{}_0+\gamma {}_0}I\hfill \end{array}$$

The time derivative is given by

$$\begin{array}{cc}\dot{\mathcal{L}}\hfill & =\frac{(\psi +d{}_0+\gamma {}_0)\alpha \beta {}_C(1-\delta )(1-\epsilon )\nu +(\theta +{\gamma }_a)(1-\nu )\beta {}_C(1-\delta )(1-\epsilon )}{(\theta +{\gamma }_a)(\psi +d{}_0+\gamma {}_0)}\dot{E}\hfill \\ & +\frac{\alpha \beta {}_C(1-\delta )(1-\epsilon )}{\theta +{\gamma }_a}\dot{A}+\frac{\beta {}_C(1-\delta )(1-\epsilon )}{\psi +d{}_0+\gamma {}_0}\dot{I}\hfill \end{array}$$

Substituting the expressions for the derivatives, $\dot{E},\dot{A}\text{and}\dot{I}$ from (2.2), into the Lyapunov derivative, $\dot{\mathcal{L}},$ and carrying out some algebraic manipulations, we have

$(\text{noting}\text{that}S\left(t\right)\le [N_h\left(t\right)-I{}_D\left(t\right)]\text{for}\text{all}\text{time},t)$

$$\begin{array}{cc}\dot{\mathcal{L}}\hfill & =\frac{\mathcal{R}{}_{\mathrm{0C}}(\alpha \beta {}_C(1-\delta )(1-\epsilon )A+\beta {}_C(1-\delta )(1-\epsilon )A)S}{N_h-I{}_D}-(\alpha \beta {}_C(1-\delta )(1-\epsilon )A\hfill \\ & +\beta {}_C(1-\delta )(1-\epsilon )A)\hfill \\ \hfill & \le (\alpha \beta {}_C(1-\delta )(1-\epsilon )A+\beta {}_C(1-\delta )(1-\epsilon )A)(\mathcal{R}{}_{\mathrm{0C}}-1)\hfill \end{array}$$

Hence, $\mathcal{L}<0$ if and only if $\mathcal{R}{}_C<1,$ and $\mathcal{L}=0$ if and only if $E=A=I=0$. Therefore, $\mathcal{L}$ is a Lyapunov function for the system (2.2). Thus, it follows by the La Salle’s Invariance Principle [21], that the DFE of the model (2.2) is globally asymptotically stable whenever $\mathcal{R}{}_C<1$.

4. Numerical simulations and results

In this section, we shall carry out uncertainty and sensitivity analyses on the parameters of the model due to uncertainties which may arise in the estimation of some of the parameters of the model. We also carry out numerical simulations of the model, in order to assess the impact of various control strategies on the dynamics of the disease. The equations of the model (2.2) are solved numerically using the MATLAB ode45 solver which is based on the fourth-order Runge-Kutta method. The stability of the method is well established in [23].

4.1. Uncertainty and sensitivity analysis

As a result of the uncertainties which may come up in parameter estimates used in the numerical simulations, a Latin Hypercube Sampling (LHS) [5] is implemented on the parameters of the model. For the sensitivity analysis, we carry out a Partial Rank Correlation Coefficient (PRCC) between values of the parameters in the response function and the values of the response function derived from the sensitivity analysis. 1000 simulations of the model (2.2) were run. Using the reproduction number, $\mathcal{R}{}_C,$ as the response function, it is observed in Table 2 that the top-ranked parameters that drive the dynamics of the model are transmission rate, $\beta {}_C,$ the case detection rates for asymptomatic and symptomatic infectious humans, θ and ψ, respectively, the modification parameter accounting for infectiousness of asymptomatic infectious humans, α. $\beta {}_C$ and α are positively correlated whereas θ and ψ are negatively correlated. The public health implication of this is that, COVID-19 can be controlled effectively in the population by reducing the transmission rate, achieved through preventive measures like strict social distancing regulations and compulsory face-masks wearing in public, and also reducing the infectiousness of asymptomatic humans through proper treatment. In addition, the disease burden can be significantly reduced in the population if efforts are put in place to step up detection rates for asymptomatic and symptotic infectious humans so as to isolate and offer them adequate treatment.

Table 2.

ePRCC values for the model (2.1) parameters using the total number of infected individuals and the reproduction number, $\mathcal{R}{}_C,$ as response functions. Parameters which strongly influence the dynamics of the model with respect to each of the response functions are shown in bold fonts.

Parameters	E	A	I	$I{}_D$	$\mathcal{R}{}_C$
$\beta {}_C$	0.9169	0.5601	0.5426	0.6205	0.9342
θ	−0.2273	−0.8068	−0.1703	0.6167	−0.5721
ψ	−0.6288	−0.2266	−0.9497	0.7729	−0.7656
α	0.3620	0.1591	0.2000	0.1728	0.6610
γa	−0.0303	−0.2526	0.08597	−0.2098	−0.0967
γo	0.3231	0.0822	−0.0097	−0.2854	−0.1698
d0	0.1113	−0.0512	−0.1094	−0.0785	−0.0784
ν	0.0364	0.8994	−0.8442	−0.0040	−0.3490
σ	−0.6068	0.6903	0.6524	0.5775	−
γi	0.1448	0.0781	0.0699	−0.6961	−
dD	0.1747	0.1487	0.2146	−0.3579	−

Using the exposed class, E, as response function, the parameters that strongly influence the dynamics of the disease are the effective contact rate, $\beta {}_C,$ the case detection rate for symptomatic infected, ψ and the transition rate out of the exposed class, σ. Also, when the total number of asymptomatic infectious, A, is used as the response function, the parameters that strongly dominate the dynamics of COVID-19 disease are the transmission rate, $\beta {}_C,$ the fraction of exposed individuals who progress to the asymptomatic stage, ν, the transition rate out of the exposed class, σ and the detection rate for asymptomatic infectious humans, θ. Using the population of symptomatic infectious humans, I, as the response function, the top-ranked parameters that drive the dynamics of the disease are the transmission rate, $\beta {}_C,$ the transition rate out of the exposed class, σ, the detection rate for asymptomatic humans, ψ and the fraction of exposed humans who progress to asymptomatic stage, ν. Moreover, using the population of detected infectious humans, $I{}_D,$ as the response function the five top-ranked parametrs that drive the dynamics of the disease are the transmission rate, $\beta {}_C,$ the detection rates for asymptomatic and symptomatic infectious, ψ and θ, respectively, the transition rate out of exposed class, σ and the recovery rate for detected infectious humans, γ_i.

4.2. Baseline values of the parameters for model (2.2)

We now apply our model (2.2) to study the dynamics of COVID-19 in the city of Lagos, Nigeria. We will be making use of the outbreak data released daily by the Nigeria Center for Disease Control (NCDC) [26]. Specifically, we will use the cumulative number of reported cases and the number of active cases for our data and model fitting since the reported cumulative number of deaths is relatively small to give a good fit for parameter estimation. We implement our model and conduct numerical simulations for an epidemic period starting from when the index case was announced in Lagos, i.e., March 16, 2020 to May 2, 2020, two days before a total city-wide lockdown was lifted (and replaced with a partial lockdown with strict measures on enforcing social distancing and the use of face masks when in public).

The incubation period for COVID-19 is estimated to average 5.2 days [32], with a range of 3 to 14 days, so that we set $\sigma =1/5.2$. The relatively infectiousness of asymptomatically infected individuals when compared to symptomatic individuals is still unknown; however, several studies have assumed that transmissibility of asymptomatic infection was 0.5 times that of symptomatic infections [8], hence we set $\alpha =0.5$. The fraction of infectious cases that are asymptomatic is uncertain; however some studies have suggested setting this to 0.5 [8], hence we set $\nu =0.5$. The average recovery period is about 15 days [7], [8], so that we set ${\gamma }_i=1/15$. We also set the natural recovery rates 0.13978 per day, so that ${\gamma }_a={\gamma }_o=0.13978$ [37], although the value 0.111 was used in [1]. The disease induced death rates was set to 0.015, following the work in [13], so that $d_o=d_D=0.015$.

We estimate the following parameters in model (2.2) by fitting the model with the daily cumulative number of reported cases and number of active cases: the transmission rate (β_c), the case detection rate for the asymptomatic individuals (θ) and the case detection rate for the symptomatic individuals (ψ). We will also estimate the initial number of infected individuals (latent and infectious) as at the time the index case was reported for Lagos, on March 16, 2020 i.e., E(0), A(0) and I(0).

We have that the total population of Lagos is estimated to be 14,368,332 [40]. Hence, since the first case was announced in March 16, 2020 (the start period for all the simulations herein), we set our initial conditions to be $S\left(0\right)=14,367,982,$ $I_D\left(0\right)=1$ and $R\left(0\right)=0,$ taking into account the fact that, as at the date of the first reported infected case, it is expected that some undetected infected within the population (since wide spread population screening and testing for COVID-19 had not begun at the time). Therefore, as stated above, it is imperative to estimate the likely values of the other initial conditions, namely, E(0), A(0) and I(0).

Table 3 gives the values of the parameters used in the simulations.

Table 3.

Values of parameters in the model (2.1).

Parameter	Baseline value	Range	Reference
βc	Fitted		Estimated
α	0.5 /day	[0,1]/day	[8]
ν	0.5 /day	[0,1]/day	[8]
σ	$\frac{1}{5.2}$ /day	$[\frac{1}{14},\frac{1}{3}]$ /day	[32]
θ	Fitted /day		Estimated
ψ	Fitted /day		Estimated
γi	$\frac{1}{15}$ /day	$[\frac{1}{30},\frac{1}{3}]$ /day	[7], [8]
${\gamma }_a={\gamma }_o$	0.13978 /day	$[\frac{1}{30},\frac{1}{3}]$ /day	[37]
$d_o=d_D$	0.015 /day	[0.001 - 0.1]	[13]

4.3. Model fitting

The model fitting was performed using a genetic algorithm (GA) [24] for our function optimizer, implemented in MATLAB; the GA algorithm helps us find the correct basin of attraction, which provides the starting values (for the parameters being estimated) for use in the fmincon function in the Optimization Toolbox of MATLAB. Hence, we will be combining two optimization algorithms for data fitting, a GA algorithm and the fmincon algorithm in MATLAB to get a more accurate estimate. We implement our model fitting for an epidemic period starting from when the index case was announced in Lagos, i.e., March 16, 2020 to May 2, 2020.

Most of the days captured in the model fitting for Lagos was for the period when there was a government imposed lockdown in the city (from March 30, 2020 to May 3, 2020). Hence, the impact of the lockdown on the dynamics of the disease in Lagos will inherently be captured in the transmission rate of the disease (β_c).

Using the data available for the daily cumulative number of reported cases and number of active cases, we seek to estimate the values of β_c, ψ, θ, and the initial conditions E(0), A(0) and I(0). It is imperative to state, that the reported number of COVID-19 cases in Lagos is from a population that has only had very small number of tests carried out, thereby resulting in a likely gross under-reporting of the actual disease burden in the population. Also, all fittings were done with $\delta =0$ and $\epsilon =0,$ since during the period being fitted in this work, both measures (social distancing when in public and the use of face masks) were not strictly monitored or enforced until after a partial lockdown (which was a relaxing of the previous ‘total’ 24 h lockdown, with debatable level of compliance from the entire population) was introduced starting from May 4, 2020. The values of other parameters of the model (2.2), used in all simulations herein, are as stated in Table 3.

We observe that we had, approximately, the same fitted values for β_c, ψ and θ, as well as the calculated disease reproduction number (R_c), when we used the cumulative number of reported cases, the number of active cases and when we combined both datasets for the model fitting. However, there were significant differences in the estimated values of E(0), A(0) and I(0). Table 4 gives the estimated values of β_c, ψ, θ, and the initial conditions E(0), A(0) and I(0), together with the calculated reproduction number (R_c), when we used the cumulative number of reported cases, the number of active cases and both sets of data for fitting the model; we make use of the following notations:

• I: Cumulative Number of Reported Cases (detected after testing).
• II: Number of Active Cases.
• III: Cumulative Number of Reported Cases and the Number of Active Cases.

Table 4.

Estimated parameters fitted using three different data sets.

	I	II	III
βc	0.4236	0.4410	0.4385
θ	$1.8999\times {10}^{-12}$	$4.2719\times {10}^{-11}$	$2.3752\times {10}^{-4}$
ψ	0.0135	0.0264	0.0059
E(0)	441	610	1234
A(0)	188	10	10
I(0)	212	52	470
Rc	2.0161	2.0060	2.1469

As seen from Table 4, the estimated parameters β_c, ψ and θ, as well as the calculated disease reproduction number (R_c), are approximately the same (for the three different datasets used for the model fitting); however, there are significant differences in the estimated values of the initial values E(0), A(0) and I(0). It is very imperative to state that, as at the time when the first detected case was announced in Lagos (16 March, 2020), it will be difficult to determine the exact number of individuals in the population who were already infected with COVID-19. Hence, we are not surprised that the model fitting carried out using the above 3 different data sets gave different values for the initial conditions (even though each set of estimated parameters and initial conditions resulted in good model fits with the actual data).

These differences in the initial conditions (E(0), A(0) and I(0)), expectedly, affected the values of the projections (future predictions) made with regards to the likely number of infected individuals (asymptomatic and symptomatic) who are yet to be detected (via testing), the cumulative number of reported cases and the number of active cases, as we shall see in the numerical simulation results in the following subsections.

4.3.1. Results when data and model fitting was done using the cumulative number of reported cases

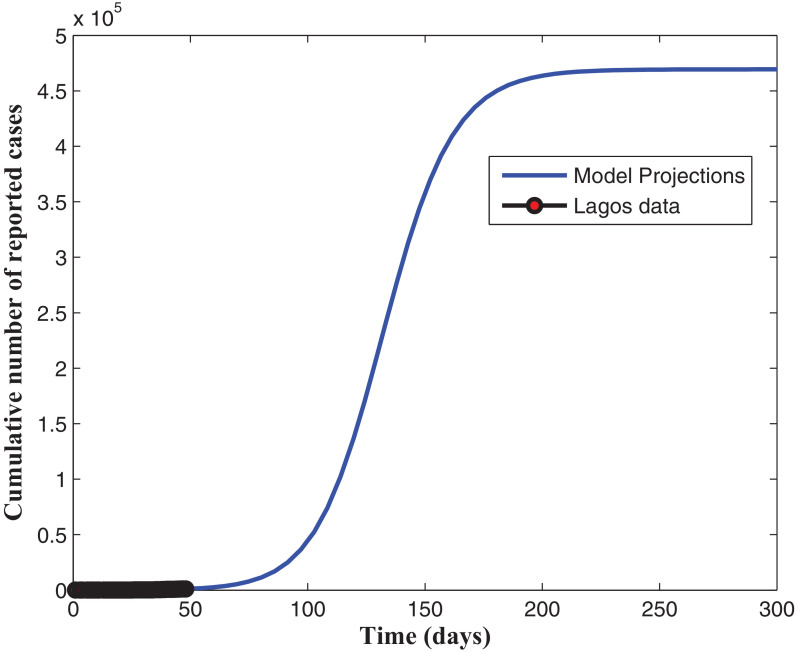
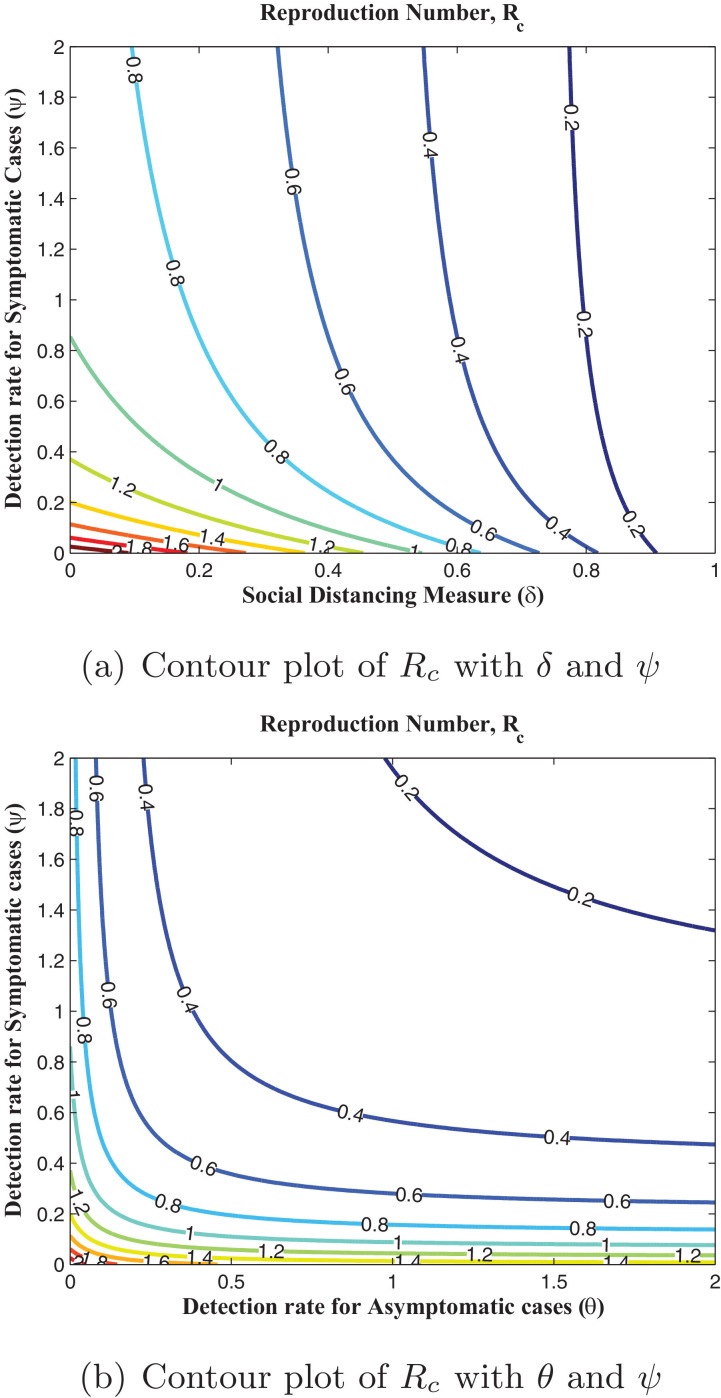
In this section, simulations of the model when fitted using the daily cumulative number of reported cases for Lagos, from March 16, 2020 to May 2, 2020 are presented. It is appropriate to note, except otherwise stated, that all fittings were done with $\delta =0$ and $\epsilon =0$ as explained in Section 4.3. Fig. 2 shows that our model fitted well with the Lagos data (daily cumulative number of reported cases). The projection in Fig. 3 reveals that, without enforcing the social distancing regulation and the use of face masks, when in public places, with the present case detection rates (for asymptomatic and asymptomatic infectious individuals), the daily cumulative number of reported cases may get up to 460,000 in 300 days (from March 16, 2020). As seen in Fig. 4 , an increase in the detection rate for symptomatic humans resulted in an increase in the number of active and an expected decrease in the number of undetected symptomatic cases, with the peak period varying between 130 and 150 days (counting from March 16, 2020). The simulation results depicted in Fig. 5 (a) shows two pandemic peaks: the first occuring between 120 and 150 days (counting from March 16, 2020), when the social distancing regulations and face-mask usage are not enforced in the population and the second occuring after 200 days (by the end of September, 2020), when 20% of the population observe only face-mask usage as a preventive measure. However, Fig. 5(b) shows that if 20% of the population complied with only the social distancing regulation from the beginning (starting from March 16, 2020), then we observe an infection peak after 200 days (by the end of September, 2020). Moreso, if 20% complied with both the social distancing regulations and face-mask usage, then infection peak occurs between 330 and 360 days (counting from March 16, 2020), as depicted by Fig. 5(b). It is important to note that infection peaks are lower and takes longer time to attain when social distancing regulation compliance and face-mask usage are combined than when they are not. Fig. 6 (a) shows that if at least 55% of the population comply with the social distancing regulation with about 55% of the population effectively making use of face masks while in public, the reproduction number of the disease can be brought below 1, which indicates that the disease will eventually die out in the population. Fig. 6(b) reveals that, if we can step up the case detection rate for symptomatic individuals to about 0.8 per day, with about 55% of the population complying with the social distancing regulations, we can also get the reproduction number of the disease below 1, with a great decrease in the incidence (and prevalence) of COVID-19 guaranteed. In addition, Fig. 7 (a) reveals that if the detection rate for symptomatic humans can be up to 0.5 per day, then if at least 55% of the population comply with the social distancing regulation while in public, the reproduction number of the disease can be brought below 1, indicating that the disease will eventually die out in the population. Fig. 7(b) reveal that, if we can step up the case detection rate for symptomatic individuals to about 0.8 per day, with about 0.5 case detection rate for asymptomatic individuals, we can equally bring the reproduction number of the disease below unity, with a great decrease in the incidence (and prevalence) of COVID-19 certain.

Fig. 2.

Fitting the cumulative number of reported cases.

Fig. 3.

Projections for the cumulative number of reported cases.

Fig. 4.

active and symptomatic (undetected): effect of ψ.

Fig. 5.

Effect of social distancing measure and face mask usage.

Fig. 6.

Contour plots of R_c.

Fig. 7.

Contour plots of R_c.

4.3.2. Results when data and model fitting was done using the number of active cases

In this section, simulations of the model when fitted using the daily cumulative number of active cases for Lagos, from March 16, 2020 to May 2, 2020 are presented. Please note, except otherwise stated, all fittings were done with $\delta =0$ and $\epsilon =0$ as explained in Section 4.3.

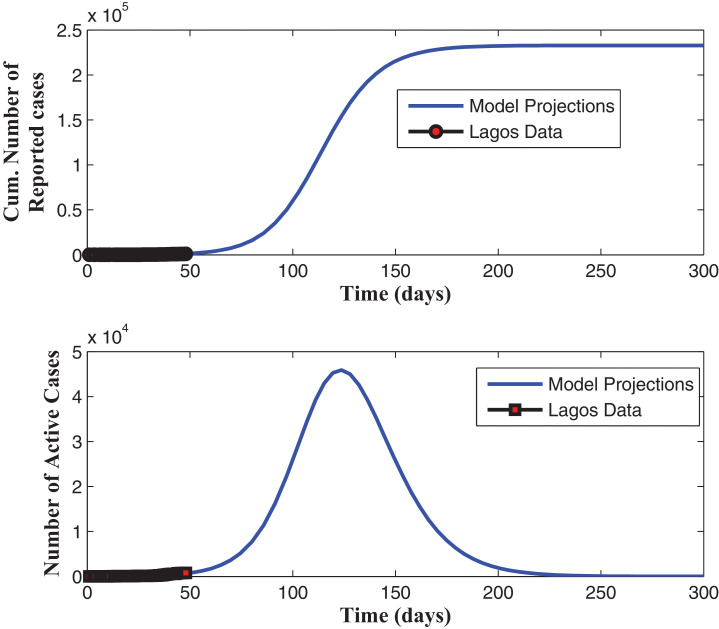
Fig. 8 shows that our model fitted well with the Lagos data (daily cumulative number of active cases). The projection in Fig. 9 , when the cumulative number of active cases are used to fit the model, reveals also that, without enforcing the social distancing regulation and the use of face masks, when in public places, and with the present case detection rates (for asymptomatic and asymptomatic infectious individuals), the daily cumulative number of active cases may get up to 160,000 by mid August, 2020. It is observed in Fig. 10 , that an increase in the detection rate for symptomatic humans led to an increase in the number of reported cases and an expected decrease in the number of undetected symptomatic cases, with the peak period varying between 130 and 150 days (counting from March 16, 2020), before the curve flattens. The simulation results depicted in Fig. 11 (a) shows two pandemic peaks: the first occuring between 120 and 150 days (counting from March 16, 2020), when the social distancing regulations and face-mask usage are not enforced in the population and the second occuring after 200 days (by the end of September, 2020), when 20% of the population observe only face-mask usage as a control measure. However, Fig. 11(b) shows that if 20% of the population complied with only the social distancing regulation from the beginning (starting from March 16, 2020), then we observe an infection peak after 200 days (by the end of September, 2020). Moreso, if 20% complied with both the social distancing regulations and face-mask usage, then a lower infection peak occurs between 330 and 360 days (counting from March 16, 2020), as depicted by Fig. 11(b). It is interesting to note here, that the peak figures vary in comparison to when the cumulative number of reported cases are used to estimate the parameters and initial conditions. Fig. 12 (a) reveals that if face-masks are effectively used by at least 55% of the population and at least 55% of the population observe strict social distancing rule in public then the disease will be effectively eliminated from the population. Fig. 12(b) shows that, if we can step up the case detection rate for asymptomatic individuals to about 0.8 per day, with about 55% of the population complying with the social distancing regulations, we can also get the reproduction number of the disease below 1, with a great decrease in the incidence (and prevalence) of COVID-19 guaranteed. Fig. 13 (a) reveals that, if we can step up the case detection rate for symptomatic individuals to about 0.9 per day, with about 50% of the population complying with the social distancing regulations, we can also get the reproduction number of the disease below unity. In addition, Fig. 13(a) reveals that if the detection rate for symptomatic humans can be up to 0.5 per day, then if at least 55% of the population comply with the social distancing regulation while in public, the reproduction number of the disease can be brought below 1, indicating that the disease will eventually die out in the population. Fig. 13(b) reveal that, if we can step up the case detection rate for symptomatic individuals to about 0.8 per day, with about 0.5 case detection rate for asymptomatic individuals, we can equally bring the reproduction number of the disease below unity, with a great decrease in the incidence (and prevalence) of COVID-19 certain.

Fig. 8.

Fitting the number of active cases.

Fig. 9.

Projections for the number of active cases.

Fig. 10.

active and symptomatic (undetected): effect of ψ.

Fig. 11.

Effect of social distancing measure and face mask usage.

Fig. 12.

Contour plots of R_c.

Fig. 13.

Contour plots of R_c.

4.3.3. Results when data and model fitting was done using the cumulative number of reported cases and the number of active cases

In this section, simulations of the model when fitted using the daily cumulative number of reported cases and the number of active cases for Lagos, from March 16, 2020 to May 2, 2020 are presented. It is imperative to note, except otherwise stated, that all fittings were done with $\delta =0$ and $\epsilon =0$ as explained in Section 4.3. As shown in Fig. 14 , our model fit well to the Lagos data, when the cumulative number of reported cases and the number of active cases are simulataneously used to fit the model. The cumulative number of reported cases and active cases are projected to attain their peak figures of 240,000 and 48,000, respectively, by mid July, 2020, when preventive measures like the social distancing rule and face-mask wearing in public are not strictly enforced (Fig. 15 ). It is observed from Fig. 16 that cumulative number of reported and active cases increase steadily, while the undetected asymptomatic and symptomatic infectious cases reduce, as efforts are intensified to increase detection of new cases (via testing). Simulations of the total number of infected humans at different detection rates for asymptomatic and symptomatic infected are depicted in Fig. 16. It is observed that as detection rate for symptomatic infected is stepped up, more confirmed cases are identified and isolated for adequate treatment. In Fig. 17 , different infection peaks are observed for reported and active COVID-19 cases, between 100 and 200 days (from March 16, 2020). The simulation results depicted in Fig. 18 (a) shows two pandemic peaks: the first occuring after 150 days (by mid August, 2020), when the social distancing regulations and face-mask usage are not enforced in the population and the second occuring after 180 days (by mid September, 2020), when 20% of the population observe only face-mask usage as a preventive measure. However, Fig. 18(b) shows that if 20% of the population complied with only the social distancing regulation from the beginning (starting from March 16, 2020), then we observe an infection peak between 180 and 200 days (counting from March 16, 2020). Moreso, if 20% complied with both the social distancing regulations and face-mask usage, then infection peak occurs between 220 and 300 days (counting from March 16, 2020), as depicted by Fig. 18(b). It is observed that Infection peaks are lower than the peaks reported when social distancing regulations are not complied with. It is also imperative to note, that the peak figures vary in comparison to when the cumulative number of reported or active cases are used to estimate the parameters and initial conditions of the model. Fig. 19 shows that if 60% of the population comply with the social distancing regulations and effectively use face-masks in public and detection rates stepped up to 0.9 per day, then we can get the reproduction number below unity and the burden of the disease brought very low. Similar conclusions are reached for the plots in Fig. 20 .

Fig. 14.

Fitting the cumulative number of reported cases and active cases.

Fig. 15.

Projections for the cumulative number of reported cases and active cases.

Fig. 16.

effect of ψ.

Fig. 17.

effect of ψ.

Fig. 18.

Effect of social distancing measure and face mask usage.

Fig. 19.

Contour plots of R_c.

Fig. 20.

Contour plots of R_c.

4.4. Remarks on the impact of variations in the initial conditions for the model fitting

In this section, we want to demonstrate the fact that, while different data fitting runs, using the optimization routines implemented in this work, the significant difference in the values of the initial conditions (E(0), A(0) and I(0)) gave markedly different projections for the number of cumulative reported cases and the number of active cases, even when the different runs gave good model fits to the data being used. Please note, except otherwise stated, all fittings were done with $\delta =0$ and $\epsilon =0$ as explained in Section 4.3.

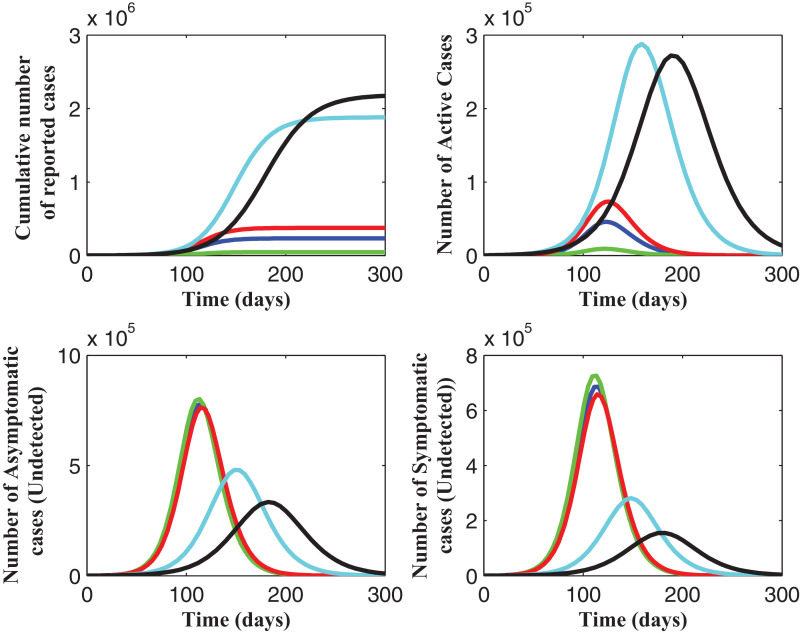
Table 5 shows the values of the estimated parameters when the model was fitted using the cumulative number of reported cases. These estimates were from the six ‘best fits’ after multiple runs of both the GA and the fmincon optimization routines; all estimates resulted in a very good match between the data and the numbers from the simulated model. As seen from Fig. 21 , as these parameter values (the estimated values in Table 5) are used to make future projections on the cumulative number of reported cases for 300 days, starting from March 16, 2020, we see the significant differences in the projections, which is due to the differences in the values of the estimated (unknown) initial number of exposed individuals (E(0)) and infectious individuals (asymptomatic and symptomatic, A(0) and I(0), respectively) in the population at the time the first reported case was announced on the start day of the simulation results herein.

Table 5.

Estimated parameters when the model (2.2) was fitted using the cumulative number of reported cases. These estimates were from the six ‘best fits’.

Colour Code in Fig. 21	βc	θ	ψ	E(0)	A(0)	I(0)	Rc
Magenta (Fitted 1)	0.4603	$4.2719\times {10}^{-11}$	0.0430	198	24	64	1.9872
Blue (Fitted 2)	0.4701	$1.1815\times {10}^{-10}$	0.0523	183	10	50	1.9763
Green (Fitted 3)	0.4346	$3.2611\times {10}^{-10}$	0.0222	279	110	131	2.0051
Red (Fitted 4)	0.4236	$1.8999\times {10}^{-12}$	0.0135	441	188	212	2.0161
Black (Fitted 5)	0.4239	$1.9249\times {10}^{-11}$	0.0135	440	185	213	2.0175
Cyan (Fitted 6)	0.4692	$2.9163\times {10}^{-12}$	0.0513	186	10	51	1.9778

Fig. 21.

Estimated parameters when the model (2.2) was fitted using the cumulative number of reported cases. The dark, red circles (at the beginning of the simulation) represents the actual data. These estimates were from the six ‘best fits’. See Table 5. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 6 shows the values of the estimated parameters when the model was fitted using the number of active cases. These estimates were from the five ‘best fits’ after multiple runs of both the GA and the fmincon optimization routines; all estimates resulted in a very good match between the data and the numbers from the simulated model. These parameter values (the estimated values in Table 6) were used to make future projections on the number of active cases for 300 days, starting from March 16, 2020. Again, as seen from Fig. 22 , just as was observed when we performed data fitting using the cumulative number of reported cases (Table 5 and Fig. 21), we see the significant differences in the projections, which is due to the differences in the values of the estimated (unknown) initial number of exposed individuals (E(0)) and infectious individuals (asymptomatic and symptomatic, A(0) and I(0),

Table 6.

Estimated parameters when the model (2.2) was fitted using the number of active cases. These estimates were from the five ‘best fits’.

Colour Code in Fig. 21	βc	θ	ψ	E(0)	A(0)	I(0)	Rc
Magenta (Fitted 1)	0.4410	$4.2719\times {10}^{-11}$	0.0264	610	10	52	2.0060
Blue (Fitted 2)	0.4661	$4.1215\times {10}^{-10}$	0.0396	361	10	50	2.0324
Green (Fitted 3)	0.4648	$1.4271\times {10}^{-10}$	0.0386	370	10	51	2.0332
Red (Fitted 4)	0.4675	0.0114	0.0290	235	10	89	2.0446
Black (Fitted 5)	0.4544	0.0061	0.0162	325	63	165	2.1074

Fig. 22.

Estimated parameters when the model (2.2) was fitted using the number of active cases. The dark, red circles (at the beginning of the simulation) represents the actual data. These estimates were from the five ‘best fits’. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 7 shows the values of the estimated parameters when the model was fitted using the cumulative number of reported cases and the number of active cases. These estimates were from the seven ‘best fits’ after multiple runs of both the GA and the fmincon optimization routines; all estimates resulted in a very good match between the data and the numbers from the simulated model. These parameter values (the estimated values in Table 7) were used to make future projections on the number of active cases for 300 days, starting from March 16, 2020. Again, as seen from Fig. 23 , just as was observed in the two previous cases above (in this subsection), we see the significant differences in the projections, which is due to the differences in the values of the estimated (unknown) initial number of exposed individuals (E(0)) and infectious individuals (asymptomatic and symptomatic, A(0) and I(0),

Table 7.

Estimated parameters when the model (2.2) was fitted using the cumulative number of reported cases and the number of active cases. These estimates were from the seven ‘best fits’.

Colour Code in Fig. 21	βc	θ	ψ	E(0)	A(0)	I(0)	Rc
Magenta	0.4502	$4.2415\times {10}^{-11}$	0.0236	426	10	100	2.0668
Blue	0.4721	$7.8119\times {10}^{-11}$	0.0432	245	10	55	2.0366
Green	0.4767	$1.2689\times {10}^{-12}$	0.0476	225	10	50	2.0301
Red	0.4724	$2.2179\times {10}^{-11}$	0.0435	241	12	56	2.0359
Black	0.4613	$4.2414\times {10}^{-4}$	0.0273	296	25	102	2.0895
Cyan	0.4385	$2.3752\times {10}^{-4}$	0.0059	1234	10	470	2.1469
Yellow	0.4566	$3.2989\times {10}^{-11}$	0.0257	352	16	102	2.0815

Fig. 23.

Estimated parameters when the model (2.2) was fitted using the cumulative number of reported cases and the number of active cases. The dark, red circles (at the beginning of the simulation) represents the actual data. These estimates were from the seven ‘best fits’. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

It is important to state that we picked the ‘best fit’ with the lowest figures (peaks and cumulative values) for the numerical simulations and parameter estimations used in Sections 4.3.1 to 4.3.3.

5. Discussions

Based on the model fitting that was carried out in this work, with three sets of data, we observe an approximately similar estimates for the β_c, ψ, θ and the control reproduction number R_c but some significant variations for the initial values of individuals in the E, A and I classes. Fig. 2, Fig. 8 and 14 showed that our model fits well to the data, irrespective of the data set used. However, we observed that the significant difference in the values of the initial conditions (E(0), A(0) and I(0)) gave markedly different projections for the number of cumulative reported cases and the number of active cases, even when the different runs gave good model fits to the data being used (as shown in Fig. 3, Fig. 9 and 15). This strongly reveals that our lack of knowledge and understanding of how long community transmission may have been going on in the population (as at the time the first (index) case was announced on March 16, 2020) could hinder our knowledge of the actual burden of COVID-19 in Lagos. Hence, very strict measures must be taken to identify other cases as quickly as possible, through aggressive screening and testing of the population, especially for asymptomatic cases, and strict enforcement of the other control measures.

6. Conclusion

This work has revealed the impact of different non-pharmaceutical control measures on the population dynamics of the novel coronavirus disease 2019 (COVID-19) in Lagos, Nigeria, using an appropriately formulated mathematical model. Using the available data, since its first reported case on 16 March 2020, we developed a predicative tool for the cumulative number of reported cases and the number of active cases in Lagos; we also estimated the basic reproduction number of the disease outbreak in the aforementioned State in Nigeria. Using numerical simulations, we showed the effect of control measures, specifically the common social distancing, use of face mask and case detection (via contact tracing and subsequent testings) on the dynamics of COVID-19. We also provided forecasts for the cumulative number of reported cases and active cases for different levels of the control measures being implemented. Numerical simulations of the model show that if at least 55% of the population comply with the social distancing regulation with about 55% of the population effectively making use of face masks while in public, the disease will eventually die out in the population and that, if we can step up the case detection rate for symptomatic individuals to about 0.8 per day, with about 55% of the population complying with the social distancing regulations, it will lead to a great decrease in the incidence (and prevalence) of COVID-19.

Therefore, to curtail the spread of COVID-19 at the community level, this study recommends, as a matter of urgency, very strict measures to be taken by policy makers and those in authority to identify new cases, through aggressive screening and testing of the population and strict enforcement of the use of face-masks and the social distancing regulations.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.