Retrieving neuronal orientations using 3D scanning SAXS and comparison with diffusion MRI

Abstract

While diffusion MRI (dMRI) is currently the method of choice to non-invasively probe tissue microstructure and study structural connectivity in the brain, its spatial resolution is limited and its results need structural validation. Current ex vivo methods employed to provide 3D fiber orientations have limitations, including tissue-distorting sample preparation, small field of view or inability to quantify 3D fiber orientation distributions. 3D fiber orientation in tissue sections can be obtained from 3D scanning small-angle X-ray scattering (3D sSAXS) by analyzing the anisotropy of scattering signals. Here we adapt the 3D sSAXS method for use in brain tissue, exploiting the high sensitivity of the SAXS signal to the ordered molecular structure of myelin. We extend the characterization of anisotropy from vectors to tensors, employ the Funk-Radon-Transform for converting scattering information to real space fiber orientations, and demonstrate the feasibility of the method in thin sections of mouse brain with minimal sample preparation. We obtain a second rank tensor representing the fiber orientation distribution function (fODF) for every voxel, thereby generating fODF maps. Finally, we illustrate the potential of 3D sSAXS by comparing the result with diffusion MRI fiber orientations in the same mouse brain. We show a remarkably good correspondence, considering the orthogonality of the two methods, i.e. the different physical processes underlying the two signals. 3D sSAXS can serve as validation method for microstructural MRI, and can provide novel microstructural insights for the nervous system, given the method’s orthogonality to dMRI, high sensitivity to myelin sheath’s orientation and abundance, and the possibility to extract myelin-specific signal and to perform micrometer-resolution scanning.

Graphical Abstract

1. Introduction

1.1. Axonal orientation, diffusion MRI and the need for validation

Understanding brain function requires knowledge of its connectivity both at the microscopic and at the whole organ scale. The anatomical substrate for connectivity is a highly structured network of fibres consisting of myelinated axons ensuring efficient propagation of information between neurons even when located a distant locations within the CNS. Hence, methods providing accurate information of cerebral fiber architecture (connectome) have become important tools for neuroscientists. Diffusion MRI (dMRI) assessing the diffusion properties of water molecules has evolved as the method of choice for microstructural investigations of the whole brain, given that water proton displacement for typical dMRI diffusion times happens at the micrometer scale, commensurate to dimensions of cells, and, in particular, axons. Moreover, the method allows probing the orientation distribution of water diffusion. Following the introduction of diffusion tensor imaging (DTI) by Basser et al. [1], a wealth of dMRI methods have emerged, aiming to retrieve the fiber orientation distribution function (fODF) for every voxel in the brain [2-5]. However, diffusion MRI has typical resolutions in the millimeter scale in humans and ~100μm in rodents, while axons have a diameter of about 1 μm [6, 7]. Moreover, oriented displacement of water molecules is not only influenced by axonal alignment, but also by other factors [8] such as myelin density [9], intra- and extra-axonal diffusion heterogeneities [10, 11], or cross-membrane water exchange [12].

1.2. Ex vivo validation methods, and their shortcomings

Multiple ex vivo methods have been proposed to validate dMRI outputs, among them electron microscopy [13, 14], traditional histology [15], 3D histology (involving tissue clearing methods) [16, 17], synchrotron micro-CT [18], polarized light imaging (PLI) [19] and more. However, these methods are limited in providing quantitative 3D fODFs for sample volumes comparable to those analyzed by dMRI. In electron microscopy, the investigated volumes are typically restricted to sub-millimeter size; moreover, extensive sample preparation affects its microstructure [20]. Traditional 2D histology cannot provide quantitative information on 3D fiber orientation; artifacts from sample preparation, sectioning and staining affect its outcome, while the slice thicknesses of few to several microns cannot capture myelin-dense white matter regions where the packed axons appear as a homogeneous material. Similar issues arise with 3D histology; despite the elimination of the need for physical sectioning with inherent artifacts, brain tissue clearing [21] usually introduces inhomogeneous sample deformations, rendering registration to MRI datasets difficult [17], whereas homogeneous clearing and staining of several millimeter-thick samples remains challenging. At the same time, imaging of cleared samples using confocal, multi-photon, light- or lattice-sheet microscopy, can achieve high in-plane but limited through-plane resolutions, typically above 1μm, introducing a bias in retrieving quantitative 3D fODFs. Synchrotron micro-CT methods [22], usually based on phase-contrast imaging, can provide very high resolution (sub-millimeter) and isotropic tomographic reconstructions of brain tissue [23]. However, typically extended sample preparation and contrast-enhancing staining steps are needed, while single axons cannot yet be resolved either, which precludes quantification of fiber orientation in dense white matter regions. Finally, PLI, exploiting myelin birefringence to provide high-resolution and quantify in-plane orientations, suffers from an inherent difficulty in assessing out-of-plane fiber angles [24]. Thus, correlation of fiber orientations from 3D histology, synchrotron micro-CT or PLI with dMRI data for extended tissue volumes has not been achieved to date.

1.3. Small-angle X-ray scattering (SAXS) to probe brain microstructure

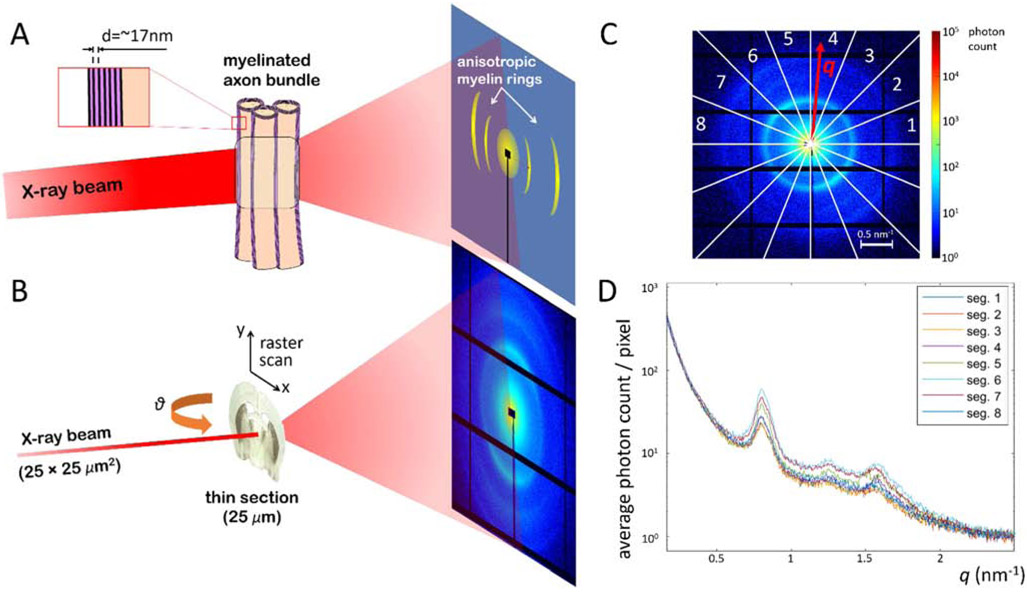
In small-angle X-ray scattering, a monochromatic photon beam interacts with the electrons of the sample, with part of the photons undergoing elastic scattering at small angles (~0.1-10°). A detector placed some meters downstream collects the scattered photons, which form a diffraction pattern (Fig. 1A,B). When the beam interacts with a collection of identical particles, the detected SAXS signal can be expressed as a product of a form factor, which is related to the scattered intensity from the single particle, and a structure factor, which is related to the ordering of particles with respect to each other. For samples comprising repetitive or periodic arrangement of these particles, the structure factor presents distinct local maxima related to the repeat distance d of the particles, at values of the momentum transfer q that are inversely proportional to d, i.e. q = n · 2π/d, where n is an integer larger than 0. Similar to crystallography, the repeated structure produces a coherent amplification of the signal, which boosts the local signal-to-noise ratio significantly at these momentum transfer values. The shape, relative height, and width of the scattering peaks is also affected by the single-particle form factor, the electron density difference between the particle and the environment, how regular the particle periodicity is, the duty cycle of the periodic structure, and the underlying non-periodic SAXS signal arising from other molecules in the sample.

Figure 1.

Principles of 3D sSAXS applied on brain tissue. A) The X-ray photons scatter elastically on the layered structure of the myelin sheath, and produce characteristic maxima on the photon-counting detector, at a distance from the center, i.e. momentum transfer value q, corresponding to the myelin sheath’s repeat distance d. B) During the 3D sSAXS experiment, the thin section is raster-scanned through a pencil beam, moving at a plane perpendicular to the beam and parallel to the detector, for a series of sample rotation angles θ. Black horizontal and vertical lines correspond to “blank” detector areas that accommodate the detector’s electronics. Signal in these areas is filled in by taking into account the center-symmetry of the SAXS diffraction pattern. The black rectangle in the center and the black line connected to it are caused by the beamstop and its support, respectively. The beamstop is used to block the main unscattered beam and thereby protect the detector. C) For each scan point, a diffraction pattern is recorded and analyzed. It is divided in 16 azimuthal segments in order to capture the signal anisotropy, and then each segment is integrated as a function of momentum transfer q. In practice, values of diagonal segments are averaged weighted by the corresponding number of pixels, thereby exploiting the center symmetry of the pattern, resulting in analysis for 8 segments. D) Plot of the signal for the 8 segments, as a function of the momentum transfer q, whose values correspond to real space features as a function of d = 2π/q.

Many nanostructural components of biological tissue produce such distinct maxima in their diffraction patterns [25, 26], including DNA molecules [27], collagen fibers [28], keratin [26], or myelin. Concerning myelin, which is of particular relevance for studying brain microstructure, the interaction of X-ray photons with the repeated structure of the myelin sheath produces characteristic scattering maxima, as illustrated in Fig. 1A. While a SAXS signal from a complex mixture of molecules can be difficult to disentangle, SAXS signal at the values corresponding to the known periodicity of myelin sheath is heavily weighted by the ordered myelin present in myelinated axons. This has allowed investigations of the myelin sheath structure in different types of human and animal myelinated axons [29-33] as well as the assessment of alterations in the integrity of the myelin structure under pathological conditions [34-39]. Also, since the myelin sheath periodicity occurs primarily radially to the axon’s main axis, the angle in which the myelin-specific peak appears can be related directly to the axon orientation. Hence, feasibility of probing the anisotropy of the myelin-related SAXS scattering signal and axonal orientation has been demonstrated [25, 40-43].

In recent years, further development of X-ray scattering methods has enabled analysis of the anisotropic scattering signal to retrieve the 3D ODF of the sample’s micro- and nanostructure [43-48]. Here, we present a method based on 3D scanning small-angle X-ray scattering (3D sSAXS) [46] that provides quantitative 3D fODFs for samples with minimal sample preparation, such as sections of fixed mouse brain cut with a vibratome. We compare structural data derived from 3D sSAXS with results obtained from dMRI, and show the high degree of similarity and complementarity of the information provided by the two methods.

2. Methods

2.1. Samples

A healthy 5-month-old C57BL/6 female mouse brain was used in this study, within the animal license ZH242/14 of the Animal Imaging Center of ETH Zurich/University of Zurich. After transcardial perfusion fixation with 4% parafolmaldehyde (PFA) in phosphate-buffered saline (PBS), the brain was surgically extracted and post-fixed in a 4% PFA solution for 48 hours. The brain was thereafter scanned with MRI ex vivo (scan details below). Following MRI scanning, the brain was cut into thin sections of varying thickness using a vibratome (Leica VT 1000S, Leica Biosystems Nussloch GmbH, Germany). The sections were then preserved in PBS at 4°C, until the synchrotron X-ray scattering experiments.

All procedures in the paper and animal handling have been performed according to the ARRIVE guidelines¹, and EU Directive 2010/63/EU for animal experiments².

2.2. MRI experiments and analysis

Ex vivo MRI experiments were carried out in a BioSpec 94/30 scanner (Bruker Biospin GmbH, Ettlingen, Germany) equipped with a 9.4T magnet with 30cm bore diameter and a BG-A 12S gradient system with maximum gradient amplitude of 440mT/m. A whole body resonator was used for excitation combined with a cryogenic 4-channel coil (CryoProbe, Bruker Biospin GmbH, Fälanden, Switzerland) for reception. dMRI was performed using a segmented 2D EPI readout, with a field of view of FOV = 15.875 × 13 × 9.5 mm³ FOV, imaging matrix dimensions 212 x 173 x 127 corresponding to 75μm isotropic voxel size, repetition and echo delays of TR/TE = 500/43 ms, 4 segments, diffusion time Δ=12ms, gradient duration δ=5.5ms, two b-values at 2,000 and 4,000 s/mm² with 96 q-space directions each, 5 b₀ scans (b=0s/mm²), and 2 averages. Analysis of the dMRI dataset was performed using the DESIGNER pipeline [49], which includes algorithms for denoising [50, 51], Gibbs ringing removal [52], Rician floor bias and corrections for rf field (B₁) inhomogeneities, registration of the diffusion volumes using FSL Eddy [53], and simultaneous estimation of the diffusion and kurtosis tensors using the weighted linear least square method [54]. In this study, we used the information from the diffusion tensor for comparison to 3D sSAXS.

2.3. X-ray scattering experiments

For the synchrotron X-ray scattering experiments, two vibratome-cut sections from the MRI-scanned brain were used, with thicknesses of 25μm and 50μm. The 25μm-thin section was enclosed within two adhesive 12μm-thick Kapton tapes (Benetec, Wettswil, Switzerland). The “sandwich” was then glued on a metallic frame with a 20×20mm² square hole at the center (Supplementary Fig. 1A). Since dehydration was observed during data acquisition from the 25μm-thick section (Supplementary Fig. 1B), the 50μm-thick section was enclosed in a 15×15×0.5mm³ chamber filled with PBS, constructed from 0.5mm thick metallic frame covered on both sides with Kapton adhesive tape (Supplementary Fig. 1C). This prevented sample dehydration, at the expense of signal attenuation by the 0.5mm water layer.

For the experiment on the 25μm-thin section, beam energy was set at 12.4 KeV (1 Å), beam and motor step x- and y-size was 25μm, with an exposure time of 50ms, and 3ms readout time. Raster-scanning the 400×256 matrix, corresponding to a FOV of 10×6.4mm², under 7 rotation angles (θ=−60°, −40°, −20°, 0°, 20°, 40°, 60°), similar to [46], took ~14 hrs. A flux of 4.47·10¹¹ photons/s resulted in an imparted dose of 26.8 MGy on the tissue.³ For the 50μm-thin section, beam energy was increased to 16.3 KeV (0.76 Å), beam and motor step x- and y-size was 50μm, with an exposure time of 300ms, and 5ms readout time. The higher energy and longer exposure time were used to counteract the beam attenuation by the water chamber. A FOV of 5.1×4mm², covering part of the section, was raster-scanned under 7 rotation angles (θ=−60°, −40°, −20°, 0°, 20°, 40°, 60°). Scanning the 102×80 matrix at 7 angles took a total of ~7hrs. A flux of 8.5·10¹⁰ photons/s resulted in an imparted dose of 9.5 MGy on the tissue.

For both experiments, SAXS photons were collected by a Pilatus 2M detector [55] positioned at a distance of 2.2m from the sample, and a photodiode was used to record the direct beam’s transmitted intensity. The reciprocal-space q-range 0.64-0.84nm⁻¹ that included the 2^nd myelin peak, which has been shown to give the strongest scattering intensity [30], was used for the analysis of SAXS orientation and anisotropy. This q-range is named q_myelin hereafter.

X-ray scattering experiments were performed at the cSAXS beamline of the Swiss Light Source, Paul Scherrer Institute, whose setup can accommodate fast raster-scanning and sample rotations.

2.4. X-ray scattering analysis - from 2D intensities to 3D tensors

The scans from the different sample rotation angles were registered to the scan at θ=0°. Registration was performed using the integrated scattering intensity at q_myelin as a contrast. In the original 3D sSAXS method [46] a rigid registration was applied [56]. In the analysis of the mouse brain sections however, non-rigid registration was required, to compensate for the curvature of the Kapton sections across the 5.1×4mm² and 10×6.4mm² FOVs. The non-rigid registration was implemented by customizing an existing Matlab solution [57], and enabled identifying the diffraction patterns corresponding to the same brain location for all rotation angles, to be used in subsequent single-voxel analysis.

Within the Born approximation, each SAXS diffraction pattern probes the 3D reciprocal space of the scanned voxel at a plane perpendicular to the beam direction, with the curvature of the Ewald sphere being negligible at the SAXS regime [58]. By rotating the sample, we sample the reciprocal space along different 3D orientations (Fig. 3A), each of which corresponds to the 3D orientation of one of the 16 azimuthal segments, and is encoded by the vector g_i. In order to reconstruct the 3D reciprocal space at q_myelin, the scattering intensity I was retrieved at q_myelin for each of the 16 azimuthal segments of every diffraction pattern (Fig. 1C) and for every sample rotation angle By assuming that this 3D intensity distribution can be captured by a symmetric positive definite rank-2 tensor T_scat, we then followed a procedure similar to the one introduced by DTI [59, 60] and recently adapted for 3D X-ray scattering [43], in order to identify the components of T_scat, by seeking for each voxel the solution to the equation system:

$$\overline{I}=\overline{\widehat{\mathit{g}}}\cdot \overline{{\mathit{T}}_{scat}}.$$ (1)

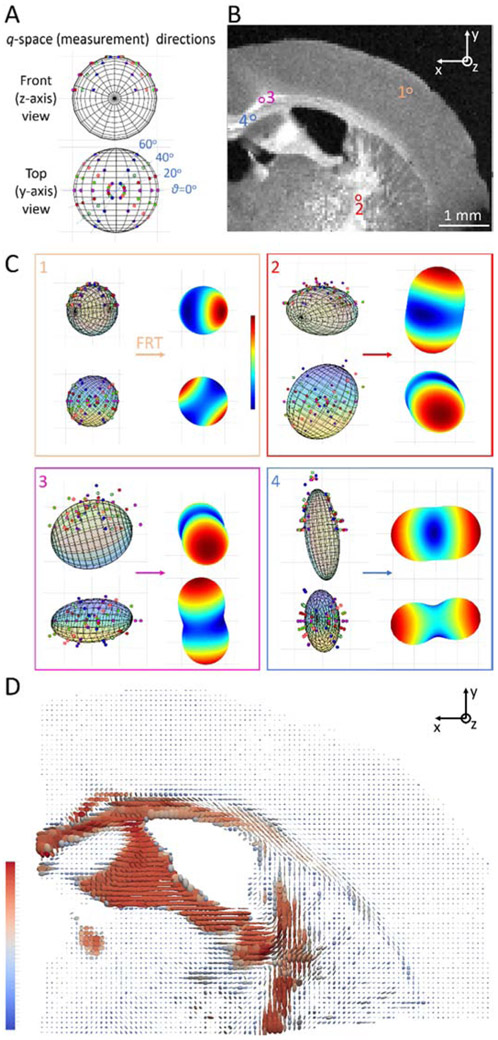
Figure 3.

Generating fODF map from scattering signal. A) The measurement directions of the scattering signal plotted on the surface of a sphere, and visualized for two (front and top) views. At a single sample rotation angle, we probe points at 8 directions g_i along a specific great circle, that correspond to the direction of the azimuthal segments along the circle in Fig. 1C. Measuring at different sample rotation angles allows to probe the 3D reciprocal space across the sphere. Front view is the beam (z-axis) direction, looking into the plane of the section (and of the page). Top view corresponds to the -y direction, as indicated in (B). B) Azimuthally averaged scattering intensity at q_myelin for θ=0° sample rotation. White matter areas display higher intensity, while intensity of gray matter areas is lower but clearly higher than the background (cf. Fig. 2A, panels 1&6). The position of one gray matter and 3 white matter voxels further analyzed in (C) is indicated. C) Orientation-dependent scattering intensities and corresponding fODFs for the 4 voxels indicated in Fig. 3B. Scattering intensities are displayed on the left side of the panels, together with the fitted tensor, for both front (z-axis) and top (y-axis) view. Subsequent to the FRT, the fODF is obtained for each of the voxels (right side of panels), with the front (z-axis) view, which corresponds to the reader looking at the plane of the page, given in the top right corner. fODF color ranges from blue to red, showing for each fODF the closest and furthest distance to the center respectively. D) Analysis of all scanned voxels yields the fODF map of the section, where the fODF is represented by a rank-2 tensor. Tensors are color-coded according to their first, i.e. largest, eigenvalue.

$\overline{I}=[I_1\cdots I_n{]}^T$ represents the vector comprising the measured scattering intensities along the n different unit vector directions g₁ … g_n. The matrix $\overline{\widehat{\mathit{g}}}=[{\widehat{\mathit{g}}}_1\cdots {\widehat{\mathit{g}}}_n{]}^T$ comprises the directional information from each unit vector g_i = [g_ix g_iy g_iz] , where ${\widehat{\mathit{g}}}_{\mathit{l}}$ was encoded in the form ${\widehat{\mathit{g}}}_{\mathit{l}}=[g_{ix}^2{g}_{iy}^2{g}_{iz}^{2}2g_{ix}{g}_{iy}2g_{ix}{g}_{iz}2g_{iy}{g}_{iz}]$ in order to linearize the equation system. The 6 independent elements of the 3×3 rank-2 tensor T_scat are represented by $\overline{{\mathit{T}}_{scat}}=[T_{sca{t}_{{}_{xx}}}{T}_{sca{t}_{{}_{yy}}}{T}_{sca{t}_{{}_{zz}}}{T}_{sca{t}_{{}_{xy}}}{T}_{sca{t}_{{}_{xz}}}{T}_{sca{t}_{{}_{yz}}}{]}^T$. Eq. (1) is a linear equation system, expressing the scattering intensity I_i along the direction g_i according to I_i = g_i^T · T_scat · g_i.

The equation system (1) has to be solved for every voxel, e.g. by using the ordinary least squares method:

$$\overline{{\mathit{T}}_{scat}}=({\overline{\widehat{\mathit{g}}}}^{{}_T}\overline{\widehat{\mathit{g}}}{)}^{-1}{\overline{\widehat{\mathit{g}}}}^{{}_T}\overline{I}.$$ (2)

2.5. X-ray scattering analysis – from 3D tensors to fODFs

Constructive scattering from the repeated layers of the myelin sheath occurs perpendicular to the fiber’s main axis, forming a series of concentric “thin circles” around the fiber axis in the 3D reciprocal space, at multiples of the momentum transfer value q corresponding to myelin sheath’s repeat distance d. If we only consider the main scattering maximum at q_myelin, we can say that the 3D scattering footprint of a single myelinated fiber is a circle around the fiber axis, of which we are probing two points only with each diffraction pattern (unless the fiber is parallel to the beam, in which case we probe the full circle at q_myelin). In theory, this implies that the “circular” 3D scattering signal from a single fiber can be transformed into signal along the fiber direction by the use of the Funk-Radon Transform (FRT) [61, 62]. The FRT integrates all points along a great circle of a sphere to derive the value that corresponds to the direction perpendicular to the plane of the circle⁴. All fibers in each voxel, which can be hundreds or thousands fibers in white matter regions, contribute to the overall 3D scattering signal, which we approximate with a rank-2 tensor as described in the previous paragraph. By applying the FRT to the overall 3D scattering signal from a distribution of myelinated fibers, we can retrieve the corresponding fODF. Effectively, this means that we can apply the FRT to the scattering tensor T_scat to derive the corresponding tensor T_fODF representing the fODF in every voxel:

$${\mathit{T}}_{fODF}=FRT({\mathit{T}}_{scat}).$$ (3)

In practice, we use the isomorphic 3D rotation group representation SO(3) of tensors in terms of spherical harmonics (SH) basis, using the formulae provided in Appendix C of ref [5]. We then apply the FRT to the derived SH components P_lm. Since the symmetric rank-2 tensor SH representation needs only the even SH components corresponding to l=0 (m=0) and l=2 (m=0,±1,±2), the conversion, as derived by Funk [61], is trivial namely by changing the SH associated Legendre polynomials P_lm:

$$P_{fOD{F}_{{}_{00}}}=P_{sca{t}_{{}_{00}}}\text{and}{P}_{fOD{F}_{{}_{2m}}}={}^{-P_{sca{t}_{{}_{2m}}}}∕_2.$$ (4)

When applied to every tensor corresponding to each voxel of the structure, the outcome is a map of the fODFs of the structure, in a SH basis. In order to derive the rank-2 tensor T_fodf representing the fDOF of each voxel, we use the inverse of the tensor-SH relationships applied before.

2.6. Comparison with dMRI

MRI volumes were affine-registered to the SAXS sections using FSL FLIRT [53, 66]. For 2D orientation analysis and comparison, the processing described in [63] was employed on both X-ray scattering and dMRI data. For the SAXS data, the isotropic and anisotropic components of the signal, as well as the principal 2D (in-plane) angle, were determined by applying a discrete Fourier transform to the data points of the 16 azimuthal segments [63] -here we include a 90° offset to retrieve the main fiber orientation instead of the main scattering orientation. In order to determine the in-plane orientation information from the dMRI virtual slice (Fig. 2C), the in-plane component of the tensor was retrieved, by probing the tensor along 16 directions along that plane, analogous to the 16 azimuthal segments of the diffraction patterns. These 16 points were then subjected to the same analysis as the X-ray scattering data.

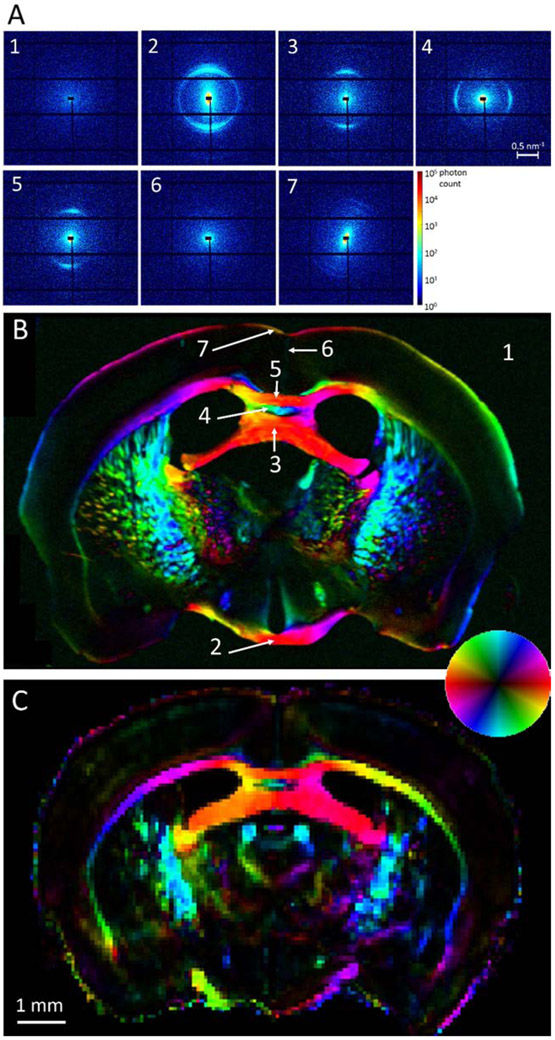
Figure 2.

Scanning SAXS of the 25μm-thick mouse brain section, and comparison with dMRI. A) Diffraction patterns from the section points indicated in (B). Background signal (panel 1) is featureless, whereas signal from white matter regions (panels 2-5) displays characteristic maxima, along the repeat structure of the myelin sheath and perpendicular to the fiber orientation. Gray matter areas displayed very little or no peak (panel 6), with the exception of the molecular layer (panel 7), where faint peaks were consistently detected. B) Color-coded map depicting microstructure orientation of the brain section, at 25μm resolution. Color hue indicates the main 2D orientation, interpreted by the inset colorwheel, whereas color intensity corresponds to signal anisotropy, defined as anisotropic over isotropic component [63]. C) Color-coded map depicting main diffusion orientation from the same virtual section of the whole-brain dMRI dataset, at 75μm resolution. Color interpretation is similar to the SAXS map, where 2D orientation information was extracted as explained in Section 2.6.

For the 3D orientation, two different approaches were employed. First, for the 25μm-thick section, the principal orientation and degree of anisotropy in every voxel was represented by a vector using the 3D sSAXS algorithm described in [46], and not by a tensor. This was because signal intensity changed significantly during the measurement for different sample orientations θ due to dehydration (Supplementary Fig. 1), so fitting a tensor to scattering intensities as described in Section 2.4 was no longer possible. However, the original 3D sSAXS method [46], where a vector represents the main fiber orientation and degree of anisotropy, could still be applied, because it does not rely on absolute but relative intensities in each diffraction pattern.

For the 50μm-thick section, the main orientation was derived by the eigenvector of the larger eigenvalue of the rank-2 tensor. The degree of tensor anisotropy was quantified for both methods by the fractional anisotropy ( $FA=\frac{\sqrt{({\lambda }_1-{\lambda }_2{)}^2+({\lambda }_1-{\lambda }_3{)}^2+({\lambda }_3-{\lambda }_2{)}^2}}{\sqrt{2}\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$ ), where λ₁, λ₂ and λ₃ are the tensor eigenvalues. For quantitative comparisons of fiber orientation and anisotropy, the physical SAXS and virtual MRI sections were non-linearly registered using [57].

All data and analysis codes are available from the first author upon request.

3. Results

3.1. Diffraction patterns from brain tissue

X-ray scanning of the 25μm-thick mouse brain section at 25μm in-plane resolution produced diffraction patterns with distinct maxima at q_myelin in areas of myelinated axons (Fig. 2A-B). Gray matter regions produced a diffuse central scattering only (Fig. 2A, pattern #6), occasionally displaying a very weak maximum at q_myelin, indicating the very low amounts of myelin in these brain regions. A consistent exception to this was the outermost layer of the cortex (layer I or molecular layer), which produced a faint but consistently present and anisotropic myelin peak (Fig. 2A, pattern #7). This can be attributed to the myelinated horizontal axons in the layer [64, 65]. In white matter, the signal at q_myelin displayed strongly anisotropic intensity along the circumference (Fig. 2A, patterns #2-5). Since scattering maxima occur along the repeat direction of the layered structure, perpendicular to the axon’s main axis (cf. Fig. 1A), strongly anisotropic scattering perpendicular to the expected fiber orientation was observed in areas with highly aligned myelinated axons (Fig. 2A-B), such as the optic chiasm (pattern #2), hippocampal commissure (pattern #3), dorsal fornix (pattern #4) and body of the corpus callosum (pattern #5). It is also worth noticing that the diffraction patterns from the optic chiasm consistently displayed a second maximum near the main peak, indicating the existence of two ordered structures with slightly different repeat distances.

3.2. 2D orientation analysis and comparison with dMRI

The color-coded orientation map of the brain section in Fig. 2B shows the principal in-plane fiber orientations, assessed by SAXS, for every voxel of the section. These are compared to the corresponding principal in-plane alignment of the fibers derived from the same virtual dMRI section (Fig. 2C). Visual comparison shows good agreement both with regard to orientation and degree of anisotropy. Small differences, e.g. anatomical discrepancies, can be attributed to sectioning artifacts, imperfect registration and to the different physical mechanism underlying the respective signals.

3.3. fODF map

The principal orientation and degree of anisotropy in every voxel could be retrieved and represented by a vector for both 25 and 50μm-thick sections using the 3D sSAXS reconstruction algorithm described in [46] (Supplementary Figs. 2, 3). Additionally, for the 50μm-thick section, we used the extended 3D sSAXS method, as presented in Section 2.4; we could thus fit the scattering intensity data at the measurement directions (Fig. 3A), for all scanned points (Fig. 3B), to a rank-2 tensor (Fig. 3C – left side of panels), and convert that to fODF using the FRT (Fig. 3C – right side of panels). The fODF represents the orientation distribution of the axons -heavily weighted by the myelinated ones- in each voxel. The procedure is illustrated for the 4 voxels indicated in Fig. 3B, one gray matter and 3 white matter voxels with almost perpendicular alignment to one another (Fig. 3C).

The fODF map for all points of the investigated section is shown in Fig. 3D, with the rank-2 tensor T_fODF visualized as an ellipsoid. As expected, tensors are larger for white matter regions compared to the gray matter, mainly due to the scattering by the repeated layers of the myelin sheath. Also, tensors seem to be oriented according to known anatomical directions. For instance, for the corpus callosum body, fimbria and stria terminalis, the main orientation is left-right, for the internal capsule and the dorsal fornix it is in the superior-inferior axis, and fibers in some structures such as the cingulate bundle or the stria medullaris are principally oriented antero-posteriorly. Moreover, there are white matter regions such as the corpus callosum tapetum or parts of the internal capsule, where tensors are highly anisotropic, with fibers aligned along one orientation only. In most white matter regions however, voxels seem to include fiber populations with more distributed orientations, as has been previously reported [66], resulting to a lesser degree of tensor anisotropy

3.4. Comparison of 3D orientation between 3D sSAXS and dMRI

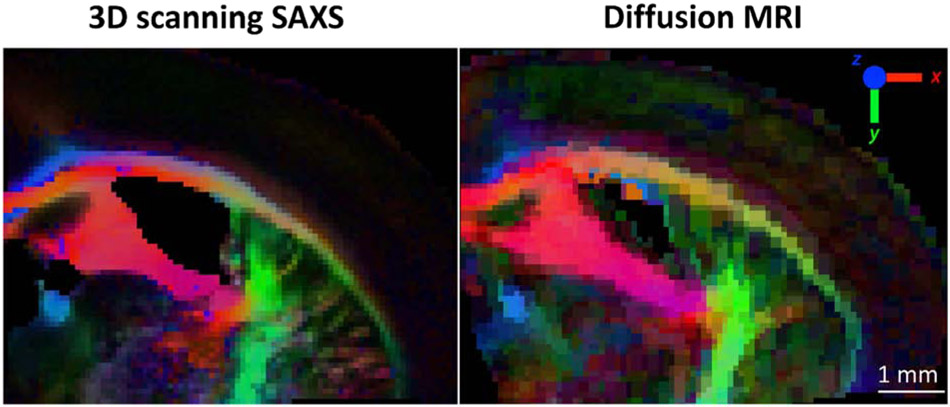
Figure 4 shows the comparison of the principal fiber orientation as derived using 3D sSAXS and dMRI for the same region of the mouse brain.

Figure 4.

3D orientation comparison between 3D sSAXS and dMRI. The dMRI volume dataset has been non-linearly-registered to the 3D sSAXS section. Fiber orientations are color-coded following the typical dMRI convention (inset), weighted by the fractional anisotropy from the tensors for both methods.

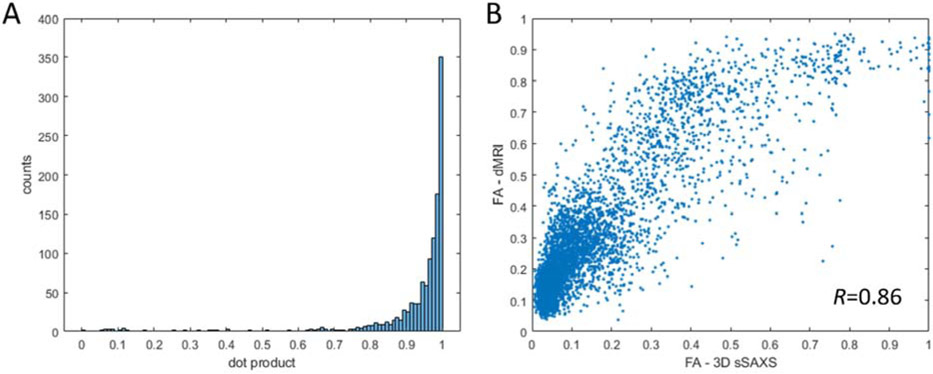
The side-by-side comparison of the color-coded main 3D orientation from the two methods reveals a remarkable correspondence. The principal white matter structures in the section show analogous orientations in both visualizations. This is further confirmed by quantitative analysis in Fig. 5A, which shows very high degree of alignment between the orientations from the two methods. Overall, the X-ray scattering-generated image in Fig. 4 looks slightly sharper, due to the difference in voxel size (50μm for SAXS vs. 75μm for dMRI). This enables a better discrimination of smaller tracts, e.g. of those emerging from the internal capsule and connecting it to the corpus callosum tapetum. Finally, color intensity, reflecting different degrees of anisotropy, seems to be similar in both methods. Quantitative analysis in Fig. 5B shows that there is a monotonic, though non-linear, relationship between fractional anisotropies from 3D sSAXS and dMRI.

Figure 5.

Quantification of the correspondence between the orientation and FA from the 50μm-thick section. A) Correspondence of the main orientation as quantified by the dot product of the two vectors from the two methods, excluding areas of low anisotropy (FA<0.25). Values of 0 correspond to no alignment (vectors at 90°), values of 1 to perfect alignment (vectors at 0°). B) Plot of the fractional anisotropy values, calculated from the eigenvalues of the tensors from both methods. The relationship shows a high correlation (Pearson’s R=0.86), while the relationship seems to be non-linear.

Comparison between 3D sSAXS and dMRI outcomes was performed for the 25μm-thick section as well (Supplementary Fig. 4), but in this case using the vector to describe the SAXS-derived fiber orientation and degree of orientation, as explained in Section 2.6. Visual comparison shows good agreement in terms of principal orientation. The 3D sSAXS result is much sharper, because of the differences in resolution (25μm vs. 75μm for dMRI). Further, in this case the anisotropy metric was the degree of orientation as described in [46] for 3D sSAXS, while it was FA for dMRI, so the color correspondence in the figure is not as good as for the 50μm section (Fig. 4), where the same metric (FA) was used.

4. Discussion

We present the application of the 3D scanning SAXS method [46] to mouse brain tissue with minimal sample preparation, in order to retrieve the 3D fiber orientation distribution function for every voxel of a section. We extend the method from vectors to tensors, make use of the Funk-Radon-Transform to convert the scattering signal to real space, and derive a rank-2 tensor that represents the fODF. We compare the outcome of the method with fiber orientations derived from diffusion MRI. Comparison of the main 2D (in-plane) and 3D orientation for every voxel reveals the qualitative (Figs. 2, 4, Supplementary Fig. 4) and quantitative (Fig. 5) similarity between the two methods. Overall, we propose 3D scanning SAXS as a directly structural method that can be used on mouse and human nervous tissue not only to structurally validate diffusion MRI measurements, but also to provide novel microstructural insights, given its orthogonality to dMRI, its sensitivity to myelin and the possibility for micrometer-scale resolution.

4.1. SAXS studies on myelin and brain tissue anisotropy

3D sSAXS is sensitive to the myelin structure based on scattering maxima due to repeated layers of the myelin sheath. Moreover, the signal probes the orientation of the myelin sheath with respect to the incident X-ray beam. X-ray scattering studies from nervous tissue have contributed to the understanding of the myelin sheath structure as such [30-33], and have been used for characterizing differences between the central and peripheral nervous system of different species [29, 31, 67], in development and aging [68, 69] and in diseases such as multiple sclerosis [34], allergic neuritis [35], brain tumors [36, 37] or in myelin deficiencies [38, 39].

Yet, very few studies have addressed the pronounced anisotropy of the myelin signal. Muller et al. demonstrated that SAXS is sensitive to brain tissue anisotropy showing a map depicting fiber orientations within the human thalamus [25]. Inouye and colleagues studied structure and 2D orientation of myelin sheath in a single myelinated fiber, with spatial resolutions of 1μm [41] and 250nm [40], and Carboni et al. showed 2D orientation and anisotropy in a part of human midbrain with 3μm resolution [42]. Wieczorek et al. used the anisotropic dark-field signal in order to tomographically derive orientation maps of a small part of a human cerebellum [70]. Although the latter study is an important step for demonstrating the use of X-ray scattering in investigations of neuronal orientations, the sample underwent critical-point-drying before scanning, rendering a direct comparison with methods such as dMRI difficult. Also, the assumption of rotational invariance of the scattering signal is not valid for anisotropic structures [71], as highlighted by the plotted scattering intensities in Fig. 3C. Moreover, the ultra-small-angle (USAXS) regime probed with dark-field imaging is not structure-specific, so the anisotropic signal can emerge from any interface, and has contribution from all sample molecules. In contrast, SAXS signal is greatly enhanced at q-values corresponding to the myelin structural repeats, while it also gives the possibility for extraction of the myelin signal in order to provide local myelination estimates[69, 72]. This implies that for the same amount of photons the generated contrast from myelinated axons is significantly higher than in the corresponding USAXS signal. In a recent study, Gao et al. presented a method to reconstruct the 3D nanostructure orientation distribution function based on the anisotropic SAXS signal and showcased it, apart from other anisotropic samples, for a mouse brain [43]. The aforementioned purely methodological study focused on the reconstruction method, and did not discuss the biological and structural implications of the mouse brain data.

4.2. 3D sSAXS-MRI comparison

3D sSAXS and dMRI were compared in terms of fiber orientation and degree of anisotropy. Visual comparison of the results from the two modalities (Figs. 2, 4, Supplementary Fig. 4) suggests similarity in terms of fiber orientation and fiber anisotropy, as is evidenced by the quantitative comparison of Fig. 5. Especially concerning fiber orientation, the highly skewed dot product histogram in Fig. 5A suggests a high degree of agreement between the two methods, since a dot product value of 1 indicates perfect fiber alignment. Despite the high similarity, discrepancies were observed. In both the 25- and the 50μm-thick sections, the size of the ventricles appeared larger in the SAXS data (Figs 2, 4 and Supplementary Fig. 4). This can be attributed to the physical sectioning of the tissue with the vibratome, which may lead to geometric distortion, in particular in regions exhibiting a large difference in mechanical properties, such as the interfaces between the fluid-filled ventricles and the surrounding white-matter structures. It should be noted that non-linear registration in Fig. 4 alleviated this difference, which was even bigger when using linear registration schemes.

Further, the quantification of anisotropy shows both similarities and differences between the methods. The color intensity in Figs. 2, 4, and Supplementary Fig. 4, demonstrate consistent anisotropy values extracted by the two methods. This agreement is further supported by the quantitative comparison in Fig. 5B for the 50μm-thick section, where FA values of the two methods are highly correlated (Pearson correlation coefficient R=0.86). However, the plotted points deviate from the identity line. This shows the different basis and complementary nature of the information retrieved from the two orthogonal methods. In areas such as the cortex, dMRI signal seems to display higher anisotropy (Figs. 2 and 4), also demonstrated in Fig. 5, where the curve is skewed towards the dMRI-derived FA for low FA values. This is attributed to the different mechanism underlying the dMRI and SAXS signals: in dMRI, the signal in tissue (excluding CSF) can be attributed to the intra- and extra-axonal water, with both contributing to the anisotropy, even in the absence of myelinated fibers. On the other hand, in SAXS the anisotropy comes almost exclusively from the myelin component, while the other tissue components contribute an almost isotropic signal with no scattering peaks, effectively lowering the overall FA values. Similar observations can be made for the gray matter regions in all three comparative figures (Fig. 2, 4, Supplementary Fig. 4), where SAXS-derived anisotropy, as depicted by color intensity, seems to be lower.

Nevertheless, it should be noted that SAXS is also sensitive, though to a lower extent, to tissue anisotropy in regions which display low myelin content, or are even devoid of myelin: in this case, X-ray photons will be scattered by oriented tissue interfaces, such as the unmyelinated axon membranes. This can be seen in Supplementary Figs. 2 and 3, where fiber orientations in the cortex can be observed, and different layers of the cortex can be distinguished. Moreover, in some cases SAXS FA reaches values close to unity (Fig. 5b), presumably because these voxels have the highest volume fraction of myelinated fibers, and their anisotropy dominates the overall signal. Finally, it is worth noting that if the myelin-specific signal is isolated [43, 69, 72], FA values, representing the myelinated fiber dispersion only, are expected to be higher than the corresponding dMRI at all voxels containing myelinated axons. This hypothesis remains to be tested in future experiments.

4.3. Limitations

The application of 3D sSAXS on brain tissue has limitations. As in all methods that require tissue sectioning, this may impact tissue shape and integrity, rendering exact registration to a volumetric scan (such as in dMRI) difficult. In addition, the quasi 2D geometry of the sample renders the complete probing of the reciprocal space impossible. In practice, sample rotation angles up to θ = ±75° are feasible; the missing angular coverage has to be complemented by the model (cf. Fig. 3C). Moreover, sample dehydration during the scan has to be avoided e.g. by embedding in a thin PBS-filled chamber. We think that ~200μm-thick chambers would warrant adequate specimen hydration during the scanning experiment, without excessive photon absorption.

Dose imparted on the tissue is an important issue when it comes to biological samples. For the two samples presented here, dose was in the range of few tens of MGys (cf. Section 2.3), which is in the same range of what we have deposited in previous experiments on brain tissue [43] without seeing any radiation damage when comparing scans pre- and post-experiment. Also, it is an order of magnitude less than the calculated 440 MGy deposited in previous brain tissue SAXS study [72]. Future micrometer or sub-micrometer 3D sSAXS experiments will increase the imparted dose, since signal will need to be generated from much smaller voxels compared to the current study. The increase of dose, however, can be mitigated by sacrificing signal-to-noise ratio. Besides, radiation damage assessment in micrometer-resolution raster-scanning experiments [41] showed no radiation damage for exposure times up to 10 times the exposure needed to collect the SAXS signal.

Finally, in this study the total intensity of the SAXS signal at q_myelin was used, rather than extracting the myelin peak as was performed previously [43, 69, 72]. However, the SAXS intensity at any given q has contributions from all sample molecules. In this way, the studied SAXS signal is heavily myelin-sheath-weighted, but not myelin-sheath specific; it would be possible to increase the specificity of contrast to the repetitive myelin sheath by peak extraction, but this goes beyond the scope of the current paper.

4.4. Outlook

4.4.1. Higher order models

We extracted information on axonal anisotropy by fitting a rank-2 tensor to sSAXS signals. This renders the results directly comparable to tensor-based dMRI approaches such as DTI. Higher-order fitting would be possible, e.g. by fitting the scattering to models with higher order spherical harmonics [44, 47] and could be used for direct comparisons with higher-order models available for dMRI [3-5]. This may require denser SAXS angular sampling to capture more complex reciprocal space maps, and thus enable disambiguation of fiber orientations in case of fiber crossings, similar to analogous MRI procedures [73, 74]. Such angular sampling could be increased at will, similar to dMRI, with the corresponding time and dose penalty for the additional measurements. Moreover, while in dMRI the signal is based on average water diffusion over intra- and extra-axonal space, which limits the effective angular resolution, in SAXS the anisotropy in myelin-related scattering maxima should reflect solely the fiber anisotropy. This should allow contributions from different fibers to be disentangled, hence allowing higher angular resolution than dMRI.

4.4.2. High-resolution scanning

Spatial resolution of SAXS data was adjusted to the thickness of tissue specimen obtained by vibratome sectioning. The vibratome was chosen instead of microtome or cryotome to keep the tissue under the same condition as during the dMRI scan, without any further preparation. However, higher-resolution maps may be obtained from thinner sections (prepared with either a micro- or cryotome), by simultaneously decreasing the beam diameter and motor step-size. In such cases, 3D sSAXS studies could be carried out at a micrometer or sub-micrometer resolution. In principle, resolution in the 3D sSAXS technique is only limited by the available scan time, and can reach micrometer or sub-micrometer levels, such as in [40-42], depending on the beamline hardware, in particular the scanning hardware and X-ray shaping optics.

Higher resolution scans might be considered for brain regions displaying a complex structural architecture, where dMRI resolution cannot yet provide adequate spatial information, such as the hippocampal layers [75, 76]. Further, a direct comparison with fODFs from the same sections using diffusion tensor microscopy methods is possible, where similar resolutions on vibratome-cut sections have been reported [77, 78].

4.4.3. Possibilities for myelin content and elemental analyses

Moreover, throughout the extended literature on SAXS myelin studies [29-39, 67-69, 72], it has been established that the scattering maximum corresponding to repeat distances of 15-17nm is directly linked to the layered structure of the myelin sheath, with no other nervous system structure displaying such a repeat distance. In that sense, in nervous system studies, the maximum at q_myelin can be considered to be mostly contributed to by myelin and thereby considered as the “footprint” of layered myelin structure. Thus, by removing the background signal, i.e. the underlying scattering from air and other molecules and structures in the sample, the myelin-specific part of the SAXS signal can be isolated, as has been demonstrated previously [43, 69, 72], and the corresponding tensors, attributed solely to myelinated axons, reconstructed. This could also enable intra- and inter-sample myelin content assessment [69, 72], and hence provide critical information when considering e.g. demyelinating pathologies or studies of the myelination and de-myelination process. Taking into account the signal anisotropy, instead of performing the analysis in 2D [69] or with the assumption of the signal’s rotational invariance [72], should provide more accurate myelin sheath content estimates.

Furthermore, the presented method can be combined with X-ray fluorescence (XRF) by adding an XRF detector at 90 degrees to the beam direction [26, 42], so that simultaneous quantification of elements such as iron, zinc or copper in the section can be performed [42].

4.4.4. Extension to non-sectioned samples

Finally, recent advent of tomographic methods for reconstructing the 3D fODFs from sSAXS data [43, 44, 47] should allow full 3D characterization of axonal orientations, neuronal tracts and structural connectivity of the mammalian brain. Such outcomes would be directly comparable with 3D dMRI scans, enabling comparisons and microstructural feature correlations on the exact same sample, while allowing for further sample-destructive investigations by other methods, eg. 2D/3D histology or electron microscopy.

It should also be mentioned that myelin SAXS is not limited to a specific sample preparation method, and can performed on fresh [29-33, 40], dried [42], fixed [37, 40, 41, 43], resin- embedded [20] samples, or even in vivo [35].

5. Conclusion

We present a method to retrieve 3D axonal orientations on brain tissue based on the small-angle X-ray scattering signal of neuronal fibers. The method derives a rank-2 tensor representing the fiber orientation distribution function (fODF) for each voxel, by non-linear registration of section scans for different rotation angles, followed by fitting the scattering intensities of every voxel with a rank-2 tensor, and application of the Funk-Radon-Transform. The resulting fODF maps are compared to diffusion MRI maps from the same sections extracted from a 3D dMRI dataset. SAXS and dMRI data displayed an excellent correspondence of fiber principal orientations and good correspondence of the degree of anisotropy (R=0.86) across the tissue regions examined, which is remarkable in view of the different physical principles underlying the signals.

3D sSAXS is an attractive validation tool as well as complement to dMRI as it provides 1) directly structural information, which opens possibilities for structural validation of dMRI fODFs and corresponding tractography and connectivity, 2) the possibility to derive this information for myelinated axons only, and at the same time provide myelin content estimates, and 3) enhanced spatial resolution reaching micrometer or sub-micrometer levels, attractive for studying microstructural connectivity.