Altered hippocampal replay is associated with memory impairment in mice heterozygous for the Scn2a gene

Abstract

An accumulating body of experimental evidence has implicated hippocampal replay occurring within sharp wave ripples (SPW-Rs) as crucial for learning and memory in healthy subjects. This raises speculation that neurological disorders impairing memory disrupt either SPW-Rs or their underlying neuronal activity. We report that mice heterozygous for the gene Scn2a, a site of frequent de novo mutations in humans with intellectual disability, displayed impaired spatial memory. While we observed no changes during encoding, to either single place cells or cell assemblies, we identified abnormalities restricted to SPW-R episodes that manifest as decreased cell assembly reactivation strengths and truncated hippocampal replay sequences. Our results suggest that alterations to hippocampal replay content may underlie disease-associated memory deficits.

The hippocampal formation has been identified as a crucial circuit for spatial memory¹ and in concert with other cortical structures has been implicated in working memory tasks². It achieves this in multiple steps, initially encoding spatial information sequentially during exploratory behavior through place-specific modulation of pyramidal cell firing rates. Place cell sequences are subsequently time compressed to a scale that presumably invokes synaptic plasticity during their repetitive replay both during behavior, as theta sequences^3,4, and during goal-directed behavior⁵ and sleep^6,7, as SPW-Rs. The formation of cell assemblies (groups of anatomically distributed neurons exhibiting transient periods of enhanced synchrony) during behavior⁸ and their subsequent reactivation during SPW-Rs⁹ has often been highlighted as a key mechanism underlying memory. Although artificial SPW-R disruption has been demonstrated to degrade performance in memory-dependent tasks^10–12 and altered SPW-Rs have been observed in several disease models^13–15, how this influences the information content replayed during SPW-R episodes is unclear.

The Scn2a gene encodes the Na_v1.2 α-subunit protein, and its homozygous deletion in mice results in perinatal lethality¹⁶. The gene is a site frequently mutated in human neurological disorders, including, but not limited to, an inherited missense mutation in an epilepsy patient¹⁷, a nonsense mutation leading to sporadic epileptic encephalopathy associated with severe intellectual disability and autism¹⁸, and a range of mutations described in people with epilepsy, intellectual disability¹⁹, autistic spectrum disorder and schizophrenia^20–23. We therefore took advantage of the previously described16 Scn2a^+/− heterozygous mouse and focused specifically on hippocampal activity, given its prominent role in memory dependent processes, to probe how altered SPW-R activity might relate to neurological dysfunction.

Results

Scn2a^+/− mice show delayed learning in spatial working memory tasks.

To assess spatial learning, Scn2a^+/− (SCN) and wild-type littermate control (CTR) mice were trained over the course of several weeks to obtain a food reward by navigating to the correct goal location depending on the randomly assigned starting box (Fig. 1a). Control subjects learned the task faster, exceeding the upper chance level following 9 d training, while Scn2a^+/− mice continued to perform at chance level until day 13 (Fig. 1b) and remained consistently poorer than controls until day 15 (genotype × training day: F = 19.3, P = 0.0006, two-way repeated measures ANOVA, post hoc comparison Bonferroni test P < 0.05 days 12–14, Fig. 1b). An analogous acquisition phenotype was seen in the Barnes maze, a test of spatial reference memory. Here Scn2a^+/− mice learned more slowly, reflected in increased escape latencies, particularly on the third day of training (genotype × training day: F(_3,72) = 5.19, P = 0.0027, two-way repeated measures ANOVA, post hoc comparison Bonferroni test P < 0.01 on day 3; latency (day 3): CTR: 89.5 ± 13.6 s, N = 14; SCN: 148.3 ± 21.4 s, N = 14, Supplementary Fig. 1), despite similar average speeds between the groups (F(_3,72) = 0.878, P = 0.46, two-way repeated measures ANOVA).

Fig. 1|. Spatial encoding is unaltered despite deficits in spatial working memory task performance.

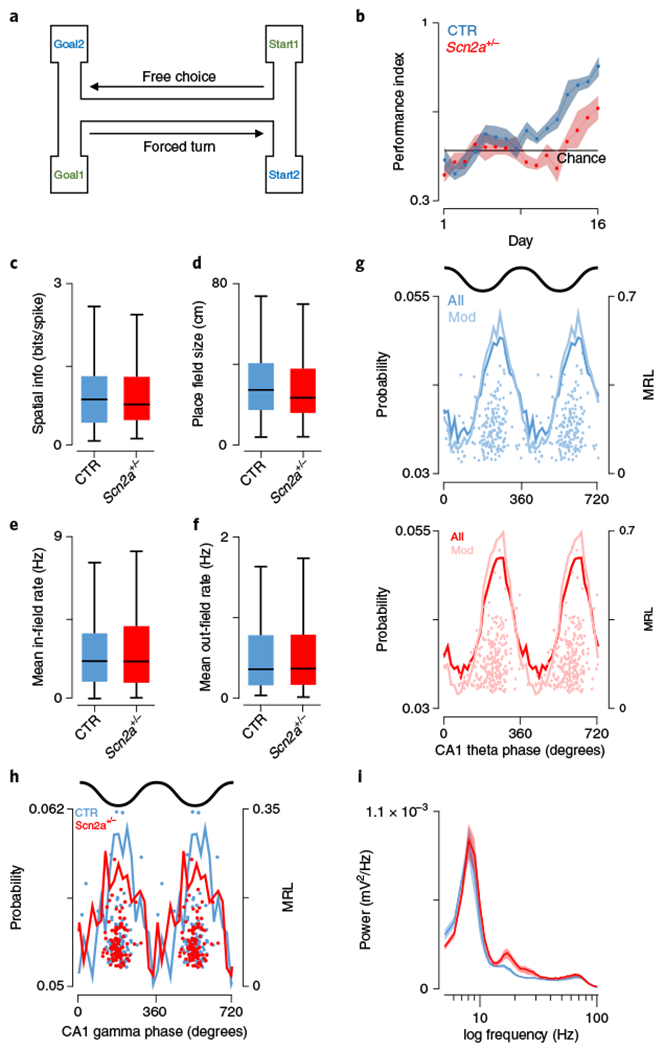
a, Schematic representation of the spatial working memory task, in which subjects needed to choose the correct goal location dependent on a brief holding period in a forced start location. b, Performance over time (blue, controls (CTR); Scn2a^+/− (SCN), red; shaded region, s.e.m.) in a spatial working memory task, highlighting faster learning and significantly better performance overall in control mice (P = 0.0006, F = 19.3, two-way repeated-measures ANOVA, followed by post hoc Bonferroni test P < 0.05 on days 12–14; CTR: N = 8 animals; SCN: N = 8 animals). c, Spatial information of place cell populations did not differ between groups (P = 0.74, Z = 0.33, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 229 cells; SCN: N = 7 animals, n = 282 cells). d, Place fields in a 1.5-m linear track were comparable in size between genotypes (P = 0.13, Z = 1.54, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 229 cells; SCN: N = 7 animals, n = 282 cells). e,f, Firing rates for pyramidal neurons either within place fields (e) (P = 0.97, Z = 0.038, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 229 cells; SCN: N = 7 animals, n = 282 cells) or outside of their receptive fields (f) (P = 0.39, Z = 0.86, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 229 cells; SCN: N = 7 animals, n = 282 cells) were not significantly different across groups. g, Theta phase preference was similar between groups in both strength (P = 0.77, F = 0.088, ANOVA; CTR: N = 7 animals, n = 184 cells; SCN: N = 7 animals, n = 233 cells) and the preferred phase angle (P = 0.87, F = 0.026, circular ANOVA; CTR: N = 7 animals, n = 184 cells; SCN: N = 7 animals, n = 233 cells). Mean phase probabilities are shown for all (dark lines) and significantly modulated cells (Mod; light lines); top, control; bottom, Scn2a^+/−. Scatter plots show the preferred phase and mean resultant length for all significantly modulated cells. h, Significantly gamma-modulated place cells were entrained by gamma rhythms to the same extent (P = 0.15, F = 2.05, ANOVA; CTR: N = 7 animals, n = 89 cells; SCN: N = 7 animals, n = 97 cells); however, Scn2a^+/− cells discharged at significantly earlier phases (P = 0.006, F = 7.74, circular ANOVA; CTR: N = 7 animals, n = 89 cells; SCN: N = 7 animals, n = 97 cells). i, Spectral power of CA1 stratum pyramidale local field potentials were not significantly different in either the theta (6–12 Hz, P = 0.65, t(12) = 0.47, Student’s two-sided t-test; CTR: N = 7 animals; SCN: N = 7 animals) or gamma frequency bands (30–80 Hz, P = 0.54, t(12) = 0.63, Student’s t-test; CTR: N = 7 animals; SCN: N = 7 animals); controls, blue; red, Scn2a^+/−; shaded areas, s.e.m. All box plots represent median (black line) and 25th–75th percentiles, with whiskers extending to the extreme data points excluding outliers, which are plotted as individual crosses. *P < 0.05.

Place field properties and spike-LFP interactions are not disrupted in Scn2a^+/− mice.

Spatial memory is a hippocampus-dependent process^2,10,24, and therefore, to better understand the decreased behavioral performance we observed, we recorded CA1 place cell activity in control and Scn2a^+/− mice during exploration of a linear track (Supplementary Fig. 1). The spatial information of CA1 place cells, a metric of their ability to effectively code precise locations, was comparable across groups (CTR: 0.95 ± 0.045 bits/spike, N = 7 mice, n = 229 cells; SCN: 0.88 ± 0.034 bits/spike, N = 7, n = 282, Z = 0.33, P = 0.742, Wilcoxon rank-sum, Fig. 1c). Consistent with this observation, place fields were similar in size (CTR: 31.29 ± 1.29 cm, N = 7, n = 229; SCN: 29.65 ± 1.18 cm, N = 7, n = 282, Z = 1.54, P = 0.125, Wilcoxon rank-sum, Fig. 1d) and single-cell mean firing rates did not differ within (CTR: 2.65 ± 0.13 Hz, N = 7, n = 229; SCN: 2.74 ± 0.13 Hz, N = 7, n = 282, Z = 0.038, P = 0.97, Wilcoxon rank-sum, Fig. 1e) or outside of (CTR: 0.49 ± 0.032 Hz, N = 7, n = 229; SCN: 0.54 ± 0.034 Hz, N = 7, n = 282, Z = 0.86, P = 0.39, Wilcoxon rank-sum, Fig. 1f) their receptive fields. Given the potential link between neuronal oscillations and memory performance^2,25 and the strong phase relationship between local field potentials (LFPs) and spike timing in hippocampal circuits²⁶, we compared spike-LFP interactions across groups. Coupling to theta frequency (6–12 Hz) oscillations was consistent across groups in both phase angle (CTR: 228.59° ± 53.31, N = 7, n = 184, (80.4% were significantly modulated); SCN: 229.61° ±46.13, N = 7, n = 233, (82.6% were significantly modulated), F = 0.026, P = 0.87, circular ANOVA, Fig. 1g) and strength (mean resultant length (MRL) CTR: 0.18 ± 0.006, N = 7, n = 184; SCN: 0.18 ± 0.006, N = 7, n = 233, F = 0.088, P = 0.77, ANOVA, Fig. 1g). Similarly, we observed only a minor difference in gamma frequency (30–80 Hz)-related spike timing (preferred phase CTR: 192.96 ± 35.58°, N = 7, n = 89 (38.9% significantly modulated); SCN: 178.91 ± 30.16°, N = 7, n = 97 (34.4% significantly modulated), F = 7.74, P = 0.006, circular ANOVA, Fig. 1h), while the extent of phase locking was comparable (MRL CTR: 0.11 ± 0.006, N = 7, n = 89; SCN: 0.096 ± 0.004, N = 7, n = 97, F = 2.05, P = 0.15, ANOVA, Fig. 1h). This was consistent with the LFP powers we observed in the theta and gamma bands in Scn2a^+/− mice, which were not different from controls (area power theta (6–12 Hz) CTR: 0.0032 ± 3.34 × 10⁻⁴, N = 7; SCN: 0.0034 ± 3.21 × 10⁻⁴, N = 7, t(12) = 0.47, P = 0.65, t-test; area power gamma (30–80 Hz) CTR: 0.0032 ± 3.94 × 10⁻⁴, N = 7; SCN: 0.0035 ± 4.40 × 10⁻⁴, N = 7, t(12) = 0.63, P = 0.54, t-test, Fig. 1i).

Place cell discharge during SPW-Rs is reduced in Scn2a^+/− mice.

Our comparison of place coding and rhythmic LFP activity in CA1 suggested that the behavioral deficits we observed were unlikely to be related to changes in physiology during the encoding of spatial environments. We therefore turned our attention to the consolidation process proposed to occur during periods of postlearning²⁷, where groups of cells coding previously traversed trajectories reactivate in a time-compressed manner during SPW-Rs (Supplementary Fig. 2). While individual ripple episodes vary in their frequency and duration, across all events they were not significantly different between genotypes (SPW-R frequency: CTR: 154.6 ± 1.36 Hz, N = 7; SCN: 156.4 ± 0.53 Hz, N = 7, t(12) = 1.26, P = 0.23, t-test; SPW-R duration: CTR: 122.5 ± 8.7 ms, N = 7; SCN: 114.6 ± 1.8 ms, N = 7, t(12) = 0.89, P = 0.39, t-test, Fig. 2a) and were of similar length to those reported previously^5,28–31. It has been proposed that slow gamma activity during SPW-Rs may play an important role in synchronizing networks, leading to higher quality ensemble reactivations³²; this is supported by recent data showing a reduction in animals with memory deficits³³. While our data demonstrate that SPW-R episodes were accompanied by robust slow gamma oscillations, we observed no change in their amplitude between groups (wavelet amplitude 140–160 Hz CTR: 7.99 ± 0.046, N = 7, n = 2,372; SCN: 8.01 ± 0.058, N = 7, n = 1,811, Z = 1.24, P = 0.21, Wilcoxon rank-sum, Fig. 2b; wavelet amplitude 20–40 Hz CTR: 1.34 ± 0.033, N = 7, n = 2,372; SCN: 1.37 ± 0.058, N = 7, n = 1,811, Z = 1.36, P = 0.17, Wilcoxon rank-sum, Fig. 2b). Phase locking to slow gamma during SPW-Rs was relatively weak, with only a small fraction of cells significantly phase locked (phase CTR: −41.2 ± 75.4°, N = 7, n = 30; SCN: 29.1 ± 76.1°, N = 7, n = 18, F = 1.11, P = 0.30, circular ANOVA; MRL CTR: 0.29 ± 0.18, N = 7, n = 30; SCN: 0.37 ± 0.21, N = 7, n = 18, F = 1.83, P = 0.18, ANOVA), while the high-frequency ripple oscillation induced strong phase locking across both genotypes (phase CTR: 188.60 ± 33.9°, N = 7, n = 190 (53.1% significantly phase locked); SCN: 182.74 ± 38.3°, N = 7, n = 131 (58.4% significantly phase locked), F = 1.86, P = 0.17, circular ANOVA; MRL CTR: 0.24 ± 0.12, N = 7, n = 190; SCN: 0.23 ± 0.14, N = 7, n = 131, F = 0.33, P = 0.57, ANOVA, Fig. 2c), in contrast to changes previously reported in a mouse model of dementia³⁴. We did, however, observe a significant decrease in the peak firing rate of pyramidal cells during SPW-R events in Scn2a^+/− mice (CTR: 2.30 ± 0.15 Hz, N = 7, n = 190; SCN: 1.45 ± 0.14 Hz, N = 7, n = 131, Z = 4.36, P = 1.30 × 10⁻⁴, Wilcoxon rank-sum, Fig. 2d and Supplementary Table 1), suggesting alterations in neural coding during the memory consolidation process. As SPW-Rs primarily occur during periods of quiescence or sleep, it was essential to rule out systematic changes in sleep between genotypes that may adversely affect SPW-R generation. To this end we quantified sleep episodes by using LFPs to calculate the percentage of time mice spent in high theta/delta ratio states and found no difference between groups (CTR: 42.1 ± 3.0%, N = 7; SCN: 39.4 ± 1.8%, N = 7, P = 0.26, Wilcoxon rank-sum).

Fig. 2|. Altered CA1 place cell activity during SPW-R episodes.

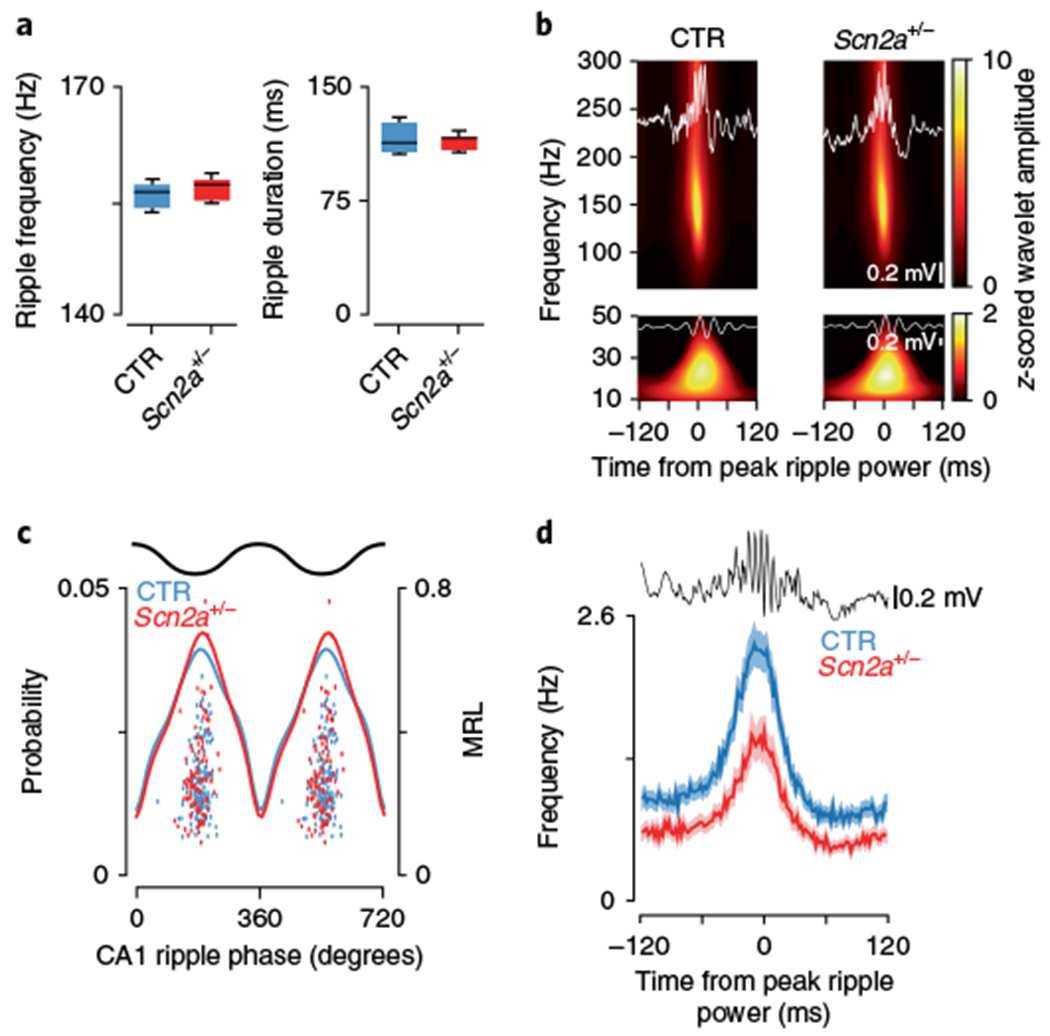
a, SPW-Rs had a similar frequency (left, P = 0.23, t(12) = 1.26, Student’s two-sided t-test; CTR: N = 7 animals; SCN: N = 7 animals) and duration (right, P = 0.39, t(12) = 0.89, Student’s two-sided t-test; CTR: N = 7 animals; SCN: N = 7 animals) in both experimental groups. b, Spectral analysis during SPW-R periods revealed that z-scored wavelet amplitudes were not significantly different in either the ripple band (top, 140–160 Hz, P = 0.21, Z = 1.24, Wilcoxon rank-sum; CTR: N = 7 animals, n = 2,372 ripples; SCN: N = 7 animals, n = 1,811 ripples) or the low gamma band (bottom, 20–40 Hz, P = 0.17, Z = 1.36, Wilcoxon rank-sum; CTR: N = 7 animals, n = 2,372 ripples; SCN: N = 7 animals, n = 1,811 ripples). c, Ripple phase preference was similar between groups in both strength (P = 0.57, F = 0.33, ANOVA; CTR: N = 7 animals, n = 190 cells; SCN: N = 7 animals, n = 131 cells) and the preferred phase angle (P = 0.17, F = 1.86, circular ANOVA; CTR: N = 7 animals, n = 190 cells; SCN: N = 7 animals, n = 131 cells). Mean phase probabilities are shown for all significantly modulated cells (solid lines), with overlaid scatter plots showing the preferred phase and mean resultant length for all significantly modulated neurons. d, Place cells in control mice (blue) had significantly elevated peak firing rates during SPW-Rs compared with the Scn2a^+/− (red) group (P = 1.30 × 10⁻⁴, Z = 4.36, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 190 cells; SCN: N = 7 animals, n = 131 cells); shaded area signifies s.e.m. All box plots represent median (black line) and 25th–75th percentiles, with whiskers extending to the extreme data points excluding outliers, which are plotted as individual crosses. *P < 0.05.

Cell assembly activation is specifically altered during SPW-Rs.

We reasoned that the changes observed in single-cell activities during SPW-Rs may affect the precise organization of activity across the population. To address this we used a combination of principal component and independent component analyses to identify the coactivation of groups of neurons (cell assemblies; Supplementary Fig. 3) and track their activity over time (Fig. 3a). Cell assemblies were initially identified from place cell activity during linear track exploration, where their expression strengths were comparable between groups (CTR: 43.67 ± 47.98, N = 7, n = 96 cell assemblies; SCN: 44.30 ± 60.93, N = 7, n = 132 cell assemblies, Z = 0.22, P = 0.83, Wilcoxon rank-sum, Supplementary Fig. 3). Within a session, cells in the same assembly had consistently higher co-firing coefficients (members: 0.065 ± 0.005, n = 59 cell pairs; nonmembers: 0.0034 ± 0.0012, n = 105 cell pairs, Z = 9.92, P = 3.32 × 10⁻²³, Wilcoxon rank-sum, Supplementary Fig. 3) and place-field similarity scores (members: 0.62 ± 0.038, n = 59 cell pairs; nonmembers: 0.024 ± 0.035, n = 105 cell pairs, Z = 8.25, P = 1.62 × 10⁻¹⁶, Wilcoxon rank-sum, Supplementary Fig. 3) than nonmembers. This was consistent across all mice, of both groups (co-firing coefficient CTR: members: 0.080 ± 0.006, N = 7; nonmembers: 0.006 ± 3.74 × 10⁻⁴, N = 7, Z = 15.3, P = 1.28 × 10⁻⁵², Wilcoxon rank-sum, Supplementary Fig. 3; place field similarity CTR: members: 0.44 ± 0.040, N = 7; nonmembers: 0.014 ± 0.01, N = 7, Z = 9.55, P = 1.25 × 10⁻²¹, Wilcoxon rank-sum; co-firing coefficient SCN: members: 0.080 ± 0.005, N = 7; nonmembers: 0.004 ± 3.41 × 10⁻⁴, N = 7, Z = 17.3, P = 7.82 × 10⁻⁶⁷, Wilcoxon rank-sum, Supplementary Fig. 3; place field similarity SCN: members: 0.38 ±0.033, N = 7; nonmembers: 0.004 ±0.009, Z = 10.3, P = 4.31 × 10⁻²⁵, Wilcoxon rank-sum, Supplementary Fig. 3). Further, across genotypes there were no differences in place field similarity for either assembly members (N = 7, 7, Z = 1.02, P = 0.31, Wilcoxon rank-sum, Supplementary Fig. 3) or assembly nonmembers (N = 7, 7, Z = 0.35, P = 0.73, Wilcoxon rank-sum, Supplementary Fig. 3). In contrast to run sessions, the strength of assembly reactivation during SPW-Rs (in the subsequent rest session) was higher in controls, suggesting alterations in Scn2a^+/− mice to the normally precisely controlled population organization of SPW-R-associated neuronal discharge (reactivation strength CTR: 334.6 ± 35.60, N = 7, n = 85; SCN: 181.1 ± 7.19, N = 7, n = 123, Z = 2.13, P = 0.034, Wilcoxon rank-sum, Fig. 3b). Next we specifically considered only SPW-R activations of multiple cell assemblies (Fig. 3c), which would be expected to encode sequences of spatial trajectories, the basis of spatial memory consolidation. On average, when considering only SPW-Rs with more than one significant (reactivation strength (R) > 5) assembly activation, the fraction of cell assemblies coactivated per ripple in mutant mice was significantly lower (CTR: 0.22 ± 0.003, N = 7, n = 2,049; SCN: 0.21 ± 0.002, N = 7, n = 2,946, Z = 2.37, P = 0.018, Wilcoxon rank-sum, Fig. 3d). Moreover, we tracked repeated activations of the same multiple assembly groups throughout the session, allowing us to establish how accurately and to what extent they were reinstated. Compared with controls, both lower strength (normalized strength CTR: 0.110 ± 0.008, N = 7, n = 227; SCN: 0.108 ± 0.005, N = 7, n = 232, Z = 2.29, P = 0.022, Wilcoxon rank-sum, Fig. 3e) and lower rate (normalized rate CTR: 0.12 ± 0.005, N = 7, n = 227; SCN: 0.086 ± 0.005, N = 7, n = 232, Z = 7.85, P = 4.11 × 10⁻¹⁵, Wilcoxon rank-sum, Fig. 3f,g) was observed in Scn2a^+/− mice. Taken as a whole, these data suggest that SPW-Rs in mutant mice are associated with either poorer or less complete trajectory information compared with control subjects, which manifests as reduced performance in spatial memory-dependent tasks.

Fig. 3|. Altered CA1 cell assembly properties in Scn2a^+/− mice.

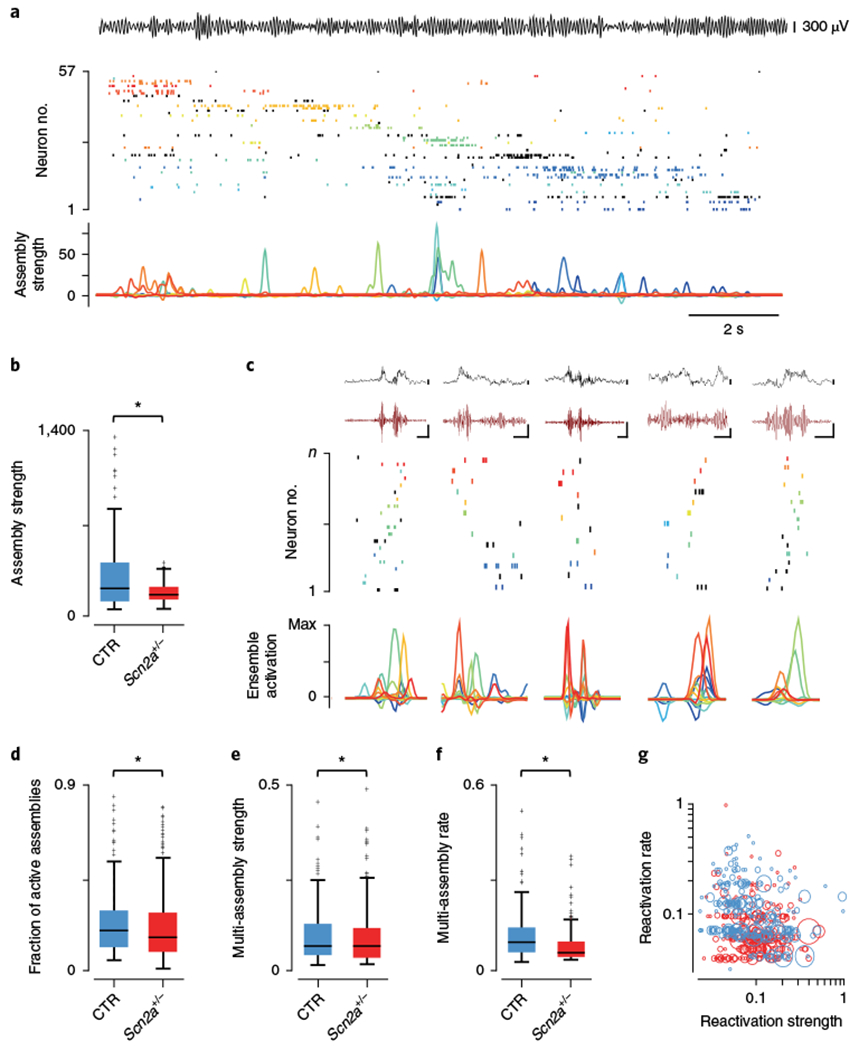
a, Example showing a single lap of the linear track with the theta (6–12 Hz) filtered CA1 stratum pyramidale LFP shown at top. The middle raster plot shows spiking activity during this run of all 57 simultaneously recorded place cells, with separate colors denoting groups of neurons identified as belonging to a single cell assembly (13 assemblies in total). Neurons shown in black are included for completeness but did not form part of any significant cell assembly during the principal component analysis. Shown below is the expression strength of each cell assembly over time. b, Assembly reactivation strength during SPW-R periods was significantly reduced (P = 0.034, Z = 2.13, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 85 cell assemblies; SCN: N = 7 animals, n = 123 cell assemblies) in Scn2a^+/− mice (red) compared to controls (blue). c, Examples of reactivation, during postexploration rest, of cell assemblies identified from linear track sessions. Top: raw (black) and filtered (120–240 Hz, dark red) CA1 SPW-R LFPs. Scale bars represent 100 ms (horizontal) and 100μV (vertical) throughout. Middle: concurrent spiking activity with individual cell assemblies color coded and ordered by their track position. Bottom: relative reactivation strength and temporal ordering across the SPW-R episode. d, A significantly higher proportion of cell assemblies were active on average during SPW-Rs in control animals (P = 0.018, Z = 2.37, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 2,049 events; SCN: N = 7 animals, n = 2,946 events). e,f, The normalized strength of reactivation for multicell-assembly-containing SPW-Rs was also significantly higher in control subjects (e, P = 0.022, Z = 2.29, two-sided Wilcoxon rank-sum; CTR: N = 7 animals; SCN: N = 7 animals), while the frequency at which they were reactivated was also greater (f, P = 4.11 × 10⁻¹⁵, Z = 7.85, two-sided Wilcoxon rank-sum; CTR: N = 7 animals; SCN: N = 7 animals). g, Scatter plot showing the normalized rate and strength at which each repeatedly reactivated group of cell assemblies were active together during SPW-Rs. Multi-assembly groups are colored according to genotype (blue, control; red, Scn2a^+/−) and scaled according to the number of active cell assemblies. All box plots represent median (black line) and 25th–75th percentiles, with whiskers extending to the extreme data points excluding outliers, which are plotted as individual crosses. *P < 0.05.

Changes in SPW-R inhibitory/excitatory balance are accompanied by truncated replay sequences.

To determine the effect of altered firing during SPW-Rs, firing rate vectors constructed from place cells during track exploration were used to decode³⁵ ripple-associated place cell activity in subsequent sleep sessions (Fig. 4a and Supplementary Fig. 4). Since decoding is sensitive to the number of simultaneously recorded neurons, we first confirmed that both the number of cells (CTR: 32.7 ± 4.2 cells/animal, N = 7; SCN: 41.0 ± 3.9 cells/animal, N = 7, P = 0.13, Wilcoxon rank-sum) and the quality of decoding (whole exploratory sessions) were comparable between genotypes (error CTR: 16.6 ± 2.0%, N = 7; SCN: 16.6 ± 2.2%, N = 7, P = 0.99, Wilcoxon rank-sum, Supplementary Fig. 4). To assess the quality of replayed trajectories detected from significant increases in multiunit activity (MUA), nonsignificant sequences were first excluded (see Methods), after which weighted correlations of decoded position and time were calculated for each remaining event and normalized as Z scores (rZ sequence score²⁹). Across the population, replays during SPW-Rs were of equivalent quality between genotypes (rZ, CTR: 2.31 ± 0.037, N = 7, n = 203 events; SCN: 2.34 ± 0.034, N = 7, n = 271 events, Z = 0.55, P = 0.58, Wilcoxon rank-sum, Fig. 4b). However, individual events on average spanned shorter track lengths in Scn2a^+/− subjects (place field shuffling CTR: 80.87 ± 2.17 cm, N = 7, n = 203; SCN: 71.09 ± 1.96 cm, N = 7, n = 271, Z = 3.39, P = 7.03 × 10⁻⁴, Wilcoxon rank-sum, Fig. 4c; cell identity shuffling CTR: 82.0 ± 3.0 cm, N = 7; SCN: 73.1 ± 2.8 cm, N = 7, Z = 2.2, P = 0.031, Wilcoxon rank-sum), together with corresponding decreases in both replay speed (CTR: 6.36 ± 0.22 m/s, N = 7, n = 203; SCN: 5.73 ± 0.20 m/s, N = 7, n = 271, Z = 2.53, P = 0.012, Wilcoxon rank-sum, Fig. 4d) and the mean jump distance between adjacent decoded positions (CTR: 15.37 ± 0.44 cm, N = 7, n = 203; SCN: 13.44 ± 0.40 cm, N = 7, n = 271, Z = 3.48, P = 4.94 × 10⁻⁴, Wilcoxon rank-sum, Fig. 4e). Since inhibition plays a key role in pacing pyramidal cell ensemble spiking during ripples³⁶ and we observed SPW-R-specific decreases in pyramidal cell firing rates (but not waveform properties: amplitude CTR: 0.27 ± 0.009 mV, N = 7, n = 229; SCN: 0.27 ± 0.006 mV, N = 7, n = 287, Z = 0.95, P = 0.34, Wilcoxon rank-sum, Supplementary Fig. 4; half-width CTR: 0.21 ± 0.002 ms, N = 7, n = 229; SCN: 0.22 ± 0.0004 ms, N = 7, n = 287, Z = 1.88, P = 0.06, Wilcoxon rank-sum, Supplementary Fig. 4), we next identified par-valbumin-like (PV) interneurons (Supplementary Fig. 4) to characterize changes that might underlie the altered replay dynamics observed in Scn2a^+/− mice. Within SPW-Rs, PV interneurons fired at later phases of the ripple cycle in mutants, but were phase locked to a similar degree (CTR: 227.3 ± 71.8°, N = 7, n = 23 (73.1% significantly phase locked); SCN: 313.4 ± 70.4°, N = 7, n = 34 (72.7% significantly phase locked), F = 4.14, P = 0.047, circular ANOVA; MRL CTR: 0.12 ± 0.016, N = 7, n = 23; SCN: 0.095 ± 0.012, N = 7, n = 34, Z = 1.50, P = 0.13, Wilcoxon rank-sum, Fig. 4f). Moreover, SPW-R associated firing rates of interneurons were significantly elevated in Scn2a^+/− mice (Fig. 4g and Supplementary Table 1) when considering only PV cells (CTR: 34.91 ± 3.15 Hz, N = 7, n = 23; SCN: 43.15 ± 2.75 Hz, N = 7, n = 34, Z = 2.10, P = 0.036, Wilcoxon rank-sum). We hypothesized that this shift in inhibition to later ripple phases may have consequences for the precise maintenance of pyramidal cell timing during ripples. To this end, we calculated mean relative spike phases for every pyramidal cell, with the first spike in every ripple assigned to the first cycle and all subsequent spike phases calculated relative to this. Here, while we observed a relatively consistent phase locking to the trough of the ripple cycle (as in Fig. 2c), as SPW-Rs progressed significant deviations in phase occurred earlier in Scn2a^+/− mice (12th cycle CTR: 147.5 ± 77.2°, N = 7, n = 77; SCN: 325.1 ± 79.5°, N = 7, n = 84, F = 6.82, P = 0.009, circular ANOVA, Fig. 4h) than controls (14th cycle CTR: 191.8 ± 70.9°, N = 7, n = 76; 15th cycle CTR: 265.2 ± 77.4°, N = 7, n = 73, F = 4.24, P = 0.041, circular ANOVA, Fig. 4h). In agreement with our observations that these changes were specific to SPW-Rs, another form of population organization, the frequency of the unit relative to LFP, that occurs during theta (phase precession) remained intact (CTR: + 0.63 ± 0.04 Hz, N = 7, n = 224; SCN: + 0.68 ± 0.04 Hz, N = 7, n = 274, Z = 1.16, P = 0.24, Wilcoxon rank-sum, Supplementary Fig. 4).

Fig. 4|. Replayed trajectory sequences are truncated in Scn2a^+/− mice.

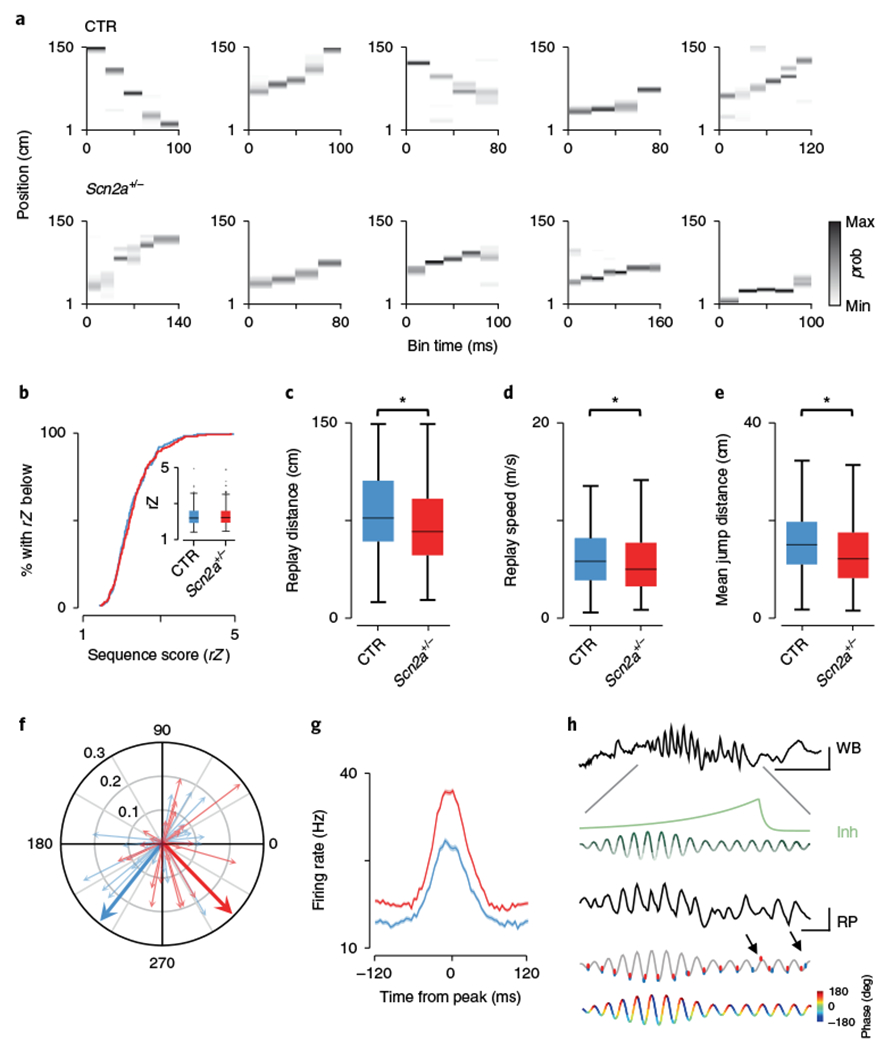
a, Examples of trajectory sequences derived from Bayesian decoding of spiking activity during SPW-Rs. Top, controls; bottom, Scn2a^+/− mice; p, probability. b, Cumulative distribution of replay event sequence scores (rZ) for control (blue) and Scn2a^+/− (red), with medians and data distribution displayed in the inset (P = 0.58, Z = 0.55, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 203 events; SCN: N = 7 animals, n = 271 events). c, Mean distance of the linear track spanned by all replay events (P = 7.03 × 10⁻⁴, Z = 3.39, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 203 events; SCN: N = 7 animals, n = 271 events). d, Average speed in m/s of progression from starting position to end position for all replay events (P = 0.012, Z = 2.53, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 203 events; SCN: N = 7 animals, n = 271 events). e, The average spatial jump in centimeters for decoded positions in adjacent temporal bins, for each replay event (P = 4.94 × 10⁻⁴, Z = 3.48, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 203 events; SCN: N = 7 animals, n = 271 events). f, Polar plot showing the mean phase angle at which all PV fast-spiking interneurons discharge during SPW-Rs (130–180 Hz). Individual neurons are shown as thin pastel arrows, with length indicating the mean resultant length and 0° and 180° representing the peak and trough of the ripple oscillation. Genotype means are displayed as thick arrows and indicate only phase (MRL: P = 0.13, Z = 1.50, Wilcoxon rank-sum; CTR: N = 7 animals, n = 23 putative PV cells; SCN: N = 7 animals, n = 34 putative PV cells; angle: P = 0.047, F = 4.14, circular ANOVA; CTR: N = 7 animals, n = 23 putative PV cells; SCN: N = 7 animals, n = 34 putative PV cells). g, Mean firing rate of all PV interneurons across a 240-ms window centered on the peak power of each ripple event; shaded areas, s.e.m. (P = 0.036, Z = 2.10, two-sided Wilcoxon rank-sum; CTR: N = 7 animals, n = 23 putative PV cells; SCN: N = 7 animals, n = 34 putative PV cells). h, WB: an unfiltered example of a SPW-R event recorded from CA1 stratum pyramidale. In green is a schematic showing the predicted build-up of inhibition (Inh) across the expanded ripple event (RP), based on ref. ⁴¹, together with cycle-by-cycle fluctuations in inhibition (with darker colors representing greatest inhibition). In gray is the same ripple bandpass filtered (130–180 Hz); overlaid on this are mean data for all place cells showing mean spike phase of all ripple spikes per cycle relative to the first spike (controls, blue; Scn2a^+/−, red). Arrows denote significant changes from mean ripple discharge phase (first arrow: cycle phase CTR vs. Scn2a^+/−, P = 0.0099, F = 6.82, circular ANOVA; CTR: N = 7 animals; SCN: N = 7 animals; second arrow: preceding 14th (CTR) vs. current 15th cycle (CTR) phase, P = 0.041, F = 4.24, circular ANOVA; N = 7 animals). Ripple phase is shown at the bottom for clarity; scale bars represents 10 ms and 300 μV throughout. All box plots represent median (black line) and 25th–75th percentiles, with whiskers extending to the extreme data points excluding outliers, which are plotted as individual crosses. *P < 0.05.

Since increases in MUA can occur independently of SPW-R activity, we confirmed our findings by including an additional 1.5 s.d. threshold for ripple power (in addition to the MUA threshold) for event detection. Replay quality during SPW-Rs was equivalent between genotypes (rZ, CTR: 2.14 ± 0.03, N = 7, n = 241 events; SCN: 2.21 ± 0.03, N = 7, n = 255, Z = 0.98, P = 0.33, Wilcoxon rank-sum, Supplementary Fig. 5), with time and space strongly correlated (CTR: 0.65 ± 0.01, N = 7, n = 241; SCN: 0.63 ± 0.01, N = 7, n = 255, Z = 1.1, P = 0.26, Wilcoxon rank-sum). As in events detected solely from MUA activity, we observed sequences than spanned significantly shorter distances in Scn2a+^/− subjects (CTR: 84.4 ± 2.2 cm, N = 7, n = 241; SCN: 71.5 ± 2.0 cm, N = 7, n = 255, Z = 4.23, P = 2.4 ×10⁻⁵, Wilcoxon rank-sum, Supplementary Fig. 5), progressed slower (CTR: 6.7 ± 0.24 m/s, N = 7, n = 241; SCN: 5.5 ± 0.22 m/s, N = 7, n = 255, Z = 3.5, P = 4.1 × 10⁻⁴, Wilcoxon rank-sum, Supplementary Fig. 5) and had reduced jump distance between adjacent decoded positions (CTR: 22.1 ± 0.61 cm, N = 7, n = 241; SCN: 19.6 ± 0.61 cm, N = 7, n = 255, Z = 2.41, P = 0.016, Wilcoxon rank-sum, Supplementary Fig. 5) when ripple power was included as a detection parameter (Supplementary Fig. 5).

Several independent studies have focused on manipulating SPW-R activity in both the awake and sleep states^{5,6,12,28,29,35}, revealing there to be substantial overlap for their roles in spatial learning and consolidation^{10–12,31,37}. With this in mind, we identified awake SPW-Rs from concurrent rises in MUA and ripple-band LFP activity to establish whether the changes we observed were state dependent or common to all SPW-R events. In the awake state, decoded events during SPW-Rs (Supplementary Fig. 5) had similar sequence scores (CTR: 2.3 ±0.06, N = 7, n = 59; SCN: 2.3 ± 0.05, N = 7, n = 88, Z = 0.03, P = 0.97, Wilcoxon rank-sum, Supplementary Fig. 5) but displayed the same reductions in decoded path lengths (CTR: 101.0 ± 5.0 cm, N = 7, n = 59; SCN: 87.5 ± 4.1 cm, N = 7, n = 88, Z = 2.0, P = 0.044, Wilcoxon rank-sum, Supplementary Fig. 5) and speed (CTR: 8.5 ± 0.47 m/s, N = 7, n = 59; SCN: 7.2 ± 0.37 m/s, N = 7, n = 88, Z = 2.2, P = 0.027, Wilcoxon rank-sum, Supplementary Fig. 5).

Discussion

Our study is centered on the hypothesis that SPW-Rs represent the process by which spatial memories are consolidated and used to plan behavior. This is based on several previous studies that either demonstrated a correlation between SPW-Rs and memory^5,6,9 or demonstrated that artificial disruption of the events produce reductions in behavioral performance^10–12; however, perhaps the most convincing proof—that SPW-R information content is altered in a disease associated with impaired memory—has remained elusive. We directly addressed this question by taking advantage of the Scn2a^+/− mouse, which displays impaired learning in multiple spatial memory tasks, and were able to characterize changes in neural coding specifically occurring during SPW-Rs.

An accumulating body of experimental observations have identified SPW-Rs as fundamental to learning and memory^{5–7,9,10,27,29,30,32,34,35,38}, suggesting that neurological disorders resulting in memory or learning deficits might exert their effect through alterations to neural coding specifically during these transient events. Our characterization of place cell activity during linear track exploration appears consistent with this, as in this mouse model of impaired learning, neural activity was qualitatively not different from control mice. No changes to either excitability (Fig. 1e,f), receptive field size (Fig. 1d) or the ability of principal cells to generate a rate map of space (Supplementary Fig. 1) were associated with the heterozygous deletion of the Scn2a gene, suggesting the process of initially encoding spatial representations remained intact. Consistent with these observations, no changes were observed in phase locking to either theta or gamma frequency rhythms (Fig. 1g,h), which constitute an important mechanism by which neurons within the hippocampal–entorhinal loop can organize and temporally segment their outputs³⁹. Notably, when we began to compare SPW-Rs between genotypes, many of their characteristic features were identical, including their intrinsic frequency, duration of the episodes, the power of co-occurring gamma oscillations (Fig. 2) and the phase preference of place cells with respect to the high-frequency oscillation (120–200 Hz) component. This is somewhat in contrast to previously observed changes to both the amplitude and temporal dynamics of SPW-Rs reported in a model of neurodegenerative disease; however, those profound changes are most likely attributable to the substantial neuronal losses associated with the rTg4510 mouse line³⁴.

Although no differences were observed to the oscillatory component of SPW-Rs, changes to the underlying neuronal activity were clearly evident. Specifically, the decreased pyramidal cell firing rates and corresponding increase in putative PV interneuron activity point to a shift in the inhibitory/excitatory balance in the CA1 network, skewed toward increased levels of inhibition. Such a change to the degree of drive in the CA1 network would, unsurprisingly, have implications for coding, given that strong phasic inhibitory inputs to pyramidal cells govern ripple dynamics^36,40,41. In this regard, both the cell assembly and Bayesian decoding analyses of SPW-R population activity point to impaired replay of previously encoded sequences of spatial trajectories in Scn2a^+/− mice compared with controls. Specifically, the weaker reactivation strength of cell assemblies (Fig. 3b) and the shift toward fewer (a smaller fraction of) assemblies reactivating during single SPW-Rs (Fig. 3d) suggest incomplete replay, which was supported by the finding that decoded events spanned shorter portions (Fig. 4c) of the track in Scn2a^+/− mice. As hippocampal replay is proposed to be crucial for both memory^{7,9,10,32,35,38,42} and planning^5,6,28 during memory based tasks, the perturbations we observed to this process during both the quiescent (Fig. 4c) and awake (Supplementary Fig. 5) states would have consequences for learning any memory-dependent behavior, as we observed for both spatial memory tasks tested. Moreover our data further blur the distinction between awake and sleep SPW-Rs, particularly when viewed in the context of previous studies that disrupted SPW-Rs in both the awake¹² and quiescent states^10,11, but produced similar performance deficits. These findings, together with recent data showing that ripples in both states engage prefrontal cortex³¹, suggest that assigning functionally distinct roles for awake and sleep SPW-Rs may be an oversimplification³⁷.

Although the specific mechanism by which SPW-Rs are naturally terminated remains unclear, a realistic assumption would be that the inhibitory input exceeds the excitatory drive to the principal cell population, preventing discharge. This is consistent with in vivo whole-cell data from awake mice that shows a ramping inhibitory input to principal cells throughout the SPW-R episode, with the peak inhibition temporally corresponding to the end of the event⁴¹. Moreover, firing is tightly modulated over each ripple cycle by inhibition, with the probability of pyramidal cell discharge highly skewed toward the troughs of the LFP oscillation (Fig. 2c)⁴³. Our results highlight a significant shift in PV inhibitory cell spiking in Scn2a^+/− mice to later phases of the ripple oscillation (Fig. 4f), moving them closer to the preferred discharge window of pyramidal cells. While this change may be tolerable initially in the SPW-R event when pyramidal cells can overcome the still relatively weak inhibition, this shift has the potential, as inhibition continues to rise as the ripple progresses, to delay pyramidal cell spiking to later phases (until inhibition has sufficiently faded), leading to cycle skipping and thus ending the event prematurely (Fig. 4h). While it has been reported that ripples can occur in close temporal proximity³⁵ leading to the possibility that these concatenated ripples may simply not have been present in Scn2a^+/− mice, our data show this was not the case (Supplementary Table 1).

This study adds evidence to the already extensive literature detailing the importance of SPW-Rs in forming stable, retrievable memories that can direct the appropriate behavioral response in cognitively demanding tasks. In contrast to other mutant studies that have detailed changes to SPW-Rs themselves, we demonstrate in Scn2a^+/− mice that an overall increase and altered timing of inhibition specifically during SPW-Rs most likely leads to the early termination of trajectories encoded during SPW-Rs, while leaving the LFP events themselves intact. While it might be tempting to speculate that this represents a common mechanism shared by multiple neurodegenerative diseases, it is more likely that similarly subtle alterations to the precise balance of excitatory and inhibitory drive, or alterations in the timing of these phasic inputs to cell-assemblies, lead to abnormal population organization during SPW-Rs that varies across diseases.

Methods

Methods, including statements of data availability and any associated accession codes and references, are available at https://doi.org/10.1038/s41593-018-0163-8.

Methods

Subjects.

In total 29 male Scn2a^+/− heterozygous knockout mice (MGI: 2180186) and 29 male wild-type littermate mice were used in this study; of those, 8 of each genotype were used exclusively to test behavioral performance in the alternation task, 14 in the Barnes maze and the remaining 7 for in vivo electrophysiology (1 experimental session per animal was used for place cell, replay and SPW-R analyses, in order not to skew the results with outlier subjects). All subjects were aged between 4 and 6 months before commencement of experiments and were maintained on a 12-h light-dark cycle with ad libitum access to food and water. All procedures were approved by the RIKEN Institutional Animal Care and Use Committee and complied with all relevant ethical regulations. Experimenters were blind to the genotype of each animal throughout the course of experiments.

Spatial working memory alternation task.

Prior to training, mice were handled daily and mildly food deprived to 80% of their free-feeding weight. Mice were trained over successive days to run the continuous spatial-alternation task (Fig. 1a), which consisted of subjects being forced to the right during the forced turn epoch and having to make a left turn to obtain a food reward during the subsequent choice epoch, or vice versa. Dustless precision pellets for rodents weighing 20 mg (BioServ) constituted rewards for correct choice trials. Incorrect choices were penalized with a 20-s holding period at the incorrect goal location, without reward. Choice epochs began with a brief 5-s holding period in the starting box before release into the central arm and subsequent choice. Forced-turn direction was varied pseudorandomly to prevent more than three consecutive turns from occurring in the same direction; randomization was performed between animals and days. A total of 20 trials were performed per subject each day, with the performance index calculated as the number of correct trials divided by the total.

Barnes maze task.

The Barnes maze comprised a white circular platform with 12 circular holes, affixed 60 cm above the floor and illuminated at approximately 700 lx (O’Hara & Co). A black plastic escape box (17 × 13 × 7 cm) was located under one of the holes numbered 1, 4, 7 and 10. One day before training (day 0), mice were allowed to explore the maze without the escape box for 5 min and then placed into an escape box, which was placed underneath the target hole during training. On days 1–4, mice performed three trials per day, which consisted of mice being placed in a center column for 10 s and then allowed 5 min to find and enter the target hole. The mouse was allowed to remain in the box for 60 s, regardless of whether it found the target hole. The location of the target hole was consistent for a given mouse but randomized across mice. The maze was rotated between trials to eliminate the use of intra-maze cues.

Surgery, recording and histology.

Animals were implanted (1.82 mm posterior and 1.6 mm right-lateral from bregma) with a microdrive consisting of nine independently adjustable nichrome (14 μm diameter) tetrodes arranged in a circular bundle. Prior to surgery, tetrodes were gold plated to a resistance of 175–250 kΩ. Over the course of several, days tetrodes were slowly lowered to CA1 stratum pyramidale while the animal was contained in a small sleep box (30 cm long × 30 cm wide × 30 cm high). Data were acquired using a 32-channel Digital Lynx 4SX acquisition system (Neuralynx, Bozeman, MT). Signals were sampled at 32,556 Hz and spike waveforms filtered between 0.6 and 6 kHz. Stainless steel screws located in the skull lying above the cerebellum served as a ground, and a single tetrode situated in the superficial layers of the neocortex (devoid of spikes) was used for referencing. Position and head direction were concurrently tracked using a pair of red and green light-emitting diodes affixed to the microdrive. At the conclusion of the experiment mice underwent terminal anesthesia and electrode positions were marked by electrolytic lesioning of brain tissue (with 50 μA current for 8 s through each tetrode individually). Transcardial perfusion with 4% paraformaldehyde (PFA) followed, after which brains were removed and postfixed for a further 24 h in 4% PFA. Coronal slices 50 jam thick were prepared on a vibratome (Leica) and inspected by standard light microscopy to confirm electrode placement.

Experimental protocol.

Once tetrodes were situated in stratum pyramidale, evident by numerous large amplitude pyramidal cell spikes and sharp wave ripples during periods of immobility, recording commenced. Linear track recordings were conducted on a long rectangular arena (150 cm long × 15 cm wide × 15 cm high) and lasted either 10 min or until 20 laps had been completed, whichever occurred first. Prior to this, and immediately following, a 1-h sleep session in a small, high-walled square enclosure was recorded, allowing spike stability to be assessed.

Statistics.

All analyses were performed in Matlab (The MathWorks, Inc). Data were first tested for normality with the Kolmogorov–Smirnov test before further statistical analysis, to determine whether parametric or non-parametric statistical tests were suitable. No statistical methods were used to predetermine sample sizes; instead, we opted to use group sizes similar to those in previously published studies^4,44 to ensure variance was kept to a minimum between genotypes and cell quantities.

Unit isolation and classification.

Spike sorting was performed using SpikeSort3D software (Neuralynx), with putative cells clustered manually in three-dimensional projections of multidimensional parameter space (using both waveform amplitude and energy). To ensure tetrode stability, spikes were clustered in the sleep session preceding linear track exploration; three-dimensional cluster boundaries were then transposed onto the latter sleep session, and clusters whose spikes fell outside the original bounds were excluded from further analyses. Moreover, clusters with > 0.5% of spikes displaying an interspike interval < 2 ms, a total number of spikes not exceeding 75 or having a cluster isolation distance < 20 were discarded⁴⁵. Cells were considered pyramidal neurons if mean spike width exceeded 200 μs and had a complex spike index⁴⁶ ≥5. Putative interneurons were initially classified⁴⁷ as units having a mean firing rate > 10 Hz during exploration (velocity > 5 cm/s). These were further classified by calculating the burst index—the amplitude of the baseline-subtracted (mean between 40 and 50 ms) autocorrelogram (calculated with 1-ms bins) peak between 0 and 10 ms—and the refractory period: the first time bin of the instantaneous derivative of the autocorrelogram (between 0 ms and the peak) exceeding 1 s.d. PV interneurons were defined as having a burst index > 0 and a refractory period < 7 ms⁴⁸. We further ensured pyramidal cell and interneurons formed two separate, non-overlapping clusters by calculating their mean firing rates and an asymmetry score of their waveforms, defined as the absolute amplitude of the trough divided by the peak amplitude, multiplied by the area of the trough divided by the area of the peak. For near-symmetric waveforms like those of PV interneurons, this produced values close to 1, while asymmetric pyramidal cells yielded much lower values (Supplementary Fig. 4).

Sleep analyses.

To compare sleep between genotypes in postexploration sessions, LFPs were filtered and powers calculated in both the delta (0–4 Hz) and theta (6–12 Hz) bands. The instantaneous theta/delta ratio was then binned into 10-s epochs for the whole session, with a mean value calculated for each bin. Sleep epochs were calculated as periods of sustained immobility (velocity < 0.5 cm/s) that co-occurred with a theta/delta ratio exceeding 1 s.d. above the mean.

Ripple analyses.

To assess simultaneous changes in the gamma and ripple frequency bands, CA1 stratum pyramidale LFPs were low-pass filtered to the Nyquist frequency of the target sampling rate and then downsampled by a factor of 20 (to 1,628 Hz). The continuous wavelet transform (CWT) was then applied to the unfiltered LFP using complex Morlet wavelets (cmor 1–1.5), returning amplitudes at 146 intervals between 10 and 300 Hz. For the purpose of comparison across genotypes, powers during SWR episodes were subsequently z-scored in the low gamma (20–40 Hz) and ripple (140–160 Hz) frequency bands. To address concatenated ripple events we bandpass filtered raw LFPs (80–200 Hz) and calculated ripple power as the Gaussian smoothed (5 ms s.d.) absolute of the Hilbert transform. Peaks exceeding 5 s.d. above the mean were classified as ripple events, with the start and termination of events defined as times when power returned to the mean plus 0.5 s.d. on either side of the peak. Concatenated ripples were identified as pairs of peaks exceeding the upper threshold (of 5 s.d.) separated by < 50 ms, which were subsequently merged into single events.

Putative replay event detection.

To identify replay events we employed two methods. First all clustered pyramidal cell spike times were concatenated, binned into 1-ms windows and subsequently smoothed with a Gaussian kernel (s.d. = 15 ms). From the resulting multi-unit spike rate across time, episodes were identified as periods exceeding 3 s.d. above the mean³⁵ (related to Fig. 4a–e). The maximum within this window was defined as the peak of the event, with the edges on either side of the peak identified when the rate returned to the mean. Mean animal velocity was calculated for each event, with those exceeding 0.5 cm/s excluded from further analyses. Additionally, to ensure that the rises in population activity coincided with ripple events, we separately detected concurrent rises in both MUA (exceeding 2 s.d. above the mean) and ripple band power (band-pass filtered between 80 and 200 Hz, exceeding 1.5 s.d. above the mean). Similarly, a mean velocity above 0.5 cm/s led to events being discarded and event edges were defined when the values either side of the peak returned to the mean (related to Supplementary Fig. 5).

Local field potential power analyses.

Spectral power was estimated using the pwelch function in Matlab during linear track exploration for all periods during which velocity exceeded 5 cm/s. Power was calculated across the frequency range 5–100 Hz, using 1-s segments and a 50% overlap. All LFP analyses (including phase analyses) were conducted using a single electrode from each animal situated in CA1 stratum pyramidale.

Spike-LFP phase analyses.

Spike phase preferences for theta (6–12 Hz), gamma (30–80 Hz) and ripples (130–180 Hz) were calculated by interpolating spike times against the phase of LFPs recorded from the CA1 pyramidal cell layer. Phase time series were generated from wavelet decomposition of LFPs (performed at 150 levels from 2 to 300 Hz) with the mean phase taken across the relevant bands frequency range. Individual spike phases for theta and gamma analysis were excluded if the mean animal velocity in a 500-ms window surrounding the spike was <5 cm/s. Similarly for ripples, only spikes occurring within the previously detected speed-thresholded ripple events were included. Cells were considered to be phase-locked only if they had a distribution significantly different from uniform, P < 0.05 by circular Rayleigh test. The mean angle and mean resultant length (a measure of phase-locking strength) were calculated for each cell using CircStat, the circular statistics toolbox⁴⁹. Peaks of oscillations were defined as occurring at 0° and 360°, with troughs corresponding to 180° and 540°.

Place cell analyses.

Clusters identified as pyramidal neurons containing more than 75 spikes occurring during high-velocity intervals (>5 cm/s) were further sorted into two separate spike time series according to the animal’s direction on the linear track. Spike times were interpolated (separately for each direction) against animal positions, which were subsequently binned into 100 evenly spaced intervals (each 1.5 cm wide). A Gaussian smoothing kernel (s.d. = 5 cm) was applied to the raw spike map, which was then divided by the smoothed occupancy map (using the same kernel) to create a smoothed rate map. Place fields were defined as any region encompassing the maximum bin of the firing rate map that remained uninterrupted for >6 bins (7.5 cm) above 10% of the peak rate. The place field boundaries were classified as the first bin either side of the maximum bin where the firing rate fell below 10% of the peak rate. Additional fields were identified outside the primary field as peaks in the rate map exceeding 50% of maximum rate. Place fields were only included if the peak firing rate was > 2 Hz. Spatial information was calculated as previously described⁵⁰:

$$\text{Spatial information}=\sum _i{P}_i\frac{{\lambda }_i}{\lambda }{\log }_2\frac{{\lambda }_i}{\lambda }$$

where i corresponds to a single spatial bin, P_i being the probability of the animal being in that bin, λ_i representing the mean firing rate in that bin and λ equal to the mean firing rate of the cell.

Phase precession analysis.

To characterize changes in phase precession across the whole population of CA1 place cells, we estimated the spectra of spike trains using the multi-taper method, allowing us to calculate the frequency of cells relative to LFP frequency by unwrapping the theta phase of LFPs (in radians) and assigning each spike’s theta phase by linear interpolation⁵¹.

Cell assembly analyses.

Spike trains for each neuron were binned into 25-ms time windows and z-score transformed. Assemblies were identified as previously described^9,52, by first calculating the principal components of the binned spike time matrix (Z):

$$\sum _{j=1}^n{\lambda }_j{P}_j{P}_j^{\text{T}}=\frac{1}{n}Z{Z}^{\text{T}}$$

where p_j is the jth principal component with the corresponding eigenvalue λ_j and $\frac{1}{n}Z{Z}^{\text{T}}$ represents the correlation matrix of Z. The Marčenko–Pastur law was then used to determine the number of significant patterns: briefly, for an n × B matrix, an eigenvalue value exceeding λ_max signifies that the pattern given by the corresponding principal component explains more correlation than would be expected if the neurons were independent of each other⁵³. λ_max is defined by

$${\lambda }_{\max }={(1+\sqrt{n/B})}^2$$

The number of eigenvalues exceeding λ_max was defined as N_A. Significant principal components only were then projected back onto the binned spike data as follows:

$$Z_{\mathrm{PROJ}}={P_{\mathrm{SIGN}}}^{\text{T}}Z$$

where P_SIGN is the n × N_A matrix with the N_A principal components as columns. Using the fastICA⁵⁴ Matlab package, independent component analysis (ICA) was applied to Z_PROJ. The resulting unmixing matrix W was used to derive each cell’s weight within each assembly (Supplementary Fig. 3), as follows:

$$V=P_{\mathrm{SIGN}}W$$

Cell assemblies were identified, as described above, exclusively from linear track exploration sessions (Fig. 3a). Assembly reactivation was then assessed by tracking assemblies over time in the postexploration sleep session immediately following:

$$R_k(t)=z{(t)}^{\text{T}}{P}_{k}z(t)$$

where R_k(t) is the strength of activation of assembly k at time t and z(t) is the neuron spike trains convolved with a Gaussian kernel and subsequently z-scored. P_k is the projection matrix of assembly k, derived from the outer product of its weight vector v_k, with the diagonal of P_k zeroed to ensure that only coactivation of multiple members of a cell assembly can produce increases in R_k. Activations were only included in analyses if R exceeded 5 and assemblies were repeatedly activated. Assembly strength was defined as the mean activation strength of all events (R > 5) across single postexploration sessions occurring during time periods detected as sharp wave ripples (described above). Activation of multiple assemblies within single ripple events were quantified as the number active, as a fraction of the total number identified for that session. Mean strength, rate and number of active assemblies were calculated for all assembly groups that were repeatedly activated across multiple ripples.

Cell-pair analyses.

For place cells pairs either forming part of an assembly or not part of any assembly, co-firing coefficients were calculated as the Pearson correlation of the binned (25-ms temporal bins) spike counts of that pair⁵⁵. Similarly, during exploration sessions, place-field similarities were calculated as the Pearson correlation between cell-pair rate maps, separately for assembly and nonassembly pairs.

Bayesian decoding.

Ripples were detected in the post-track exploration sleep session as described above using thresholded rises in multi-unit spiking. These events were further refined by excluding those lasting less than 80 ms or having fewer than five place cells participate. Ripples were segmented into 20-ms non-overlapping windows, for which firing rate vectors were constructed for all place cells. Each temporal window’s place cell activity was decoded to generate a virtual position using the Bayesian method³⁵, with the smoothed firing rates across space from the previous linear track session serving as templates:

$$\mathrm{Pr}(\mathrm{pos}|\mathrm{spikes})=\left(\prod _{i=1}^n{f}_i{(\mathrm{pos})}^{{\mathrm{sp}}_i}\right)\exp \left(-\tau \sum _{i=1}^n{f}_i(\mathrm{pos})\right)$$

where f_i(pos) represents the firing rate in the template of the ith place cell at position pos. The number of spikes fired by the ith place cell in the temporal bin being decoded is denoted by sp_i, while n is the total number of place cells and τ is the temporal duration of the decoding bin (0.02 s). All of the posterior probabilities were subsequently normalized to 1 using the following equation, where P_n is the total number of positions:

$$\mathrm{Pr}(\mathrm{pos}|\mathrm{spikes})=\frac{\mathrm{Pr}(\mathrm{pos}|\mathrm{spikes})}{{\sum }_{i=1}^{P_n}\mathrm{Pr}({\mathrm{pos}}_i|\mathrm{spikes})}$$

Additionally, using this method we decoded sessions of linear track exploration (excluding periods where velocity <0.5 cm/s) and calculated the error between the decoded and actual position as a percentage for each temporal bin, which was then averaged across the full session.

Sequence scoring.

For each decoded event, the correlation of time and position was calculated by both a standard Pearson correlation and as a sequence score (r) weighted by the posterior probability²⁹. This was achieved by calculating the weighted mean (m), where pos_j is the jth spatial bin, bin_i is the ith temporal bin and Pr_ij is the posterior probability in that bin. M and N represent the total numbers of temporal and spatial bins, respectively:

$$m(\mathrm{pos};\mathrm{Pr})=\frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{\mathrm{Pr}}_{ij}{\mathrm{pos}}_j}{{\sum }_{i=1}^M{\sum }_{j=1}^N{\mathrm{Pr}}_{ij}}$$

From this the weighted covariance (cov) was derived,

$$\mathrm{cov}(\mathrm{pos},\mathrm{bin};\mathrm{Pr})=\frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{\mathrm{Pr}}_{ij}({\mathrm{pos}}_j-m(\mathrm{pos};\mathrm{Pr}))({\mathrm{bin}}_i-m(\mathrm{bin};\mathrm{Pr}))}{{\sum }_{i=1}^M{\sum }_{j=1}^N{\mathrm{Pr}}_{ij}}$$

followed by the weighted correlation r(pos, bin; Pr):

$$r(\mathrm{pos},\mathrm{bin};\mathrm{Pr})=\frac{\mathrm{cov}(\mathrm{pos},\mathrm{bin};\mathrm{Pr})}{\sqrt{\mathrm{cov}(\mathrm{pos},\mathrm{pos};\mathrm{Pr})(\mathrm{cov}(\mathrm{bin},\mathrm{bin};\mathrm{Pr})}}$$

Next, for each event, the firing rate template (used for decoding) for each place cell was circularly shuffled, shifting each place fields position on the track by a random distance. The newly shuffled template was then used to decode the event as described above, generating a new (shuffled) weighted correlation. This process of shuffling and decoding was repeated 1,000 times to generate a set of r(null) values for each ripple event. A final sequence score rZ was derived by taking the absolute value of the weighted correlation r(observed) as a z-score relative to its expected absolute null weighted correlation distribution:

$$rZ=\frac{|r(\mathrm{observed})|-|\overline{r(\mathrm{null})}|}{\mathrm{s.d.}(|r(\mathrm{null})|)}$$

Isolating significant replay sequences.

While the sequence score was calculated for all putative replay events irrespective of the replay content or quality, we independently calculated a Monte Carlo P-value for each event⁵⁶. Here, place field maps (tuning curves) for each place cell were circularly shifted by a random distance and a new weighted correlation calculated. This process was repeated 1,000 times, to generate a P-value:

$$P=\frac{(n+1)}{(r+1)}$$

where r represents the total number of shuffles (1,000) and n is equal to the number of shuffles with a weighted correlation greater than or equal to the unshuffled value. Additionally, while each putative event was decoded twice, using directional (left and right track runs) smoothed tuning curves, only the event (in one particular direction) yielding the highest sequence score was tested for significance. Sequence scores presented in the text and Fig. 4b refer to events with a P < 0.05. Additionally, we used a secondary method of cell identity shuffling to confirm our results, whereby the 1,000 shuffles were decoded from tuning curves whose identities were randomly permuted, thus attributing spike times to a place field other than its own.