Abstract
Violations of economic rationality principles in choices between three or more options are critical for understanding the neural and cognitive mechanisms of decision making. A recent study reported that the relative choice accuracy between two options decreases as the value of a third (distractor) option increases, and attributed this effect to divisive normalization of neural value representations. In two preregistered experiments, a direct replication and an eye-tracking experiment, we assessed the replicability of this effect and tested an alternative account that assumes value-based attention to mediate the distractor effect. Surprisingly, we could not replicate the distractor effect in our experiments. However, we found a dynamic influence of distractor value on fixations to distractors as predicted by the value-based attention theory. Computationally, we show that extending an established sequential sampling decision-making model by a value-based attention mechanism offers a comprehensive account of the interplay between value, attention, response times, and decisions.
Introduction
A central tenet of neuroeconomics is to exploit knowledge of the neural and cognitive principles of decision making in order to provide explanations and predictions of seemingly irrational choice behavior1. A prominent example of this research agenda is the concept of divisive normalization of neural value representations. According to divisive normalization, the firing rates of single neurons are normalized by the summed firing rates of a pool of neurons2. This property allows the brain to maintain efficient coding of information in changing environments. Importantly, divisive normalization appears to also influence the encoding of subjective values, in the sense that the neural value signal of a choice option is normalized by the sum of the value signals of all options3. Based on this finding, Louie and colleagues4 predicted a new choice phenomenon: When deciding between three options of different subjective values (V1 > V2 > V3), the relative choice accuracy between the two targets (i.e., the probability of choosing the best option relative to the probability of choosing the second-best option) should depend negatively on the value of the third (distractor) option. This is because higher distractor values lead to higher summed values and thus to stronger normalization, which in turn implies reduced neural discriminability of the target values. Louie and colleagues4 confirmed their prediction in a behavioral experiment, in which human participants made ternary decisions between food snacks (they also conducted an experiment with two monkeys, but our study is only concerned with the human experiment). Notably, this finding has strong implications for economics, as it constitutes a violation of the axiom of independence of irrelevant alternatives (IIA), according to which the choice ratio between two options must not depend on any third option5,6.
The purpose of the current study was twofold. First, we assessed the replicability of the distractor effect reported by Louie and colleagues4 by conducting a direct replication that followed the original experimental procedures as closely as possible (with the exception that we tested more than 2.5 times as many participants). This attempt was motivated by the fact that the reported IIA violation in the ternary food-choice task differs from other violations of this axiom7, which are usually found in decisions between options that are characterized by multiple and distinct attributes, such as price and quality of consumer goods8 or magnitude and delay of rewards9. Moreover, the lack of direct replications has been identified as a central weakness of current research practices10.
The second goal of this study was to test an alternative account of the distractor effect, which proposes that the distractor effect is mediated by value-based attention11,12. Notably, the idea that violations of IIA in multi-alternative choice are caused by interactions between value and attention has been entertained in previous work, including the selective-integration model13–15. Our specific hypothesis was that the amount of overt attention (gaze time) spent on a choice option is a function of the option’s subjective value. As a consequence, low-value distractors are quickly identified as unattractive candidates and receive little attention during the choice process. This could reserve cognitive capacity for making more accurate decisions between the two target options. Thus, the value-based attention account could in principle incorporate a distractor effect (though it does not need to predict it12). Importantly, the account also makes specific predictions about the allocation of attention during decision making and how this allocation interacts with the distractor effect: The distractor effect emerges, because the amount of gaze time spent on the distractor is a function of its value, and because more attentional distraction reduces relative choice accuracy. This mediation of the distractor effect by eye movements is not predicted by divisive normalization. Therefore, we conducted a second study in which we recorded participants’ eye movements in the ternary choice task. We preregistered both experiments at the Open Science Framework (https://osf.io/qrv2e/registrations) prior to data acquisition.
Unexpectedly, neither the direct replication nor the eye-tracking experiment replicated the distractor effect on choice reported in the original study4. In fact, we obtained very strong evidence in favor of the null hypothesis of no distractor effect. As predicted by the value-based attention account, on the other hand, the influence of distractor value on the amount of gaze time spent on distractors was confirmed by the data (i.e., low-value distractors were fixated less often than high-value distractors). In addition, we found that high-value distractors slowed down response times (RT) of target choices. Finally, we take these findings to propose an extension of the attentional Drift Diffusion Model (aDDM)16,17, a sequential sampling decision-making model7,18,19 that accounts for the influence of attention on choice. According to our proposal, the probability to fixate an option depends on the option’s accumulated value. We show that this computational model offers a comprehensive account of all qualitative patterns in our choice, RT, and eye-tracking data.
Results
Choice task and descriptive statistics
Both experiments consisted of two computerized tasks each (Fig. 1). In the first task, participants indicated their subjective value of each food snack on a continuous scale. Based on the results of this task, the choice sets for the second task were created such that on each trial, two targets from the third of snacks with the highest values and one distractor from the two-thirds of snacks with the lowest values were presented. Participants were then asked to choose their preferred snack in every trial. In the direct replication, we followed the procedures of Louie and colleagues4 as closely as possible using the original computer codes provided to us by the study’s first author. The setup of the eye-tracking experiment differed in some aspects including the arrangement of options in the ternary choice task (see Fig. 1b and Methods). All tasks were incentivized.
Figure 1. Valuation and choice task in the two experiments.
a Trial designs in the direct replication experiment. As in the original study4, subjective values for all snacks were assessed via a willingness-to-pay auction (left panel), and options in the choice task were arranged horizontally (right panel). b Trial designs in the eye-tracking experiment. Subjective values were assessed via incentivized ratings (left panel); options in the choice task were arranged in a triangle (right panel). A gray background was used. Instead of the snack icons shown here, photographs of the actual food products were presented in both experiments.
In the direct replication experiment, participants chose the best option in 68.6% of trials on average, which was slightly higher compared to the original study (60.5%). In the eye-tracking experiment, participants made even more accurate decisions (75.3%), partially due to preregistered exclusion criteria that were added in this experiment (see Methods). Table 1 summarizes the essential descriptive statistics.
Table 1. Descriptive statistics of the two experiments.
| Experiment | N | best chosen | second-best chosen | distractor chosen | RT in ms |
|---|---|---|---|---|---|
| Direct replication | 102 | 68.6% (13.0) | 28.6% (11.0) | 2.8% (4.5) | 2261 (800) |
| Eye tracking | 37 | 75.3% (9.0) | 22.6% (6.8) | 2.0% (3.4) | 1862 (650) |
Note. Group means are reported together with standard deviations in parentheses. N = number of participants included in the data analysis.
No evidence for distractor effect on target choices
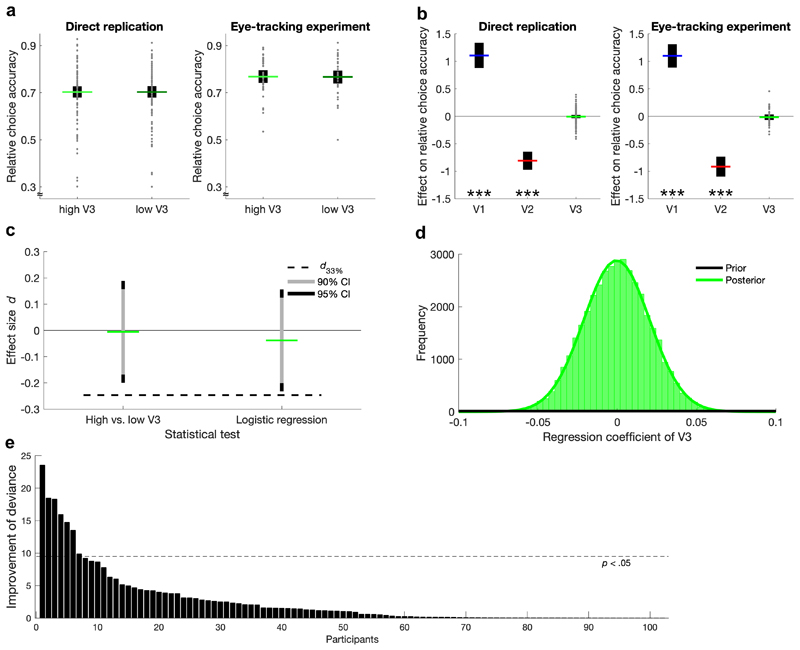
To investigate the distractor effect on relative choice accuracy, we performed two statistical tests. First, we compared the accuracy averaged over trials that included a high- vs. a low-value distractor (Fig. 2a). In contrast to Louie and colleagues4, we did not find significantly lower accuracy for high-value distractor trials, neither in the direct replication (one-sided paired t-test, t(101) = -0.05, p = .479, effect size Cohen’s d = -0.01, 95% confidence interval [CI] of the difference = [-0.01, 0.01]), nor in the eye-tracking experiment (t(36) = 0.21, p = .583, d = 0.03, 95% CI = [-0.02, 0.02]). For the second test, we performed a random-effects logistic regression analysis, for which relative choice accuracy was regressed onto the value of each option (i.e., V1, V2, V3) in every participant, and a one-sample t-test on the regression coefficients was performed on the group level (Fig. 2b). Expectedly, V1 had a significantly positive influence on accuracy (direct replication: t(101) = 9.53, p < .001, d = 0.94, 95% CI = [0.88, 1.34]; eye-tracking experiment: t(36) = 10.52, p < .001, d = 1.73, 95% CI = [0.89, 1.31]), and V2 had a significantly negative influence (direct replication: t(101) = -9.75, p < .001, d = -0.97, 95% CI = [-0.97, -0.64]; eye-tracking experiment: t(36) = -10.17, p < .001, d = -1.67, 95% CI = [-1.10, -0.73]). However, there was no statistically significant effect of V3 on choice accuracy (direct replication: t(101) = -0.38, p = .351, d = -0.04, 95% CI = [-0.04, 0.02]; eye-tracking experiment: t(36) = -0.67, p = .254, d = -0.11, 95% CI = [-0.07, 0.03]). Notably, our analyses deviated from that of Louie and colleagues4, as we performed a random-effects rather than a fixed-effects analysis and replaced the normalized V3 predictor variable (normV3 = V3 / 0.5*[V1 + V2]) by the ‘raw’ V3. Briefly, our reason for deviating from the original analysis was that normV3 is confounded with the target-value difference V1 – V2 and thus with difficulty, which is particularly problematic for the fixed-effects analysis (detailed information and analyses with the original settings are provided in the Supplementary Information). These deviations from the original analyses were preregistered.
Figure 2. Analyses of distractor effects on relative choice accuracy.
a Comparison of trials with high- vs. low-value distractors. Individual data points (gray dots) are shown together with group means (colored lines) and 95% CIs (black error bars). b Regression coefficients for the influence of target and distractor values. Individual data points for effects of V1 and V2 are omitted for better visualization of the V3 effect. c Assessment of replicability using the Small Telescopes approach21. The 90% (and 95%) CIs of the effect sizes in the direct replication did not overlap with d33% (i.e., the effect size that would give the original study 33% statistical power), indicating replication failure. d Prior and posterior distributions of the V3 coefficient according to a hierarchical Bayesian logistic regression (direct replication data). The posterior density at 0 is much higher than the prior density, indicating very strong evidence for the null hypothesis. e Improvement of model fit (i.e., deviance) for the more complex divisive normalization model compared to the probit model for each participant of the direct replication. A statistically significant improvement was found for only few participants (the normalization model was also rejected on the group level). The Bayesian analysis and model comparison for the eye-tracking experiment are shown in Supplementary Figure 4. ***p < .001
It is important to note that inferring the replicability of an effect based on its significance in the replication study has been criticized20,21. For this reason we adopted the “Small Telescopes” approach21 to determine the sample size of our direct replication experiment and to infer the success of replication. According to this approach, one should test whether the 90% CI of the effect size in the replication study is closer to 0 than a (hypothetical) effect size that would give the original study a statistical power of only 33%. Using this rationale, we found that the 90% CIs (and even the 95% CIs) of the effect sizes from the two distractor effect analyses described in the previous paragraph did not overlap with the 33% threshold, indicating that our direct replication was indeed unsuccessful (Fig. 2c).
Given the absence of an influence of V3 on relative choice accuracy, we sought to quantify the evidence in favor of the null hypothesis by conducting the above-mentioned logistic regression analysis within a hierarchical Bayesian framework. For the direct replication, this analysis yielded a Bayes factor in favor of the null hypothesis of BF01 = 241 which is seen as very strong evidence22 (Fig. 2d) (95% Highest Density Interval [HDI] = [-0.04, 0.04]). Additionally, we performed a nested model comparison between the divisive normalization model, the probit model23, and a baseline model that assumed random choices (because the divisive normalization model assumes normally distributed errors, it can be understood as a generalization of the probit model). Both the probit and the normalization models predicted decisions of participants in the direct replication significantly better than the baseline model (probit: χ2(102) = 25’160; p < .001; normalization: χ2(510) = 25’425; p < .001). Critically, only for a minority of 7 out of 102 participants choices were explained significantly better by the normalization model than by the probit model (Fig. 2e). Similarly, a likelihood ratio test on the group level indicated that the higher complexity of the divisive normalization model was not statistically justified by the small improvement in goodness-of-fit (χ2(408) = 265; p > .999). The Bayesian analysis and model comparison for the eye-tracking experiment yielded equivalent results (Supplementary Figure 4). We regard these Bayesian analyses and model comparisons together with the negative results from the adopted “Small Telescopes” approach for direct replications as providing crucial and strong evidence against a negative influence of distractor value on the relative probability to choose the better out of the two targets and against the normalization model as offering additional precision in explaining multi-alternative value-based decisions.
Higher distractor values slow down choices of targets
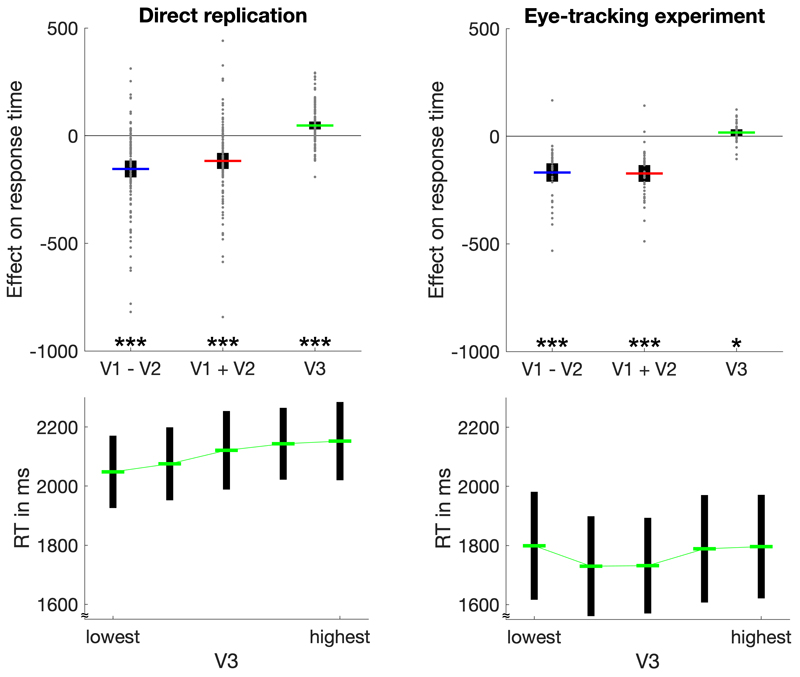
Contrary to the absence of an impact on relative choice accuracy, we found a significantly positive effect of distractor value on RT of target choices (Fig. 3). As statistical test, we performed a random-effects linear regression analysis, for which the RT of target choices was regressed onto V3 as well as onto the difference and the sum of target values (i.e., V1 – V2; V1 + V2). In line with previous research12,24–26, RT in both experiments were significantly reduced by higher target-value differences (direct replication: t(101) = -7.83, p < .001, d = -0.78, 95% CI = [-194, -116]; eye-tracking experiment: t(36) = -8.01, p < .001, d = -1.32, 95% CI = [-211, -126]) and by higher target-value sums (direct replication: t(101) = -6.26, p < .001, d = -0.62, 95% CI = [-155, -80]; eye-tracking experiment: t(36) = -9.02, p < .001, d = -1.48, 95% CI = [-211, -134]). More importantly, RT increased as a function of distractor value (direct replication: t(101) = 5.10, p < .001, d = 0.51, 95% CI = [29, 65]; eye-tracking experiment: t(36) = 2.27, p = .029, d = 0.37, 95% CI = [2, 32]). Notably, this effect does not provide evidence for the divisive normalization model, which does not make any RT predictions. However, the effect is predicted by the extended aDDM (see section “Computational modelling” below).
Figure 3. Analyses of distractor effects on RT.
The upper panels depict regression coefficients for the influence of target-value difference, target-value sum, and distractor value on RT in both experiments. Individual data points (gray dots) are shown together with group means (colored lines) and 95% CIs (black error bars). The lower panels show average RT (with 95% CIs) for five levels of V3 from lowest to highest. The increase of RT with increasing V3 is clearly visible in the direct replication. In the eye-tracking experiment, the effect is less pronounced (consistent with the comparatively small effect size in this experiment). *p < .05, ***p < .001
In addition to the RT effects, participants were also more likely to choose high- compared to low-value distractors (direct replication: t(101) = 5.52, p < .001, d = 0.55, 95% CI = [2.51, 5.33]; eye-tracking experiment: t(36) = 3.69, p < .001, d = 0.61, 95% CI = [1.72, 5.90]), confirming that they were not simply ignoring the distractors. Importantly, this effect does not constitute a violation of IIA and is not specific evidence for divisive normalization12.
Dynamic influences of value on attention
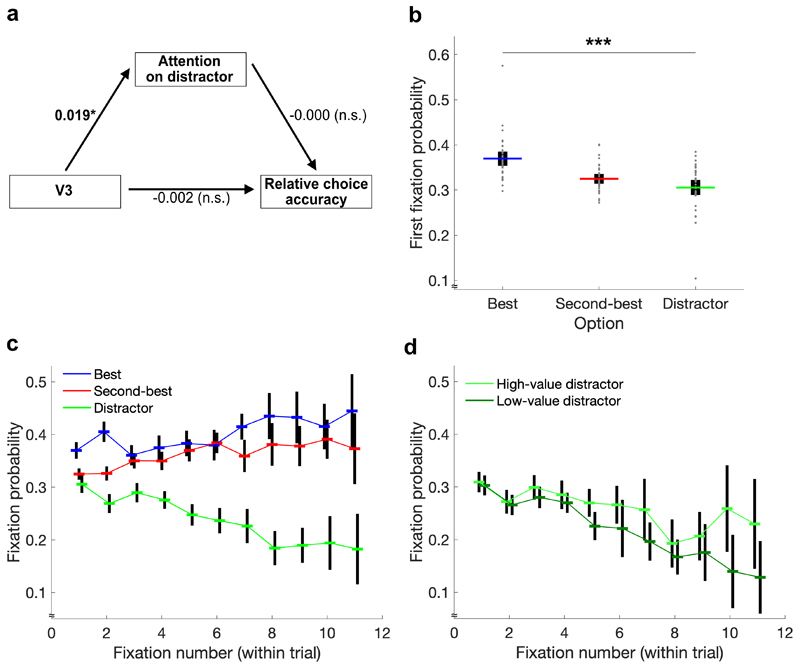
Our primary eye-tracking hypothesis examined an alternative account of the distractor effect that was not based on divisive normalization but on attentional capacity. More specifically, we applied a random-effects path analysis to test whether a (potential) negative influence of the distractor value on relative choice accuracy was mediated by the amount of attention spent on the distractor (Fig. 4a). In line with the attentional account, the path coefficient from V3 to relative gaze duration on the distractor was significantly positive (t(36) = 1.80, p = .040, d = 0.30, 95% CI = [0, 0.04]). On the other hand, there was no statistically significant effect of gaze duration on relative choice accuracy (t(36) = -0.01, p = .497, d = 0, 95% CI = [-0.01, 0.01]). This is not surprising given the above-mentioned absence of a distractor effect on target choices. For the same reason, there was also no statistically significant direct effect of V3 on accuracy. Consistent with our previous work12, we found evidence for a mediating role of attention with respect to absolute (rather than relative) choice accuracy, that is, when including trials in which the distractor was chosen (Supplementary Figure 5).
Figure 4. Evidence for value-based attention.
a Path analysis testing a mediation of the distractor effect by attention. As predicted, distractor value was positively linked to relative gaze duration on the distractor. Due to the absence of a distractor effect on relative choice accuracy, however, there was no mediation. b The probability to fixate different option types at the first fixation was not random. Individual data points (gray dots) are shown together with group means (colored lines) and 95% CIs (black error bars). The effect remains significant when excluding the outlier with 58% / 10% first fixations on the best option / the distractor. c Development of fixations per option type over the course of single trials. d Development of fixations on high- and low-value distractors over the course of single trials. Consistent with value-based attention, the decline of fixation probability is modulated by distractor value. *p < .05, ***p < .001
Alongside the path analysis, we predicted to find additional evidence for value-dependent gaze patterns in more detailed analyses of the eye-tracking data. First, we tested for early effects of value-based attentional capture11,12,27 by looking at the first fixation in each trial. While there was no statistically significant influence of V3 on the probability to fixate the distractor first (t(36) = -0.26, p = .604, d = -0.04, 95% CI = [-0.17, 0.13]), we found strong evidence that the first fixation depended on the type of option (F(2,72) = 14.51, p < .001, effect size partial eta squared = .39): On average, 37.0% of first fixations were on the best option, 32.4% on the second-best option, and 30.6% on the distractor (Fig. 4b). This effect remained significant even after excluding one participant with an exceptionally high dependency (F(2,70) = 16.57, p < .001, = .32). Second, we predicted a top-down effect of value on attention, meaning that fixations on low-value options should become less likely during the choice process. Consistent with our hypothesis, the probability to fixate the distractor decreased as decisions emerged (interaction effect of option type and fixation number: F(12,432) = 8.09, p < .001, = .78) (Fig. 4c). Most importantly, the slope of this decrease was modulated by V3 with a steeper decline for distractors of lower values (interaction effect of V3 and fixation number: t(36) = 3.65, p < .001, d = 0.60, 95% CI = [0.02, 0.09]) (Fig. 4d). We also found effects of value on attention within the two target options, as participants looked more often at the best compared to the second-best option, both at the first fixation (t(36) = 4.52, p < .001, d = 0.74, 95% CI = [0.02, 0.05]) as well as at ensuing fixations (t(36) = 3.88, p < .001, d = 0.64, 95% CI = [0.01, 0.03]). Notably, the last fixation in each trial was excluded from these analyses to avoid confusion with the tendency to fixate the chosen option last16,28.
In summary, our primary eye-tracking analyses revealed both early and late (top-down) influences of value on attention. The first fixation was made more often on target options than on distractors, but this comparatively small difference of about 5% increased to more than 20% during the emerging decision and was most pronounced in the presence of low-value distractors.
Successful replication of an influence of attention on choice
Many eye-tracking studies on value-based decisions reported an influence of attention on choice: Options that are looked at longer are more likely to be chosen12,16,17,28–32. We tested this effect using a random-effects logistic regression analysis that regressed whether an option was chosen or not onto the option’s relative gaze duration while controlling for the option’s relative value. Again, the last fixation per trial was excluded from this analysis. In line with the previous literature, we found strong evidence for an influence of gaze on choice (t(36) = 7.81, p < .001, d = 1.28, 95% CI = [1.45, 2.47]).
Reanalysis of a related dataset (Krajbich & Rangel, 2011)
To test the robustness of our findings across labs, we reanalyzed an existing dataset of an eye-tracking study on ternary food choices17 (note that choice sets were created differently in this study, so that its statistical power for finding a distractor effect might be lower). Consistent with our results, there was no statistically significant distractor effect on relative choice accuracy in this dataset (random-effects logistic regression: t(29) = -0.67, p = .510, d = -0.12, 95% CI = [-0.18, 0.09]), and the hierarchical Bayesian analysis provided strong evidence for the null hypothesis (BF01 = 77, 95% HDI = [-0.07, 0.14]). As in our data, there were negative effects of the target-value difference (t(29) = -5.99, p < .001, d = -1.09, 95% CI = [-202, -99]) and target-value sum (t(29) = -4.02, p < .001, d = -0.73, 95% CI = [-235, -76]) on RT of target choices. However, RT did not depend statistically significantly on distractor value (t(29) = -0.58, p = .568, d = -0.11, 95% CI = [-61, 34]). Finally, we found some evidence for an influence of value on attention: While there was no statistically significant effect of value-based attentional capture on the first fixation (F(2,58) = 1.01, p = .349, = .05), we found a significantly positive interaction of option value and fixation number on the probability to fixate an option (t(29) = 2.81, p = .009, d = 0.51, 95% CI = [0.01, 0.06]), indicating that fixations on high-value options became more likely over the period of single decisions (see also Figure 4A in the original study17). Overall, the reanalysis of an existing dataset yielded mostly consistent results with our data, in particular the absence of a distractor effect on target choices and a top-down influence of value on attention.
Computational modeling
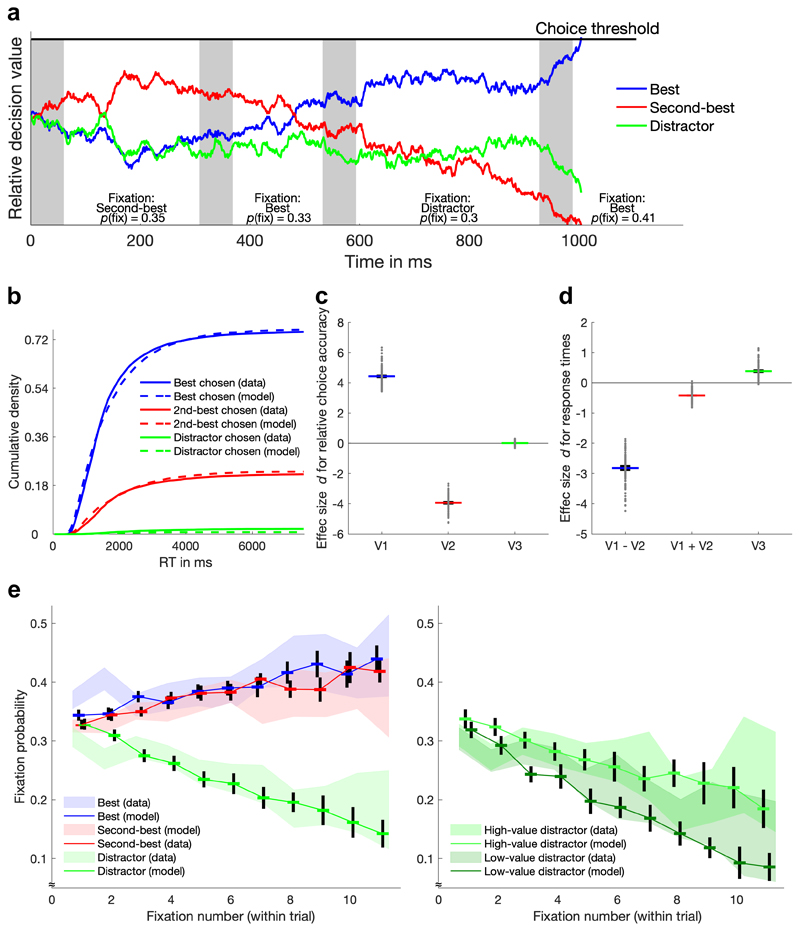
Our behavioral and eye-tracking results draw a complex picture of the interplay between value, attention, RT, and decisions: no distractor effect on target choices but on RT and a small effect of option value on the first fixation that develops into a large value-dependency of fixations as decisions emerge. We reasoned that all of these effects could be captured computationally within the framework of the multi-alternative version of the aDDM17 – but only if this model is extended by a mechanism of value-based attention. The aDDM assumes that (noisy) evidence for each option is accumulated proportional to the option’s value, and that as soon as the difference of accumulated evidence between the highest and second-highest accumulator exceeds a threshold, the option represented by the highest accumulator is chosen (Fig. 5a). To account for the influence of attention on choice, the inputs to the accumulators of options that are currently not fixated are reduced. Importantly, the aDDM does not assume a dependency of the probability to fixate an option on the option’s value. As a consequence, the model does not allow to account for the effects of value on early and late fixations seen in our data (Supplementary Figure 6). Therefore, we extended the model by a mechanism that couples fixation probabilities with accumulated value signals: The higher the accumulated value of an option, the more likely it is fixated. Additionally, we initiated the evidence-accumulation process 60 ms prior to the first fixation (Fig. 5a). These two assumptions should enable the aDDM to predict a small influence of value on the first fixation and an increase of this influence over the period of the emerging decision.
Figure 5. Illustration and predictions of the aDDM with value-based attention.
a Sequential sampling process of the aDDM for an example trial. The depicted relative decision values are based on a comparison between each option’s accumulator and the best alternative accumulator. The choice process terminates when one decision value reaches the threshold. Fixations of options are indicated by a white background, gaps before the first fixation and between fixations are indicated by a gray background (gaps between fixations were implemented to match the empirical gaps between fixations, which lasted ~60 ms on average). The probability of each fixation is stated at the bottom and is based on accumulated value (via a logistic function; see Equation 8 in the Supplementary Information). Fixation durations are drawn from a log-normal distribution (whose parameters were fitted to the empirical fixation durations). b Cumulative density of empirical and model-predicted RT distributions for each option type. c and d Effect sizes of the influence of V1, V2, and V3 on relative choice accuracy (c) and on target-choice RT (d) for 100 simulations of the eye-tracking experiment with the extended aDDM. Gray dots show the effect sizes for each simulation, colored lines and black error bars show the overall means and their 95% CIs, respectively. e Comparison of the empirical and model-predicted development of fixations for different options types over the course of single trials. Shaded areas represent the 95% CIs of the data.
Based on simulating the data of our eye-tracking experiment, we searched for a parameter set that allowed the extended aDDM to capture as many qualitative patterns in our choice, RT, and gaze data as possible. Indeed, we found that the model offered a full account of our results. First, the model described the choice probabilities and RT distributions for all three options sufficiently (Fig. 5b). Second, it did not predict a statistically significant distractor effect on relative choice accuracy (average effect size d = 0.01, 95% CI = [-0.02, 0.04]) (Fig. 5c). Third, the model accounted for the negative influences of the difference (d = -2.82, 95% CI = [-2.92, -2.72])) and sum (d = -0.42, 95% CI = [-0.46, -0.38])) of target values on RT (the target-value difference effect is essentially a difficulty effect that is predicted by any sequential sampling model; the target-value sum effect results from the multiplicative relationship between value and attention in the aDDM33: high values amplify the influence of attention, inducing stronger deflections of the decision variable and thus faster crossing of the threshold). More importantly, the model also accounts for the positive influence of distractor value on RT (d = 0.39, 95% CI = [0.32, 0.45]) (Fig. 5d). Fourth, the model predicted an influence of relative gaze duration on the probability to choose an option (d = 1.46, 95% CI = [1.41, 1.51]). Finally, the model captured the development of fixation probabilities on targets and distractors in its entirety (Fig. 5e), including a small effect of option value on the first fixation (d = 0.17, 95% CI = [0.14, 0.20]), a steeper within-trial decay of fixations for low- compared to high-value distractors (d = 1.58, 95% CI = [1.53, 1.62]), and a higher likelihood to fixate the best compared to the second-best option initially (d = 0.04, 95% CI = [0.01, 0.08]) and at ensuing fixations (d = 0.61, 95% CI = [0.58, 0.65]). Alternative variants of the aDDM with divisive normalization or with different implementations of value-based attention did not provide such a comprehensive account of the behavioral and eye-tracking results (Supplementary Figures 6-10).
Discussion
In the present study, we set out to assess the replicability of the distractor effect on relative choice accuracy reported by Louie and colleagues4 and to test an alternative underlying mechanism that does not rely on divisive normalization of neural value signals but on value-based attention. The results of our two studies and the reanalysis of a previously published dataset17 suggest that there is no reliable distractor effect on choices (and thus no violation of the IIA axiom), and that the distribution of attention depends on value with the predicted dynamics. An extension of the multi-alternative aDDM17, in which the probability to fixate an option is coupled with the option’s accumulated value signal, allowed us to capture a total of ten different behavioral and eye-movement patterns: effects of V1 and V2 on relative choice accuracy, no effect of V3 on choices, effects of V1 – V2, V1 + V2 and V3 on RT, an influence of attention on choice, an effect of option type on the first fixation, the development of fixations for the three option types over time, and finally a dependency of the within-trial decay of distractor fixations on V3.
Divisive normalization has been proposed as a canonical neural computation that is remarkably ubiquitous in the brain2, and there is substantial evidence that neural representations of subject value also exhibit this3,34 or related forms35–37 of adaptation to the range of offered values. However, the evidence for a behavioral impact of divisive normalization or value-range adaptation appears to be mixed, with some studies reporting positive evidence4,38 but other studies reporting null findings12,34,36,39 or even contradictory effects40. Importantly, the above-mentioned studies are not direct replications of the seminal study by Louie and colleagues4. Assessing the replicability of an effect via direct replications is essential for establishing the robustness of empirical research, which in turn is a prerequisite for scientific progress10,20. Notably, researchers were not only inspired by the results reported by Louie and colleagues4 when conducting new behavioral and neuroscientific experiments but have also started to develop computational models that attempt to take the distractor effect into account41,42. Therefore, we consider our unsuccessful replication being essential to open up the discussion on the implications of neural value-range adaptations on overt behavior. Notably, our study does not speak to potential dynamic effects of divisive normalization across multiple decisions43 or to the robustness of the effects of the monkey experiment reported by Louie and colleagues4 (note, however, that another monkey study reported that changing the range of values does not affect economic preferences39).
Violations of the IIA axiom have been found and replicated in various settings of multi-alternative decision making including consumer choice8, risky decision making44, and intertemporal choice9. In fact, the ability to account for specific IIA violations such as the attraction effect8,9 has become a benchmark for decision-making models in cognitive science7. What all of the choice settings in which robust violations of IIA can be found have in common is that options are characterized by two (or more) distinct and well quantifiable attributes (e.g., amount and delay in the case of intertemporal choices). On the contrary, when attribute values are fuzzy45 or when decision are made under time pressure12, such that careful attribute-wise comparisons are hindered, violations of IIA are less likely to occur. Similarly, violations of IIA in experience-based decisions, in which attribute values can only be learned via feedback, appear to emerge from specific mechanisms during the processing of feedback rather than during the choice process itself46. We argue that the absence of IIA violations in the present study is consistent with the previous literature, given that decisions between food snacks appear to rely on a single attribute (taste) as long as people are not instructed to also consider other attributes (for example, health)47. On a computational level, our findings indicate that divisive normalization is not a necessary element to take into account when trying to develop models of decision making that relax the IIA assumption.
While our results provide strong evidence against a negative distractor effect on choices, we obtained significantly positive effects on RT in both experiments. This finding might motivate the speculation that our results and those of the original study could be reconciled by assuming that participants of the two different studies employed two different choice strategies, one leading to a distractor effect on choices and the other leading to a distractor effect on RT. More specifically, one could devise a DDM variant with normalized input values and two different choice-rule strategies, one strategy being that the option with the highest accumulator value is chosen at a pre-determined time point (i.e., a “deadline” strategy), and the other strategy being that the option whose accumulator reaches the decision threshold first is chosen (i.e., a “threshold” strategy). In Supplementary Figure 11, we show that such a model indeed predicts a distractor effect on choices under the “deadline” strategy and a distractor effect on RT under the “threshold” strategy. For the following reasons, however, we consider this model and the speculation that participants of the two studies employed different strategies implausible. First, under the “deadline” strategy, the model does not predict an effect of target-value difference (and thus of difficulty) on RT. Although, we do not know whether this effect was present in the original study, which did not report RT effects, we consider this prediction very unlikely given the robustness of the influence of difficulty on RT in the current study as well as in virtually any study on decision making12,16,17,24,26,30,32,33,47–49. Second, under the “threshold” strategy, the model neither provides a sufficient account of the overall choice and RT distributions, nor does it predict the gaze patterns in our eye-tracking experiment. Third, the assumption of normalized input values is not necessary for the prediction of a distractor effect on RT. The prediction that high-value distractors slow down responses emerges naturally from the sequential sampling framework and does not provide evidence for divisive normalization. Finally, the model does not provide a rationale for the speculation that participants in the original and the current study might have employed two extremely different choice strategies (despite the fact that the direct replication was kept as similar as possible to the original study, including the same instructions). In our view, it is much more plausible to assume that participants in the two studies (as well as in Krajbich & Rangel, 201117) employed similar strategies, which are best described by our proposed extension of the aDDM.
Beyond speaking against a role of divisive normalization in shaping multi-alternative decisions, our study provides strong evidence for a dynamic dependency of attention on value. While people engage in the choice process and accumulate evidence for each option, they focus more and more on the two options that appear to be most attractive (usually the targets) and disregard more and more the seemingly worst option (usually the distractor). Notably, a positive feedback-loop between attention and preference formation that results in a “gaze cascade effect” has been proposed in a previous eye-tracking study28. This proposal has been criticized by a simulation study50, which showed that the tendency to fixate the chosen option at late choice stages could be explained without assuming that preferences drive attention. However, we found robust effects of value on attention already at the first fixation, lending new support for the feedback-loop idea51.
It is interesting to note that the developers of the aDDM have reported some initial evidence of value-based attention in their dataset on ternary decisions17 but not in their dataset on binary decisions16, even though a systematic mechanism was not implemented in either of the two aDDM versions. Our data provide more compelling evidence for value-based attention, possibly due to an increase in statistical power given the larger number of participants (37 vs. 30) and trials per participant (300 vs. 100), and the superior sampling rate of the eye tracker (500 vs. 50 Hz) in our study (similarly, we attribute the absence of a distractor effect on RT in the dataset of Krajbich & Rangel, 2011, to a lack of statistical power). In general, the partially divergent findings from binary and ternary decisions could indicate that people adapt their distribution of attention strategically (top-down) to reduce cognitive effort in multi-alternative decision making and to mainly sample information about the two options that appear to be better than all remaining candidates52,53. Even if this does not improve choice accuracy, it leads to faster and thus more efficient decisions.
Importantly, our model simulations suggest that alternative implementations of value-based attention which are not based on accumulated but on input values12,54 do not provide the same comprehensive account of all behavioral and gaze patterns. In a related study of our group12, we proposed a sequential sampling model that assumed an attentional mechanism based on input-values, the Mutual Inhibition with Value-based Attentional Capture (MIVAC) model. MIVAC offered a sufficient account of the behavioral and eye-tracking data in this previous study. Regarding the current study, however, MIVAC would not be able to predict the dynamic dependency of attention on (accumulated) value. Notably, the two studies differ in several aspects, including the stimulus material (food snacks vs. colored rectangles) and the amount of time available for making decisions. Thus, the comparatively weak effect of value-based attention on the first fixation in the current study (which then developed into a larger effect during the ongoing decision) could be explained by the difficulty to identify food snacks and their subjective value through initial peripheral viewing. More work and a better integration of knowledge from vision science and decision-making research will be critical to reconcile these different accounts of the influence of value on attention. Furthermore, our model simulations do not rule out that combinations of different mechanisms (e.g., value-based attention together with interim rejections of low-value options) might provide the most accurate account of the behavioral and eye-movement data. Therefore, future research should develop more principled ways of assessing goodness-of-fit of choices, RT, and gaze patterns on the single-trial level, possibly via the joint modeling approach55. Finally, it should be noted that the aDDM does not analyze options on the attribute level but assumes a single input value per option. Consequently, the model cannot account for the above-mentioned (robust) IIA violations in multi-attribute decision making7, and further extensions of the model are required to address this gap.
In conclusion, our study refutes the proposal that divisive normalization of neural value signals has a sizeable impact on multi-alternative value-based decisions. At the same time, it provides compelling evidence for a dynamic influence of value on the allocation of attention during decision making and offers a comprehensive account of the complex interplay of value, attention, response times and decisions within a well-established computational framework.
Methods
Ethics statement
All participants gave written informed consent, and the study was approved by the Ethics Committee of the Department of Psychology at the University of Basel. All experiments were performed in accordance with the relevant guidelines and regulations.
Preregistration protocols
Prior to data collection, each experiment was preregistered on the Open Science Framework (OSF) (https://osf.io/qrv2e/registrations). The direct replication experiment was preregistered on September 24, 2018. The eye-tracking experiment was preregistered on March 1, 2019. Preregistrations comprised descriptions of the rationale of the study, the main hypotheses, experimental procedures, power analyses, exclusion criteria, and data analysis. The protocol of the direct replication also outlined and justified the planned deviations from the original study (e.g., use of V3 instead of normV3 for testing distractor effects). For this protocol, we used OSF’s “Replication Recipe” template which is based on Brandt et al.56. For the protocol of the eye-tracking experiment, we used the “OSF Preregistration” template. Before preregistering the direct replication, the associated protocol was sent to the first author of Louie and colleagues4, who approved it.
Participants
A total of 148 participants took part in the study, 103 in the direct replication experiment, 45 in the eye-tracking experiment. One participant in the direct replication had to be excluded, resulting in a final sample of 102 participants in this experiment (72 female, age: 18-51, M = 24.78, SD = 6.37; four participants did not report their age). The excluded participant did not bid any money in the auction task for more than 50% of the snacks, making it impossible to perform a median-split of high- and low-value distractors and a random-effects regression analysis with distractor value impossible (in the Supplementary Information we show that including this participant in a fixed-effects regression analysis can induce spuriously significant effects). Eight participants in the eye-tracking experiment had to be excluded, resulting in a final sample of 37 participants in this experiment (26 female, age: 19-61, M = 27.63, SD = 11.14; one participant did not report their age). Four participants were excluded due to incompatibilities with the eye-tracking device, and another four participants were excluded for not passing one of the preregistered exclusion criteria (three participants rated more than 40% of the food snacks with 0, one participant chose the low-value target more often than the high-value target). As in the original study, convenience sampling was used, and most of the participants were students of the University of Basel (87 in direct replication, 33 in the eye-tracking experiment). Participants were not allowed to be on a diet or to suffer from food allergies, food intolerances, or mental illnesses, and they had to be willing to eat (in principle) all of these food types: chocolate, crisps, nuts, candy. Participants with insufficient knowledge of the project language (German) were not invited.
Sample size determination
We adopted the “Small Telescopes” approach21 to determine the sample size of the direct replication experiment. According to this method, the sample size of the replication study should be based on achieving ≥ 80% statistical power to find that – when assuming a true effect size of 0 – the effect size in the replication study is significantly lower than the (hypothetical) effect size that would give the original study only 33% statistical power. Applying this rationale to the case of Louie et al.4, who tested 40 participants, and our planned statistical tests (i.e., paired or one-sample t-tests, effect size Cohen’s d) resulted in a suggested sample size of 103.
The sample size of the eye-tracking experiment was based on a power analysis that assumed a medium effect size of d = 0.5 for an effect of value-based attention on relative choice accuracy (one-sided, one-sample t-tests, alpha error = 5%, power = .90). This analysis resulted in a suggested sample size of 36 participants. Due to known incompatibility issues of eye-tracking devices, we tested 45 participants and then checked whether ≥ 36 full datasets that also met the behavioral inclusion criteria were collected. These procedures were described in the preregistration protocol.
Experimental design of the direct replication experiment
Following recommendations in the literature56, we contacted the first author of the original study before data acquisition to resolve any ambiguities regarding recruitment of participants, experimental design, and statistical analyses. Thankfully, Kenway Louie answered our questions and provided us with their codes for instructions and tasks. Instructions were translated into German by two co-authors independently (N.K., C.L.V.). Inconsistencies were resolved in a discussion with all authors.
Participants were asked to refrain from eating for four hours prior to the experiment. At the beginning of the experiment, they read and signed the consent form and filled out a brief demographic questionnaire. Participants were informed that after completing the experiment, they were required to stay in the lab for one hour and were only allowed to eat the snack they could win in the computer tasks. Snacks were present and visible in the lab, so that participants were sure of their availability. Afterwards, participants were given instructions about the first task, which was a BDM auction57 to assess their willingness to pay money for eating a randomly selected food snack at the end of the experiment. They were endowed with a 5 Swiss francs coin and were told that this money could be used to place a bid for each snack in the auction task. The instructions explained the rationale of the BDM auction: For each snack, a bid had to be placed on a continuous scale from CHF 0 to CHF 5. If a trial from the auction was selected at the end of the experiment, they would be asked to draw one chip from a bag that contained chips with values ranging from CHF 0 to CHF 5 in steps of CHF 0.10. The value of the drawn chip would determine the price of the snack of the selected trial. If bid ≥ price, then the snack would be paid out for the price, otherwise no transaction would happen. Two practice trials were provided. Each of the 30 snacks was presented twice during the auction. The order of presented snacks was randomized for each participant anew.
The average bid of each snack was taken as its subjective value to generate choice sets for the second task, the ternary choice task. The algorithm for generating the snack worked as follows: Snacks were ordered by value, the 10 highest snacks were used as targets, and from the remaining 20 snacks 10 distractors were selected by taking the lowest, third-lowest, …, 19-lowest snack. Then, possible pairs of targets were generated, ordered by value difference, and binned into 5 levels. For each of the 10 distractors, 5 pairs from each value-difference level were drawn randomly (without replacement) resulting in 10*5*5 = 250 trials. These procedures ensured large and uncorrelated ranges of distractor values (V3) and target-value differences (V1 – V2) (but did not ensure that normV3 and V1 – V2 would be uncorrelated; see Supplementary Figure 1). The order of trials and the assignment of options to screen locations were randomized. Instructions of the choice task together with two practice trials were provided after the BDM auction. Participants were told that if a trial from the choice task was selected at the end of the experiment, they would receive the chosen snack from that trial.
Following Louie et al.4, stimuli were presented on a 13-inch laptop (Apple Inc. Mac book, year 2012) and only one participant at a time was tested. Responses were made with a computer mouse. For stimulus presentation, the Matlab-based software package Psychtoolbox-3 was used. Snack stimuli (size 400x400, resolution 72x72) were presented on a black background. In the BDM auction, a snack option was presented at the center of the screen together with the current bid amount and a horizontal bar beneath it. At the beginning of each trial, the bid was initialized at half of the maximum bid and half of the bar was filled with white (the rest with gray). By moving the bar to the left or right, participants could reduce or increase their bid, which was indicated to them by the displayed amount and the white filling of the bar. By pressing the left mouse button, they confirmed their bids. The mouse cursor was displayed by the “CrossHair” setting of Psychotoolbox-3 and was enforced to stay within the bar. An intertrial interval (ITI) of 1 s separated trials (blank screen). In the choice task, the three options of a trial were presented along the horizontal midline from left to right. The mouse cursor was initialized beneath the middle option. When moving the cursor over one of the options, the option was highlighted by a surrounding white rectangle. The option could then be chosen by pressing the left mouse button. Trials were separated with a variable ITI between 1 and 1.5 s (in steps of 0.1 s).
Food snacks were products from local Swiss supermarkets. Selection of the food snacks for the two experiments were based on a pilot study with a different pool of 21 participants that rated 60 food snacks with respect to liking, familiarity, distinctiveness and category matching (details can be found in Mechera-Ostrovsky and Gluth58). As in the original study, participants received a monetary reimbursement for their participation (CHF 20 per hour).
Experimental design of the eye-tracking experiment
The procedures of the eye-tracking experiment were largely identical to those of the direct replication. Here, we only describe the differences between the two experiments. A higher number of snacks (45) was used to reduce the number of repetitions of options in consecutive choice trials. A higher number of decisions (300) was used to increase statistical power. The algorithm to create choice sets was adjusted accordingly (i.e., 15 distractors * 5 target-value difference levels * 4 random draws of target pairs per difference level). Instead of a BDM auction, participants rated their subjective liking of each snack on a continuous bar (from “like not at all” to “like very much”). The bar included red vertical lines at 20, 40, 60, 80% of its size as orientation. No monetary value was displayed. The mouse cursor for the rating task was a yellow arrow. Importantly, the rating task was incentivized: Participants were informed that if their reward at the end of the experiment was determined from the rating task, two rating trials would be selected randomly and they would receive the higher rated snack. A gray background was used during the rating and choice tasks. ITI screens included a white fixation cross at the center of the screen. Options in the choice task were presented in triangular orientation (lower left, upper middle, lower right), so that the first fixation was not automatically on the middle option. Choices were not made with the computer mouse but with the left, upper, and right arrow keyboard buttons. When a decision was made, the chosen option was highlighted by a white frame for 0.5 s. The Matlab-based software package Cogent 2000 was used for stimulus presentation. A desktop PC with a 22-inch monitor was used and the display resolution was set to 1280x1024. Participants were required to wait for 30 minutes in the lab after completing the computer tasks. During this time, they were asked to rate the snacks with respect to their distinctiveness and familiarity using the same rating scheme as for the subject value ratings (for one participant, these ratings were not recorded due to a computer crash; because these ratings were not central to any of our analyses, we decided to include this participant). The 19 psychology students of the University of Basel that took part in the experiment could choose between money (20 CHF per hour) or course credits as reimbursement.
In addition to these changes, the task was adjusted for eye-tracking purposes. Gaze positions were recorded using an SMI RED500 eye-tracking device with 500 Hz sampling rate. Eye-movements were recorded only during the choice task. Instructions of the choice task included information about the calibration procedures. The initial calibration was conducted before the first choice task. Between trials, participants were required to look at the fixation cross. If their gaze stayed within an (invisible) area of interest (AOI) with a diameter of 205 pixels around the fixation cross, a counter was initialized at 0 and increased by 1 every 10 ms until it reached 100, which started the next trial. If the gaze went out of the AOI, the counter decreased by 1 every 10 ms. Thus, in the optimal case of purely within-AOI gazes, a trial was started after 1 s. This procedure ensured a high calibration quality throughout the experiment. If a choice trial could not be started within 10 s, the eye-tracker was recalibrated. If more than 3 re-calibrations within a single trial or more than 5 re-calibrations over 10 consecutive trials were required, the experiment was aborted.
Preregistered data analyses of the direct replication experiment
The replicability of the distractor effect was assessed by two statistical tests, a comparison of relative choice accuracy between trials with high- vs. low-value distractors and a logistic regression of relative choice accuracy with V3 (together with V1 and V2) as predictor variable. These tests were also conducted by Louie and colleagues4, but we modified the analyses in the following ways (modifications were preregistered): The median-split between high- and low-value distractors was performed within each participant to ensure equal trial numbers per level; the median-split was based on V3 rather than normV3; similarly, normV3 was replaced by V3 in the logistic regression; the regression was conducted within each participant and the resulting coefficients were tested against 0 (one-sample t-test). Our reasons for deviating from the original analyses were as follows: We replaced normV3 by V3, because normV3 is confounded with the target-value difference V1 – V2 and thus with the difficulty of choosing between the targets (detailed information are provided in the Supplementary Information). We replaced the fixed-effects by the random-effects analysis approach, because the random-effects analysis approach allows a better generalization to the population59 and avoids spuriously significant effects (detailed information are provided in the see Supplementary Information). Importantly, we also provide additional analyses including analyses with normV3 and fixed-effects analyses in the Supplementary Information. None of these analyses provided evidence that would support the normalization model. Data distribution was assumed to be normal but this was not formally tested. One-sided p-values are reported for preregistered tests.
As stated above, replication success was assessed based on the Small Telescopes approach21. The effect size that would give the original study (with 40 participants) only 33% statistical power was d33% = -0.25 for both tests. The critical effect size for the replication study (with 102 participants) at which replication failure would be concluded (because the 90% CI of the replication effect size does not overlap with d33%) was d = -0.08. Notably, this is a more lenient criterion than inferring replication success based on statistical significance in the replication study, which would have required d = -0.16.
Additional data analyses of the direct replication experiment
The Small Telescopes approach provides a systematic test of replication success within the realm of frequentist statistics without making (unjustified) inferences on the basis of non-significant hypothesis tests21. In addition, we sought to quantify the evidence in favor of the null hypothesis of no distractor effect on relative choice accuracy, by repeating the logistic regression analysis with V1, V2, and V3 as predictors in a hierarchical Bayesian framework. Individual regression coefficients were assumed to be drawn from group-level normal distributions with means μ(Vi) and standard deviations σ(Vi). Priors for group-level parameters were normal distributions with means 0 and standard deviations 5 (choosing different priors for the standard deviations did not affect the results qualitatively). Priors for group-level standard deviations were truncated to be ≥ 0. Gibbs sampling as implemented in JAGS was performed within Matlab (function matjags.m) with 4 chains, 2’000 burn-in samples, 10’000 recorded samples and a thinning of 10. Convergence was ensured by requiring R-hat values for all parameters to be < 1.01. The Bayes Factor was determined using the Savage-Dickey density ratio test60. Notably, the hierarchical Bayesian approach circumvents the disadvantages of both the fixed-effects approach (which let to spurious effects, see Supplementary Information) and the random-effects approach (which could not be performed in one participant, see above). Therefore, we performed the Bayesian analysis twice, with and without the excluded participant, and obtained the same Bayes Factor of 241 in favor of the null hypothesis.
Random-effects linear regression analyses were conducted to test influences of V1 – V2, V1 + V2, and V3 on RT in both experiments. RT beyond 4 SD of the group mean were excluded. Two-sided p-values are reported for these analyses.
Preregistered data analyses of the eye-tracking experiment
Eye-tracking data was preprocessed by recoding the raw gaze positions into events (fixations, saccades, blinks) in SMI’s BeGaze software package using the high-speed detection algorithm with default values. For one participant, recoding with BeGaze did not work properly and SMI’s Event Detection software was used instead. AOIs for the left, middle, and right option were defined such that fixations on the entire stimulus picture (including the black space around the snack) counted towards the respective option. The main dependent variables were relative gaze duration (i.e., the amount of time within a trial during which an option was looked at relative to the amount of time during which any option was looked at) and the number of fixations.
The behavioral data analyses matched those of the direct replication experiment. In addition, we tested for a mediation of the distractor effect by value-based attention via a path analysis, in which relative choice accuracy was regressed onto V3 and onto relative gaze duration while relative gaze duration was also regressed onto V3. A random-effects approach was applied with the path analysis being performed within each participant and the resulting regression coefficients being subjected to one-sample t-tests against 0 on the group level. To test for early effects of value-based attention, a random-effects logistic regression analysis was conducted regressing whether the first fixation was on the distractor onto V3. Trials with only one fixation were excluded from this analysis. To test for late effects of value-based attention, a random-effects logistic regression analysis was conducted regressing whether any fixation (except the last) was on the distractor onto V3, the within-trial fixation number, and the interaction between V3 and fixation number. To avoid nonessential multicollinearity12,61, predictor variables were standardized before generating their interaction term. The critical test is whether the interaction term is significantly positive, as this indicates a stronger decline of attention on low- compared to high-value distractors. Trials in which the distractor was chosen were excluded from this analysis to ensure that the influence of V3 on looking at the distractor was not driven by the fact that high-value distractors are more likely to be chosen than low-value distractors. Further note that this regression analysis requires a sufficient amount of fixations at each fixation number, across trials. Therefore, we included only those fixation numbers per participant for which we had ≥ 30 fixations (e.g., if a participant had 32 fixations at fixation number 6 but only 25 fixations at fixation number 7, for that participant we would only analyze up to the 6th fixation). This procedure was described in the preregistration protocol.
Additional data analyses of the eye-tracking experiment
As an additional test for early effects of value-based attention, a repeated-measures ANOVA was conducted with option type (best, second-best, distractor) as factor and fixation probability as dependent variable. As an additional test for late effects of value-based attention, a repeated-measures ANOVA was conducted with option type and within-trial fixation number as factors and fixation probability as dependent variable. Greenhouse-Geisser correction was used when assumptions of sphericity were violated. To test for early and late effects of value-based attention on the allocation of attention between target options, paired t-tests were performed that compared the frequency of fixations on the best vs. the second-best option, separately for the first and for later fixations. To test for an influence of attention on choice16,17, a random-effects logistic regression analysis was conducted with relative gaze duration towards an option and relative value of an option (i.e., the value of an option relative to the sum of values in the choice set) as predictor variables and choice of an option as dependent variable. The critical test is whether the influence of gaze is positive. The relative value predictor serves as a control variable. The last fixation per trial was excluded from all these analyses.
Statistical analyses were performed in Matlab (regression analyses) and R (path analyses with the lavaan package, ANOVAs with the packages car and heplots). Information about the re-analysis of the dataset of Krajbich & Rangel (2011)17 are provided in the Supplementary Information.
Computational modeling
Information about the model comparison between probit and divisive normalization as well as on the extended aDDM are provided in the Supplementary Information
Supplementary Material
Acknowledgements
We thank Kenway Louie for providing us with a lot of materials from the original study and for approving the preregistration protocol of the direct replication experiment. Further thanks go to Ian Krajbich and Antonio Rangel for sharing their data, and to Ian Krajbich and Jörg Rieskamp for comments on an earlier version of the manuscript. S.G. was supported by a grant from the Swiss National Science Foundation (SNSF 100014_172761). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Footnotes
Sebastian Gluth: ORCID: 0000-0003-2241-5103
Data availability
Data of all participants included in the final samples of the two experiments are publicly available on OSF (https://osf.io/qrv2e/).
Code availability
Custom code that supports the findings of this study is publicly available on OSF (https://osf.io/qrv2e/).
Author Contributions
All authors designed the study, N.K., M.K. and C.L.V. collected the data, all authors analyzed the data, S.G. wrote the manuscript, N.K., M.K., and C.L.V. revised the manuscript.
Competing Interests
The authors declare no competing interests.
References
- 1.Glimcher PW, Rustichini A. Neuroeconomics: the consilience of brain and decision. Science. 2004;306:447–452. doi: 10.1126/science.1102566. [DOI] [PubMed] [Google Scholar]
- 2.Carandini M, Heeger DJ. Normalization as a canonical neural computation. Nat Rev Neurosci. 2012;13:51–62. doi: 10.1038/nrn3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Louie K, Grattan LE, Glimcher PW. Reward value-based gain control: divisive normalization in parietal cortex. J Neurosci. 2011;31:10627–10639. doi: 10.1523/JNEUROSCI.1237-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Louie K, Khaw MW, Glimcher PW. Normalization is a general neural mechanism for context-dependent decision making. Proc Natl Acad Sci. 2013;110:6139–6144. doi: 10.1073/pnas.1217854110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Savage LJ. The Foundations of Statistics. Wiley; 1954. [Google Scholar]
- 6.Luce RD. Individual Choice Behavior: A Theoretical Analysis. Dover Publications; 1959. [Google Scholar]
- 7.Busemeyer JR, Gluth S, Rieskamp J, Turner BM. Cognitive and neural bases of multi-attribute, multi-alternative, value-based decisions. Trends Cogn Sci. 2019;23:251–263. doi: 10.1016/j.tics.2018.12.003. [DOI] [PubMed] [Google Scholar]
- 8.Huber J, Payne JW, Puto C. Adding asymmetrically dominated alternatives: Violations of regularity and the similarity hypothesis. J Consum Res. 1982;9:90–98. [Google Scholar]
- 9.Gluth S, Hotaling JM, Rieskamp J. The attraction effect modulates reward prediction errors and intertemporal choices. J Neurosci. 2017;37:371–382. doi: 10.1523/JNEUROSCI.2532-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Munafò MR, et al. A manifesto for reproducible science. Nat Hum Behav. 2017;1 doi: 10.1038/s41562-016-0021. 0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Anderson BA, Laurent PA, Yantis S. Value-driven attentional capture. Proc Natl Acad Sci. 2011;108:10367–10371. doi: 10.1073/pnas.1104047108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gluth S, Spektor MS, Rieskamp J. Value-based attentional capture affects multi-alternative decision making. eLife. 2018;7:e39659. doi: 10.7554/eLife.39659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tsetsos K, Chater N, Usher M. Salience driven value integration explains decision biases and preference reversal. Proc Natl Acad Sci U S A. 2012;109:9659–9664. doi: 10.1073/pnas.1119569109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Glickman M, Tsetsos K, Usher M. Attentional selection mediates framing and risk-bias effects. Psychol Sci. 2018;29:2010–2019. doi: 10.1177/0956797618803643. [DOI] [PubMed] [Google Scholar]
- 15.Usher M, Tsetsos K, Glickman M, Chater N. Selective integration: an attentional theory of choice biases and adaptive choice. Curr Dir Psychol Sci. 2019 doi: 10.1177/0963721419862277. 096372141986227. [DOI] [Google Scholar]
- 16.Krajbich I, Armel C, Rangel A. Visual fixations and the computation and comparison of value in simple choice. Nat Neurosci. 2010;13:1292–1298. doi: 10.1038/nn.2635. [DOI] [PubMed] [Google Scholar]
- 17.Krajbich I, Rangel A. Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions. Proc Natl Acad Sci. 2011;108:13852–13857. doi: 10.1073/pnas.1101328108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Forstmann BU, Ratcliff R, Wagenmakers E-J. Sequential sampling models in cognitive neuroscience: advantages, applications, and extensions. Annu Rev Psychol. 2016;67:641–666. doi: 10.1146/annurev-psych-122414-033645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- 20.Asendorpf JB, et al. Recommendations for increasing replicability in psychology. Eur J Personal. 2013;27:108–119. [Google Scholar]
- 21.Simonsohn U. Small telescopes: detectability and the evaluation of replication results. Psychol Sci. 2015;26:559–569. doi: 10.1177/0956797614567341. [DOI] [PubMed] [Google Scholar]
- 22.Kass RE, Raftery AE. Bayes factors. J Am Stat Assoc. 1995;90:773–795. [Google Scholar]
- 23.McFadden D. Economic choices. Am Econ Rev. 2001;91:351–378. [Google Scholar]
- 24.Polanía R, Krajbich I, Grueschow M, Ruff CC. Neural oscillations and synchronization differentially support evidence accumulation in perceptual and value-based decision making. Neuron. 2014;82:709–720. doi: 10.1016/j.neuron.2014.03.014. [DOI] [PubMed] [Google Scholar]
- 25.Palminteri S, Khamassi M, Joffily M, Coricelli G. Contextual modulation of value signals in reward and punishment learning. Nat Commun. 2015;6 doi: 10.1038/ncomms9096. 8096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fontanesi L, Gluth S, Spektor MS, Rieskamp J. A reinforcement learning diffusion decision model for value-based decisions. Psychon Bull Rev. 2019 doi: 10.3758/s13423-018-1554-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pearson D, et al. Value-modulated oculomotor capture by task-irrelevant stimuli is a consequence of early competition on the saccade map. Atten Percept Psychophys. 2016;78:2226–2240. doi: 10.3758/s13414-016-1135-2. [DOI] [PubMed] [Google Scholar]
- 28.Shimojo S, Simion C, Shimojo E, Scheier C. Gaze bias both reflects and influences preference. Nat Neurosci. 2003;6:1317–1322. doi: 10.1038/nn1150. [DOI] [PubMed] [Google Scholar]
- 29.Fiedler S, Glöckner A. The dynamics of decision making in risky choice: an eye-tracking analysis. Front Psychol. 2012;3 doi: 10.3389/fpsyg.2012.00335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cavanagh JF, Wiecki TV, Kochar A, Frank MJ. Eye tracking and pupillometry are indicators of dissociable latent decision processes. J Exp Psychol Gen. 2014;143:1476–1488. doi: 10.1037/a0035813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stewart N, Gächter S, Noguchi T, Mullett TL. Eye movements in strategic choice. J Behav Decis Mak. 2016;29:137–156. doi: 10.1002/bdm.1901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Thomas AW, Molter F, Krajbich I, Heekeren HR, Mohr PNC. Gaze bias differences capture individual choice behaviour. Nat Hum Behav. 2019 doi: 10.1038/s41562-019-0584-8. [DOI] [PubMed] [Google Scholar]
- 33.Smith SM, Krajbich I. Gaze amplifies value in decision making. Psychol Sci. 2019;30:116–128. doi: 10.1177/0956797618810521. [DOI] [PubMed] [Google Scholar]
- 34.Holper L, et al. Adaptive value normalization in the prefrontal cortex is reduced by memory load. eneuro. 2017;4 doi: 10.1523/ENEURO.0365-17.2017. ENEURO.0365-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Padoa-Schioppa C. Range-adapting representation of economic value in the orbitofrontal cortex. J Neurosci. 2009;29:14004–14014. doi: 10.1523/JNEUROSCI.3751-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cox KM, Kable JW. BOLD subjective value signals exhibit robust range adaptation. J Neurosci. 2014;34:16533–16543. doi: 10.1523/JNEUROSCI.3927-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kobayashi S, Pinto de Carvalho O, Schultz W. Adaptation of reward sensitivity in orbitofrontal neurons. J Neurosci. 2010;30:534–544. doi: 10.1523/JNEUROSCI.4009-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Furl N. Facial-Attractiveness Choices Are Predicted by Divisive Normalization. Psychol Sci. 2016;27:1379–1387. doi: 10.1177/0956797616661523. [DOI] [PubMed] [Google Scholar]
- 39.Rustichini A, Conen KE, Cai X, Padoa-Schioppa C. Optimal coding and neuronal adaptation in economic decisions. Nat Commun. 2017;8 doi: 10.1038/s41467-017-01373-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chang LW, Gershman SJ, Cikara M. Comparing value coding models of context-dependence in social choice. J Exp Soc Psychol. 2019;85 103847. [Google Scholar]
- 41.Li V, Michael E, Balaguer J, Herce Castañón S, Summerfield C. Gain control explains the effect of distraction in human perceptual, cognitive, and economic decision making. Proc Natl Acad Sci. 2018;115:E8825–E8834. doi: 10.1073/pnas.1805224115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tajima S, Drugowitsch J, Patel N, Pouget A. Optimal policy for multi-alternative decisions. Nat Neurosci. 2019;22:1503–1511. doi: 10.1038/s41593-019-0453-9. [DOI] [PubMed] [Google Scholar]
- 43.Khaw MW, Glimcher PW, Louie K. Normalized value coding explains dynamic adaptation in the human valuation process. Proc Natl Acad Sci. 2017;114:12696–12701. doi: 10.1073/pnas.1715293114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mohr PNC, Heekeren HR, Rieskamp J. Attraction effect in risky choice can be explained by subjective distance between choice alternatives. Sci Rep. 2017;7 doi: 10.1038/s41598-017-06968-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Frederick S, Lee L, Baskin E. The limits of attraction. J Mark Res. 2014;51:487–507. [Google Scholar]
- 46.Spektor MS, Gluth S, Fontanesi L, Rieskamp J. How similarity between choice options affects decisions from experience: The accentuation-of-differences model. Psychol Rev. 2019;126:52–88. doi: 10.1037/rev0000122. [DOI] [PubMed] [Google Scholar]
- 47.Tusche A, Hutcherson CA. Cognitive regulation alters social and dietary choice by changing attribute representations in domain-general and domain-specific brain circuits. eLife. 2018;7 doi: 10.7554/eLife.31185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Grueschow M, Polania R, Hare TA, Ruff CC. Automatic versus choice-dependent value representations in the human brain. Neuron. 2015;85:874–885. doi: 10.1016/j.neuron.2014.12.054. [DOI] [PubMed] [Google Scholar]
- 49.Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychol Sci. 1998;9:347–356. [Google Scholar]
- 50.Mullett TL, Stewart N. Implications of visual attention phenomena for models of preferential choice. Decision. 2016;3:231–253. doi: 10.1037/dec0000049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cavanagh SE, Malalasekera WMN, Miranda B, Hunt LT, Kennerley SW. Visual fixation patterns during economic choice reflect covert valuation processes that emerge with learning. Proc Natl Acad Sci. 2019;116:22795–22801. doi: 10.1073/pnas.1906662116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Callaway F, Griffiths T. Attention in value-based choice as optimal sequential sampling. PsyArXiv. doi: 10.31234/osf.io/57v6k. [DOI] [Google Scholar]
- 53.Sims CA. Implications of rational inattention. J Monet Econ. 2003;50:665–690. [Google Scholar]
- 54.Towal RB, Mormann M, Koch C. Simultaneous modeling of visual saliency and value computation improves predictions of economic choice. Proc Natl Acad Sci. 2013;110:E3858–E3867. doi: 10.1073/pnas.1304429110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Turner BM, et al. A Bayesian framework for simultaneously modeling neural and behavioral data. NeuroImage. 2013;72:193–206. doi: 10.1016/j.neuroimage.2013.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Brandt MJ, et al. The Replication Recipe: What makes for a convincing replication? J Exp Soc Psychol. 2014;50:217–224. [Google Scholar]
- 57.Becker GM, DeGroot MH. MarschakJ: Measuring utility by a single-response sequential method. Behav Sci. 1964;9:226–232. doi: 10.1002/bs.3830090304. [DOI] [PubMed] [Google Scholar]
- 58.Mechera-Ostrovsky T, Gluth S. Memory beliefs drive the memory bias on value-based decisions. Sci Rep. 2018;8 doi: 10.1038/s41598-018-28728-9. 10592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Holmes AP, Friston KJ. Generalisability, random effects & population inference. NeuroImage. 1998;7:S754. [Google Scholar]
- 60.Lee MD, Wagenmakers E-J. Bayesian cognitive modeling: a practical course. Cambridge University Press; 2013. [Google Scholar]
- 61.Aiken LS, West SG. Multiple Regression: Testing and Interpreting Interactions. SAGE; 1991. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.