Abstract
Arterial spin labeling (ASL) imaging is a powerful magnetic resonance imaging technique that allows to quantitatively measure blood perfusion non-invasively, which has great potential for assessing tissue viability in various clinical settings. However, the clinical applications of ASL are currently limited by its low signal-to-noise ratio (SNR), limited spatial resolution, and long imaging time. In this work, we propose an unsupervised deep learning-based image denoising and reconstruction framework to improve the SNR and accelerate the imaging speed of high resolution ASL imaging. The unique feature of the proposed framework is that it does not require any prior training pairs but only the subject’s own anatomical prior, such as T1-weighted images, as network input. The neural network was trained from scratch in the denoising or reconstruction process, with noisy images or sparely sampled k-space data as training labels. Performance of the proposed method was evaluated using in vivo experiment data obtained from 3 healthy subjects on a 3T MR scanner, using ASL images acquired with 44-min acquisition time as the ground truth. Both qualitative and quantitative analyses demonstrate the superior performance of the proposed txtc framework over the reference methods. In summary, our proposed unsupervised deep learning-based denoising and reconstruction framework can improve the image quality and accelerate the imaging speed of ASL imaging.
Keywords: Unsupervised deep learning, neural network, arterial spin labeling, denoising, sparse sampling, reconstruction with prior
1 |. INTRODUCTION
Perfusion is an important physiological biomarker which is commonly used to assess tissue viability in clinical settings. Arterial spin labeling (ASL) is a powerful magnetic resonance imaging (MRI) technique that measures blood perfusion without exposure to ionizing radiation or involvement of contrast agent injection1,2. Due to the non-invasive, repeatable, and quantitative nature of the technique, ASL has great potential for studying perfusion in research settings as well as in clinical scenarios with contraindications of gadolinium, especially for pediatric patients or patients with renal failure. However, since only a small portion of blood is labeled compared to the whole tissue volume, conventional ASL suffers from low signal-to-noise ratio (SNR), poor spatial resolution, and long acquisition time.
Because ASL has great potential in clinical and basic research applications, developing advanced data acquisition schemes and processing methods for fast, high-resolution, high-SNR ASL has been a very active research area. For data acquisition, three-dimensional (3D) ASL sequences, e.g., 3D rapid acquisition with relaxation enhancement (RARE) stack-of-spirals3,4, 3D gradient and spin echo (GRASE)5,6,7,8,9, and 3D balanced steady-state free precession (bSSFP)10,11, have been developed to achieve whole-brain perfusion mapping within a clinically feasible scan time with higher SNR efficiency than the conventional 2D acquisitions. For data processing, partial volume correction methods using linear regressions12 or modified least trimmed squares13 have been developed for more accurate estimation of perfusion signal from ASL images with limited spatial resolutions. To improve the robustness of ASL, methods utilizing selective averaging14, wavelet-based filters15, independent component analysis16 have been proposed to suppress errors due to instabilities during acquisition (e.g., subject motion and physiological noise attributed to cardiac pulsation) and improve SNR. More importantly, many methods have been proposed to recover high-SNR, artifact-free ASL images from noise-corrupted and/or sparsely sampled k-space data by incorporating parallel imaging17,18, compressed sensing10, spatial19 or spatiotemporal constraints20,21, and physical and physiological model22 into the conventional image reconstruction. However, despite these significant technical advances in the past decade, the clinical applications of ASL are still limited by SNR and imaging time. In practice, a number of repetitive measurements are often required to achieve reliable image quality, which greatly hinders the clinical translation of the technique.
Deep neural networks (DNNs) have emerged as a powerful tool for image processing and reconstruction. DNN-based methods have made breakthroughs in numerous computer vision tasks. Recently, DNN has been applied to various applications of MR to improve image quality via image denoising23,24,25,26 or reconstruction approaches27,28,29,30,31,32,33,34,35. Specifically, several pioneering works have applied DNN to improve ASL36,37,38,39. Up to date, all previously proposed DNN-based frameworks require either a large set of images reconstructed from fully sampled dataset or multiple measurements as training labels for network training. However, collecting such training labels can be challenging due to difficulties in recruiting, collecting, and processing data from a large number of subjects. And there are cases, e.g., ASL, where acquiring fully sampled 3D MR images with high-resolution and high-SNR itself can be challenging due to the long acquisition time and limitations of the current MR hardware systems. Apart from high-quality training labels, structural priors40,41,42,43, extra information from other domains44,45, or similarities shared across multi-contrast images46,47,26, can be also employed in network training to further boost the performance of DNN. Recently, the deep image prior framework48 shows that DNN can learn intrinsic structural information from the corrupted images. In this framework, random noise is used as the network input and no high-quality training labels are needed. Furthermore, it has been shown that when the network input is not random noise but high-resolution anatomical prior from the same subject, the denoising results can be further improved49.
Inspired by these prior arts, in this work, we explored the possibility of utilizing anatomical prior to perform image denoising and image reconstruction for ASL. In this proposed framework, no high-quality training labels are needed. Hence it is an unsupervised deep learning approach. To train the network, we used T1-weighted anatomical image as network input, with noisy ASL image as training label for denoising task or k-space data as training label for image reconstruction from sparsely sampled data application. The 3D U-net50 was adopted as the network structure, and L-BFGS algorithm51 was chosen as the optimization algorithm for network training because of its monotonic property and better performance observed in experiments. The performance of the proposed framework was evaluated via in vivo experiments with healthy volunteers from a 3T MR scanner. State-of-the-arts methods, i.e., guided image filtering, non-local mean denoising, total variation penalty-based reconstruction and anatomically constrained reconstruction, were employed as comparison methods to evaluate the performance of the proposed framework.
2 |. METHODS
For MR inverse problems such as image denoising and reconstruction, the measured data, , can be written as
| (1) |
where is the transformation matrix, is the unknown image to be estimated, is the noise, M is the size of measured data, and N is the number of pixels in image space. Supposing y is independent and identically distributed (i.i.d.) and the ith element of y, yi, follows a distribution of p(yi|x), we can estimate x based on the maximum likelihood framework as
| (2) |
The maximum-likelihood solution of (2) can be prone to noise and/or undersampling artifacts. Previous works have focused on incorporating sparsity52, dictionary-learning representation 53 or low-rank54 constraints into the image reconstruction. In the dictionary learning framework, the unknown image is linearly represented by an over-complete dictionary. Following the deep image prior framework48 and associated works55,49, we propose to nonlinearly represent the image x by a deep neural network as
| (3) |
where f represents the neural network, θ denotes the unknown parameters of the neural network, and z denotes the prior image which is the input to the neural network. This representation can exploit multiple-contrast prior images, simply by increasing the number of network-input channels. With x substituted by the neural network representation in (3), the original data model in (1) becomes
| (4) |
where θ are the only unknown parameters to be determined. The task of recovering unknown image x from the measured data y is translated to finding an optimal set of network parameters θ that maximize the likelihood function:
| (5) |
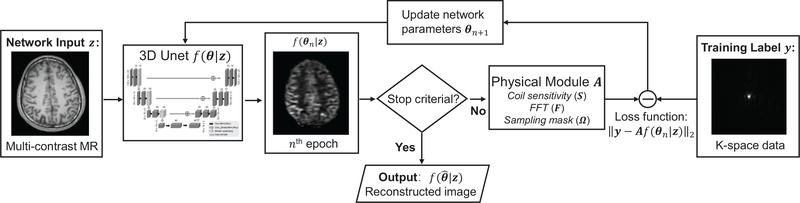
Once θ is determined, the reconstructed image is simply the output of the neural network, . Figure 1 shows the flowchart of the proposed framework for denoising and reconstruction tasks. Optimization details for each case are explained below.
FIGURE 1.
Diagram of the proposed framework for under-sampling reconstruction task. For denoising task, the physical module A is an identity matrix and the training label is the noisy image itself.
2.1 |. Image Denoising
For denoising applications, the transformation matrix A becomes an identity matrix and y is the noisy image. Supposing the image noise w follows i.i.d. Gaussian distribution56,57, the maximum likelihood estimation in (5) can be explicitly written as
| (6) |
Optimization of (6) is a network training problem with the commonly used ℓ2 norm as the loss function. A unique advantage of this framework is that only the measured data from the subject is employed in the training process, with no additional training pairs needed. This significantly reduces the training data size and thus allows using high-order optimization methods to train the network with better convergence properties. We propose to use the L-BFGS algorithm51 to solve (6), which is a Quasi-Newton method, using a history of updates to approximate the Hessian matrix. Compared to the commonly used first-order stochastic algorithms, L-BFGS is a monotonic algorithm and is preferred to solve (6) due to its stability and better performance observed in our previous work49.
2.2 |. Reconstruction from sparsely sampled data
For image reconstruction, y is the measured k-space data and A is the forward model of imaging, which can be written as
| (7) |
where Ω is the k-space sampling mask, denotes Fourier transform, and S represents the coil sensitivities. Assuming i.i.d. Gaussian noise in the k-space data 56,57, the maximum likelihood estimation in (5) becomes
| (8) |
Directly training the neural network (estimating θ) using the loss function in (8) can be time consuming because the forward operator A and its adjoint is often computationally expensive and the neural network training needs more update steps compared to traditional iterative image reconstruction. Instead alternating direction method of multipliers (ADMM)58 was used to separate the reconstruction and network training steps. Another advantage is that this separation allows direct use of penalized image reconstruction methods at the image reconstruction step, which have been extensively studied in the past. We first introduced one auxiliary variable x to convert (8) to the constrained format as below
| (9) |
The augmented Lagrangian format for the constrained optimization problem in (9) is
| (10) |
where y is the dual variable and ρ is the penalty parameter. It can be solved by the ADMM algorithm iteratively in three steps
| (11) |
| (12) |
| (13) |
where μ = (1/ρ)y is the scaled dual variable. Detailed derivations from the objective function (10) to the three update steps can be found in the review paper58. With the ADMM algorithm, we decoupled the original constrained optimization problem into a network training problem (11) and a penalized reconstruction problem (12). At each step of iteration, the parameters of the neural network (θn+1) are estimated by minimizing the ℓ2 norm difference between the output of the network (f(θ|z)) and the training label (xn + μn). The training label are updated consecutively by solving subproblem (12) and (13), respectively. For subproblem (11), the L-BFGS algorithm described in the denoising section 2.1 is used to solve it. By setting the first order derivative to zero, the normal equation for subproblem (12) can be expressed as
| (14) |
Preconditioned conjugate gradient (PCG) algorithm59 was used to solve the above normal equation.
2.3 |. Network Structure
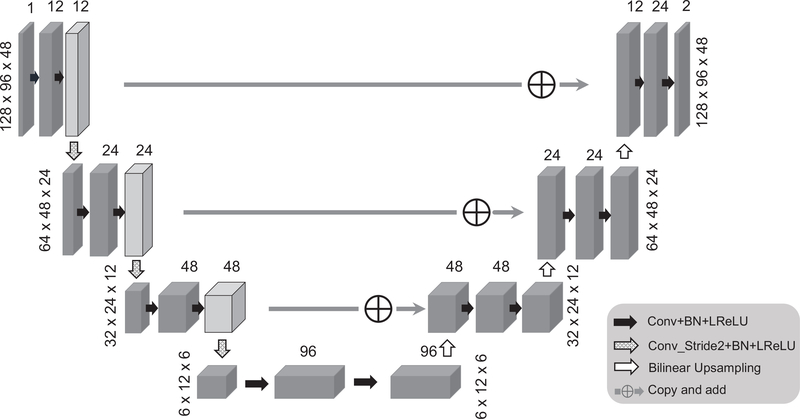
The network structure employed in this work is based on a modified 3D U-net50 shown in Fig. 2, where several modifications were made to accommodate the proposed framework: (1) convolutional layer with stride 2 was used to down-sample the image instead of using max-pooling layer, to construct a fully convolutional network; (2) the left side feature was directly added to the right side instead of concatenation operations, to reduce the number of training parameters; (3) for up-sampling layer, bi-linear interpolation was used instead of transposed convolution, to reduce the checkerboard artifact; (4) leaky ReLU was used instead of ReLU. The magnitude component of the prior image was used as input. Note that the phase of the prior image is not used in our current implementation because the phase information often does not represent high-resolution structural information and is sequence dependent. The image denoising/reconstruction was performed from the complex domain. Accordingly, the network output has two channels: real and imaginary parts of the ASL image. The proposed method can also be applied for denoising of magnitude images by reducing the output channel number to one. The whole network was implemented based on TensorFlow 1.6 on a NVIDIA GTX 1080 Ti graphic card. The denoising task running 500 epochs takes around 4 min and the reconstruction from sparsely sampled data application takes around 40 min, running 100 iterations of the ADMM framework.
FIGURE 2.
The schematic plot of the 3D Unet structure used in this work. The spatial size for each layer is based on the matrix size of the ASL dataset used in this work. The network input is the magnitude of the prior image and the network output has two channels: real and imaginary parts of the ASL image.
3 |. EXPERIMENTS
3.1 |. Data acquisition
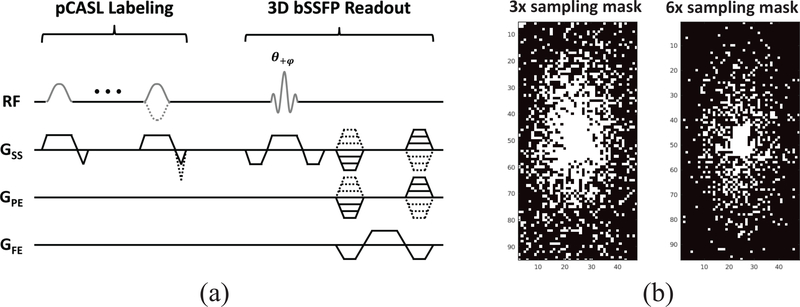
All experiments were performed on a 3T whole-body scanner (Magnetom Tim Trio, Siemens Healthcare, Erlangen, Germany). Three healthy volunteers (two males and one female, 29–31 years old) were examined for the study. The study protocol was approved by the local Institutional Review Board (IRB) and informed written consent was obtained from all subjects before the scan. A three-plane localizer and a T1-weighted magnetization-prepared rapid gradient echo (MPRAGE) were performed followed by a series of ASL acquisitions. All ASL images were acquired using pseudo-continuous ASL (pCASL)60,4 with bSSFP readout61,10,11 (Fig. 3(a)). The pCASL labeling parameters were: RF pulse shape = Hanning window; flip angle = 25°; RF duration/spacing = 0.5/0.92 ms; total labeling duration (τ) =1500 ms; post-labeling delay (PLD) time=1.2 s; max slice-selective gradient (Gss) = 6.0 mT/m; labeling plane= 8.5 cm inferior to the AC-PC line; and unbalanced tagging scheme4 (i.e., mean Gss of 1 and 0 mT/m for label and control pulses, respectively). The imaging parameters for each set of pCASL scans were as follows: matrix size = 128 × 96 × 48; voxel size = 1.875 × 1.875 × 2.5 mm3; image plane = axial; slice thickness = 2.5 mm; TR/TE = 3.93/1.73 ms; flip angle = 30°; acquisition bandwidth = 592 Hz/pixel; partial Fourier factor in the slice direction = 6/8; delay between acquisitions = 0.6 sec; number of segments = 12; number of excitations (NEX) = 3; total acquisition time= 5.5 min. A total of eight sets of pCASL scans were acquired and a separate scan without labeling but with the same readout was acquired for M0. The MPRAGE image was registered to the same pixel size as the ASL image and was used as an anatomical prior for network input. Retrospective undersampling was performed to evaluate the performance of the proposed method in the case of image reconstruction from sparsely sampled data. The three repetitions of each pCASL dataset were retrospectively undersampled using different variable density sampling masks with acceleration factors of 3 and 6, respectively (Fig. 3(b)). The equivalent scanning time for 3- and 6-times acceleration is 1.8 min and 0.9 min, respectively. The coil sensitivity maps were estimated from the low-frequency region of the fully sampled k-space data and was used for all SENSE62-based reconstruction algorithm.
FIGURE 3.
(a) A schematic diagram of the 3D bSSFP pCASL sequence. (b) Sampling masks used in a 96 × 48 phase encoding plane.
3.2 |. Comparison methods
For the denoising case, the nonlocal-mean (NLM) method using the T1-weighted MPRAGE image as prior was chosen as a comparison method63. The final denoised image at voxel i is , where wij is the filter weight between voxels i and j, y is the original noisy image and Ni is the searching neighborhood around voxel i. In this paper, wij was calculated based on the T1-weighted image as
| (15) |
where fi represents the patch around the ith voxel in theT1-weighted image. σ2 was set to the image variance inside the brain region. The patch size was set to 3 based on previous literatures64,65 and the searching window size was set to 7 based on the maximizing the peak signal-to-noise ratio (PSNR) of the whole image. In addition, the guided image filtering (GIF) method66 was also employed as a reference method. The parameter settings of the GIF method followed the default parameter settings in Matlab R2018a (MathWorks Inc., Natick, MA, USA). For the image reconstruction from sparsely sampled data case, SENSE reconstruction62 with Tikhonov regularization was adopted as the baseline method to reconstruct the under-sampled image,
| (16) |
In addition, SENSE reconstruction with total variation (TV) regularization10 was included as a reference method,
| (17) |
Finally, the anatomically constrained (AC) reconstruction with edge weights derived from the T1-weighted image was also adopted as the comparison method40,
| (18) |
Here wij was calculated according to (15) with the same parameter settings as the NLM denoising. Penalty parameter β in (16), (17) and (18) was chosen by setting the data consistency error similar to the k-space noise level. The PCG algorithm was used to solve (16) and (18) and the ADMM algorithm was used to solve (17)10.
3.3 |. CBF quantification
The cerebral blood flow (CBF) was calculated using the standard single-compartment model67,68 for bSSFP readout10,
| (19) |
where denotes the label-control subtraction signal, which is the result of denoising or image reconstruction described in Sec. 2.1 and Sec. 2.2, respectively, λ denotes the blood-tissue water partition coefficient, T1b denotes the longitudinal relaxation time of blood, α denotes the labeling efficiency, and D denotes the signal decay rate from the repetitive RF excitations pulses in bSSFP readout. λ = 0.9 mL/g, α = 0.85, T1b = 1650 ms, D = 0.996, were assumed for the calculation of CBF68,10. To quantitatively evaluate the performance of different methods, the PSNR was calculated for the gray matter region68,69 and the structural similarity index (SSIM)70 was calculated based on the whole image. The PSNR was calculated as , where stands for the maximum value of the estimated image, and stands for the jth pixel of the estimated image and the ground truth, respectively. The SSIM was calculated based on the default parameter settings in Matlab R2018a (MathWorks Inc., Natick, MA, USA). The averaged perfusion map from the eight sets of pCASL scans, equivalent to 44 min of imaging time, was considered as the ground truth. The Wilcoxon signed-rank test was performed between the proposed method and the comparison method based on the PSNR and SSIM values calculated from the ground truth.
4 |. RESULTS
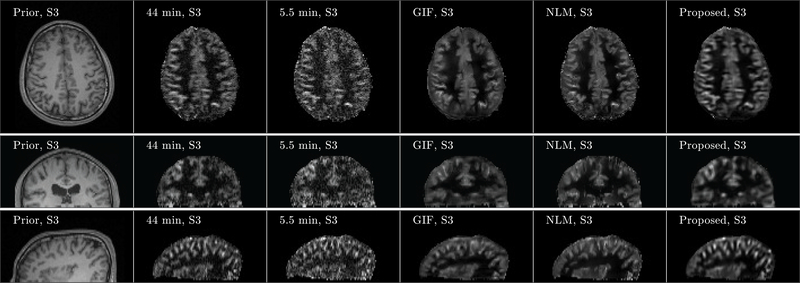
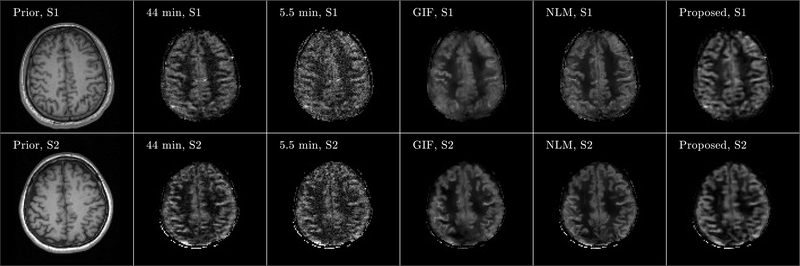
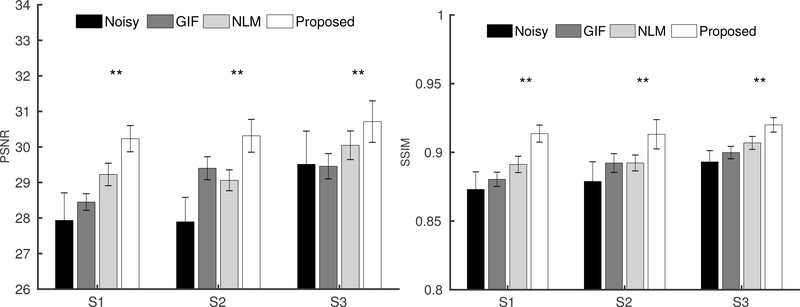
Figure 4 shows three orthogonal views of denoising results from Subject 3. Although noisy, the perfusion map from the 5.5 min acquisition showed signal details within the gray matter cortex regions well along the coronal and sagittal views, which demonstrates the feasibility of high-resolution ASL imaging. Compared to the ground truth image obtained from the 44 min acquisition, the GIF, NLM and the proposed method successfully reduced the noise in the perfusion maps, while the proposed method recovered signal details more accurately in the cortex regions than the GIF and NLM methods. Axial views of the denoising results from the other two subjects are shown in Figure 5, which also confirm that the proposed method can reduce the image noise while preserving the perfusion signal details well. Quantitative comparison results based on PSNR and SSIM from all three subjects are shown in Figure 6. Statistical analysis shows that regarding SSIM, the proposed method performs better than the NLM method in all three subjects at p-value< 0.01. Using PSNR, the performance of the proposed method is better than NLM in all three subjects at p-value< 0.01. All these results demonstrate the superiority of the proposed method compared to the reference methods.
FIGURE 4.
Three orthogonal views of denoising result from Subject 3 (S3). Images of anatomical prior (first column) and averaged perfusion maps from 44 min acquisition (second column), 5.5 min acquisition (third column), 5.5 min acquisition with GIF denoising (fourth column), 5.5 min acquisition with NLM denoising (fifth column), and 5.5 min acquisition with the proposed denoising method (sixth column) are shown. Note that the averaged perfusion maps from 44 min acquisition serve as the ground-truth image.
FIGURE 5.
Axial view of denoising results from Subject 1 (S1) and Subject 2 (S2). Images of anatomical prior (first column) and averaged perfusion maps from 44 min acquisition (second column), 5.5 min acquisition (third column), 5.5 min acquisition with GIF denoising (fourth column), 5.5 min acquisition with NLM denoising (fifth column), and 5.5 min acquisition with the proposed denoising method (sixth column) are shown. Note that the averaged perfusion maps from 44 min acquisition serve as the ground-truth image.
FIGURE 6.
The PSNR(left) and SSIM (right) bar plots from the three subjects (S1, S2 and S3) based on the eight datasets. The Wilcoxon signed-rank test was performed between the NLM and the proposed denoising methods. Correspondingly, ** located at the top of each bar plot, represents p-value<0.05.
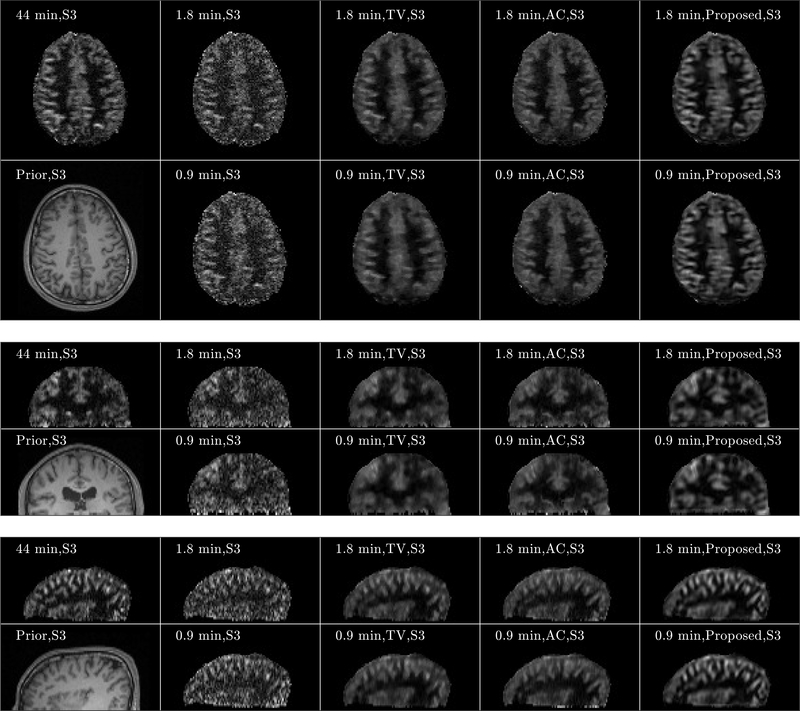
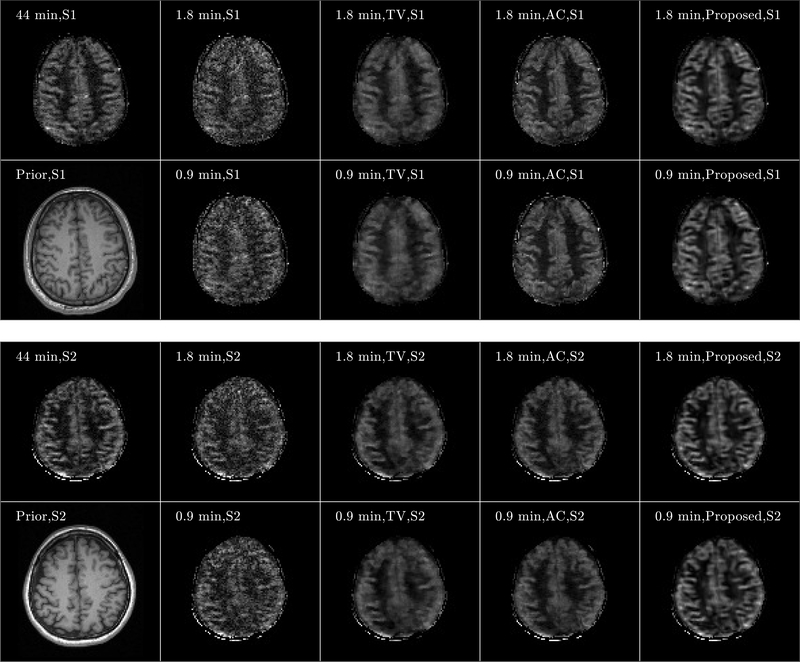
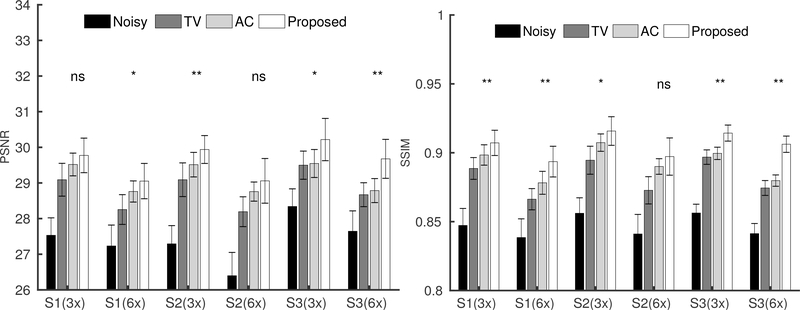
Figure 7 shows three orthogonal views of the image reconstruction results from Subject 3. The equivalent scan time for 3- and 6-times acceleration is 1.8 and 0.9 min, respectively. For both 1.8- and 0.9-min scans, the perfusion maps reconstructed by the SENSE method displayed higher levels of noise compared to those from the fully sampled 5.5 min scan shown in Figure 4. The anatomically constrained and the proposed reconstruction methods can better reduce the noise in the reconstructed perfusion maps, while preserving the perfusion signal details in the cortex regions, compared to other reference methods. Furthermore, the proposed method reconstructed the perfusion signal details in the cortex region more accurately than those from the anatomically constrained reconstruction method. Figure 8 shows the axial views of the image reconstruction results from the other two subjects, which also reflects better performance of the proposed method compared to the other methods regarding noise suppression and preservation of signal details in the cortex region. Fig. 9 shows the PSNR and SSIM comparisons of the eight sets along with the statistical analysis. Regarding SSIM, the proposed method is significantly better than the anatomically constrained method for Subject 1 and Subject 3 for all sparse sampling scenarios at p-value < 0.01 and for Subject 2 with 1.8-min scan at p-value < 0.05. For PSNR, the proposed method is better than the anatomically constrained method in Subject 1 for 0.9-min scan at p-value < 0.05, in Subject 2 for 1.8-min scan at p-value < 0.01, and in Subject 3 for both 0.9-min and 1.8-min scans at p-value < 0.05 and p-value < 0.01, respectively. For 0.9-min scan in Subject 2, there is no significant difference between the proposed method and the anatomically constrained method for both PSNR and SSIM values. We presume this to be due to motion effect in the noisy image, since two out of eight sets of pCASL scans in Subject 2 were affected by motion, which resulted in dissimilar structures compared to the anatomical prior and thereby lowered performance of the proposed reconstruction method.
FIGURE 7.
Three orthogonal views of image reconstruction results from Subject 3 (S3). Transversal, sagittal, and coronal views of the results are shown from the top, middle, and bottom subfigures, respectively. For each subfigure, images of anatomical prior (1st column, 2nd row) and averaged perfusion maps from 44-min acquisition (1st row, 1st column), SENSE reconstruction with Tikhonov regularization for 1.8-min (2nd column, 1st row) and 0.9-min (2nd column, 2nd row) acquisitions, TV penalized reconstruction for 1.8-min (3rd column, 1st row) and 0.9-min (3rd column, 2nd row) acquisitions, anatomically constrained (AC) penalized reconstruction for 1.8-min (4rd column, 1st row) and 0.9-min (4rd column, 2nd row) acquisitions, and reconstruction with the proposed framework for 1.8 min (5th column, 1st row) and 0.9 min (5th column, 2nd row) acquisitions are shown. Note that the averaged perfusion maps from 44-min acquisition serve as the ground-truth image.
FIGURE 8.
Axial view of image reconstruction results from Subjects 1 (S1) and Subject 2 (S2). Results from S1 and S2 are shown from the top and bottom subfigures, respectively. For each subfigure, images of anatomical prior (1st column, 2nd row) and averaged perfusion maps from 44-min acquisition (1st row, 1st column), SENSE reconstruction for 1.8-min (2nd column, 1st row) and 0.9-min (2nd column, 2nd row) acquisitions, TV penalized reconstruction for 1.8-min (3rd column, 1st row) and 0.9-min (3rd column, 2nd row) acquisitions, anatomically constrained (AC) penalized reconstruction for 1.8-min (4rd column, 1st row) and 0.9-min (4rd column, 2nd row) acquisitions, and reconstruction with the proposed framework for 1.8 min (5th column, 1st row) and 0.9 min (5th column, 2nd row) acquisitions are shown. Note that the averaged perfusion maps from 44-min acquisition serve as the ground-truth image.
FIGURE 9.
The PSNR (left) and SSIM (right) bar plots from the three subjects (S1, S2 and S3) based on eight datasets, in the scenarios of 3-times sparse-sampling(1.8 min scan) and 6-times sparse-sampling(0.9 min scan). The Wilcoxon signed-rank test was performed between the anatomically constrained (AC) penalized reconstruction and the proposed reconstruction method. Correspondingly, *, **, and ns, located at the top of each bar plot, represents p-value<0.05, p-value <0.01, and non-significant, respectively.
5 |. DISCUSSION
In this work, we have developed a novel, unsupervised-deep-learning based framework that requires only the subject’s own anatomical information as prior for training. Our in vivo experimental results show that the proposed framework can be used for both denoising and image reconstruction to improve the SNR and imaging speed in ASL imaging and generate high-resolution CBF maps. Statistical analysis based on multiple measurements per subject demonstrates the robustness of this proposed framework. As a feasibility study, only the T1-weighted image was employed as the network input in current work. If multi-contrast images are available, they can be supplied as additional network inputs to provide more information.
The proposed framework showed superior performance compared to comparison methods in terms of SSIM than PSNR, which reflects the strength of the proposed method in better preserving the structural information than reducing the pixel-to-pixel error. This might be due to the acknowledged performance of U-net structure in terms of capturing global features as a result of the specially designed encoder and decoder paths. In our deployed U-net structure, the total number of unknown network parameters are set to be similar to the image matrix size. Further improvements can be made by designing a network structure with less unknown parameters while keeping similar representation power. This will reduce the dimension size of the original denoising/reconstruction problem and thereby making the whole denoising/reconstruction process less ill-conditioned. In addition, when fxing the number of trainable parameters, the U-net structure employed in our experiments is not guaranteed to be optimal. Exploring better network structures with equivalent or less trainable parameters for this proposed unsupervised deep learning framework will be one of our future works.
We noticed that in one of the subjects, two out of the eight scans were affected by subject motion, which resulted in blurring in the reconstructed images. One possible explanation for this is that if the training label is motion-corrupted, it does not share structure similarities with the anatomical priors. Correspondingly during the network training process, the network output will be closer to the motion-corrupted images and cannot benefit much from the high-quality prior images. Further analysis regarding the tolerance of the proposed framework to noise levels and motion artifacts deserves further investigations. As for the stopping criterion used in the network training, we calculated the likelihood L(f(θn|z)) along with the iteration number n based on one dataset. The iteration number was chosen such that L(f(θn|z)) converges. This iteration number was used for all the other datasets. This method of checking L(f(θn|z)), works well in practice, but is not the most optimal method. Exploring options for better stopping criteria deserves further investigations.
6 |. CONCLUSION
In this work, we propose a new, unsupervised-deep-learning based framework for image denoising and reconstruction of ASL signal. The proposed framework does not require any prior training pairs and only requires the subject’s own anatomical images as prior for network input. Denoising and image reconstruction results from three subjects show that the proposed method performs better than the comparison methods. Future work will focus on exploring efficient network structures, finding better stopping criterion, and performing more evaluations.
7 |. ACKNOWLEDGEMENTS
This work was supported in part by National Institute of Biomedical Imaging and Bioengineering (NIBIB) grants P41EB022544 and T32EB013180, National Institute on Aging (NIA) grant R01AG052653, National Heart, Lung, and Blood Institute (NHLBI) grants R01HL118261 and R01HL137230, and National Cancer Institute (NCI) grant R01CA165221.
Abbreviations
- DNN
deep neural network
- ASL
arterial spin labeling
- SNR
signal-to-noise ratio
- PSNR
peak signal-to-noise ratio
- SSIM
structural similarity index
- ADMM
alternating direction method of multipliers
- CBF
cerebral blood flow
References
- 1.Detre JA, Leigh JS, Williams DS, Koretsky AP. Perfusion imaging. Magnetic resonance in medicine 1992; 23(1): 37–45. [DOI] [PubMed] [Google Scholar]
- 2.Williams DS, Detre JA, Leigh JS, Koretsky AP. Magnetic resonance imaging of perfusion using spin inversion of arterial water. Proceedings of the National Academy of Sciences 1992; 89(1): 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ye FQ, Frank JA, Weinberger DR, McLaughlin AC. Noise reduction in 3D perfusion imaging by attenuating the static signal in arterial spin tagging (ASSIST). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2000; 44(1): 92–100. [DOI] [PubMed] [Google Scholar]
- 4.Dai W, Garcia D, De Bazelaire C, Alsop DC. Continuous flow-driven inversion for arterial spin labeling using pulsed radio frequency and gradient fields. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2008; 60(6): 1488–1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fernández-Seara MA, Wang Z, Wang J, Rao HY, Guenther M, Feinberg DA, Detre JA. Continuous arterial spin labeling perfusion measurements using single shot 3D GRASE at 3 T. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2005; 54(5): 1241–1247. [DOI] [PubMed] [Google Scholar]
- 6.Günther M, Oshio K, Feinberg DA. Single-shot 3D imaging techniques improve arterial spin labeling perfusion measurements. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2005; 54(2): 491–498. [DOI] [PubMed] [Google Scholar]
- 7.Tan H, Hoge WS, Hamilton CA, Günther M, Kraft RA. 3D GRASE PROPELLER: improved image acquisition technique for arterial spin labeling perfusion imaging. Magnetic resonance in medicine 2011; 66(1): 168–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Feinberg D, Ramanna S, Guenther M. Evaluation of new ASL 3D GRASE sequences using parallel imaging, segmented and interleaved k-space at 3T with 12-and 32-channel coils. In:; 2009: 623.
- 9.Vidorreta M, Balteau E, Wang Z, De Vita E, Pastor MA, Thomas DL, Detre JA, Fernández-Seara MA. Evaluation of segmented 3D acquisition schemes for whole-brain high-resolution arterial spin labeling at 3 T. NMR in Biomedicine 2014; 27(11): 1387–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Han PK, Ye JC, Kim EY, Choi SH, Park SH. Whole-brain perfusion imaging with balanced steady-state free precession arterial spin labeling. NMR in biomedicine 2016; 29(3): 264–274. [DOI] [PubMed] [Google Scholar]
- 11.Han PK, Choi SH, Park SH. Investigation of control scans in pseudo-continuous arterial spin labeling (p CASL): Strategies for improving sensitivity and reliability of p CASL. Magnetic resonance in medicine 2017; 78(3): 917–929. [DOI] [PubMed] [Google Scholar]
- 12.Asllani I, Borogovac A, Brown TR. Regression algorithm correcting for partial volume effects in arterial spin labeling MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2008; 60(6): 1362–1371. [DOI] [PubMed] [Google Scholar]
- 13.Liang X, Connelly A, Calamante F. Improved partial volume correction for single inversion time arterial spin labeling data. Magnetic resonance in medicine 2013; 69(2): 531–537. [DOI] [PubMed] [Google Scholar]
- 14.Tan H, Maldjian JA, Pollock JM, Burdette JH, Yang LY, Deibler AR, Kraft RA. A fast, effective filtering method for improving clinical pulsed arterial spin labeling MRI. Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine 2009; 29(5): 1134–1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bibic A, Knutsson L, Stahlberg F, Wirestam R. Denoising of arterial spin labeling data: wavelet-domain filtering compared with Gaussian smoothing. Magnetic Resonance Materials in Physics, Biology and Medicine 2010; 23(3): 125–137. [DOI] [PubMed] [Google Scholar]
- 16.Wells JA, Thomas DL, King MD, Connelly A, Lythgoe MF, Calamante F. Reduction of errors in ASL cerebral perfusion and arterial transit time maps using image de-noising. Magnetic resonance in medicine 2010; 64(3): 715–724. [DOI] [PubMed] [Google Scholar]
- 17.Boland M, Stirnberg R, Pracht ED, Kramme J, Viviani R, Stingl J, Stöcker T. Accelerated 3D-GRASE imaging improves quantitative multiple post labeling delay arterial spin labeling. Magnetic resonance in medicine 2018; 80(6): 2475–2484. [DOI] [PubMed] [Google Scholar]
- 18.Wang S, Tan S, Gao Y, Liu Q, Ying L, Xiao T, Liu Y, Liu X, Zheng H, Liang D. Learning joint-sparse codes for calibration-free parallel MR imaging. IEEE transactions on medical imaging 2017; 37(1): 251–261. [DOI] [PubMed] [Google Scholar]
- 19.Petr J, Ferré JC, Gauvrit JY, Barillot C. Denoising arterial spin labeling MRI using tissue partial volume. In:. 7623. International Society for Optics and Photonics.; 2010: 76230L. [Google Scholar]
- 20.Spann SM, Kazimierski KS, Aigner CS, Kraiger M, Bredies K, Stollberger R. Spatio-temporal TGV denoising for ASL perfusion imaging. Neuroimage 2017; 157: 81–96. [DOI] [PubMed] [Google Scholar]
- 21.Fang R, Huang J, Luh WM. A spatio-temporal low-rank total variation approach for denoising arterial spin labeling MRI data. In: IEEE.; 2015: 498–502. [Google Scholar]
- 22.Zhao L, Fielden SW, Feng X, Wintermark M, Mugler III JP, Meyer CH. Rapid 3D dynamic arterial spin labeling with a sparse model-based image reconstruction. Neuroimage 2015; 121: 205–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. In: IEEE.; 2016: 514–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection-reconstruction MR. Magnetic resonance in medicine 2018; 80(3): 1189–1205. [DOI] [PubMed] [Google Scholar]
- 25.Hauptmann A, Arridge S, Lucka F, Muthurangu V, Steeden JA. Real-time cardiovascular MR with spatio-temporal artifact suppression using deep learning-proof of concept in congenital heart disease. Magnetic resonance in medicine 2019; 81(2): 1143–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xiang L, Chen Y, Chang W, Zhan Y, Lin W, Wang Q, Shen D. Deep Leaning Based Multi-Modal Fusion for Fast MR Reconstruction. IEEE Transactions on Biomedical Engineering 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sun J, Li H, Xu Z. Deep ADMM-Net for compressive sensing MRI. In:; 2016: 10–18.
- 28.Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine 2018; 79(6): 3055–3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mardani M, Gong E, Cheng JY, Vasanawala S, Zaharchuk G, Alley M, Thakur N, Han S, Dally W, Pauly JM, Xing L. Deep generative adversarial networks for compressed sensing automates MRI. arXiv preprint arXiv:1706.00051 2017. [Google Scholar]
- 30.Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE transactions on Medical Imaging 2018; 37(2): 491–503. [DOI] [PubMed] [Google Scholar]
- 31.Yang G, Yu S, Dong H, Slabaugh G, Dragotti PL, Ye X, Liu F, Arridge S, Keegan J, Guo Y, Firmin D. DAGAN: deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE transactions on medical imaging 2018; 37(6): 1310–1321. [DOI] [PubMed] [Google Scholar]
- 32.Yoon J, Gong E, Chatnuntawech I, Bilgic B, Lee J, Jung W, Ko J, Jung H, Setsompop K, Zaharchuk G, Kim EY, Pauly J, Lee J. Quantitative susceptibility mapping using deep neural network: QSMnet. NeuroImage 2018; 179: 199–206. [DOI] [PubMed] [Google Scholar]
- 33.Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE transactions on medical imaging 2019; 38(2): 394–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang S, Ke Z, Cheng H, Jia S, Leslie Y, Zheng H, Liang D. Dimension: Dynamic mr imaging with both k-space and spatial prior knowledge obtained via multi-supervised network training. NMR in Biomedicine 2019. [DOI] [PubMed] [Google Scholar]
- 35.Jin KH, Unser M, Yi KM. Self-Supervised Deep Active Accelerated MRI. arXiv preprint arXiv:1901.04547 2019. [Google Scholar]
- 36.Kim KH, Choi SH, Park SH. Improving arterial spin labeling by using deep learning. Radiology 2017; 287(2): 658–666. [DOI] [PubMed] [Google Scholar]
- 37.Gong E, Pauly J, Zaharchuk G. Boosting SNR and/or resolution of arterial spin label (ASL) imaging using multi-contrast approaches with multilateral guided filter and deep networks. In:; 2017. [Google Scholar]
- 38.Xie D, Bai L, Wang Z. Denoising Arterial Spin Labeling Cerebral Blood Flow Images Using Deep Learning. arXiv preprint arXiv:1801.09672 2018. [Google Scholar]
- 39.Ulas C, Tetteh G, Kaczmarz S, Preibisch C, Menze BH. DeepASL: Kinetic Model Incorporated Loss for Denoising Arterial Spin Labeled MRI via Deep Residual Learning. In: Springer.; 2018: 30–38. [Google Scholar]
- 40.Haldar JP, Hernando D, Song SK, Liang ZP. Anatomically constrained reconstruction from noisy data. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2008; 59(4): 810–818. [DOI] [PubMed] [Google Scholar]
- 41.Eslami R, Jacob M. Robust reconstruction of MRSI data using a sparse spectral model and high resolution MRI priors. IEEE transactions on medical imaging 2010; 29(6): 1297–1309. [DOI] [PubMed] [Google Scholar]
- 42.Gnahm C, Bock M, Bachert P, Semmler W, Behl NG, Nagel AM. Iterative 3D projection reconstruction of 23Na data with an 1H MRI constraint. Magnetic resonance in medicine 2014; 71(5): 1720–1732. [DOI] [PubMed] [Google Scholar]
- 43.Lam F, Ma C, Clifford B, Johnson CL, Liang ZP. High-resolution 1H-MRSI of the brain using SPICE: data acquisition and image reconstruction. Magnetic resonance in medicine 2016; 76(4): 1059–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gal Y, Mehnert AJ, Bradley AP, McMahon K, Kennedy D, Crozier S. Denoising of dynamic contrast-enhanced MR images using dynamic nonlocal means. IEEE transactions on medical imaging 2010; 29(2): 302–310. [DOI] [PubMed] [Google Scholar]
- 45.Chen G, Wu Y, Shen D, Yap PT. Noise Reduction in Diffusion MRI Using Non-Local Self-Similar Information in Joint x- q Space. Medical image analysis 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gong E, Huang F, Ying K, Wu W, Wang S, Yuan C. PROMISE: Parallel-imaging and compressed-sensing reconstruction of multicontrast imaging using SharablE information. Magnetic resonance in medicine 2015; 73(2): 523–535. [DOI] [PubMed] [Google Scholar]
- 47.Bilgic B, Kim TH, Liao C, Manhard MK, Wald LL, Haldar JP, Setsompop K. Improving parallel imaging by jointly reconstructing multi-contrast data. Magnetic resonance in medicine 2018; 80(2): 619–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ulyanov D, Vedaldi A, Lempitsky V. Deep Image Prior. arXiv preprint arXiv:1711.10925 2017. [Google Scholar]
- 49.Gong K, Catana C, Qi J, Li Q. PET Image Reconstruction Using Deep Image Prior. IEEE transactions on medical imaging 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. In: Springer.; 2016: 424–432. [Google Scholar]
- 51.Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical programming 1989; 45(1–3): 503–528. [Google Scholar]
- 52.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2007; 58(6): 1182–1195. [DOI] [PubMed] [Google Scholar]
- 53.Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE transactions on medical imaging 2011; 30(5): 1028–1041. [DOI] [PubMed] [Google Scholar]
- 54.Ma C, Clifford B, Liu Y, Gu Y, Lam F, Yu X, Liang ZP. High-resolution dynamic 31P-MRSI using a low-rank tensor model. Magnetic resonance in medicine 2017; 78(2): 419–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gong K, Guan J, Kim K, Zhang X, Fakhri GE, Qi J, Li Q. Iterative PET image reconstruction using convolutional neural network representation. arXiv preprint arXiv:1710.03344 2017. [Google Scholar]
- 56.Macovski A Noise in MRI. Magnetic Resonance in Medicine 1996; 36(3): 494–497. [DOI] [PubMed] [Google Scholar]
- 57.Chen Cn, Hoult DI. Biomedical magnetic resonance technology. Hilger. 1989. [Google Scholar]
- 58.Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning 2011; 3(1): 1–122. [Google Scholar]
- 59.Barrett R, Berry MW, Chan TF, Demmel J, Donato J, Dongarra J, Eijkhout V, Pozo R, Romine C, Vorst V. dH. Templates for the solution of linear systems: building blocks for iterative methods. 43. Siam. 1994. [Google Scholar]
- 60.Wu WC, Fernandez-Seara M, Detre JA, Wehrli FW, Wang J. A theoretical and experimental investigation of the tagging efficiency of pseudocontinuous arterial spin labeling. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2007; 58(5): 1020–1027. [DOI] [PubMed] [Google Scholar]
- 61.Park SH, Wang DJ, Duong TQ. Balanced steady state free precession for arterial spin labeling MRI: initial experience for blood flow mapping in human brain, retina, and kidney. Magnetic resonance imaging 2013; 31(7): 1044–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine 1999; 42(5): 952–962. [PubMed] [Google Scholar]
- 63.Buades A, Coll B, Morel JM. A non-local algorithm for image denoising. In:. 2. IEEE.; 2005: 60–65. [Google Scholar]
- 64.Wang G, Qi J. Penalized likelihood PET image reconstruction using patch-based edge-preserving regularization. IEEE transactions on medical imaging 2012; 31(12): 2194–2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Chan C, Fulton R, Barnett R, Feng DD, Meikle S. Postreconstruction nonlocal means filtering of whole-body PET with an anatomical prior. IEEE Transactions on medical imaging 2013; 33(3): 636–650. [DOI] [PubMed] [Google Scholar]
- 66.He K, Sun J, Tang X. Guided image filtering. IEEE transactions on pattern analysis and machine intelligence 2012; 35(6): 1397–1409. [DOI] [PubMed] [Google Scholar]
- 67.Buxton RB, Frank LR, Wong EC, Siewert B, Warach S, Edelman RR. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magnetic resonance in medicine 1998; 40(3): 383–396. [DOI] [PubMed] [Google Scholar]
- 68.Alsop DC, Detre JA, Golay X, Günther M, Hendrikse J, Hernandez-Garcia L, Lu H, Macintosh BJ, Parkes LM, Smits M, Van Osch MJ, Wang DJ, Wong EC, Zaharchuk G. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magnetic resonance in medicine 2015; 73(1): 102–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Okell TW, Chappell MA, Kelly ME, Jezzard P. Cerebral blood flow quantification using vessel-encoded arterial spin labeling. Journal of Cerebral Blood Flow & Metabolism 2013; 33(11): 1716–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 2004; 13(4): 600–612. [DOI] [PubMed] [Google Scholar]