Highlights
-
•
Disparities among Chinese cities in centralities of HSR network are examined from 2010 to 2015.
-
•
Both scheduled travel time and service frequency are incorporated into centrality measures.
-
•
Inequality between economic regions or between megalopolises has reduced.
-
•
Small/medium-sized cities are further lagged behind in HSR development.
-
•
In major megalopolises, non-core cities are catching up but they rely more on core cities to access other regions.
Keywords: High-speed rail, Network centralities, Regional disparity, China
Abstract
This research examines whether cities are getting more equally accessible and connected via high-speed rail (HSR) in China over the period from 2010 to 2015. Existing studies mainly use network centralities to describe the spatial pattern of HSR network without measuring the spatial disparity of these centralities, and most of them rely on the infrastructure network and thus fail to incorporate HSR service quality in the centrality measures. Using HSR timetable data, we incorporate both scheduled travel time and daily frequency of each origin-destination city pair into three centrality measures and further quantify their inequalities using Theil’s T index. We find that as the HSR network expands, cities appear to be more equal in terms of accessibility, but their disparities in connectivity and transitivity depend on the dimensions of comparison. In general, although the difference between economic regions or between megalopolises has reduced, small/medium-sized cities not belonging to any major city cluster are further lagged behind in HSR development. The difference between core and non-core cities in the same megalopolises has decreased despite that non-core cities are increasingly relying on core cities to access other regions.
1. Introduction
Transportation planners and policy makers are interested in understanding the impacts of high-speed rail (HSR) development on regional integration or disparities. For example, in China’s 12th and 13th Five-Year Plans for Railway Development issued in 2011 and 2017 respectively, one objective of future HSR development is to reduce regional inequality and promote inter-regional cooperation via the improvement of connectivity between the rich and poor regions. However, it remains unclear how HSR can affect regional economy. In theory, the new economic geography model predicts that regional disparity can increase as a result of transportation infrastructure development (Fujita and Thisse, 1996). This is because reduced transportation cost may reinforce the “siphone effect”, i.e. the tendency of having resources being attracted from small cities to large cities. Furthermore, HSR stations in large cities generally have better locations, since large cities have stronger bargaining power when negotiating with the central planner, and hence they are more attractive for HSR service providers (Zhu et al., 2015). Empirically, the findings are mixed. Some studies find HSR development increases regional disparity (e.g. Loukaitou-Sideris et al., 2013, Kim and Sultana, 2015, Chen and Haynes, 2017, Diao, 2018), while others find HSR does not contribute to regional dispersion (e.g. Sasaki et al., 1997, Zheng and Kahn, 2013, Monzon et al., 2013, Vickerman, 2018, Wang, 2018).1 For instance, in the context of China, Zheng and Kahn (2013) find that HSR facilitates market integration, leading to reduced disparity between mega cities and nearby second- and third-tier cities. Diao (2018) reveals, on the other hand, that second-tier cities with relatively large population benefit more in attracting investment than small cities and mega cities.
Quantifying the impact of HSR on regional development and testing the underlying mechanisms are empirically challenging. Whether a city is benefited from HSR depends, among others, on how the city is linked to the other cities in the HSR network. Sanchez-Mateos and Givoni (2012) find that only very few cities with good accessibility to metropolis along the newly constructed line in the UK could gain benefits. Scholars have warned that the situation of small cities might even become worse due to the lack of adequate services or inappropriate station design (e.g. Preston and Wall, 2008, Moyano and Dobruszkes, 2017). In fact, being linked to the HSR network is not equivalent to being well-served by HSR. Small intermediate cities on an HSR line are found to be bypassed by HSR services in favor of the metropolises in both Europe (Urena et al., 2009, Moyano and Dobruszkes, 2017) and China (Qin, 2017). As suggested by Qin (2017), this bypassing behavior may weaken the relative economic position of small cities, since small cities are further marginalized while the linkages among large cities are enhanced. To better understand the impact of HSR on regional economy, therefore, we need first to investigate the important question of whether cities in an HSR network are getting more equally accessible and connected as the network expands.
This study focuses on the spatial disparity of HSR development among Chinese cities and the inter-temporal changes of such disparity as the HSR network expands. The objective is to examine whether the gap between cities in terms of HSR service supply has been reduced over time. After recent years of HSR development in China, many small cities have been linked to the HSR network, but it is unclear whether such linkages have helped small cities to catch up with the large ones. As the levels of economic development are highly uneven within China, it is essential to assess the disparity of HSR development among cities in different regions, of different sizes, and in different megalopolises. This approach may shed light on the regional disparity from the viewpoint of provision of HSR services and pave the way for a better understanding of the HSR impact on regional economy. From a planning point of view, an increased disparity in service provision may imply low utilization of HSR infrastructure at small cities. This can serve as a signal for policy makers to seek ways to better utilize the existing infrastructure, instead of further expanding the infrastructure to small cities. Furthermore, policy makers may pay more attention to improve the attractiveness of small cities as a support policy of an overall HSR development.
To address our research questions, we use HSR timetable data over the 2010-2015 period to evaluate a city’s status in HSR development from a network perspective. In particular, we employ the weighted degree, betweenness and harmonic centralities to measure, respectively, a city’s connectivity, transitivity and accessibility. The degree centrality is weighted by daily service frequency, whereas the betweenness and harmonic centralities are weighed by the generalized travel time that takes into account scheduled travel time and daily train frequency. Then, by calculating the Theil’s T indices of these centrality measures across HSR cities, we explore whether inequalities among cities have increased or decreased over the study period. Theil’s T index allows us to examine both the disparity within a group and the disparity across city groups, after grouping cities according to geographic regions, city sizes, and megalopolises, respectively. We include all Chinese cities over a certain population threshold in the study, regardless of the availability of HSR stations in the cities. By doing so, we can take into account the impact of having more cities being served by HSR as the network expands. We find that the disparity in accessibility has been gradually reduced as the HSR network expands, but this is not the case for connectivity and transitivity, suggesting that a comprehensive assessment on all the three aspects might be necessary during the planning of HSR network and services.
The rest of the paper is organized as follows. Section 2 reviews the related literature. Section 3 presents the methodology and describes the data. Section 4 compares HSR infrastructure network and service network and explains why the latter is chosen for further analysis. Section 5 displays the disparity analysis on the three dimensions, namely, economic regions, tiers of cities, and megalopolises. Section 6 concludes the study and discusses policy implications and avenues for further research.
2. Literature review
Our study is most related to the stream of studies that apply complex network theories to measure centralities of cities in Chinese HSR network. This kind of analysis may have different purposes: e.g. quantification of the spatial evolutional pattern (Chen et al., 2018), projection of the growth pattern of future HSR network based on the national railway planning proposal (Xu et al., 2018a), comparison of the configurations of China’s HSR system and airline networks (Yang et al., 2018), introduction of an integrated connectivity and accessibility indicator (Xu et al., 2018b), assessment of the robustness of HSR network (Li et al., 2019, Li and Rong, 2020), and examination of the hierarchical impacts of HSR on the city networks (Jiao et al., 2017).
Most of these studies measure centralities based on the HSR infrastructure; as such, they treat all the edges in HSR network equally (no weights are imposed on each edge of the HSR network by service quality). However, infrastructure only provides the potential of offering HSR services but does not capture the actual provision and usage of HSR services (Zhang et al., 2016, Yang et al., 2019). Evidence shows that HSR can positively affect regional economies only if the location of a region and its external factors such as the commuting frequency are effectively matched (Jia et al., 2017). Chen et al., 2018, Jiao et al., 2017, Li et al., 2019, Li and Rong, 2020 are exceptions here,2 but they either fail to fully utilize the timetable data or focus on another question. For instance, Li et al., 2019, Li and Rong, 2020 employ a comprehensive HSR timetable data that takes into account travel time and passenger flow to explore the volunerability and robustness of HSR network. Chen et al. (2018) weigh edges by estimated travel time only, while Jiao et al. (2017) only consider service frequency. None of them uses the generalized travel time, which takes into account both scheduled travel time and service frequency, to construct transitivity and accessibility, as well as considers the directional difference in scheduled HSR services.3 In addition, all of the studies use the closeness centrality to measure accessibilty. By contrast, we use the harmonic centrality since this measure can better deal with disconnected networks that are common in the earlier stages of HSR development in China. Moreover, none of the above studies track the disparities in the provision of HSR services as the HSR network expands. This is the most crucial difference between our study and those in the literature.
Our study is also relevant to the measure of regional inequalities in the context of HSR development. The literature mainly adopts three measures, i.e., coefficient of variation (e.g. Gutierrez, 2001, Jiao et al., 2014, Kim and Sultana, 2015, Chen and Haynes, 2017, Wang, 2018, Wang and Duan, 2018), Gini coefficient (e.g. Kim, 2000, Chen and Haynes, 2017, Wang et al., 2019) and Theil index (e.g. Chen and Haynes, 2017), to evaluate disparity. All studies cited above apply the view of New Economic Geography which associates accessibility with regional development. As a result, these studies mainly measure disparity in accessibility. However, we argue that other centrality measures, namely connectivity and transitivity, also deserve investigation. In fact, Jiao et al. (2017) find that changes in connectivity resulted from HSR expansion plays a more vital role in economic development than in time saving, a key element of accessibility. Campante and Yanagizawa-Drott (2018) establish empirically that more and better air connectivity (and network centrality) can contribute to local economic growth.4 Connectivity improvement brought by HSR is also recognized as a key factor in driving economic growth (Chong et al., 2019). In addition to geographical condition and topography, connectivity is highly affected by policy interventions and the disparity in connectivity is also associated with the inequalities in development opportunities (Rodrigue, 2019). Further, it is evident that transit station proximity is positively correlated with new business creation (Credit, 2019). Therefore, it is essential to comprehensively explore the uneven development of HSR with various centrality measurements.
Among studies measuring disparities in HSR development listd above, our work is most relevant to Jiao et al., 2014, Chen and Haynes, 2017. Jiao et al. (2014) use the coefficient of variation to predict changes in the disparities of Chinese cities’ accessibility based on future HSR expansion plans. Therefore, unlike our study, they did not include connectivity and transitivity and they based their assessment on planned infrastructure network instead of the actual provision of HSR services. Moreover, we explore inequalities not only among different regions and different sizes of cities, but also among five megalopolises which is again not included in Jiao et al. (2014). Although both Chen and Haynes (2017) and our paper use Theil index to assess disparity, the subjects being studied are different. The objective of Chen and Haynes (2017) is to identify the impact of HSR development on regional economic disparity. Thus, they used Theil index to evaluate the inequality of regional economy and then applied panel regression analysis to explain how HSR may potentially associate with regional economic disparity. Unlike Chen and Haynes (2017), we focus on HSR development per se and hence measure the disparities of connectivity, transitivity and accessibility of HSR service provision.
3. Methodology
3.1. Network representation and data
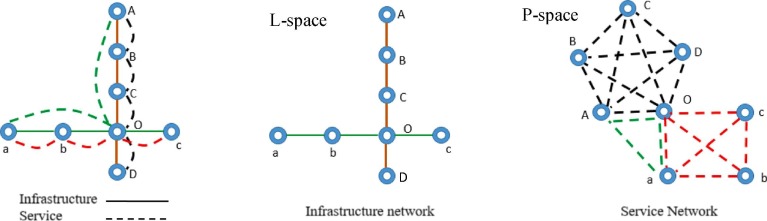
The topology of a transportation network can vary by taking different views of “space”, namely the space of stations, space of stops, or space of changes (Kurant and Thiran, 2006). These three views of space affect how two nodes (cities or stations) are defined as connected and hence the construction of edges. The space of stations reflects the physical infrastructure, i.e. railway tracks. In a space of stations, two stations are considered as connected only if they are directly linked by at least one railway track without going through any other station in between. Both space of stops and space of changes are based on the schedule of train services. In a space of stops, two stations are connected if there exists at least one direct train making two consecutive stops at these stations. In a space of changes, two stations are connected when there exists at least one direct train that stops at both stations regardless the number of stops between these two stations. In other words, two nodes are connected as long as they can be directly reached without changing trains. In this way, all stations served by the same train are fully connected with each other. The space of stations and the space of stops are also called L-space in the literature (e.g. Barthelemy, 2011), while the space of changes is also called P-space.
In this paper, we use L-space (space of stations) to represent HSR infrastructure network and P-space to represent HSR service network.5 Fig. 1 distinguishes these two representations of an example HSR network. The P-space emphasizes the accessibility of two nodes and is more effective for reflecting the socio-economic connections of two locations (Lu et al., 2018). As a result, it is very popular in analysing service networks and has been proven to be practical in the analysis of public transport networks (Chatterjee, 2016). In both views of “space”, the edges can be weighted to reflect the strength of the links.
Fig. 1.
Representations of HSR infrastructure network versus service network.
In the HSR infrastructure network, nodes represent cities, and edges are physical railway tracks of two consecutive cities. As shown in Fig. 1, the solid line segment AB is an edge in the infrastructure network. From A to C, one needs to go through two edges, AB and BC. In the HSR service network, nodes represent cities, and edges represent the existence of direct rail services between two cities. For example, in the service network of Fig. 1, the dashed line segment between A and C is one edge despite that there is one stop (B) between A and C, because there is one direct train service which stops at A, B, C, O and D in sequence. To travel from C to b, one needs to go through two edges, i.e. making a train transfer. The black dashed line and green dashed line between A and O represent the same edge (not two different edges), despite that there are two direct trains serving these two nodes.
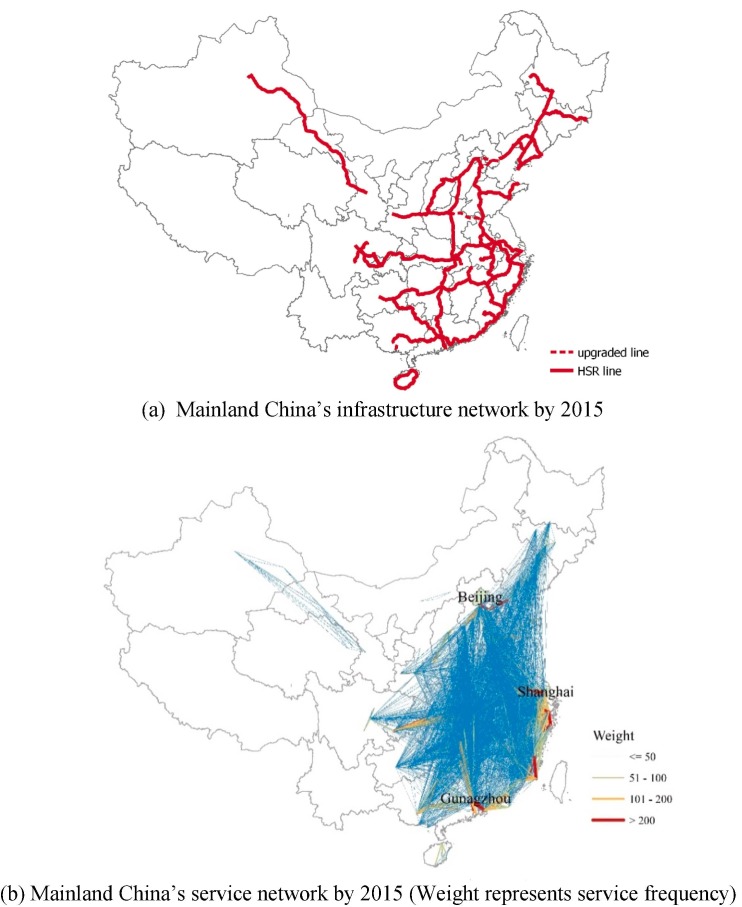
Our study examines Chinese cities’ centralities in the HSR network and inequality in their HSR development during the period of 2010–2015. China’s HSR network has experienced remarkable growth since 2008 and the network has reached a total length of 19730 km by 2015, covering 28 out of 31 provincial-level regions in mainland China and forming a grid network consisting of four vertical corridors and four horizontal corridors. This makes China’s HSR network the largest in the world in terms of both total length and traffic volume. Fig. 2 (a)-(b) show the development of HSR network reflected by infrastructure and service respectively by 2015. According to the Medium- and Long-Term Railway Network Plan approved by China’s Cabinet and the 13th Five-Year Plan for Railway Development issued by China’s National Development and Reform Commission, 80% of the cities with over one million population will be connected by HSR by 2020 and all cities with more than 0.5 million urban population will be linked by HSR by 2025. Therefore, cities with population over 1 million and urban population over 0.5 million in mainland China are all included in our study, resulting in 341 cities being assessed. We include all cities which have been or will potentially be linked into the HSR network, because we consider the individual cities’ HSR development and hence the measure of disparity should capture the effect of having an increasing number of cities linked to the HSR system over the study period. Note that the inclusion of cities without HSR stations does not affect the calculation of centralities and these cities will be assigned a value of zero for each centrality indicator.
Fig. 2.
Development of HSR network in mainland China by 2015.
The HSR infrastructure data is obtained from international union of railways (UIC), while train timetable data is retrieved from China Train Timetable (2010–2015, July editions), and all types of bullet trains (G, C and D) are considered. China Railway Corporation releases several editions of train timetable each year. We choose the July edition mainly for two reasons. First, July editions are the most available throughout our study period. We are not able to obtain a complete collection (from 2010 to 2015) of editions published in the other months. Second, significant changes in the timetable tend to occur in each July because many HSR lines were opened around the 1st of July to celebrate a major public holiday of the country. Demographic and socio-economic data for each city is obtained from CEIC China database. We focus on cities, and hence multiple stations in one city are merged into one station. We consider the infrastructure network as undirected whereas the service network directed as intensity and quality of train services from one city to the other are not necessarily the same in the return direction.
3.2. Centrality measures
Our paper focuses on the microscopic properties of China’s HSR network. Thus, we use centrality, a fundamental concept in network analysis, to capture the importance of a node in the HSR network.6 Among various centrality measures, degree, betweenness and closeness are the most popular indices in transportation studies. These three measures can be interpreted respectively as the connectivity (Mishra et al., 2012), transitivity and accessibility (Jiao et al., 2017, Wang et al., 2011) of a node in the HSR network. However, Opsahl et al. (2010) argued that closeness centrality may not work in a network composed by multiple disconnected components (subgraphs), which is the case of China’s HSR network, especially in the early stage of its development. In particular, the closeness centrality may overstate the accessibility of nodes in small subgraphs disconnected from the larger main subgraph (See Appendix B for an example). Therefore, in this study we use harmonic centrality proposed by Marchiori and Latora (2000) as a transformation of closeness centrality.
Traditional topology measures treat all connections equally without taking into account the quality of each connection. This treatment may overstate (understate) the centralities of nodes that are mainly served by low (high) quality connections. As HSR connections between cities are highly heterogeneous, all the three centrality measures in our study are weighted.7 The following provides the detailed definitions of the three measures.
Degree measures the importance of a node, i.e. city in our case, by considering the number of other nodes being directly connected (Freeman, 1978, Newman, 2010). In an undirected graph (e.g. HSR infrastructure network), the weighted degree centrality of city i is defined as:
| (1) |
where N is the set of cities in the HSR network. equals to 1 when there exists a direct connection via HSR, i.e. an edge in L-space, between city i and city j, and equals to 0 otherwise. The weight is the number of rail tracks that directly link city i and city j.
In a directed graph (e.g. HSR service network), degree centrality is the sum of in-degree and out-degree which measure the number of inbound links and outbound links respectively. Then, the weighted degree centrality of city i in the service network is formalized as:
| (2) |
where indicates the presence of direct HSR service from city i to city j (i.e. outbound links), i.e. an edge pointing from i to j in P-space, and indicates the presence of direct HSR service from city j to city i (i.e. inbound links). Again, and equal to 1 when the corresponding HSR service exists and 0 otherwise. Givoni and Banister (2012) argued that service frequency, safety, and reliability are more important than speed in affecting the experience with HSR. Therefore, we use daily service frequency to weight the in-degree and out-degree of city i. That is, and are the number of daily train services from city i to city j and from city j to city i respectively. This weighted degree centrality is also called strength in the literature.
Harmonic centrality captures the average level of convenience that one can travel from a node to all the other nodes in the network. Nodes with higher harmonic centrality can access to the whole network more quickly. In the infrastructure network, it is defined as:
| (3) |
where
Here, is the length of the shortest path between city i and city j. To see this, note that is the set of paths linking city i and city j. A particular path p consists a series of edges which form the path. Each edge k along path p is considered as an element of path p. In the literature, in many cases indicates the presence of the edge k along a path and hence is assigned a value of 1. Therefore, the length of shortest path in fact counts the smallest number of edges needed to link city i and city j. In our study, each edge is weighted by the estimated travel time along the edge. That is, equals to the ratio of rail distance of this edge and planned operating speed. In this way, we capture not only the number of edges involved in a path but also the quality of the edges (in the form of the travel time). Note that is the sum of the reciprocals of . That is, the longer the travel time between cities i and j, the lower the value of the harmonic centrality. In the directed service network, the formula is rewritten as:
| (4) |
where
where . That is, each directional edge k is weighted by the generalized travel time which is the sum of the average scheduled in-vehicle time along the edge () and the estimated maximum waiting time between two train services on this edge. According to the schedule data, the daily operating time of HSR services in China is 18 h and thus the ratio of 18 h and service frequency, , is a proxy of maximum waiting time, assuming services are evenly distributed throughout the operating time. Thus, the length of each path captures both the number of trains to change to move from city i to city j and the generalized travel time of each train ride. In both infrastructure and service networks, we assume and its inverse becomes zero when there exists no path linking city i and city j (i.e., ). This case occurs when city i and city j belong to two disconnected subgraphs.
Betweenness centrality of a node measures the extent to which a node lies on the shortest paths between two other nodes (Freeman, 1978, Newman, 2010). Nodes on the shortest paths of many origin-destination pairs tend to become the bottleneck of the network. For infrastructure network, the betweenness of city i is written as:
| (5) |
where is the number of shortest paths between city j and city k, and is the number of shortest paths between city j and city k that pass city i. The identification of shortest path between nodes is discussed above when defining harmonic centrality. For directed service network, the formula is rewritten as:
| (6) |
To measure the overall centrality of one city, we generate an aggregated centrality indicator by first standardizing the three centrality measures and then taking the linear combination of the standardized indicators. The formula of the aggregated indicator is:
| (7) |
where μ and σ indicate the mean and standard deviation of the corresponding centrality measure. , and are weights for each centrality measure. In this paper, we assume a city’s capability of connectivity, transitivity and accessibility are equally important. Thus, we set .
3.3. Disparity measures
Measures of regional inequality have been well documented in literature and can be classified into three groups: dispersion indices, Lorenz curve indices, and entropy indices. Coefficient of variation is a popular dispersion index which is defined as the ratio of the standard deviation over the mean, and Gini coefficient is a popular indicator based on Lorenz curve. However, both indicators cannot be easily decomposed. The main advantage of entropy indices, such as Theil’s T index, is that the total disparity can be decomposed into the between-group and within-group disparities. This feature is particularly useful when identifying the sources of inequality. For example, it can be used to distinguish whether the inequality mainly occurs between large and small cities or within cities with similar size.8 Since the objective of this research is to examine the disparities among regions, tiers of cities, and megalopolises, Theil’s T index fits this purpose better.
Theil’s T index (Theil, 1967) is defined as:
| (8) |
where n is the number of cities included in measuring the inequality, is the centrality measure for city i, and is the average centrality measure of all the n cities. Equation (8) can be decomposed into between-group inequality () and with-in group inequality ():
| (9) |
In equation (9), m is the number of groups, is the number of cities in group j, is the Theil’s T index of group j, and is the average centrality measure of group j.
4. Infrastructure network versus service network
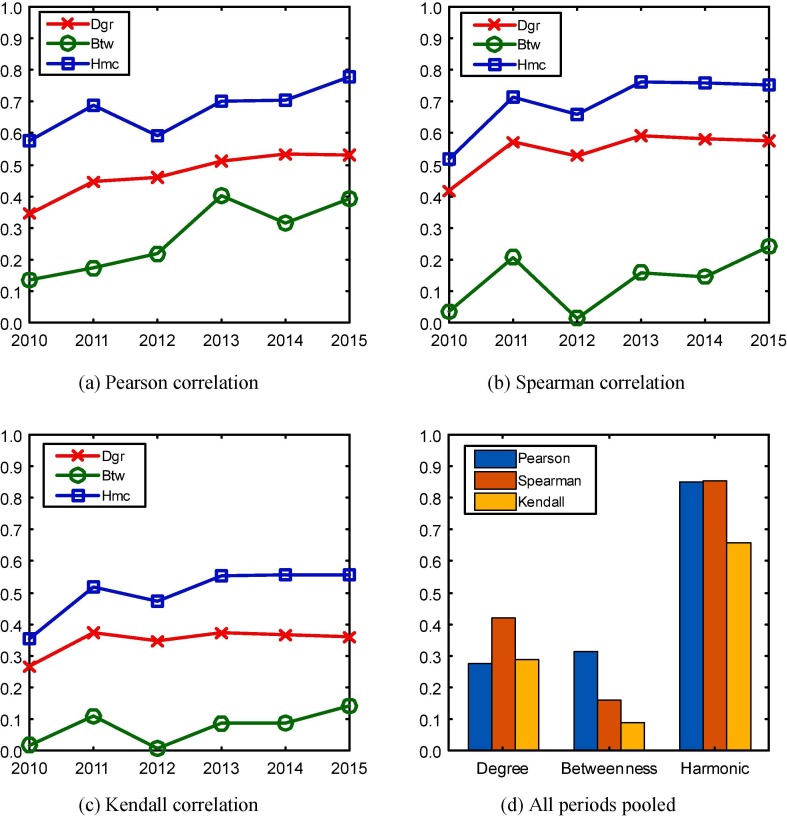
In this section, we explore whether infrastructure network and service network generate similar assessment on a city’s centrality in the HSR network. We calculate, for each centrality measure, the correlation between these two network representations. Fig. 3 (a)-(c) presents three correlation coefficients, Pearson, Spearman and Kendall, over the time. All three centrality measures obtained from service networks appear to have weak correlations with those derived from infrastructure networks. This is especially the case for degree and betweenness, as the correlation coefficients of and (denoted as Dgr in Fig. 3) are in most of the cases below 0.5, and so are the correlation coefficients of and (denoted as Btw in Fig. 3). Harmonic centralities of these two types of networks have a stronger correlation with a coefficient mostly ranging from 0.5 to slightly over 0.7. After pooling the centrality measures over the time, the correlation coefficients of and (denoted as Hmc in Fig. 3) are substantially improved, exceeding 0.8 in the case of Pearson and Spearman correlations (Fig. 3(d)). These inter-temporal correlations are weaker when degree and betweenness centralities are in concern.
Fig. 3.
Correlations between centralities obtained from infrastructure network and service network.
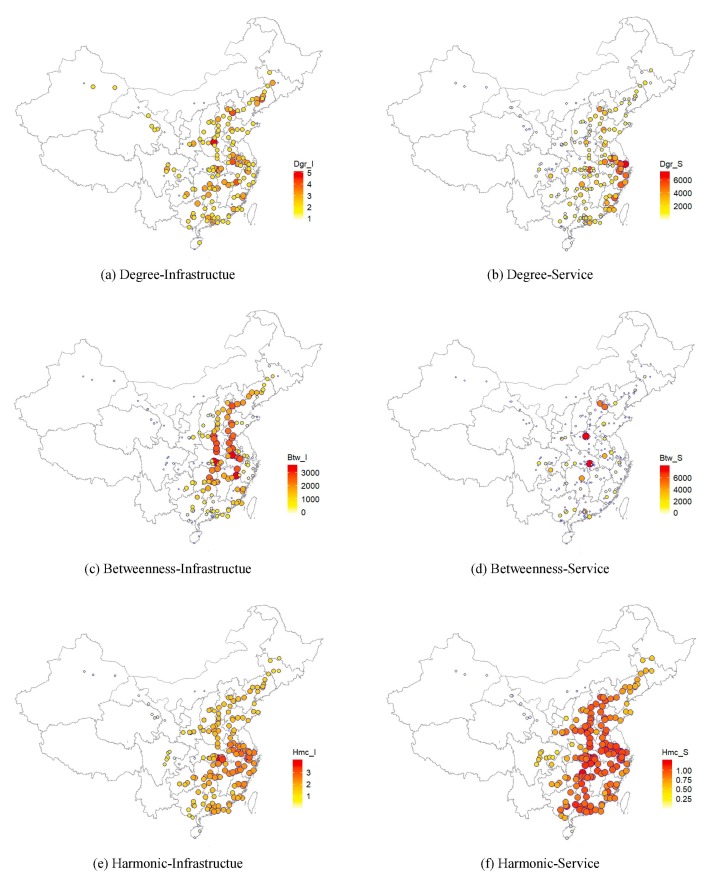
Fig. 4 shows centralities of individual cities in 2015 based on infrastructure network and service network respectively. Centralities, esp. degree and betweenness, in the service network show stronger variations across cities than in the infrastructure network. This is because centrality measures in the infrastructure network does not incorporate service frequency and scheduled travel time which vary significantly across edges and nodes. In addition, rankings of cities also differ in these two networks. Specifically, the five cities with the highest degree centrality are Shanghai, Nanjing, Wuhan, Hangzhou and Guangzhou in service network, whereas they are Wuhan, Nanjing, Chengdu, Zhuzhou and Shangrao in infrastructure networks. The top-5 cities in terms of betweenness are Wuhan, Zhengzhou, Beijing, Tianjin and Changsha in service network, while Wuhan, Tianjin, Shangrao, Jinan and Changsha are the top-5 cities in infrastructure network. In terms of harmonic centrality, the top-5 cities are Wuhan, Zhengzhou, Changsha, Nanjing and Hangzhou in service networks, whereas only Wuhan and Hangzhou appear in the top-5 list of infrastructure network.
Fig. 4.
Comparison between HSR infrastructure network and service network in 2015 (Cities without HSR are excluded from the figure.)
According to Fig. 4, we can observe a number of differences with respect to the spatial distributions of centralities between infrastructure and service networks. For example, in the infrastructure network, cities with the highest degrees (red and orange dots) are scattered throughout the country, but in the service network, these cities are concentrated in Yangtze River Delta. Similarly, many cities along the Beijing-Shanghai line and the Beijing-Guangzhou line can achieve high betweenness in the infrastructure network, but only a handful of cities, mostly located in central China, can achieve high transitivity in the service network in terms of transitivity. Both networks have similar patterns in the spatial distribution of harmonic centrality, but there is some slight difference. In the service network, there is a much clearer polarization of strong and weak cities. Although the service network has a lot more cities with high accessibility than the infrastructure network, the rest of the cities in the service network have much lighter colors, indicating a much larger difference between the strong and weak cities. In the infrastructure network, however, although only a few cities enjoy high accessibility, the difference between strong and weak cities is much milder, as majority of the cities have medium level accessibility.
Table 1 shows that centralities obtained from infrastructure networks have weak association with cities’ demographic and economic characteristics. Centralities obtained from service networks, especially degree and betweenness, have stronger association with economic activities. Harmonic centrality of service network appears to have a weaker linkage with population and GDP. A possible explanation is that harmonic centrality is considerably driven by the physical location of the city in the network. Cities with locational advantages, such as those located in Central China, generally have high values of harmonic centrality despite their lower levels of economic activities compared with cities in East China. Taken together, the centrality measures from service networks are more consistent with the level of development of individual cities and better reflect the true importance of a city in the HSR network. This is consistent with the preference of flow approach (service network) over node approach (infrastructure network) in characterizing urban networks (Yang et al., 2019). Thus, discussions in the next section are based on the centralities generated from service networks.
Table 1.
Correlation between centrality measures and population or GDP.
| Degree |
Betweenness |
Harmonic |
||||
|---|---|---|---|---|---|---|
| Infrastructure | Service | Infrastructure | Service | Infrastructure | Service | |
| Population | 0.286 | 0.469 | 0.206 | 0.435 | 0.222 | 0.298 |
| GDP | 0.364 | 0.685 | 0.276 | 0.545 | 0.373 | 0.417 |
| GDP per capita | 0.242 | 0.414 | 0.175 | 0.239 | 0.321 | 0.326 |
5. Disparity analysis
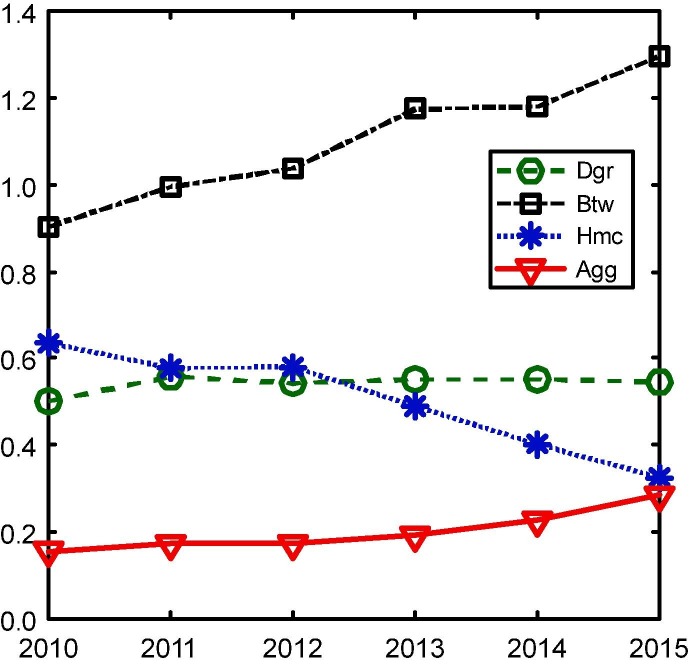
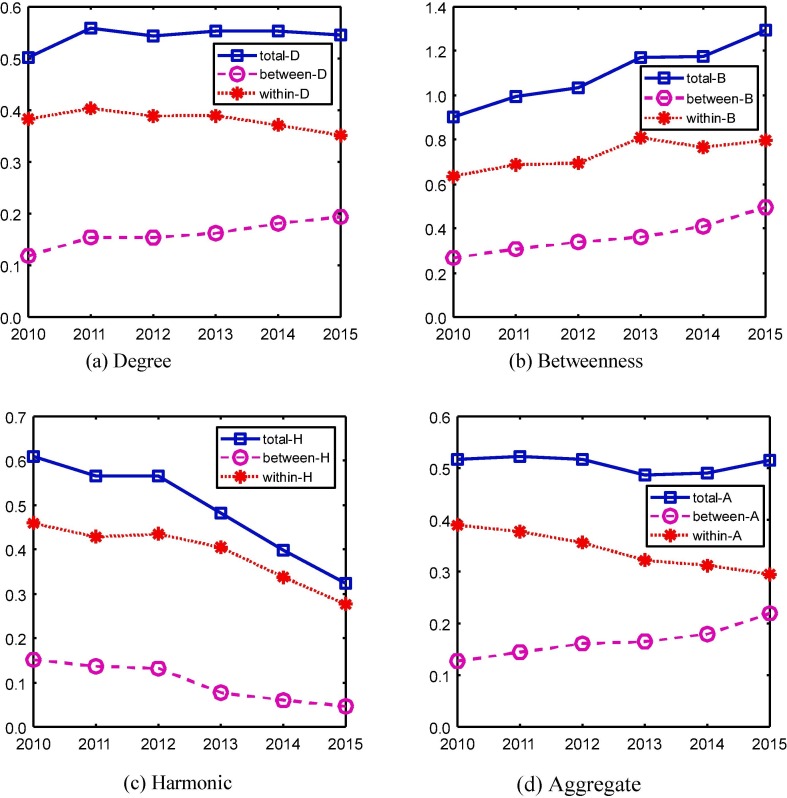
Fig. 5 shows the overall disparities among all the studied cities. Theil’s T index of harmonic centrality (Hmc) have decreased over time, suggesting that cities are becoming more equal in terms of accessibility. On the contrary, cities appear to be more unequal regarding betweenness centrality (Btw) which reflects a city’s transitivity, indicating that metropolises’ capability of channelling traffic between different HSR train services has been enhanced. As a result, the inequality in aggregate measure (Agg) remains almost unchanged with a slight increase. The remainder of Section 5 will focus on the inequalities within and between different economic regions, tiers of cities, and megalopolises.
Fig. 5.
Overall disparity of all sampled cities (Theil’s T index).
5.1. Disparities by economic regions
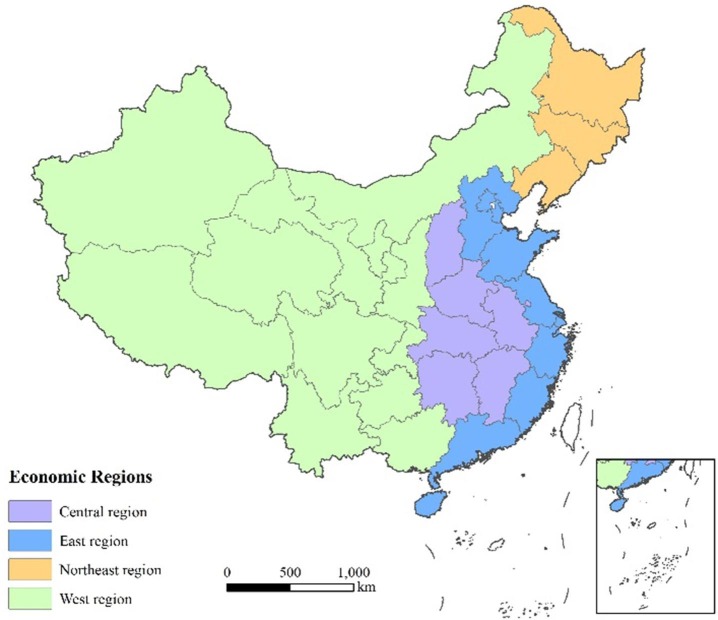
Based on the socio-economic status of different provinces, the State Council of China divides the country into four major regions, namely East, Central, Northeast, and West. Fig. 6 shows the geographical location of each region. Following this standard, we examine the inter-temporal changes in inequalities of HSR development (more precisely, provision of HSR services) within these four regions as well as inequalities between these regions.
Fig. 6.
Four economic regions of China.
Table 2 presents the mean values of the centralities across all studied cities in each region during the study period. All four regions have seen a considerable growth in centrality values. However, the east and central regions dominate the development of HSR in this period. Among the three centrality measures, betweenness is the most sensitive to opening of new HSR lines and is not necessarily increasing throughout the period. The impact of the system-wide deceleration of HSR trains after the ‘Wenzhou train collision’ happened in 2011 can be immediately seen, as there is a decrease in the average harmonic centrality values in all the regions in the following year.
Table 2.
Mean centrality values by economic regions.
| Region (number of cities) | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|
| East (1 2 6) | Dgr | 164.07 | 398.59 | 378.71 | 547.09 | 787.85 | 1057.62 |
| Btw | 420.8 | 486.9 | 504.5 | 831.5 | 1081.0 | 1230.6 | |
| Hmc | 0.1251 | 0.2615 | 0.2449 | 0.3643 | 0.5027 | 0.7160 | |
| Agg | 0.3711 | 0.4163 | 0.4196 | 0.4889 | 0.5760 | 0.6243 | |
| Central (91) | Dgr | 76.73 | 115.49 | 117.15 | 222.44 | 378.73 | 701.54 |
| Btw | 217.8 | 288.5 | 268.8 | 453.0 | 744.8 | 1394.9 | |
| Hmc | 0.1056 | 0.1933 | 0.1803 | 0.3528 | 0.5028 | 0.8146 | |
| Agg | 0.2626 | 0.2610 | 0.2592 | 0.3870 | 0.4864 | 0.6399 | |
| Northeast (39) | Dgr | 16.59 | 34.44 | 36.59 | 171.08 | 264.18 | 307.85 |
| Btw | 36.6 | 82.5 | 66.3 | 309.6 | 238.4 | 305.2 | |
| Hmc | 0.0363 | 0.0850 | 0.0786 | 0.2269 | 0.2883 | 0.3690 | |
| Agg | 0.0792 | 0.1072 | 0.1048 | 0.2559 | 0.2813 | 0.2782 | |
| West (85) | Dgr | 8.55 | 10.96 | 12.38 | 17.60 | 68.64 | 215.95 |
| Btw | 11.4 | 39.0 | 12.6 | 23.5 | 192.0 | 569.7 | |
| Hmc | 0.0093 | 0.0245 | 0.0148 | 0.0238 | 0.1238 | 0.2829 | |
| Agg | 0.0214 | 0.0313 | 0.0200 | 0.0254 | 0.1146 | 0.2205 |
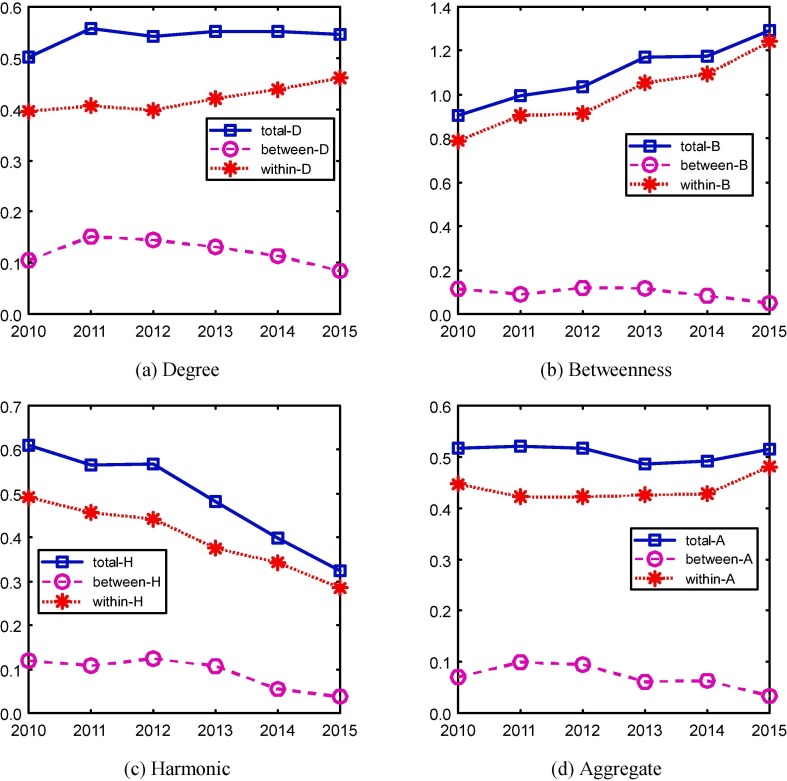
By applying Theil’s T index, we decompose the total inequality across all cities sampled into between-region inequality and with-region inequality (Fig. 7 ). Disparity among cities within the same region is much stronger than the disparity between different regions. As a result, the trend of total disparity of each centrality measure is mainly driven by the trend of within-region disparity. That is, although the disparity between different regions tends to decrease, the total disparity may not decrease. In particular, the four regions show a trend of convergence in HSR development. Among cities in the same region, as more cities are connected to the HSR network, the inequality in accessibility (harmonic) has been quickly reduced, but the inequalities in connectivity (degree) and transitivity (betweenness) appear to increase. This implies that although cities are getting more inter-connected with each other, the provision of HSR service is progressively concentrated in only a few cities of a region.
Fig. 7.
Between-region and within-region disparity: Theil’s T index 2010–2015.
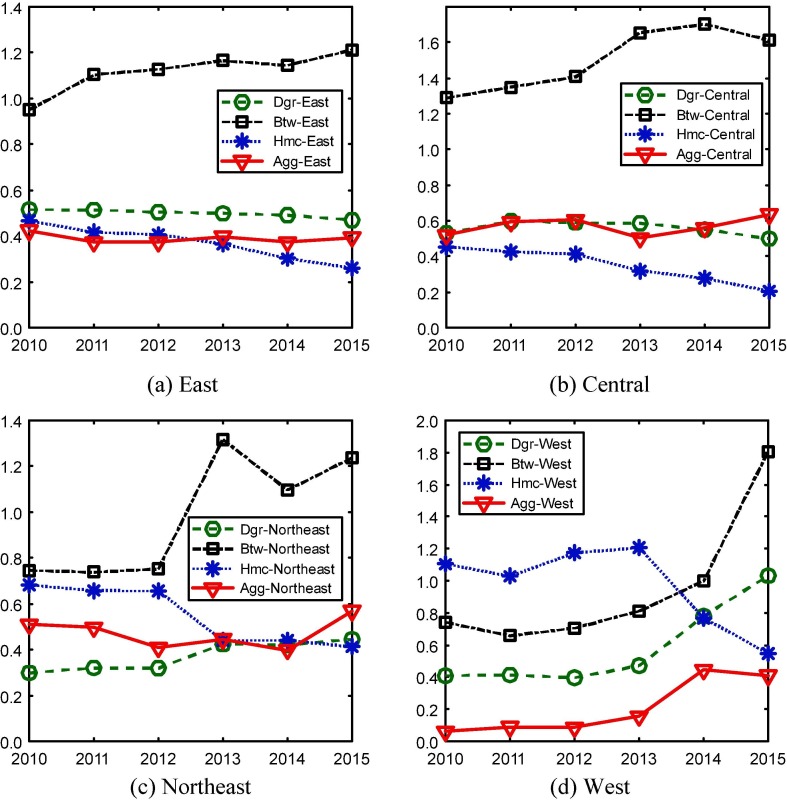
The within-region disparity shown in Fig. 7 is the average disparity across all the four regions. However, the inter-temporal variations of individual regions may differ (Fig. 8 ). Aggregating all the three centralities, the inequalities within the East, Central and Northeast regions remain stable, whereas the inequality within the West has experienced a notable increase. This is mainly contributed by the widening inequality in degree centralities of cities in the West. In particular, the inequalities in degree centralities have barely changed within the East and Central regions and slightly increased in the Northeast region, whereas the inequality in the West has been almost doubled. Unlike small cities in the East, those in the West are left behind probably because of lower service frequency. Given that small cities in the West have lower levels of urbanization and economic activities, they are bypassed by many HSR trains. On the other hand, every region sees a convergent trend in harmonic centralities and a divergent trend in betweenness centralities among its cities. That is, each region has been increasingly relying on a few large cities to channel inter-city traffic. These large cities include Beijing, Tianjin, Nanjing, Hangzhou and Guangzhou in the East, Wuhan, Zhengzhou and Changsha in the Central, Shenyang and Changchun in the Northeast, and Chengdu and Chongqing in the West. This observation is consistent to the National Urban Hierarchical Plan (2006–2020) in which cities nominated as the national central cities are expected to lead regional development and radiate their impacts to others in the country. Thus, these cities may have advantages over the others in gaining national resources including transportation services.
Fig. 8.
Within-region disparities by regions.
In addition, it is worth noting that the Northeast and the West regions have experienced more dramatic changes in within-region disparities than the other two regions. This could partially be attributed to the opening of new HSR lines in the Northeast, e.g. Harbin-Dalian line at the end of 2012, and in the West, e.g. Chongqing-Lichuan segment at the end of 2013. These two regions are the least developed in terms of HSR services and therefore opening of new lines affects inequality within these two regions more than the other well-developed regions. For example, the Harbin-Dalian line make more cities in the Northeast to be accessible by HSR, leading to reduced inequality of accessibility, but it also strengthens the bridging role of Shenyang between the Northeast and the other parts of China, as Harbin-Dalian line and Qinhuangdao-Shenyang line join in Shenyang. Similarly, the transitivity of Changchun is also enhanced since Changchun-Jilin line and Harbin-Dalian line join in Changchun. Therefore, Shenyang and Changchun experienced a significant increase in betweenness centrality whereas the values of the other cities remained unchanged, contributing to the increase in with-region disparity. In the West region, the increased inequality in transitivity and connectivity could be caused by the enhanced roles of several metropolises in long-haul services after opening of new lines. For instance, the Chongqing-Lichuan segment is the final piece of the Shanghai-Wuhan-Chengdu corridor, one of the east-west HSR corridors in China, and hence its opening completes this corridor by linking the west and east rail segments. As a result, Chongqing and Chengdu, being the two major cities on the west segment of the corridor, are served by new direct long-haul HSR trains linking the east part of China. Meanwhile, the topography and landform of the West region limit the operating speed of HSR. To reduce the travel time between large cities in the west and other parts of China, newly added long-haul HSR services may bypass small and medium cities in the west. Consequently, small cities enjoyed relatively marginal improvement in HSR services, and their residents may find it more convenient to transfer at Chongqing and Chengdu when traveling to the East region.
5.2. Disparities by city tiers
Several studies argue that smaller intermediate cities are more likely to be bypassed by HSR services in favour of the metropolises, and as a result HSR has intensified the polarization between small and large cities (Urena et al., 2009, Moyano and Dobruszkes, 2017). In this section, we investigate the disparities between and within different tiers of cities. We classify all the selected cities into three tiers based on their total and permanent urban population sizes.9 This classification incorporates the standard set by the Ministry of Housing and Urban-Rural Development of China. In particular, tier 1, tier 2 and tier 3 denote large, medium and small cities respectively.
Table 3 presents the average centrality values of each tier of cities. Although cities of tier 1 are clearly much better-developed in HSR than those of the other two tiers, which is consistent with Xu et al. (2018), medium and small cities have experienced faster growth since 2013. For example, during this six-year period, the average aggregated indicator of tier 1 cities has increased by 0.4 times, while those of tier 2 cities and tier 3 cities have increased by 1.2 and 3.1 times respectively. This is expected as more medium and small cities are connected by HSR over the time. Based on the growth rates, while the development of tier 2 cities is mostly contributed by the increase in degree, the most remarkable development of tier 3 cities is the dramatic increase in betweenness.
Table 3.
Mean centrality values by tiers of cities.
| Tier (number of cities) | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|
| Tier 1 (49) | Dgr | 397.86 | 875.10 | 834.45 | 1240.06 | 1747.53 | 2408.12 |
| Btw | 2137.4 | 3005.8 | 2961.2 | 4367.2 | 6383.4 | 9658.0 | |
| Hmc | 0.2495 | 0.4790 | 0.4380 | 0.6332 | 0.8315 | 1.1371 | |
| Agg | 0.9615 | 0.9409 | 0.9457 | 1.1046 | 1.2590 | 1.3643 | |
| Tier 2 (68) | Dgr | 64.97 | 156.04 | 151.68 | 272.99 | 450.76 | 726.50 |
| Btw | 127.4 | 109.8 | 102.8 | 285.0 | 367.4 | 536.7 | |
| Hmc | 0.0969 | 0.2116 | 0.1968 | 0.3478 | 0.5028 | 0.7796 | |
| Agg | 0.2474 | 0.2855 | 0.2775 | 0.3662 | 0.4614 | 0.5531 | |
| Tier 3 (2 2 4) | Dgr | 22.84 | 42.48 | 43.10 | 80.43 | 149.95 | 268.13 |
| Btw | 0.1 | 1.4 | 0.6 | 2.3 | 34.2 | 62.6 | |
| Hmc | 0.0392 | 0.0807 | 0.0747 | 0.1527 | 0.2496 | 0.4199 | |
| Agg | 0.0635 | 0.0737 | 0.0769 | 0.1290 | 0.1874 | 0.2606 |
Fig. 9 shows the variation in disparities between and within city tiers. As reflected by the aggregated indicator, the inequality between different tiers has been increasing, but it has been offset by a decrease in inequality within each city tier. Similar pattern is also observed in degree centrality. In terms of betweenness, both within-tier and between-tier disparities have increased, whilst the within-tier disparity has been mitigated slightly since 2013. In contrast, there is a clear trend of convergence in harmonic centrality both between different tiers and within the same tier. In general, although medium and small cities are gradually catching up with large cities in terms of accessibility, they are still increasingly disadvantaged in terms of connectivity and transitivity.
Fig. 9.
Between-tier and within-tier disparities: Theil’s T index 2010–2015.
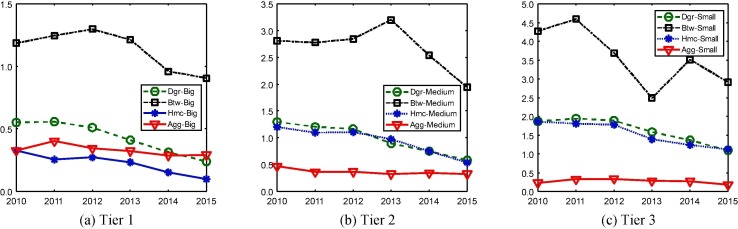
Fig. 10 reports the changes in within-tier inequalities of tier 1, tier 2 and tier 3 cities respectively. In general, HSR development among tier1 cities is more balanced, while the development in tier 2 and tier 3 cities is not quite equal. This is because small cities are not the main target of HSR network planning. Provision of HSR services in small cities is commonly a by-product of linking large cities. As a result, small cities which are luckily located along the routes linking large cities are much better served by HSR than the others. As large cities are concentrated in the east part of China, small cities in the East China are much stronger than those in the West in terms of HSR development. However, as the HSR network expands to the west part of China, more medium and small cities in the West China are connected. As a result, for each of the three tiers, among cities belong to the same tier, there seems to be a convergent trend, especially in degree and harmonic centralities (Fig. 10). The inequality in betweenness within each tier also shows a decreasing trend, but it has experienced substantial increase and decrease in various years until 2014, especially for tier 2 and tier 3 cities. These variations lead to the increasing pattern of average within-tier disparity during 2010–2013 (Fig. 9(b)) and little change in the within-tier inequality of aggregated indicator of all the three tiers.
Fig. 10.
Within-tier disparities by tiers of cities.
5.3. Disparities by megalopolises
Megalopolis (officially termed as a “city cluster” in China) is defined as a region that results from the coalescence of a chain of metropolitan areas (Gottmann, 1957). Consequently, megalopolis is a highly developed urban spatial form in the process of industrialization and urbanization. According to China’s new urbanization plan, i.e. the New-Type Urbanization Plan (2014–2020), the Chinese government gives priority to the development of five world-class city clusters, namely Yangtze River Delta (YRD), Pearl River Delta (PRD), Jing-Jin-Ji (JJJ), Middle-Yangtze River (MYR), and Cheng-Yu Region (CY). These five megalopolises account for 40% of China’s population but only 11% of the nation’s land (Table 4 ), and they play a key role in Chinese economy, accounting for 55% of China’s GDP. According to the new urbanization plan, these megalopolises have the highest priority over the other cities in developing through the integration of public resources, together with enhanced connections among cities within the megalopolises via tight and efficient transportation links, such as highways and HSR. Thus, it is relevant to compare cities in these megalopolises with others as well as HSR development in these megalopolises.
Table 4.
Economic and population sizes of the five megalopolises (Source: China index academy).
| Megalopolis | Land area (km2) |
2016 GDP (1000 billion CNY) |
2015 population (10 million) |
GDP per capita (1000 CNY) |
GDP Density (10,000 CNY/km2) |
|---|---|---|---|---|---|
| Pearl River Delta | 5.5 | 6.8 | 58.74 | 115.6 | 12,346 |
| Yangtze River Delta | 21.2 | 14.7 | 150 | 97.5 | 6949 |
| Jing-Jin-Ji | 21.5 | 7.5 | 110 | 67.5 | 3499 |
| Middle-Yangtze River | 34.5 | 7.1 | 120 | 56.8 | 2049 |
| Cheng-Yu Region | 24.0 | 4.8 | 98.19 | 49.1 | 2007 |
| China total | 963.4 | 74.4 | 1370 | 54.0 | 772 |
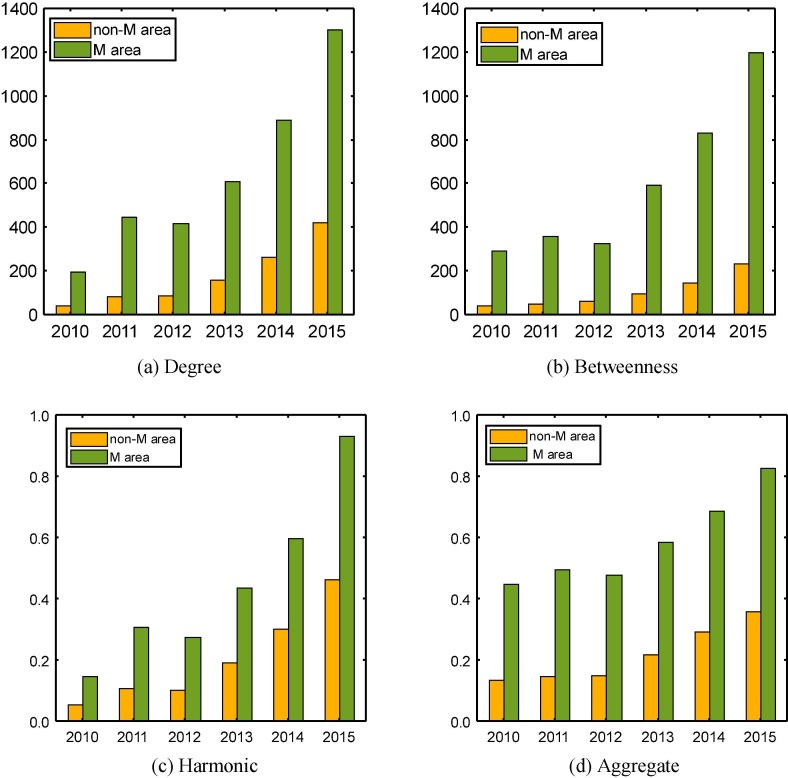
Fig. 11 compares the average centralities between cities belong to the five megalopolises (M-area) and those not belonging to any of the five megalopolises (nonM-area). Clearly, megalopolises are better served by HSR than non-megalopolises, as these five megalopolises contribute over 50% of the total HSR services. The non-megalopolises’ share of HSR services has increased by about 10%, but in terms of centrality measures, the gap between megalopolises and non-megalopolises has been widened during the study period. This finding is somewhat consistent to the new urbanization plan.
Fig. 11.
Mean centrality values: megalopolises versus non-megalopolises.
Table 5 lists the evolution of average HSR centralities in each megalopolis. Yangtze River Delta performs the best in connectivity, Jing-Jin-Ji achieves the best in transitivity, and Pearl River Delta surpassed Middle-Yangtze River in 2015 and became the most accessible region. Cheng-Yu Region experienced a significant growth after 2014 even though it performs the worst among the five megalopolises.
Table 5.
Mean centrality values by megalopolises.
| Megalopolis (number of cities) | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
|---|---|---|---|---|---|---|---|
| Yangtze River Delta (26) | Dgr | 391 | 941 | 879 | 1276 | 1555 | 2087 |
| Btw | 1033.7 | 1306.5 | 1184.4 | 2327.2 | 1943.5 | 2032.4 | |
| Hmc | 0.2342 | 0.4217 | 0.3900 | 0.5650 | 0.6501 | 0.9445 | |
| Agg | 0.7704 | 0.7774 | 0.7681 | 0.9052 | 0.8668 | 0.9333 | |
| Pearl River Delta (9) | Dgr | 227 | 673 | 563 | 671 | 1026 | 1376 |
| Btw | 69.2 | 324.3 | 325.9 | 321.1 | 1269.4 | 1935.2 | |
| Hmc | 0.1260 | 0.3978 | 0.3648 | 0.4577 | 0.7289 | 1.1890 | |
| Agg | 0.3759 | 0.6205 | 0.5945 | 0.5777 | 0.8039 | 0.9806 | |
| Jing-Jin-Ji (13) | Dgr | 171 | 400 | 404 | 684 | 1123 | 1405 |
| Btw | 1551.0 | 1115.8 | 985.3 | 2086.2 | 4259.4 | 5345.6 | |
| Hmc | 0.1762 | 0.4252 | 0.3929 | 0.6205 | 0.7854 | 0.9791 | |
| Agg | 0.5806 | 0.6428 | 0.6339 | 0.8086 | 0.9663 | 0.9588 | |
| Middle-Yangtze River (28) | Dgr | 132 | 179 | 177 | 330 | 621 | 995 |
| Btw | 436.6 | 597.8 | 589.4 | 973.5 | 1334.2 | 2379.8 | |
| Hmc | 0.1419 | 0.2524 | 0.2308 | 0.4836 | 0.6819 | 1.0389 | |
| Agg | 0.3892 | 0.3708 | 0.3660 | 0.5425 | 0.6748 | 0.8843 | |
| Cheng-Yu Region (16) | Dgr | 28 | 36 | 36 | 45 | 161 | 320 |
| Btw | 2.0 | 138.9 | 1.5 | 1.6 | 485.6 | 1579.6 | |
| Hmc | 0.0102 | 0.0598 | 0.0174 | 0.0190 | 0.1457 | 0.3922 | |
| Agg | 0.0343 | 0.0835 | 0.0288 | 0.0265 | 0.1592 | 0.3327 |
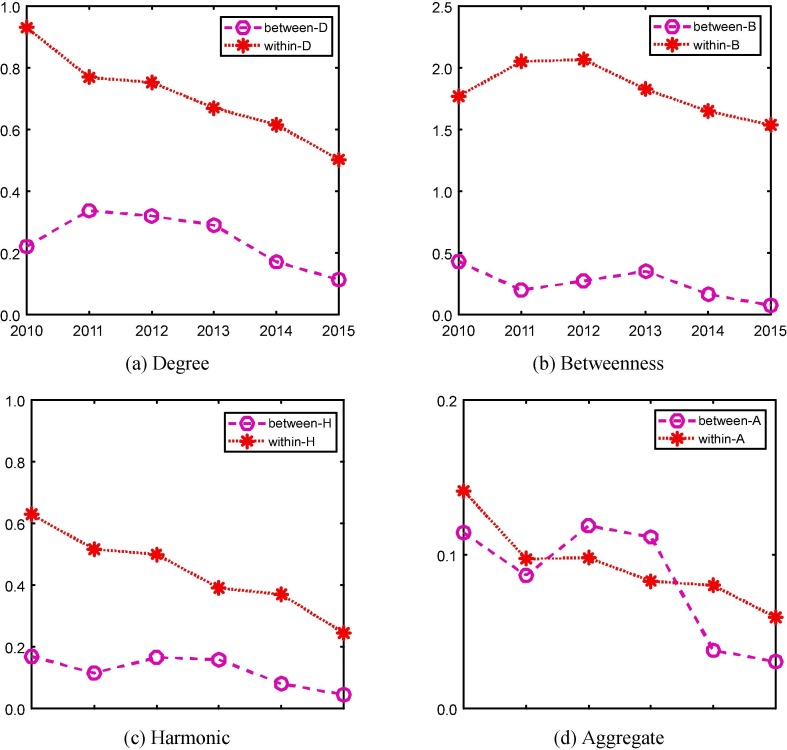
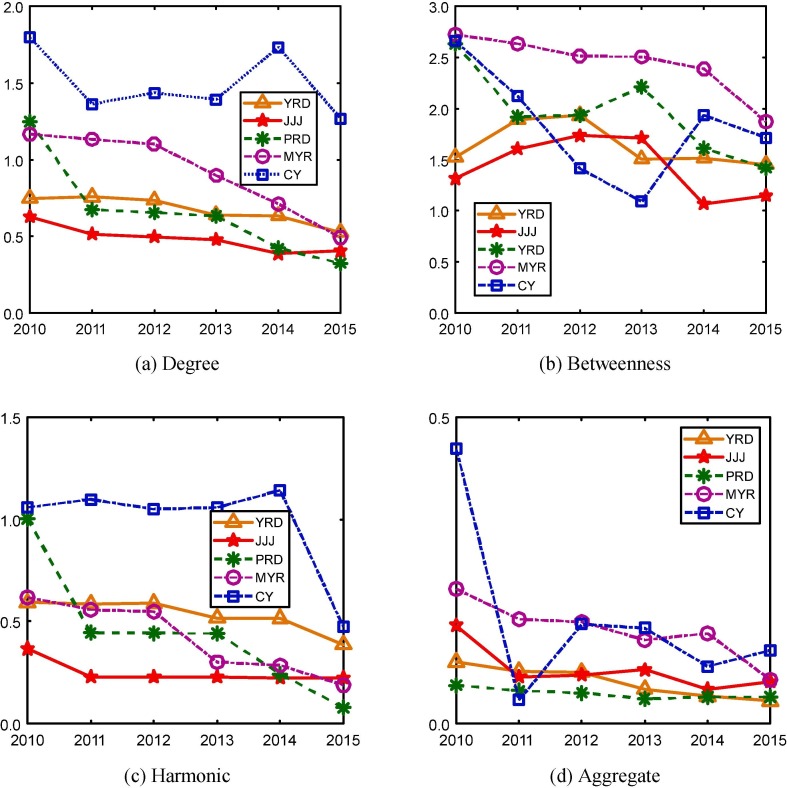
On average, both between-megalopolis disparity and within-megalopolis disparity have a decreasing trend (Fig. 12 ), especially in terms of connectivity and accessibility. Another interesting observation from Fig. 12(d) is that the aggregated indicator has very low Theil’s T indexes throughout the period. This implies that cities belonging to these megalopolises have balanced HSR development overall, although some may be stronger in connectivity while others may be stronger in transitivity or accessibility. For each megalopolis, the within-megalopolis inequality has been reduced comparing 2015 with 2010 (Fig. 13 ). However, the inequality within Cheng-Yu Region experienced a substantial increase in 2014 in all the three centrality measures. This is caused by the opening of Chongqing-Lichuan line which greatly improved the position of Chongqing and Chengdu, the two largest cities of the Cheng-Yu Region, while the other cities in the region are only marginally improved. In the Pearl River Delta, the within-megalopolis inequality in betweenness experienced a jump in 2013. This is because the extension of Guangzhou-Zhuhai line at the end of 2012 has weakened the transit function of intermediate cities, such as Foshan and Zhongshan, but strengthened the transitivity of Guangzhou, the largest city in Pearl River Delta.
Fig. 12.
Between-megalopolis and within-megalopolis disparities: Theil’s T index 2010–2015.
Fig. 13.
Within-megalopolis disparities by megalopolises: 2010–2015.
The final question is whether cities in a megalopolis play different roles in the HSR network. That is, some cities may specialize in connecting to the outside regions (out-region connection) while others are mainly linked to cities within the same megalopolis (intra-region connection). To do so, we calculate the “out-region” (“intra-region”) centrality values by only taking into account HSR services which link a city with other cities outside (inside) of its own megalopolis. The corresponding Theil’s T indices of each megalopolis are shown in Table 6 . The Theil’s T indices of all the centrality measures calculated based on “intra-region” services have decreased comparing 2010 and 2015, suggesting that cities within the same megalopolis have become increasingly similar in their ability to connect with each other by HSR. This again conforms to the new urbanization plan. However, the Theil’s T indices based on “out-region” services tend to increase. In fact, only Jing-Jin-Ji and Yangtze River Delta see a reduced inequality in “out-region” connectivity and accessibility. Cities in all the other three megalopolises become more divergent in terms of reaching cities outside of their own megalopolises. In other words, inter-regional HSR services become more concentrated in a few core cities in these three megalopolises, and other non-core cities have to rely more on core cities to access cities in other megalopolises. This is consistent to the increased inequality of “out-region” betweenness in all megalopolises. In fact, our data suggest that in each megalopolis, intra-region connections have grown much faster than out-region connections during the period. In conclusion, as China’s HSR network expands, core cities of each megalopolis start to play a major role in bridging the megalopolis and other regions, which gradually weakened non-core cities’ capability of reaching other regions directly. Nevertheless, non-core cities have achieved stronger connection with core cities in the same megalopolis in terms of higher frequency and shorter travel time.
Table 6.
Disparity by megalopolises: intra-region versus out-region HSR services.
| megaopolis | Degree |
Betweenness |
Harmonic |
Aggregate |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intra-region |
Out-region |
Intra-region |
Out-region |
Intra-region |
Out-region |
Intra-region |
Out-region |
|||||||||
| 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | |
| JJJ | 0.367 | 0.184 | 0.241 | 0.185 | 0.845 | 0.065 | 0.498 | 0.737 | 0.203 | 0.084 | 0.148 | 0.084 | 0.467 | 0.395 | 0.446 | 0.431 |
| YRD | 0.230 | 0.191 | 0.153 | 0.128 | 0.287 | 0.232 | 0.730 | 0.794 | 0.161 | 0.096 | 0.115 | 0.045 | 0.389 | 0.304 | 0.413 | 0.582 |
| PRD | 0.298 | 0.263 | 0.267 | 0.302 | 0.698 | 0.365 | 0.517 | 0.699 | 0.140 | 0.138 | 0.055 | 0.115 | 0.434 | 0.256 | 0.458 | 0.479 |
| MYR | 0.513 | 0.264 | 0.377 | 0.504 | 0.495 | 0.329 | 0.992 | 1.475 | 0.355 | 0.105 | 0.198 | 0.297 | 0.687 | 0.424 | 0.506 | 0.559 |
| CY | 0.786 | 0.330 | 0.012a | 1.210 | 0.562 | 0.316 | 0.038 | 0.250 | 0.416 | 0.188 | 0.010 | 0.510 | 0.754 | 0.568 | 0.263 | 0.283 |
a. Cheng-Yu Region was not connected to cities outside by HSR until 2011. Thus, we report the out-region service disparity in 2011 for CY.
6. Concluding remarks
In this paper, we have examined whether cities in China are getting more equally served by HSR as the HSR network expands. Using HSR timetable data, our research explored Chinese cities’ spatial disparities in connectivity, transitivity and accessibility in the HSR network. We emphasized on the intertemporal trend of these disparities from 2010 to 2015 during which the four-by-four grid network of China’s HSR was formed. While the literature focuses mainly on the impact of HSR on regional economy and on whether HSR reduces or increases spatial disparity in economic development, our focus is HSR development per se instead of its economic impact. We view that a better understanding on how cities are served by HSR can shed light on their economic development.
The answer to our research question is complex and depends on the dimensions in concern. There are three main insights as summarized in Table 7 . First, the difference between the economic regions has been reduced in all the three centrality measures. However, within each region, the inequalities tend to increase except for accessibility and the east region. Second, between the cities of different sizes, the disparities in connectivity and transitivity have increased, whilst the inequalities among cities in the same tiers have reduced, especially among large cities (Tier 1). Third, the disparities between and within the five megalopolises have both been reduced after pooling all HSR services together. However, when distinguishing HSR services within the megalopolis and those linking to cities outside of the megalopolis, we found that the reduced disparity mainly applies to HSR services within each megalopolis. Nevertheless, non-core cities have been further falling behind in connecting to cities outside of their own megalopolises. The only exceptions are JJJ and YRD in “out-region” connectivity and accessibility. In sum, interconnections among core metropolises have been increasingly enhanced as well as the importance of core metropolises in the HSR network. Cities nearby these core metropolises also benefit in HSR development by being more tightly connected to these core metropolises and other cities in the same region. Meanwhile, these non-core cities in major clusters are increasingly relying on core metropolises to access other parts of the country, showing a sign of specialization among core and non-core cities in the same cluster. However, small/medium-sized cities not belonging to any major city cluster appear to be further lagged behind in HSR development.
Table 7.
Summary of inter-temporal changes in disparities.
| Classification | Degree | Betweenness | Harmonic | Aggregate | |
|---|---|---|---|---|---|
| Economic regions | Between | ↓ | ↓ | ↓ | ↓ |
| Within | ↑ East and Central (no change) |
↑ | ↓ | ↑ East (no change) |
|
| City tiers | Between | ↑ | ↑ | ↓ | ↑ |
| Within | ↓ | ↓ | ↓ | ↓ Tier 2 and Tier 3 (no change) |
|
| Megalopolises | Between | ↓ | ↓ | ↓ | ↓ |
| Within | ↓ | ↓ | ↓ | ↓ | |
| Intra-region | ↓ | ↓ | ↓ | ↓ | |
| Out-region | ↑ JJJ and YRD (↓) |
↑ |
↑ JJJ and YRD (↓) |
↑ |
Our study revealed the differentiated impacts on a city’s HSR connectivity, transitivity and accessibility. Naturally, as more small cities are linked to the HSR network, the disparity in accessibility will be reduced. However, despite being weighted by the generalized travel time, accessibility is less effective, compared with connectivity and transitivity, in distinguishing the real status of HSR development among highly diverse cities.
Findings of this research provide several insights for policy makers. First, although many small and weak cities have been linked to HSR network and their HSR accessibilities have been improved, it is still difficult for them to catch up with large cities in connectivity and transitivity, as the large cities have developed in an even faster pace. The enlarged gap in the supply of HSR services may be attributed to insufficient opportunities. In other words, it is questionable whether these small cities have been benefited from HSR. Therefore, small cities in remote regions should pay much more attention to increasing their attractiveness (via, for example, industrial upgrading) in addition to building railroads and stations. This point is relevant to China’s future HSR expansion plan. According to the plan, an increasing number of small cities in the central and western parts of China will be linked to the HSR system. Considering these cities’ relative low attractiveness and low population density, together with the region’s complex geographical conditions which raises difficulty in constructing HSR and achieving high operating speed, a serious cost-benefit analysis comparing the development of HSR infrastructure with other options, such as air transport, is warranted, before such heavy investment is materialized (see also Wang et al., 2017). As HSR connectivity is expected to remain at a low level at these small cities, the utilization of such expensive infrastructure will be a cause for concern.
Second, except YRD and JJJ, all the other megalopolises have experienced an increase in the disparities of out-region connectivity, transitivity, and accessibility. This increasing reliance of non-core cities on core cities to reach outside opportunities might be unavoidable in the short term. However, these non-core cities should also plan ahead so as to improve their own attractiveness. On the other hand, the reduction of both the intra-region and out-region disparities in Yangtze River Delta and Jing-Jin-Ji may imply more balanced development opportunities among cities in these two megalopolises.
Third, the substantial increase in the disparity of transitivity (betweenness centrality) may be a warning signal for the potential risk of the HSR system or for the existing scheduling approach. Although having passengers transfer at a few large stations is an efficient way of routing passengers between small cities (similar to the hub-and-spoke system in air transport), it increases the vulnerability of the system when the main transfer point is in trouble. The recent outbreak of novel coronavirus (COVID-19) in the city of Wuhan is a good example. As Wuhan has the highest transitivity among all the cities we studied (Table A2), the city’s position in the HSR network plays an important role in spreading the epidemic across China.
This paper has two major limitations which can lead to two avenues for future studies. First, caution should be taken when interpreting our results as we only include HSR in the picture. In fact, introduction of HSR services may be accompanied with reduction in other services, such as inter-city coaches, conventional trains and short/medium haul flights. Evidence shows that conventional trains suffer the most from the modal substitution of HSR, leading to the reduced service levels on conventional lines (Givoni and Dobruszkes, 2013).10 In the case of China, for example, the inauguration of Beijing-Shanghai HSR line resulted in a reduction of 47 conventional trains which had served many small cities. The recent opening of Datong-Xi’an line has, for instance, led to the termination of several conventional routes that served small cities. Even though these cities used to be served frequently by conventional trains, they tend to be bypassed by HSR of which the primary focus is on large cities. The deterioration of conventional trains may widen the gap between small and large cities in terms of accessing rail services. As a result, excluding conventional trains would likely cause an underestimation on the disparities among regions. Similarly, although harmonic centrality can be interpreted as a city’s accessibility via HSR alone, it is different from the concept of accessibility in measuring a city’s capacity and potential to access markets and resources. The latter would be better measured by considering all possible modes of transportation.
Second, it would be useful to investigate the economic drivers underlying these disparity impacts by HSR in the spirit of the recent work on connectivity at Chinese airports (e.g. Zhang et al., 2017). The new urbanization plan might be a driver, but the plan may also be inspired by the evolving HSR service network. The key is to understand the mechanism behind the flows of capital and human resources and the changing relationships between cities (see detailed discussion in Zhang et al., 2019). For example, what we observe might be a net outcome of both agglomeration and spill-over effects of HSR. That is, while HSR facilitates metropolises to attract more resources from other smaller cities, it also helps with diverting certain activities to nearby cities by offering a tight connection between the metropolises and the nearby cities.
CRediT authorship contribution statement
Shuli Liu: Conceptualization, Methodology, Formal analysis, Visualization, Data curation, Writing - original draft, Writing - review & editing. Yulai Wan: Conceptualization, Methodology, Writing - original draft, Writing - review & editing, Project administration, Funding acquisition. Anming Zhang: Conceptualization, Writing - review & editing, Supervision.
Acknowledgement
We are very grateful to the three anonymous reviewers for providing constructive comments and suggestions. We also thank Chunan Wang, Haoran Yang, Weiyang Zhang, and the seminar participants at School of Urban and Regional Science, East China Normal University, at Beijing Jiaotong University, and at Beihang University (Beijing) for helpful comments. We are grateful to the financial support from the Research Grants Council of Hong Kong (RGC/PolyU 152195/17E).
Footnotes
For a recent survey of the literature, see Zhang et al. (2019).
See also Takebayashi (2015) and Zhu et al., 2018, Zhu et al., 2019 who use timetables for HSR and airlines to examine multi-modal connections and connectivity radiations of transportation infrastructure.
According to the train timetables, we find that the numbers of inbound and outbound train services are not necessarily close to each other, especially for the small cities. Large cities tend to have more balanced inbound and outbound services (see Appendix A).
See also Wong et al. (2019) and Cheung et al. (2020), among others, for the recent studies on airports using various centrality measures.
Zhang et al., 2016 mentioned that actual passenger flow data is the best to analyse urban networks. Yang et al. (2019) found that timetable data and passenger flow data can generate very different results. However, passenger flow data is not available for our study. Moreover, passenger flow data may reflect the demand for HSR services, while our focus is on the supply, since connectivity, transitivity and accessibility are all referring to passengers’ ability to reach other cities instead of demand for travel.
This is also done in, e.g., Liu et al. (2019).
In transportation systems, the weights can be ridership, travel cost, geodesic distance and so on.
One weakness of Theil’s T index is that it cannot be directly compared across populations with different sizes. However, this is not a problem in our study. We do not compare inequality between different groups of cities. Rather, our focus is to assess the inter-temporal changes in inequality among cities belonging to the same group. That is, we are interested in which group of cities has experienced increased inequality, but not which group of cities has experienced high inequality than the other groups.
Tier 1 includes cities with total population over 5 million and permanent urban population over 1 million. Tier 2 includes cities with total population in the range of 3–5 million and permanent urban population over 0.5 million. Tier 3 includes cities with total population in the range of 1–3 million and permanent urban population below 0.5 million.
The deterioration of conventional train services can be caused by various reasons. For example, conventional trains and high-speed trains may share the same track with the latter having a higher priority than the former. Consequently, the expansion of HSR services would leave less infrastructure available for conventional trains. There can also be a natural adjustment on the supply of conventional services due to a shift of demand from conventional trains to HSR.
The formula of Jiao et al. (2017)’s degree centrality can be rewritten into . The strength of node i is defined as .
Appendix A. Imbalance of inbound and outbound HSR services
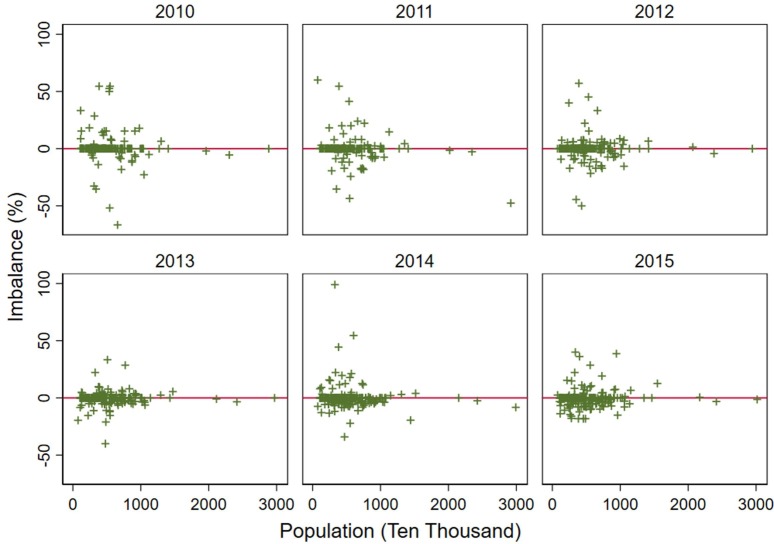
We use the difference between the numbers of inbound and outbound HSR services of a node to indicate the imbalance of inbound and outbound services. The imbalance indicator is calculated by using the formula below.
That is, a negative (positive) imbalance indicator suggests that there is more (fewer) outbound services than inbound services. Cities with imbalance indicator closer to zero have more balanced services. In Fig. A1 , we plot the imbalance indicator against the city size measured by the cities’ population. In general, cities with lower population size tend to have stronger imbalance.
Fig. A1.
Imbalance of inbound and outbound services by city size (2010–2015).
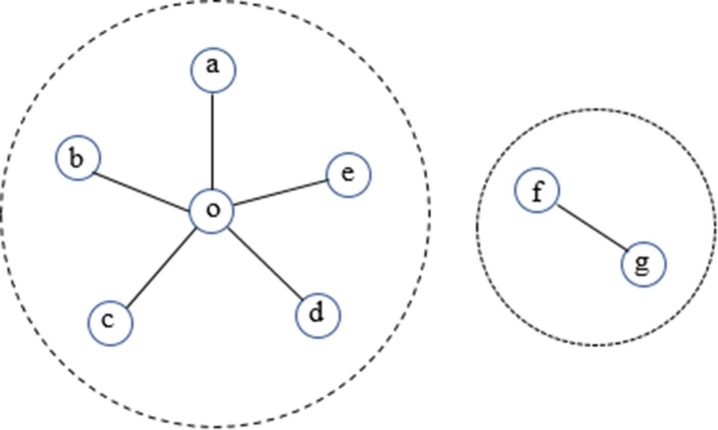
Appendix B. Difference of closeness and harmonic centralities in a disconnected network
Closeness centrality may not be applicable to the network that consists of several disconnected components. Fig. A2 shows an example of disconnected network. In this case, closeness centrality can be inaccurate in measuring accessibility. This is because most nodes in the larger subgraph need to go through more edges to reach the other nodes in the same subgraph than nodes f and g in the smaller subgraph. For example, node a needs to go through 1 edge to reach node o but 2 edges to reach nodes b, c, d and e. Whist, node f only needs to go through 1 edge to reach g. As a result, nodes g and f in the smaller subgraph appear to have a larger closeness than nodes in the larger subgraph (Table A1 ). Obvious this does not reflect the true situation that nodes in the larger subgraph is in fact more accessible. Harmonic centrality in Table A1 reflects the true accessibility better.
Table A1.
Network analysis of the disconnected network.
| a | b | c | d | e | o | f | g | Farness | Closeness | Harmonic | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | – | 2 | 2 | 2 | 2 | 1 | Inf | Inf | a | Inf | 1/9 | 3 |
| B | 2 | – | 2 | 2 | 2 | 1 | Inf | Inf | b | Inf | 1/9 | 3 |
| C | 2 | 2 | – | 2 | 2 | 1 | Inf | Inf | c | Inf | 1/9 | 3 |
| D | 2 | 2 | 2 | – | 2 | 1 | Inf | Inf | d | Inf | 1/9 | 3 |
| E | 2 | 2 | 2 | 2 | – | 1 | Inf | Inf | e | Inf | 1/9 | 3 |
| O | 1 | 1 | 1 | 1 | 1 | – | Inf | Inf | o | Inf | 1/5 | 5 |
| F | Inf | Inf | Inf | Inf | Inf | Inf | – | Inf | f | Inf | 1/1 | 1 |
| G | Inf | Inf | Inf | Inf | Inf | Inf | 1 | – | g | Inf | 1/1 | 1 |
| (a) Distance matrix | (b) Accessibility measure |
Fig. A2.
An example of a disconnected network.
Appendix C. Comparison of our results with Jiao et al. (2017)
Table A2 compares our city-level rankings with those of Jiao et al. (2017). Since both studies employ the same data source (China railway timetable), all major rail hubs such as Shanghai, Beijing, Guangzhou, Wuhan, and Nanjing are on the top-20 lists of both studies. Nonetheless, only 60% of the cities on our list appear on Jiao et al. (2017)’s list when degree centrality is in concern, and the level of similarity in terms of closeness (harmonic) and betweenness centralities are 65%. This low level of similarity might be contributed by three major differences. First, when calculating degree centrality, Jiao et al. (2017) also take service frequency into account, but their approach is equivalent to taking the geometric mean of unweighted degree and strength, while our degree centrality is equivalent to strength.11 Our approach is more likely to upgrade cities with fewer connections but higher HSR service frequencies. Second, when generating the other two centralities, we incorporate both in-vehicle travel time and service frequency while Jiao et al. (2017) only take service frequency into account. As the in-vehicle time vary significantly across edges depending on geographical locations and types of HSR services provided, ignoring this feature can substantially change the results. Third, Jiao et al. (2017) use closeness centrality to measure accessibility, while we use harmonic centrality.
Table A2.
Comparison of city-level rankings in year 2014.
| Rank |
Jiao et al. (2017) |
Our analysis |
||||
|---|---|---|---|---|---|---|
| Degree | Accessibility - closeness | Betweenness | Degree | Accessibility - harmonic | Betweenness | |
| 1 | Shanghai | Shanghai | Beijing | Shanghai | Wuhan | Wuhan |
| 2 | Beijing | Nanjing | Wuhan | Nanjing | Nanjing | Zhengzhou |
| 3 | Nanjing | Beijing | Guangzhou | Wuhan | Wuxi | Tianjin |
| 4 | Wuhan | Wuhan | Zhengzhou | Hangzhou | Changzhou | Nanjing |
| 5 | Zhengzhou | Zhengzhou | Shenyang | Wenzhou | Suzhou | Beijing |
| 6 | Guangzhou | Hangzhou | Shanghai | Guangzhou | Zhenjiang | Huzhou |
| 7 | Hangzhou | Guangzhou | Hangzhou | Fuzhou | Hangzhou | Guangzhou |
| 8 | Xuzhou | Suzhou | Xi’an | Suzhou | Huzhou | Jinan |
| 9 | Suzhou | Xuzhou | Jinan | Ningbo | Shanghai | Qinhuangdao |
| 10 | Shijiazhuang | Changsha | Nanjing | Wuxi | Ezhou | Fuzhou |
| 11 | Wuxi | Wuxi | Chengdu | Beijing | Zhengzhou | Ningbo |
| 12 | Changsha | Shijiazhuang | Tianjin | Shaoxing | Jinan | Shenzhen |
| 13 | Jinan | Changzhou | Harbin | Jinan | Yixing | Shenyang |
| 14 | Tianjin | Tianjin | Shijiazhuang | Shenzhen | Xianning | Hangzhou |
| 15 | Shenyang | Jinan | Xuzhou | Changzhou | Guangzhou | Chongqing |
| 16 | Changzhou | Zhenjiang | Changsha | Tianjin | Beijing | Hefei |
| 17 | Hengyang | Shenyang | Nanchang | Putian | Hefei | Xuzhou |
| 18 | Zhenjiang | Hengyang | Baoji | Xiamen | Tianjin | Sanming |
| 19 | Zhuzhou | Xi’an | Shenzhen | Hefei | Huanggang | Changsha |
| 20 | Xi’an | Bengbu | Lanzhou | Xuzhou | Shaoxing | Shijiazhuang |
| Similarity | 60% | 65% | 65% | |||
References
- Barthelemy M. Spatial networks. Phys. Rep. 2011;499(1–3):1–101. [Google Scholar]
- Campante F., Yanagizawa-Drott D. Long-range growth: Economic development in the global network of air links. Q. J. Econ. 2018;133(3):1395–1458. [Google Scholar]
- Chatterjee, A., 2016. Studies on the Structure and Dynamics of Urban Bus Networks in Indian Cities. Working Paper, 1–47.
- Chen C., D'Alfonso T., Guo H., Jiang C. Graph theoretical analysis of the Chinese high-speed rail network over time. Res. Transp. Econ. 2018;72:3–14. [Google Scholar]
- Chen Z., Haynes K. Impact of high-speed rail on regional economic disparity in China. J. Transp. Geogr. 2017;65:80–91. [Google Scholar]
- Cheung T.K.Y., Wong C.W.H., Zhang A. The evolution of aviation network: Global airport connectivity index 2006–2016. Transp. Res. Part E: Transp. Logist. Rev. 2020;133 [Google Scholar]
- Chong Z., Qin C., Chen Z. Estimating the economic benefits of high-speed rail in China: A new perspective from the connectivity improvement. J. Transp. Land Use. 2019;12(1):287–302. [Google Scholar]
- Diao M. Does growth follow the rail? The potential impact of high-speed rail on the economic geography of China. Transp. Res. Part A. 2018;113:279–290. [Google Scholar]
- Credit K. Transitive properties: A spatial econometric analysis of new business creation around transit. Spatial Econ. Anal. 2019;14(1):26–52. [Google Scholar]
- Fujita M., Thisse J.-F. Economics of Agglomeration. J. Jpn. Int. Econ. 1996;10(4):339–378. [Google Scholar]
- Freeman L. Centrality in social networks conceptual clarification. Soc. Netw. 1978;1(3):215–239. [Google Scholar]
- Givoni M., Banister D. Speed: the less important element of the High-Speed Train. J. Transp. Geogr. 2012;22:306–307. [Google Scholar]
- Givoni M., Dobruszkes F. A review of ex-post evidence for mode substitution and induced demand following the introduction of high-speed rail. Transp. Rev. 2013;33(6):720–742. [Google Scholar]
- Gottmann J. Megalopolis or the urbanization of the northeastern seaboard. Econ. Geogr. 1957;33(3):189–200. [Google Scholar]
- Gutierrez J. Location, economic potential and daily accessibility: An analysis of the accessibility impact of the high-speed line Madrid–Barcelona–French border. J. Transp. Geogr. 2001;9(4):229–242. [Google Scholar]
- Jia S., Zhou C., Qin C. No difference in effect of high-speed rail on regional economic growth based on match effect perspective? Transp. Res. Part A. 2017;106:144–157. [Google Scholar]
- Jiao J., Wang J., Jin F. Impacts of high-speed rail lines on the city network in China. J. Transp. Geogr. 2017;60:257–266. [Google Scholar]
- Jiao J., Wang J., Jin F., Dunford M. Impacts on accessibility of China’s present and future HSR network. J. Transp. Geogr. 2014;40:123–132. [Google Scholar]
- Kim K. High-speed rail developments and spatial restructuring: A case study of the Capital region in South Korea. Cities. 2000;17(4):251–262. [Google Scholar]
- Kim H., Sultana S. The impacts of high-speed rail extensions on accessibility and spatial equity changes in South Korea from 2004 to 2018. J. Transp. Geogr. 2015;45:48–61. [Google Scholar]
- Kurant M., Thiran P. Extraction and analysis of traffic and topologies of transportation networks. Phys. Rev. E. 2006;74(3) doi: 10.1103/PhysRevE.74.036114. [DOI] [PubMed] [Google Scholar]
- Li T., Rong L. A comprehensive method for the robustness assessment of high-speed rail network with operation data: A case in China. Transp. Res. Part A. 2020;132:666–681. [Google Scholar]
- Li T., Rong L., Yan K. Vulnerability analysis and critical area identification of public transport system: A case of high-speed rail and air transport coupling system in China. Transp. Res. Part A. 2019;127:55–70. [Google Scholar]
- Liu S., Wan Y., Ha H.-K., Yoshida Y., Zhang A. Impacts of high-speed rail network development on airport traffic and traffic distribution: Evidence from China and Japan. Transp. Res. Part A: Policy Pract. 2019;127:115–135. [Google Scholar]
- Loukaitou-Sideris A., Higgins H., Piven M., Wei W. Tracks to change or mixed signals? A review of the Anglo-Saxon literature on the economic and spatial impacts of high-speed rail. Transp. Rev. 2013;33(6):617–633. [Google Scholar]
- Lu S., Huang Y., Zhao Z., Yang X. Exploring the Hierarchical structure of China's railway network from 2008 to 2017. Sustanability. 2018;10:3173. [Google Scholar]
- Marchiori M., Latora V. Harmony in the small-world. Physica A. 2000;285(3–4):539–546. [Google Scholar]
- Mishra S., Welch T., Jha M. Performance indicators for public transit connectivity in multi-modal transportation networks. Transp. Res. Part A. 2012;46(7):1066–1085. [Google Scholar]
- Monzon A., Ortega E., Lopez E. Efficiency and spatial equity impacts of high-speed rail extensions in urban areas. Cities. 2013;30:18–30. [Google Scholar]
- Moyano A., Dobruszkes F. Mind the services! High-speed rail cities bypassed by high-speed trains. Case Stud. Transp. Policy. 2017;5(4):537–548. [Google Scholar]
- Newman M. Oxford University Press; Oxford, UK: 2010. Networks: An introduction. [Google Scholar]
- Opsahl T., Agneessens F., Skvoretz J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 2010;32(3):245–251. [Google Scholar]
- Preston J., Wall G. The ex-ante and ex-post economic and social impacts of the introduction of high-speed trains in South East England. Plan. Pract. Res. 2008;23(3):403–422. [Google Scholar]
- Qin Y. 'No county left behind?’ The distributional impact of high-speed rail upgrades in China. J. Econ. Geogr. 2017;17(3):489–520. [Google Scholar]
- Rodrigue J.-P. fifth ed. Routledge; New York: 2019. The Geography of Transport Systems. [Google Scholar]
- Sanchez-Mateos H.S.M., Givoni M. The accessibility impact of a new High-Speed Rail line in the UK – a preliminary analysis of winners and losers. J. Transp. Geogr. 2012;25:105–114. [Google Scholar]
- Sasaki K., Ohashi T., Ando A. High-speed rail transit impact on regional systems: does the Shinkansen contribute to dispersion? Ann. Reg. Sci. 1997;31:77–98. [Google Scholar]
- Takebayashi M. Multiple hub network and high-speed railway: connectivity, gateway, and airport leakage. Transp. Res. Part A. 2015;79:55–64. [Google Scholar]
- Theil H. North Holland; Amsterdam, The Netherlands: 1967. Economics and information theory. [Google Scholar]
- Urena J., Menerault P., Garmendia M. The high-speed rail challenge for big intermediate cities: A national, regional and local perspective. Cities. 2009;26(5):266–279. [Google Scholar]
- Vickerman R. Can high-speed rail have a transformative effect on the economy? Transp. Policy. 2018;62:31–37. [Google Scholar]
- Wang J., Mo H., Wang F., Jin F. Exploring the network structure and nodal centrality of China’s air transport network: A complex network approach. J. Transp. Geogr. 2011;19(4):712–721. [Google Scholar]
- Wang K., Xia W., Zhang A. Should China further expand its high-speed rail network? Consider the low-cost carrier factor. Transp. Res. Part A: Policy Pract. 2017;100:105–120. [Google Scholar]
- Wang L. High-speed rail services development and regional accessibility restructuring in megaregions: A case of the Yangtze River Delta, China. Transp. Policy. 2018;72:34–44. [Google Scholar]
- Wang L., Duan X. High-speed rail network development and winner and loser cities in megaregions: The case study of Yangtze River Delta, China. Cities. 2018;83(31):71–82. [Google Scholar]
- Wang L., Zhang W., Duan X. Understanding accessibility changes from the development of a high-speed rail network in the Yangtze River Delta, China: Speed increases and distance deductions. Appl. Spatial Anal. Policy. 2019;12:1011–1029. [Google Scholar]
- Wong W., Cheung T., Zhang A., Wang Y. Is spatial dispersal the dominant trend in air transport development? A global analysis for 2006–2015. J. Air Transp. Manage. 2019;74:1–12. [Google Scholar]
- Xu W., Zhou J., Qiu G. China's high-speed rail network construction and planning over time: a network analysis. J. Transp. Geogr. 2018;70:40–54. [Google Scholar]
- Xu W., Zhou J., Yang L., Li L. The implications of high-speed rail for Chinese cities: Connectivity and accessibility. Transp. Res. Part A. 2018;116:308–326. [Google Scholar]
- Yang H., Dijst M., Witte P., van Ginkel H., Wang J. Comparing passenger flow and time schedule data to analyse High-Speed Railways and urban networks in China. Urban Stud. 2019;56(6):1267–1287. [Google Scholar]
- Yang H., Dobruszkes F., Wang J., Dijst M., Witte P. Comparing China's urban systems in high-speed railway and airline networks. J. Transp. Geogr. 2018;68:233–244. [Google Scholar]
- Zhang A., Wan Y., Yang H. Impacts of high-speed rail on airlines, airports and regional economies: A survey of recent research. Transp. Policy. 2019;81:A1–A19. [Google Scholar]
- Zhang, W., Derudder, B., Wang, J., Witlox, F., 2016. Approximating actual flows in physical infrastructure networks: the case of the Yangtze River Delta high-speed railway network. In: Szymańska, D., Rogatka, K. (Eds.), Bulletin of Geography. Socio-economic Series, No. 31, Toruń: Nicolaus Copernicus University, pp. 145–160.
- Zhang Y., Zhang A., Zhu Z., Wang K. Connectivity at Chinese airports: The evolution and drivers. Transp. Res. Part A: Policy Pract. 2017;103:490–508. [Google Scholar]
- Zheng S., Kahn M.E. China’s bullet trains facilitate market integration and mitigate the cost of megacity growth. PNAS. 2013;110:E1248–E1253. doi: 10.1073/pnas.1209247110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu P., Yu T., Chen Z. High-speed rail and urban decentralization in China. Transp. Res. Rec. 2015;2475(1):16–26. [Google Scholar]
- Zhu Z., Zhang A., Zhang Y. Connectivity of intercity passenger transportation in China: A multi-modal and network approach. J. Transp. Geogr. 2018;71:263–276. [Google Scholar]
- Zhu Z., Zhang A., Zhang Y. Measuring multi-modal connections and connectivity radiations of transport infrastructure in China. Transportmetrica A: Transport Science. 2019;15:1762–1790. [Google Scholar]