Abstract.
Purpose: For many patients with intracranial tumors, accurate surgical resection is a mainstay of their treatment paradigm. During surgical resection, image guidance is used to aid in localization and resection. Intraoperative brain shift can invalidate these guidance systems. One cause of intraoperative brain shift is cavity collapse due to tumor resection, which will be referred to as “debulking.” We developed an imaging-driven finite element model of debulking to create a comprehensive simulation data set to reflect possible intraoperative changes. The objective was to create a method to account for brain shift due to debulking for applications in image-guided neurosurgery. We hypothesized that accounting for tumor debulking in a deformation atlas data framework would improve brain shift predictions, which would enhance image-based surgical guidance.
Approach: This was evaluated in a six-patient intracranial tumor resection intraoperative data set. The brain shift deformation atlas data framework consisted of simulated deformations to account for effects due to gravity-induced and hyperosmotic drug-induced brain shift, which reflects previous developments. An additional complement of deformations involving simulated tumor growth followed by debulking was created to capture observed intraoperative effects not previously included.
Results: In five of six patient cases evaluated, inclusion of debulking mechanics improved brain shift correction by capturing global mass effects resulting from the resected tumor.
Conclusions: These findings suggest imaging-driven brain shift models used to create a deformation simulation data framework of observed intraoperative events can be used to assist in more accurate image-guided surgical navigation in the brain.
Keywords: data science, computational modeling, biomechanics, finite element modeling, poroelastic, brain tumor
1. Introduction
Between 2011 and 2015, malignant brain and other central nervous system tumors were diagnosed in the United States with a 5-year survival rate of 35.0%.1 Initial treatment of accessible intracranial tumors is surgical resection. In a meta-analysis studying the extent of resection with patient survival in glioblastoma, the authors concluded that gross total resection of the tumor engendered the reduction of 1- and 2-year mortality.2 Others have found that of a glioma’s volume must be resected to provide maximal increased life expectancy.3,4 Accurate resection is also tied closely to tumor recurrence; 80% of recurrent glioblastomas recur within 2 cm of the original resection. 5 In low-grade gliomas, the extent of resection is also a predictor of improved overall patient survival.6 Therefore, optimal resection of intracranial tumors, regardless of etiology, requires accurate intraoperative localization of diseased brain tissue.
Image-guided neurosurgical systems (IGNS) are used during neurosurgery to aid in tumor localization and maximal resection while minimally disturbing the surrounding healthy tissue.7–9 Neuronavigation involves registering preoperative imaging into intraoperative physical space to provide neurosurgeons guidance.9 IGNS are effectively a data-driven technology with preoperative imaging providing the geography of resection. Unfortunately, IGNS are not always accurate. IGNS treat the patient’s preoperative imaging data as static and nonevolving with the events of surgery, which is not necessarily reflective of intraoperative changes to the neuroanatomy due to sources of error associated with brain shift.7–9
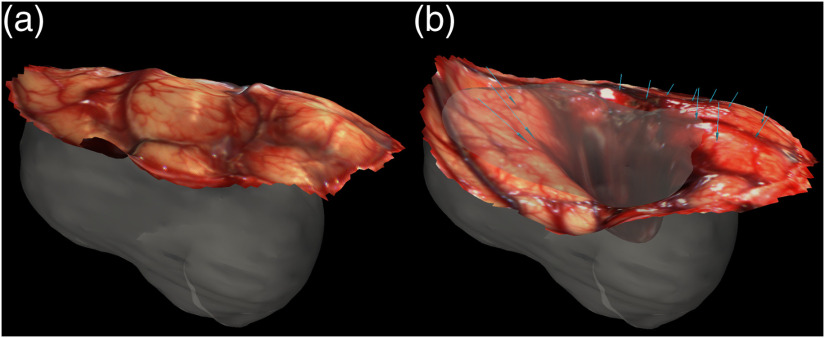
Intraoperative brain shift can cause IGNS to inaccurately localize the patient’s tumor by violating the assumed static relationship between the preoperative image and physical space.8,10 When one considers that brain shifts up to 24 mm have been measured during tumor resection,11 the potential impact to the accuracy of IGNS is alarming. There are numerous causes of brain shift, including gravity, hyperosmotic drugs, loss of cerebrospinal fluid (CSF), removal of the tumor, edema presence, and extent of craniotomy.7,8,12,13 Multiple methods to compensate for brain shift intraoperatively have been researched including intraoperative magnetic resonance imaging (iMR), a finite element model (FEM) coupled with intraoperative measurements such as laser range scanners (LRS) or stereo vision cameras, and intraoperative ultrasound (iUS).3,7,8,14 These intraoperative measurement techniques, however, are not available in all hospital facilities. This study focuses on brain shift correction using an imaging-driven FEM of brain biomechanics to create a comprehensive deformation simulation data set to reflect possible intraoperative changes, and in particular, the effects of intraoperative cavity collapse due to tumor resection.11,15 More specifically, extensive work has been done for modeling brain shift due to hyperosmotic drugs, swelling, gravity, retraction, and resection.16–19 However, to the best of our knowledge, no groups have developed an FEM of tumor cavity collapse during resection, despite measured and observational evidence supporting its prominent impact on brain shift. The cavity collapse effect can be seen in Fig. 1 using LRS measurements. In Fig. 1, the opaque region is the meshed patient tumor. The LRS surface immediately after the dura was opened is shown in (a), and the LRS surface taken postresection is shown in (b). The blue arrows are the displacement vectors measured using corresponding features in the LRS scans, and they demonstrate tumor cavity collapse. In addition, several studies in intraoperative brain shift recovery work have noted measured displacements with cortical surface motion deforming in a direction toward the center of the tumor cavity, i.e., cavity collapse. It has been noted in these studies with brain shift recovery methods that current approaches are considerably limited in accommodating this confounding factor.12,20,21
Fig. 1.
An illustration of cavity collapse during tumor resection for patient 1. The opaque shape in (a) and (b) is a visualization of the segmented tumor. (a) The postcraniotomy, cranial surface can be visualized with the laser range scan obtained intraoperatively. The cranial surface was scanned again after the tumor was resected, and this laser range scan is shown in (b). The tissue movement was quantified using these scans, and the measured displacement vectors (pre- to intraoperative) are indicated by the blue arrows in (b).
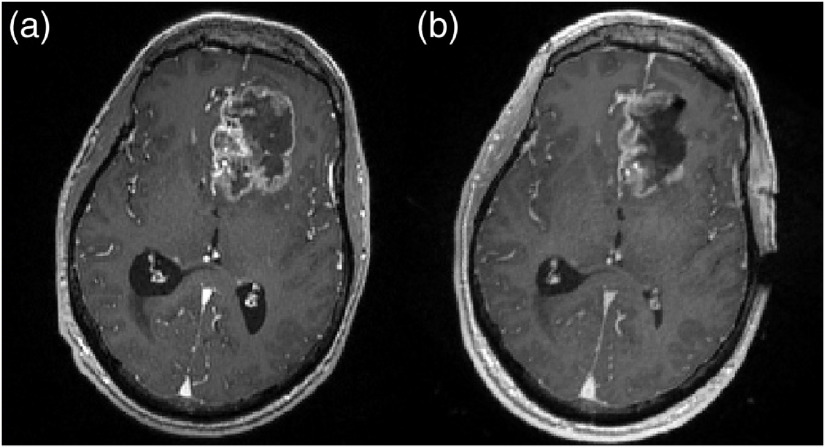
Tumor cavity collapse has been observed and quantified by multiple groups.22,23 For example, intraoperative cavity collapsing was observed using iMR to quantify surface and subsurface brain shift that involved the resection cavity.24 In another study, patients’ preoperative MRIs were compared with their postoperative MRI counterparts; the mean preoperative tumor volume was while the mean postoperative cavity volume was .25 Another group compared preoperative and postoperative MRIs of 68 lesions and noted a decrease in postoperative cavity size related to the original tumor volume.26 An example of intraoperative magnetic resonance (MR) used in documenting cavity collapse is shown in Fig. 2. Here, the preoperative patient MR and iMR were registered to one another, and Figs. 2(a) and 2(b) are corresponding slices. The boundary of the tumor can be visualized in Fig. 2(a), and it qualitatively decreases in size during tumor resection, illustrating collapse, as shown in Fig. 2(b).
Fig. 2.
An exemplar illustration of cavity collapse during tumor resection. The two -weighted MRI scans were taken (a) preoperatively and (b) intraoperatively. (a), (b) An image of the same slice of the scan after the complete MRI volumes were registered. (a) The total tumor can be visualized. (b) The collapse in the tumor’s original cavity can be perceived in this intraoperative, postresection MRI.
Overall, extensive evidence supporting improved patient survival with improved extent of tumor resection 27 highlights the clinical need for accurate resection, which could be improved by advanced models of brain shift. Compensating for brain shift would improve the fidelity of IGNS and effectively improve patient outcomes. In the description above, a new deformation event, namely cavity collapse due to resection or “debulking,” is a remaining challenge that can compromise image-guided surgical navigation systems. One of the principle challenges is that it is extremely difficult to estimate the mechanics environment from a grown tumor within a preoperative image volume. Questions regarding the effects of edema, stored elastic mechanical energy from the tumor mass and necrosis, extent of encapsulation, influence of nearby structures and surgical planes, and mechanical discrepancies between contrast enhancing features versus true infiltrative tumor boundaries persist and are difficult to determine from preoperative imaging data alone. It should also be noted that for the purpose of this study, the term debulking will be used to reflect the process of brain shift associated with tumor cavity collapse due to the resection of diseased tissue. In this investigation, a deformation data framework is described that involves using numerous FEM biophysical simulations to estimate the impact of tumor growth mass and their subsequent cavity collapse mechanics when resected. We hypothesize that accounting for tumor debulking in a deformation atlas data framework will improve computational methods to compensate for errors in navigation due to brain shift.
2. Materials and Methods
2.1. Retrospective Patient Selection
There were a total of 18 possible tumor resection cases in 18 distinct patients with intraoperative data considered in this study. All tumors were manually segmented, and measured intraoperative displacement vectors were registered into the same space. The methods of data collection are discussed in Sec. 2.2. Expanding upon prior work,11,12 metrics are proposed to determine if tumor cavity collapse was present within the measured shift data. More specifically, as noted above, the mechanics environment is complex, and significant debulking does not always occur. For the purposes of this study, we attempted to identify those cases with significant cavity collapse. In addition, to reduce bias incurred by choice of selection criteria, four separate metrics, which are four different debulking assessment metrics, were investigated. These four metrics were tested to prevent bias toward a specific intraoperative measurement type or the selection of a metric that only works on the 18 cases evaluated here.
For all cases at every intraoperative data measurement, the debulk vector was calculated. The debulk vector is the unit vector between the start of the displacement measurement and the tumor centroid. The centroid was calculated by taking the average of the three-dimensional (3D) coordinates prescribing the outer contour of the segmented tumor per patient. The debulk vector estimates the vector of pure tumor-centroid-cavity collapse. [Eq. (1)] quantifies the amount of cavity collapse by taking the mean of the normalized dot product of the measured displacement vector for each measurement () and the debulk vector at each measurement (). [Eq. (2)] quantifies the amount of debulking by taking the mean of the dot product of the measured displacement vector for each measurement () and the debulk vector at each measurement (). Methods one and two both weight all measured points equally.
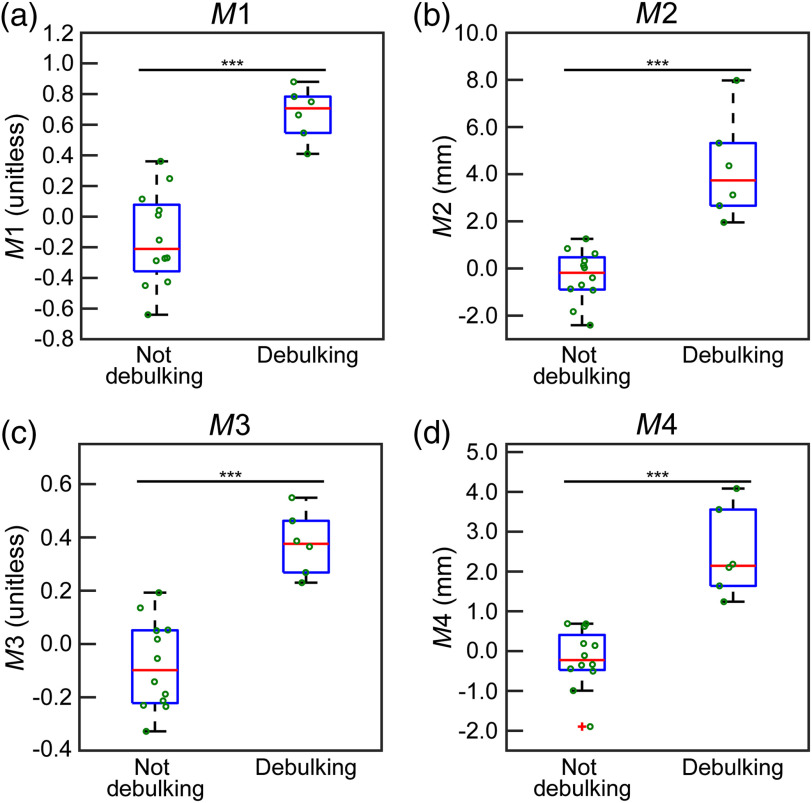
[Eq. (3)] and [Eq. (4)] weight debulking motion closer to the tumor larger than measurements taken further away. Therefore, we generated a weighting scheme from 0.1 (to prevent measurement exclusion) to 1, where 0.1 was assigned to the largest distance to the centroid, and 1 was assigned to the smallest distance to the centroid for a given patient. The weights of the remaining measurements points were calculated by normalizing the weights from 0.1 to 1 based on a given patient. Using this weighting schema, each measurement () had an associated weight based on its proximity to the tumor. [Eq. (3)] and [Eq. (4)] are the weighted versions of and , respectively. For each quantification type, the values for all candidate patients were plotted (Fig. 5), and a threshold was qualitatively selected based on the observed grouping; the threshold was used to determine if the measured displacements per patient were classified as debulking or not. This selection was based on the distribution of the values obtained within the sample population. In Eqs. (1)–(4), represents measured displacements, represents weight, and represents debulk vector
| (1) |
| (2) |
| (3) |
| (4) |
Fig. 5.
The box plots representing sorting the patients into debulking or not using the four different classification equations described in Sec. 2.1. In all panels, the axis is the value obtained using Eqs. (1)–(4). The box on the left side of each panel is the distribution of values below or equal to the threshold of the method (not debulking), and the right side is the distribution of values above the threshold (debulking). In all plots, the central red line designates the median, and the bottom and top of the boxes are the 25th and 75th percentiles, respectively. The green circles visualize all patient data. (a), (b), (c), and (d) The results of , , , and , respectively. (*** indicates ).
2.2. Patient Data Collection
Using the quantification methods described above, six patients were selected. This is elaborated on in Sec. 3.1. For the remainder of this study, the cases are referred to as patients 1 to 6. Multiple modalities were employed for intraoperative data collection for these patients and included the use of LRS data (patients 1 to 3) of the cortical surface deformation, available iMR data (patient 4), and available tracked iUS data (patients 5 and 6). Preoperatively, the surgeons provided an estimate of the patient’s head orientation during surgery and the approximate size and location of the craniotomy they would perform intraoperatively.
For patients 1 to 3, intraoperative data were acquired using LRS. The patients were enrolled in a study at Vanderbilt University Medical Center and gave consent in accordance with the Vanderbilt Institutional Review Board.22 The preoperative MRI scans were collected as a part of standard clinical care.22 Tracking of measurement instruments was accomplished intraoperatively using an optical tracking system (Polaris Spectra, Northern Digital Inc., Waterloo, Ontario).22 Intraoperatively, an optical tracking rigid body (Medtronic, Minneapolis, Minnesota), attached to the patient was used to obtain all of the collected data in the same coordinate frame.22 An optically tracked LRS (Pathfinder Therapeutic Inc., Nashville, Tennessee) was used to obtain scans of the region of interest at two intraoperative time points: (i) after the initial opening of the dura [ Fig. 1(a)] and (ii) after resection of the tumor [ Fig. 1(b)].22 The measured brain shift was calculated by tracking homologous points in the pre- and postresection LRS collected data.
Patient 4 had their preoperative MR data collected using an Ax MPRAGE sequence.20 Patient 4 consented for imaging in accordance with the Brigham and Women’s Hospital Institutional Review Board.20 The iMR scanner was a 3T, wide bore MRI scanner (Siemens Magnetom Verio, Erlangen, Germany).20 The preoperative MR and iMR scans were rigidly registered to one another. Using Analyze 9.0 (AnalyzeDirect, Overland Park, Kansas) and a 3D-Slicer,28 homologous surface and subsurface points were collected in both scans to quantify the brain shift.20
Patients 5 and 6 had intraoperative data acquired using 3D iUS. The data were collected under the Institutional Review Board protocol at Brigham and Women’s Hospital’s Advanced Multimodality Imaged Guided Operating (AMIGO) suite.29 Preoperatively, patient MRs were obtained in accordance with standard clinical care. Intraoperatively, iUS was collected using a 2D BK5000 cranial probe through the patients’ craniotomy.30 To construct the 3D iUS, the collected sequences of 2D ultrasound images were registered and combined as described in our prior work.29 The 3D iUS data used in this investigation were collected at two time points: (i) after the dura was opened and (ii) after a maximal portion of the tumor had been resected.29 Features were manually matched in pairs of iUS images and using a matched feature extraction method detailed in our prior work.31 The brain shift was quantified using both the automatic and manual iUS data and pre- and postresection automatic and manual iUS data.
2.3. Segmentation and FEM Mesh Construction
All six patients were analyzed in the same manner. The brains and tumors were expertly segmented from the preoperative -weighted MRI scans using ITK-Snap.32 The segmentations for the patients were registered to an atlas image set using the adaptive bases algorithm and the normalized mutual information algorithm.33,34 A marching cubes algorithm was then used, followed by a custom mesh generator to create a 3D tetrahedral mesh.35 The average number of nodes in the six patient meshes was 26,764, and the average number of elements was 134,393. This generated six patient-specific finite element meshes describing the six patients and their tumors.
2.4. Brain Shift Atlas without Debulking
Atlases describing sources of brain shift other than cavity collapse have been developed.16,17 In this work, we assume measured brain shift consists of debulking plus these previously studied factors. We tested our mechanism retrospectively using a framework called model-updated image-guided neurosurgery (MUIGNS).36 MUIGNS uses sparse measurements of intraoperative brain shift in an inverse problem framework using patient-specific FEM solutions. These FEM solutions are calculated preoperatively and represent the possible intraoperative brain deformations.22 The solution of the inverse problem is then used to deform the preoperative scans to correct for intraoperative brain shift.
In order to assess the influence of our proposed atlas, we first performed brain shift corrections with a baseline brain shift FEM deformation atlas data framework that has been extensively studied and that did not include debulking.16,20 This atlas accounts for gravity-induced and hyperosmotic drug-induced brain shift. Controlling variables were perturbed for both categories of induced brain shift to generate a distribution of possible motion due to each category. For gravity-induced brain shift, these variables included CSF drainage levels, the presence of the tumor, and possible head orientations. For hyperosmotic drug-induced brain shift, these variables include permeability conditions, the presence of the tumor, and possible head orientations.20 A poroelastic biomechanical FEM description of brain tissue is used that was based on Biot’s theory of consolidation.37 A detailed description of this biomechanical model can be found in prior work.15,16,38 A total of 378 possible deformations due to gravity and 378 possible deformations due to hyperosmotic drugs of the brain comprise the 756 total possible deformation solutions in the deformation atlas without cavity collapse.12,20 Next, we created an additional deformation atlas data that included debulking FEM solutions (simulated tumor growth and resection) in the same patients.
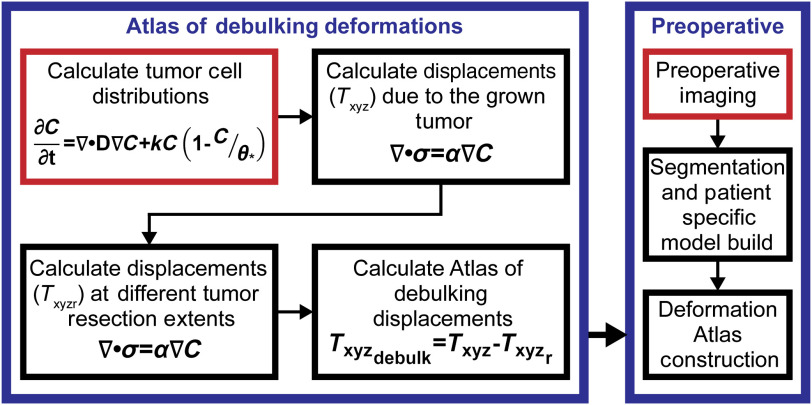
2.5. Physics of Debulking
In this investigation, we created an atlas of debulking and hypothesized that our description could capture intraoperative cavity collapse elements of brain shift not included in previous atlases. The flowchart of the proposed physics of the debulking process is illustrated in Fig. 3. For all six patients ultimately included in this study, a unique, patient-specific finite element mesh reflecting their brain and tumor geometry was constructed. These six meshes were then used for all finite element calculations and reconstructions. Given that only the final endpoint of tumor growth is known from imaging data, a simulation process to capture possible growth mechanics trajectories is needed. This is accomplished by varying the seeding of tumor within the simulation environment. The proposed seeding of tumors employed herein can be visualized in Fig. 4. The cellular distribution was computed using a custom FEM as
| (5) |
In Eq. (5), is the tumor cell concentration, is the time, () is the tumor cell proliferation rate, () is the tumor cell diffusion rate, and () is the cellular carrying capacity.39 The Galerkin method of weighted residuals was used to spatially integrate Eq. (5) in the 3D domain of tetrahedral elements,40 and temporal evolution was performed using a forward Euler explicit formulation.
Fig. 3.
The flowchart illustrates the general debulking brain shift prediction methods. The right block in blue illustrates where the atlas of debulking deformations is introduced into the brain shift correction method. The left block in blue is the flowchart of the physics of debulking as described in this study. In the two halves of the flowchart, the red indicates the start of the processes.
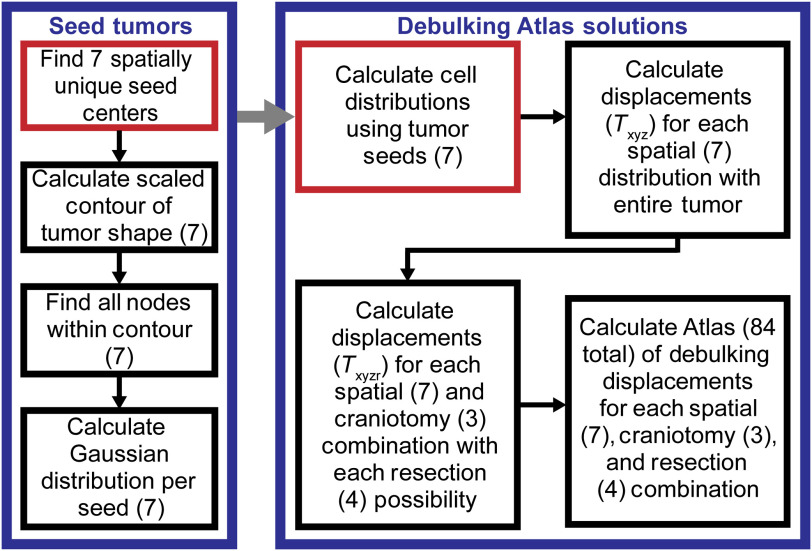
Fig. 4.
The flowchart illustrates the generation of the debulking atlas solutions. The right block in blue reflects the range of possible deformations captured by the atlas. The left block in blue shows how the seven possible tumors were seeded. The red indicates the start of the processes, and the gray arrow shows how the seed tumor block fits into the debulking atlas solutions block. Each number () represents the number of variations for a given step.
Building upon a poroelastic model of brain tissue and a biomechanically coupled model of tumor growth, Eq. (6) was used to account for the tumor’s (Fig. 3) mechanical effects.41,42 An isotropic Hookean linear elastic constitutive model was assumed. The constant coefficient () is an empirically derived constant, which dictates the amount of influence of the tumor cells.38 Poisson’s ratio is set to 0.45 and the Young’s modulus is 2100 Pa based on previous work.38 The Galerkin method of weighted residuals was used to spatially integrate Eq. (6),40 and a custom FEM model was generated to solve the equation. The displacements of the brain when the fully grown tumor was present were calculated with Eq. (6). Then, the displacements of the brain after the tumor was resected at variable extents were calculated (Fig. 3). The resection of the tumor was accomplished by removing the model equation contributions associated with the resected tissue elements from the finite element matrix system19
| (6) |
The atlas of debulking solutions is calculated with Eq. (7) (Fig. 3). In Eq. (7), is the brain shift displacement associated with debulking. is the displacement when the entire tumor is present (preoperative state). is the displacement when the tumor has been resected at different extents (intraoperative and postoperative states)
| (7) |
This description of physics was used to generate the deformation atlas data of debulking solutions. The solutions were then incorporated into the entire deformation atlas data framework, i.e., gravity-, mannitol-, and debulking-induced simulated brain shifts.
2.6. Brain Shift Atlas with Debulking
The debulking atlas component comprises a total of 84 deformation solutions. Since there was no imaging beyond -weighted MRI available for these patients, it was necessary to capture a variety of cellular distributions and possible tumors. In order to do this, it was necessary to define possible tumors. The first step in the generation of this atlas is seeding seven distinct tumors, since no serial imaging was available (Fig. 4). Using the segmentation of patient’s tumor from their preoperative MRI, the centroid of the original tumor was calculated. The distance from the centroid to the boundaries of the tumor was calculated, and the average of these lengths (average axis length) was calculated. Seven distinct spatial locations were identified, which serve as the centers of the seven tumors. The first center is the centroid of the tumor. The other six centers are based on a Cartesian axis, with the centroid serving as the origin. The other six centers are placed at of the average axis length on the , , and axes. For each center, a scaled contour of the original tumor was defined (Fig. 4). This was done by finding the chord between the center and original tumor boundary and defining the contour point at 50% of the total chord length. For the seven spatial locations, all the mesh nodes within the scaled contour are found (Fig. 4). Finally, for all seven groups of nodes, a Gaussian cellular distribution was assumed and calculated (Fig. 4). It was specified that the tumor cell density decreases outwardly from the designated center with a minimum tumor cell density of at the maximal long dimension.43 These seven tumor seeds served as an initial condition fed into Eq. (5) in order to calculate tumor cell distributions reflecting the tumor’s condition before resection.
In our patient data, the length of time the tumor grew was unknown. For each of the seven tumor seeds, seven unknown time finals were calculated. While Eq. (5) was being solved, every five time steps the distance between the closest-point from the isocontour of the growing tumor to the segmented tumor contour was compared and stored. The seven time finals were the times when the closest point distance is minimized for each possible cellular distribution. A total of seven tumor cell distributions were grown using the calculated time finals (Fig. 4). With respect to boundary conditions for these models, the boundary condition was no flux across the dural septa and skull.
For each of the seven tumors, the displacements possible with the entire tumor present were calculated [Eq. (6)]. Following this, the displacements of the brain due to possible resections were calculated [Eq. (6)]. With respect to the above tumor growth variants, each was considered with respect to three different craniotomy sizes, where one size corresponds with the surgeon’s preoperative plan and the other two are smaller and larger than the planned size to accommodate variability in intraoperative execution, which does not necessarily match the exact preoperative plan. Of note, nodes associated with the craniotomies were considered stress free while the remainder of the skull nodes was fixed in displacement. In addition to the above variants, four possible resection extents were allowed when estimating the atlas of debulking. This was performed by allowing for elements within four possible isocontours [ max (cell count in solution), max (cell count in solution), max (cell count in solution), and max (cell count in solution)] of the grown tumors being treated as resected tissue. Finally, the preoperative and postoperative displacements were subtracted from one another generating the debulking atlas solutions. In summary, a total of 84 solutions account for seven spatial locations and cellular distributions, three possible craniotomies, and four possible resection extents.
2.7. Brain Shift Reconstruction and Quantification
The displacements describing the movement between the preoperative and intraoperative features were used to drive the inverse problem for brain shift reconstruction. The reconstruction was performed for each patient using each of the two atlases (one without and one with debulking). The optimization problem is a constrained minimization of a least-squared error between the model predicted displacements and the measured experimental displacements.12,43 The objective function is Eq. (8). This equation’s variables are defined as
| (8) |
In Eq. (8), are the non-negative regression coefficients being solved, which is the size of the number of atlas solutions (). The inverse problem is constrained such that the coefficients must be non-negative and their sum is less than or equal to one. is an matrix containing the deformation atlas data where is the number of measured displacements and is the number of atlas solutions.20 In Eq. (8), are the sparse measured displacements collected (). Once the weighting coefficients are solved for, they are used to combine the deformations of the atlas to reconstruct the displacements of the full patient brain. This brain shift reconstruction procedure was applied to all the experiments performed.
The percent brain shift correction was calculated using Eq. (9), where and are the model estimated and experimentally measured displacements, respectively.38 For statistical testing, Eq. (10) was calculated on the measured displacements for each patient to assess the changes in correction using the debulking atlases.38 Since we could not assume normality of the values obtained from Eq. (10), we used a nonparametric test. In addition, since the samples were not guaranteed to be independent, we used a two-sided Wilcoxon signed rank test to test statistical significance. It is important to note how the percent correction and statistical significance for the patient analysis was performed. The data used to drive the inverse problem and the data for validation were the same. This was due to the limited intraoperative data available.
| (9) |
| (10) |
3. Results
3.1. Retrospective Patient Selection
All four quantification methods of debulking were applied to the 18 patients. The results are summarized in Fig. 5. Cases larger than the selected threshold were debulking cases. Qualitatively, Fig. 5 reflects that to resulted in the classification of patient cases. The values in the two groups generated (debulking and not debulking) were compared to one another using a two-sided Wilcoxon rank sum test. All four of the tests indicated that the groups created were different from one another (, two-sided Wilcoxon rank sum). Furthermore, the same six patients were identified as debulking cases using all four classifications. The six identified patients were used in this investigation to test our proposed physics.
3.2. Brain Shift Atlas with Debulking
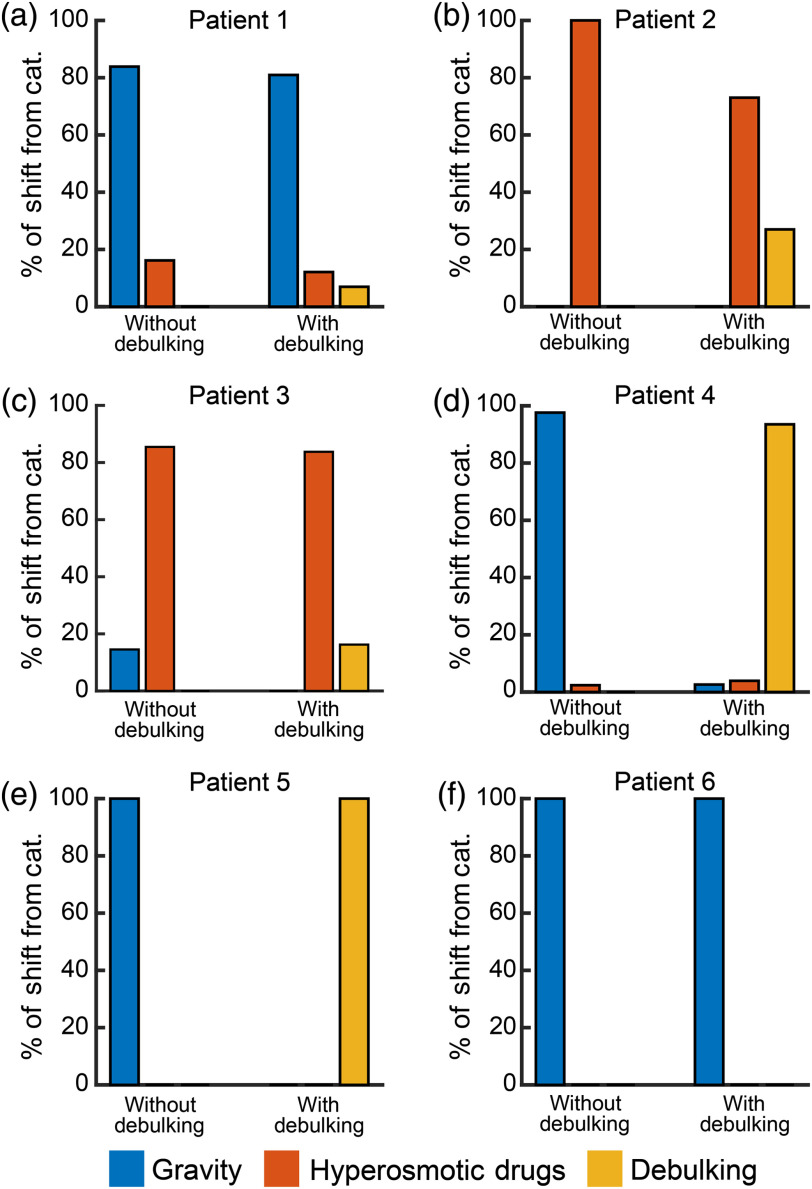
The results of including the debulking atlas solutions are in Figs. 6 and 7 and Table 1. Figure 6 visualizes the types of brain shift solutions used in order to reconstruct the six patients’ measurements using the atlases without and with debulking. The types of brain shifts included resulted from gravity, hyperosmotic drugs, and tumor cavity collapse. Qualitatively, from Fig. 6, we can see that cavity collapse solutions were used in five of the six patients. In these patients, the inclusion of the new atlas changed the distribution of the other two categories relative to the reconstructions without them. The percent of debulking solutions used in patients 1 to 6 were 6.95%, 26.99%, 16.25%, 93.50%, 100.00%, and 0.00%, respectively. Comparing when the cavity collapse atlas was utilized in the shift reconstruction (patients 1 to 5) versus when the correction was performed without including it, the average error magnitude tended to decrease, the standard deviation error magnitude always decreased, the maximum error magnitude always decreased, and the percent shift correction always increased (Table 1).
Fig. 6.
The percent of the brain shift categories used to reconstruct the patients’ measured displacements based on atlas type. The three general shift categories (cat.) are gravity, hyperosmotic, and debulking. In all six panels, without debulking refers to the atlas without debulking solutions present. With debulking refers to the atlas with the debulking solutions present. The percent of solutions from the three categories in every reconstruction adds up to 100%. (a)–(f) The distributions of patients 1 to 6, respectively.
Fig. 7.
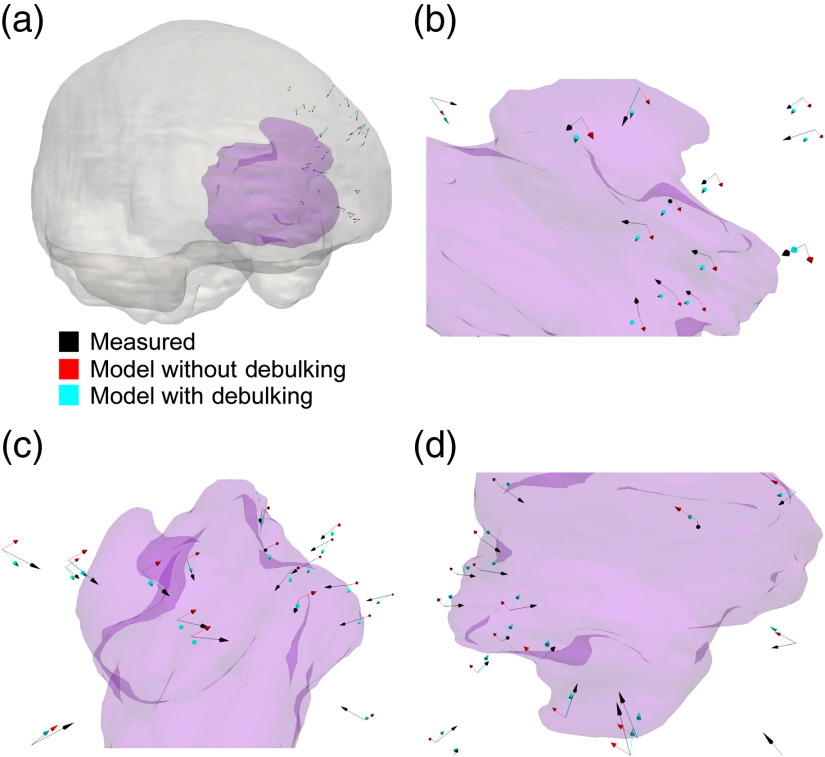
The results of patient 4. The opaque purple structure in all panels is the tumor in patient 4. (a) The tumor relative to the brain (opaque grey) can be visualized. (b)–(d) Portions of the tumor and the arrows at various angles and magnifications. In all of the panels, the black arrows are the measured deformations, the red arrows are the estimated deformations when no debulking was included in the atlas, and the cyan arrows are the estimated deformations when the debulking solutions were included in the atlas of solutions for the reconstruction. The size of the arrows is proportional to the magnitude of the deformation.
Table 1.
A summary of the shift correction of the measured points in all six patients in the types of atlas corrections performed. Magnitude is abbreviated with mag.
| Type of atlas correction | Average error mag. (mm) | Standard deviation error mag. (mm) | Maximum error mag. (mm) | Percent shift correction (%) |
|---|---|---|---|---|
| Patient 1 | ||||
| No correction | 4.82 | 4.52 | 14.10 | N/A |
| Correction without debulking | 3.07 | 2.58 | 8.91 | 21.40 |
| Correction with debulking | 2.87 | 2.38 | 8.44 | 24.00 |
| Patient 2 | ||||
| No correction | 19.94 | 4.69 | 28.52 | N/A |
| Correction without debulking | 0.74 | 0.54 | 1.82 | 88.79 |
| Correction with debulking | 0.44 | 0.41 | 1.30 | 89.48 |
| Patient 3 | ||||
| No correction | 7.70 | 4.85 | 22.81 | N/A |
| Correction without debulking | 1.07 | 1.13 | 4.76 | 61.72 |
| Correction with debulking | 1.29 | 0.96 | 3.87 | 63.52 |
| Patient 4 | ||||
| No correction | 3.73 | 1.25 | 6.77 | N/A |
| Correction without debulking | 1.75 | 1.11 | 3.72 | −2.67 |
| Correction with debulking | 1.20 | 0.90 | 3.66 | 37.43 |
| Patient 5 | ||||
| No correction | 8.47 | 3.89 | 15.71 | N/A |
| Correction without debulking | 7.38 | 3.66 | 14.33 | 0.18 |
| Correction with debulking | 5.58 | 3.22 | 14.01 | 21.49 |
| Patient 6 | ||||
| No correction | 3.03 | 1.02 | 5.12 | N/A |
| Correction without debulking | 2.30 | 1.09 | 4.28 | 9.53 |
| Correction with debulking | 2.30 | 1.09 | 4.28 | 9.53 |
A paired, two-sided Wilcoxon signed rank test revealed statistically significant differences between the corrections per measured displacement [Eq. (10)] in the reconstructions without and with debulking in patient 4 (, two-sided Wilcoxon signed rank test) and patient 5 (, two-sided Wilcoxon signed rank test). There were also statistically significant differences between the angles between the measured shift and the reconstructed shift (without and with debulking atlas) per corrections. These differences in angles were found in patient 2 (, two-sided Wilcoxon signed rank test), patient 3 (, two-sided Wilcoxon signed rank test), and patient 4 (, two-sided Wilcoxon signed rank test). These differences in reconstruction can also be visualized in Fig. 7, which illustrates the results of patient 4.
4. Discussion
We present a mathematical representation of intraoperative tumor cavity collapse, that we propose captures physics of brain shift not accounted for in previous models. By utilizing the calculated cellular distribution, we generated atlases that capture brain shift due to this mechanism. We were able to improve the percent brain shift correction in multiple cases by approximating these mechanics. Our methodology changed the distribution of brain shift types included as well as improved the quality of results relative to when the solutions were not a part of the reconstruction.
The debulking atlas solutions captured a new movement type, reflecting tumor cavity collapse. Figure 7 shows the differences in the measured shift vectors, the vectors from the reconstructions without and with debulking. The strength of the cavity collapse atlas is its ability to capture global mass effect as well as calculate possible cellular distributions using established mechanisms of cellular growth. By seeding the possible tumors in a contour-based method, accurately fitting the geometry of asymmetric tumors was possible. A potential improvement of this technique for future work would be the use of a more sophisticated model of tumor growth, the incorporation of tissue heterogeneity, and mechanical coupling.43–45
The debulking atlas was unable to achieve shift correction improvements in patient 6, despite all proposed metrics indicating cavity collapse in patient 6 (Figs. 5 and 6). When comparing tumor volumes, it became evident that patient 6 had a substantially smaller tumor relative to the other patients. Another study into resection cavity dynamics noted that the preresection tumor volume was a predictor of postoperative cavity volume change.26 While we cannot conclusively state it, we believe the tumor’s small volume caused the discrepancy in correction.
Two of the simplifications made in this work are areas of improvement for future work. The first is the exclusion of the influence of edema on tumor cavity collapse. This was made due to a lack of access to -weighted MRI scans. Segmenting the edema from this scan type would provide patient-specific edema distributions. It could easily be incorporated into the proposed framework by solving for pressure distributions with
| (11) |
where is the pressure, () is the hydraulic conductivity, () is the capillary permeability, and (3633 Pa) is the intracapillary pressure.16 This could then be incorporated into the brain displacement calculations [Eq. (6)] by introducing a gradient pressure term. Second, we only used the preoperative scan taken immediately prior to surgical resection, meaning we had no knowledge of how long the tumor grew or its final cellular density distribution. This would influence how diffuse the tumor was and its associated gradients. In future studies, incorporation of serial imaging and biopsy specimen pathology may lead to more accurate calculated tumor cell distributions and higher fidelity brain shift corrections.
Other limitations of this investigation are the number of patients studied, the variability of intraoperative modalities, and the variability in tumors. Therefore, while the results of this study are encouraging, further investigation is necessary to determine the fidelity of the proposed physics and the corresponding atlases. Despite these challenges, we were able to identify and correct for the tumor cavity collapse mechanism with patient data collected at multiple sites with multiple modalities (LRS, iMR, and iUS). This suggests not only the significant impact of accounting for cavity collapse when correcting for brain shift, but also indicates the robustness of our method.
Overall, based on the results of this investigation, the proposed atlas captured global mass effects from the tumor and its influence. It provided statistically significantly different results in shift correction and angle relative to the baseline atlas. Accurate resection of tumors is critical for patient survival.3,4 Knowledge of how the tumor cavity is evolving intraoperatively has the potential to improve the fidelity of tumor resections and inform tumor margin planning. While we have focused on applications in IGNS, there are a variety of other possible applications for our model of debulking. One of these applications is the prediction of the boundaries of the tumor cavity postoperatively to aid in planning stereotactic radiosurgery treatments.26 Knowledge of how the cavity moves could help with patient treatment planning. Despite the noted limitations of this investigation, our multimodal study of tumor cavity collapse during resection demonstrates an ability to improve brain shift correction relative to a model-based atlas that does not account for it.
5. Impact on Interventional and Surgical Data Science
It is important to prescribe a working definition of this emerging field. Interventional and surgical data science is a field of investigation that curates data (real or simulated) associated with planning, control, delivery, and/or the distribution of procedural medical therapy for the purposes of codifying best surgical practices, assessing surgical performance, optimizing procedural therapy outcomes, and/or realizing innovative procedural therapies and predicting efficacy. While quite broad, it is distinctive in that the source of data is within the procedural environment, and the goals of the field are to utilize that data to affect concerns in procedural outcome.
The investigation presented here represents just one form of this emerging area of research. More specifically, sophisticated biophysical simulations driven by imaging data are utilized to create a distribution of biomechanical effects that cannot be curated from physical data easily; in this case, the underlying biomechanically coupled reactive-diffuse environment associated with tumor growth could not be found with imaging alone. Once created, the entire distribution of brain shift simulated data was fit to a real intraoperative environment by optimally matching sparse observed measurements of real brain deformations. The procedural outcome that is facilitated is enhanced navigational assistance in the image-guided removal of the tumor. In this context, the simulated data environment provided a biophysically constrained scaffold, which, when combined with sparse measurements of deformation within the operating room, could provide a tool for enhanced localization for improved resection of disease.
We would suggest that this represents a fairly innovative viewpoint of the use of simulation within the field of interventional and surgical data science. The more conventional framework would involve the availability of large-scale data sets, and the curation of those data sets such that effective training algorithms can generate desirable clinical solutions to a pressing procedural problem (i.e., a real-data trained approach to unique conditions). This is also an important objective within the field. However, in the case where driving data are quite sparse, we suggest good biophysical simulation as a source of data to weight and constrain solutions to pressing procedural questions. This is what this study offers. Finally, an underlying aspect to this work is its reliance on an optimization framework rather than artificial intelligence methods. Machine learning methods could decidedly be used to create networks that represent physical simulations, and these would offer advantages of speed with only small sacrifices in error. Recent literature has reflected such efforts.46–49 While these are important steps for simplifying implementation, the more important underlying precept is that interventional/surgical environments can be incredibly challenging for data acquisition. In these instances, the roles of high-fidelity simulation could have profound impact in shaping the implementation of data science in the areas of intervention and surgery.
6. Conclusions
The purpose of this investigation was to develop a method of predicting intraoperative brain shifts due to tumor cavity collapse to improve tumor resection therapy. Imaging-driven models that simulated tumor growth and debulking due to resection were employed to generate a deformation atlas data framework that could be employed to recover a new mechanism of deformation that is extraordinarily difficult to measure. Using sparsely measured deformation data from a series of intracranial resection cases, the approach demonstrated additional compensation capabilities. While we cannot conclusively say that our method is ready for clinical implementation without further investigation, the results of this study are encouraging. Furthermore, albeit still preliminary in nature, the work presented could improve patient outcomes through applications in actively updating IGNS navigation as well as treatment planning in other neurointerventional procedures (e.g., stereotactic radiosurgery).
Acknowledgments
This work was supported by the NIH—National Institute of Neurological Disorders and Stroke R01NS049251. It was also supported by the National Center for Image Guided Therapy Grant No. P41-EB015898-09 and the National Cancer Institute Grant No. K25CA204599. NIH Grant No. R01EB027134-01 also partially funded this work.
Biographies
Saramati Narasimhan is currently a postdoctoral research fellow in the Department of Neurosurgery at Vanderbilt University Medical Center. She received her BS degree in biomedical engineering from the University of Miami in December 2013 and her PhD in biomedical engineering from Vanderbilt University in June 2019. Her research interests include translational work in surgery and diagnostics, computational modeling, and functional modeling.
Biographies of the other authors are not available.
Disclosures
The authors of this paper have no conflicts of interest or disclosures.
Contributor Information
Saramati Narasimhan, Email: saramati.narasimhan.1@vumc.org.
Jared A. Weis, Email: jared.a.weis@vanderbilt.edu.
Ma Luo, Email: m.luo@vanderbilt.edu.
Amber L. Simpson, Email: amber.simpson@queensu.ca.
Reid C. Thompson, Email: reid.thompson@vanderbilt.edu.
Michael I. Miga, Email: michael.miga@vanderbilt.edu.
References
- 1.Ostrom Q. T., et al. , “CBTRUS statistical report: primary brain and other central nervous system tumors diagnosed in the United States in 2011–2015,” Neuro-oncology 20(Suppl. 4), iv1–iv86 (2018). 10.1093/neuonc/noy131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brown T. J., et al. , “Association of the extent of resection with survival in glioblastoma: a systematic review and meta-analysis,” JAMA Oncol. 2(11), 1460–1469 (2016). 10.1001/jamaoncol.2016.1373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eyüpoglu I. Y., Buchfelder M., Savaskan N. E., “Surgical resection of malignant gliomas—role in optimizing patient outcome,” Nat. Rev. Neurol. 9(3), 141–151 (2013). 10.1038/nrneurol.2012.279 [DOI] [PubMed] [Google Scholar]
- 4.Lacroix M., et al. , “A multivariate analysis of 416 patients with glioblastoma multiforme: prognosis, extent of resection, and survival,” J. Neurosurg. 95(2), 190–198 (2001). 10.3171/jns.2001.95.2.0190 [DOI] [PubMed] [Google Scholar]
- 5.Eljamel S., et al. , “Comparison of intraoperative fluorescence and MRI image guided neuronavigation in malignant brain tumours, a prospective controlled study,” Photodiagn. Photodyn. Ther. 10(4), 356–361 (2013). 10.1016/j.pdpdt.2013.03.006 [DOI] [PubMed] [Google Scholar]
- 6.Ius T., et al. , “Low-grade glioma surgery in eloquent areas: volumetric analysis of extent of resection and its impact on overall survival. A single-institution experience in 190 patients,” J. Neurosurg. 117(6), 1039–1052 (2012). 10.3171/2012.8.JNS12393 [DOI] [PubMed] [Google Scholar]
- 7.Bayer S., et al. , “Intraoperative imaging modalities and compensation for brain shift in tumor resection surgery,” Int. J. Biomed. Imaging 2017, 6028645 (2017). 10.1155/2017/6028645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gerard I. J., et al. , “Brain shift in neuronavigation of brain tumors: a review,” Med. Image Anal. 35, 403–420 (2017). 10.1016/j.media.2016.08.007 [DOI] [PubMed] [Google Scholar]
- 9.Schulz C., Waldeck S., Mauer U. M., “Intraoperative image guidance in neurosurgery: development, current indications, and future trends,” Radiol. Res. Pract. 2012, 197364 (2012). 10.1155/2012/197364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Orringer D. A., Golby A., Jolesz F., “Neuronavigation in the surgical management of brain tumors: current and future trends,” Expert Rev. Med. Devices 9(5), 491–500 (2012). 10.1586/erd.12.42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nimsky C., et al. , “Quantification of, visualization of, and compensation for brain shift using intraoperative magnetic resonance imaging,” Neurosurgery 47(5), 1070–1080 (2000). 10.1097/00006123-200011000-00008 [DOI] [PubMed] [Google Scholar]
- 12.Chen I., et al. , “Intraoperative brain shift compensation: accounting for dural septa,” IEEE Trans. Biomed. Eng. 58(3), 499–508 (2011). 10.1109/TBME.2010.2093896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Miga M. I., et al. , “Clinical evaluation of a model-updated image-guidance approach to brain shift compensation: experience in 16 cases,” Int. J. Comput. Assist. Radiol. Surg. 11(8), 1467–1474 (2016). 10.1007/s11548-015-1295-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nimsky C., et al. , “Intraoperative high-field-strength MR imaging: implementation and experience in 200 patients,” Radiology 233(1), 67–78 (2004). 10.1148/radiol.2331031352 [DOI] [PubMed] [Google Scholar]
- 15.Dumpuri P., et al. , “An atlas-based method to compensate for brain shift: preliminary results,” Med. Image Anal. 11(2), 128–145 (2007). 10.1016/j.media.2006.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sun K., et al. , “Near real-time computer assisted surgery for brain shift correction using biomechanical models,” IEEE J. Transl. Eng. Health Med. 2, 2500113 (2014). 10.1109/JTEHM.2014.2327628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dumpuri P., et al. , “A fast and efficient method to compensate for brain shift for tumor resection therapies measured between preoperative and postoperative tomograms,” IEEE Trans. Biomed. Eng. 57(6), 1285–1296 (2010). 10.1109/TBME.2009.2039643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fan X., et al. , “Simulation of brain tumor resection in image-guided neurosurgery,” Proc. SPIE 7964, 79640U (2019). 10.1117/12.878104 [DOI] [Google Scholar]
- 19.Miga M. I., et al. , “Modeling of retraction and resection for intraoperative updating of images,” Neurosurgery 49(1), 75–85 (2001). 10.1097/00006123-200107000-00012 [DOI] [PubMed] [Google Scholar]
- 20.Luo M., et al. , “Retrospective study comparing model-based deformation correction to intraoperative magnetic resonance imaging for image-guided neurosurgery,” J. Med. Imaging 4(3), 035003 (2017). 10.1117/1.JMI.4.3.035003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Coffey A. M., et al. , “Toward a preoperative planning tool for brain tumor resection therapies,” Int. J. Comput. Assist. Radiol. Surg. 8(1), 87–97 (2013). 10.1007/s11548-012-0693-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Simpson A. L., et al. , “Evaluation of conoscopic holography for estimating tumor resection cavities in model-based image-guided neurosurgery,” IEEE Trans. Biomed. Eng. 61(6), 1833–1843 (2014). 10.1109/TBME.2014.2308299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Grabowski M. M., et al. , “Residual tumor volume versus extent of resection: predictors of survival after surgery for glioblastoma,” J. Neurosurg. 121(5), 1115–1123 (2014). 10.3171/2014.7.JNS132449 [DOI] [PubMed] [Google Scholar]
- 24.Nabavi A., et al. , “Serial intraoperative magnetic resonance imaging of brain shift,” Neurosurgery 48(4), 787–798 (2001). 10.1097/00006123-200104000-00019 [DOI] [PubMed] [Google Scholar]
- 25.Jarvis L. A., et al. , “Tumor bed dynamics after surgical resection of brain metastases: implications for postoperative radiosurgery,” Int. J. Radiat. Oncol. Biol. Phys. 84(4), 943–948 (2012). 10.1016/j.ijrobp.2012.01.067 [DOI] [PubMed] [Google Scholar]
- 26.Atalar B., et al. , “Cavity volume dynamics after resection of brain metastases and timing of postresection cavity stereotactic radiosurgery,” Neurosurgery 72(2), 180–185 (2013). 10.1227/NEU.0b013e31827b99f3 [DOI] [PubMed] [Google Scholar]
- 27.Li Y. M., et al. , “The influence of maximum safe resection of glioblastoma on survival in 1229 patients: can we do better than gross-total resection?” J. Neurosurg. 124(4), 977–988 (2016). 10.3171/2015.5.JNS142087 [DOI] [PubMed] [Google Scholar]
- 28.Fedorov A., et al. , “3D slicer as an image computing platform for the quantitative imaging network,” Magn. Reson. Imaging 30(9), 1323–1341 (2012). 10.1016/j.mri.2012.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frisken S., et al. , “A comparison of thin-plate spline deformation and finite element modeling to compensate for brain shift during tumor resection,” Int. J. Comput. Assist. Radiol. Surg. 15(1), 75–85 (2020). 10.1007/s11548-019-02057-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.BK Medical, Analogic Corporation, Peabody, https://bkultrasound.com/ (2018). [Google Scholar]
- 31.Machado I., et al. , “Non-rigid registration of 3D ultrasound for neurosurgery using automatic feature detection and matching,” Int. J. Comput. Assist. Radiol. Surg. 13(10), 1525–1538 (2018). 10.1007/s11548-018-1786-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yushkevich P. A., et al. , “User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability,” NeuroImage 31(3), 1116–1128 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Maes F., et al. , “Multimodality image registration by maximization of mutual information,” IEEE Trans. Med. Imaging 16(2), 187–198 (1997). 10.1109/42.563664 [DOI] [PubMed] [Google Scholar]
- 34.Rohde G. K., Aldroubi A., Dawant B. M., “The adaptive bases algorithm for intensity-based nonrigid image registration,” IEEE Trans. Med. Imaging 22(11), 1470–1479 (2003). 10.1109/TMI.2003.819299 [DOI] [PubMed] [Google Scholar]
- 35.Sullivan J. M. J., Charron G., Paulsen K. D., “A three-dimensional mesh generator for arbitrary multiple material domains,” Finite Elem. Anal. Des. 25(3–4), 219–241 (1997). 10.1016/S0168-874X(96)00027-3 [DOI] [Google Scholar]
- 36.Roberts D. W., et al. , “Intraoperatively updated neuroimaging using brain modeling and sparse data,” Neurosurgery 45(5), 1199–1207 (1999). 10.1097/00006123-199911000-00037 [DOI] [PubMed] [Google Scholar]
- 37.Biot M. A., “General theory of three-dimensional consolidation,” J. Appl. Phys. 12(2), 155–164 (1941). 10.1063/1.1712886 [DOI] [Google Scholar]
- 38.Narasimhan S., et al. , “In vivo modeling of interstitial pressure in a porcine model: approximation of poroelastic properties and effects of enhanced anatomical structure modeling,” J. Med. Imaging 5(4), 045002 (2018). 10.1117/1.JMI.5.4.045002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Weis J. A., Miga M. I., Yankeelov T. E., “Three-dimensional image-based mechanical modeling for predicting the response of breast cancer to neoadjuvant therapy,” Comput. Methods Appl. Mech. Eng. 314, 494–512 (2017). 10.1016/j.cma.2016.08.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lynch D. R., Numerical Partial Differential Equations for Environmental Scientists and Engineers: A First Practical Course, Springer Science & Business Media, New York: (2005). [Google Scholar]
- 41.Narasimhan S., et al. , “Biophysical model-based parameters to classify tumor recurrence from radiation-induced necrosis for brain metastases,” Med. Phys. 46(5), 2487–2496 (2019). 10.1002/mp.13461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Narasimhan S., et al. , “Development of a mechanics-based model of brain deformations during intracerebral hemorrhage evacuation,” Proc. SPIE 10135, 101350F (2017). 10.1117/12.2255830 [DOI] [Google Scholar]
- 43.Narasimhan S., et al. , “Differentiating tumor recurrence from radiation-induced necrosis: an image-based mathematical modeling framework,” in IEEE Int. Symp. Biomed. Imaging, IEEE, Washington D.C., pp. 839–842 (2018). 10.1109/ISBI.2018.8363702 [DOI] [Google Scholar]
- 44.Dumpuri P., Miga M. I., “Model-updated image guidance: a statistical approach to gravity-induced brain shift,” Lect. Notes Comput. Sci. 2878, 375–382 (2003). 10.1007/978-3-540-39899-8_47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Swanson K. R., Alvord E. C. J., Murray J. D., “A quantitative model for differential motility of gliomas in grey and white matter,” Cell Prolif. 33(5), 317–329 (2000). 10.1046/j.1365-2184.2000.00177.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Brunet J.-N., et al. , “Physics-based deep neural network for augmented reality during liver surgery,” Lect. Notes Comput. Sci. 11768, 137–145 (2019). 10.1007/978-3-030-32254-0_16 [DOI] [Google Scholar]
- 47.Mendizabal A., Márquez-Neila P., Cotin S., “Simulation of hyperelastic materials in real-time using deep learning,” Med. Image Anal. 59, 101569 (2020). 10.1016/j.media.2019.101569 [DOI] [PubMed] [Google Scholar]
- 48.Feng R., et al. , “Deep learning guided stroke management: a review of clinical applications,” J. Neurointerventional Surg. 10(4), 358–362 (2018). 10.1136/neurintsurg-2017-013355 [DOI] [PubMed] [Google Scholar]
- 49.Tonutti M., Gras G., Yang G.-Z., “A machine learning approach for real-time modelling of tissue deformation in image-guided neurosurgery,” Artif. Intell. Med. 80, 39–47 (2017). 10.1016/j.artmed.2017.07.004 [DOI] [PubMed] [Google Scholar]