Depletion interactions modulate the binding between disordered proteins in crowded environments

Significance

The molecular environment in a biological cell is much more crowded than the conditions commonly used in biochemical and biophysical experiments in vitro. It is therefore important to understand how the conformations and interactions of biological macromolecules are affected by such crowding. Addressing these questions quantitatively, however, has been challenging owing to a lack of sufficiently detailed experimental information and theoretical concepts suitable for describing crowding, especially when polymeric crowding agents and biomolecules are involved. Here, we use the combination of extensive single-molecule experiments with established and recent theoretical concepts to investigate the interaction between two intrinsically disordered proteins. We observe pronounced effects of crowding on their interactions and provide a quantitative framework for rationalizing these effects.

Abstract

Intrinsically disordered proteins (IDPs) abound in cellular regulation. Their interactions are often transitory and highly sensitive to salt concentration and posttranslational modifications. However, little is known about the effect of macromolecular crowding on the interactions of IDPs with their cellular targets. Here, we investigate the influence of crowding on the interaction between two IDPs that fold upon binding, with polyethylene glycol as a crowding agent. Single-molecule spectroscopy allows us to quantify the effects of crowding on a comprehensive set of observables simultaneously: the equilibrium stability of the complex, the association and dissociation kinetics, and the microviscosity, which governs translational diffusion. We show that a quantitative and coherent explanation of all observables is possible within the framework of depletion interactions if the polymeric nature of IDPs and crowders is incorporated based on recent theoretical developments. The resulting integrated framework can also rationalize important functional consequences, for example, that the interaction between the two IDPs is less enhanced by crowding than expected for folded proteins of the same size.

Intrinsic disorder is a widespread phenomenon among eukaryotic proteins, manifesting itself in unstructured segments of larger proteins or proteins that are entirely disordered under physiological conditions (1). Such intrinsically disordered proteins (IDPs) are particularly prevalent in the context of signaling and regulation (2), where they form complex interaction networks (3), often involving many partners (4). IDPs lack the stable tertiary structure familiar from folded proteins—instead, they sample a heterogeneous ensemble of conformations on timescales from nanoseconds to seconds (5–8). Their disorder and the lack of pronounced minima in their conformational free energy landscapes makes the ensembles particularly sensitive to external factors such as ligands (9), posttranslational modifications (10), and salt concentration (11), which can even induce the folding of IDPs. The cellular milieu, densely packed with globular and polymeric macromolecules (12–14), is thus also expected to influence the conformational distributions and dynamics of IDPs. Experimental evidence, simulations, and theory suggest that the effects of such macromolecular crowding are moderate but detectable, including the compaction and local structure formation of unfolded proteins and IDPs (8, 11, 15–31), which may have important effects on their function. However, a quantitative understanding of the effects of crowding on IDPs is largely lacking.

The influence of macromolecular crowding on the conformational properties of individual IDPs and on the binding interactions of folded proteins has been studied (32–35), but little is known about the effect of crowding on the binding process involving IDPs, which is essential for many of their functions (9, 36). Here, we aim to fill this gap with a systematic investigation of the effects of the size and concentration of polymeric crowding agents on the interaction between two IDPs by simultaneously monitoring complex stability, kinetics, and translational diffusion. We find that the effects on all these observables can be rationalized quantitatively within the framework of depletion interactions, the effective attractive force that arises between particles in a solution of solutes that are preferentially excluded from the vicinity of the particles (37–39). The depletion effects that cause the interaction between two proteins in a crowded solution have the same entropic origin as those leading to the conformational collapse of IDPs in the presence of crowding agents (20, 40). It is worth noting that our use of terminology, especially regarding “depletion interactions” and “crowding,” is influenced by different schools of thought that have traditionally been separated, but the underlying quantitative concepts are equivalent (40). The coherent framework we use is enabled by theoretical developments, some of them quite recent, that allow us to combine the influence of polymer physics (19) with the enhanced attractive interactions between the proteins in a crowded solution (39).

Results

Single-Molecule Spectroscopy Enables a Comprehensive Investigation of Crowding Effects.

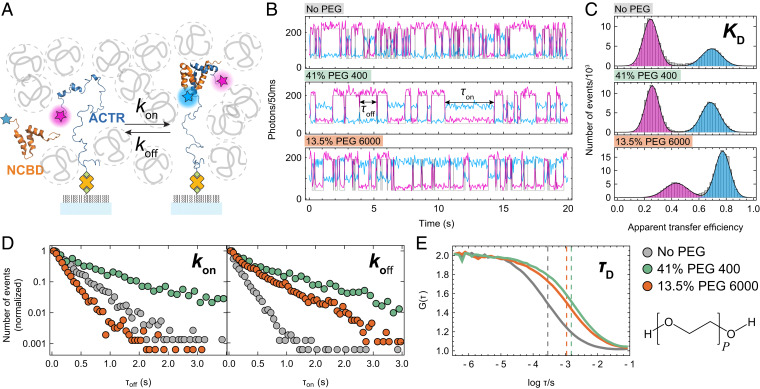
We investigate the interaction between the intrinsically disordered activation domain of the steroid receptor coactivator 3 (ACTR) and the molten-globule-like nuclear coactivator binding domain of CBP/p300 (NCBD), a paradigm of coupled folding and binding (41, 42). Upon binding to each other, ACTR and NCBD form a stable, structured complex (41) with an equilibrium dissociation constant of ∼30 nM. Association is fast (∼10⁸ M⁻¹⋅s⁻¹) and electrostatically favored by the opposite net charge of the two proteins (7, 43, 44). We monitor the binding of NCBD to surface-immobilized ACTR molecules in confocal single-molecule Förster resonance energy transfer (FRET) experiments (Fig. 1 A and B) (7). To follow the binding reaction, we labeled ACTR on its C terminus with a fluorescent donor dye and NCBD on its N terminus with a fluorescent acceptor dye. In the unbound state of ACTR, only donor fluorescence is observed (with some background in the acceptor channel from freely diffusing NCBD). Upon binding, the donor and acceptor dyes of ACTR and NCBD come into proximity, resulting in FRET between them, as evident from the increase in acceptor intensity and simultaneous decrease in donor intensity. When NCBD dissociates, acceptor emission ceases, and the donor fluorescence returns to its original intensity, leading to anticorrelated signal changes of donor and acceptor (Fig. 1B).

Fig. 1.

Probing IDP interactions and crowding in single-molecule experiments. (A) Schematic representation of acceptor-labeled NCBD (orange, Protein Data Bank ID code 2KKJ) binding to surface-immobilized donor-labeled ACTR (blue, Protein DataBank ID code 1KBH) in the presence of polymeric crowders (gray). (B) Examples of single-molecule time traces recorded at different PEG concentrations (first 20 s each, binning: 50 ms, donor signal: magenta, acceptor signal: light blue; not corrected for background, quantum yields, detection efficiencies, etc.). The most likely state trajectory identified by the Viterbi algorithm is depicted in gray. Note that the quantitative trajectory analysis is based on 1-ms binning to avoid averaging over fast events (Materials and Methods). From top to bottom: buffer without PEG; 41% PEG 400; 13.5% PEG 6000. (C) Histograms of the apparent transfer efficiency (from time traces binned at 20 ms) can be used to quantify the equilibrium dissociation constant, K_D. Apparent efficiencies at 13.5% PEG 6000 are shifted to higher values because of the increased background in the acceptor channel owing to residual nonspecific surface adsorption of NCBD. (D) Normalized dwell-time distributions (conditions and color code as in B) from the state trajectories of 30 to 40 ACTR molecules each (gray: 9,300 transitions, green: 3,475 transitions, orange: 12,192 transitions). The dwell time distributions in the unbound and bound states reflect k_on (Left) and k_off (Right), respectively (Materials and Methods). (E) Normalized FCS curves of freely diffusing acceptor-labeled NCBD measured above the surface under the same conditions as the time traces (B) yield the diffusion times of NCBD through the confocal volume (dashed lines), which can be related to translational diffusion coefficients.

Fig. 1 illustrates that each such measurement enables us to acquire a comprehensive set of observables. From the fluorescence time traces, both the equilibrium dissociation constant, $K_{\text{D}}$ (Fig. 1C), and the kinetic on- and off-rate coefficients of the binding reaction, $k_{\text{on}}$ and $k_{\text{off}}$ (Fig. 1D), can be quantified (Materials and Methods). From fluorescence correlation spectroscopy (FCS) measurements in the solution above the surface (Fig. 1E), we can further determine the diffusion time, ${\tau }_{\text{D}}$, of acceptor-labeled NCBD through the confocal volume of the instrument to quantify the translational diffusion coefficient, D. Finally, FCS also reports on the average number of molecules in the confocal volume via its amplitude, which allows us to correct for small variations in NCBD concentration.^† The complementarity of these observables, all of which are obtained under identical solution conditions, is essential for the integrated analysis of the effects of crowding that we present below.

As crowding agents (crowders), we chose (poly)ethylene glycol (PEG) because it is widely used for mimicking inert crowders (45, 46), its interaction with proteins is dominated by excluded-volume effects (especially for longer PEG chains) (47, 48), and it is available over a wide range of degrees of polymerization at a purity suitable for single-molecule fluorescence experiments, even at physiologically realistic mass fractions of up to ∼40% (19). We can thus investigate a large range of relative protein-crowder dimensions, including crowders that are much smaller, of similar size, and much larger than the proteins used. NCBD and ACTR have hydrodynamic radii of $R_{\text{H}}=1.74$ nm and $R_{\text{H}}=2.3$ nm, respectively, as determined by NMR (49) and two-focus FCS (50), so we selected 10 different degrees of polymerization, P, of PEG (SI Appendix, Fig. S1 A and B), ranging from the monomer, ethylene glycol $\left(R_{\text{g}}\approx 0.2\hspace{0.17em}\mathrm{nm}\right)$, to PEG 35000 $\left(R_{\text{g}}\approx 10\hspace{0.17em}\mathrm{nm}\right)$ (SI Appendix, Fig. S1). For every set of solution conditions (71 in total), 34 to 83 min of cumulative single-molecule time traces were analyzed, each set containing 3·10³ to 2.5·10⁴ association/dissociation transitions (SI Appendix, Table S1), to enable a comprehensive quantitative analysis. We also tested polyvinylpyrrolidone, polyvinyl alcohol, and dextran as crowding agents. They show effects on the ACTR–NCBD interaction qualitatively similar to PEG (SI Appendix, Fig. S2), but they are not available over a broad range of chain lengths, and at high concentrations they often cause background problems in single-molecule experiments. The type of quantitative analysis we present for PEG is thus not feasible for these crowders.

It is worth noting that we recently found that NCBD exists in two conformations corresponding to different peptidyl-prolyl cis/trans isomers, both of which are molten-globule-like and able to bind ACTR, but with different affinities and dissociation rates (7). The relative effects of crowders on the kinetics and affinities of both isomers is, however, equal to within experimental error (SI Appendix, Fig. S3 and Table S1). The parameters extracted for each set of conditions are compiled in SI Appendix, Table S1 for both types of analysis, including and excluding isomerization (see Materials and Methods). For the sake of clarity, we focus on the simpler two-state analysis here.

Polymeric Crowders and Relevant Length Scales.

For investigating the effects of a polymeric crowder, it is essential to recognize that we do not only cover a large range of PEG sizes but also two different concentration regimes (SI Appendix, Fig. S1). At low polymer concentrations, in the dilute regime, the sizes of the polymeric crowders can be approximated by their radii of gyration, $R_{\text{g}}$, since the chains do not overlap (Fig. 2 A and B) (51). With increasing crowder concentration, the chains fill the available volume more and more, until they start to overlap, at which point the solution enters the semidilute regime. The overlap concentration, c*, separating the two regimes [used here in units of mass per volume (39)] is given by

$$c*=M/\left(N_{\text{A}}\frac{4}{3}\pi \hspace{0.17em}{R}_{\text{g}}^3\right)\propto P^{-0.749},$$ [1]

where M is the molar mass of the crowder and N_A Avogadro’s constant. The overlap concentration of PEG thus strongly decreases with increasing P (SI Appendix, Fig. S1C). Within the accessible range of c, we reach the semidilute regime for PEGs with M ≥ 1,000 g/mol; for M ≥ 4,600 g/mol, most of the recorded data points are in the semidilute regime (SI Appendix, Fig. S1C).^‡ In the semidilute regime, the characteristic length scale is no longer given by R_g of the individual polymer chains but by the average mesh size, ξ, in the network of overlapping polymers. In this sense, the solution can also be viewed as a solution of “blobs” of size ξ. Inside a blob, the monomers of a chain do not overlap with other chains, whereas on length scales greater than a blob (or correlation length), the excluded volume interactions within the protein and within the crowding agents are screened by other overlapping chains (52). Importantly, ξ is independent of P but decreases steeply with increasing c (Theory) (39, 52).

Fig. 2.

Depletion interactions stabilize the IDP complex. (A) Depletion interaction between two spherical colloidal particles in a solution of noninteracting polymers (37, 38). Each particle has a depletion layer into which the centers of mass of the polymers cannot enter. When the depletion layers of the two particles overlap, the volume available to the polymer chains increases by the overlap volume $V_{\text{overlap}}$ (green), which increases their entropy and causes an attractive potential between the two particles via the osmotic pressure, $\mathit{\Pi }=n\hspace{0.17em}{k}_{\text{B}}T$. (B) The theory is modified to account for the smaller overlap volume between the compact, molten-globule-like protein NCBD (orange) and the largely unstructured IDP ACTR (blue), whose depletion layer arises from the size of the interacting segment instead of $R_{\text{H}}$ of the whole protein. (C) Equilibrium dissociation constant, K_D, for the interaction between ACTR and NCBD, $K_{\text{D}}=k_{\text{off}}/k_{\text{on}}$, as a function of PEG concentration, c, for different sizes of PEG (see color scale). (D) Change in interaction free energy between ACTR and NCBD caused by crowding, ΔΔG/k_BT (Eq. 2), versus the number density of PEG, n. Data for n > 1 M (shaded range) were excluded from the analysis. (E) Linear fit of ΔΔG/k_BT as a function of c for $n\le 1\hspace{0.17em}\mathrm{M}$. (F) Magnitude of the crowder concentration dependence, ΔΔG/ck_BT, that is, the slope from the linear fit in E, as a function of crowder size. The black dashed line indicates the dilute-limit prediction for two spherical particles with R = 1.74 and 2.3 nm, the measured $R_{\text{H}}$ values of NCBD and ACTR (Eq. 4) [note that using the R_g of ACTR (∼2.5 nm) (19) instead of R_H has only a minor effect on the result]. The dark gray line shows the dilute-limit prediction using instead a segment size of 0.4 nm for ACTR (Eq. 4). The light gray line shows the corresponding prediction in the semidilute regime (39), where the overlap volume is determined by the correlation length $\xi$, and the osmotic pressure is approximated by renormalization group theory (Eq. 11). Shaded bands indicate the uncertainty from a variation in the segment size of ACTR by ± 0.1 nm.

Depletion Interactions Stabilize the IDP Complex.

Fig. 2C shows that the complex between ACTR and NCBD is increasingly stabilized both with increasing crowder concentration and crowder size. From $K_{\text{D}}=k_{\text{off}}/k_{\text{on}}$ (which yields, within error, the same $K_{\text{D}}$ as calculated from the transfer efficiency histograms; see SI Appendix, Table S1), we obtain the effect of crowding on the free energy of binding between the two IDPs according to (54)

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }G-\mathrm{\Delta }{G}_0=-k_{\text{B}}T\ln \frac{K_{\text{D,0}}}{K_{\text{D}}}.$$ [2]

$\mathrm{\Delta }G$ and $\mathrm{\Delta }{G}_0$ are the binding free energies in the presence and absence of crowder, respectively, $K_{\text{D},0}$ is the equilibrium dissociation constant in the absence of crowder $\left(K_{\text{D},0}=31\pm 3\hspace{0.17em}\mathrm{nM}\right)$, and $k_{\text{B}}$ and $T$ are the Boltzmann constant and absolute temperature, respectively. The largest measured stabilization by about an order of magnitude in $K_{\text{D}}$, or $\mathrm{\Delta }\mathrm{\Delta }G\approx -2\hspace{0.17em}{k}_{\mathrm{B}}T$, was observed in 0.13 to 0.17 g/mL of the largest PEGs (4600 to 35000). We note that for the smallest crowders (up to PEG 200), the stabilizing trend reverts at a number density of PEG above ∼1 M (Fig. 2D), possibly caused by the repulsive interactions between two particles at high concentrations of small crowders, as observed in optical tweezer experiments, owing to entropically stabilized layers of small crowders filling the interparticle space (55). Since such contributions go beyond the excluded-volume effects of interest here, we restrict our analysis to data points with n < 1 M. Another effect we do not consider here are enthalpic interactions (56–58), in particular the stabilization of the complex by ethylene glycol (and to a lesser extent by di- and triethylene glycol), which is not caused by excluded-volume effects but by the unfavorable chemical interactions of the terminal hydroxyl groups with proteins (47). The relative contribution of these end effects decreases with increasing degrees of polymerization and becomes negligible for longer PEG chains (19).

What is the cause of the crowder size- and concentration-dependent stabilization of the ACTR–NCBD complex we observe? A commonly employed framework for crowding effects is scaled-particle theory (59), which estimates the free energy required for creating a cavity of the size of the biomolecules of interest in a solution of hard spheres equivalent to the size of the crowder. The total volume occupied by the two individual IDPs is greater than that of their folded complex, so complex stabilization with increasing crowder concentration is expected because the solution volume available to the proteins decreases (45, 60). However, scaled-particle theory predicts that with increasing crowder size (at fixed volume [or mass] fraction of crowding agent), the free energy cost for creating a cavity of a given volume decreases (61), and so complex stabilization should decrease, the opposite of what we observe (Fig. 2C). This marked discrepancy is reminiscent of the effect of polymeric crowders on the chain dimensions of IDPs (19) and indicates that a different theoretical framework is required.

Here, we utilize the concept of depletion interactions (37–39), which allows us to combine the influence of polymer physics (19) with the attractive interactions between particles (the proteins in our case) in a solution of crowders (39), as well as to describe the effect of crowders on viscosity and association kinetics. The origin of these effects is the existence of a depletion layer around a colloidal particle with radius R, in a solution of polymeric crowders with radius of gyration $R_{\text{g}}$ (Fig. 2A and SI Appendix, Fig. S1D) (39). The segments of the polymer cannot penetrate the particle, which leads to a loss of configurational entropy of the polymer near the surface of the colloid and thus a vanishing concentration of polymer segments in a layer around the surface. The thickness, δ, of this depletion layer is proportional to R_g of the polymer in the dilute regime, whereas it depends on the average mesh size, $\xi$, in the semidilute regime (SI Appendix, Fig. S1E) (62):

$${\delta }^{-2}={\delta }_0^{-2}+{\xi }^{-2},$$ [3]

where ${\delta }_0$ is the thickness of the depletion layer in dilute solution. A common approach to quantify the resulting attractive depletion force is via the osmotic pressure in a solution of polymers, $\mathit{\Pi }=n\hspace{0.17em}{k}_{\text{B}}T$, where $n$ is the number density of polymer.^§ If the particles are far apart, they are uniformly surrounded by polymers, and the resulting osmotic pressure around them is isotropic. If instead the depletion layers of the particles overlap, polymer chains cannot enter between them, leading to a nonisotropic osmotic pressure that pushes the particles together. Their distance-dependent attractive interaction potential, $W\left(r\right)$, then results as the product of $\mathit{\Pi }$ and the overlap volume of the depletion layers, $V_{\mathrm{overlap}}\left(r\right)$: $W\left(r\right)=-n\hspace{0.17em}{k}_{\text{B}}T\hspace{0.17em}{V}_{\mathrm{overlap}}\left(r\right)$. We assume that the net stabilization of the complex, $\mathrm{\Delta }\mathrm{\Delta }G$, corresponds to the interaction potential of the two particles at contact, $W\left(0\right)$ [which has previously been suggested to be a reasonable approximation for proteins (63)]:

$$\mathrm{\Delta }\mathrm{\Delta }G=W\left(0\right)=-n\hspace{0.17em}{k}_{\text{B}}T\hspace{0.17em}{V}_{\mathrm{overlap}}\left(0\right)=-\frac{c}{M}{k}_{\text{B}}T\hspace{0.17em}{V}_{\mathrm{overlap}}\left(0\right),$$ [4]

where c is the mass concentration and M is the molar mass of the polymeric crowder. Eq. 8 (Theory) describes the calculation of $V_{\mathrm{overlap}}\left(0\right)$ for two interacting spherical particles. Since larger crowders increase the size of the depletion layer and thus V_overlap, Eq. 4 rationalizes the observed stabilization of the ACTR–NCBD complex both with increasing crowder concentration and increasing crowder size. However, can this simple theory account for our experimentally observed extent of stabilization quantitatively?

The dependence of $\mathrm{\Delta }\mathrm{\Delta }G$ on crowder concentration is approximately linear (Fig. 2E), as predicted by Eq. 4. However, the magnitude of this concentration dependence for two particles with radii corresponding to the experimentally determined hydrodynamic radii of ACTR and NCBD clearly overestimates the experimentally observed stabilization (black dashed line in Fig. 2F; for details of the calculation see Theory). Within the framework of Eq. 4, this discrepancy indicates that V_overlap for the two proteins is too large. Fig. 2B illustrates that the size of the relevant depletion layer around an IDP is indeed expected to be much smaller than around a globular protein, because the polymeric crowders can penetrate the hydrodynamic sphere of the IDP, which is a polymer itself. The dark gray line in Fig. 2F takes this effect into account and shows the prediction of the stabilization calculated for two particles in dilute crowder solution, one with R₁ = 1.74 nm (corresponding to R_H of NCBD, which is rather compact owing to its molten-globule-like character), and one with R₂ = 0.4 ± 0.1 nm, corresponding to the approximate size of a chain segment of an IDP such as ACTR. We note that R₂ is the only adjustable parameter in this context.

The resulting small stabilization of the complex describes the data up to PEG 2050 reasonably well,^¶ but for larger PEGs it predicts an effective destabilization, in contrast to the experimental observation. In this range of PEG lengths, however, we leave the dilute regime already at low PEG concentrations, so the overlap volume becomes a function of the correlation length (64), and the osmotic pressure must be treated in terms of blobs of volume $\sim {\xi }^3$ and concentration $\sim {\xi }^{-3}$ (since PEG fills the solution completely at $c>c^{\ast }$). We thus use a corresponding expression from renormalization group theory (RGT) for the osmotic pressure in the semidilute regime (64) (Theory), with R₁ = 1.74 nm and R₂ = 0.4 ± 0.1 nm. The result indeed agrees with the experimentally observed stabilization of the protein complex reasonably well, even for large crowder sizes (light gray line in Fig. 2F). The pronounced improvement compared to the simple picture of the interaction between two spherical colloidal particles in dilute crowder solution suggests that the polymeric properties of both the crowders and the IDPs need to be taken into account: for the IDPs in terms of the relevant overlap volume of the highly disordered ACTR, and for the polymeric crowders in terms of a decrease of the correlation length in the semidilute regime, where the chains overlap and screen each other’s excluded-volume interactions. Notably, ΔΔG approaches saturation for PEGs with M ≳ 4,600 g/mol, as expected for polymers above c*, where $\xi$ is independent of P (39, 52).

Diffusion in a Solution of Polymeric Crowders.

A key contribution to the rate of binding is the diffusivity of the interaction partners. Since in our measurements ACTR is surface-immobilized, we only need to account for the diffusion of NCBD in solutions with different sizes and concentrations of PEG. We obtain the translational diffusion coefficients from FCS measurements of the acceptor-labeled NCBD in the solution directly above the surface by measuring the diffusion time, ${\tau }_D$, through the confocal volume and relating it to the diffusion time in the absence of crowder (Fig. 3 and SI Appendix, Fig. S4 A and B). The diffusion coefficient of NCBD without crowder follows from its $R_{\text{H}}$ and the Stokes–Einstein relation as $D_0=1.3\cdot {10}^8\hspace{0.17em}\mathrm{n}{\mathrm{m}}^2\cdot {\mathrm{s}}^{-1}$. The diffusion coefficients in the presence of crowders, $D_1$, result from the corresponding measured diffusion times (SI Appendix, Fig. S4D) as $D_1=D_0\hspace{0.17em}{\tau }_{\text{D,}0}/{\tau }_{\text{D}}$, with the index “0” specifying the value in the absence of crowder. According to the Stokes–Einstein equation, $1/D_1$ is expected to scale with the bulk viscosity of the solution, ${\eta }_{\text{bulk}}$, as $1/D_1\propto 6\pi {\eta }_{\text{bulk}}{R}_{\text{H}}/k_{\text{B}}T$ (Fig. 3B and SI Appendix, Fig. S4E), where $R_{\text{H}}$ is the hydrodynamic radius of the diffusing particle. Up to PEG 2050 $\left(R_{\text{g}}=1.8\hspace{0.17em}\mathrm{nm}\right)$, where the crowders are smaller than or similar in size to NCBD $\left(R_{\text{H}}=1.74\hspace{0.17em}\mathrm{nm}\right)$, this relation describes the data reasonably well (Fig. 3B), but pronounced deviations are apparent for larger PEGs. In the presence of 0.1 g/mL PEG 35000, for example, the observed diffusion time of NCBD corresponds to only ∼20% of the value expected for ${\eta }_{\text{bulk}}$. We quantify the observed microscopic viscosity relevant for the translational diffusion of NCBD, ${\eta }_{\text{micro}}$, according to ${\eta }_{\text{micro}}/{\eta }_{\text{s}}={\tau }_D/{\tau }_{\text{D,0}}=D_0/D_1$, where η_s is the viscosity of the solution in the absence of crowders (1.0 mPa⋅s at 22 °C).

Fig. 3.

Probing the microviscosity of PEG solutions with FCS. (A) Diffusion of a particle through a solution of crowders with different sizes, with the respective thickness of the depletion layer, δ (red dashed circles). With increasing size of the depletion layer, the effect of the bulk viscosity of the solution on the local diffusion of the particle decreases. (B) Relation between relative bulk viscosity and microviscosity, quantified via the translational diffusion coefficient of NCBD according to ${\eta }_{\text{micro}}/{\eta }_{\text{s}}=D_0/D_1$ for solutions containing different concentrations and sizes of PEG (color scale above), where η_micro is the microscopic viscosity, η_s the neat solvent viscosity, and D₀ the diffusion coefficient in the absence and D₁ in the presence of crowder. The black dashed line shows the behavior expected from the Stokes–Einstein equation and the bulk viscosity. (C) Microviscosity analyzed with a model using solvent viscosity within the depletion layer and bulk viscosity outside (Eq. 5). A global fit of $D_0/D_1={\eta }_{\text{micro}}/{\eta }_{\text{s}}$ across all PEG sizes and concentrations yields R = 1.8 ± 0.1 nm for NCBD.

The theory of depletion interactions provides an adequate framework for describing the effect of microviscosity as probed by the diffusion of a molecule in a solution of polymeric crowders. The observed dependence on PEG size can be explained by the larger thickness of the depletion layer around NCBD in the presence of larger polymeric crowders (Fig. 3A). Within the depletion layer, where the polymer segment concentration is reduced, the microviscosity is expected to be closer to the viscosity of pure solvent. Hence, the larger the depletion layer around the particle, the less the particle is influenced by ${\eta }_{\text{bulk}}$. This effect can be described by the theory of Tuinier et al. (65), according to which

$${\eta }_{\text{micro}}={\eta }_{\text{s}}\frac{Q\left(\lambda ,\epsilon \right)}{Z\left(\lambda ,\epsilon \right)},$$ [5]

where $Q\left(\lambda ,\epsilon \right)$ and $Z\left(\lambda ,\epsilon \right)$ are algebraic functions of the ratio of solvent and bulk viscosity, $\lambda ={\eta }_s/{\eta }_{bulk}$, and of the ratio of depletion layer thickness and particle radius, $\epsilon =\delta /R$ (Theory). The known values of $\delta$, ${\eta }_{\text{s}}$, and ${\eta }_{\text{bulk}}$ are used in a global fit of the diffusion data for all PEG sizes and concentrations (Fig. 3C). The single free fit parameter is R, which yields a value of 1.8 ± 0.1 nm, remarkably close to the size of NCBD (R_H = 1.74 nm) (49). The fit is best for small PEGs, but even for larger PEGs the theory predicts the observed microviscosities to within ∼25%, suggesting that depletion effects are the dominant contribution to the low microviscosity experienced by NCBD in the presence of large PEGs.

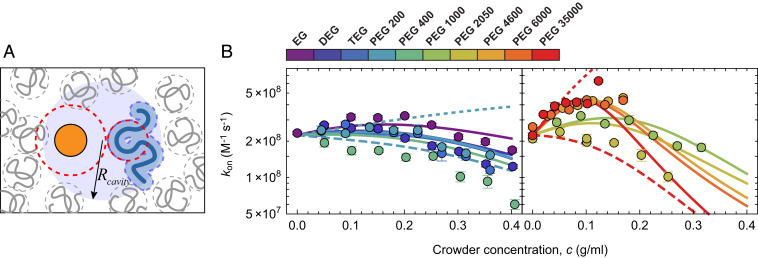
Depletion Effects Influence the Association Rate.

The kinetics of binding under crowded conditions should be affected by both of the depletion effects discussed above (66). On the one hand, the crowder-induced attractive interaction potential should accelerate binding; on the other hand, the reduced diffusion coefficient should decelerate it. Based on the quantitative analysis of these two competing effects in the previous sections, we can now analyze their joint influence. An expression recently derived by Berezhkovskii and Szabo (67) explicitly combines the two effects on the association rate coefficient, $k_{\text{on}}$ (Fig. 4A):

$$\frac{1}{k_{\text{on}}}=\left(\frac{1}{k_0}+\frac{1}{4\pi D_0}\left(\frac{1}{R_{\text{contact}}}-\frac{1}{R_{\text{cavity}}}\right)\right)e^{-\frac{\mathrm{\Delta }\mathrm{\Delta }G}{k_{\text{B}}T}}+\frac{1}{4\pi D_1{R}_{\text{cavity}}}.$$ [6]

This special case of the Collins–Kimball–Debye (68, 69) formula generalized to a distance-dependent diffusivity (70) accounts for the following effects:

• 1)In the crowded solution, the reactants diffuse relative to each other with a diffusion coefficient $D_1$. Crowding decreases $D_1$ with respect to $D_0$, their relative diffusivity in pure solvent ($D_1<D_0$, cf. SI Appendix, Fig. S4D), which slows down association. Since ACTR is surface-immobilized, only the diffusion coefficient of NCBD needs to be considered in our case, which was quantified in the previous section (Fig. 3).
• 2)Once the reactants come to within their contact radius, $R_{\text{contact}}$, they form a product with the intrinsic/reaction-controlled rate constant, $k_0$.
• 3)If the crowders are sufficiently large, they can accommodate the reactants within a cavity of radius $R_{\text{cavity}}$ that is devoid of crowders, so the diffusion coefficient of the reactants within the cavity is $D_0$. This effect speeds up the association reaction if $R_{\text{cavity}}>R_{\text{contact}}$, since the proteins can make contact faster than if they are separated by the crowder solution. $R_{\text{cavity}}$ is related to the thickness of the depletion layer, $\delta$, around the proteins. We calculated $\delta$ using Eq. 3 for a sphere with $R=1.74\hspace{0.17em}\mathrm{nm}$, the size of NCBD, and introduce a proportionality factor, a, yielding $R_{\text{cavity}}=a\cdot \delta$. We assume a > 1, that is, $R_{\text{cavity}}>\delta$, since the cavity needs to accommodate two proteins.
• 4)A square-well potential localized in the cavity devoid of crowders leads to an attraction between the reactants and increases the association rate coefficient. As previously suggested (71), we assume that the depth of the potential equals the depletion interaction free energy, $\mathrm{\Delta }\mathrm{\Delta }G$, which we measured as a function of crowder concentration (Fig. 2 E and F).

Fig. 4.

Depletion effects on the association rate coefficient. (A) Schematic depiction of NCBD (orange) and ACTR (blue) within a cavity formed by the crowder molecules. Inside the cavity, the proteins diffuse with the diffusion coefficient in pure solvent, outside with a reduced relative diffusion coefficient. Within the cavity, the proteins experience an attractive interaction due to the osmotic pressure of the crowders. (B) Measured association rate coefficients, $k_{\text{on}}$ (filled circles), with global fit using Eq. 6 (lines) as a function of the concentration of PEGs of different size (see color scale) using the values of ΔΔG from the fits in Fig. 2E. For clarity, the dataset is split in two: the left shows PEGs up to 400 g/mol and the right 1,000 g/mol and above. The counteracting effects of depletion attraction (short-dashed lines) and viscosity (long-dashed lines) predicted by Eq. 6 are illustrated for PEG 200 (Left) and PEG 35000 (Right).

To probe the competing effects of viscosity-induced deceleration and depletion-induced acceleration of binding, we extracted $k_{\text{on}}$ from the single-molecule time traces (Fig. 1) recorded over the entire range of PEG sizes and concentrations (Fig. 4B). Overall, $k_{\text{on}}$ tends to exhibit an initial increase at low crowder concentrations, which is most pronounced for the largest PEGs. At higher crowder concentrations, the trend is reversed, and association slows down again—exactly the nonmonotonic behavior predicted by the competing effects that contribute to Eq. 6: The initial acceleration is caused by the attractive potential between the reactants owing to the depletion force, whereas at higher crowder concentrations the strong decrease of $D_1$ due to the increase in viscosity dominates and leads to a deceleration (66, 67).

We fit all data in Fig. 4B globally using Eq. 6, with $R_{\text{contact}}$, $k_0$, and $a$ as shared fit parameters.^# The resulting fit yields $R_{\text{contact}}=0.54\pm 0.06\hspace{0.17em}\mathrm{nm}$, $k_0=\left(4.0\pm 0.5\right)\cdot {10}^8{\mathrm{M}}^{-1}\cdot {\mathrm{s}}^{-1}$, and $a=1.8\pm 0.1$, and captures the overall behavior. The small value of $R_{\text{contact}}$ indicates a relatively compact encounter complex, in line with recent measurements (44), and k₀ is only about a factor of two lower than the purely diffusion-limited rate constant, $4\pi D_0{R}_{\text{contact}}$, in keeping with the low association barrier of the protein pair identified previously (44). The value of a suggests that the cavity radius is roughly twice the thickness of the depletion layer, which appears reasonable. A turnover and subsequent drop in $k_{\text{on}}$ is also predicted for the largest PEGs (4,600 to 35,000 g/mol), but only at crowder concentrations that were experimentally inaccessible owing to increased fluorescence background at high PEG concentrations. Finally, given the quantitative description of both the stability (Fig. 2) and the association kinetics of ACTR–NCBD binding (Fig. 4) based on depletion interactions, we note that the dissociation kinetics can be inferred according to $k_{\text{off}}=K_{\text{D}}{k}_{\text{on}}$.

Discussion

We probed the effects of (macro)molecular crowding on microviscosity, diffusion, and the equilibrium and kinetic properties of the interactions between two IDPs. The comprehensive dataset we obtained enables an advanced quantitative analysis that integrates classical concepts and more recent developments in the theory of depletion interactions (37–39). These developments allow us to combine the role of polymer effects, such as chain overlap and excluded-volume screening (19), with the attractive interactions between proteins caused by the crowding agent (or depletant) (39), as well as with the effect of crowders on microviscosity and association kinetics (67). In this way, the transition from the dilute to the semidilute regime can be treated quantitatively, which has previously been shown to be essential for understanding the interactions of folded proteins (32) and IDP dimensions (19) under the influence of polymeric crowding agents.^‖ The approach thus goes beyond the more commonly employed scaled particle theory (59), which is based on the free energy of insertion of a particle into a hard-sphere fluid and successfully describes many crowding-induced phenomena (45, 60, 61), especially as a function of crowder concentration. However, at fixed volume or mass fraction of crowder, scaled-particle theory predicts for a process such as coupled folding and binding that the stability of the complex decreases with increasing crowder size, because the free energy cost for creating a cavity is smaller for larger crowders (19, 59). This trend is opposite to what we observe here experimentally (Fig. 2), illustrating the need for extending the theoretical approach for the analysis.

We find that all our experimental observations can be explained remarkably well by depletion effects of the polymeric crowders on the interacting proteins, including the enhanced stability of the complex as a function of crowder size and concentration, the underlying changes in kinetics, and the link to translational diffusion, which is governed by the crowder-dependent microviscosity. The decrease in polymer segment concentration near a protein creates a cavity within which the protein diffuses according to the viscosity of the crowder-free solvent rather than the bulk viscosity. This effect on translational diffusion is only expected if the size of the cavity is larger than the protein, so that it can effectively slip through the polymer network. A related length scale dependence has previously been observed by varying the diameter of the probe instead of the crowder (72): When the crowder-related length scale was larger than the probe, translational diffusion was significantly faster than the bulk value. The theory by Tuinier et al. (65) accounts for these different length scales and successfully predicts the observed translational diffusion coefficient. Similarly, depletion-enhanced diffusion relative to the bulk viscosity is the basis for the acceleration of binding that we observe for large crowders, as explained by a recent model for the influence of crowding on bimolecular association rates (67). Accounting for the acceleration of binding additionally requires an attractive potential (67), which is caused by the depletion interactions between the two proteins and can be described by the theory of Asakura and Oosawa (37) extended to the semidilute regime (62, 64).

The combined framework of depletion interactions and polymer physics may be useful for quantitatively describing the effect of crowding on a wide range of biopolymers. For instance, single-molecule measurements have been used to investigate the effect of crowding on hairpin formation in RNA (73) and ribozyme compaction (74). The results indicate a stabilization of more compact structures upon addition of PEG 8000, similar to the effects observed here. The crowder concentrations we use extend into the range of cellular concentrations of macromolecules (∼0.1 to 0.15 g/mL in eukaryotes and 0.2 to 0.4 g/mL in Escherichia coli) (12–14, 75, 76). It will be interesting to investigate the relevant crowding length scales directly in the cell (14, 31, 77) and compare how diffusion, binding equilibria, and kinetics compare with the depletion interactions we observed in vitro. However, the framework of depletion interactions and polymer physics we employed here is currently limited to excluded-volume interactions, and extensions will be required to quantitatively account for additional contributions, such as enthalpic interactions (56) [for which we found indications for the smallest PEGs, in accord with previous work (47)], mixtures of different types of globular and polymeric crowders of different lengths, and the role of meshworks and small solutes in the cell (58, 79–81). Such an extended framework could be further tested with the experimental approach used here, complemented, for example, by site-directed amino acid exchanges to probe protein–crowder interactions or help to disentangle effects on protein folding and binding in detail.

An important result of our analysis is not only the general insight that polymer effects need to be included for quantitative understanding but, more specifically, that the disordered nature of ACTR has important consequences for its interactions with NCBD. In particular, we observe a lower equilibrium stabilization of the complex by crowding than expected for folded proteins of the same size. The theoretical analysis suggests that the relevant length scale for the depletion interactions of ACTR corresponds not to its overall chains dimensions but to the size of a chain segment. The result implies that the interactions of IDPs should in general be less affected by crowding than the interactions of folded proteins. Interestingly, it has also been demonstrated that the translational diffusion of IDPs is less reduced by crowding than that of globular proteins of the same size (81). IDPs are usually more sensitive to environmental changes than folded proteins owing to the lack of deep minima in their free-energy landscapes (82), but the effects of crowding may thus be less pronounced than expected, with potentially important implications for their cellular functions, including their role in cellular condensates (83), where the concentrations of biomolecules can be exceedingly high (84).

Theory

Relevant Length Scales in the Dilute and Semidilute Regimes.

For our analysis, we used the values for the radius of gyration of PEG, $R_{\text{g}}$, according to its dependence on P, the degree of polymerization, $R_{\text{g}}=0.21\hspace{0.17em}\text{nm}\cdot P^{0.583}$ (85), where the scaling exponent indicates that water is a good solvent for PEG (51). Each of the polymer chains occupies on average a volume $V=\left(4\pi /3\right)R_{\text{g}}^3$. The scaling law for the correlation length in the good-solvent regime (52), $\xi \approx R_{\text{g}}{\left(c/c^{\ast }\right)}^{-0.77}$, indicates that $\xi$ decreases steeply with increasing polymer concentration. Equivalently, $\xi \propto b^{-1.335}{\left(c{N}_{\text{A}}/M_{\text{monomer}}\right)}^{-0.77}$, where $b$ is the segment length of PEG, and $M_{\text{monomer}}$ is the molar mass of a monomer. This relation shows that in the semidilute regime $\xi$ is independent of $P$ and only a function of the polymer concentration (which follows from substituting the length scaling of $R_{\text{g}}$ into Eq. 1) (39).

Depletion Interactions.

The basis of depletion interactions between particles of radius R in a solution of polymers is that the segments of the polymer cannot penetrate the particle, which leads to a loss of configurational entropy of the polymer near the surface of the colloid and thus a vanishing concentration of polymer segments in a depletion layer around the surface. In the dilute regime, we calculate the change in interaction free energy, $\mathrm{\Delta }\mathrm{\Delta }G$, due to the depletion layer with the classic Asakura–Oosawa model (37), assuming that the net stabilization corresponds to the depletion potential at contact, $W\left(0\right)$:

$$\mathrm{\Delta }\mathrm{\Delta }G=W\left(0\right)=-n\hspace{0.17em}{k}_{\text{B}}T{V}_{\mathrm{overlap}}\left(0\right)=-\frac{c}{M}{k}_{\text{B}}T{V}_{\mathrm{overlap}}\left(0\right).$$ [7]

The terms $n\hspace{0.17em}{k}_{\text{B}}T$ or $\frac{c}{M}{k}_{\text{B}}T$, respectively, describe the osmotic pressure, $\mathit{\Pi }$, where n is the number density (or molar concentration), c the mass concentration, and M the molar mass of the polymeric crowder. The overlap volume, $V_{\mathrm{overlap}}\left(0\right)$, of two spherical particles of radii $R_1$ and $R_2$ in contact, with depletion layers of thickness δ_s, is calculated based on elementary geometrical considerations according to

$$\begin{array}{l}{V}_{\text{overlap}}=\frac{\pi {\left(r+R-d\right)}^2\left(d^2-3{\left(r-R\right)}^2+2d\left(r+R\right)\right)}{12\hspace{0.17em}d}.\\ \text{with}\hspace{1em}r=R_1+{\delta }_s\left(R_1\right),\hspace{1em}R=R_2+{\delta }_s\left(R_2\right),\hspace{1em}d=R_1+R_2.\end{array}$$ [8]

A common approximation for the depletion layer in a solution of polymers is to replace the resulting smooth segment concentration profile near the particle surface by a step function that is zero up to a depletion layer thickness, $\delta$, and equal to the bulk concentration above (86). $\delta$ then corresponds to the thickness of the layer around the particle surface from which the centers of mass of the polymer chains are excluded (SI Appendix, Fig. S1D). In the dilute regime, $\delta \propto R_{\text{g}}$ for $R\gg R_{\text{g}}$; the smaller the crowder, the closer its center of mass can be to the colloidal particle. The depletion layer thickness near a flat plate in a dilute solution of excluded volume polymers with radius of gyration $R_{\text{g}}$ was calculated by Hanke et al. using RGT (39, 87):

$${\delta }_0=1.07\hspace{0.17em}{R}_g.$$ [9]

The conversion of ${\delta }_0$ near a flat plate to the corresponding value, ${\delta }_{\text{s}}$, near a sphere with radius R is a geometrical problem. If $R_{\text{g}}$ is similar to or greater than R, a correction term needs to be introduced to account for the interpenetration between particle and polymers. For excluded volume chains in the dilute regime (up to PEG 2050), we use the following expression that has been found using RGT (64, 87):

$$\frac{{\delta }_{\text{s}}}{R}={\left[1+3\frac{{\delta }_0}{R}+2.273\hspace{0.17em}{\left(\frac{{\delta }_0}{R}\right)}^2-0.0975\hspace{0.17em}{\left(\frac{{\delta }_0}{R}\right)}^3\right]}^{1/3}-1.$$ [10]

To calculate the depletion potential at contact in the semidilute regime (polymer concentration $c>c^{\ast }$), we employed a relation based on the generalized Gibbs adsorption equation (64):

$$\mathrm{\Delta }\mathrm{\Delta }G=W\left(0\right)=-k_{\text{B}}T{\displaystyle \underset{0}{\overset{n}{\int }}\frac{1}{n^{\prime }}}\left(\frac{\partial \mathit{\Pi }}{\partial n^{\prime }}\right)\left(\mathrm{\Gamma }\left(0,n^{\prime }\right)-\mathrm{\Gamma }\left(\infty ,n^{\prime }\right)\right)d{n}^{\prime },\hspace{1em}\text{with}\hspace{0.17em}n=\frac{c}{M}.$$ [11]

Eq. 11 is also valid in the dilute regime, where it simplifies to Eq. 7. The expression for the osmotic compressibility, $\partial \mathit{\Pi }/\partial n$, based on RGT (88), is

$$\left(\frac{\partial \mathit{\Pi }}{\partial n}\right)=1+2.63\hspace{0.17em}\varphi {\left(\frac{1+3.25\hspace{0.17em}\varphi +4.15\hspace{0.17em}{\varphi }^2}{1+1.48\hspace{0.17em}\varphi }\right)}^{0.309}\text{,}\hspace{1em}\text{with}\hspace{0.17em}\varphi =\frac{c}{c^{*}}.$$ [12]

$\mathrm{\Gamma }\left(h,n\right)$ corresponds to the (negative) amount of adsorbed polymer segments when the spheres are a distance $h$ apart. It equals the product of n and the overlap volume, thus

$$\mathrm{\Gamma }\left(0,n\right)=n\hspace{0.17em}{V}_{\mathrm{overlap}}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{\Gamma }\left(\infty ,n\right)=0.$$ [13]

The overlap volume was again calculated with Eq. 8, but in this case with ${\delta }_{\text{s}}$ evaluated in the semidilute regime, where the size of the interacting entity (the “blob”) is determined by $\xi$, so $\delta$ becomes a function of $\xi$ instead of $R_{\text{g}}$, and $\delta \approx \xi$ in the semidilute regime (52). To this end, we employed a simple relation derived by Fleer et al. (62) for calculating the depletion thickness near a flat plate in the semidilute regime, which we used for all PEG sizes and concentrations:

$$\begin{array}{c}{\delta }^{-2}={\delta }_0^{-2}+{\xi }^{-2}\text{,}\\ \text{with}\hspace{0.17em}\xi =R_{\text{g}}{\left(c/c^{*}\right)}^{-0.77}\hspace{0.17em}\text{and}\hspace{0.17em}{c}^{*}=3M/\left(4\pi N_{\text{A}}{R}_{\text{g}}^3\right),\end{array}$$ [14]

and used $\delta$ instead of ${\delta }_0$ in Eq. 10 for calculating the thickness of the depletion layer around a sphere in the semidilute regime.

Diffusion through a Solution of Polymers.

The microviscosity experienced by a sphere with radius $R$ that is diffusing through a polymer solution with bulk viscosity ${\eta }_{\text{bulk}}$ and solvent viscosity ${\eta }_{\text{s}}$ is calculated with the relation obtained by Tuinier et al. (65):

$$\begin{array}{l}\frac{{\eta }_{\text{micro}}}{{\eta }_{\text{micro,0}}}=\frac{Q\left(\lambda ,\epsilon \right)}{Z\left(\lambda ,\epsilon \right)},\hspace{0.17em}\text{with}\\ Q\left(\lambda ,\epsilon \right)=2\left(2+3\lambda \right){\left(1+\epsilon \right)}^6-4\left(1-\lambda \right)\left(1+\epsilon \right)\hspace{0.17em}\text{and}\\ Z\left(\lambda ,\epsilon \right)=2\left(2+3\lambda \right){\left(1+\epsilon \right)}^6-9\left(1-\frac{1}{3}\lambda -\frac{2}{3}{\lambda }^2\right){\left(1+\epsilon \right)}^5\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+10\left(1-\lambda \right){\left(1+\epsilon \right)}^3-9\left(1-\lambda \right)\left(1+\epsilon \right)+4{\left(1-\lambda \right)}^2\\ \epsilon =\frac{{\delta }_{\text{s}}}{R},\hspace{0.17em}\lambda =\frac{{\eta }_{\text{s}}}{{\eta }_{\text{bulk}}}.\end{array}$$ [15]

${\delta }_{\text{s}}$, the depletion layer thickness around a sphere of radius R, was calculated from Eq. 10 with the approximation for the semidilute regime, Eq. 14.

It is worth mentioning that the approach we use here neglects solute–solute interactions beyond excluded volume effects (40). Integrating such higher-order contributions, which are likely to be responsible for the deviations we observe for ethylene glycol and diethylene glycol (47) (Fig. 2F), with the polymer effects we focus on here is one of the next challenges in refining the quantitative understanding of the effect of solutes on macromolecular conformations and interactions (56).

Materials and Methods

Protein Expression, Purification, and Labeling.

ACTR and NCBD were purified, expressed, and labeled as described before (7). Briefly, a single-cysteine Avi-tagged (89) ACTR variant was in vivo-biotinylated in E. coli and purified with immobilized metal ion chromatography (IMAC) via a C-terminal His₆-tag. The tag was cleaved off with thrombin and the protein further purified with high-performance liquid chromatography (HPLC) on a C18 column (Reprosil Gold 200; Dr. Maisch HPLC GmbH). Lyophilized protein was labeled with a 0.8-fold molar ratio of Cy3B maleimide dye (GE Healthcare); the single-labeled protein was purified with HPLC (Sunfire C18; Waters).

A single-cysteine NCBD variant was coexpressed with ACTR as described before (41). Purification was carried out using IMAC via an N-terminal His₆-tag. The tag was cleaved off with HRV 3C protease and the protein was further purified with HPLC on a C18 column (Reprosil Gold 200). Lyophilized protein was labeled with a 1.5-fold molar ratio of CF680R maleimide dye (Biotium); the single-labeled protein was purified with HPLC (Reprosil Gold 200). We note that the amino acid exchanges, dye labeling, and biotinylation can affect the binding affinity (7). However, since we investigate the relative change in affinity and rates due to crowding for a single labeled molecular system, the absolute affinity and rates in the absence of crowder do not affect our conclusions.

Preparation of Crowder Solutions.

PEG solutions were prepared as described before (19). Briefly, crowding experiments were carried out in 50 mM sodium phosphate buffer, pH 7.0 (NaP buffer). The highest mass-per-volume concentration for each PEG stock solution was prepared by weighing in the appropriate amount of PEG in a volumetric flask. This stock solution was then mixed in different ratios with buffer of the same composition without PEG to yield the other buffers of the series. PEG solutions were prepared by mixing acidic (50 mM NaH₂PO₄ + PEG) and alkaline (50 mM Na₂HPO₄ + PEG) stock solutions to a final pH of 7.0 (± 0.05). PEGs were from Sigma, except PEG 400 (ROTIPURAN; Roth) and ethylene glycol (SPECTRANAL; Riedel-de Haën). The solutions of dextran 40K, PVA 40K, and PVP 40K were prepared analogously, with dextran from Leuconostoc spp. (average molecular weight [M_w] 40,000), poly(vinyl alcohol) (M_w 31,000 to 50,000), and polyvinylpyrrolidone (average M_w 40,000), all from Sigma. The bulk viscosity of the crowder solutions was measured with a digital rotational viscometer (DV-I+; Brookfield).

Surface Immobilization.

The single-molecule binding experiments were conducted as described before (7). In short, adhesive silicone hybridization chambers (Secure Seal Hybridization Chambers, SA8R-2.5; Grace Bio-Labs) were fixed onto PEGylated, biotinylated quartz coverslips (Bio_01; MicroSurfaces, Inc.); 0.2 mg/mL Avidin D (Vector Labs) were incubated for 5 min in a reaction chamber, followed by addition of 10 pM ACTR–Cy3B to yield a surface coverage of 0.1 to 0.3 molecules per µm². Binding experiments were conducted in the appropriate PEG solution, supplied with 16 nM CF680R-labeled NCBD, 0.01% Tween 20, 1% (wt/vol) glucose, 0.4 mg/mL glucose oxidase, 400 U/mL catalase as oxygen scavenging system, as well as 1 mM methyl viologen and 1 mM ascorbic acid as triplet quenchers. Addition of these components led to a 0.1-fold dilution of the PEG solution, which was taken into account.

Single-Molecule Experiments.

All single-molecule experiments were conducted at 22 °C on a MicroTime 200 (PicoQuant) equipped with a 532-nm continuous-wave laser (LaserBoxx LBX-532-50-COL-PP; Oxxius) and a 635-nm diode laser (LDH-D-C-635M; PicoQuant). Florescence photons were separated from the scattered laser light with a triple-band mirror (zt405/530/630rpc; Chroma). A dichroic mirror was used to separate donor and acceptor emission (T635LPXR; Chroma). Donor photons were filtered with an ET585/65m band-pass filter (Chroma) and acceptor photons with a LP647RU long-pass filter (Chroma), followed by detection with two SPCM-AQRH-14 single-photon avalanche diodes (PerkinElmer). For FCS measurements, acceptor photons were split according to their polarization, filtered with LP647RU long-pass filters and detected on two SPCM-AQRH-14 single-photon avalanche diodes. To enable surface scanning, the objective (UPlanApo 60×/1.20-W; Olympus) was mounted on a piezo stage (P-733.2 and PIFOC; Physik Instrumente GmbH).

Single Cy3B-labeled ACTR molecules were localized on the surface as described before (7) and recorded at a laser power of 0.5 µW (measured at the back aperture of the objective) until photobleaching occurred. Time traces from a total of 30 to 40 molecules were recorded for each PEG concentration. Note that the fluorescence signal was not corrected for background, quantum yields, channel cross-talk, and so on since none of the observables used for our analysis depends on these corrections. We thus only report apparent transfer efficiencies in Fig. 1C. Before and after recording the time traces at a given set of conditions, the diffusion time and concentration of NCBD were estimated from FCS measurements using the 635-nm diode laser (10 µW, measured at the back aperture of the objective). For this purpose, the laser was focused 20 µm above the cover slide surface where ACTR was immobilized, and the fluorescence signals of the two acceptor detection channels were cross-correlated.

Analysis of Single-Molecule Time Traces.

Single-molecule time traces were analyzed using 1-ms time binning and a maximum-likelihood approach based on a hidden Markov model (90, 91), as described before (7). We previously showed that NCBD binds to ACTR in two conformations, NCBD1 and NCBD2, which correspond to the peptidyl–prolyl bond involving Pro20 being in trans or cis configuration, respectively (7). The binding and dissociation rates of these states to ACTR differ, but the relative donor and acceptor photon rates of the bound states are identical. We used the following rate matrix to describe the kinetics of freely diffusing NCBD1 and NCBD2 interacting with a surface-immobilized ACTR molecule [see kinetic scheme in figure 2E of Zosel et al. (7)]:

$${\mathbf{K}}_{3\text{state,blink}}=\left(\begin{array}{cccc}-\left({k^{\prime }}_{\text{on,}1}+{k^{\prime }}_{\text{on,}2}+k_{+\text{b}}\right)& k_{\text{off,}1}& k_{\text{off,}2}& k_{-\text{b}}\\ {k^{\prime }}_{\text{on,}1}& -k_{\text{off,}1}& 0& 0\\ {k^{\prime }}_{\text{on,}2}& 0& -k_{\text{off,}2}& 0\\ k_{+\text{b}}& 0& 0& -k_{-\text{b}}\end{array}\right).$$ [16]

The first three states correspond to free ACTR, NCBD1 bound to ACTR, and NCBD2 bound to ACTR, respectively. The two association rates are given by ${k^{\prime }}_{\text{on,}i}=k_{\text{on,}i}\cdot c_{\text{NCBD}i}$ with i = 1,2. $k_{\text{off,}i}$ are the corresponding dissociation rate coefficients. An additional dark state was introduced to represent photon blinking of the donor dye while no NCBD is bound to ACTR [the fluorescence blinking occurring in other states can be neglected (7)]. Assuming that the relative populations of NCBD1 and NCBD2 do not depend on the crowder concentration, we set $c_{\text{NCBD}2}=0.56\hspace{0.17em}{c}_{\text{NCBD}1}$ and determined $k_{\text{on,}1}$, $k_{\text{on,}2}$, $k_{\text{off,}1}$, and $k_{\text{off,}2}$ for all concentrations of crowders using the maximum-likelihood procedure based on a hidden Markov model as described previously (7). The results, displayed in SI Appendix, Fig. S3 and Table S1, show that the relative effects of crowders are identical for ACTR interacting with NCBD1 and NCBD2. Hence, we present in the main text a simpler analysis, in which we neglect the difference between the two binding kinetics for the sake of clarity. We thus analyzed the data using the rate matrix

$${\mathbf{K}}_{2\text{state,blink}}=\left(\begin{array}{ccc}-\left({k^{\prime }}_{\text{on}}+k_{+\text{b}}\right)& k_{\text{off}}& k_{-\text{b}}\\ {k^{\prime }}_{\text{on}}& -k_{\text{off}}& 0\\ k_{+\text{b}}& 0& -k_{-\text{b}}\end{array}\right),$$ [17]

where ${k^{\prime }}_{\text{on}}=k_{\text{on}}\cdot c_{\text{NCBD}}$ and $k_{\text{off}}$ are the observed association and dissociation rates, respectively. This procedure is justified because the relative dependencies of $k_{\text{on}}$ and $k_{\text{off}}$ on crowder size and crowder concentration are within error the same as for the individual $k_{\text{on,}i}$ and $k_{\text{off,}i}$ values. For both the two-state and the three-state analysis, the time traces were binned in 1-ms intervals. The error bars in Figs. 2 and 4 and SI Appendix, Figs. S2 and S3 were obtained from bootstrapping; 10 synthetic datasets of photon traces were randomly sampled from the measured data and analyzed in the same way as the original data set. Error bars for all derived quantities were propagated.

FCS.

The mean diffusion time, ${\tau }_{\text{D}}$, of NCBD molecules (labeled with CF680R) through the confocal volume and the average number of NCBD molecules in the confocal volume, $\langle N\rangle$, were determined before and after recording the time traces as described by Zosel et al. (7) (with the aspect ratio of the confocal volume set to 0.165). The variations between the two FCS measurements (before and after recording single-molecule time traces) are depicted as error bars in SI Appendix, Fig. S4 C and D. The values of $\langle N\rangle$ from all measurements (with exception of the highest concentrations of PEG 2050, 6000, and 35000; see SI Appendix, Fig. S4C) were averaged to calculate the mean number of molecules, ${\langle N\rangle }_{\text{avg}}$, present in the confocal volume at an NCBD concentration of 16 nM. To account for preparative sample-to-sample variation, the NCBD concentrations were corrected with $c=\langle N\rangle /{\langle N\rangle }_{\text{avg}}$ 16 nM. The association rate coefficients were then calculated from $k_{\text{on}}={k^{\prime }}_{\text{on}}/c$.

Data Availability.

The data supporting the findings of this study are available within the paper, SI Appendix, and SI Appendix, Table S1 and Dataset S1.