Biomechanics of the Human Brain during Dynamic Rotation of the Head

Abstract

Traumatic brain injuries (TBI) are a substantial societal burden. The development of better technologies and systems to prevent and/or mitigate the severity of brain injury requires an improved understanding of the mechanisms of brain injury, and more specifically, how head impact exposure relates to brain deformation. Biomechanical investigations have used computational models to identify these relations, but more experimental brain deformation data are needed to validate these models and support their conclusions. The objective of this study was to generate a dataset describing in situ human brain motion under rotational loading at impact conditions considered injurious.

Six head-neck human post-mortem specimens, unembalmed and never frozen, were instrumented with 24 sonomicrometry crystals embedded throughout the parenchyma that can directly measure dynamic brain motion. Dynamic brain displacement, relative to the skull, was measured for each specimen with four loading severities in the three directions of controlled rotation, for a total of 12 tests per specimen. All testing was completed 42–72 h post-mortem for each specimen. The final dataset contains approximately 5,000 individual point displacement time-histories that can be used to validate computational brain models. Brain motion was direction-dependent, with axial rotation resulting in the largest magnitude of displacement. Displacements were largest in the mid-cerebrum, and the inferior regions of the brain—the cerebellum and brainstem—experienced relatively lower peak displacements. Brain motion was also found to be positively correlated to peak angular velocity, and negatively correlated with angular velocity duration, a finding that has implications related to brain injury risk-assessment methods. This dataset of dynamic human brain motion will form the foundation for the continued development and refinement of computational models of the human brain for predicting TBI.

Introduction

Traumatic brain injury (TBI) is a common but poorly understood injury to the body. In the United States, an estimated 1.7 million TBIs occur annually, and TBI is a contributing factor in one-third of all injury-related deaths.¹ TBIs are caused by many factors including falls, motor vehicle crashes, and sports and recreational activity.² A majority of TBI cases occur from head impacts without skull fracture, and their effects range on a spectrum from mild to severe.³ Seventy-five percent are classified as mild TBI, or concussion.⁴ Brain injuries can also be classified as either diffuse, including concussion and diffuse axonal injury (DAI), or focal injuries, such as contusion or hemorrhage.⁵ With closed-head, diffuse TBIs, the mechanisms that transform head motion into gross brain deformation and localized neuronal tissue strain, which ultimately lead to neurological dysfunction, are an ongoing research focus.⁶

The biomechanics of TBI have been studied for decades in an attempt to link a threshold for impact or motion of the head to brain tissue responses or injury. Computational finite element (FE) models have been vital to improving understanding of the brain's biomechanics during an impact. In the past two decades, there have been numerous FE models of the human brain described in the literature.⁷ Most of these models use tissue-level, strain-based injury metrics, such as maximum principal strain (MPS)^8–11 and maximum axonal strain,^12,13 under the assumption that brain strain is related to brain injury. The FE models allow for regional and macroscopic investigations into the brain response under a wide variety of loading conditions and severities that would not otherwise be possible experimentally. The biofidelity of these models in predicting the deformation of the brain is requisite for their role in predicting and mitigating TBI. Verifying the fidelity of these models relies on comparing the deformation responses with reference data measuring brain motion during dynamic experiments.

Most of the earliest criteria used to assess brain injury risk, such as the Head Injury Criterion,¹⁴ were developed using linear acceleration loading to the head as the sole predictor of injury. As a result, previous attempts to quantify brain biomechanics under impact loading have focused on impacts resulting in primarily linear translation of the head. Such studies have formed the basis of current tools for evaluating the safety of protective equipment such as helmets^15,16 and automotive restraint systems.^10,14,17,18

Despite the historical focus on linear head acceleration, rotational impact has long been theorized to be the primary mechanism of TBI.¹⁹ Holbourn¹⁹ suggested that rotation-driven mechanisms may lead to diffuse injury to the brain, ranging from mild concussion to DAI. The importance of rotational kinematics as a predictor of TBI severity has recently been substantiated through numerous experimental^20–24 and computational studies,^9,10,18,25 prompting the development of new injury metrics based on rotational kinematics of the head.^10,26,27 Thus, FE models of the brain seeking to predict diffuse injury must be able to predict motion of the brain during dynamic rotation events.

Few methods are available to measure three-dimensional (3D) motion of the brain during dynamic rotation of the head. Measuring human brain deformation in vivo has been explored using magnetic resonance imaging (MRI),^28–31 although this methodology limits the loading to low-speed, non-injurious head motion that results in low magnitudes of brain deformation. Post-mortem human subjects (PMHS) have been the best available in situ model to study brain deformation under potentially injurious loading, with various methods being utilized to measure human brain motion in response to head impacts.^32–34 Bi-planar X-ray imaging is a technique that measures in situ brain motion by tracking the motion of radiopaque targets implanted in PMHS brain tissue. Stalnaker and colleagues³⁴ measured brain motion during pressurization of the vasculature and ventricles of a PMHS using lead markers embedded in the brain. Nusholtz and associates³⁵ quantified the two-dimensional brain motion in PMHS during padded frontal impacts using high-speed X-ray, with head linear accelerations ranging from 25 to 450g and head rotational velocities ranging from 18 to 52 rad/sec. Hardy and co-workers^32,36 measured the 3D motion of the brain during frontal, occipital, and coronal impacts to the head, resulting in head linear accelerations ranging from 38 to 291g, rotational velocities ranging from 4 to 30 rad/sec, and head rotational accelerations ranging from 2370 to 24,206 rad/sec². The observed motion of the brain had peak excursions of 13.4 mm.

Although the bi-planar X-ray methodology provided good quality data for FE model validation, the method has inherent limitations arising from line-of-sight requirements and other factors.³⁷ A novel methodology using sonomicrometry was recently described by Alshareef and colleagues³⁷ as an alternative to high-speed radiography. Sonomicrometry uses ultrasound time-of-flight to dynamically measure distances between pairs of small piezoelectric crystals implanted within a tissue. Sonomicrometry does not have line-of-sight limitations, which allows for a larger number of crystals to be tracked in the brain, and it also allows for testing under multiple directions and loading conditions for each specimen. This methodology was demonstrated by Alshareef and colleagues,³⁷ whereby an unembalmed and never frozen PMHS head-neck specimen was instrumented with an array of 32 sonomicrometry crystals embedded in the brain. The specimen was subjected to dynamic rotation tests that were applied about the three principal anatomical directions (sagittal, coronal, and axial) through the head center of mass, with angular velocity pulses ranging from 20 to 40 rad/sec in amplitude and 30 to 60 msec in duration, which resulted in peak angular accelerations from 600 to 5500 rad/sec². The sonomicrometry and experimental techniques were able to reliably and repeatedly capture 3D dynamic in situ whole-brain motion during the dynamic head-rotation tests.

The objective of this study was to apply the sonomicrometry methodology to generate a reference dataset of human brain motion under rotational loading with multiple specimens, to form the basis for biofidelity evaluation of human brain FE models. A secondary aim was to examine the relationship between brain motion, loading magnitude and duration, and the direction of rotation. The data presented in this study will provide valuable insight on fundamental brain biomechanics that has only been theorized using computer models and will provide a comprehensive set of experimental targets for more rigorous model validation during the development of the next generation of FE brain models.

Methods

Six PMHS head-neck specimens were tested using the methodology described by Alshareef and colleagues.³⁷ A comprehensive description of the methodology used to measure brain motion, including the test device, specimen preparation, and use of sonomicrometry can be found in the referenced study. A concise explanation of the methods that includes any changes relevant to the full dataset of six specimens is presented below.

Specimen acquisition and information

All tissue donation, testing, and handling procedures were approved by the University of Virginia Institutional Review Board – Human Surrogate Use (IRB-HSU) Committee. Exclusion criteria for the acquisition of the PMHS included any factors that may have compromised the anatomy or material properties of the skull and/or brain tissue, and included any diagnosed skull lesions or trauma, neurological disease, or neurological lesions. PMHS were also screened for blood-borne pathogens (HIV, hepatitis B and C). The donated PMHS (Tables 1 and 2) were acquired unembalmed and never frozen, 10–24 h post-mortem. Pre-test radiographs of the PMHS confirmed no abnormalities of the skull. T1-weighted MRI scans of the brain were obtained for four of the PMHS. Finally, a cervical spine transection was performed at the C7-T1 joint of each PMHS to obtain a head-neck specimen for testing.

Table 1.

Specimen Information and Identification Number (ID) for All Tested PMHS

Specimen ID	Age (years)	Sex	Cause of death	Imaging	Testing completea (h)
846	53	Male	Congestive heart failure	CT	56
896	57	Female	Esophageal cancer	CT, MRI	42
900	66	Female	Carcinoma	CT, MRI	72
902	61	Female	Cardiac arrest	CT, MRI	64
903	80	Female	Cardiac arrest	CT	54
904	67	Male	Colon cancer	CT, MRI	63

^aIndicates hours post-mortem.

CT, computed tomography; MRI, manetic resonance imaging; PMHS, post-mortem human subjects.

Table 2.

PMHS Anthropometry and Mass Measurements

	Anthropometric measurement	846	896	900	902	903	904	Average
Whole body	Stature (cm)	173	163	165	168	156	177	167 ± 8
	Mass (kg)	116	31.1	56.2	97.1	90.2	54.9	74.3 ± 31.9
	BMI	38.8	11.7	20.6	34.4	37.1	17.5	26.7 ± 11.5
Skull	Circumference (mm)	510	500	520	539	506	514	514.8 ± 13.7
	Length (A-P, mm)	172	176	184	181	180	186	179.8 ± 5.15
	Breadth (L-M, mm)	144	129	131	148	129	135	136.0 ± 8.15
	Height (Vertex-Mentum, mm)	240	196	230	226	220	234	224.3 ± 15.5
	Height (Vertex-Occiput, mm)	156	135	146	137	130	153	142.8 ± 10.5
	Brow-to-Occiput Arc Length (mm)	315	305	320	315	292	352	316.5 ± 20.1
Mass	Head/Neck (kg)	7.79	3.35	4.53	4.11	4.09	4.73	4.44 ± 0.84
	Brain (kg)a	1.27	1.21	1.34	1.30	1.11	1.49	1.28 ± 0.13
Intracranial volume (from CT, cm3)		1442	1435	1558	1481	1298	1692	1484 ± 132

^aBrain mass measured post-test during specimen dissection.

BMI, body mass index; CT, computed tomography; PMHS, post-mortem human subject;

Specimen preparation

All instrumentation and hardware were installed in positions relative to the head center of gravity (CG), which was estimated based on anatomical landmarks according to the protocol outlined by Robbins and associates.³⁸ The skull was denuded and secured to fixture plates that were attached to the superior, lateral, and posterior surfaces using a custom-built locating jig. The specimen were perfused with artificial cerebrospinal fluid (aCSF)³⁹ throughout preparation and testing. The perfusion was applied through the carotid arteries and ports at the sagittal sinus and occiput and was allowed to drain through the jugular veins and the spinal canal. A recirculation pump was used to maintain continuous perfusion with a hydrostatic pressure of approximately 78 mm Hg.

Sonomicrometry crystals (Sonometrics Corporation, London, Ontario, Canada) were implanted to quantify 3D brain motion during the tests. A total of 40 crystals were utilized for each specimen. Ten crystals were affixed to the inner surface of the skull (epidural) to serve as transmitters with a fixed-location reference frame. The transmitters were fixed in locations that were designed to ensure that all receivers within the brain measured at least four transmitting signals. Only 8 of the 10 transmitters were used during testing, with the remaining 2 transmitters used as backups in the case of improperly placed or non-functioning crystals.

Thirty receiving crystals were inserted into the brain tissue using a stereotactic cannula system. The positions of the crystals were controlled by a guide plate that was fixed to the posterior surface of the skull. Only 24 of the 30 receivers were activated during the tests (dictated by the data acquisition system channel capacity), with the additional 6 serving as backups in case of noisy or non-functioning crystals. The chosen crystal positions were designed to avoid skull boundaries and ventricles while maximizing dispersion throughout the brain. Slack was intentionally introduced to the ultra-fine wires attached to each crystal during insertion to ensure they did not snag or pull taught during the testing.

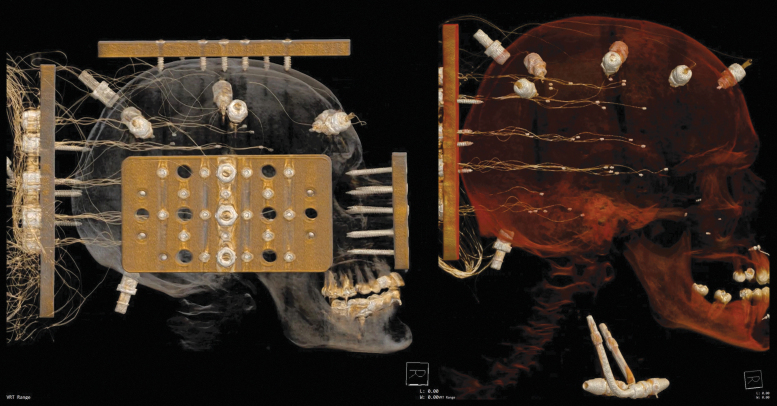
After the installation of the sonomicrometry sensors, computed tomography (CT) images were acquired at a resolution of 0.625 mm to determine the initial coordinates of each receiver and transmitter relative to the head CG (Fig. 1). Perfusion was applied during CT scans to ensure that the intracranial space was fully filled and to obtain an accurate measurement of the initial position of all implanted sensors.

FIG. 1.

Representative computed tomography images following the specimen preparation and crystal insertion procedure. Specimen 903 (left) includes the mounting plates and instrumentation plate. Specimen 904 (right) shows the transmitters affixed to the skull, the receivers in the brain (note that slack is intentionally introduced in the wires during insertion), and the perfusion ports in the carotid arteries and occipital skull. Color image is available online.

Test fixture and matrix

A custom-built rotational test device (RTD) was designed to apply repeatable, controlled dynamic rotations (CDR) to the head in the sagittal (posterior to anterior rotation), coronal (right to left rotation), or axial directions, depending on how the specimen was mounted to the RTD. For all test cases, the specimen was mounted with the head inverted at the beginning of every test to allow for consistent perfusion and brain geometry for each test. The dynamic rotation was applied through the head CG, and the specimen was returned to its initial position after every test.

The rotation severities were selected to simulate a representative spectrum of automotive and sports head impacts.²⁵ Four severities were chosen and consisted of half-sine pulses with a nominal peak angular velocity of 20 or 40 rad/sec and a nominal duration of 30 or 60 msec. Peak angular accelerations ranged from 600 to 5600 rad/sec². The four severities were applied in each of the three anatomical axes for a total of 12 tests per specimen.

Head kinematics

The six degree-of-freedom (DOF) kinematics of the head were measured using an array consisting of three Endevco 7264B-500 linear accelerometers (Meggit Sensing Systems, Irvine, CA) and three angular rate sensors (ARS) (ARS PRO-8k angular rate sensors; Diversified Technical Systems Inc., Seal Beach, CA). The sensor array was rigidly mounted to the head mounting plates. The array kinematics were transformed to the head coordinate system according to SAE J211 definitions.⁴⁰ A SlicePRO data acquisition system (Diversified Technical Systems Inc.) was used to acquire the data at a sampling rate of 10 kHz with an anti-aliasing filter of 2900 Hz. The linear acceleration data were filtered with a CFC 180 filter, and the angular velocity was filtered with a CFC 60 filter. Angular acceleration was calculated by forward differentiating the filtered angular velocity data. The peak angular velocity and duration of every test for each specimen was calculated from the measured head kinematics.

Sonomicrometry acquisition and data processing

Sonomicrometry data were recorded using a 32-channel TRX-USB Acquisition System (Sonometrics Corporation, London, Ontario, Canada). Unfiltered data were collected at a sampling rate of 600 Hz for all tests, which was sufficient for capturing the dynamic displacements of the sonomicrometry crystals. There were a total of 192 distance traces for each test. Before and after each test, static sonomicrometry data were collected to confirm that all receivers had returned to their original position. Sonomicrometry data were processed according to the manufacturer's recommended practice to remove any data artifacts (obvious point outliers and level shifts) that may appear in sonomicrometry signals. Excessively noisy sonomicrometry signals were removed and not included in subsequent analyses. All sonomicrometry analyses were performed using an acoustic speed of sound of 1540 m/sec for brain tissue, which was calibrated based on the static sonomicrometry data and the crystal positions measured from the pre-test CT images.

Sonomicrometry trilateration

Trilateration was utilized to determine the 3D coordinate time-history of each receiver crystal relative to the reference frame defined by the transmitting crystals affixed to the skull. This method uses the geometry of spheres to determine the absolute location of a point based on multiple redundant distance measurements from fixed reference points (the transmitters). A custom script was written in MATLAB (Mathworks Inc., Natick, MA) to trilaterate the displacement of each crystal using Kalman filtering. Kalman filtering iteratively estimates the position of receivers based on the distances at the next time-step, assuming errors in the measured distances, allowing for a more accurate and reliable solution in the presence of redundant measurement information.⁴¹

Brain displacement statistics

For every receiver crystal (i) embedded in the brain, the peak displacement (${\delta }_i$) of that crystal from its initial position was recorded for each test and specimen. For each test and specimen, two metrics were calculated to summarize the overall brain displacement response: the maximum displacement metric [${\delta }_{max}=max\left({\delta }_i\right)$] represents the largest displacement of any one crystal within the brain during a test, and the average displacement metric [${\delta }_{mean}=mean\left({\delta }_i\right)$] represents the average displacement of all crystals within the brain during a test. The relationship between the brain displacement metrics and head kinematics was then examined using linear regression analysis with the maximum angular velocity and angular velocity duration as independent variables. A separate regression model was fit for each axis of rotation (sagittal, coronal, and axial), using the 24 measurements for each loading condition (four tests, six specimens) in that direction. The linear regression model for ${\delta }_{max}$ is shown in Equation 1 and includes an interaction term.

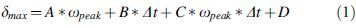
where ${\omega }_{peak}$ denotes the measured peak angular velocity (rad/sec), $\Delta t$ denotes the measured duration (msec), and A, B, C, and D are the regression coefficients. A regression model for ${\delta }_{mean}$ was developed using the same form as in Equation 1.

Results

All specimens were acquired, prepared, and tested within 72 h post-mortem. There was a total of 72 tests conducted on a total of six specimens. The dataset included 1652 3D receiver displacement time-histories, which corresponded to approximately 5000 response curves for motion relative to the skull, in the principal Cartesian directions.

Rotational head kinematics

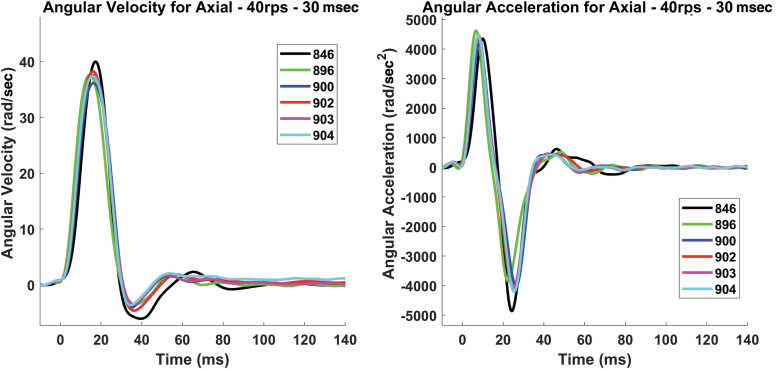
Due to differences in the inertia of each specimen in each rotational direction, and differences between the specimens and the surrogate used for tuning the RTD, there were slight variations in the head kinematics from the nominal targets (Fig. 2). There were minimal linear accelerations and off-axis rotations of the head for all loading severities. The average peak linear acceleration, angular velocity, angular acceleration, and duration are given in Table 3.

FIG. 2.

An example of the repeatability of a single loading case (axial – 40 rad/sec – 30 msec) for the six specimens in controlled dynamic rotation (CDR) using the rotational test device (RTD) (left: angular velocity; right: angular acceleration). Color image is available online.

Table 3.

A Summary of Peak Linear and Angular Head Kinematics for All Specimens (Means and Standard Deviations Shown)

	Test	Max acceleration (g)	Max angular velocity (rad/sec)	Angular velocity duration (msec)	Max angular acceleration (rad/sec2)
Sagittal	20 rps-60 msec	3.5 ± 0.6	23.1 ± 1.5	58.9 ± 3.0	1641 ± 291
	20 rps-30 msec	6.9 ± 2.1	16.7 ± 3.1	38.2 ± 12.2	1908 ± 574
	40 rps-60 msec	9.4 ± 2.3	43.6 ± 2.7	54.5 ± 4.0	3753 ± 692
	40 rps-30 msec	16.7 ± 6.5	39.9 ± 2.3	33.1 ± 2.0	5209 ± 525
Coronal	20 rps-60 msec	4.6 ± 1.3	23.7 ± 1.5	62.2 ± 2.7	1455 ± 266
	20 rps-30 msec	7.8 ± 3.4	15.9 ± 2.3	40.4 ± 7.1	1527 ± 355
	40 rps-60 msec	10.7 ± 2.3	42.2 ± 2.9	60.6 ± 2.4	3826 ± 731
	40 rps-30 msec	18.0 ± 6.7	33.8 ± 3.1	35.7 ± 2.4	4342 ± 563
Axial	20 rps-60 msec	4.6 ± 2.3	22.8 ± 0.7	64.7 ± 8.6	1803 ± 102
	20 rps-30 msec	7.0 ± 2.0	17.7 ± 1.4	36.4 ± 12.5	2193 ± 188
	40 rps-60 msec	10.6 ± 3.7	43.4 ± 2.0	61.1 ± 5.9	3363 ± 79
	40 rps-30 msec	24.0 ± 9.6	37.8 ± 1.3	29.1 ± 0.5	4484 ± 236

Brain motion (sonomicrometry)

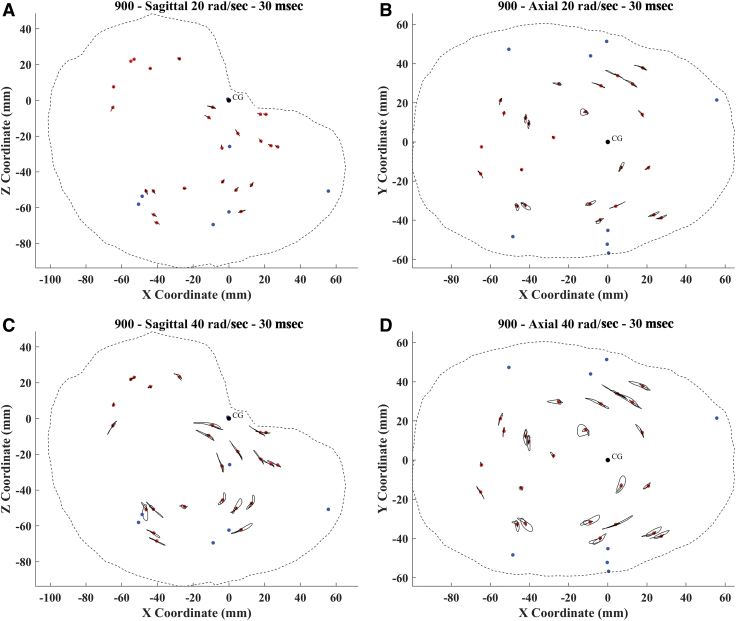
The trilaterated trajectories of the sonomicrometry crystals in the brain were similar, temporally and spatially, to the coronal rotation traces presented in the study by Alshareef and colleagues.³⁷ An example of the trajectories of all receivers for a single specimen tested in two directions and two severities is given in Figure 3. The brain motion in the plane of rotation follows an arcing trajectory about a point posterior and superior to the head CG (located at 0,0 in Fig. 3) where the dynamic rotation was applied. There were clear increases in displacement magnitude for the 40 rad/sec tests compared with the 20 rad/sec tests.

FIG. 3.

Trajectory plot for the 20 rad/sec – 30 msec (A,B) and 40 rad/sec – 30 msec (C,D) sagittal and axial tests for specimen 900. The red dots symbolize the initial position of each receiver. The black dot represents the CG of the head, about which the rotation was applied. Blue dots represent the transmitter crystals in the skull. Color image is available online.

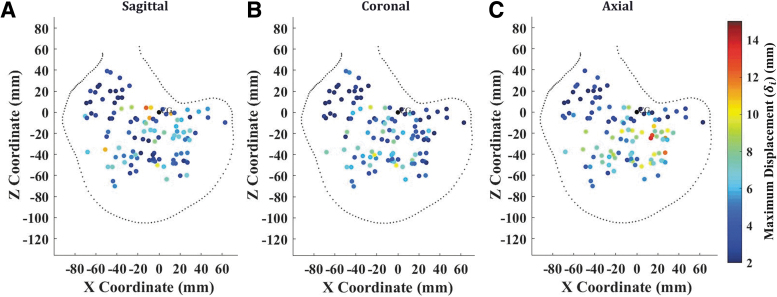
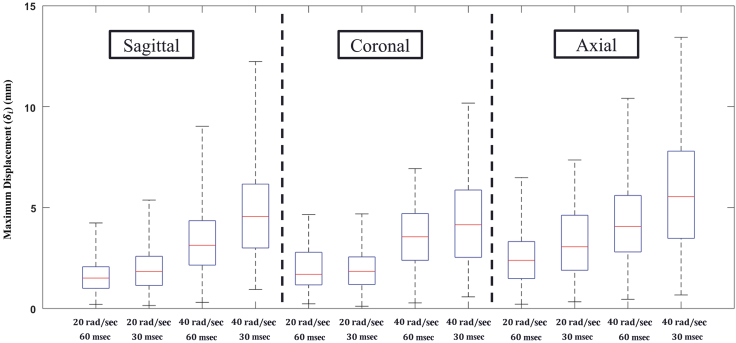
The ${\delta }_i$ values for each receiver, and for all specimens registered to a common anatomical space, are shown in Figure 4 for the most severe loading condition tested in this study (40 rad/sec – 30 msec). There was a spatial dependence of brain motion, with receivers in the inferior brain regions, including the cerebellum and brainstem, experiencing the lowest levels of displacement across all rotation directions and severity. The range of ${\delta }_i$ for all crystals for each test condition are depicted in the box plot in Figure 5. The highest displacements were recorded for the axial, 40 rad/sec, 30 msec test. For all rotation severities, the axial rotations resulted in greater displacements than the sagittal and coronal rotations, which experienced similar ranges of ${\delta }_i$. Within each loading direction, there were distinct increases in crystal displacement with increasing angular velocity. However, with regard to duration of the head rotation, there were mixed results: for the 20 rad/sec cases there was little difference in ${\delta }_i$ between the 30 msec and 60 msec cases, but for the 40 rad/sec cases there was a noticeable increase in ${\delta }_i$ with decreasing loading duration (i.e., increasing acceleration). This phenomenon is most pronounced in the coronal rotation cases.

FIG. 4.

Maximum displacement (${\delta }_i$) of all crystals for all specimens for the axial – 40 rad/sec – 30 msec tests in the sagittal (A), coronal (B), and axial (C) directions. Color image is available online.

FIG. 5.

Box plots of maximum displacement (${\delta }_i$) for all specimens for each test. The blue boxes represent the 25th and 75th quartile values, the red line represents the median, and the dashed lines represent the maximum and minimum values. Color image is available online.

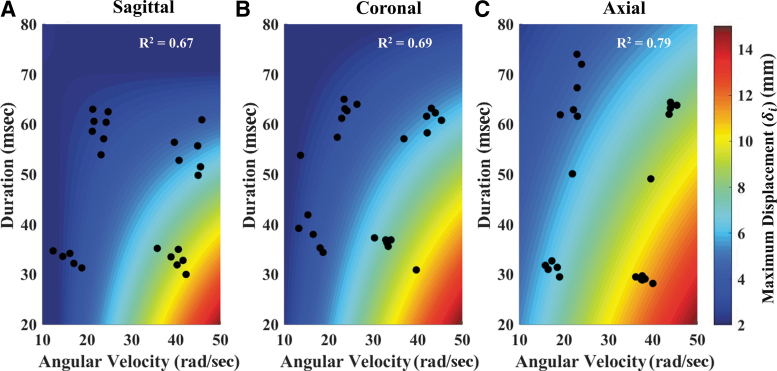
The ${\delta }_{max}$ for every test was used in a linear regression to determine the dependence of brain displacement on angular head kinematics, shown in Figure 6. The model fits had R² ranging from 0.67 to 0.79, and all coefficients in the linear regression were significant (p < 0.05). The regressions showed a dependence of brain displacement on angular kinematics, with increasing angular velocity and decreased duration causing increases in ${\delta }_{max}$. The sagittal and coronal rotation directions had similar trends and magnitudes of maximum ${\delta }_{max}$, whereas the axial direction resulted in higher displacements for the same input kinematics. Similar trends are identified for the averaged brain displacement response when using ${\delta }_{mean}$ as the regressed variable.

FIG. 6.

Surface plots depicting the results of the linear regression model for maximum brain displacement (${\delta }_{max}$) using the maximum angular velocity and duration for the sagittal (A), coronal (B), and axial (C) tests. The black dots correspond to the data points (${\delta }_{max}$) used in the regression fit. The sagittal regression model had an R² of 0.67. The coronal regression model had an R² of 0.69. The axial regression model had an R² of 0.79. All estimated coefficients of the regression model were statistically significant (p < 0.05). Color image is available online.

Discussion

An understanding of the biomechanics of the brain during injurious loading of the head is essential to predicting and mitigating injury. A human brain motion dataset with accurate, repeatable, and well-defined loading conditions partially fulfills a major need in the TBI biomechanics field. Expanding on a methodology developed in Alshareef and colleagues,³⁷ this study generated a dataset of human brain displacement with six subjects varying in sex, age, and anthropometry. The dataset contains approximately 5000 brain motion traces that can each be used to improve and validate FE brain models.

Experimental methodology

The sonomicrometry method was utilized to measure brain displacement relative to the skull. With the development of this new application of the method, there were concerns about the effect on the brain response after conducting multiple tests on the same specimen, as well as the chosen sequence of kinematic severities and loading directions. Within the experiments, three assessments were conducted to ensure that the sonomicrometry method produced accurate and repeatable results and that the brain tissue was not experiencing permanent displacement (i.e., plastic damage) or any material damage or property changes (e.g., dynamic softening).

The first assessment was to verify that all crystals returned to their initial position after every test. On average, crystals distances (relative to all eight transmitters in the skull) returned to within 0.1 mm of their initial measurement after every test. The “return to zero” gives us two key pieces of information: 1) the crystals are moving with the brain tissue and not being tethered in any way, and 2) the brain is not experiencing inelastic deformation resulting in a change in shape or position. The second assessment was a repeatability experiment across kinematic severity. As reported in Alshareef and colleagues,³⁷ the repeatability, tested for the 40 rad/sec – 30 msec case in specimen 846, was excellent across all three orientations of loading, with a root mean square error (RMSE) of 0.375 ± 0.26 mm between the original and repeat tests. The repeatability tests were also conducted on various kinematic loading cases for the remaining five specimens, with the average RMSE ranging from 0.124 mm to 0.561 mm. The repeatability results show that the brain tissue is not damaged or experiencing inelastic deformation, even at the highest severity. They also show that the dynamic motion response of the brain, in both magnitude and phase, remains unaltered.

The third assessment was a repeatability experiment across the orientation of rotation and the chosen sequence of experiments. The sagittal tests, which were conducted first for all specimens, were repeated for specimen 896 at the conclusion of the other two orientations. The sequence of tests was sagittal, coronal, axial, and sagittal (repeat). All four kinematic severities were repeated, with an RMSE of 0.587 ± 0.42 mm between the first set of the sagittal test and the repeats at the end of the test series. The larger RMSE for the brain deformation results can be attributed partially to the differences in applied head kinematics between the first set of sagittal tests and the last set, which can arise due to the environmental variables of the pneumatics of the test device when a repeat test is conducted hours later. Nonetheless, all measurements of repeatability resulted in differences less than the radius of the sonomicrometry crystals used in the study. Further, the results of the sagittal repeat experiments show that effect of testing sequence had little effect on the measured brain deformation.

There are a few limitations of the sonomicrometry method that were addressed in this study. The experimental limitations of sonomicrometry have been described by Alshareef and colleagues,³⁷ as well as limitations associated with noise and signal processing.⁴¹ The experimental limitations included: a maximum of 24 crystals embedded in the brain tissue due to a limitation of the number of channels used in the sonomicrometry data acquisition, the presence of crystal wires that must be routed and given sufficient slack, and an arduous preparation procedure. Meticulous design and insertion procedures mitigated these limitations through a diffuse spatial distribution of crystals and verification of wire slack through CT and repeatability experiments.

From a signal processing perspective, noise errors can occur in sonomicrometry data from electrical noise, acoustic reflections off the skull, or delayed wave-front triggering. Signal bias errors (or magnitude shifts) can occur in sonomicrometry data from an error in the speed of sound defined for the tissue, CT measurement of the initial position, and in level shifts that occur as a result of the chosen receiver wave-front triggering sensitivity.^42–44 Both types of error were considered in the design stage to reduce their effects, such as choosing a sampling rate that sufficiently captures the brain response and eliminates reflections associated with the sequential triggering of each transmitter. Additionally, these errors were considered in the trilateration stage, where various non-linear filtering and trilateration algorithms were evaluated to mitigate their effects.⁴¹ The Kalman filtering trilateration method used in this study was the least sensitive to measurement and signal errors.

Brain biomechanics

An extensive dataset of human brain motion allows for insight into brain biomechanics that has previously relied on animal experiments and FE models. Although previous human brain deformation experiments conducted included a breadth of tests and severities with different specimens,³⁶ this is the first dataset to produce data for multiple loading directions and severities for the same set of specimens. The consistency and repeatability of this dataset allows for comparisons of the same point in the brain across different angular velocities, loading durations, and rotation directions to systematically identify the effects of head motion on the resulting displacement of the brain. The head rotation in the axial plane caused the largest brain displacements for all four loading severities. The sagittal and coronal directions had similar displacement magnitudes, with the sagittal direction resulting in slightly greater maximum displacements. The dependence of brain deformation on rotation loading direction has been investigated using analytical, physical, and computational models of the brain,^10,19,25 and from this work hypotheses were formed regarding the brain strain sensitivity to axial rotations. The current study validates these earlier hypotheses and supports the use of the direction-dependence in criteria used to assess the efficacy of equipment designed to mitigate TBI.

Brain motion also depended on the angular velocity and duration of the head-rotation pulse (Fig. 6). Increasing angular velocity and decreasing pulse duration resulted in larger brain displacements across all loading directions. The purpose of the regression analysis (Fig. 6) used to investigate the dependence on brain displacement on head angular velocity was only to objectively determine a dependence on head rotational kinematics, not to predict or interpolate brain deformation at various magnitudes and duration of angular velocity. Although each regression had a high R² value, only 24 data points across a limited number of loading conditions were used to create each regression fit. The quantification of ${\delta }_i$ was also limited to the spatial distribution of crystals in each specimen, so this measure is inherently biased depending on where the crystals are placed. Because there was small variability in crystal placement, differences in maximum displacement could be partially attributed to the sampled brain regions, and not the angular kinematics. These limitations prevent the use of the regression surface (Fig. 6) to interpolate brain deformation or to predict injury risk.

Rotational pulse severities

The rotational severities applied to the specimens were chosen to represent head impact conditions observed in automotive and sports impacts associated with mild-to-moderate risk of TBI. The rotational pulses applied to the head-neck specimen were chosen based on previous work that examined brain deformation from nearly 1600 reconstructed automotive and impact tests using a human FE brain model,⁴⁵ with interquartile ranges for angular velocity between 23.2 rad/sec and 41.0 rad/sec and angular acceleration between 1540 rad/sec² and 4120 rad/sec². The reconstructed cases span a range of plausible head kinematics, from non-injury to concussion to moderate and severe TBI, based on the developed injury criteria.⁴⁵ Additional studies have identified rotational head kinematics in human volunteer tests,⁴⁶ with angular velocities up to 37 rad/sec and angular accelerations up to 2500 rad/sec², and in football reconstruction impacts,⁴⁷ with angular velocity ranging from 10.1 rad/sec to 64.5 rad/sec and angular acceleration ranging from 1099 rad/sec² to 10875 rad/sec².

The correlation between human brain deformation and associated head impact severity has only been investigated systematically using FE models. Experimental brain motion measurements have been made using impact testing on PMHS,³⁶ with rotational velocities ranging from 4 to 30 rad/sec, and head rotational accelerations ranging from 2370 to 24,206 rad/sec². However, these tests, being a primarily linear acceleration model with a limited sample of brain motion points, were insufficient to provide any statistical quantification on the dependence of brain motion to head rotational kinematics. Brain deformation measurements using tagged MRI on human volunteers³¹ were tested at rotational severities of 2 to 3 rad/sec and approximately 300 rad/sec², but the small amount of deformation and single loading severity precludes a correlation between head kinematics and brain deformation. Although this study provides a limited set of four severities across three loading directions, it is a valuable initial step into improving our understanding of the link between head kinematics, brain deformation, and clinical injury risk.

Finite element model validation

Direct measurement of tissue-level deformation of a living brain under head impact, outside of controlled laboratory experiments, remains elusive and challenging. Anatomically detailed FE models provide a valuable alternative and have been vital to approximating the temporal and spatial mechanical behavior of the brain. These models allow for a cost-effective investigation of the brain response under various loading conditions at a level that is not possible using cadaveric or human experiments, and their potential ability to predict injury has started to influence consumer safety standards across multiple industries. Therefore, it is essential that FE brain models are validated using human brain motion under injurious loading conditions. The availability of this digital dataset of human brain motion with precise measurement location and six DOF loading conditions, as well as similar loading conditions for multiple specimens, allows for thorough and rigorous validation of FE models. The biofidelity of these models is of utmost importance to the TBI field, and meticulous comparison of model-simulated brain motion to this human experimental brain motion is essential.

Extension of the sonomicrometry method

One of the most prominent debates in the field of TBI injury biomechanics has been on the injury tolerance of the brain as it relates to either the linear or rotational kinematics of the head. Due to the incompressible nature of brain tissue and closed volume of the skull, the prevailing hypothesis is that rotational, not linear, head kinematics are responsible for the shear deformations of brain tissue that lead to the diffuse injuries associated with TBI.^19,21 Although this concept has been demonstrated using computational brain models,^7,10,45 this is the first experimental study to demonstrate the large magnitudes of brain displacement caused by controlled, dynamic rotation of the head without impact. The sonomicrometry methodology developed in this project provides a unique platform for investigating the influence of head kinematics on the ensuing brain deformation in a controlled and repeatable manner. To expand this line of research, future investigations may be performed in pure linear loading conditions or combined rotational and linear loading conditions using the platform developed in this study to examine the relative contributions of each type of loading to brain deformation.

The sonomicrometry method can also be extended to animal models, allowing correlation of brain motion to clinical injury. Matched-pair testing may then be performed with sonomicrometry and survival cohorts receiving identical loading to identify injury prediction metrics and pathological outcomes. Such studies would help “close the loop” that has existed between biomechanical input, brain deformation, and injury.

Conclusion

The sonomicrometry method was utilized to generate a dataset of human brain motion containing six specimens, 12 test severities, and approximately 5000 individual brain displacement traces. The measurements collected during this study demonstrate the dependence of brain motion on rotation severity, loading direction, and location within the brain. This dataset can be used to investigate fundamental brain mechanics, create kinematics injury criteria for safety standards, and develop and validate FE brain models. The full dataset of the sonomicrometry experiments can be obtained from the National Highway Traffic Safety Administration, or by requests made to Dr. Panzer.

Funding Information

This study was sponsored by the National Highway Traffic Safety Administration under contract number DTNH221500022/0002.

Author Disclosure Statement

No competing financial interests exist.