Abstract
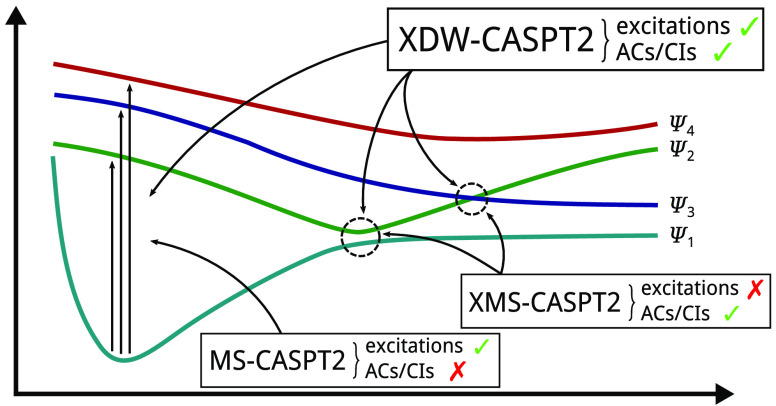
We introduce a new variant of the complete active space second-order perturbation theory (CASPT2) method that performs similarly to multistate CASPT2 (MS-CASPT2) in regions of the potential energy surface where the electronic states are energetically well separated and is akin to extended MS-CASPT2 (XMS-CASPT2) in case the underlying zeroth-order references are near-degenerate. Our approach follows a recipe analogous to that of XMS-CASPT2 to ensure approximate invariance under unitary transformations of the model states and a dynamic weighting scheme to smoothly interpolate the Fock operator between state-specific and state-average regimes. The resulting extended dynamically weighted CASPT2 (XDW-CASPT2) methodology possesses the most desirable features of both MS-CASPT2 and XMS-CASPT2, that is, the ability to provide accurate transition energies and correctly describe avoided crossings and conical intersections. The reliability of XDW-CASPT2 is assessed on a number of molecular systems. First, we consider the dissociation of lithium fluoride, highlighting the distinctive characteristics of the new approach. Second, the invariance of the theory is investigated by studying the conical intersection of the distorted allene molecule. Finally, the relative accuracy in the calculation of vertical excitation energies is benchmarked on a set of 26 organic compounds. We found that XDW-CASPT2, albeit being only approximately invariant, produces smooth potential energy surfaces around conical intersections and avoided crossings, performing equally well to the strictly invariant XMS-CASPT2 method. The accuracy of vertical transition energies is almost identical to MS-CASPT2, with a mean absolute deviation of 0.01–0.02 eV, in contrast to 0.12 eV for XMS-CASPT2.
1. Introduction
The theoretical modeling of excited states processes is undoubtedly of fundamental and practical importance.1 The investigation of physical mechanisms at the base of chemi- and bioluminescence,2 spectroscopy,3 singlet fission,4 and many other scientifically and technologically relevant applications require methodologies that are able to describe the entire potential energy surface (PES), providing accurate relative energies between different electronic states, their correct orderings, and the right morphology in regions of near-degeneracies.5 Single-reference approaches, despite their widespread success, do not generally have the necessary flexibility to be applied indistinctly in any situation that one might encounter in the realm of excited states chemistry: a multireference approach is unavoidable. From the several available options, multireference perturbation theory (MRPT) stands out: its accuracy, general applicability, and moderate computational cost elected it during the last few decades as the method of choice for the investigation of full potential energy surfaces.5 In particular, formalisms that allow the relaxation of the reference states under the influence of the perturbation have seen the most success,6−20 with the multistate complete active space second-order perturbation theory (MS-CASPT2)11 approach being one of the most popular. Relying on the multipartitioning technique,8 this methodology is well suited for the calculation of transition energies between states that are well separated, with deviations within 0.1–0.2 eV from the best theoretical estimates.21,22 On the other hand, even though MS-CASPT2 follows the “diagonalize-then-perturb-then-diagonalize” philosophy, it may still suffer from unphysical behaviors at molecular geometries with near-degenerate reference states. A theoretical understanding of this shortcoming is known,23 and it can be solved by enforcing the states to be invariant under unitary transformations within the model space, leading to the so-called extended MS-CASPT2 (XMS-CASPT2)24 method. However, XMS-CASPT2 requires a unique partitioning of the Hamiltonian, which is achieved through the use of a state-average Fock operator at zeroth-order. Employing a state-average operator might degrade the accuracy of the zeroth-order approximation as the dimension of the model space is increased or when the states under consideration are of different character (e.g., valence and Rydberg). This is because several states have to be described simultaneously by a single operator, in contrast to having operators tailored for each state individually.
The main objective of this work is to formulate a new CASPT2 variant that retains the accuracy of MS-CASPT2 in the calculation of transition energies and at the same time yields smooth potential energy surfaces with no artifacts in regions where the excited states manifold is near-degenerate. Our approach is based on the same transformation carried out in the initial step of XMS-CASPT2 and then uses a dynamical weighting scheme to interpolate between state-specific and state-average operators; hence we call it extended dynamically weighted CASPT2 (XDW-CASPT2). From a theoretical standpoint, XDW-CASPT2 corresponds to a new and somewhat sophisticated partitioning of the Hamiltonian, thus retaining the underlying structure of the parent theory. Recently, an analogous attempt to find a zeroth-order Hamiltonian that coincides with the canonical MS-CASPT2 one and at the same time is invariant as in XMS-CASPT2 was carried out by Park.25 XDW-CASPT2 also shares some similarities with the recently introduced dynamically weighted driven similarity renormalization group (DW-DSRG)26 as well as the dynamically weighted complete active space self-consisted field method.27,28
This Article is structured as follows: In section 2, we first selectively review important aspects of quasidegenerate perturbation theory (QDPT), MS-CASPT2, and XMS-CASPT2 necessary to define XDW-CASPT2 in the remainder of the section. Next, section 3 is devoted to the assessment of the new methodology and is divided in three parts. First, an extensive study on the dissociation of LiF is presented: this problem being a prototypical example to show all features of the new method. Second, the conical intersection in the distorted allene molecule is investigated, which represents a difficult case for QDPT-based approaches. Third, the accuracy of vertical transition energies to the lowest singlet excited state is evaluated on a set of 26 small to medium organic compounds. At last, in section 4, we conclude by summarizing the results obtained in this contribution and with an outlook on future directions regarding XDW-CASPT2.
2. Theory
As in any perturbation theory approach, the starting point is to partition the full Hamiltonian into a zeroth-order part Ĥ0, with known eigenfunctions Ψα(0) and associated eigenvalues Eα, and a perturbation operator V̂ = Ĥ – Ĥ0. The Hilbert space is also partitioned into a model space, spanned by model functions (also called reference functions) selected from the set of zeroth-order ones, and a complementary space, spanned by all other functions orthogonal to the model ones. The projector onto the model space is defined as
| 1 |
where 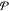 denotes the
set of indices labeling the
reference states. The projector onto the complementary space is simply
defined as Q̂ = 1̂ – P̂. Note that the complementary space does not necessarily have to
be spanned by the remaining zeroth-order functions not included in
the model space: other types of many-electron functions can be used.
The wave operator,29 Ω̂, defined
as an operator that acting on a model state Ψα(0) generates the exact one
(i.e., of the full Hamiltonian Ĥ)
denotes the
set of indices labeling the
reference states. The projector onto the complementary space is simply
defined as Q̂ = 1̂ – P̂. Note that the complementary space does not necessarily have to
be spanned by the remaining zeroth-order functions not included in
the model space: other types of many-electron functions can be used.
The wave operator,29 Ω̂, defined
as an operator that acting on a model state Ψα(0) generates the exact one
(i.e., of the full Hamiltonian Ĥ)
| 2 |
is governed by the generalized Bloch equation30
| 3 |
Assuming intermediate normalization, an effective Hamiltonian is constructed according to
| 4 |
whose eigenvalues and eigenfunctions (within the model space) correspond to the exact ones. To arrive at a practical implementation of QDPT, Ω̂ is expanded in powers of the perturbation operator
| 5 |
and substituted into eq 4 leading to the second-order effective Hamiltonian
| 6 |
with the superscript (n) denoting the order in V̂. Expressing Ĥeff(2) in the model space basis and diagonalizing the resulting matrix provides the second-order correction to the energies and the perturbatively modified zeroth-order wave functions. To determine Ω̂(1) in eq 6, one has to solve the first-order generalized Bloch equation
| 7 |
which is obtained upon inserting eq 5 into eq 3 and equating only the terms which are of first order in V̂. Note that the application of Ω̂(1) to Ψα(0) generates the first-order correction to the wave function
| 8 |
for all 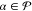 .
.
2.1. MS-CASPT2
In the
multistate CASPT2
method,11 the zeroth-order functions defining
the model space are of complete active space self-consistent field
(CASSCF) type. For each 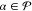 ,
there is a separate partitioning of the
full Hamiltonian,31Ĥ = Ĥ0α + V̂α, with the zeroth-order part defined by
,
there is a separate partitioning of the
full Hamiltonian,31Ĥ = Ĥ0α + V̂α, with the zeroth-order part defined by
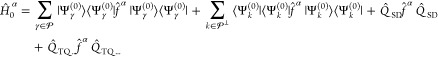 |
9 |
The first sum is restricted to states
in the model space (including γ = α), while the second
one runs over all other states of the complete active space, with 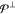 being the set of indices labeling them.
The remaining part of the complementary space is spanned by internally
contracted configurations (ICCs)32,33 obtained by
the application of excitation operators to the reference states Ψα(0). The operator Q̂SD projects onto the so-called first-order
interacting space that, for the sake of this theoretical discussion,
we shall assume is always generated from the union of all model states.a Similarly, Q̂TQ... projects onto the space spanned by higher-order ICCs. Note that
the use of ICCs allows to study larger systems compared to an uncontracted
approach, for which the steep computational scaling would severely
limit its applicability. On the downside, the use of ICCs constitutes
an approximation: for a detailed comparison in the context of multireference
configuration interaction, see the work by Sivalingam et al.34 The generalized Fock operator f̂α is given by
being the set of indices labeling them.
The remaining part of the complementary space is spanned by internally
contracted configurations (ICCs)32,33 obtained by
the application of excitation operators to the reference states Ψα(0). The operator Q̂SD projects onto the so-called first-order
interacting space that, for the sake of this theoretical discussion,
we shall assume is always generated from the union of all model states.a Similarly, Q̂TQ... projects onto the space spanned by higher-order ICCs. Note that
the use of ICCs allows to study larger systems compared to an uncontracted
approach, for which the steep computational scaling would severely
limit its applicability. On the downside, the use of ICCs constitutes
an approximation: for a detailed comparison in the context of multireference
configuration interaction, see the work by Sivalingam et al.34 The generalized Fock operator f̂α is given by
| 10 |
where Êpq is the second-quantized spin-summed one-particle excitation operator and fpqα are entries of the Fock matrix expressed in the molecular orbital basis
| 11 |
Here, hpq and (pq|rs) are elements of the one-particle Hamiltonian and the two-electron repulsion integrals, respectively, while Drsα = ⟨Ψα|Êrs|Ψα(0)⟩ are entries of the one-particle reduced density matrix (1-RDM or also simply called density matrix) of state Ψα. The indices p, q, r, and s label general molecular orbitals. The use of projectors in eq 9 for the definition of Ĥ0 is necessary because the CASSCF states are not eigenfunctions of the generalized Fock operator. Furthermore, note that every Ĥ0α is diagonal within the model space since f̂α is projected directly onto the reference states rather than onto the space spanned by them. In other words, even though in general
| 12 |
for 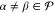 and
and 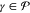 , these elements are arbitrarily set to
zero in MS-CASPT2. This constitutes an approximation that we will
call, hereafter, diagonal approximation and that
was already strongly emphasized by Granovsky.23 The immediate consequence of this choice is that, upon inserting eq 9 into eq 7, the solution of the first-order generalized
Bloch equation can be obtained for each state of the model space separately,
as these are not coupled anymore. The substantial advantage gained
is the possibility to use state-specific Fock operators in Ĥ0, allowing for a formalism based on
multipartitioning that should provide more accurate zeroth-order energies.
In particular, for states that are energetically well separated or
have considerably different character, state-specific Fock operators
are in principle better suited to describe them than, for instance,
a single operator that requires the flexibility to account for all
states in an average way.
, these elements are arbitrarily set to
zero in MS-CASPT2. This constitutes an approximation that we will
call, hereafter, diagonal approximation and that
was already strongly emphasized by Granovsky.23 The immediate consequence of this choice is that, upon inserting eq 9 into eq 7, the solution of the first-order generalized
Bloch equation can be obtained for each state of the model space separately,
as these are not coupled anymore. The substantial advantage gained
is the possibility to use state-specific Fock operators in Ĥ0, allowing for a formalism based on
multipartitioning that should provide more accurate zeroth-order energies.
In particular, for states that are energetically well separated or
have considerably different character, state-specific Fock operators
are in principle better suited to describe them than, for instance,
a single operator that requires the flexibility to account for all
states in an average way.
On the other hand, the diagonal approximation has a profound impact on the invariance properties of the method as elucidated by Granovsky23 in the context of multiconfigurational QDPT (MCQDPT). There are two main issues. First, when two reference states interact strongly at zeroth-order, meaning that the element ⟨Ψα(0)|f̂γ|Ψβ⟩ is significantly larger than zero, it can be shown23 that neglecting it leads to large systematic errors in the corresponding off-diagonal element of the second-order effective Hamiltonian. Second, it is known that zeroth-order states at a conical intersection (CI) and, to a large extent, at an avoided crossing (AC) as well are not well-defined: in such situations any linear superposition of the involved states constitutes an equally valid or almost equally valid wave function. Hence, simply projecting the Fock operator onto the individual components entails an arbitrary choice, which often leads to the appearance of artifacts on the potential energy surface in the vicinity of the AC or CI.
In conclusion, we should note that it is possible to adopt a unique partitioning in MS-CASPT2, for instance with the use of a state-average Fock operator. Such an approach, however, would lose the advantages of multipartitioning but keep the issues related to the lack of invariance. Nevertheless, this strategy has been recently explored by Kats and Werner35 in the context of pair natural orbital MS-CASPT2, finding systematic deviations from canonical MS-CASPT2 by 0.1 to 0.2 eV for transitions to the lowest singlet excited state.
2.2. XMS-CASPT2
The main flaw of MS-CASPT2 is the lack of invariance under unitary transformations within the model space. The result obtained with a particular set of reference states should always be the same to the one obtained with a set of states generated by a unitary transformation of the original ones. This shortcoming is ascribed to the diagonal approximation of Ĥ0, and the solution to this problem was first proposed by Granovsky23 for MCQDPT and was, shortly thereafter, applied to MS-CASPT2 by Shiozaki et al.24 The key difference of the new methodology, XMS-CASPT2, is in the zeroth-order Hamiltonian
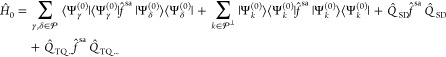 |
13 |
The Fock operator is now projected onto the full model space rather than onto the individual components alone. This implies a unique partitioning of the Hamiltonian because the first-order generalized Bloch equation, eq 7, does not decouple the states anymore. The Fock operator f̂sa is constructed from the state-average density matrix
| 14 |
for a model space containing d statesb. The fact that Ĥ0 is no longer diagonal in the zeroth-order basis makes the solution of eq 7 somewhat harder. However, this complication can be fully overcome by a unitary transformation of the reference states, such that the rotated wave functions
| 15 |
diagonalize the Fock operator within the model space. In other words, the rotated model states satisfy
| 16 |
for 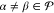 .
Using the wave functions Ψ̃α(0), the zeroth-order
Hamiltonian can now be rewritten as
.
Using the wave functions Ψ̃α(0), the zeroth-order
Hamiltonian can now be rewritten as
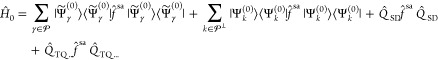 |
17 |
which has the same form of eq 9, albeit the use of the state-average Fock operator. Therefore, MS-CASPT2 truly corresponds to an approximation of XMS-CASPT2, provided that the same unique partitioning of the Hamiltonian is used in both variants. The generalizations introduced with eq 13 make this method invariant under unitary transformations of the model space wave functions, solving the issues intrinsic to the diagonal approximation of MS-CASPT2. As a result, XMS-CASPT2 is more robust in general, with energies that are continuous and smooth functions of the molecular geometry even in the vicinity of ACs and CIs. The price to pay is the use of f̂sa in Ĥ0, treating the states in an average fashion at zeroth-order, which, as more states are included in the model space, might decrease the accuracy of the method. An instance of this behavior is reported for glycine in the Supporting Information, thereby showing the dependence on two vertical excitations as a function of the model space dimension. By averaging over different numbers of states, XMS-CASPT2 shows a strong dependence on the model space dimension, which tends to deteriorate its accuracy as this increases. For example, the nO → π* transition (experimentally reported to be in the range 5.8–6.0 eV47) goes from an estimated value of 5.82 eV obtained with the smallest model space considered (1 state) to a value of 5.08 eV for the largest one (7 states). This deterioration of the accuracy is ascribed to the use of a state-average Fock operator instead of a state-specific one, such as in MS-CASPT2 (see Supporting Information for a detailed discussion). However, we should point out that this does not imply that XMS-CASPT2 transition energies are less accurate than MS-CASPT2 in general, but at the very least, one should expect a stronger dependence on the model space dimension for the former. Ultimately, only a systematic and comprehensive benchmark of XMS-CASPT2 will shed more light on its accuracy, which, to the best of our knowledge, is not available in the literature contrary to the case of MS-CASPT2.21,22
2.3. XDW-CASPT2
The necessary ingredients to design a hybrid approach that interpolates between MS-CASPT2 and XMS-CASPT2 are the use of state-specific Fock operators in a multipartitioning formalism and the projection of Ĥ0 onto the full model space rather than onto individual reference states. The objective is a method that performs as well as MS-CASPT2 in situations where states are clearly discernible and is as robust as XMS-CASPT2 when these are instead quasidegenerate. We note from our previous discussion that in case the zeroth-order Hamiltonian has negligible off-diagonal elements within the model space, that is
| 18 |
the diagonal approximation is a sound simplification of the generalized Bloch equation. Crucially, it allows for a formalism based on multipartitioning. Thus, we are seeking a unitary transformation as in eq 15, whereby the rotated states satisfy
| 19 |
for 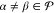 ,
with the Fock operator
,
with the Fock operator 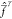 (note the bar to differentiate this operator
from the normal state-specific one) having the following property
(note the bar to differentiate this operator
from the normal state-specific one) having the following property
 |
20 |
for all 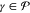 . Note that we shall better specify further
below what do weak and strong interactions mean in this context.
. Note that we shall better specify further
below what do weak and strong interactions mean in this context.
We are able to satisfy eqs 19 and 20 with the following scheme. In
a first step, completely analogous to XMS-CASPT2, a set of rotated
model states Ψ̃α(0) is obtained by diagonalization of the state-average
Fock operator 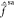 . These
functions are then used to construct
dynamically weighted density matrices of the form
. These
functions are then used to construct
dynamically weighted density matrices of the form
| 21 |
with weights satisfying the condition
| 22 |
for all 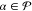 .
The use of tildes emphasizes that D̃β is the 1-RDM associated with the
rotated state Ψ̃β(0). Using the densities defined in eq 21, state-specific Fock
operators are constructed according to eqs 10 and 11 for all
.
The use of tildes emphasizes that D̃β is the 1-RDM associated with the
rotated state Ψ̃β(0). Using the densities defined in eq 21, state-specific Fock
operators are constructed according to eqs 10 and 11 for all 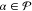 and used to define the partitioning of
the Hamiltonian for a subsequent MS-CASPT2 calculation. Thus, XDW-CASPT2
substantially consists in a MS-CASPT2 calculation employing zeroth-order
states defined by eq 15 and state-specific Fock operators constructed with densities
and used to define the partitioning of
the Hamiltonian for a subsequent MS-CASPT2 calculation. Thus, XDW-CASPT2
substantially consists in a MS-CASPT2 calculation employing zeroth-order
states defined by eq 15 and state-specific Fock operators constructed with densities 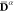 .
.
The weights ωαβ are chosen such that the resulting Fock
operators 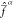 satisfy the prescription of eq 20. This is achieved by using a scheme
recently introduced by one of the authors of this contribution and
his collaborators,26 whereby ωα is
defined by the following Boltzmann-like function
satisfy the prescription of eq 20. This is achieved by using a scheme
recently introduced by one of the authors of this contribution and
his collaborators,26 whereby ωα is
defined by the following Boltzmann-like function
| 23 |
where Δαβ (Δαγ) quantifies
the interaction between states Ψ̃α(0) and Ψ̃β (Ψ̃γ(0)) and 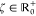 is a parameter controlling the sharpness
of the transition between mixed-density and state-specific regimes.
Let us list the asymptotic properties of eq 23 with respect to Δαβ
is a parameter controlling the sharpness
of the transition between mixed-density and state-specific regimes.
Let us list the asymptotic properties of eq 23 with respect to Δαβ
| 24 |
| 25 |
A physical quantity that satisfies eqs 24 and 25 is given by the energy difference between the rotated states
| 26 |
When computing the contribution of state Ψβ(0) to the density of Ψα, if their energy difference is large, Δαβ ≫ 0, then Ψβ(0) should not contribute: ωα ≈ 0. This situation corresponds to the case in which the two states are weakly or not interacting. Vice versa, if the energy difference is small, Δαβ ≈ 0, then Ψβ(0) is quasidegenerate with Ψα and should receive approximately the same weight: ωαβ ≈ ωβ. This situation corresponds to the case in which the two states are strongly interacting. Note that, somewhat counterintuitively, strong interaction is associated with a small value of the parameter Δαβ and conversely weak interaction with a large one. Simply using an energetic criterion to parametrize the interaction strength between two states can lead to unphysical averaging: for example, two states of different symmetry (spin or spatial) should not be mixed together irrespective of their relative energy. In this work, this problem has been circumvented by treating states of different symmetry separately, however, a more general solution is possible. For instance, by multiplying the right-hand side of eq 26 by a factor dependent on the off-diagonal element of the full Hamiltonian expressed in the basis of rotated references, ⟨Ψ̃α(0)|Ĥ|Ψ̃β⟩, Δαβ would account for the physical nature of the states without resorting on external constraints (e.g., forcing symmetries). Importantly, such a modification would correctly model changes of the molecular geometry that break the symmetry of the system.
For a fixed state Ψα(0), the parameter ζ modulates the importance of other states in a collective manner: a small value tends to make them all equally important, whereas a large value favors the state under consideration. The asymptotic behavior of ωα with respect to ζ is given by
| 27 |
| 28 |
where d is the number of
model states. The situation depicted in eq 27 results in purely state-specific Fock operators
alike MS-CASPT2, albeit using densities of rotated reference functions.
On the other hand, if all weights are equal as shown in eq 28, the original XMS-CASPT2 is restored.
For the particular choice of Δαβ made in eq 26, ζ assumes Eh–2 units and its value can be regarded
as a threshold. When the value of Δαβ is in the same order of magnitude as ζ–1/2 or smaller, the state Ψβ will contribute significantly to 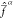 ; if instead Δαβ ≫
ζ–1/2, it will play little
to no role in
; if instead Δαβ ≫
ζ–1/2, it will play little
to no role in 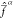 .
.
As a final remark, we should note that eq 23 was used in a similar fashion in the recent work by Li et al.,26 where not only the 1-RDM was averaged with dynamical weights but also higher-order RDMs. Importantly, the latter were introduced in the flow equations, whose solution provides the diagonal matrix elements of the effective Hamiltonian. In the approach presented here, the densities defined by eq 21 are only used to obtain an alternative partitioning of the Hamiltonian; the first-order equations that determine the correction to the wave function, and accordingly Ĥeff, make use of purely state-specific densities.
3. Results
In this section, we present the results obtained for a series of calculations representing typical use-case scenarios to assess the reliability of XDW-CASPT2. First, the avoided crossings in LiF are investigated. This prototypical system is an ideal model to highlight the strengths, weaknesses, and features of XDW-CASPT2 as compared to MS-CASPT2 and XMS-CASPT2. Since this example touches every aspect of the theory, the discussion of this case is quite extensive. Second, the conical intersection in the distorted allene molecule is considered. This system provides a tougher test for the invariance properties of the theory, thereby probing the robustness of the approach. At last, singlet vertical excitation energies are computed for a series of organic compounds in order to evaluate the accuracy of the method and the effect of the dynamical weighting scheme.
All calculations were performed with a development branch of OpenMolcas36 based on the master branch, version v18.09-617-g5a96a25e. Note that the CASPT2 implementation of OpenMolcas uses the SS-SR ICC basis, thereby never fully preserving invariance, not even for XMS-CASPT2.
3.1. Avoided Crossings in LiF
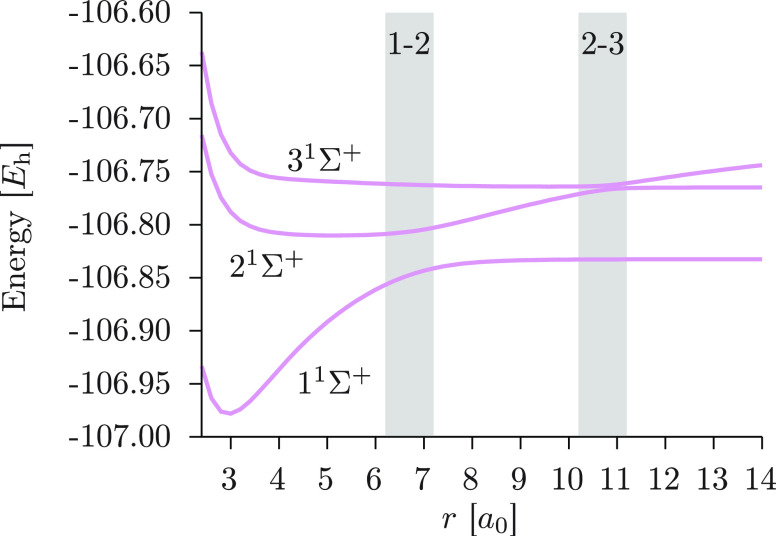
It is well-known that during the dissociation of lithium fluoride the two lowest singlet states of 1Σ+ symmetry undergo a rapid change of character switching between ionic and covalent.37 A state-average CASSCF (SA-CASSCF) calculation predicts the avoided crossing at a much shorter distance compared to the reference values (e.g., full configuration interaction) because of the missing dynamical electron correlation.11,38,39 Introduction of the latter in a state-specific manner, for instance through single-state CASPT2, results in an artificial double crossing of the two potential energy curves (PECs), which, alongside other issues present in the theory, has been a main motivation for the development of its multistate generalization. Nevertheless, even though MS-CASPT2 provides much more satisfactory results, it still faces severe complications at internuclear distances where the underlying reference states are quasidegenerate. This is particularly visible when considering the three lowest 1Σ+ states rather than the usual two. Instead, XMS-CASPT2 does not incur in any unphysical behavior irrespective of the number of states, however at the expense of a reduced accuracy in their relative energy at the equilibrium distance. Thus, lithium fluoride is an ideal system to test XDW-CASPT2, and to this end, we calculated its dissociation considering the three lowest singlet states simultaneously.
The reference wave functions were obtained by a SA-CASSCF40 calculation using equal weights for all three states and imposing the C2v molecular point group symmetry. The active space was composed of six electrons in 2 a1, 2 b1, and 2 b2 orbitals, while the remaining 3 occupied a1 orbitals were relaxed during optimization. The cc-pVTZ41 and aug-cc-pVTZ42 basis sets were used on lithium and fluorine, respectively. The potential energy curves were computed for internuclear distances between 2.4 and 14 a0 in steps of 0.2 a0. The results obtained with the CASSCF method are shown in Figure 1. At an internuclear distance comprised between 6.2 and 7.2 a0, the ground state wave function quickly changes from an ionic to a covalent character, whereas the opposite happens for the 21Σ+ one. The inclusion of a third state in the calculation plays a little role here: the position of this avoided crossing is slightly shifted to a shorter internuclear distance compared to a 2-state calculation (see Supporting Information for 2-state PECs). From 10.2 to 11.2 a0, a second avoided crossing between the 21Σ+ and the 31Σ+ states appear, where the character of the 31Σ+ wave function becomes ionic. These quasi-degeneracies among the CASSCF states have important consequences on the accuracy and effectiveness of the perturbative approach used to recover the dynamic electron correlation.
Figure 1.
SA-CASSCF potential energy curves of the three lowest 1Σ+ states of lithium fluoride. There are two avoided crossing regions (highlighted in gray), one between the ground and the first excited states, labeled 1–2, and one between the first and the second excited states, labeled 2–3.
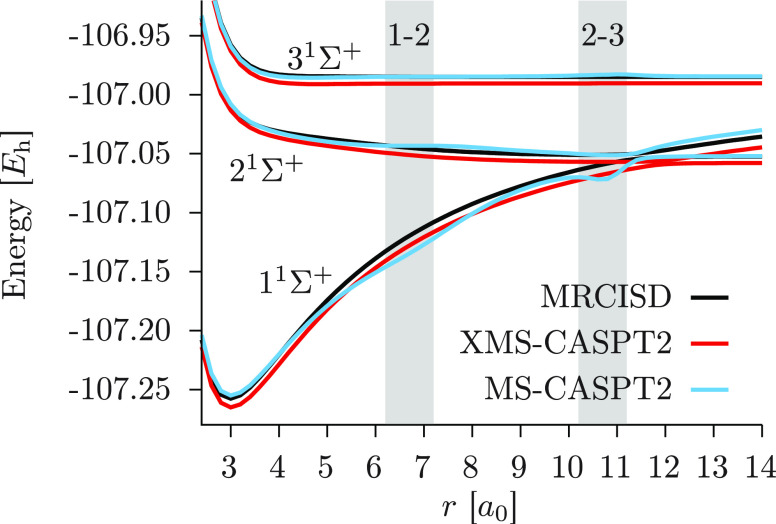
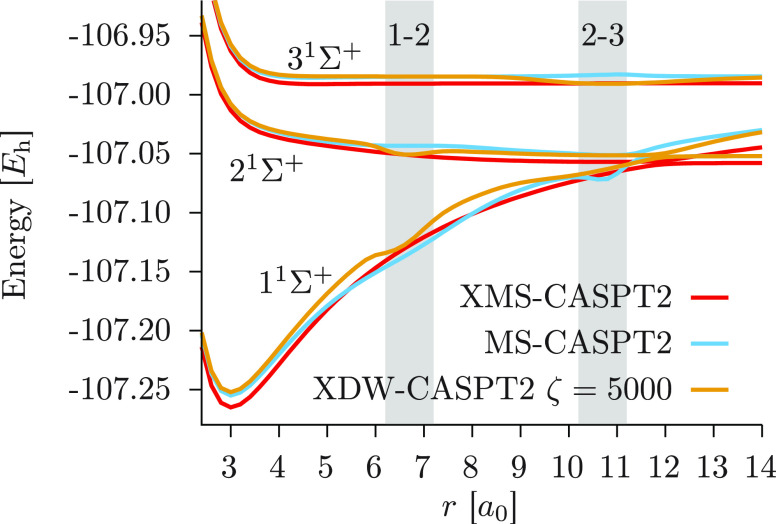
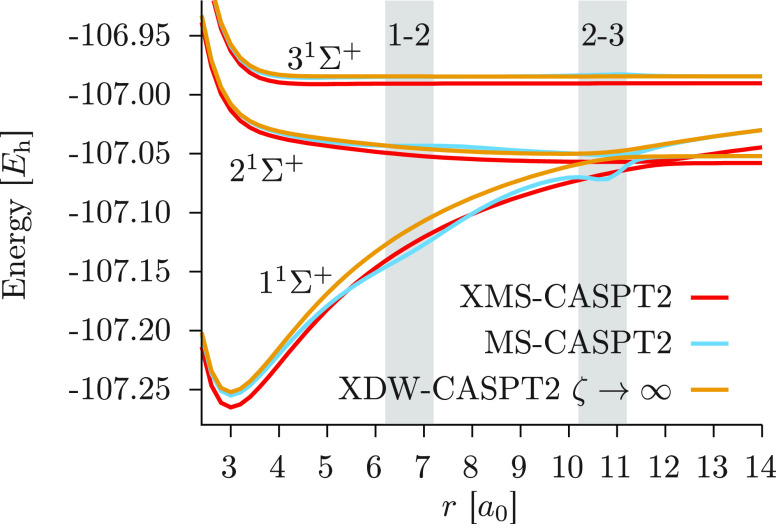
To establish reference curves, we report, in Figure 2, the PECs computed with MS-CASPT2, XMS-CASPT2, and multireference configuration interaction with singles and doubles (MRCISD), considering the latter the most accurate result. The use of MRCISD without Davidson’s correction as the reference instead of MRCISD+Q is supported by a better agreement to full CI (FCI) by the former (see the work by Varandas43 for more details). Nonetheless, we report in the Supporting Information the results obtained with MRCISD+Q, where an artificial double crossing is observed around an internuclear distance of 12 a0. For all three methodologies, the two 1s core orbitals were kept frozen, and the 2s orbital of fluorine was the only doubly occupied orbital correlated.c No shift was used in any CASPT2 calculation: neither real nor imaginary nor IPEA. In both regions where the avoided crossings happen at CASSCF level, we note a significant, unphysical distortion of the MS-CASPT2 curves, but not for the other two methods. The 1–2 AC is responsible for a “hump” in both the ground and first excited states, while around the 2–3 AC, we observe a clear artifact for the 11Σ+ state and, again, a small hump on the 31Σ+ curve. Remarkably, besides the issues in the AC regions, the MS-CASPT2 PECs fall right on top of the MRCISD ones: this is not the case for a 2-state calculation, in which the three methodologies provide three distinct results. Around the equilibrium distance MS-CASPT2 is in very good agreement with MRCISD, with transition energies to the first and second excited states underestimated by only 0.05 and 0.11 eV, respectively. In contrast, XMS-CASPT2 overestimates these excitations by 0.2 and 0.25 eV, respectively. On the other hand, the plot shown in Figure 2 demonstrates the effectiveness of XMS-CASPT2 in correcting the erratic behavior of the original theory, with PECs that are smooth throughout the entire range of r.
Figure 2.
Potential energy curves of the three lowest 1Σ+ states of lithium fluoride. The zones highlighted in gray correspond to the avoided crossing regions at the CASSCF level of theory.
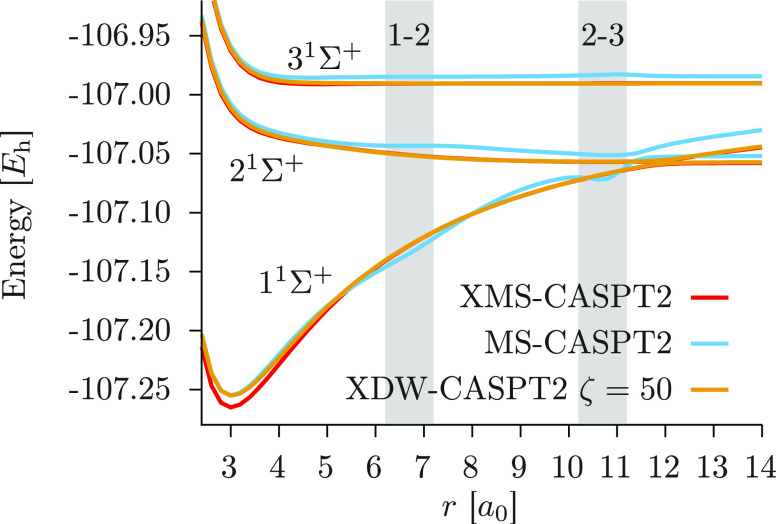
Let us now investigate the performance
of XDW-CASPT2 and study
the dissociation of LiF as a function of the exponent ζ. Recalling
that, for ζ = 0, all states receive the same weight regardless
of their energy difference (and thus the methodology is exactly equivalent
to XMS-CASPT2), we show in Figure 3 the results obtained by setting ζ = 50. The
XDW-CASPT2 potential energy curves substantially overlap the XMS-CASPT2
ones for most of the dissociation, showing no sign of artifacts at
any place. Crucially, the 11Σ+ state,
and to some extent the 21Σ+ and 31Σ+ states, smoothly slide over to the MS-CASPT2
curves for r < 5 a0, with an excellent agreement around the equilibrium distance. To
rationalize this result, we first analyze the structure of the transformation
matrix that diagonalizes 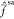 and inspect the magnitude of zeroth-order
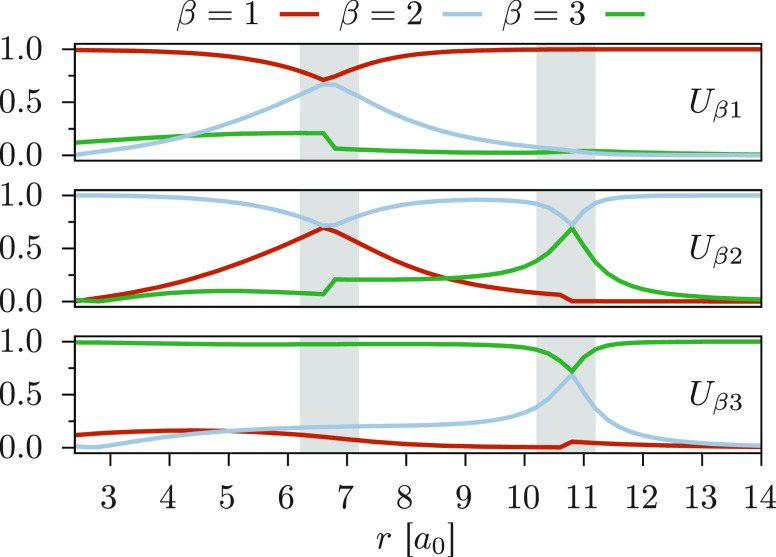
mixing among the states. In Figure 4, we show the absolute value of the rotation matrix
elements Uβα (cf., eq 15) as a
function of the internuclear distance. The top plot represents the
components of the ground state wave function. The magnitude of U31, that is, the curve corresponding to β
= 3, never exceeds 0.25 for the entire range of distances, meaning
that the contribution of Ψ3(0) to Ψ̃1 is very limited. In contrast, the
magnitude of U21, that is, the curve corresponding
to β = 2, increases when approaching r ≈
6.75 a0, with a peak at the SA-CASSCF avoided crossing.
Reciprocally, U11 decreases in the same
region substantially attaining the same value of U21 at r ≈ 6.75 a0,
implying an equal mix of these two states. Lastly, note that U11 is approximately 1 for most part of the plot,
that is the off-diagonal elements of
and inspect the magnitude of zeroth-order
mixing among the states. In Figure 4, we show the absolute value of the rotation matrix
elements Uβα (cf., eq 15) as a
function of the internuclear distance. The top plot represents the
components of the ground state wave function. The magnitude of U31, that is, the curve corresponding to β
= 3, never exceeds 0.25 for the entire range of distances, meaning
that the contribution of Ψ3(0) to Ψ̃1 is very limited. In contrast, the
magnitude of U21, that is, the curve corresponding
to β = 2, increases when approaching r ≈
6.75 a0, with a peak at the SA-CASSCF avoided crossing.
Reciprocally, U11 decreases in the same
region substantially attaining the same value of U21 at r ≈ 6.75 a0,
implying an equal mix of these two states. Lastly, note that U11 is approximately 1 for most part of the plot,
that is the off-diagonal elements of 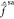 are
very small and therefore Ψ̃1(0) ≈ Ψ1. An analogous
analysis for the other two plots leads to the following general observations.
The magnitude of mixing is a signature of the quasi-degeneracies between
the states: around 6.75 a0 the ground and first excited
states are equally mixed, while the first and second excited states
mix just before 11 a0. Both cases are around the ACs. At r = 3 a0, U11 ≈ U22 ≈ U33 ≈
1, meaning that the original CASSCF wave functions are barely coupled
by
are
very small and therefore Ψ̃1(0) ≈ Ψ1. An analogous
analysis for the other two plots leads to the following general observations.
The magnitude of mixing is a signature of the quasi-degeneracies between
the states: around 6.75 a0 the ground and first excited
states are equally mixed, while the first and second excited states
mix just before 11 a0. Both cases are around the ACs. At r = 3 a0, U11 ≈ U22 ≈ U33 ≈
1, meaning that the original CASSCF wave functions are barely coupled
by 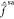 and
thus remain virtually the same after
the transformation. Note that the transformation matrix elements Uβα appear to be
discontinuous at certain internuclear distances. For instance, U31 (top plot) suddenly drops at the first avoided
crossing, while U32 (center plot) does
the opposite. This is because the wave functions of the first and
second states abruptly change character from r =
6.6 a0 to 6.8 a0, and essentially the off-diagonal
elements U31 and U32 are swapped. This is not an actual discontinuity but rather
a fictitious effect as a result of working with adiabatic states that
are labeled according to their energy, rather than diabatic ones identified
by their wave function character. Thus, if one would instead follow
a particular wave function, that is, by tracking the diabatic state
with the same label throughout the dissociation, the resulting curve
would be perfectly smooth. In general we can expect to see this effect
every time two states go through an AC or CI and will be visible for
other quantities too, for example, the off-diagonal Fock matrix elements.
and
thus remain virtually the same after
the transformation. Note that the transformation matrix elements Uβα appear to be
discontinuous at certain internuclear distances. For instance, U31 (top plot) suddenly drops at the first avoided
crossing, while U32 (center plot) does
the opposite. This is because the wave functions of the first and
second states abruptly change character from r =
6.6 a0 to 6.8 a0, and essentially the off-diagonal
elements U31 and U32 are swapped. This is not an actual discontinuity but rather
a fictitious effect as a result of working with adiabatic states that
are labeled according to their energy, rather than diabatic ones identified
by their wave function character. Thus, if one would instead follow
a particular wave function, that is, by tracking the diabatic state
with the same label throughout the dissociation, the resulting curve
would be perfectly smooth. In general we can expect to see this effect
every time two states go through an AC or CI and will be visible for
other quantities too, for example, the off-diagonal Fock matrix elements.
Figure 3.
Potential energy curves of the three lowest 1Σ+ states of lithium fluoride. Note that to a large extent the XMS-CASPT2 curves are covered by the XDW-CASPT2 ones.
Figure 4.
Absolute value of the elements Uβα of the rotation matrix mixing the zeroth-order CASSCF wave functions. The ground state (α = 1) is shown at the top; the first excited state (α = 2) is in the center, and the second excited state (α = 3) is at the bottom. The zones highlighted in gray correspond to SA-CASSCF ACs.
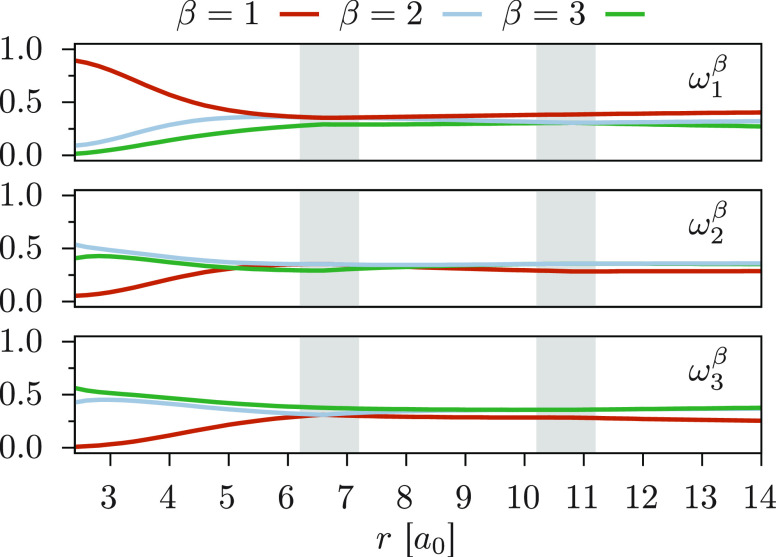
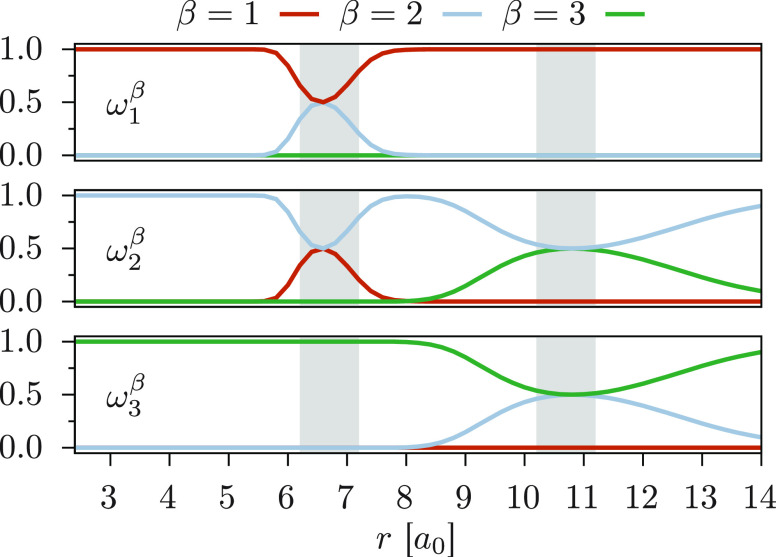
To further understand the results shown in Figure 3, the weights used in the construction of
the density matrices are depicted in Figure 5 in a plot similar to the one for Uβα. At r = 3 a0, the ground state weight
ω1β with β = 1 is about 0.80, meaning that 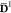 closely
resembles D1, thereby resulting in a Fock
operator similar to the MS-CASPT2 one.
The latter is ultimately responsible for the very good agreement between
the XDW-CASPT2 and the MS-CASPT2 energies. The densities of the other
two states are instead approximately a 50% mixture (central and bottom
plots); as a consequence, the energy of the 21Σ+ and 31Σ+ states is somewhere
in-between the MS-CASPT2 and XMS-CASPT2 ones. Note that such straightforward
analogies are facilitated by the fact that the zeroth-order states
are very weakly coupled through
closely
resembles D1, thereby resulting in a Fock
operator similar to the MS-CASPT2 one.
The latter is ultimately responsible for the very good agreement between
the XDW-CASPT2 and the MS-CASPT2 energies. The densities of the other
two states are instead approximately a 50% mixture (central and bottom
plots); as a consequence, the energy of the 21Σ+ and 31Σ+ states is somewhere
in-between the MS-CASPT2 and XMS-CASPT2 ones. Note that such straightforward
analogies are facilitated by the fact that the zeroth-order states
are very weakly coupled through 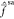 at r = 3 a0. In case of strong mixing,
such an analysis would be much harder.
At geometries with r > 6 a0, the weights
are roughly equal for all the states. This results in Fock operators
at r = 3 a0. In case of strong mixing,
such an analysis would be much harder.
At geometries with r > 6 a0, the weights
are roughly equal for all the states. This results in Fock operators 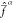 resembling
resembling 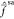 for
α = 1, 2, 3, and thus, XDW-CASPT2
essentially performs as XMS-CASPT2.
for
α = 1, 2, 3, and thus, XDW-CASPT2
essentially performs as XMS-CASPT2.
Figure 5.
Weights ωαβ for ζ = 50. The ground state (α = 1) is shown at the top; the first excited state (α = 2) is in the center, and the second excited state (α = 3) is at the bottom.
The invariance properties of XDW-CASPT2 rely on
the assumption
made in eq 19, that
is the off-diagonal terms 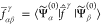 are approximately
zero. It is interesting
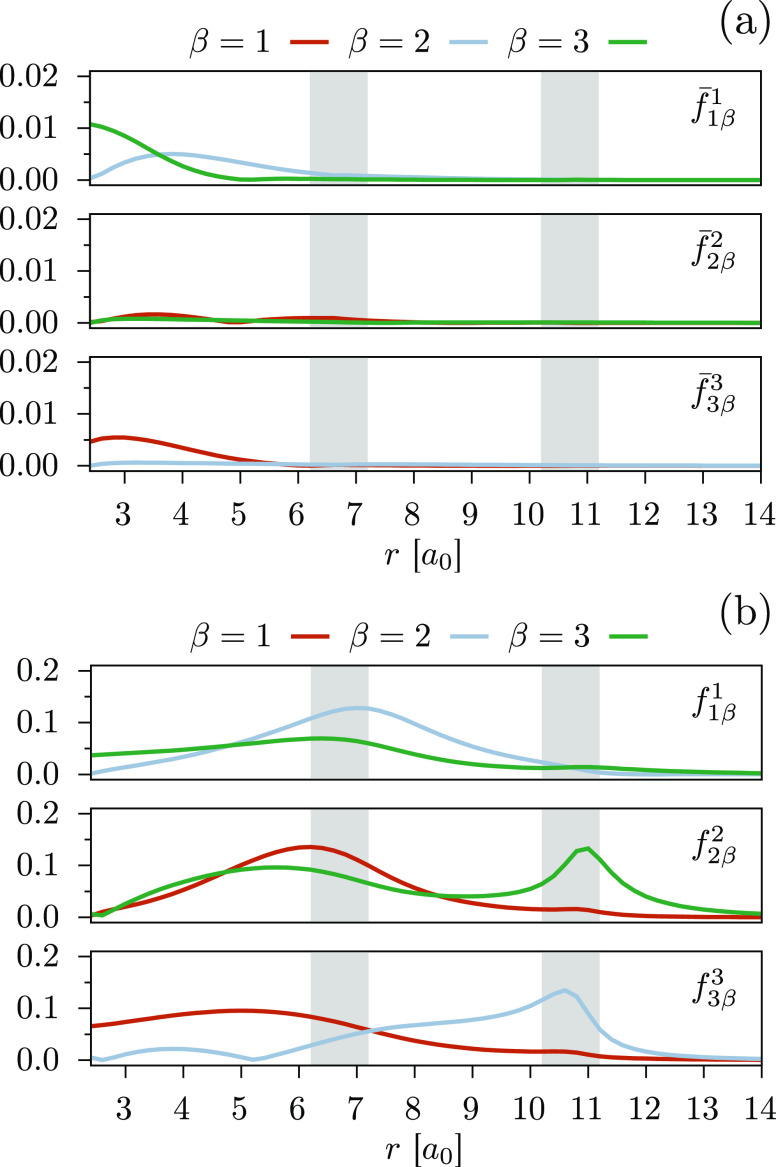
to investigate if this is the case for LiF. In Figure 6a, we show the absolute values of the Fock
couplings for each of the three states. The largest elements are observed
for the ground state around the equilibrium distance; this is not
surprising since the Fock operator is essentially state-specific in
that region. On the other hand the opposite is true past r = 6 a0, with the three Fock operators being roughly equivalent
and equal to
are approximately
zero. It is interesting
to investigate if this is the case for LiF. In Figure 6a, we show the absolute values of the Fock
couplings for each of the three states. The largest elements are observed
for the ground state around the equilibrium distance; this is not
surprising since the Fock operator is essentially state-specific in
that region. On the other hand the opposite is true past r = 6 a0, with the three Fock operators being roughly equivalent
and equal to 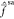 (cf., Figure 5). Recalling that
the rotated zeroth-order
states diagonalize
(cf., Figure 5). Recalling that
the rotated zeroth-order
states diagonalize 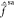 , their coupling must be approximately zero.
The elements
, their coupling must be approximately zero.
The elements 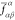 , albeit different
from zero, are in practice
small enough to yield smooth potential energy curves. As a matter
of comparison, the MS-CASPT2 zeroth-order off-diagonal elements between
the original CASSCF states are shown in Figure 6b: the difference is striking, with values
that are one order of magnitude larger compared to XDW-CASPT2. The
strongest couplings are around the avoided crossings, exactly where
MS-CASPT2 performs poorly.
, albeit different
from zero, are in practice
small enough to yield smooth potential energy curves. As a matter
of comparison, the MS-CASPT2 zeroth-order off-diagonal elements between
the original CASSCF states are shown in Figure 6b: the difference is striking, with values
that are one order of magnitude larger compared to XDW-CASPT2. The
strongest couplings are around the avoided crossings, exactly where
MS-CASPT2 performs poorly.
Figure 6.
Absolute values of the Fock operator off-diagonal entries for (a) XDW-CASPT2 with ζ = 50 (elements f̅αβγ) and (b) MS-CASPT2 (elements fαβ). For each method (three plots), the ground state (α = 1) is shown at the top; the first excited state (α = 2) is in the center, and the second excited state (α = 3) is at the bottom. Note that the Fock operator used to compute the couplings is different for each state, and only the case γ = α is of relevance.
Increasing the value of ζ sharpens the transition between state-specific and state-average regimes. As already observed in the context of DW-DSRG,26 this leads to the appearance of wiggles along the potential energy curves because of sudden changes of the zeroth-order weights. This behavior can be seen in Figure 7 for ζ = 5000. For instance, near the 1–2 AC, the XDW-CASPT2 curve for state 21Σ+ rapidly switches between the XMS-CASPT2 and MS-CASPT2 references. Inspection of the weights in Figure 8 reveals a clear correlation between the weights ωαβ and these oscillations. Whenever the weights undergo a rapid and significant change, the energy does so accordingly. Despite this oscillatory behavior, the off-diagonal elements of the Fock operators for ζ = 5000 are in the same order of magnitude as for ζ = 50 and, hence, are still 10-fold less than those of MS-CASPT2, as can be seen in Figure 9. Therefore, it appears that the cause of the wiggles in the PECs is not due to the diagonal approximation.
Figure 7.
Potential energy curves of the three lowest 1Σ+ states of lithium fluoride.
Figure 8.
Weights ωαβ for ζ = 5000.
Figure 9.
Absolute values of the elements f̅αβ for ζ = 5000.
Lastly, the results obtained taking the limit ζ → ∞ are reported in Figure 10. For this case, the weights never change
and correspond to unit vectors, hence the densities are state-specific: 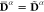 . This leads
to potential energy curves
that mostly overlap with the MS-CASPT2 ones, however without the artifacts around the SA-CASSCF near-degeneracies. Notably, state-specific
Fock operators built with densities D̃ do not couple
the states as strong as the original operators, f̂α, since the zeroth-order off-diagonal elements
for ζ → ∞ are as large as those
for ζ = 5000 (see Supporting Information). This result is important because it corroborates the conjecture
that the PEC wiggles observed for intermediate values of ζ are
strictly caused by the rapid change of the weights.
. This leads
to potential energy curves
that mostly overlap with the MS-CASPT2 ones, however without the artifacts around the SA-CASSCF near-degeneracies. Notably, state-specific
Fock operators built with densities D̃ do not couple
the states as strong as the original operators, f̂α, since the zeroth-order off-diagonal elements
for ζ → ∞ are as large as those
for ζ = 5000 (see Supporting Information). This result is important because it corroborates the conjecture
that the PEC wiggles observed for intermediate values of ζ are
strictly caused by the rapid change of the weights.
Figure 10.
Potential energy curves of the three lowest 1Σ+ states of lithium fluoride.
3.2. Conical Intersection in Allene
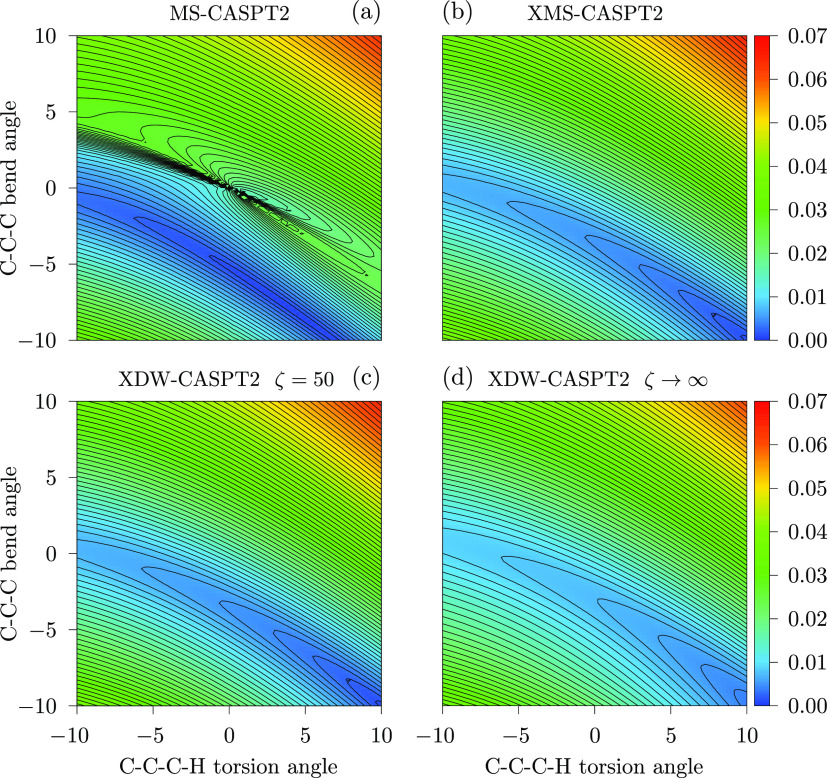
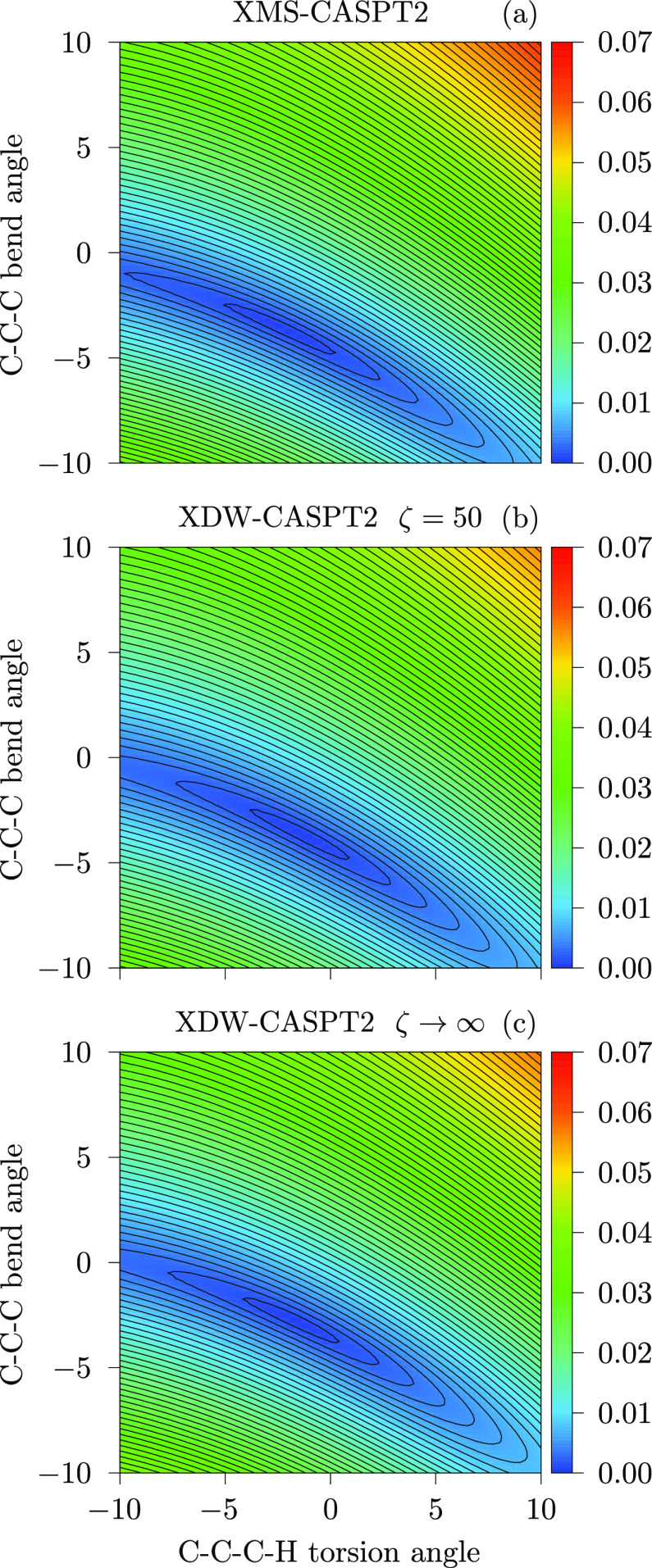
Projection of the zeroth-order Hamiltonian onto the individual states of the model space defines a MRPT that is not invariant under unitary transformations of the model states. Failure to satisfy eq 19 leads to unphysical results at conical intersections or in the vicinity of avoided crossings. This situation has been already observed in the LiF dissociation, however a more challenging test is that of the minimum energy conical intersection (MECI) of the distorted allene molecule, depicted in Figure 11. Around that point, the 11A′ and 21A′ states are quasidegenerate and thus only the space spanned by them is well-defined. To investigate the behavior of the various CASPT2 variants in this situation, we performed two-dimensional, nonrelaxed scans by varying the C–C–C bend angle and the C–C–C–H torsional angle in steps of 0.25 degrees in the range of −10 to +10 degrees from the CASSCF MECI point, respectively.d The computational details are the same as in ref (23) and are fully described in the Supporting Information; here, we report only the essential points. The reference wave functions were obtained in a SA-CASSCF calculation with 4 electrons in 3 orbitals of a′ symmetry and 1 orbital of a″ symmetry. This amounts to a complete active space of 12 totally symmetric configuration state functions, thus allowing to study the behavior of the potential energy surface as a function of the number of states, up to the complete active space limit. Given that the calculation focuses on the 11A′ and 21A′ conical intersection, the CASSCF orbital optimization was carried out for the two lowest states only, while the remaining 10 states were obtained by diagonalization of the configuration interaction matrix. The basis set used was the GAMESS (US)-style variation of the Dunning–Hays basis, augmented by a single polarization spherical d function on each carbon. In Figure 12, we report the color-mapped isosurface plots of the energy difference between the 11A′ and 21A′ states computed with a model space spanned by the 2 lowest roots only. Figure 12a shows the result obtained with MS-CASPT2. At the CASSCF MECI point, the origin of the plot, there is a singularity and the surface around this point is completely compromised, showing the deficiency of this methodology. On the contrary, as can be seen from Figure 12b, the surface obtained with XMS-CASPT2 does not show any sign of artifacts, demonstrating the importance of invariance to obtain physically sound results. The plot in Figure 12c illustrates the behavior of XDW-CASPT2 for ζ = 50. The surface is virtually identical to that obtained with XMS-CASPT2, a result that is easily explained upon analyzing the density weights. Recalling that the model space only has a dimension of two, the largest and smallest values of ωαβ observed in the entire scan were 0.53 and 0.47, respectively, meaning that the difference between the XDW-CASPT2 and XMS-CASPT2 partitions are very small across the board. Lastly, in Figure 12d is shown the surface obtained by letting ζ → ∞. Remarkably, albeit the use of purely state-specific operators, the PES around the MECI point is perfectly smooth. The overall morphology is analogous to the last two cases, even though a slightly larger width of the potential well is noticeable.
Figure 11.
11A′ and 21A′ MECI geometry of the allene molecule.
Figure 12.
Color-mapped isosurface plot of the absolute energy difference (in Eh) between the 11A′ and 21A′ states for a model space including 2 states. The same calculation was carried out with different methodologies: (a) MS-CASPT2, (b) XMS-CASPT2, (c) XDW-CASPT2 with ζ = 50, and (d) XDW-CASPT2 with ζ → ∞.
Repeating the same calculation
with XMS-CASPT2 including all 12
states of the complete active space results again in a smooth surface
as shown in Figure 13a. The position of the MECI at the correlated level changes according
to the number of states and, for XMS-CASPT2, is substantially converged
with a model space of 6 states (see Supporting Information). In Figure 13b and c, we report the result obtained with XDW-CASPT2
for ζ = 50 and ζ → ∞. Once
again the PESs are smooth everywhere and on par with the XMS-CASPT2
one. Moreover, we note that all three plots of Figure 13 are remarkably similar to the one obtained
by Granovsky23 with extended MCQDPT. In
contrast to the 2-state case, the dynamical weights obtained with
ζ = 50 are significantly different from the state-average ones.
The Fock operators 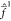 and
and 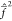 are
substantially defined by the first
four states, since the weights assigned starting from the fifth one
are less than 0.03, thereby contributing little to nothing to the
11A′ and 21A′ 1-RDMs. Crucially,
this does not imply that PESs obtained with a model space of dimension
four are the same as those obtained with one of higher dimension.
Both eqs 15 and 23 directly depend on the total number of model states
and their wave function. As a result, different model space dimensions
give rise to distinct partitions of Ĥ, which
are ultimately coupled together in a nontrivial way through the formation
of the second-order effective Hamiltonian.
are
substantially defined by the first
four states, since the weights assigned starting from the fifth one
are less than 0.03, thereby contributing little to nothing to the
11A′ and 21A′ 1-RDMs. Crucially,
this does not imply that PESs obtained with a model space of dimension
four are the same as those obtained with one of higher dimension.
Both eqs 15 and 23 directly depend on the total number of model states
and their wave function. As a result, different model space dimensions
give rise to distinct partitions of Ĥ, which
are ultimately coupled together in a nontrivial way through the formation
of the second-order effective Hamiltonian.
Figure 13.
Color-mapped isosurface plot of the absolute energy difference between the 11A′ and 21A′ states for a 12-state model space computed with different methodologies: (a) XMS-CASPT2, (c) XDW-CASPT2 (ζ = 50), and (c) XDW-CASPT2 (ζ → ∞).
3.3. Vertical Excitation Energies
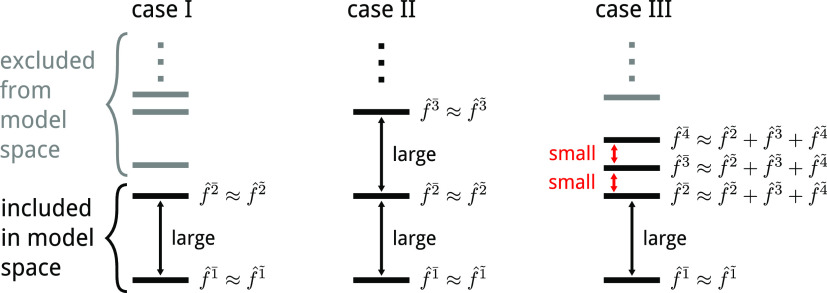
One of the design objectives of XDW-CASPT2 is to maintain the accuracy of MS-CASPT2 in the calculation of transition energies. If we consider a molecule in its electronic ground state, the dynamical weighting scheme is such that when the energy gap to the first excited state is larger than ζ–1/2, then the density matrices of both these states will barely mix with each other, remaining predominantly state-specific. It is reasonable to assume that in this situation the energy separation between these states is sizable and that their associated wave functions have well-defined, but distinct character. Hence, the rotated reference states obtained from eq 15 will be similar to the original ones: Ψ̃α(0) ≈ Ψα. Under these circumstances, all the quantities in XDW-CASPT2 will not be very different from those in MS-CASPT2, such that we expect the two methods to have a comparable accuracy. This was indeed observed in the previous section for lithium fluoride. In principle, the same logic applies when the model space dimension is larger than two: as long as all states are energetically well separated from each other and the rotated reference wave functions maintain their original character, we expect similar results for XDW-CASPT2 and MS-CASPT2. A different and much more complicated situation occurs when many model states lie within a limited region of the spectrum and interact strongly with each other at zeroth-order. Although it is conceptually easy to visualize the amount of density mixing by inspecting the weights ωαβ, the fact that the rotated model states are linear combinations of the original reference wave functions, makes it hard to rationalize the physical content of the Fock operator in these terms. The three different cases are summarized in Scheme 1.
Scheme 1. Three Main Scenarios for the Calculation of Excited States Energies.
In case I, only the well-separated ground and first excited states are included in the model space. In case II, many states are included in the calculation, but all of them are well separated. In case III, several low-lying excited states are included in the model space, and these are energetically very close to each other. Therefore, their Fock operators will be approximately state-average in contrast to the other cases.
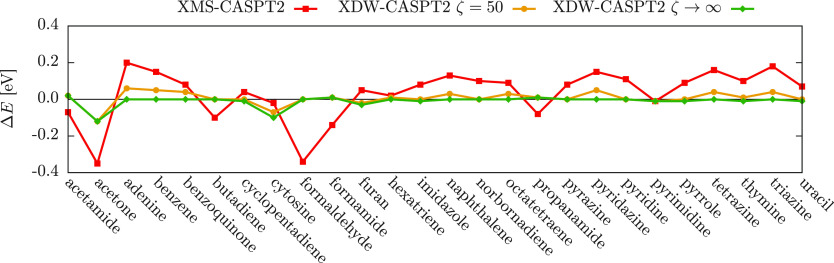
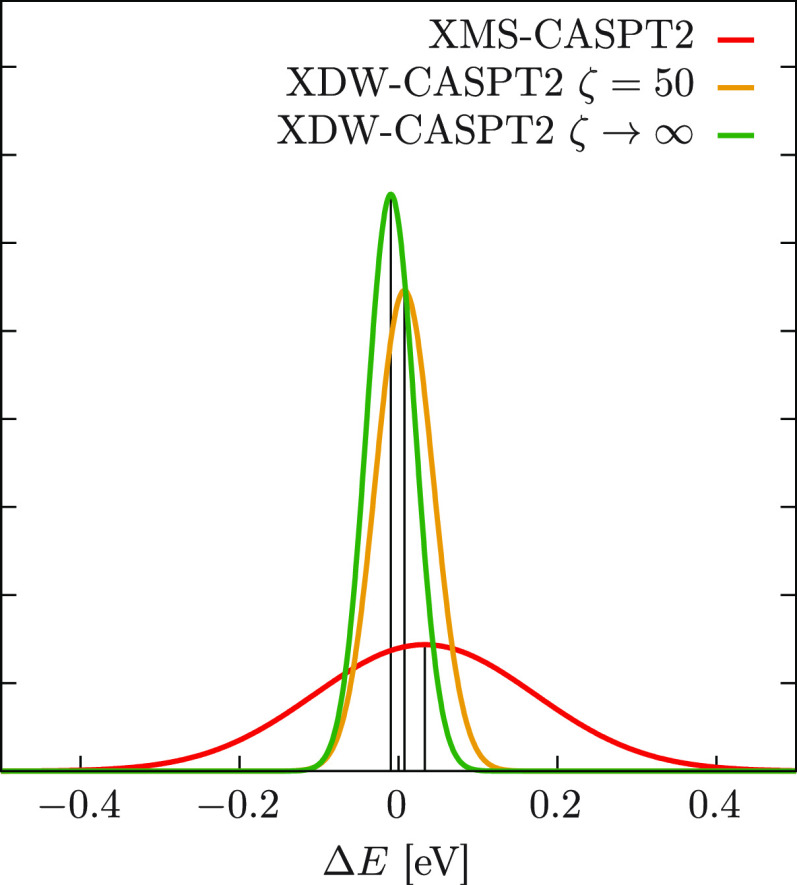
To assess the accuracy of XDW-CASPT2 for the calculation of electronically excited states, we computed the vertical energy gap between the ground and the first excited singlet state for a series of small to medium organic compounds and compared the results to MS-CASPT2. This case corresponds to the first scenario illustrated in Scheme 1. The molecules were taken from Thiel’s benchmark set,21 excluding ethene and cyclopropene since no singlet excited state was considered for these two systems. To appreciate the effects of the dynamical weighting scheme, the calculated first excited states always belonged to the same irreducible representation as the ground state. The geometries were taken from ref (21) and correspond to structures optimized at MP2/6-31G* level of theory. The reference wave functions were obtained by a 2-state SA-CASSCF calculation using the TZVP basis set44 and the RICD approximation.45 Full computational details are available in the Supporting Information. Vertical transition energies were calculated with MS-CASPT2, XMS-CASPT2, and XDW-CASPT2 with two values of ζ and setting the IPEA shift to zero for all methods. A real shift was used when necessary and equally applied to all methods to obtain comparable energies. Since one of the design objectives of XDW-CASPT2 is to reproduce the transition energies obtained with MS-CASPT2, we report all the calculated values as differences with respect to the MS-CASPT2 ones in Figure 14. As expected for case I, the largest deviation is observed for XMS-CASPT2, with a general tendency to slightly overestimate the MS-CASPT2 excitation energies by up to 0.2 eV. The results of XDW-CASPT2 are instead on par with MS-CASPT2, with transitions that are exactly reproduced for several systems, more so for ζ → ∞ than for ζ = 50, even though the general performance of both is virtually the same. The results shown in Figure 14 are neatly summarized by normal distributions with respect to MS-CASPT2 as reported in Figure 15. Despite the mean of all three methods is quite close to the reference, energies obtained by XDW-CASPT2 are clearly closer than the XMS-CASPT2 ones. In terms of mean absolute deviations, XMS-CASPT2 excitation energies differ by 0.12 eV on average, whereas the agreement is excellent for XDW-CASPT2, with a discrepancy of only 0.02 and 0.01 eV for ζ = 50 and ζ → ∞, respectively. It is important to note that the results presented so far only provide a relative measure rather than an absolute one, as we rely on the fact that MS-CASPT2 has an established, acceptable accuracy, such that for most applications it is sufficient to be able to reproduce it. Case I particularly highlights the difficulties of a state-average Fock operator to replicate it, whereby excitations that are energetically far apart from the ground state deviate the most. Most notably is the case of acetone and formaldehyde, for which the excitation energy is considerably underestimated by XMS-CASPT2: these transitions, 8.93 and 10.06 eV, respectively, correspond to the largest of the entire set. Note that the MS-CASPT2 values of 9.28 and 10.40 eV agree well with the CC3/TZVP21 values at 9.65 and 10.45 eV.
Figure 14.
Signed deviations of singlet vertical excitation energies with respect to MS-CASPT2.
Figure 15.
Normal distributions of excitation energy deviations with respect to MS-CASPT2.
Lastly, we would like to stress out that the results obtained here do not imply that XMS-CASPT2 is worse than XDW-CASPT2 (or MS-CASPT2) in general but, rather, that under certain circumstances (e.g., those akin to case I) the state-average Fock operator might decrease the accuracy of the method or, at least, it will significantly deviates from results obtained by its state-specific counterpart. It is likely that the same discussion holds for case II, whereas, we are aware that the relative and absolute accuracy of XDW-CASPT2, as well that of XMS-CASPT2, still have to be fully assessed for case III (see also the discussion on glycine in the Supporting Information).
4. Conclusions
In this work we have proposed and investigated a new variant of the CASPT2 method. By a careful analysis of the properties of MS-CASPT2 and XMS-CASPT2, we have identified the two key components that characterize the success of each variant and included them in the newly developed XDW-CASPT2 approach. First, diagonalization of the state-average Fock operator in the reference basis provides a new set of zeroth-order states. Second, this is followed by the construction of state-specific Fock operators with dynamically adjusted weights that depend on the energy separation between the states. These operators are then used to partition the Hamiltonian in a MS-CASPT2 calculation. The resulting method is approximately invariant under unitary transformations of the model states, a property that ensures a physical behavior in the vicinity of avoided crossings and conical intersections, and at the same time shows an accuracy comparable to conventional MS-CASPT2. The dynamical weighting scheme introduces a parameter ζ which acts as a threshold controlling the state-specificity of the Fock operator, thereby allowing the method to interpolate between XMS-CASPT2 and MS-CASPT2 (with rotated reference functions). Unfortunately, we were not able to identify a universal value for this parameter; however, for typical applications involving a moderate number of low-lying excited states, we suggest keeping it small (≲150) or taking the limit to ∞. Importantly, even though XDW-CASPT2 employs the diagonal approximation, in practice it approximately satisfies all important properties listed by Granovsky.23
The reliability of XDW-CASPT2 is demonstrated in the typical benchmark system LiF, whose avoided crossings represent a difficult task for multireference approaches. The obtained potential energy curves overlap with the XMS-CASPT2 ones in the regions where the underlying zeroth-order states are quasidegenerate, hence do not show the wiggles typical of MS-CASPT2, but at the same time the vertical transitions to the first two excited states are in better agreement than XMS-CASPT2 with the reference MRCISD values. The robustness of XDW-CASPT2 is further tested by studying the conical intersection in the allene molecule, for which smooth PESs were obtained for different values of ζ and dimensions of the model space. At last, vertical excitation energies are shown to be in almost perfect agreement with MS-CASPT2 for singlet transitions in a set of 26 organic compounds, unlike XMS-CASPT2 that shows an average deviation on the order of 0.1 eV and maximum deviations as large as 0.4 eV.
The XDW-CASPT2 method can be viewed as a bridge between MS-CASPT2 and XMS-CASPT2, thereby attempting to bring together what in our opinion are the best features of both methods, that is, the established accuracy of MS-CASPT2 in the calculation of excitation energies and the ability of XMS-CASPT2 to produce smooth surfaces for any molecular geometry. It is in this context that we envision XDW-CASPT2 to bring together the best of two worlds, providing a valid alternative to other quasidegenerate multireference perturbation theories. Moreover, being based on the CASPT formalism constitutes a practical advantage: any existing implementation can be easily adapted to provide XDW-CASPT2 as an option and at the same time it only requires an additional input parameter from the final user. Analytical energy gradients and derivative couplings can be derived and implemented in a similar manner to MS-CASPT2 and XMS-CASPT2. The similarity with its parent theory also means that XDW-CASPT2 can be used with zeroth-order wave functions obtained with modern approaches, such as the density matrix renormalization group.46 From the computational perspective, the only difference with (X)MS-CASPT2 is a small overhead for the construction of the dynamically weighted densities and thus it is applicable to systems of the same size where the parent methods are an option. At last, we envision XDW-CASPT2 to be a very interesting method in the context of ab initio molecular dynamics, once the restriction of imposing molecular symmetries is lifted, for example, through the use of the off-diagonal elements of the full Hamiltonian.
Acknowledgments
S.B. acknowledges the Swiss National Science Foundation (SNSF) for the funding received through the Early Postdoc. Mobility fellowship (Grant P2SKP2_184034). R.L. acknowledges the Swedish Research Council (VR, Grant 2016-03398). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.9b01129.
Computational details and results obtained for the glycine molecule, additional results on the dissociation of lithium fluoride and the conical intersection of the distorted allene molecule, supplementary computational details on the allene molecule, and information necessary to reproduce the calculation of the singlet vertical excitation energies (PDF)
The authors declare no competing financial interest.
Footnotes
This seemingly insignificant choice avoids a discussion on single-state single-reference (SS-SR) and multistate multireference (MS-MR) variants of internally contracted theories, which is not the primary focus of this work. For a thorough comparison between them in the context of CASPT2, see, for example, the recent work by Park.25
Note that using the state-average density matrix to construct the Fock operator or averaging the state-specific Fock operators lead to the same f̂sa.
Note that the presence of at least one doubly occupied orbital is important to have contributions from all possible excitation classes in a second-order perturbation theory approach, allowing for a fair comparison with the MRCISD method.
Note that the C–C–C−H torsion angle is simultaneously changed on both sides of the molecule to preserve the Cs symmetry.
Supplementary Material
References
- Matsika S.; Krylov A. I. Introduction: Theoretical Modeling of Excited State Processes. Chem. Rev. 2018, 118, 6925–6926. 10.1021/acs.chemrev.8b00436. [DOI] [PubMed] [Google Scholar]
- Vacher M.; Fdez. Galván I.; Ding B.-W.; Schramm S.; Berraud-Pache R.; Naumov P.; Ferré N.; Liu Y.-J.; Navizet I.; Roca-Sanjuán D.; Baader W. J.; Lindh R. Chemi- and Bioluminescence of Cyclic Peroxides. Chem. Rev. 2018, 118, 6927–6974. 10.1021/acs.chemrev.7b00649. [DOI] [PubMed] [Google Scholar]
- Norman P.; Dreuw A. Simulating X-ray Spectroscopies and Calculating Core-Excited States of Molecules. Chem. Rev. 2018, 118, 7208–7248. 10.1021/acs.chemrev.8b00156. [DOI] [PubMed] [Google Scholar]
- Casanova D. Theoretical Modeling of Singlet Fission. Chem. Rev. 2018, 118, 7164–7207. 10.1021/acs.chemrev.7b00601. [DOI] [PubMed] [Google Scholar]
- Lischka H.; Nachtigallová D.; Aquino A. J.; Szalay P. G.; Plasser F.; MacHado F. B.; Barbatti M. Multireference Approaches for Excited States of Molecules. Chem. Rev. 2018, 118, 7293–7361. 10.1021/acs.chemrev.8b00244. [DOI] [PubMed] [Google Scholar]
- Cave R. J.; Davidson E. R. Quasidegenerate variational perturbation theory and the calculation of first–order properties from variational perturbation theory wave functions. J. Chem. Phys. 1988, 89, 6798–6814. 10.1063/1.455354. [DOI] [Google Scholar]
- Nakano H. Quasidegenerate perturbation theory with multiconfigurational self–consistent–field reference functions. J. Chem. Phys. 1993, 99, 7983–7992. 10.1063/1.465674. [DOI] [Google Scholar]
- Malrieu J.-P.; Heully J.-L.; Zaitsevskii A. Multiconfigurational second-order perturbative methods: Overview and comparison of basic properties. Theor. Chim. Acta 1995, 90, 167–187. 10.1007/BF01113846. [DOI] [Google Scholar]
- Hoffmann M. R. Third-order complete active space self-consistent field based generalized Van Vleck perturbation theory. Chem. Phys. Lett. 1993, 210, 193–200. 10.1016/0009-2614(93)89123-Y. [DOI] [Google Scholar]
- Hoffmann M. R. Canonical Van Vleck Quasidegenerate Perturbation Theory with Trigonometric Variables. J. Phys. Chem. 1996, 100, 6125–6130. 10.1021/jp952753r. [DOI] [Google Scholar]
- Finley J.; Malmqvist P.-Å.; Roos B. O.; Serrano-Andrés L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. 10.1016/S0009-2614(98)00252-8. [DOI] [Google Scholar]
- Mahapatra U. S.; Datta B.; Mukherjee D. Development of a size-consistent state-specific multireference perturbation theory with relaxed model-space coefficients. Chem. Phys. Lett. 1999, 299, 42–50. 10.1016/S0009-2614(98)01227-5. [DOI] [PubMed] [Google Scholar]
- Shavitt I. Multi-state Multireference Rayleigh–Schrödinger Perturbation Theory for Mixed Electronic States: Second and Third Order. Int. J. Mol. Sci. 2002, 3, 639–655. 10.3390/i3060639. [DOI] [Google Scholar]
- Angeli C.; Borini S.; Cestari M.; Cimiraglia R. A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach. J. Chem. Phys. 2004, 121, 4043–4049. 10.1063/1.1778711. [DOI] [PubMed] [Google Scholar]
- Fink R. F. The multi-reference retaining the excitation degree perturbation theory: A size-consistent, unitary invariant, and rapidly convergent wavefunction based ab initio approach. Chem. Phys. 2009, 356, 39–46. 10.1016/j.chemphys.2008.10.004. [DOI] [Google Scholar]
- Roskop L.; Gordon M. S. Quasi-degenerate second-order perturbation theory for occupation restricted multiple active space self-consistent field reference functions. J. Chem. Phys. 2011, 135, 044101. 10.1063/1.3609756. [DOI] [PubMed] [Google Scholar]
- Sharma S.; Jeanmairet G.; Alavi A. Quasi-degenerate perturbation theory using matrix product states. J. Chem. Phys. 2016, 144, 034103. 10.1063/1.4939752. [DOI] [PubMed] [Google Scholar]
- Giner E.; Angeli C.; Garniron Y.; Scemama A.; Malrieu J.-P. A Jeziorski-Monkhorst fully uncontracted multi-reference perturbative treatment. I. Principles, second-order versions, and tests on ground state potential energy curves. J. Chem. Phys. 2017, 146, 224108. 10.1063/1.4984616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garniron Y.; Scemama A.; Giner E.; Caffarel M.; Loos P.-F. Selected configuration interaction dressed by perturbation. J. Chem. Phys. 2018, 149, 064103. 10.1063/1.5044503. [DOI] [PubMed] [Google Scholar]
- Bozkaya U. Efficient Implementation of the Second-Order Quasidegenerate Perturbation Theory with Density-Fitting and Cholesky Decomposition Approximations: Is It Possible To Use Hartree–Fock Orbitals for a Multiconfigurational Perturbation Theory?. J. Chem. Theory Comput. 2019, 15, 4415–4429. 10.1021/acs.jctc.9b00378. [DOI] [PubMed] [Google Scholar]
- Schreiber M.; Silva-Junior M. R.; Sauer S. P. A.; Thiel W. Benchmarks for electronically excited states: CASPT2, CC2, CCSD, and CC3. J. Chem. Phys. 2008, 128, 134110. 10.1063/1.2889385. [DOI] [PubMed] [Google Scholar]
- Silva-Junior M. R.; Schreiber M.; Sauer S. P. A.; Thiel W. Benchmarks of electronically excited states: Basis set effects on CASPT2 results. J. Chem. Phys. 2010, 133, 174318. 10.1063/1.3499598. [DOI] [PubMed] [Google Scholar]
- Granovsky A. A. Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory. J. Chem. Phys. 2011, 134, 214113. 10.1063/1.3596699. [DOI] [PubMed] [Google Scholar]
- Shiozaki T.; Győrffy W.; Celani P.; Werner H.-J. Communication: Extended multi-state complete active space second-order perturbation theory: Energy and nuclear gradients. J. Chem. Phys. 2011, 135, 081106. 10.1063/1.3633329. [DOI] [PubMed] [Google Scholar]
- Park J. W. Single-State Single-Reference and Multistate Multireference Zeroth-Order Hamiltonians in MS-CASPT2 and Conical Intersections. J. Chem. Theory Comput. 2019, 15, 3960–3973. 10.1021/acs.jctc.9b00067. [DOI] [PubMed] [Google Scholar]
- Li C.; Lindh R.; Evangelista F. A. Dynamically weighted multireference perturbation theory: Combining the advantages of multi-state and state-averaged methods. J. Chem. Phys. 2019, 150, 144107. 10.1063/1.5088120. [DOI] [PubMed] [Google Scholar]
- Deskevich M. P.; Nesbitt D. J.; Werner H.-J. Dynamically weighted multiconfiguration self-consistent field: Multistate calculations for F+H2O → HF+OH reaction paths. J. Chem. Phys. 2004, 120, 7281–7289. 10.1063/1.1667468. [DOI] [PubMed] [Google Scholar]
- Glover W. J. Communication: Smoothing out excited-state dynamics: Analytical gradients for dynamically weighted complete active space self-consistent field. J. Chem. Phys. 2014, 141, 171102. 10.1063/1.4901328. [DOI] [PubMed] [Google Scholar]
- Bloch C. Sur la théorie des perturbations des états liés. Nucl. Phys. 1958, 6, 329–347. 10.1016/0029-5582(58)90116-0. [DOI] [Google Scholar]
- Lindgren I. The Rayleigh–Schrödinger perturbation and the linked-diagram theorem for a multi-configurational model space. J. Phys. B: At. Mol. Phys. 1974, 7, 2441–2470. 10.1088/0022-3700/7/18/010. [DOI] [Google Scholar]
- Zaitsevskii A.; Malrieu J.-P. Multi-partitioning quasidegenerate perturbation theory. A new approach to multireference Møller-Plesset perturbation theory. Chem. Phys. Lett. 1995, 233, 597–604. 10.1016/0009-2614(94)01503-N. [DOI] [Google Scholar]
- Meyer W. In Methods of Electronic Structure Theory; Schaefer H. F., Ed.; Springer US: Boston, MA, 1977; Chapter (11), , pp 413–446. [Google Scholar]
- Siegbahn P. E. M. Direct configuration interaction with a reference state composed of many reference configurations. Int. J. Quantum Chem. 1980, 18, 1229–1242. 10.1002/qua.560180510. [DOI] [Google Scholar]
- Sivalingam K.; Krupicka M.; Auer A. A.; Neese F. Comparison of fully internally and strongly contracted multireference configuration interaction procedures. J. Chem. Phys. 2016, 145, 054104. 10.1063/1.4959029. [DOI] [PubMed] [Google Scholar]
- Kats D.; Werner H.-J. Multi-state local complete active space second-order perturbation theory using pair natural orbitals (PNO-MS-CASPT2). J. Chem. Phys. 2019, 150, 214107. 10.1063/1.5097644. [DOI] [PubMed] [Google Scholar]
- Clark L. B. Polarization Assignments in the Vacuum UV Spectra of the Primary Amide, Carboxyl, and Peptide Groups. J. Am. Chem. Soc. 1995, 117, 7974–7986. 10.1021/ja00135a017. [DOI] [Google Scholar]
- Fdez. Galván I.; Vacher M.; Alavi A.; Angeli C.; Aquilante F.; Autschbach J.; Bao J. J.; Bokarev S. I.; Bogdanov N. A.; Carlson R. K.; Chibotaru L. F.; Creutzberg J.; Dattani N.; Delcey M. G.; Dong S. S.; Dreuw A.; Freitag L.; Frutos L. M.; Gagliardi L.; Gendron F.; Giussani A.; González L.; Grell G.; Guo M.; Hoyer C. E.; Johansson M.; Keller S.; Knecht S.; Kovačević G.; Källman E.; Li Manni G.; Lundberg M.; Ma Y.; Mai S.; Malhado J. P.; Malmqvist P. Å.; Marquetand P.; Mewes S. A.; Norell J.; Olivucci M.; Oppel M.; Phung Q. M.; Pierloot K.; Plasser F.; Reiher M.; Sand A. M.; Schapiro I.; Sharma P.; Stein C. J.; Sørensen L. K.; Truhlar D. G.; Ugandi M.; Ungur L.; Valentini A.; Vancoillie S.; Veryazov V.; Weser O.; Wesołowski T. A.; Widmark P.-O.; Wouters S.; Zech A.; Zobel J. P.; Lindh R. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. 10.1021/acs.jctc.9b00532. [DOI] [PubMed] [Google Scholar]
- Sand A. M.; Hoyer C. E.; Truhlar D. G.; Gagliardi L. State-interaction pair-density functional theory. J. Chem. Phys. 2018, 149, 024106. 10.1063/1.5036727. [DOI] [PubMed] [Google Scholar]
- Kahn L. R.; Hay P. J.; Shavitt I. Theoretical study of curve crossing: ab initio calculations on the four lowest 1 Σ + states of LiF. J. Chem. Phys. 1974, 61, 3530–3546. 10.1063/1.1682533. [DOI] [Google Scholar]
- Bauschlicher C. W.; Langhoff S. R. Full configuration-interaction study of the ionic–neutral curve crossing in LiF. J. Chem. Phys. 1988, 89, 4246–4254. 10.1063/1.455702. [DOI] [Google Scholar]
- Roos B. O.; Taylor P. R.; Sigbahn P. E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
- Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Kendall R. A.; Dunning T. H. Jr.; Harrison R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. 10.1063/1.462569. [DOI] [Google Scholar]
- Varandas A. J. C. Accurate ab initio potential energy curves for the classic Li–F ionic-covalent interaction by extrapolation to the complete basis set limit and modeling of the radial nonadiabatic coupling. J. Chem. Phys. 2009, 131, 124128. 10.1063/1.3237028. [DOI] [PubMed] [Google Scholar]
- Schäfer A.; Huber C.; Ahlrichs R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. 10.1063/1.467146. [DOI] [Google Scholar]
- Aquilante F.; Lindh R.; Bondo Pedersen T. Unbiased auxiliary basis sets for accurate two-electron integral approximations. J. Chem. Phys. 2007, 127, 114107. 10.1063/1.2777146. [DOI] [PubMed] [Google Scholar]
- White S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. 10.1103/PhysRevLett.69.2863. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.