Unveiling the Delicate Balance of Steric and Dispersion Interactions in Organocatalysis Using High-Level Computational Methods

Abstract

High-level quantum electronic structure calculations are used to provide a deep insight into the mechanism and stereocontrolling factors of two recently developed catalytic asymmetric Diels–Alder (DA) reactions of cinnamate esters with cyclopentadiene. The reactions employ two structurally and electronically very different in situ silylated enantiopure Lewis acid organocatalysts: i.e., binaphthyl-allyl-tetrasulfone (BALT) and imidodiphosphorimidate (IDPi). Each of these catalysts activates only specific substrates in an enantioselective fashion. Emphasis is placed on identifying and quantifying the key noncovalent interactions responsible for the selectivity of these transformations, with the final aim of aiding in the development of designing principles for catalysts with a broader scope. Our results shed light into the mechanism through which the catalyst architecture determines the selectivity of these transformations via a delicate balance of dispersion and steric interactions.

Introduction

Over the last two decades, numerous chiral organocatalysts that efficiently facilitate highly stereo- and regioselective transformations by activating the reactants through either covalent¹⁻³ or noncovalent interactions⁴⁻⁷ have been reported.⁸⁻¹⁰

In the vast majority of cases, the design of new organocatalysts relies on a trial and error procedure where different prototypes are synthesized and tested under variable experimental conditions. Hence, guidelines and rules of thumb for developing better catalysts are crucial, as they allow a significant reduction in laboratory efforts. From a computational point of view, accurate predictions require the calculation of relative reaction rates with high accuracy for systems with hundreds of atoms as well as the identification and quantification of the key covalent and noncovalent interactions responsible for the selectivity of a given transformation. In particular, the last aspect has proven to be critical for the rational design of more effective catalysts.^7,11−14

Herein, a computational protocol for addressing these issues is introduced and used to elucidate the mechanism and the stereocontrolling factors of two challenging enantioselective Diels–Alder (DA) reactions recently developed by List and co-workers^15,16 in the context of asymmetric ion-pairing catalysis.¹⁷⁻²¹

In this type of chemistry, enantioselectivity is induced via the formation of an ion pair between a chiral catalyst and a reaction intermediate of opposite charge. This includes the well-known phase-transfer catalysis²² and the more recent area of asymmetric counteranion-directed catalysis (ACDC).^19,20,23 While in the former the reaction proceeds through anionic intermediates ion-paired with chiral cations, chiral anions and positively charged intermediates are the key components in the latter. In particular, the List group has pioneered the use of highly reactive silylium-based Lewis acids (LAs) to control many of the key C–C bond forming reactions through cationic intermediates (Scheme 1A).^{15,16,24−36}

Scheme 1. (A) Catalyst Activation and Proposed Catalytic Cycle of Silylium-ACDC and (B) Application of This Synthetic Strategy to the Diels-Alder Reaction of Cp with Cinnamate Esters.

[Si]⁺[X*]^– denotes the activated catalyst, [Si]⁺ is the silylium ion, [X*]⁻ indicates the chiral counteranion, S is the achiral substrate, [Si–S]⁺[X*]^– denotes the chiral ion pair, and P* is the enantioenriched product.

The proposed mechanism for the silylium-ACDC can be summarized in three steps. First, in situ silylation of a chiral Brønsted acid, HX*, generates an extremely active catalyst, [Si]⁺[X*]^–, whose formation can be probed by proton nuclear magnetic resonance (¹HNMR) spectroscopy.^15,26 Second, an exchange of the Lewis base leads to an activated substrate, which is a cationic intermediate, [Si–S]⁺. This species ion-pairs with the enantiopure counteranion [X*]^–, responsible for inducing the enantioselectivity, leading to the formation of a chiral ion pair (CIP), [Si–S]⁺[X*]^–. Third, the interaction of a reagent with the CIP yields the enantioenriched product P* and the catalyst is regenerated.^37,38

Recently,^15,16 the List group used this strategy to catalyze the enantioselective DA reaction of unreactive trans-cinnamate esters with cyclopentadiene (Cp) (see Scheme 1B). An in situ silylated enantiopure binaphthyl-allyl-tetrasulfone ((S)-BALT) Lewis acid organocatalyst (5a) was used for the enantioselective DA reaction of 9-fluorenylmethyl (Fm) trans-cinnamates (1a) with Cp (“reaction A”, RA, in Scheme 2). Under the experimental conditions, the endoproduct (S,S)-4a was furnished in 94% yield, with enantiomeric ratios (er) of up to 97:3 and diastereomeric ratios (dr) of 25:1. A subsequent computational study by Wheeler and co-workers suggested that dispersive “π-stacking” interactions³⁹ favor the addition of Cp to the more hindered face of 1a and determine the enantioselectivity of the reaction.

Scheme 2. Reactions and Experimental Conditions Considered in This Work.

RA: cycloaddition of 9-fluorenylmethyl (Fm) cinnamate 1a to Cp catalyzed by 5a.¹⁵ Note that, under optimized conditions (solvent Et₂O, temperature −20 °C, Si = tert-butyldimethylsilyl) the same reaction can be achieved with an er of 97:3 and a dr of 25:1.¹⁵RB: cycloaddition of methyl (Me) cinnamate 1b to Cp catalyzed by 5b.¹⁶

Interestingly, 5a was found to selectivity activate only Fm-cinnamates and was unable to asymmetrically activate the simplest cinnamate ester, i.e. methyl (Me) cinnamate (1b), giving nearly racemic mixtures of the endo product.^16,33 A more quantitative discussion of the activation mode of 5a would be highly desirable and might provide useful information for the development of new catalysts with broader scope.

Experimentally, to tackle structurally/functionally challenging substrates such as 1b, efforts have been focused on the design and synthesis of highly acidic functionalities sterically constrained by means of bulkier Ar substituents. In this sense, List and co-workers proposed a C₂-symmetric imidodiphosphorimidate (IDPi) acid (5b) as a new type of Lewis acid precursor. This designed enzyme-like catalyst^{16,32−36,40−55} is extremely sterically demanding, featuring the active center inside a compact rigid chiral pocket formed by two BINOL-phosphate moieties bonded via the imide nitrogen. Under mild conditions, 5b was able to effectively activate methyl trans-cinnamate 1b(16) in an enantioselective fashion (“reaction B”, RB, in Scheme 2).

In our preliminary computational investigation of these systems,¹⁶ we suggested that a chiral ion pair held together by highly directional electrostatic interactions is formed between the chiral anion and the activated substrate. This encounter complex revealed a striking geometrical match, which is also retained in the stereocontrolling transition states (TSs): the Me group of 1b was pointing inside the chiral pocket of the counteranion 5b in order to maximize the electrostatic attraction between the activated substrate and the chiral anion. To corroborate these findings, bulkier substituents at the alkyloxy group of the cinnamate were experimentally tested, and significantly diminished enantioselectivities were found (er 75:25 with ethyl cinnamate; er 57.5:42.5 with benzyl cinnamate). Despite these promising results, a detailed understanding of the activation mode of this chiral counteranion and the molecular recognition that leads to the CIP is still missing, together with a clear-cut explanation of the origin of the enantioselectivity.

This work provides a thorough description of the mechanism, the intermediate structures, and the stereocontrolling factors for the aforementioned enantioselective DA reactions of cinnamate esters (RA and RB in Scheme 2) using a generally applicable computational protocol. As outlined above, the reactions were chosen due to the markedly different shape of the associated catalysts, i.e. open (5a) vs confined active sites (5b), and their different selectivities, i.e. 5a exclusively activates Fm-cinnamates (1a) while 5b enantioselectivities decrease with the size of the alkyloxy group, i.e. methyl (1b) > ethyl > phenyl cinnamate. A summary of the substrate-dependent selectivity of 5a,b is shown Table 1.

Table 1. Selectivity of DA Reactions of Cinnamate Esters Catalyzed by 5a,b.

entry	R group	silylating reagent	catalyst	erendo
1a	Fm	6a	5a	86.5:13.5
2a	Me	6a	5a	51:49
3b	Me	6b	5b	97:3
4b	Et	6b	5b	75:25
5b	Ph	6b	5b	57.5:42.5

^aReaction at 25 °C for 24 h.

^bReaction at −40 °C for 24 h.

In our study, emphasis is placed on identifying the key noncovalent interactions responsible for the selectivity of the studied transformations, with the final aim of aiding in the development of designing principles for catalysts with tailored properties. To achieve this goal in the case of ACDC, the first challenge is to identify the thermally accessible conformations for intermediates and TSs from among the thousands of potential structures.⁵⁶ Moreover, extremely accurate free energy calculations are needed to get reliable selectivities.⁵⁷ Finally, the identification and quantification of the most important attractive/repulsive interactions that take place at the TSs is fundamental to develop designing principles for better catalysts.⁵⁶

To tackle these challenges, a computational protocol was developed that relies on four key components. First, an extensive conformational sampling was performed using molecular meta-dynamics simulations (MTD) as implemented in XTB code.^58,59 Second, free energy calculations for all low-energy conformers were carried out using density functional theory (DFT). Third, the free energy was further refined using accurate quantum electronic structure calculations based on highly correlated wave function based methods: i.e., a local variant of the coupled cluster method with single and double excitations and perturbative triple substitutions (CCSD(T)).⁶⁰ Specifically, the domain-based local pair natural orbital CCSD(T) (DLPNO-CCSD(T)) method was used.⁶¹⁻⁶⁷ Finally, in order to achieve a quantitative understanding of the stereocontrolling factors, catalyst–substrate interactions in the enantiodetermining TSs were quantified using the well-established local energy decomposition (LED)^68,69 scheme for DLPNO-CCSD(T) energies. This approach allowed us to exactly decompose the relative energy between the low-lying enantiodetermining TSs into steric and London dispersion (LD) energy (see refs (70 and 71) for reviews on the role that LD plays in molecular chemistry), thus providing a quantitative framework in which to discuss the origin of the stereoselectivity.

Methodological Aspects

In order to identify the thermally accessible reaction intermediates and TSs under the experimental conditions, we applied a filtration strategy, in which the number of candidate structures is progressively reduced while ascending a hierarchy of levels of theory. Our computational approach consists of five steps, as detailed in the following sections. Importantly, all steps rely on quantum electronic structure methods rather than on empirical force fields. This makes our computational strategy generally applicable, irrespective of the nature of the reaction. Unless otherwise specified, all calculations were carried out using a development version of the ORCA suite of programs based on version 4.2.⁷²

Step 1: Definition of Initial Guess Structures

In the first step of our protocol, we generate an initial set of reaction intermediates and TSs to be used as input in the subsequent conformational sampling procedures. For CIPs, initial structures were obtained by placing the chiral anion and the activated substrate (in their various conformations) in different relative orientations. Then, the structures were fully optimized at the DFT level of theory by using the PBE-exchange correlation functional⁷³ in conjunction with the D3-dispersion correction of Grimme^74,75 and making use of the resolution of identity approximation.⁷⁶ The def2-SVP basis set⁷⁷ was used for all atoms with matching auxiliary basis sets.⁷⁸ The optimized CIPs with significantly different structural features were used to generate the initial guesses for the TSs. These correspond to the attack of Cp to either face of the dienophile in the CIP.

Analytical frequency calculations were done to characterize local minima (no imaginary frequencies) and TSs (one imaginary frequency). Note that, for the studied reactions, TS and intermediate geometries are rather independent by the nature of the exchange correlation functional employed or by the level of theory used for incorporating solvation effects, as shown in Tables S1 and S2 in the Supporting Information. Moreover, this strategy has been already successfully used for the study of related transformations.¹⁶

Step 2: Conformational Sampling

Starting from the initial set of candidate structures for the relevant TSs and intermediates, a large set of conformers was generated using a semiempirical method. For these calculations, the XTB code (version 6.1) was used.⁵⁸ A slightly different procedure was adopted for the reaction intermediates (e.g., counteranions and CIPs) and TSs, as detailed in the following.

The conformational space for reaction intermediates was sampled using the conformer–rotamer ensemble sampling (CREST) algorithm⁷⁹ that relies on the semiempirical tight-binding based quantum chemistry methods GFN1-xTB⁸⁰ and GFN2-xTB.⁸¹ We used the default settings and thresholds for the MTD-GC(RMSD)/GFN2-xTB simulations, where an extensive root mean square deviation (RMSD) based meta-dynamic sampling (MTD) is performed with an extra genetic z matrix crossing (GC) step at the end.⁵⁹ The MTD simulations were done in a canonical NVT ensemble using the Berendsen thermostat⁸² at a heat transfer time constant of 0.5 ps. The SHAKE⁸² algorithm was used to constrain the covalent bonds (based on covalent radii) with an MD time step dτ of 5 fs. The average temperatures in the conformational MTD were between 400 and 500 K with a length that is unique to each molecule (automatically determined as a function of the molecule flexibility). The structural similarity was assessed by the RMSD, and conformers for which their RMSD is less than 0.25 Å were removed.

For TS conformers, the sampling was performed using the procedure just discussed but keeping the two forming C···C bond lengths of the cycloadduct fixed to the values obtained from the initial DFT optimization (d_1,C···C ≈ 2.0 Å and d_2,C···C ≈ 2.7 Å).

Step 3: Energy Sorting, Geometry Optimizations and Free Energy Corrections

For intermediates, the conformers obtained from the conformational sampling were further optimized at the PBE-D3/def2-SVP level, leading to a total of 301, 81, and 397 unique conformers for anions, activated dienophiles, and CIPs, respectively. Free energy corrections were computed at 298.15 K (RA) and 233.15 K (RB), consistent with the experimental conditions, at the same level of theory used for the geometry optimizations. The quasi-rigid-rotor harmonic oscillator (RRHO) approximation was used,⁸³ as implemented in ORCA.

For TSs, all structures obtained from the conformational sampling procedure were further optimized by means of constrained-geometry optimizations at the PBE-D3/def2-SVP level, using the same constraints defined in the previous step. This led to 142 approximate TSs for RA and 707 approximate TSs for RB. Fully relaxed TS optimizations were performed for the low-lying TSs as well as for those TSs with remarkably different structural features. Note that the energy difference between constrained and fully relaxed TS geometries is typically very small, as shown in Figure 1 for the RB case. Hence, the TSs obtained from the constrained optimizations can be considered to be very good approximations to the fully relaxed TSs.

Figure 1.

Energy of the TS conformers obtained from constrained geometry optimizations (C-TS) at the PBE-D3/def2-svp level for RB. The TSs leading to the major (3b) and minor (3b′) enantiomers are shown with black and red points, respectively. Empty circles denote the corresponding TSs obtained from fully relaxed TS optimizations.

Step 4: Final Single-Point Energies and Free Energies

For the low-energy structures identified in the previous step, DLPNO-CCSD(T)⁶¹⁻⁶⁷ single-point energies were determined using def2-TZVPP⁷⁷ (for RA) and def2-TZVP⁷⁷ (for RB) basis sets in conjunction with their matching auxiliary counterparts.^84,85A solvation correction was computed in toluene using the continuum solvation model C-PCM⁸⁶ at the B3LYP⁸⁷-D3 level with the basis set def2-TZVP and added to the DLPNO-CCSD(T) energy together with the free energy correction. The method is denoted hereafter as DLPNO-CCSD(T) + B3LYP(C-PCM).

Step 5: Analysis of the Key Intermolecular Interactions

Having identified the low-energy structures for intermediates and TSs, an in-depth analysis of the key noncovalent interactions responsible for their relative energy (and thus for the stereoselectivity of the studied transformations) is required.

A useful tool in this context is the local energy decomposition (LED) analysis, whose theory has been described in detail in a series of recent publications,^68,88,89 (See ref (69) for a review). Herein, we recall only the features of this scheme that are relevant to the present work. The total DLPNO-CCSD(T) binding energy between a pair of fragments (X and Y) in a molecule can be partitioned as

1

where the geometric preparation energy ΔE_geo-prep (also called strain⁹⁰ or distortion^91,92) is the energy required to distort the fragments from their equilibrium structure into the geometry they have in the adduct; while ΔE_int is the interaction energy between the distorted fragments. The latter can be further defined as the sum of the HF (ΔE_int^HF) and correlation (ΔE_int) contributions:

2

The ΔE_int^HF term already accounts for some of the key interaction components such as electrostatics, polarization effects, and exchange interactions, while ΔE_int provides a correction for the energy terms that are approximately descibed at the HF level and also incorporates an additional physical contribution to the interaction: i.e., the London dispersion (LD) energy. The LD energy term can be extracted from ΔE_int^C by summing up all the instantaneous dipole–dipole excitations between the two fragments, as detailed in ref (69). This procedure allows us to define the LD energy at the DLPNO-CCSD level. Moreover, an effective triple correction contribution to the LD energy can also by estimated and added to it, as detailed in refs (69 and 93), leading to the final LD energy at the DLPNO-CCSD(T) level: i.e., E_disp.

Finally, by summing up the nondispersive components in ΔE_int^C with ΔE_int, one can define the overall nondispersive component to the interaction, ΔE_no-disp. This term accounts for all the physical components of the interaction energy except for LD: i.e., electrostatics, orbital interactions, steric repulsion, and polarization effects. This term can be further decomposed into various energy components, as detailed in the Supporting Information.

Herein, this approach is used to decompose the free energy of association for the interaction between the counteranion and the activated substrate to form the CIP using the expression

3

where ΔG_corr incorporates all solvent, thermal, and entropy corrections to the association energy. An analogous approach can also be used to decompose the reaction barrier for the attack of Cp to the CIP (ΔG^⧧) using

4

where the fragments in this case are the CIP and the diene in the stereocontrolling TSs.

To provide an additional visual insight into the electrostatic interactions that contribute to the stability of CIPs and TSs, molecular electrostatic potential (MEP) surfaces are discussed. MEP was mapped on isodensity surfaces (0.002 au) in the range from −0.1 (red) to +0.1 (blue) and was generated with UCSF Chimera.⁹⁴ Optimized geometries were plotted using the CYLview⁹⁵ program using the following atom color code: H, white; C, gray; N, blue; O, red; F, green; Si, beige; P, orange; S, yellow.

Results and Discussion

As already mentioned, RA and RB are expected to proceed through the mechanism highlighted in Scheme 1. In their seminal work,³⁹ Wheeler and co-workers were already able to identify the key TSs responsible for the stereoselectivity of RA by combining molecular mechanics and DFT optimizations. However, the complete energy profile for this reaction has not been discussed so far, and the structure and properties of the chiral anion, of the activated catalyst, and of the most stable CIP are still unknown. The computational modeling of RB is even more challenging due to the larger size and flexibility of the associated catalyst (see ref (16) for preliminary results). In this work, a thorough discussion of the mechanism and sterecontrolling factors of both reactions is reported.

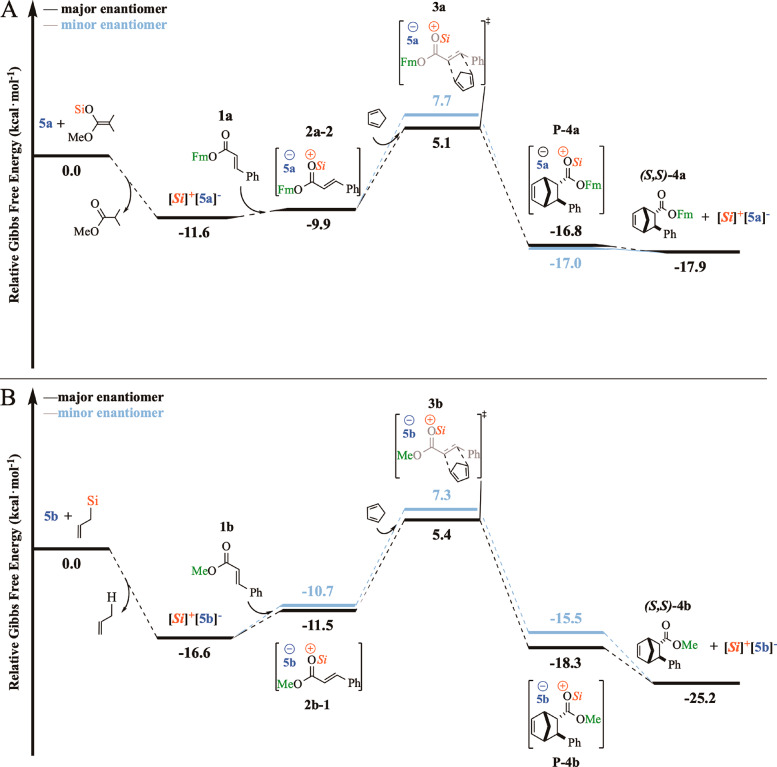
Our discussion starts by analyzing their energy profiles (Figure 2), which were obtained using the computational protocol outlined in the previous section.

Figure 2.

Proposed reaction mechanisms for RA (top) and RB (bottom) at the DLPNO-CCSD(T) + B3LYP(C-PCM) level.

The activation of the catalyst to give the [Si]⁺[X*]^– species is highly exergonic for both reactions. In fact, these species have been characterized by ¹H NMR spectroscopy.^15,26 The second step of the reaction is the formation of the CIPs, which are lower in energy in comparison with the separated species (ΔG(2a-2) = −9.9 kcal mol^–1 for RA; ΔG(2b-1) = −11.5 kcal mol^– for RB) but higher in energy than the activated catalyst. Note that, for RB, the pathways leading to the major and the minor endo enantiomers feature different CIPs, as will be discussed in more detail in the following sections. Afterward, the attack of the Cp leads to the TSs. A lower activation barrier was found for the formation of the favored endoenantiomer 3a (ΔΔG^⧧ = 2.6 kcal mol^–1) and 3b (ΔΔG^⧧ = 1.9 kcal mol^–1), consistent with the experimental observation. Once the activation barrier is overcome, the product P (interacting with the counteranion) is formed and then liberated by direct Lewis base exchange with another molecule of the dienophile.^15,16 Finally, it is worth mentioning that cycloadducts 4a,b are predicted to be formed in slightly greater enantiomeric excesses (99 and 98, respectively) in comparison to the experimental findings (86 and 97, respectively). Given the challenging nature of these transformations, these results appear as extremely promising.

In the following sections, we will provide a thorough discussion of the stereocontrolling factors of these transformations. In particular, to clearly illustrate the molecular recognition mechanism responsible for the CIP formation, we start by exploring the structure of its constituting charged species: i.e., the chiral counteranion and the activated dienophile. In this context, it is worth mentioning that an experimental characterization of the CIP intermediate would be highly desirable, because it could provide an experimental insight into the stereocontrolling factors of these reactions (provided that the CIP structure is retained in the enantiodetermining TSs). Unfortunately, the CIP intermediate for RA and RB has proven elusive to experimental characterization so far: e.g., by NMR spectroscopy. This observation is consistent with the profile shown in Figure 2.

Counteranions

The (S)-BALT counteranion features a relatively rigid geometry with only a few possible conformers, which differ in the relative orientation of the Tf substituents directly bonded to the active center (see emphasized atoms in Figure 3A). On comparison to the two more stable isomers 5a-1 and 5a-2, the staggered conformation of the Tf groups is 3.6 kcal mol^–1 more stable than the eclipsed conformation. Their relative population in solution can be estimated by a standard Boltzmann distribution analysis. Our results suggest that only the conformer 5a-1 exists at room temperature in toluene (99.8% weight). Indeed, this conformation is retained in the most stable CIP and TSs, as discussed in the next sections.

Figure 3.

Low-energy conformers for (A) (S)-BALT and (B) (S,S)-IDPi counteranions with expected percentage populations in solution and relative free energy stabilities (kcal mol^–1) with respect to the most stable geometry. Only the conformers with significantly different structures are shown (see Figure S1 in the Supporting Information for additional conformers). Emphasized atoms show the major structural changes from these references. Hydrogens are omitted for the sake of clarity. MEP shows that the negative charge excess in (S)-BALT is delocalized between eight oxygens and two carbons, while that in (S,S)-IDPi is delocalized between four oxygens and three nitrogens.

Visual inspection of the MEP surfaces of the conformers can be used to identify the region of the anion that features a more negative electrostatic potential: i.e., the region of the anion in which the negative charge is mostly delocalized (see red region in Figure 3A and Scheme S1). As expected, the negative charge is delocalized between the two carbons of the allyl group and eight oxygens. Hence, all conformers reveal extended “red” surfaces. These results indicate that the (S)-BALT counteranion lacks a clear recognition site to favorably engage with the substrate. Thus, the electrostatic interaction stabilizing the ion pair is expected to be poorly directional.

In contrast to the (S)-BALT counteranion, the (S,S)-IDPi counteranion (5b) has a rather flexible structure with hundreds of possible conformers. The most stable conformers 5b-1 and 5b-2 feature a C₂ axis, as do 5b-3 and 5b-4 (see Figure 3B). These results are consistent with previous experimental findings indicating that the 5b structure is C₂ symmetrical on the NMR time scale.⁵³ It is important to note here that a direct geometry optimization of the X-ray coordinates³² leads to the nonsymmetric minimum 5b-5, which is less stable than 5b-1 by 3.8 kcal mol^–1. Other nonsymmetrical geometries lying in a range of only 1.2 kcal mol^–1 (computed population >6% at T = 233.15 K in toluene) are shown in Figure S1 in the Supporting Information.

The most stable conformers of 5b differ for the relative orientation of the Tf groups and of the two sterically demanding Ar substituents (Scheme 2) closer to the N–P–N–P–N inner core. For instance, 5b-1 differs from 5b-2 in the relative orientation of the Ar groups (2.0 kcal mol^–1) and from 5b-4 in that of the Tf groups (2.6 kcal mol^–1). This flexibility affects the shape and size of the chiral pocket, which is expected to be responsible for the induction of asymmetry in the substrate. The extreme cases are conformers 5b-3 and 5b-4, which feature a widely open and closed pocket, respectively.

Consistent with chemical intuition, the analysis of the MEP surfaces reveals that the negative charge is highly delocalized between the nitrogens and the oxygens of the Tf groups, as shown clearly for the “open” isomer 5b-3 in Figure 3B (see also Scheme S1 in the Supporting Information). Thus, all IDPi conformers, except for 5b-4, feature a region of negative electrostatic potential that might act as a recognition site, to which the positive regions of the substrate can interact via attractive electrostatic forces.

To summarize, it is worth highlighting here the main differences between the counteranions of RA and RB: (i) 5a is structurally more rigid than 5b and hence only a single conformer is thermally accessible at room temperature, while several conformers are in principle accessible for 5b (although 5b-1 is by far the most stable); (ii) 5a features a highly delocalized negative charge, thus lacking a well-defined recognition site, while in 5b the negative charge is essentially confined into the chiral pocket. As will be demonstrated in the following, these differences in the structural features of the anions are responsible to a large extent for their different selectivity.

Activated Dienophiles

Experimentally, only the trans stereoisomer of the α,β-unsaturated cinnamates 1a and 1b were used. Note that the carbonyl group can be placed either s-trans or s-cis to the olefin, while the silyl and alkoxy groups can be bonded either on the same side (Z) or on the opposite side (E) of the carbonyl. In all cases, the Z s-cis form was found to be slightly more stable than the other isomers in solution (see Figure 4).

Figure 4.

Low-energy conformers for the trans-cinnamate (A) 1a activated with LA SiMe₃⁺ and (B) 1b activated with LA SiEt₃⁺. Their relative free energy stabilities (kcal mol^–1) with respect to the most stable geometry are also reported together with the associated percentage populations in solution. Emphasized atoms show the s-cis and s-trans conformations.

A common feature of all conformers is that the coordination of the silylium LA makes 1a,b electron-poorer dienophiles, which is consistent with the positive region observed in the MEP surface for the reactive C=C atoms (dark blue in Figure 4). Moreover, an analysis of the MEP surface indicates that the positive charge delocalizes toward the alkyloxy group of both cinnamates: i.e., in the CH₂ group of the Fm substituent of Si-1a and in the CH₃ group of Si-1b.

Activation Mode within the Chiral Ion Pair

Initially, several ion-pair complexes formed between the different conformers of 5a,b (Figure 3) with Si-1a and Si-1b (Figure 4), respectively, were located at the DFT level and used as a guess for the subsequent conformational sampling, as detailed in Methodological Aspects.

For RA, a large number of CIP structures were identified that differ significantly in the relative orientation of the anion and of the activated dienophile. A complex pattern of interactions is responsible for the relative stability of the various CIPs. This observation is consistent with the aforementioned findings on the (S)-BALT counteranion, which lacks a well-defined recognition zone to engage with the substrate. Despite these structural differences, some common features can be identified among the most stable CIP complexes 2a-1 and 2a-2 (see Figure 5A). First, they involve the interaction of the most stable anion 5a-1 with an s-cis conformation of the dienophile Si-1a. Second, all CIP conformers feature nonconventional C–H···O hydrogen bonds and/or C–H···F interactions between C–H groups of the dienophile and oxygens and/or fluorines of the counteranion. Interestingly, structure 2a-2, which is 1.7 kcal mol^–1 higher in energy than 2a-1, features a “π-stacking” interaction between the Fm group of the dienophile and the parallel alignment of 9-phenanthryl substituent of the counteranion. This interaction is reminiscent of that found by Wheeler as one of the key factors contributing to the selectivity of RA.³⁹ The fact that this interaction is not present in the most stable CIP is interesting and will be discussed in more detail in the following section.

Figure 5.

Low-energy conformers for (A) Si-1a···5a and (B) Si-1b···5b chiral ion pairs with percentage populations in solution sorted by their relative free energy stabilities (kcal mol^–1) with respect to the most stable geometries 2a-1 and 2b-1, respectively. All of the structures keep the same orientation of the anion. C–H···O (dotted red lines), C–H···N (dotted blue lines), and C–H···F (dotted green lines) interactions between CH groups of the dienophile and emphasized oxygens, nitrogens ,and fluorines of the counteranions are identified. Nonactive hydrogens are omitted for the sake of clarity. MEP surfaces of the distorted interacting fragments are superimposed on the geometry of the CIP.

In contrast to the RA case, the most stable CIPs for RB involves a relatively high energy conformer of the (S,S)-IDPi counteranion (5b-3, 2.4 kcal mol^–1), which features an open chiral pocket (see Figure 5B). Closer inspection of these geometries reveals that the methoxy group of the dienophile is pointing inside the pocket of the anion, leading to a perfect geometric and electrostatic match between the binding partners. The close proximity between the methyl group of the silylated dienophile and the inner core of the IDPi counteranion is consistent with the experimental observation that a significant amount of catalyst methylation occurs at high temperatures.¹⁶ This molecular recognition is favored regardless of the substrate conformation, since 2b-1 involves the Si-1b-1 (s-cis) dienophile, while 2b-2 is formed with the s-trans conformation. Note that these results differ in part from those found in previous preliminary computational investigations of these systems,¹⁶ in which the s-trans dienophile was predicted to be involved in the most stable CIPs. This difference originates from the more extended conformational sampling approach used in the present work. It is also worth mentioning that, in addition to the C–H···O and C–H···F interactions, a nonconventional C–H···N hydrogen bond between a C–H of the methoxy group and a nitrogen of the counteranion is present in structures 2b-1 and 2b-2.

A further insight into the nature of the ion-pair interaction can be obtained by decomposing association energies into additive contributions via the LED scheme, as shown in Table 2. Importantly, the free energies of formation for the CIPs are highly exergonic, irrespective of the different nature of the ionic moieties (about −25 kcal mol^–1, see Table 2). Note that this does not necessarily imply that their structure can be detected via NMR spectroscopy under the experimental conditions, because the silylating agent could in principle bond preferentially to the anion rather than to the dienophile. In fact, our calculations predict that the activated catalyst [Si]⁺[X*]^– is generally more stable than the CIP, which might explain why the latter has not been yet characterized experimentally in the context of ACDC.

Table 2. Computed Free Energies (ΔG) for the Association of the Counteranion with the Activated Dienophile To Form the CIPs Si-1a···5a and Si-1b···5b in Solution^a.

	CIP
	RA		RB
	2a-1	2a-2	2b-1	2b-2
ΔGb,c	–26.3	–24.6	–25.4	–24.6
ΔE	–82.6	–79.5	–78.9	–77.3
ΔEgeo-prep	4.3	4.1	12.4	9.0
ΔEint	–86.9	–83.6	–91.3	–86.3
Edisp	–36.4	–33.8	–35.4	–35.5
ΔEno-disp	–50.5	–49.8	–55.9	–50.8

^aThe ΔG values are also decomposed using the LED scheme (eq 3). All energies are in kcal mol^–1.

^bReaction RA at 25 °C.¹⁵

^cReaction RB at −40 °C.¹⁶

As can be readily seen in Table 2, all systems exhibit similar ΔE values, while more pronounced differences can be observed in the magnitude of the various LED terms. In particular, 2b-1 and 2b-2 feature larger ΔE_geo-prep values than 2a-1 and 2a-2, which is due to the fact that the (S,S)-IDPi counteranion is significantly distorted in the CIP structure to maximize the electrostatic interaction with the activated dienophile. In fact, the largest stabilizing term in all cases is the electrostatic interaction between the ions (which is included in ΔE_no-disp, see Table S3 and Figure S3 in the Supporting Information), which is consistent with the ionic nature of the CIP complex. The significance of the LD interactions in stabilizing these systems is also evident. In fact, the LD energy (ΔE_disp) between the ions amounts to about 34 kcal mol^–1. This result is consistent with the notion that the dispersion increases with the polarizability of the interacting fragments, and thus with their size, leading to a large and stabilizing contribution for CIPs involving bulky anions. Importantly, 2a-1 features a more compact structure than 2a-2, and hence LD preferentially stabilizes the former (see Figure S2 in the Supporting Information). This result explains the greater stability of 2a-1 with respect to that of 2a-2, despite the fact that the latter features an additional “π-stacking” interaction.

To summarize, the most stable CIP structure in RA is essentially determined by the relative orientation of the rigid (S)-BALT counteranion with the activated dienophile, which in turn determines a complex pattern of noncovalent interactions. In contrast, the most stable CIP structure for RB features an “electrostatic lock and key” binding mode mechanism, in which both the activated dienophile and the anion distort significantly to maximize their electrostatic interaction. This mechanism is consistent with the notion that these organocatalysts mimic the activation mode of enzymes.^32,40−47 For both reactions, the association process between the ions is further supported by London dispersion forces.

Origin of the Selectivity

Having established the mechanism through which the chiral anion and the activated substrate interact to form the CIP, we now discuss how the CIP structure influences the enantioselectivity of the reaction. Once the CIP is formed, a Cp molecule can attack either face of the activated dienophile, leading to the corresponding enantiomeric cycloadducts through a four-membered TS. Thus, the CIP structure determines the face of the dienophile that is preferentially attacked and hence the reaction stereoselectivity. For the sake of simplicity, only the most stable competing endo-TSs are discussed (see 3a and 3a′ in Figure 6 for RA and 3b and 3b′ in Figure 7 for RB; the prime denotes TSs leading to the minor product enantiomer). However, all of the results discussed in the following remain valid for all TS structures within a range of 2 kcal mol^–1 from the most stable geometry.

Figure 6.

Cp attack to the CIP 2a-2 leading to the formation of the stereocontrolling TSs. TSs 3a and 3a′ lead to 4a (major) and 4a′ (minor) product enantiomers, respectively. Forming C···C σ-bonds at the TSs are shown in red. The er is calculated as the free energy difference between both TSs in toluene at 298.15 K. MEP shows the more positive region (dark blue) localized in the dienophile, while the negative region (red) belongs to the counteranion. MEP surfaces of the distorted anion and dienophile are superimposed on the geometry of the TSs including the diene. Energies are given in kcal mol^–1.

Figure 7.

Comparison between the formation of the CIPs 2b-1 and 2b-2 that are retained at the corresponding competing TSs 3b and 3b′ for each endo enantiomer 4b (major) and 4b′ (minor) of cycloaddition RB. Forming C···C σ-bonds at the TSs are shown in red. The er is calculated as the free energy difference between both TSs in toluene at 233.15 K. MEP shows the more positive region, in dark blue, localized in the dienophile, while the negative region, in red, belongs to the counteranion. MEP surfaces of the distorted anion and dienophile are superimposed on the geometry of the TSs including the diene. Energies are given in kcal mol^–1.

As mentioned above, the most stable CIP for RA is 2a-1, which features a compact structure stabilized by LD forces. However, in 2a-1, both faces of the dienophile are sterically hindered from attacking Cp, and hence the associated TSs are very high in energy (see Figure S2 in the Supporting Information). The most stable TSs obtained from the computational sampling procedure, i.e., 3a and 3a′, correspond to the attack of Cp to the same CIP, that is, 2a-2. For RB, 3b and 3b′ correspond to the attack of Cp to slightly different CIPs: namely, 2b-1 (for 3b) and 2b-2 (for 3b′).

According to the computed free energies shown in Table 3, our results predict the formation of the final product with an er of 98.8:1.2 (ΔΔG^⧧ = 2.6 kcal mol^–1, RA) and 98:2 (ΔΔG′ = 1.9 kcal mol^–1, RB), which are in good agreement with the experimental outcomes (er 86.5:13.5, ΔΔG^⧧ = 1.1 kcal mol^–1 for RA and er 97:3, ΔΔG^⧧ = 1.6 kcal mol^–1 for RB).

Table 3. Reaction Barriers (ΔG^⧧) for the Attack of Cp to the CIP and Their Decomposition Based on the DLPNO-CCSD(T)/LED Scheme (eq 4)^a.

	TS
	RA			RB
	3a	3a′	3a′ – 3a	3b	3b′	3b′ – 3b
ΔG⧧b,c	16.7	19.3	2.6 (exp 1.1d)	16.9	18.8	1.9 (exp 1.6d)
ΔE⧧	–3.4	0.0	3.4	4.6	7.3	2.7
ΔEgeo-prep⧧	27.3	28.4	1.1	36.2	37.1	0.9
ΔEint⧧	–30.7	–28.4	2.3	–31.6	–29.8	1.8
ΔEdisp⧧	–34.7	–29.6	5.1	–37.7	–37.0	0.7
ΔEno-disp⧧	4.0	1.2	–2.8	6.1	7.2	1.1

^aAll energies are in kcal mol^–1. The free energy difference between the TSs is also reported (and decomposed) and compared with available experimental data.

^bReaction RA at 25 °C.¹⁵

^cReaction RB at −40 °C.¹⁶

^dObtained from the experimental er^15,16 according to the Curtin–Hammett principle.

The TS geometries reveal a concerted mechanism via highly asynchronous TSs, where the β carbon reacts before the α carbon with the diene: i.e., the forming C···C σ-bond distances are not equal (the difference between the lengths are 0.734 Å in 3a, 0.710 Å in 3a′, 0.676 Å in 3b, and 0.701 Å in 3b′). Although the most important features of the CIP structure are retained also in the stereocontrolling TSs, a closer inspection of the TS geometries reveals that the interaction of the diene with the CIP leads to substantial structural changes in both the interacting dienophile and the counteranion.

Surprisingly, in TS 3a of RA as well as for TSs 3b and 3b′ of RB the cycloaddition takes place preferentially at the congested face of the activated substrate, while only in TS 3a′ does the Cp attack the bare face of the dienophile. To understand the origin of this unexpected behavior as well as the stereocontrolling factors of these transformations, we analyzed the interaction between the Cp and the CIP using our DLPNO-CCSD(T)/LED methodology. Table 3 contains the LED terms for the CIP–Cp interactions in the enantiodetermining TSs of RA and RB, together with their relative energies.

For all of the TSs, the interaction energy between the CIP and the Cp fragment is highly stabilizing and is essentially compensated by the energy investment required to distort the fragments from their equilibrium geometry to the geometry they have in the TS. For RA, a comparison between 3a and 3a′ demonstrates that TS 3a is favored from both, a less destabilizing ΔE_geo-prep^⧧ (by 1.1 kcal mol^–1) and a stronger ΔE_int (by 2.3 kcal mol^–1). A similar result is found for RB.

A decomposition of the interaction energy into dispersive and nondispersive components reveals that the latter preferentially stabilizes TS 3a′ (ΔE_no-disp^⧧ = –2.8 kcal mol^–1), thus favoring the formation of the minor product enantiomer. Intuitively, this can be associated with the fact that TS 3a′ arises from the addition of Cp to the less congested face of the substrate, which is sterically favored (see Figure 6). However, the LD energy is significantly larger in the competing TS 3a, thus reversing the energetic ordering of the two TSs. In fact, 3a features a much more compact structure than 3a′. These results demonstrate that a balance of steric repulsion and LD is responsible for the experimentally observed enantioselectivity. In particular, LD appears to be the main stereocontrolling factor in RA.

As discussed above, the (S,S)-IDPi counteranion is bulkier and more flexible than (S)-BALT. A consequence of this enhanced flexibility is that it can rearrange in order to maximize the electrostatic interactions with the activated dienophile to form the CIP. Moreover, the CIP structure is rather flexible and hence can easily accommodate the activated substrate within its chiral pocket, thus maximizing CIP–Cp LD interactions. In fact, our results for RB demonstrate that TS 3b and 3b′ feature very similar structures, in which the Cp settled within the pocket formed between the dienophile and one of the Ar substituents on the BINOL backbone of the (S,S)-IDPi counteranion (see Figure 7). Hence, in both cases LD dominates over steric repulsion and Cp always attacks the more congested face of the dienophile. The relative energy between the TS 3b and 3b′ is in this case the result of a delicate balance of steric and dispersion, with both effects contributing similarly to stabilize TS 3b over 3b′.

Conclusions

A computational protocol combining a thorough conformational sampling with accurate coupled-cluster based energies was used to shed light on the mechanism, stereocontrolling factors, and key intermolecular interactions of two asymmetric catalytic Diels–Alder reactions (RA and RB) in the context of asymmetric counteranion-directed catalysis. The computed er values for these reactions were found to be in excellent agreement with experimental data, and the computed mechanism was found to be fully consistent with previous experimental observations.

In this type of chemistry, the chiral counteranion induces the enantioselectivity by ion pairing with a cationic intermediate to form a so-called “chiral ion pair” (CIP). It was found that the smaller BALT anion is structurally more rigid than the IDPi anion. Hence, only one BALT anion conformer features a non-negligible population at room temperature in solution. Moreover, the BALT anion lacks a well-defined recognition site to engage with the positively charged activated substrate. As a consequence, the various CIP conformers involving this anion differ in the relative orientation of the “rigid” ions, which in turn determines a complex pattern of noncovalent interactions that are responsible for their relative stability. The most stable CIP structure is extremely compact and is significantly stabilized by London dispersion forces.

In contrast, the IDPi anion is much more flexible, with several conformers that are relatively close in energy. Hence, it can distort in order to maximize the electrostatic interaction with the activated substrate, giving rise to a characteristic “electrostatic lock-and-key” binding mode that is reminiscent of that found in enzymes. Again, the association process between the ions is further supported by highly stabilizing London dispersion forces.

Once the CIP is formed, a Cp molecule can attack either face of the activated dienophile, leading to the corresponding enantiomeric products. Interestingly, the most stable CIP structure involving BALT is not retained in the sterecontrolling TSs for RA. This is a consequence of its rigid and compact structure that does not allow an easy access to the Cp molecule. For RA, Cp attacks the second most stable CIP. Importantly, it attacks preferentially the more congested face of the activated dienophile due to attractive London dispersion forces. Hence, such noncovalent interactions overcome the repulsive steric interactions at the more congested face of the dienophile, thus determining the most stable TS structure and the selectivity of the transformation.

For RB, the attack of the Cp to the different faces of the dienophile involves two slightly different CIPs that feature the same electrostatic lock-and-key binding mode. This is a consequence of the structural flexibility of the IDPi counteranion and related CIP. In fact, the CIP structure can distort slightly in order to accommodate a Cp molecule into its pocket, giving rise to TS structures that are greatly stabilized by London dispersion forces. As a consequence, the selectivity of these transformations is governed by a delicate balance of dispersion and steric effects.

These results suggest that London dispersion could be used as a valuable catalyst design element in the future. This is especially true for IDPi catalysts, which feature a clear recognition site to engage with the activated substrates. By modifying the size and polarizability of the substituents on the BINOL backbone, one can tune the shape and the electronic properties of the chiral pocket, thus influencing the structure of the CIP and of the corresponding TSs. We hope that the computational strategy presented in this work will aid in the rational design of new catalysts with tailored electronic and steric properties.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.9b13725.

• Detailed computational results and XYZ coordinates for all the structures computed in this work (PDF)

The authors declare no competing financial interest.