Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Feb 24;124(12):2380–2397. doi: 10.1021/acs.jpca.9b10880

Performance of Electronic Structure Methods for the Description of Hückel–Möbius Interconversions in Extended π-Systems

Tatiana Woller †,‡, Ambar Banerjee §, Nitai Sylvetsky §, Golokesh Santra §, Xavier Deraet †, Frank De Proft †, Jan M L Martin §,*, Mercedes Alonso †,*
PMCID: PMC7307915  PMID: 32093467

Abstract

graphic file with name jp9b10880_0014.jpg

Expanded porphyrins provide a versatile route to molecular switching devices due to their ability to shift between several π-conjugation topologies encoding distinct properties. DFT remains the workhorse for modeling such extended macrocycles, when taking into account their size and huge conformational flexibility. Nevertheless, the stability of Hückel and Möbius conformers depends on a complex interplay of different factors, such as hydrogen bonding, π···π stacking, steric effects, ring strain, and electron delocalization. As a consequence, the selection of an exchange–correlation functional for describing the energy profile of topological switches is very difficult. For these reasons, we have examined the performance of a variety of wave function methods and density functionals for describing the thermochemistry and kinetics of topology interconversions across a wide range of macrocycles. Especially for hexa- and heptaphyrins, the Möbius structures have a stronger degree of static correlation than the Hückel and twisted-Hückel structures, and as a result the relative energies of singly twisted structures are a challenging test for electronic structure methods. Comparison of limited orbital space full CI calculations with CCSD(T) calculations within the same active spaces shows that post-CCSD(T) correlation contributions to relative energies are very minor. At the same time, relative energies are weakly sensitive to further basis set expansion, as proven by the minor energy differences between the extrapolated MP2/CBS energies estimated from cc-pV{T,Q}Z, diffuse-augmented heavy-aug-cc-pV{T,Q}Z and explicitly correlated MP2-F12/cc-pVDZ-F12 calculations. Hence, our CCSD(T) reference values are reasonably well-converged in both 1-particle and n-particle spaces. While conventional MP2 and MP3 yield very poor results, SCS-MP2 and particularly SOS-MP2 and SCS-MP3 agree to better than 1 kcal mol–1 with the CCSD(T) relative energies. Regarding DFT methods, the range-separated double hybrids, such as ωB97M(2) and B2GP-PLYP, outperform other functionals with RMSDs of 0.6 and 0.8 kcal mol–1, respectively. While the original DSD-PBEP86 double hybrid performs fairly poorly for these extended π-systems, the errors drop down to 1.9 kcal mol–1 for the revised revDOD-PBEP86-NL, which eliminates the same-spin correlation energy. Minnesota meta-GGA functionals with high fractions of exact exchange (M06-2X and M08-HX) also perform reasonably well, outperforming more robust and significantly less empirically parametrized functionals like SCAN0-D3.

Introduction

Expanded porphyrins have attracted considerable attention over the past few decades in view of their large conformational flexibility, facile redox interconversions, novel metal coordination behaviors, and versatile electronic states.1 The rich chemistry of these extended macrocycles has led to diverse applications including near-infrared dyes,2 nonlinear optical materials,3 magnetic resonance imaging contrast agents,4 and molecular switches.5

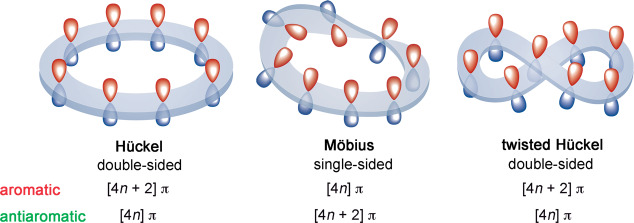
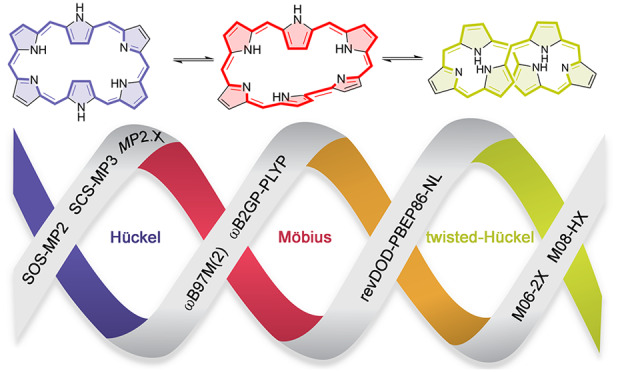
In contrast to the regular porphyrin, expanded porphyrins are flexible enough to switch between different π-conjugation topologies (Hückel, Möbius, and twisted-Hückel), each with different properties (Figure 1).6−8 Such a change of topology involves a Hückel–Möbius aromaticity switch in a single molecule and it can be induced by solvent, pH, and metalation, among others.9,10 These Hückel–Möbius aromaticity switches combine both mechanical and π-electron switching, providing a new route to molecular optoelectronic devices.11 Indeed, we have recently demonstrated the applicability of these unique aromaticity switches as conductance switching and bithermoelectric devices12,13 and as efficient nonlinear optical switches.14

Figure 1.

Figure 1

Open in a new tab

Schematic representation of different π-conjugation topologies of expanded porphyrins and their expected aromaticity as a function of the number of π-electrons.

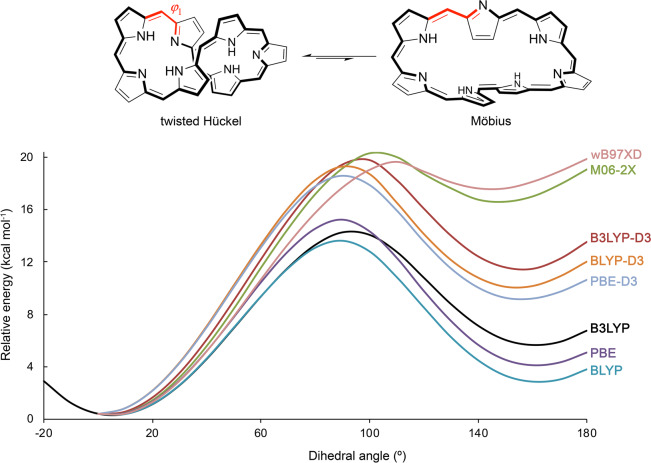
Through extensive density functional theory calculations,15,16 we have demonstrated that the molecular topology is highly influenced by the number of π-electrons and the size of the macrocycle. While [4n + 2] π-electron expanded porphyrins adopt Hückel conformations that are almost planar and highly aromatic, antiaromatic Hückel and aromatic Möbius conformers coexist in dynamic equilibrium for [4n] π-electrons expanded porphyrins.17 The larger heptaphyrins and octaphyrins prefer a twisted-Hückel topology (also known as figure-eight conformation) in the neutral state, but the Möbius topology became the most stable in protonated species.18,19 The stability of these conformers depends on the complex interplay of different factors, such as hydrogen bonding, π···π stacking, steric effects, ring strain, and aromaticity.19 As a consequence, the selection of an exchange–correlation functional for describing the energy profile of these topological switches remains challenging. An illustrative example is the potential energy curve for the Hückel–Möbius interconversion of neutral [32]heptaphyrin computed with different density functionals (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Influence of the density functional on the energetic profile for the interconversion between the twisted-Hückel and Möbius topologies in the neutral [32]heptaphyrin.

In previous studies, we investigated the performance of several exchange–correlation functionals in reproducing the molecular structure of different meso-substituted expanded porphyrins by comparison with the X-ray diffraction data. Our results indicate that the degree of bond-length alternation and π-electron delocalization along the conjugation pathway is highly dependent on the amount of exact Hartree–Fock (HF) exchange.15,16,18,19 Functionals with a small amount of HF exchange predict more delocalized and bond-length equalized structures than functionals including a larger percentage of exact exchange.20 Nevertheless, the bond lengths for Möbius and Hückel structures obtained with B3LYP and M06 are in better agreement with the crystallographic data than the bond lengths computed with M06-2X with double the amount of nonlocal exchange.16,18,19 From the geometrical parameters, it seems that π–π stacking interactions in the twisted-Hückel topology are overemphasized in functionals like M06-2X, which generally yields reduced inter-ring distances and interplanar angles for the stacked rings compared to the experimental geometries (Figure S1). These geometrical changes influence the relative energies of twisted-Hückel and Möbius conformations of large expanded porphyrins, resulting in likely overestimation of the stability of twisted-Hückel topologies. As a consequence, the M06-2X functional fails in predicting the Möbius topology as the most stable configuration upon protonation of [32]heptaphyrin and [36]octaphyrins,18,19 in disagreement with the spectroscopic data and solid-state structures.21,22

The critical role of the density functional on the energetic, geometric and magnetic results of expanded porphyrins was recently established by Torrent-Sucarrat et al.23 In this benchmark study, the performance of 11 DFT functionals was assessed with respect to the local pair natural orbital coupled cluster DLPNO-CCSD(T) method24−26 for topological switches based on [26]hexaphyrin and [32]heptaphyrin. They conclude that CAM-B3LYP, M05-2X, and M06-2X functionals provide a more consistent description of these topological switches. Nevertheless, it is important to underline that the reference values were obtained with the DLPNO-CCSD(T0) approach using default settings, in which off-diagonal Fock matrix elements are neglected in the (T) contribution.27 In line with previous findings,28,29 our recent efforts to assess the performance of localized coupled cluster methods for Hückel–Möbius interconversions suggest larger errors for Möbius-type structures for the DLPNO-CCSD(T0) approach, even with TightPNO cutoffs.30

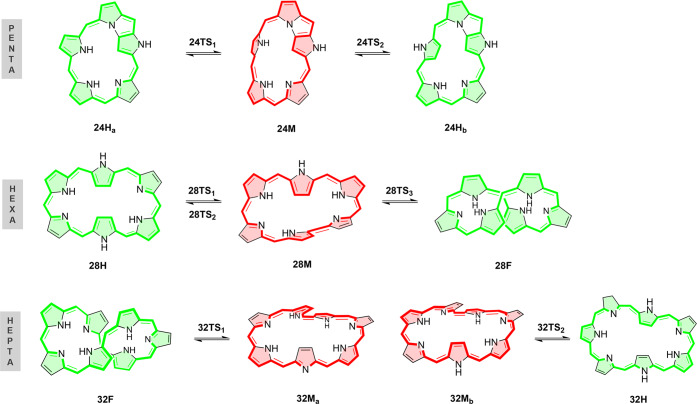
For all these reasons, we decide to examine the performance of a large variety of density functionals and wave function methods for describing the thermochemistry and kinetics of topological switches involving the interconversion between Hückel, Möbius and twisted-Hückel structures. A number of exchange–correlation functionals, ranging from generalized gradient approximations to double hybrids, has been tested and their performance to describe such unique interconversions has been carefully assessed with respect to canonical CCSD(T)/CBS calculations. To this aim, we have considered a variety of topology interconversions in N-fused [24]penta-, [28]hexa-, and [32]heptaphyrins (Figure 3). On the basis of our previous conformational analyses,15,16,18 the more stable conformations for the different expanded porphyrins were selected. In the case of [28]hexaphyrin and [32]heptaphyrin, these conformers correspond to Hückel (H), Möbius (M), and twisted-Hückel topologies (F), also known as figure-eight structures, whereas only Hückel and Möbius structures correspond to energy minima in the smaller N-fused [24]pentaphyrin. Besides the performance on the description of the conformational energies, we considered the key isomerization transition states for these topological interconversions.

Figure 3.

Figure 3

Open in a new tab

Hückel (H), Möbius (M), and figure-eight (F) conformations of selected expanded porphyrins and their aromaticity character. Aromatic macrocycles are colored in red, while green is indicative of antiaromatic systems.

Computational Details

Calculations

The geometries of all stationary points involved in the topology interconversions of N-fused [24]pentaphyrin, [28]hexaphyrin, and [32]heptaphyrin were fully optimized and characterized by harmonic vibrational frequency calculations at the B3LYP31/6-311G(d,p) level of theory. The performance of the B3LYP hybrid functional on the geometries of expanded porphyrins was assessed in our previous benchmarks toward crystallographic data.16,18,19 The nature of the stationary points was ascertained from the appropriate number of negative eigenvalues of the Hessian matrix from the frequency calculations. Minima are characterized by positive eigenvalues, whereas transition states exhibit one negative eigenvalue corresponding to the rotation of one internal dihedral angle. Starting from those optimized geometries, single-point energy calculations were performed using various DFT functionals and wave function methods. Most density functional calculations were carried out using either the Gaussian 09/Gaussian16 software package32 or ORCA versions 4.0 through 4.2,33 whereas Molpro 201834 was used to perform several Møller–Plesset (MP2) and coupled cluster calculations. MP2.X and MP2.5 calculations were conducted with the Turbomole program system.35

As byproducts of the MP2 and MP2-F12 calculations, we also obtained spin-component-scaled varieties such as SCS-MP2-F1236 and S2-MP2.37 The spin-component scaled MP2 theory treats the correlation effects of electron pairs with opposite spin and same spin differently by means of different scaling parameters.38,36 Next to SCS-MP2, MP2.5 and MP2.X methods were also considered. MP2.5 is constructed as the average between MP2 and MP3 energies and produces accurate energies at a computational cost significantly lower than that of CCSD(T).39 MP2.X is a generalized MP2.5 method of the form40

graphic file with name jp9b10880_m001.jpg 1

where C is a basis set-specific empirical scaling parameter for the third-order correction term (C = 0.72 for cc-pVDZ). MP2.X is designed to reduce the errors exhibited by MP2.5 when using smaller basis sets.

Spin-component scaled coupled-cluster singles and doubles, such as SCS-CCSD41 and SCS(MI)-CCSD,42 were also considered, as they are a zero-cost byproduct of the CCSD results. SCS(MI)-CCSD is a reparametrized version of the SCS-CCSD method, in which the same- and opposite-spin scaling parameters were optimized to minimize the error toward CCSD(T)/CBS interaction energies for various noncovalent interaction dimers. Furthermore, the performance of the distinguishable cluster approach DCSD43 and its spin-component scaled version SCS-DCSD44 was assessed.

In our benchmark, the following set of DFT functionals was considered, classified according to Jacob’s ladder:45

  • on the second rung corresponding to generalized gradient approximation functionals (GGA): BLYP,46 PBE,47 and revPBE48

  • on the third rung, we consider the following meta-generalized gradient approximation functionals (mGGA): TM,49 TMTPSS,50 SCAN,51 and TPSS52

  • on the fourth rung, we consider the global hybrid functionals (B3LYP,31 BHLYP,53 PBE0,54 revPBE0,54 SCAN0,55 PW6B95,56 TPSSh,57 M06,58 M06-2X,58 and M08-HX59), several range-separated hybrid functionals (CAM-B3LYP,60 CAM-QTP00,61 CAM-QTP01,61 M11,62 LC-ωPBE,63 ωB97XD,64 ωB97MV,65 and ωB97XV66), and the nonseparable gradient approximation functionals (MN1567)

  • finally, on the fifth and top rung, we assessed the double hybrid functionals (B2PLYP,68 SCAN0-2,55 PWPB95,69 and PTPSS69), the range-separated double hybrids (ωB2PLYP,70 ωB97M(2),71 ωB97X-2(TQ),72 ωB2GP-PLYP73), the spin-component scaled double hybrids74 (DSD-PBEP86,75 revDSD-PBEP86, revDOD-PBEP86,76 revDSD-PBEB95, revDOD-PBEB95, DSD-SCAN66, DOD-SCAN66, DSD-SCAN69, DOD-SCAN69,77 SOS0-PBE0-278), and a random-phase-approximation dRPA-based double hybrid (dRPA7579)

We have also considered Grimme’s DFT-D3 atom-pairwise dispersion corrections80 with the Becke–Johnson (BJ) damping function81 for most of the DFT energies. For the M06-2X functional, the zero-damping version D3(0)82 was used since the parameter optimization for the M06-2X-D3(BJ) diverge. For the revDSD-PBEP86 and revDOD-PBEP86 functionals, the newly developed atomic-charge dependent London dispersion correction DFT-D483,84 dispersion correction was also considered, aside from the Vydrov–Van Voorhis “nonlocal” (NL) dispersion functional,85 in which an a posteriori correction is obtained from the electron density.

For orbital-based ab initio calculations, we mostly employed correlation-consistent polarized basis sets.86,87 For the canonical CCSD(T) calculations, the cc-pVDZ with no p-type polarization functions on hydrogen atoms was employed due to the systems’ sizes. For the explicitly correlated methods MP2-F12, the cc-pVDZ-F12 basis set88 together with the associated complementary auxiliary basis sets (CABS)89 was used. The latter accelerate the basis set convergence of explicitly correlated methods.90 For most DFT calculations, the Weigend–Ahlrichs basis set def2-TZVP91 was employed using the corresponding auxiliary basis sets for simultaneously fitting Coulomb and exchange.92 For several functionals, we compare the def2-TZVP basis set with the 6-311G(d,p) basis set, which is commonly used in the modeling of expanded porphyrins.15,19,23 The small differences in the RMSDs (Figure S3) indicate that basis set sensitivity for the DFT energies of Hückel and Möbius expanded porphyrins is relatively weak. In addition, to assess the influence of the expansion of the basis set on the DFT energies, we explore the basis set convergence of several functionals using the def2-QZVP basis set (Table S2), which approaches the CBS limit for the rung 1–4 functionals.93,94 It is encouraging that the differences between the def2-TZVP and def2-QZVP are remarkably small, with RMSD differences below 0.3 kcal mol–1. These results suggest that a triple-ζ basis set is sufficient for more efficient yet acceptably accurate DFT calculations for the considered systems.

Choice of the Reference Method

As a reference, we employed fully canonical CCSD(T) calculations, widely regarded as the gold-standard in quantum chemistry.95 More specifically, relative energies evaluated at the CCSD(T)/cc-pVDZ and CCSD(T)/CBS levels serve as a reference to benchmark the relative energies obtained with wave function and DFT methods, respectively, for each family of macrocycles shown in Figure 3. The accuracy of the different computational methods was assessed through the mean unsigned error (MUE) and the root-mean-square deviation (RMSD) relative to the fully canonical CCSD(T) energies:

graphic file with name jp9b10880_m002.jpg 2
graphic file with name jp9b10880_m003.jpg 3

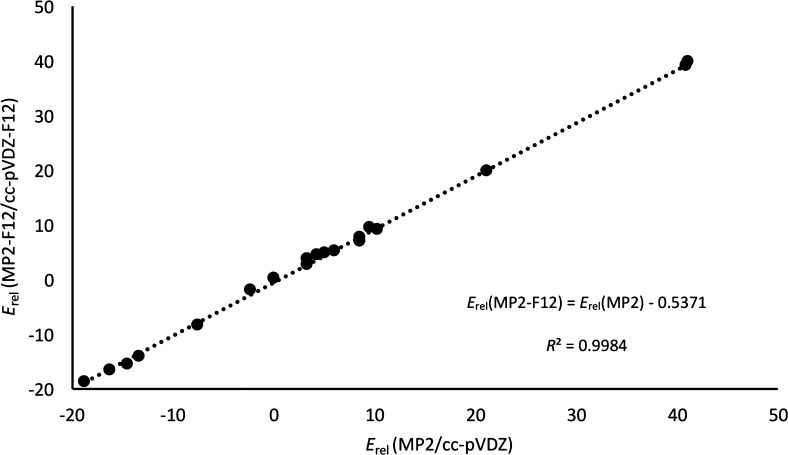
It is noteworthy that the computational resources for performing canonical CCSD(T)/cc-pVDZ on these extended systems were enormous in terms of CPU and disk space, precluding the use of a larger basis set. To assess the effect of expanding the basis set, we tried different composite schemes to estimate the CCSD(T)/CBS energies. First, we performed explicitly correlated96,90 RI-MP2-F12 calculations with the cc-pVDZ-F12 basis set88 and associated auxiliary basis sets89 for all species. We note in passing that for the largest systems, even cc-pVDZ-F12 already required about 10 TB of scratch space per run. As the largest nodes at Weizmann only had about 5 TB of SSD scratch space available, we achieved this feat by cross-mounting scratch file systems from other nodes via NFS over InfiniBand. Typically, the explicitly correlated calculations with appropriate basis set gain about two angular momenta in basis set convergence.97 Hence, the MP2-F12/cc-pVDZ-F12 energies ought to be comparable or superior to MP2/cc-pVQZ in terms of convergence. This statement was verified by carrying out additional RI-MP2/cc-pVTZ and cc-pVQZ calculations and extrapolating to the complete basis set limit using the Helgaker formula.98 Interestingly, the resulting MP2/cc-pV{T,Q}Z relative energies deviate from their MP2-F12/cc-pVDZ-F12 counterparts by just 0.1 kcal mol–1 RMSD. The basis set extension effect itself, from MP2/cc-pVDZ, is just 0.9 kcal mol–1 RMS in both cases. As shown in Figure 4, the MP2 relative energies computed with the cc-pVDZ and the cc-pVDZ-F12 basis sets are almost perfectly linearly related (coefficient of determination R2 = 0.998) and the MUE is 0.74 kcal mol–1 for the complete set of structures. We might hence safely assume that the coupling term C in the equation below is negligible:

graphic file with name jp9b10880_m004.jpg 4
graphic file with name jp9b10880_m005.jpg 5

And thus, we can apply the familiar “high-level correction” (HLC) approximation:

graphic file with name jp9b10880_m006.jpg 6

In order to further assess the influence of the diffuse functions, we performed additional MP2 calculations with the heavy-aug-cc-pV{T,Q}Z, in which only the heavy (non-hydrogen) atoms are augmented with diffuse functions. Similarly, the extrapolated MP2/CBS energies estimated from cc-pV{T,Q}Z and diffuse-augmented heavy-aug-cc-pV{T,Q}Z are rather similar. A perfect linear correlation is obtained for the two sets of MP2/CBS energies (R2 = 1.000) and the MUE is only 0.14 kcal mol–1 for the complete set of structures (Figure S2). Overall, these results reinforce the hypothesis that the relative energies of topology interconversions are comparatively insensitive to basis set expansion and that our estimated CCSD(T)/CBS should be close to the basis set limit. These results are in line with those previously obtained which showed that the expansion of the Pople basis set from 6-31G to 6-311G(d,p) hardly influences the relative stabilities and energy barriers for topological switches based on hexaphyrins.99 Our best estimates for the relative energies of the expanded porphyrin database are collected in Table 1.

Figure 4.

Figure 4

Open in a new tab

Influence of expanding the basis set on the relative energies of our test set. Linear correlation between MP2-F12/cc-pVDZ-F12 and MP2/cc-pVDZ relative energies for 21 porphyrinoid structures.

Table 1. Best Estimates for the Relative Energies of the Expanded Porphyrin Database (in kcal mol–1)a.

  CCSD(T)/cc-pVDZ CCSD(T)/CBS CCSD(T)/cc-pVDZ-F12 CCSD(T)/CBS
extrap scheme none MP2/cc-pV{T,Q}Z + [CCSD(T) – MP2]/cc-pVDZ MP2-F12/cc-pVDZ-F12 + [CCSD(T) – MP2]/cc-pVDZ MP2/heavy-aug-cc-pV{T,Q}Z + [CCSD(T) – MP2]/cc-pVDZ
24Ha 9.12 7.92 8.06 7.82
24Hb 0.00 0.00 0.00 0.00
24M 6.06 6.38 6.48 6.35
24TS1 9.05 8.93 9.01 8.83
24TS2 4.87 5.12 5.18 5.07
28H 0.00 0.00 0.00 0.00
28M –0.73 –1.77 –1.75 –1.64
28M1A 0.46 0.28 0.28 0.46
28M1B 1.82 1.39 1.39 1.57
28F –0.38 0.16 –0.08 0.29
28TS1A 6.33 4.65 4.58 4.70
28TS1B 2.86 2.00 1.92 2.05
28TS2A 6.87 6.10 6.02 6.29
28TS2B 9.89 8.88 8.79 9.07
28TS3 5.17 4.50 4.36 4.60
32F 0.00 0.00 0.00 0.00
32Ma 16.81 15.45 15.65 15.13
32Mb 16.74 16.59 16.52 16.45
32H 34.60 32.59 32.72 32.16
32TS1 17.49 16.08 16.16 15.78
32TS2 33.79 32.33 32.36 31.97
RMSD 0.95   0.10 0.19
MUE 0.74 REFERENCE 0.08 0.14
MaxD 2.01   0.23 0.43
Open in a new tab
a

The CCSD(T)/CBS energies were obtained from extrapolation of the MP2 energies at the complete basis set limit from the (heavy-aug-)cc-pVTZ and (heavy-aug-)cc-pVQZ basis sets. Alternatively, the CCSD(T)/cc-pVDZ-F12 were estimated from explicitly correlated MP2-F12/cc-pVDZ-F12 calculations.

Although the extrapolation to the complete basis set limit does not affect significantly the energetic description of Hückel–Möbius interconversions, energy deviations larger than 1 kcal mol–1 are found for several conformations. Accordingly, we employed the CCSD(T)/CBS energies as a reference to assess the performance of the DFT methods, whereas the CCSD(T)/cc-pVDZ energies were used to benchmark the lower-level electron correlation methods.

Results and Discussion

Database of Hückel and Möbius Expanded Porphyrins

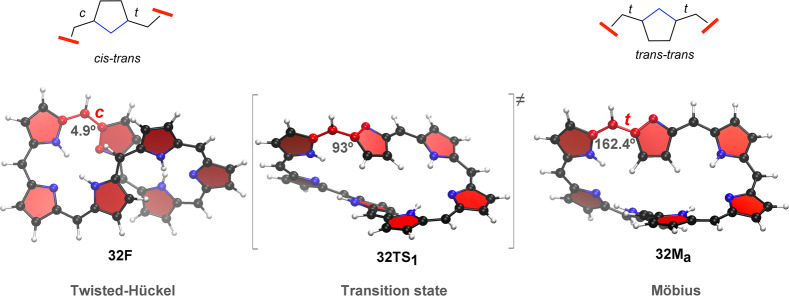
In the present work, we introduce a representative database of topological switches based on expanded porphyrins with varying ring size. The database covers a broad spectrum of structures with Hückel (H), Möbius (M), and twisted-Hückel (F) topologies for representative [4n] π-electron expanded porphyrins (Figure 3). Besides the more stable configurations, we also considered the key isomerization transition states for the topological interconversions. Here, it is important to note that the topology switching is achieved via internal rotations,11 without “dissecting” the ring. This interesting feature is displayed in Figure 2, which shows that the interconversion between the twisted-Hückel and the Möbius conformers is achieved only by variation of one torsional angle (φ1). As a result of the rotation of φ1, a ct-aligned pyrrole ring is transformed into a tt-aligned subunit, leading to an odd number of trans bonds in the Möbius topology.17 The macrocycle is preserved during the switching process, but the π system is temporarily broken when one torsion angle becomes close to 90°. The latter can be better visualized in Figure 5. For these reasons, these Hückel–Möbius interconversions can be regarded as challenging isomerization processes for future benchmark studies.

Figure 5.

Figure 5

Open in a new tab

Optimized geometries for the minima and transition state involved in the twisted-Hückel/Möbius topology interconversion in [32]heptaphyrin. Such interconversion is triggered by rotation of the dihedral angle highlighted in red.

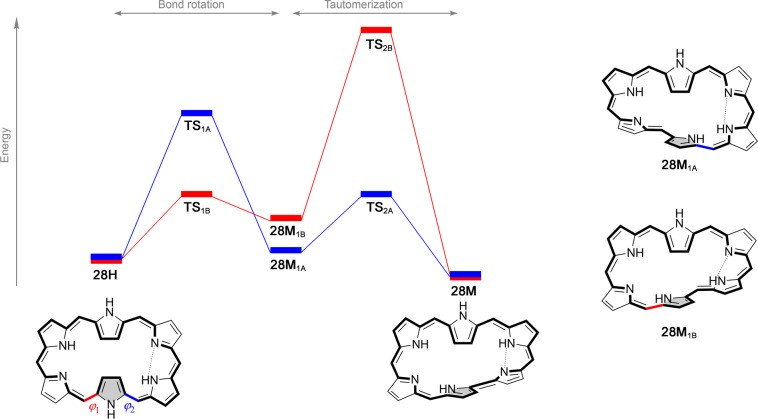
In the case of N-fused [24]pentaphyrin, the low-energy pathway for the rotation of an imine-type pyrrole ring corresponds to a two-step mechanism, as shown in Figure S4. Accordingly, two transition structures are considered for the Hückel–Möbius interconversions in the pentapyrrolic system.16 In the case of [28]hexaphyrin, two different pathways for the interconversion between the Hückel planar (28H) and the Möbius structure (28M) were considered, on the basis of the exhaustive study of the reaction mechanism reported by Torrent-Sucarrat et al.99 The two pathways differ in the rotating carbon–carbon bond leading to the intermediate Möbius structures (28M1A and 28M2A), as indicated in Figure 6. Mechanism A involves the rotation of the φ1 angle (in blue), whereas mechanism B involves the variation of the dihedral angle φ2 (in red). The second step in both mechanisms corresponds to the proton transfer between both nitrogen atoms, leading to the most stable tautomer of the Möbius topology (28M). The rate-determining step can be either the bond rotation or the proton transfer, depending on the rotating bond and the meso-substituents.99,100 For this particular switch, several density functionals were benchmarked against CCSD(T)/6-31G data, concluding that both CAM-B3LYP and M05-2X provide the most reliable results.99 Besides the Hückel–Möbius interconversion, we also considered the switching from 28M to 28F with the associated transition state (28TS3), as shown in Figure S5.

Figure 6.

Figure 6

Open in a new tab

Schematic energetic profile for the Hückel–Möbius interconversion in [28]hexaphyrin via two different mechanisms.

For the [32]heptaphyrin, we have considered the interconversions between twisted-Hückel (32F), Möbius (32M), and Hückel (32H) topologies with the associated transition states (32TS1 and 32TS2). The schematic energetic profile for the three-level topology switching in [32]heptaphyrin is displayed in Figure S6. In total, 21 structures with varying topology and ring size are included in our database of expanded porphyrins.

Multireference Character of Expanded Porphyrins

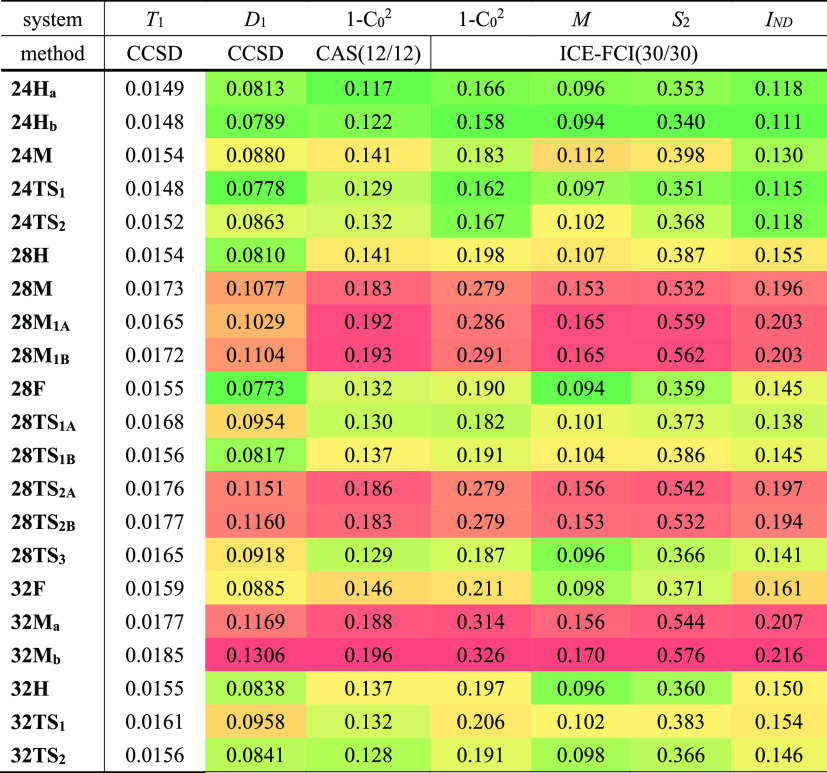
In order to assess the reliability of single reference quantum methods for this set of expanded porphyrins, several diagnostics for static correlation have been examined (Table 2).101 The single-excitation amplitude vector t1 from the CCSD calculations offers up two diagnostics. The first, the T1 diagnostic of Lee and Taylor,102 is the vector norm of t1 normalized by the number of correlated electrons, ||t1||/N1/2 = (t1T·t1/N)1/2. The second, the D1 diagnostic of Janssen and Nielsen,103,104 is the square of the largest eigenvalue of the matrix product t1·t1T. For the didactic example of a complex between ozone (strong static correlation) and octadecane (purely dynamical correlation) at very long distance, it is obvious from the structure of t1T·t1 and of t1·t1T that D1 will approach its value for the worst monomer (in this case, ozone), while T1 will approach its value for the largest monomer (octadecane). For our set of expanded porphyrins, we see that T1 varies in a rather narrow band (Table 2) and deceptively stays below the allegedly “safe” limit of 0.02, while D1 shows a more pronounced variation, ranging from 0.08 to 0.13. D1 is largest for the Möbius conformers and transition states with Möbius topology, and smallest for the Hückel and twisted-Hückel structures. In a recent benchmark study of explicitly correlated coupled cluster methods for the W4-17 thermochemical benchmark,105 we obtained a set of diagnostics for a broad spectrum of small molecules as a byproduct. Even the lowest D1 diagnostics in the porphyrinoid set are already in the same range as O3 (0.077), FOOF (0.087), and C2(1Σ+g) (0.086)—all cases with strong static correlation. Despite the fairly large correlation (R2 = 0.93) between the T1 and D1 diagnostics (Figure S7), these results suggest that the T1 diagnostic is not informative in terms of the degree of multireference character in Hückel and Möbius porphyrins.

Table 2. Diagnostics for Hückel and Möbius Expanded Porphyrins with Varying Ring Size.

graphic file with name jp9b10880_0013.jpg

Open in a new tab

Another diagnostic, nearly as old as CASSCF and CI calculations, that can shed light about the multireference character is 1 – C02, where C0 is the coefficient of the reference determinant in a CASSCF or CI calculation.106 1 – C02 is intuitively understood as the weight of determinants other than the reference in the energy. Generally, the system is regarded to possess significant multireference character if the coefficient C0 is smaller than 0.95 or the weight C02 is smaller than 0.90.107 The specific values given in Table 2 were obtained from both iterative full CI (ICE-CI) calculations with 30 electrons in 30 orbitals and CASSCF(12,12) wave functions. The 1 – C02 values obtained from CASSCF(12,12) and ICE-CI(30,30) methods provide very similar information with R2 = 0.95. Similar to D1, we see a much more pronounced variation in static correlation among the different π-conjugation topologies than for T1.

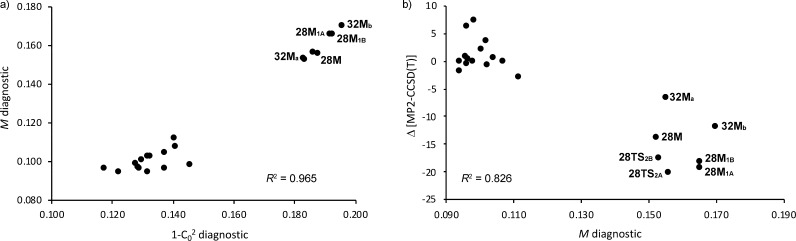
Yet a fourth is Truhlar’s M diagnostic,108 which for closed-shell systems is effectively the average of the deviations from 2 and 0, respectively, of the HOMO and LUMO natural orbital occupations; therefore, one must always have 0 ≤ M ≤ 1 for closed-shell species. 1 – C02 and M are statistically very similar for the problem at hand, with R2 = 0.965 (Figure 7a). Interestingly, the relationship M vs 1 – C02 shows the separation of the porphyrinoid structures into two groups that exhibit different degree of static correlation: (a) the Hückel and twisted-Hückel topologies as well as the Möbius pentaphyrins and (b) the Möbius structures of hexa- and heptaphyrins.

Figure 7.

Figure 7

Open in a new tab

(a) Relationship between M and 1 – C02 diagnostics for static correlation within our set of 21 expanded porphyrins. (b) Relationship between the energy differences computed with MP2 and canonical CCSD(T) methods and the M diagnostic.

A fifth diagnostic to measure the importance of static correlation is IND of Matito and co-workers,109 as defined in eq 20 of that paper and obtained from the 30-in-30 FCI natural orbital occupations. We found it to be statistically most similar to 1 – C02 for the same wave function (R2 = 0.97), less so to M (R2 = 0.84), and still less to T1 (R2 = 0.81) and D1 (R2 = 0.79).

Finally, there is the von Neumann correlation entropy,110 where the ni are the natural orbital occupation numbers:

graphic file with name jp9b10880_m007.jpg 7

S2 is not size intensive. In the present work, we use just the HOMO–1, HOMO, LUMO, and LUMO+1 orbitals out of the 30-in-30 FCI to mitigate size disintensivity. Thus, the S2 obtained contains basically the same information as M (R2 = 0.995, Figure S7) and, accordingly, we have hence not considered it further. The M diagnostic, in particular, turns out to be a fair predictor for the energy difference between canonical CCSD(T) and MP2 calculations, with R2 = 0.83 (Figure 7b); CASSCF 1 – C02 has a more modest but still respectable R2 = 0.79, while remaining diagnostics (S2 aside, see above) fare more poorly (R2 = 0.65 or less). The CCSD(T) – MP2 energy differences can be seen as a pragmatic measure of the importance of higher-order correlation effects.

In addition, we have computed the fractional occupation number weighted density (FOD) as a real-space measure for static electron correlation effects.111 This density is obtained by performing finite-temperature DFT calculations and allows for the localization of strongly correlated electrons in molecules with a complicated electronic structure.112 A representative example of the FOD plots for the different topologies of [28]hexaphyrin (28F, 28M1A, and 28H) is shown in Figure S8. For the three topologies, the FOD is significantly delocalized over the entire macrocyclic ring and not localized on any particular moiety of the molecules, which would indicate that the whole system is strongly correlated. Unexpectedly, no significant differences are observed in the FOD plots for the Hückel and Möbius topologies, in contrast to other diagnostics computed from the ICE-FCI(30,30) wave functions which clearly show that the 28M1A exhibits stronger multireference character than 28H and 28F.

This prompts the question whether we can trust CCSD(T) at all for such extended π-systems. Unfortunately, higher-order correlated methods with the full complement of orbitals are not a practical option. We can, however, carry out iterative full CI calculations in a small orbital “active space” by means of the ICE-CI method,113 and we have done so for 12-in-12, 18-in-18, 24-in-24, and 30-in-30 active spaces and then carried out CCSD(T) in the same restricted spaces for comparison. The results are collected in Table S3 and summarized in Table 3. It is clear that, at least for the relative energies of topology interconversions in expanded porphyrins, CCSD(T) closely tracks FCI for all orbital spaces (see also Figure S9). The fact that post-CCSD(T) contributions are surprisingly small might arise from a fortunate compensation of errors between the repulsive contribution of higher-order iterative triple excitations [CCSDT–CCSD(T)] and the attractive contribution of connected quadruple excitations [CCSDTQ-CCSDT]. Similar cancellations have been already observed for small molecules with strong multireference character, such as the C2 (1Σ+g) molecule.114,115

Table 3. Statistical Analysis of Deviations in Relative Energies of Hückel–Möbius Interconversions between ICE-CI and CCSD(T) Methods for Different Orbital Active Spaces (in kcal mol–1)a.

  (12,12) (18,18) (24,24) (30,30)
RMSD 0.15 0.14 0.13 0.21
MUE 0.10 0.10 0.09 0.16
MaxD 0.28 0.30 0.32 0.50
Open in a new tab
a

MaxD represents the maximum deviation.

Then, what sets the Möbius structures’s CI wave functions apart from those for the twisted-Hückel and Hückel structures? Table 4 shows the coefficients of the leading configurations in a 30-in-30 full CI expansion for the different structures involved in the topology interconversions of [28]hexaphyrin. From Table 4, it is clear that the Möbius structures have qualitatively different multireference character than the twisted-Hückel and Hückel-untwisted structures, with a prominent second component that effectively corresponds to exciting one electron each from the two quasidegenerate HOMO and HOMO–1 orbitals to the quasidegenerate LUMO and LUMO+1 orbitals. There are six unique determinants that fit this pattern, which generate three singlet and three MS = 0 triplet configuration state functions. The same pattern is seen for the TS2A and TS2B Möbius transition states. Effectively, a single Slater determinant is a fairly poor zero-order reference for these systems, and a 4-in-4 CASSCF would be required. This would also embrace most of the other prominent determinants in the expansions.

Table 4. CI Coefficients of Leading Configurations (Ci ≥ 0.07) in a 30-in-30 Full CI Expansion for the Different Structures Involved in the Topology Interconversions of [28]Hexaphyrina.

28H 28F 28M1A 28M1B 28M
0.895 222||000 0.900 222||000 0.845 222||000 0.842 222||000 0.849 222||000
0.120 121||110 0.082 121||110 0.224 211||110 0.226 211||110 0.211 211||110
0.112 211||101 0.077 211||101 0.123 202||200 0.138 212||100 0.122 221||010
0.081 112||011 0.074 112||000 0.123 212||010 0.131 221||010 0.120 212||100
0.074 212||010     0.122 221||100 0.096 220||200 0.101 220||200
        0.107 220||020 0.085 202||200 0.090 202||020
        0.071 112||101 0.082 202||020    
            0.079 220||020    
28TS1A 28TS1B 28TS2A 28TS2B 28TS3
0.904 222||000 0.900 222||000 0.849 222||000 0.849 222||000 0.902 222||000
0.101 211||110 0.110 211||110 0.217 211||110 0.215 211||110    
0.077 220||200 0.084 220||200 0.113 221||010 0.121 221||010    
        0.112 212||100 0.120 212||100    
        0.101 220||200 0.099 220||200    
        0.088 202||020 0.088 202||020    
        0.077 202||200 0.075 202||200    
        0.072 220||020        
Open in a new tab
a

Determinants are represented by the occupation vector of the frontier orbitals: occupied and virtual orbitals are separated by a double vertical line ||.

In contrast, despite having significant contributions from excited determinants, the HF reference determinant of the twisted-Hückel and Hückel structures as well as the transition structures (28TS1A, 28TS1B, and 28TS3) has a coefficient of 0.895 or more. For them, a 6-in-6 CASSCF would be preferable over 4-in-4, but even a single HF determinant is still a reasonable reference unlike for the Möbius structures.

Performance of Lower-Level Electron Correlation Methods

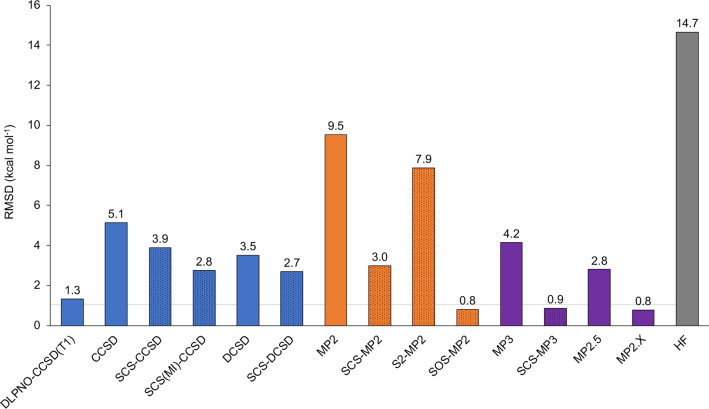
Having assessed the reliability of the canonical CCSD(T) method for this set of Hückel and Möbius expanded porphyrins, the next step involves the performance of lower-level wave function methods. Tables S4 and S5 collect the relative energies computed with different CCSD-based approaches and MP-based procedures, respectively, together with the mean unsigned error (MUE) and root-mean-square deviation (RMSD). For the purpose of assessing the performance of CCSD and MP-based methods against canonical CCSD(T) results, we resort to the CCSD(T)/cc-pVDZ reference energies, since the same basis set is employed in all wave function approaches. The RMSD deviations for each wave function approach with respect to canonical CCSD(T)/cc-pVDZ energies are visualized in Figure 8.

Figure 8.

Figure 8

Open in a new tab

Root-mean-square deviations (RMSDs in kcal mol–1) for all wave function approaches over the relative energies in the expanded porphyrin database relative to canonical CCSD(T)/cc-pVDZ reference values. Spin-component-scaled methods are represented by dotted columns.

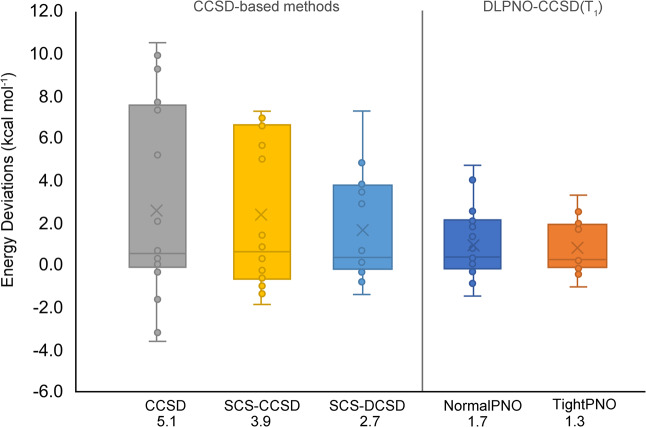
First of all, the importance of connected triple excitations is illustrated by the RMSD of 5.1 kcal mol–1 for CCSD. The breakdown of the CCSD/cc-pVDZ reference energies into the SCF, CCSD, and (T) components (Table S6) shows that the inclusion of triple excitations has a major effect on the relative energies of the Möbius topologies, which become greatly stabilized upon inclusion of higher excitations into the coupled cluster calculations. The statistical error drops to 3.9 kcal mol–1 for SCS-CCSD and 2.8 kcal mol–1 for SCS(MI)CCSD,42,116 or to 3.5 kcal mol–1 for the distinguishable cluster singles and doubles (DCSD) method,43 which costs the same as CCSD. Adding spin-component scaling, i.e., SCS-DCSD,44 improves the distinguishable cluster approach to an RMSD of 2.7 kcal mol–1. As expected, the larger statistical errors of all CCSD-based approaches are found for the Möbius structures of [28]hexaphyrin and [32]heptaphyrin, which exhibit a more pronounced multireference character. These results confirm that the DCSD is less sensitive to static correlation than CCSD and that the addition of the SCS correction improves the accuracy of coupled-cluster-based approaches. Figure 9 shows the box-and-whisker plots for different CCSD-based approaches. It becomes clear that the error distribution becomes progressively narrower for the series CCSD, SCS-CCSD, and SCS-DCSD. The RMSD decreases to 3.9 and 2.7 kcal mol–1 for SCS-CCSD and SCS-DCSD, showing that spin-component scaled approaches improves the accuracy of coupled-cluster-based approaches. Among spin-component-scaled approaches, the distinguishable SCS-DCSD approach results in a narrower error distribution as compared to SCS-CCSD for the expanded porphyrin database.

Figure 9.

Figure 9

Open in a new tab

Box-and-whisker plots for several CCSD-based methods and the DLPNO-CCSD(T1) approach (with different settings), showing the error spread for the expanded porphyrin database. The energy deviations are estimated with respect to canonical CCSD(T)/cc-pVDZ reference energies. The average RMSDs (in kcal mol–1) are also displayed below each method.

Since the localized orbital coupled cluster theory has recently emerged as an efficient quantum chemical method for coupled cluster calculations on large systems,26 we have also investigated the accuracy of the DLPNO-CCSD(T1) approach for these extended π-systems using two different sets of truncation thresholds, termed “NormalPNO” and “TightPNO”.29 The energy differences with respect to canonical CCSD(T)/cc-pVDZ relative energies are collected in Table S6 and the box-and-whisker plots of the energy deviations for the different settings are shown in Figure 9. With the TightPNO setup, DLPNO-CCSD(T1)/cc-pVDZ delivers relative energies with an RMSD of 1.3 kcal mol–1 with respect to canonical CCSD(T)/cc-pVDZ calculations. Loosening of the thresholds results in a slightly larger error distribution and the RMSD increases to 1.7 kcal mol–1 for NormalPNO. Although the statistical errors increased with the default PNO settings, the wall time is reduced by 75–80%.

Overall, similar trends are provided by the local pair natural orbital coupled-cluster theory, but the errors for the Möbius structures reach up to 4.7 kcal mol–1 due to their more pronounced multireference character. Indeed, the M diagnostic turns out to be a good predictor for the energy difference between canonical CCSD(T) and localized DLPNO-CCSD(T) calculations, with R2 = 0.89 (Figure S10). For these reasons, we conclude that canonical coupled-cluster theory is needed for benchmarking purposes in the case of Hückel–Möbius interconversions in expanded porphyrins. The assessment of the performance of a large variety of localized coupled cluster methods for these challenging structures is currently underway.30

With HF being a poor zero-order wave function for the Möbius species, it is not surprising that the statistics for normal MP2 are also not good (RMSD = 9.5 kcal mol–1). In contrast to the CCSD approach, MP2 overstabilizes the Möbius-type structures to a huge extent, leading to energy deviations up to 20 kcal mol–1 relative to canonical CCSD(T) method (Table S5). Orbital-optimized Møller–Plesset perturbation (OO-MP2) theory117 in fact performs worse than conventional MP2, leading to an RMSD of 12.0 kcal mol–1. By contrast, spin-component scaling36 greatly mitigates the problem, with an RMSD = 3.0 kcal mol–1 for SCS-MP2. Intriguingly, Fink’s S2-MP2,37 despite its sounder theoretical foundation, actually performs worse at RMSD = 7.9 kcal mol–1. A possible reason for the bad performance of S2-MP2 is the high coefficient for the same-spin MP2 correlation energy (css = 0.75), which seems to have a negative impact on the performance of spin-component-scaled approaches for the description of these topology interconversions. SOS-MP2,118 however, which completely neglects same-spin correlation, achieves a stunning RMSD = 0.8 kcal mol–1. This behavior is not specific to this subset of systems. For the MOBH35 organometallic transition state benchmark,119 standard MP2 has an RMSD = 6.0 kcal mol–1, compared to 2.8 and 2.5 kcal mol–1, respectively, for SCS-MP2 and SOS-MP2 (Table 2 in ref (74)). This is not the case for problems less driven by static correlation, as shown for the very extensive GMTKN55 (General Main-group Thermochemistry, Kinetics, and Noncovalent interactions, 55 problem types) benchmark of Grimme, Goerigk, and co-workers,120 in which SOS-MP2 is clearly inferior to standard MP2 and SCS-MP2.74

Inclusion of damped third-order contributions, however, appears to improve on the shortcomings of same-spin MP2 for strongly correlated systems, as seen from the RMSDs of SCS-MP3121 (0.9 kcal mol–1) and to MP2.X40 (0.8 kcal mol–1).

Performance of Density Functional Methods Belonging to Different Rungs of Jacob’s Ladder

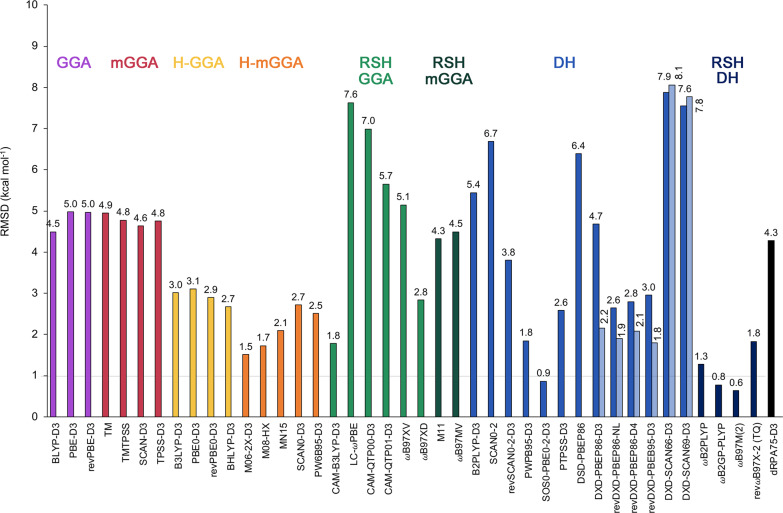
Since DFT remains the workhorse for modeling expanded porphyrins, we have investigated the performance of a variety of exchange–correlation functionals from different rungs of Jacob’s ladder.45,93Tables S8–S15 collect all the relative energies for our expanded porphyrin database computed with all the DFT methods. RMSDs for each functional relative to canonical CCSD(T)/CBS energies are visualized in Figure 10.

Figure 10.

Figure 10

Open in a new tab

Root-mean-square deviations (RMSDs in kcal mol–1) for all the DFT methods over the relative energies of the expanded porphyrin database relative to canonical CCSD(T)/CBS reference values. For the several spin-component-scaled double hybrids, the RMSDs of the spin-component (DSD) and spin-opposite (DOD) scaled version are shown.

Overall, Figure 10 reveals a poor performance for GGAs, meta-GGAs, GGA hybrids, range-separated hybrids, and double hybrids for describing the thermochemistry and kinetics of topological interconversions in expanded porphyrins. Among all the functionals tested in this work, the range-separated double hybrids, such as ωB97M(2)71 and ωB2GP-PLYP,73 are the most reliable approaches for describing the relative energies of Hückel–Möbius interconversions, providing RMSDs within chemical accuracy. In contrast, range-separated hybrids perform badly for these topological interconversions, including the promising ωB97MV functional with nonlocal correlation.65 In a recent benchmark study of 200 density functionals,93 ωB97MV emerges as the best choice for nearly all interaction types with the exception of systems highly sensitive to the self-interaction/delocalization errors. For our set of highly delocalized π-systems,20 the Minnesota meta-GGA functionals with high fractions of exact exchange (M06-2X and M08-HX) perform reasonably well, outperforming more robust and significantly less empirically parametrized functionals within their class (SCAN0-D3 and PW6B95-D3). It is important to note that the conclusions regarding the performance of the different type of functionals remain the same when the relative errors per functional is analyzed separately for reaction energies and barrier heights (Figure S11).

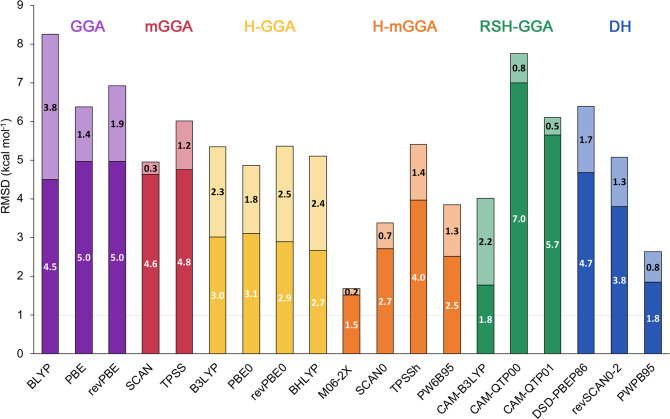
GGA functionals, like BLYP, PBE, or revPBE, exhibit very poor performance, similarly to the meta-GGA functionals. Global hybrids outperform GGA and meta-GGA functionals, but still they are not accurate enough to describe these Hückel–Möbius topological interconversions. Dispersion corrections significantly improve the performance of the standard functionals, in contrast to previous findings (Figure 11).18,23 For nearly all the tested functionals across the rungs of Jacob’s Ladder, we found a significant improvement for describing the relative energies of these challenging systems upon addition of atom-pairwise dispersion corrections. The improvement of performance upon addition of the D3(BJ) dispersion can be linked to the variety of noncovalent interactions present in the different conformations, ranging from hydrogen bonding to π···π stacking interactions (Figure S13). For the M06-2X functional, we found that the D3(0) yields only 0.2 kcal mol–1 improvement with respect to the uncorrected functional, while for B2PLYP we found that D3(BJ) yields almost the same RMSD as the uncorrected functional. Similarly, for the SCAN functional, the dispersion correction yields only 0.3 kcal mol–1 improvement.

Figure 11.

Figure 11

Open in a new tab

Stacked root-mean-square deviations (kcal mol–1) for different density functionals with and without dispersion corrections. The RMSDs of the DFT-D3(BJ)-corrected functionals are shown in white. For the M06-2X functional, the D3(0) correction was used.

The different impact of the dispersion correction on the performance of different types of functionals can be rationalized in terms of the optimized parameters for the DFT-D3(BJ) correction (Table S16). These are the prefactors s6 and s8 for the R–6 and R–8 terms, respectively, and the damping function turnover parameters a1 and a2 (eq 7).

graphic file with name jp9b10880_m008.jpg 8

where the C6AB and C8 are dispersion coefficients specific to the atom pair and 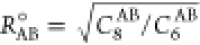Inline graphic. The larger a1 and a2 become, the further out to the periphery is the dispersion correction pushed. Conversely, the larger s8 becomes (for typical values of a1 and a2), the more prominent medium-distance noncovalent interactions become, to the extent that they may interfere with static correlation effects.

For typical GGAs and hybrid GGAs, the large values of s8, combined with typical values of a1 and a2, ensure large D3BJ contributions. The role of the dispersion is perhaps best understood as favoring the spatially more compact twisted-Hückel and Möbius structures over the spatially more spread-out untwisted Hückel topology. For SCAN, SCAN0, and M06-2X, s8 = 0, so the effect of D3BJ is mitigated.

An alternative way to improve the accuracy of GGA hybrids is introducing additional ingredients into the density functional form, as in meta-GGAs hybrids. Within this group, we have considered several Minnesota density functionals with variable fraction of HF exchange, highly parametrized functionals, and extreme sensitivity to the integration grid,122 but showing good performance for main group thermochemistry and kinetics.93,123,124 However, none of them are state-of-the art for noncovalent interaction data sets.120,124 The fraction of exact exchange across these functionals varies from 27% (M06) to 44% (MN15) to 52% (M08-HX) and 54% (M06-2X). M06-2X and M08-HX exhibit the best performance with an RMSD about 1.7 kcal mol–1, followed by MN15 (RMSD = 2.1 kcal mol–1). The lower performance of MN15 with respect to M06-2X for expanded porphyrins is rather unexpected considering the partial multireference character of Möbius structures. MN15 was specifically developed for preserving the performance of M06-2X for single-reference main-group thermochemistry, while improving its description of multireference cases.67 The fact that more exact exchange reduces the errors reinforce the idea that the delocalization error represents an additional issue in Hückel and Möbius expanded porphyrins.125

Range-separated hybrid functionals show significantly poorer performance compared to the meta-GGA hybrids, except for CAM-B3LYP-D3 (RMSD = 1.8 kcal mol–1), as pointed out in previous benchmark studies on expanded porphyrins.23,99 We recently proved that M06-2X and CAM-B3LYP exhibit very similar degrees of π-electron delocalization in expanded porphyrins.20 Disappointingly, the promising range-separated hybrid ωB97M-V with nonlocal correlation,65 designed using a combinatorial approach and containing only 12 parameters, clearly underperforms the older ωB97XD for topology interconversions in expanded porphyrins. Similarly, the range-separated GGA hybrid with 10 parameters ωB97XV exhibits larger errors than the original ωB97XD.

Regarding DSD double hybrids, one might expect these functionals to suffer from the same issues as the MP2 method. Indeed, the original DSD-PBEP86 performs poorly at RMSD = 6.4 kcal mol–1, but the error drops to 4.7 kcal mol–1 upon addition of the D3(BJ)-dispersion correction. However, the entire DSD family of functionals has recently been reparametrized126 against the much larger and more chemically diverse GMTKN55 database,120 which led to a substantial change in parameters and improved performance across the board. Our revDSD-PBEP86-NL functional indeed reduces the RMSD to 2.6 kcal mol–1, presumably due to the much smaller coefficient for same-spin MP2-like correlation in revDSD compared to DSD. As we have seen earlier for transition metals reaction energies,127 the revDSD parametrizations are not only more accurate than the original DSD but more robust as well. Furthermore, the comparison of spin-component (DSD) and spin-opposite (DOD) scaled double hybrids (Figure S12) again shows that elimination of the same-spin correlation in DOD-type functionals results in a significant improvement over DSD-type functionals, except for the DSD-SCANx-D3 functionals. Consequently, the best performers, among the spin-component scaled dispersion-corrected double hybrids, are the revDOD-PBEB95-D3 (RMSD = 1.8 kcal mol–1), revDOD-PBEP86-NL (RMSD = 1.9 kcal mol–1), and especially the nonempirical SOS0-PBE0-2-D3(BJ)78 (RMSD = 0.9 kcal mol–1).

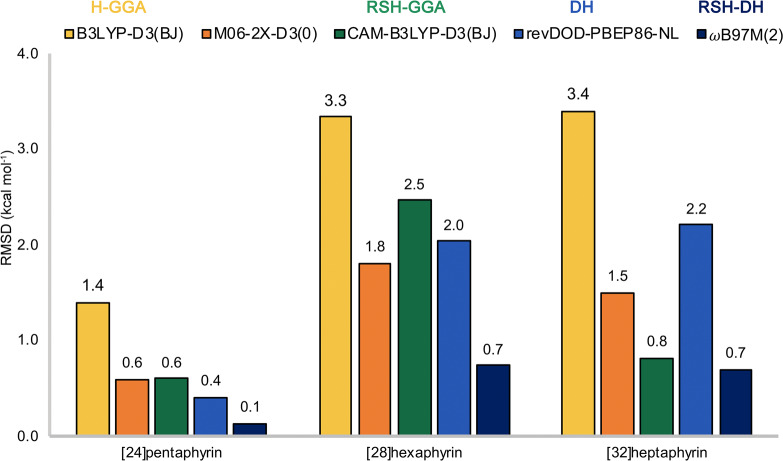
Finally, the RMSDs of selected hybrids and double hybrid functionals for each family of expanded porphyrin are carefully analyzed. Figure 12 summarizes the errors for the B3LYP-D3(BJ) (GGA hybrid), M06-2X-D3(0) (meta-GGA hybrid), CAM-B3LYP-D3(BJ) (range-separated GGA hybrid), revDOD-PBEP86-NL (double hybrid), and ωB97M(2) (range-separated double hybrid) for N-fused [24]pentaphyrin, [28]hexaphyrin, and [32]heptaphyrin. The performance of the functionals is clearly different for each type of macrocycle, and only ωB97M(2) shows errors within 1 kcal mol–1 for all three expanded porphyrins considered here. Not surprisingly, most of the functionals perform worse for the relative energies of [28]hexaphyrin, which contain a larger number of Möbius structures with a more challenging electronic structure. By contrast, the relative energies of Hückel and Möbius structures of the pentapyrrolic macrocycle are relatively well described by the different functionals except B3LYP-D3, which can be expected from the minor degree of static correlation in the smallest macrocycle. In this case, the five functionals predict the same global minimum (24Hb) and similar activation barriers for the Hückel and Möbius interconversion, in good agreement with experimental studies.128

Figure 12.

Figure 12

Open in a new tab

Root-mean-square deviations of five density functionals (RMSDs in kcal mol–1) for each family of expanded porphyrins relative to canonical CCSD(T)/CBS reference values.

In the case of [28]hexaphyrin, only ωB97M(2) provides reasonably accurate energies relative to CCSD(T)/CBS, followed by the M06-2X-D3(0) functional. According to canonical CCSD(T)/CBS calculations, unsubstituted [28]hexaphyrin can adopt three different topologies with small energy differences (28H, 28M, and 28F), explaining why meso-aryl substituted [28]hexaphyrin exists in solution as an equilibrium of several equivalent twisted Möbius conformations and a Hückel rectangular conformation.129 According to CCSD(T)/CBS energies, the Möbius topology 28M corresponds to the thermodynamically more stable conformation, in line with the experimental findings from spectroscopic investigations.130 Here, it is important to note that M06-2X-D3(0) and CAM-B3LYP-D3(0) both predict the Hückel untwisted topology 28H to be the global minimum.

For the flexible [32]heptaphyrin, the canonical CCSD(T) calculations reveal the predominance of the twisted-Hückel conformer (32F), in agreement with the experimental findings.21,22 The five functionals predict the twisted-Hückel as most stable, but important energy differences between functionals appear for the relative energies of the Möbius topologies (32Ma and 32Mb), belonging to the group of structures with larger multireference character. The difficulty to describe the relative energies of the interconversion between the twisted-Hückel and Möbius topologies in [32]heptaphyrin arise from the partial multireference character of the Möbius topologies as well as the delocalization error. In this regard, we observe that the statistical errors for B3LYP arises mainly from the overstabilization of the Möbius topologies with respect to the Hückel ones. This overstabilization can be traced to the delocalization error, since B3LYP exaggerates the degree of π-electron delocalization in aromatic macrocycles.20 This overstabilization is mitigated to a great extent by means of the D3(BJ) dispersion. Overall, these results highlight the critical role of the exchange–correlation functional for studying the conformational preferences and topology interconversions in expanded porphyrins.

Conclusions

The ultimate goal of this study is to identify affordable wave function methods and density functionals for the prediction of accurate relative energies for Hückel-Möbius topology interconversions in expanded porphyrins. Such topology interconversions can be exploited in the development of molecular switches for multiple applications; computational chemistry represent a powerful tool toward the design of efficient switches. DFT remains the workhorse for modeling such extended macrocycles, but these macrocycles are challenging from an electronic structure point of view. In this work, we demonstrate that the degree of static correlation largely varies between the different topologies, as revealed by several diagnostics for static correlation. Although the T1 diagnostic values stay deceptively below 0.02 for all the investigated systems, D1, M, IND, S2, and 1 – C02 diagnostics show a more pronounced variation between Hückel and Möbius π-systems. According to these tests, the selected porphyrinoid structures can be split into two groups as a function of the degree of static correlation, with the Möbius structures of hexa- and heptaphyrins being more “troublesome” for single-reference methods.

Accordingly, we assess the performance of a variety of wave function methods and density functionals for thermochemistry and kinetics of topology interconversions across a wide range of macrocycles. As a reference, fully canonical CCSD(T) energies were used; post-CCSD(T) correlation effects were estimated by comparing CCSD(T) with approximate full configuration interaction (ICE-CI) in an expanding sequence of active orbital spaces. According to our results, the contributions of post-CCSD(T) correlation and basis set expansion to relative energies are minor. Hence, our CCSD(T) reference values are reasonably well-converged in both 1-particle and n-particle spaces.

Regarding lower-cost wave function methods, we found that conventional CCSD, MP2, and MP3 perform very poorly, while spin-component scaling approaches like SOS-MP2 or SCS-MP3 reproduce the CCSD(T) relative energies within chemical accuracy. Third-order contributions become important to mitigate the shortcomings of same-spin MP2 for strongly correlated systems; lower-cost MP2.X approaches CCSD(T) quality for the description of topology interconversions.

The accurate description of the relative energies of our expanded porphyrin database becomes difficult for most of the density functionals tested in this work, in particular for the largest macrocycles. The largest errors are found for the Möbius topologies, which exhibit a stronger multireference character. Inclusion of atom-pairwise dispersion corrections and a large percentage of exact HF exchange improve the performance of the exchange–correlation functionals. Overall, the safest choice to describe the energetic profile of Hückel–Möbius interconversions in expanded porphyrins appears to be the range-separated double hybrids ωB97M(2) and ωB2GP-PLYP, which clearly outperform GGAs, hybrid-GGAs, range-separated hybrids, and double hybrids.

Acknowledgments

M.A. thanks the FWO for a postdoctoral fellowship (12F4416N) and the VUB for financial support. F.D.P. acknowledges the Vrije Universiteit Brussel (VUB) for a Strategic Research Program and the Francqui foundation for a position as Francqui research professor. Computational resources and services at the VUB were provided by the Shared ICT Services Centre funded by the VUB, the Flemish Supercomputer Center (VSC), and FWO. Research at Weizmann was funded by the Israel Science Foundation (grant 1358/15) and by the Yeda-Sela-SABRA Fund (Weizmann). A.B. and N.S. acknowledge postdoctoral and doctoral fellowships, respectively, from the Feinberg Graduate School at the Weizmann Institute. The authors thank Dr. Mark Vilensky (scientific computing manager of ChemFarm) for his assistance with the somewhat exorbitant mass storage requirements of the largest calculations. T.W. thanks Dr. Johannes Teunissen for his in-house program CINDES to run a large number of calculations.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.9b10880.

  • Figures and tables encompassing the comparison of B3LYP and M06-2X optimized geometries and geometrical descriptors, sensitivity of the DFT and MP2 relative energies with the basis set, database of Hückel and Möbius expanded porphyrins, diagnostic criteria to assess the suitability of single-reference methods, comparison between limited orbital space full CI and CCSD(T) calculations, relative energies computed with different wave function and DFT approaches, schematic representations of the topology interconversions included in the porphyrin database, and the Cartesian coordinates of the optimized geometries included in the porphyrinoid database (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Paul Geerlings Festschrift”.

Supplementary Material

jp9b10880_si_001.pdf (6.2MB, pdf)

References

  1. Tanaka T.; Osuka A. Chemistry of meso-aryl-substituted expanded porphyrins: Aromaticity and molecular twist. Chem. Rev. 2017, 117, 2584–2640. 10.1021/acs.chemrev.6b00371. [DOI] [PubMed] [Google Scholar]
  2. Barbieri A.; Bandini E.; Monti F.; Praveen V. K.; Armaroli N. The rise of near-infrared emitters: organic dyes, porphyrinoids, and transition metal complexes. Top. Curr. Chem. 2016, 374, 39. 10.1007/s41061-016-0048-9. [DOI] [PubMed] [Google Scholar]
  3. Torrent-Sucarrat M.; Navarro S.; Marcos E.; Anglada J. M.; Luis J. M. Design of Hückel–Möbius topological switches with high nonlinear optical properties. J. Phys. Chem. C 2017, 121, 19348–19357. 10.1021/acs.jpcc.7b05900. [DOI] [Google Scholar]
  4. Higashino T.; Nakatsuji H.; Fukuda R.; Okamoto H.; Imai H.; Matsuda T.; Tochio H.; Shirakawa M.; Tkachenko N. V.; Hashida M.; Murakami T.; Imahori H. Hexaphyrin as a potential theranostic dye for photothermal therapy and 19F magnetic resonance imaging. ChemBioChem 2017, 18, 951–959. 10.1002/cbic.201700071. [DOI] [PubMed] [Google Scholar]
  5. Higashino T.; Kumagai A.; Sakaki S.; Imahori H. Reversible π-system switching of thiophene-fused thiahexaphyrins by solvent and oxidation/reduction. Chem. Sci. 2018, 9, 7528–7539. 10.1039/C8SC02448K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Sung Y. M.; Oh J.; Cha W.-Y.; Kim W.; Lim J. M.; Yoon M.-C.; Kim D. Control and switching of aromaticity in various all-aza-expanded porphyrins: spectroscopic and theoretical analyses. Chem. Rev. 2017, 117, 2257–2312. 10.1021/acs.chemrev.6b00313. [DOI] [PubMed] [Google Scholar]
  7. Szyszko B.; Białek M. J.; Pacholska-Dudziak E.; Latos-Grażyński L. Flexible porphyrinoids. Chem. Rev. 2017, 117, 2839–2909. 10.1021/acs.chemrev.6b00423. [DOI] [PubMed] [Google Scholar]
  8. Soya T.; Mori H.; Osuka A. Quadruply twisted Hückel-aromatic dodecaphyrin. Angew. Chem., Int. Ed. 2018, 57, 15882–15886. 10.1002/anie.201811433. [DOI] [PubMed] [Google Scholar]
  9. Shin J. Y.; Kim K. S.; Yoon M. C.; Lim J. M.; Yoon Z. S.; Osuka A.; Kim D. Aromaticity and photophysical properties of various topology-controlled expanded porphyrins. Chem. Soc. Rev. 2010, 39, 2751–2767. 10.1039/b925417j. [DOI] [PubMed] [Google Scholar]
  10. Tanaka Y.; Saito S.; Mori S.; Aratani N.; Shinokubo H.; Shibata N.; Higuchi Y.; Yoon Z. S.; Kim K. S.; Noh S. B.; Park J. K.; Kim D.; Osuka A. Metalation of expanded porphyrins: a chemical trigger used to produce molecular twisting and Mobius aromaticity. Angew. Chem., Int. Ed. 2008, 47, 681–684. 10.1002/anie.200704407. [DOI] [PubMed] [Google Scholar]
  11. Stępień M.; Szyszko B.; Latos- Grażyński L. Three-level topology switching in a molecular Möbius band. J. Am. Chem. Soc. 2010, 132, 3140–3152. 10.1021/ja909913y. [DOI] [PubMed] [Google Scholar]
  12. Stuyver T.; Perrin M.; Geerlings P.; De Proft F.; Alonso M. Conductance switching in expanded porphyrins through aromaticity and topology changes. J. Am. Chem. Soc. 2018, 140, 1313–1326. 10.1021/jacs.7b09464. [DOI] [PubMed] [Google Scholar]
  13. Stuyver T.; Geerlings P.; De Proft F.; Alonso M. Toward the design of bithermoelectric switches. J. Phys. Chem. C 2018, 122, 24436–24444. 10.1021/acs.jpcc.8b07753. [DOI] [Google Scholar]
  14. Woller T.; Geerlings P.; De Proft F.; Champagne B.; Alonso M. Fingerprint of aromaticity and molecular topology on the photophysical properties of octaphyrins. J. Phys. Chem. C 2019, 123, 7318–7335. 10.1021/acs.jpcc.8b10908. [DOI] [Google Scholar]
  15. Alonso M.; Geerlings P.; De Proft F. Viability of Möbius topologies in [26]- and [28]hexaphyrins. Chem. - Eur. J. 2012, 18, 10916–10928. 10.1002/chem.201200511. [DOI] [PubMed] [Google Scholar]
  16. Alonso M.; Geerlings P.; De Proft F. Exploring the structure-aromaticity relationship in Hückel and Möbius N-fused pentaphyrins using DFT. Phys. Chem. Chem. Phys. 2014, 16, 14396–14407. 10.1039/C3CP55509G. [DOI] [PubMed] [Google Scholar]
  17. Stępień M.; Sprutta N.; Latos-Grażyński L. Figure eights, Möbius bands, and more: conformation and aromaticity of porphyrinoids. Angew. Chem., Int. Ed. 2011, 50, 4288–4340. 10.1002/anie.201003353. [DOI] [PubMed] [Google Scholar]
  18. Alonso M.; Geerlings P.; De Proft F. Topology switching in [32]heptaphyrins controlled by solvent, protonation, and meso-substituents. Chem. - Eur. J. 2013, 19, 1617–1628. 10.1002/chem.201203295. [DOI] [PubMed] [Google Scholar]
  19. Woller T.; Contreras-Garcia J.; Geerlings P.; De Proft F.; Alonso M. Understanding the molecular switching properties of octaphyrins. Phys. Chem. Chem. Phys. 2016, 18, 11885–11900. 10.1039/C5CP07413D. [DOI] [PubMed] [Google Scholar]
  20. Casademont-Reig I.; Woller T.; Contreras-García J.; Alonso M.; Torrent-Sucarrat M.; Matito E. New electron delocalization tools to describe the aromaticity in porphyrinoids. Phys. Chem. Chem. Phys. 2018, 20, 2787–2796. 10.1039/C7CP07581B. [DOI] [PubMed] [Google Scholar]
  21. Lim J. M.; Shin J.-Y.; Tanaka Y.; Saito S.; Osuka A.; Kim D. Protonated [4n] π and [4n+2] π octaphyrins choose their Möbius/Hückel aromatic topology. J. Am. Chem. Soc. 2010, 132, 3105–3114. 10.1021/ja909744z. [DOI] [PubMed] [Google Scholar]
  22. Saito S.; Shin J.-Y.; Lim J. M.; Kim K. S.; Kim D.; Osuka A. Protonation-triggered conformational changes to Möbius aromatic [32]heptaphyrins(1.1.1.1.1.1.1). Angew. Chem., Int. Ed. 2008, 47, 9657–9660. 10.1002/anie.200804457. [DOI] [PubMed] [Google Scholar]
  23. Torrent-Sucarrat M.; Navarro S.; Cossío F. P.; Anglada J. M.; Luis J. M. Relevance of the DFT method to study expanded porphyrins with different topologies. J. Comput. Chem. 2017, 38, 2819–2828. 10.1002/jcc.25074. [DOI] [PubMed] [Google Scholar]
  24. Riplinger C.; Sandhoefer B.; Hansen A.; Neese F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. 10.1063/1.4821834. [DOI] [PubMed] [Google Scholar]
  25. Riplinger C.; Pinski P.; Becker U.; Valeev E. F.; Neese F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. 10.1063/1.4939030. [DOI] [PubMed] [Google Scholar]
  26. Sparta M.; Neese F. Chemical applications carried out by local pair natural orbital based coupled-cluster methods. Chem. Soc. Rev. 2014, 43, 5032–5041. 10.1039/C4CS00050A. [DOI] [PubMed] [Google Scholar]
  27. Schütz M. Low-order scaling local electron correlation methods. III. Linear scaling local perturbative triples correction (T). J. Chem. Phys. 2000, 113, 9986–10001. 10.1063/1.1323265. [DOI] [Google Scholar]
  28. Guo Y.; Riplinger C.; Becker U.; Liakos D. G.; Minenkov Y.; Cavallo L.; Neese F. Communication: An improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)]. J. Chem. Phys. 2018, 148, 011101. 10.1063/1.5011798. [DOI] [PubMed] [Google Scholar]
  29. Liakos D. G.; Sparta M.; Kesharwani M. K.; Martin J. M. L.; Neese F. Exploring the accuracy limits of local pair natural orbital coupled-cluster theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. 10.1021/ct501129s. [DOI] [PubMed] [Google Scholar]
  30. N. Sylvetsky N.; Banerjee A.; Alonso M.; Martin J. M. L., Performance of localized coupled cluster methods in a moderately strong correlation regime: Hückel-Möbius interconversions in expanded porphyrins. Preprint available at https://arxiv.org/abs/2001.08641. [DOI] [PMC free article] [PubMed]
  31. Becke A. D. Density-functional thermochemistry III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. 10.1063/1.464913. [DOI] [Google Scholar]
  32. Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Mennucci B.; Petersson G.; et al. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2016.
  33. Neese F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1327 10.1002/wcms.1327. [DOI] [Google Scholar]
  34. Werner H. J.; Knowles P. J.; Knizia G.; Manby F.; Schütz M.; Celani P.; Korona T.; Lindh R.; Mitrushenkov A.; Rauhut G.; et al. MOLPRO, version 2018.1, A package of ab initio programs; Cardiff, United Kingdom, 2012.
  35. Furche F.; Ahlrichs R.; Hättig C.; Klopper W.; Sierka M.; Weigend F. Turbomole. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 91–100. 10.1002/wcms.1162. [DOI] [Google Scholar]
  36. Grimme S.; Goerigk L.; Fink R. F. Spin-component-scaled electron correlation methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 886–906. 10.1002/wcms.1110. [DOI] [Google Scholar]
  37. Fink R. F. Spin-component-scaled Møller–Plesset (SCS-MP) perturbation theory: A generalization of the MP approach with improved properties. J. Chem. Phys. 2010, 133, 174113. 10.1063/1.3503041. [DOI] [PubMed] [Google Scholar]
  38. Grimme S. Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. 10.1063/1.1569242. [DOI] [Google Scholar]
  39. Sedlak R.; Riley K. E.; Řezáč J.; Pitoňák M.; Hobza P. MP2.5 and MP2.X: Approaching CCSD(T) quality description of noncovalent interaction at the cost of a single CCSD iteration. ChemPhysChem 2013, 14, 698–707. 10.1002/cphc.201200850. [DOI] [PubMed] [Google Scholar]
  40. Riley K. E.; Řezáč J.; Hobza P. MP2.X: a generalized MP2.5 method that produces improved binding energies with smaller basis sets. Phys. Chem. Chem. Phys. 2011, 13, 21121–21125. 10.1039/c1cp22525a. [DOI] [PubMed] [Google Scholar]
  41. Takatani T.; Hohenstein E. G.; Sherrill C. D. Improvement of the coupled-cluster singles and doubles method via scaling same- and opposite-spin components of the double excitation correlation energy. J. Chem. Phys. 2008, 128, 124111. 10.1063/1.2883974. [DOI] [PubMed] [Google Scholar]
  42. Pitoňák M.; Řezáč J.; Hobza P. Spin-component scaled coupled-clusters singles and doubles optimized towards calculation of noncovalent interactions. Phys. Chem. Chem. Phys. 2010, 12, 9611–9614. 10.1039/c0cp00158a. [DOI] [PubMed] [Google Scholar]
  43. Kats D. The distinguishable cluster approach from a screened Coulomb formalism. J. Chem. Phys. 2016, 144, 044102. 10.1063/1.4940398. [DOI] [PubMed] [Google Scholar]
  44. Kats D. Improving the distinguishable cluster results: spin-component scaling. Mol. Phys. 2018, 116, 1435–1442. 10.1080/00268976.2017.1417646. [DOI] [Google Scholar]
  45. Perdew J. P.; Schmidt K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2000, 577, 1–20. 10.1063/1.1390175. [DOI] [Google Scholar]
  46. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  47. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  48. Zhang Y.; Yang W. Comment on “Generalized gradient approximation made simple. Phys. Rev. Lett. 1998, 80, 890. 10.1103/PhysRevLett.80.890. [DOI] [Google Scholar]
  49. Tao J.; Mo Y. Accurate semilocal density functional for condensed-matter physics and quantum chemistry. Phys. Rev. Lett. 2016, 117, 073001. 10.1103/PhysRevLett.117.073001. [DOI] [PubMed] [Google Scholar]
  50. Mo Y.; Tian G.; Tao J. Performance of a nonempirical exchange functional from density matrix expansion: comparative study with different correlations. Phys. Chem. Chem. Phys. 2017, 19, 21707–21713. 10.1039/C6CP08761B. [DOI] [PubMed] [Google Scholar]
  51. Sun J.; Ruzsinszky A.; Perdew J. P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
  52. Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Climbing the density functional ladder: nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
  53. Becke A. D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. 10.1063/1.464304. [DOI] [Google Scholar]
  54. Adamo C.; Barone V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  55. Hui K.; Chai J.-D. SCAN-based hybrid and double-hybrid density functionals from models without fitted parameters. J. Chem. Phys. 2016, 144, 044114. 10.1063/1.4940734. [DOI] [PubMed] [Google Scholar]
  56. Zhao Y.; Truhlar D. G. Design of density functionals that are broadly accurate for thermochemistry, thermochemical kinetics, and nonbonded interactions. J. Phys. Chem. A 2005, 109, 5656–5667. 10.1021/jp050536c. [DOI] [PubMed] [Google Scholar]
  57. Staroverov V. N.; Scuseria G. E.; Tao J.; Perdew J. P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. 10.1063/1.1626543. [DOI] [Google Scholar]
  58. Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  59. Zhao Y.; Truhlar D. G. Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. 10.1021/ct800246v. [DOI] [PubMed] [Google Scholar]
  60. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  61. Ranasinghe D. S.; Margraf J. T.; Jin Y.; Bartlett R. J. Does the ionization potential condition employed in QTP functionals mitigate the self-interaction error?. J. Chem. Phys. 2017, 146, 034102. 10.1063/1.4973727. [DOI] [PubMed] [Google Scholar]
  62. Peverati R.; Truhlar D. G. Improving the accuracy of hybrid meta-GGA density functionals by range separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. 10.1021/jz201170d. [DOI] [Google Scholar]
  63. Vydrov O. A.; Scuseria G. E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. 10.1063/1.2409292. [DOI] [PubMed] [Google Scholar]
  64. Chai J.-D.; Head-Gordon M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
  65. Mardirossian N.; Head-Gordon M. ωB97M-V: A combinatorially optimized, range-separated hybrid, meta-GGA density functional with VV10 nonlocal correlation. J. Chem. Phys. 2016, 144, 214110. 10.1063/1.4952647. [DOI] [PubMed] [Google Scholar]
  66. Mardirossian N.; Head-Gordon M. ωB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Phys. Chem. Chem. Phys. 2014, 16, 9904–9924. 10.1039/c3cp54374a. [DOI] [PubMed] [Google Scholar]
  67. Yu H. S.; He X.; Li S. L.; Truhlar D. G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. 10.1039/C6SC00705H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
  69. Goerigk L.; Grimme S. Efficient and accurate double-hybrid-meta-GGA density functionals—evaluation with the extended GMTKN30 database for general main group thermochemistry, kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2011, 7, 291–309. 10.1021/ct100466k. [DOI] [PubMed] [Google Scholar]
  70. Casanova-Páez M.; Dardis M. B.; Goerigk L. ωB2PLYP and ωB2GPPLYP: the first two double-hybrid density functionals with long-range correction optimized for excitation energies. J. Chem. Theory Comput. 2019, 15, 4735–4744. 10.1021/acs.jctc.9b00013. [DOI] [PubMed] [Google Scholar]
  71. Mardirossian N.; Head-Gordon M. Survival of the most transferable at the top of Jacob’s ladder: Defining and testing the ωB97M(2) double hybrid density functional. J. Chem. Phys. 2018, 148, 241736. 10.1063/1.5025226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Chai J.-D.; Head-Gordon M. Long-range corrected double-hybrid density functionals. J. Chem. Phys. 2009, 131, 174105. 10.1063/1.3244209. [DOI] [PubMed] [Google Scholar]
  73. Karton A.; Tarnopolsky A.; Lamère J.-F.; Schatz G. C.; Martin J. M. L. Highly accurate first-principles benchmark data sets for the parametrization and validation of density functional and other approximate methods. Derivation of a robust, generally applicable, double-hybrid functional for thermochemistry and thermochemical kinetics. J. Phys. Chem. A 2008, 112, 12868–12886. 10.1021/jp801805p. [DOI] [PubMed] [Google Scholar]
  74. For a very recent review of double hybrids, see:Martin J. M. L.; Santra G. Empirical double-hybrid density functional theory: a ‘third way’ in between WFT and DFT. Isr. J. Chem. 2019, 10.1002/ijch.201900114. [DOI] [Google Scholar]
  75. Kozuch S.; Martin J. M. L. DSD-PBEP86: in search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104–20107. 10.1039/c1cp22592h. [DOI] [PubMed] [Google Scholar]
  76. Kozuch S.; Martin J. M. L. Spin-component-scaled double hybrids: An extensive search for the best fifth-rung functionals blending DFT and perturbation theory. J. Comput. Chem. 2013, 34, 2327–2344. 10.1002/jcc.23391. [DOI] [PubMed] [Google Scholar]
  77. Santra G.; Sylvetsky N.; Martin J. M. L. Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 2019, 123, 5129–5143. 10.1021/acs.jpca.9b03157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Alipour M. Seeking for spin-opposite-scaled double-hybrid models free of fitted parameters. J. Phys. Chem. A 2016, 120, 3726–3730. 10.1021/acs.jpca.6b03406. [DOI] [PubMed] [Google Scholar]
  79. Mezei P. D.; Csonka G. I.; Ruzsinszky A.; Kállay M. Construction and application of a new dual-hybrid random phase approximation. J. Chem. Theory Comput. 2015, 11, 4615–4626. 10.1021/acs.jctc.5b00420. [DOI] [PubMed] [Google Scholar]
  80. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  81. Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  82. Goerigk L.; Grimme S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. 10.1039/c0cp02984j. [DOI] [PubMed] [Google Scholar]
  83. Grimme S.; Bannwarth C.; Caldeweyher E.; Pisarek J.; Hansen A. A general intermolecular force field based on tight-binding quantum chemical calculations. J. Chem. Phys. 2017, 147, 161708. 10.1063/1.4991798. [DOI] [PubMed] [Google Scholar]
  84. Caldeweyher E.; Ehlert S.; Hansen A.; Neugebauer H.; Spicher S.; Bannwarth C.; Grimme S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. 10.1063/1.5090222. [DOI] [PubMed] [Google Scholar]
  85. Vydrov O. A.; Voorhis T. V. Nonlocal van der Waals density functional: the simpler the better. J. Chem. Phys. 2010, 133, 244103. 10.1063/1.3521275. [DOI] [PubMed] [Google Scholar]
  86. Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  87. Woon D. E.; D T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  88. Peterson K. A.; Adler T. B.; Werner H.-J. Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B–Ne, and Al–Ar. J. Chem. Phys. 2008, 128, 084102. 10.1063/1.2831537. [DOI] [PubMed] [Google Scholar]
  89. Yousaf K.; Peterson K. Optimized complementary auxiliary basis sets for explicitly correlated methods: Aug-cc-pVnZ orbital basis sets. Chem. Phys. Lett. 2009, 476, 303. 10.1016/j.cplett.2009.06.003. [DOI] [PubMed] [Google Scholar]
  90. Kong L.; Bischoff F. A.; Valeev E. F. Explicitly correlated R12/F12 methods for electronic structure. Chem. Rev. 2012, 112, 75–107. 10.1021/cr200204r. [DOI] [PubMed] [Google Scholar]
  91. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  92. Weigend F. Hartree–Fock exchange fitting basis sets for H to Rn. J. Comput. Chem. 2008, 29, 167–175. 10.1002/jcc.20702. [DOI] [PubMed] [Google Scholar]
  93. Mardirossian N.; Head-Gordon M. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. 10.1080/00268976.2017.1333644. [DOI] [Google Scholar]
  94. Witte J.; Neaton J. B.; Head-Gordon M. Push it to the limit: characterizing the convergence of common sequences of basis sets for intermolecular interactions as described by density functional theory. J. Chem. Phys. 2016, 144, 194306. 10.1063/1.4949536. [DOI] [PubMed] [Google Scholar]
  95. Crawford T. D.; Schaefer H. F. III An introduction to coupled cluster theory for computational chemists. Rev. Comput. Chem. 2007, 14, 33–136. 10.1002/9780470125915.ch2. [DOI] [Google Scholar]
  96. Hättig C.; Klopper W.; Köhn A.; Tew D. P. Explicitly correlated electrons in molecules. Chem. Rev. 2012, 112, 4–74. 10.1021/cr200168z. [DOI] [PubMed] [Google Scholar]
  97. Spackman P. R.; Jayatilaka D.; Karton A. Basis set convergence of CCSD(T) equilibrium geometries using a large and diverse set of molecular structures. J. Chem. Phys. 2016, 145, 104101. 10.1063/1.4962168. [DOI] [PubMed] [Google Scholar]
  98. Halkier A.; Helgaker T.; Jørgensen P.; Klopper W.; Koch H.; Olsen J.; Wilson A. K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998, 286, 243–252. 10.1016/S0009-2614(98)00111-0. [DOI] [Google Scholar]
  99. Marcos E.; Anglada J. M.; Torrent-Sucarrat M. Theoretical study of the switching between Hückel and Möbius topologies for expanded porphyrins. J. Phys. Chem. C 2012, 116, 24358–24366. 10.1021/jp3083612. [DOI] [Google Scholar]
  100. Marcos E.; Anglada J. M.; Torrent-Sucarrat M. Effect of the meso-substituent in the Hückel-to-Möbius topological switches. J. Org. Chem. 2014, 79, 5036–5046. 10.1021/jo500569p. [DOI] [PubMed] [Google Scholar]
  101. For a brief overview of static correlation diagnostics, see:Fogueri U. R.; Kozuch S.; Karton A.; Martin J. M. L. A simple DFT-based diagnostic for nondynamical correlation. Theor. Chem. Acc. 2013, 132, 1291. 10.1007/s00214-012-1291-y. [DOI] [Google Scholar]
  102. Lee T. J.; Taylor P. R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. 1989, 36, 199–207. 10.1002/qua.560360824. [DOI] [Google Scholar]
  103. Janssen C. L.; Nielsen I. M. B. New diagnostics for coupled-cluster and Møller–Plesset perturbation theory. Chem. Phys. Lett. 1998, 290, 423–430. 10.1016/S0009-2614(98)00504-1. [DOI] [Google Scholar]
  104. Lee T. Comparison of the T1 and D1 diagnostics for electronic structure theory: A new definition for the open-shell D1 diagnostic. Chem. Phys. Lett. 2003, 372, 362–367. 10.1016/S0009-2614(03)00435-4. [DOI] [Google Scholar]
  105. Karton A.; Sylvetsky N.; Martin J. M. L. W4–17: A diverse and high-confidence dataset of atomization energies for benchmarking high-level electronic structure methods. J. Comput. Chem. 2017, 38, 2063–2075. 10.1002/jcc.24854. [DOI] [PubMed] [Google Scholar]
  106. Sears J. S.; Sherrill C. D. Assessing the performance of Density Functional Theory for the electronic structure of metal–salens: the d2-metals. J. Phys. Chem. A 2008, 112, 6741–6752. 10.1021/jp802249n. [DOI] [PubMed] [Google Scholar]
  107. Jiang W.; DeYonker N. J.; Wilson A. K. Multireference character for 3d transition-metal-containing molecules. J. Chem. Theory Comput. 2012, 8, 460–468. 10.1021/ct2006852. [DOI] [PubMed] [Google Scholar]
  108. Tishchenko O.; Zheng J.; Truhlar D. G. Multireference model chemistries for thermochemical kinetics. J. Chem. Theory Comput. 2008, 4, 1208–1219. 10.1021/ct800077r. [DOI] [PubMed] [Google Scholar]
  109. Ramos-Cordoba E.; Salvador P.; Matito E. Separation of dynamic and nondynamic correlation. Phys. Chem. Chem. Phys. 2016, 18, 24015–24023. 10.1039/C6CP03072F. [DOI] [PubMed] [Google Scholar]
  110. Zanardi P. Quantum entanglement in fermionic lattices. Phys. Rev. A: At., Mol., Opt. Phys. 2002, 65, 042101.and references therein. 10.1103/PhysRevA.65.042101. [DOI] [Google Scholar]
  111. Grimme S.; Hansen A. A practicable real-space measure and visualization of static electron-correlation effects. Angew. Chem., Int. Ed. 2015, 54, 12308–12313. 10.1002/anie.201501887. [DOI] [PubMed] [Google Scholar]
  112. Bauer C. A.; Hansen A.; Grimme S. The fractional occupation number weighted density as a versatile analysis tool for molecules with a complicated electronic structure. Chem. - Eur. J. 2017, 23, 6150–6164. 10.1002/chem.201604682. [DOI] [PubMed] [Google Scholar]
  113. ICE-CI is effectively ORCA’s implementation of Malrieu’s CIPSI algorithm.Evangelisti S.; Daudey J.-P.; Malrieu J.-P. Convergence of an improved CIPSI algorithm. Chem. Phys. 1983, 75, 91–102. 10.1016/0301-0104(83)85011-3. [DOI] [Google Scholar]
  114. Karton A. Basis set convergence of high-order coupled cluster methods up to CCSDTQ567 for a highly multireference molecule. Chem. Phys. Lett. 2019, 737, 136810. 10.1016/j.cplett.2019.136810. [DOI] [Google Scholar]
  115. Karton A.; Daon S.; Martin J. M. L. W4–11: A high-confidence benchmark dataset for computational thermochemistry derived from first-principles W4 data. Chem. Phys. Lett. 2011, 510, 165–178. 10.1016/j.cplett.2011.05.007. [DOI] [Google Scholar]
  116. Distasio R. A. Jr; Head-Gordon M. Optimized spin-component scaled second-order Møller-Plesset perturbation theory for intermolecular interaction energies. Mol. Phys. 2007, 105, 1073–1083. 10.1080/00268970701283781. [DOI] [Google Scholar]
  117. Neese F.; Schwabe T.; Kossmann S.; Schirmer B.; Grimme S. Assessment of orbital-optimized, spin-component scaled second-order many-body perturbation theory for thermochemistry and kinetics. J. Chem. Theory Comput. 2009, 5, 3060–3073. 10.1021/ct9003299. [DOI] [PubMed] [Google Scholar]
  118. Jung Y.; Lochan R. C.; Dutoi A. D.; Head-Gordon M. Scaled opposite-spin second order Møller–Plesset correlation energy: an economical electronic structure method. J. Chem. Phys. 2004, 121, 9793–9802. 10.1063/1.1809602. [DOI] [PubMed] [Google Scholar]
  119. Iron M. A.; Janes T. Evaluating transition metal barrier heights with the latest density functional theory exchange–correlation functionals: the MOBH35 benchmark database. J. Phys. Chem. A 2019, 123, 3761–3781. 10.1021/acs.jpca.9b01546. [DOI] [PubMed] [Google Scholar]; J. Phys. Chem. A 2019, 123, 6379. 10.1021/acs.jpca.9b0613531306024
  120. Goerigk L.; Hansen A.; Bauer C.; Ehrlich S.; Najibi A.; Grimme S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. 10.1039/C7CP04913G. [DOI] [PubMed] [Google Scholar]
  121. Grimme S. Improved third-order Møller–Plesset perturbation theory. J. Comput. Chem. 2003, 24, 1529–1537. 10.1002/jcc.10320. [DOI] [PubMed] [Google Scholar]
  122. Wheeler S. E.; Houk K. N. Integration grid errors for meta-GGA-predicted reaction energies: origin of grid errors for the M06 suite of functionals. J. Chem. Theory Comput. 2010, 6, 395–404. 10.1021/ct900639j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  123. Zhao Y.; Truhlar D. G. Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. 10.1021/ct800246v. [DOI] [PubMed] [Google Scholar]
  124. Mardirossian N.; Head-Gordon M. How accurate are the Minnesota density functionals for noncovalent interactions, isomerization energies, thermochemistry, and barrier heights involving molecules composed of main-group elements?. J. Chem. Theory Comput. 2016, 12, 4303–4325. 10.1021/acs.jctc.6b00637. [DOI] [PubMed] [Google Scholar]
  125. Li C.; Zheng X.; Su N. Q.; Yang W. Localized orbital scaling correction for systematic elimination of delocalization error in density functional approximations. National Science Rev. 2018, 5, 203–215. 10.1093/nsr/nwx111. [DOI] [Google Scholar]
  126. Santra G.; Sylvetsky N.; Martin J. M. L. Minimally empirical double-hybrid functionals trained against the GMTKN55 Database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 2019, 123, 5129–5143. 10.1021/acs.jpca.9b03157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  127. Efremenko I.; Martin J. Coupled cluster benchmark of new density functionals and domain pair natural orbital methods: mechanisms of hydroarylation and oxidative coupling catalyzed by Ru(II) chloride carbonyls. AIP Conf. Proc. 2019, 2186, 030005. 10.1063/1.5137916. [DOI] [Google Scholar]
  128. Park J. K.; Yoon Z. S.; Yoon M.-C.; Kim K. S.; Mori S.; Shin J.-Y.; Osuka A.; Kim D. Möbius aromaticity in N-fused [24]pentaphyrin upon Rh(I) metalation. J. Am. Chem. Soc. 2008, 130, 1824–1825. 10.1021/ja7100483. [DOI] [PubMed] [Google Scholar]
  129. Sankar J.; Mori S.; Saito S.; Rath H.; Suzuki M.; Inokuma Y.; Shinokubo H.; Suk Kim K.; Yoon Z. S.; Shin J.-Y.; et al. Unambiguous identification of Möbius aromaticity for meso-aryl-substituted [28]hexaphyrins(1.1.1.1.1.1). J. Am. Chem. Soc. 2008, 130, 13568–13579. 10.1021/ja801983d. [DOI] [PubMed] [Google Scholar]
  130. Kim K. S.; Yoon Z. S.; Ricks A. B.; Shin J.-Y.; Mori S.; Sankar J.; Saito S.; Jung Y. M.; Wasielewski M. R.; Osuka A.; Kim D. Temperature-dependent conformational change of meso-hexakis(pentafluorophenyl) [28]hexaphyrins(1.1.1.1.1.1) into Möbius structures. J. Phys. Chem. A 2009, 113, 4498–4506. 10.1021/jp8111205. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp9b10880_si_001.pdf (6.2MB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES