The Amide I Spectrum of Proteins—Optimization of Transition Dipole Coupling Parameters Using Density Functional Theory Calculations

Abstract

The amide I region of the infrared spectrum is related to the protein backbone conformation and can provide important structural information. However, the interpretation of the experimental results is hampered because the theoretical description of the amide I spectrum is still under development. Quantum mechanical calculations, for example, using density functional theory (DFT), can be used to study the amide I spectrum of small systems, but the high computational cost makes them inapplicable to proteins. Other approaches that solve the eigenvalues of the coupled amide I oscillator system are used instead. An important interaction to be considered is transition dipole coupling (TDC). Its calculation depends on the parameters of the transition dipole moment. This work aims to find the optimal parameters for TDC in three major secondary structures: α-helices, antiparallel β-sheets, and parallel β-sheets. The parameters were suggested through a comparison between DFT and TDC calculations. The comparison showed a good agreement for the spectral shape and for the wavenumbers of the normal modes for all secondary structures. The matching between the two methods improved when hydrogen bonding to the amide oxygen was considered. Optimal parameters for individual secondary structures were also suggested.

Introduction

The main application of infrared (IR) spectroscopy in the biological sciences is the analysis of the amide I region of the spectrum. The vibrations in this region of the spectrum are mainly due to the stretching vibrations of the C=O bonds in the amide groups of the protein backbone. The spectrum is sensitive to the backbone conformation of proteins,¹⁻¹¹ but the interpretation of the experiments is limited by an incomplete theoretical description.

To aid the understanding of the experimental results, several approaches were suggested to describe the interactions in proteins and to simulate the infrared spectrum in the amide I region.^{2−4,12−17} A quantum mechanical method to analyze molecular vibrations is density functional theory (DFT). Because of the large computational cost, DFT calculations cannot be applied to entire proteins, although fragmentation approaches are possible.¹⁸⁻²⁰ Even though these are successful in the hand of specialists, there is a demand in the vibrational spectroscopy community for widely applicable and rapid computational methods to model experimental spectra. Such methods are often based on the floating oscillator model,¹² where each amide group is considered as a vibrating oscillator with a specific, intrinsic frequency of vibration and a local transition dipole moment (TDM). The individual oscillators are coupled electrostatically, which is often described by the transition dipole coupling (TDC) approximation.^{2,4,12,21−23} TDC is known not to reproduce nearest neighbor couplings, which are therefore taken from quantum chemical calculations of small peptides.^{13,14,24−27} Additional properties can influence the intrinsic frequency of the individual amide I oscillators, such as the local dihedral angles^13,14,26 and hydrogen bonding, which causes a downshift of the intrinsic frequencies of vibration.²⁸⁻³⁰

The calculation of TDC requires the determination of the relevant parameters. In particular, the quantity that describes the coupling between amide I oscillators is the TDM; the properties to be optimized are its position, its magnitude, and its angle in relation to the direction of the C=O bond. Several studies^{4,12,24,25,31−33} suggested different values for the TDM parameters, and there is still no agreement regarding the optimal parameters. This work aims to find these parameters for the TDM by comparing DFT and TDC calculations.

Computational Details

Model Structures

All structural models are in the form of poly-l-alanine. The antiparallel and parallel β-sheets were composed of two and four strands, with five amide groups per strand. The initial structures of these sheets were created in our Matlab program,^34,35 according to the atomic coordinates suggested by Fraser and MacRae³⁶ and by Pauling,³⁷ respectively. The α-helices were composed of 11 and 21 amide groups. Their initial structures were generated with PyMOL. The structural models were created with the following dihedral angles: ϕ = −138.6°, φ = 134.5° for the antiparallel β-sheets; ϕ = −121.0°, φ = 114.8° for the parallel β-sheets; and ϕ = −57.0°, φ = −47.0°, ω = 180.0° for the α-helices. The three largest structures are shown in Figures S1–S3 of the Supporting Information.

DFT Calculations

The calculations were performed using the Gaussian 09³⁸ program package. The BPW91³⁹⁻⁴² density functional and the 6-31G** basis set were used first for the geometry optimization of the model structures and then for the frequency calculations with the optimized geometries. This combination of functional and basis set was chosen because it provides a good compromise between accuracy of the vibrational frequencies and computational time.^5,43−45 It yields good agreement with experimental data regarding the frequencies and dipole strengths of the amide I and amide II vibrations of N-methylacetamide.⁴⁴ In addition, the vibrational couplings are reproduced well, as evidenced by the good description of the effects of site-specific ¹³C labeling.⁴⁶

During the geometry optimization, the Ramachandran angles were kept frozen. The dihedral angle ω was not kept frozen for the β-sheet model structures because the ω values were close to 180.0° after the preliminary geometry optimization. In contrast, the ω value for the N terminal amide group of the α-helix structures was close to 167.0° after the preliminary geometry optimization. New geometry optimizations were then performed for the α-helix model structures, with the ω angles kept frozen.

The infrared spectra were calculated placing a Lorentzian line shape function at the spectral position of each normal mode, with 16 cm^–1 as the full width at half-maximum. The maximum of the line shape function was equal to the dipole strength of the particular normal mode.

The coupling constants between individual amide groups were retrieved from the DFT calculations using the carbonyl population analysis method as a Hessian reconstruction method.²⁷ It approximates the contribution of each amide group to a particular amide I normal mode by the carbon and oxygen displacements. The method is equivalent to the use of the carbonyl bond length change,²⁷ which in turn produces very similar results as a more complete consideration of all of the atoms that vibrate in the amide I mode.²⁶ According to this method, the reconstructed Hessian matrix is given by

where Λ is the wavenumber eigenvalue matrix obtained from the DFT calculations and U is a matrix whose elements are obtained from the displacements of the C=O atoms

where u_Cαxj is the displacement of the carbonyl carbon atom of amide group α along the x direction for the jth normal mode and u_Oαxj is the displacement of the carbonyl oxygen atom of the amide group α along the x direction for the jth normal mode. The normalization constant N_j is calculated according to the formula

where N is the number of amide groups. The sign of the elements of the U matrix is assigned according to whether the C=O bond length increases or decreases according to the displacements stated in the Gaussian output file. The resulting Hessian matrices were converted to F matrices through the transformation of the elements from wavenumbers to mass-normalized force constants.^21,47 The F matrices were then made symmetrical, by averaging the elements f_ij and f_ji. The resulting matrix is termed the DFT F matrix in the following.

TDC Calculations—F Matrix

TDC calculations were performed on the optimized geometries from the DFT calculations using a Matlab program.⁴⁸ Diagonal elements and nearest neighbor diagonal elements in the F matrices were copied from DFT F matrices. In this way, the calculated spectrum depends only on the parameters for TDC coupling and not on the modeling of other interactions, such as hydrogen bonding,²⁸⁻³⁰ the local dihedral angles, and nearest neighbor interactions.^13,14,26 All other elements were calculated using coupling constants from TDC, using the following formula

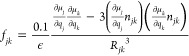where ∂μ_α/∂q_α is the dipole derivative of the amide group α in D Å^–1 u^–1/2, R_jk is the distance between the two dipole derivatives in Å, n_jk is the unit vector of the distance, ε is the dielectric constant (assumed to be unity), and 0.1 is the factor for conversion from D² Å^–5 to mdyn Å^–1. The magnitude of the dipole derivative is proportional to that of the transition dipole moment, according to the formula⁴⁷

where |TDM| is in D, ∂μ/∂q is the dipole derivative in D Å^–1 u^–1/2, 4.1058 is equal to h/(8π²c)^1/2 in units of u^1/2 Å cm^–1/2, and υ̃ is the intrinsic wavenumber of a local amide I oscillator in cm^–1. The resulting F matrices are termed TDC F matrices in the following.

A hydrogen bond to the carbonyl oxygen polarizes the C=O bond. The larger partial charges lead to a larger change of dipole moment during the amide I vibration, i.e., to a larger dipole derivative. Therefore, we considered the magnitude of the dipole derivative to depend on the hydrogen bond to the amide oxygen. As a first approximation, we assumed the change induced by hydrogen bonding to be proportional to the C=O bond length change and to the energy of the hydrogen bond. Both are proportional to the change in the intrinsic wavenumber^29,49,50 of the hydrogen bonded amide group. This gives

where ∂μ/∂q is the magnitude of the dipole derivative used for the calculation of TDC, ∂μ₀/∂q is the magnitude of the dipole derivative in the absence of a hydrogen bond, A describes the effect of a hydrogen bond on the magnitude of the dipole derivative, and Δυ̃ is the shift of the intrinsic wavenumber due to hydrogen bonding to the oxygen atom, calculated from the Kabsch–Sander energy.^50,51 The hydrogen bond shift is a measure of the strength of the hydrogen bond. When a hydrogen bond is present, it leads to a downshift (Δυ̃ < 0), which increases the magnitude of the dipole derivative.

The TDM is oriented at an angle with respect to the C=O bond. The resulting TDM points from a location close to the oxygen atom toward the vicinity of the nitrogen atom.

TDC Calculations—Optimization of TDM Parameters

The magnitude of ∂μ₀/∂q, the angle and the position of the TDM, as well as the hydrogen bonding parameter A were optimized in our Matlab program in order to minimize the sum of the squared differences between TDC and DFT F matrices. These parameters were the same for all amide groups. Fixed positions for the TDM suggested by Krimm and co-workers³³ and by Chirgadze and Nevskaya⁴ were also tested. The latter is similar to the position used by Torii and Tasumi¹² for amide groups that were neither in α-helices nor in β-sheets.

Two different optimization procedures were performed. The first optimization was performed on all six model structures together, while the second optimization was performed for each of the three secondary structures separately. The optimization procedure minimized the R value, which is the sum of the squared differences between the coupling constants of the DFT and TDC F matrices of all considered structures. To compensate for the smaller number of elements in the F matrix of the smaller model structures (β-sheets with 10 amide groups or α-helix with 11 amide groups) as compared to the larger model structures (β-sheets with 20 amide groups and α-helix with 21 amide groups), the squared differences for the smaller model structures were doubled in both optimization procedures.

TDC Calculations—Calculating the Spectrum

A subsequent normal-mode analysis diagonalized the optimized TDC F matrices, which retrieved the wavenumbers of the normal modes as eigenvalues (υ̃_k in the following) and the participation of each amide group to the normal modes as eigenvectors. The IR intensities of the normal modes (I_k in the following) are calculated according to

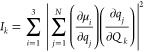where ∂μ_i/∂q_j is the ith Cartesian component of the dipole derivative for the jth amide group, ∂q_j/∂Q_k is the vibrational amplitude of the local amide I oscillator on group j in the kth normal mode, and N is the number of amide groups.

The dipole strengths were obtained from the intensities I_k and the wavenumbers υ̃_k using the following formula

where D_k is the dipole strength of the normal mode k in D², I_k is the intensity of the normal mode k in D² u^–1 Å^–2, υ̃_k is the wavenumber of the normal mode k in cm^–1, and 10⁴ is a factor of conversion between esu² cm² and D². Finally, the infrared spectra were calculated from the dipole strengths as described for the DFT calculations.

Results

TDM Parameter Optimization Using All Structural Models

In order to find the optimized TDM parameters, the optimization program minimized the sum of the squared differences between the coupling constants obtained from DFT and those obtained from TDC. In a first optimization procedure, the TDM parameters were optimized for all six model structures together. The results are summarized in Table 1. The R value reflects the deviations between DFT and TDC F matrices (see the Computational Details), with a lower value indicating a better match.

Table 1. Optimized Parameters for the Three Tested Positions of the TDM^a.

TDM position reference	TDM position along C=O (Å)	TDM position along C—N (Å)	∂μ0/∂q (∂μ/∂qmax) (D Å–1 u–1/2)	TDM angle (deg)	A (cm)	R (10–4 mdyn2 Å–2 u–2)
Moore and Krimm33	0.868	0	2.26 (2.47)	17	0.007	15.7
Chirgadze and Nevskaya4	0.893	0.357	2.24 (2.52)	22	0.009	8.8
this work	1.043	0.513	2.20 (2.51)	22	0.010	7.5

^aOptimized parameters are indicated in bold, while the fixed parameters are in normal print. The parameters were optimized using all six structural models together. The TDM positions are the distances from the C-atom along the specified bonds. ∂μ₀/∂q is the dipole derivative in the absence of hydrogen bonding and ∂μ/∂q_max (value in brackets) the maximum dipole derivative in the presence of hydrogen bonding.

The R value decreases when hydrogen bonding to the oxygen atom is considered to increase the magnitude of the dipole derivative (hydrogen bonding parameter A > 0). From the optimized A values and a typical hydrogen bonding induced shift of 20 cm^–1, our optimization indicates a 20% increase of the dipole derivative magnitude upon formation of a typical hydrogen bond. We considered also hydrogen bonding to the amide hydrogen, but this did not improve the R value and was therefore not implemented in the calculations presented here.

Regarding the TDM position, our optimized position and Chirgadze and Nevskaya’s position for the TDM are the best choices. The magnitude of the TDM and the A parameter are similar for the three positions, while the angle is different for Moore and Krimm’s TDM position. In the following, the term “our optimized parameters” refers to the parameter optimization where also the TDM position was allowed to optimize (last row of Table 1).

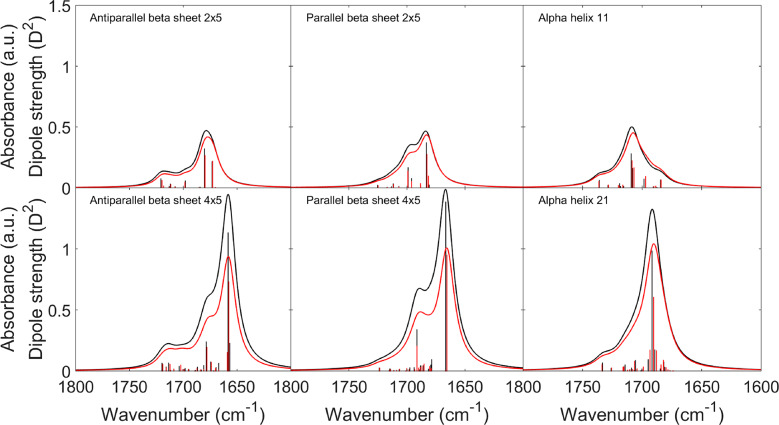
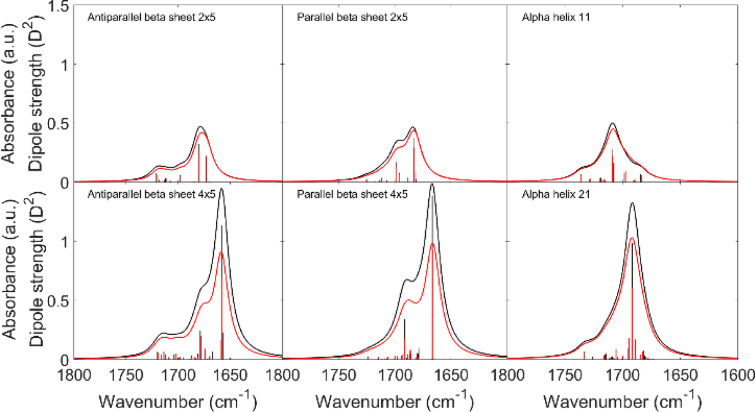
Figure 1 shows a comparison between amide I spectra and dipole strengths from DFT and from the normal mode calculation with the TDC F matrix using our optimized parameters. A very good agreement is reached for the wavenumbers of the normal modes for all model structures. Also, most dipole strengths are well reproduced, but the strongest dipole strengths are underestimated.

Figure 1.

Comparison between IR spectra from DFT calculations (black) and TDC calculations which used our optimized TDM parameters (Table 1) for the F matrix and for the dipole strength calculations (red). The dipole strengths of the normal modes are shown as bars.

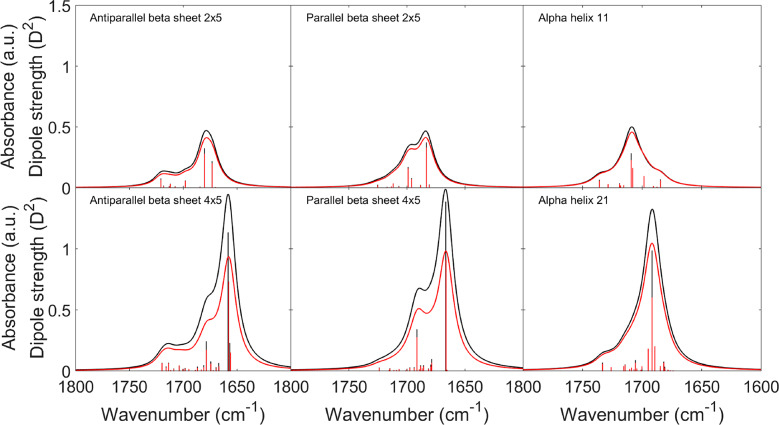
To test whether this underestimation is due to a deficiency of the TDC F matrix, we calculated the dipole strengths and the IR spectra from a normal-mode analysis that used the reconstructed DFT F matrices without modification. The dipole strengths were then calculated with the optimized TDM parameters as for the spectra shown in Figure 1 (see the Computational Details). The comparison with the DFT calculations is shown in Figure 2. As for the previous calculations, the dipole strengths of the strongest normal modes are still weaker in the normal mode calculations. Therefore, this effect is not due to a deficiency of the TDC approximation.

Figure 2.

Comparison between IR spectra from DFT calculations (black) and calculations which used DFT F matrices and our optimized TDM parameters (Table 1) for the intensity calculations (red). The dipole strengths of the normal modes are shown as bars.

In our normal-mode analysis, the TDM parameters are used twice: (i) to calculate the TDC terms in the F matrix and (ii) to calculate the dipole strengths of the normal modes. Therefore, a solution for the mismatch problem could be the use of different sets of TDM parameters for the TDC F matrix and for the dipole strength calculations. We tested this approach and optimized the TDM parameters for dipole strength calculations starting from normal mode calculations with DFT F matrices. In the optimization process, the squared deviations between the obtained spectrum and the DFT spectrum were minimized. The most important parameter to improve the overall agreement of the spectra was the hydrogen bonding parameter A, which needed to be increased. This selectively increased the dipole derivative for the hydrogen bonded amide groups. The required A value was smaller for the small structures (0.013 cm) than for the large structures (0.020 cm). A value of 0.019 cm (keeping the other parameters constant as in the last row of Table 1) provided the best match for all structures. The resulting spectra are shown in Figure 3. Also, a general increase of only the dipole magnitude by 15% improved the overall agreement, but not as much as the increase of A. While the overall best parameters of both measures increased the spectral agreement for the three large structures, the small structure spectra deviated more from the DFT spectra than with the original parameters, but the deviations were more balanced between the six different structures.

Figure 3.

Comparison between IR spectra from DFT calculations (black) and calculations which used DFT F matrices, our optimized TDM parameters (Table 1), and A = 0.019 for the dipole strength calculations (red). The dipole strengths of the normal modes are shown as bars.

The change of the hydrogen bonding parameter A did not alter the spectral shapes significantly. However, when we allowed angle, magnitude, and A to vary, the shape of the spectra was less well reproduced (data not shown) than in the calculations with the optimized TDM parameters listed in Table 1. As we consider the shape to be the more important spectral feature for the interpretation of experimental data, we did not pursue this approach further. If both spectral shape and absolute intensities are important, then we suggest to increase the hydrogen bonding parameter for the calculation of the dipole strengths.

With this information, we returned to the coupling constants in the F matrix and explored the effect of an A value of 0.019 cm on the R value. The R value increased by more than a factor of 4, when the other parameters were kept constant (last row of Table 1). When these parameters were allowed to vary, the R value became nearly as low as in the original optimization, the angle decreased to 21°, the magnitude decreased to 1.9 D Å^–1 u^–1/2, and the TDM position moved 2 pm toward the nitrogen atom. The resulting spectra had a similar intensity mismatch as those in Figure 2 (not shown), indicating again that a unified set of parameters cannot provide a good match both of the coupling constants and of the dipole strengths.

TDM Parameter Optimization for Each Secondary Structure

The TDM parameters were also optimized separately for each pair of α-helix, antiparallel β-sheet, and parallel β-sheet model structures. Because of the smaller number of coupling constants, the optimization procedure did not converge when all parameters were left free. Therefore, we fixed the TDM position to the optimum position for all six structures but also fixed A, which describes the hydrogen bonding to the oxygen atom, and optimized the other parameters for several A values. The results confirmed that the introduction of the hydrogen bonded parameter A improved the result, providing a better match between TDC and DFT F matrices. The optimal values of the parameters are shown in Table 2. If we compare the optimal TDM parameters for each secondary structure with the optimal parameters for all structures together in Table 1, the magnitudes of the dipole derivative and the hydrogen bonding parameter A are similar, whereas the TDM angle differs. It is considerably larger for the α-helical structures than for the β-sheets, and this effect is observed for all tested TDM positions.

Table 2. Optimized TDM Parameters for Individual Secondary Structures^a.

secondary structure	fixed position of the TDM	∂μ0/∂q (∂μ/∂qmax) (D Å–1 u–1/2)	TDM angle (deg)	A - best value (cm)	R (10–4 mdyn2 Å–2 u–2)
antiparallel β-sheet	Moore and Krimm33	2.20 (2.55)	12	0.012	3.7
	Chirgadze and Nevskaya4	2.29 (2.58)	18	0.010	3.7
	optimized	2.33 (2.62)	18	0.010	2.0
parallel β-sheet	Moore and Krimm33	2.18 (2.42)	9	0.008	2.3
	Chirgadze and Nevskaya4	2.28 (2.59)	24	0.010	1.7
	optimized	2.25 (2.56)	22	0.010	1.6
α-helix	Moore and Krimm33	2.76 (2.93)	40	0.006	2.8
	Chirgadze and Nevskaya4	2.40 (2.57)	35	0.006	0.8
	optimized	2.32 (2.49)	33	0.006	0.6

^aThe parameters were obtained for each secondary structure individually. “Optimized” in the position column indicates the TDM position obtained for the optimization for all six structures together (see Table 1). Optimized parameters are indicated in bold, while the fixed parameters are in normal print. ∂μ₀/∂q is the dipole derivative in the absence of hydrogen bonding and ∂μ/∂q_max (value in brackets) the maximum dipole derivative in the presence of hydrogen bonding.

Analysis of the Deviations between DFT and TDC Coupling Constants

To analyze whether TDC managed or failed to describe the DFT coupling constants, we compared their relative deviations for both optimization procedures. They are plotted separately for each secondary structure as a function of the optimized TDC coupling constants in Figure 4.

Figure 4.

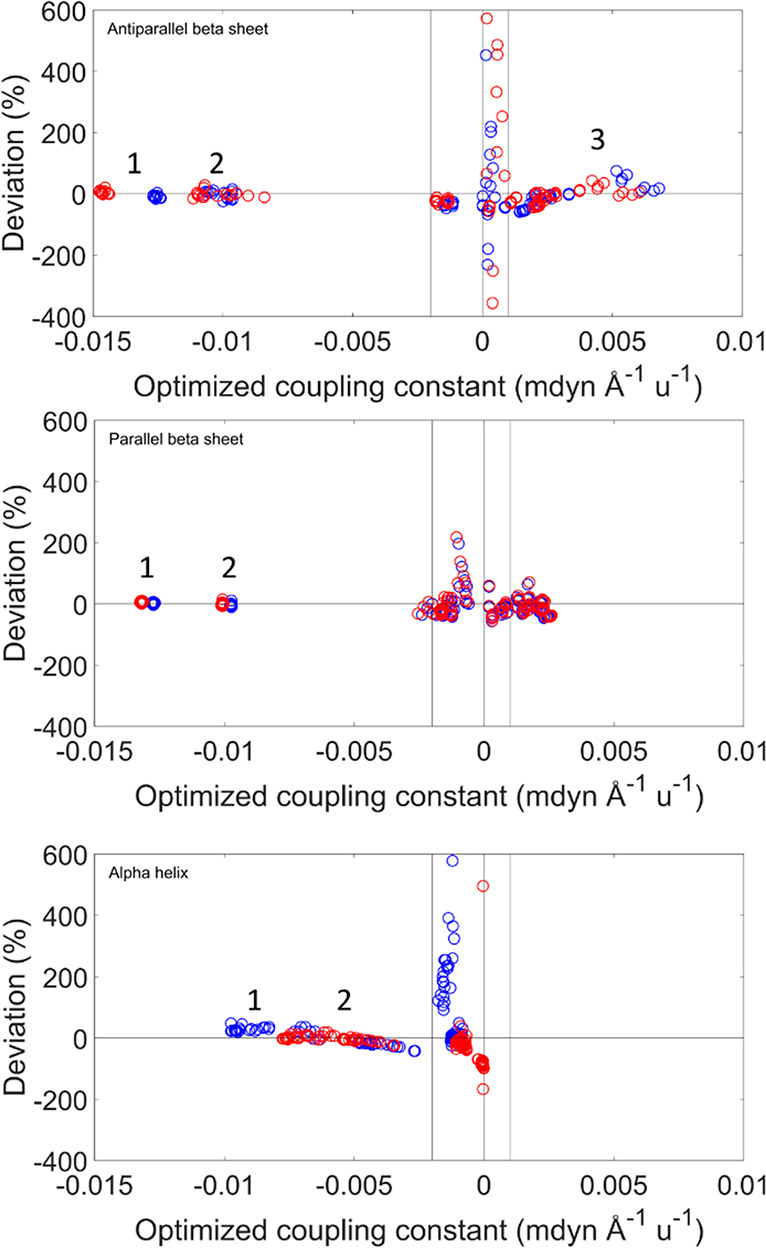
Relative deviations as a function of the TDC coupling constant for the three secondary structures. The relative deviations were calculated by the equation (f_ijTDC/f_ijDFT) – 1. The deviations are colored according to the type of optimization procedure: optimization on all structural models is shown in blue, and optimization by secondary structure, in red. The vertical lines represent the cutoff values suggested from this analysis. For the largest coupling constants, the relative arrangement of the coupled groups is indicated in the following. Hydrogen bonding refers to the hydrogen bond with the carbonyl oxygen. Antiparallel β-sheet: (1) inline between nearest strands (hydrogen bonded); (2) large hydrogen bonded loop and inline between nearest strands where one oxygen is not hydrogen bonded; (3) small hydrogen bonded loop. Parallel β-sheet: (1) inline between nearest strands (hydrogen bonded); (2) inline between nearest strands (one oxygen not hydrogen bonded). α-helix: (1) hydrogen bonded (i, i + 3); (2) interaction between next-nearest amide groups in the sequence (i, i + 2).

The coupling constants in Figure 4 can be grouped according to the relative arrangement of the two interacting amide groups. In the antiparallel β-sheet, we can distinguish three arrangements that produce large coupling constants: inline interstrand (aligned amide groups in different strands which are hydrogen bonded), small hydrogen bonded loop (interaction with the amide group that follows the hydrogen bonded amide group in the sequence), and large hydrogen bonded loop (interaction with the amide group that precedes the hydrogen bonded amide group in the sequence).⁵² For the parallel β-sheet, the latter two arrangements are equivalent and termed diagonal. In the α-helix, the strongest interaction occurs between amide groups that are hydrogen bonded (between amide groups i and i + 3 in the sequence); additional important interactions are with the amide groups that precede the hydrogen bonded group in the sequence (between groups i and i + 2). These arrangements are indicated in Figure 4, and the coupling constants for these arrangements are grouped and listed in the Supporting Information.

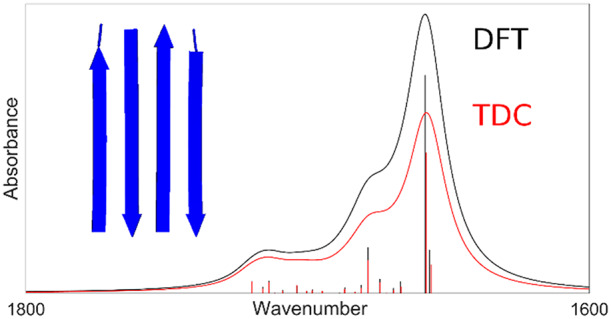
The large coupling constants are generally well reproduced, with the exception of the groups in the small hydrogen loop arrangement of antiparallel β-sheets.

The largest relative deviations are observed for small coupling constants, i.e., when the interaction between the amide groups is weak. This behavior is observed because the optimization program is focused to optimize the stronger interactions between the amide groups because it minimizes the absolute deviations.

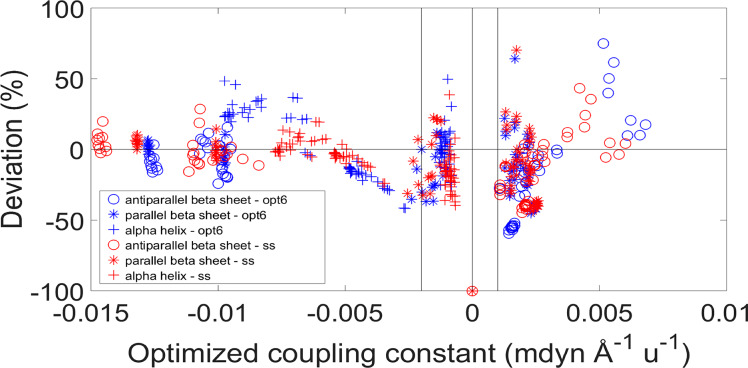
The same deviations, plotted as a function of the angle between the transition dipole moments of the interacting amide groups, are shown in Figure 5. The coupling constants are generally well reproduced, except when the angle is lower than 30° and larger than 170°.

Figure 5.

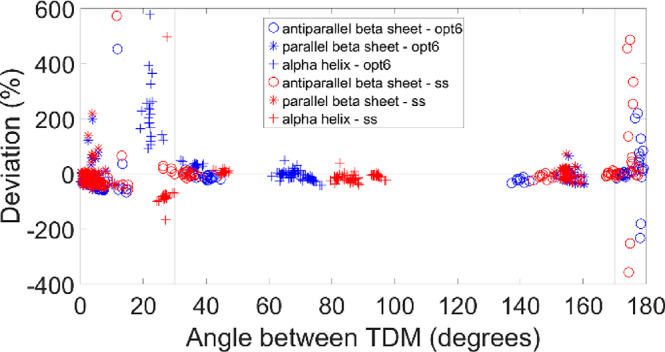
Relative deviations between the coupling constants of TDC and DFT F matrices as a function of the angle between the transition dipole moments. TDC was calculated with our optimized TDM position. See Figure 4 for the calculation of the relative deviations and significance of the vertical lines. The deviations are colored according to the type of optimization procedure: optimization on all structural models (“opt6”) is shown in blue, optimization by secondary structure (“ss”) in red.

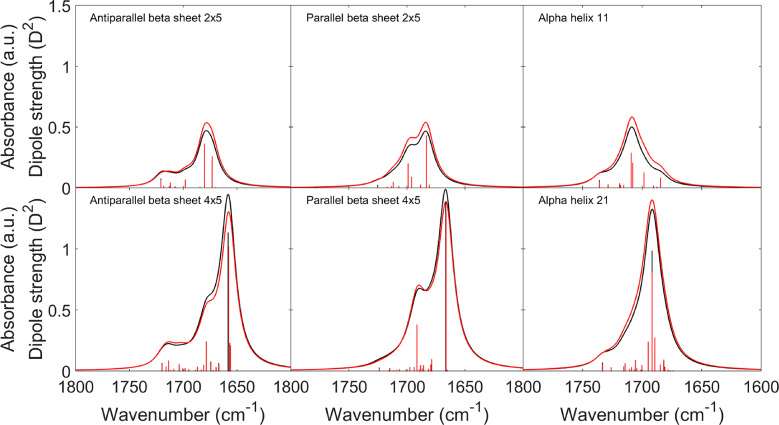
Figures 4 and 5 suggest a cutoff for the TDC coupling constants in order to focus on the stronger interactions and to avoid the large deviations for the small coupling constants. The cutoff we decided to apply was to consider as zero all of the coupling constants between −0.002 and 0.001 mdyn Å^–1 u^–1 for the interactions whose angle between their TDMs is smaller than 30° or larger than 170°. Applying this cutoff, the largest deviations disappeared (as shown in Figure 6), while many of the small negative coupling constants were kept. Figure 6 demonstrates that optimization of the TDM parameters for each secondary structure reduces the deviations between TDC and DFT coupling constants. The sign of the coupling constants was calculated correctly by the TDC approximation, with only very few exceptions for small coupling constants. Our cutoff results in a slightly better agreement between the wavenumbers calculated by DFT and from the TDC F matrices (Figure 7), in particular for the α-helices.

Figure 6.

Relative deviations between the coupling constants of TDC and DFT F matrices as a function of the TDC coupling constants, after applying the cutoff on the TDC coupling constants (between −0.002 and 0.001 mdyn Å^–1 u^–1) and on the angle between the transition dipole moments (lower than 30° and higher than 170°). See Figure 4 for the calculation of the relative deviations and significance of the vertical lines. The deviations are colored according to the type of optimization procedure: optimization on all structural models (“opt6”) is shown in blue, optimization by secondary structure (“ss”) in red.

Figure 7.

Comparison between IR spectra from DFT calculations (black) and TDC calculations (red) as in Figure 1, using our optimized TDM parameters (Table 1) to calculate dipole strengths and TDC, but after applying the cutoff on the coupling constants (between −0.002 and 0.001 mdyn Å^–1 u^–1) and on the angle between the transition dipole moments (lower than 30° and higher than 170°). The dipole strengths of the normal modes are shown as bars.

Further cutoffs were applied to the optimized F matrices (the coupling constants were considered as zero if their intensities were between −0.002 and 0.001 mdyn Å^–1 u^–1, between −0.002 and 0.002 mdyn Å^–1 u^–1, or between −0.005 and 0.005 mdyn Å^–1 u^–1). The resulting spectra and dipole strengths are shown in Figures S4–S6 in the Supporting Information. The increase of the cutoff values and the removal of the angle constraint led to visible changes in the IR spectra and to a shift of the position of the main normal modes. This indicates that cutoffs should be applied with care.

Discussion

DFT calculations were performed on models of three main secondary structures occurring in proteins. The amide I vibrations obtained were further analyzed by a reconstruction of the Hessian matrix, which provided the coupling constants between local amide I oscillators. These DFT coupling constants can be compared to those determined by a combination of isotope-edited experimental infrared spectra and calculations. This approach has indicated coupling constants for nearest neighbors in extended polypeptide chains between 4 and 7 cm^–1 (our average DFT value: 4.9 cm^–1).^53,54 Interstrand coupling constants in parallel β-sheets⁵⁵ were found to be −4 cm^–1 for coupling between hydrogen bonded amide groups in adjacent strands (our average DFT value: −5.4 cm^–1) and between −0.5 and 1 cm^–1 for groups that are diagonally positioned and connected by a hydrogen bonded loop (e.g., groups 1 and 7 in Figure S2, our average DFT value: −0.9 cm^–1). In antiparallel β-sheets, the interstrand coupling constants⁴⁶ were determined to be 4 cm^–1 for the groups in a large hydrogen bonded loop (e.g., groups 2 and 8 in Figure S1, our average DFT value: −5.1 cm^–1) and to be −4 cm^–1 for the small hydrogen bonded loop (e.g., groups 2 and 10 in Figure S1, our average DFT value: 2.3 cm^–1). In α-helices, the strongest coupling was found for nearest neighbors (approximately 8 cm^–1, our average DFT value: 7.3 cm^–1) and somewhat weaker but considerable couplings between amide group i and groups i + 2 and i + 3 (approximately −2 cm^–1, our average DFT value: −2.9 cm^–1). The values of our DFT coupling constants agree well with these experimentally derived values, but the signs for the small and large hydrogen bonded loop interactions in antiparallel β-sheets are different. This discrepancy is possibly due to a sign error in the original article, because a positive constant for the small loop interaction⁵⁶ and a negative coupling constant for the large loop interaction^56,57 are mentioned in other publications. These signs are consistent with the out-of-phase character of the most intense mode⁴⁶ and with the observed down- and upshift for the small and large loop interactions, respectively.^46,56

The DFT coupling constants were then approximated by coupling constants calculated with the TDC mechanism, using optimized TDM parameters to achieve the best match. With these TDC coupling constants, we successfully reproduced DFT IR spectra of three main secondary structures. While the overall agreement of the F matrices is good and the strongest coupling constants are generally well reproduced, a perfect matching of the coupling constants was not reached. Using TDM parameters optimized for the antiparallel β-sheet, the TDC model overestimates the small hydrogen bonded loop interactions, which are the largest positive coupling constants (see Figure 4). For the parallel β-sheet and optimized parameters for this structure, an underestimation of the diagonal interactions can be found, which generate small negative coupling constants (approximately −0.002 mdyn Å^–1 u^–1). With optimized parameters for the α-helix, there is a slight overestimation of the interaction between hydrogen bonded amide groups (i, i + 3) and a slight underestimation of the interaction between next-nearest amide groups in the sequence (i, i + 2).

The accuracy of the TDC approximation is debated in the literature. Several studies verified that the TDC model is appropriate to describe long-range interactions but not short-range interactions.^{13,14,58−60} Cho and co-workers^27,31 concluded that the TDC model underestimates the coupling for β-sheets, whereas Chung and Tokmakoff⁶⁰ note an overestimation of short-range coupling constants. Wang⁶¹ deduced that the TDC model can provide a good description of turns but not of α-helices and extended chains.

On the other hand, TDC coupling was found to reproduce experimental isotope effects,^54,55,62 but the agreement depended on the TDM parameters.⁵⁵ The parameter set of Torii and Tasumi,²⁴ developed for second-nearest neighbor interactions, performed better for a parallel β-sheet than a parameter set with Moore and Krimm’s TDM position and angle³³ and Torii and Tasumi’s dipole derivative.¹² The TDM position of Chirgadze and Nevskaya,⁴ which performed better than that of Moore and Krimm in our study, was not tested.⁵⁵ All TDC and transition charge models tested calculated a too negative value for the coupling between hydrogen bonded amide groups in a parallel β-sheet. This is not the case for our TDM parameters, where the TDC coupling constant is ∼14% and ∼20% less negative than the DFT coupling constant for parameters optimized for parallel β-sheets and parameters optimized for all six structures, respectively. For α-helices, it was concluded that the description of coupling constants by TDC has significant deficiencies.⁵⁹

These partly conflicting conclusions regarding the validity of the TDC model may be due to the different TDM parameters used: a specific choice of the TDM position, magnitude, and angle can lead to underestimation or overestimation of interactions between amide groups in a specific arrangement relative to the interactions for other arrangements. For example, the latter investigation of coupling in α-helices used a TDM that was aligned along the C=O bond, which is very different from the optimum angle of more than 30° found in this study. However, even with the best TDM parameters, TDC is only an approximation of the true electrostatic interactions and ignores higher multipoles. Their consideration in, for example, the transition charge coupling model^13,27,63 might further improve the description of these interactions. However, this expectation does not generally seem to be fulfilled.^{13,27,54,55,61,63} Furthermore, even a complete description of the through-space electrostatic interactions would still ignore through-bond couplings. The present work shows, however, that the TDC approximation describes the amide I spectrum remarkably well in spite of the mentioned simplifications. Regarding the neglect of through-bond couplings, the success of the TDC description can be rationalized by (i) the small contribution of the CN stretching vibration to the amide I mode, which is the main reason for through-bond coupling,⁶⁴ and (ii) the restriction of the TDC model to non-nearest neighbor couplings.

Our optimized magnitude of the dipole derivative is 10–20% smaller than dipole derivatives calculated for trans-N-methylacetamide in apolar solvents from experimental data^65,66 or from quantum chemical calculations in the gas phase.^61,67 Our optimized dipole derivative refers to amide groups without hydrogen bonding to the oxygen atom. It will be increased by the effect of the hydrogen bond, expressed by the hydrogen bonding parameter A in our calculations. The magnitude of the dipole derivative increases because a hydrogen bond polarizes the C=O bond, which increases its permanent dipole moment and therefore also its change during the C=O stretching vibration. This effect increases with the strength of the hydrogen bond. Accordingly, it has been found that solvation in water increases the dipole derivative by 4–20% in quantum chemical calculations with N-methylacetamide.^61,67,68 This is in line with the increase of ∼15% obtained with our optimized parameters (Table 1).

Our dipole derivatives may be compared to local amide I dipole derivatives in peptides that have been determined previously.^32,54,61 For a β-hairpin, the local dipole derivatives are between 2.7 and 3.4 D Å^–1 u^–1/2 (average 3.2 D Å^–1 u^–1/2),³² and for a set of small peptides in different conformations, they ranged between 2.1 and 3.2 D Å^–1 u^–1/2.^54,61 Our values for free and hydrogen bonded amide groups (Tables 1 and 2) are in the lower half of the combined ranges of these studies, which may be related to the intensity mismatch obtained with these parameters as discussed in the following.

In our optimization, the TDM parameters were optimized so that the coupling constants obtained by TDC matched as good as possible those obtained from the DFT calculations. When these parameters are used to calculate the dipole strengths of the normal modes, many dipole strengths are underestimated, in particular those of the strongest absorbing modes in the three larger structures. Such a size effect on the infrared intensity has been noted before for antiparallel β-sheets.⁶ An increase of the hydrogen bonding parameter A, which selectively increases the dipole derivative magnitude of hydrogen bonded amide groups, in the calculation of the dipole strengths improves the agreement. The required increase is larger for the large structures than for the small structures. This might indicate that our implementation of the hydrogen bonding effect is imperfect, possibly because it considers only the local interaction between hydrogen bonding donor and acceptor but ignores more long-range interactions.

The observation that different parameters are optimum for calculating the coupling constants on the one hand and the dipole strengths on the other hand seems to be counterintuitive. A possible explanation is the following: Our optimization of the TDM parameters is based on calculating DFT coupling constants from TDC, which is an approximation of the true electrostatic interactions. The optimization focused on the strongest interactions, which occur between close neighbors, where deficiencies of the TDC approximation can be expected. Therefore, our optimized parameters might not be the true TDM parameters; they are just those which describe the strongest interactions best. In consequence, they might not be the best choice for calculating the dipole strengths.

In our calculations, the magnitudes of the dipole derivative and the hydrogen bonding parameter A do not change drastically between the optimization for all secondary structures and the optimizations for individual secondary structures. The difference between the two optimization procedures can be found in the angle of the TDM. When the TDM parameters are optimized for each secondary structure, the optimum angle varied between 9 and 40°, with the largest angles found for the α-helix. The angle depended also on the choice of the TDM position. The position on the C=O bond suggested by Moore and Krimm led to the smallest angle for the β-sheets (∼9°) and the largest angle for the α-helix (40°).

These angles can be compared to TDM angles of individual amide I oscillators, which have been determined in previous studies. They varied between 20 and 32° (average 28°) in a β-hairpin³² and between 7 and 33° in a number of small peptide molecules in different conformations.^54,61 These ranges are in good agreement with the angles used in this work. However, there is no indication that the local TDM angle in a helical peptide should be larger than that in extended chains when the local parameters are calculated for short peptides with three amide groups.⁶¹ Therefore, the different angles obtained in this work might not be the true local TDM angles but rather reflect a compensation for deficiencies of the TDC model as mentioned earlier.

The angle obtained with the optimized position of this work for the two β-sheets (18 and 22°) and in the optimization with all structures (22°) is close to the values used in the original studies of Chirgadze and Nevskaya⁴ and Krimm and Abe.²³ It is also in the range of experimentally determined angles for crystalline trans-N-methylacetamide⁶⁹ and antiparallel β-sheets in a protein⁷⁰ and close to the angles calculated for trans-N-methylacetamide in the gas phase or an aqueous environment (13–20°).^61,67

We conclude that the TDM positions suggested in this work and by Chirgadze and Nevskaya⁴ lead to the most consistent TDM parameters for the different secondary structures. However, the best parameters for α-helices and β-sheets are still different. This need for different parameters for the two structures has been noted before.⁷¹ It is a hinder for the implementation of these parameters in calculations of the amide I spectrum of proteins for two reasons: (i) the optimum parameters for other secondary structures are not known, and (ii) small changes in the dihedral angles or the hydrogen bonding pattern might lead to rather abrupt changes in the TDM parameters. Instead of specific parameters for different secondary structures, it seems to be advisible to use the parameters optimized for all three secondary structures together. While these reproduce the coupling constants with less accuracy, the resulting wavenumbers and spectral shapes are in very good agreement with the DFT spectra.

Conclusions

This work optimized TDM parameters for a modeling of the non-nearest neighbor amide I coupling constants by TDC. The reference for the optimization was a set of DFT calculations at the BPW91/6-31G** level for different secondary structures. Such calculations reproduce amide I vibrational frequencies, dipole strengths, and couplings well,^44,46 as discussed in the Computational Details. Nevertheless, a certain modification of our optimized parameters might be required when they are used to model experimental spectra because our DFT calculations neglect the consequences of anharmonicity and dispersion interactions.

Our optimization minimized the discrepancy between the DFT-derived coupling constants and those obtained by TDC. In other words, we did not optimize the parameters by comparison with DFT-calculated infrared spectra. Therefore, our parameters are not specific for infrared absorption spectroscopy—they are also optimized for the computation of other vibrational properties that require the knowledge of the coupling constants. Examples are vibrational circular dichroism and Raman scattering.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.9b11793.

• Details about the Supporting Information spreadsheets and Figures S1–S6 showing the antiparallel and parallel β-sheet model structures, the α-helix with 21 amide groups, and comparisons between IR spectra from DFT calculations and TDC calculations (PDF)

• Optimization using the six structural models together; the F matrices from Matlab are obtained using the optimized parameters for our optimized position for the TDM (see Table 1 of the main text) (XLSX)

• Optimization for each secondary structure separately; the F matrices from Matlab are obtained using our optimized position for the TDM (see Table 1 of the main text) and the best value for A for each secondary structure (see Table 2 of the main text) (XLSX)

The authors declare no competing financial interest.