Abstract
Kelvin-probe measurements on ferromagnetic thin film electrodes coated with self-assembled monolayers of chiral molecules reveal that the electron penetration from the metal electrode into the chiral molecules depends on the ferromagnet’s magnetization direction and the molecules’ chirality. Electrostatic potential differences as large as 100 mV are observed. These changes arise from the applied oscillating electric field, which drives spin-dependent charge penetration from the ferromagnetic substrate to the chiral molecules. The enantiospecificity of the response is studied as a function of the magnetization strength, the magnetization direction, and the handedness and length of the chiral molecules. These new phenomena are rationalized in terms of the chiral-induced spin selectivity (CISS) effect, in which one spin orientation of electrons from the ferromagnet penetrates more easily into a chiral molecule than does the other orientation. The large potential changes (>kT at room temperature) manifested here imply that this phenomenon is important for spin transport in chiral spintronic devices and for magneto-electrochemistry of chiral molecules.
The control and detection of electron spin dynamics is essential for the realization of spintronic1 and quantum information technologies. Recent developments in molecular spintronics have pointed to the “spinterface” (ferromagnet surface/molecular semiconductor interface) as playing an important role in determining device behavior.2 This work demonstrates the use of chiral molecules to control the electron spin density at an interface and its effect on the electrostatic potential. Thus, it suggests that chiral molecules and the constraints they impose on the interface through the chiral-induced spin selectivity (CISS) effect provide a new approach to controlling the “spinterface.” This work also provides new insight into the mechanism of the chiral-induced spin selectivity effect discovered more than a decade ago,3 for which a full quantitative theory has not yet been provided.
A number of different experiments have shown that chiral organic molecules exhibit strongly spin-dependent electron transport at room temperature. For example, one experimental method has examined the spin distribution of photoelectrons that transit from a metal substrate through a layer of chiral molecules and are detected with a Mott polarimeter.4−6 In another method, the effect was established by measuring the spin polarization of electron tunneling currents through individual chiral molecules adsorbed on a magnetized substrate.7−9 The effect was also observed via the magnetization generated by chiral films10,11 and by the dissymmetry in electron transfer rates of chiral molecules12,13 and chiral quantum dots,14−17 among others.18−26 In addition, CISS has been shown by the enantiospecific adsorption rate of chiral molecules on magnetized ferromagnetic films.27,28 Abendroth et al.29 used photoemission spectroscopy to reveal work function shifts of ferromagnet/chiral molecule interfaces that depend on the magnetization direction. The current work explores the interfacial effects of chiral molecules assembled on a ferromagnetic substrate.
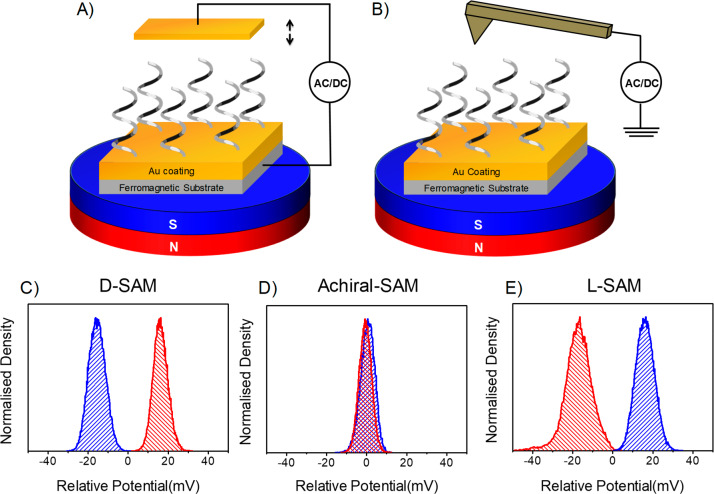
This study uses Kelvin-probe force microscopy (KPFM)30 and macroscopic Kelvin-probe31 measurements to investigate the spin-dependent resistance at metal–chiral molecule interfaces. Self-assembled monolayers (SAMs) of chiral organic molecules were adsorbed on ferromagnetic substrates, which were magnetized either parallel or antiparallel to the surface normal. Using the Kelvin probe, we investigated the effect of an oscillating electric field on charge injection from the magnetic substrate into the molecule as a function of the magnetization direction and the handedness of the molecule. An important advantage of this method over the existing ones, such as magneto-optic Kerr effect (MOKE) and tunneling microscopy methods, lies in its simplicity. The basic Kelvin-probe setup consists of a metallic probe electrode that is placed near the sample surface to form a capacitor (see Figure 1A). Then, the distance between the probe electrode and the sample surface is changed periodically to generate a frequency-dependent capacitance. Thus, an AC voltage is created across the gap, and it is proportional to the voltage difference between the probe electrode and the sample. Rather than record the AC voltage directly, it is common to apply a DC voltage, referred to as the contact potential difference (CPD), to null the response. The concept of Kelvin-probe force microscopy is similar, except the probe in this case is a conductive cantilever, which is scanned over the surface to record an electrostatic potential map (see Figure 1B). This work focuses on changes in the CPD, or electrostatic surface potential, that arise as one changes the adsorbate’s enantiomeric form and the surface magnetization. These enantiospecific changes in the measured CPD arise from the spin-dependence of charge penetration from the ferromagnet into the adsorbed chiral molecules, at the chiral molecule/ferromagnet interface.
Figure 1.
Schematic diagrams illustrating the principle of the Kelvin-probe measurement. In the macroscopic measurement (panel A), the distance of a Au electrode from the chiral-SAM/ferromagnetic sample is varied sinusoidally. In the microscopy version of the Kelvin-probe measurement (panel B), an AFM conducting tip is used as the counter-electrode, and its lateral position is scanned to image the substrate’s potential distribution. The diagrams illustrate how a static magnet is placed under the sample in order to saturate the magnetization of the ferromagnetic layer. Measured CPD distributions are shown for the (panel C) d-AL5-peptide-, (panel E) l-AL5-peptide-, and (panel D) achiral-SAM-coated ferromagnetic substrate under two different magnetizations. The blue color represents the potential distribution for a magnetization pointing to the south, and red corresponds to a north direction. These two directions are defined to be along the axis perpendicular to the surface. The zero voltage is set by the averaged contact potential difference found in the two measurements.
Several ferromagnetic substrates (with a Ni or Co layer) and different types of chiral SAMs were measured. For chiral SAMs, the CPD depends on the molecules’ handedness and the ferromagnetic substrate’s magnetization direction. This dependence arises from the difference between the probabilities of electrons with spin up and spin down tunneling into the chiral molecule layer, i.e., of the CISS effect. More specifically, the use of the ferromagnetic substrate affects the spin-dependent part of the contact resistance. For opposite magnetization directions of the ferromagnetic substrate, the change in the CPD corresponds to a difference in the induced dipole moments in the chiral SAM; it implies a strong penetration of the spin wave function through the molecular layer for one chirality and a weaker penetration for the opposite chirality.
Panels C, D, and E of Figure 1 show histograms of the CPD, which were measured using the KPFM method (see Supporting Information for more details), as a function of the magnetization direction for three self-assembled monolayer (SAM) systems: a d-AL5 peptide (−S–CH2–CH2–(Ala–Aib)5–COOH) denoted as d-SAM, an l-AL5 peptide (−S–CH2–CH2–(Ala–Aib)5–COOH) denoted as l-SAM, and an achiral SAM composed of mercaptoalkylcarboxylates (−S–(CH2)15–COOH). The ferromagnetic substrates consist of a 10 nm thick layer of Ni with a 10 nm capping layer of Au. For the d-SAM, the CPD was found to be 30–40 mV higher under north (red) magnetization than under south (blue) magnetization (the two directions are along the axis perpendicular to the surface), whereas the opposite was found for the l-SAM. In a control experiment with achiral SAMs, the CPD does not show any dependence on the applied magnetization direction. These data show that for a magnetization direction that “matches” the SAM chirality, the charge density extends farther into the chiral SAM.
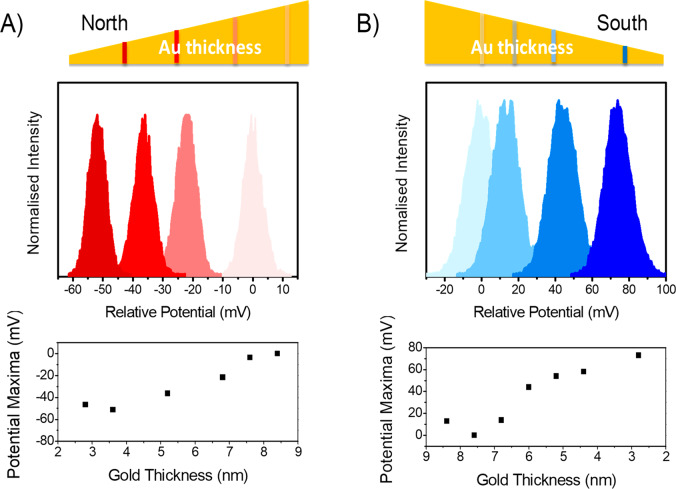
To confirm that the observations originate from the preferential tunneling of one electron spin over the other (i.e., the CISS effect), the dependence of the CPD on the Au layer thickness (wedge shape layer), which covers the ferromagnetic cobalt thin film exhibiting a perpendicular anisotropy (see Figure 2), was measured. As the thickness of the Au layer increases, the spin-polarized electron density emanating from the ferromagnetic layer will depolarize more prior to entering the chiral molecules.32 Thus, as the Au capping layer becomes thinner, the measured dependence of the potential difference on the magnetization direction should become stronger. Figure 2 shows KPFM results from measurements with l-AL5 SAMs adsorbed on a magnetic substrate comprising a 1.8 nm thick Co film that is covered with an Au wedge layer whose thickness is varied uniformly from 2 to 10 nm over a lateral distance of 10 mm (represented by the wedge shape at the top of Figure 2). The CPD was measured along the thickness gradient of the Au layer for two different film magnetization vertical orientations, north and south. Under application of a north magnetic field (Figure 2A), the CPD becomes more negative as the gold thicknesses decreases from 10 to 2 nm (light to dark red). The lower panel shows a plot of the most probable CPD value (peak of the distribution) measured at different gold thicknesses. Conversely, for the south magnetization direction (Figure 2B) the CPD becomes more positive as the gold thickness decreases (light to dark blue color). In both cases, changing the Au capping thickness from 10 to 2 nm results in a 60–80 mV shift in the CPD. These data indicate that the spin polarization persists through more than 10 nm of Au but that it is strongly attenuated. More importantly, these findings support the claim that spin delocalization from the chiral molecule into the magnetized substrate is responsible for the observed changes in CPD. Note that the MBE grown ferromagnetic Co layer in this sample has a higher saturation magnetization than the polycrystalline Ni layer used for the measurements in Figure 1 and that in a Au/Co/Au configuration such nanostructures feature a perpendicular anisotropy,33 i.e., the easy axis points directly out-of-plane. This feature results in a larger difference in the CPD for the Co ferromagnetic substrates than for the Ni ferromagnetic substrates.
Figure 2.
Change in the CPD as a function of the Au layer thickness for the opposite Co magnetization directions with adsorbed l-AL5 SAMs. The top diagram shows the distribution of a potential in different regions of the magnetic sample along the Au wedge. The color of each plot corresponds to the region indicated on the gradient bar by the same shade. The zero voltage is set by the measurement at the region of the highest Au thickness of 10 nm. The maxima of the potential distribution curves versus the thickness of the gold layer are plotted at the bottom of the Figure. As shown in panel (A), the CPD becomes more negative as the gold thickness decreases for a north magnetization. In contrast, in panel (B) where the magnetization is south, the CPD becomes positive, and its value increases with decreasing gold layer thickness. To estimate the error in the measurements, see the full-width-at-half-maximum of the histograms.
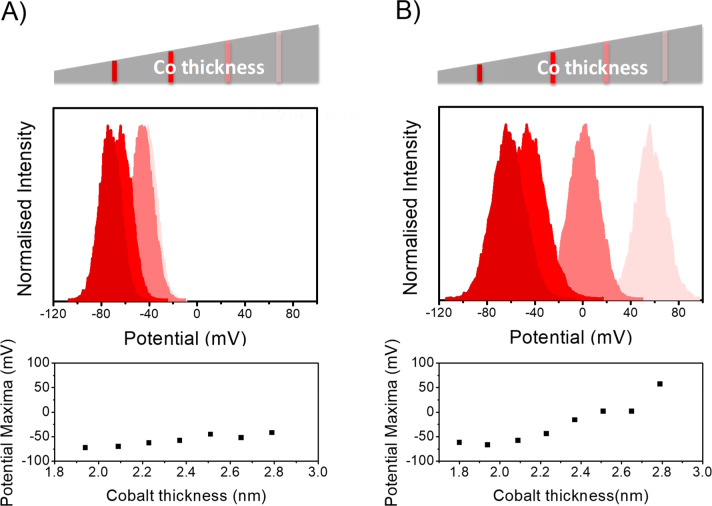
Previous work on the interaction of chiral molecules with ferromagnetic thin film surfaces showed that the enantiospecificity arose from the projection of the magnetic moment on the direction perpendicular to the film surface.34 To examine this feature, measurements on the l-AL5 SAMs were conducted using Au/Co/Au ferromagnetic substrates, in which the cobalt layer thickness was varied from 1.6 to 3 nm and the Au capping layer thickness was fixed at 2 nm. The coercivity and easy-axis direction of the magnetic layer (Co) changes with thickness; below 2 nm, the easy axis of the Co is mainly out-of-plane, while for Co layer thicknesses above 2 nm, a spin reorientation transition takes place, and the magnetization easy axis rotates to an in-plane direction (see the Supporting Information for more details on the ferromagnetic sample coercivity).33,35
Figure 3A shows the CPD measured along the Co thickness gradient under north magnetization for substrates with the l-AL5 SAM. Note that the magnet was placed underneath the substrate during the measurements, i.e., the Co layer magnetization was oriented perpendicular to the sample normal, even for Co thicknesses above the spin reorientation transition, along the applied magnetic field direction. In this configuration, a large negative shift of CPD was observed; however, the CPD distributions vary only weakly with the Co thickness. Figure 3B shows experimental results for the same sample as in Figure 3A but upon removal of the permanent magnet. When the magnetic field is removed, the magnetization of the Co layer (for thicknesses of Co layer above 2 nm) is no longer oriented normal to the surface and instead rotates toward the “easy” axis as a function of thickness. When the easy axis is not aligned with the electron injection direction into the SAM, the electron density injected into the SAM is lower, and the CPD becomes more positive. These results imply that the tilt angle of chiral molecules adsorbed on the substrate surface, in an ordered chiral monolayer, could be probed by changing the magnetization direction.
Figure 3.
Coercivity-dependent changes in the CPD. The Co thickness is changed from 1.5 to 3 nm, and the coercive field decreases as the Co layer thickness increases. The color of each plot corresponds to the region indicated on the gradient bar by the same shade. The bottom diagram plots the maxima of the potential distribution curve for the substrate with adsorbed l-AL5 SAMs vs the thickness of the Co layer. The CPD measured in the presence of a constant magnetic field well above the coercive field (panel A) shows a weak dependence on the Co thickness. In contrast, a strong Co layer thickness-dependence is measured in the absence of constant magnetic field (panel B). Here, the external magnetic field has been applied to orient a magnetization in a given direction and is then removed prior to the measurement.
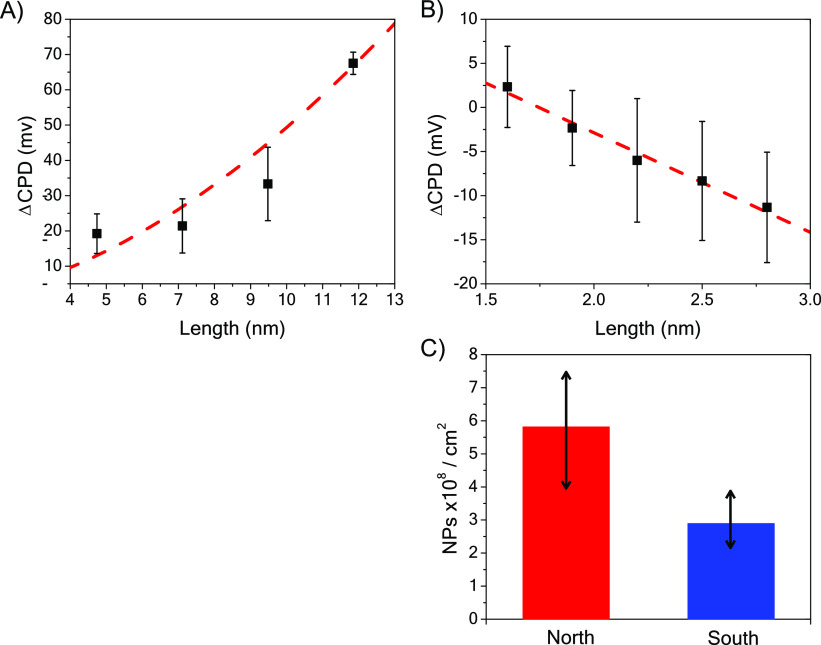
Lastly, the dependence of the CPD’s asymmetry on the substrate magnetization was studied as a function of the chiral molecule length (L); see Figure 4. The CPD of the SAM-coated substrate electrode arises from the potential drop across the SAM and thus should be proportional to the dipole moment of the molecules, D ∝ LQ, in the SAM, where Q is the amount of charge transferred between the metal surface and the monolayer, and L is the effective distance between this charge and the surface. As the molecules become longer, the injected charge can delocalize farther from the metal substrate, and a larger potential drop is expected. If the delocalization length changes with the chiral molecule length, then the asymmetry in the contact potential difference, ΔCPD = CPD(north) – CPD(south), should change with length. Figure 4A shows the ΔCPD for north and south magnetized films with chiral DNA, and Figure 4B shows the case for oligopeptides (ALn with n = 3–7) SAMs. See the Supporting Information for molecular sequences of the DNA and oligopeptides. Interestingly, a different length dependence was observed for the two types of molecules: ΔCPD ∝ L2 for the DNA, and ΔCPD ∝ L for the oligopeptides.
Figure 4.
Panels A and B show a change in CPD for molecules of different length; (A) double stranded DNA and (B) ALn oligopeptides on a magnetized Ni/Au electrode. The red lines are fits of the data by a quadratic dependence in panel (A) and by a linear fit in panel (B). See the SI for details on the SAM compositions. Panel C shows the number of Au NPs that electrostatically bind to an l-polyalanine monolayer in 2 s, for north (red) and south (blue) magnetization directions. The experiments were repeated five times and measured at several different areas to reduce fluctuations.
Given that the ΔCPD of the SAM-coated electrodes is proportional to the dipole moment of the molecules D ∝ LQ, a linear dependence on L implies that the amount of charge displacement in the SAM layer is independent of molecular length, whereas a supralinear dependence on L implies that the amount of charge displacement in the SAM increases with the molecular length. In DNA, the molecule’s polarizability has been shown to scale linearly with the molecule’s length,36 and this could account for the quadratic growth in the dipole moment with the length, D ∝ L2. The data suggest that the polarizability in the oligopeptides does not change significantly over the short lengths studied (1.5 to 3 nm), and therefore, the dipole moment appears to change linearly with the molecular length. While the ΔCPD signal has a different sign for DNA and oligopeptides, these data are consistent with previous reports; conductive AFM measurements showed a higher tunneling barrier for DNA under north magnetization than south magnetization7 and the opposite for oligopeptides.8
Large changes in the surface potential can affect surface chemical processes. Figure 4C illustrates this fact by demonstrating how the change in surface charge of an l-polyalanine SAM on a magnetized Ni/Au substrate can be used to control the electrostatic adsorption of achiral gold NPs. The substrate was immersed for 2 s, and the number of particles was normalized to a 1 cm2 substrate area. The gold NPs were counted using SEM images. The experiment was repeated five times. By simply changing the magnetization direction applied to the substrate, a 2-fold change in the adsorption rate was found.
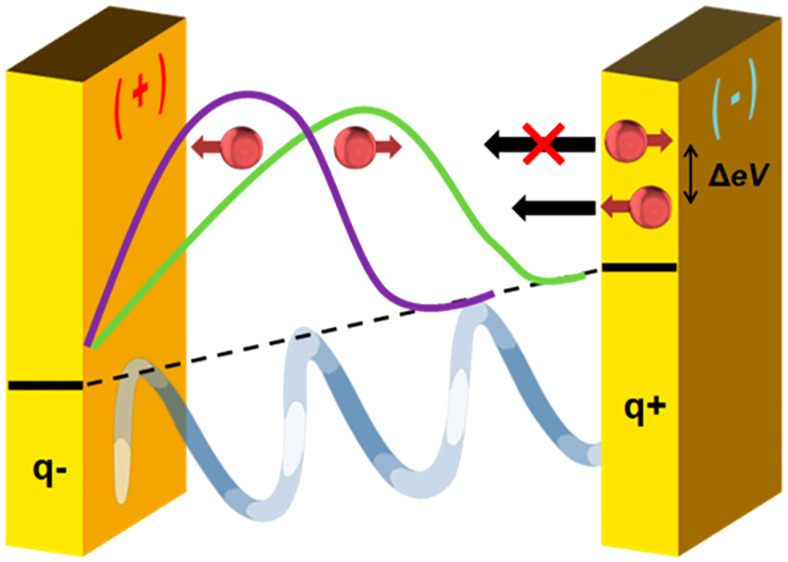
Here we sketch a model that rationalizes the observations and is consistent with the many other CISS effect observations for electron transmission through chiral molecules. First we describe the time-dependence of the response, which results from the oscillating electric polarization in the molecule, and second, we discuss the large magnitude of the effect. In the Kelvin-probe experiment, a time-dependent response of the chiral SAM/ferromagnet sample is measured. Namely, charge flows between the ferromagnetic substrate and the SAM in response to the oscillating electric field that is applied by the Kelvin probe. As is known, the Kelvin-probe measurement can be modeled by an AC electrical circuit comprising a capacitance for the probe and the interface. The situation studied here (metal with an insulating monolayer film) requires an effective capacitance comprising the capacitance of the SAM/Kelvin-probe junction, Cmol-p, in series with a resistance and capacitance for the ferromagnet/chiral-SAM interface, R and Cfm-mol. The resistance R determines the rate at which charge is transferred between the chiral molecules and the substrate.
While the effect of molecular films on a metal substrate’s work function has been studied widely, much less is known about the difference in the behavior that arises for chiral molecules on ferromagnetic surfaces. An electric field that is acting on a molecule or molecular monolayer at an electrode modifies the molecular electronic states. The electric fields at an electrode surface can be as high as 108–109 V/m,37 and this field induces a dipole moment in the molecule, i.e., an electron charge displacement. For chiral molecules, this charge displacement in the molecule is accompanied by a spin polarization.38 Based on spin–orbit coupling strengths of about 5 meV in chiral organic molecules, one expects a spin polarization, ΔP, of a few percent, or less.39,40
Upon application of an oscillating electric field onto the magnetic substrate coated with the chiral monolayer, charge reorganization in the molecule takes place, but also, charge flow between the substrate and the molecules occurs. This charge flow implies charge exchange (electron cloud overlap) between the molecule and the metal. Electron density permeating from the metal into the positive electric pole of the molecule, polarized by the oscillating field, can have either the same spin as that of the electrons which remain at the positive pole or it can have the opposite spin. To estimate the difference in energy ΔE between the two possibilities, we take the product of the spin polarization ΔP, which is a metric for the difference in the two spin densities, and the typical value of the singlet–triplet energy splitting, which is a metric for the electronic orbital energy difference between the two spin types. In a Heitler–London valence bond picture,41 this approximation results in
where Q is the Coulomb integral, S is the electron overlap integral, and Jexc is the exchange integral. The values found for these different parameters are sensitive to the level of theory used for calculation. Thus, we approximate this term in the equation by the triplet–singlet energy difference of an excited electronic configuration. Given that the typical energy splitting between singlet and triplet states in hydrocarbons is of the order of 1 eV,42 a spin polarization of 3% yields an energy splitting ΔE = 30 meV. This energy splitting at 300 K amounts to a spin selectivity in the spin injection of about 1:4, namely a spin polarization of approximately 60%. Clearly, if the singlet–triplet energy difference is larger or the initial spin polarization on the formation of the dipole is higher, then a higher spin polarization can be observed in the CISS effect. Consequently, a significant energy bias exists for injecting one spin orientation over the other, and the magnitudes are sufficient to account for the observed contact potential differences. This mechanism is reminiscent of a “spin blockade”43 that restricts the spin injection from the substrate to the molecule despite an apparent small spin–orbit coupling in the chiral molecule. Thus, this mechanism could give rise to the large spin selectivity reported in CISS processes and account for the large CPD values reported here.
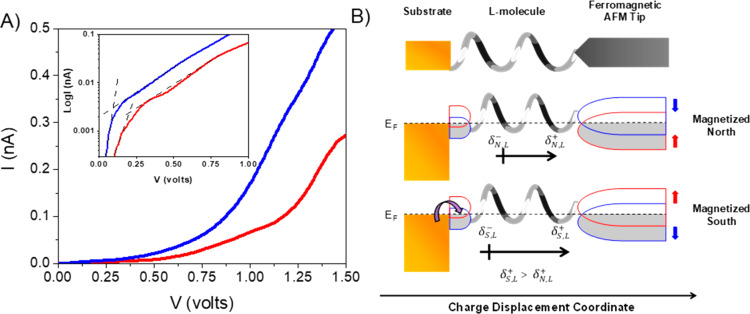
The mechanism presented here indicates that the transport is nonlinear,44 and it is consistent with the current versus voltage (I–V) curves that are observed in magnetic conducting probe measurements of oligopeptides. For convenience, I–V curves for the AL7 molecule, which are taken from ref (8), are reproduced in Figure 5A under different magnetization directions. The data show that nonlinear conduction occurs after an electric field is applied to the molecules. The current under the south (blue) magnetization direction begins to occur when the applied voltage is approximately 93 mV, and the current for the north (red) direction appears at a higher voltage, ∼200 mV. The inset in Figure5A shows a plot of log(I) versus voltage for the same data, which illustrates more clearly the difference in the voltage (difference in on-state and off-state voltage slopes) for the two curves. According to the suggested model vide supra, the difference of 100 mV between the voltage of the two spin currents is associated with a “spin blockade”. Note, in this experiment, the tip is ferromagnetic, as opposed to the experiments in Figures 1–4 where the substrate is ferromagnetic; hence, the geometry of the experiment is inverted, and the effect on the magnetization is reversed; panel B illustrates this difference. The sub-band splittings of the AFM tip, blue and red semicircles, are controlled by the applied magnetization, whereas the spin injection from the substrate into the chiral molecule, blue and red semicircles, is determined by the helicity of the molecule.
Figure 5.
Panel A shows I–V curves from magnetic conductive probe atomic force microscopy measurements in the presence of a magnetic field pointing south (blue) and magnet pointing north (red) for an AL7 oligopeptide. The inset is a log plot, in which the dashed lines illustrate the changeover from off-state to on-state voltages. Panel B shows a corresponding cartoon depicting the interaction of the ferromagnetic substrate with the chiral SAM to create a “spin blockade”. The red and blue semicircles indicate a splitting of the spin sub-bands.
Based on the presented model, the difference in the resistance of the chiral molecules can be rationalized by the spin-dependence of the electron penetration into the molecular layer. Figure 3B provides further evidence corroborating the suggested model. Here, the contact potential difference of the same sample is measured but in regions with two different thickness ranges. When Co is 1.8 nm thick, the easy axis is pointing out-of-plane, and the potential shift is much larger than that found for a 2.5 nm thick cobalt region, in which the easy axis is in-plane. For the 1.8 nm thick Co thick, both spin–orbit coupling and spin exchange interactions should be considered, whereas for the 2.5 nm thick Co, the spin–orbit coupling term may dominate.
It was shown that coating a ferromagnetic film electrode with a self-assembled monolayer of chiral molecules leads to contact potential differences (measured via the Kelvin-probe method) that depend on the magnetization direction of the ferromagnetic film with respect to the SAM’s chirality. The data show that the asymmetry in the potential difference can be as large as 100 mV and is controlled by the magnetization direction of the ferromagnetic film electrode. The use of Kelvin-probe measurements for extracting spin dynamics inside chiral organic monolayer films demonstrates a new way to probe spin penetration in ultrathin films without the need for external contacts. The phenomena were interpreted using the CISS effect and AC transient charge redistribution, and the magnitude of the effect is explained by the nonlinearity of the spin exchange interactions. These observations rationalize how large spin polarizations can be generated in the experiments despite the apparent small spin–orbit coupling in the chiral hydrocarbons and should thus motivate more detailed calculations on the interaction of chiral molecules with ferromagnetic substrates in the future.
Acknowledgments
S.G. thanks Nathaniel Miller for helpful discussions and advice. S.G. acknowledges the support of a Mellon Fellowship during part of this work. D.H.W. and R.N. acknowledge the support of the Department of Energy (Grant No. ER46430). D.H.W., Y.P., and R.N. acknowledge the support from the John Templeton Foundation. The authors thank Professor Karen Michaeli for helpful discussions.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.9b03487.
Experimental details, coercivity measurements, DNA and peptide sequences, electrical model for the measurement setup (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Varignon J.; Vila L.; Barthélémy A.; Bibes M. A new spin for oxide interfaces. Nat. Phys. 2018, 14, 322–325. 10.1038/s41567-018-0112-1. [DOI] [Google Scholar]
- Cinchetti M.; Dediu V. A.; Hueso L. E. Activating the molecular spinterface. Nat. Mater. 2017, 16, 507–515. 10.1038/nmat4902. [DOI] [PubMed] [Google Scholar]
- Naaman R.; Paltiel Y.; Waldeck D. H. Chiral molecules and the electron’s spin. Nat. Rev. Chem. 2019, 3, 250–260. 10.1038/s41570-019-0087-1. [DOI] [Google Scholar]
- Göhler B.; Hamelbeck V.; Markus T. Z.; Kettner M.; Hanne G. F.; Vager Z.; Naaman R.; Zacharias H. Spin Selectivity in Electron Transmission Through Self-Assembled Monolayers of dsDNA. Science 2011, 331, 894–897. 10.1126/science.1199339. [DOI] [PubMed] [Google Scholar]
- Kettner M.; Göhler B.; Zacharias H.; Mishra D.; Kiran V.; Naaman R.; Fontanesi C.; Waldeck D. H.; Sęk S.; Pawłowski J.; et al. Spin Filtering in Electron Transport Through Chiral Oligopeptides. J. Phys. Chem. C 2015, 119, 14542–14547. 10.1021/jp509974z. [DOI] [Google Scholar]
- Kettner M.; Maslyuk V. V.; Nürenberg D.; Seibel J.; Gutierrez R.; Cuniberti G.; Ernst K.-H.; Zacharias H. Chirality-Dependent Electron Spin Filtering by Molecular Monolayers of Helicenes. J. Phys. Chem. Lett. 2018, 9, 2025–2030. 10.1021/acs.jpclett.8b00208. [DOI] [PubMed] [Google Scholar]
- Xie Z.; Markus T. Z.; Cohen S. R.; Vager Z.; Gutierrez R.; Naaman R. Spin specific electron conduction through DNA oligomers. Nano Lett. 2011, 11, 4652–4655. 10.1021/nl2021637. [DOI] [PubMed] [Google Scholar]
- Kiran V.; Cohen S. R.; Naaman R. Structure Dependent Spin Selectivity in Electron Transport through Oligopeptides. J. Chem. Phys. 2017, 146, 092302 10.1063/1.4966237. [DOI] [Google Scholar]
- Aragonès A. C.; Medina E.; Ferrer-Huerta M.; Gimeno N.; Teixidó M.; Palma J. L.; Tao N.; Ugalde J. M.; Giralt E.; Díez-Pérez I.; et al. Measuring the Spin-Polarization Power of a Single Chiral Molecule. Small 2017, 13, 1602519. 10.1002/smll.201602519. [DOI] [PubMed] [Google Scholar]
- Ben Dor O.; Yochelis S.; Radko A.; Vankayala K.; Capua E.; Capua A.; Yang S.-H.; Baczewski L. T.; Parkin S. S. P.; Naaman R.; et al. Magnetization switching in ferromagnets by adsorbed chiral molecules without current or external magnetic field. Nat. Commun. 2017, 8, 14567. 10.1038/ncomms14567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smolinsky E. Z. B.; Neubauer A.; Kumar A.; Yochelis S.; Capua E.; Carmieli R.; Paltiel Y.; Naaman R.; Michaeli K. Electric field controlled magnetization in GaAs/AlGaAs heterostructures-chiral organic molecules hybrids. J. Phys. Chem. Lett. 2019, 10, 1139–1145. 10.1021/acs.jpclett.9b00092. [DOI] [PubMed] [Google Scholar]
- Mondal P. C.; Fontanesi C.; Waldeck D. H.; Naaman R. Spin-dependent Transport through Chiral Molecules Studied by Spin-dependent Electrochemistry. Acc. Chem. Res. 2016, 49, 2560–2568. 10.1021/acs.accounts.6b00446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mondal P. C.; Fontanesi C.; Waldeck D. H.; Naaman R. Magnetic Field and Chirality Effects on Electrochemical Charge Transfer Rates: Spin Dependent Electrochemistry. ACS Nano 2015, 9, 3377–3384. 10.1021/acsnano.5b00832. [DOI] [PubMed] [Google Scholar]
- Ben Dor O.; Morali N.; Yochelis S.; Baczewski L. T.; Paltiel Y. Local Light-Induced Magnetization Using Nanodots and Chiral Molecules. Nano Lett. 2014, 14, 6042. 10.1021/nl502391t. [DOI] [PubMed] [Google Scholar]
- Bloom B. P.; Kiran V.; Varade V.; Naaman R.; Waldeck D. H. Spin Selective Charge Transport through Cysteine Capped CdSe Quantum Dots. Nano Lett. 2016, 16, 4583–4589. 10.1021/acs.nanolett.6b01880. [DOI] [PubMed] [Google Scholar]
- Bloom B. P.; Graff B. M.; Ghosh S.; Beratan D. N.; Waldeck D. H. Chirality Control of Electron Transfer in Quantum Dot Assemblies. J. Am. Chem. Soc. 2017, 139, 9038–9043. 10.1021/jacs.7b04639. [DOI] [PubMed] [Google Scholar]
- Bloom B. P.; Liu R.; Zhang P.; Ghosh S.; Naaman R.; Beratan D.; Waldeck D. H. Directing Charge Transfer in Quantum Dot Assemblies. Acc. Chem. Res. 2018, 51, 2565–2573. 10.1021/acs.accounts.8b00355. [DOI] [PubMed] [Google Scholar]
- Carmeli I.; Skakalova V.; Naaman R.; Vager Z. Magnetization of Chiral Monolayers of Polypeptide-A Possible Source of Magnetism in Some Biological Membranes. Angew. Chem., Int. Ed. 2002, 41, 761–764. . [DOI] [PubMed] [Google Scholar]
- Zwang T. J.; Hürlimann S.; Hill M. G.; Barton J. K. Helix-Dependent Spin Filtering through the DNA Duplex. J. Am. Chem. Soc. 2016, 138, 15551–15554. 10.1021/jacs.6b10538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckshtain-Levi M.; Capua E.; Refaely-Abramson S.; Sarkar S.; Gavrilov Y.; Mathew S. P.; Paltiel Y.; Levy Y.; Kronik L.; Naaman R. Cold denaturation induces inversion of dipole and spin transfer in chiral peptide monolayers. Nat. Commun. 2016, 7, 10744. 10.1038/ncomms10744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suda M.; Thathong Y.; Promarak V.; Kojima H.; Nakamura M.; Shiraogawa T.; Ehara M.; Yamamoto H. M. Light-driven molecular switch for reconfigurable spin filters. Nat. Commun. 2019, 10, 2455. 10.1038/s41467-019-10423-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dor O. B.; Yochelis S.; Ohldag H.; Paltiel Y. Optical Chiral Induced Spin Selectivity XMCD Study. Chimia 2018, 72, 379–383. 10.2533/chimia.2018.379. [DOI] [PubMed] [Google Scholar]
- Santos J. I.; Rivilla I.; Cossío F. P.; Matxain J. M.; Grzelczak M.; Mazinani S. K. S.; Ugalde J. M.; Mujica V. Chirality-Induced Electron Spin Polarization and Enantiospecific Response in Solid-State Cross-Polarization Nuclear Magnetic Resonance. ACS Nano 2018, 12, 11426–11433. 10.1021/acsnano.8b06467. [DOI] [PubMed] [Google Scholar]
- He X.; Zhou Y.; Wen X.; Shpilman A. A.; Ren Q. Effect of Spin Polarization on the Exclusion Zone of Water. J. Phys. Chem. B 2018, 122, 8493–8502. 10.1021/acs.jpcb.8b04118. [DOI] [PubMed] [Google Scholar]
- Abendroth J. M.; Nakatsuka N.; Ye M.; Kim D.; Fullerton E. E.; Andrews A. M.; Weiss P. S. Analyzing Spin Selectivity in DNA-Mediated Charge Transfer via Fluorescence Microscopy. ACS Nano 2017, 11, 7516–7526. 10.1021/acsnano.7b04165. [DOI] [PubMed] [Google Scholar]
- Ravi S.; Sowmiya P.; Karthikeyan A. Magnetoresistance and Spin-filtering Efficiency of DNA-Sandwiched Ferromagnetic Nanostructures. SPIN 2013, 03, 1350003. 10.1142/S2010324713500033. [DOI] [Google Scholar]
- Banerjee-Ghosh K.; Ben Dor O.; Tassinari F.; Capua E.; Yochelis S.; Capua A.; Yang S.-H.; Parkin S. S. P.; Sarkar S.; Kronik L.; et al. Separation of enantiomers by their enantiospecific interaction with achiral magnetic substrates. Science 2018, 360, 1331–1334. 10.1126/science.aar4265. [DOI] [PubMed] [Google Scholar]
- Tassinari F.; Steidel J.; Paltiel S.; Fontanesi C.; Lahav M.; Paltiel Y.; Naaman R. Enantioseparation by crystallization using magnetic substrates. Chem. Sci. 2019, 10, 5246–5250. 10.1039/C9SC00663J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abendroth J. M.; Cheung K. M.; Stemer D. M.; El Hadri M. S.; Zhao C.; Fullerton E. E.; Weiss P. S. Spin-Dependent Ionization of Chiral Molecular Films. J. Am. Chem. Soc. 2019, 141, 3863–3874. 10.1021/jacs.8b08421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nonnenmacher M.; O’Boyle M. P.; Wickramasinghe H. K. Kelvin probe force microscopy. Appl. Phys. Lett. 1991, 58, 2921–2923. 10.1063/1.105227. [DOI] [Google Scholar]
- Melitz W.; Shen J.; Kummel A. C.; Lee S. Kelvin probe force microscopy and its application. Surf. Sci. Rep. 2011, 66, 1–27. 10.1016/j.surfrep.2010.10.001. [DOI] [Google Scholar]
- Mondal P. C.; Fontanesi C.; Waldeck D. H.; Naaman R. Magnetic Field and Chirality Effects on Electrochemical Charge Transfer Rates: Spin Dependent Electrochemistry. ACS Nano 2015, 9, 3377–3384. 10.1021/acsnano.5b00832. [DOI] [PubMed] [Google Scholar]
- Kisielewski M.; Maziewski A.; Tekielak M.; Wawro A.; Baczewski L. T. New possibilities for tuning ultrathin cobalt film magnetic properties by a noble metal overlayer. Phys. Rev. Lett. 2002, 89, 087203 10.1103/PhysRevLett.89.087203. [DOI] [PubMed] [Google Scholar]
- Koplovitz G.; Leitus G.; Ghosh S.; Bloom B. P.; Yochelis S.; Rotem D.; Vischio F.; Striccoli M.; Fanizza E.; Naaman R.; et al. Single Domain 10 nm Ferromagnetism Imprinted on Superparamagnetic Nanoparticles Using Chiral Molecules. Small 2019, 15, 1804557. 10.1002/smll.201804557. [DOI] [PubMed] [Google Scholar]
- Kisielewski M.; Maziewski A.; Kurant Z.; Tekielak M.; Wawro A.; Baczewski L. T. Magnetic ordering in ultrathin cobalt film covered by an overlayer of noble metals. J. Appl. Phys. 2003, 93, 7628. 10.1063/1.1543914. [DOI] [Google Scholar]
- Ying L.; White S. S.; Bruckbauer A.; Meadows L.; Korchev Y. E.; Klenerman D. Frequency and Voltage Dependence of the Dielectrophoretic Trapping of Short Lengths of DNA and dCTP in a Nanopipette. Biophys. J. 2004, 86, 1018–1027. 10.1016/S0006-3495(04)74177-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zangwill A.Physics at Surfaces; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Kumar A.; Capua E.; Kesharwani M. K.; Martin J. M. L.; Sitbon E.; Waldeck D. H.; Naaman R. Spin Polarization Accompanies Charge Polarization in Chiral Molecules- Implication for Enantio-selectivity and Bio-recognition. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 2474–2478. 10.1073/pnas.1611467114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeganeh S.; Ratner M. A.; Medina E.; Mujica V. Chiral electron transport: Scattering through helical potentials. J. Chem. Phys. 2009, 131, 014707 10.1063/1.3167404. [DOI] [PubMed] [Google Scholar]
- Michaeli K.; Naaman R. Origin of Spin Dependent Tunneling Through Chiral Molecules. J. Phys. Chem. C 2019, 123, 17043–17048. 10.1021/acs.jpcc.9b05020. [DOI] [Google Scholar]
- Shaik S. S.; Phillipe C. H.. A Chemist’s Guide to Valence Bond Theory; Wiley-Interscience, 2007. [Google Scholar]
- See, for example:Köhler A.; Beljonne D. The singlet-triplet exchange energy in conjugated polymers. Adv. Funct. Mater. 2004, 14, 11–18. 10.1002/adfm.200305032. [DOI] [Google Scholar]
- de Bruijckere J.; Gehring P.; Palacios-Corella M.; Clemente-Leon M.; Coronado E.; Paaske J.; Hedegard P.; van der Zant H. S. J. Ground-State Spin Blockade in a Single-Molecule Junction. Phys. Rev. Lett. 2019, 122, 197701. 10.1103/PhysRevLett.122.197701. [DOI] [PubMed] [Google Scholar]
- Matityahu S.; Utsumi Y.; Aharony A.; Entin-Wohlman O.; Balseiro C. A. Spin-dependent transport through a chiral molecule in the presence of spin-orbit interaction and nonunitary effects. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 075407 10.1103/PhysRevB.93.075407. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.