Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jan 28;53(3):844–851. doi: 10.1021/acs.macromol.9b01813

Dynamics of Soft and Hairy Polymer Nanoparticles in a Suspension by NMR Relaxation

Young-Gon Kim 1, Manfred Wagner 1, Héloïse Thérien-Aubin 1,*
PMCID: PMC7307961  PMID: 32587417

Abstract

graphic file with name ma9b01813_0008.jpg

The design of surface-modified functional nanoparticles (NPs) is used to control the properties of the NPs and the NP/environment interactions. The efficient control of the final behavior of the NPs demands a comprehensive understanding of the resulting system. This is particularly challenging for systems with an architecture of the type polymer core–polymer canopy. In such systems, one of the key parameters influencing the behavior of the NPs is the local dynamics of the polymer canopy. However, because the grafting points of the canopy are experiencing their own local dynamics, predicting the final behavior of such systems is difficult. To get a deeper understanding of NPs made of a soft and swollen polymer core and a swollen polymer canopy, we prepared a library of hairy NPs made of a polystyrene (PS) core and a canopy of grafted poly(methyl acrylate) (PMA) chains. The softness of the PS core and the thickness of the PMA canopy were controlled, and the behavior and dynamics of the soft and hairy PS–PMA NPs in suspension were measured by 1H NMR relaxation and dynamic light scattering. It was observed that the rigid PS core slowed down the subsegmental dynamics of the PMA chains, while thick PMA canopies accelerated the relaxation of the PS core. The dynamics of the NPs in suspension was the result of the interplay between the PS core and the PMA canopy.

Introduction

End-tethered polymer chains, or polymer brushes, are used extensively to modify the properties of nanoparticles (NPs) such as stability, solvent compatibility, dispersibility, and assembly. However, there are currently no guidelines to design the ideal canopy of end-tethered polymer chains, especially when grafted onto soft and deformable NPs. Understanding the behavior of the polymer canopy and its effect on the NP would improve the design of future NP-based systems. We designed a comprehensive library of functionalized NPs with a variable degree of core softness and an increasing length of grafted polymer chains and studied the local movement of the core and the canopy using NMR spectroscopy to get an understanding about the interplay between the local dynamics of the core and the canopy.

Controlling the thickness of the grafted polymer layer and the surface coverage is one of the most important parameters to be considered when designing hairy NPs because these parameters determine the conformation of the grafted chains.1−7 As the grafting density increases, polymer chains start to overlap and hence stretch because of steric repulsion. In a densely crowded regime, as described by the Alexander–de Gennes model, polymer chains are highly stretched and only local polymer movement confined within a polymer blob unit can be observed.3 When such a polymer layer is immobilized on a spherical surface, the size of the blobs expands as the distance with the substrate increases.8 Consequently, the influence of the neighboring chains on the stretching and extension of the chains decreases with respect to the distance from the curved substrate or with the degree of polymerization (N) of the grafted chains. This radial dependency results in a transition between brush regimes from stretched chains to coiled polymer chains.8

In order to precisely control both the grafting density and the molecular weight, different surface-initiated controlled radical polymerizations have been used.9 Among these, surface-initiated atom transfer radical polymerization (SI-ATRP) has been employed to graft polymer chains on a wide range of substrates, from metal to polymer, because of its versatility with respect to monomers, solvents, and reaction conditions.

Studies of the relaxation dynamics of grafted chains, both experimentally and by simulation, have demonstrated that the presence of a substrate significantly affects the subsegmental dynamics of the tethered polymer chains and can impact the mechanical properties of the resulting materials.10−13 The presence of the substrate usually creates a confinement effect influencing the relaxation of the tethered polymer chains, and this effect decreases with increase in N.14−16 For example, studies of the relaxation dynamics of a polymer chain grafted on inorganic NPs have shown that the relaxation rate of short tethered chains was increased by orders of magnitude in comparison to the untethered chains because of the conformational changes of the polymer chains, and as the chain length increased, the relaxation rate of the tethered chains converged to the relaxation rate observed for untethered chains of a similar molecular weight.10 Other studies have shown that the relaxation of grafted polymer chains was impeded in comparison to free polymer chains of the same molecular weight because of their immobilization on a substrate.17

Such differences arise from different methods used to analyze the polymer dynamics, which can probe different types of relaxation processes and give access to different physical characteristics. For example, a study, using neutron spin echo (NSE), has shown significantly faster chain dynamics for poly(methyl acrylate) (PMA) grafted to silica particles when the length of the chain was increased above the threshold for the transition from the concentrated brush region, close to the substrate, and the semidiluted brush region.11 However, a recent study using neutron backscattering (BS) of a similar system of PMA chains grafted to silica NPs has shown that there is only a limited effect of N of the grafted chain on the local relaxation of the polymer.18 These studies were not probing the same dynamics; NSE measures the global dynamics over a wide range of correlation time,19 whereas BS was used to probe the subsegmental dynamics.20 Similarly, nuclear magnetic resonance (NMR) spectroscopy can be used to probe local subsegmental relaxation of grafted polymer chains and gives access to faster subsegmental dynamics that involve motions, vibrations, and rotation of side groups.21

NMR spectroscopy is a versatile method to interpret the local dynamics of polymers22 and has been used to study functionalized NPs in suspension.23−25 NMR relaxation is an ideal method to study the behavior of swollen soft NPs functionalized with polymer chains because it allows for the simultaneous and independent characterization of the local behavior of the core particle and the canopy of end-tethered polymer chains. In NMR spectroscopy, the spin–lattice (T1) and spin–spin (T2) relaxation times can be correlated with the local molecular motions in the molecules.26 In particular, unlike other methods used to probe polymer dynamics, such as dielectric spectroscopy, NMR relaxation provides information on the local dynamics of specific chemical groups in the macromolecular structure without the need for labeling.21

Most of the studies devoted to the relaxation of end-tethered polymer chains have focused on the polymer grafted to rigid solid substrates, such as silica or gold NPs, where the tethering points can be considered as fixed. The effect of having softer substrates with faster relaxation dynamics has been largely overlooked so far.27−29 In such systems, in addition to the dynamics of the canopy of end-tethered polymer chains, the dynamics of the core also need to be taken into account. Then, the system becomes more complex, and the interpretation of the results is more challenging in comparison to polymer chains grafted on rigid inorganic cores.

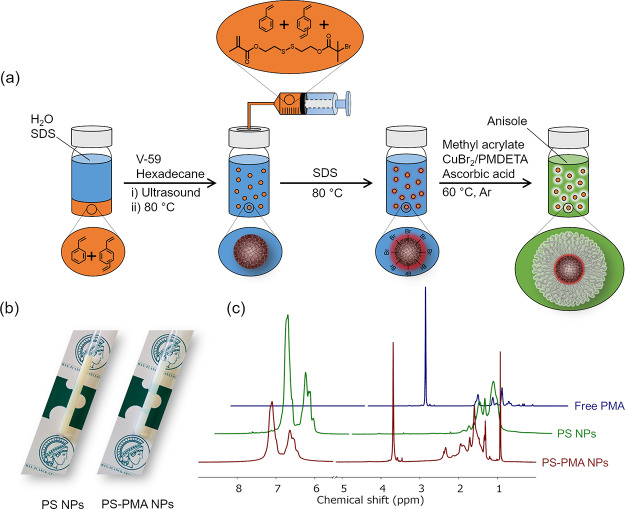
Here, to address the complex dynamics in a system where both the canopy of the end-grafted polymer and the particle core undergo relaxation in a similar frequency range, the study of the local dynamics of hairy NPs with a polymer–polymer core–canopy architecture was studied by NMR spectroscopy. The core–canopy architecture was designed with a polystyrene (PS) core and a canopy of PMA (Figure 1). The cross-linking density of the core, and thus the softness of the core of the particle, was tuned by the addition of different amounts of divinylbenzene (DVB) during the synthesis of the PS nanonetwork. Then, SI-ATRP was used to grow the PMA chains from the initiators immobilized on the PS surface. The relaxation dynamics of the resulting PS–PMA hairy NPs in suspension was investigated by NMR relaxation at different temperatures and magnetic fields. The length of the PMA chains and the cross-linking density of PS cores were controlled to understand the relationship between the rigidity of core and the degree of polymerization of the polymer canopy and the local dynamics in NPs.

Figure 1.

Figure 1

Open in a new tab

(a) Synthesis of PS NPs and PS–PMA NPs by a tandem approach based on miniemulsion polymerization and SI-ATRP. (b) Photographs of stable suspensions of PS NPs and PS–PMA NPs in DCM. (c) NMR spectra of free PMA chains, PS NPs, and PS–PMA NPs (CD2Cl2, 700.02 MHz, 298 K).

Experimental Section

Synthesis of PS–PMA Core–Canopy NPs

PS–PMA core–canopy NPs were prepared by two-step synthesis (Figure 1). The core made of cross-linked PS NPs (PS–DVB NPs) functionalized with the ATRP initiator was prepared by miniemulsion polymerization followed by starve-fed emulsion polymerization.30 The resulting NPs functionalized with the ATRP initiator were washed by precipitation using methanol followed by redispersion in tetrahydrofuran (THF) and precipitation in hexane followed by redispersion in THF and then dried. ATRP was used to grow the PMA canopy from the initiating sites at the surface of the PS core.31,32 After different polymerization times, the polymerization was quenched, and the PMA-tethered PS NPs were precipitated in hexane and washed by centrifugation and then redispersed in dichloromethane (DCM). The details of the preparation of PS–PMA core–canopy NPs are available in the Supporting Information.

Characterization

The radius of the NPs was determined by dynamic light scattering (DLS) measured with a Malvern Instruments Zetasizer Nano S90 at a fixed angle of 90°. The NPs were dispersed either in DCM or in an aqueous solution of cetyltrimethylammonium chloride. All the measurements were carried out at 25 °C. The grafting density was measured by inductively coupled plasma atomic emission spectrometry (ICP-AES) with an ACTIVA M spectrometer (Horiba Jobin Yvon) and processed by the software ACTIVAnalyst 5.4. NMR relaxation experiments were performed on a series of NMR AVANCE spectrometers (Bruker) working at nominal frequencies of 500.13, 700.02, and 850.27 MHz. The details of NMR experiments are described in the Supporting Information.

Results and Discussion

The synthesis of a library of PS NPs functionalized with PMA chains was carried out in a multistep manner. First, PS–DVB NPs were prepared by miniemulsion polymerization using different amounts of DVB (from 0.5 to 10 mol % of cross-linkers). Afterward, a layer of cross-linked PS containing 5 mol % of the ATRP initiator was polymerized at the surface of the PS–DVB NPs in a starved–fed regime. The resulting cross-linked PS NPs swelled in a good solvent, such as DCM, and their swelling varied between 370 and 1000% depending on the cross-linking density (Table S1) and provided NPs with different softness used as the “core” to graft a “canopy” of PMA. Then, using a “grafting from” approach, PMA chains were polymerized from the ATRP initiators immobilized at the surface of the PS NPs. The molecular weight of the resulting end-tethered polymer chains varied from 3.5 to 26.2 kg mol–1 (or 41 to 305 units). The density of the ATRP initiators on the surface of the PS–DVB NPs was ca. 0.8 chains nm–2 in water and after redispersion and swelling in DCM ca. 0.2 chains nm–2 (Table S1).

Dispersing the hairy PS–PMA NPs in a good solvent, such as DCM, resulted in a stable suspension because of the combined swelling of the core and the polymer canopy. The change of the solvated radii (Rh) of PS–PMA NPs with different degrees of cross-linking was studied in DCM, a good solvent for both PS and PMA (Figure 2). The results show that the size distribution of the unfunctionalized NPs was systematically larger than for the NPs functionalized with short PMA chains, although the unfunctionalized PS NPs were used as the substrate to grow the PMA chains for the preparation of the PS–PMA samples. DCM is a better solvent for PMA than for PS, and the addition of PMA likely increased the colloidal stability of the NPs by preventing particle agglomeration more efficiently. Nevertheless, all the PS–PMA NPs cross-linked with different amounts of DVB showed a similar overall trend; as N of the grafted PMA chains increased, an increase in the size of the NP was observed and the relationship between the thickness of the grafted polymer layer (H) and N of the PMA chains scaled as H ≈ N0.75∼0.72 (Figure S3). This scaling relationship was similar to what has been observed for chains grafted on spherical NPs adopting a stretched brush conformation (H ≈ N0.83 for poly(methyl methacrylate) in acetone and H ≈ N0.7 for PS in benzene).1,7,33,34 These stretching factors suggest that in the PS–PMA NPs, the end-tethered PMA chains were in a stretched brush regime.

Figure 2.

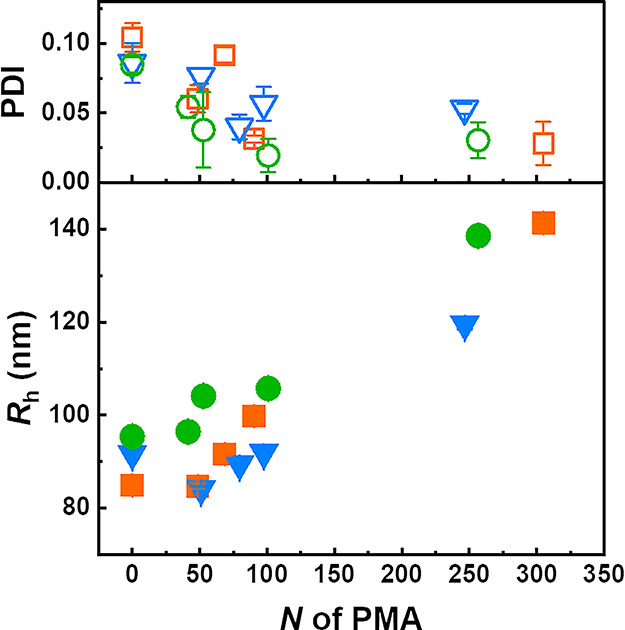
Figure 2

Open in a new tab

Size (Rh) and size distribution (PDI) of PS–PMA NPs functionalized with PMA chains with a degree polymerization (N) ranging from 0 to 305 units, measured by DLS in DCM. NPs with cross-linked PS cores prepared with 0.5 mol % of DVB (green circle), 3 mol % of DVB (blue triangle), and 10 mol % of DVB (orange square).

NMR spectroscopy was used to individually study the average relaxation of the PS and PMA in different PS–PMA NPs. All the relaxation curves could be fitted to a monoexponential decay (Figure S4), indicating that the relaxation process of every type of proton could be described by one single relaxation mechanism or by a distribution of T1 averaged by spin diffusion. T1 is the measure of the rate of energy transfer from an excited nucleus (the spin) to other molecules or nucleus in its immediate environment (the lattice) and is influenced by the local dynamics of the group bearing the spin under observation and the presence of other spins in the immediate environment as described by the Bloembergen–Purcell–Pound (BPP) model (eqs S2 and S3).35 The influence of swelling and cross-linking density on the relaxation of the NP core was studied by measuring the T1 of naked PS NPs (Figure S5). The longest T1 observed was 2.8 s for highly cross-linked PS NPs and decreased gradually with the decrease in the cross-linker concentration. The variation of T1 with the correlation time of the local relaxation process describes a parabola with a frequency-dependent minimum, and for relatively slow local subsegmental motions, like those observed in the systems under study, one would expect T1 to decrease as the subsegmental dynamics becomes faster.35 The increase in T1 observed with the increasing cross-linking density was in agreement with the expected trend for macromolecules and gels,36 where, as the network becomes more cross-linked and rigid, the local subsegmental dynamics slows down leading to an increase in T1.

Figure 3 shows that for any length of the PMA chains, the T1 of the PS aromatic protons in the samples of PS–PMA–DVB10 was systematically longer than the T1 of PS in PS–PMA with a lower degree of cross-linking in the PS core. This result was consistent with the decrease of T1 observed for the naked PS NPs when the cross-linking density was decreased (Figure S5). Additionally, all NPs prepared using 3 and 10 mol % of cross-linker showed a decrease in T1 when increasing N of the PMA chains. This result suggests that the grafting of PMA chains on the cross-linked PS core speeded up the local dynamics of the PS and that longer PMA chains facilitate more efficiently the relaxation of the PS network. The effect of the end-tethered chains was the most prominent with the relatively rigid core and less effective in NPs with a softer core because of the initially faster subsegmental dynamics of the PS in the sparsely cross-linked core associated with the larger swelling of the softer NP core.

Figure 3.

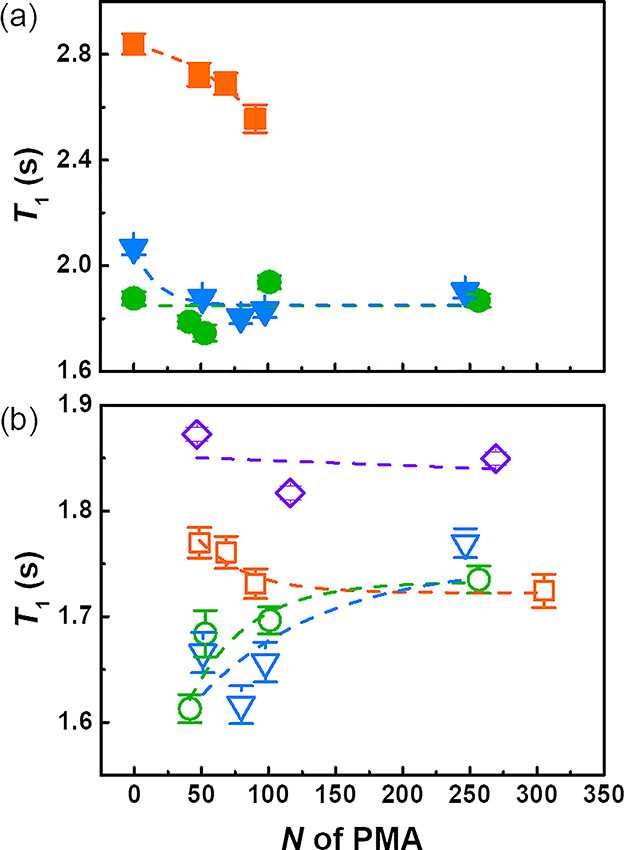
Figure 3

Open in a new tab

1H spin–lattice relaxation of the (a) aromatic ring of PS and (b) methoxy group of PMA in PS–PMA NPs with different degrees of polymerization of the PMA chains (N) grafted on PS cores with different cross-linking densities, measured at a Larmor frequency of 850.27 MHz at 298 K. NPs with cross-linked PS cores prepared with 0.5 mol % of DVB (green circle), 3 mol % of DVB (blue triangle), 10 mol % of DVB (orange square), and untethered PMA chains (violet diamond).

Figure 3b shows the relaxation of the protons in the methoxy group of PMA for free PMA chains and PMA chains tethered to a PS surface in PS–PMA NPs. In the range of N studied, the T1 of the free PMA chains did not vary significantly and the T1 values of the free chains were consistently longer than the T1 values of the grafted chains. This decrease in T1 upon grafting could be the consequence of an increase in the local subsegmental chain dynamics of the tethered PMA triggered by changes to the polymer chain conformation caused by grafting, in agreement with other studies,18 or to an increase in the efficiency of the spin–lattice interaction. The T1 of the PMA chains grafted to the more rigid PS cores, cross-linked with 10 mol % of DVB, remained constant over the range of N analyzed. However, for chains grafted to the softer PS cores (PS–DVB0.5 and PS–DVB3), an increase in T1 was observed when N increased. The T1 observed for three different systems all converged to a similar value, independent of the cross-linking density of the PS cores when long PMA chains were immobilized to the surface of the PS NPs. However, when short PMA chains were grafted to the PS NPs, the decrease in T1 observed between the free PMA chains and the end-tethered chains was more pronounced for the chains grafted to the soft and deformable PS cores in comparison to chains grafted to PS–DVB10. The T1 values measured by NMR are the average values over every methoxy group in the PMA chains, and the results suggest that the PMA units close to the surface of the PS core were experiencing a larger variation in T1 than the PMA units further removed from the grafting point. The T1 values measured could be the average of the relaxation time of PMA units located close to the PS surface and others further removed from the substrate. However, the difference observed between the T1 of the PMA chains with similar N grafted to PS cores with different cross-linking degrees decreased as N increased. Thus, the results suggested that the substrate effect only had a short-range influence. The substrate effect on the T1 values measured did not disappear for long PMA chains but was masked because of the increased number of methoxy groups not experiencing the effect of the substrate.

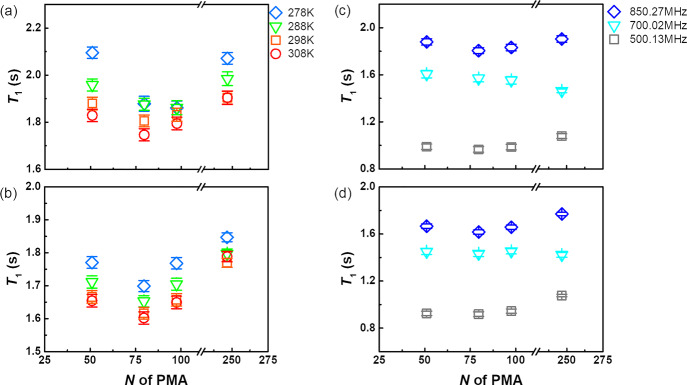
To better understand the local chain dynamics in both the core and the canopy of the PS–PMA NPs, the correlation between the T1 of PS and PS–PMA NPs was measured at different temperatures and Larmor frequencies. An increase in temperature should result in faster local subsegmental dynamics, and thus, shorter T1. While most of the NPs analyzed displayed the expected decrease in T1 with increasing temperature (Figure 4), it was not the case for the PS core of highly cross-linked NPs (Figures S6 and S7). Both the unfunctionalized PS NPs and the PS–PMA NPs cross-linked with 10 mol % of DVB showed an increase in T1 with increasing temperature, suggesting the existence of a slower relaxation mechanism at high temperatures in these samples. This result could be attributed to changes in the swelling of the PS core. In the same temperature range, the size of the densely cross-linked PS NPs in DCM decreased with increasing temperature, while the size of sparsely cross-linked PS NPs increased (Figure S8). Similarly, deswelling of highly cross-linked PS gels in toluene has been observed when increasing temperatures.37 Thus, counterintuitively, in highly cross-linked NPs, although the local dynamics of the solvated free PS chains should be faster with increasing temperature, an overall increase in T1 was observed and was related to the deswelling of the highly cross-linked PS NPs resulting in a more rigid polymer network.

Figure 4.

Figure 4

Open in a new tab

Temperature and magnetic field strength dependence of 1H spin–lattice relaxation time of PS–PMA hairy NPs cross-linked with 3 mol % of DVB. (a,b) Influence of the temperature on the relaxation of the aromatic ring of the PS core (a) and of the methoxy group of PMA chains (b) at 278, 288, 298, and 308 K measured with a Larmor frequency of 850.27 MHz. (c,d) Influence of the magnetic field on the relaxation of the aromatic ring of the PS core (c) and of the methoxy groups of PMA chains (d) measured at 298 K with Larmor frequencies of 500.13, 700.02, and 850.27 MHz.

When using NMR relaxometry, molecular motions that are occurring at a rate similar to the resonance frequency of the nucleus under investigation are more effective in influencing the efficiency of the spin–lattice relaxation. In addition to the temperature and the resonance frequency of the nucleus, the observed T1 is also a function of the distance between two interacting spins. The BPP model take those last two factors into account in describing the subsegmental motions and can be used to relate T1 to the local chain dynamics in the PS–PMA NPs (eqs S2 and S3)35 and to evaluate the correlation time (τc) associated with the local subsegmental motions in the PS–PMA NPs.

For all NPs, an increase of T1 was observed when the magnetic field was increased, indicative of a relatively slow local motion (Figure 4). When using different NMR magnets to vary the magnetic field, the relaxation time will change. This effect is attributed to the fact that a minimum T1 is observed when the rotational correlation time of the relaxation under study is equal to the inverse of the Larmor frequency of the nucleus observed.35 This variation in T1 at different magnetic fields was used to calculate the correlation time (τc) of the segmental motions of PS–PMA NPs (Figure 5) with the BPP model (eq S2). For the naked PS NPs, τc increased with an increase in the degree of cross-linking in agreement with the reduction of the subsegmental dynamics of the PS network as the cross-linking increased. The τc of PS in PS–PMA NPs decreased with increasing N of the PMA because the PMA chains were promoting the local relaxation of the PS core. The τc of PMA chains also showed a variation with the degree of cross-linking of the PS core and N of the PMA chains. The τc of the methoxy group of the free PMA chains with an N of 36 units was 135 ps in DCM. The τc of all the grafted PMA was either equal or longer than that of the free chains. As the cross-linking of the PS core increased, the τc,PMA increased indicative of a reduction in the subsegmental dynamics of the grafted PMA chains. Furthermore, as N of the PMA chains increased, the average τc,PMA decreased because of the faster subsegmental dynamics of the PMA units located farther from the substrate, and as N increased, the effect of the substrate decreased, and consequently, τc,PMA for the grafted PMA chains converged to the τc,PMA measured for free PMA chains.

Figure 5.

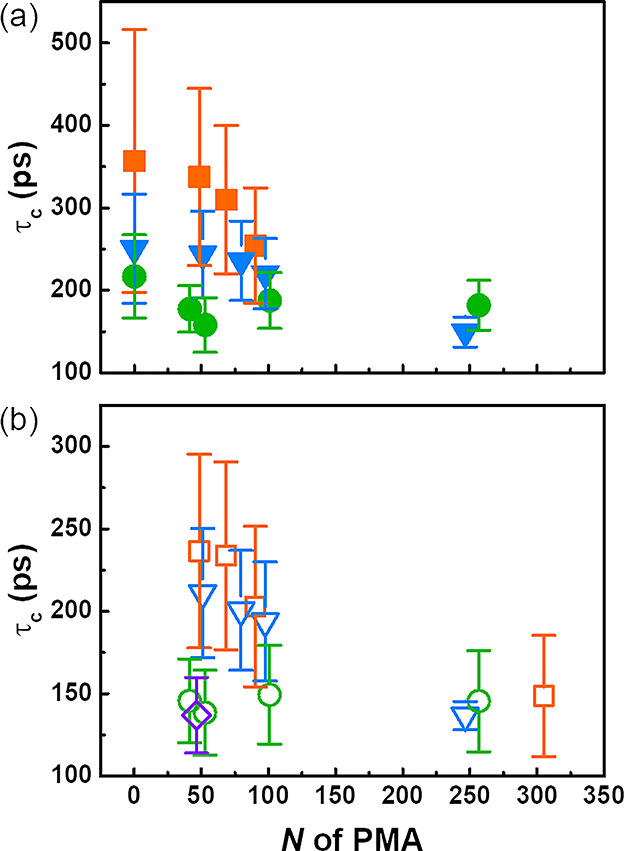
Figure 5

Open in a new tab

Correlation time of the 1H spin–lattice relaxation in the (a) PS core and the (b) PMA chains in PS–PMA hairy NPs at 298 K. NPs with cross-linked PS cores prepared with 0.5 mol % of DVB (green circle), 3 mol % of DVB (blue triangle), 10 mol % of DVB (orange square), and untethered PMA chains (violet diamond).

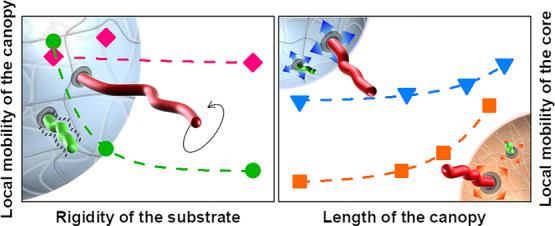
The τc for both PS and PMA was faster with lower cross-linking and a longer PMA canopy, suggesting that covalently tethering PMA chains to the PS core accelerated the subsegmental dynamics of the PS core and that this effect increased with the increasing degree of polymerization of the PMA chains. Similarly, the presence of the substrate slowed down the subsegmental dynamics of the tethered chains, and this effect was more pronounced for more rigid substrates and decreased for longer chains. Figure 6 summarizes the interrelation between the composition of the core and the local dynamics of the canopy and between the composition of the canopy and the local dynamics of the core. On the one hand, the presence of PMA chains softened the PS core and facilitated the local relaxation. This effect increased as N increased, and was more pronounced when the rigidity of the substrate increased. On the other hand, grafting the PMA chains to the PS substrate impeded the local relaxation of the PMA in comparison to free PMA chains in solution; this effect was stronger when the PMA chains were grafted to a more rigid PS core, and more visible for short chains wich can be relatively more strongly influenced by the substrate effect than long chains.

Figure 6.

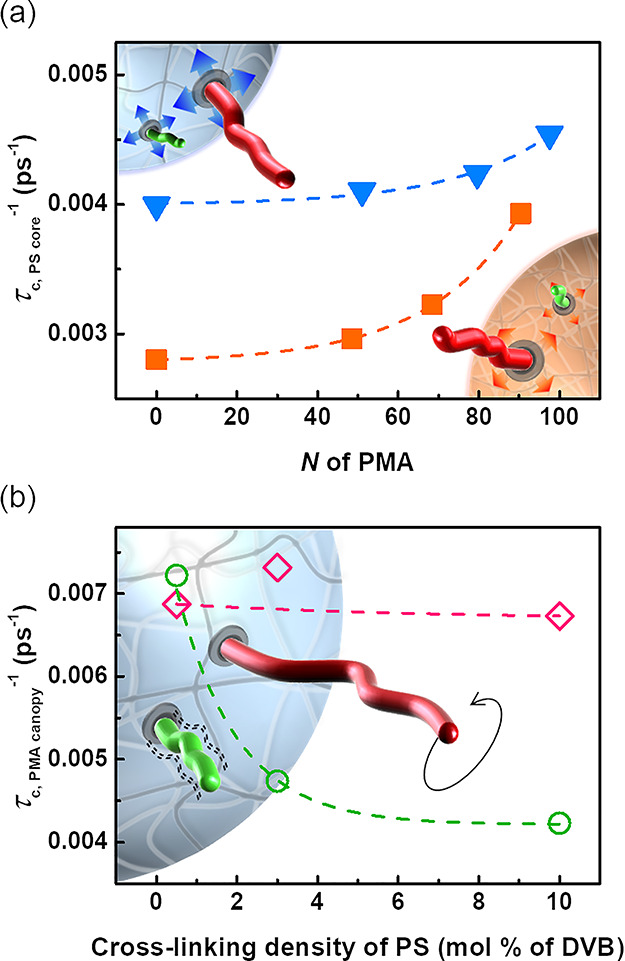
Figure 6

Open in a new tab

Effect of the interplay between the PS core and the PMA canopy on the local dynamics of PS–PMA NPs. (a) Effect of the length of the PMA canopy on the local dynamics of the PS core measured for the PS core cross-linked with 3 mol % of DVB (blue triangle) and 10 mol % of DVB (orange square). (b) Effect of the rigidity of the PS core on the local dynamics of the PMA canopy measured for PMA chains of N ca. 50 units (green circle) and N ca. 250 units (pink diamond).

To fully understand the relaxation mechanism in the PS–PMA NPs, the temperature influence on τc of the core and the canopy of PS–PMA NPs was measured between 278 and 308 K (Figure 7). An increase in temperature is associated with a faster local subsegmental chain dynamics resulting in a decrease of τc. The dynamics of the free PMA chains and PMA chains grafted to sparsely cross-linked PS cores followed the expected trend with the increase in temperature. However, τc,PS of highly cross-linked PS NPs increased at higher temperatures. When PMA chains were grafted to the NPs, the τc,PS of the highly cross-linked core in PS–PMA NPs showed an even more severe increase. In contrast, sparsely cross-linked PS NPs and the PS core in PS–PMA NPs only exhibited a slight increase in τc,PS as the temperature increased. This effect of temperature on the τc,PS observed for different cross-linking densities was in accordance with the negative thermal expansion observed for highly cross-linked PS NPs swollen in DCM (Figure S8); the deswelling of NPs at high temperatures led to a slower local relaxation dynamics. The subsegmental dynamics of PMA chains grafted on the highly cross-linked PS core followed a similar trend and τc,PMA increased at higher temperatures. Thus, the local dynamics of the PS core directly affected the local dynamics of the PMA canopy.

Figure 7.

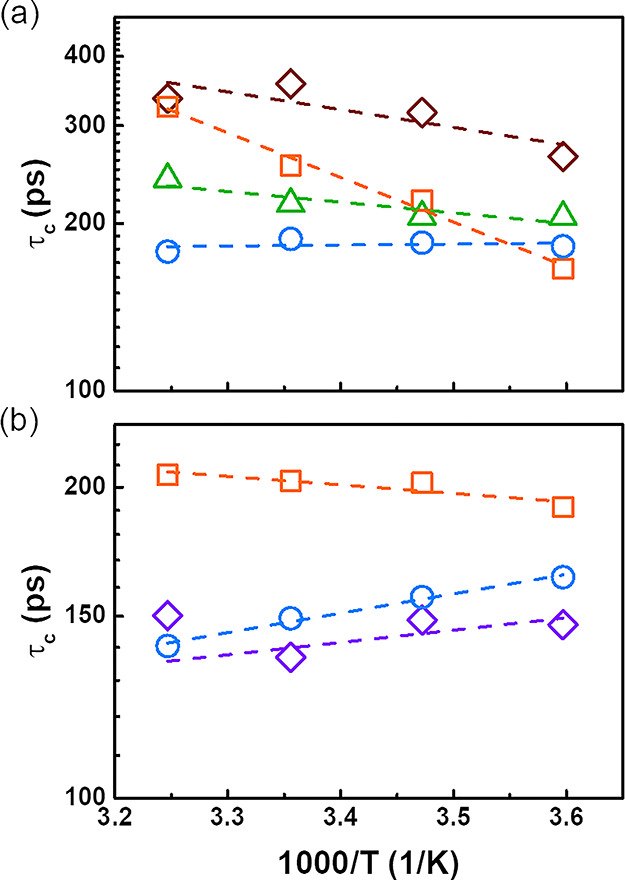
Figure 7

Open in a new tab

Effect of temperature on the correlation time (τc) for the 1H spin–lattice relaxation. (a) Relaxation of the aromatic 1H of PS for unfunctionalized PS NPs prepared with 10 mol % of DVB (brown diamond) and with 0.5 mol % of DVB (green triangle) and for the PS core of PS–PMA NPs cross-linked with 10 mol % of DVB (orange square) and 0.5 mol % of DVB (blue circle). (b) Relaxation of the methoxy 1H of PMA for free PMA chains (N = 46) (violet diamond), PMA chains (N = 100) of PS–PMA NPs prepared with 10 mol % of DVB (orange square) and with 0.5 mol % of DVB (blue circle).

Conclusions

In summary, 1H spin–lattice NMR relaxation was used to characterize the dynamics of soft and hairy PS–PMA NPs in suspension in DCM, a good solvent for both the PMA canopy and the PS core. The length of the PMA chains and the amount of the cross-linker in the PS cores were controlled by miniemulsion followed by SI-ATRP. The resulting NPs had a low size dispersity, formed stable suspensions in DCM, and the grafted polymer chains were in an extended brush conformation in all samples. DLS measurements showed that the swelling of the PS–PMA NPs was influenced both by the degree of cross-linking of the PS core and the length of the PMA canopy. NMR relaxation was used to analyze the subsegmental dynamics of the system. As observed by other techniques, grafting polymer chains slowed down the subsegmental relaxation dynamics of the grafted chain, but more interestingly, grafting polymer chains on soft and deformable NPs allowed us to address a new phenomenon, the relation between the local relaxation dynamics of the core and the local relaxation dynamics of the canopy. We observed a clear interplay between the PMA canopy and the PS core. More rigid PS cores slowed down the subsegmental relaxation dynamics of the PMA chains more efficiently than softer cores, whereas the presence of longer chains in the PMA canopy accelerated the local relaxation dynamics of the PS cores more efficiently than short chains. Canopies prepared with long PMA chains showed marginally faster subsegmental dynamics than the ones made with shorter chains because of the stronger influence of the substrate on short PMA chains. However, the local dynamics of the grafted chains, especially short ones, was strongly influenced by the local dynamics of the substrate. The relaxation dynamics of the PS cores was mainly determined by the degree of cross-linking, but the tethering of long PMA chains accelerated the constrained subsegmental motions in the cross-linked PS.

Our results show the influence of the local dynamics of the substrates on the overall dynamics of the system. We have found a clear relationship between the local dynamics of the core particles and the local dynamics of the end-tethered polymer chains. Grafting a canopy of polymer chains that are pulling and tugging on the tethering points on a soft and deformable NP influences the local dynamics of the soft core. Moreover, the local dynamics of the tethered chains is affected by the softness and the dynamics of the substrate.

Acknowledgments

The authors are grateful to Prof. Dr. Kartharina Landfester for her continuous support. The authors acknowledge the financial support of the Max Planck Society and the support of the Max Planck Center for Complex Fluid Dynamics. H.T.-A. is grateful to the Alexander von Humboldt Foundation for financial support. The authors thank Michael Steiert for ICP-AES measurements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.9b01813.

  • Additional details of chemicals, synthetic methods, NMR experiments, and thermoresponsive swelling behaviors of PS NPs (PDF)

The authors declare no competing financial interest.

Supplementary Material

ma9b01813_si_001.pdf (907.2KB, pdf)

References

  1. Dukes D.; Li Y.; Lewis S.; Benicewicz B.; Schadler L.; Kumar S. K. Conformational Transitions of Spherical Polymer Brushes: Synthesis, Characterization, and Theory. Macromolecules 2010, 43, 1564–1570. 10.1021/ma901228t. [DOI] [Google Scholar]
  2. Devaux C.; Cousin F.; Beyou E.; Chapel J.-P. Low Swelling Capacity of Highly Stretched Polystyrene Brushes. Macromolecules 2005, 38, 4296–4300. 10.1021/ma047478y. [DOI] [Google Scholar]
  3. de Gennes P. G. Conformations of Polymers Attached to an Interface. Macromolecules 1980, 13, 1069–1075. 10.1021/ma60077a009. [DOI] [Google Scholar]
  4. Wu T.; Efimenko K.; Genzer J. Combinatorial Study of the Mushroom-to-Brush Crossover in Surface Anchored Polyacrylamide. J. Am. Chem. Soc. 2002, 124, 9394–9395. 10.1021/ja027412n. [DOI] [PubMed] [Google Scholar]
  5. Brittain W. J.; Minko S. A Structural Definition of Polymer Brushes. J. Polym. Sci., Part A: Polym. Chem. 2007, 45, 3505–3512. 10.1002/pola.22180. [DOI] [Google Scholar]
  6. Moh L. C. H.; Losego M. D.; Braun P. V. Solvent Quality Effects on Scaling Behavior of Poly(methyl methacrylate) Brushes in the Moderate- and High-Density Regimes. Langmuir 2011, 27, 3698–3702. 10.1021/la2002139. [DOI] [PubMed] [Google Scholar]
  7. Hore M. J. A. Polymers on s: Structure & Dynamics. Soft Matter 2019, 15, 1120–1134. 10.1039/c8sm02110d. [DOI] [PubMed] [Google Scholar]
  8. Daoud M.; Cotton J. P. Star Shaped Polymers: A Model For the Conformation and Its Concentration-Dependence. J. Phys. 1982, 43, 531–538. 10.1051/jphys:01982004303053100. [DOI] [Google Scholar]
  9. Zoppe J. O.; Ataman N. C.; Mocny P.; Wang J.; Moraes J.; Klok H.-A. Surface-Initiated Controlled Radical Polymerization: State-of-the-Art, Opportunities, and Challenges in Surface and Interface Engineering with Polymer Brushes. Chem. Rev. 2017, 117, 1105–1318. 10.1021/acs.chemrev.6b00314. [DOI] [PubMed] [Google Scholar]
  10. Kim S. A.; Mangal R.; Archer L. A. Relaxation Dynamics of Nanoparticle-Tethered Polymer Chains. Macromolecules 2015, 48, 6280. 10.1021/acs.macromol.5b00791. [DOI] [Google Scholar]
  11. Wei Y.; Xu Y.; Faraone A.; Hore M. J. A. Local Structure and Relaxation Dynamics in the Brush of Polymer-Grafted Silica Nanoparticles. ACS Macro Lett. 2018, 7, 699–704. 10.1021/acsmacrolett.8b00223. [DOI] [PubMed] [Google Scholar]
  12. Cang Y.; Reuss A. N.; Lee J.; Yan J.; Zhang J.; Alonso-Redondo E.; Sainidou R.; Rembert P.; Matyjaszewski K.; Bockstaller M. R.; Fytas G. Thermomechanical Properties and Glass Dynamics of Polymer-Tethered Colloidal Particles and Films. Macromolecules 2017, 50, 8658–8669. 10.1021/acs.macromol.7b01752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Midya J.; Cang Y.; Egorov S. A.; Matyjaszewski K.; Bockstaller M. R.; Nikoubashman A.; Fytas G. Disentangling the Role of Chain Conformation on the Mechanics of Polymer Tethered Particle Materials. Nano Lett. 2019, 19, 2715–2722. 10.1021/acs.nanolett.9b00817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ndoro T. V. M.; Böhm M. C.; Müller-Plathe F. Interface and Interphase Dynamics of Polystyrene Chains near Grafted and Ungrafted Silica Nanoparticles. Macromolecules 2012, 45, 171–179. 10.1021/ma2020613. [DOI] [Google Scholar]
  15. Lo Verso F.; Yelash L.; Binder K. Dynamics of Macromolecules Grafted in Spherical Brushes under Good Solvent Conditions. Macromolecules 2013, 46, 4716–4722. 10.1021/ma400446r. [DOI] [Google Scholar]
  16. Ghanbari A.; Rahimi M.; Dehghany J. Influence of Surface Grafted Polymers on the Polymer Dynamics in a Silica-Polystyrene Nanocomposite: A Coarse-Grained Molecular Dynamics Investigation. J. Phys. Chem. C 2013, 117, 25069–25076. 10.1021/jp407109r. [DOI] [Google Scholar]
  17. Savin D. A.; Pyun J.; Patterson G. D.; Kowalewski T.; Matyjaszewski K. Synthesis and Characterization of Silica-graft-Polystyrene Hybrid Nanoparticles: Effect of Constraint on the Glass-Transition Temperature of Spherical Polymer Brushes. J. Polym. Sci., Part B: Polym. Phys. 2002, 40, 2667–2676. 10.1002/polb.10329. [DOI] [Google Scholar]
  18. Jhalaria M.; Buenning E.; Huang Y. C.; Tyagi M.; Zorn R.; Zamponi M.; Garcia-Sakai V.; Jestin J.; Benicewicz B. C.; Kumar S. K. Accelerated Local Dynamics in Matrix-Free Polymer Grafted Nanoparticles. Phys. Rev. Lett. 2019, 123, 6. 10.1103/PhysRevLett.123.158003. [DOI] [PubMed] [Google Scholar]
  19. Richter D.; Kruteva M. Polymer Dynamics under Confinement. Soft Matter 2019, 15, 7316–7349. 10.1039/c9sm01141b. [DOI] [PubMed] [Google Scholar]
  20. Ghugare S. V.; Chiessi E.; Telling M. T. F.; Deriu A.; Gerelli Y.; Wuttke J.; Paradossi G. Structure and Dynamics of a Thermoresponsive Microgel around Its Volume Phase Transition Temperature. J. Phys. Chem. B 2010, 114, 10285–10293. 10.1021/jp100962p. [DOI] [PubMed] [Google Scholar]
  21. Cendoya I.; Alegría A.; Alberdi J. M.; Colmenero J.; Grimm H.; Richter D.; Frick B. Effect of Blending on the PVME Dynamics. A Dielectric, NMR, and QENS Investigation. Macromolecules 1999, 32, 4065–4078. 10.1021/ma9819539. [DOI] [Google Scholar]
  22. Malveau C.; Baille W. E.; Zhu X. X.; Ford W. T. Molecular Dynamics of Hydrophilic Poly(propylene imine) Dendrimers in Aqueous Solutions by H-1 NMR Relaxation. J. Polym. Sci., Part B: Polym. Phys. 2003, 41, 2969–2975. 10.1002/polb.10584. [DOI] [Google Scholar]
  23. Pinto L. F.; Correa J.; Martin-Pastor M.; Riguera R.; Fernandez-Megia E. The Dynamics of Dendrimers by NMR Relaxation: Interpretation Pitfalls. J. Am. Chem. Soc. 2013, 135, 1972–1977. 10.1021/ja311908n. [DOI] [PubMed] [Google Scholar]
  24. de Graaf A. J.; Boere K. W. M.; Kemmink J.; Fokkink R. G.; van Nostrum C. F.; Rijkers D. T. S.; van der Gucht J.; Wienk H.; Baldus M.; Mastrobattista E.; Vermonden T.; Hennink W. E. Looped Structure of Flowerlike Micelles Revealed by H-1 NMR Relaxometry and Light Scattering. Langmuir 2011, 27, 9843–9848. 10.1021/la2019605. [DOI] [PubMed] [Google Scholar]
  25. Sayed J. E.; Lorthioir C.; Perrin P.; Sanson N. PEGylated NiPAM Microgels: Synthesis, Characterization and Colloidal Stability. Soft Matter 2019, 15, 963–972. 10.1039/c8sm02156b. [DOI] [PubMed] [Google Scholar]
  26. Pietrasik J.; Sumerlin B. S.; Lee H.-i.; Gil R. R.; Matyjaszewski K. Structural Mobility of Molecular Bottle-Brushes Investigated by NMR Relaxation Dynamics. Polymer 2007, 48, 496–501. 10.1016/j.polymer.2006.11.057. [DOI] [Google Scholar]
  27. Martin H. J.; White B. T.; Scanlon C. J.; Saito T.; Dadmun M. D. Tunable Synthetic Control of Soft Polymeric Nanoparticle Morphology. Soft Matter 2017, 13, 8849–8857. 10.1039/C7SM01533J. [DOI] [PubMed] [Google Scholar]
  28. Wei W.-C.; Feng S.; Zheng C.-X.; Liang G.-D.; Gao H.-Y.; Wu Q.; Zhu F.-M. Glass Transition and Quantum Yield for Fluorescent Labelled Polystyrene Core-forming Block in Self-assembled Nanomicelles of Amphiphilic Diblock Copolymers. J. Polym. Res. 2015, 22, 212. 10.1007/s10965-015-0855-7. [DOI] [Google Scholar]
  29. Kang E.; Graczykowski B.; Jonas U.; Christie D.; Gray L. A. G.; Cangialosi D.; Priestley R. D.; Fytas G. Shell Architecture Strongly Influences the Glass Transition, Surface Mobility, and Elasticity of Polymer Core-Shell Nanoparticles. Macromolecules 2019, 52, 5399–5406. 10.1021/acs.macromol.9b00766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Landfester K. Miniemulsion Polymerization and the Structure of Polymer and Hybrid Nanoparticles. Angew. Chem., Int. Ed. 2009, 48, 4488–4507. 10.1002/anie.200900723. [DOI] [PubMed] [Google Scholar]
  31. Min K.; Gao H.; Matyjaszewski K. Use of Ascorbic Acid as Reducing Agent for Synthesis of Well-defined Polymers by ARGET ATRP. Macromolecules 2007, 40, 1789–1791. 10.1021/ma0702041. [DOI] [Google Scholar]
  32. Schreiber E.; Ziener U.; Manzke A.; Plettl A.; Ziemann P.; Landfester K. Preparation of Narrowly Size Distributed Metal-Containing Polymer Latexes by Miniemulsion and Other Emulsion Techniques: Applications for Nanolithography. Chem. Mater. 2009, 21, 1750–1760. 10.1021/cm802796y. [DOI] [Google Scholar]
  33. Ohno K.; Morinaga T.; Takeno S.; Tsujii Y.; Fukuda T. Suspensions of Silica Particles Grafted with Concentrated Polymer Brush: Effects of Graft Chain Length on Brush Layer Thickness and Colloidal Crystallization. Macromolecules 2007, 40, 9143. 10.1021/ma071770z. [DOI] [Google Scholar]
  34. Birshtein T. M.; Zhulina E. B. Conformations of Star-Branched Macromolecules. Polymer 1984, 25, 1453–1461. 10.1016/0032-3861(84)90109-5. [DOI] [Google Scholar]
  35. Bloembergen N.; Purcell E. M.; Pound R. V. Relaxation Effects in Nuclear Magnetic Resonance Absorption. Phys. Rev. 1948, 73, 679–712. 10.1103/PhysRev.73.679. [DOI] [Google Scholar]
  36. O’Connor P. J.; Cutié S. S.; Smith P. B.; Martin S. J.; Sammler R. L.; Harris W. I.; Marks M. J.; Wilson L. H-1 NMR Characterization of Swelling in Cross-linked Polymer Systems. Macromolecules 1996, 29, 7872–7884. 10.1021/ma960650g. [DOI] [Google Scholar]
  37. Erman B.; Baysal B. Temperature Dependence of Swelling of Polystyrene Networks. Macromolecules 1985, 18, 1696–1700. 10.1021/ma00151a010. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma9b01813_si_001.pdf (907.2KB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES