Summary
Biclustering techniques can identify local patterns of a data matrix by clustering feature space and sample space at the same time. Various biclustering methods have been proposed and successfully applied to analysis of gene expression data. While existing biclustering methods have many desirable features, most of them are developed for continuous data and few of them can efficiently handle -omics data of various types, for example, binomial data as in single nucleotide polymorphism data or negative binomial data as in RNA-seq data. In addition, none of existing methods can utilize biological information such as those from functional genomics or proteomics. Recent work has shown that incorporating biological information can improve variable selection and prediction performance in analyses such as linear regression and multivariate analysis. In this article, we propose a novel Bayesian biclustering method that can handle multiple data types including Gaussian, Binomial, and Negative Binomial. In addition, our method uses a Bayesian adaptive structured shrinkage prior that enables feature selection guided by existing biological information. Our simulation studies and application to multi-omics datasets demonstrate robust and superior performance of the proposed method, compared to other existing biclustering methods.
Keywords: Adaptive shrinkage prior, Bayesian, Biclustering, Biological information, Integrative analysis, -omics data
1. Introduction
Advances in high-throughput technologies have enabled researchers to uncover secrets of human genome on various levels. From microarray to next-generation sequencing, these tools can reveal understandings of genomic activity including DNA composition, abundance of transcriptome, epigenetic modification, etc. Recently, there have been growing interests on integrative analysis of data from multiple -omic modalities for identifying disease subtypes (Verhaak and others, 2010), inferring omics network (Ideker and others, 2001; Tanay and others, 2004), and uncovering disease culprit genes (Network and others, 2011). One significant challenge in integrating multiple -omics data sources is that these data have different characteristics and are difficult to be unified and explored by one single method. Although multiple attempts have been made, more analytical techniques are needed to fully realize the potential of existing vast omics data.
Biclustering is a popular unsupervised learning and data mining technique which can identify local patterns of a data matrix by clustering feature space and sample space at the same time. The idea of biclustering was first discussed by Hartigan (1972) using the term “direct clustering.” Biclustering of gene expression microarray data was first formally introduced by Cheng and Church (2000). Since then, various biclustering methods have been proposed and successfully applied to the analysis of microarray data (Lazzeroni and Owen, 2002; Murali and Kasif, 2002; Bergmann and others, 2003; Sheng and others, 2003; Ben-Dor and others, 2003; Gu and Liu, 2008; Caldas and Kaski, 2008; Hochreiter and others, 2010; Liu and others, 2014; Yu and others, 2017). Biclustering methods have been systematically compared in several review papers (Prelić and others, 2006; Eren and others, 2012; Pontes and others, 2015; Padilha and Campello, 2017).
Following the review paper by Padilha and Campello (2017), the existing biclustering methods can be categorized as greedy algorithms, divide-and-conquer algorithms, exhaustive enumeration algorithms, and distribution parameter identification algorithms. Greedy algorithms including CC (Cheng and Church, 2000), xMotifs (Murali and Kasif, 2002), ISA (Bergmann and others, 2003), etc.; divide-and-conquer algorithms include Bimax (Prelić and others, 2006) and MTBGD (Huda and Noureen, 2016); exhaustive enumeration algorithms include SAMBA (Tanay and others, 2002) and BiBit (Rodriguez-Baena and others, 2011); distribution parameter identification algorithms include Plaid (Caldas and Kaski, 2008), Bayesian Biclustering (BBC) (Gu and Liu, 2008), FABIA (Hochreiter and others, 2010), etc. BBC uses a Bayesian framework and extends the Plaid model by constraining overlaps to 1D and allowing per-bicluster error variance specification. But BBC only focuses on Gaussian data and does not impose any sparsity constraint to model formulation. In addition to BBC, FABIA is of particular interest to us, as it is closely related to our model formulation. FABIA uses a multiplicative model and imposes standard Laplace priors on latent variables. Both Hochreiter and others (2010) and Padilha and Campello (2017) show that FABIA achieves robust performance in their simulation studies and real data applications.
Although many biclustering approaches have been developed, few of them can utilize existing biological information for identifying biclustering patterns such as those from functional genomics or proteomics. An example of such biological information is demonstrated in Figure S1 of the supplementary material available at Biostatistics online. Such gene network can be obtained from publicly available databases such as KEGG pathway (Kanehisa and Goto, 2000; Keshava Prasad and others, 2008; Mi and others, 2015). In addition, recent work has shown that incorporating biological information can improve variable selection and prediction performance in methods such as linear regression and multivariate analysis (Li and Li, 2008; Zhao and others, 2016; Li and others, 2017; Safo and others, 2018; Chang and others, 2018). Furthermore, most, if not all, existing biclustering methods focus on analyzing gene expression microarray data which are of continuous data type. Our simulation results have shown that the current methods cannot identify biclusters with good accuracy on inputs of mixed data types, for example, data generated from Gaussian distribution and Binomial distribution. To address this challenge, we develop a more generalized approach to identify the biclustering patterns using one or multiple -omics datasets. Our work takes advantage of recent work by Polson and others (2013), which developed a unified Bayesian inference framework for analysis of data from exponential family distributions through the use of Pólya-Gamma latent variables. Polson and others (2013) transforms common discrete data distributions into a mixture of Gaussian distributions by introducing auxilary variables. By combining Pólya-Gamma latent variables with a multiplicative modeling framework, we formulate a BBC model similar in spirit with Hochreiter and others (2010) but can accept different data types as inputs. In addition, our approach allows the incorporation of prior biological knowledge in the process of biclustering, if such biological information exists. We call this approach Generalized Biclustering (GBC).
The structure of this article is as follows. Section 2 introduces our model formulation including the adaptive structured prior and the computation of GBC for different data types. Section 3 presents the simulations comparing the proposed method with other popular biclustering methods. Section 4 presents the applications on real datasets.
2. Methodology
Suppose we have a random sample of 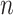 subjects for which data are obtained from
subjects for which data are obtained from 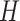 -omics platforms, such as microarray and next-generation sequencing, denoted by
-omics platforms, such as microarray and next-generation sequencing, denoted by 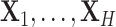 . Each of them is a
. Each of them is a 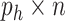 matrix,
matrix, 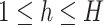 , where
, where 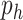 is the number of features and
is the number of features and 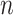 is the number of samples. Let
is the number of samples. Let  be their vertical concatenation with size
be their vertical concatenation with size 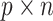 ,
, 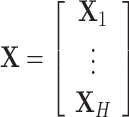 , where
, where 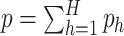 . It follows that the rows represent the feature space and the columns represent the sample space. Let
. It follows that the rows represent the feature space and the columns represent the sample space. Let 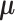 denote the mean of
denote the mean of 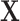 and
and 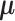 is related with latent components through
is related with latent components through 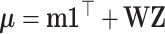 where
where 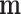 is a
is a 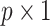 location vector,
location vector, 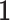 is a
is a 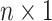 vector of ones,
vector of ones, 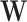 is a
is a 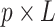 factor loading matrix, and
factor loading matrix, and 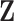 is a
is a 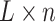 latent factor matrix. To understand this model formulation, one may make an analogy between this framework and the generalized linear model
latent factor matrix. To understand this model formulation, one may make an analogy between this framework and the generalized linear model 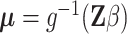 with observations
with observations 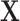 , covariates
, covariates 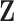 , and link function
, and link function 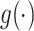 .
. 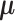 in both models are latent components related with observations. Although data from different platforms are concatenated in the first step, our model allows the use of different distributions for data from different platforms. Assuming the observations
in both models are latent components related with observations. Although data from different platforms are concatenated in the first step, our model allows the use of different distributions for data from different platforms. Assuming the observations 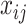 ’s are independent one from each other conditional on
’s are independent one from each other conditional on 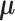 , the likelihood of observations
, the likelihood of observations 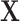 is the multiplication of the likelihood of each individual observation and
is the multiplication of the likelihood of each individual observation and 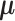 is the parameter of the likelihood function,
is the parameter of the likelihood function, 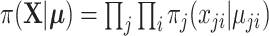 . In the remaining of Section 2, we only consider
. In the remaining of Section 2, we only consider 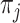 to be an exponential family likelihood for the random variable
to be an exponential family likelihood for the random variable 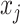 .
.
Using the above notations, a number of distributions can be considered to model observed variables. For instance, if the observation  from the
from the 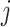 th platform is continuous and after appropriate transformation as needed, one can assume
th platform is continuous and after appropriate transformation as needed, one can assume 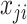 follows the Gaussian distribution having mean
follows the Gaussian distribution having mean 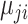 and precision
and precision 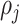 with density function as
with density function as
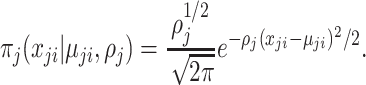 |
(2.1) |
If the observation 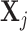 is discrete and one can assume that
is discrete and one can assume that 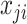 follows a Binomial distribution with parameter
follows a Binomial distribution with parameter 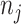 and
and 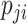 . Using the logit link function, the likelihood function is
. Using the logit link function, the likelihood function is
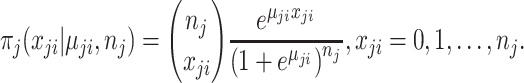 |
(2.2) |
If assuming 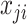 follows Negative Binomial with
follows Negative Binomial with 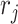 and
and 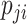 and again using the logit link function for
and again using the logit link function for 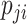 , the likelihood is given by
, the likelihood is given by
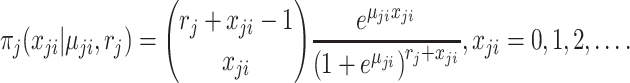 |
(2.3) |
Lastly, if assuming 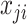 follows Poisson distribution with parameter
follows Poisson distribution with parameter  , the likelihood can be approximated with large
, the likelihood can be approximated with large 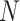 and small
and small 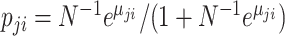 in the form of Binomial distribution. It follows that the likelihood is given by
in the form of Binomial distribution. It follows that the likelihood is given by
 |
(2.4) |
In the following derivations, we take the above four distributions—Gaussian, Binomial, Negative-Binomial, and Poisson—as examples to illustrate the proposed method. Other exponential family distribution such as Bernoulli, Log-normal can be handled similarly.
2.1. Prior specification
We employ a Bayesian adaptive structured shrinkage prior formulation similar to Chang and others (2018), and the goal is to achieve sparse estimations for  and
and  while incorporating existing biological information simultaneously. There are multiple components in this prior. First, a Bayesian Laplacian shrinkage prior is imposed on
while incorporating existing biological information simultaneously. There are multiple components in this prior. First, a Bayesian Laplacian shrinkage prior is imposed on  :
:
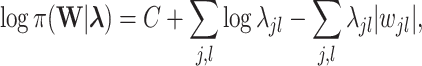 |
where 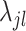 is a parameter controlling the shrinkage level of
is a parameter controlling the shrinkage level of 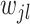 . Unlike standard Laplacian prior that uses the same shrinkage parameter
. Unlike standard Laplacian prior that uses the same shrinkage parameter 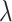 for all
for all 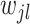 ’s, our approach adapts the shrinkage parameter to individual
’s, our approach adapts the shrinkage parameter to individual 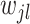 , hence the term of adaptive shrinkage. We further impose a Bayesian shrinkage prior on
, hence the term of adaptive shrinkage. We further impose a Bayesian shrinkage prior on 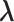 to incorporate biological information, also known as structural information, hence the term of structured shrinkage prior.
to incorporate biological information, also known as structural information, hence the term of structured shrinkage prior.
Suppose the biological information is given through graphs. 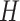 graphs
graphs 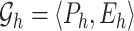 are given where
are given where 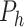 is the set of variables
is the set of variables 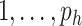 in the
in the 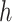 th dataset and
th dataset and 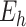 is the set of edges between pairs of variables. The presence of edges represents the correlations of corresponding variable pairs are non-zero. We combine these
is the set of edges between pairs of variables. The presence of edges represents the correlations of corresponding variable pairs are non-zero. We combine these 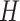 graphs into a single graph
graphs into a single graph 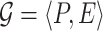 by setting
by setting 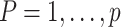 and
and 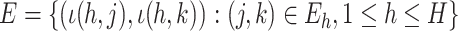 where
where 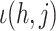 is the index in the matrix
is the index in the matrix 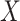 of the
of the 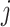 th variable in the
th variable in the 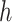 th dataset. Intuitively, consider the situation when there is an edge between
th dataset. Intuitively, consider the situation when there is an edge between 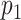 and
and  and another edge between
and another edge between  and
and 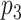 . If
. If 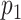 is selected, we encourage
is selected, we encourage 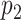 to be selected, and if
to be selected, and if 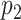 is selected, we encourage
is selected, we encourage 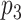 to be selected. In the case when
to be selected. In the case when 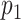 is selected, as long as
is selected, as long as 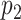 is not selected, we do not encourage
is not selected, we do not encourage 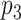 to be selected. One way to achieve such effects is to encourage one variable to load on a factor if the other connected variable has non-zero loading on the same factor. Translating this to notations shows that, if
to be selected. One way to achieve such effects is to encourage one variable to load on a factor if the other connected variable has non-zero loading on the same factor. Translating this to notations shows that, if 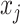 and
and 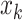 are directly connected in
are directly connected in 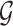 and
and 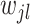 is non-zero for some
is non-zero for some 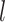 ,
, 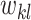 should also be encouraged to have non-zero values. To this end, we employ a graph-Laplacian prior for
should also be encouraged to have non-zero values. To this end, we employ a graph-Laplacian prior for 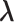 given the precision matrix
given the precision matrix 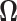 as:
as:
 |
(2.5) |
where 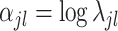 and
and 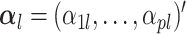 for
for 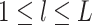 .
. 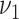 and
and 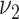 are hyper-parameters needed to be specified a priori. The precision matrix
are hyper-parameters needed to be specified a priori. The precision matrix 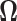 is defined as
is defined as
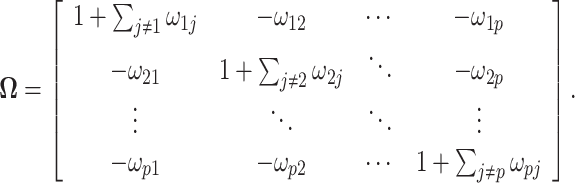 |
Note that 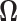 is a symmetric matrix, i.e.,
is a symmetric matrix, i.e.,  . The following prior is assigned on set
. The following prior is assigned on set 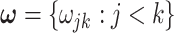
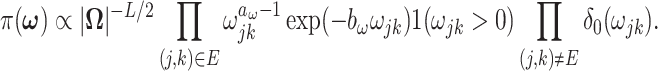 |
(2.6) |
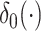 is the Dirac delta function concentrated at 0 and
is the Dirac delta function concentrated at 0 and 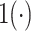 is the indicator function. It can be shown that (2.6) is a proper prior (Chang and others, 2018). Thus if
is the indicator function. It can be shown that (2.6) is a proper prior (Chang and others, 2018). Thus if 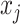 and
and 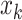 are directly connected in graph
are directly connected in graph 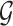 , the prior formula (2.6) encourages precision matrix components
, the prior formula (2.6) encourages precision matrix components  to be non-zero and the shrinkage terms
to be non-zero and the shrinkage terms 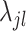 and
and 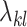 are encouraged to be correlated through prior (2.5). Since
are encouraged to be correlated through prior (2.5). Since 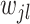 and
and  receive a similar level of shrinkage under this prior specification, they tend to be zero or non-zero at the same time. In other words, if genes
receive a similar level of shrinkage under this prior specification, they tend to be zero or non-zero at the same time. In other words, if genes  and
and 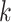 are directly connected in a pathway, they are encouraged to be selected together (or not selected together) in bicluster
are directly connected in a pathway, they are encouraged to be selected together (or not selected together) in bicluster 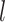 . As such, a salient feature of our approach is that the selected feature set in each bicluster tends to include gene pathways rather than individual genes, leading to biologically more meaningful results. Our current construction of the edge set automatically assumes that there are no edges between features across distinct platforms. This assumption makes it easier to construct biological information from real datasets, since such information is usually given per platform. But our formulation allows the use of edges connecting nodes from different platforms. For example, one can connect the nodes related to the same gene from different platforms.
. As such, a salient feature of our approach is that the selected feature set in each bicluster tends to include gene pathways rather than individual genes, leading to biologically more meaningful results. Our current construction of the edge set automatically assumes that there are no edges between features across distinct platforms. This assumption makes it easier to construct biological information from real datasets, since such information is usually given per platform. But our formulation allows the use of edges connecting nodes from different platforms. For example, one can connect the nodes related to the same gene from different platforms.
To obtain sparse estimates for  , we employ a Bayesian Laplacian shrinkage prior on
, we employ a Bayesian Laplacian shrinkage prior on  as
as
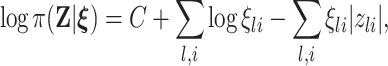 |
where 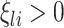 are the shrinkage parameters. Since no prior biological information is available for subjects, we impose a conjugate prior, i.e., a Gamma prior on
are the shrinkage parameters. Since no prior biological information is available for subjects, we impose a conjugate prior, i.e., a Gamma prior on 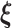 as
as
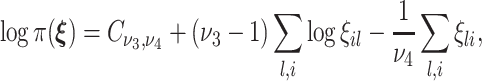 |
(2.7) |
where 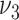 and
and 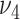 need to be specified a priori. After
need to be specified a priori. After 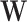 and
and 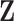 are estimated, the product of the kth column of
are estimated, the product of the kth column of 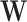 and the
and the 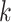 th row of
th row of 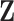 forms the
forms the 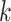 th bicluster. Because the priors specified above yield exact zeros when estimating
th bicluster. Because the priors specified above yield exact zeros when estimating 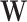 and
and 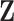 , non-zero elements in
, non-zero elements in 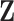 represent the subset of subjects belonging to the
represent the subset of subjects belonging to the 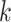 th bicluster, and non-zero elements in
th bicluster, and non-zero elements in 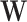 represent the subset of features that contribute to the
represent the subset of features that contribute to the  th bicluster, which is different from the thresholding method used in FABIA.
th bicluster, which is different from the thresholding method used in FABIA.
2.2. Computation
As the likelihoods given in functions (2.1) to (2.4) are dissimilar with inputs of different data types, usually the computation procedures to optimize such likelihoods are also not the same. However, by introducting the Pólya-Gamma latent variables as in Polson and others (2013), we are able to build a unified likelihood for inputs of different data types. Such unified likelihood facilitates the subsequent computations and allows the proposed method to have the flexibility in analyzing data from various sources. We use the identity formula provided in Polson and others (2013):
 |
where  and
and 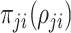 is the density of the Pólya-Gamma class
is the density of the Pólya-Gamma class  . This approach transforms a non-trivial density function into a mixture of Gaussian formulation. Thus the likelihood functions (2.1) to (2.4) can be written in the following universal form:
. This approach transforms a non-trivial density function into a mixture of Gaussian formulation. Thus the likelihood functions (2.1) to (2.4) can be written in the following universal form:
 |
(2.8) |
where the unknown components are summarized in Table 1. Besides offering a unified likelihood function, the augmentation with Pólya-Gamma latent variable 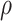 enables the use of efficient lasso algorithms for solving for
enables the use of efficient lasso algorithms for solving for 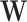 and
and  in the M-steps of EM algorithms, which otherwise is not possible. In addition, the approach of Polson and others (2013) also enables the use of Gibbs sampling via Markov chain Monte Carlo (MCMC) instead of Metropolis–Hastings, if MCMC was implemented.
in the M-steps of EM algorithms, which otherwise is not possible. In addition, the approach of Polson and others (2013) also enables the use of Gibbs sampling via Markov chain Monte Carlo (MCMC) instead of Metropolis–Hastings, if MCMC was implemented.
Table 1.
Formula components of Pólya-Gamma classes
| Data type |

|
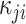
|
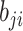
|
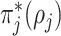
|
|---|---|---|---|---|
| Gaussian |

|
0 | NA |

|
| Binomial | 0 |
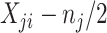
|
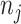
|
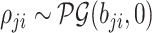
|
| Neg binomial | 0 |

|
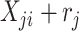
|
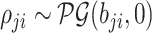
|
| Poisson |

|
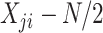
|
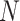
|

|
Similar to Hochreiter and others (2010), we use expectation–maximization (EM) algorithm to compute maximum a posteriori (MAP) estimation of the likelihood function (2.8). To the best of our knowledge, this is the first paper to propose EM algorithm using Pólya-Gamma variables. The MAP estimator 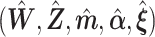 is defined as,
is defined as,
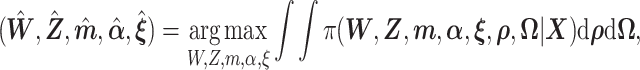 |
with 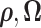 marginalized out. Of note, our EM algorithm treats
marginalized out. Of note, our EM algorithm treats  and
and  as missing variables which are to be imputed, and yields sparse solutions for
as missing variables which are to be imputed, and yields sparse solutions for 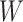 and
and  . Although MCMC could also provide solutions, EM algorithm is more scalable to high dimensional settings of our interest while a full MCMC can be very expensive. Moreover, it requires additional steps to define bicluster membership from MCMC solutions, which is further complicated by the fact that MCMC solutions do not have exact zeroes under the proposed shrinkage priors, and hence may not be sparse. We adopt a recent computational technique called dynamic weighted lasso (Chang and Tsay, 2010) in each EM iteration which further speeds up the algorithm.
. Although MCMC could also provide solutions, EM algorithm is more scalable to high dimensional settings of our interest while a full MCMC can be very expensive. Moreover, it requires additional steps to define bicluster membership from MCMC solutions, which is further complicated by the fact that MCMC solutions do not have exact zeroes under the proposed shrinkage priors, and hence may not be sparse. We adopt a recent computational technique called dynamic weighted lasso (Chang and Tsay, 2010) in each EM iteration which further speeds up the algorithm.
EM algorithm
The inputs of this algorithm include a 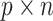 observed data matrix
observed data matrix 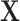 , a
, a 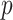 element vector for data types, and a
element vector for data types, and a 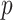 element vector for specific parameter values of each data type. If prior biological information is available, edges between directly connected variables should also be provided. The vector for parameter values for different data types is defined as follows. For Gaussian, Binomial, Negative Binomial and Poisson data, prior parameter for variance specification
element vector for specific parameter values of each data type. If prior biological information is available, edges between directly connected variables should also be provided. The vector for parameter values for different data types is defined as follows. For Gaussian, Binomial, Negative Binomial and Poisson data, prior parameter for variance specification 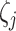 (Gaussian), number of trials
(Gaussian), number of trials  (Binomial), number of failures
(Binomial), number of failures 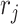 (Negative Binomial), and large number
(Negative Binomial), and large number  (Poisson) should be specified. Definitions of these parameters are demonstrated in the likelihood functions (2.1) to (2.4).
(Poisson) should be specified. Definitions of these parameters are demonstrated in the likelihood functions (2.1) to (2.4).
We develop an EM algorithm for obtaining MAP. The objective function to be optimized at the  -th EM iteration step is given by
-th EM iteration step is given by
 |
where 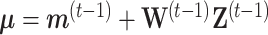 ,
,  , and
, and  The detailed steps of the EM algorithm are explained in Section S1 of the supplementary material available at Biostatistics online. In Figure S2 of the supplementary material available at Biostatistics online, we plot the likelihood by the number of iterations which suggests that our algorithm converges fairly quickly.
The detailed steps of the EM algorithm are explained in Section S1 of the supplementary material available at Biostatistics online. In Figure S2 of the supplementary material available at Biostatistics online, we plot the likelihood by the number of iterations which suggests that our algorithm converges fairly quickly.
Initialization
We initialize 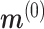 by
by 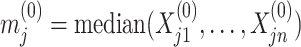 , where
, where
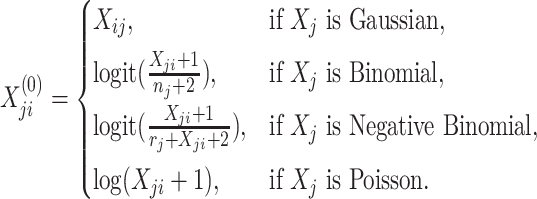 |
 and
and  are initialized by the singular value decomposition of
are initialized by the singular value decomposition of  , and let
, and let  and
and 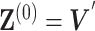 .
.
Tuning
The parameters needed to be specified a priori include 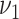 and
and 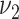 from (2.5),
from (2.5),  and
and  from (2.6), and
from (2.6), and 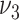 and
and 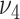 from (2.7). Based on our experience in numerical experiments, we fix
from (2.7). Based on our experience in numerical experiments, we fix  as 4 and
as 4 and 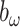 as 1 so that the prior of
as 1 so that the prior of  has large prior correlation and at the same time is relatively uninformative. We also fix
has large prior correlation and at the same time is relatively uninformative. We also fix  as
as  and
and 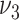 as
as 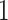 so that the corresponding priors for
so that the corresponding priors for  and
and 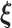 have a unit coefficient of variation.
have a unit coefficient of variation. 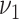 and
and 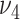 control the sparseness of the solutions to
control the sparseness of the solutions to  and
and  , i.e., the size of each bicluster. We choose
, i.e., the size of each bicluster. We choose 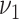 and
and 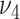 by the Bayesian information criterion (BIC). The BIC is given by
by the Bayesian information criterion (BIC). The BIC is given by
 |
where  is the observed likelihood of
is the observed likelihood of  ,
, 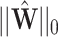 and
and 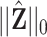 are the cardinalities of
are the cardinalities of 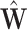 and
and 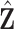 . We conduct grid search and the combinations of
. We conduct grid search and the combinations of 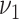 and
and 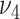 with the smallest BIC value are chosen as the optimal tuning parameter values for each simulation dataset and real data application.
with the smallest BIC value are chosen as the optimal tuning parameter values for each simulation dataset and real data application.
3. Simulation
We design a series of simulation studies to examine the performance of the proposed method and compare it with existing methods. GBC represents the proposed method without utilizing any biological information and sGBC is the version incorporating biological information. As discussed in Section 2, GBC incorporates structural information by employing a graph-Laplacian prior on the shrinkage parameter 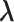 . For each simulation dataset, an working edge matrix is generated by assuming that each bicluster is a fully connected graph and randomly sampling 5% of true edges from all the underlying true biclusters. These edge matrices are used as structural information in sGBC.
. For each simulation dataset, an working edge matrix is generated by assuming that each bicluster is a fully connected graph and randomly sampling 5% of true edges from all the underlying true biclusters. These edge matrices are used as structural information in sGBC.
The existing methods used as comparators are plaid (Caldas and Kaski, 2008), CC (Cheng and Church, 2000), FABIA (Hochreiter and others, 2010), xMotifs (Murali and Kasif, 2002), and ISA (Bergmann and others, 2003). All the methods have implementations in R. Specifically, FABIA is implemented in R/Bioconductor package FABIA, ISA is implemented in R/CRAN package isa2, and plaid, CC, and xMotifs are implemented in R/CRAN package biclust. To choose appropriate tuning parameters for each method, we have evaluated the tuning parameter options provided in Padilha and Campello (2017) and Eren and others (2012). We follow the parameter selections suggested in Padilha and Campello (2017). For methods which parameter tuning is not specifically discussed about in Padilha and Campello (2017), including FABIA and CC, we use the default settings of these methods. For Plaid, we find the best combination of row.release and col.release in the interval 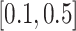 with steps of 0.1. For xMotifs, we relax the
with steps of 0.1. For xMotifs, we relax the 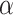 to 0.05 as suggested by Padilha and Campello (2017) and used sd = 5 in synthetic datasets and sd = 1 in real data applications, because otherwise no biclusters can be identified. BBC is not included in our comparison, since Eren and others (2012) demonstrated that FABIA, ISA, xMotifs, and Plaid have overall better performance. The searching area for
to 0.05 as suggested by Padilha and Campello (2017) and used sd = 5 in synthetic datasets and sd = 1 in real data applications, because otherwise no biclusters can be identified. BBC is not included in our comparison, since Eren and others (2012) demonstrated that FABIA, ISA, xMotifs, and Plaid have overall better performance. The searching area for 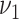 and
and 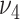 of GBC and sGBC is
of GBC and sGBC is 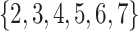 by
by 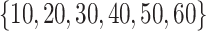 in simulation study.
in simulation study.
Two evaluation criteria are used in both the simulation study and real data applications: clustering error (CE) (Patrikainen and Meila, 2006) and consensus score (CS) (Hochreiter and others, 2010). CE finds the maximum overlapping proportions of two biclusters after an optimal matching of clusters. Similarly, CS finds the optimal mapping between clusters that maximizes the sum of similarities between matched pairs. The only difference between CE and CS is that CS uses the size of bicluster union at the denominator, i.e., CS does not take bicluster size into consideration and gives same weights on all biclusters. Big biclusters may have greater impact on CE than CS. It is worth noting that our CE is one minus the CE defined in Patrikainen and Meila (2006). Both CE and CS lie between 0 and 1. Higher CE, CS values mean greater overlaps between estimated biclusters and true biclusters. Besides CE and CS, we also compute sensitivity (SEN), specificity (SPE), and Matthews correlation coefficient (MCC) in the simulation studies. All these metrics also have values between 0 and 1, and higher values indicate better performance.
3.1. Settings
In each simulation setting, we generate 100 simulation datasets. Each dataset has 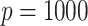 genes and
genes and 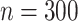 samples. We assume
samples. We assume 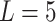 underlying true biclusters. The parameter
underlying true biclusters. The parameter 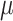 is computed by a multiplicative model
is computed by a multiplicative model 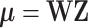 where
where 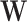 is a
is a  matrix and
matrix and 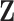 is a
is a  matrix. The number of non-zero elements in each column of
matrix. The number of non-zero elements in each column of 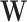 is set as 50 and the number of non-zero elements in each row of
is set as 50 and the number of non-zero elements in each row of 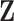 is randomly drawn from Poisson distribution with parameter 30. The row numbers with non-zero elements in
is randomly drawn from Poisson distribution with parameter 30. The row numbers with non-zero elements in  are consecutive while the column numbers with non-zero elements in
are consecutive while the column numbers with non-zero elements in 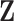 are randomly drawn from
are randomly drawn from  to
to 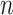 . And the elements of different columns of
. And the elements of different columns of 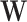 are allowed to have overlaps. The non-zero elements of both
are allowed to have overlaps. The non-zero elements of both 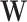 and
and 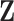 are generated from normal distribution with mean 1.5 and standard deviation 0.1, and are randomly assigned to be positive or negative. We use
are generated from normal distribution with mean 1.5 and standard deviation 0.1, and are randomly assigned to be positive or negative. We use  to represent the number of overlapping rows/columns between adjacent biclusters.
to represent the number of overlapping rows/columns between adjacent biclusters.  is set to
is set to 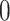 or
or 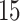 .
.
Four simulation settings are generated: Gaussian, Binomial, Negative Binomial, and mixed data types. For the Gaussian case, the observed  data matrix
data matrix  is generated by
is generated by 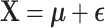 . The noise elements
. The noise elements  are randomly chosen from
are randomly chosen from  . For the Binomial case, each element of
. For the Binomial case, each element of 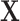 is generated from Binomial
is generated from Binomial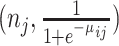 and
and 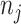 is randomly sampled from 5 to 20. Similarly, each element in Negative Binomial case of
is randomly sampled from 5 to 20. Similarly, each element in Negative Binomial case of 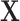 is generated from
is generated from  and the parameter
and the parameter 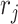 is randomly sampled from 5 to 20. For the mixed data type, we randomly sample each row from these three distributions with the same parameter values as the previous three settings. We demonstrate the general overflow of our simulation study in Figure S3 of the supplementary material available at Biostatistics online.
is randomly sampled from 5 to 20. For the mixed data type, we randomly sample each row from these three distributions with the same parameter values as the previous three settings. We demonstrate the general overflow of our simulation study in Figure S3 of the supplementary material available at Biostatistics online.
3.2. Results
Tables 2 and 3 and Tables S1 and S2 of the supplementary material available at Biostatistics online present simulation results for Gaussian, Binomial, Negative Binomial, and mixed data type settings, respectively. All the results are generated based on 100 Monte Carlo datasets. Table 2 shows that in the Gaussian case, FABIA, GBC, and sGBC outperforms all the other methods. GBC and FABIA have similar CE and CS values, around 0.5 for both non-overlapping scenario and overlap ( ) scenario. sGBC has higher CE and CS, around 0.7 for non-overlapping scenario, and around 0.6 for overlapping scenario. CC, xMotifs, and ISA have the worst results with CE and CS around 0, suggesting that they fail to identify any biclusters. Plaid has better performance than CC, xMotifs, and ISA, but is worse than GBC and FABIA, with CE and CS values around 0.2.
) scenario. sGBC has higher CE and CS, around 0.7 for non-overlapping scenario, and around 0.6 for overlapping scenario. CC, xMotifs, and ISA have the worst results with CE and CS around 0, suggesting that they fail to identify any biclusters. Plaid has better performance than CC, xMotifs, and ISA, but is worse than GBC and FABIA, with CE and CS values around 0.2.
Table 2.
Simulation results for Gaussian settings. Results are generated based on 100 simulated datasets: mean(sd)
| Gaussian | ||||||
|---|---|---|---|---|---|---|
| Overlap | Method | CE | CS | SEN | SPE | MCC |
| 0 | Plaid | 0.24(3e 02) 02) |
0.24(3e 02) 02) |
0.29(2e 02) 02) |
1(5e 06) 06) |
0.43(5e 02) 02) |
| CC | 0(0e+00) | 0(0e+00) | 0(0e+00) | 1(5e 05) 05) |
 0.0025(1e 0.0025(1e 04) 04) |
|
| FABIA | 0.54(3ev02) | 0.54(3e 02) 02) |
0.57(3e 02) 02) |
1(1e 04) 04) |
0.72(3e 02) 02) |
|
| XMotifs | 0(0e+00) | 0(0e+00) | 0(0e+00) | 1(0e+00) | 0(0e+00) | |
| ISA | 0(0e+00) | 0(0e+00) | 0(0e+00) | 0(0e+00) | 0(0e+00) | |
| GBC | 0.64(9e 02) 02) |
0.63(9e 02) 02) |
0.88(1e 01) 01) |
0.99(4e 03) 03) |
0.78(6e 02) 02) |
|
| sGBC | 0.76(7e 02) 02) |
0.76(8e 02) 02) |
0.95(8e 02) 02) |
0.99(2e 03) 03) |
0.86(5e 02) 02) |
|
| 15 | Plaid | 0.24(2e 02) 02) |
0.23(3e 02) 02) |
0.28(2e 02) 02) |
1(1e 04) 04) |
0.42(4e 02) 02) |
| CC | 0(0e+00) | 0(0e+00) | 0(0e+00) | 1(5e 05) 05) |
 0.0027(1e 0.0027(1e 04) 04) |
|
| FABIA | 0.51(8e 02) 02) |
0.52(7e 02) 02) |
0.56(3e 02) 02) |
1(1e 03) 03) |
0.68(9e 02) 02) |
|
| XMotifs | 0(0e+00) | 0(0e+00) | 0(0e+00) | 1(0e+00) | 0(0e+00) | |
| ISA | 0(0e+00) | 0(0e+00) | 0(0e+00) | 0(0e+00) | 0(0e+00) | |
| GBC | 0.57(1e 01) 01) |
0.57(1e 01) 01) |
0.91(1e 01) 01) |
0.98(7e 03) 03) |
0.76(7e 02) 02) |
|
| sGBC | 0.66(9e 02) 02) |
0.66(9e 02) 02) |
0.95(9e 02) 02) |
0.99(4e 03) 03) |
0.81(5e 02) 02) |
|
Table 3.
Simulation results for binomial settings. Results are generated based on 100 simulated datasets: mean(sd)
| Binomial | ||||||
|---|---|---|---|---|---|---|
| Overlap | Method | CE | CS | SEN | SPE | MCC |
| 0 | Plaid | 0.01(9e 04) 04) |
0.18(2e 02) 02) |
0.4(2e 02) 02) |
0.9(1e 01) 01) |
0.036(3e 03) 03) |
| CC | 0.0048(8e 04) 04) |
0.0022(4e 04) 04) |
0.015(2e 03) 03) |
0.99(2e 04) 04) |
0.003(2ev03) | |
| FABIA | 0.072(1e 02) 02) |
0.37(2e 02) 02) |
0.41(2e 02) 02) |
0.98(2e 03) 03) |
0.17(2e 02) 02) |
|
| XMotifs | 0.0013(9e 04) 04) |
0.0013(9e 04) 04) |
0.0014(1e 03) 03) |
1(4e 05) 05) |
0.003(3e 03) 03) |
|
| ISA | 0(0e+00) | 0(0e+00) | 0(0e+00) | 0(0e+00) | 0(0e+00) | |
| GBC | 0.57(1e 01) 01) |
0.6(1e 01) 01) |
0.99(1e 02) 02) |
0.98(9e 03) 03) |
0.77(7e 02) 02) |
|
| sGBC | 0.61(1e 01) 01) |
0.63(9e 02) 02) |
1(8e 04) 04) |
0.98(6e 03) 03) |
0.79(6e 02) 02) |
|
| 15 | Plaid | 0.012(1e 03) 03) |
0.17(2e 02) 02) |
0.4(2e 02) 02) |
0.82(5e 02) 02) |
0.039(4e 03) 03) |
| CC | 0.0064(1e 03) 03) |
0.0027(4e 04) 04) |
0.017(3e 03) 03) |
0.99(2e 04) 04) |
0.005(2e 03) 03) |
|
| FABIA | 0.1(3e 02) 02) |
0.34(4e 02) 02) |
0.39(3e 02) 02) |
0.98(4e 03) 03) |
0.21(4e 02) 02) |
|
| XMotifs | 0.0014(9e 04) 04) |
0.0014(9e 04) 04) |
0.0015(1e 03) 03) |
1(5e 05) 05) |
0.0036(3e 03) 03) |
|
| ISA | 0.012(4e 03) 03) |
0.0033(1e 03) 03) |
0.017(7e 03) 03) |
1(2e 04) 04) |
0.025(8e 03) 03) |
|
| GBC | 0.43(2e 01) 01) |
0.48(1e 01) 01) |
1(9e 03) 03) |
0.97(1e 02) 02) |
0.7(8e 02) 02) |
|
| sGBC | 0.6(1e 01) 01) |
0.61(9e 02) 02) |
1(3e 03) 03) |
0.98(6e 03) 03) |
0.79(5e 02) 02) |
|
Table 3 shows that in the Binomial case, GBC and sGBC still perform best with CE and CS more than 0.5, but FABIA performs worse than in the Gaussian case. In addition, all the other methods, Plaid, CC, xMotifs, and ISA all perform poorly in this setting. It is worth noting that incorporating structural information in GBC is shown to effectively improve performance in both settings. For example, in Gaussian setting with zero overlap, sGBC improves CE from 0.557 to 0.724, which is about a 30% increase.
Tables S1 and S2 of the supplementary material available at Biostatistics online show that in the Negative Binomial and mixed data types, GBC and sGBC still perform best among all the methods. Their CE and CS reach around 0.6 in Negative Binomial, around 0.5 in mixed data types. FABIA also outperforms the rest of the methods, obtaining CE and CS values ranging from 0.1 to 0.2. Plaid, CC, xMotifs, and ISA still have the worst results, with CE and CS around 0.
In addition to CE and CS, the proposed methods also have better performance in sensitivity, specificity, and MCC. We find all the methods generally have high specificity and low sensitivity, suggesting that they fail to identify biclusters instead of misidentifying biclusters. And sGBC usually has higher sensitivity than GBC, indicating that considering structural information helps improve the sensitivity of identifying true biclusters.
4. Real data applications
To evaluate our methods in comparison with the existing methods in real data applications, we obtain one proteomics dataset, one RNAseq dataset, and one integrative dataset. The first two datasets have validated or known subgroup/cluster information on subject level, which are used as the gold standard to compute all evaluation metrics. In the integrative data set, there are no known or validated subgroups. To assess performance, we use patient survival time to define subgroups, which provides evidence that clusters detected by a method are clinically meaningful. Again we followed the tuning parameter options provided in Padilha and Campello (2017) and Eren and others (2012) for existing methods. For GBC and sGBC, we use search area 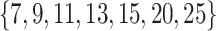 by
by 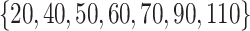 for
for 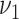 and
and 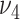 , as previous experience shows real datasets need larger tuning parameter to achieve the smallest BIC.
, as previous experience shows real datasets need larger tuning parameter to achieve the smallest BIC.
4.1. Proteomics dataset
A proteomics dataset is obtained from the AMP-AD knowledge portal of the Synapse website (www.synapse.org) with ID syn3607470. Synapse is an organization dedicated to the research of brain diseases and service patients who have brain injuries. This proteomics dataset includes the measurements for 6533 protein levels from 20 Alzheimer’s Disease (AD) patients, 13 Asymptomatic Alzheimer’s Disease (AsymAD) patients, and 14 controls. All the measurements are conducted on post-mortem brain tissues from both the dorsolateral prefrontal cortex and precuneus. Both regions have been previously reported to be affected in AD (Cox and others, 2011). The disease status of all subjects was confirmed through post-mortem neuropathological evaluation and is used as ground truth in our analyses. According to the data description, the dataset has been normalized based on isotopically labeled retention time peptide standards and the central limit tendency theorem 3 (Callister and others, 2006). To remove noise, we use the top 300 variables with the largest variance.
We apply all the methods on this dataset and report CE and CS in the second and third columns of Table 4. We set the maximum number of clusters to 5 in all the methods. Pathway information is extracted from KEGG Pathway and used in the sGBC. GBC and sGBC achieves the highest CE and CS among all the methods. CC, xMotifs, and FABIA have relatively good performance with CE more than 0.20. On this dataset Plaid does not find any biclusters.
Table 4.
Results of real data applications
| Method | ASD: proteomics data | ASD: RNAseq data | GBM: mixed data | |||
|---|---|---|---|---|---|---|
| CE | CS | CE | CS | CE | CS | |
| PLAID | 0 | 0 | 0 | 0 | 0.263 | 0.175 |
| CC | 0.238 | 0.200 | 0.147 | 0.125 | 0.004 | 0.004 |
| FABIA | 0.254 | 0.140 | 0.147 | 0.103 | 0.260 | 0.186 |
| xMotif | 0.106 | 0.081 | 0 | 0 | 0 | 0 |
| ISA | 0.045 | 0.010 | 0.113 | 0.096 | 0.045 | 0.015 |
| GBC | 0.313 | 0.167 | 0.239 | 0.211 | 0.265 | 0.263 |
| sGBC | 0.313 | 0.160 | 0.239 | 0.211 | 0.281 | 0.221 |
4.2. RNAseq dataset
An RNA-seq dataset is obtained from the AMP-AD knowledge portal of the Synapse website with ID syn5223705. This dataset include next-generation RNA sequencing (RNAseq) from 82 AD, 84 progressive supranuclear palsy, 28 pathologic aging subjects, and 77 elder controls. These measurements are from cerebellum RNA samples collected by the Mayo Clinic Brain Bank and Banner Sun Health Research Institute. Reads are aligned by the SNAPR software1 with the GRCh38 reference and Ensembl v77 gene models and data are normalized by the R/Bioconductor package edgeR (Robinson and others, 2010). The original dataset has 64 253 features, and we use the top 300 features with largest variability for the biclustering analysis. Pathway information is extracted from KEGG Pathway and used in the sGBC as prior biological information.
We apply all the methods on this dataset and CE and CS are reported in the fourth and fifth columns of Table 4. We set the maximum number of clusters to 4 in all the methods. In Table 4, GBC and sGBC have similar CE and CS performance and are the best performing methods among all the methods. CC and FABIA are the second best methods and have CE 0.147 and CS around 0.1. PLAID and xMotif do not find any biclusters in this dataset.
4.3. Integrative dataset
The data of this integrative analysis are obtained from a TCGA study in glioblastoma multiforme (GBM), which is the most common and aggressive type of malignant brain tumor (Holland, 2000). From the TCGA data portal2, microarray gene expression data, DNA methylation data, and DNA copy number data are downloaded for a cohort of 233 GBM patients. All the data are pre-processed, normalized, and annotated to the gene level (see Wang and others 2012 for details). Our analysis focus on 48 genes that overlap with the three critical signaling pathways—RTK/PI3K, p53, and Rb, which have been found to relate with migration, survival, and apoptosis progression of cell cycles (Furnari and others, 2007). Thus the data matrix consists of 48 genes mapped to these core pathways from three platforms resulting in 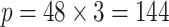 for
for 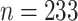 subjects. Note that both microarray gene expression data and DNA methylation data are continuous, while copy number is converted to binary data via thresholding, having
subjects. Note that both microarray gene expression data and DNA methylation data are continuous, while copy number is converted to binary data via thresholding, having 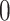 corresponding to normal probes and
corresponding to normal probes and  corresponding to abnormal (gain or loss) probes. The survival information of all subjects is obtained. We use Kaplan–Meier imputed survival time in the case that the subjects are censored, and we categorize the subjects into four groups according to their survival time (or imputed survival time) using 25th, 50th, 75th percentile as cutoffs. These four groups are used as ground truth for clustering patients.
corresponding to abnormal (gain or loss) probes. The survival information of all subjects is obtained. We use Kaplan–Meier imputed survival time in the case that the subjects are censored, and we categorize the subjects into four groups according to their survival time (or imputed survival time) using 25th, 50th, 75th percentile as cutoffs. These four groups are used as ground truth for clustering patients.
We conduct biclustering analysis using the existing methods and the proposed methods. Five are given to all methods as maximum number of biclusters. In GBC and sGBC, we use normal distribution for both microarray gene expression data and DNA methylation data, and binomial distribution for copy number data. A total of  edges are extracted from the KEGG Pathway and are used as biological information in sGBC. We have visualized the gene interaction graph of these
edges are extracted from the KEGG Pathway and are used as biological information in sGBC. We have visualized the gene interaction graph of these  edges in Figure S1 of the supplementary material available at Biostatistics online. We present CE and CS in the last two columns of Table 4. GBC and sGBC have highest CE and CS values among all the methods. Plaid and FABIA also have similar CE values as GBC, which is around 0.26. GBC has higher CS value while sGBC has higher CE value, which may indicate that GBC identify more biclusters regardless of their sizes while GBC with biological information incorporated can identify biclusters with larger size.
edges in Figure S1 of the supplementary material available at Biostatistics online. We present CE and CS in the last two columns of Table 4. GBC and sGBC have highest CE and CS values among all the methods. Plaid and FABIA also have similar CE values as GBC, which is around 0.26. GBC has higher CS value while sGBC has higher CE value, which may indicate that GBC identify more biclusters regardless of their sizes while GBC with biological information incorporated can identify biclusters with larger size.
5. Conclusion
In this article, we propose a BBC algorithm which not only adapts to inputs of different types but also can incorporate biological information. Although a large number of different biclustering approaches have been developed, we are not aware of any existing biclustering methods that can incorporate prior biological information. In addition, our simulation study demonstrates that none of the existing methods considered can efficiently identify biclusters using input data of various distribution types. The proposed methods fill these gaps and become a useful tool in integrative analysis of multiple -omics datasets or analysis of single -omics dataset including proteomic data and genomic data. In the integrative data set, there are no known or validated subgroups. To assess performance, we use patient survival time to define subgroups, which provides evidence that clusters detected by a method are clinically meaningful.
Future directions of research may address two challenges. One is to include more input datatypes in addition to Gaussian, Binomial, and Negative Binomial, for example, beta-Binomial distribution as in bisulfite sequencing data. To achieve this goal, one may need to seek other solutions instead of using the Pólya-Gamma framework. The other one is that the current methods may not be able to retrieve useful biclustering information when input matrix is very sparse, such as data matrices containing the information of somatic mutations. Thus the direction of developing biclustering methods for sparse data matrix is worth further investigation.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Footnotes
6. Software
Software in the form of R code, together with a sample input data set and sample code is available on Github at https://github.com/ziyili20/GBC.
Funding
National Institutes of Health (R01GM124111, R21NS091630, and P30CA016520 to Q.L.), in part.
References
- Ben-Dor A., Chor B., Karp R. and Yakhini Z. (2003). Discovering local structure in gene expression data: the order-preserving submatrix problem. Journal of Computational Biology 10, 373–384. [DOI] [PubMed] [Google Scholar]
- Bergmann S., Ihmels J. and Barkai N. (2003). Iterative signature algorithm for the analysis of large-scale gene expression data. Physical Review E 67, 031902. [DOI] [PubMed] [Google Scholar]
- Caldas J. and Kaski S. (2008). Bayesian biclustering with the plaid model. In: IEEE Workshop on Machine Learning for Signal Processing, 2008. MLSP 2008. Cancun, Mexico:IEEE, pp. 291–296. [Google Scholar]
- Callister S. J., Barry R. C., Adkins J. N., Johnson E. T., Qian W., Webb-Robertson B.-J. M., Smith R. D. and Lipton M. S. (2006). Normalization approaches for removing systematic biases associated with mass spectrometry and label-free proteomics. Journal of Proteome Research 5, 277–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C., Kundu S. and Long Q. (2018). Scalable Bayesian variable selection for structured high-dimensional data. Biometrics. doi: 10.1111/biom.12882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. and Tsay R. S. (2010). Estimation of covariance matrix via the sparse Cholesky factor with lasso. Journal of Statistical Planning and Inference 140, 3858–3873. [Google Scholar]
- Cheng Y. and Church G. M. (2000). Biclustering of expression data. Proceedings of the International Conference on Intelligent Systems for Molecular Biology 8, 93–103. [PubMed] [Google Scholar]
- Cox J., Neuhauser N., Michalski A., Scheltema R. A., Olsen J. V. and Mann M. (2011). Andromeda: a peptide search engine integrated into the maxquant environment. Journal of Proteome Research 10, 1794–1805. [DOI] [PubMed] [Google Scholar]
- Eren K., Deveci M., Küçüktunç O. and Çatalyürek Ü. V. (2012). A comparative analysis of biclustering algorithms for gene expression data. Briefings in Bioinformatics 14, 279–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furnari F. B., Fenton T., Bachoo R. M., Mukasa A., Stommel J. M., Stegh A., Hahn W. C., Ligon K. L., Louis D. N., Brennan C.. and others (2007). Malignant astrocytic glioma: genetics, biology, and paths to treatment. Genes & Development 21, 2683–2710. [DOI] [PubMed] [Google Scholar]
- Gu J. and Liu J. S. (2008). Bayesian biclustering of gene expression data. BMC Genomics 9, S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartigan J. A. (1972). Direct clustering of a data matrix. Journal of the American Statistical Association 67, 123–129. [Google Scholar]
- Hochreiter S., Bodenhofer U., Heusel M., Mayr A., Mitterecker A., Kasim A., Khamiakova T., Van Sanden S., Lin D., Talloen W.. and others (2010). Fabia: factor analysis for bicluster acquisition. Bioinformatics 26, 1520–1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland E. C. (2000). Glioblastoma multiforme: the terminator. Proceedings of the National Academy of Sciences United States of America 97, 6242–6244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huda S. B. and Noureen N. (2016). Mtbgd: multi type biclustering for genomic data. In: 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), IEEE; pp. 1113–1119. [Google Scholar]
- Ideker T., Thorsson V., Ranish J. A., Christmas R., Buhler J., Eng J. K., Bumgarner R., Goodlett D. R., Aebersold R. and Hood L. (2001). Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science 292, 929–934. [DOI] [PubMed] [Google Scholar]
- Kanehisa M. and Goto S. (2000). KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Research 28, 27–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshava Prasad T. S., Goel R., Kandasamy K., Keerthikumar S., Kumar S., Mathivanan S., Telikicherla D., Raju R., Shafreen B., Venugopal A.. and others (2008). Human protein reference database 2009 update. Nucleic Acids Research 37(suppl_1), D767–D772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazzeroni L. and Owen A. (2002). Plaid models for gene expression data. Statistica Sinica, 61–86. [Google Scholar]
- Li C. and Li H. (2008). Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics 24, 1175–1182. [DOI] [PubMed] [Google Scholar]
- Li Z., Safo S. E. and Long Q. (2017). Incorporating biological information in sparse principal component analysis with application to genomic data. BMC Bioinformatics 18, 332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Gu Q., Hou J. P., Han J. and Ma J. (2014). A network-assisted co-clustering algorithm to discover cancer subtypes based on gene expression. BMC Bioinformatics 15, 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mi H., Poudel S., Muruganujan A., Casagrande J. T. and Thomas P. D. (2015). Panther version 10: expanded protein families and functions, and analysis tools. Nucleic Acids Research 44, D336–D342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murali T. M. and Kasif S. (2002). Extracting conserved gene expression motifs from gene expression data. In: Biocomputing 2003. World Scientific, pp. 77–88. [PubMed] [Google Scholar]
- Cancer Genome Atlas Research Network. (2011). Integrated genomic analyses of ovarian carcinoma. Nature 474, 609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padilha V. A. and Campello R. J. G. B. (2017). A systematic comparative evaluation of biclustering techniques. BMC Bioinformatics 18, 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patrikainen A. and Meila M. (2006). Comparing subspace clusterings. IEEE Transactions on Knowledge and Data Engineering 18, 902–916. [Google Scholar]
- Polson N. G., Scott J. G. and Windle J. (2013). Bayesian inference for logistic models using Pólya–Gamma latent variables. Journal of the American statistical Association 108, 1339–1349. [Google Scholar]
- Pontes B., Giráldez R. and Aguilar-Ruiz J. S. (2015). Biclustering on expression data: a review. Journal of Biomedical Informatics 57, 163–180. [DOI] [PubMed] [Google Scholar]
- Prelić A., Bleuler S., Zimmermann P., Wille A., Bühlmann P., Gruissem W., Hennig L., Thiele L. and Zitzler E. (2006). A systematic comparison and evaluation of biclustering methods for gene expression data. Bioinformatics 22, 1122–1129. [DOI] [PubMed] [Google Scholar]
- Robinson M. D., McCarthy D. J. and Smyth G. K. (2010). edger: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26, 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Baena D. S., Perez-Pulido A. J. and Aguilar-Ruiz J. S. (2011). A biclustering algorithm for extracting bit-patterns from binary datasets. Bioinformatics 27, 2738–2745. [DOI] [PubMed] [Google Scholar]
- Safo S. E., Li S. and Long Q. (2018). Integrative analysis of transcriptomic and metabolomic data via sparse canonical correlation analysis with incorporation of biological information. Biometrics 74, 300-312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheng Q., Moreau Y. and De Moor B. (2003). Biclustering microarray data by Gibbs sampling. Bioinformatics 19(suppl 2), ii196–ii205. [DOI] [PubMed] [Google Scholar]
- Tanay A., Sharan R., Kupiec M. and Shamir R. (2004). Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data. Proceedings of the National Academy of Sciences of the United States of America 101, 2981–2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanay A., Sharan R. and Shamir R. (2002). Discovering statistically significant biclusters in gene expression data. Bioinformatics 18(suppl_1), S136–S144. [DOI] [PubMed] [Google Scholar]
- Verhaak R. G. W., Hoadley K. A., Purdom E., Wang V., Qi Y., Wilkerson M. D., Miller C. R., Ding L., Golub T., Mesirov J. P.. and others (2010). Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in pdgfra, idh1, egfr, and nf1. Cancer Cell 17, 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., Baladandayuthapani V., Morris J. S., Broom B. M., Manyam G. and Do K.-A. (2012). ibag: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 29, 149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu G. and Wang J. (2017). Network-aided bi-clustering for discovering cancer subtypes. Scientific Reports 7, 1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Chung M., Johnson B. A., Moreno C. S. and Long Q. (2016). Hierarchical feature selection incorporating known and novel biological information: identifying genomic features related to prostate cancer recurrence. Journal of the American Statistical Association 111, 1427–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


