Summary
With the advent of next-generation sequencing, investigators have access to higher quality sequencing data. However, to sequence all samples in a study using next generation sequencing can still be prohibitively expensive. One potential remedy could be to combine next generation sequencing data from cases with publicly available sequencing data for controls, but there could be a systematic difference in quality of sequenced data, such as sequencing depths, between sequenced study cases and publicly available controls. We propose a regression calibration (RC)-based method and a maximum-likelihood method for conducting an association study with such a combined sample by accounting for differential sequencing errors between cases and controls. The methods allow for adjusting for covariates, such as population stratification as confounders. Both methods control type I error and have comparable power to analysis conducted using the true genotype with sufficiently high but different sequencing depths. We show that the RC method allows for analysis using naive variance estimate (closely approximates true variance in practice) and standard software under certain circumstances. We evaluate the performance of the proposed methods using simulation studies and apply our methods to a combined data set of exome sequenced acute lung injury cases and healthy controls from the 1000 Genomes project.
Keywords: Genetic association studies, Hypothesis testing, Maximum likelihood, Misclassification, Regression calibration, Sequencing depth
1. Introduction
Next-generation sequencing (NGS) is becoming a popular trend in genetic association studies (Shendure and others, 2017). Despite the recent advances, it can still be prohibitively expensive to conduct a NGS study by sequencing both cases and controls using study-specific resources. To make efficient use of available resources, one could sequence disease cases and combine them with controls from publicly available sequenced data, such as data from 1000 Genomes Project Consortium (2012). This increases available sample size and can lead to more efficient use of available resources. To combine data from multiple sources for valid analysis, however, one needs to account for the varied data quality from different data sources, such as called genotype quality, in order to avoid biases in analysis (Kim and others, 2011).
This work is motivated by a case-only sequencing study of Acute Lung Injury (ALI) from the National Heart, Lung, and Blood Institute (NHLBI) Exome Sequencing Project (ESP) (Fu and others, 2013). The ALI exome sequencing study performed whole exome sequencing of 89 ALI cases without healthy controls. To identify variants associated with ALI, it is of interest to use external controls, e.g. 1000 Genomes. However, the average depth of the Phase I of the 1000 Genomes data is 4 , and that of the ALI data set is over 70
, and that of the ALI data set is over 70 . The average depth is the average number of times a locus is read, and the more reads, the higher the accuracy. This constitutes a stark difference in data quality between study cases and publicly available controls.
. The average depth is the average number of times a locus is read, and the more reads, the higher the accuracy. This constitutes a stark difference in data quality between study cases and publicly available controls.
One existing cost-effective strategy for an association study with NGS data is to use sequenced cases for variant discovery and genotype a larger sample size on the identified variants for association analysis (Liu and Leal, 2012; Longmate and others, 2010; Sanna and others, 2011). These study designs prevent type I error inflation, but have been found to be conservative, are unable to detect protective variants, and do not allow the use of publically available controls (Derkach and others, 2014). There is also existing work for genetic association analysis that incorporate the quality of the genotype calls. Skotte and others (2012) introduced such a method, which only considers the prospective setting and assumes non-differential misclassification. In this setting, it assumes the sequencing quality is the same between cases and controls. Derkach and others (2014) build on Skotte and others (2012) by considering the retrospective setting and differential sequencing depths but is unable to control for confounding. Both methods take a score approach and do not compute regression coefficients. A few authors consider a similar but different settings. Hu and others (2015) study a situation where there is a mixture of sequencing data and genotyping array data, whereas we only have sequencing data that contain systematic difference in sequencing quality. Lee and others (2017) investigate incorporating external controls to a sample that contains internal controls, while our method and the data example do not have internal controls. Hence these methods are not applicable to our setting.
Regression calibration (RC) and maximum likelihood (ML) are popular methods for handling measurement error and misclassification. The existing RC methods primarily focus on measurement error of the covariates (Carroll and others, 2006; Rosner and others, 1989), with some exceptions (Spiegelman and others, 2000). ML has been developed for both measurement error and misclassification (Carroll and others, 1993). Both methods commonly consider non-differential measurement error/misclassification in the presence of validation data, where a subset of the data has both error-free and error-prone observations, or in the presence of replicates of error-prone observations (Carroll and others, 2006; Liu and Liang, 1991). A few authors have developed methods for differential measurement error/misclassification in the presence of validation data (Lyles, 2002; Freedman and others, 2008; Tang and others, 2015), However, little work has been done using RC and ML for differential misclassification in the absence of validation data.
This article fills this gap by developing statistical methods for genetic association analysis in the sequencing setting when cases and controls are subject to systematic difference in sequencing depths and validation data are unavailable. We propose RC and ML methods based on sequencing reads that can handle differential misclassification. Our methods allow for adjusting of non-confounding covariates to increase power as well as controlling for confounding, in the form of population stratification, which is the primary confounder in genetic association studies. We focus on analysis of common variants in this article.
Our methods control type I error when combining data sequenced for the current study and previously available data, such as publically available controls. Under balanced case–control sampling with different sequencing quality, we show that our RC method can use naive variance estimate, which approximates the true variance well in practice, to give non-inflated type I error, allowing for ease of analysis with standard software packages. This is not a general result for existing RC methods in other settings, where hypothesis testing usually proceeds with the sandwich estimator or bootstrap (Carroll and others, 2006). We show that the parameters of interest are identifiable with our proposed ML approach, which gives unbiased estimate of regression coefficients under retrospective sampling without covariates.
This article is organized as the following. In Section 2, we present the model in case–control sequencing studies subject to different sequencing depths and describe the assumptions about the distribution of the data as well as the reads. In Section 3, we propose the RC and ML methods without covariates, with non-confounding covariates, and with confounding in the form of population stratification, as well as discussion for general confounding. In Section 4, we describe the simulations for evaluating the performance of the proposed methods as well as the results. In Section 5, we apply our methods to analysis of the combined ALI exome-sequencing and 1000 Genomes data. Lastly, we conclude with discussions in Section 6.
2. Models and assumptions
Suppose for the 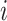 th of
th of 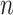 independent subjects,
independent subjects, 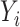 is the observed case–control status,
is the observed case–control status, 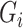 the unobserved genotype of a biallelic locus of interest, and
the unobserved genotype of a biallelic locus of interest, and 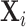 the vector of potential additional covariates. Conditional on
the vector of potential additional covariates. Conditional on 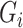 and
and 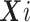 , assume the disease risk
, assume the disease risk 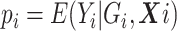 is logistic
is logistic
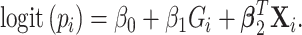 |
(2.1) |
The information for the unobserved genotype 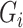 is obtained from the observed
is obtained from the observed 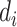 reads
reads 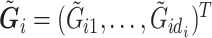 and quality information for each read. Here
and quality information for each read. Here 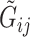 is the
is the 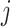 th read of subject
th read of subject 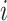 for
for 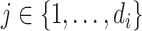 , where
, where 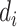 is the read depth for subject
is the read depth for subject 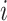 . Denote the two alleles of
. Denote the two alleles of 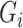 as
as 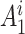 and
and 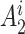 , and the allele randomly chosen for read
, and the allele randomly chosen for read 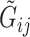 as
as 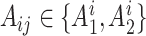 . Then, for read
. Then, for read 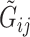 , there is an associated quality score
, there is an associated quality score 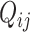 , which can be mapped to base-calling error probability (referred to as misclassification rate for simplicity for the remainder)
, which can be mapped to base-calling error probability (referred to as misclassification rate for simplicity for the remainder) 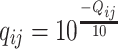 for this read. For each subject, we observe
for this read. For each subject, we observe 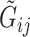 and
and 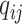 , for
, for 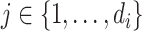 , from the reads directly.
, from the reads directly.
We assume some distributions for 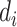 and
and 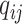 . In the setting of interest where the sequencing quality depends only on the case–control status, the distributions of
. In the setting of interest where the sequencing quality depends only on the case–control status, the distributions of 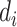 and
and 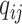 depends only on the case–control status, i.e.,
depends only on the case–control status, i.e., 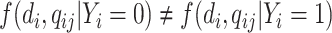 , where
, where 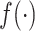 is the density function. This implies differential misclassification. While
is the density function. This implies differential misclassification. While 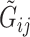 depends on
depends on 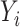 through
through 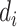 and
and 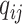 , we assume that the
, we assume that the 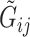 and
and 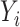 are independent conditional on
are independent conditional on 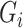 ,
, 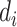 , and
, and 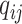 , i.e.
, i.e. 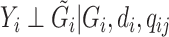 , and the reads
, and the reads 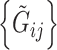 are mutually independent conditional on
are mutually independent conditional on 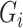 ,
, 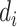 , and
, and 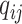 . We are interested in estimating the regression coefficients
. We are interested in estimating the regression coefficients 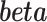 using the observed data
using the observed data 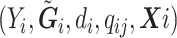 .
.
3. Methods
3.1. Regression calibration
The RC method approximates 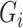 using
using 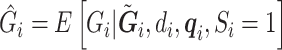 , where
, where 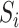 is an indicator for a subject in a cohort being sampled in a case–control study, and plugs
is an indicator for a subject in a cohort being sampled in a case–control study, and plugs 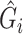 in the logistic model (2.1) for estimation of
in the logistic model (2.1) for estimation of 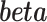 . Multiple sequencing reads
. Multiple sequencing reads 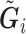 and the quality scores
and the quality scores 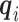 enable the computation of the desired conditional expectation
enable the computation of the desired conditional expectation 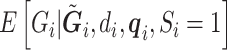 without the need of a validation set. We calculate
without the need of a validation set. We calculate 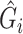 by following Derkach and others (2014).
by following Derkach and others (2014).
First consider the case in the absence of confounding. Given 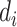 and
and 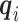 , we can compute the conditional distribution of the observed reads,
, we can compute the conditional distribution of the observed reads, 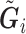 , given the true genotype,
, given the true genotype, 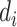 and
and 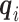 as
as
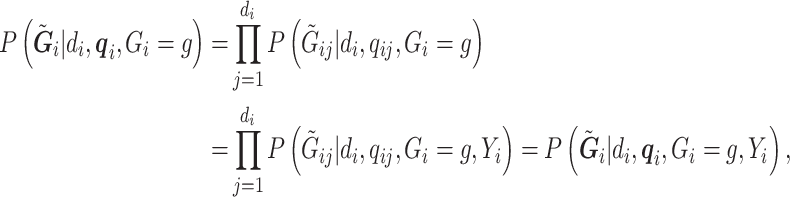 |
(3.2) |
with the first equality due to the conditional independence assumption of 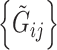 and the second due to conditional independence of
and the second due to conditional independence of 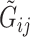 and
and 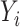 given
given 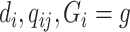 . Assuming that the case–control sampling indicator
. Assuming that the case–control sampling indicator 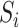 only depends on
only depends on 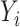 , then we can rewrite (3.2) as
, then we can rewrite (3.2) as
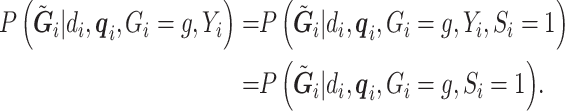 |
(3.3) |
To calculate 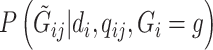 , we follow the formulation in Derkach and others (2014):
, we follow the formulation in Derkach and others (2014): 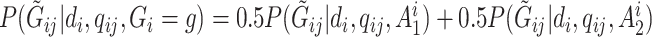 , where
, where 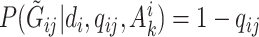 if
if 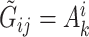 and
and 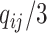 if
if 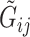 is any of the other three base pairs, and
is any of the other three base pairs, and 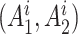 are two alleles of
are two alleles of 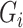 and
and 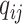 is defined in Section 2. This can be used to compute
is defined in Section 2. This can be used to compute 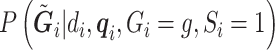 through (3.2) and (3.3). Then, we compute the desired conditional expectation of the genotype as
through (3.2) and (3.3). Then, we compute the desired conditional expectation of the genotype as 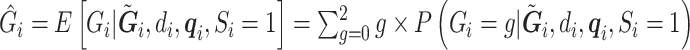 , where
, where
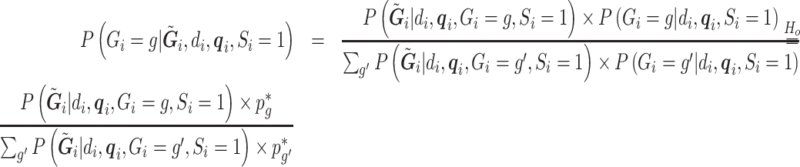 |
is constructed from 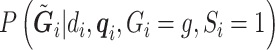 and an estimate of the retrospective distribution of the genotype,
and an estimate of the retrospective distribution of the genotype, 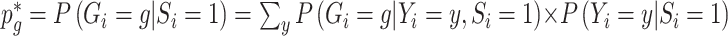 . The second equality holds under the null, since
. The second equality holds under the null, since 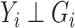 under
under 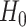 and
and 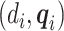 only depends on
only depends on 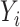 . The unknown parameters
. The unknown parameters 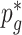 ’s are estimated from the full sample (cases and controls) using an EM algorithm (McKenna and others, 2010; Skotte and others, 2012), where the marginal likelihood of the reads (see Section S2 of supplementary material available at Biostatistics online) is maximized over
’s are estimated from the full sample (cases and controls) using an EM algorithm (McKenna and others, 2010; Skotte and others, 2012), where the marginal likelihood of the reads (see Section S2 of supplementary material available at Biostatistics online) is maximized over 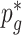 . This corresponds to solving the estimating equations in (3.4), and
. This corresponds to solving the estimating equations in (3.4), and 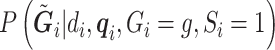 is again computed as in (3.2) and (3.3). Note that in the retrospective setting, we are conditioning on
is again computed as in (3.2) and (3.3). Note that in the retrospective setting, we are conditioning on 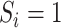 everywhere.
everywhere.
We first consider the case without any additional covariates. After computing 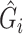 , we proceed to use it in place of
, we proceed to use it in place of 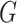 in logistic regression to obtain the RC estimator
in logistic regression to obtain the RC estimator 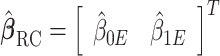 , which maximizes the logistic “likelihood” obtained from model (2.1) with
, which maximizes the logistic “likelihood” obtained from model (2.1) with 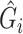 in place of
in place of 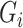 . The resulting estimator,
. The resulting estimator, 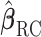 , along with estimates of
, along with estimates of 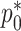 and
and 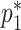 , can be framed within a set of four estimating equations
, can be framed within a set of four estimating equations 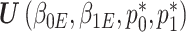 , two for the RC estimators and two for maximizing the marginal likelihood of the reads
, two for the RC estimators and two for maximizing the marginal likelihood of the reads 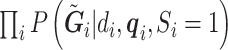 in terms of
in terms of 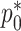 and
and 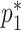 as stated above. Under the null, the estimating equations are unbiased when evaluated at
as stated above. Under the null, the estimating equations are unbiased when evaluated at 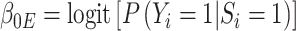 and
and 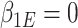 (shown in Section S3 of supplementary material available at Biostatistics online). This implies the RC estimators are unbiased under the null. Variance of
(shown in Section S3 of supplementary material available at Biostatistics online). This implies the RC estimators are unbiased under the null. Variance of 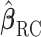 can be estimated with the sandwich estimator resulting from these four estimating equations. The test statistic is formed by dividing
can be estimated with the sandwich estimator resulting from these four estimating equations. The test statistic is formed by dividing 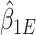 by the sandwich variance estimate and will be asymptotically normal under the null.
by the sandwich variance estimate and will be asymptotically normal under the null.
The estimating equations of the RC procedure 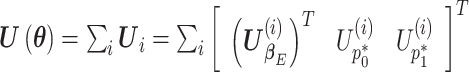 are functions of
are functions of 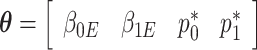 with individual contributions
with individual contributions 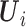 , where
, where
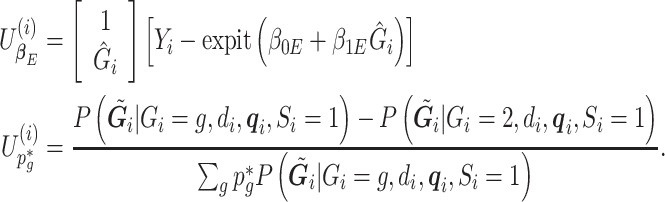 |
(3.4) |
Note that 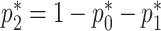 . The sandwich variance estimator is defined
. The sandwich variance estimator is defined 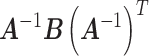 , where
, where  and
and 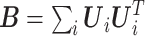 , with asymptotic limits
, with asymptotic limits 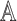 and
and 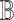 . The naive information matrix of the logistic regression fit for RC is
. The naive information matrix of the logistic regression fit for RC is 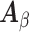 , the submatrix of
, the submatrix of 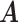 corresponding to
corresponding to 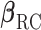 , with asymptotic limit
, with asymptotic limit 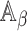 , a submatrix of
, a submatrix of 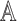 . Under the null, with balanced case–control sampling, the submatrices of
. Under the null, with balanced case–control sampling, the submatrices of 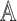 and
and 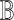 corresponding to
corresponding to 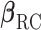 are the same. In this situation, the naive variance estimator,
are the same. In this situation, the naive variance estimator, 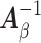 , overestimates the true variance (shown in Section S4 of supplementary material available at Biostatistics online), i.e., the element corresponding to
, overestimates the true variance (shown in Section S4 of supplementary material available at Biostatistics online), i.e., the element corresponding to 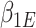 of
of 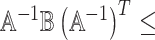 that of
that of 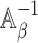 . So the naive variance estimator, from inverting the “observed information”
. So the naive variance estimator, from inverting the “observed information” 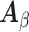 like in regular logistic regression, gives non-inflated type I error when the sampling is balanced, though it can be conservative.
like in regular logistic regression, gives non-inflated type I error when the sampling is balanced, though it can be conservative.
Simulation results suggest that if the distribution of the read depth and misclassification rate between cases and controls are not too dissimilar or if both cases and controls have reasonable read depth, then conservativeness with the naive variance is negligible. Under the alternative, simulations suggest that power loss and bias are minor with fairly large differences in data quality.
Now, we consider the context with presence of covariates: i.e., in the 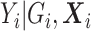 model. If adjusting for non-confounding covariates
model. If adjusting for non-confounding covariates 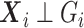 , we first need to compute the conditional expectation
, we first need to compute the conditional expectation 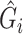 as before. Note that this conditional expectation does not take
as before. Note that this conditional expectation does not take 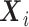 into account since
into account since 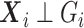 . The RC estimates are
. The RC estimates are 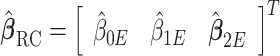 , which maximizes the logistic likelihood from the
, which maximizes the logistic likelihood from the 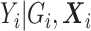 model with
model with 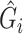 in place of
in place of 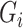 in terms of
in terms of 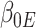 ,
, 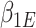 , and
, and 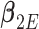 . Just as the case without covariates, the corresponding set of estimating equations are unbiased when evaluated at
. Just as the case without covariates, the corresponding set of estimating equations are unbiased when evaluated at 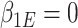 . Hypothesis testing can once again proceed with the corresponding sandwich estimator, or the naive variance estimator when sampling is balanced.
. Hypothesis testing can once again proceed with the corresponding sandwich estimator, or the naive variance estimator when sampling is balanced.
If 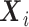 are confounders, i.e.
are confounders, i.e. 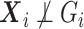 , one needs to compute the conditional expectation of the genotype given
, one needs to compute the conditional expectation of the genotype given  and
and 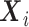 ,
, 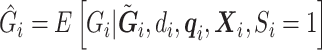 . If correctly done, then
. If correctly done, then 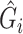 can be used in place of
can be used in place of 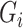 as before. The corresponding estimating equations will have expectation 0. However, this requires a model for
as before. The corresponding estimating equations will have expectation 0. However, this requires a model for 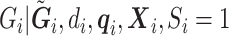 , which may be difficult to ascertain.
, which may be difficult to ascertain.
In practice, however, the main confounder of concern in the sequencing setting is population stratification. One unique aspect of confounding due to population stratification is that it is weak with respect to a single SNP. We empirically verified this assumption in the 1000 Genomes data used later in the data analysis, where the first principal components (PCs) calculated from both the conditional expectation of the genotype as well as the called genotype show low correlation with the expected/called genotype throughout the genome [25%, 50%, 75% quartiles about ( 0.056, 0.001, 0.057) for both]. Mathematically, this can be expressed as:
0.056, 0.001, 0.057) for both]. Mathematically, this can be expressed as:
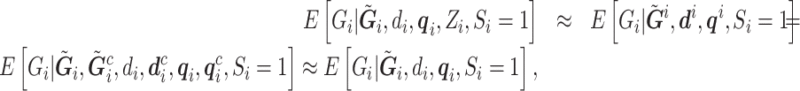 |
where 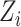 is the population marker,
is the population marker, 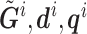 is the set of reads, read depth, and quality score for all SNPs in the genome. While
is the set of reads, read depth, and quality score for all SNPs in the genome. While 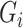 still represent the genotype of the locus of interest and
still represent the genotype of the locus of interest and 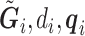 are its associated reads, read depth, and quality scores,
are its associated reads, read depth, and quality scores, 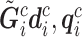 represent that for all loci except the one of interest. The first line says that the information of the population membership is encoded in the information over the whole genome, the second line simply partitions
represent that for all loci except the one of interest. The first line says that the information of the population membership is encoded in the information over the whole genome, the second line simply partitions 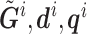 in the conditioning, and the last line states that reads at other loci give little information for the locus of interest given
in the conditioning, and the last line states that reads at other loci give little information for the locus of interest given 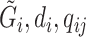 .
.
Given these assumptions, 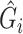 can be computed as if without any confounding. We propose to adjust for population stratification with RC by including the PCs derived from
can be computed as if without any confounding. We propose to adjust for population stratification with RC by including the PCs derived from 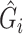 as covariates in model (2.1) by defining
as covariates in model (2.1) by defining 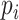 as
as 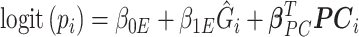 .
.  are the vector of loadings for the PCs from
are the vector of loadings for the PCs from 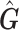 (the matrix of the conditional expectation of the true genotype for all loci and all subjects) of the
(the matrix of the conditional expectation of the true genotype for all loci and all subjects) of the 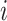 th subject, and inference proceeds as before.
th subject, and inference proceeds as before.
Since 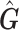 is an approximation of
is an approximation of 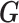 (the genotype matrix for all loci and all subjects), then the PCs resulting from
(the genotype matrix for all loci and all subjects), then the PCs resulting from 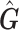 should be an approximation of those from
should be an approximation of those from 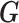 . Although
. Although 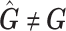 and the two associated sets of PCs are not equal, the PCs from
and the two associated sets of PCs are not equal, the PCs from 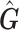 can be used to control for population stratification as long as they adequately separate the different populations. Our simulation results suggests PCs from
can be used to control for population stratification as long as they adequately separate the different populations. Our simulation results suggests PCs from 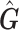 do achieve this.
do achieve this.
3.2. Maximum likelihood
Again, first consider in the context of the 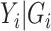 model without covariates. Since the sampling is retrospective and assume that the sampling fraction is unknown, the parameters related to the marginal distribution of the data, i.e. the minor allele frequency
model without covariates. Since the sampling is retrospective and assume that the sampling fraction is unknown, the parameters related to the marginal distribution of the data, i.e. the minor allele frequency 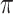 and
and 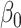 , are not identifiable (Prentice and Pyke, 1979). From Prentice and Pyke (1979), if the sampling status only depends on the outcome, we know that we can write
, are not identifiable (Prentice and Pyke, 1979). From Prentice and Pyke (1979), if the sampling status only depends on the outcome, we know that we can write 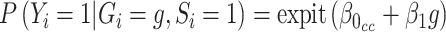 , where
, where 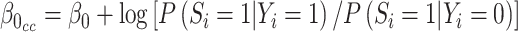 and
and 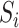 is the indicator of being sampled. Thus, we need to form the likelihood based on parameters related to the distribution of the data given being sampled, i.e.
is the indicator of being sampled. Thus, we need to form the likelihood based on parameters related to the distribution of the data given being sampled, i.e. 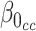 ,
, 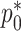 , and
, and 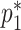 . The retrospective likelihood can be written as
. The retrospective likelihood can be written as 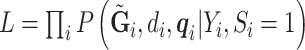 , with individual contributions:
, with individual contributions:
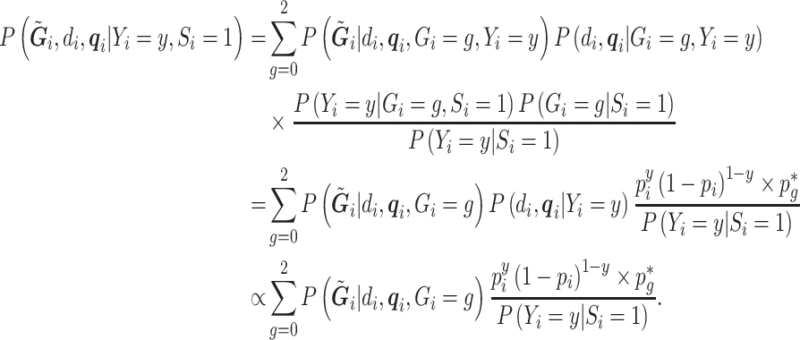 |
(3.5) |
Note that the 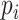 are defined as in model (2.1). In the third line, the conditioning of
are defined as in model (2.1). In the third line, the conditioning of 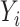 is dropped from
is dropped from 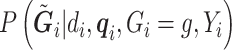 as shown in the previous section. The conditioning of
as shown in the previous section. The conditioning of 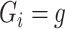 is dropped from
is dropped from 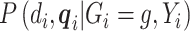 since
since 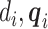 only depend on
only depend on 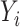 per assumptions in Section 2. Then, the term
per assumptions in Section 2. Then, the term 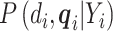 , which does not depend on the parameters of interest
, which does not depend on the parameters of interest 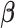 , can be factored out. The identifiability of the model in (3.5) is shown in Section S5 of supplementary material available at Biostatistics online.
, can be factored out. The identifiability of the model in (3.5) is shown in Section S5 of supplementary material available at Biostatistics online.
Since 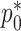 and
and 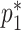 are both probabilities and given their interpretations, the parameter space for
are both probabilities and given their interpretations, the parameter space for 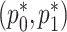 is restricted:
is restricted: 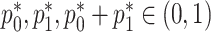 . Optimization in a restricted parameter space can be difficult, so we propose to reparameterize
. Optimization in a restricted parameter space can be difficult, so we propose to reparameterize 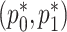 as
as 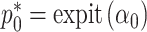 and
and 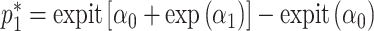 . This ensures that
. This ensures that 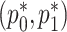 respect the bounded parameter space while allowing for optimization in terms of
respect the bounded parameter space while allowing for optimization in terms of 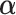 , which can take any value in
, which can take any value in 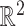 . For the RC procedure based on (3.4), the two estimation equations corresponding to
. For the RC procedure based on (3.4), the two estimation equations corresponding to 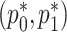 does not involve
does not involve 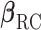 , so the estimation of
, so the estimation of 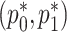 is completely separate from that of
is completely separate from that of 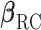 . The estimation for
. The estimation for 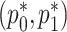 in RC always gives estimates that respect the bounded parameter space, so no reparameterization is needed. In ML, on the other hand, all parameters are jointly estimated, and may violate the parameter space without the reparameterization. Finally, to further simplify the parameter space for ML,
in RC always gives estimates that respect the bounded parameter space, so no reparameterization is needed. In ML, on the other hand, all parameters are jointly estimated, and may violate the parameter space without the reparameterization. Finally, to further simplify the parameter space for ML, 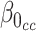 can be substituted into (3.5) as a function of
can be substituted into (3.5) as a function of 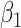 ,
, 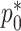 , and
, and 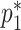 , by solving:
, by solving:
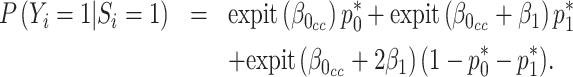 |
(3.6) |
Although there is no closed form solution to equation (3.6), it can be numerically solved during each step of the fitting process. Following this reparameterization, (3.5) can be rewritten with the 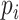 as a function of
as a function of 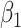 and
and 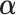 , and
, and 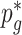 as a function of
as a function of 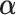 .
.
Estimation and inference both proceed in the likelihood framework. The MLE can be obtained by numerically maximizing 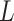 , while testing of the null
, while testing of the null 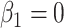 is done by dividing
is done by dividing 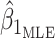 by its corresponding standard error derived from the information matrix and comparing the quotient to the normal distribution. An issue arises in this parameterization when allele frequency is low. In this case,
by its corresponding standard error derived from the information matrix and comparing the quotient to the normal distribution. An issue arises in this parameterization when allele frequency is low. In this case, 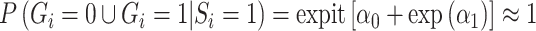 . The column of the information matrix corresponding to
. The column of the information matrix corresponding to 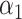 contain products of
contain products of 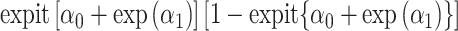 , which is very close to 0. Thus, this column will be of terms very to 0. Inverting the information matrix in this case may run into numerical issues. We found that, at minor allele frequency of 0.01, ML can become unstable for the sample size we considered in this article, although its performance improves for large sample sizes, while RC did not suffer from such stability issues. Thus, when allele frequency is low, we recommend RC instead.
, which is very close to 0. Thus, this column will be of terms very to 0. Inverting the information matrix in this case may run into numerical issues. We found that, at minor allele frequency of 0.01, ML can become unstable for the sample size we considered in this article, although its performance improves for large sample sizes, while RC did not suffer from such stability issues. Thus, when allele frequency is low, we recommend RC instead.
In the context of the  model when
model when 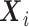 is not a confounder, i.e.,
is not a confounder, i.e., 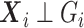 ,
, 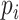 is still defined according to model (2.1), and the retrospective likelihood can be rewritten as:
is still defined according to model (2.1), and the retrospective likelihood can be rewritten as:
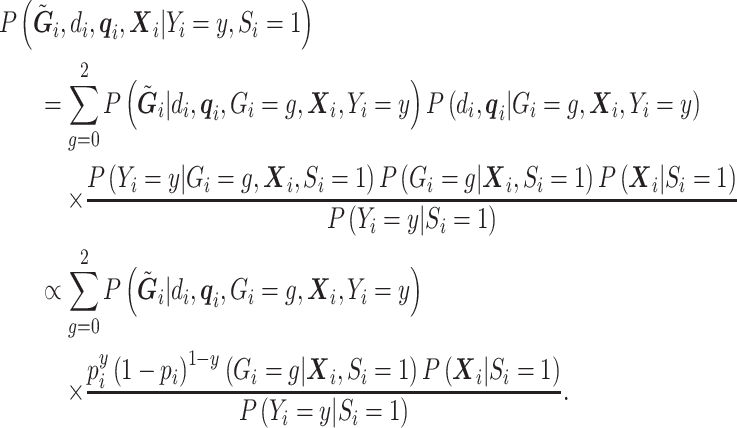 |
(3.7) |
Similar to the case without covariates, 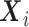 and
and 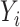 are dropped from
are dropped from 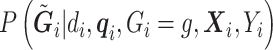 per earlier assumptions and the fact that
per earlier assumptions and the fact that 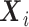 is independent of
is independent of 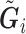 conditional on
conditional on 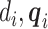 , and
, and 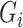 , thus
, thus 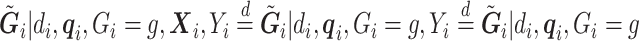 . In addition,
. In addition, 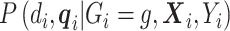 does not depend on
does not depend on 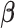 and can be factored out. Although
and can be factored out. Although 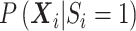 can be factored out also,
can be factored out also, 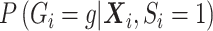 cannot be ignored, regardless of whether
cannot be ignored, regardless of whether 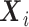 is a confounder or not. If
is a confounder or not. If 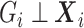 marginally and both
marginally and both 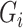 and
and  are associated with
are associated with 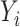 , i.e.
, i.e. 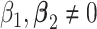 , then
, then 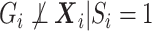 after averaging over
after averaging over 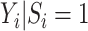 . In this case, under the null, it can be shown that
. In this case, under the null, it can be shown that 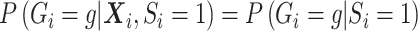 :
:
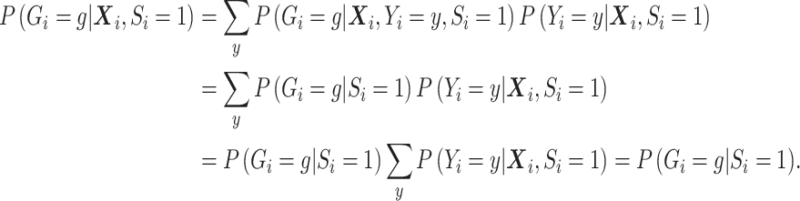 |
The second equality is due to 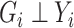 and
and 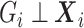 . So if
. So if 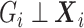 marginally and replace
marginally and replace 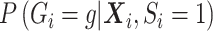 with
with 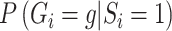 in the likelihood, then it is correct under the null, i.e. correct type I error, but incorrect under the alternative, i.e. some bias in the estimator.
in the likelihood, then it is correct under the null, i.e. correct type I error, but incorrect under the alternative, i.e. some bias in the estimator.
If 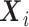 were confounding, the likelihood still takes form of (3.7). However, compared to when
were confounding, the likelihood still takes form of (3.7). However, compared to when 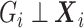 , the main difference is
, the main difference is 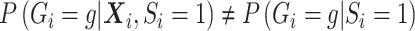 under the null as well as the alternative. If the marginal conditional distribution of
under the null as well as the alternative. If the marginal conditional distribution of 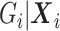 is correctly specified, then we can correctly specify the null likelihood. Just as with non-confounding
is correctly specified, then we can correctly specify the null likelihood. Just as with non-confounding 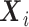 , under the null,
, under the null, 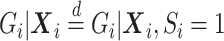 , but under the alternative,
, but under the alternative, 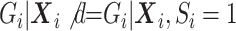 due to averaging over
due to averaging over 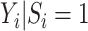 . Thus, given
. Thus, given 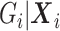 is correct, type I error would be correct under the null, but there will be some bias under the alternative. To avoid the bias, one would need a flexible functional form for
is correct, type I error would be correct under the null, but there will be some bias under the alternative. To avoid the bias, one would need a flexible functional form for 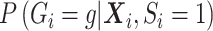 . Since this quantity changes under the null versus under the alternative, a flexible functional form allows close approximation of the true
. Since this quantity changes under the null versus under the alternative, a flexible functional form allows close approximation of the true 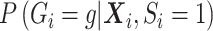 in either case. If
in either case. If 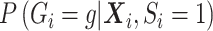 is sufficiently well specified, then the bias should be small under the alternative, but the likelihood is an approximation of the true likelihood.
is sufficiently well specified, then the bias should be small under the alternative, but the likelihood is an approximation of the true likelihood.
This approach for general confounding can be used to control for population stratification by specifying 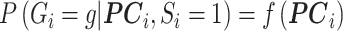 , with a flexible
, with a flexible 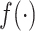 , to replace
, to replace 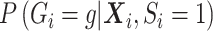 in (3.7). However, the weak confounding with respect to a single SNP for population stratification assumption, as made for RC, translates to
in (3.7). However, the weak confounding with respect to a single SNP for population stratification assumption, as made for RC, translates to 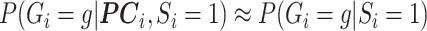 here. This implies that the PCs, as defined in Section 3.1, can be approximated as non-confounding covariates by adding them to the specification of
here. This implies that the PCs, as defined in Section 3.1, can be approximated as non-confounding covariates by adding them to the specification of 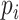 but ignoring the dependence of
but ignoring the dependence of 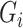 on the PCs.
on the PCs. 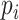 in (3.7) becomes
in (3.7) becomes 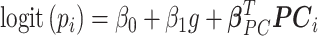 , and the resulting likelihood can be maximized as before. We show the efficacy of this approach in simulation.
, and the resulting likelihood can be maximized as before. We show the efficacy of this approach in simulation.
4. Simulation studies
We perform simulation studies to evaluate the performance of the proposed methods under scenarios with varying differences in data quality between cases and controls. We consider three situations: (i) the distribution of both read depth and misclassification rates are similar, (ii) both are quite different, and (iii) the read depth is similar and misclassification rate is quite different. Situation (i) corresponds to using data from similar platforms; situation (ii) corresponds to using data from a newer and an older platform; and situation (iii) corresponds to using data from a newer platform and an older platform with increased number of reads. The distribution for the misclassification rates for cases and controls in (i) are chosen to be similar to that from the simulations in Derkach and others (2014). In (ii) and (iii), the mean of the misclassification for the controls are chosen to an order of magnitude higher for an exaggerated difference.
For simulation without other covariates, given fixed number of cases and controls, we first generate the genotype 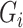 of cases and controls separately, based on the distribution of
of cases and controls separately, based on the distribution of 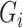 given
given 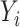 . Then, for subject
. Then, for subject 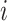 , we generate the read depth
, we generate the read depth 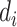 and a sequence of misclassification rates
and a sequence of misclassification rates 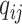 for
for 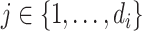 . Now, we generate the sequence of reads
. Now, we generate the sequence of reads 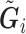 for individual
for individual  based on
based on 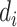 and
and 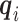 . The
. The 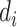 ’s are generated from various normal distributions truncated from below at 1 and rounded to the nearest integer. The
’s are generated from various normal distributions truncated from below at 1 and rounded to the nearest integer. The 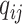 ’s are generated from various normal distributions truncated from below at 0 and from above at 1. The means and standard deviations of the normal distributions truncated for each situation are specified in Table 1. From the reads, we can computed the desired
’s are generated from various normal distributions truncated from below at 0 and from above at 1. The means and standard deviations of the normal distributions truncated for each situation are specified in Table 1. From the reads, we can computed the desired 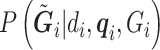 as above, with which we can compute
as above, with which we can compute 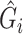 for RC or form the likelihood for ML.
for RC or form the likelihood for ML.
Table 1.
The normal distributions (mean, standard deviation) used to generate the read depth and misclassification rate in our simulations. (i) Refers to similar read depth and misclassification rates. (ii) Refers to dissimilar read depth and misclassification rates. (iii) Refers to similar read depth but dissimilar misclassification rates
| (i) | (ii) | (iii) | ||
|---|---|---|---|---|
| Case | Read depth |
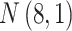
|
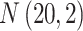
|
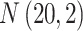
|
| Misclassification |
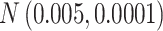
|
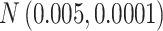
|
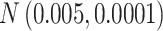
|
|
| Control | Read depth |
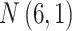
|
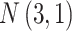
|
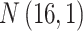
|
| Misclassification |
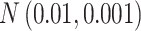
|
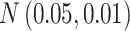
|
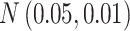
|
For simulation with population stratification, we generate two population minor allele frequencies from the Balding–Nichols model (Balding and Nichols, 1995) with 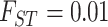 and ancestral allele frequency 0.2, then generate the genotype and the phenotype based on the population membership. We sample the desired number of cases and controls independently of the population membership and generate the sequence of reads as before. The parameters used for the simulation with population stratification are listed in Table S1(a) of supplementary material available at Biostatistics online.
and ancestral allele frequency 0.2, then generate the genotype and the phenotype based on the population membership. We sample the desired number of cases and controls independently of the population membership and generate the sequence of reads as before. The parameters used for the simulation with population stratification are listed in Table S1(a) of supplementary material available at Biostatistics online.
4.1. Type I error
For simulations under the null, we generated a case–control sample from the following prospective models 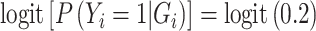 and
and 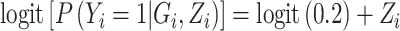 . The first model refers to the null model without any other covariates, the second refers to the null model with population stratification with binary population marker
. The first model refers to the null model without any other covariates, the second refers to the null model with population stratification with binary population marker 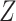 . Note that
. Note that 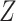 is only used for data generation and is considered unobserved for the analysis, which uses the PCs only as per Section 3. The true genotype
is only used for data generation and is considered unobserved for the analysis, which uses the PCs only as per Section 3. The true genotype 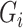 is generated with minor allele frequency 0.2. For simulation with population stratification, we generate two population minor allele frequencies from the specified Balding–Nichols model, then generate the true genetype for both populations. After the genotype is generated, we simulate the read depth and misclassification rates
is generated with minor allele frequency 0.2. For simulation with population stratification, we generate two population minor allele frequencies from the specified Balding–Nichols model, then generate the true genetype for both populations. After the genotype is generated, we simulate the read depth and misclassification rates 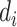 and
and 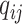 with the distribution as specified in the three situations stated above. The results are from 100 000 replications for each scenario, except for with population stratification, which is from 1 000 000 replications.
with the distribution as specified in the three situations stated above. The results are from 100 000 replications for each scenario, except for with population stratification, which is from 1 000 000 replications.
The parameters used in the simulations are summarized in Table S1(b) of supplementary material available at Biostatistics online, and entail scenarios with 1:1 and 1:2 case to control sampling ratio. In each setting, we compare the performance of analysis with the true genotype with the Wald statistic versus RC and ML. RC with the naive variance estimator will only be considered when the sampling is balanced. We also performed the naive analysis using the called genotype calculated using the Wald statistic to investigate the degree of inflation in each situation when the differential sequencing quality is ignored.
When the read depth and misclassification distribution are both similar between cases and controls and sampling is balanced, RC with naive and sandwich variance both control type I error well (scenario A, Figure S1(a)–(b) of supplementary material available at Biostatistics online). On the other hand, if the distribution of read depth and misclassification both differ significantly between cases and controls with balanced sampling, RC with naive variance is conservative, while RC with sandwich variance continues to perform well (scenario B, Figure S2(a)–(b) of supplementary material available at Biostatistics online). This is consistent with results in Section 3.1. Next, we consider a similar read depth distribution but significantly different misclassification distribution between cases and controls with balanced sampling. In this case, RC with both naive and sandwich variances control the type I error well, so a sufficient number of reads can make up for an order of magnitude of difference in misclassification rate (scenario C, Figure S3(a)–(b) of supplementary material available at Biostatistics online). Lastly, if we have scenario B with unbalanced sampling, RC with naive variance gives inflated type I error, but RC with sandwich variance still performs well (scenario D, Figure S4(a)–(b) of supplementary material available at Biostatistics online). In each of these scenarios, ML controls type I error well consistently. The naive analysis using the called genotypes that ignores differential sequencing quality between cases and controls showed obvious inflation of various degrees in all the scenarios except for scenario C, which had similar read depths in both cases and controls. Table 2 gives a summary of all the scenarios considered and of the performance of each method in each scenario. Results with the true genotype are included for comparison. QQ plots and parameters used in simulation are in Section S1 of supplementary material available at Biostatistics online.
Table 2.
Summary of the scenarios considered in the type I error simulations. The first column is used for identification in the article; the second refers to the distributions of read depth and misclassification rate as described above; the third refers to whether the sampling is balanced; the fourth refers to the section in the supplementary materials to refer to for the QQ plots as well as power results. The next five columns gives the empirical type I error at 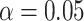 for each method, including analysis with the true genotype (True G) and naive analysis with the called genotype via the Wald statistic. Significant departures from
for each method, including analysis with the true genotype (True G) and naive analysis with the called genotype via the Wald statistic. Significant departures from 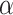 are bolded
are bolded
| Scenario | Dep/Mis | Balanced | Plots | True G | RC Naive | RCsandwich | ML | Called |
|---|---|---|---|---|---|---|---|---|
| A | (i) | Yes | S1.1 | 0.050 | 0.050 | 0.051 | 0.049 | 0.060 |
| B | (ii) | Yes | S1.2 | 0.050 | 0.047 | 0.050 | 0.050 | 0.203 |
| C | (iii) | Yes | S1.3 | 0.049 | 0.049 | 0.049 | 0.049 | 0.050 |
| D | (ii) | No | S1.4 | 0.050 | 0.059 | 0.049 | 0.050 | 0.190 |
For simulation with population stratification, we generated data in the aforementioned fashion and performed naive analysis with no PCs as well as analysis that controls for the first two PCs as described in Section 3. As noted above, the population marker 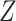 is considered unobserved for the analysis, with PCs taking its place in the analysis. Both analysis with RC and ML proceed by changing the specification of
is considered unobserved for the analysis, with PCs taking its place in the analysis. Both analysis with RC and ML proceed by changing the specification of 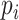 with
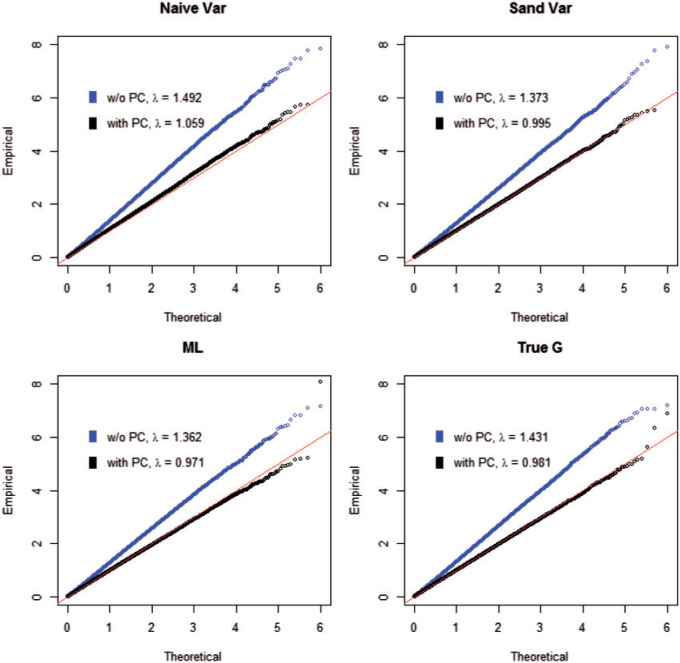
with 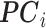 as stated in Section 3. With the weak confounding with respect to a single SNP assumption made in Section 3, both RC and ML approximate the PCs as non-confounding covariates. As expected, the naive analysis shows significant inflation for RC, ML, and analysis with the true genotype when population structure is ignored. After controlling for the two PCs, we can see that the control of type I error is much improved. Due to the unbalanced sampling, however, RC with naive variance still shows some inflation as expected, but RC with sandwich variance performs well. All corresponding QQ plots are in Figure 1.
as stated in Section 3. With the weak confounding with respect to a single SNP assumption made in Section 3, both RC and ML approximate the PCs as non-confounding covariates. As expected, the naive analysis shows significant inflation for RC, ML, and analysis with the true genotype when population structure is ignored. After controlling for the two PCs, we can see that the control of type I error is much improved. Due to the unbalanced sampling, however, RC with naive variance still shows some inflation as expected, but RC with sandwich variance performs well. All corresponding QQ plots are in Figure 1.
Fig. 1.
The QQ plots for the type I error simulation with population stratification. The four plots correspond to analysis with RC and naive variance, RC and sandwich variance, ML, and with the true genotype. The lighter plots correspond to the naive analysis without PCs, and the darker plots correspond to analysis with PCs. The estimate of the inflation factor 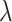 for each method of analysis for each scenario is in the legend.
for each method of analysis for each scenario is in the legend.
4.2. Power
For simulations under the alternative, the data are generated with the same procedure as simulations under the null, except with 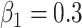 . For each scenario assessed for type I error, we generate data with the same parameters, but with a non-zero effect for the genotype as stated above. We evaluate power at various significance levels as well as bias in the estimators for analysis with the true genotype against RC and ML. RC with naive variance is still only considered with balanced sampling since it gives inflated type I error when sampling is unbalanced. Each QQ-plot in the supplementary materials is accompanied by the corresponding tables of averages of the estimates and empirical power at various significance levels. In each scenario, the power for the methods based on the reads is expectedly lower than that with the true genotype, but power loss is minimal when data quality is sufficient for both cases and controls (scenarios A and C). The results are from 20 000 replications, and results for
. For each scenario assessed for type I error, we generate data with the same parameters, but with a non-zero effect for the genotype as stated above. We evaluate power at various significance levels as well as bias in the estimators for analysis with the true genotype against RC and ML. RC with naive variance is still only considered with balanced sampling since it gives inflated type I error when sampling is unbalanced. Each QQ-plot in the supplementary materials is accompanied by the corresponding tables of averages of the estimates and empirical power at various significance levels. In each scenario, the power for the methods based on the reads is expectedly lower than that with the true genotype, but power loss is minimal when data quality is sufficient for both cases and controls (scenarios A and C). The results are from 20 000 replications, and results for 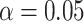 are presented in Table 3.
are presented in Table 3.
Table 3.
Empirical power for each of the four scenarios in the simulation study described in Supplementary Table S1(b) of supplementary material available at Biostatistics online under the the alternative at 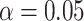 , with effect size
, with effect size 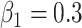
| Scenario | True G | RC Naive | RC Sandwich | ML |
|---|---|---|---|---|
| A | 0.74 | 0.72 | 0.72 | 0.71 |
| B | 0.74 | 0.64 | 0.66 | 0.65 |
| C | 0.74 | 0.73 | 0.73 | 0.74 |
| D | 0.69 | NA | 0.64 | 0.63 |
In the scenarios examined, RC and ML have very similar power, with undetectable to fairly minor bias in the various settings for the RC estimates. The power comparison between RC with naive and sandwich variance varies for the scenarios with balanced sampling. For scenario A, with similar distributions for read depth and misclassification distributions, power is similar for RC with naive and sandwich variance. In scenario B, in which the distribution of read depth and misclassification rate both differ significantly between cases and controls, there is a small but noticeable power gain from using the sandwich variance. In scenario C, read depth for both cases and controls are sufficiently high, but there is significant difference in misclassification rates. Here, power is similar for RC with both variances. Lastly, in scenario D, the distribution of read depth and misclassification rate both differ significantly and sampling is unbalanced, so there is no comparison since the naive variance gives inflated type I error here.
In general, the power loss compared to analysis with the true genotype is more severe in cases where the data quality of one group is poor, such as in scenarios B and D. The bias of the RC estimator follows a similar pattern, as the bias goes from undetectable in situation (i) and (iii) to noticeable but not too severe in situation (ii). For ML, there is no appreciable bias even under situation (ii). Note that (i)–(iii) are described at the beginning of Section 4.
5. Application on ALI exome and 1000 genomes data
We performed analysis with RC and ML as well as naive analysis with the called genotype on the combined data set of the case-only sample from the NHLBI ALI cohort project and phase 1 of 1000 Genomes project. The sample from the ALI cohort project consists of exome-sequencing data from 89 Caucasian subjects with varying severity of lung injury, who are considered cases. The data from phase 1 of 1000 Genomes consist of exome-sequencing data from 174 CEU and GBR subjects, who are considered controls.
To compute the desired 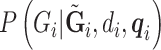 , we need
, we need 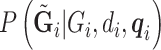 from all the subjects. This information is encoded as PL in the VCF files for the ALI subjects, and as GL for the 1000 Genomes subjects. To combine the data set, we matched up SNPs that are both in the 1000 Genomes phase 1 exome data and the ALI exome data that have the same name (RS number), physical location, and definition of major and minor alleles. SNPs with quality (QUAL)
from all the subjects. This information is encoded as PL in the VCF files for the ALI subjects, and as GL for the 1000 Genomes subjects. To combine the data set, we matched up SNPs that are both in the 1000 Genomes phase 1 exome data and the ALI exome data that have the same name (RS number), physical location, and definition of major and minor alleles. SNPs with quality (QUAL) 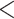 30, quality by depth (QD)
30, quality by depth (QD) 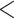 5, allele balance (AB)
5, allele balance (AB) 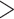 0.75, % missing
0.75, % missing 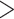 10%, or strand bias (SB)
10%, or strand bias (SB) 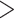
 0.1 were removed due to low quality. We also removed SNPs that exhibit low allele frequencies by filtering out SNPs that have estimated minor allele frequency
0.1 were removed due to low quality. We also removed SNPs that exhibit low allele frequencies by filtering out SNPs that have estimated minor allele frequency 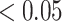 . Lastly, due to the lack of genotype data and small sample sizes (89 cases and 174 controls), we were unable to filter based on the exact or asymptotic Hardy–Weinberg equilibrium tests. So as a substitute, we filtered out SNPs that had estimated probability for genotype 1
. Lastly, due to the lack of genotype data and small sample sizes (89 cases and 174 controls), we were unable to filter based on the exact or asymptotic Hardy–Weinberg equilibrium tests. So as a substitute, we filtered out SNPs that had estimated probability for genotype 1 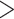 0.5, which is the upper bound had the SNP been under Hardy–Weinberg equilibrium. 22 619 SNPs remained after this filtering.
0.5, which is the upper bound had the SNP been under Hardy–Weinberg equilibrium. 22 619 SNPs remained after this filtering.
The remaining SNPs post-filtering are analyzed with RC, ML as well as the naive Wald test with the called genotype. Since we have unequal number of cases and controls, we did not consider RC with naive variance estimator just as in the simulations. For the three methods of analysis, we control for population stratification with two PCs. For RC and ML, the PCs are computed from the conditional expectation of the genotype, while the naive analysis used PCs computed from the called genotypes. The PCs are included in the analysis as specified in Section 3. The naive analysis demonstrates the biased inference due to ignoring differential sequencing quality between cases and controls but taking population stratification into account.
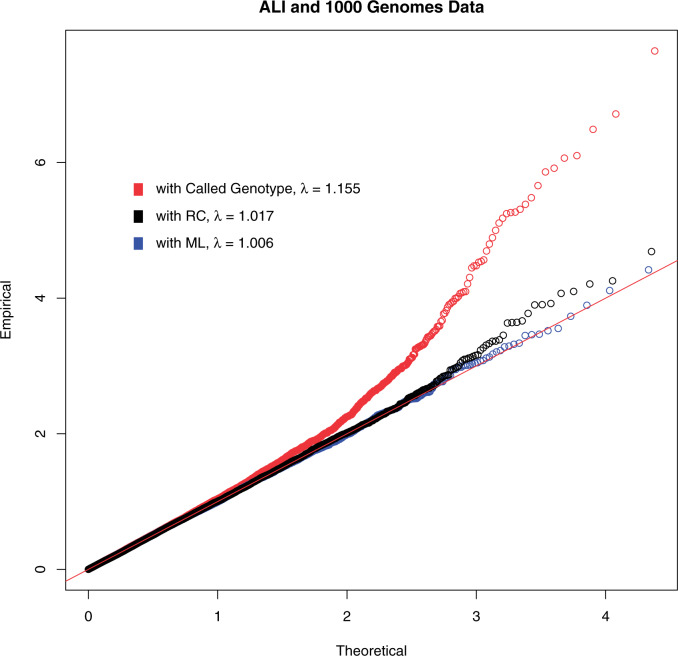
The resulting QQ plots for both RC and ML are close to the 45 degree line (Figure 2), with the tail of the QQ plot for RC showing a little more signal than ML. On the other hand, the QQ plot for the naive analysis with called genotypes is much more liberal in comparison, with the QQ plot well above the 45 degree line. This suggests that naive analysis with such a combined data set can lead to lots of false positives. This is due to the called genotypes that are subject to systematic difference in confidence in the calls between cases and controls, resulting in differential misclassification errors between cases and controls in called genotypes.
Fig. 2.
The QQ plots for analysis of combined ALI and 1000 Genomes data. The red plot is analysis with the called genotypes, the blue plot is analysis with ML, the black plot is analysis with RC. The estimate of the inflation factor 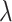 for each method of analysis is in the legend.
for each method of analysis is in the legend.
There were no SNPs that reach genotype-wide significance. There were 5 SNPs that had p-value 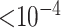 and 30 SNPs that had p-value
and 30 SNPs that had p-value 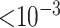 with RC, while the same numbers were 2 and 27 for ML. One of the top hits with both RC and ML is rs2943521 from the MUC5B gene. This gene is associated with mucus secretion, including lung mucus, and has been linked to other lung diseases (Seibold and others, 2011). Looking at the QQ-plots from RC and ML, we can see that the two look very similar, with RC having a few more smaller p-values in the tail.
with RC, while the same numbers were 2 and 27 for ML. One of the top hits with both RC and ML is rs2943521 from the MUC5B gene. This gene is associated with mucus secretion, including lung mucus, and has been linked to other lung diseases (Seibold and others, 2011). Looking at the QQ-plots from RC and ML, we can see that the two look very similar, with RC having a few more smaller p-values in the tail.
6. Discussion
We propose methods for association analysis when there is a systematic difference in sequencing quality between cases and controls while controlling for population stratification. Such a data set arises when combining sequenced cases with publicly available controls, or more generally, when the cases and controls are sequenced on different sequencing platforms. The RC method requires the sandwich estimator for inference with unbalanced case–control sampling but can use the naive estimator with balanced sampling. The latter can be useful when speed is of importance. The ML estimator is unbiased under the alternative when there are no covariates and is approximately unbiased when controlling for population stratification. The RC estimator provides a good approximation of the ML estimator and is much faster/easier to compute. In practice, the type I error and power of the two methods are very similar, the bias of RC is quite small, and its efficiency loss is negligible.
We proposed a solution for controlling for population stratification for both RC and ML, but it is of future research interest for more complex methods to control for general confounders. In addition, forming the sandwich estimator for RC and maximizing the likelihood for ML can be time consuming at the moment. Speeding up both is also of interest and can potentially be achieved through a higher performance language.
In the simulations, RC and ML have similar power. With balanced sampling, the difference in control of type I error between the sandwich and naive estimator appears negligible, though the power seems to be slightly better for the sandwich estimator in some cases. Compared to the existing score-based methods, our methods gives an estimate of the effect size, allows the use of the naive variance estimator with balanced sampling, and controlling for population stratification.
Our method does not require BAM files, which contain sequence reads. It only requires VCF files and that VCF files for cases and controls use the same reference genome, which is generally the case. In other words, the person level data from the VCF files should suffice for applying our methods. Batch effects are an important factor to control for in sequencing studies. In practice, VCF files are usually generated using the joint calling algorithm, which controls for batch effects. Additionally, the PCs are also able to capture additional batch effects.
The methods in this article are for the additive model, but can be extended for the dominant and recessive model by simply substituting in the probability of the desired homozygous genotype for the indicator of said genotype, and the results still hold. Our methods can also be extended to accommodate data sets where cases and controls are both taken from multiple sources of differing quality. We consider common variants in this article, but our RC approach can be extended for analysis of rare variants by modifying the method for association testing using variant set analysis (Lee and others, 2014), such as SKAT (Wu and others, 2011), burden (Li and Leal, 2008), with the true genotype for each variant in the set substituted by their conditional expectation.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
National Institute of Health (R35-CA197449, P01-CA134294, U01-HG009088, U19CA203654, R01-HL113338, and P42-ES016454). The data sets were obtained as part of the identification of SNPs Predisposing to Altered ALI Risk (iSPAAR) study funded by the National Heart, Lung, and Blood Institute (RC2 HL101779).
References
- 1000 Genomes Project Consortium. (2012). An integrated map of genetic variation from 1,092 human genomes. Nature 491, 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balding, D. J. and Nichols, R. A. (1995). A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica 96, 3–12. [DOI] [PubMed] [Google Scholar]
- Carroll, R. J., Gail, M. H. and Lubin, J. H. (1993). Case-control studies with errors in covariates. Journal of the American Statistical Association 88(421), 185–199. [Google Scholar]
- Carroll, R. J., Ruppert, D., Stefanski, L. A. and Crainiceanu, C. M. (2006). Measurement Error in Nonlinear Models: A Modern Perspective. Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- Derkach, A., Chiang, T., Gong, J., Addis, L., Dobbins, S., Tomlinson, I., Houlston, R., Pal, D. K. and Strug, L. J. (2014). Association analysis using next-generation sequence data from publicly available control groups: the robust variance score statistic. Bioinformatics 30, 2179–2188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman, L. S., Midthune, D., Carroll, R. J and Kipnis, V. (2008). A comparison of regression calibration, moment reconstruction and imputation for adjusting for covariate measurement error in regression. Statistics in Medicine 27, 5195–5216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu, W., Oconnor, T. D., Jun, G., Kang, H. M., Abecasis, G., Leal, S. M., Gabriel, S., Rieder, M. J., Altshuler, D., Shendure, J.. and others (2013). Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants. Nature 493, 216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu, Y.-J., Li, Y., Auer, P. L. and Lin, D.-Y. (2015). Integrative analysis of sequencing and array genotype data for discovering disease associations with rare mutations. Proceedings of the National Academy of Sciences United States of America 112, 1019–1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, S. Y., Lohmueller, K. E., Albrechtsen, A., Li, Y., Korneliussen, T., Tian, G., Grarup, N., Jiang, T., Andersen, G., Witte, D.. and others (2011). Estimation of allele frequency and association mapping using next-generation sequencing data. BMC Bioinformatics 12, 231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, S., Abecasis, G. R., Boehnke, M. and Lin, X. (2014). Rare-variant association analysis: study designs and statistical tests. The American Journal of Human Genetics 95, 5–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, S., Kim, S. and Fuchsberger, C. (2017). Improving power for rare-variant tests by integrating external controls. Genetic Epidemiology 41, 610–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, B. and Leal, S. M. (2008). Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. The American Journal of Human Genetics 83, 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, D. J. and Leal, S. M. (2012). Seqchip: a powerful method to integrate sequence and genotype data for the detection of rare variant associations. Bioinformatics 28, 1745–1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, X. and Liang, K.-Y. (1991). Adjustment for non-differential misclassification error in the generalized linear model. Statistics in Medicine 10, 1197–1211. [DOI] [PubMed] [Google Scholar]
- Longmate, J. A., Larson, G. P., Krontiris, T. G. and Sommer, S. S. (2010). Three ways of combining genotyping and resequencing in case-control association studies. PLoS One 5, e14318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyles, R. H. (2002). A note on estimating crude odds ratios in case–control studies with differentially misclassified exposure. Biometrics 58, 1034–1036. [DOI] [PubMed] [Google Scholar]
- McKenna, A., Hanna, M., Banks, E., Sivachenko, A., Cibulskis, K., Kernytsky, A., Garimella, K., Altshuler, D., Gabriel, S., Daly, M.. and others (2010). The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Research 20, 1297–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice, R. L. and Pyke, R. (1979). Logistic disease incidence models and case-control studies. Biometrika 66, 403–411. [Google Scholar]
- Rosner, B., Willett, W. C. and Spiegelman, D. (1989). Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Statistics in Medicine 8, 1051–1069. [DOI] [PubMed] [Google Scholar]
- Sanna, S., Li, B., Mulas, A., Sidore, C., Kang, H. M., Jackson, A. U., Piras, M. G., Usala, G., Maninchedda, G., Sassu, A.. and others (2011). Fine mapping of five loci associated with low-density lipoprotein cholesterol detects variants that double the explained heritability. PLoS Genetics 7, e1002198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seibold, M. A., Wise, A. L., Speer, M. C., Steele, M. P., Brown, K. K., Loyd, J. E., Fingerlin, T. E., Zhang, W., Gudmundsson, G., Groshong, S. D.. and others (2011). A common muc5b promoter polymorphism and pulmonary fibrosis. New England Journal of Medicine 364, 1503–1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shendure, J., Balasubramanian, S., Church, G. M., Gilbert, W., Rogers, J., Schloss, J. A. and Waterston, R. H. (2017). DNA sequencing at 40: past, present and future. Nature 550, 345. [DOI] [PubMed] [Google Scholar]
- Skotte, L., Korneliussen, T. S. and Albrechtsen, A. (2012). Association testing for next-generation sequencing data using score statistics. Genetic Epidemiology 36, 430–437. [DOI] [PubMed] [Google Scholar]
- Spiegelman, D., Rosner, B. and Logan, R. (2000). Estimation and inference for logistic regression with covariate misclassification and measurement error in main study/validation study designs. Journal of the American Statistical Association 95, 51–61. [Google Scholar]
- Tang, L., Lyles, R. H., King, C. C., Celentano, D. D. and Lo, Y. (2015). Binary regression with differentially misclassified response and exposure variables. Statistics in Medicine 34, 1605–1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, M. C., Lee, S., Cai, T., Li, Y., Boehnke, M. and Lin, X. (2011). Rare-variant association testing for sequencing data with the sequence kernel association test. The American Journal of Human Genetics 89, 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.