Neural Selectivity, Efficiency, and Dose Equivalence in Deep Brain Stimulation through Pulse Width Tuning and Segmented Electrodes

Abstract

Background:

Achieving deep brain stimulation (DBS) dose equivalence is challenging, especially with pulse width tuning and directional contacts. Further, the precise effects of pulse width tuning are unknown, and recent reports of the effects of pulse width tuning on neural selectivity are at odds with classic biophysical studies.

Methods:

We created multicompartment neuron models for two axon diameters and used finite element modeling to determine extracellular influence from standard and segmented electrodes. We analyzed axon activation profiles and calculated volumes of tissue activated.

Results:

We find that long pulse widths focus the stimulation effect on small, nearby fibers, suppressing distant white matter tract activation (responsible for some DBS side effects) and improving battery utilization when equivalent activation is maintained for small axons. Directional leads enable similar benefits to a greater degree. Reexamining previous reports of short pulse stimulation reducing side effects, we explore a possible alternate explanation: non-dose equivalent stimulation may have resulted in reduced spread of neural activation. Finally, using internal capsule avoidance as an example in the context of subthalamic stimulation, we present a patient-specific model to show how long pulse widths could help increase the biophysical therapeutic window.

Interpretations:

We find agreement with classic studies and predict that long pulse widths may focus the stimulation effect on small, nearby fibers and improve power consumption. While future pre-clinical and clinical work is necessary regarding pulse width tuning, it is clear that future studies must ensure dose equivalence, noting that energy- and charge-equivalent amplitudes do not result in equivalent spread of neural activation when changing pulse width.

Introductory figure:

Short pulse widths cannot focus the stimulation effect on small, nearby fibers. We use chronaxies from Reich et al.³ for large, side effect-inducing axons, and small, therapeutic axons. Strength-duration curves show that, for short pulses, threshold amplitudes diverge, and small fibers require more amplitude than large fibers, contradicting that short pulse widths could focus the stimulation effect on small, nearby fibers.

Introduction

Deep brain stimulation (DBS) programming has become more complex in recent years with the introduction of directional electrodes^1,2 and interest in pulse width modulation^3–5. Testing the effects of changing the pulse width or using segmented contacts requires a notion of dose equivalence. Various groups have tested changes in parameterization while maintaining various metrics of equivalence, including energy – sometimes referred to as total electrical energy delivered^4,6,7 – charge⁸, strength-duration relationships³, and other quantities similar to energy^9,10.

In the context of thalamic stimulation for essential tremor and subthalamic stimulation for Parkinsonism, smaller, nearby fibers have been associated with therapy, while distant, large fibers have been associated with side effects, supported by chronaxie values for side effects versus therapy³. Long pulse widths have been associated with cognitive deficits in thalamic stimulation for essential tremor⁶, while short pulse widths have been associated with increased therapeutic window^3,5,11 and decreased side effects^4,12. In fact, recent results have suggested that pulse width tuning may be superior to directional segmentation in side effect avoidance⁴ due to the focusing of electrical stimulation on smaller diameter fibers near the electrode while avoiding larger fibers far away from the electrode. However, classic biophysical studies demonstrated that short pulse widths increase selectivity for large diameter fibers¹³, and that selectivity increases with increased distance¹⁴. As seen in the introductory figure, short pulse widths create a divergence between the threshold amplitudes of large and small fibers, with selective activation moving towards large, not small fibers, necessitating an investigation of the biophysical properties underlying the benefits of short-pulse stimulation.We carried out modeling studies focused on axon size selectivity, volume of tissue activated¹⁵ (VTA), and patient-specific modeling to understand the benefits of short-pulse stimulation.

Our modeling results led us to surprising conclusions, generating possible alternate interpretations that need to be investigated for several sets of results on pulse width tuning and directional electrodes. Our work predicts that reduced side effects found with short pulse width could have possibly arisen through controlling amplitude vianon-dose-equivalent metrics, resulting in smaller volumes of neuronal activation when using short pulse widths. Further, we question whether finer amplitude titration on programming devices would enable easy avoidance of side effects associated with long-pulse stimulation, enabling more optimal treatment and substantially increasing battery life. In-so-doing, we predict that longer (cf. shorter) pulse widths should optimally focus the stimulation effect more on small, nearby, and therapeutic axons, and less on large, distant, side effect-inducing fiber tracts, thus maximizing energy efficiency. We demonstrate that directional electrodes, with decreased contact surface area, can focus the effect of stimulation on small, nearby axons to an even greater extent than pulse width modulation. Finally, we use patient-specific modeling of STN stimulation as an example to predict that it is possible to activate more of the subthalamic nucleus before stimulating into the internal capsule with longer-than-standard pulse widths. While our results were found in the context of deep brain stimulation, they hold broad implications regarding invasive electrical stimulation and may serve to guide development of neuromodulation devices for a variety of disease states.

Methods

Overview

We modeled stimulation influence on activation volumes through multicompartment NEURON models, with fibers arranged tangentially around the electrodes. We determined activation profiles for 2.0 and 5.7 μm diameter neurons for the Medtronic 3387 and Abbott 6173 electrodes at pulse widths from 20 to 450 μs and amplitudes from 0 to 10 mA or 0 to 10 V, depending on whether the lead geometry is voltage or current controlled. We calculated the total charge injected and energy for each parameter set. We analyzed the relationships between pulse width and directional segmentation on the shaping of volumes of tissue activated (VTA)^16,17 for each fiber size.

Finite element model

We used the finite element method, implemented in SCIRun 4.7 (Scientific Computing and Imaging (SCI), Institute, University of Utah, Salt Lake City, UT), to solve the bioelectric field problem. Electrode contacts were modeled as ideal conductors, and electrode shafts were modeled as ideal insulators¹⁸. The volume of tissue surrounding the electrode was modeled using isotropic conductivities, using 0.2 S/m for tissue, and 0.1 S/m for the 0.5 mm encapsulation layer¹⁹. We solved for the electric potential solution for pulse widths of 20, 30, 40, 50, 60, 90, 120, 180, 300, and 450 μs for each contact on the Medtronic 3387 and Abbott 6173 leads using −1 V and −0.5 mA, respectively. The outer boundary of the computational model (100 mm × 100 mm × 100 mm) was set using Dirichlet boundary conditions to stimulate the distant anode for monopolar cathodic stimulations²⁰.

NEURON Modeling

Briefly, we used multicompartment axon models to quantify neuron response to extracellular stimulation and used these results to compute the volume of tissue activated¹⁶ (VTA) and spread of activation, applying what we recently referred to as the axon model method²¹. We provided monopolar stimulation, and as we found in that recent work, various methods of activation estimation all yield highly similar results with monopolar (cf. bipolar) stimulation²¹. The waveform consisted of biphasic pulses, with a cathodic pulse, followed by a 100 μs interphase delay, then a 10% amplitude / 10 times duration charge-balancing pulse.

More specifically, we performed simulations in NEURON 7.4 using the MRG neuron model²² to model 5.7 μm diameter myelinated fibers and modified parameters of the MRG model to represent 2.0 μm diameter myelinated axons^23,24. We simulated 2.0 μm diameter fibers to quantify therapeutic activation and 5.7 μm diameter fibers to quantify side-effect activation¹⁶. For the Medtronic 3387 lead, tangential neurons were distributed evenly around the electrode in 0.4 mm increments from 0 to 10 mm in the radial direction and across a range of 20 mm in the axial direction. Electric potential solutions were linearly interpolated onto each node, paranode, and internode segments of the MRG model in MATLAB. To generate a VTA, the voltage data are rotated at 2° steps around the lead to take advantage of the axisymmetry of the cylindrical leads. For the directional Abbott 6173 lead, tangential neurons were arranged in 0.4 mm increments on the xy-plane through the first row of directional contacts. No axons were spaced in the axial direction to reduce computational time, and for this reason, we do not quantify volumes for the directional lead. Based on our previous work²⁵, cathode stimulation preferentially activates passing axons, and therefore, tangentially oriented axons are the most excitable orientation during cathodic stimulation. Most clinical stimulation paradigms involve cathodic stimulation, so we applied that in this work. Thus, given that tangential axons are the most appropriate orientation to quantify activation due to cathodic stimulation, the use of tangential neurons alone is sufficient to describe the influence of extracellular cathodic stimulation.

Selectivity of Pulse Width and Directional Modulation

We first tested the effects of pulse width tuning on neural selectivity. We found the maximum distances for which 2.0 and 5.7 μm axons are activated by 60 μs, −1.0 V pulses from the Medtronic 3387 lead. Maintaining 2.0 and 5.7 μm axons at these distances, we found activation thresholds for both axons with pulse widths from 20 to 450 μs to determine the effect of pulse width on selectivity. To test the effects of directional stimulation on neural selectivity, we found the maximum distances for which 2.0 and 5.7 μm fibers are activated by 60 μs, −1.0 mA pulses from the Abbott 6173 lead with two active contacts. Maintaining 2.0 and 5.7 μm axons at these distances, we found activation thresholds for both axons during ring mode and single contact directional simulation to determine the effect of segmented contacts on selectivity.

Charge, Energetic Demand, and Battery Life Calculations

Charge per pulse (Q) is defined simply as (V × pw) / Z. We computed energy (E) as (V² × f × pw × 1 sec) / Z, where V is voltage, f is frequency, pw is pulse width, and Z is impedance²⁶. We normalized the energy required for each pulse width (E_pw) by that required for a nominal 60 μs pulse (E₆₀) to compute the relative theoretical battery life as 100% / (E_pw / E₆₀). We computed voltages for equivalent spread of activation for 2.0 μm fibers across pulse widths from 20–450 μs and determined energetic demand for these parameter combinations.” For conversion from ring mode to directional contacts, we computed currents for equivalent spread in the intended direction for 2.0 μm fibers across pulse widths from 20–450 μs. Calculations were done using current, with conversion following Ohm’s law: V = I × Z.

Clinical Evaluation of dose equivalence

For previous clinical experiments that have used pulse width as an independent variable in human subjects research, we computed VTAs with reported stimulation parameters to evaluate fiber size selectivity and equivalence in the context of pulse width tuning in humans:

• Reich et al., 2015: We analyzed the clinical data from the 2015 paper by Reich et al.³ We computed VTAs at thresholds for rigidity control (2.0 μm fibers) and contraction side effects (5.7 μm fibers) for all pulse widths: 20, 30, 40, 50, 60, 90, and 120 μs. For simplicity, we modeled with Medtronic 3387 electrodes, and converted current to voltage via Ohm’s law with a typical impedance of 1 kΩ. We compared VTA sizes across all combinations of pulse width and amplitudes used in Reich et al. to verify dose equivalence.

• Choe et al., 2018: We also analyzed the pulse width and directional experiment from Choe et al.³ We modeled spread over 5.7 μm fibers with Abbott 6173 leads at given parameters for ring mode (−3.44 mA at 60 μs vs. −4.85 mA at 30 μs). Additionally, we found the spread of activation for energy-equivalent stimulation from ring mode stimulation to single-contact directional stimulation as well as with strength-duration dose equivalence described in supplementary material, Appendix C: Dose equivalence with segmented contacts and directional stimulation.

• Woods et al., 2003: To simulate VTAs derived from Woods et al.⁶, we modeled activation by 105 μs and 80 μs pulses, for both large and small fibers, to approximate the average pulse widths they reported for subjects exhibiting (105.37 μs) and not exhibiting (79.09 μs) cognitive decline. We isosurfaced VTAs at the reported −3.18 V and −3.51 V for both large and small diameter VTAs to generalize VTA spread in Woods et al., to determine the influence of activation volume on clinical outcomes.

Patient-specific direct axon modeling

We obtained diffusion-weighted MRI from a patient with Parkinson’s disease prior to implantation with a DBS lead to the STN and then obtained the lead location through postoperative CT. We processed the diffusion-weighted imaging according to methods described in our previous work^18,27. We generated 1000 tracts for the internal capsule by seeding the anterior limb of the internal capsule, and then we resampled node spacing along the tracts to match node, paranode, and internode segments. We linearly interpolated electric potential on the internal capsule based on patient lead location. Importantly, we modeled the activation of the STN through 2.0 μm axons, while internal capsule fibers were modeled with 5.7 μm axons.

Statistics

When relevant, we present results as mean +/− standard error. We use the following abbreviations: Student t-test is referred to as t-test and Pearson correlation coefficient t-test is referred to as Pearson t-test.

Results

We used the finite element method (in SCIRun) to solve the bioelectric field problem for monopolar stimulation from Medtronic 3387 and Abbott 6173 electrodes for 0–10 V and 0–10 mA amplitudes, respectively. We mapped this extracellular voltage field to multicompartment myelinated axon models (in NEURON) projecting tangentially around the electrode, with 2.0 and 5.7 μm diameters. From these simulations, we reexamine the relationships between stimulation amplitude, pulse width, strength duration curves, contact size, energy efficiency, charge delivered, and the different volumes of tissue activated when considering 2.0 versus 5.7 μm diameter fibers.

Long pulses and segmented contacts focus stimulation on small, nearby axons

We began by exploring the ability of pulse-width tuning to differentially activate axons of different sizes. First, we found maximum distances at which 2.0 and 5.7 μm axons were activated by −1.0 V, 60 μs pulses from a cylindrical electrode: 1.31 and 2.06 mm, respectively (Fig. 1A). We shortened the pulse width to 30 μs and found that the large, distant fiber required less voltage than the small, nearby fiber to fire at 30 μs. With a 90 μs pulse, the small, nearby fiber was activated with less voltage. Tracking axonal firing thresholds as a function of distance, we found that lengthening the pulse width progressively increases selectivity for small, nearby axons (Fig. 1B).

Figure 1:

Longer pulses and smaller contacts focus the stimulation effect on small, nearby fibers. A. We determined maximum distances where 2.0 and 5.7 μm axons are activated by −1.00 V, 60 μs pulses from the Medtronic lead, then found minimum amplitudes to activate axons at these distances with 30 and 90 μs pulses. 30 μs stimulation more easily activated the large fiber, while the opposite was true with 90 μs. B. Ratios of threshold amplitudes as a function of pulse width show that longer pulses focus stimulation more effectively on small, nearby fibers, and that the effect is greater for smaller voltages. C. We determined maximum distances at which 2.0 and 5.7 μm axons are activated by −1.00 mA, 60 μs pulses per contact from the Abbott lead using 2 segmented contacts, then found thresholds with ring mode and 1 contact. Ring mode more easily activated the large fiber, while one segmented contact focused the effect on the small fiber. D. Small fiber selectivity increases as contact surface area decreases, and the effect was greater for smaller amplitude currents. Note the different scale from B to D.

We next examined whether similar selective activation of small fibers was also achievable with directional contacts. We found distances at which 2.0 and 5.7 μm axons were both activated by −1.0 mA, 60 μs pulses from two segmented contacts on the same axial plane of a directionally segmented electrode: 1.78 and 2.52 mm, respectively. During ring mode stimulation, we found that the large, distant axon was activated with less current than the small, nearby axon. With one segmented contact, the small, nearby axon was activated with less current (Fig. 1C). In fact, decreasing the number of segmented contacts focused the stimulation effect on small, nearby axons to a degree that is even more powerful than lengthening the pulse width (Fig. 1D, note scale change in ordinate axis from 1B).

We fit strength-duration curves to our simulation results for 5.7 and 2.0 μm diameter axons at several distances from the electrode. The shapes of the curves for different axon sizes were similar, and the relative selectivity for small axons improved with increased pulse width and increased proximity to the contact (Fig. 2A). We similarly derived strength-duration curves using one, two, and all three segmented contacts on the same level of a directionally segmented electrode. Once again, longer pulse widths and increased proximity to the contact improved selectivity for smaller axons in all contact configurations, as did reducing the number of contacts (Fig. 2B). To summarize, selectivity for smaller fibers is best achieved by segmented contacts in close proximity to the fibers of interest and using long stimulation pulses.

Figure 2:

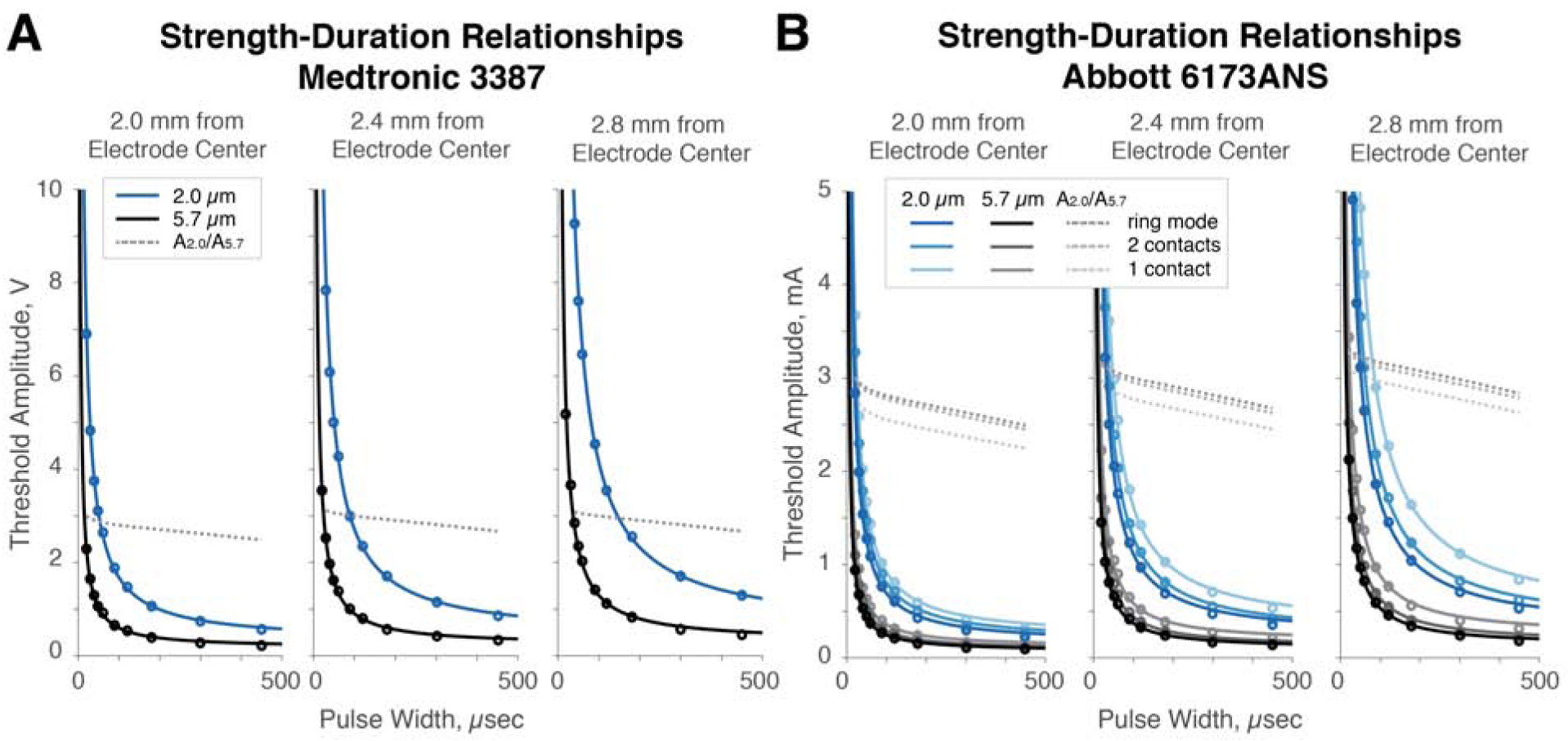
Strength-duration curves reveal that long pulse widths, proximity to electrode, and small, segmented contacts reduce preferential selectivity for large fibers. A. We derived strength-duration relationships for 5.7 and 2.0 μm fibers at 2.0 and 3.2 mm from the electrode center given a Medtronic 3387 electrode. Computing the ratio of the amplitudes needed to activate 2.0 vs 5.7 μm fibers (A2.0/A5.7), we find that the preferential selectivity for the large fiber decreases with distance. Further, increasing the pulse width decreases this preferential selectivity. B. We derived similar relationships for 5.7 and 2.0 μm fibers at the same distances with an Abbott 6173 electrode given the use of ring mode, two, and one segmented contacts. Similar results were found as in A; further, using fewer segmented contacts decreased the preferential selectivity for large fibers.

Long pulses and small contacts minimize energetic demand, improving battery life

Given that longer pulses and segmented contacts improved selectivity for smaller axons, we evaluated the energy efficiency of waveforms featuring long pulse widths and directional configurations. When constrained to a strength-duration curve, using a pulse width that equals the chronaxie of an axon minimizes energetic demand and maximizes theoretical battery life (Fig. 3A; see Supplemental Appendix A for mathematical derivation, different from those previously published^28,29). Specifically, given a model chronaxie of ~341 μs, shortening pulse width from 60 to 30 μs increased energetic demand by 71%, while further shortening to 20 μs increased energetic demand by 143%. Lengthening pulse width from 60 to 150 μs decreased energetic demand by 40%, while further lengthening the pulse width to equal the chronaxie decreased energetic demand by 49%.

Figure 3:

Energy efficiency and theoretical battery life are optimized by lengthening the pulse width to the value of the chronaxie and using a single directional segmented contact. A. Moderately long pulses (specifically, the chronaxie) optimize energy efficiency, while charge increases linearly with pulse width. B. Energy is reduced substantially by dose-equivalent stimulation (same spread in the intended direction) with one segmented contact. Theoretical battery improvements when switching to a single contact are slightly greater at short pulse widths due to poor efficiency with short pulses. C. For a given spread in the intended direction, single contact stimulation at a moderately long pulse width maximizes theoretical battery life.

Decreasing the number of active contacts to one active segmented contact substantially decreased energetic demand (Fig. 3B, left). In general, stimulating with one contact to create an equivalent spread of activation in the intended direction decreased energy utilization by an average of more than 50%. This relative effect is slightly greater for very short pulses (Fig. 3B, right) for which all stimulation modes are particularly inefficient (Fig. 3A). In absolute terms, however, longer pulse widths on single directional contacts minimize energetic demand (Fig. 3C).

Strength duration

There is no consensus on how to define a dose for stimulation therapy; therefore, we investigate how different metrics of dose equivalence can change the volume of tissue activated (VTAs: Supplemental Appendix B; Supplemental Fig. 1). We determined relationships between pulse width and voltage to maintain energy, charge, and VTA size equivalence for 2.0 and 5.7 μm fibers, starting from a 60 μs pulse (Fig. 4A). At short pulse widths, energy equivalence required less voltage than VTA equivalence, which required less voltage than charge equivalence. Thus, for short pulse widths, maintaining energy equivalence creates a smaller VTA, while maintaining charge equivalence creates a larger VTA. The opposite results were found for long pulse widths (Fig. 4B), and thus, supports the notion that longer pulse widths have improved energetic efficiency over short pulse widths when maintaining a consistent spread of activation.

Figure 4:

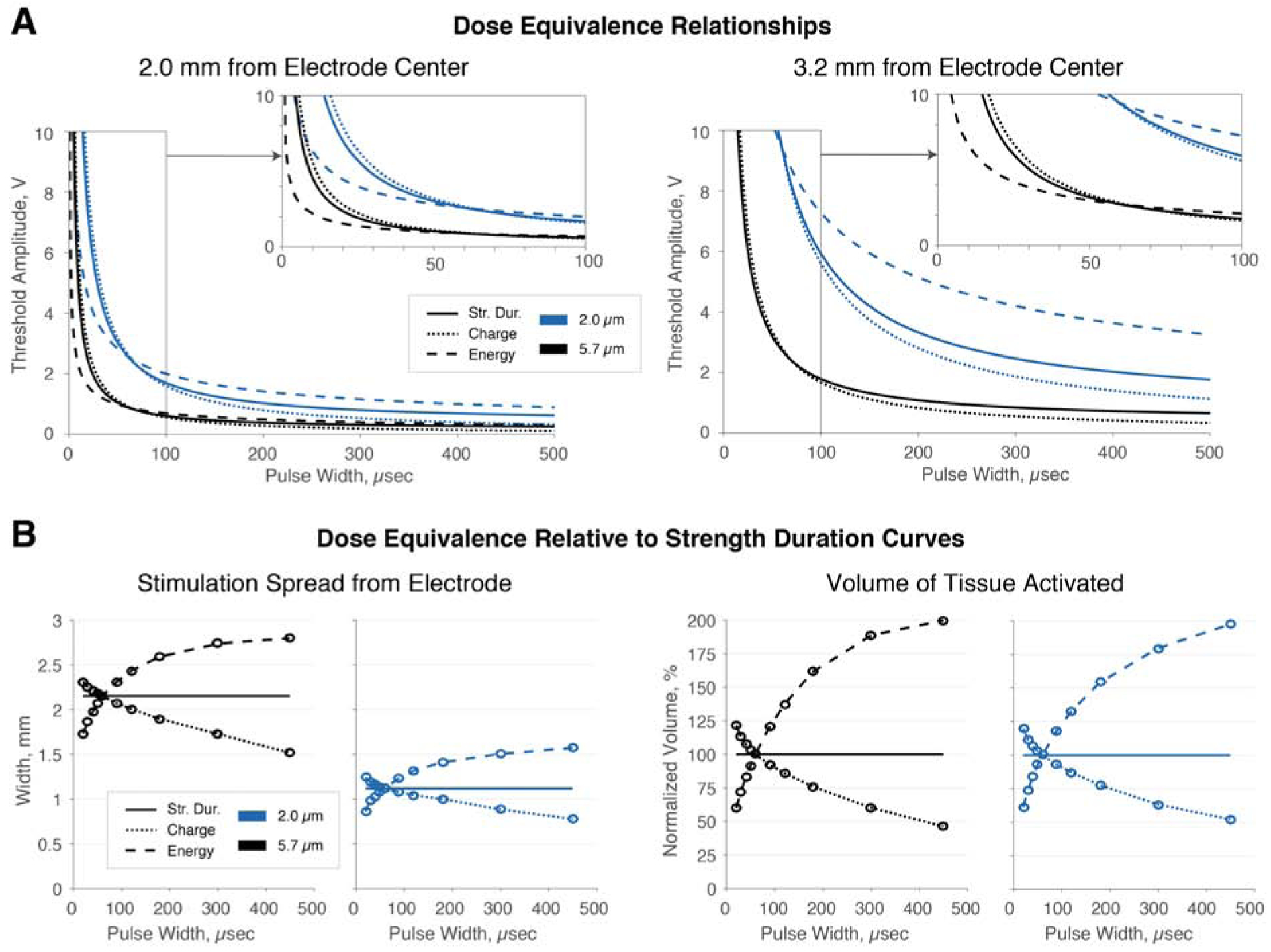
Comparison of strength-duration relationship, charge, and energy as equivalence metrics. A. Each of strength-duration equivalence, charge equivalence, and energy equivalence have been used as metrics to maintain equivalent neural activation when changing parameters. For short pulses, the voltage required to maintain energy equivalence is less than that required to maintain a strength-duration relationship, while the voltage required to maintain equivalent charge per pulse is greater. With long pulses, the trend reverses. B. Energy equivalence results in reduced spread of activation and VTA for short pulses and increases these for long pulses. Charge equivalence reverses this trend. Thus, both energy- and charge-equivalent parameters, with pulse width tuning, result in non-equivalent neural activation. Taken together, these results indicate that energy and charge equivalence are an inappropriate means for maintaining dose equivalence when changing pulse width and will always result in greater or reduced, never identical, spread of neural activation.

Analysis of Reich et al., 2015: pulse width modulation does not modify stimulation spread for side effects or rigidity control.

Across both rigidity control and contraction thresholds, reported combinations of pulse width and threshold amplitudes yielded insignificant changes in VTA (p=.199, rigidity control; p=.105, contractions; Pearson t-test) or spread (p=.129, rigidity control; p=.095 for contractions; Pearson t-test) (Fig. 5A). As reported, 20 μs pulses failed to generate contractions in most patients due to a 10 mA limitation. Thus, we analyzed contraction thresholds excluding 20 μs data, finding higher p-values (p=.277 for volume, p=.265 for width, Pearson t-test). Dose equivalence in Reich et al., was determined by symptom response, and therefore closely followed the strength-duration curve of dose equivalence. As a result, VTAs were not significantly different across tested pulse widths. We conclude that from a biophysical perspective, the therapeutic window was unchanged using pulse width modulation; however, only the range of stimulation amplitude between therapy and side effect thresholds increased. The interpretation that short pulse widths focus the stimulation effect on small, nearby fibers is not supported; our data presented in the introductory figure, Fig. 1A, and Fig. 2A suggest the opposite.

Figure 5:

Evaluation of example and human data sets. A. Reich et al.³ report that short pulse widths increase therapeutic window and better focus the stimulation effect within small, nearby axons. In our simulations of their therapeutic and side effect thresholds, activation spread did not vary significantly across pulse widths. Pulse-width tuning therefore did not impact therapeutic window from a biophysical perspective. B. Woods et al.⁶ associated long pulse widths with cognitive decline in thalamic DBS. Simulations with their parameters yielded larger VTAs in those with decline than in those without, supporting that VTA size (cf. pulse width per se) may be predictive of cognitive decline. C. Choe et al.⁴ found that, when balanced for energy use, short pulses reduce side effects, but directional stimulation does not. From our simulations of their parameters, overall spread reduced with pulse width for both fiber sizes (5.7 μm shown on left). Maintaining amplitude with one contact increased spread in the intended direction, but also largely in the opposite direction. Using our equivalence equation from supplemental appendix C, we match the intended spread for 2.0 μm fibers with more directionality and reduced 5.7 μm spread.

Analysis of Woods et al., 2003: Patients with cognitive decline had larger VTAs.

Woods et al.⁶ found that thalamic DBS patients with cognitive decline had, on average, ~33% longer pulse width than those without. We modeled VTAs for large and small fibers with their average reported settings. VTAs for both fiber ize were significantly smaller in those without cognitive decline than in those with cognitive decline (p=.027, t-test, Fig. 5B). We propose that another possible mechanism by which cognitive decline occurred was the larger spread of stimulation in patients with cognitive decline could potentially reach more side effect-inducing fibers.

Analysis of Choe et al., 2018: reduced side effects with short pulse widths may have resulted from smaller VTAs; maintaining energy equivalence with directional contacts reduces directionality.

Choe et al.⁴ showed that decreasing thalamic pulse width from 60 to 30 μs while modulating amplitude to maintain energy dose equivalence resulted in reduced ataxic side effects. We found that activation spread was significantly greater for 60 μs parameters than for 30 μs (p=.000042, t-test) (Fig. 5C, left). We propose an alternate conclusion that the 30 μs case reduced ataxic side effects because the spread of activation was substantially reduced from the 60 μs case. In such a suprathreshold case, a reduction in VTA size could decrease activation of fibers responsible for side effects, yet remain greater than the minimum VTA spread required for therapy.

We also analyzed results showing that directional stimulation was ineffective for side effect avoidance. Maintaining energy equivalence from ring mode stimulation to single-contact directional stimulation results in a loss of the electrode’s capability to avoid stimulation in the unintended direction (Fig. 5C, right). Axons of both sizes are activated in the intended direction across greater distances (p=.000013, t-test), and energy-equivalent stimulation results in ~50% of the spread from ring mode in the opposition direction. The overall spread across intended and opposite directions is over 90% of the original linear spread, just shifted slightly in the intended direction. We propose an alternate conclusion: directional stimulation failed to generate consistent reductions in side effects because using energy for dose equivalence is particularly ineffective when switching between numbers of contacts. In the supplemental work, we show parameters that may have been a more effective means of maintaining spread in the intended direction from the ring-mode case, generated from our segmented contact dose equivalence equation (Supplemental Appendix C, Supplemental Fig. 2).

Patient-specific direct axon modeling predicts that longer-than-standard pulse widths enable greater activation of STN when avoiding stimulating into the internal capsule.

Given diffusion-weighted MRI data from a patient implanted with an electrode to the subthalamic nucleus, we generated a model including the subthalamic nucleus comprised of small grey matter axons, and larger internal capsule (IC) white matter axons generated from diffusion tensor imaging. We simulated the neural response to stimulation through a Medtronic 3387 electrode. In this particular patient, the electrode was situated on the dorsolateral edge of STN near the IC. Thus, even activating a little over 20% of the STN with 60 μs pulses would result in stimulation of a small percentage of the internal capsule (Fig. 6A). We found the maximum achievable percentage of STN activation before the IC is activated increases with increases in pulse width (Fig. 6B). We repeated this simulation 9 times first using randomized node locations, and then shifting nodes 8 times from node to internode positions. We found that 450 μs stimulation enabled greater STN activation prior to IC activation than any other pulse width tested (p<.00001, t-test). We found significant increases in maximum achievable STN activation prior to IC activation when increasing the pulse width from 30 to 40 μs (p=.0265, t-test) and each of 60 to 90, 90 to 120, 120 to 180, 180 to 300, and 300 to 450 μs (p<.00001 for each, t-test), while increasing from 40 to 50 and 50 to 60 trended towards increased maximum STN activation. Note that we do not present 20 μs pulses because 20 μs stimulation with a standard amplitude maximum of 10 V, implemented in our model, could not generate a large enough VTA to reach the IC. With a pulse width of 60 μs for this particular lead location, we found that 16.86% of STN could be activated before the IC is stimulated, while the maximum achievable percentage of STN activation was 19.41% at 450 μs. Further, increases in maximum STN activation prior to IC activation were highly predicted by pulse width, with r^2 = .9953. We determined the voltages required to maintain this equivalent STN activation at 60 μs as well as the voltages to begin activating the IC (Fig. 6C). Comparing the ratios of these voltages at all tested pulse widths, we found that shorter pulse widths could not maintain equivalent STN activation without stimulating into the IC, while longer pulse widths enabled equivalent activation at substantially lower voltages than those required to stimulate into the IC (Fig. 6D).

Figure 6:

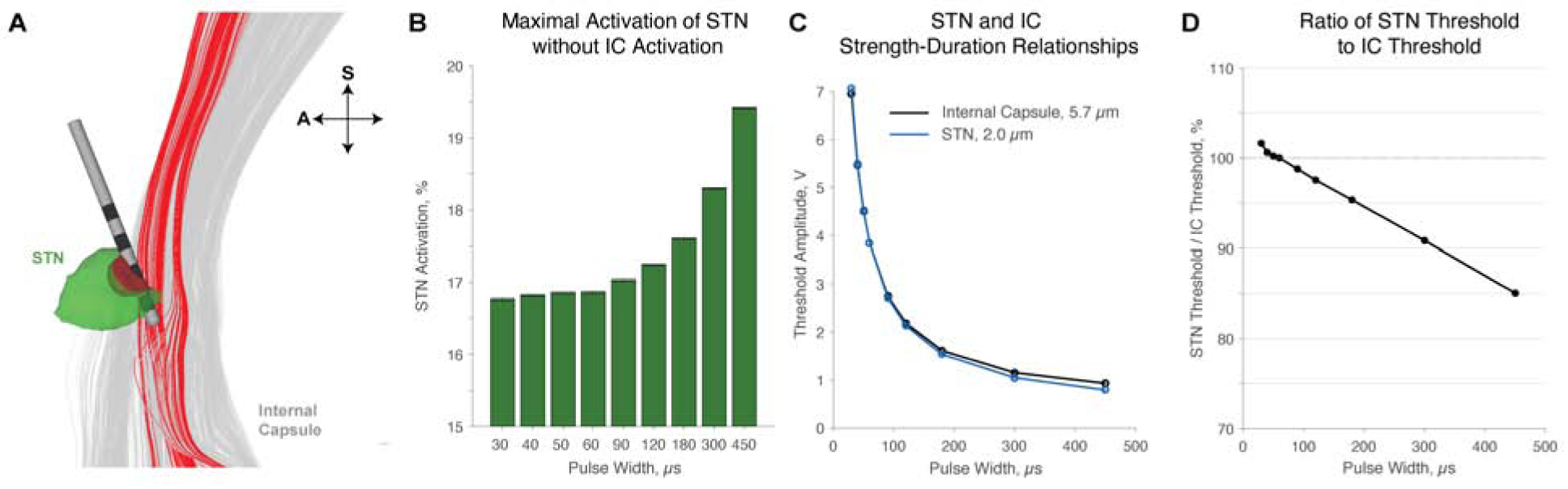
Activation of STN and avoidance of IC with patient-specific direct-axon modeling. A. We modeled Medtronic 3387 lead placement, IC axons, and STN using diffusion-weighted MRI and DTI. In this patient, the electrode is situated on the dorsolateral edge of STN. In this example, applying 60 μs, −5V pulses is predicted to activate 21.17% of the STN (green is inactivated, while red and in-between color is activated) and 4.9% of IC (grey is inactivated, while red is activated). A is anterior, while S is superior. B. Error bars represent standard error of the mean. The maximum achievable percentage of STN activation before IC is activated is predicted to increase with pulse width, and increasing the pulse width beyond standard values significantly increases the maximum achievable activation of STN prior to IC activation. C-D. From B, 60 μs pulses would enable a maximum of 16.8% of STN to be activated before IC is activated. As pulse width decreases, the necessary voltage to maintain this equivalent 16.8% STN activation increases above the threshold to activate IC. With longer pulses, equivalent STN activation is achieved at a lower voltage than that required to activate IC.

Discussion

In this work, we provide computational evidence that short pulse widths may drive preferential selectivity for large axons, while long pulse widths focus the stimulation effect on small, nearby axons, in agreement with classic literature^13,14. Large, distant axons are often associated with side-effects; whereas small, nearby axons are often associated with therapeutic benefits. If the goal of therapy is to target stimulation to small grey matter axons, pulse widths longer than common clinical values require less energy to activate the same tissue when compared with shorter pulse widths, plus there is reduced activation of larger fiber populations. Thus, our modeling work predicts that longer pulse widths can better contain the effect of stimulation within local grey matter while prolonging battery life. While these effects using pulse width modulation are potentially quite useful for patient programming, we demonstrate that directional segmentation of electrodes can provide these benefits to a greater degree.

Pulse width and therapeutic window

Short pulse widths widen the therapeutic window of DBS in terms of a wider range of amplitudes. However, analysis of data from Reich et al. shows that the ratio between the minimum and maximum amplitudes in the therapeutic window did not significantly change over pulse widths from 20 to 120 μs³. While amplitude is the simplest way to define therapeutic window³⁰, we believe that it could be misleading to define therapeutic window on one programming variable whose effects can be countered by accommodations of other programming variables (i.e. amplitude and pulse width). Ideally, the field should consider therapeutic window from a biophysical perspective, based on the specific volume or set of neurons that are activated by a combination of parameters. While this is a substantially more complicated manner of thought, using a dose equivalence metric based on neuron response will ensure that studies are properly controlled when testing different DBS programming variables. Using this biophysical definition of dose equivalent, we find is a minor, yet significant, difference in the therapeutic windows generated with different pulse widths. Specifically, longer pulse widths enable greater activation spread over small axons before reaching a population of large axons, as further demonstrated in our final figure with patient-specific modeling (Fig. 6). While it is not precisely clear why this focusing effect occurs for small fibers, it could stem in part from the fact that larger fibers have more surface area and reduced membrane resistance; thus, they have reduced time constants, and could possibly respond more rapidly to a shorter stimulation pulse, i.e. larger diameter fibers would be even more likely to fire during short pulses. Finally, in regards to therapeutic window as defined by range in amplitude from therapeutic to side effect thresholds, one must consider that short pulse stimulation can truncate the therapeutic window based on the maximal amplitude a device could stimulate. Some clinical devices are incapable of stimulating above 10 mA or 10 V, which would make it difficult in some cases to reach similar activation spread with short pulse stimulation.³

Distance and selectivity

We note that all results taken at a specified distance were repeated at 400 μm intervals from just outside the electrode to a distance 10 mm away, of course bounded by maximal voltages. At all points tested, results held. This stated, we note, as have others¹⁴, that distance has a subtle, but interesting impact on axon size selectivity relationships. Previous work found that distance from the electrode can slightly modulate strength-duration curves for all axon sizes³¹ and that chronaxie increases with distance from the electrode³². Our results find agreement and suggest that the change in chronaxie of different axon sizes do not scale identically with distance from the electrode.

Longer pulse widths are predicted to have benefits over shorter pulse widths in many DBS cases.

Our results provide an alternate explanation for the reductions in side effects shown with short-pulse stimulation when calculating dose equivalence through energy equivalence⁴ and with voltages averaging lower than those with energy equivalence:¹² while further validation of the modeling results is necessary, our results suggest that when decreasing the pulse width and adjusting the amplitude using energy equivalence, creates a smaller spread of activation and may result in fewer side effect-inducing distant, large axons being activated. However, even if our alternate explanation is correct, short pulses do have some benefits. Given biophysical dose equivalence, they decrease charge injection, a nearly 10% reduction found when converting from 60 to 30 μs³, which could help with reducing charge density. Additionally, very long pulse widths and long interphase intervals can result in incomplete charge recovery by the charge-balancing pulse, bringing about safety concerns^33,34. That stated, however, it is unclear that shortening the pulse width below 60 μs will have much positive impact on stimulation safety, and pulse widths are sometimes lengthened to 450 μs clinically without obvious negative effects. Given that implantable pulse generators are programmed across device-specified amplitude increments, small pulse widths provide more steps through the therapeutic window. Thus, using a shorter pulse width and having more amplitude settings to choose from could more finely titrate the stimulation amplitude and provide programmers with more flexibility when programming. However, many devices currently available already have adjustable amplitude step sizes, and long pulses may achieve better utility through the simple solution by device companies to allow smaller amplitude steps for longer pulse widths. Using longer pulse widths could decrease energetic demand, increasing time between battery replacement surgeries. Additionally, longer pulse widths are predicted to decrease preferential activation of larger fibers, and may enable better side effect avoidance in patients.

Long, not short, pulse widths improve battery life; battery life does not vary inversely with charge.

Numerous reports have asserted that short pulse widths improve battery life due to reduced charge. Charge scales with pulse width, but decreasing charge does not increase battery life. Battery life depends on energy, the multiple of charge and voltage, not just charge. When voltage is help constant, only then does energetic demand scale with charge. In contrast, in DBS, decreasing pulse width below requires substantially increased voltage to maintaining similar neural activation and overall raises the energetic demand. On the other hand, increasing pulse width increases charge but decreases voltage enough to reduce overall energetic demand. However, one cannot increase pulse width indefinitely and expect reduced energy demand. Past the chronaxie, increasing pulse width does not result in enough voltage decrease to overcome the increased charge, and energetic demand increases. An energetically optimal pulse width is the chronaxie of an axon, which is 200–700 μs in grey matter³⁵. This is in line with previous findings that decreasing axon diameter – which corresponds to an increase in the chronaxie – increases the energetically optimal pulse width.³⁶

Programming directional electrodes and gaining their benefits

In the context of directionally segmented electrodes, it is particularly important to consider biophysical dose-equivalence parameters when changing the number of active segmented contacts, rather than modulating amplitude through equivalence in measures like energy. As recently well established, segmenting contacts significantly alters the VTA shape and size.³⁷ Applying the same amplitude from ring mode on only one portion of a segmented electrode can result in overshooting stimulation in the direction of the segmented contact and spillover of stimulation around the back of the electrode in the unintended direction, reducing the utility of the directional electrode. Achieving equivalent stimulation in the intended direction for one contact depends on creating a VTA with similar spread to that achieved in ring mode, which requires less overall amplitude than the amplitude determined by energy dose equivalence. Further, we found that segmented contacts decrease selectivity for distant, large fibers. Mechanistically, this may result from decreasing the effective width of the stimulation source, introducing a narrower voltage profile along the length of an axon. Smaller diameter fibers with shorter internodal spacing between nodes may be better able to capture the rapidly changing spatial field, while large diameter fibers, which can still respond more easily due to greater internodal spacing, will be less sensitive to rapid spatial changes in electric potential produced from smaller contacts.

Another benefit of directional stimulation is that using only one segmented contact decreases energy usage. When switching from ring mode to a single segmented contact, the amplitude on one contact must be increased from the amplitude used on each of the three contacts to maintain equivalent spread in the intended direction. However, the new amplitude is substantially smaller than the previous sum across three contacts. Since the amplitude term is squared in power and energy, the energy savings are substantial with one contact instead of three.

Finally, segmented contacts would be predicted to always, at the very least, be capable of matching the results of standard electrodes. As we note, one can always at least program segmented electrodes in ring mode to match the benefits of standard electrodes. Thus, given the predicted improvements in therapeutic benefits of directional leads, as well as improved efficiency, we believe our results should promote their use.

Potential caveats

Results derived from computational models must be clinically validated; given that our work is not in full agreement with some clinical work, it is especially important that it is fully validated before being considered clinically valid. However, the computational models used here are based on validated models and have been well studied. Recent attention has been placed on the importance of patient-specific modeling^38,39; however, we have performed studies primarily aimed at determining general relationships, and only the final figure employs patient-specific modeling, though the patient-specific modeling results closely match the generalized results we found. While it may be predicted that the specific methods of modeling may influence the results obtained, we recently found that methods currently used for VTA all generate highly similar results for monopolar stimulation.²¹ Therefore, it is highly unlikely that the specific methods influenced the general relationships found in this work. Fundamentally, without a specific axon model in mind, strength duration curves as defined by the chronaxie show an undisputable divergence in activating small fiber diameters with shorter pulse widths from their larger diameter counterparts. Future work could examine additional metrics of membrane biophysics. It is true that internodal distance is quite proportional to fiber diameter over the range of fiber sizes and species⁴⁰ -- this relationship is necessary to optimize conduction velocity^41,42. That said, it may be useful in the future to examine models with a biologically valid degree of fluctuation within internodal spacing. On this note, encapsulation layers fluctuating in size or resistivity can influence spread over all axon sizes¹⁹, and it would be interesting to explore selectivity in the context of these variables in the future. Given that every patient’s lead implantation is different and distance from electrode influences chronaxie, our dose equivalence equations presented in supplemental appendix C are most useful theoretically. If a chronaxie estimate is incorrect, the voltage required for an equivalent dose will vary, particularly with large changes in pulse width. While our work champions longer pulse widths in relevant scenarios, one must consider charge density safety when increasing pulse widths. Charge density should not exceed 30 μC/cm²; this has not been an issue on standard electrodes with pulse widths commonly reaching 450 μs in some indications. However, as we move towards segmented contacts with reduced surface areas, one must continue to evaluate charge densities, which rise with increased pulse width and decreased stimulation surface area. Our work solely employed rectangular waveforms, as this is what is typically clinically employed; however, the energetically optimal waveform shape changes with pulse width⁴³. Finally, in situations in which white matter may be primarily responsible for both therapy and side effects, such as when aiming to treat the intention tremor component of essential tremor⁴⁴, pulse width tuning would not likely have substantial effect on the biophysical therapeutic window.

Conclusions

Strength-duration-based dose equivalence metrics, rather than energy or charge injected equivalence, should be used to maintain equivalent neural activation and properly control studies investigating the clinical response to changing DBS parameters. Future work studying the effects of modulating parameters should consider how to maintain consistent volume of tissue activated. Lengthening the pulse width to match the chronaxie maximizes battery life through energy minimization. When grey matter contributes significantly to therapy, longer pulse widths decreases the preferential selection of large, distant fibers that can cause side effects, thus, widening the therapeutic window from a biophysical standpoint. Directional stimulation through smaller, segmented contacts reduces energetic demand, effectively steers stimulation, and may also decrease the preferential selection of large, distant fibers, to an even greater extent than when using longer pulse widths. Future work will need to be completed to pre-clinically and clinically test the claims made in this paper. For now, even if we do not currently recommend changing the clinical pulse widths used, the biophysical explanations generated in our work regarding neuronal selectivity should serve to guide contact sizes and segmentation in future device design, as well as future studies regarding pulse width in DBS and related areas.

Highlights.

• Long pulse widths are predicted to focus the effect of deep brain stimulation on small, nearby axons.

• From a biophysical perspective, long pulse widths may widen the therapeutic window when grey matter is responsible for therapy and white matter is responsible for side effects.

• Long pulse widths, up to several hundred microseconds, improve energetic efficiency.

• Segmented electrodes may achieve the benefits of pulse width tuning to a greater degree, capable of increasing both the therapeutic window and energetic efficiency.

• Future studies of pulse width tuning must assign amplitudes using strength duration-based equivalence metrics; amplitudes derived from energy and charge equivalence lead to substantially non-equivalent neural activation.