Abstract
In order to simulate hemodynamics within centrifugal blood pumps and to predict pump hemolysis, CFD simulations must be thoroughly validated against experimental data. They must also account for and accurately model the specific working fluid in the pump, whether that is a blood-analog solution to match an experimental PIV study or animal blood in a hemolysis experiment. Therefore, the FDA benchmark centrifugal blood pump and its database of experimental PIV and hemolysis data were used to thoroughly validate CFD simulations of the same blood pump. A Newtonian blood model was first used to compare to the PIV data with a blood analog fluid while hemolysis data was compared using a power-law hemolysis model fit to porcine blood data. A viscoelastic blood model was then incorporated into the CFD solver to investigate the importance of modeling blood’s viscoelasticity in centrifugal pumps. The established computational framework, including a dynamic rotating mesh, animal blood specific fluid properties and hemolysis modeling, and a k-ω SST turbulence model, was shown to more accurately predict pump pressure heads, velocity fields, and hemolysis compared to previously published CFD studies of the FDA centrifugal pump. The CFD simulations were able to match the FDA pressure and hemolysis data for multiple pump operating conditions, with the CFD results being within the standard deviations of the experimental results. While CFD radial velocity profiles between the impeller blades also compared well to the PIV velocity results, more work is still needed to address the large variability among both experimental and computational predictions of velocity in the diffuser outlet jet. Small differences were observed between the Newtonian and viscoelastic blood models in pressure head and hemolysis at the higher flow rate cases (FDA Conditions 4 and 5) but were more significant at lower flow rate and pump impeller speeds (FDA Condition 1). These results suggest that the importance of accounting for blood’s viscoelasticity may be dependent on the specific blood pump operating conditions. This detailed computational framework with improved modeling techniques and an extensive validation procedure will be used in future CFD studies of centrifugal blood pumps to aid in device design and predictions of their biological responses.
Keywords: FDA, computational fluid dynamics, centrifugal blood pump, hemolysis, validation
1. Introduction
Computational fluid dynamics (CFD) modeling is an important tool for designing and predicting the performance of cardiovascular devices. While increasingly used as part of regulatory submissions to the U.S. Food and Drug Administration (FDA), CFD data often lack credibility due to inadequate verification and validation [1]. In an effort to improve and standardize the use of CFD for blood contacting device regulatory submissions, the FDA developed benchmark nozzle and centrifugal blood pump models in which in vitro experimental data were collected at multiple independent laboratories [1,2] and compared with round-robin CFD data [3,4,5]. However, an analysis of the submitted CFD data revealed significant variability between the computational and experimental velocity fields [5]. Additionally, in the centrifugal pump study, only 8 of the 25 submissions included any predictions of device hemolysis [5].
Much of the variability in the centrifugal pump CFD flow fields and hemolysis predictions can be attributed to differences in the computational methods and strategies used in the round-robin submissions. Of the 25 CFD submissions, 14 used steady-state or multiple reference-frame approaches that do not actually model the rotating impeller and are not able to predict the fluctuations as each rotor blade passes the cut-water region of the pump. There was also an extremely large range in computational grid sizes with meshes ranging from 0.53 to 76.5 million cells [5]. Gross-Hardt et al. demonstrated in centrifugal pump blade geometries that significant underpredictions in both wall shear stress (WSS) and hemolysis were observed when using coarser CFD meshes [6]. Additionally, only 13 of the CFD submissions used the k-ω shear-stress transport (SST) turbulence model while the others applied variations of the k-ϵ turbulence model despite the k-ω SST model being shown to better match experimental PIV data in centrifugal pumps [7].
Many groups have performed experimental [8–20] and/or CFD [11–18,21–28] studies of centrifugal blood pumps to investigate pump performance, hemodynamics, and device induced hemolysis. While several have been able to show similar pressure-flow curves and hemolysis to experimental results, very few have thoroughly validated the computational flow fields within their respective pumps. As suggested by Malinauskas et al. [5] to use CFD to predict hemolysis in blood pumps, validation should be performed at two different levels: first on the fluid dynamics within the pump including pressure, velocity, and viscous and turbulent stresses and second on predictions of the biological response including hemolysis and thrombosis. Burgreen et al. performed flow visualization studies in a HeartMate III blood pump (Abbott, Chicago, Ill, USA) model but only provided qualitative comparisons to the CFD flow fields [21]. Nishida et al. similarly compared experimental and CFD flow fields in a monopivot circulatory assist pump (Senko Medical Instrument Mfg. Co. Ltd., Kasukabe, Saitama, Japan) but only used one flow condition and one pump location for validation. Recently, a few studies have used some of the available PIV data of the FDA centrifugal blood pump (https://nciphub.org/wiki/FDA_CFD) to validate their own CFD modeling efforts [27,28,29,30]. However, at the time of their work, PIV data was only available from a single flow condition and at two pump cross-sections, which hindered the groups’ abilities to fully validate their CFD.
A further limitation in much of the previous CFD work, both with the FDA pump and with other centrifugal blood pumps, is the lack of accurate blood modeling and accounting for the specific species of animal blood. For example, Trias et al. found that using a Newtonian blood model in the FDA nozzle geometry significantly underpredicted hemolysis compared to a non-Newtonian constitutive model [31]. This could also be one of the reasons for discrepancies between the PIV and CFD data (which used Newtonian fluids and models) and the experimental hemolysis data (which was performed with viscoelastic porcine blood). Therefore, to establish a more accurate computational framework for predicting hemodynamics and hemolysis in centrifugal blood pumps, the FDA benchmark centrifugal pump and its database of available velocity, pressure, and hemolysis data [1,5] will be used to thoroughly validate blood pump CFD simulations. A Newtonian fluid model will first be used to match the PIV experimental working fluid and a viscoelastic blood model [32] fit to porcine data [33] will then incorporated into the CFD solver to investigate the importance of modeling blood’s viscoelasticity in centrifugal blood pump studies.
2. Methods
2.1. FDA Centrifugal Blood Pump Model
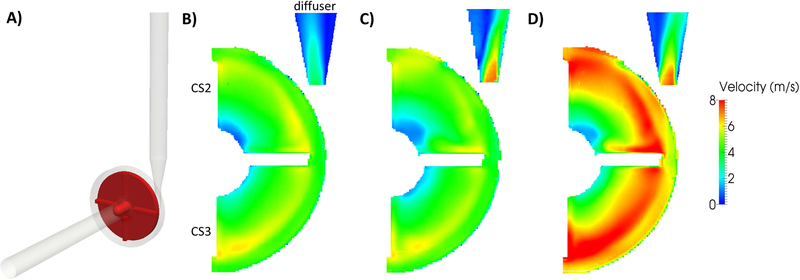
The FDA benchmark centrifugal blood pump model (Fig. 1A) was designed to have simple geometrical features and to operate over a wide range of operating conditions [5]. PIV data was collected at three laboratories using Newtonian blood analog fluids and with an acrylic model of the blood pump incorporated into a closed recirculating flow loop that allowed for flow rate, pressure head, and rotor speed to be measured and controlled [5]. Measurements of the two-dimensional velocity fields were collected at several sampling planes across the pump and the cross-correlation results of image pairs captured at the same rotor position (with one of the blades positioned 90° to the outlet) were ensemble-averaged. Cross-section (CS) 2 and CS 3 (labeled in Fig. 1B), were chosen for detailed analysis because they encompass many important regions around the pump impeller blades and hub. Additionally, the cutwater region of the pump diffuser was analyzed in order to investigate the outlet velocity jets and separation regions. Further details of the experimental data collection can be found in Hariharan et al. [1]. Hemolysis testing, using the same closed recirculating experimental flow loop, was performed at a single laboratory with porcine blood and plasma-free hemoglobin (pfHb) levels were measured [5].
Figure 1.
A) Computational model of the FDA benchmark centrifugal pump. PIV velocity magnitude (m/s) fields at cross-section (CS) 2, CS 3, and the diffuser region for FDA B) Condition 1 (Q= 2.5 L/min and Ω=2500 rpm), C) Condition 4 (Q= 6 L/min and Ω=2500 rpm), and D) Condition 5 (Q= 6 L/min and Ω=3500 rpm). Note that all but the Condition 4 diffuser region data were reconstructed from PIV data on the FDA database (https://nciphub.org/wiki/FDA_CFD) [1]. The Condition 4 diffuser region PIV data was collected at the Pennsylvania State University in the same acrylic centrifugal pump model and flow loop.
2.2. Viscoelastic Blood Modeling
While it is well established that blood is a viscoelastic fluid, most studies of rotary blood pumps choose to model blood as a Newtonian fluid due to the predominance of higher shear rates (>100 s−1) within the devices. However, depending on specific device designs and operating conditions, regions of low shear rate (<100 s−1) can occur and alter the predictions of stress and residence time, ultimately affecting hemolysis. For simulating the viscoelastic behavior of porcine blood, the fluid used in the FDA hemolysis experiments [5], a previously validated CFD solver [34] was modified to incorporate a generalized Oldroyd-B (GOB) blood model [32,35,36]. In brief, the GOB constitutive model splits the fluid’s deviatoric stress tensor (Eq. 1) into a solvent component representing the Newtonian blood plasma (Eq. 2) and a polymeric component representing the viscoelastic red blood cells (RBCs). The polymeric stress component is modeled with a neo-Hookean elastic response and a dissipative response that is quadratic in the stretch tensor (Eqs. 3 and 4):
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
| (Eq. 4) |
where is the total viscous stress tensor composed of solvent () and polymeric () parts, is the solvent viscosity, D is the symmetric part of the velocity gradient, is the polymeric viscosity, is the elastic shear modulus, is the Giesekus mobility parameter, is the relaxation time, B is the left Cauchy stretch tensor, and is the upper-convected time derivative of the polymeric stress. For determining the GOB model coefficients, the porcine blood density (1030 kg/m3) and infinite-shear rate viscosity (3.4 cP) were taken from the FDA study [5], the zero-shear rate viscosity (20 cP) was taken from experimental porcine blood data [33], and the elastic shear modulus (3.38 cP/s) was determined from a least-squares fit of the GOB model to the same porcine data. For the Newtonian blood simulations, constant density (1030 kg/m3) and dynamic viscosity (3.4 cP) were used that matched the FDA study.
2.3. Hemolysis Modeling
A power-law relationship between hemolysis (), shear stress (), and exposure time () was first developed by Giersiepen et al. [37] (Eq. 5) with a set of coefficients (, and ) found by fitting to experimental hemolysis data [38]:
| (Eq. 5) |
where represents the ratio of released hemoglobin due to hemolysis to the total hemoglobin concentration within RBCs. The original model was fit to experimental data on human RBCs, where shear stresses up to 255 Pa and exposure times up to 700 ms were imposed [38]. Another set of constants was fit to experimental data on porcine RBCs with shear stresses up to 600 Pa and exposure times between 0.0034 and 0.69 s (C=1.8e−8, α=1.991, and β=0.765) [33]. Based on the types of flows in the FDA blood pump and the fact that porcine blood was used for the experimental hemolysis tests, this set of coefficients [33] was chosen for the CFD simulations herein.
In order to incorporate the Giersiepen power-law model into a CFD solver and simulate flow in complex 3-D blood pumps, an Eulerian approach was developed [39] that linearized Eq. 5 with respect to time (Eq. 6):
| (Eq. 6) |
The blood damage () was then formulated as a partial differential equation where the time derivative along a streamline of the linear blood damage is constant and given by the source term, (Eq. 7):
| (Eq. 7) |
A hyperbolic transport equation was then derived (Eq. 8):
| (Eq. 8) |
To account for the 3-D nature of the viscous stress tensor and to define a single parameter to relate to hemolysis, a scalar von Mises stress (Eq. 9) is computed in terms of the principal stresses, , of the total stress tensor:
| (Eq. 9) |
After the scalar stress field is calculated, is obtained by integrating Eq. 8. Finally, the normalized index of hemolysis (NIH) is evaluated by Eq. 10 over the pump outlet:
| (Eq. 10) |
where is the hemoglobin concentration and assumed to be 10.12 g/dL for porcine blood [40]. This Eulerian approach [39] transforms the more computationally intensive Lagrangian method and allows for Eq. 8 to be directly solved along with the Navier-Stokes equations over the whole domain.
2.4. Computational Modeling
OpenFOAM (OpenCFD Ltd.), a C++ open-source computational software, was used for all simulations in this study. For simulating the viscoelastic behavior of porcine blood, a previously validated OpenFOAM solver called ‘viscoelasticFluidFoam’ [34] was used as the base structure and modified to solve the constitutive model presented in Eqs. 1–4 [32,35,36]. A time-step was chosen for each FDA case such that the fluid Courant number remained below 1 throughout the entire simulation (6e−6 s for the 2.5 L/min cases and 4e−6 for the 6 L/min cases) and the residuals of all variables were converged to below 10−6 at every time step. To capture the complex flow patterns caused by the pump’s rotating impeller, fully transient simulations with sliding mesh boundaries were used. To do this, the entire blood domain was split into two adjacent regions; the rotating region containing the bladed impeller and the stationary region containing the rest of the fluid. The connection between these two regions was handled by OpenFOAM’s arbitrary mesh interface (AMI) library, which enables simulations across disconnected but adjacent mesh domains and uses rotational transformations to account for the adjacent cell face motion at each time step [42]. Similar to previous CFD studies of centrifugal blood pumps [11, 13, 17, 18, 23, 24, 26–28], the k-ω SST turbulence model [41], a two-equation model to solve the turbulent eddy viscosity in Reynolds-averaged Navier-Stokes (RANS) equations, was used. This model has been shown to be optimal for centrifugal pump applications [7] because it combines the standard low-Reynolds number k-ω model in the near-wall region with the high Reynolds number k-ϵ model in the far field.
2.5. Computational Grid Refinement and Boundary Conditions
Three high-quality unstructured meshes were generated using OpenFOAM’s ‘snappyHexMesh’ utility (coarse ~1,900,000; medium ~4,700,000; and fine ~9,400,000 cells) in order to perform a systematic grid refinement study. The interior cells were primarily hexahedral with nearly isotropic sizes of 1, 0.75, and 0.5 mm in the coarse, medium, and fine meshes, respectively. Additionally, three wall layers were added to each mesh such that the near-wall cell heights were approximately 0.15, 0.1125, and 0.075 mm, respectively. After obtaining preliminary flow results with each mesh, y+ values were calculated to determine the non-dimensional wall distances and the average y+ value over the entire pump wall was found to be less than 1 for all flow conditions.
To cover multiple flow rates and rotational speeds, three of the FDA conditions were chosen for detailed CFD investigation and validation: Condition 1 (Q= 2.5 L/min and Ω=2500 rpm), Condition 4 (Q= 6 L/min and Ω=2500 rpm) and Condition 5 (Q= 6 L/min and Ω=3500 rpm). The bulk flow rates were prescribed as boundary conditions at the inlet of the pump and far enough upstream to ensure fully developed velocity profiles. The impeller rotational speeds were imposed on the cyclic AMIs defining the boundary between the inner rotating impeller region and the outer stationary fluid region. No-slip boundary conditions were applied to all other stationary walls and the outlet boundary condition was a fixed pressure of 0 mmHg. Both the pressure and velocity fields converged within a few full rotations of the impeller blade. Hemolysis, however, which was measured at the outlet of the pump and based Eq. 8, required 600 ms of simulation time in the 6 L/min flow rate cases and 1.4 s of simulation time in the 2.5 L/min flow rate case to achieve convergence. Hemolysis was considered converged when NIH at the pump outlet changed by less than 1% over an impeller rotation.
3. Results
3.1. PIV Velocity Fields
PIV velocity fields were reconstructed from the FDA centrifugal blood pump database (https://nciphub.org/wiki/FDA_CFD) [1] for Conditions 1, 4, and 5 using Paraview (Kitware Inc, Clifton Park, NY). It is important to note that data for Condition 4 in the diffuser region is currently unavailable on the FDA website database, and thus, PIV data collected at the Pennsylvania State University with the same acrylic centrifugal pump model and flow loop was used for this single condition and location. Qualitatively comparing the flow fields (Fig. 1B–D) between the three pump conditions, flow patterns and velocity magnitudes in CS 2 and CS 3 were primarily influenced by the pump rotor speed while the position and magnitude of the diffuser outlet jet were influenced by the pump flow rate. Conditions 1 (Fig. 1B) and 4 (Fig. 1C) were both operated at 2500 rpm and displayed similar velocity fields with peak magnitudes of 4 to 6 m/s between the impeller blades. In Condition 5, which was operated at 3500 rpm, higher velocity magnitudes of 6 to 8 m/s were measured between the blades (Fig. 1D). In the diffuser outlet region, however, Condition 1 (2.5 L/min) had a velocity jet skewed toward the inner wall of the diffuser while Conditions 4 and 5 (6 L/min) had velocity jets skewed toward the outer wall.
Figure 4.
A) Velocity magnitude (m/s) profiles were collected along radial line (r2) from CS 2 in the centrifugal pump. PIV (blue) and CFD (red) velocity profiles were compared for B) Condition 1, C) Condition 4, and D) Condition 5.
3.2. CFD Grid Refinement
A systematic grid study was performed to verify that the numerical solutions in the CFD simulations were independent of the mesh they were solved on. Three meshes (coarse, medium, and fine) were created in OpenFOAM consisting of approximately 1.9, 4.7, and 9.4 million cells, respectively. Hemodynamic parameters of velocity, pressure, and NIH were each evaluated for FDA Condition 4 as to their respective mesh sensitivities. Examples of the medium computational mesh at key pump regions of the diffuser cutwater and around the impeller blade tip are shown in Fig. 2A.
Figure 2.
A) Velocity magnitude (m/s) profiles were collected along radial lines from CS 2 (r2) and CS 3 (r3) and across the diffuser outlet (d) in the centrifugal pump CFD results. Images of the medium mesh are also shown to highlight key pump regions of the diffuser cutwater and impeller blade tip. Comparison of Condition 4 velocity profiles in B) CS 2, C) CS 3, and D) across the diffuser outlet for the coarse (blue), medium (red), and fine (black) computational meshes.
3.2.1. Velocity Grid Refinement Results
Shown in Fig. 2A and similar to the analysis by Malinauskas et al. [5], time-averaged mean radial velocity profiles from the impeller hub to the outer pump casing in CS 2 and CS 3 (r2 and r3, respectively) and the velocity profile across the diameter of the diffuser outlet (d) were investigated. Along radial profile r2, the average difference in velocity magnitude between the coarse and medium meshes was 7.3% and between the medium and fine meshes was 4.9% (Fig. 2B). Along radial profile r3, the average difference in velocity magnitude between the coarse and medium meshes was 10.1% and between the medium and fine meshes was 5.1% (Fig. 2C). Looking at the velocity profile across the diffuser outlet (d) (Fig. 2D), the coarse mesh showed a slightly more skewed and lower magnitude outlet jet while the medium and fine meshes predicted nearly identical outlet jet location and peak velocity magnitude (2.3% higher with the medium mesh).
3.2.2. Pressure Head and Hemolysis Grid Refinement Results
The effects of mesh refinement on pump pressure head and hemolysis are shown in Fig. 3. Between the coarse and medium meshes, a 15.5% difference in pressure was observed while only a 3.6% difference was shown between the medium and fine meshes (Fig. 3A). In Fig. 3B, predictions of NIH were 9.6% higher in the medium mesh compared to the coarse mesh and only 6.4% higher in the fine mesh compared to the medium mesh. As recommended by Roache [43], to quantitatively assess mesh convergence for unstructured meshes via Richardson extrapolation theory, global quantities as opposed to local values should be used to calculate a grid convergence index (GCI). The GCI uses a factor of safety (1.25 in this case) and provides an upper bound on the relative discretization error. Here, Richardson extrapolation theory was used to calculate the GCI’s of the NIH and pump pressure values averaged over the pump outlet and were found to be 10.3% and 2.1% for the medium mesh, respectively. Based on these results and the relatively small differences observed between the medium and fine mesh velocity fields, the medium mesh was used for all further CFD simulations.
Figure 3.
Comparison of Condition 4 A) pressure head (mmHg) and B) NIH (g/100L) for the coarse (blue), medium (red), and fine (black) computational meshes.
3.3. Validation of CFD with FDA PIV and Hemolysis Data
Following the guidance of Malinauskas et al. [5], the CFD simulations were validated at two different levels: first on the fluid dynamics within the pump (velocity and pressure) and second on predictions of the biological response (hemolysis).
3.3.1. Velocity Validation Results
To account for the unsteady nature of the centrifugal pump flow field, primarily the velocity fluctuations occurring around the blades and in the diffuser outlet, the velocity fields were time-averaged over two full impeller rotations and the comparisons to experimental data were presented as mean velocity profiles with their respective standard deviations. Along radial profile r2, the average difference in mean velocity magnitude between the experimental and mean computational results in Condition 1 was 5.4% (Fig. 4B), in Condition 4 was 8.1% (Fig. 4C), and in Condition 5 was 6.9% (Fig. 4D). Peak velocities, occurring along the outer wall of the pump, were slightly higher in the CFD results (2 to 7%) compared to the experimental results. Along radial profile r3, the average difference in mean velocity magnitude in Condition 1 was 4.5% (Fig. 5B), in Condition 4 was 4.8% (Fig. 5C), and in Condition 5 was 4.5% (Fig. 5D). Peak velocities, occurring along the outer wall of the pump, were also slightly higher in the CFD results (1 to 4%) compared to the experimental results.
Figure 5.
A) Velocity magnitude (m/s) profiles were collected along radial line(r3) from CS 3 in the centrifugal pump. PIV (blue) and CFD (red) velocity profiles were compared for B) Condition 1, C) Condition 4, and D) Condition 5.
In Condition 1, across the diffuser outlet profile (d), the CFD predicted a jet more skewed toward the inner wall of the diffuser while the PIV showed a blunter and more central jet (Fig. 6B). The peak mean velocity magnitude was 1.77 m/s in the PIV data and 3.01 m/s in the CFD results. In both Conditions 4 and 5, the CFD more closely matched the shapes of the experimental flow profiles showing jets skewed toward the outer wall of the diffuser but over-predicted the peak velocity magnitudes in both cases. In Case 4 (Fig. 6C), the CFD peak mean velocity was 5.26 m/s compared to 4.02 m/s in the PIV data and in Case 5 (Fig. 6D), the CFD peak mean velocity was 5.52 m/s compared to 3.6 m/s in the PIV data. Comparing to the FDA round-robin CFD results [5], there was substantial variability in the presented predictions of the diffuser outlet flow field. For Condition 5, 7 of the 12 group’s data showed peak velocity magnitudes between 5 and 7 m/s for Condition 5, which is very similar to the peak mean velocity of 5.52 m/s in Fig. 6D. In other studies that used the FDA PIV data for CFD validation [29,30], large CFD overpredictions of the Condition 5 velocity jet magnitude were also shown (5.85 m/s [29] and 4.6 m/s [30], respectively).
Figure 6.
A) Velocity magnitude (m/s) profiles were collected across the diffuser outlet (d) in the centrifugal pump. PIV (blue) and CFD (red) velocity profiles were compared for B) Condition 1, C) Condition 4, and D) Condition 5.
3.3.2. Pressure Head and Hemolysis Validation Results
Experimental pressure heads from both the FDA’s PIV [1,5] and hemolysis [5] studies were compared to those predicted by CFD (Fig. 7A). The CFD predicted pressure heads were 164.6 mmHg for Condition 1, 51.1 mmHg for Condition 4 and 251.4 mmHg for Condition 5, which were all within the standard deviations of the FDA PIV experimental data. Condition 4 was also within the FDA blood experimental data standard deviations while Conditions 1 and 5 were just outside. Plasma free hemoglobin (pfHb) results from the FDA’s hemolysis experiments [5] were also compared to those predicted by CFD (Fig. 7B). The CFD predicted pfHb hemolysis levels of 42.73 mg/dl on Condition 1, 31.24 mg/dL in Condition 4, and 59.92 mg/dL in Condition 5. For all three pump flow conditions, the CFD hemolysis results were within the standard deviations of the FDA experimental hemolysis data.
Figure 7.
Comparison of A) experimental PIV (blue) [1,5], experimental hemolysis (red) [5], and CFD (black) pressure head (mmHg) measurements. B) Comparison of experimental hemolysis (red) [5] and CFD (black) plasma free hemoglobin (mg/dL) measurements.
3.4. Comparison of Newtonian and Viscoelastic Blood Models
Similar to the previous grid refinement and CFD validation sections, the key parameters of velocity, pressure, and hemolysis were evaluated in the FDA pump using both Newtonian and viscoelastic blood models to determine the importance of using such rheological models in future centrifugal blood pump studies.
3.4.1. Velocity Comparison Results
Similar to Section 3.3.1, the velocity fields were time-averaged over two full impeller rotations to account for the unsteady nature of the centrifugal pump. Along radial profiles r2 and r3, the differences in mean velocity between the Newtonian and viscoelastic blood model were very minimal with average differences in mean velocity magnitude between 2 and 8% for the different flow conditions. Much larger differences between the blood models, however, were apparent in the diffuser outlet region (Fig. 8). In Condition 1, velocity profiles across the diameter of the diffuser outlet (d) were similar in shape but the Newtonian model had a 5.8% higher peak mean velocity (Fig. 8B). While the viscoelastic model in Condition 4 had a higher peak mean velocity than the Newtonian model, the biggest discrepancies for this flow condition occurred along the inner wall of the diffuser in the flow separation region (Fig. 8C). While only the velocity magnitudes are presented here, significant recirculation occurred in this region with velocity in the negative streamwise direction. A similar feature was observed in Condition 5, where a more pronounced and larger recirculation region was located along the inner wall of the diffuser with the viscoelastic model and resulted in larger variability in velocity compared to the Newtonian model (Fig. 8D). Additionally, in Condition 5, a lower peak mean velocity was predicted with the viscoelastic blood model as well as an outlet jet skewed more towards the outer wall of the diffuser.
Figure 8.
A) Velocity magnitude (m/s) profiles were collected across the diffuser outlet (d) in the centrifugal pump CFD results. Newtonian (blue) and viscoelastic (red) blood models were compared for B) Condition 1, C) Condition 4, and D) Condition 5.
3.4.2. Pressure Head and Hemolysis Comparison Results
Comparing the Newtonian and viscoelastic blood models, higher pressures were predicted with the Newtonian model at the lower rotational speed Conditions 1 and 4 (1.6% and 7.9% higher, respectively) but a lower pressure at the higher rotational speed Condition 5 (1.7%) (Fig. 9A). With regards to NIH, the viscoelastic blood model predicted higher hemolysis in all three pump conditions. In Condition 1 this difference was more pronounced (6.2% higher) compared to Condition 4 (1.2% higher) and Condition 5 (0.2% higher) (Fig. 9B). Overall, the choice of blood model had minimal effect on pump pressure head while substantially higher NIH was predicted with the viscoelastic model for the lower flow rate Condition 1.
Figure 9.
Comparison of Newtonian (blue) and viscoelastic (red) CFD blood model predictions of A) pressure head (mmHg) and B) NIH (g/100L).
4. Discussion
To the authors’ knowledge, this is the first study to leverage the full set of published PIV and hemolysis data of the FDA’s benchmark centrifugal blood pump for validation of CFD modeling. To date, a few studies [27,28,29,30] have used some of the early published PIV data [5] and compared their CFD results to the inlet velocity profiles [27] and the Condition 5 velocity profiles in CS 2 [28,29] and in the diffuser outlet [29,30]. Only using a single pump condition (FDA Condition 5) with one or two pump regions is insufficient to fully validate a centrifugal pump CFD simulation. Additionally, besides the most recent work by Morrison et al. [30], no comparisons were made between the available FDA hemolysis data for validation. Compared to these CFD studies, the results presented herein include a much more thorough validation and show significant improvement in predictions of the pump pressure heads, velocity fields, and hemolysis. For all three flow conditions investigated, the CFD pressure head predictions were within the FDA’s experimental PIV testing standard deviations, compared to only 57% of the previous round-robin CFD submissions [5].
As shown in Figs. 4, 5, and 6, there was substantial variability in the CFD velocity predictions due to the inherent unsteadiness of the centrifugal pump impeller rotations. For Condition 4, the standard deviations of the time-averaged mean velocity were as high as 0.5 m/s in along radial profile r2 near the impeller hub but were nearly 1.5 m/s at the peak of the diffuser outlet jet. There was also substantial variability in the round-robin predictions of velocity along radial profile r2 and diffuser outlet profile d, with several groups reporting velocity jets skewed toward the opposite walls compared to the PIV data. For Condition 5, 7 of the 12 round-robin groups showed peak velocity magnitudes in the outlet jet between 5 and 7 m/s [5], while Ozturk et al. [29] and Morrison et al. [30] also showed overpredictions of the Condition 5 velocity jet magnitude in their CFD studies (5.85 and 4.6 m/s, respectively). Based on these previous results, the CFD peak velocity of 5.26 m/s for the Condition 5 outlet jet (Fig. 6D) in this study compares very well. The large variability in accurately predicting and validating the flow field in the diffuser outlet jet is further highlighted by the variability observed amongst the three independent laboratories that collected the experimental PIV data for the FDA [1]. Differences in the peak velocity magnitudes in the diffuser region varied from 5 to 25% and the coefficients of variation for velocity were also the highest in the diffuser region with mean inter-laboratory values exceeding 35% [1].
Heck et al. [27] reported Eulerian hemolysis indices for their simulations of the FDA centrifugal pump, which indicated the percentage increase of pfHb in the device. For Condition 1, their hemolysis indices varied between 0.0075% and 0.019% depending on the turbulence and rheological models used. An Eulerian damage index was calculated for the Condition 1 hemolysis results in this study from Eq. 13 and was found to be 0.042%. Morrison et al. [30] also reported hemolysis results with the FDA centrifugal pump but normalized their data with that from a commercially available blood pump. While direct comparisons to their exact levels of hemolysis were not possible, they did show the same trends as observed in this work between Conditions 1 and 5. Due to the lack of available CFD data for the FDA centrifugal pump to thoroughly compare hemolysis predictions, comparisons were made to similar flow conditions in other commercially available blood pumps. Fraser et al. found in axial and centrifugal pumps that hemolysis decreased when the pump flow rate was increased while maintaining a fixed rotor speed [17], which was the same trend shown between Conditions 1 and 4 (NIH decreased from 0.00436 to 0.00309 g/100 L) (Fig. 7B). They also found, along with Taskin et al. [23], that hemolysis increased when the rotor speed was increased while maintaining a fixed flow rate, which was the same trend shown between Conditions 4 and 5 (NIH increased from 0.00309 to 0.00592 g/100 L) (Fig. 7B). In a study of hemolysis in the CentriMag centrifugal pump [14], NIH values of 0.0029±0.006 g/100 L were measured experimentally, and 0.0033 g/100 L predicted computationally, operating the pump at 5 L/min and 4000 RPM. At a higher flow rate of 6 L/min [18], hemolysis in a separate CentriMag pump study was reported as a hemolysis index of approximately 0.0005%. These two flow conditions were most similar to FDA Condition 5 (6 L/min and 3500 RPM) used in this study and compared well to the CFD prediction of hemolysis (NIH value of 0.0059 g/100L and hemolysis index of 0.00059%).
Only a few groups have investigated the effect of blood’s non-Newtonian behavior on the hemodynamics and hemolysis in blood pumps. In an experimental study of the Kyoto-NTN centrifugal blood pump [44], measured pressure heads were higher with Newtonian blood analogs compared to non-Newtonian analogs at lower pump RPMs. However, the opposite occurred at higher rotor speeds where the pump pressure heads were lower with Newtonian blood analogs. The same trends occurred in this study, where the Newtonian pressure head was larger than the viscoelastic pressure head in Conditions 1 and 4 but smaller in Condition 5 (Fig. 11A). Shown in Fig. 11B, the viscoelastic effects on hemolysis were most pronounced in Condition 1, where velocity and shear rates were the lowest. Post-analysis of the Condition 1 simulation results showed that over 21% of the total computational cells experienced shear rates less than 500 s−1 and about 2% experienced shear rates less than 100 s−1. This was much larger than in Conditions 4 and 5 where only 8% of cells experienced shear rates under 500 s−1 and 0.8% under 100 s−1. These values were also very similar to those in a CentriMag pump study where approximately 2% of all computational cells experienced shear rates less than 100 s−1 [18]. A further factor that could be responsible for the larger viscoelastic hemolysis in Condition 1 was the peak WSS calculated at the cutwater region of the pump’s diffuser outlet. For Condition 1, the Newtonian model predicted peak WSS values of 527 Pa while the viscoelastic model predicted WSS values of 621 Pa, an increase of 16%. In contrast, Conditions 4 and 5 only had WSS increases of 2 and 9%, respectively, using the viscoelastic blood model.
5. Limitations
As displayed in the analysis of the FDA PIV data [1], there was still variability among the three independent laboratories’ velocity measurements (mean percent coefficient of variations was approximately 10% overall and greater than 35% in the diffuser region). The lab-to-lab variability in the blood-analog fluid’s density and viscosity introduced uncertainty in the diffuser Reynolds number of about 10% that was enough to cause variations in each data sets velocity fields [1]. Therefore, validation of the flow fields in this particular region of the pump are much more challenging and uncertain and will require future investigation of the best turbulence models to improve outlet jet flow predictions. Additionally, in this study, the hemolysis power-law coefficients determined by Heuser and Opitz [33] for porcine RBCs were used. While the range of shear stresses (30 to 600 Pa) and exposure times (0.0034 to 0.69 s) for their experimental hemolysis study is valid for many centrifugal blood pumps, we acknowledge the limitations of applying coefficients derived from uniform-shear experiments in Couette-type flow to the more complicated flow fields experienced in a centrifugal blood pump.
6. Conclusions
In order to simulate hemodynamics within centrifugal blood pumps and to predict pump hemolysis, CFD simulations must be thoroughly validated against experimental data. They must also account for and accurately model the specific working fluid in the pump (i.e. a blood-analog solution in an experimental PIV study or animal blood in an experimental hemolysis study). Therefore, the FDA benchmark centrifugal blood pump and its database of experimental PIV and hemolysis data were used to thoroughly validate CFD simulations of the same blood pump. Hemodynamics within the pump were first validated against the FDA PIV data using a Newtonian blood model to match the experimental working fluid. Additionally, a viscoelastic blood model was used in the CFD solver and compared to the simplified Newtonian model results to investigate the importance of incorporating blood’s viscoelastic behavior in centrifugal blood pumps.
For the first time, the full set of experimental data of the FDA’s centrifugal blood pump (pressure, velocity, and hemolysis) were used to thoroughly validate CFD simulations. The established computational framework, including a dynamic rotating mesh, animal blood specific fluid properties and hemolysis modeling, and a k-ω SST turbulence model, was shown to more accurately predict pump pressure heads, velocity fields, and hemolysis compared to previously published CFD studies of the FDA centrifugal pump [5,29,30]. Additionally, blood’s viscoelastic behavior was shown to have an effect on hemolysis predictions at the lower flow rate Condition 1 but was nearly identical to the Newtonian model hemolysis predictions at the higher flow rate Conditions 4 and 5. These results suggest that accounting for blood’s viscoelasticity may be important at certain low flow and rotational speed operating conditions. This detailed computational framework with improved modeling techniques and an extensive validation procedure will be used in future CFD studies of centrifugal blood pumps to aid in device design and predictions of their biological responses.
Acknowledgements
This work was supported in part by the Department of Defense W81XWH-16–1–0536, National Institutes of Health HL136369, and by the American Heart Association Postdoctoral Fellowship 19POST34370040.
Footnotes
Disclosure
The authors declare no conflict of interest.
References
- 1.Hariharan P, Aycock KI, Buesen M, Day SW, Good BC, Herbertson LH, Steinseifer U, Manning KB, Craven BA, Malinauskas RA. Inter-laboratory characterization of the velocity field in the FDA blood pump model using particle image velocimetry (PIV). Cardiovascular engineering and technology 2018;9(4):623–640. [DOI] [PubMed] [Google Scholar]
- 2.Hariharan P, Giarra M, Reddy V, Day SW, Manning KB, Deutsch S, Stewart SF, Myers MR, Berman MR, Burgreen GW, Paterson EG. Multilaboratory particle image velocimetry analysis of the FDA benchmark nozzle model to support validation of computational fluid dynamics simulations. Journal of biomechanical engineering 2011;133(4):041002. [DOI] [PubMed] [Google Scholar]
- 3.Stewart SF, Paterson EG, Burgreen GW, Hariharan P, Giarra M, Reddy V, Day SW, Manning KB, Deutsch S, Berman MR, Myers MR. Assessment of CFD performance in simulations of an idealized medical device: results of FDA’s first computational interlaboratory study. Cardiovascular Engineering and Technology 2012;3(2):139–160. [Google Scholar]
- 4.Stewart SF, Hariharan P, Paterson EG, Burgreen GW, Reddy V, Day SW, Giarra M, Manning KB, Deutsch S, Berman MR, Myers MR. Results of FDA’s first interlaboratory computational study of a nozzle with a sudden contraction and conical diffuser. Cardiovascular Engineering and Technology 2013;4(4):374–391. [Google Scholar]
- 5.Malinauskas RA, Hariharan P, Day SW, Herbertson LH, Buesen M, Steinseifer U, Aycock KI, Good BC, Deutsch S, Manning KB, Craven BA. FDA benchmark medical device flow models for CFD validation. ASAIO Journal 2017;63(2):150–160. [DOI] [PubMed] [Google Scholar]
- 6.Gross-Hardt S, Boehning F, Steinseifer U, Schmitz-Rode T, Kaufmann T. Mesh sensitivity analysis for quantitative shear stress assessment in blood pumps using computational fluid dynamics. J Biomech Eng 2019;141(2):021012. [DOI] [PubMed] [Google Scholar]
- 7.Song X, Wood HG, Day SW, Olsen D. Studies of Turbulence Models in a Computational Fluid Dynamics Model of a Blood Pump. Artif Organs 2003;27(10):935–937. [DOI] [PubMed] [Google Scholar]
- 8.Kawahito K, Yukihiko N. Hemolysis in different centrifugal pumps. Artif Organs 1997;21(4):323–326. [DOI] [PubMed] [Google Scholar]
- 9.Chan WK, Wong YW, Ding Y, Chua LP, Yu SC. Numerical investigation of the effect of blade geometry on blood trauma in a centrifugal blood pump. Artif Organs 2002;26(9):785–793. [DOI] [PubMed] [Google Scholar]
- 10.James NL, Wilkinson CM, Lingard NL, Meer AL, Woodard JC. Evaluation of hemolysis in the VentrAssist implantable rotary blood pump. Artif Organs 2003;27(1):108–113. [DOI] [PubMed] [Google Scholar]
- 11.Arvand A, Hormes M, Reul H. A validated computational fluid dynamics model to estimate hemolysis in a rotary blood pump. Artif Organs 2005;29(7):531–540. [DOI] [PubMed] [Google Scholar]
- 12.Arora D, Behr M, Pasquali M. Hemolysis estimation in a centrifugal blood pump using a tensor-based measure. Artif Organs 2006;30(7):539–547. [DOI] [PubMed] [Google Scholar]
- 13.Kido K, Hoshi H, Watanabe N, Kataoka H, Ohuchi K, Asama J, Shinshi T, Yoshikawa M, Takatani S. Computational fluid dynamics analysis of the pediatric tiny centrifugal blood pump (TinyPump). Artif Organs 2006;30(5):392–399. [DOI] [PubMed] [Google Scholar]
- 14.Zhang J, Gellman B, Koert A, Dasse KA, Gilbert RJ, Griffith BP, Wu ZJ. Computational and experimental evaluation of the fluid dynamics and hemocompatibility of the CentriMag blood pump. Artif Organs 2006;30(3):168–177. [DOI] [PubMed] [Google Scholar]
- 15.Zhang J, Koert A, Gellman B, Gempo TM, Dasse KA, Gilbert RJ, Griffith BP, Wu ZJ. Optimization of a miniature maglev ventricular assist device for pediatric circulatory support. ASAIO J 2007;53(1):23–31. [DOI] [PubMed] [Google Scholar]
- 16.Nishida M, Maruyama O, Kosaka R, Yamane T, Kogure H, Kawamure H, Yamamoto Y, Kuwana K, Sankai Y, Tsutsui T. Hemocompatibility evaluation with experimental and computational fluid dynamic analyses for a monopivot circulatory assist pump. Artif Organs 2009;33(4):378–386. [DOI] [PubMed] [Google Scholar]
- 17.Fraser KH, Zhang T, Taskin ME, Griffith BP, Wu ZJ. A quantitative comparison of mechanical blood damage parameters in rotary ventricular assist devices: shear stress, exposure time and hemolysis index. Journal of biomechanical engineering 2012;134(8):081002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Taskin ME, Fraser KH, Zhang T, Wu C, Griffith BP, Wu ZJ. Evaluation of Eulerian and Lagrangian models for hemolysis estimation. ASAIO J 2012;58(4):363–372. [DOI] [PubMed] [Google Scholar]
- 19.Sobieski MA, Giridharan GA, Ising M, Koenig SC, Slaughter MS, 2012. Blood trauma testing of CentriMag and RotaFlow centrifugal flow devices: a pilot study. Artif organs 2012;36(8):677–682. [DOI] [PubMed] [Google Scholar]
- 20.Ding J, Niu S, Chen Z, Zhang T, Griffith BP, Wu ZJ. Shear‐induced hemolysis: species differences. Artif organs 2015;39(9):795–802. [DOI] [PubMed] [Google Scholar]
- 21.Burgreen GW, Loree HM, Bourque K, Dague C, Poirier VL, Farrar D, Hampton E, Wu ZJ, Gempp TM, Schöb R. Computational fluid dynamics analysis of a maglev centrifugal left ventricular assist device. Artif organs 2004;28(10):874–880. [DOI] [PubMed] [Google Scholar]
- 22.Song X, Throckmorton AL, Wood HG, Antaki JF, Olsen DB. Quantitative evaluation of blood damage in a centrifugal VAD by computational fluid dynamics. Journal of fluids engineering 2004;126(3):410–418. [Google Scholar]
- 23.Taskin ME, Fraser KH, Zhang T, Gellman B, Fleischli A, Dasse KA, Griffith BP, Wu ZJ. Computational characterization of flow and hemolytic performance of the UltraMag blood pump for circulatory support. Artif Organs 2010;34(12):1099–1113. [DOI] [PubMed] [Google Scholar]
- 24.Selgrade BP, Truskey GA. Computational fluid dynamics analysis to determine shear stresses and rates in a centrifugal left ventricular assist device. Artif organs 2012;36(4):89–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pauli L, Nam J, Pasquali M, Behr M. Transient stress‐based and strain‐based hemolysis estimation in a simplified blood pump. International journal for numerical methods in biomedical engineering 2013;29(10):1148–1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Thamsen B, Blümel B, Schaller J, Paschereit CO, Affeld K, Goubergrits L, Kertzscher U. Numerical analysis of blood damage potential of the HeartMate II and HeartWare HVAD rotary blood pumps. Artificial organs 2015;39(8):651–659. [DOI] [PubMed] [Google Scholar]
- 27.Heck ML, Yen A, Snyder TA, O’rear EA, Papavassiliou DV. Flow‐field simulations and hemolysis estimates for the food and drug administration critical path initiative centrifugal blood pump. Artif organs 2017;41(10):129–140. [DOI] [PubMed] [Google Scholar]
- 28.Khoo DP, Cookson AN, Gill HS, Fraser KH. Normal fluid stresses are prevalent in rotary ventricular assist devices: A computational fluid dynamics analysis. The International journal of artificial organs 2018;41(11):738–751. [DOI] [PubMed] [Google Scholar]
- 29.Ozturk C, Aka IB, Lazoglu I. Effect of blade curvature on the hemolytic and hydraulic characteristics of a centrifugal blood pump. Int J Artif Organs 2018;41(11):730–737. [DOI] [PubMed] [Google Scholar]
- 30.Morrison T, Hariharan P, Funkhouser C, Afshari P, Goodin M, Horner M. Assessing Computational Model Credibility Using a Risk-Based Framework: Application to Hemolysis in Centrifgual Blood Pumps. ASAIO J 2019;65(4):349–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Trias M, Arbona A, Massó J, Miñano B, Bona C. FDA’s nozzle numerical simulation challenge: non-Newtonian fluid effects and blood damage. PloS one 2014;9(3):e92638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Good BC, Deutsch S, Manning KB. Hemodynamics in a pediatric ascending aorta using a viscoelastic pediatric blood model. Annals of biomedical engineering 2016;44(4):1019–1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Heuser G, Opitz R. A Couette viscometer for short time shearing of blood. Biorheology 1980;171(1–2):17–24. [DOI] [PubMed] [Google Scholar]
- 34.Favero JL, Secchi AR, Cardozo NS, Jasak H. Viscoelastic flow analysis using the software OpenFOAM and differential constitutive equations. J Non-Newton Fluid 2010;165(23–24):1625–36. [Google Scholar]
- 35.Good BC, Deutsch S, Manning KB. Continuous and pulsatile pediatric ventricular assist device hemodynamics with a viscoelastic blood model. Cardiovascular engineering and technology 2016;7(1):23–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Good BC, Weiss WJ, Deutsch S, Manning KB. Asynchronous Pumping of a Pulsatile Ventricular Assist Device in a Pediatric Anastomosis Model. World Journal for Pediatric and Congenital Heart Surgery 2017;8(4):511–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Giersiepen M, Wurzinger LJ, Opitz R, Reul H. Estimation of shear stress-related blood damage in heart valve prostheses—in vitro comparison of 25 aortic valves. Int J Artif Organs 1990;13:300–306. [PubMed] [Google Scholar]
- 38.Wurzinger LJ, Opitz R, Eckstein H. Mechanical blood trauma, an overview. Angeiologie 1986;38:81–97. [Google Scholar]
- 39.Garon A, Farinas MI. Fast three‐dimensional numerical hemolysis approximation. Artif Organs 2004;28(11):1016–25. [DOI] [PubMed] [Google Scholar]
- 40.Ihedioha JI, Onwubuche RC. Artifactual changes in PCV, hemoglobin concentration, and cell counts in bovine, caprine, and porcine blood stored at room and refrigerator temperatures. Veterinary clinical pathology 2007;36(1):60–63 [DOI] [PubMed] [Google Scholar]
- 41.Menter FR. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA journal 1994;32(8):1598–1605. [Google Scholar]
- 42.Mangani L, Buchmayr M, Darwish M, Moukalled F. A fully coupled OpenFOAM® solver for transient incompressible turbulent flows in ALE formulation. Numerical Heat Transfer, Part B: Fundamentals 2017;71(4):313–326. [Google Scholar]
- 43.Roache PJ. Perspective: a method for uniform reporting of grid refinement studies. Journal of Fluids Engineering 1994;116(3):405–413. [Google Scholar]
- 44.Zhang G, Zhang M, Yang W, Zhu X, Hu Q. Effects of Non-Newtonian fluid on centrifugal blood pump performance. International Communications in Heat and Mass Transfer 2008;35(5):613–617. [Google Scholar]