Abstract
Assessing the risk of fall in elderly people is a difficult challenge for clinicians. Since falls represent one of the first causes of death in such people, numerous clinical tests have been created and validated over the past 30 years to ascertain the risk of falls. More recently, the developments of low-cost motion capture sensors have facilitated observations of gait differences between fallers and nonfallers. The aim of this study is twofold. First, to design a method combining clinical tests and motion capture sensors in order to optimize the prediction of the risk of fall. Second to assess the ability of artificial intelligence to predict risk of fall from sensor raw data only. Seventy-three nursing home residents over the age of 65 underwent the Timed Up and Go (TUG) and six-minute walking tests equipped with a home-designed wearable Inertial Measurement Unit during two sets of measurements at a six-month interval. Observed falls during that interval enabled us to divide residents into two categories: fallers and nonfallers. We show that the TUG test results coupled to gait variability indicators, measured during a six-minute walking test, improve (from 68% to 76%) the accuracy of risk of fall’s prediction at six months. In addition, we show that an artificial intelligence algorithm trained on the sensor raw data of 57 participants reveals an accuracy of 75% on the remaining 16 participants.
Keywords: risk of fall, elderly, wearable sensor, gait variability, clinical tests
1. Introduction
Falls are an inevitable part of aging and their prediction and prevention are of paramount importance to health care. According to the World Health Organization (WHO), falls are the second cause of accidental death and approximately 646,000 people die every year following falls, particularly people over the age of 65. In the European Union (EU), an average of 35,848 elderly people/y (65 and above) are reported to have died from falls [1]. As the population of elderly people in the EU is expected to grow by 60% by 2050, the number of fall-related deaths is expected to increase to almost 60,000/y by 2050, unless additional measures are taken to predict and prevent falls. Additionally, falls result in significant physical and psychosocial costs that have to be incurred by patients and social security. The social security cost for treating fall-related injuries in the EU is estimated to be €25 billion each year [2].
In nursing homes, falls frequency is higher for elderly people than at home with a yearly rate of falls of 50% [3]. This phenomenon is foreseen to increase in the future in view of the population aging. Risk factors for falls in elderly people are higher among nursing home residents compared to home-based individuals [4]. Those factors are usually grouped in three main categories: intrinsic (age, sex, cognitive disorders, eyesight impairment, sarcopenia, multiple medication use, sensory impairment, gait disorders, postural instability and neurodegenerative diseases), behavioral (inappropriate footwear, alcohol use), and environmental (slippery surfaces, poor lighting, worn carpeting) [3,4,5].
It is well-known that the assessment of the risk of falls is better achieved through screening tools designed for that purpose. One of the most well-known tests is the Timed Up and Go (TUG) test [6]. It is considered as the gold standard in fall risk assessment and has numerous advantages. It is simple and easy to describe and to perform, and, therefore, widely used [7]. It is also recommended by the American Geriatric Society and the British Geriatric Society [8]. The typical time to perform the test is around 20–30 s. Unfortunately, this is too short to enable a full assessment of the gait kinematics and more specifically the long-term variability of the stride interval. This is correlated to the risk of fall in home-based older people [9] but requires a time series of a typical duration of 10 min. More recently, the TUG test has been performed with patients equipped with an accelerometer. This allowed an analysis focusing on sit-to-stand and stand-to-sit subtasks, which is useful to identify fall risk in home-based fallers versus healthy controls [10]. The findings of this study show that the TUG test allows successfully identifying 63% of fallers and this is increased by up to 87% in accelerometer-equipped patients.
Another widely used tool in clinical practice that allows the study of gait for a longer period is the six-minute walking test [11]. Similar to the TUG test, the accelerometer-based six-minute walking test has been used in patients with chronic heart failure [12] and chronic obstructive pulmonary disease [13]. To the best of our knowledge, the accelerometer-based six-minute walking test has not been performed in elderly people to assess risk of fall.
Today, the availability of low-cost inertial sensors enables 3D measurement of acceleration and angular speed during human movements. In a recent study, we successfully used a homemade ultralow-cost wearable inertial sensor (DYSKIMOT) to capture the rotational movements of the head during a standardized test [14]. It is part of the DYSKIMOT project to show the relevance of the proposed sensor in a wide variety of clinically relevant situations, and the present study aims at extending the range of applications of the DYSKIMOT sensor. Of course, many other wearable sensors are relevant in gait analysis, e.g., smart socks [15] or instrumented shirts [16]. Our results can also be transposed in principle to other systems using inertial sensors. Here, we used this sensor to capture locomotor movements during the six-minute walking test to increase the predictive power of the TUG test on the risk of falls among elderly nursing home fallers and nonfallers during two sets of measurements at six months interval (TUG+ test). We also present an analysis of kinematic data based on variability assessment and on artificial intelligence (AI) techniques. Current hardware capacities the processing and management of huge datasets required for such tools to converge to a solution. That is why these techniques have gained popularity in recent years and are recognized as efficient tools in fall detection in particular [17].
The main objective of this study is to show that it is possible to design a test identifying nursing home residents presenting a risk of fall, the test’s accuracy being assessed by comparison to their actual falls during six months after the test. A secondary objective is to present three different ways of assessing the risk of falls: a standard clinical test (TUG), a standard clinical test augmented by sensor measurements (TUG+), and an AI algorithm based on sensor measurements only. The first two tests require the presence of a therapist, while the third could be implemented in an autonomous wearable system.
2. Materials and Methods
2.1. Population
Participants in this survey (Table 1) were at least 65 years old or over and lived in 4 nursing homes in the Charleroi area in Belgium. The experiment protocol was designed according to the Helsinki declaration and was approved by the Bioethical Academic Committee (No. B200-2017-144). Exclusion criteria were as follows: lower limb musculoskeletal or cardio-respiratory disorders preventing a six-minute walking test or major cognitive disorders preventing a full patient’s cooperation. During the experiment, participants who experienced a major illness such as stroke or limb fracture were excluded.
Table 1.
Main characteristics, comorbidities and number of medications increasing the risk of fall of the participants. Fallers were identified according to the fall records between the 6 months interval (t1 and t2).
| t1 | t2 | |
|---|---|---|
| N | 80 | 73 |
| Age (years) | 83.2 ± 8.2 | 83.0 ± 8.3 |
| Male/Female | 28/52 | 28/45 |
| Walking aid required | 49 | 52 |
| Hypertension (%) | 44 | 42 |
| Number of medications | 4 [2–5] | 4 [2–5] |
| Cerebrovascular accident (%) | 10 | 10 |
| Dementia (%) | 14 | 16 |
| Previous heart surgery (%) | 21 | 23 |
| Diabetes (%) | 16 | 15 |
| Hip or knee replacement (%) | 16 | 16 |
| Fallers | 23 | |
| TUG (s) | 20 [17–27] | 17 [14–23] |
Age is indicated under the form mean ± standard deviation. Medications increasing the risk of fall: psychotrope, antiarrhythmic, diuretics [18]. Timed Up and Go (TUG) and number of medications results are given under the form median [1st quartile–3rd quartile]. Hypertension is defined as a value >140/90 mmHg.
Participants who chose to discontinue their participation, were admitted to hospital, had their medication changed thus preventing the continuation of the experiment or died before the completion of the experiment were also excluded.
Ninety-two individuals started the initial test. Twelve of them were excluded from the survey in view of the above criteria. Seventy-three participants completed the experiment.
2.2. Protocol
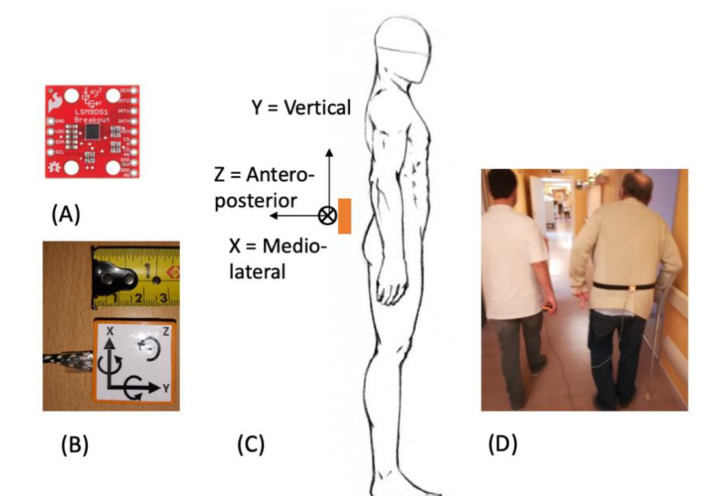
The survey took place between the month of May (t1) and the month of November (t2) 2018. At t1, the TUG test was performed in all participants. Participants sat down with their back against a 46 cm high chair rest. When signaled, participants were asked to get up, walk three meters, turn around and sit down again. Participants then performed the six-minute walking test with the right to take short pauses as required. Measurements were taken by the two same experimenters (L.C. and R.G.), who always walked aside the patient to prevent any fall in case they lost balance. Six-minute tests were performed by walking a typical point-to-point track of 25 m with serial turnarounds. The turnaround points were clearly marked with strong adhesive tape stuck on the floor. During the six-minute walking test, participants were equipped with a homemade sensor collecting several kinematic data. The ultralow-cost sensor, called DYSKIMOT, was presented in a previous survey [14]. It is based on the Magnetic Angular Rate and Gravity (MARG) sensor LSM9DS1 (SparkFun), composed of a 3-axis accelerometer, gyrometer and magnetometer, plus a temperature sensor (Figure 1A,B). It is light (10.44 g) and small enough (3 × 3 cm) to be worn by a patient without any disturbance (Figure 1B). Among other quantities, the MARG sensor measures acceleration, (in [g], ±16 [g]), and angular velocity, (in °/s, ±2000 °/s) at a sampling frequency of 100 Hz. The data are transmitted to a PC via an Arduino Uno Rev 3 and a USB cable (RS232 serial link) and then transferred to a homemade acquisition software for further analysis. More details can be found in [14], including a comparison between DYSKIMOT and a gold standard optoelectronic sensor. The sensitivity depends on the sensor and on the selected range; detailed information is given in the datasheet (https://www.st.com/en/mems-and-sensors/lsm9ds1.html). For example, the gyrometer sensitivity is 8.75 × 10−3 °/s/LSB at the range ±245 °/s, i.e., the range we use in the present study, and the accelerometer sensitivity is 0.322× mg/LSB at the range ±4× g. During the experiment, the DYSKIMOT was positioned in the lumbar region of the individual at the level of the L4 vertebra (Figure 1C,D) in such a way that the sensor’s cartesian frame matched with walking directions.
Figure 1.
(A) The LSM9DS1 sensor (SparkFun) used to record acceleration and angular speed. (B) LSM9DS1 sensor within the DYSKIMOT system. Sensor’s cartesian frame is indicated. The curved arrows give rotation’s positive direction. (C) Schematic placement of a DYSKIMOT sensor on a patient. The sensor’s cartesian frame matches the walking directions. (D) A patient equipped with DYSKIMOT sensor (right) with one experimenter (R.G.) walking aside.
Between t1 and t2, each fall of a participant was recorded by the nursing home staff. The fall records were used at t2 to categorize participants into fallers and nonfallers. At the end of the survey, 23 fallers and 50 nonfallers were noted. Among the 23 fallers, 17 participants made 1 fall, while 2 participants fell two, three and four times. The lack of “frequent fallers” (more than 1 fall) in our population has led us to consider a binary classification rather than a more detailed description in terms of, say, the number of falls between t1 and t2.
2.3. Data Analysis
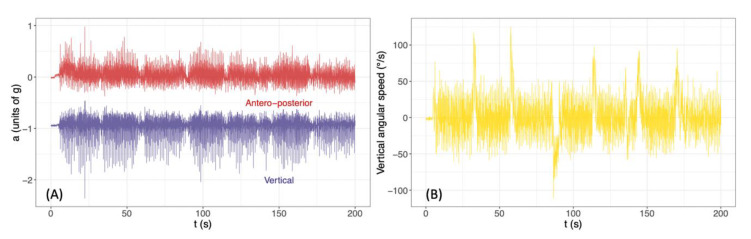
Time series included and (2 times 3 components). Typical traces of selected time series are shown in Figure 2. The indices ml, v and ap stand for mediolateral, vertical and anteroposterior, respectively. We recorded for analysis the data at t1 and t2 of the 73 participants still included at t2.
Figure 2.
(A) Typical traces of anteroposterior ( and vertical ( accelerations measured by the DYSKIMOT during the six-minute walking test. (B) Typical trace of vertical angular speeds () measured by the DYSKIMOT during the six-minute walking test. The regularly spaced peaks correspond to turnarounds made by the participants.
We chose to focus on the assessment of time series variability. As shown in [5], gait variability can be correlated with the risk of fall. Further studies such as [9] have analyzed it using mathematical tools such as fractal dimension and have demonstrated that those tools can discriminate between healthy and disabled individuals, healthy individuals showing a higher fractal dimension. The parameters identified in the present study are the standard deviation (SD) and fractal dimension (D) obtained from the six time series ( and ) recorded during the six-minute walking test. Fractal dimension was computed by resorting to the box counting method: If is the number of square boxes of side necessary to cover the plot of the time series under study, then scales as when . D is, therefore, the slope of vs. in a log–log plot for small values of . Computational details about the method we use are presented in [19] and additional mathematical references can be found in [20]. SD and D give complementary information about gait variability: SD provides an indication about the magnitude of the fluctuations while D represents the time series complexity, i.e., smooth (D close to 1) or abrupt (D close to 2) relative changes in successive measurements.
Due to failed normality tests on data, a Mann–Whitney test was performed with a significance level of 0.05 in order to ascertain potential differences between fallers and nonfallers at t1.
Three classification algorithms were then defined to classify participants as presenting a risk of fall or not: the TUG test, the TUG+ test and the AI algorithm (see below for more details). Standard tools belonging to binary classification were then used to compare our “diagnostic” (risk of fall or not) to the actual faller or nonfaller status of our participants. Sensitivity (), specificity (), positive () and negative () predictive values, and accuracy () were calculated, with TP the true positives, FP the false positives, FN the false negatives, and TN the true negatives. The positive () and negative () likelihood ratios were also computed.
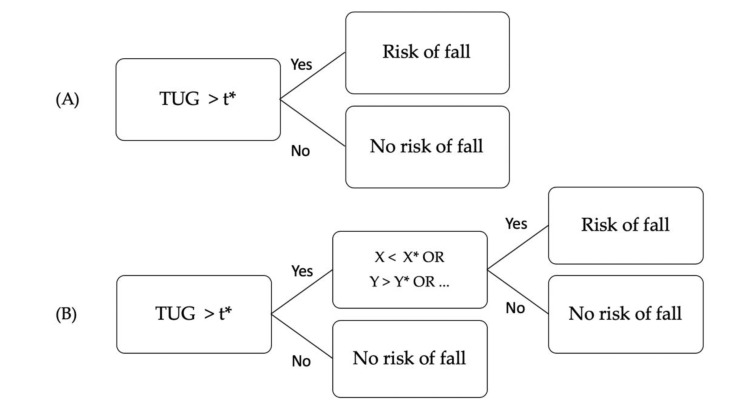
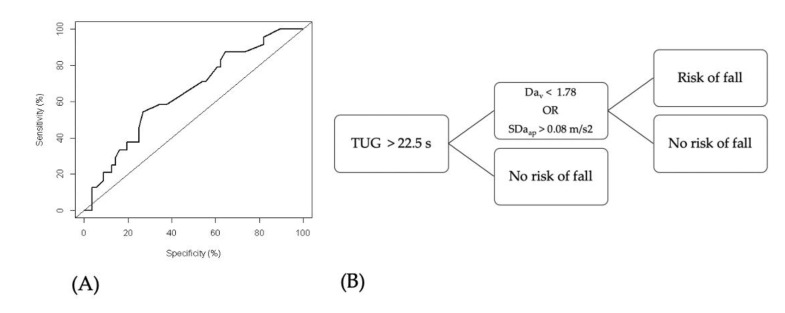
The TUG test at t1 was first analyzed by computing a Receiver Operating Characteristic (ROC) curve. The time maximizing Youden’s index was computed and chosen as the threshold, t*, to separate participants with and without risk of fall. An augmented TUG test (TUG+) was then designed following the decision tree shown in Figure 3. It includes information from the variability indices that showed a significant difference between fallers and nonfallers at t1. If an individual is recognized by the clinical test as a faller, then he/she is assessed a second time by one or more kinematic parameters displaying a significant difference between fallers and nonfallers (according to fall recording). Threshold values were chosen after several attempts at designing an augmented TUG test as it provided the best accuracy.
Figure 3.
(A) Decision tree illustrating the TUG test. T* is the threshold time maximizing Youden’s index. (B) Decision tree illustrating the TUG+ test. X, Y, etc., are variability indices and X*, Y*, etc., are threshold values. The selected indices and thresholds are given in Figure 5B.
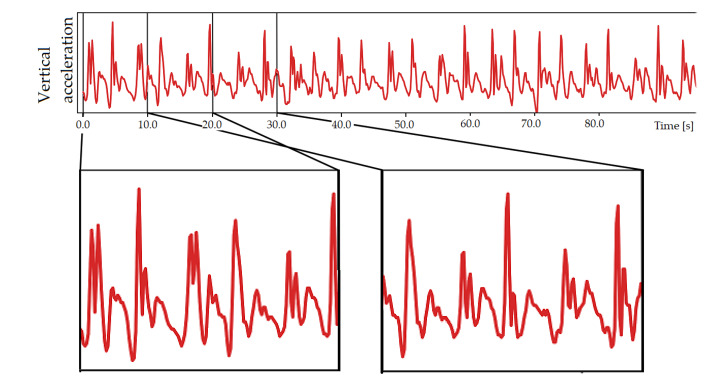
The AI algorithm was designed as follows. The times series related to a participant were divided into fixed-duration windows so that the inputs of our model are fixed-size vectors. Models were trained and tested for different window sizes; the value 20 s was chosen, see Section 3.3 for a justification. Splitting one 6 min time series into smaller ones may also have the advantage of avoiding the AI to learn long-term autocorrelations which are typical of human walk [9,21]. We used a 10 s overlapping during the frame generation of the training dataset (Figure 4) to increase its size and to remove any bias regarding the starting position of the frames. The obtained dataset was divided by test/validation datasets and training as a compromise between having enough fallers data for test/validation and for training. The test/validation is made up of 16 participants (8 fallers and 8 nonfallers randomly chosen) and the training dataset is made up of 57 participants (16 fallers and 41 nonfallers). Models based on Convolutional Neural Network (CNN) [22] have then been trained and tested to find the optimal accuracy on the risk of fall prediction in the test/validation dataset. We have chosen an AI classification based on deep learning (CNN) among other machine learning solutions because of its capacity to extract features by itself. Since TUG and TUG+ methods are based on features we selected (TUG time and variability indices), such a deep learning approach was preferred because it is complementary.
Figure 4.
Example of sequence splitting for the train dataset. A duration of 20 s is chosen with 10 s overlapping.
Sigmaplot (v. 11.0) and R (v. 3.5.0) software were used to perform the statistical calculations. AI algorithm was designed by using the standard software Keras over Tensorflow 2.0. R package pROC was used.
3. Results
3.1. Variability Indices
The variability indices (SD and D) computed from the six time series recorded during the six-minute test are shown in Table 2. The medians are compared and the p-values are indicated. Two parameters are significantly different for the fallers and nonfallers: SDaap is significantly larger for fallers and Dav is significantly smaller. Those parameters will then be selected in the TUG+ test. Note that the fractal dimensions are globally smaller for fallers than for nonfallers.
Table 2.
Comparison between various indices of fallers and nonfallers at t1. Data are given under the form median [1st quartile–3rd quartile]. SD = standard deviation, D = fractal dimension. These indices are followed by a subscript labeling the time series from which it was obtained. Results of the TUG test are given in the last line. Significant differences are written in bold font.
| Fallers | Nonfallers | p | |
|---|---|---|---|
| SDav (m/s2) | 0.0949 [0.0810–0.149] | 0.101 [0.0868–0.130] | 0.245 |
| SDaml (m/s2) | 0.0864 [0.0752–0.109] | 0.0950 [0.0747–0.109] | 0.891 |
| SDaap (m/s2) | 0.120 [0.0901–0.173] | 0.0900 [0.0753–0.120] | 0.010 |
| SDωv (°/s) | 17.4 [15.5–20.2] | 18.4 [15.0–21.9] | 0.957 |
| SDωml (°/s) | 15.8 [12.3–20.3] | 13.7 [11.1–19.2] | 0.480 |
| SDωap (°/s) | 8.29 [6.77–11.6] | 8.79 [7.44–12.6] | 0.487 |
| Dav | 1.78 [1.73–1.82] | 1.81 [1.77–1.85] | 0.044 |
| Daml | 1.78 [1.66–1.81] | 1.81 [1.77–1.83] | 0.088 |
| Daap | 1.73 [1.68–1.80] | 1.79 [1.73–1.83] | 0.072 |
| Dωv | 1.71 [1.67–1.76] | 1.74 [1.69–1.76] | 0.376 |
| Dωml | 1.74 [1.71–1.78] | 1.78 [1.72–1.82] | 0.098 |
| Dωap | 1.81 [1.75–1.83] | 1.82 [1.78–1.85] | 0.149 |
| TUG (s) | 23 [19–31] | 19 [16–25] | 0.035 |
3.2. TUG and TUG+ Tests
Fallers perform the TUG test significantly slower than nonfallers. ROC curve and confusion matrix for the TUG test are shown in Figure 5 and Figure 6. Related parameters are shown in Table 3. Youden’s statistics for the TUG test leads to an optimal threshold of 22.5 s. An individual performing the TUG test over that threshold is likely to be considered as presenting a risk of fall in our population.
Figure 5.
(A) ROC curve for TUG test. An area under the curve of 0.621 is obtained, a Youden’s J of 0.256 and a threshold of 22.5 s. (B) TUG+ test classification algorithm.
Figure 6.
Confusion matrices in our study. (A) General definitions. TP = True Positives, FP = False Positives, FN = False Negatives, TN = True Negatives. (B) Results for the TUG test. (C) Results for the TUG+ test. (D) Results for the AI classification. The validation data set has 16 participants.
Table 3.
Characterization of the TUG and TUG+ test. The following parameters are displayed: sensitivity (Se), specificity (Sp), positive (LR+) and negative (LR−) likelihood ratios, positive (PPV) and negative (NPV) predictive values and accuracy (Acc). Improvements of TUG+ and AI methods with respect to TUG are emphasized in bold font.
| TUG | TUG+ | AI | |
|---|---|---|---|
| Se | 0.714 | 0.857 | 0.750 |
| Sp | 0.541 | 0.500 | 0.750 |
| LR+ | 1.56 | 1.71 | 3.00 |
| LR− | 0.529 | 0.286 | 0.333 |
| PPV | 0.481 | 0.778 | 0.750 |
| NPV | 0.761 | 0.632 | 0.750 |
| Acc | 0.657 | 0.739 | 0.750 |
The threshold of 22.5 s is kept in the TUG+. The SDaap and Dav thresholds were adjusted in order to maximize the TUG+ test’s accuracy: They are shown in Figure 5. The TUG+ test has better accuracy than the TUG test—an Mc Nemar test performed on the TUG and TUG+ classifications confirm that both tests are significantly different (p = 0.013). A detailed comparison between both tests is given in Table 3. The confusion matrix for the TUG+ test is also shown in Figure 6.
We have purposely designed TUG and TUG+ tests in a simple way, like how clinical tests are usually designed. For example, the TUG+ test can be seen as a checklist with three questions: Does the patient lie above the TUG and SDaap, or below Dav thresholds? A “diagnostic” of the risk/no risk of fall can be made from these three answers. Both tests could have been designed in a more complex way by resorting to logistic regressions: We present that approach in Appendix A. The performances of both versions of the TUG+ test are equivalent.
3.3. AI Classification
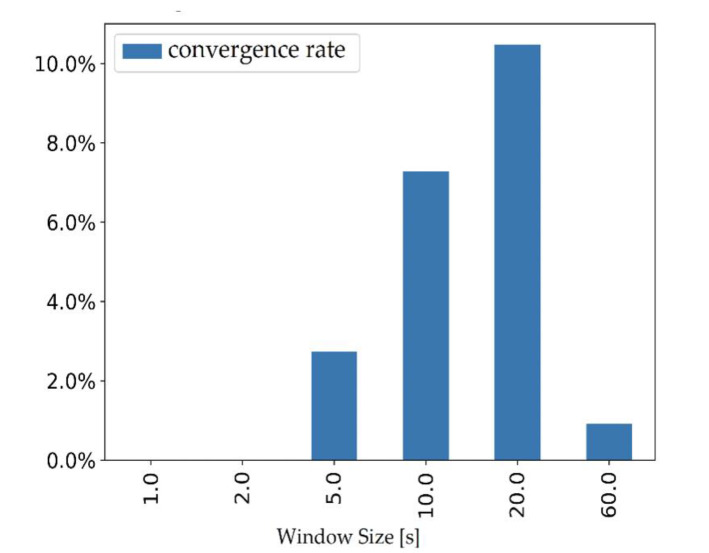
Models were trained and tested for the following window sizes: 1, 2, 5, 10, 20 and 60 s. Twenty seconds windows showed the best convergence rate as shown in Figure 7. We have then performed a random search hyperparametric study to optimize the accuracy of our AI algorithm [23]. The convergence rate may seem small but it is the consequence of the small (with respect to deep learning) dataset at our disposal and of the wide range of parameters we explored in the parameter space.
Figure 7.
Convergence rate of the AI algorithm versus window size. The convergence rate is the ratio of models that reached a precision of at least 65% on test data and the total amount of models trained for a specific window size.
We have kept the solution presented in Figure 8, leading to the confusion matrix displayed in Figure 6D. It showed maximal accuracy while being equally specific and sensitive (Sp = Se). One solution with higher accuracy was found (Acc = 81%) but at the expense of sensitivity (Se = 62.5%) and was, therefore, not kept.
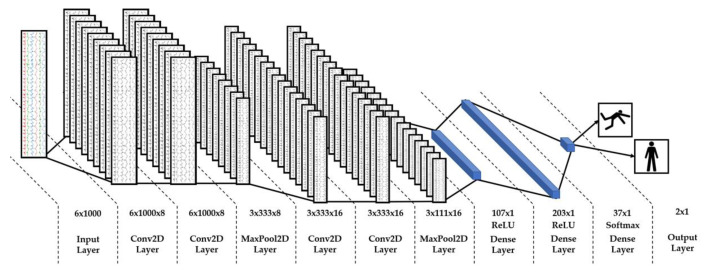
Figure 8.
CNN-based AI algorithm used to predict the risk of fall. The input layer receives a 20 s frame from the 6 inputs of the DYSKIMOT sensor. The convolutional layers (Conv2D layer) extract meaningful features from its input and present it to the next stage. Pooling layers (MaxPool2D Layer) reduce the dimension of the feature space by retaining the meaningful inputs of its layer only. After several convolutional stages, the remaining features are injected in a three layers neural network (dense layer) in order to classify the participant’s frames (output layer). The risk of fall is the mean (ranging from 0 to 1) of prediction on all frames of the participant’s sequence. A mean greater than 0.5 denotes a participant with risk of fall.
4. Discussion
Our study aimed at designing tests assessing the risk of fall in nursing home patients. The predictions of these tests were compared to the faller/nonfaller status of the participants. The originality of the present work is that two examination times separated by six months were included, and that the fall records of the nursing home during that time was used to classify participants as fallers or nonfallers.
We first confirm that the TUG test alone may predict falls despite its simplicity. We do not observe sensitivity and specificity as high as in [24] (Sp and Se of 87%). This could be explained by the fact that their sample only included 30 participants. Furthermore, a difference of 3.9 s between fallers and nonfallers is observed in our survey, which correlates with that of [25] (difference of 3.59 s). The threshold defining the risk of falls varies between 13 and 32.6 s according to the studies quoted by [26]. Our value of 22.5 s is intermediate. This latter study shows that the TUG test is a test that allows a better division between fallers and nonfallers when they are nursing home residents but not when they are home-based. This conclusion is shared by [26].
Kinematic analysis of the six-minute walking using the DYSKIMOT sensor reveals that this low-cost wearable device is able to measure significant differences between fallers and nonfallers. It is the first time our homemade system is applied to a geriatric population. The homemade sensor we used is not wireless yet. Placing the sensor in the lower limb (e.g., in one shoe) would have been relevant, as it is known from the literature, that instrumented socks are able to identify gait events [27,28], but the wire was uncomfortable for participants. This is coherent with the findings of [29] showing that patients mostly favor devices placed in the upper part of the body. The most comfortable solution we found is the placement in the lumbar region, which leads moreover to a sensor near the participant’s body center of mass, i.e., a crucial point as far as stability and balance are concerned.
The magnitude of anteroposterior acceleration’s fluctuations is significantly larger in fallers. It is coherent with the findings of [30] showing that elderly people who have already fallen have longer deceleration periods during a walking cycle than healthy young people. This behavior aims at reducing the swing phase to shorten unstable periods during the walking cycle. fallers also present smaller fractal dimensions. This observation can be related to the optimal complexity framework of [31]. They argued that physiological signals recorded in a healthy individual have a maximal complexity (e.g., high fractal dimension or entropy). A loss in complexity is associated with aging or disease. For instance, a smaller complexity in the walking pattern of healthy aged participants was observed in [32]. In our population, fallers are less able to perform quick modifications of their walking pattern and show a less complex behavior than nonfallers. Note that the six-minute walking test was interrupted by turnarounds due to the typical 25 m length of the nursing home corridors. Even if in the case of a point-to-point track, a walking course of 30 m is preferred, the minimum recommended length is 15 m [33]. Still, it is worth noticing that turnarounds are complex motor tasks that are representative of the daily activities of nursing home residents. Therefore, the kinematic information contained in the turnarounds could be isolated from the straight gait time series for separate analysis.
According to the review [34], techniques combining sensors and clinical tests are encouraging but the protocols used have yet to be standardized (sensor position, choice of clinical tests, data analysis). It is, therefore, possible to find combinations of clinical tests and kinematic parameters with an accuracy between 47.9% and 100% in a given sample [34]. The choice of the TUG test appears adequate in view of its intensive use in the field of geriatric rehabilitation and simplicity to perform. This test provides important information to predict the risk of fall when combined with kinematic data. The position of the inertial sensor in the lumbar area is relevant as it is close to the body center of mass. Studies such as [35] show that it is at this position that the best information can be gathered in order to differentiate between fallers and nonfallers. Furthermore, our choice of a six-minute walking test with an inertial sensor provides long-term information about an individual’s gait. Such information is not available with the TUG test alone. It appears from our study that the TUG test combined with kinematic parameters such as SCaap and Dav collected during the six-minute walking test improves the accuracy in predicting falls.
We report here for the first time on the increase of accuracy of TUG+ compared to TUG in predicting falls in elderly nursing home people. The novelty of this TUG+ is to combine TUG stopwatch-based duration results to gait variability indicators measured during a six-minute walking test by the DYSKIMOT sensor. Previous studies followed a similar approach. The study [36] is an attempt to improve the TUG test by increasing the walking distance and by timing each phase of this move (chair lifting, walking time, turnaround time) in order to get more information during the test. Others chose to complement the TUG test with additional sensors in order to improve its effectiveness [37,38]. In [38], the TUG test is specifically coupled with inertial sensors and shows an accuracy of 88%. In another survey, the same authors combined a questionnaire-based clinical evaluation with kinematic data measured by an inertial sensor during the TUG test [37]. They obtained accuracies of 68% for clinical evaluation alone, 73% for inertial sensors alone and 76% for combined evaluation. Those results are similar to ours: We find that the TUG+ test is a better way to predict the risk of falls in the elderly than the TUG test alone: We managed to increase the accuracy of the TUG test by 8.2% (Table 3). Using the TUG+ test, about 74% of the individuals on our sample were correctly categorized. To our knowledge, it is the first time that TUG and six-minute walking test results are merged that way.
We finally have built a complementary approach: AI analysis of six-minute walking kinematical time series in view of predicting the risk of fall. AI techniques are nowadays able to detect falls in real-time [39,40,41]. The particularity of our first attempt is to focus on a six-month prediction rather than on real-time detection. The obvious weakness of our AI classification, based on a convolutional neural network, is the size of our data set. Still, it shows the feasibility of risk of fall prediction from the kinematic data of an elderly walking six minutes, with an accuracy, specificity and sensibility of 75%.
The TUG+ test is an interesting solution in nursing homes because patients generally favor systems that do not replace a therapist [42]. Since our thresholds were fitted on the full population, we can safely conclude that a simple augmented clinical test is able to assess the risk of fall in our sample. The next step in this research is to study a different sample of nursing home patients with the tests built in the present study in order to fully assess our test’s predictive power. We hope to present such results in future work.
AI classification of the risk of fall, combined with a wearable sensor, gives hope that relevant tools monitoring the risk of fall of home-based elderly will become available in the near future. The MARG sensor we used is small (9 cm2) and light (10.44 g) enough to imagine several sensors attached on a wearable shirt, as proposed in [16,43] where it is shown that an undershirt equipped with 11 sensors is able to recognize several complex manual material handling tasks and basic postures (sitting, standing and lying down) as well as walking and running. In view of these promising results, it can be hoped that increasing the number of sensors in our system will increase the AI’s accuracy in the assessment of risk of fall. We leave such a program for future works.
Acknowledgments
The authors thank the following Belgian nursing homes for their support to the project: l’Adret (Gosselies), le Centenaire (Châtelet), le home Notre-Dame De Bonne Espérance (Châtelet) and Au Temps des Cerises (Châtelet). The authors also thank CeREF’s technical department for having allowed the use of DYSKIMOT sensor.
Appendix A. TUG and TUG+ Tests with Logistic Regressions
Instead of computing the threshold for TUG time from the ROC curve, a logistic regression of vs. the TUG time can be performed, P being the probability of being a faller (the R package caret is used). This test, called TUG (Logit), is defined by and the threshold P* = 0.41; its confusion matrix is presented in Figure A1 and its parameters are given in Table A1. The threshold was fitted to reach optimal accuracy.
Figure A1.
Confusion matrices for the logistic regression-based versions of the TUG and TUG+ tests. (A) TUG test. (B) TUG+ test.
Table A1.
Characterization of the TUG (Logit) and TUG+ (Logit) tests. Values in bold font represent improvements of TUG+ (Logit) test with respect to TUG (Logit) test.
| TUG (Logit) | TUG+ (Logit) | |
|---|---|---|
| Se | 0.837 | 0.898 |
| Sp | 0.250 | 0.333 |
| LR+ | 1.12 | 1.35 |
| LR− | 0.652 | 0.306 |
| PPV | 0.695 | 0.733 |
| NPV | 0.439 | 0.615 |
| Acc | 0.644 | 0.712 |
The TUG+ test can also be reformulated by using a logistic regression of LOGIT vs. TUG time, SDaap and Dav. This test, called TUG+ (Logit), is defined by . With the same threshold, one is led to the results presented in Figure A1 and Table A1.
The features of TUG (Logit) test are significantly different from TUG test: A Mc Nemar test leads to p < 0.01. The TUG test has a higher accuracy than the TUG (Logit) one. However, the performance of TUG+ (Logit) and TUG+ tests are very similar. A Mc Nemar test leads to p = 0.149.
Author Contributions
Conceptualization, F.B., F.D., R.G. and L.C.; methodology, F.D., R.G., L.J., D.F. and L.C.; software, F.B., R.G., L.J., D.F. and L.C.; validation, F.B., F.D. and V.B.; investigation, R.G. and L.C.; data curation, F.B., R.G. and L.C.; writing—original draft preparation, F.B., F.D. and V.B.; writing—review and editing, F.B., F.D., V.B., L.J., D.F., R.G. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Fatal Falls: WHO, Mortality Database 2010–2012. [(accessed on 12 February 2020)]; Available online: http://www.who.int/healthinfo/mortality_data/en/
- 2.Hartholt K. Falls and Drugs in Older Population: Medical and Societal Consequences. Erasmus University; Rotterdam, The Netherlands: 2011. [Google Scholar]
- 3.Moreland J.D., Richardson J.A., Goldsmith C.H., Clase C.M. Muscle weakness and falls in older adults: A systematic review and meta-analysis. J. Am. Geriatr. Soc. 2004;52:1121–1129. doi: 10.1111/j.1532-5415.2004.52310.x. [DOI] [PubMed] [Google Scholar]
- 4.Rossat A., Fantino B., Nitenberg C., Annweiler C., Poujol L., Herrmann F.R., Beauchet O. Risk factors for falling in community-dwelling older adults: Which of them are associated with the recurrence of falls? J. Nutr. Health Aging. 2010;14:787–791. doi: 10.1007/s12603-010-0089-7. [DOI] [PubMed] [Google Scholar]
- 5.Ambrose A.F., Paul G., Hausdorff J.M. Risk factors for falls among older adults: A review of the literature. Maturitas. 2013;75:51–61. doi: 10.1016/j.maturitas.2013.02.009. [DOI] [PubMed] [Google Scholar]
- 6.Posdiadlo D., Richardson S. The time “Up & Go”: A test of basic functional mobility for frail elderly persons. J. Am. Geriatr. Soc. 1991;39:142–148. doi: 10.1111/j.1532-5415.1991.tb01616.x. [DOI] [PubMed] [Google Scholar]
- 7.Herman T., Giladi N., Hausdorff J.M. Properties of the ‘timed up and go’ test: More than meets the eye. Gerontology. 2011;57:203–210. doi: 10.1159/000314963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Panel on Prevention of Falls in Older Persons. American Geriatrics Society. British Geriatrics Society Summary of the Updated American Geriatrics Society/British Geriatrics Society clinical practice guideline for prevention of falls in older persons. J. Am. Geriatr. Soc. 2011;14:148–157. doi: 10.1111/j.1532-5415.2010.03234.x. [DOI] [PubMed] [Google Scholar]
- 9.Hausdorff J.M., Rios D.A., Edelberg H.K. Gait variability and fall risk in community-living older adults: A 1-year prospective study. Arch. Phys. Med. Rehabil. 2001;82:1050–1056. doi: 10.1053/apmr.2001.24893. [DOI] [PubMed] [Google Scholar]
- 10.Weiss A., Herman T., Plotnik M., Brozgol M., Giladi N., Hausdorff J.M. An instrumented timed up and go: The added value of an accelerometer for identifying fall risk in idiopathic fallers. Physiol. Meas. 2011;32:2003–2018. doi: 10.1088/0967-3334/32/12/009. [DOI] [PubMed] [Google Scholar]
- 11.ATS Committee on Proficiency Standards for Clinical Pulmonary Function Laboratories ATS statement: Guidelines for the six-minute walk test. Am. J. Respir. Crit. Care Med. 2002;166:111–117. doi: 10.1164/ajrccm.166.1.at1102. [DOI] [PubMed] [Google Scholar]
- 12.Jehn M., Schmidt-Trucksäess M.D., Schuster T., Hanssen H., Weis M., Halle M., Koehler F. Accelerometer-Based Quantification of 6-Minute Walk Test Performance in Patients with Chronic Heart Failure: Applicability in Telemedicine. J. Card. Fail. 2009;15:334–340. doi: 10.1016/j.cardfail.2008.11.011. [DOI] [PubMed] [Google Scholar]
- 13.Annegarn J., Spruit M.A., Savelberg H.H.C.M., Willems P.J.B., van de Bool C., Schols A.M.W.J., Wouters E.F.M., Meijer K. Differences in Walking Pattern during 6-Min Walk Test between Patients with COPD and Healthy Subjects. PLoS ONE. 2012;7:e37329. doi: 10.1371/journal.pone.0037329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hage R., Detrembleur C., Dierick F., Pitance L., Jojczyk L., Estievenart W., Buisseret F. DYSKIMOT: An Ultra-Low-Cost Inertial Sensor to Assess Head’s Rotational Kinematics in Adults during the Didren-Laser Test. Sensors. 2020;20:833. doi: 10.3390/s20030833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Oks A., Katashev A., Zadinans M., Rancans M., Litvak J. Development of Smart Sock System for Gate Analysis and Foot Pressure Control. In: Kyriacou E., Christofides S., Pattichis C.S., editors. XIV Mediterranean Conference on Medical and Biological Engineering and Computing. Springer International Publishing; Paphos, Cyprus: 2016. pp. 466–469. [Google Scholar]
- 16.Esfahani M.I.M., Nussbaum M.A., Kong Z. Using a smart textile system for classifying occupational manual material handling tasks: Evidence from lab-based simulations. Ergonomics. 2019;62:823–833. doi: 10.1080/00140139.2019.1578419. [DOI] [PubMed] [Google Scholar]
- 17.Rajagopalan R., Litvan I., Jung T.-P. Fall Prediction and Prevention Systems: Recent Trends, Challenges, and Future Research Directions. Sensors. 2017;17:2509. doi: 10.3390/s17112509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Moulias S., Peigne V., Guérin O., Daire R. Gériatrie, Cahier des EC. 3rd. Elsevier Masson; Paris, France: 2015. p. 95. [Google Scholar]
- 19.Dierick F., Nivard A.-L., White O., Buisseret F. Fractal analyses reveal independent complexity and predictability of gait. PLoS ONE. 2017;12:e0188711. doi: 10.1371/journal.pone.0188711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kantz H., Schreiber T. Nonlinear Time Series Analysis. Cambridge University Press; Cambridge, UK: 2004. [Google Scholar]
- 21.Hausdorff J.M., Peng C.K., Ladin Z., Wei J.Y., Goldberger A.L. Is walking a random walk? Evidence for long-range correlations in stride interval of human gait. J. Appl. Physiol. 1995;78:349–358. doi: 10.1152/jappl.1995.78.1.349. [DOI] [PubMed] [Google Scholar]
- 22.Goodfellow I., Bengio Y., Courville A. Deep Learning. MIT Press; Cambridge, MA, USA: 2016. [Google Scholar]
- 23.Bergstra J., Bengio Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012;13:281. [Google Scholar]
- 24.Shumway-Cook A., Brauer S., Woollacott M. Predicting the Probability for Falls in Community-Dwelling Older Adults Using the Timed Up & Go Test. Phys. Ther. 2000;80:896–903. [PubMed] [Google Scholar]
- 25.Schoene D., Wu S.M.-S., Mikolaizak A.S., Menant J.C., Smith S.T., Delbaere K., Lord S.R. Discriminative ability and predictive validity of the timed up and go test in identifying older people who fall: Systematic review and meta-analysis. J. Am. Geriatr. Soc. 2013;61:202–208. doi: 10.1111/jgs.12106. [DOI] [PubMed] [Google Scholar]
- 26.Viccaro L.J., Perera S., Studenski S.A. Is timed up and go better than gait speed in predicting health, function, and falls in older adults? J. Am. Geriatr. Soc. 2001;59:887–892. doi: 10.1111/j.1532-5415.2011.03336.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Preece S.J., Kenney L.P., Major M.J., Dias T., Lay E., Fernandes B.T. Automatic identification of gait events using an instrumented sock. J. Neuroeng. Rehabil. 2011;8:32. doi: 10.1186/1743-0003-8-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tirosh O., Begg R., Passmore E., Knopp-Steinberg N. Wearable textile sensor sock for gait analysis; Proceedings of the Seventh International Conference on Sensing Technology; Wellington, New Zealand. 3–5 December 2013. [Google Scholar]
- 29.Bergmann J.H.M., Chandaria V., McGregor A. Wearable and implantable sensors: The patient’s perspective. Sensors. 2012;12:16695–16709. doi: 10.3390/s121216695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kavanagh J.J., Barrett R.S., Morrison S. Upper body accelerations during walking in healthy young and elderly men. Gait Posture. 2004;20:291–298. doi: 10.1016/j.gaitpost.2003.10.004. [DOI] [PubMed] [Google Scholar]
- 31.Goldberger A.L., Amaral L.A.N., Hausdorff J.M., Ivanov P.C., Peng C.-K., Stanley H.E. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. USA. 2002;99(Suppl. 1):2466–2472. doi: 10.1073/pnas.012579499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kobsar D., Olson C., Paranjape R., Hadjistavropoulos T., Barden J.M. Evaluation of age-related differences in the stride-to-stride fluctuations, regularity and symmetry of gait using a waist-mounted tri-axial accelerometer. Gait Posture. 2014;39:553–557. doi: 10.1016/j.gaitpost.2013.09.008. [DOI] [PubMed] [Google Scholar]
- 33.Sciurba F., Criner G.J., Lee S.M., Mohsenifar Z., Shade D., Slivka W., Wise R.A. National Emphysema Treatment Trial Research Group. Six-minute Walk Distance in Chronic Obstructive Pulmonary Disease: Reproducibility and Effect of Walking Course Layout and Length. Am. J. Respir. Crit. Care Med. 2003;167:1522–1527. doi: 10.1164/rccm.200203-166OC. [DOI] [PubMed] [Google Scholar]
- 34.Sun R., Sosnoff J.J. Novel sensing technology in fall risk assessment in older adults: A systematic review. BMC Geriatr. 2014;18:14. doi: 10.1186/s12877-018-0706-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Howcroft J., Lemaire E.D., Kofman J. Wearable-Sensor-Based Classification Models of Faller Status in Older Adults. PLoS ONE. 2016;11:e0153240. doi: 10.1371/journal.pone.0153240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wall J.C., Bell C., Campbell S., Davis J. The Timed Get-up-and-Go test revisited: Measurement of the component tasks. J. Rehabil. Res. Dev. 2000;37:109–113. [PubMed] [Google Scholar]
- 37.Greene B.R., Doheny E.P., Kenny R.A., Caulfield B. Classification of frailty and falls history using a combination of sensor-based mobility assessments. Physiol. Meas. 2014;35:2053–2066. doi: 10.1088/0967-3334/35/10/2053. [DOI] [PubMed] [Google Scholar]
- 38.Greene B., Redmond S., Caulfield B. Fall Risk Assessment through Automatic Combination of Clinical Fall Risk Factors and Body-Worn Sensor Data. IEEE J. Biomed. Health Inform. 2016;21:725–731. doi: 10.1109/JBHI.2016.2539098. [DOI] [PubMed] [Google Scholar]
- 39.Luna-Perejón F., Domínguez-Morales M.J., Civit-Balcells A. Wearable Fall Detector Using Recurrent Neural Networks. Sensors. 2019;19:4885. doi: 10.3390/s19224885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Santos G.L., Endo P.T., Monteiro K.H.C., Rocha E.S., Silva I., Lynn T. Accelerometer-Based Human Fall Detection Using Convolutional Neural Networks. Sensors. 2019;19:1644. doi: 10.3390/s19071644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhang J., Wu C., Wang Y. Human Fall Detection Based on Body Posture Spatio-Temporal Evolution. Sensors. 2020;20:946. doi: 10.3390/s20030946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bergmann J.H.M., McGregor A.H. Body-worn sensor design: What do patients and clinicians want? Ann. Biomed. Eng. 2011;39:2299–2312. doi: 10.1007/s10439-011-0339-9. [DOI] [PubMed] [Google Scholar]
- 43.Mokhlespour Esfahani M.I., Nussbaum M.A. Classifying Diverse Physical Activities Using “Smart Garments”. Sensors. 2019;19:3133. doi: 10.3390/s19143133. [DOI] [PMC free article] [PubMed] [Google Scholar]