Sensitivity of comorbidity network analysis

Abstract

Objectives

Comorbidity network analysis (CNA) is a graph-theoretic approach to systems medicine based on associations revealed from disease co-occurrence data. Researchers have used CNA to explore epidemiological patterns, differentiate populations, characterize disorders, and more; but these techniques have not been comprehensively evaluated. Our objectives were to assess the stability of common CNA techniques.

Materials and Methods

We obtained seven co-occurrence data sets, most from previous CNAs, coded using several ontologies. We constructed comorbidity networks under various modeling procedures and calculated summary statistics and centrality rankings. We used regression, ordination, and rank correlation to assess these properties’ sensitivity to the source of data and construction parameters.

Results

Most summary statistics were robust to variation in link determination but somewhere sensitive to the association measure. Some more effectively than others discriminated among networks constructed from different data sets. Centrality rankings, especially among hubs, were somewhat sensitive to link determination and highly sensitive to ontology. As multivariate models incorporated additional effects, comorbid associations among low-prevalence disorders weakened while those between high-prevalence disorders shifted negative.

Discussion

Pairwise CNA techniques are generally robust, but some analyses are highly sensitive to certain parameters. Multivariate approaches expose additional conceptual and technical limitations to the usual pairwise approach.

Conclusion

We conclude with a set of recommendations we believe will help CNA researchers improve the robustness of results and the potential of follow-up research.

INTRODUCTION

Systems medicine consists in the adoption into medical research of principles and techniques from systems biology, described as global, integrative, and holistic.^1–3 Networks have become a staple of systems biology⁴ and seen extensive use in systems medicine.⁵ An ongoing focus is the “diseaseome” characterized by comorbid associations among disorders. Clinical comorbidity refers to disease that complicates an index condition for an individual patient. These patterns can reveal clinically relevant differences in prognosis or response to treatment and produce statistical associations in population studies called epidemiological comorbidities.^6,7Comorbidity network analysis (CNA) is a systems approach to epidemiology that studies networks aggregated from measures of co-occurrence between pairs or larger subsets of disorders.^8,9 CNAs seek to uncover novel clinical associations, to stratify patient populations, and to identify disorders and multimorbidities for further investigation, among other aims.¹⁰

Network science¹¹ rests predominantly on the theory of mathematical graphs. The relations that constitute a comorbidity network are usually discretized from incidence data, which makes the analysis of large data sets more computationally tractable but for which no standard procedure exists and which may result in confounding of covariance and loss of sign and magnitude information. Moreover, network tools often rely on theoretical assumptions that do not hold for association data, such as the importance of indirect connections between nodes for the transfer of material, activity, or information, which underpin concepts such as community, brokerage, and centrality.^12,13 The graph-theoretic operationalizations of these concepts do not have natural epidemiological interpretations.

OBJECTIVES

We distinguish four concerns with conventional CNA, adapting terminology from¹⁴ and:¹⁵ (1) Source of incidence data differ in their conventions, completeness, and representativeness, and the consequent differences in network structure have not been explored (results reproducibility). (2) The method of link determination, with respect to statistical signal and association strength, varies across studies, and the effects of adjusting these parameters have not been assessed (stability). (3) Networks aggregated from pairwise associations discard information about higher-order interactions, though these potential effects are important to epidemiological understanding and to the systems paradigm (robustness). (4) The use of network statistics relies on correspondences between theoretical constructs and instrumental definitions, but little theoretical guidance is available for network representations of comorbid associations (interpretability).

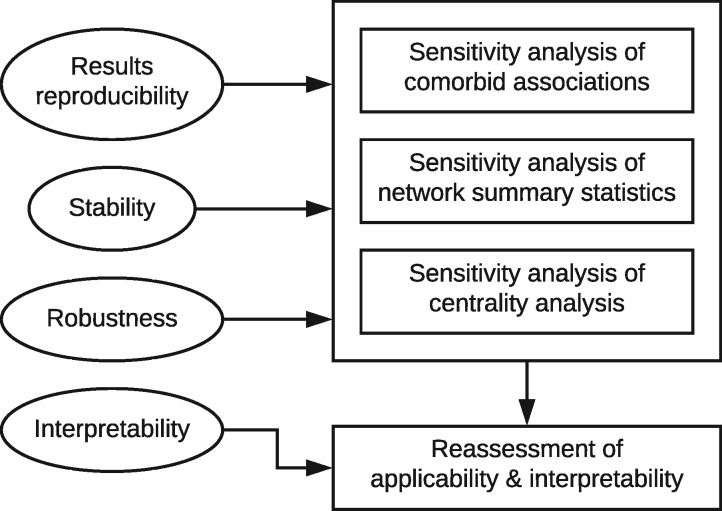
Motivated by these concerns, we set out to answer four research questions (Figure 1): (1) How sensitive are the measured strengths of pairwise associations to the choice of network model, in particular whether the model takes additional comorbid associations or patient-level covariates into account? (2) How sensitive are network summary statistics to network model parameters, including the choice of model and model-specific parameters like the choice of association measure and the cutoff for link determination? Does this sensitivity impair the use of these statistics to characterize and distinguish underlying populations? (3) How sensitive is centrality analysis to these parameters? Does this sensitivity problematize the identification of highly comorbid “hub” disorders or the centrality rankings of less central disorders? (4) How does the relational origin of network-analytic tools limit their application or interpretability on co-occurrence data? Do the sensitivity results help inform the answer?

Figure 1.

Motivation and design of this study.

MATERIALS AND METHODS

Data sets

We acquired eight data sets for our analysis (Table 1): Six were provided by the authors of previous CNAs, but only in a form suitable for pairwise analysis.^16–20 One (MIMIC-III) is freely available to researchers upon submission of a study design and completion of a short online course.²¹ For computational feasibility, we crosswalked diagnosis codes to the Clinical Classification Software (CCS) ontology.²² The last, results of the 2011 National Ambulatory Medical Care Survey (NAMCS), was obtained from the website of the Centers for Disease Control and Prevention (https://www.cdc.gov/nchs/ahcd/index.htm). We extracted indicators for 13 chronic disorders for analysis purposes. Coded ontologies included the International Classification of Diseases, 9th and 10th Revisions, Clinical Modifications (ICD9 and ICD10) and the custom ontology of reference 16. The data sets vary widely in the underlying patient population, in the collection of their data by healthcare institutions, and in the researchers’ pre-processing protocols; variation along each of these dimensions contributes to overall variation due to the data source. Disentangling these factors would require a more thorough study using several sources of patient-level data.

Table 1.

Sources of pairwise disorder co-occurrence data used in this study, originally aggregated from patient-level data for previous studies and made available by their authors (except MIMIC-III and NAMCS)

Source	Time period	Patients	Ontology	Terms
Columbia University Medical Center16	Unreported	1.5 million	Rzhetsky et al.16	161
MedPAR17	1990–1993	32 million	ICD9 (level 5)	16 459
			ICD9 (level 3)	657
Sct. Hans Hospital18	1998–2008	5543	ICD10 (level 3)	351
University of Michigan Health System19	Unreported	1.62 million	ICD9 (level 5)	14 489
STRIDE (Stanford University)20	2008–2013	277 290	Rzhetsky et al. 16	161
MIMIC-III (Beth Israel Deaconess)21	2001–2012	38 645	CCS	113–273
NAMCS	2011	10 908	Chronic disorders	13

SOFTWARE

We performed analyses in R,²³ using the tidyverse collection²⁴ and a combination of igraph,²⁵ tidygraph,²⁶ and ggraph.²⁷ English descriptions of ICD9 and ICD10 codes were obtained from icd.²⁸ Full code to reproduce our analyses is available at https://bitbucket.org/corybrunson/comorbidity.

Pairwise constructions

The majority of CNAs construct networks from pairwise co-occurrence data, that is, the values that fill a $2\times 2$ contingency table. From these data, we calculated both evidential and evaluative thresholds: Evidential thresholds were test-wise error rates (TWERs), optionally adjusting for multiple comparisons using the family-wise error rate (FWER) Bonferroni correction or the false discover rate (FDR) Benjamini–Hochberg correction, both of which have been used in the CNA literature.^{18,20,29–31} Evaluative thresholds were minimum absolute values of a binary association measure (BAM). We used four BAMs, two risk ratios and two correlation coefficients: the odds ratio $\mathit{OR}=\frac{a/b}{c/d};$^32,33Pearson’s binary correlation coefficient $\varphi =\frac{\mathit{ad}-\mathit{bc}}{\sqrt{(a+b)(a+c)(b+d)(c+d)}},$³⁴Forbes’ coefficient of association $F=\frac{a/(a+b)}{(a+c)/(a+b+c+d)},$³⁴ and the tetrachoric correlation coefficient $r_t$ calculated using a latent bivariate normal model.³⁵$\mathrm{OR}$ is recommended as a standard measure of epidemiological comorbidity³² and has been used in several CNA studies.^19,36,37 Several other studies have used $\varphi$ and $F$ together, in part to check the robustness of their results,^17,38–41 though these refer to $F$ as “relative risk.”⁴²$r_t$ has not appeared in CNA literature but enables later comparisons between pairwise and multivariate models. We calculated $r_t$ using psych⁴³ and implemented the approximation of reference 44 to calculate standard errors. In the pairwise analysis, only positive associations were included.

Pairwise network construction was thus based on five parameters: the source of data $D$; the TWER $\alpha$; the error rate correction $C$, if any; the BAM $m$ (possibly none); and the BAM cutoff $\theta$. We notate specific networks $N(D,\alpha ,C,m,\theta )$ and substitute bullets $•$ for values to indicate families of networks taken over all values in the following ranges:

• $D$: Columbia, MedPAR(3), MedPAR(5), Sct. Hans, Michigan, Stanford, Columbia*, MIMIC

• $\alpha$: ${10}^{-p}, p=1,\dots , 6$

• $C$: none (ø), Bonferroni (FWER), Benjamini–Hochberg (FDR)

• $m$: $1$ (unit), $\mathrm{OR}$, $\varphi$, $F$, $r_t$

• $\theta$: each of four values specific to each measure: (The threshold ranges of ${\theta }_m$ for each BAM $m$ were chosen so that the corresponding quantiles of pairs in each data set are roughly equal.) ${\mathrm{\theta }}_{\mathrm{OR}}=1, 2, 6, 60$, ${\theta }_{\varphi }=0, 0.005, 0.05, 0.2$, ${\theta }_F=1, 2, 6, 60$, ${\theta }_{r_t}=0, 0.1, 0.4, 0.6$.

Multivariate constructions

Conventional measures of comorbidity fail to account for incidence rates of other disorders. Clinically unrelated disorders may co-occur due to common risk factors or complications, and such “transitive correlations”⁴⁵ are important potential explanations for clustering patterns observed in comorbidity networks.³⁶ Partial correlations account for these confounding effects by generalizing the calculation of regression coefficients: the full partial correlation $r{\text{'}}_{\mathit{ij}}={\widehat{\beta }}_{\mathit{ij}}{\widehat{\sigma }}_j/{\widehat{\sigma }}_i$ between response variables $y_i$ and $y_j$ is a standardized effect estimate from the regression model of $y_i$ on all other responses, including $y_j$ (and satisfies $r{\text{'}}_{\mathit{ij}}=r{\text{'}}_{\mathit{ji}}$).⁴⁶ This concept relies on normality assumptions for regression; we use a matrix formulation $R_t\text{'}$ to obtain partial tetrachoric correlations $r_t\text{'}$ from the tetrachoric correlations $R_t$. We computed $r_t\text{'}$ differently for high-volume, low-dimension data⁴³ and, via shrinkage estimates, for low-volume, high-dimension data.^47,48

Another way to account for such confounding is to use an interaction model based on an underlying covariance matrix. An estimator of this matrix can be scaled to obtain an estimated correlation matrix $\mathrm{P}=\left({\rho }_{\mathit{ij}}\right)$. Epidemiological comorbidities may also arise from patient-level covariates, as when clinically relevant subpopulations (eg, elderly or infirm patients) are at heightened risk of multiple, otherwise etiologically unrelated disorders. We adapted the joint interaction–distribution model (JIDM) of reference 49 to jointly model disorder interactions and patient-level covariates, and by omitting covariates other than intercepts we obtain a comparable interaction model. We denote the models JIDM0 and JIDM1 and their correlation matrices ${\widehat{\mathrm{P}}}_0$ and ${\widehat{\mathrm{P}}}_1$. We adapted this workflow from reference 49 using JAGS⁵⁰ via R2jags.⁵¹

From the NAMCS data, we generated a $13\times 13$ correlation matrix for each model, controlling for age, gender, ethnicity, insurance status, region, and metropolitan status in JIDM1. From the MIMIC data, we excluded JIDM1, to reduce computational cost and to limit the scope of the analysis. Each model included every CCS code. We compared all four models on the chronic disorders in NAMCS using correlation biplots. We visualized the relationships among the correlation estimates using scatterplots. Of the two data sources, one (NAMCS) is low-dimensional but high-volume while the other (MIMIC-III) is comparatively high-dimensional and low-volume. This enables us to more confidently take general lessons from the model comparisons.

Global network structure

To assess the effects of the construction parameters on the pairwise models, we calculated several unweighted summary statistics on the networks $N(•,•,ø,•,•)$ and fit two regression models to each vector of statistics. The first model (Equation 1) included only the predictors $D_i$ (categorical) and $\text{log}\left({\alpha }_i\right)$ (continuous) and was evaluated on the networks $N(•,•,ø, 1,ø)$, while the second (Equation 2) was evaluated on the lot and also included an interaction effect of $m_i$ (categorical) with ${\theta }_i$ (continuous) in order to allow for the different effects of the evaluative cutoff using different association measures. To simplify computations, we took as the response variable the difference $y_i=s_i-\overline{s}$ between $s_i$ and the average value $\overline{s}$ on the networks $N(•,•,ø)$. The coefficient ${\beta }_{D_i}$ associated with each dataset $D_i$ then indicates the direction in which a statistic deviates, on $D_i$, from its values on the other $D_j$.

Equation 1

$$y_i={\sum }_D{\beta }_{d}I\left(D_i=D\right)+{\beta }_{\alpha }\log \left({\alpha }_i\right)+{ϵ}_i$$

Equation 2

$$y_i={\sum }_D{\beta }_{d}I\left(D_i=D\right)+{\beta }_{\alpha }\log \left({\alpha }_i\right)+{\sum }_m{\beta }_{m,\theta }I\left(m_i=m\right){\theta }_i+{ϵ}_i$$

$${ϵ}_i\sim N(0,{\sigma }^2)$$

The statistics included the proportion of disorders in the largest connected component LCP, the graph density $\delta$, the mean degree $\overline{k}$, the Gini index $G,$⁵² the degree assortativity $r,$⁵³ the triad closure $C$, the mean graph distance $\overline{\ell }$, the modularity $Q$ using Walktrap,^54,55 and the location and scale parameters $\widehat{\mu }$ and $\widehat{\sigma }$ of the log-normal family, which best fit the degree sequence tails.^56,57 We complemented these regressions with a principal components analysis (PCA) on the same centered and scaled statistics.

Centrality rankings

CNAs often characterize disorders by their centrality in a comorbidity network:¹⁷ and⁵⁸ used (weighted and unweighted, respectively) degree centrality to measure the connectedness of disorders, or their “total” epidemiological comorbidity;⁵⁸ also used betweenness centrality to measure the potential influence of an index disorder on a patient’s comorbidities. Several other teams invoked degree, betweenness, and closeness centrality as general indicators of a disorder’s importance.^39,59,60 Three studies corroborated the exceptionally high centrality of hypertension in comorbidity networks,^39,58,61 while another examined the centralities of disorders comorbid with hypertension.⁶⁰ An increasingly popular approach is to compare centralities across study populations:⁶¹ compared the betweenness centralities of diagnoses between demographic strata such as low- and high-income populations, and⁶² compared degree centralities of disorders between COPD and non-COPD populations in a case–control design.⁶¹ found that the betweenness rankings of disorders were sensitive to their link pruning procedure, and⁵⁹ noted that the centralities of adverse events in their VAERS networks changed noticeably from month to month.

We calculated degree, betweenness, and closeness centralities in the networks $N(•, 0.01,•,•,ø)$. We compared centrality rankings on entire ontologies using Kendall rank correlations,^63,64 which we analyzed geometrically using variance decompositions and biplots. We also identified the several most central disorders from each network and assessed their consistency directly. Finally, we used many-to-one maps between ontologies (level-5 to level-3 ICD9 and level-5 ICD9 to the ontology of reference 16) to compare group centrality measures for concepts in the finer ontology with node centralities for concepts in the coarser ontology.⁶⁵

Ethical considerations

This study did not involve human or other animal subjects. We conducted secondary analysis on data sets collected and aggregated by other researchers, which are available either publicly or upon request. Of these, patient-level data were only available in MIMIC-III, but our analysis relied exclusively on aggregated data.

RESULTS

Global network structure

Table 2 ⁶⁶ summarizes the linear model of Equation 2 fit to various global statistics. The effect estimates ${\beta }_{m,\theta }$ of the interactions $m\times {\theta }_m$ can be compared after scaling the ranges of the ${\theta }_m$. Almost all effects are discernible with $P<.001$. The PCA biplot (Figure 2⁶⁷) complements these estimates with information about their relative differences.

Table 2.

LMs of network statistics on data source, test-wise error rate, and binary association measure

	Dependent variable
	LCP	$r$	$G$	$\overline{k}$	$\widehat{\mu }$	$\widehat{\sigma }$	$\overline{\ell }$	$Q$	$C$
Columbia	0.24***	0.06*	−0.19***	−51.04***	−0.001	−0.34***	−0.68*	−0.03	0.01
	(0.03)	(0.03)	(0.02)	(11.46)	(0.18)	(0.05)	(0.27)	(0.03)	(0.02)
MedPAR(3)	0.31***	0.13***	−0.18***	−31.79**	0.31*	−0.08	0.30	0.12***	−0.09***
	(0.03)	(0.03)	(0.02)	(11.46)	(0.17)	(0.05)	(0.27)	(0.03)	(0.02)
MedPAR(5)	0.21***	−0.12***	0.03*	−39.54***	0.24	0.31***	1.38***	0.18***	−0.28***
	(0.03)	(0.03)	(0.02)	(11.46)	(0.17)	(0.05)	(0.27)	(0.03)	(0.02)
Sct. Hans	0.13***	0.04	−0.11***	−59.58***	−1.16***	0.03	0.20	0.10**	−0.22***
	(0.03)	(0.03)	(0.02)	(11.46)	(0.18)	(0.05)	(0.27)	(0.03)	(0.02)
Michigan	0.51***	−0.18***	−0.11***	158.43***	2.07***	0.23***	0.31	0.12***	−0.12***
	(0.03)	(0.03)	(0.02)	(11.46)	(0.17)	(0.05)	(0.27)	(0.03)	(0.02)
Stanford	−0.21***	0.39***	−0.07***	−60.66***	−2.20***	0.23***	−1.50***	−0.13***	0.09***
	(0.03)	(0.03)	(0.02)	(11.46)	(0.19)	(0.05)	(0.27)	(0.03)	(0.02)
Columbia*	−0.19***	0.07*	−0.14***	−58.96***	−0.93***	−0.45***	−1.63***	−0.14***	0.01
	(0.03)	(0.03)	(0.02)	(11.46)	(0.19)	(0.05)	(0.27)	(0.03)	(0.02)
MIMIC	0.31***	0.02	−0.07***	−37.21**	−0.09	0.43***	1.62***	0.15***	−0.21***
	(0.03)	(0.03)	(0.02)	(11.46)	(0.17)	(0.05)	(0.27)	(0.03)	(0.02)
$\log \left(p\right)$	0.02***	−0.003	−0.01***	1.95*	0.06***	−0.01**	−0.05**	−0.01***	−0.01***
	(0.002)	(0.002)	(0.001)	(0.80)	(0.01)	(0.003)	(0.02)	(0.002)	(0.001)
$F\times {\theta }_F$	−0.01***	0.001*	0.002***	−1.17***	−0.04***	−0.003*	0.02***	0.002***	−0.003***
	(0.001)	(0.001)	(0.0003)	(0.20)	(0.004)	(0.001)	(0.005)	(0.001)	(0.0003)
$\widehat{\mathit{OR}}\times {\theta }_{\widehat{\mathit{OR}}}$	−0.01***	0.003***	0.002***	−1.14***	−0.03***	−0.003**	0.02***	0.003***	−0.003***
	(0.001)	(0.001)	(0.0003)	(0.20)	(0.004)	(0.001)	(0.005)	(0.001)	(0.0003)
$\varphi \times {\theta }_{\varphi }$	−3.24***	2.20***	1.46***	−422.14***	−19.35***	0.47	3.70**	0.57***	−0.51***
	(0.15)	(0.17)	(0.09)	(59.45)	(1.08)	(0.30)	(1.38)	(0.16)	(0.11)
$r_t\times {\theta }_{r_t}$	−0.63***	0.19***	0.19***	−125.11***	−4.50***	−0.04	2.64***	0.34***	−0.22***
	(0.05)	(0.05)	(0.03)	(17.70)	(0.30)	(0.08)	(0.41)	(0.05)	(0.03)
Observations	576	568	576	576	504	504	576	576	568
Adjusted $R^2$	0.78	0.59	0.57	0.66	0.79	0.51	0.43	0.56	0.65

Note:

^* P < .1;

^** P < .01;

^*** P < .001.

Figure 2.

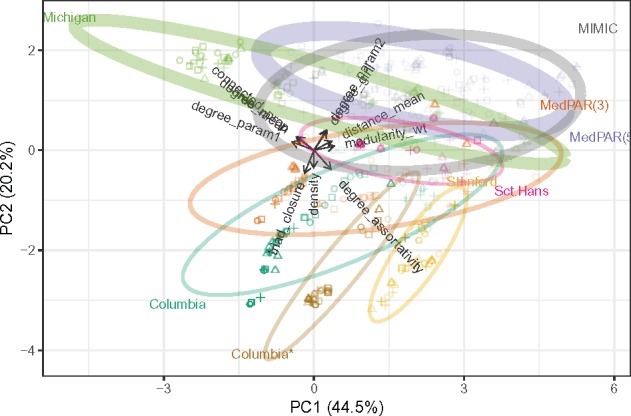
Row-principal PCA biplot for the summary statistics with networks (cases) in principal coordinates and statistics (variables) in standard coordinates. The values for graphs constructed from a common dataset are summarized by 95% confidence ellipses. Symbol corresponds to BAM, color indicates data source, and opacity is proportional to network density. Ellipse thicknesses are proportional to the number of clinical concepts (nodes) in the ontology (graph).

The evidential and evaluative thresholds effect dramatic changes in graph density $\delta$, which largely explain their effects on connectivity ($\text{LCP},\overline{k},\mu ,\overline{\ell }$). Stricter thresholds also led to greater hierarchical structure ($r,Q$). Uniquely, triad closure increased with stricter evidential cutoffs but decreased with stricter evaluative cutoffs. Graph density aligned with the first principal component, which accounted for 40% of the variation among the global statistics.

The second principal component separated more connected and homogeneous networks from those with greater assortativity and triad closure, and more effectively discriminated among the data sources. Each data source produced networks with distinctive properties, and stricter thresholds enhanced these distinctions. Stanford and Columbia* yielded similar networks via identical ontology and processing, though MedPAR(3) and Michigan produced similar networks with no such commonalities; MedPAR(3) and MedPAR(5), like Columbia and Columbia*, differed only in ontology, but the former yielded similar networks while the latter highly dissimilar ones.

Centrality rankings

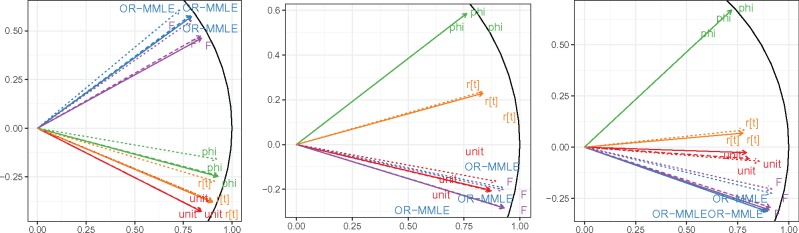
For each data source and centrality measure, different error rate corrections and BAMs yielded very different rankings of disorders in the underlying ontology. For an example taken at random, rankings of full ICD9 codes based on Michigan data were sensitive to the BAM though robust to the correction (Figure 3). In other cases, rankings were variably more sensitive to the BAM (MedPAR(3), Columbia*) or to the correction (Sct. Hans, MIMIC). Overall, degree centrality was more sensitive to the correction and closeness and betweenness centrality more sensitive to the BAM.

Figure 3.

Eigendecomposition biplots for the Kendall correlations among (left to right) degree, betweenness, and closeness centrality rankings of disorders in networks constructed from the Michigan data, using a 5% TWER with each error rate correction and each BAM. The linetype of each arrow indicates the correction (solid for none, dotted for FWER, dashed for FDR) and its color and label indicate the BAM.

In contrast, the hubs identified using each centrality measure were consistent across constructions for each data source. Hubs identified from regional EHR data included epilepsy, limb pain, respiratory problems, vitamin deficiency, benign neoplasms, and tuberculosis; other data sources produced their own distinctive hubs: non-specific diagnoses of fluid and electrolyte imbalances, urinary tract disorders, and bacterial infections (MedPAR), which may be associated with increased hospital and nursing home care as well as with aging itself; gait and mobility disorders, which are strongly associated with nervous disorders (Sct. Hans); and acute posthemorrhagic anemia (APHA), a common symptom of injury-induced blood loss (MIMIC). Prevalence did not strongly predict centrality, but all hubs were highly prevalent disorders.

Centrality rankings using node versus group centrality on networks constructed using different ontologies were weakly concordant or else discordant, even when constructed using crosswalked data from the same source. Group betweenness centrality was computationally prohibitive, so only degree and closeness centrality were used.

Multivariate constructions

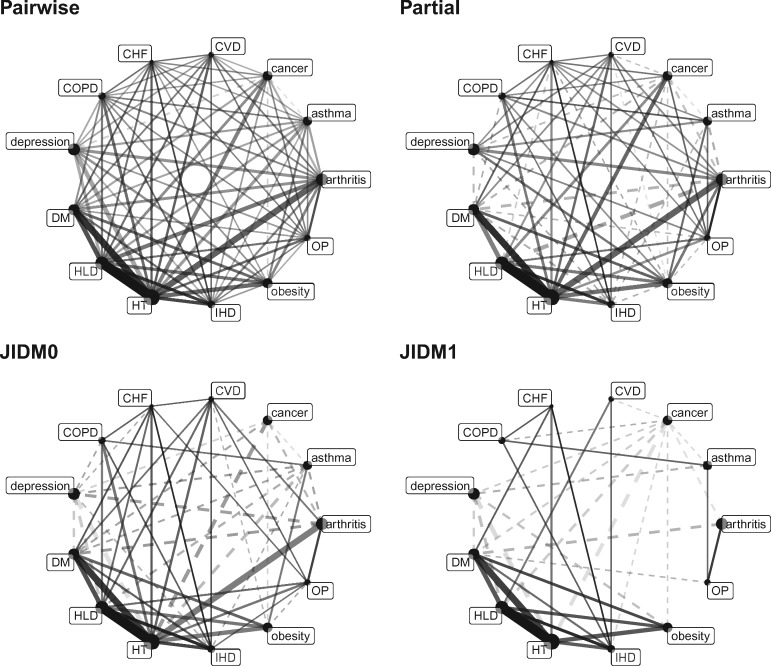
The four correlation matrices $R_t,R_t\text{'},{\widehat{\mathrm{P}}}_0,{\widehat{\mathrm{P}}}_1$ yielded both increasingly noisy and progressively less positive association estimates; each set of estimates was roughly linearly related to the others. In $R_t$ and $R_t\text{'}$, all 13 disorders loaded positively onto the first eigenvector, which was most aligned with HT, HLD, and IHD; whereas ${\widehat{\mathrm{P}}}_0$ and ${\widehat{\mathrm{P}}}_1$ oriented some disorders, including depression and cancer, in opposition. Several associations changed sign or discernibility as well as magnitude from model to model, though negative associations in $R_t$ were negative throughout and positive associations in ${\widehat{\mathrm{P}}}_1$ were positive in $R_t$ (Figure 4).

Figure 4.

Four comorbidity networks constructed from the NAMCS chronic disease incidence data. From left to right, then top to bottom: conventional comorbidity network with links determined from a 5% TWER and weighted by r_t; partial correlation comorbidity network adapted from the conventional network; JDM network controlling only for disease prevalence, with links weighted by $\widehat{\text{P}}$; JDM network also controlling for patient-level demographics. Black (respectively, grey) links indicate positive (negative) associations.

These patterns were reproduced using MIMIC data from each critical care unit. The roughly linear relationships between model estimates held only among more prevalent disorders, while those among less prevalent disorders amounted to noise. In contrast to the robustness in pairwise analyses, and despite the correlation between prevalence and centrality, hub identification was highly inconsistent across network models based on a common care unit.

DISCUSSION

Robustness

We found that data sources are generally more determinative of global network properties and top centrality rankings than network construction parameters, which lends support to the use of CNA to assess differences in network structures between different populations.^61,68,69 These differences both sustain and become clearer as links are pruned (up to conventional limits). Global network properties that rely on link weights, including weight distributions and distance-based centrality rankings, are less robust to the relevant parameter choices of error rate correction and of association measure.

Uniquely, triad closure $C$ was affected differently by evidential and evaluative link pruning: removing statistically fainter associations increased $C$, while removing lower-magnitude associations decreased $C$. This suggests that many weak but discernible comorbidities are transitive, arising from mutual associations in the incidence data. This further motivates the use of multivariate models to obtain association estimates controlled for such effects.

Among high-prevalence disorders, the primary spectrum from lower to higher incidence observable in the pairwise and partial correlation networks is obscured in the joint interaction–distribution networks. These models also reveal that much observed epidemiological comorbidity can be accounted for by patient-level factors such as age, ethnicity, and insurance status. Whereas these differences nevertheless follow predictable patterns, differences in associations among less prevalent disorders appeared to amount to noise.

Overall, conventional pairwise CNA is robust to the researcher degrees of freedom inherent to network construction, but multivariate models call into question not only global network properties but the signs and magnitudes of the constituent pairwise associations.

Insufficiency of pairwise models

Network analysis is fundamentally dyadic, and comorbidity network construction hinges on the method of link determination, which we have shown to depend profoundly on the network model employed. This raises the prospect that pairwise association mining, while certain to reveal many thitherto unknown comorbidities, may turn up a mixed bag of novel associations, including many that would turn out to be unremarkable or even inverted after controlling for co-related disorders. For example, the unexpected associations between hypothyroidism and shingles ($\mathrm{OR}=2.9$) and between Keloids and a history of asthma ($\mathrm{OR}=17.4$) uncovered by reference 36 might turn out to be negatively associated once the confounding associations they propose (cancer treatments and racial identity, respectively) are accounted for. Such differences could be epidemiological, but it is also plausible that they are in part administrative, for example, if a limited number of diagnoses are recorded during patient encounters even though others may be present in each patient (see also reference [19]). The authors of reference [39] point out that mined associations do not imply relevance or validity, and that some detected associations may be spurious. However, one lesson of our analysis is that mining for pairwise associations in a system as complex as human health may be little better than chance at selecting comorbidities that survive even statistical scrutiny.

A great deal of statistical machinery exists to facilitate this. In adapting JIDMs in particular, we appeal to the field ecology literature, on the basis of an ecological–epidemiological analogy: Disorders afflicting persons and communities are analytically similar to species occupying geographical sites—in the case of viral, bacterial, and fungal infections, indeed a special case. Association network analysis itself is rooted in ecology, which produced many if not most of the measures commonly used to weight association networks.^70,71 More recently, ecologists have honed several other methods to account for the same limitations of pairwise network construction discussed here.^72–74 The assumptions underlying an ecological data analytic technique will frequently be met by epidemiological data, in which case the results will be interpretable in a way that translates between the settings.

Interpretability

Though we have focused on the robustness of numerical results, equally important is the validity of interpretations. Association network models are increasingly popular for high-dimensional data sets, and the conclusions drawn about an underlying complex system must be informed by the process that converts the raw data to the network model. Though arising from fundamentally different constructions, these networks are often characterized using concepts grounded in the study of social networks, electrical circuits, and other relational data.

A chronic triad

The triad of hypertension, diabetes, and arthritis help illustrate these problems (Figure 4, Table 3): Each of the three pairs is positively correlated, based on their $2\times 2$ contingency tables. The HT–DM correlation weakens but remains in the multivariate models; the HT–arthritis correlation weakens more dramatically, to the point that it is not discerned at $P<.05$ in the JIDM controlling for demographic covariates; and the DM–arthritis correlation is discernibly negative in each of the multivariate models.

Table 3.

Point estimates and their upper and lower bounds on 95% confidence or credible intervals for the HT–DM–arthritis triad in network models of the NAMCS data

Disorder 1	Disorder 2	Model	Lower	Estimate	Upper
Arthritis	DM	Pairwise	0.144	0.163	0.182
Arthritis	DM	Partial	−0.083	−0.064	−0.045
Arthritis	DM	JIDM0	−0.101	−0.054	−0.005
Arthritis	DM	JIDM1	−0.142	−0.091	−0.039
Arthritis	HT	Pairwise	0.360	0.377	0.393
Arthritis	HT	Partial	0.165	0.184	0.202
Arthritis	HT	JIDM0	0.018	0.060	0.102
Arthritis	HT	JIDM1	−0.072	−0.026	0.021
DM	HT	Pairwise	0.563	0.576	0.588
DM	HT	Partial	0.334	0.351	0.368
DM	HT	JIDM0	0.299	0.341	0.382
DM	HT	JIDM1	0.201	0.245	0.291

What to make of these differences? The correlation between HT and arthritis may be mediated by gender, the only demographic variable found to have opposite effects on their incidence in JIDM1 (effects on HT and DM all had the same sign); though the correlation was very weak already in JIDM0, suggesting that it was largely attributable to other comorbid associations. The more puzzling relationship is that between HT and DM, which is complicated by the coarseness of the ontology: NAMCS does not distinguish types 1 versus 2 DM, nor osteo- (OA) versus rheumatoid (RA) arthritis. It is not obvious, though, that parsing these subtypes would explain away the association: Systematic reviews^75,76 have cemented an epidemiological comorbidity between type 2 DM and OA, and there is emerging agreement on one between DM and RA,⁷⁷ in both cases likely mediated by BMI.

In any event, the DM–arthritis correlation turns negative upon accounting for the effects of the other chronic disorders; it is less likely due to a protective effect than to diabetic and arthritic populations generally having different multimorbid profiles. The disorders statistically associated with both in the partial correlation and endogenous joint interaction–distribution networks include cancer (negatively), CVD (positively), and depression (differently), in addition to HT, and only cancer remains as a discernible covariate of both after accounting for demographics. The coarseness of these indicators precludes drill-down analysis, but their relative uniqueness and their obviation while controlling for demographics suggest that their effect on the DM–arthritis association may be a proxy for a demographic stratification.

Meanings of centrality

The use of centrality measures is another case in point. The degree of a disorder, calculated as the number of disorders it is comorbid with in a patient population, is sensible enough a measure of its “total comorbidity”¹⁷ and a useful concept both epidemiologically and clinically. The weights (using BAMs) associated with these comorbidities are also clearly useful for discriminating between stronger and weaker co-occurrence rates, hence higher or lower risk factors for patients with an index disorder. However, we found that the choice of disease ontology has a significant impact on comorbidity rankings, so much so that the centralities of disorders before crosswalking to a coarser ontology are not predictive of the centralities of their counterparts after crosswalking. For the following discussion, we constructed a typical comorbidity network, using the Rzhetsky data and ontology with a Bonferroni-corrected $5\%$ evidential cutoff and weighting (positive) links by the Forbes coefficient $F$.

First note that none of the weights commonly used to quantify total comorbidity are additive: In our example network, amebiasis, a gastrointestinal infection rare in the United States, and rheumatoid arthritis, a common chronic autoimmune disorder, have 5 and 67 comorbid relations, respectively. Though having very different etiologies and afflicting very different patient populations, these disorders have approximately the same weighted degree (529 and 561). This does not translate to their being similarly severe in any recognized sense, or to their belonging at a similar ranking amidst the other disorders in the ontology.

Betweenness and closeness centrality rely on a different version of additivity that is equally problematic. The graph distance in this network (To calculate graph distances, replace edge weights $F$ with $\frac{1}{F-1}+1$.) between type 1 diabetes and breast cancer (in female patients) is the same as that between multiple epiphyseal dysplasia (MED) and hepatitis E (HepE), approximately $0.30$, though the former two disorders are significantly correlated (ie, directly linked, $P<{10}^{-27}$) while the latter two can only be reached from each other via three intermediate disorders: multiple epiphyseal dysplasia $\leftrightarrow$ Albright–Sternberg syndrome $\leftrightarrow$ cerebral palsy $\leftrightarrow$ hepatitis C $\leftrightarrow$ HepE. Yet this indirect sequence of associations leading to HepE is does not have an established clinical interpretation, nor does it imply a natural comparison to the relative risk of MED encoded by the direct link. Furthermore, controlling for covariates and subsetting populations may significantly alter the magnitudes and signs of these links, with unpredictable effects on indirect distances.

These limitations are highlighted by weighting issues, but they arise from the network model itself, which is premised on a principle of “guilt by association” that implicates one node in the effects of another according to their proximity in the network. In the related field of genomics, this principle “does not reflect the dynamic nature of biological networks,”¹³ and the same may be said of epidemiological networks. As in genomics, comorbidity network centrality analysis is demonstrably effective at prioritization, but without underlying theory it will be difficult to know what critical patterns it may miss, or even what it means for a disorder to be “central” in any specific sense (Such concerns are not specific to CNA. Inconsistency and uncertainty over the interpretations of centrality measures in the study of human communication networks led [12] to propose the concise set of conceptualizations and measures discussed above: degree, based on the idea of communication activity with other nodes; betweenness, based on the control of communication among other actors, and closeness, based on either independence from the control of others or efficiency of dissemination. These interpretations extend to other kinds of resource exchange, but they do not have straightforward interpretations on correlation networks.).

Limitations

Our results come with their own limitations. As discussed above, the data sets best-suited to the investigations undertaken here were only available to us as pairwise contingency tables, rather than as case-level incidence data, so that multivariate comparisons were performed only on open-access sources with important caveats beyond those of all administrative healthcare data. Necessarily, we evaluated only a handful of CNA techniques. Our focus was cross-sectional, whereas many recent CNAs have used longitudinal or case–control designs, often tailoring conventional techniques to these settings. Additional work will be necessary to evaluate these approaches. Additionally, though we have discussed some use cases from our analysis, we have not conducted the kinds of follow-up studies CNA is often used to support. It will be necessary to validate this longer-term workflow as methods are standardized and basic science driven by CNA accumulates. Finally, the companion goal of validating CNA techniques is made difficult by the lack of any ground truth underneath the real-world incidence data used in CNA. Some headway may be gained in future through simulation studies, for instance making use of the generative framework underlying the JIDM, though ultimately this may require network analyses of data generated from artificial complex systems, such as multi-level, whole-system models.

CONCLUSION

To pre-empt and mitigate the concerns raised in the introduction, we urge CNA researchers to include the following steps (according to their objectives):

• Make patient-diagnosis incidence data available for secondary use. This will enable ontological crosswalking and multivariate modeling, though it may require additional processing to address privacy concerns.

• Provide theoretical justification for the disorder ontology from which networks are constructed. This choice can have dramatic effects on the resulting network structure, including which nodes are identified as hubs.

• Provide theoretical justification for weighting networks. Indirect relations are highly sensitive to the association measure; if weighting is important, then results using different measures should be compared.

• To summarize global structure, report at least the largest component size, assortativity, and clustering coefficient. These statistics are likely to effectively discriminate between networks constructed from different populations.

• Provide theoretical justification for using pairwise versus partial correlations. Controlling for confounding effects can radically change the network structure, and free efficient software exists to calculate partial correlations from pairwise.

• Validate associations among common disorders or within specific subsets of disorders using multivariate (eg, joint interaction–distribution) models. These methods do not yet scale but can distinguish primary from secondary or transitive associations among a manageable set of variables.

Funding

JCB was supported in part by an NIDCR T90 training grant (5T90DE021989-07).

AUTHOR CONTRIBUTIONS

JCB, TPA, and RCL conceived the study questions and design. JCB acquired data and performed computational analyses. JCB and TPA interpreted results and examined use cases. JCB, TPA, and RCL contributed to the discussion, wrote and approved the final manuscript, and take responsibility for the integrity of the work.

CONFLICT OF INTEREST STATEMENT

None declared.