Accounting for data variability in multi-institutional distributed deep learning for medical imaging

Abstract

Objectives

Sharing patient data across institutions to train generalizable deep learning models is challenging due to regulatory and technical hurdles. Distributed learning, where model weights are shared instead of patient data, presents an attractive alternative. Cyclical weight transfer (CWT) has recently been demonstrated as an effective distributed learning method for medical imaging with homogeneous data across institutions. In this study, we optimize CWT to overcome performance losses from variability in training sample sizes and label distributions across institutions.

Materials and Methods

Optimizations included proportional local training iterations, cyclical learning rate, locally weighted minibatch sampling, and cyclically weighted loss. We evaluated our optimizations on simulated distributed diabetic retinopathy detection and chest radiograph classification.

Results

Proportional local training iteration mitigated performance losses from sample size variability, achieving 98.6% of the accuracy attained by centrally hosting in the diabetic retinopathy dataset split with highest sample size variance across institutions. Locally weighted minibatch sampling and cyclically weighted loss both mitigated performance losses from label distribution variability, achieving 98.6% and 99.1%, respectively, of the accuracy attained by centrally hosting in the diabetic retinopathy dataset split with highest label distribution variability across institutions.

Discussion

Our optimizations to CWT improve its capability of handling data variability across institutions. Compared to CWT without optimizations, CWT with optimizations achieved performance significantly closer to performance from centrally hosting.

Conclusion

Our work is the first to identify and address challenges of sample size and label distribution variability in simulated distributed deep learning for medical imaging. Future work is needed to address other sources of real-world data variability.

INTRODUCTION

In recent years, deep learning has brought about rapid progress in image classification and object detection.^1,2 Due to the proficiency of convolutional neural networks (CNNs) at pattern recognition, these innovations have also translated to progress in automating clinical tasks within medical imaging. For instance, deep CNNs have allowed breakthroughs in areas such as retinopathy diagnosis,^3,4 lung nodule detection,⁵ and brain tumor segmentation.^6,7

Training deep learning models for medical applications is often challenged by insufficient quantities of patient data, especially for rare diseases. Further, it has been shown that models trained at a single institution have limited generalizability when applied to data from other institutions.^8,9 Thus it is desirable for multiple institutions with patient data to collaborate to pool data to create larger, more diverse datasets. However, patient data-sharing efforts are often complicated by regulatory, technical, and privacy concerns. Specifically, there are legal and ethical barriers to sharing patient data that have made institutions very protective in their willingness to disperse data. Additionally, there is the cost to develop the necessary infrastructure to securely store pooled data.¹⁰ As such, data-distributed learning, or federated learning, where the partially trained model weights are transferred between institutions instead of the data itself, has become an attractive alternative.^11,12 Indeed, distributed learning has been highlighted as a foundational area of research within medical imaging.¹³ Recently, data-distributed deep learning methods have been successfully developed for training medical image classification models with a cyclical weight transfer (CWT) approach.¹⁰

In the CWT approach, models are trained at 1 institution at a time for a number of iterations before transferring the updated weights to the next institution in a cyclical fashion until model convergence.¹⁰ A key limitation with the existing implementation of CWT is that it is not optimized to handle variability in sample sizes, label distributions, resolution, and acquisition settings in the training data across institutions. In fact, CWT performance decreases when these variabilities are introduced.¹⁰ In order for CWT to be utilized in practice, it must be capable of handling such institutional variabilities that would be found in most real-world medical imaging datasets.

Cyclical learning rates (CLR) have been used for hyperparameter optimization for more efficient model training in nondistributed machine learning tasks,¹⁴ but it is unclear whether they could be applied towards distributed tasks to optimize performance. Additionally, weighted sampling of data in random minibatch selection during training^15,16 as well as weighted loss functions¹⁷ have been used in literature with standard machine learning tasks to handle data with label imbalances, but, again, it is unclear how these approaches could affect model performance in a distributed setting.

In this study, to our knowledge, we are the first to identify that data variability in training sample sizes and label distributions across institutions can significantly decrease performance of distributed learning models for medical imaging. We present modifications to CWT to mitigate performance losses that arise from introducing variability in training sample sizes and label distributions across institutional training splits, and we evaluate the efficacy of our modifications to simulated distributed tasks for (DR) detection and abnormal chest radiograph classification. Specifically, we use proportional local training iterations (PLTI) and a CLR to address sample size variability, and we use locally weighted minibatch sampling and cyclically weighted loss to address label distribution variability. Such modifications allow CWT to be more practically useful and more generalizable to real-world medical image classification tasks where such variability is likely to arise.

MATERIALS AND METHODS

In this section we detail the binary classification datasets used to evaluate our methods, the deep learning image classification model used to classify images, our distributed training method (CWT), and our modifications to CWT designed to account for variability in sample sizes across institutions and variability in label distribution across institutions. We use 2 different datasets to evaluate our methods: the Kaggle Diabetic Retinopathy Detection dataset¹⁸ and the NIH Chest X-ray14 dataset.¹⁹

Diabetic retinopathy dataset

The Kaggle Diabetic Retinopathy Detection dataset consists of a total of 88 702 left and right eye retinal fundus images from 44 351 patients. Each image is given a label from 0–4 for severity of diabetic retinopathy (DR), where 0 is “No DR,” 1 is “Mild,” 2 is “Moderate,” “3 is Severe,” and 4 is “Proliferative DR.” The image pixel resolutions range from 433 px × 289 px to 5184 px × 3456 px. For our distributed tasks, we binarized the labels to 0 for “No DR” and 1 for “Moderate,” “Severe,” or “Proliferative DR” (“Mild” images, which represent a middle ground between Healthy and Diseased, were excluded), so 0 and 1 represent negative and positive images respectively. Additionally, we only utilized right eye images to avoid the possibility of confounding resulting from using multiple images from the same patient. Of the remaining images, we randomly selected 3200 positive images and 3200 negative images to comprise the training set, 1600 positive images and 1600 negative images to comprise a validation set, and 1600 positive images and 1600 negative images to comprise a held-out test set. We preprocessed these 12 800 images using the approach outlined by the Kaggle Diabetic Retinopathy Competition winner Benjamin Graham.²⁰ To summarize, the preprocessing consisted of rescaling the images to have the same eye radius of 300 pixels, subtracting the local average color in each image, and clipping images to remove boundaries. We further resized the preprocessed images to 256px × 256px for memory efficiency to serve as the input to our deep learning models.

Chest X-ray dataset

To assess the reproducibility of our methods, we repeated all experiments on the NIH Chest X-ray14 dataset. The preprocessing and splitting of this dataset are outlined in the Supplementary Material.

Deep image classification model

For both datasets, we used a 22-layer GoogLeNet as our deep classification model.²¹ We included a batch normalization layer after each convolutional layer and a dropout layer with probability 0.5 before the final readout layer. We used random minibatch sampling with batch size of 32. We used the Adam optimization algorithm for model weight optimization with an initial learning rate of 0.001 for the DR dataset and an initial learning rate of 0.0015 for the chest X-ray (CXR) dataset.²² Weights were initialized with Xavier Initialization. For both datasets, we had an exponential learning rate decay with a decay rate of 0.99 every 200 training iterations (every epoch). We used cross-entropy loss with an L2 regularization coefficient of 0.0001 as the loss function for both datasets. We also terminate model learning early if there are 4000 consecutive training iterations (20 epochs) without improvement in validation loss. Finally, during training, we perform real-time data augmentation by introducing random 0–360-degree rotations, random shading, and random contrast adjustment to each image in a minibatch at every training iteration. We repeated all experiments using a 50-layer ResNet²³ instead of a 22-layer GoogLeNet for classification to assess any CNN architecture-dependent effects on distributed model performance. All computation was performed on NVIDIA Tesla K80 GPUs.

Distributed training

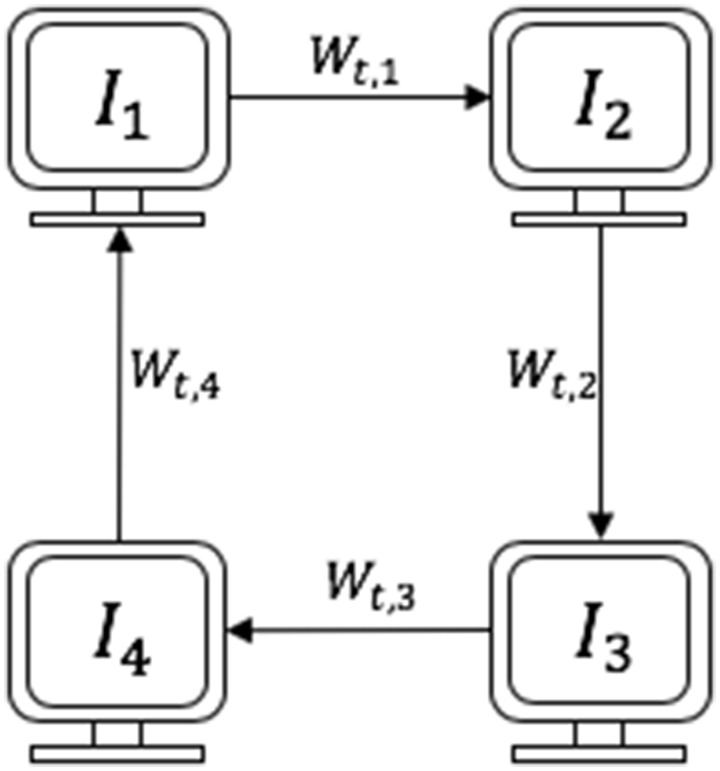
We performed a simulated distributed learning task involving 4 participating institutions by dividing the training data into 4 institutional splits (details on the 4 splits for our distributed experiments are explained in the sections below). We use CWT as our baseline distributed approach because it is a synchronous nonparallel approach, and therefore robust to discrepancies in machine configurations across training institutions.¹⁰ Cyclical weight transfer involves starting training a newly initialized model at 1 of the institutions for a certain number of iterations, transferring the updated model weights to initialize the subsequent institution and training at that institution for a certain number of iterations, transferring the updated weights to the next institution, and so on until model convergence. A schematic of CWT with 4 participating institutions is included in Figure 1. We also repeated all experiments with a reversed ordering of institutions (4 to 1).

Figure 1.

Schematic of cyclical weight transfer with 4 participating institutions ($I_1$, $I_2$, $I_3$, and $I_4$), where $I_1$ is the starting institution. Each arrow represents transfer of updated model weights $W_{t,i}$ at cycle $t$ for $i\in \{\mathrm{1,2},\mathrm{3,4}\}$.

Sample size variability

A common variability that is likely to arise in real (nonsimulated) distributed learning tasks is differing sample sizes across institutional training splits, especially in a setting whether there are both small (eg, community hospitals) and large institutions (eg, academic university hospitals). Figure 2A shows an example of a distributed training split with variability in sample sizes across institutions. It has been demonstrated that introducing variability in sample sizes across institutional training splits results in performance losses with CWT.¹⁰ In vanilla CWT (CWT without any optimizations), the model is trained for a fixed, equal number of iterations at each institution. If 1 of the institutions has a smaller training sample than the other institutions do, then on average over the course of training, each training example from that institution will be sampled with higher frequency than the training examples from other institutions. Thus, when the CWT model is being trained at this institution, the model is susceptible to overfitting to the training data from this institution and catastrophic forgetting of the data from other institutions. And likewise, if 1 of the institutions has a larger training sample than the other institutions do, then on average each training example from that institution will be sampled with lower frequency than the training examples from other institutions. Thus, when the CWT model is being trained at this institution, the model is susceptible to underfitting the training data from this institution. We developed the following 2 modifications to CWT to mitigate performance losses arising from variability in sample sizes across institutional training splits.

Figure 2.

Examples of heterogeneous training splits of the diabetic retinopathy dataset with 4 participating institutions consisting of 20 total images (10 healthy and 10 diseased). (A) Training split with sample size variability; institutions 1, 2, 3, and 4 have 2, 4, 6, and 8 samples respectively, and the data at each institution have a balanced label distribution. (B) Training split with label distribution variability; each institution has equal number of data samples but varying label distribution.

Proportional local training iterations

Instead of a fixed number of training iterations at each institution, we will train the model at each institution for a number of iterations proportional to the training sample size at the institution. Formally, if there are $i$ participating institutions $1,\dots ,i$, with training sample sizes of $n_1,\dots ,n_i$ respectively, then the number of training iterations at institution $k$ will be $f\cdot \frac{n_k}{{\sum }_{j=1}^i{n}_j}$ where $f$ is some scaling factor. With this modification, each training example across all institutions is expected to appear the same number of times on average over the course of training. If $f=\frac{{\sum }_{j=1}^i{n}_j}{B}$ where $B$ is the batch size, then a single full cycle of CWT represents an epoch over the full training data.

Cyclical learning rate

Another way of equalizing the contribution of each image across the entire training set to the model weights is to adjust the learning rate at each training institution. Having a smaller learning rate at institutions with smaller sample sizes and a larger learning rate at institutions with larger sample sizes will prevent disproportionate impact of the images at institutions with small or large sample sizes on the model weights. Specifically, we expect that lowering the learning rate at institutions with smaller training samples will mitigate the overfitting and catastrophic forgetting that occurs at institutions with smaller training sample sizes, and increasing the learning rate at institutions with larger training samples will mitigate the underfitting that occurs at institutions with larger training sample sizes. We do this by constructing a CLR where the learning rate at an institution is proportional to the number of training samples at the institution. If there are $i$ participating institutions $1,\dots ,i$, with training sample sizes of $n_1,\dots ,n_i$ respectively, then the learning rate ${\alpha }_k$ while training at institution $k$ is

$${\alpha }_k=\frac{n_{k}i\alpha }{{\sum }_{j=1}^i{n}_j}$$

where $\alpha$ is the global learning rate. Note that we include $i$ in the numerator and the total number of training samples in the denominator as scaling factors so that the average learning rate across the institutions is equal to the global learning rate. It is important for the average learning rate to be equal to the global learning rate to control for hyperparameter differences that could confound results.

Label distribution variability

Another common variability that is likely to arise in real distributed learning tasks is differing label distributions across institutional training splits, due to local differences in prevalence of the disease of interest. Figure 2B shows an example of a distributed training split with variability in sample sizes across institutions. It has been demonstrated that introducing variability in the label distributions across institutional training splits results in performance losses with CWT.¹⁰ We developed the following 2 modifications to CWT to mitigate performance losses arising from variability in label distribution across institutional training splits.

Locally weighted minibatch sampling

With this modification at each institution, the local training samples are weighted by label during minibatch sampling so that the data from each label are equally likely to get selected. Suppose there are $L$ possible labels, and for each label $m\in \{1,\dots ,\mathrm{L}\}$ there are $n_{k,m}$ samples with label $m$ at institution $k$. Then each training sample at institution $k$ with label $m$ is given a weight of $\frac{1}{l\cdot n_{k,m}}$ for random minibatch sampling at each local training iteration. With such a sampling approach, we can ensure that the minibatches during training have a balanced label distribution at each institution even if the overall label distribution at the training institution is imbalanced.

Cyclically weighted loss

The standard cross-entropy loss function for sample $x$ is $CE\left(x\right)=-{\sum }_{j=1}^L{y}_{x,j}\hspace{0.17em}\text{log}\left(p_{x,j}\right)$ where $L$ is the number of labels, $y_x\in {\mathfrak{R}}^L$is a one-hot ground truth vector for sample $x$ with $1$ at the entry corresponding to the true label of $x$ and $0$ at all other entries, and $p_{x,j}$ is the model prediction probability that sample $x$ has label $j$. We introduce a cyclically weighted loss function that gives smaller weight to the loss contribution from labels overrepresented at an institution, and vice versa for underrepresented labels. The modified cyclically weighted cross-entropy loss function at institution $k$ becomes

$$C{E}_k\left(x\right)=-\frac{{\sum }_{j=1}^L{y}_{x,j}\hspace{0.17em}\text{log}\left(p_{x,j}\right)}{L\cdot n_{k,j}}$$

where $n_{k,j}$ is the proportion of samples at institution $k$ with label $j$.

RESULTS

We create institutional training splits with varying degrees of sample size or label distribution variability across institutions. The specific splits are detailed in the sections below. We then evaluate the performance of a model trained on centrally hosted data and distributed models on these institutional splits. Centrally hosted data is when all data are located at a central repository and serve as our benchmark. The distributed models we consider are the originally described CWT method (“vanilla CWT”),¹⁰ CWT with PLTI or CLR to address sample size variability, and CWT with label distribution variability or cyclically weighted loss to address label distribution variability. In both the DR and CXR datasets, CWT with PLTI produced significantly higher performance than did CWT without optimizations in institutional splits with high sample size heterogeneity. In both datasets, both locally weighted minibatch sampling and cyclically weighted loss significantly increased vanilla CWT performance in institutional splits with high label distribution heterogeneity. Note that in Figures 3 and 4, if the number of training runs were increased to a large enough number, the mean central hosting accuracy would converge to horizontal lines. The differences in central hosting performance across experiments can be attributed to run-to-run variations in model performance due to stochasticity in model initialization, minibatch selection, and dropout.

Figure 3.

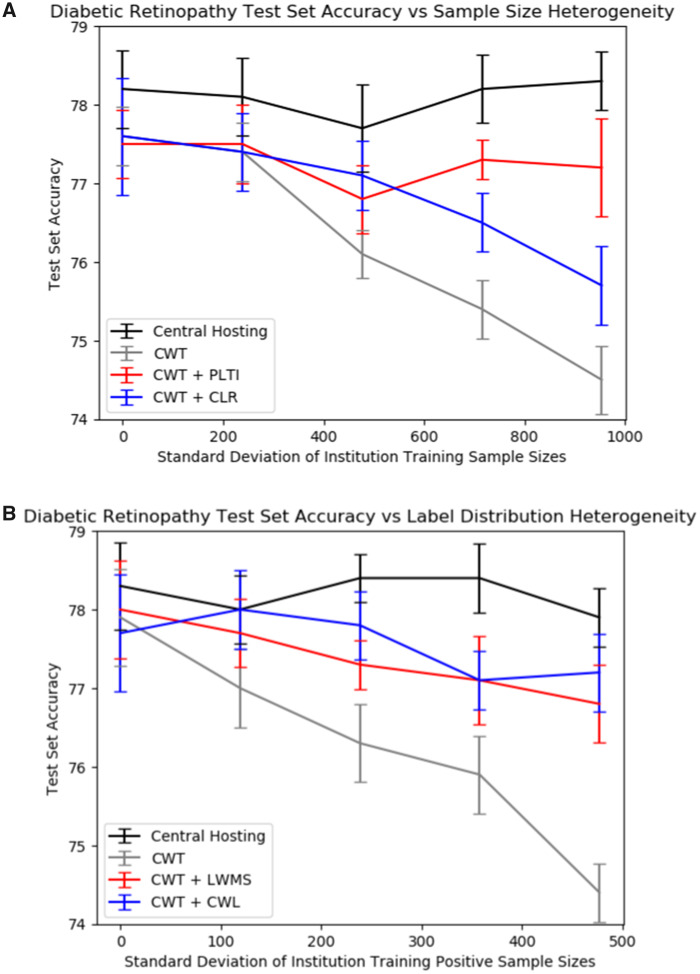
Results on the diabetic retinopathy test set. Each point represents the mean accuracy across 10 runs, and error bars are 95% confidence intervals for the mean accuracy. (A) Diabetic retinopathy test set accuracies vs sample size standard deviation for the various sample size splits with centrally hosted and distributed training. (B) Diabetic retinopathy test set accuracies vs sample size standard deviation for the various label distribution splits with centrally hosted and distributed training.

Figure 4.

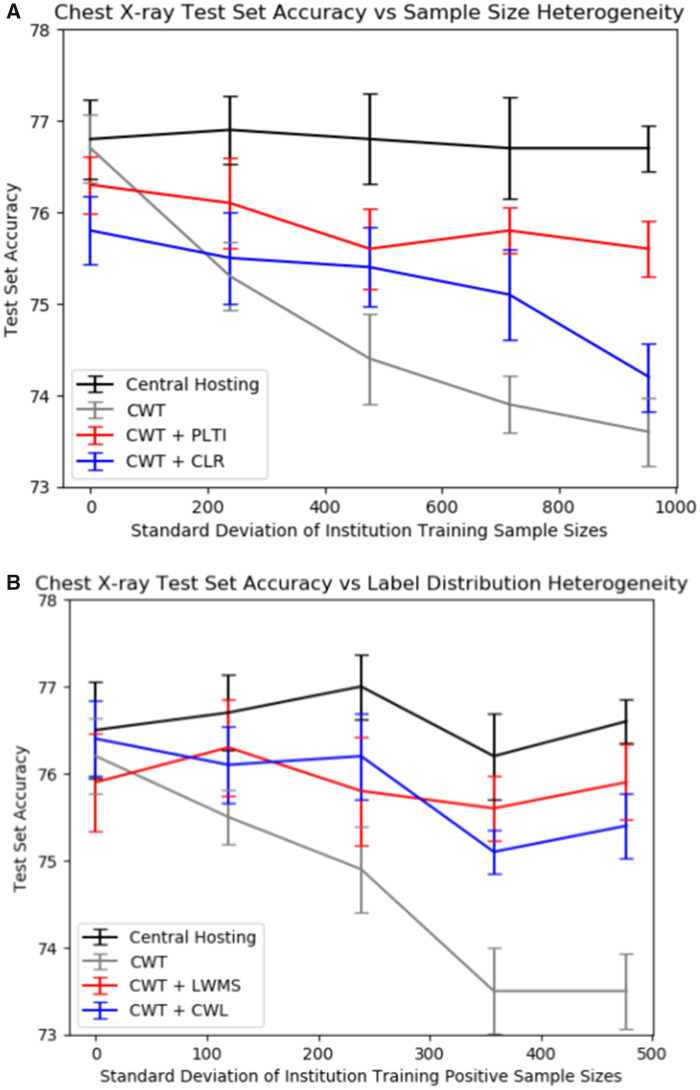
Results on the chest X-ray test set. Each point represents the mean accuracy across 10 runs, and error bars are 95% confidence intervals for the mean accuracy. (A) Chest X-ray test set accuracies vs sample size standard deviation for the various sample size splits with centrally hosted and distributed training. (B) Chest X-ray test set accuracies vs sample size standard deviation for the various label distribution splits with centrally hosted and distributed training.

Sample size variability

In order to test our methods on sample size variability for both the DR and CXR datasets, we created the institutional training splits as given in Table 1. The institutional splits were randomly selected from the training sets of size 6400. The results of centrally hosting (pooling all institutional data together) as well as distributed learning—vanilla CWT, cyclical weight transfer with PLTI (CWT + PLTI), and cyclical weight transfer with cyclical learning rate (CWT + CLR) using the splits from Table 1—are given in Table 2, Figure 3A for the DR dataset, and Figure 4A for the CXR dataset. Repeating these experiments with reversed ordering of institutions during training of CWT models produced similar results, as shown in Supplementary Material Table 1 and Supplementary Material Figures 1A and 1B. Repeating these experiments with a 50-layer ResNet instead of a 22-layer GoogLeNet for classification also produced similar results, as shown in Supplementary Material Table 2 and Supplementary Material Figures 2A and 2B.

Table 1.

Institutional training splits with varying degrees of sample size standard deviation across the 4 institutions. The number of positive (+) and negative (−) samples at each institution are also indicated (each split is balanced)

Split	Inst 1 +/−	Inst 2 +/−	Inst 3 +/−	Inst 4 +/−	Sample size Std. Dev.
1	800/800	800/800	800/800	800/800	0.0
2	960/960	853/853	747/747	640/640	238.4
3	1120/1120	907/907	693/693	480/480	477.2
4	1280/1280	960/960	640/640	320/320	715.5
5	1440/1440	1013/1013	587/587	160/160	953.9

Table 2.

Diabetic retinopathy (DR) and Chest X-ray (CXR) mean and standard deviation test set accuracies across 10 runs for the various sample size splits with centrally hosted and distributed training. Bold entries represent optimizations that resulted in significantly better performance than performance of cyclical weight transfer without optimizations for the same split

Model	DR test set accuracyMean ± Std. Dev.	CXR test set accuracyMean ± Std. Dev.
Split 1
Central hosting	78.2 ± 0.8	76.8 ± 0.7
CWT	77.6 ± 0.6	76.7 ± 0.6
CWT + PLTI	77.5 ± 0.7	76.3 ± 0.5
CWT + CLR	77.6 ± 1.2	75.8 ± 0.6
Split 2
Central Hosting	78.1 ± 0.8	76.9 ± 0.6
CWT	77.4 ± 0.6	75.3 ± 0.6
CWT + PLTI	77.5 ± 0.8	76.1 ± 0.8
CWT + CLR	77.4 ± 0.8	75.5 ± 0.8
Split 3
Central Hosting	77.7 ± 0.9	76.8 ± 0.8
CWT	76.1 ± 0.5	74.4 ± 0.8
CWT + PLTI	76.8 ± 0.7	75.6 ± 0.7
CWT + CLR	77.1 ± 0.7	75.4 ± 0.7
Split 4
Central Hosting	78.2 ± 0.7	76.7 ± 0.9
CWT	75.4 ± 0.6	73.9 ± 0.5
CWT + PLTI	77.3 ± 0.4	75.8 ± 0.4
CWT + CLR	76.5 ± 0.6	75.1 ± 0.8
Split 5
Central hosting	78.3 ± 0.6	76.7 ± 0.4
CWT	74.5 ± 0.7	73.6 ± 0.6
CWT + PLTI	77.2 ± 1.0	75.6 ± 0.5
CWT + CLR	75.7 ± 0.8	74.2 ± 0.6

Label distribution variability

In order to test our methods on label distribution variability for both the DR and CXR datasets we created the institutional training splits as given in Table 3. The institutional splits were randomly selected from the training sets of size 6400, with increasing degrees of label imbalance in splits 6–10. The results of centrally hosting (pooling all institutional data together) as well as distributed learning—vanilla CWT, cyclical weight transfer with locally weighted minibatch sampling (CWT + LWMS), and cyclical weight transfer with cyclically weighted loss (CWT + CWL) using the splits from Table 3—are given in Table 4, Figure 3B for the DR dataset, and Figure 4B for the CXR dataset. Repeating these experiments with reversed ordering of institutions during training of CWT models produced similar results, as shown in Supplementary Material Table 3 and Supplementary Material Figures 1C and 1D. Repeating these experiments with a 50-layer ResNet instead of a 22-layer GoogLeNet for classification also produced similar results, as shown in Supplementary Material Table 4 and Supplementary Material Figures 2C and 2D.

Table 3.

Institutional training splits with varying degrees of positive label sample size standard deviation across the 4 institutions. The number of positive and negative samples at each institution are also indicated (each split has equal total sample size across institutions)

Split	Inst 1 +/−	Inst 2 +/−	Inst 3 +/−	Inst 4 +/−	+ Sample Size Std. Dev.
6	800/800	800/800	800/800	800/800	0.0
7	960/640	853/747	747/853	640/960	119.2
8	1120/480	907/693	693/907	480/1120	238.6
9	1280/320	960/640	640/960	320/1280	357.8
10	1440/160	1013/587	587/1013	160/1440	477.0

Table 4.

Diabetic retinopathy (DR) and Chest X-ray (CXR) mean and standard deviation test set accuracies across 10 runs for the various label distribution splits with centrally hosted and distributed training. Bold entries represent optimizations that resulted in significantly better performance than performance of cyclical weight transfer without optimizations for the same split

Model	DR test set accuracyMean ± Std. Dev.	CXR test set accuracyMean ± Std. Dev.
Split 6
Central hosting	78.3 ± 0.9	76.5 ± 0.9
CWT	77.9 ± 1.0	76.2 ± 0.7
CWT + LWMS	78.0 ± 1.0	75.9 ± 0.9
CWT + CWL	77.7 ± 1.2	76.4 ± 0.7
Split 7
Central hosting	78.0 ± 0.7	76.7 ± 0.7
CWT	77.0 ± 0.8	75.5 ± 0.5
CWT + LWMS	77.7 ± 0.7	76.3 ± 0.9
CWT + CWL	78.0 ± 0.8	76.1 ± 0.7
Split 8
Central hosting	78.4 ± 0.5	77.0 ± 0.6
CWT	76.3 ± 0.8	74.9 ± 0.8
CWT + LWMS	77.3 ± 0.5	75.8 ± 1.0
CWT + CWL	77.8 ± 0.7	76.2 ± 0.8
Split 9
Central hosting	78.4 ± 0.7	76.2 ± 0.8
CWT	75.9 ± 0.8	73.5 ± 0.8
CWT + LWMS	77.1 ± 0.9	75.6 ± 0.6
CWT + CWL	77.1 ± 0.6	75.1 ± 0.4
Split 10
Central hosting	77.9 ± 0.6	76.6 ± 0.4
CWT	74.4 ± 0.6	73.5 ± 0.7
CWT + PLTI	76.8 ± 0.8	75.9 ± 0.7
CWT + CWL	77.2 ± 0.8	75.4 ± 0.6

DISCUSSION

Distributed learning is a promising approach to train deep learning models on multi-institutional patient data, with only model parameters being transferred among institutions. By circumventing the need for sharing patient data, such approaches could catalyze development of deep learning models with medical datasets. Existing distributed learning approaches focus on nonmedical applications, but there are unique, unaddressed challenges to distributed learning with medical data. Specifically, unlike typical distributed learning approaches where the data are distributed optimally to maximize performance of the learning method, in medical scenarios the data are not shared, and consequently there are variations in the amount of data, distribution of labels, and resolution of images across institutions, which we have observed in preliminary work to decrease model performance in CWT. To our knowledge, we are the first to study the deleterious impact of data variability on distributed learning for medical imaging and to develop strategies to address it. Specifically, our goal is to optimize CWT to overcome these challenges.

We implemented various strategies to mitigate performance losses that arise from distributed training with CWT when data across institutional splits are heterogeneous. Specifically, we modified cyclical weighted transfer by including PLTI and CLR to address sample size variability across institutional training splits, and locally weighted minibatch sampling and cyclically weighted loss to address label distribution variability across institutional training splits. We evaluated our methods with simulated distributed learning tasks with 4 participating institutions using the Kaggle Diabetic Retinopathy Detection and Chest X-ray14 datasets. We used performance from centrally hosting all training data as a theoretical maximum performance (and therefore goal performance) for our distributed methods.

When we introduced sample size variability across the institutional training splits, vanilla CWT performance on both the DR and CXR datasets decreased. For the DR dataset, vanilla CWT test set accuracy decreased from 77.6% with split 1 (equal sample sizes) to 74.5% with split 5 (highest variance in sample sizes). For both datasets, including PLTI was the most effective at mitigating this performance loss when variability was introduced. The DR test set accuracy with PLTI with split 5 was 77.2%, so PLTI almost completely bridged performance losses from sample size variability across institutional training splits. The DR test set accuracy with a CLR with split 5 was 75.7%. While the improvement over vanilla CWT performance was significant, the improvement was not as significant as that from PLTI.

Additionally, when we introduced label distribution variability across the institutional training splits, again, vanilla CWT performance on both the DR and CXR datasets decreased. For the DR dataset, vanilla CWT test set accuracy decreased from 77.9% with split 6 (balanced label distributions across all institutions) to 74.4% with split 10 (highest variance in positive training samples across institutions, representing highest label imbalance). Neither locally weighted minibatch sampling nor cyclically weighted loss was as effective as PLTI at completely eradicating performance losses arising from variability, but for both datasets, both modifications improved CWT performance when label distribution variability was introduced. The DR test set accuracy with locally weighted minibatch sampling and cyclically weighted loss with split 10 were 76.8% and 77.2% respectively, so both modifications are promising for bridging performance losses from CWT when label distribution variability across institutional training splits is introduced.

Furthermore, there are no notable effects of reversing institution order on the performance of our models. Our CWT models train for hundreds of cycles until the validation loss stops improving and training is terminated. Starting training with different institutions may result in significantly different models after 1 cycle. However, the subsequent hundreds of cycles of training make the effects of the first training institution on the model negligible. There are also no notable differences in model performance as a result of using a 50-layer ResNet instead of a 22-layer GoogLeNet for classification, indicating the exact choice of deep CNN architecture is not important for the use cases in our article.

Sample sizes and label distributions are likely sources of data heterogeneity across institutions in real-world distributed learning tasks for medical image analysis because patient distributions are likely to vary across healthcare institutions. Thus, our optimizations extend the applicability of distributed training with CWT to real-world scenarios where such patient data heterogeneity across institutions is present. Our work has the potential to propel the multi-institutional collaborative training of deep learning models in these scenarios without the need for any patient data-sharing.

There are several limitations to our study. First, our institutional splits are created from single datasets, so introducing heterogeneity across institutions in number of data samples and label distribution of data samples may still not fully capture other forms of heterogeneity that may be present across real-world institutions such as race, gender, and image acquisition settings. Furthermore, another possible source of data heterogeneity that is possible is variance in image resolution across institutions, due to the use of nonstandardized imaging equipment and methods across sites. It has been observed that variability in resolution can also result in decreases in cyclically weighted loss performance.¹⁰ It remains future work to address this variability. A potential approach to address resolution imbalance includes training image super-resolution networks²⁴ to improve data quality of institutions with low-resolution or low-quality images, which may ultimately improve classification accuracy. Also, in this study, we focused on the utilization of CWT as our distributed learning approach. Future work can explore performance loss mitigation for other distributed learning methods such as asynchronous stochastic gradient descent and split learning.^25,26

CONCLUSION

In this study, we identified that variability in training sample sizes and label distributions across institutional data results in significant performance losses in distributed learning for medical imaging, and we developed modifications to CWT to mitigate these performance losses. We evaluated our methods in 2 simulated distributed medical image classification tasks of DR detection and thoracic disease classification from chest radiographs. Proportional local training iterations was effective in almost completely mitigating performance losses from introducing sample size variability. Locally weighted minibatch sampling and cyclically weighted loss were both effective at mitigating performance losses from variations in the label distribution. Our optimizations to CWT make it more robust to data variability in sample size and label distribution in simulated multi-institutional distributed learning, and future work is needed to address other sources of real-world data variability.

FUNDING

This work was supported by the National Cancer Institute grant number U01CA242879 to DR, by the National Institute of Biomedical Imaging and Bioengineering grant number 5T32EB1680 and National Cancer Institute grant number F30CA239407 to KC, by National Institutes of Health grant numbers U01CA154601, U24CA180927, and U24CA180918 to JK-C, and by the Stanford AstraZeneca Collaboration program. This research was carried out in part at the Athinoula A. Martinos Center for Biomedical Imaging at the Massachusetts General Hospital, using resources provided by the Center for Functional Neuroimaging Technologies supported by National Institute of Biomedical Imaging and Bioengineering grant number P41EB015896. The content in this publication is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

AUTHOR CONTRIBUTIONS

NB and KC performed the experiments, interpreted the results, and wrote the main body of the manuscript. DR and JK conceived the study, designed the experiments, and supervised the work. All authors reviewed the manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST

JK is a consultant/advisory board member for Infotech, Soft. The other authors have no competing interests to declare.