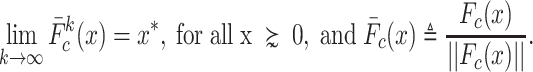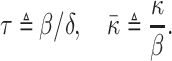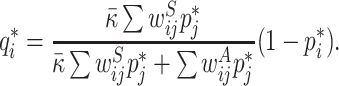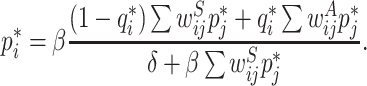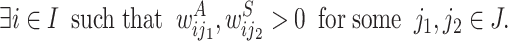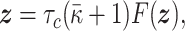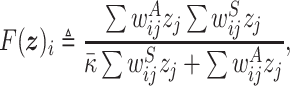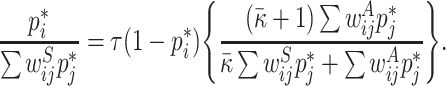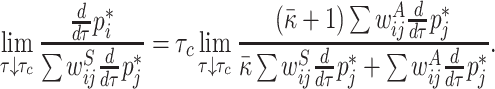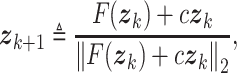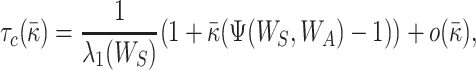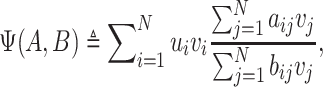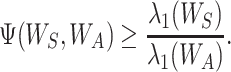Abstract
People change their physical contacts as a preventive response to infectious disease propagations. Yet, only a few mathematical models consider the coupled dynamics of the disease propagation and the contact adaptation process. This paper presents a model where each agent has a default contact neighborhood set, and switches to a different contact set once she becomes alert about infection among her default contacts. Since each agent can adopt either of two possible neighborhood sets, the overall contact network switches among 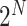 possible configurations. Notably, a two-layer network representation can fully model the underlying adaptive, state-dependent contact network. Contact adaptation influences the size of the disease prevalence and the epidemic threshold—a characteristic measure of a contact network robustness against epidemics—in a nonlinear fashion. Particularly, the epidemic threshold for the presented adaptive contact network belongs to the solution of a nonlinear Perron-Frobenius (NPF) problem, which does not depend on the contact adaptation rate monotonically. Furthermore, the network adaptation model predicts a counter-intuitive scenario where adaptively changing contacts may adversely lead to lower network robustness against epidemic spreading if the contact adaptation is not fast enough. An original result for a class of NPF problems facilitate the analytical developments in this paper.
possible configurations. Notably, a two-layer network representation can fully model the underlying adaptive, state-dependent contact network. Contact adaptation influences the size of the disease prevalence and the epidemic threshold—a characteristic measure of a contact network robustness against epidemics—in a nonlinear fashion. Particularly, the epidemic threshold for the presented adaptive contact network belongs to the solution of a nonlinear Perron-Frobenius (NPF) problem, which does not depend on the contact adaptation rate monotonically. Furthermore, the network adaptation model predicts a counter-intuitive scenario where adaptively changing contacts may adversely lead to lower network robustness against epidemic spreading if the contact adaptation is not fast enough. An original result for a class of NPF problems facilitate the analytical developments in this paper.
Keywords: Epidemics, contact adaptation, state-dependent switching networks, multilayer networks, nonlinear Perron-Frobenius
1. Introduction
Mathematical models of infectious diseases transmission are one of the primary tools for understanding the propagation of infectious diseases among plant, animal, or human populations [1], [2], [3]. Understanding how spreading dynamics are affected by individual-level transmission characteristics and large-scale properties of interactions aids endeavors to control and mitigate epidemics, making it critical for the public health and security.
In addition to their critical role in public health decision making [4], infectious disease models are appealing from complex systems perspective. Take for instance the Susceptible-Infected-Susceptible (SIS) model [3], where each individual in the population is either ‘Susceptible’ or ‘Infected’. The SIS model simply states that susceptible individuals may become infected when interacting with infected individuals, and infected individuals will become susceptible immediately after recovery. Rich dynamics of the SIS model, such as the phase transition observed between fast die-out of infections and long-term epidemic persistence [5], exemplify the ability of simple individual-level interactions to give rise to emergent phenomena.
Understanding disease transmission dynamics in human social networks is particularly challenging [6], partly because humans take preventive measures and alter their interactions in response to disease spreading [7], which subsequently change the course of the spreading [8]. As such, coupled modeling of behavioral change and infection transmission dynamics has seen significant attention recently [8], [9], [10], [11]. Medical treatments, quarantines, illness management practices, and individual preventive behaviors are a few examples of ways society works to reduce disease spreading.
Common preventive behaviors of individuals to the emergence of an epidemic are (1) adopting hygiene/pharmaceutical actions such as wearing a mask, using condoms, improving bodily/environmental cleanliness, and receiving vaccinations, and (2) altering contacts to avoid infection. In the first case, individuals are intending to reduce the probability of infection by cleansing themselves and their environment—or at least placing barriers between the two [12], [13], [14], [15], [16], [17]. In the second case, when individuals change who they come in contact with, the fundamental topology of the network itself is changing. As individuals remove certain contacts with people, while possibly creating new ones, the structural paths available to dynamic processes are being altered, resulting in rich dynamic interplay between network topology and the spreading process on top of it [18], [19], [20], [21], [22], [23], [24], [25], [26].
Existing approaches to incorporate preventive behaviors in mathematical models of infectious diseases fall into two general categories. First approach incorporates the effect of preventive behaviors directly into disease model parameters [27], [28], [29], [30], [31], [32], [33]. The second approach introduces additional dynamic states into a disease model to explicitly distinguish those who have adopted a preventive behavior from those who have not [13], [17], [34], [35], [36], [37], [38]. One example of individual-based models taking the second approach is the susceptible–alert–infected–susceptible (SAIS) framework, first introduced in [17].
The SAIS framework adds an ‘Alert’ state to the networked SIS model of [39]. The alert state represents individuals who (similar to susceptible individuals) can potentially become infected, but has adopted a preventive behavior. In the original SAIS model [17], alert individuals have a lower infection rate compared to the susceptible individuals, and susceptible individuals could become alert in presence of infection among their local contacts. The lower infection rate of alert individuals would correspond to their type-1 preventive behaviors (such as wearing masks or using condoms). This model predicts possibility of total eradication of an epidemics through preventive behaviors[34]. In a subsequent study [40], authors considered an information-dissemination network as an alternative alerting mechanism, and proposed the optimal design solution for an information-dissemination network based on eigenvector centralities [41] in the contact network graph. The SAIS model has been further explored in [42], [43], [44].
In this paper, we introduce the AC-SAIS model, where AC stands for ‘Adaptive Contact’, to model a scenario in which individuals change their contact neighborhood upon becoming alert. More specifically, each susceptible individual 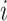 is in contact with a given set of individuals
is in contact with a given set of individuals 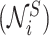 , and when she becomes alert, she switches to another set of individuals
, and when she becomes alert, she switches to another set of individuals 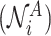 . We will use the terms default neighborhood and adapted neighborhood to distinguish the two. In our model, we assume both of these neighborhoods are known a priori. Yet, we do no make any restrictive assumptions on these neighborhood sets and deliver our results in the most generic setup. In practice, the default and adapted neighborhood sets might be closely related. For example, in a social distancing scenario [45], the adapted neighborhood would be a subset of the default neighborhood. Social distancing is not the only possible scenario of contact adaptation. In the context of sexually transmitted infections, for example, when a person is notified that one of his sexual partners is infected, in response, he may abandon all or some of his set of partners and seek partnership from a new venue.
. We will use the terms default neighborhood and adapted neighborhood to distinguish the two. In our model, we assume both of these neighborhoods are known a priori. Yet, we do no make any restrictive assumptions on these neighborhood sets and deliver our results in the most generic setup. In practice, the default and adapted neighborhood sets might be closely related. For example, in a social distancing scenario [45], the adapted neighborhood would be a subset of the default neighborhood. Social distancing is not the only possible scenario of contact adaptation. In the context of sexually transmitted infections, for example, when a person is notified that one of his sexual partners is infected, in response, he may abandon all or some of his set of partners and seek partnership from a new venue.
When nodes adapt their contacts to a neighborhood constituting a more robust network, one might intuitively expect that the robustness of the network against epidemic spreading increases monotonically with the contact adaptation rate. This is true in the case of social distancing (where the alert neighborhood is a subset of the default ones) as it always help mitigating epidemic spreading, and the faster the social distancing is implemented, the better. However, when the set of adapted contacts of an individual is not restricted to be a subset of their default contacts, the network robustness against epidemic spreading can be a non-monotone function of the contact adaptation rate. Indeed, our model detects a counter-intuitive scenario where adaptively changing contacts may adversely lead to lower network robustness against epidemic spreading if the adaptation is not fast enough.
From dynamical systems perspective, this study contains several contributions. First, we propose a novel state-dependent switching network framework and show that a multilayer-network [46] formulation can be successfully employed. Second, we develop an original result of nonlinear Perron-Frobenius theory, where we find necessary and sufficient conditions for existence and uniqueness of a strictly positive eigenvector for the class of non-negative, concave maps. We apply this tool to find the epidemic threshold for our AC-SAIS model. Furthermore, we introduce a novel notion of connectivity for multilayer networks, which is novel for the new research field of multilayer networks.
The rest of the paper is organized as follows: After the literature review in Section 2, Section 3 introduces a novel notion of multilayer connectivity and an original result for nonlinear Perron-Frobenius theory, which are pivotal for the subsequent modeling and analysis. Section 4 develops the AC-SAIS model, showing that the proposed adaptive contact can be equivalently modeled by multilayer networks. Analyses in Section 5 are followed by numerical experiments in Section 6. Several proofs to theorems and lemmas are omitted for the sake of brevity, and can be found in the Supplemental Materials of this article, which can be found on the Computer Society Digital Library at http://doi.ieeecomputersociety.org/10.1109/TNSE.2017.2770091.
2. Literature Review
Typical approaches to modeling spreading processes on networks consider network topologies as independent of individual node states, such is the case when nodes retain the same set of contacts regardless of whether or not they, or their neighbors, are infected. This assumption is made for simplicity’s sake and is not representative of real world networks; especially in regards to social networks where a person’s contacts are in constant fluctuation. The notion of state-dependent topologies is especially poignant in the context of disease dynamics where a person will adjust who they come in contact with when in the presence of an infection. The extent to which this occurs can vary greatly—from removing a single contact to completely changing all of them—depending on the perceived severity of an infection.
Several formulations of adaptive contact exist in the literature of infectious disease modeling, including: 1) social distancing [47], where healthy individuals lower their contact with the rest of the population, 2) delete-and-reactivate [48], where healthy break their contact with infected population and reactivate after some time, 3) rewiring [49], [50], where healthy break their contact with infected population and create new links with healthy members [21] or any other randomly chosen individual [23].
Altering the local contacts can have a strong effect on disease dynamics, which in turn influences the contact adaptation process; a complicated mutual interaction between a time varying network topology and the dynamics of the nodes emerges. For example, Gross et al. [21] presented a model where susceptible individuals rewire their links from other infected individuals toward susceptible ones in an SIS model, resulting in the formation of two loosely connected clusters. Several researches have built on this model: Marceau et al. [22] additionally include the infection state of its neighbors in the node information. Risau et al. [23] rewire susceptible individuals from infected neighbors to random nodes, which in some cases completely suppresses epidemic spreading.
Most of contact adaptation schemes have been implemented for well-mixed populations or random network models of physical interactions. Studies that work with generic graphs as their contact network are scarce in the literature. Among a few existing research endeavors is the Adaptive-SIS (ASIS) model developed by Guo et al. [48], who studied an SIS epidemic model where contacts between susceptible and infected nodes are removed at some rate and reactivated later. They showed the epidemic threshold increases as a function of the link removal rate, while the network topology exhibits binomial-like degree distribution, assortative mixing, and modularity. This approach was rigorously extended by Ogura and Preciado [51], who additionally considered heterogeneous node and edge parameters, as well as a method for optimizing adaptation rates to mitigate epidemic outbreaks. This approach of adaptation for generic graphs considers a dynamic equation for the edge weights which is coupled with the epidemic model. Another approach would be through the notion of switching networks in dynamical systems.
A switching contact network is defined as a set of distinct networks where the “active” network at any given time is determined by some switching signal. More precisely, we denote a switching network 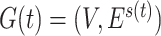 , where
, where 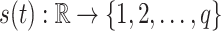 is a signal that determines which of the
is a signal that determines which of the 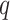 networks are active at time
networks are active at time 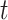 . Usually this signal is external and independent of the system states. For example, a common approach is to consider
. Usually this signal is external and independent of the system states. For example, a common approach is to consider 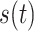 as a Markov process independent from the disease states [52], [53]. The collection of possible edge sets
as a Markov process independent from the disease states [52], [53]. The collection of possible edge sets 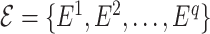 may be given a priori as in [52], or they might be generated from local processes as in [53]. In the latter, Ogura and Preciado considered a base graph with
may be given a priori as in [52], or they might be generated from local processes as in [53]. In the latter, Ogura and Preciado considered a base graph with 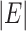 edges where each edge can become active or inactive according to an externally defined Markov process, leading to an overall
edges where each edge can become active or inactive according to an externally defined Markov process, leading to an overall 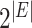 possible configurations for the switching contact network. We can also think of a more complex situation where the switching signal is dependent on the system states. In this way, the topology of the active network determines the evolution of the dynamic process and in turn, the state of the process itself signals network switching. Here lies our proposed contact adaptation scheme.
possible configurations for the switching contact network. We can also think of a more complex situation where the switching signal is dependent on the system states. In this way, the topology of the active network determines the evolution of the dynamic process and in turn, the state of the process itself signals network switching. Here lies our proposed contact adaptation scheme.
We consider a class of switching networks where the neighborhood set of each node depends on the state it occupies. Specifically, each node 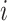 has one of two contact sets
has one of two contact sets 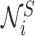 and
and 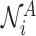 , depending on whether is is ‘susceptible’ or ‘alert’. Therefore, for a network of size
, depending on whether is is ‘susceptible’ or ‘alert’. Therefore, for a network of size 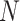 , the entirety of the switching network is composed of
, the entirety of the switching network is composed of 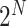 separate topologies. In this case, not only the network state-space size exponentially increases by
separate topologies. In this case, not only the network state-space size exponentially increases by 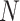 , but also the switching signal depends on the collective system state.
, but also the switching signal depends on the collective system state.
3. Fundamental Concepts and Tools
Before diving into the modeling and analysis, we first start with a novel notion of connectivity for multilayer networks and an original results for a class of nonlinear Perron–Frobenius problems that will facilitate the subsequent developments in this paper.
3.1. Nonlinear Perron Frobenius
The classical Perron-Frobenius theorem [54] concerns the eigenvalue problem 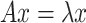 for a nonnegative and irreducible matrix
for a nonnegative and irreducible matrix 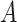 . Let
. Let 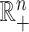 be the non-negative cone in the
be the non-negative cone in the 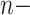 dimensional Euclidean space
dimensional Euclidean space
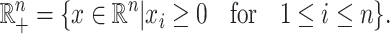 |
Assuming 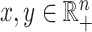 , here
, here 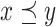 (
(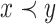 ) means
) means 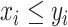 (
(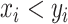 ) for
) for 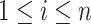 and
and 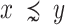 denotes
denotes 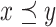 but
but 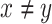 . A matrix
. A matrix 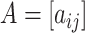 is called non-negative if all of its entries are either positive or zero. We can construct a graph
is called non-negative if all of its entries are either positive or zero. We can construct a graph 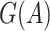 associated with
associated with 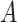 such that the edge
such that the edge 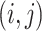 exists if
exists if 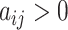 . The matrix
. The matrix 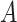 is irreducible if and only if its associated graph
is irreducible if and only if its associated graph 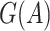 is strongly connected. The classical Perron-Frobenius theorem may be stated as the following:
is strongly connected. The classical Perron-Frobenius theorem may be stated as the following:
Theorem 1 (Perron–Frobenius Theorem [54]). —
Let
be a nonnegative, irreducible matrix. Then
has a positive eigenvalue
which has multiplicity one and any eigenvalue of
has a magnitude smaller than or equal to
. Furthermore the eigenvector
corresponding to
is strictly positive (i.e.,
) and is the only eigenvector of
in the nonnegative cone.
From mappings perspective, the classical Perron–Frobenius theory concerns solutions to the eigenvalue problem 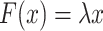 where
where 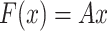 is a linear self-map of the non-negative cone. By “self-map of the non-negative cone,” we mean that
is a linear self-map of the non-negative cone. By “self-map of the non-negative cone,” we mean that 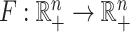 maps the non-negative cone to itself. But what if the map
maps the non-negative cone to itself. But what if the map 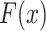 is not linear? Can we still get powerful results for nonlinear maps analogous to the Perron–Frobenius theorem? The whole area of the nonlinear Perron–Frobenius theory [55], [56], [57], [58], [59] seeks answer to these questions. A thorough review of nonlinear Perron–Frobenius theory is out of the scope of this paper. In short, results are usually more limited in that existence, uniqueness, or strictly positivity of an eigenvector is seldom guaranteed unless under restrictive assumptions on the nonlinear map.
is not linear? Can we still get powerful results for nonlinear maps analogous to the Perron–Frobenius theorem? The whole area of the nonlinear Perron–Frobenius theory [55], [56], [57], [58], [59] seeks answer to these questions. A thorough review of nonlinear Perron–Frobenius theory is out of the scope of this paper. In short, results are usually more limited in that existence, uniqueness, or strictly positivity of an eigenvector is seldom guaranteed unless under restrictive assumptions on the nonlinear map.
The following properties are among the possibilities to relax the linearity assumption for the non-negative map 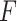 . Note that the linear map
. Note that the linear map 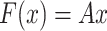 with non-negative matrix
with non-negative matrix 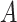 has all of these properties.
has all of these properties.
Definition 1. —
Assume
is a self-map of nonnegative cone. We say
is
- 1)
homogeneous, if for any
and
,
,
- 2)
concave, if
for all
and
,
- 3)
super-additive, if
for all
,
- 4)
monotone,1 if
for all
.
The homogeneity property indicates that if 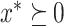 is an eigenvector of
is an eigenvector of  , so is
, so is 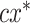 for any
for any 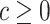 . Furthermore, the following lemma indicates that the class of homogeneous, concave self-maps of the non-negative cone is a special case of homogeneous, monotone maps.
. Furthermore, the following lemma indicates that the class of homogeneous, concave self-maps of the non-negative cone is a special case of homogeneous, monotone maps.
Lemma 1. —
If
is a homogeneous, concave map of the non-negative cone, then
is also monotone and super-additive.
Several results in the literature concern the more general class of homogeneous, monotone maps [56], [57]. While existence and strict positivity of an eigenvector can be proved for this class of maps, uniqueness cannot be guaranteed without quite restrictive assumptions [56]. For example,2 for the homogeneous, monotone function 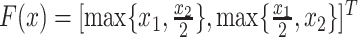 , any vector
, any vector 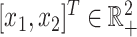 with
with 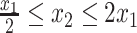 is an eigenvector of
is an eigenvector of 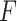 with eigenvalue
with eigenvalue 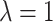 . On the contrary, existence and strict positivity of a unique eigenvector can be proved for the special class of homogeneous, concave maps.
. On the contrary, existence and strict positivity of a unique eigenvector can be proved for the special class of homogeneous, concave maps.
The nonlinear map of interest in this paper falls in the special class of homogeneous and concave maps. Therefore, we focus on this class of nonlinear maps and develop a new result.
So far, we relaxed the linearity restriction by assuming that our nonlinear map is homogeneous and concave. The next question is what would be the counter part to irreducibility of 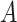 in the linear map
in the linear map 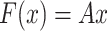 for a homogeneous, concave map. For homogeneous, concave maps, Krause [58] proposes the following condition:
for a homogeneous, concave map. For homogeneous, concave maps, Krause [58] proposes the following condition:
Definition 2 (Krause [58], Section 3). —
We say the homogeneous, concave self-map
satisfies condition3 C1 in
if for any non-empty subset
, there exists
and
such that
, where
is the
th unit vector in
and
denotes the
th component of
.
Furthermore, Krause proves that condition C1 is a sufficient condition for existence and uniqueness of a positive eigenvector:
Theorem 2 (Krause [58], Theorem 13). —
For the self-map
, which is concave, homogeneous, and satisfies condition C1, the equation
has a strictly positive solution
,
, and
is the only eigenvector in the non-negative cone (up to scaling).
We argue that the condition C1 for the notion of irreducibility in [58] may be restrictive, and same strong results would be still valid under a more relaxed condition. Indeed, the nonlinear map of our interest in this paper may not satisfy the condition C1 in Definition 2.
To illustrate, suppose 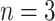 and the nonlinear map is
and the nonlinear map is 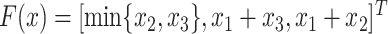 . This map is both homogeneous and concave. However, it does not satisfy condition C1 of [58] stated in Definition 2. To test this, let
. This map is both homogeneous and concave. However, it does not satisfy condition C1 of [58] stated in Definition 2. To test this, let 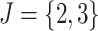 ; no
; no 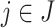 leads to
leads to 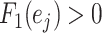 because
because 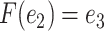 and
and  . However, this map has a unique, strictly positive eigenvector
. However, this map has a unique, strictly positive eigenvector 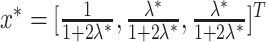 and
and 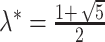 with
with  . Another example is
. Another example is 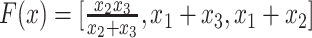 . Again,
. Again, 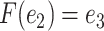 and
and 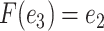 , so it does not satisfy condition C1. However, this map has a unique, strictly positive eigenvector
, so it does not satisfy condition C1. However, this map has a unique, strictly positive eigenvector 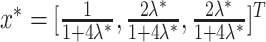 and
and 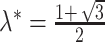 with
with 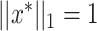 .
.
Definition 3. —
We say the homogeneous, concave self-map
of the non-negative cone satisfies condition C2 in
if for any choice of
, there exists
such that
, where
is defined as
.
The example function 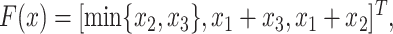 which does not satisfy condition C1, does satisfy C2. For instance, selecting
which does not satisfy condition C1, does satisfy C2. For instance, selecting 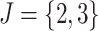 yields
yields 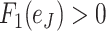 because
because 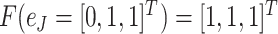 . The following lemma proves that C2 is indeed less restrictive than C1.
. The following lemma proves that C2 is indeed less restrictive than C1.
Lemma 2. —
A homogeneous, concave self-map
of the nonnegative cone that satisfies condition C1 also satisfies condition C2.
We would like to emphasize that there is nothing special about usage of 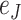 in Definition 3. The following lemma shows that any vector that has positive values on elements corresponding to
in Definition 3. The following lemma shows that any vector that has positive values on elements corresponding to 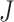 and is zero on other elements would be equivalently applicable.
and is zero on other elements would be equivalently applicable.
Lemma 3. —
For any choice
, we have
if and only if
where the symbol
denotes the Hadamard (entry-wise) multiplication.
In the linear domain, we know that if a non-negative matrix 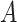 is irreducible, the matrix
is irreducible, the matrix 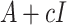 is primitive for any
is primitive for any 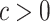 [60, Theorem 9], and vice versa. How would be the extension of this idea to the nonlinear domain? First, let us precisely define a primitive map.
[60, Theorem 9], and vice versa. How would be the extension of this idea to the nonlinear domain? First, let us precisely define a primitive map.
Definition 4. —
The self-map
of the non-negative cone is called primitive if there exists
such that
for all
and
. Here,
denotes the
th iterate of
, i.e.,
and
.
The following theorem states that 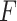 satisfying C2 and
satisfying C2 and 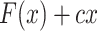 being primitive are equivalent.
being primitive are equivalent.
Theorem 3. —
The map
with
is primitive if and only if the homogeneous, concave self-map
of the non-negative cone satisfies condition C2.
The duality between  satisfying C2 and
satisfying C2 and 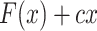 being primitive leads to the main theorem in this paper:
being primitive leads to the main theorem in this paper:
Theorem 4. —
Statements of Theorem 2 still holds if condition C1 is replaced with condition C2. Furthermore, if
is a unique eigenvector of the homogeneous concave map
in
then
must satisfy condition C2. Moreover, iterations of
with
converge to
i.e.,
Compared with Theorem 1, it is evident that results for the nonlinear Perron–Frobenius problem in case of homogeneous, concave maps are very strong; existence and uniqueness of a strictly positive eigenvector can be guaranteed. Our contribution to the theory of nonlinear Perron–Frobenius theory for homogeneous, concave maps is that we relaxed the sufficient condition of [58] (through replacing C1 by C2) and proved that this new4 condition is also the necessary condition for uniqueness of the eigenvector in the non-negative cone.
3.2. Multilayer Networks and an Algorithmic Notion of Connectivity
Graph theory is the mathematics of networks. In graph theory, a directed graph is formally defined as an ordered pair 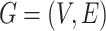 , where
, where 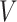 is the set of nodes and
is the set of nodes and 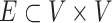 is the set of ordered pairs of nodes representing their directed relation. We say node
is the set of ordered pairs of nodes representing their directed relation. We say node 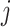 is a neighbor of node
is a neighbor of node 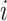 , if
, if 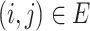 . The set
. The set 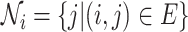 denotes the neighbors of node
denotes the neighbors of node 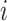 . A path
. A path 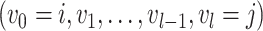 of length
of length 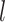 is an ordered tuple of edges than connects
is an ordered tuple of edges than connects 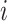 to
to 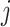 , i.e.,
, i.e., 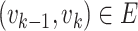 . A directed graph is strongly connected if there exists a path between all ordered pair of nodes in the network [54].
. A directed graph is strongly connected if there exists a path between all ordered pair of nodes in the network [54].
Several natural and technological systems show complex patterns of interactions among their heterogeneous entities. To capture the complexities of such systems, the network science community has recently shown substantial interest in the notion of multilayer networks [46], [61] and developing proper mathematics for them beyond the classical graph theory [62].
In this paper, we denote a multilayer network5 as an ordered tuple 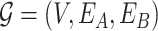 where nodes in
where nodes in 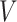 are connected through two link types
are connected through two link types 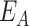 and
and 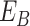 . Corresponding to the multilayer network
. Corresponding to the multilayer network 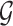 , we define
, we define 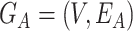 and
and 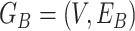 as the layers of
as the layers of 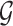 . Motivated by the notion of strong connectivity for directed graphs, we propose a novel notion of connectivity for multilayer networks in the following.
. Motivated by the notion of strong connectivity for directed graphs, we propose a novel notion of connectivity for multilayer networks in the following.
Our proposed notion of multilayer connectivity, which from now on we will refer to it as M–connectivity, has an algorithmic definition. To motivate and acquaint our definition to the reader, we first point out a straight-forward property of simple strongly connected graphs. Suppose for the graph 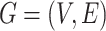 we have an arbitrary partition
we have an arbitrary partition  of the node set
of the node set 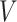 , i.e., members of
, i.e., members of  are non-empty disjoint subsets of
are non-empty disjoint subsets of  that cover
that cover  , more precisely
, more precisely
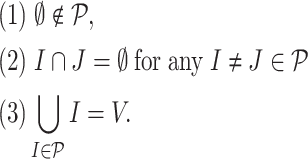 |
We can build a graph 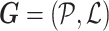 , where the partition set
, where the partition set 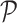 is the node set of
is the node set of 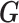 . Note that each node
. Note that each node 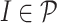 of
of 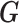 is a partitioning subset of
is a partitioning subset of 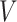 . As such, to avoid possible confusion, we will refer to nodes of
. As such, to avoid possible confusion, we will refer to nodes of 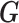 as hypernodes from now on. We assign a directed link from one hypernode
as hypernodes from now on. We assign a directed link from one hypernode 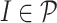 to another hypernode
to another hypernode 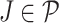 , if there is a node
, if there is a node 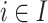 of
of 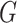 that is connected to a node
that is connected to a node 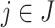 , i.e.,
, i.e., 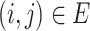 . Trivially, yet importantly, strong connectivity of
. Trivially, yet importantly, strong connectivity of 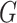 implies strong connectivity of
implies strong connectivity of  . For a multilayer network
. For a multilayer network 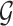 , we use a related notion to define connectivity.6 The main difference is that connection among subsets must be through both layers. Following provides a formal definition.
, we use a related notion to define connectivity.6 The main difference is that connection among subsets must be through both layers. Following provides a formal definition.
For a multilayer network 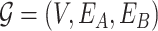 , we iteratively build graphs
, we iteratively build graphs 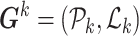 , starting with
, starting with 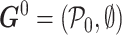 , where
, where 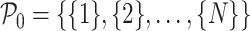 is the trivial partition of
is the trivial partition of 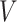 singletons. From the graph
singletons. From the graph 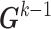 , we build
, we build 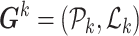 in the following way:
in the following way:
Step 1. Define the hypernode set 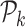 of cardinality equal to the number of strongly connected components of
of cardinality equal to the number of strongly connected components of 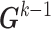 where each element
where each element 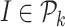 groups one and only one strongly connected component of
groups one and only one strongly connected component of 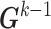 (i.e.,
(i.e., 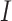 is the union of all the hypernodes in that strongly connected component). Note that, doing so, the hypernode set
is the union of all the hypernodes in that strongly connected component). Note that, doing so, the hypernode set 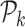 always denotes a partitioning of the node set
always denotes a partitioning of the node set 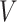 .
.
Step2. We assign the directed link 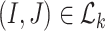 if at least one single node in
if at least one single node in 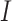 is connected to
is connected to 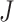 through both layers simultaneously,7 i.e.,
through both layers simultaneously,7 i.e.,
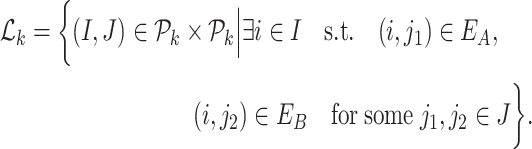 |
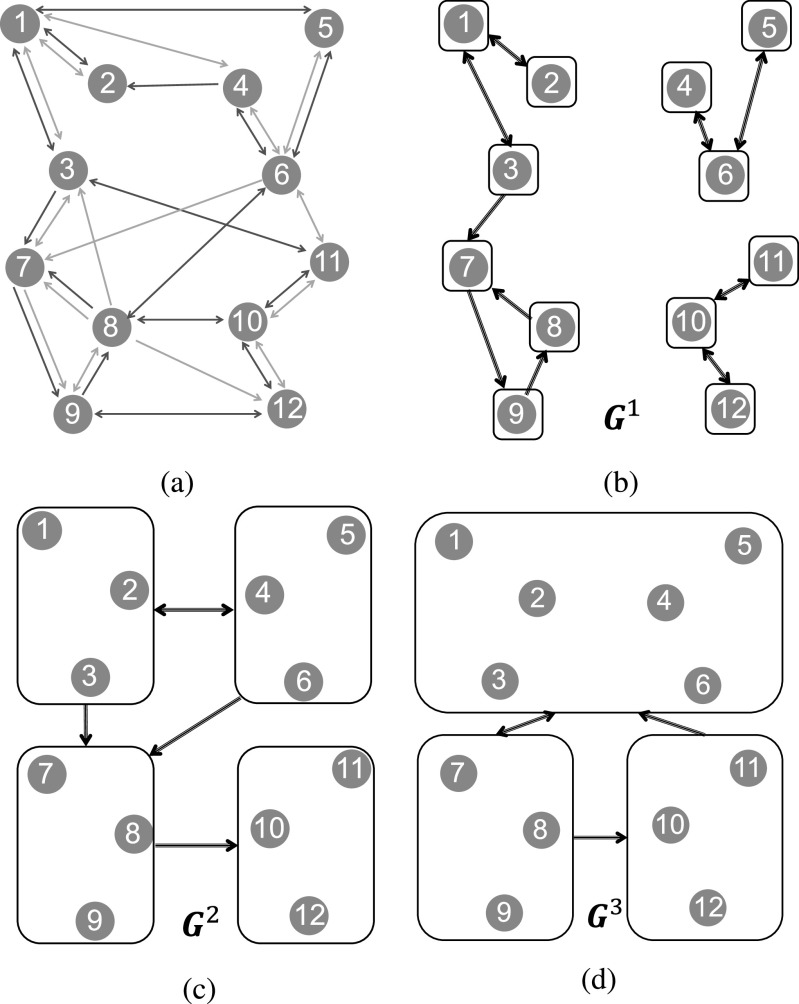
Fig. 1 illustrates the iterative procedure explained above.
Fig. 1.
Example of an M-connected multilayer network according to Definition 1. (a) In the two-layer graph, the red arrows represent 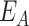 edges and green arrows represent
edges and green arrows represent 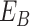 edges. (b) The first graph
edges. (b) The first graph 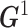 has the hypernodes set
has the hypernodes set 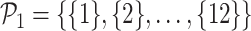 , and its links are the intersection of
, and its links are the intersection of 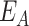 and
and 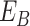 edges. Hypernodes are depicted by black squares, and links between them are shown by black arrows. The graph
edges. Hypernodes are depicted by black squares, and links between them are shown by black arrows. The graph 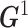 is not strongly connected. (c) The second aggregate graph
is not strongly connected. (c) The second aggregate graph 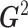 has the strongly connected components of
has the strongly connected components of 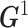 as its hypernodes set
as its hypernodes set 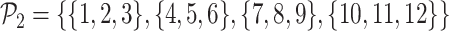 . The links among the hypernodes is according to Step 2 in Section 3.2. For example, the directed link
. The links among the hypernodes is according to Step 2 in Section 3.2. For example, the directed link  is due to node 6, a member of
is due to node 6, a member of  , being connected to the hypernode
, being connected to the hypernode 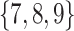 through both layers (because,
through both layers (because, 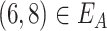 and
and 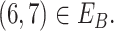 ). The graph
). The graph 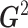 is not strongly connected either. (d) The third aggregated graph
is not strongly connected either. (d) The third aggregated graph 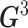 groups strongly connected components of
groups strongly connected components of 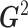 as its hypernodes set
as its hypernodes set 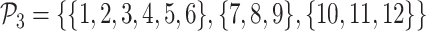 . The graph
. The graph 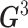 is strongly connected. Therefore, the two-layer network in (a) is M–connected according to Definition 1.
is strongly connected. Therefore, the two-layer network in (a) is M–connected according to Definition 1.
Definition 5. —
A multilayer network
is M– connected, if starting with with
—where
is the trivial partition of
singletons—and inductively building
following Step 1 and Step 2 described above, there exists an iteration step
such that
is strongly connected.
Intuitively, M–connectivity of 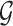 implies that if we split the node set
implies that if we split the node set  into any two subsets
into any two subsets 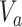 and
and 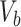 , there is always a node in
, there is always a node in 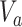 (resp.
(resp. 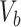 ) that is connected to
) that is connected to 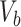 (resp.
(resp.  ) through both edge types. A necessary condition for M–connectivity of
) through both edge types. A necessary condition for M–connectivity of 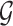 is that both individual layers
is that both individual layers 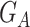 and
and 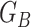 are strongly connected. Moreover, a sufficient condition for M–connectivity of
are strongly connected. Moreover, a sufficient condition for M–connectivity of 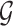 is that the intersection graph
is that the intersection graph 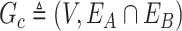 is strongly connected (because,
is strongly connected (because, 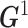 which is similar to
which is similar to 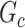 , will be already strongly connected).
, will be already strongly connected).
M–Connectivity and Condition C2. Consider a multilayer network 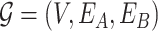 , where the node set are labeled from 1 to
, where the node set are labeled from 1 to  , i.e.,
, i.e., 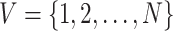 . By defining a real valued vector
. By defining a real valued vector 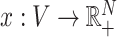 on node set
on node set 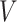 , we show the relation between M–connectivity and condition C2 for functions
, we show the relation between M–connectivity and condition C2 for functions 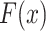 .
.
Theorem 5. —
Associated with the multilayer network
where
, suppose a homogeneous, concave map
of the non-negative cone is such that for any nontrivial subset
of
and
,
if and only if there exists
for which
and
. Then,
satisfies condition C2 if and only if the multilayer network
is M-connected.
4. Model Development
Before introducing our model, we first review a background on the networked SIS epidemic process.
4.1. A Background on Networked SIS Model
Susceptible–infected–susceptible model is a paradigmatic epidemic spreading model. In the SIS model, each individual is either susceptible or infected, and individuals are assumed to immediately become susceptible to the disease after recovery. SIS model is thus suitable for modeling sexually transmitted infections such as Gonorrhea and Syphilis [2].
Classical compartmental epidemic models assume homogeneous (fully mixed) interactions among individuals. In networked epidemic models, interactions among individuals are explicitly modeled using a contact network, represented by the graph 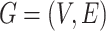 , where individuals are represented by nodes
, where individuals are represented by nodes 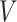 of a graph and possible interactions are the edges
of a graph and possible interactions are the edges 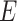 of a graph. Node
of a graph. Node 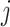 is a neighbor of node
is a neighbor of node 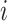 , denoted as
, denoted as 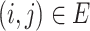 , if she can infect node
, if she can infect node 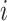 directly. We can also use weighted graphs to represent contact networks. Doing so, the weight value of a link would serve as a proxy for heterogeneity of contact levels among pairs of individuals. For example, if both nodes
directly. We can also use weighted graphs to represent contact networks. Doing so, the weight value of a link would serve as a proxy for heterogeneity of contact levels among pairs of individuals. For example, if both nodes 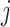 and
and 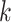 are infected and
are infected and 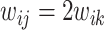 , the likelihood that a susceptible node
, the likelihood that a susceptible node 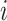 contracts the disease from node
contracts the disease from node 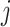 is double the likelihood of contracting it from node
is double the likelihood of contracting it from node 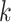 . In this paper, we allow the contact graph be directed and weighted.
. In this paper, we allow the contact graph be directed and weighted.
In the networked SIS model [63], the state of node 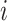 at time
at time 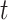 is denoted by
is denoted by 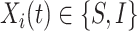 , where
, where 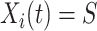 if the node is susceptible or
if the node is susceptible or 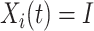 if it is infected. In this model, a susceptible nodes becomes infected if it is exposed to an infected individual. Moreover, an infected individual recovers and becomes susceptible again after a recovery period. The infection and curing times are commonly assumed to have a memoryless property, leading to exponentially distributed time intervals in continuous time descriptions. More general time distributions are also possible and addressed in the literature to some extent [53], [64], [65], [66], [67].
if it is infected. In this model, a susceptible nodes becomes infected if it is exposed to an infected individual. Moreover, an infected individual recovers and becomes susceptible again after a recovery period. The infection and curing times are commonly assumed to have a memoryless property, leading to exponentially distributed time intervals in continuous time descriptions. More general time distributions are also possible and addressed in the literature to some extent [53], [64], [65], [66], [67].
The overall evolution of the nodes states are due to their interactions with each other. Hence, mathematical description of the SIS model requires utilization of the collective state 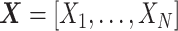 , which is the joint state of all
, which is the joint state of all 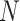 nodes in the network. The network state is a continuous-time Markov process that undergoes transition over a space consisting of
nodes in the network. The network state is a continuous-time Markov process that undergoes transition over a space consisting of 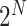 possible network states. In this description, we say an event has occurred if the state of a single node changes. Furthermore, the time interval for the event occurrence is exponentially distributed. This time interval can equivalently be described as the minimum of transition times of a set of statistically independent processes on node states, denoted by
possible network states. In this description, we say an event has occurred if the state of a single node changes. Furthermore, the time interval for the event occurrence is exponentially distributed. This time interval can equivalently be described as the minimum of transition times of a set of statistically independent processes on node states, denoted by 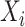 , and pair states, denoted by
, and pair states, denoted by 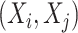 , as the following:
, as the following:
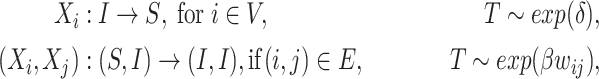 |
where 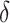 and
and 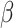 are called curing and infection rates, respectively, and
are called curing and infection rates, respectively, and 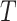 represents the corresponding exponentially distributed transition duration.
represents the corresponding exponentially distributed transition duration.
Describing the network Markov process as competition among statistically independent nodal and edge-based transitions, similar to the above formulation of the SIS process, allows for a much more general framework for modeling networked epidemic processes (see, [68]). We will use this approach to describe our adaptive contact epidemic model.
Finally, the Kolmogorov equation, which governs probability distribution of the SIS Markov process, is a system of 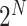 coupled differential equations which is neither computationally nor analytically tractable for large number of nodes. Moment closure approximations [39], [68], [69], [70] or Monte Carlo simulations are thus necessary to study the networked SIS process. The SIS process shows a phase transition behavior where initial infections die out quickly for small values of
coupled differential equations which is neither computationally nor analytically tractable for large number of nodes. Moment closure approximations [39], [68], [69], [70] or Monte Carlo simulations are thus necessary to study the networked SIS process. The SIS process shows a phase transition behavior where initial infections die out quickly for small values of 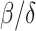 , while infections can persist in the network for long time (coined as metastable state) for large values of
, while infections can persist in the network for long time (coined as metastable state) for large values of 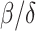 [71]. The critical value separating these regions is called the epidemic threshold. As such, epidemic threshold suggests a measure of networks robustness against epidemic spreading. In this paper, whenever we say network
[71]. The critical value separating these regions is called the epidemic threshold. As such, epidemic threshold suggests a measure of networks robustness against epidemic spreading. In this paper, whenever we say network  is more robust against epidemic spreading than network
is more robust against epidemic spreading than network 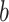 , we mean network
, we mean network 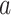 has a larger value of epidemic threshold that network
has a larger value of epidemic threshold that network  .
.
4.2. AC-SAIS Markov Model
Consider a population of 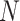 individuals, where each individual is either susceptible, alert, or infected. For each individual
individuals, where each individual is either susceptible, alert, or infected. For each individual 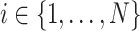 , let the random variable
, let the random variable  if the individual
if the individual 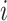 is susceptible at time
is susceptible at time 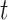 ,
, 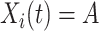 if alert, and
if alert, and 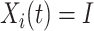 if infected. In the AC-SAIS model of this paper, contacts of a node depends on her state. Specifically, we define
if infected. In the AC-SAIS model of this paper, contacts of a node depends on her state. Specifically, we define 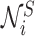 as the neighbors of node i when she is susceptible, and
as the neighbors of node i when she is susceptible, and  as her neighbors when she is alert. Associated with these neighborhood sets, we consider weight values
as her neighbors when she is alert. Associated with these neighborhood sets, we consider weight values  if
if 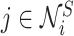 and
and 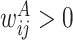 if
if  as a proxy for heterogeneity of the contact levels.
as a proxy for heterogeneity of the contact levels.
Four competing stochastic transitions describe the AC-SAIS model, as Fig. 2 depicts:
-
1)Infection of susceptible nodes: A susceptible individual becomes infected from her infected neighbor (among
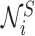 ) after an exponentially distributed random time duration with the infection rate
) after an exponentially distributed random time duration with the infection rate 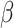
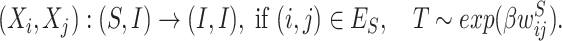
-
2)Alerting of susceptible nodes: A susceptible individual becomes alert from her infected neighbor (among
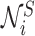 ) after an exponentially distributed random time duration with the alerting rate
) after an exponentially distributed random time duration with the alerting rate 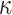
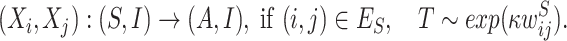
-
3)Infection of alert nodes: An alert individual becomes infected due to having an infected neighbor among her switched neighborhood set
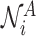 after an exponentially distributed random time duration with the infection rate
after an exponentially distributed random time duration with the infection rate 
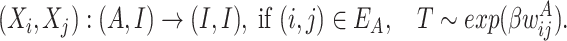
-
4)Recovering of infected nodes: An infected individual recovers to the susceptible state after an exponentially distributed random time duration with recovery rate
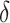

Fig. 2.
Schematic of the AC-SAIS model. Black edges correspond to neighborhood 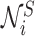 of susceptible node
of susceptible node 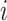 , while red edges represent the neighborhood
, while red edges represent the neighborhood 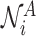 when node
when node 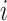 is in the alert state. Here,
is in the alert state. Here, 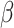 ,
, 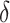 , and
, and 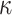 are the infection rate, curing rate, and alerting rate, respectively.
are the infection rate, curing rate, and alerting rate, respectively. 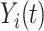 is the number of infected neighbors of
is the number of infected neighbors of 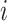 in
in 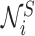 at time
at time 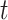 and
and  is the number of infected neighbors of
is the number of infected neighbors of 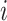 in
in 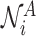 at time
at time 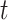 .
.
A Few Remarks on the AC-SAIS Model. The disease dynamics component of the AC-SAIS model is according to the networked SIS model, elaborated in Section 4.1. Therefore, a representative example would be the spread of Syphilis or Gonorrhea for which the sexual contact network is well-defined and disease dynamics are SIS-type. In this scenario, the alerting process can be the result of a partner notification effort.
In the AC-SAIS model, we assume that if an alert individual never gets infected, she will remain in the alert state indefinitely. In other words, we do not consider an awareness decay process where alert individuals can transition to the susceptible state directly. In practice, we are assuming that the awareness decay process is so much slower than the disease dynamics that it becomes irrelevant for the disease spreading. Interested readers can refer to [44] for analysis of an SAIS model with awareness decay.
The current setup of the AC-SAIS model only considers a type-2 preventive behavior of altering contacts, whereas the original SAIS model considered a type-1 preventive behavior by assuming a lower infection rate for alert individuals. It would be possible to also incorporate type-1 behaviors in the AC-SAIS model by lowering the infection rate for the alert individuals to 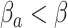 . In order to isolate the role of network adaptation, we do not change the infection rate in this study.
. In order to isolate the role of network adaptation, we do not change the infection rate in this study.
The contact alteration scheme in the AC-SAIS model assumes the contacts set of an individual only depends on her own state; it is the default set when susceptible, and the adapted set when alert. Particularly, the contact set of an alert individual is fixed and is independent of the health state of those contacts. Such contact adaptation scheme is most sensible when the identity of infected contacts are not known to the individual. For example, in the context of sexually transmitted diseases and partner notification, the identity of the infectious patient is not revealed to their partners. So, a subsequent contact adaptation may not necessarily lead to definite avoidance of infectious partners.
4.3. An Equivalent Multilayer Representation
From a networked dynamical system perspective, the network topology in the AC-SAIS model is time-varying and switches among 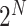 different possibilities because each node
different possibilities because each node 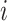 may adopt one of the two neighborhood sets
may adopt one of the two neighborhood sets 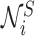 and
and 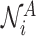 . However, the AC-SAIS model can be equivalently interpreted as a spreading process on a two-layer network. The AC-SAIS Markov process described in Section 4.2 falls in the broad class of generalized epidemic modeling framework (GEMF) introduced in [68] for spreading processes on multilayer networks. In essence, the switching contact network of the AC-SAIS model can be equivalently described as a spreading process on multilayer network
. However, the AC-SAIS model can be equivalently interpreted as a spreading process on a two-layer network. The AC-SAIS Markov process described in Section 4.2 falls in the broad class of generalized epidemic modeling framework (GEMF) introduced in [68] for spreading processes on multilayer networks. In essence, the switching contact network of the AC-SAIS model can be equivalently described as a spreading process on multilayer network 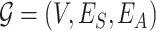 , where each layer determines the interaction neighborhood that induces state change in a node, depending on its current state. Note that we only need to include layers for susceptible and alert nodes, because the transition of an infected node towards the susceptible state is spontaneous and does not depend on other nodes states.
, where each layer determines the interaction neighborhood that induces state change in a node, depending on its current state. Note that we only need to include layers for susceptible and alert nodes, because the transition of an infected node towards the susceptible state is spontaneous and does not depend on other nodes states.
Significantly, a multilayer network formulation of adaptive contact reduces the problem from defining a process between 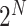 separate topologies to defining a process on top of a static two–layer network, effectively modeling complex switching dynamics with a conceptually straightforward framework. The network layers
separate topologies to defining a process on top of a static two–layer network, effectively modeling complex switching dynamics with a conceptually straightforward framework. The network layers 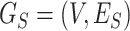 and
and 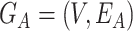 represent the two extreme cases among all possible
represent the two extreme cases among all possible 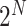 configurations. The network layer
configurations. The network layer 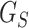 would be physical contact network if none of the nodes were alert, and the network layer
would be physical contact network if none of the nodes were alert, and the network layer 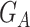 would be the physical contact network if none of the nodes were susceptible. Associated with network layers
would be the physical contact network if none of the nodes were susceptible. Associated with network layers 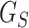 and
and 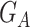 , we define the weighted adjacency matrices
, we define the weighted adjacency matrices 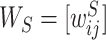 and
and 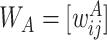 , respectively. The realized topology at a given time will be a mixture of the two network layers according to the collective node states at that time. Interestingly though, we show it is possible to characterize the behavior of the AC-SAIS model in terms of the spectral properties of
, respectively. The realized topology at a given time will be a mixture of the two network layers according to the collective node states at that time. Interestingly though, we show it is possible to characterize the behavior of the AC-SAIS model in terms of the spectral properties of 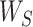 and
and 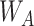 and their interrelation.
and their interrelation.
Remark. The actual, physical/social contact between the network agents is fundamentally different from those represented by the multilayer network 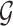 . For example, a directed edge
. For example, a directed edge 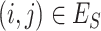 is physically relevant only if node
is physically relevant only if node 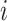 is susceptible and node
is susceptible and node  is infected. Otherwise, node
is infected. Otherwise, node  and
and  might have a different interaction if, for instance, both are susceptible. However, the later is not relevant for disease spreading and thus no need to be incorporated in our epidemic model. Take for instance the contact between node
might have a different interaction if, for instance, both are susceptible. However, the later is not relevant for disease spreading and thus no need to be incorporated in our epidemic model. Take for instance the contact between node  , who is a nurse, and node
, who is a nurse, and node  , who is a student. These two might not have any social contact in normal situation, however, when node
, who is a student. These two might not have any social contact in normal situation, however, when node 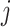 (the student) is sick, she can possibly pass infection to node
(the student) is sick, she can possibly pass infection to node 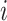 (the nurse); and this is the contact important for epidemic modeling purpose. Also, realize that this contact is directional because when the nurse is sick, she may not have a physical contact with the student. This is why in our state-dependent contact network formulation we do not make “undirectedness” assumption on the underlying graph.
(the nurse); and this is the contact important for epidemic modeling purpose. Also, realize that this contact is directional because when the nurse is sick, she may not have a physical contact with the student. This is why in our state-dependent contact network formulation we do not make “undirectedness” assumption on the underlying graph.
4.4. Mean-Field AC-SAIS Model
Similar to the networked SIS model described in Section 4.1, the collective state 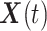 in the AC-SAIS model is a Markov process. However, this Markov process is both analytically and numerically intractable due to its exponential state space size of
in the AC-SAIS model is a Markov process. However, this Markov process is both analytically and numerically intractable due to its exponential state space size of 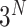 (each node can be in one of three states). We can leverage the observation that the AC-SAIS model falls in the GEMF class of stochastic spreading processes on multilayer networks—for which Sahneh et al. [68] have derived a system of nonlinear differential equations describing the evolution of state-occupancy probabilities after adopting a first-order, mean-field-type approximation.
(each node can be in one of three states). We can leverage the observation that the AC-SAIS model falls in the GEMF class of stochastic spreading processes on multilayer networks—for which Sahneh et al. [68] have derived a system of nonlinear differential equations describing the evolution of state-occupancy probabilities after adopting a first-order, mean-field-type approximation.
Following procedures explained in [68], we find the first order mean-field-type approximate model for the AC-SAIS model as
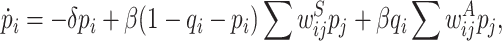 |
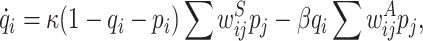 |
for 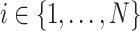 , where
, where 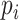 corresponds to the probability that individual
corresponds to the probability that individual 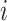 is infected, and
is infected, and 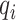 corresponds to the probability that she is alert.
corresponds to the probability that she is alert.
It is worthwhile to acknowledge the limitations of mean-field models. Statistical physics tells us that MF approximations function suitably for infinite-dimensional networks. While, they can perform very poorly for sparse or highly structured networks, such as rings or low-dimensional lattices, particularly close to critical model parameters. Despite, the approximation allows for investigating extremely complex dynamics, and discovering intriguing phenomena and key network characteristics influencing them.
5. Analysis of AC-SAIS Model
In this section, we compute and study the epidemic threshold of the mean-field AC-SAIS model in Eqs. ((2) and (3)) through analyzing its equilibrium points. Our motivation for this approach stems from the mean-field SIS model which exhibits a threshold phenomena in its equilibrium where a stable (see, [72], [73], [74]) endemic equilibrium emerges [39].
To facilitate the subsequent analysis, we make the following assumption on the structure of the default and adapted neighborhoods throughout this article.
Assumption 1. —
The edge sets
and
are such that the two-layer network
is M–connected according to Definition 5.
5.1. Mean-Field Epidemic Threshold Equation
Our approach to finding the critical value 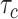 for AC-SAIS model (Eqs. (2) and (3)) is through examining the equilibrium points; as used by Van Mieghem for the SIS model in [39]. The idea is to show that for
for AC-SAIS model (Eqs. (2) and (3)) is through examining the equilibrium points; as used by Van Mieghem for the SIS model in [39]. The idea is to show that for 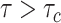 an endemic equilibrium (
an endemic equilibrium (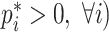 exists aside from the disease-free equilibrium.8 In this approach, strong connectivity of the underlying contact network is pivotal. In case of the SIS model, Van Mieghem [39] showed that if the contact graph is strongly connected, equilibriums of the mean-field model must either be all zero—the disease-free equilibrium—or they must be strictly positive—the endemic equilibrium. Following lemma shows that similar argument holds for the AC-SAIS model (Eqs. (2) and (3)) under the M–connectivity assumption of the multilayer network
exists aside from the disease-free equilibrium.8 In this approach, strong connectivity of the underlying contact network is pivotal. In case of the SIS model, Van Mieghem [39] showed that if the contact graph is strongly connected, equilibriums of the mean-field model must either be all zero—the disease-free equilibrium—or they must be strictly positive—the endemic equilibrium. Following lemma shows that similar argument holds for the AC-SAIS model (Eqs. (2) and (3)) under the M–connectivity assumption of the multilayer network 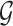 as in Definition 5.
as in Definition 5.
Lemma 4. —
Under Assumption 1, the equilibrium value of the infection probability
is either zero for all individuals, or strictly positive for all individuals. Moreover, a positive equilibrium satisfies
with effective infection rate
and relative alerting rate
respectively defined as9
Proof. —
Assume
. Letting
in Eq. (3) for any node
with
or
, yields
Therefore, according to Eq. (2), the equilibrium infection probabilities
satisfy
Replacing
from Eq. (5) in Eq. (6) yields the formula in Eq. (4).
The rest of the proof concerns choosing
deliberately, so that
guarantees
, and repeating the process until concluding positive equilibrium probabilities for all nodes. We employ the definition of graphs
associated with the multilayer network
as explained in Section 3.2. According to Definition 5, if
is M–connected, there exists
such that
is a strongly connected graph. Eq. (4) indicates that in order to get
, both
and
must be positive. Therefore, choosing
such that
(for which
and
) necessitates
. Repeating this process yields the equilibrium probability of all the nodes in the strongly connected component of
that contains
are all positive. This strongly connected component of
becomes a single hypernode, which we call
, for graph
. So far, we have proved that
. According to the definition of
, for graph
, there is a directed link from component
to component
, i.e.,
, if and only if
Since
, we get
for the above choice of
, which further indicates all the nodes of
have positive equilibrium values. As a result, all the nodes belonging to the strongly connected component of
that contains
have positive equilibrium values. This procedure can be repeated for
. Since,
is strongly connected, all the nodes of the network must have positive equilibrium values.
We can find the epidemic threshold by examining the equilibrium points in Eq. (4). For 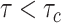 , the disease-free state is the only equilibrium. However, for
, the disease-free state is the only equilibrium. However, for 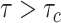 , another equilibrium point
, another equilibrium point 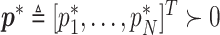 , also exists in the positive orthant. Therefore, we find the threshold value of
, also exists in the positive orthant. Therefore, we find the threshold value of 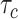 if we can find a critical value
if we can find a critical value 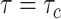 such that
such that 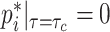 while
while 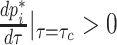 for all
for all 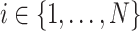 . We have the following theorem regarding the value of the epidemic threshold. We would like to emphasize that such a threshold corresponds to the mean-field approximate model (Eqs. (2) and (3)) and should not be confused as the actual threshold value in the exact AC-SAIS Markov model.
. We have the following theorem regarding the value of the epidemic threshold. We would like to emphasize that such a threshold corresponds to the mean-field approximate model (Eqs. (2) and (3)) and should not be confused as the actual threshold value in the exact AC-SAIS Markov model.
Theorem 6. —
The threshold value
for AC-SAIS model ((2) and (3)) is such that the equation
with
has a nontrivial solution
.
Proof. —
Eq. (4) can be rewritten as
Now, we take the limit of both sides as
, for which
for
according to the definition of an epidemic threshold. Since the limit of numerator and denominator of fraction terms of both sides goes to zero, we apply the L’Hôpital’s rule for limits [76]
Defining
, the above equation will lead to (8). The value of
that solves (8) is the critical value for which
, however,
, denoting a second-order phase transition at
. Therefore,
is the epidemic threshold for AC-SAIS model ((2) and (3)).
Letting 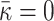 in Eq. (9) yields
in Eq. (9) yields 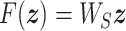 , which reduces Eq. (8) to the Perron Frobenius problem
, which reduces Eq. (8) to the Perron Frobenius problem 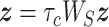 , suggesting
, suggesting 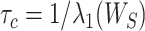 ; the SIS mean-field threshold. For the AC-SAIS model, the epidemic threshold condition pertains to the nonlinear Perron-Frobenius problem (8). Though an analytical solution is not expected, we can employ the tools of Section 3.1.
; the SIS mean-field threshold. For the AC-SAIS model, the epidemic threshold condition pertains to the nonlinear Perron-Frobenius problem (8). Though an analytical solution is not expected, we can employ the tools of Section 3.1.
In order to employ Theorem 6, we should prove our nonlinear map 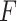 in Eq. (9) is homogeneous and concave, and it satisfies condition C2 defined in Definition 3. The map
in Eq. (9) is homogeneous and concave, and it satisfies condition C2 defined in Definition 3. The map 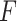 in Eq. (9) is defined for interior of the nonnegative cone. We extend the definition to the boundary of the nonnegative cone by letting
in Eq. (9) is defined for interior of the nonnegative cone. We extend the definition to the boundary of the nonnegative cone by letting 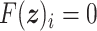 whenever
whenever  and
and 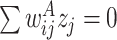 . In this way,
. In this way,  is well defined for all
is well defined for all  . It is obvious that
. It is obvious that 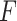 in Eq. (9) is a homogeneous map. Concavity of
in Eq. (9) is a homogeneous map. Concavity of 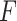 can be also deduced from the concavity of the function
can be also deduced from the concavity of the function 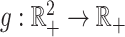 defined as
defined as 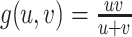 (which is half of the harmonic average) because the arguments of
(which is half of the harmonic average) because the arguments of 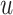 and
and 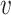 are linear transformation of
are linear transformation of 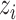 ’s. Next lemma proves that it also satisfies condition C2.
’s. Next lemma proves that it also satisfies condition C2.
Lemma 5. —
Function
, defined in Eq. (9), satisfies condition C2 if and only if the multilayer graph
is M–connected.
Proof. —
We just argued that
, as defined in Eq. (9), is homogeneous and concave. Also, for any set
,
if and only if there exists
and
for which
and
, i.e.,
and
. Therefore, Theorem 5 is applicable and proves the lemma.
Since we showed 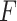 in Eq. (9) is homogeneous and concave, and satisfies condition C2, we can apply Theorem 4 to prove existence and uniqueness of a strictly positive solution for
in Eq. (9) is homogeneous and concave, and satisfies condition C2, we can apply Theorem 4 to prove existence and uniqueness of a strictly positive solution for 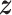 to the nonlinear Perron–Frobenius problem (8).
to the nonlinear Perron–Frobenius problem (8).
Corollary 1. —
If the multilayer graph
is M–connected, the nonlinear Perron–Frobenius problem (8) has a unique solution
with
. Furthermore, the following numerical update law will converge asymptotically to
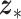
with
, and the initial state
and
. Moreover, the threshold value is
.
5.2. Possible Solutions to MF Epidemic Threshold
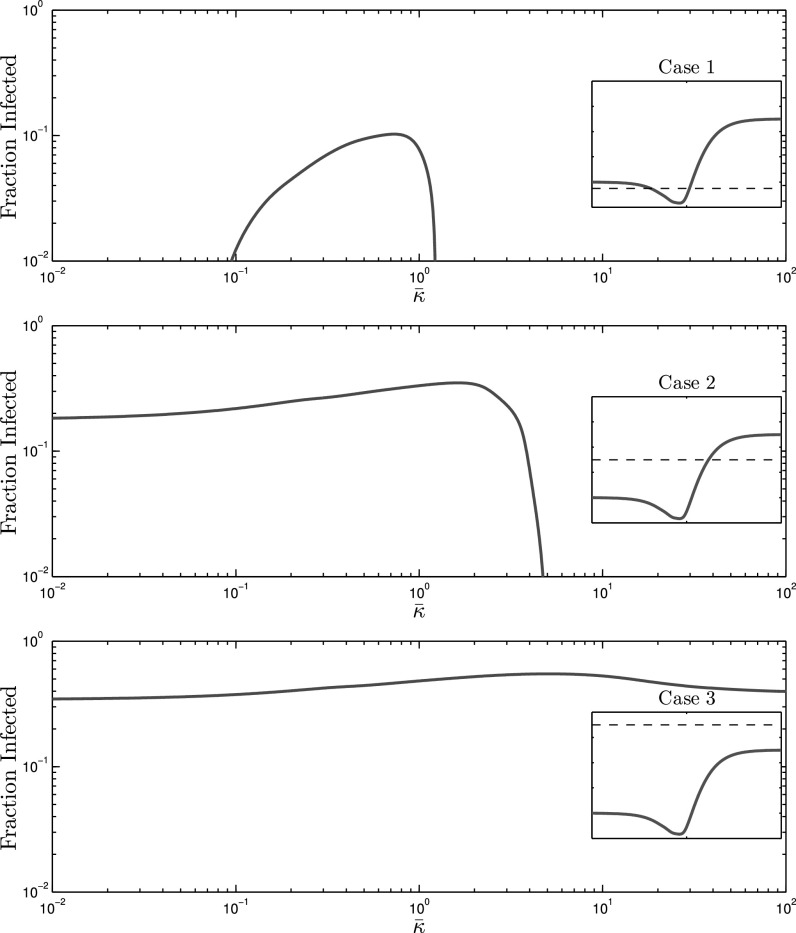
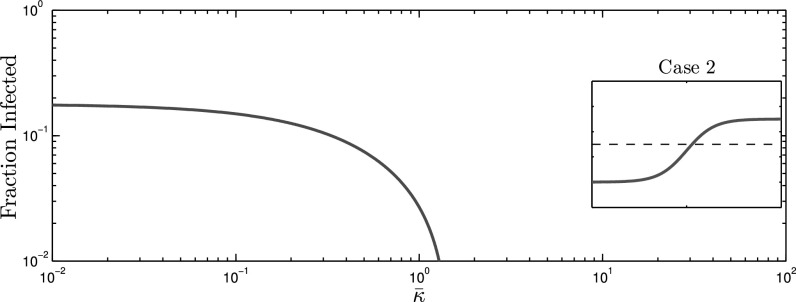
Corollary 1 proves the existence and uniqueness of a solution for the AC-SAIS threshold formula in Eq. (8). Furthermore, the update law of Eq. (10) suggests a numerical algorithm for finding the threshold value. Interestingly, a numerical experiment in the next section (see, Fig. 3) shows that the epidemic threshold value is a non-monotone function of contact adaptation rate (quantified by 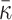 ); indicating faster contact adaptation is not necessarily always better in suppressing epidemics. Here, we aim to predict such scenarios without numerically solving the nonlinear Perron-Frobenius problem for the epidemic threshold.
); indicating faster contact adaptation is not necessarily always better in suppressing epidemics. Here, we aim to predict such scenarios without numerically solving the nonlinear Perron-Frobenius problem for the epidemic threshold.
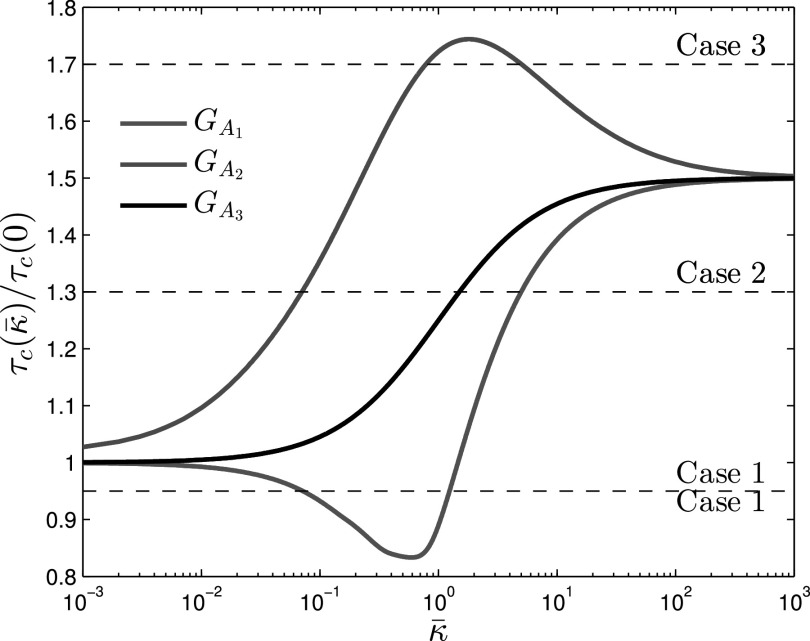
Fig. 3.
Normalized epidemic threshold 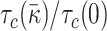 as a function of relative alerting rate
as a function of relative alerting rate 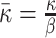 , showing three dependency scenarios. All three alert layers have the same spectral radius with respect to
, showing three dependency scenarios. All three alert layers have the same spectral radius with respect to 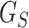 i.e.,
i.e., 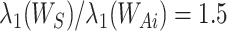 . Therefore, in all of them the threshold value
. Therefore, in all of them the threshold value 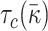 starts from
starts from 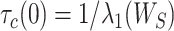 and converges to
and converges to 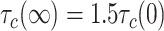 . Graph
. Graph 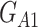 is synthesized such that
is synthesized such that 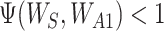 . From the red curve we can observe that
. From the red curve we can observe that 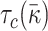 decreases for small
decreases for small 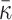 values after which it increases. Graph
values after which it increases. Graph 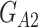 is synthesized such that
is synthesized such that 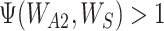 . In this case the blue curve
. In this case the blue curve 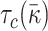 is maximal around
is maximal around 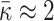 . The topology of graph
. The topology of graph 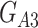 is
is 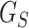 with reduced weights and is represented by the black epidemic threshold curve which increases monotonically by
with reduced weights and is represented by the black epidemic threshold curve which increases monotonically by 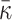 .
.
The idea is perturbing the threshold Eq. (8) around two extreme cases of 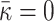 and
and 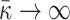 , for which we know the exact solutions. Specifically, 1) for
, for which we know the exact solutions. Specifically, 1) for 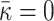 , the epidemic threshold is
, the epidemic threshold is 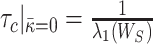 and
and 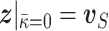 is a solution, where
is a solution, where 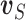 is the dominant eigenvector of matrix
is the dominant eigenvector of matrix 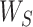 ; and 2) for
; and 2) for 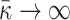 , the epidemic threshold is
, the epidemic threshold is 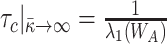 and
and 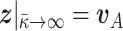 is a solution, where
is a solution, where 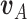 is the dominant eigenvector of matrix
is the dominant eigenvector of matrix 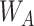 . Thus, employing spectral perturbation techniques, we can approximate the threshold value for small and large values of relative alerting rate
. Thus, employing spectral perturbation techniques, we can approximate the threshold value for small and large values of relative alerting rate 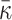 .
.
Theorem 7. —
The value of the epidemic threshold solving (8) has the forms
suitable for small values of
, and
suitable for large values of
, where
is
and
and
are the right and left dominant eigenvectors of
corresponding to
with
.
Fortunately, spectral perturbation of the nonlinear Perron-Frobenius problem (Eq. (8)) leads to analytically tractable formulas expressed in terms of spectral properties of individual layers 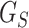 and
and 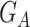 , and their interrelation (as manifested by
, and their interrelation (as manifested by 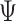 terms in Eqs. (11) and (12)). Using Eq. (11) for small values of
terms in Eqs. (11) and (12)). Using Eq. (11) for small values of 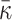 and Eq. (12) for large values of
and Eq. (12) for large values of 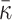 , we can categorize several solution possibilities for the full range of
, we can categorize several solution possibilities for the full range of 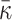 values.
values.
To reflect more realistic scenarios, we impose the constraint 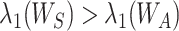 , that is, we assume that if all healthy individuals adopted their alert neighborhood simultaneously, they would collectively raise the epidemic threshold value, making their network more robust against epidemics than the default contact graph
, that is, we assume that if all healthy individuals adopted their alert neighborhood simultaneously, they would collectively raise the epidemic threshold value, making their network more robust against epidemics than the default contact graph 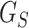 .
.
The three scenarios for the dependency of the threshold value on contact adaptation rate—as shown in Fig. 3—can be characterize as the following:
-
1)
Monotone scenario (the faster, the better): This is the simplest case where the value of the epidemic threshold increases monotonically with
 , as simulated in Section 6 and shown in Fig. 3 by the black curve. The monotone behavior happens if
, as simulated in Section 6 and shown in Fig. 3 by the black curve. The monotone behavior happens if 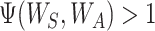 and
and 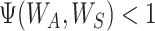 . Such monotonically increasing curve occurs, for instance, in contact-avoidance cases10 where
. Such monotonically increasing curve occurs, for instance, in contact-avoidance cases10 where 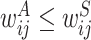 . In other words, if individuals only reduce contact with their neighbors upon becoming alert, the higher the rate they do so, the better; because the epidemic threshold increases with the alerting rate in this scenario.
. In other words, if individuals only reduce contact with their neighbors upon becoming alert, the higher the rate they do so, the better; because the epidemic threshold increases with the alerting rate in this scenario. -
2)
Overshooting scenario (moderate even better than fast): It is possible that an optimal alerting rate
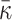 exists for which the adaptive network is most robust with respect to spreading infection. In other words, having a moderate contact adaptation rate is even better than than the case where the alerting rate is so large that alerting processes is almost instantaneous. The blue curve in Fig. 3 corresponds to this case. This scenario happens if
exists for which the adaptive network is most robust with respect to spreading infection. In other words, having a moderate contact adaptation rate is even better than than the case where the alerting rate is so large that alerting processes is almost instantaneous. The blue curve in Fig. 3 corresponds to this case. This scenario happens if 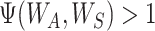 .
. -
3)
Undershooting scenario (adaptation goes wrong if slow): An interesting and important scenario is when
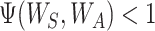 . In this case, the value of the epidemic threshold initially decreases as the value of
. In this case, the value of the epidemic threshold initially decreases as the value of 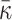 increases. If the switching rate is not fast enough, the alerting process can unintendedly worsen the infection spreading compared to keeping the default contacts! The red curve in Fig. 3 depicts such scenario.
increases. If the switching rate is not fast enough, the alerting process can unintendedly worsen the infection spreading compared to keeping the default contacts! The red curve in Fig. 3 depicts such scenario.
The following lemma shows that asymmetry of contacts is critical for observing the latter scenario.
Lemma 6. —
If
and
are both symmetric,
is lower-bounded as
Given 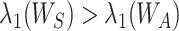 (the alert layer is more robust than the susceptible layer), the right hand side of Eq. (14) will be always greater than 1. Hence, for undirected network layers, it is impossible for the critical threshold of the adaptive contact network to go below the critical threshold of the default contacts layer,
(the alert layer is more robust than the susceptible layer), the right hand side of Eq. (14) will be always greater than 1. Hence, for undirected network layers, it is impossible for the critical threshold of the adaptive contact network to go below the critical threshold of the default contacts layer, 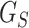 . We can conclude that asymmetry of contacts is in part responsible for this unexpected behavior.
. We can conclude that asymmetry of contacts is in part responsible for this unexpected behavior.
6. Numerical Experiments
In this section, we perform a numerical study to evaluate our findings. For 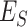 edges, we consider the well-known “Football” network from [77] with
edges, we consider the well-known “Football” network from [77] with 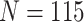 nodes and
nodes and 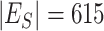 edges, and spectral radius
edges, and spectral radius 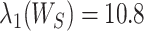 . Given
. Given  , we synthesize three adapted contact layers
, we synthesize three adapted contact layers 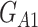 ,
, 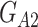 , and
, and 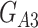 as described bellow, and compute their corresponding threshold values as a function of the relative alerting rate as shown in Fig. 3.
as described bellow, and compute their corresponding threshold values as a function of the relative alerting rate as shown in Fig. 3.
-
•
The spectral radii of
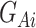 graphs are all equal to
graphs are all equal to  of the spectral radius of
of the spectral radius of 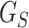 , i.e.,
, i.e., 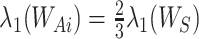 . In this way, we ensure that the adapted contacts layers are more robust to epidemic spreading compared to the default contacts layer. This can be verified in Fig. 3 where
. In this way, we ensure that the adapted contacts layers are more robust to epidemic spreading compared to the default contacts layer. This can be verified in Fig. 3 where 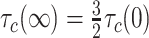 . Note that
. Note that 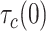 is the threshold value when
is the threshold value when 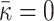 , i.e., no adaptation occurs, and
, i.e., no adaptation occurs, and  corresponds to
corresponds to 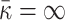 where the contact adaptation occurs instantaneously.
where the contact adaptation occurs instantaneously. -
•
For
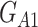 ,
, 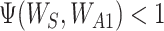 . From Eq. (11), we can predict that for small values of
. From Eq. (11), we can predict that for small values of 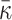 , the epidemic threshold decreases below
, the epidemic threshold decreases below 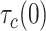 , the threshold if no contact adaptation was in place at all . Therefore, we expect an undershoot in
, the threshold if no contact adaptation was in place at all . Therefore, we expect an undershoot in 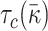 as a function of
as a function of 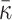 . This is the configuration where contact adaptation can “go wrong”; despite the fact that the alert contact network is more robust, switching to it can adversely aid in the spread of infection. The red curve in Fig. 3 corresponds to this scenario.
. This is the configuration where contact adaptation can “go wrong”; despite the fact that the alert contact network is more robust, switching to it can adversely aid in the spread of infection. The red curve in Fig. 3 corresponds to this scenario. -
•
For
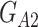 ,
, 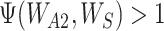 . From Eq. (12), we can predict it is possible to get
. From Eq. (12), we can predict it is possible to get 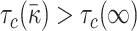 , an thus there is a value for
, an thus there is a value for 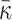 for which
for which 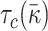 is maximum. This is in contrast to
is maximum. This is in contrast to 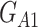 in that the epidemic threshold for the multilayer network is greater than its constituent layers. In this configuration, the characteristics are such that an enhanced robustness is created synergistically. The blue curve in Fig. 3 corresponds to this scenario.
in that the epidemic threshold for the multilayer network is greater than its constituent layers. In this configuration, the characteristics are such that an enhanced robustness is created synergistically. The blue curve in Fig. 3 corresponds to this scenario. -
•
Graph
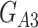 is made by decreasing the link weights from
is made by decreasing the link weights from  , representing a social-avoidance scenario. As discussed in Section 5.2, we expect to see a monotonic increase in the epidemic threshold as the contact adaptation rate increases. The black curve in Fig. 3 corresponds to this scenario.
, representing a social-avoidance scenario. As discussed in Section 5.2, we expect to see a monotonic increase in the epidemic threshold as the contact adaptation rate increases. The black curve in Fig. 3 corresponds to this scenario.
In order to synthesize 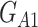 and
and 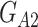 , we performed a greedy search to obtain desired values of
, we performed a greedy search to obtain desired values of  functions. For each alert contact graph,
functions. For each alert contact graph, 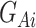 , and subsequent multilayer network representation,
, and subsequent multilayer network representation, 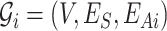 , we examine spreading behavior at three effective infection rates
, we examine spreading behavior at three effective infection rates  ,
, 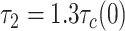 , and
, and 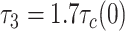 , as seen in Fig. 3 (dotted lines). In our numerical simulations, we have set
, as seen in Fig. 3 (dotted lines). In our numerical simulations, we have set 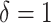 , which without loss of generality, chooses the unit of time equal to the expected curing period. Steady-state solutions to the mean-field AC-SAIS Eqs. (2) and (3) are calculated for
, which without loss of generality, chooses the unit of time equal to the expected curing period. Steady-state solutions to the mean-field AC-SAIS Eqs. (2) and (3) are calculated for 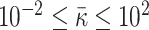 and fraction of population infected
and fraction of population infected 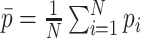 —as the indicator of severity of the spreading—is plotted as a function of the alerting rate in Figs. 4, 5, and 6.
—as the indicator of severity of the spreading—is plotted as a function of the alerting rate in Figs. 4, 5, and 6.
Fig. 4.
The effect of alerting rate on infection size for the undershooting scenario, for which the epidemic threshold dependence on 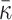 is depicted by the red curve in Fig. 3. Case 1 (top) Despite setting the effective infection rate below that of the extreme cases, i.e.,
is depicted by the red curve in Fig. 3. Case 1 (top) Despite setting the effective infection rate below that of the extreme cases, i.e., 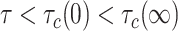 , an epidemic outbreak is still observed for small alerting rates because
, an epidemic outbreak is still observed for small alerting rates because  is larger than the minimum of
is larger than the minimum of 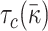 . case 2 (middle) Effective infection rate lies in between the two extreme values, i.e.,
. case 2 (middle) Effective infection rate lies in between the two extreme values, i.e., 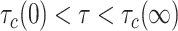 . There is a slight increase in infected individuals after which the infection size drops to 0 due to the increase in the critical threshold. Case 3 (bottom) Persistent infections are observed regardless of contact adaptation rate because
. There is a slight increase in infected individuals after which the infection size drops to 0 due to the increase in the critical threshold. Case 3 (bottom) Persistent infections are observed regardless of contact adaptation rate because 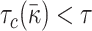 for all
for all  .
.
Fig. 5.
The effect of alerting rate on infection size for the overshooting scenario, for which the epidemic threshold dependence on 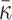 is depicted by the blue curve in Fig. 3. Case 1 This case is omitted since the infection size would be 0 regardless of the alerting rate. Case 2 (top) The behavior is similar to case 2 with
is depicted by the blue curve in Fig. 3. Case 1 This case is omitted since the infection size would be 0 regardless of the alerting rate. Case 2 (top) The behavior is similar to case 2 with 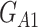 (middle graph in Fig. 4) though the transition to zero infection size occurs at a smaller alerting rate. Case 3 (bottom) This is a scenario when the effective infection rate is larger than the extreme values
(middle graph in Fig. 4) though the transition to zero infection size occurs at a smaller alerting rate. Case 3 (bottom) This is a scenario when the effective infection rate is larger than the extreme values 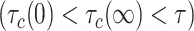 , yet it is less than the maximum of the threshold curve
, yet it is less than the maximum of the threshold curve 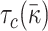 as seen by the blue curve in Fig. 3. A non-zero infection size is observed for small alerting rates, eventually
as seen by the blue curve in Fig. 3. A non-zero infection size is observed for small alerting rates, eventually 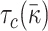 raises above
raises above 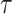 so that an epidemic cannot be sustained. As the threshold converges towards
so that an epidemic cannot be sustained. As the threshold converges towards 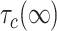 , an epidemic can once again persist, and the infection size even increases by the contact adaptation rate.
, an epidemic can once again persist, and the infection size even increases by the contact adaptation rate.
Fig. 6.
The effect of alerting rate on infection size for the monotone scenario, for which the epidemic threshold dependence on 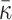 is depicted by the black curve in Fig. 3. Case 2 Similar to Sections 6.1 and 6.2, case 2 shows a transition between low and high alerting rates where epidemic outbreaks occur for the former and not the latter. Cases 1 and 3 are omitted for trivial behavior.
is depicted by the black curve in Fig. 3. Case 2 Similar to Sections 6.1 and 6.2, case 2 shows a transition between low and high alerting rates where epidemic outbreaks occur for the former and not the latter. Cases 1 and 3 are omitted for trivial behavior.
6.1. Adaptation Gone Wrong
For the multilayer network with 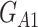 as the adaptive contact layer, we expect to observe increased epidemic sizes—due to a decreased threshold (red curve of Fig. 3)—for a range of low alerting rates.
as the adaptive contact layer, we expect to observe increased epidemic sizes—due to a decreased threshold (red curve of Fig. 3)—for a range of low alerting rates.
In Case 1, the infection rate is chosen so that 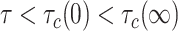 . In the top plot of Fig. 4, we can see that for most
. In the top plot of Fig. 4, we can see that for most 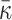 values there is no outbreak, as one would expect since the effective infection rate is below the either extreme values. However, for
values there is no outbreak, as one would expect since the effective infection rate is below the either extreme values. However, for 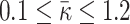 an epidemic is sustained due entirely to inter-layer dynamics creating conditions where an epidemic is more effectively carried throughout the population. In the context of persons altering who they come into contact with, although in an effort to avoid becoming infected, may in fact unintentionally contribute to the opposite outcome.
an epidemic is sustained due entirely to inter-layer dynamics creating conditions where an epidemic is more effectively carried throughout the population. In the context of persons altering who they come into contact with, although in an effort to avoid becoming infected, may in fact unintentionally contribute to the opposite outcome.
For Case 2, with 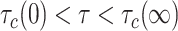 , we observe two regimes of behavior as depicted in the middle plot of Fig. 4: for lower alerting rates, where the effective infection rate is above the epidemic threshold
, we observe two regimes of behavior as depicted in the middle plot of Fig. 4: for lower alerting rates, where the effective infection rate is above the epidemic threshold  , an infection is sustained. For higher alerting rates the reverse is true since the critical threshold goes above
, an infection is sustained. For higher alerting rates the reverse is true since the critical threshold goes above 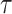 .
.
In Case 3, effective infection rate is set above the critical threshold (red curve of Fig. 3) for all values of 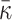 , i.e.,
, i.e., 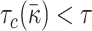 . Therefore, persistent infections are observed regardless of contact adaptation rate in bottom plot of Fig. 4.
. Therefore, persistent infections are observed regardless of contact adaptation rate in bottom plot of Fig. 4.
6.2. Enhanced Robustness
We perform the same computations on when the adapted contact layer is 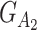 . Case 1 yields trivially zero infection size. For case 2, shown in the top plot of Fig. 5, we observe that increasing alerting rate beyond a certain value successfully suppresses the infection spreading. Case 3, shown in the bottom plot of Fig. 5, provides an interesting observation in that the critical threshold raises even larger than the alert contacts layer, indicating that a moderate rate of contact adaptation is indeed better than fast rates in enhancing the robustness of the network. Therefore, for
. Case 1 yields trivially zero infection size. For case 2, shown in the top plot of Fig. 5, we observe that increasing alerting rate beyond a certain value successfully suppresses the infection spreading. Case 3, shown in the bottom plot of Fig. 5, provides an interesting observation in that the critical threshold raises even larger than the alert contacts layer, indicating that a moderate rate of contact adaptation is indeed better than fast rates in enhancing the robustness of the network. Therefore, for 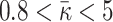 , the critical threshold increases such that no infection is sustained. While for larger values an outbreak occurs, and the infection size increases as contact adaptation rate increases.
, the critical threshold increases such that no infection is sustained. While for larger values an outbreak occurs, and the infection size increases as contact adaptation rate increases.
6.3. Monotonic Dependency
In the third scenario, the adapted contact layer is constructed by lowering the edge weights of 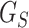 . This would correspond to a social distancing scenario, where individuals limit or abandon their contacts when they become alert. As can be seen by the black curve in Fig. 3, the threshold value increases monotonically by the alerting rate. Fig. 6 depicts the second case where
. This would correspond to a social distancing scenario, where individuals limit or abandon their contacts when they become alert. As can be seen by the black curve in Fig. 3, the threshold value increases monotonically by the alerting rate. Fig. 6 depicts the second case where 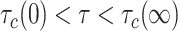 . As expected, there is a certain value of
. As expected, there is a certain value of 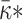 so that the epidemic infection is controlled for alerting rates
so that the epidemic infection is controlled for alerting rates 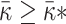 . Case 1 and 3 are omitted for trivial behavior.
. Case 1 and 3 are omitted for trivial behavior.
7. Discussions and Conclusion
The state-dependent switching (adaptive) contact network in the AC-SAIS model leads to rich dynamics for the epidemic spreading process and behavior not yet identified in literature (to the best of the authors’ knowledge). Intuitively, when nodes can “switch” to a neighborhood constituting a more robust network, the expected effect on the overall robustness of the network would be to increase monotonically with the alerting rate. As shown in Sections 6.2 and 6.1, this is not always the case. Indeed, we observed non-monotone dependency of the epidemic threshold in most of our experiment trials. We show how the adaptive switching topology of the contact network is different from fixed static graphs and can lead to regimes of extreme or unexpected behavior. In particular, it is possible that adaptive behavior towards a supposedly more resilient network can in fact worsen the severity of an outbreak, or enable the possibility where it did not exist before. On the other hand, it is possible to configure network layers such that the multilayer network is more robust than either individual layer.
It is noteworthy to mention that some results in the literature point to the observation that contact adaptation do not always aid suppressing the infection. For example, Meloni et al. [26] considered a self-initiated behavior where individuals change their mobility patterns. When travelers decide to avoid locations with high levels of infection and travel through locations with low levels of infections, this behavioral change may facilitate disease spreading because individuals effectively act as vectors of the disease transmission. It is very important to highlight the difference of the underlying mechanism between these formerly reported results and the “adaptation-gone-wrong” behavior in this paper. In our model, individuals who adapt their contacts (alerts) do not act as vectors for propagating the infection because they do not carry infection. This comes purely as a result of the adaptive behavior, signifying the importance of further analysis of state-dependent networks.
Finally, we would like to highlight several aspects of this study that go beyond the specific epidemic model considered in this paper. We developed a necessary and sufficient condition for existence and uniqueness of a positive eigenvector for homogeneous, concave maps. Furthermore, our utilization of multilayer networks to formulate dynamics on state-dependent switching networks is novel and can facilitate analysis of many networked dynamical systems. In our analysis, we come up with concepts that are genuine and novel to multilayer networks. Specifically, our analysis leads to 1) critical phenomena characterized by a nonlinear Perron Frobenius equation, and 2) the definition of M–connectivity. Our proposed concept of M–connectivity can easily scale to more than two layers. Furthermore, the joint descriptor  in Eq. (13) emphasizes the importance of joint descriptors when characterizing dynamics over multilayer networks. While network science has flourished in understanding intra-layer network topologies, intrinsic descriptors of inter-layer connectivity of multilayer networks are yet to be investigated.
in Eq. (13) emphasizes the importance of joint descriptors when characterizing dynamics over multilayer networks. While network science has flourished in understanding intra-layer network topologies, intrinsic descriptors of inter-layer connectivity of multilayer networks are yet to be investigated.
Acknowledgments
We are grateful to anonymous reviewers for their constructive feedback to improve this manuscript. We would like to thank Victor Preciado for inspiring conversations regarding use of the SAIS model in a contact adaptation context. Also, we would like to thank Heman Shakeri and Rad Niazadeh for their helpful discussions on the nonlinear Perron-Frobenius theory. This material is based on work supported by the US National Science Foundation under Grant No. CIF-1423411.
Biographies

Faryad Darabi Sahneh received the doctoral degree in electrical engineering from the Kansas State University, in 2014. In August 2014, he joined the ECE Department as a research assistant professor. Since July 2016, he has also been a visiting faculty in the School of Computing, Georgia Institute of Technology. His primary research is on the intersection of complex systems, network science, and control theory.

Aram Vajdi is working toward the PhD degree at Electrical and Computer Engineering Department, Kansas State University. His research is mainly focused on network inference and spreading processes.

Joshua Melander received the MS degree from Electrical and Computer Engineering Department, Kansas State University, in 2016. He researched interacting spreading processes on multilayer networks.

Caterina M. Scoglio received the DrEng degree from the “Sapienza” Rome University, Italy, in 1987. She is the Paslay chair professor of Electrical and Computer Engineering, Kansas State University. Before joining Kansas State University, she worked at the Fondazione Ugo Bordoni from 1987 to 2000, and at the Georgia Institute of Technology from 2000 to 2005. Her main research interests include the field of network science and engineering. She is also affiliated faculty member at the Institute of Computational Comparative Medicine (ICCM), Kansas State University.
Funding Statement
This material is based on work supported by the US National Science Foundation under Grant No. CIF-1423411.
Footnotes
Sometimes, this property is referred to as order-preserving.
This example is from [56].
In Krause [58], authors refer to this condition as being irreducible. We choose to avoid this term to avoid any confusion with other notions that tend to extend irreducibility of linear maps to nonlinear domain.
We got the inspiration for our definition of condition C2 for homogeneous, concave maps from a notion in [56] for homogeneous, monotone maps. Gaubert and Gunawardena [56] refer to the homogeneous, monotone map  as indecomposable if for any choice of
as indecomposable if for any choice of 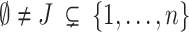 , there exists
, there exists 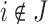 such that
such that 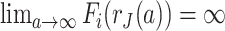 , where
, where 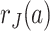 is defined as
is defined as 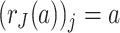 if
if 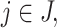 and
and 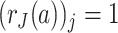 otherwise. While this may look very similar (or perhaps equivalent) to condition C2, we would like to point out a subtle difference which can be very consequential. Consider the function
otherwise. While this may look very similar (or perhaps equivalent) to condition C2, we would like to point out a subtle difference which can be very consequential. Consider the function 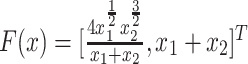 . This function is homogeneous, concave, and monotone. It does not satisfy condition C2 because for
. This function is homogeneous, concave, and monotone. It does not satisfy condition C2 because for 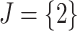 we get
we get 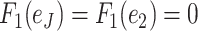 . However, it falls in the category of indecomposable maps of [56] because
. However, it falls in the category of indecomposable maps of [56] because 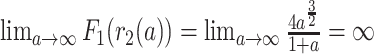 and
and 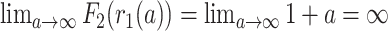 . The nonlinear eigenvalue problem for this function gives two eigenvectors in
. The nonlinear eigenvalue problem for this function gives two eigenvectors in  , namely,
, namely,  with
with 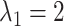 , and
, and 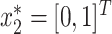 with
with 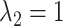 ; which is consistent with the fact that it does not satisfy condition C2.
; which is consistent with the fact that it does not satisfy condition C2.
In some literature, this may be referred to as a multiplex network.
We have been inspired by the notions of indecomposability for nonlinear maps and the method of aggregated graphs from Gaubert and Gunawardena [56, Sections 1.3 & 3.4].
Note that this is different from,  , which basically indicates that both individual layers
, which basically indicates that both individual layers 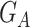 and
and 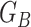 are strongly connected.
are strongly connected.
Note that 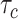 is the mean-field model threshold value which is a lower bound of the actual value in the exact stochastic SIS process.
is the mean-field model threshold value which is a lower bound of the actual value in the exact stochastic SIS process.
According to Poisson processes theory, the effective infection rate 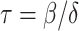 is equal to the expected number of attempts per link that an infected node makes to infect her neighbor during her infectious period [75]. The relative alerting rate
is equal to the expected number of attempts per link that an infected node makes to infect her neighbor during her infectious period [75]. The relative alerting rate 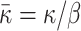 indicates the ratio of the chance that an infected neighbor cause her neighbor to become alert versus the causing her to become infected. For instance,
indicates the ratio of the chance that an infected neighbor cause her neighbor to become alert versus the causing her to become infected. For instance, 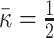 means the chance that a node becomes infected from her infected neighbor is twice the chance of becoming alert as the result of interacting with the same neighbor.
means the chance that a node becomes infected from her infected neighbor is twice the chance of becoming alert as the result of interacting with the same neighbor.
This is because having 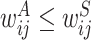 yields
yields 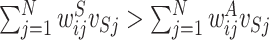 and
and 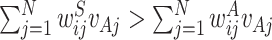 , which according to Eq. (13), leads to
, which according to Eq. (13), leads to 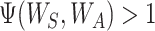 and
and 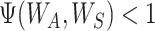 .
.
Contributor Information
Faryad Darabi Sahneh, Email: faryad@ksu.edu.
Aram Vajdi, Email: avajdi@ksu.edu.
Joshua Melander, Email: jmelander@ksu.edu.
Caterina M. Scoglio, Email: caterina@ksu.edu.
References
- [1].Hethcote H. W., “The mathematics of infectious diseases,” SIAM Rev., vol. 42, no. 4, pp. 599–653, 2000. [Google Scholar]
- [2].Keeling M. J. and Rohani P., Modeling Infectious Diseases in Humans and Animals. Princeton, NJ, USA: Princeton Univ. Press, 2008. [Google Scholar]
- [3].Anderson R. M., May R. M., and Anderson B., Infectious Diseases of Humans: Dynamics and Control, vol. 28 Hoboken, NJ, USA: Wiley, 1992. [Google Scholar]
- [4].Knight G. M., et al. , “Bridging the gap between evidence and policy for infectious diseases: How models can aid public health decision-making,” Int. J. Infectious Diseases, vol. 42, pp. 17–23, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Pastor-Satorras R., Castellano C., Van Mieghem P., and Vespignani A., “Epidemic processes in complex networks,” Rev. Modern Physics, vol. 87, no. 3, 2015, Art. no. . [Google Scholar]
- [6].Moran K. R., et al. , “Epidemic forecasting is messier than weather forecasting: The role of human behavior and internet data streams in epidemic forecast,” J. Infectious Diseases, vol. 214, no. suppl 4, pp. S404–S408, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Bish A. and Michie S., “Demographic and attitudinal determinants of protective behaviours during a pandemic: A review,” Brit. J. Health Psychology, vol. 15, no. 4, pp. 797–824, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Manfredi P. and d’Onofrio A., Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases. Berlin, Germany: Springer, 2013. [Google Scholar]
- [9].Funk S., Salathé M., and Jansen V. A., “Modelling the influence of human behaviour on the spread of infectious diseases: A review,” J. Roy. Soc. Interface, vol. 7, no. 50, pp. 1247–1256, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Verelst F., Willem L., and Beutels P., “Behavioural change models for infectious disease transmission: A systematic review (2010–2015),” J. Roy. Soc. Interface, vol. 13, no. 125, 2016, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wang Z., Andrews M. A., Wu Z.-X., Wang L., and Bauch C. T., “Coupled disease–behavior dynamics on complex networks: A review,” Physics Life Rev., vol. 15, pp. 1–29, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Chen F., “A susceptible-infected epidemic model with voluntary vaccinations,” J. Math. Biol., vol. 53, no. 2, pp. 253–272, 2006. [DOI] [PubMed] [Google Scholar]
- [13].Funk S., Gilad E., and Jansen V., “Endemic disease, awareness, and local behavioural response,” J. Theoretical Biol., vol. 264, no. 2, pp. 501–509, 2010. [DOI] [PubMed] [Google Scholar]
- [14].Funk S., Gilad E., Watkins C., and Jansen V., “The spread of awareness and its impact on epidemic outbreaks,” Proc. Nat. Academy Sci. United States America, vol. 106, no. 16, pp. 6872–6877, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Perra N., Balcan D., Gonasalves B., and Vespignani A., “Towards a characterization of behavior-disease models,” PLoS One, vol. 6, no. 8, Aug. 2011, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Poletti P., Caprile B., Ajelli M., Pugliese A., and Merler S., “Spontaneous behavioural changes in response to epidemics,” J. Theoretical Biol., vol. 260, no. 1, pp. 31–40, 2009. [DOI] [PubMed] [Google Scholar]
- [17].Sahneh F. and Scoglio C., “Epidemic spread in human networks,” in Proc. IEEE Conf. Decision Control, 2011, pp. 3008–3013. [Google Scholar]
- [18].Reluga T. C., “Game theory of social distancing in response to an epidemic,” PLoS Comput. Biol., vol. 6, no. 5, 2010, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Youssef M. and Scoglio C., “An individual-based approach to SIR epidemics in contact networks,” J. Theoretical Biol., vol. 283, no. 1, pp. 136–144, 2011. [DOI] [PubMed] [Google Scholar]
- [20].Gross T. and Blasius B., “Adaptive coevolutionary networks: A review,” J. Roy. Soc. Interface, vol. 5, no. 20, pp. 259–271, Mar. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Gross T., D’Lima C. J. D., and Blasius B., “Epidemic dynamics on an adaptive network,” Phys. Rev. Lett., vol. 96, no. 20, 2006, Art. no. . [DOI] [PubMed] [Google Scholar]
- [22].Marceau V., Noël P., Hébert-Dufresne L., Allard A., and Dubé L., “Adaptive networks: Coevolution of disease and topology,” Phys. Rev. E, vol. 82, no. 3, 2010, Art. no. . [DOI] [PubMed] [Google Scholar]
- [23].Risau-Gusmán S. and Zanette D., “Contact switching as a control strategy for epidemic outbreaks,” J. Theoretical Biol., vol. 257, no. 1, pp. 52–60, 2009. [DOI] [PubMed] [Google Scholar]
- [24].Demirel G., E. Barter, and Gross T., “Dynamics of epidemic diseases on a growing adaptive network,” Scientific Reports, vol. 7, Feb. 2017, Art. no. 42352. [DOI] [PMC free article] [PubMed]
- [25].Van Segbroeck S., Santos F. C., and Pacheco J. M., “Adaptive contact networks change effective disease infectiousness and dynamics,” PLoS Comput. Biol., vol. 6, no. 8, Aug. 2010, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Meloni S., Perra N., Arenas A., Gomez S., Moreno Y., and Vespignani A., “Modeling human mobility responses to the large-scale spreading of infectious diseases,” Sci. Rep., vol. 1, 2011, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Fenichel E. P., et al. , “Adaptive human behavior in epidemiological models,” Proc. Nat. Academy Sci. United States America, vol. 108, no. 15, pp. 6306–6311, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Liu M., Liz E., and RoÌĹst G., “Endemic bubbles generated by delayed behavioral response: Global stability and bifurcation switches in an SIS model,” SIAM J. Appl. Math., vol. 75, no. 1, pp. 75–91, 2015. [Google Scholar]
- [29].Brauer F., “A simple model for behaviour change in epidemics,” BMC Public Health, vol. 11, no. 1, 2011, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Li J., Zhao Y., and Zhu H., “Bifurcation of an SIS model with nonlinear contact rate,” J. Math. Anal. Appl., vol. 432, no. 2, pp. 1119–1138, 2015. [Google Scholar]
- [31].Morin B. R., Perrings C., Levin S., and Kinzig A., “Disease risk mitigation: The equivalence of two selective mixing strategies on aggregate contact patterns and resulting epidemic spread,” J. Theoretical Biol., vol. 363, pp. 262–270, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Xiao Y., Xu X., and Tang S., “Sliding mode control of outbreaks of emerging infectious diseases,” Bulletin Math. Biol., vol. 74, no. 10, pp. 2403–2422, 2012. [DOI] [PubMed] [Google Scholar]
- [33].Paarporn K., Eksin C., Weitz J. S., and Shamma J. S., “Epidemic spread over networks with agent awareness and social distancing,” in Proc. 53rd Annu. Allerton Conf. Commun. Control Comput., 2015, pp. 51–57. [Google Scholar]
- [34].Sahneh F. D., Chowdhury F. N., and Scoglio C. M., “On the existence of a threshold for preventive behavioral responses to suppress epidemic spreading,” Sci. Rep., vol. 2, 2012, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Misra A., Sharma A., and Singh V., “Effect of awareness programs in controlling the prevalence of an epidemic with time delay,” J. Biol. Syst., vol. 19, no. 02, pp. 389–402, 2011. [Google Scholar]
- [36].Samanta S., Rana S., Sharma A., Misra A., and Chattopadhyay J., “Effect of awareness programs by media on the epidemic outbreaks: A mathematical model,” Appl. Math. Comput., vol. 219, no. 12, pp. 6965–6977, 2013. [Google Scholar]
- [37].Misra A., Sharma A., and Shukla J., “Stability analysis and optimal control of an epidemic model with awareness programs by media,” Biosyst., vol. 138, pp. 53–62, 2015. [DOI] [PubMed] [Google Scholar]
- [38].Wang Q., Zhao L., Huang R., Yang Y., and Wu J., “Interaction of media and disease dynamics and its impact on emerging infection management,” Discr. Continuous Dynamical Syst.-Series B, vol. 20, no. 1, pp. 215–230, 2015. [Google Scholar]
- [39].Van Mieghem P., Omic J., and Kooij R., “Virus spread in networks,” IEEE/ACM Trans. Netw., vol. 17, no. 1, pp. 1–14, Feb. 2009. [Google Scholar]
- [40].Sahneh F. and Scoglio C., “Optimal information dissemination in epidemic networks,” in Proc. IEEE 51st Annu. Conf. Decision Control, Dec. 2012, pp. 1657–1662. [Google Scholar]
- [41].Bonacich P., “Some unique properties of eigenvector centrality,” Social Netw., vol. 29, no. 4, pp. 555–564, 2007. [Google Scholar]
- [42].Preciado V., Sahneh F., and Scoglio C., “A convex framework for optimal investment on disease awareness in social networks,” in Proc. Global Conf. Signal Inf. Process., Dec. 2013, pp. 851–854. [Google Scholar]
- [43].Shakeri H., Sahneh F. D., Scoglio C., Poggi-Corradini P., and Preciado V. M., “Optimal information dissemination strategy to promote preventive behaviours in multilayer epidemic networks,” Math. Biosci. Eng., vol. 12, no. 3, pp. 609–623, 2015. [DOI] [PubMed] [Google Scholar]
- [44].Juher D., Kiss I. Z., and Saldaña J., “Analysis of an epidemic model with awareness decay on regular random networks,” J. Theoretical Biol., vol. 365, pp. 457–468, 2015. [DOI] [PubMed] [Google Scholar]
- [45].Maharaj S. and Kleczkowski A., “Controlling epidemic spread by social distancing: Do it well or not at all,” BMC Public Health, vol. 12, no. 1, 2012, Art. no. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Kivela M., Arenas M. A., Barthelemy M., Gleeson J. P., Moreno Y., and Porter M. A., “Multilayer networks,” J. Complex Netw., vol. 2, no. 3, pp. 203–271, 2014. [Google Scholar]
- [47].Valdez L., Macri P. A., and Braunstein L. A., “Intermittent social distancing strategy for epidemic control,” Phys. Rev. E, vol. 85, no. 3, 2012, Art. no. . [DOI] [PubMed] [Google Scholar]
- [48].Guo D., Trajanovski S., van de Bovenkamp R., Wang H., and Van Mieghem P., “Epidemic threshold and topological structure of susceptible-infectious-susceptible epidemics in adaptive networks,” Phys. Rev. E, vol. 88, Oct. 2013, Art. no. . [DOI] [PubMed] [Google Scholar]
- [49].Juher D., Ripoll J., and Saldaña J., “Outbreak analysis of an SIS epidemic model with rewiring,” J. Math. Biol., vol. 67, pp. 411–432, 2013. [DOI] [PubMed] [Google Scholar]
- [50].Dong C., Yin Q., Liu W., Yan Z., and Shi T., “Can rewiring strategy control the epidemic spreading?” Physica A: Statistical Mech. Appl., vol. 438, pp. 169–177, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Ogura M. and Preciado V. M., “Epidemic processes over adaptive state-dependent networks,” Phys. Rev. E, vol. 93, no. 6, 2016, Art. no. . [DOI] [PubMed] [Google Scholar]
- [52].Ogura M. and Preciado V. M., “Disease spread over randomly switched large-scale networks,” in Proc. Amer. Control Conf., 2015, pp. 1782–1787. [Google Scholar]
- [53].Ogura M. and Preciado V. M., “Stability of spreading processes over time-varying large-scale networks,” IEEE Trans. Netw. Sci. Eng., vol. 3, no. 1, pp. 44–57, Jan.–Mar. 2016. [Google Scholar]
- [54].Van Mieghem P., Graph Spectra for Complex Networks. Cambridge, U.K.: Cambridge Univ. Press, 2010. [Google Scholar]
- [55].Krasnoselskij M. A., Positive Solutions of Operator Equations, Groningen, Netherlands: Noordhoff Publishers, 1964. [Google Scholar]
- [56].Gaubert S. and Gunawardena J., “The Perron-Frobenius theorem for homogeneous, monotone functions,” Trans. Amer. Math. Soc., vol. 356, no. 12, pp. 4931–4950, 2004. [Google Scholar]
- [57].Lemmens B. and Nussbaum R., Nonlinear Perron-Frobenius Theory. Cambridge, U.K.: Cambridge Univ. Press, 2012. [Google Scholar]
- [58].Krause U., “Concave perron–frobenius theory and applications,” Nonlinear Anal.: Theory Methods Appl., vol. 47, no. 3, pp. 1457–1466, 2001. [Google Scholar]
- [59].Nussbaum R. D. and Lunel S. M. V., Generalizations of the Perron-Frobenius Theorem for Nonlinear Maps. Providence, RI, USA: American Mathematical Soc., 1999. [Google Scholar]
- [60].Wood R. and O’Neill M., “An always convergent method for finding the spectral radius of an irreducible non-negative matrix,” ANZIAM J., vol. 45, pp. 474–485, 2004. [Google Scholar]
- [61].Boccaletti S., et al. , “The structure and dynamics of multilayer networks,” Physics Rep., vol. 544, no. 1, pp. 1–122, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].De Domenico M., et al. , “Mathematical formulation of multilayer networks,” Phys. Rev. X, vol. 3, no. 4, 2013, Art. no. . [Google Scholar]
- [63].Ganesh A., Massoulié L., and Towsley D., “The effect of network topology on the spread of epidemics,” in Proc. 24th Annu. Joint Conf. IEEE Comput. Commun. Societies, 2005, pp. 1455–1466. [Google Scholar]
- [64].Lloyd A. L. and May R. M., “How viruses spread among computers and people,” Sci., vol. 292, no. 5520, pp. 1316–1317, 2001. [DOI] [PubMed] [Google Scholar]
- [65].Neal P., “Endemic behaviour of SIS epidemics with general infectious period distributions,” Advances Appl. Probability, vol. 46, no. 1, pp. 241–255, 2014. [Google Scholar]
- [66].Van Mieghem P. and Van de Bovenkamp R., “Non-Markovian infection spread dramatically alters the susceptible-infected-susceptible epidemic threshold in networks,” Phys. Rev. Lett., vol. 110, no. 10, 2013, Art. no. . [DOI] [PubMed] [Google Scholar]
- [67].Cator E., Van de Bovenkamp R., and Van Mieghem P., “Susceptible-infected-susceptible epidemics on networks with general infection and cure times,” Phys. Rev. E, vol. 87, no. 6, 2013, Art. no. . [DOI] [PubMed] [Google Scholar]
- [68].Sahneh F. D., Scoglio C., and Van Mieghem P., “Generalized epidemic mean-field model for spreading processes over multilayer complex networks,” IEEE/ACM Trans. Netw., vol. 21, no. 5, pp. 1609–1620, Oct. 2013. [Google Scholar]
- [69].Gleeson J. P., Melnik S., Ward J. A., Porter M. A., and Mucha P. J., “Accuracy of mean-field theory for dynamics on real-world networks,” Phys. Rev. E, vol. 85, no. 2, 2012, Art. no. . [DOI] [PubMed] [Google Scholar]
- [70].Taylor M., Simon P. L., Green D. M., House T., and Kiss I. Z., “From Markovian to pairwise epidemic models and the performance of moment closure approximations,” J. Math. Biol., vol. 64, no. 6, pp. 1021–1042, 2012. [DOI] [PubMed] [Google Scholar]
- [71].Pastor-Satorras R., Castellano C., Van Mieghem P., and Vespignani A., “Epidemic processes in complex networks,” Rev. Modern Physics, vol. 87, no. 3, 2015, Art. no. . [Google Scholar]
- [72].Khanafer A., Basar T., and Gharesifard B., “Stability properties of infected networks with low curing rates,” in Proc. Amer. Control Conf., 2014, pp. 3579–3584. [Google Scholar]
- [73].Khanafer A., Başar T., and Gharesifard B., “Stability properties of infection diffusion dynamics over directed networks,” in Proc. IEEE 53rd Annu. Conf. Decision Control, 2014, pp. 6215–6220. [Google Scholar]
- [74].Bonaccorsi S., Ottaviano S., Mugnolo D., and Pellegrini F. D., “Epidemic outbreaks in networks with equitable or almost-equitable partitions,” SIAM J. Appl. Math., vol. 75, no. 6, pp. 2421–2443, 2015. [Google Scholar]
- [75].Van Mieghem P., Performance Analysis of Communications Networks and Systems. Cambridge, U.K.: Cambridge Univ. Press, 2009. [Google Scholar]
- [76].Rudin W., Principles of Mathematical Analysis, vol. 3 New York, NY, USA: McGraw-Hill, 1964. [Google Scholar]
- [77].Girvan M. and Newman M. E., “Community structure in social and biological networks,” Proc. Nat. Academy Sci. United States America, vol. 99, no. 12, pp. 7821–7826, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Sternberg S., Dynamical systems. North Chelmsford, MA, USA: Courier Corporation, 2010. [Google Scholar]