Abstract
Goal: Thermography-based infection screening at international airports plays an important role in the prevention of pandemics. However, studies show that thermography suffers from low sensitivity and specificity. To achieve higher screening accuracy, we developed a screening system based on the acquisition of multiple vital-signs. This multimodal approach increases accuracy, but introduces the need for sophisticated classification methods. This paper presents a comprehensive analysis of the multimodal approach to infection screening from a machine learning perspective. Methods: We conduct an empirical study applying six classification algorithms to measurements from the multimodal screening system and comparing their performance among each other, as well as to the performance of thermography. In addition, we provide an information theoretic view on the use of multiple vital-signs for infection screening. The classification methods are tested using the same clinical data, which has been analyzed in our previous study using linear discriminant analysis. A total of 92 subjects were recruited for influenza screening using the system, consisting of 57 inpatients diagnosed to have seasonal influenza and 35 healthy controls. Results: Our study revealed that the multimodal screening system reduces the misclassification rate by more than 50% compared to thermography. At the same time, none of the multimodal classifiers needed more than 6 ms for classification, which is negligible for practical purposes. Conclusion: Among the tested classifiers k-nearest neighbors, support vector machine and quadratic discriminant analysis achieved the highest cross-validated sensitivity score of 93%. Significance: Multimodal infection screening might be able to address the shortcomings of thermography.
Keywords: Classification, infection screening, machine learning, supervised learning
I. Introduction
In recent years, the outbreak of severe acute respiratory syndrome and other highly contagious diseases has highlighted the importance of rapid mass screening at international airport quarantines and places of mass gathering, like schools and hospitals, as a part of strategies for the prevention of pandemics. Currently, thermography is used for this purpose. However, studies have shown that this approach suffers from low sensitivity and specificity [1]. In addition, screening based on skin temperature alone can be insufficient for the detection of infected individuals, since it is affected by many factors, e.g., medication with antipyretics [2].
To address these problems, a novel multimodal infection screening system has been developed, which is based on the contactless acquisition of heart rate, respiration rate and facial temperature [3]–[5]. The inclusion of additional vital-signs leads to increased screening accuracy [3], but also introduces the need for more sophisticated classification methods. In contrast to traditional screening systems based solely on thermography, classification using simple thresholding is not applicable anymore.
The multimodal screening system has been tested with several classification algorithms in different application scenarios, including linear discriminant analysis (LDA) [6] and an unsupervised algorithm based on self-organizing maps with k-means clustering [3] . Classification via support vector machine has been tested on an improved version of the screening system designed for use in paediatric wards [7] and logistic regression-based classification has been tested in a study carried out in a hospital environment [8]. However, a comprehensive analysis of the information processing aspect in the context of multimodal infection screening has yet to be presented. To date, all studies evaluating the multimodal system have focused on the performance of different classification methods applied to different datasets and evaluated without cross validation.
While these studies contributed to a better understanding of the multivital-signs approach to infection screening, an important question remains open: How much performance does the multimodal system gain compared to the standard method of thermography?
In this paper, we analyze the multimodal infection screening system from a machine learning perspective. We compare the performance of six different classification algorithms on the task of classifying measurements of the new screening device into the two classes healthy and potentially infected. Based on the test results, we discuss the suitability of each algorithm for application in the multimodal screening device.
For the first time, we also perform a direct comparison between the multimodal screening system and thermography. The results indicate that the multimodal system reduces the misclassification rate by more than 50%. To gain additional insight, we present an information theoretic view on the problem by comparing the mutual information scores between the class labels and the different vital-sign readings. This analysis provides a possible explanation for the difference in performance between the multimodal screening system and thermography.
It is important to note that the idea behind any mass infection screening approach, including our system, is to screen for symptoms of a potential infection and not to provide a medical diagnosis. On the one hand, this means that although our system is tested on patients diagnosed with seasonal influenza, it will also pick up other diseases which cause similar symptoms, i.e., elevated heat rate, respiration rate, and body temperature. On the other hand, the system will not distinguish between different diseases.
The remainder of this paper is organized as follows: In Section II, we provide an overview on the hardware of the multimodal infection screening system, as well as on the dataset used. In addition, we provide a short summary of each classification algorithm included in our test. The performance of the multimodal screening system and the thermography reference are reported in Section III. Section IV presents an information theoretic analysis of the multimodal screening system. In Section V , we discuss the results of our analysis, as well as the limitations of this study. Finally, we close this paper with the conclusion in Section VI.
II. Methods and Material
A. Data Acquisition
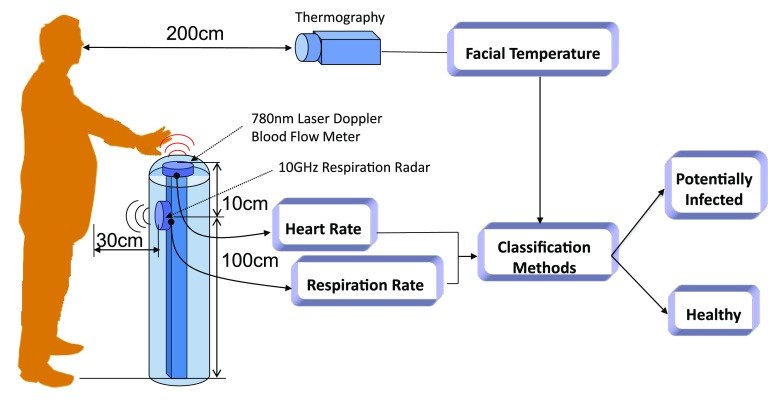
The technical details of the infection screening system are provided in our previous papers [9], [10]. The system automatically detects infected individuals within 15 s via a classification method using measured multiple vital-signs (see Fig. 1). Heart and respiration rates are determined using a noncontact laser Doppler blood-flow meter and a 10 GHz respiration radar, respectively. The facial temperature is measured via infrared thermography. As shown in Fig. 1, the heart and respiration rates and the facial temperature are measured simultaneously, while the subject holds his/her left palm over the system. The output signals of the laser Doppler blood-flow meter and the respiration radar are analyzed in real time. The heart and respiration rates are calculated by fast Fourier transform.
Fig. 1.
Schematic diagram of the multimodal infection screening system. The system acquires heart rate, respiration rate, and facial temperature readings and feeds them into a classifier, which classifies the measurement as potentially infected or healthy.
B. Subjects
We tested the classification methods using the same clinical data, which has been analyzed in our previous study using LDA [6]. A total of 92 subjects were recruited, consisting of 57 inpatients (49 male and 8 female, 19–40 years) diagnosed to have seasonal influenza using QuickVue Rapid SP Influ kits (Quidel Corporation, USA). These inpatients were treated with antiviral medications (i.e., oseltamivir or zanamivir), some of the inpatients’ body temperature dropped to normal. The 35 normal control subjects (30 male and 5 female, 20–35 years) were students at the Institute of Medical Radiology Technologists at the Japan Self-Defense Force Central Hospital. These normal control subjects had no symptoms of fever, headache, or sore throat.
The study was reviewed and approved by the Ethics Committee of the Japan Self-Defense Force Central Hospital.
C. Classification Algorithms
The algorithms considered in this study are: LDA and quadratic discriminant analysis (QDA), support vector machine (SVM), k-nearest neighbors (kNN), logistic regression (LR), and naive Bayes (NB) classifier.
In this section, we provide short introductions for each of these methods and comment on their strength and weaknesses in the context of the screening application. For all tested methods, we used the implementation provided by MATLAB's statistics toolbox.
In the following, we denote measurements with 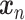 , which is a three-dimensional (3-D) vector containing the values for heart rate, respiration rate,
and facial temperature.
, which is a three-dimensional (3-D) vector containing the values for heart rate, respiration rate,
and facial temperature. 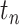 denotes ground
truth class labels, which can take on two values:
denotes ground
truth class labels, which can take on two values: 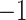 for healthy and
for healthy and 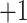 for infected. The subject index
for infected. The subject index 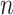 ranges from 1 to
ranges from 1 to 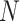 , where
, where 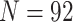 denotes the number of all
subjects.
denotes the number of all
subjects.
The symbol 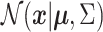 is used to denote that the random variable
is used to denote that the random variable 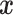 is distributed according to a multivariate
Gaussian distribution with mean
is distributed according to a multivariate
Gaussian distribution with mean 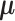 and covariance matrix
and covariance matrix 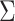 .
.
1). Discriminant Analysis
LDA is used in the original study [6], albeit without performing cross validation. Therefore, we included LDA in this paper and repeat the analysis with cross validation. In addition, we also investigate if QDA leads to better performance.
LDA and QDA assume that the class conditional distribution of the measurements is Gaussian:
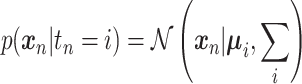 |
with 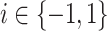 . While LDA assumes both covariance matrices to be equal (
. While LDA assumes both covariance matrices to be equal (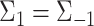 ), the covariances are allowed to be different in QDA.
Consequently, LDA's decision boundary is a hyperplane, while QDA has a quadratic decision boundary
[11]. Mean and covariances are learned from training data with known labels,
e.g., in maximum likelihood learning, the
), the covariances are allowed to be different in QDA.
Consequently, LDA's decision boundary is a hyperplane, while QDA has a quadratic decision boundary
[11]. Mean and covariances are learned from training data with known labels,
e.g., in maximum likelihood learning, the 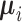 and
and 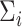 are
simply set to the empirical means and covariances of the training data of the respective classes
[11].
are
simply set to the empirical means and covariances of the training data of the respective classes
[11].
Once 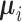 and
and 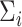 have been estimated, classifying a new measurement
have been estimated, classifying a new measurement
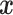 is based on the posterior class
probability, which can be obtained via Bayes rule
is based on the posterior class
probability, which can be obtained via Bayes rule
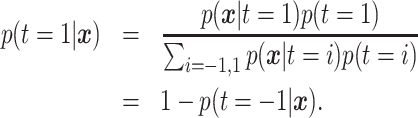 |
Here, 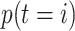 denotes
the prior probability of class
denotes
the prior probability of class 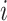 , which can
either be estimated from the fraction of training data with label
, which can
either be estimated from the fraction of training data with label 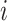 , or set by hand, if, e.g., the class proportions of the training data does not
reflect the prevalence.
, or set by hand, if, e.g., the class proportions of the training data does not
reflect the prevalence.
2). Support Vector Machine
The SVM falls into the category of sparse kernel methods. Sparse means that only a small portion of the training
data contributes to the classification process, while being a kernel method means that information from the
measurement enters only through a kernel function 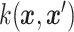 . The kernel function is a function that depends on two input
variables and returns a scalar output.
. The kernel function is a function that depends on two input
variables and returns a scalar output.
More precisely, a new observation 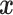 is classified by evaluating the function
is classified by evaluating the function
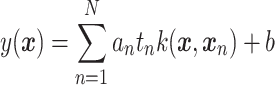 |
and making a decision based on the sign of 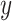 . The variables
. The variables 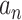 and
and 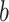 are parameters of the SVM, which are
learned from the training data
are parameters of the SVM, which are
learned from the training data 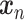 by solving a quadratic programming (QP) problem. The standard algorithm for solving the QP problem arising in SVM is
called sequential minimal optimization [12].
by solving a quadratic programming (QP) problem. The standard algorithm for solving the QP problem arising in SVM is
called sequential minimal optimization [12].
In the typical case, most of the 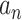 found
after solving the QP problem are equal to zero. This means that the corresponding training sample
found
after solving the QP problem are equal to zero. This means that the corresponding training sample 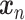 does not contribute to the classification
process, giving rise to the sparseness of SVM. A detailed description of SVM can be found in standard textbooks like
[11].
does not contribute to the classification
process, giving rise to the sparseness of SVM. A detailed description of SVM can be found in standard textbooks like
[11].
The SVM has two hyperparameters, which have to be fixed before optimization: the kernel width 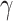 , which determines properties of the kernel function
, which determines properties of the kernel function
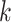 , and the so-called box constraint
, and the so-called box constraint
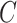 , which controls the tradeoff between
minimizing training errors and limiting model complexity. We choose the values of the
, which controls the tradeoff between
minimizing training errors and limiting model complexity. We choose the values of the 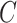 and
and 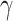 by minimizing the leave-one-out (LOO) error via grid search. This approach, however, is
susceptible to overfitting with respect to
by minimizing the leave-one-out (LOO) error via grid search. This approach, however, is
susceptible to overfitting with respect to 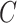 and
and 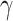 and we cannot cite the minimum LOO
error as the test performance of SVM.
and we cannot cite the minimum LOO
error as the test performance of SVM.
Therefore, we evaluate the performance of SVM using a nested cross-validation scheme: Using  samples, we calculate the LOO error for each
samples, we calculate the LOO error for each
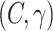 -pair on a 2-D grid and chose the
pair with the lowest LOO error. Then, we train the SVM with the chosen parameters on all
-pair on a 2-D grid and chose the
pair with the lowest LOO error. Then, we train the SVM with the chosen parameters on all  samples and test on the held out sample. This procedure is
repeated
samples and test on the held out sample. This procedure is
repeated 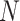 times, each time with a different
sample being held out.
times, each time with a different
sample being held out.
3). K-Nearest Neighbors
kNN is considered to be a nonparametric method and despite its simplicity, it often achieves good performance in
practice [11], [13]. One advantage
is that kNN does not require a training phase. Instead, a new measurement 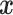 is assigned the label that holds the majority among the
is assigned the label that holds the majority among the 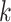 training data samples which are closest to
training data samples which are closest to 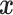 . However, this means that for classification,
the entire training set has to be stored and searched, which can be slow for large and high-dimensional training sets.
. However, this means that for classification,
the entire training set has to be stored and searched, which can be slow for large and high-dimensional training sets.
Distance between samples is often measured via Euclidean distance, but more sophisticated measures like Mahalanobis distances can also be used. In addition, preprocessing steps like, e.g., neighborhood components analysis (NCA) [14], which learns a custom Mahalanobis distance from the training data, can be applied to improve classification results. However, methods like NCA require a training phase.
Similar to SVM, there is a hyperparameter, the number of neighbors 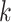 , which has to be optimized with cross validation. We use the same kind of nested
cross-validation procedure that was employed in the SVM case to optimize
, which has to be optimized with cross validation. We use the same kind of nested
cross-validation procedure that was employed in the SVM case to optimize 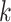 and avoid overfitting.
and avoid overfitting.
4). Logistic Regression
LR is a discriminative approach, where the logistic sigmoid function 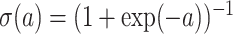 is applied to a linear function of the measurement.
The output is interpreted as posterior class probability
is applied to a linear function of the measurement.
The output is interpreted as posterior class probability
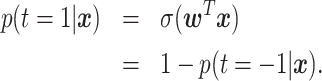 |
The vector 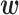 contains parameters, which can be learned from the training data using standard optimization methods
[11].
contains parameters, which can be learned from the training data using standard optimization methods
[11].
The advantage of LR is that the size of 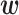 , which corresponds to the number of parameters of LR, grows linearly with the input dimensionality.
In contrast, the number of parameters in the LDA and QDA methods grows quadratic with the input dimensionality
[11]. This leads to increased training and classification speed for LR.
, which corresponds to the number of parameters of LR, grows linearly with the input dimensionality.
In contrast, the number of parameters in the LDA and QDA methods grows quadratic with the input dimensionality
[11]. This leads to increased training and classification speed for LR.
5). NB Classification
In NB class, conditional distributions for the inputs are assumed to be independent:
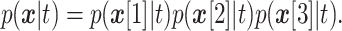 |
When learning the conditional distributions from data, the 1-D conditional distributions
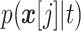 can be learned for each
dimension separately. This greatly simplifies the training process.
can be learned for each
dimension separately. This greatly simplifies the training process.
Applying Bayes law yields the posterior distribution [11]
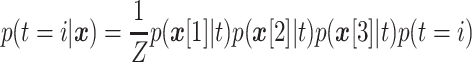 |
where 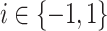 ,
, 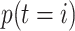 is the prior class
probability and the unknown constant
is the prior class
probability and the unknown constant 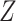 can be
obtained via normalization.
can be
obtained via normalization.
Although the independence assumption is rarely satisfied, NB performs surprisingly well in practice and is often applied to high-dimensional datasets with many features, where it holds an advantage due to the simplified training process. However, since our data has only three dimensions, we do not expect NB to outperform the other methods. We have included NB in this study mainly as a reference to compare the other methods against.
D. Reference Thermography
Since the multivital-signs screening system contains temperature as one of its modalities, it is possible to obtain thermography data by simply discarding the other modalities.
Thermography-based classification relies on simple thresholding instead of sophisticated classification algorithms. A temperature above the threshold is classified as infected and a temperature below the threshold is classified as healthy. Thus, the performance of thermography will depend on the choice of the temperature threshold.
In order to illustrate the performance of thermography, we calculated the receiver operating characteristic (ROC) curve [15], which plots the true positive rate against the false positive rate for a range of different thresholds. In addition, we calculated the area under the ROC curve (AUC), which acts as a summary statistic for the performance of the classifier [16] .
As a reference, we also provided the ROC curve for QDA and kNN classification, as well as AUC values for all classification methods tested with the multimodal infection screening system.
This approach favors the thermography only system, as cross validation is only performed for the multimodal classification. Also, it should be noted that for multimodal classifiers, the decision threshold is only one of several parameters. This means that for multimodal classifier, especially those with nonlinear decision surface like SVM or kNN, the ROC accounts for only one part of the variability of the system.
III. Classification Performance
Table I provides an overview of the classification results. The
upper half of the table presents the performance measures of the multimodal classifiers, which were obtained using LOO
cross validation or, in the case of SVM and kNN, nested cross validation. The results marked with LDA* and
QDA* were obtained by choosing uniform prior class probabilities: 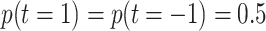 , instead of learning the prior from the
training data. This is done to test the robustness against misspecification of prior probabilities.
, instead of learning the prior from the
training data. This is done to test the robustness against misspecification of prior probabilities.
TABLE I.
Classification Results and Average Running Time
| Method | Error rate | Sensitivity | Specificity | Average training time | Average classification time | Area under curve |
|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [ms] | [ms] | [1] | |
| QDA | 9.8 | 93 | 85.7 | 34.9 | 3.9 | 0.95 |
| QDA* | 10.9 | 89.5 | 88.6 | – | – | – |
| LDA | 10.9 | 91.2 | 85.7 | 30.7 | 3.4 | 0.95 |
| LDA* | 13 | 86 | 88.6 | – | – | – |
| SVM | 9.8 | 93 | 85.7 | 15.4 | 0.7 | 0.9 |
| kNN | 10.9 | 93 | 82.9 | – | 6 | 0.93 |
| LR | 12 | 89.5 | 85.7 | 24.5 | 1.3 | 0.95 |
| NB | 14.1 | 89.5 | 80 | 7.3 | 1.4 | 0.95 |
| thermography | 0.79 | |||||
thr (32.6 (32.6  C) C) |
25 | 87.7 | 54.3 | – | – | – |
thr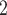 (33.1 (33.1  C) C) |
29.4 | 61.4 | 85.7 | – | – | – |
Average training time denotes the time needed on average to train the classifiers on 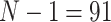 samples during the LOO scheme. Average classification
time denotes the time needed on average to classify the one held out sample. Computation was performed on a 3 GHz
Intel Xeon workstation. Note that there is no average training time for kNN, since kNN does not require a training
phase.
samples during the LOO scheme. Average classification
time denotes the time needed on average to classify the one held out sample. Computation was performed on a 3 GHz
Intel Xeon workstation. Note that there is no average training time for kNN, since kNN does not require a training
phase.
The average time needed for hyperparameter optimization was 32.5 s for kNN and 113 s for SVM. However, these times strongly depend on the size of the grid searched during optimization and are not meaningful by themselves.
The lower half of Table I, consisting of the last three lines,
reports the performance of the thermography reference for two exemplary temperature thresholds. thr was selected such that the thermography-based
classification would achieve a sensitivity comparable to that of the multimodal classifiers. However, this will lead
to a significantly lower specificity for thermography-based classification. On the other hand, thr
was selected such that the thermography-based
classification would achieve a sensitivity comparable to that of the multimodal classifiers. However, this will lead
to a significantly lower specificity for thermography-based classification. On the other hand, thr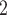 was selected such that the specificity score of the
thermography-based classification would match that of the multimodal classifiers. Now, we observe that the sensitivity
of the thermography-based classification drops below the level of the multimodal classifiers. Note that the
temperature thresholds in Table I seem very low because our device is
measuring the facial temperature, which is a few degrees lower than the body core temperature
[9].
was selected such that the specificity score of the
thermography-based classification would match that of the multimodal classifiers. Now, we observe that the sensitivity
of the thermography-based classification drops below the level of the multimodal classifiers. Note that the
temperature thresholds in Table I seem very low because our device is
measuring the facial temperature, which is a few degrees lower than the body core temperature
[9].
The last column in Table I reports AUC values for all classification methods, where the AUC values for the multimodal classifiers were obtained with LOO cross validation.
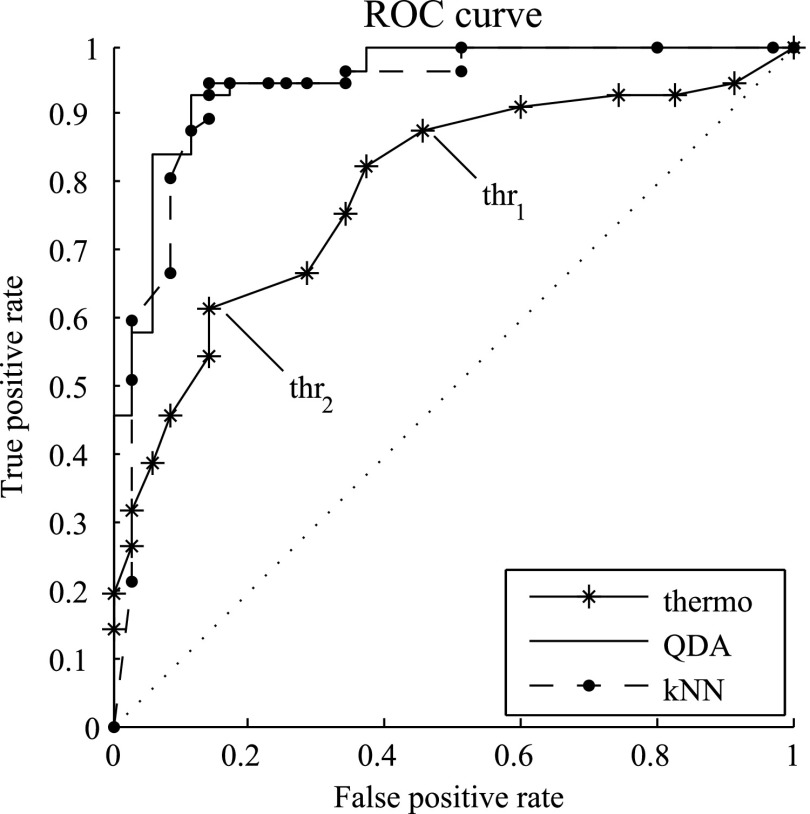
In addition, Fig. 2 shows the ROC curves for the thermography only
classification, as well as QDA and kNN. QDA and kNN were selected as representatives, since plotting ROC curves for
all multimodal classifiers would have cluttered the image. Additionally, Fig. 2
also shows the position of thr and
thr
and
thr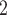 within the thermography ROC curve. The
lowest error rate achieved by thermography, using any of the thresholds, is 25%.
within the thermography ROC curve. The
lowest error rate achieved by thermography, using any of the thresholds, is 25%.
Fig. 2.
ROC plots for the thermography only classification, as well as QDA and kNN. The two exemplary facial
temperature thresholds listed in Table I are indicated by thr
 and thr
and thr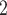 .
.
Since the performance estimates for the multimodal classifiers were obtained using cross validation, there is no unique set of parameters. Instead, we report the mean values for selected parameters for each of the classifiers in Table II. Note, however, that this serves only to provide the reader with a rough idea about the range of the parameters.
TABLE II.
Mean Value of Selected Parameters of the Multimodal Classifiers
| QDA | LDA | SVM |
|---|---|---|
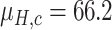 |
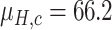 |
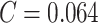 |
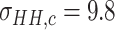 |
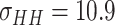 |
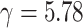 |
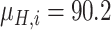 |
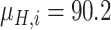 |
|
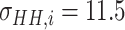 |
||
| NB | kNN | LR |
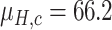 |
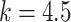 |
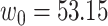 |
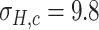 |
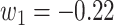 |
|
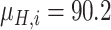 |
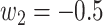 |
|
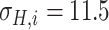 |
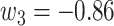 |
|
In order to supplement the information theoretic analysis presented in Section IV, we have conducted an additional experiment to assess the relative importance of the modalities. We selected one vital-sign, which was then removed from the data. The remaining bimodal input vectors were classified using QDA. This procedure was repeated for each of the vital-sings and the results are summarized in Table III. The increase in error rate provides an indicator for the importance of the left out modality.
TABLE III.
Performance of Bimodal Classification
| QDA | HR + RR | HR + FT | RR + FT |
|---|---|---|---|
| Error rate [%] | 9.8 | 10.9 | 22.8 |
| Sensitivity [%] | 93 | 91.2 | 79 |
| Specificity [%] | 85.7 | 85.7 | 74.3 |
IV. Information Theoretic Analysis
A. Mutual Information
In information theory, the concept of entropy is used to measure the information content of a random variable
[17]. For a (discrete) random variable 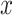 with distribution
with distribution 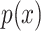 , it is defined as
, it is defined as
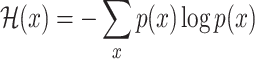 |
where 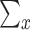 denotes summation over all possible values of
denotes summation over all possible values of 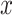 .
.
Closely related is the concept of mutual information, which measures the information content that one random
variable 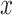 conveys about another random
variable
conveys about another random
variable 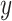 and vice versa. If
and vice versa. If 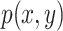 is the joint distribution of the two variables and
is the joint distribution of the two variables and
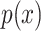 and
and 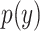 denote the marginal distribution of
denote the marginal distribution of 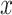 and
and 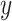 , respectively, the mutual information can be expressed as
, respectively, the mutual information can be expressed as
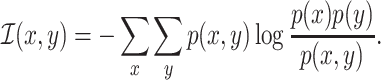 |
Furthermore, we have 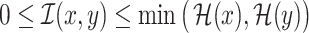 , with
, with 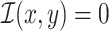 if
and only if
if
and only if 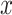 and
and 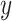 are independent [11]
, [17].
are independent [11]
, [17].
The unit of entropy and mutual information is “bit” when calculated using the logarithm to the base of
two and “nat” when calculated using the natural logarithm. Both units differ by a factor of
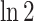 .
.
When performing a classification task, one would like to use inputs which convey as much information about the class labels as possible. Therefore, we used the data from our study to estimate the mutual information between class labels and the vital-signs acquired by the screening system.
The entropy of the class label estimated from our dataset is 0.96 bit, which is an upper bound on the mutual information. The entropy is lower than 1 because the number of patients and controls are not exactly balanced.
The marginal and joint probability distributions used to calculate the mutual information score are estimated via histograms, where the numerical values of each modality are quantized into a certain number of steps, also called bins. This method has the advantage of being simple and independent of any assumptions about the parametric form of the data's distribution [11].
On the other hand, the number of bins will affect the estimated distribution and, thus, also the mutual information score. The problem is that a very small number of bins will yield histograms which are too coarse to reflect the details of the distribution; while for very large number of bins, the number of samples is not enough to fill the bins, leading to noisy estimates of the distribution [11]. When using histograms, the aim should be to choose the number of quantization steps from an intermediate range [11], i.e., high enough to retain the details of the underlying distribution, but not much higher than the number of samples.
Taking the aforementioned points into account, we have calculated the mutual information score for several different numbers of bins chosen from an intermediate range. This allows us to check whether the conclusions drawn in Section V depend on the quantization.
Table IV contains two sets of mutual information estimates. In the first three rows, we report the mutual information between the class labels and each of the modalities, for three different numbers of bins. The lower half of Table IV contains estimates of the mutual information between the class label and the complete input vector containing all three modalities.
TABLE IV.
Mutual Information Between Class Labels and Vital-Signs
| # bins | heart rate | resp. rate | facial temp. | all modalities |
|---|---|---|---|---|
| [bit] | [bit] | [bit] | [bit] | |
| 24 | 0.58 | 0.34 | 0.39 | – |
| 32 | 0.63 | 0.32 | 0.44 | – |
| 40 | 0.67 | 0.36 | 0.45 | – |
8 (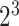 ) ) |
0.3 | 0.11 | 0.09 | 0.45 |
27 (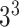 ) ) |
0.47 | 0.13 | 0.14 | 0.61 |
64 (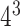 ) ) |
0.44 | 0.14 | 0.19 | 0.7 |
For the latter estimates, the input space has been quantized into a 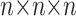 grid, where
grid, where 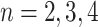 . As a reference, we have also provided the mutual information between the labels and the
single modality using the
. As a reference, we have also provided the mutual information between the labels and the
single modality using the 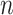 -step
quantization. However, it should be noted that both the 8-bin and 64-bin quantization are not well suited for our
dataset, since 8 bins corresponds to a very coarse binary quantization of each input dimension and 64 bins exceeds the
number of both controls (35) and patients (57) in our dataset.
-step
quantization. However, it should be noted that both the 8-bin and 64-bin quantization are not well suited for our
dataset, since 8 bins corresponds to a very coarse binary quantization of each input dimension and 64 bins exceeds the
number of both controls (35) and patients (57) in our dataset.
B. Mutual Information Versus Statistical Testing
As an alternative to the mutual information score, one could use statistical testing to assess if the vital-signs distribution of the patient group differs significantly from that of the healthy controls. For example, Welch's t-test can be used to test if the mean heart rate of patients is significantly higher than the mean heart rate of the control subjects, assuming both distributions are Gaussian. The output of a t-test is a so called p-value. If the p-value is smaller than a preselected threshold (typically 0.05), then the null hypothesis that the mean of both groups are equal can be rejected [18].
The t-test is a well-established method for testing for statistical significance. However, in our case, the aim is to assess which of the vital-signs is most suited for the classification task at hand. A low p-value signifies strong statistical evidence that the mean vital-signs readings of both groups are unequal, but it does not tell us directly how big the difference is, or if one modality is better suited for classification than the other.
For this reason, we prefer to compare the modalities on the basis of the mutual information scores, which offer a more intuitive interpretation and a direct answer to our question.
V. Discussion
A. Multimodal Screening Versus Thermography
The results in Table I show that classification based solely on
thermography suffers more heavily from the tradeoff between sensitivity and specificity than any of the multimodal
classifiers. When adjusting the threshold to match the sensitivity scores of the multimodal classifiers (thr
 ), the specificity score drops below the
level of the multimodal classifiers. Conversely, when adjusting the threshold to match specificity scores (thr
), the specificity score drops below the
level of the multimodal classifiers. Conversely, when adjusting the threshold to match specificity scores (thr
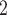 ), the sensitivity score drops.
), the sensitivity score drops.
The lowest error rate for thermography achieved with any threshold is 25%. However, unlike in the cases of the multimodal classifiers, the error rates reported for thermography are not cross validated. All multimodal classifiers, with the exception of NB, achieve cross-validated error rates, which are more than 50% lower than the minimum error rate of thermography. This shows that acquiring additional vital-signs beside temperature can significantly improve screening performance.
Training of the classifiers can be performed in advance and the time required for the classification process itself is negligible. Therefore, the only disadvantage of the multimodal approach lies in the increased cost and complexity of the hardware, compared to thermography only systems. However, with the decreasing cost of electronic components, this aspect will become less and less relevant. Also, the cost of the screening system itself has to be weighed against the cost saved due to the increased level of accuracy (e.g., less follow up examinations by quarantine personnel, less undetected infections, etc.).
B. Comparing the Classification Algorithms
Based on the classification speed, SVM is the fastest algorithm, due to being a sparse method, i.e., using only part of the training data. It also achieved the best performance. However, it has two free hyperparameters, which require a computationally expensive optimization procedure. More problematic than the complexity of hyperparameter optimization, which can be done offline, is the potential for overfitting associated with optimization. Thus, SVM is an appealing method, which requires careful training to avoid overfitting [11] .
QDA achieved good test results, but its performance depends on the prior probability, which is difficult to estimate. In reality, prior probabilities will be application dependent, e.g., at airport quarantines or in schools, the number of infected individuals is low and a reasonable choice for the prior would be the prevalence rate of infectious diseases in the general public. However, if the scanner is used in a hospital, a uniform prior might be more suitable.
Although LDA performed only slightly worse than QDA, the results show that LDA's performance is more sensitive to the choice of prior probabilities. Considering the increased accuracy of QDA and the fact that QDA is only slightly slower than LDA, QDA should be favored over LDA.
kNN performed surprisingly well, despite its simplicity. In fact, kNN achieved a sensitivity score, which is equal to the sensitivity of SVM and QDA. Applying more sophisticated preprocessing might further improve the performance. However, it is the slowest classifier, which could be problematic when making the transition to embedded hardware, combined with a much larger training dataset.
Since training and hyperparameter optimization can be performed in advance on workstations, the most important time to consider is the average classification time. Although, in practice, the classifier will be running on a slow embedded system, the classification times in our experiments were several magnitudes below the time needed for data acquisition, which is in the range of 10 s [9], [10]. Thus, the classification time can be considered as negligible for practical purposes. The only exception to this could be kNN because kNN's classification time grows linearly with the size of the training set, which might be significant larger in the actual application than in our study.
With three modalities per observation, the dimension of our dataset is low for typical machine learning applications. This also explains why simpler methods like NB and LR have no decisive advantage in speed over more complex methods like, e.g., LDA, which outperform them.
C. Mutual Information and Bimodal Classification
The result in Table IV indicates that the exact value of the mutual information depends on the number of bins. Nevertheless, we can observe a clear ordering of the modalities. Although body temperature is generally considered to be a good predictor of fever, the values in Table IV show that, for our dataset, the by far most informative single modality is heart rate, independent of the number of quantization steps. Facial temperature is only the second most informative modality, closely followed by respiration rate.
Comparing the values in the second half of Table IV reveal that the mutual information between label and temperature is smaller than the average mutual information per dimension when using all three modalities (e.g., 0.14 bit versus 0.2 bit for 27 bins). This observation also holds for all quantizations, and it explains the significant advantage in performance of the multivital-signs system compared to thermography.
A possible reason for this observation could be the fact that the patients in our study received treatment with antiviral medication. Thus, the use of fever reducing medication may lead to a reduction of the discriminative power of thermography. This is a scenario one might also encounter in mass screening applications and it has already been recognized as a potential shortcoming of thermography-based infection screening [2]. Multimodal screening might be a way to address this problem.
These findings are also supported by the results of the bimodal classification experiment given in Table III, which show that the exclusion of heart rate doubles the error rate. On the other hand, the exclusion of respiration rate or facial temperature did not affect the classification performance very much. Especially, the information conveyed by the respiration rate seems to be redundant.
A possible explanation is the difficulty of measuring respiration rate when the observation periods are very short. Given that the observation period is 15 s long [9], [10], it will most likely only contain two or three respiration cycles. Thus, respiration rate might be the noisiest modality among the three vital-sings acquired by the system.
D. Limitations of the Current Study
Our dataset contains a total of 92 subjects, which can be considered big for a medical study. However, it is small compared to typical datasets from the field of machine learning. This is a limiting factor to the accuracy of our tests.
In addition, the group of control subjects mainly consist of students, i.e., young male individuals. This introduces a certain bias to the measurements from the control group and also limits the variability of the dataset. A more realistic and, thus, more heterogeneous dataset would include patients suffering from noninfectious diseases in the control group, e.g., heart or respiratory diseases which could affect heart rate or respiratory rate.
The shortcomings of the current dataset mean that the absolute values of the performance measures reported here might be too optimistic. However, the main focus of this paper is the comparison of the performance of multimodal screening relative to thermography, as well as the comparison among the different classification algorithms which can be used with the multimodal system. In this context, the limitations of the dataset applies to all methods. In addition, our cross-validation scheme favors the results for thermography.
In order to address these limitations, we are planning to extend the current study to include a larger and more realistic dataset. We will try to recruit volunteers suffering from noninfectious diseases which affect heart or respiration rate, in order to test the robustness of the multimodal screening system. In addition, we are planning further tests of the multimodal system in different clinical settings.
VI. Conclusion
In this paper, we compared a multimodal infection screening system to screening via thermography, which is the current standard. We also compared different classification algorithms for use with the multimodal system. To our best knowledge, this is the first time when such an extensive comparison based on one common dataset has been presented. In addition, an information theoretic analysis has been carried out, which explained some of the observed results.
In this study, acquiring heart and respiration rate in addition to facial temperature allowed us to reduce the misclassification rate by more than 50%. In addition, the mutual information scores and the bimodal classification results indicate that the multiple vital-signs approach to infection screening could present a solution to the problem of identifying infected individuals who received treatment with antipyretics.
The comparison between the classification algorithms revealed that SVM and QDA are the two most promising classification methods for a multimodal screening device for infection screening. kNN can be considered as an alternative. Future studies with larger and more realistic subject population should focus on these three methods.
Biographies

Yu Yao received the Dipl.-Ing. degree in electrical engineering from RWTH Aachen University, Aachen, Germany, in 2010, and the Ph.D. degree in physics from the University of Wuppertal, Wuppertal, Germany, in 2015.
He is currently a Member of the team “Modeling and Algorithmics” at the Central Institute of Engineering, Electronics and Analytics–Electronic Systems, Research Centre Jülich, Jülich, Germany. His research interests include methods from the field of nonlinear dynamics and their application to biosignal processing.

Guanghao Sun (S’12-M’15) received the B.S. degree in medical engineering from Chiba University, Chiba, Japan, in 2011. He completed the Frontier Science Course supported by the Ministry of Education, Culture, Sports, Science and Technology in Japan, in 2011. He received the M.S. and Ph.D. degrees in system design engineering from Tokyo Metropolitan University, Tokyo, Japan, in 2013 and 2015, respectively.
From April 2013 to September 2015, he was a Research Fellow of the Japan Society for the Promotion of Science. In October 2015, he joined The University of Electro-Communications, Tokyo, as an Assistant Professor. His research interests include noncontact biomeasurement, medical device design, biomedical signal processing, and data mining.
Dr. Sun received the 2013 BES-SEC Design Silver Award for designing a multiple vital-signs-based infection screening system, and the 2014 Chinese Government Award for Outstanding Self-financed Student Abroad.

Takemi Matsui received the B.S. and M.S. degrees in physics from the University of Tsukuba, Tsukuba, Japan, in 1984 and 1986, respectively, and the Ph.D. degree in medicine from Saitama Medical School, Saitama, Japan, in 1995.
He proposed a variety of screening systems, including vital-signs-based noncontact infection screening system, and depression screening system by autonomic nerves monitoring. He joined the National Defense Medical College as a Faculty Member in 1997, and has been a Professor of medical engineering at Tokyo Metropolitan University, Tokyo, Japan, since 2005.

Yukiya Hakozaki received the Graduate degree from National Defense Medical College, Tokorozawa, Japan, in 1981, and the Ph.D. degree in medicine from Juntendo University, Tokyo, Japan, in 1986.
He was with Self-Defense Forces Central hospital for a long period of time. Since November 2014, he has been working as the Yokohama Director of a hospital. His subspecialty is gastroenterology in internal medicine, and he holds many medical specialists and advising doctors (for example, Society of Gastroenterology, Gastroenterological endoscopy, and ultrasonography). The latest research has announced the article of the relation of colorectal cancer and a lifestyle-related disease and special disaster and civil protection law in Japan.

Stefan van Waasen received the Diploma and Doctors degrees in electrical engineering from Gerhard-Mercator-University, Duisburg, Germany, in 1994 and 1999, respectively.
The topic of his doctoral thesis was optical receivers up to 60 Gb/s based on traveling wave amplifiers. In 1998, he joined Siemens Semiconductors/Infineon Technologies AG, Düsseldorf, Germany. His responsibility was BiCMOS and CMOS RF system development for highly integrated cordless systems like DECT and Bluetooth. In 2001, he changed into the IC development of front-end systems for high data rate optical communication systems. From 2004 to 2006, he was with the Stockholm Design Center responsible for the short-range analog, mixed-signal, and RF development for SoC CMOS solutions. In the period 2006 to 2010, he was responsible for the wireless RF system engineering in the area of SoC CMOS products at the headquarter in Munich, Germany, and later in the Design Center Duisburg, Duisburg. Since 2010, he has been the Director of the Central Institute of Engineering, Electronics and Analytics–Electronic Systems at Forschungszentrum Jülich GmbH, Jülich, Germany. In addition to the institute expertise for electronic system development for the research area, he is building up a new development team on SoC CMOS solutions for the experiment area.

Michael Schiek received the Diploma degree in physics and the Ph.D. degree, both from the Technical Rheinisch-Westfaelische Technische Hochschule, Aachen University, Aachen, Germany, in 1994 and 1998, respectively.
Since 1998, he has been a Scientific Assistant at the Research Center Jülich, Central Institute of Engineering, Electronics and Analytics–Electronic Systems, Jülich, Germany, where he is heading the team “Modeling and Algorythmics.” His current research interests include nonlinear time series analysis, modeling, and distributed sensor-actuator networks.
Funding Statement
This work was supported by the Tokyo Metropolitan Government Asian Human Resources Fund and the Japan Society for the Promotion of Science Research Fellowships for Young Scientists (13J05344).
References
- [1]. Bitar D. et al. , “International travels and fever screening during epidemics: A literature review on the effectiveness and potential use of non-contact infrared thermometers, ” Eurosurveillance, vol. 14, no. 6, pp. 1 –5, 2009. [PubMed] [Google Scholar]
- [2]. Nishiura H. and Kamiya K., “Fever screening during the influenza (H1N1-2009) pandemic at Narita international airport, Japan,” BMC Infectious Dis., vol. 11, no. 1, pp. 111–121, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Sun G. et al. , “A novel non-contact infection screening system based on self-organizing map with k-means clustering,” Commun. Comput. Inform. Sci., vol. 258, pp. 125–132, 2011. [Google Scholar]
- [4]. Sun G. et al. , “Development of an infection screening system for entry inspection at airport quarantine stations using ear temperature, heart and respiration rates,” in Proc. IEEE 35th Ann. Int. Conf. Eng. Med. Biol. Soc., 2013, pp. 6716 –6719. [DOI] [PubMed] [Google Scholar]
- [5]. Sun G. et al. , “Development of a stand-alone physiological monitoring system for noncontact heart and respiration rate measurements on real-time linux platform,” in The 15th International Conference on Biomedical Engineering, Goh J., Ed. New York, NY, USA: Springer-Verlag, vol. 43, pp. 649–651. [Google Scholar]
- [6]. Matsui T. et al. , “A novel screening method for influenza patients using a newly developed non-contact screening system,” J. Infection, vol. 60, no. 4, pp. 271–277, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Sun G. et al. , “A pediatric infection screening system with a radar respiration monitor for rapid detection of seasonal influenza among outpatient children,” J. Infectious Dis. Therapy, vol. 2, no. 5, pp. 1– 4, 2014. [Google Scholar]
- [8]. Nguyen V. Q. et al. , “Rapid screening for influenza using a multivariable logistic regression model to save labor at a clinic in Iwaki, Fukushima, Japan,” Amer. J. Infection Control, vol. 42, no. 5, pp. 551 –553, 2014. [DOI] [PubMed] [Google Scholar]
- [9]. Matsui T. et al. , “The development of a non-contact screening system for rapid medical inspection at a quarantine depot using a laser doppler blood-flow meter, microwave radar and infrared thermography,” J. Med. Eng. Technol., vol. 33, no. 6, pp. 481–487, 2009. [DOI] [PubMed] [Google Scholar]
- [10]. Sun G. et al. , “A portable screening system for onboard entry screening at international airports using a microwave radar, reflective photo sensor and thermography,” in Proc. 2nd Int. Conf. Instrum., Commun. Inform. Technol. Biomed. Eng., 2011, pp. 107–110. [Google Scholar]
- [11]. Bishop C., Pattern Recognition and Machine Learning (ser. Information Science and Statistics). Cambridge, MA, USA: Springer-Verlag, 2006. [Google Scholar]
- [12]. Platt J. C., “Fast training of support vector machines using sequential minimal optimization,” in Advances in Kernel Methods, Schölkopf B., Burges C. J. C., and Smola A. J., Eds. Cambridge, MA, USA: MIT Press, 1999, pp. 185–208. [Google Scholar]
- [13]. Altman N., “An introduction to kernel and nearest-neighbor nonparametric regression,” Amer. Statist., vol. 46, no. 3, pp. 175–185, 1992. [Google Scholar]
- [14]. Goldberger J. et al. , “Neighbourhood components analysis, ” in Advances in Neural Information Processing Systems 17. Cambridge, MA, USA: MIT Press, 2004, pp. 513 –520. [Google Scholar]
- [15]. Zweig M. H. and Campbell G., “Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine,” Clin. Chem., vol. 39, no. 4, pp. 561–577, 1993. [PubMed] [Google Scholar]
- [16]. Bradley A. P., “The use of the area under the ROC curve in the evaluation of machine learning algorithms,” Pattern Recog., vol. 30, no. 7, pp. 1145–1159, 1997. [Google Scholar]
- [17]. Shannon C. E., “A mathematical theory of communication,” Bell Syst. Tech. J., vol. 27, pp. 379–423, 1948. [Google Scholar]
- [18]. Privitera G., Statistics for the Behavioral Sciences. Thousand Oaks, CA, USA: SAGE, 2011. [Google Scholar]