Abstract
We study clockability for Ordinal Turing Machines (OTMs). In particular, we show that, in contrast to the situation for ITTMs, admissible ordinals can be OTM-clockable, that 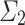 -admissible ordinals are never OTM-clockable and that gaps in the OTM-clockable ordinals are always started by admissible limits of admissible ordinals. This partially answers two questions in [3].
-admissible ordinals are never OTM-clockable and that gaps in the OTM-clockable ordinals are always started by admissible limits of admissible ordinals. This partially answers two questions in [3].
Introduction
In ordinal computability, “clockability” denotes the property of an ordinal that it is the halting time of some program. The term was introduced in [9], which was the paper that triggered the bulk of research in the area of ordinal computability by introducing Infinite Time Turing Machines (ITTMs).1 By now, a lot is known about clockability for ITTMs. To give a few examples: In [9], it was proved that there are gaps in the ITTM-clockable ordinals, i.e., there are ordinals  such that
such that  and
and 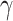 are ITTM-clockable, but
are ITTM-clockable, but 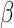 is not. Moreover, it is known that no admissible ordinal is ITTM-clockable (Hamkins and Lewis, [9]), that the first ordinal in a gap is always admissible (Welch, [14]), that the supremum
is not. Moreover, it is known that no admissible ordinal is ITTM-clockable (Hamkins and Lewis, [9]), that the first ordinal in a gap is always admissible (Welch, [14]), that the supremum  of the ITTM-writable ordinals (i.e. ordinals coded by a real number that is the output of some halting ITTM-computation) equals the supremum of the ITTM-clockable ordinals (Welch, [14]), that an ITTM-clockable
of the ITTM-writable ordinals (i.e. ordinals coded by a real number that is the output of some halting ITTM-computation) equals the supremum of the ITTM-clockable ordinals (Welch, [14]), that an ITTM-clockable  has a code that is ITTM-writable in
has a code that is ITTM-writable in  many steps (Welch, [14]) and that ITTM-writable ordinals have real codes that are ITTM-writable at the point the next clockable appears. Moreover, it is known that not every admissible below
many steps (Welch, [14]) and that ITTM-writable ordinals have real codes that are ITTM-writable at the point the next clockable appears. Moreover, it is known that not every admissible below 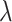 starts a gap, there are admissibles properly inside gaps, and occasionally many of them (Carl, Durand, Lafitte, Ouazzani, [6]). And indeed, clockability turned out to be a central topic in ordinal computability; it was, for example, crucial for Welch’s analysis of the computational strength of ITTMs.
starts a gap, there are admissibles properly inside gaps, and occasionally many of them (Carl, Durand, Lafitte, Ouazzani, [6]). And indeed, clockability turned out to be a central topic in ordinal computability; it was, for example, crucial for Welch’s analysis of the computational strength of ITTMs.
Besides ITTMs, clockability was also considered for Infinite Time Register Machines (ITRMs), where the picture turned out to be quite different: In particular, there are no gaps in the ITRM-clockable ordinals (see [5]), and in fact, the ITRM-clockable ordinals are exactly those below 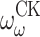 , which thus includes
, which thus includes 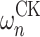 for every
for every 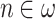 , i.e. the first
, i.e. the first  many admissible ordinals.
many admissible ordinals.
For other models, clockability received comparably little attention. This work arose out of a question of T. Kihara during the CTFM2 conference in 2019 in Wuhan who, after hearing that admissible ordinals are never ITTM-clockable, asked whether the same holds for OTMs. After most of the results of this paper had been proved, we found two questions in the report of the 2007 BIWOC (Bonn International Workshop on Ordinal Computability) [3] concering this topic: the first (p. 42, question 9), due to J. Reitz, was whether 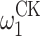 was OTM-clockable, the second, due to J. Hamkins, whether gap-starting ordinals for OTMs can be characterized as “something stronger” than being admissible. In [3], both are considered to be answered by the claim that no admissible ordinal is OTM-clockable, which is attributed to J. Reitz and S. Warner. Upon personal inquiry, Reitz told us that they had a sketch of a proof which, however, did not entirely work; what it does show with a few modifications, though, is that
was OTM-clockable, the second, due to J. Hamkins, whether gap-starting ordinals for OTMs can be characterized as “something stronger” than being admissible. In [3], both are considered to be answered by the claim that no admissible ordinal is OTM-clockable, which is attributed to J. Reitz and S. Warner. Upon personal inquiry, Reitz told us that they had a sketch of a proof which, however, did not entirely work; what it does show with a few modifications, though, is that  -admissible ordinals are not OTM-clockable, and the argument that Reitz sketched in personal correspondence to us in fact resembles the one of Theorem 6 below. We thus regard Reitz and Warner as the first discoverers of this theorem. Both the argument of Reitz and Warner from 2007 and the one we found during the CTFM in 2019 are adaptations of Welch’s argument that admissible ordinals are not ITTM-clockable.
-admissible ordinals are not OTM-clockable, and the argument that Reitz sketched in personal correspondence to us in fact resembles the one of Theorem 6 below. We thus regard Reitz and Warner as the first discoverers of this theorem. Both the argument of Reitz and Warner from 2007 and the one we found during the CTFM in 2019 are adaptations of Welch’s argument that admissible ordinals are not ITTM-clockable.
The statement actually made in [3], is, however, false: As we will show below, 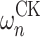 is OTM-clockable for any
is OTM-clockable for any 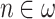 . Thus, there are plenty of admissible ordinals that are OTM-clockable, and the answer to the first question is positive. The idea is to use the ITRM-clockability of these ordinals, which follows from Lemma 3 in [5], together with a slightly modified version of the obvious procedure for simulating ITRMs on OTMs. This actually shows that
. Thus, there are plenty of admissible ordinals that are OTM-clockable, and the answer to the first question is positive. The idea is to use the ITRM-clockability of these ordinals, which follows from Lemma 3 in [5], together with a slightly modified version of the obvious procedure for simulating ITRMs on OTMs. This actually shows that  is clockable on an ITTM with tape length
is clockable on an ITTM with tape length 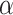 as soon as
as soon as 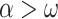 . Thus, the strong connection between admissibility and clockability seems to depend rather strongly on the details of the ITTM-architecture. We remark that this is a good example of how the studies of different models of infinitary computability can fruitfully interact: At least for us, it would not have been possible to find this result while only focusing on OTMs.
. Thus, the strong connection between admissibility and clockability seems to depend rather strongly on the details of the ITTM-architecture. We remark that this is a good example of how the studies of different models of infinitary computability can fruitfully interact: At least for us, it would not have been possible to find this result while only focusing on OTMs.
Moreover, we will answer the second question in the positive as well by showing that, if 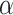 starts a gap in the OTM-clockable ordinals, then
starts a gap in the OTM-clockable ordinals, then 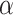 is an admissible limit of admissible ordinals.3
is an admissible limit of admissible ordinals.3
Of course, the gap between “admissible limit of admissible ordinals” and “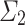 -admissible” is quite wide. In particular, we do not know whether every gap starting ordinal for OTMs is
-admissible” is quite wide. In particular, we do not know whether every gap starting ordinal for OTMs is 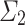 -admissible, though we conjecture this to be false.
-admissible, though we conjecture this to be false.
Ordinal Turing Machines
Ordinal Turing Machines (OTMs) were introduced by Koepke in [10] as a kind of “symmetrization” of ITTMs: Instead of having a tape of length 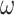 and the whole class of ordinals as their working time, OTMs have a tape of proper class length
and the whole class of ordinals as their working time, OTMs have a tape of proper class length 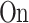 while retaining
while retaining 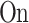 as their “working time” structure. We refer to [10] for details.
as their “working time” structure. We refer to [10] for details.
In contrast to Koepke’s definition but in closer analogy with the setup of ITTMs, we allow finitely many tapes instead of a single one. Each tape has a head, and the heads move independently of each other; the program for such an OTM is simply a program for a (finite) multihead Turing machine. At limite times, the inner state (which is coded by a natural number), the cell contents and the head positions are all determined as the inferior limits of the sequences of the respective earlier values. At successor steps, an OTM-program is carried out as if on a finite Turing machine with the addition that, when a head is moved to the left from a limit posistion, it is reset to the start of the tape. Though models of ordinal computability generally enjoy a good degree of stability under such variations as far as computational strength is concerned, this often makes a difference when it comes to clockability. Intuitively, simulating several tapes with separate read-write-heads on a single tape requires one to check the various head positions to determine whether the simulated machine has halted, which leads to a delay in halting. For ITTMs, this is e.g. demonstrated in [13]. For OTMs, insisting on a single tape would lead to a theory that is “morally” the same as the one described here, but make the results much less compelling and the proofs more technically involved and harder to follow.4 Thus, allowing multiple tapes seems to be a good idea.
An important property of OTMs that will be used below is the existence of an OTM-program P that ‘enumerates L’; in particular, P will write (a code for) the constructible level 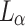 on the tape in
on the tape in 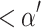 many steps, where
many steps, where 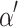 is the smallest exponentially closed ordinal
is the smallest exponentially closed ordinal 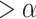 (this notation will be used throughout the paper).
(this notation will be used throughout the paper).
The following picture of OTM-computations may be useful to some readers: Let us imagine the tape split into 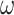 -blocks. Then an OTM-computation proceeds like this: The head works for a bit in one
-blocks. Then an OTM-computation proceeds like this: The head works for a bit in one 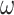 -block, then leaves it to the right, works for a bit in the new
-block, then leaves it to the right, works for a bit in the new 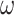 -portion, again leaves it to the right and so on, until eventually the computation either halts or the head is moved back from a limit position, i.e., goes back to 0 and starts over. Thus, if one imagines an
-portion, again leaves it to the right and so on, until eventually the computation either halts or the head is moved back from a limit position, i.e., goes back to 0 and starts over. Thus, if one imagines an 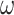 -portion as single point, then the head moves from left to right, jumps back to 0, moves right again etc. Moreover, in each
-portion as single point, then the head moves from left to right, jumps back to 0, moves right again etc. Moreover, in each 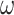 -portion, we have a classical ITTM-computation (up to the limit rules for the head position and the inner state, which make little difference).
-portion, we have a classical ITTM-computation (up to the limit rules for the head position and the inner state, which make little difference).
We fix some terminology for the rest of this paper.
Definition 1
If M is one of ITRM, ITTM or OTM and  is an ordinal, then
is an ordinal, then 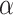 is called M-clockable if and only if there is an M-program that halts at time
is called M-clockable if and only if there is an M-program that halts at time  .5
.5
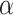 is called M-writable if and only if there is a real number coding
is called M-writable if and only if there is a real number coding 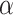 that is M-computable. An M-clockable gap is an interval
that is M-computable. An M-clockable gap is an interval  of ordinals such that
of ordinals such that  , no element of
, no element of  is M-clockable and
is M-clockable and  is maximal in the sense that there are cofinally many M-clockable ordinals below
is maximal in the sense that there are cofinally many M-clockable ordinals below 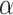 and
and  is M-clockable. In this case, we say that
is M-clockable. In this case, we say that  “starts” the gap and call
“starts” the gap and call  a “gap starting ordinal” or “gap starter” for M.
a “gap starting ordinal” or “gap starter” for M.
Basic Observations
We start with some useful observations that can mostly be obtained by easy adaptations of the corresponding results about ITTM-clockability.
We start by noting that the analogue of the speedup-theorem for ITTMs from [9] holds for multitape-OTMs. This is proved by an adaptation of the argument for the speedup-theorems for ITTMs. The main difference is that, in contrast to ITTMs, OTMs do not have their head on position 0 at every limit time and that the head may make long “jumps” when moved to the left from a limit position. This generates a few extra complications.
To simplify the proof, we start by building up a few preliminaries.
For the ITTM-speedup, the following compactnes property is used: If P halts in  many steps and the head is located at position k at time
many steps and the head is located at position k at time  , then only the n cells contents before and after the kth one at time
, then only the n cells contents before and after the kth one at time  are relevant for this. Now, this is a fixed string s of 2n bits. In [9], a construction is described that achieves that the information whether these 2n cells currently contain s at a limit time
are relevant for this. Now, this is a fixed string s of 2n bits. In [9], a construction is described that achieves that the information whether these 2n cells currently contain s at a limit time 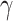 is coded on some extra tapes at time
is coded on some extra tapes at time 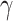 . Due to the special limit rules for ITTMs that set the head back to position 0 at every limit time, the Hamkins-Lewis-proof has this information stored at the initial tape cells, but the construction is easily modified to store the respective information on any other tape position.
. Due to the special limit rules for ITTMs that set the head back to position 0 at every limit time, the Hamkins-Lewis-proof has this information stored at the initial tape cells, but the construction is easily modified to store the respective information on any other tape position.
We will use it in the following way: Suppose that P is an OTM-program that halts at time 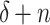 , where
, where 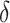 is a limit ordinal and
is a limit ordinal and 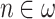 . We want to “speed up” P by n steps, i.e. to come up with a program Q that halts in
. We want to “speed up” P by n steps, i.e. to come up with a program Q that halts in  many steps. Suppose that P halts with the head on position
many steps. Suppose that P halts with the head on position 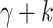 , where
, where  is a limit ordinal and
is a limit ordinal and  . Let m be
. Let m be 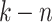 if
if 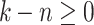 and 0, otherwise, and let s be the bit string present on positions
and 0, otherwise, and let s be the bit string present on positions 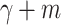 until
until  at time
at time 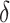 . Then we use the Hamkins-Lewis-construction to ensure that the information whether the bit string present on positions
. Then we use the Hamkins-Lewis-construction to ensure that the information whether the bit string present on positions 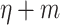 until
until  is equal to s on the
is equal to s on the 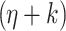 th cells of three extra tapes, for each limit ordinal
th cells of three extra tapes, for each limit ordinal  .
.
An extra complication arises from the possibility of a “setback”: Within the n steps from time 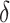 to time
to time 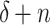 , it may happen that the head is moved left from position
, it may happen that the head is moved left from position  , thus ending up at the start of the tape. Clearly, it will then take
, thus ending up at the start of the tape. Clearly, it will then take 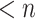 many further steps at the start of the tape and only consider the first n bits during this time. However, we need to know what these bits are - or rather, whether they are the “right ones”, i.e., the ones present at time
many further steps at the start of the tape and only consider the first n bits during this time. However, we need to know what these bits are - or rather, whether they are the “right ones”, i.e., the ones present at time  - while our head is located at position
- while our head is located at position 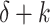 . The idea is then to store this information in the inner state of the sped-up program. We thus create extra states: The new state 2i will represent the old state i together with the information that the first n bits were the “right ones” (i.e. the same ones as at time
. The idea is then to store this information in the inner state of the sped-up program. We thus create extra states: The new state 2i will represent the old state i together with the information that the first n bits were the “right ones” (i.e. the same ones as at time  ) and
) and 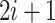 will represent the old state i together with the information that some of these bits deviated from those at time
will represent the old state i together with the information that some of these bits deviated from those at time  . To achieve this, we use an extra tape
. To achieve this, we use an extra tape  . At the start of Q, a 1 is written to each of the first n cells of
. At the start of Q, a 1 is written to each of the first n cells of  ; after that, the head on
; after that, the head on 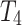 is set back to position 0 and then moved along with the head of P. In this way, we will always know whether the head of P is currently located at one of the first n cells. Whenever this is the case, we insert some intermediate steps to read out the first n bits, update the inner state and move the head back to its original position. (This requires some additional states, but we skip the details). Note that, if
is set back to position 0 and then moved along with the head of P. In this way, we will always know whether the head of P is currently located at one of the first n cells. Whenever this is the case, we insert some intermediate steps to read out the first n bits, update the inner state and move the head back to its original position. (This requires some additional states, but we skip the details). Note that, if  is a limit time and the first n bits have been changed unboundedly often before
is a limit time and the first n bits have been changed unboundedly often before  , then the head will be located at one of these positions at time
, then the head will be located at one of these positions at time  by the liminf-rule and thus, a further update will take place so that the state will correctly represent the configuration afterwards. On the other hand, if the first n bits were only changed boundedly often before time
by the liminf-rule and thus, a further update will take place so that the state will correctly represent the configuration afterwards. On the other hand, if the first n bits were only changed boundedly often before time 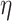 , then let
, then let  be the supremum of these times. We just saw that the state will represent the configuration correctly finitely many steps after time
be the supremum of these times. We just saw that the state will represent the configuration correctly finitely many steps after time 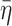 , after which the first n cell contents remain unchanged, so that the state is still correct at time
, after which the first n cell contents remain unchanged, so that the state is still correct at time 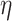 . In each case, updating this information and returning to the original configuration will take only finitely many extra steps and thus not cause a delay at limit times.6
. In each case, updating this information and returning to the original configuration will take only finitely many extra steps and thus not cause a delay at limit times.6
In the following construction, we will need to know whether the head is currently located at a cell the index of which is of the form 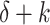 , where
, where  is a limit ordinal and k is a fixed natural number. To achieve this, we add three tapes
is a limit ordinal and k is a fixed natural number. To achieve this, we add three tapes 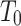 ,
,  and
and  to P. The tape
to P. The tape 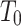 serves as a flag: By having two cells with alternating contents 01 and 10, we can detect a limit time as a time at which both cells contain 0. On
serves as a flag: By having two cells with alternating contents 01 and 10, we can detect a limit time as a time at which both cells contain 0. On  , we move the head along with the head on P and place a 1 on a cell whenever we encounter a cell on which a 0 is written. Thus, the head occupies a certain limit position for the first time if and only if the head on
, we move the head along with the head on P and place a 1 on a cell whenever we encounter a cell on which a 0 is written. Thus, the head occupies a certain limit position for the first time if and only if the head on 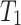 reads a 0 at a limit time. Finally, on
reads a 0 at a limit time. Finally, on  , we more the head along with the heads on
, we more the head along with the heads on  and the main tape. Whenever the head on
and the main tape. Whenever the head on 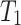 reads a 0 at a limit time, we interrupt the computation, move the head on
reads a 0 at a limit time, we interrupt the computation, move the head on  for k many steps to the right, write a 1, move the head k many places to the left, and continue. In this way, the head on
for k many steps to the right, write a 1, move the head k many places to the left, and continue. In this way, the head on 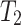 will read a 1 if and only if the head on the main tape is at a position of the desired form. As this merely inserts finitely many steps occasionally, running this procedure along with an OTM-program P will still carry out
will read a 1 if and only if the head on the main tape is at a position of the desired form. As this merely inserts finitely many steps occasionally, running this procedure along with an OTM-program P will still carry out  many steps of P at time
many steps of P at time  whenever
whenever  is a limit ordinal. We will say that the head is “at a
is a limit ordinal. We will say that the head is “at a 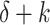 -position” if the index of the cell where it is currently located is of this form with
-position” if the index of the cell where it is currently located is of this form with  a limit ordinal and, by the construction just described, we can use formulations like “if the head is currently at a
a limit ordinal and, by the construction just described, we can use formulations like “if the head is currently at a  -position” in describing OTM-programs without affecting the running time at limit ordinals.
-position” in describing OTM-programs without affecting the running time at limit ordinals.
Lemma 1
If 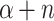 is OTM-clockable and
is OTM-clockable and  , then
, then 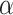 is OTM-clockable.
is OTM-clockable.
Proof
It is clear that finite ordinals are OTM-clockable and that OTM-clockable ordinals are closed under addition (by simply running one program after the other).7 Thus, it suffices to consider the case that 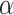 is a limit ordinal. Moreover, we assume for simplicity that P uses only one tape.8
is a limit ordinal. Moreover, we assume for simplicity that P uses only one tape.8
Let P be an OTM-program that runs for 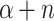 many steps, where
many steps, where  is a limit ordinal. We want to construct a program Q that runs for
is a limit ordinal. We want to construct a program Q that runs for 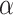 many steps. Let the head position at time
many steps. Let the head position at time 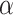 be equal to
be equal to  , where
, where  is a limit ordinal and
is a limit ordinal and  . As above, let m be
. As above, let m be  if
if 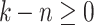 and otherwise let
and otherwise let 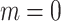 . Let s be the bit string present on the positions
. Let s be the bit string present on the positions  until
until 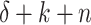 at time
at time  , and let t be the string present on the first n positions.
, and let t be the string present on the first n positions.
Using the constructions explained above, Q now works as follows: Run P. At each step, determine whether the head is currently at a location of the form  with
with 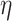 a limit ordinal and whether one of the two following conditions holds:
a limit ordinal and whether one of the two following conditions holds:
The head is currently at one of the first n positions and the bit string currently present on the positions
 up to
up to  is equal to s.
is equal to s.The head is currently not on one of the first n positions, the bit string currently present on the positions
 up to
up to 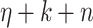 is equal to s and whether the bit string currently present on the first n positions is equal to t.
is equal to s and whether the bit string currently present on the first n positions is equal to t.
If not, continue with P. Otherwise, halt. As described above, the necessary information can be read off from the various extra tapes and the inner state simultaneously. Now it is clear that, if Q halts at time 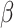 , then P will halt at time
, then P will halt at time  . Thus, Q halts at time
. Thus, Q halts at time  , as desired.
, as desired.
Definition 2
Let 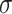 be the minimal ordinal such that
be the minimal ordinal such that  , i.e. such that
, i.e. such that  is a
is a  -submodel of L.
-submodel of L.
Proposition 3
Every OTM-clockable ordinals is 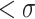 , and their supremum is
, and their supremum is  .
.
Proof
The statement ‘The program P halts’ is 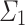 . Moreover, any halting OTM- computation is contained in L. Consequently, if P halts, its computation is con- tained in L, and hence in
. Moreover, any halting OTM- computation is contained in L. Consequently, if P halts, its computation is con- tained in L, and hence in  , and thus, the halting time of P, if it exists, is
, and thus, the halting time of P, if it exists, is  .
.
On the other hand, every real number in 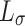 is OTM-computable (see, e.g., [12], proof of Corollary 3), including codes for all ordinals
is OTM-computable (see, e.g., [12], proof of Corollary 3), including codes for all ordinals 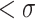 , and thus we can write such a code for any ordinal
, and thus we can write such a code for any ordinal 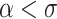 and then run through this code, which takes at least
and then run through this code, which takes at least 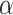 many steps. Thus, there is an OTM-clockable ordinal above
many steps. Thus, there is an OTM-clockable ordinal above 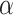 for every
for every  .
.
Proposition 4
There are gaps in the OTM-clockable ordinals. That is, there are ordinals  such that
such that  and
and  are OTM-clockable, but
are OTM-clockable, but  is not.
is not.
Proof
This works like the argument in Hamkins and Lewis ([9], Theorem 3.4) for the existence of gaps in the ITTM-clockable ordinals: Take the OTM-program that simultaneously simulates all OTM-programs and halts as soon as it arrives at a level at which no OTM-program halts. If there were no gap, then this program would halt after all OTM-halting times, which is a contradiction.
The following is an OTM-version of Welch’s “quick writing theorem” (see [14], Lemma 48) for ITTMs.
Lemma 2
If an ordinal  is OTM-clockable, then a real number coding
is OTM-clockable, then a real number coding 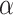 is OTM-writable in
is OTM-writable in  many steps, where
many steps, where 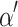 denotes the next exponentially closed ordinal after
denotes the next exponentially closed ordinal after  .
.
Proof
If  is clocked by some OTM-program P, then
is clocked by some OTM-program P, then 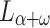 believes that P halts. Thus, there is a
believes that P halts. Thus, there is a 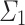 -statement that becomes true between
-statement that becomes true between 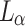 and
and 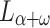 for the first time and hence, by finestructure (see [2], Lemma 1), a real number coding
for the first time and hence, by finestructure (see [2], Lemma 1), a real number coding  is contained in
is contained in  . But the OTM-program Q that enumerates L will have (a code for)
. But the OTM-program Q that enumerates L will have (a code for)  on the tape in
on the tape in 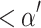 many steps. So we can simply run this program until we arrive at a code c for a limit L-level that believes that P halts for the first time. Now, we can easily find out the desired real code for
many steps. So we can simply run this program until we arrive at a code c for a limit L-level that believes that P halts for the first time. Now, we can easily find out the desired real code for 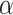 in the code for
in the code for 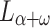 (by searching the coded structure for an element which it believes to be the halting time of P).
(by searching the coded structure for an element which it believes to be the halting time of P).
Proposition 5
If 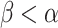 is exponentially closed and OTM-clockable and there is a total
is exponentially closed and OTM-clockable and there is a total 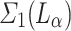 -function
-function  such that f is cofinal in
such that f is cofinal in 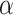 , then
, then  is OTM-clockable.
is OTM-clockable.
Proof
This works by the same argument as the “only admissibles start gaps”-theorem for ITTMs, see Welch [14]: Suppose for a contradiction that 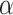 starts an OTM-gap, but is not admissible.
starts an OTM-gap, but is not admissible.
Pick  OTM-clockable and
OTM-clockable and 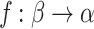 such that f is
such that f is  and cofinal in
and cofinal in  . Let B be an OTM-program that clocks
. Let B be an OTM-program that clocks 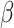 . By the last lemma, we can compute a real code for
. By the last lemma, we can compute a real code for  in
in 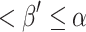 many steps. Run the OTM that enumerates L. If
many steps. Run the OTM that enumerates L. If  is exponentially closed, then we will have a code for
is exponentially closed, then we will have a code for  on the tape at time
on the tape at time 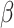 . In addition, for each new L-level, check which ordinals recieve f-images when evaluating the definition of f in that level. Determine the largest ordinal
. In addition, for each new L-level, check which ordinals recieve f-images when evaluating the definition of f in that level. Determine the largest ordinal 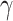 such that f is defined on
such that f is defined on 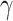 . Whenever
. Whenever 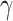 increases, say from
increases, say from  to
to  , let
, let 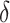 be such that
be such that  and run B for
and run B for  many steps. When B halts, all elements of
many steps. When B halts, all elements of 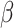 have images, so we have arrived at time
have images, so we have arrived at time  .
.
This suffices for an OTM-analogue of Welch’s theorem [14], Theorem 50:
Corollary 1
If 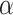 starts a gap in the OTM-clockable ordinals, then
starts a gap in the OTM-clockable ordinals, then  is admissible.
is admissible.
Proof
As 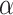 starts an OTM-gap, it is exponentially closed.
starts an OTM-gap, it is exponentially closed.
If 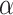 is not admissible, there is a total cofinal
is not admissible, there is a total cofinal 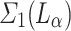 -function
-function 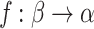 with
with 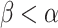 . Pick
. Pick  OTM-clockable and large enough so that all parameters used in the definition of f are contained in
OTM-clockable and large enough so that all parameters used in the definition of f are contained in  . By Lemma 2, we can write a real code for
. By Lemma 2, we can write a real code for  , and thus for all of its elements in time
, and thus for all of its elements in time 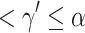 . We can now clock
. We can now clock  as in Proposition 5, a contradiction.
as in Proposition 5, a contradiction.
 -admissible Ordinals Are Not OTM-clockable
-admissible Ordinals Are Not OTM-clockable
We now show that no 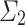 -admissible ordinal
-admissible ordinal 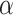 can be the halting time of a parameter-free OTM-computation. The proof is mostly an adapatation of argument in Hamkins and Lewis [9] for the non-clockability of admissible ordinals by ITTMs to the extra subtleties of OTMs.
can be the halting time of a parameter-free OTM-computation. The proof is mostly an adapatation of argument in Hamkins and Lewis [9] for the non-clockability of admissible ordinals by ITTMs to the extra subtleties of OTMs.
Theorem 6
No 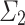 -admissible ordinal is OTM-clockable.
-admissible ordinal is OTM-clockable.
Proof
We will show this for the case of a single-tape OTM for the sake of simplicity.
Let 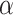 be
be 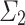 -admissible and assume for a contradiction that
-admissible and assume for a contradiction that  is the halting time of the parameter-free OTM-program P. At time
is the halting time of the parameter-free OTM-program P. At time 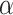 , suppose that the read-write-head is at position
, suppose that the read-write-head is at position 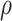 , the program is in state
, the program is in state  and the head reads the symbol
and the head reads the symbol  . As one cannot move the head more than
. As one cannot move the head more than 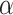 many places to the right in
many places to the right in 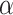 many steps, we have
many steps, we have  .
.
By the limit rules, z must have been the symbol on cell 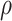 cofinally often before time
cofinally often before time  and similarly, s must have been the program state cofinally often before time
and similarly, s must have been the program state cofinally often before time 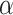 . By recursively building an increasing ‘interleaving’ sequence of ordinals of both kinds, we see that the set S of times at which the program state was s and the symbol on
. By recursively building an increasing ‘interleaving’ sequence of ordinals of both kinds, we see that the set S of times at which the program state was s and the symbol on  was z, we see that S is closed and unbounded in
was z, we see that S is closed and unbounded in  .
.
We now distinguish three cases.
Case 1:
 and the head position
and the head position 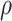 was assumed cofinally often before time
was assumed cofinally often before time  .
.
Let 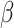 be the order type of the set of times at which
be the order type of the set of times at which 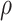 was the head position in the computation of P. We show that
was the head position in the computation of P. We show that  . If not, then
. If not, then  ; let
; let 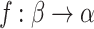 be the function sending each
be the function sending each  to the
to the  th time at which
th time at which 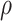 was the head position. Then f is
was the head position. Then f is  over
over  and thus, by admissibility of
and thus, by admissibility of  ,
,  is bounded in
is bounded in  , contradicting the case assumption.
, contradicting the case assumption.
Let T be the set of times at which  was the head position. Then, by the limit rules and the case assumption, T is closed and unbounded in
was the head position. Then, by the limit rules and the case assumption, T is closed and unbounded in 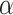 .
.
As S and T are both 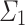 over
over  and
and  is admissible, it follows that
is admissible, it follows that  is also closed and unbounded in
is also closed and unbounded in  . In particular, there is an element
. In particular, there is an element  in
in  , i.e. there is a time
, i.e. there is a time 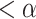 at which the head was on position
at which the head was on position  , the cell
, the cell  contained the symbol z and the inner state was s. But then, the situation that prompted P to halt at time
contained the symbol z and the inner state was s. But then, the situation that prompted P to halt at time 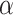 was already given at time
was already given at time  , so P cannot have run up to time
, so P cannot have run up to time 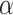 , a contradiction.
, a contradiction.
Case 2:
 and the head position
and the head position 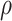 was assumed boundedly often before time
was assumed boundedly often before time  .
.
By the liminf rule for the determination of the head position at time 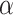 , this implies that, for every
, this implies that, for every 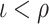 , there is a time
, there is a time  such that, from time
such that, from time 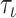 on, the head never occupied a position
on, the head never occupied a position  . The function
. The function  is
is  over
over 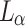 (we have
(we have  if and only if, for all
if and only if, for all  and all partial P-computations of length
and all partial P-computations of length  , the head position in the final state of the partial computation was
, the head position in the final state of the partial computation was  ) and thus in particular
) and thus in particular 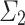 over
over  . By
. By 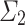 -admissibility of
-admissibility of  and the case assumption
and the case assumption 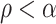 , the set
, the set  must be bounded in
must be bounded in 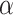 , say by
, say by  . But this implies that, after time
. But this implies that, after time 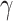 , all head positions were
, all head positions were  . As
. As  was assumed only boundedly often as the head position, this means that, from some time
was assumed only boundedly often as the head position, this means that, from some time  on, all head positions were actually
on, all head positions were actually  . But then,
. But then, 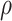 cannot be the inferior limit of the sequence of earlier head positions at time
cannot be the inferior limit of the sequence of earlier head positions at time 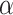 , contradicting the case assumption that the head is on position
, contradicting the case assumption that the head is on position 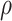 at time
at time  .
.
Case 3:
 .
.
This implies that the head is on position 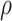 for the first time at time
for the first time at time  , so that we must have
, so that we must have  , as there was no chance to write on the
, as there was no chance to write on the 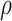 th cell before time
th cell before time  .
.
Let S be the set of times 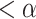 at which some head position was assumed for the first time during the computation of P. By the same reason as above, this newly reached cell will contain 0 at that time. If we can show that there is such a time
at which some head position was assumed for the first time during the computation of P. By the same reason as above, this newly reached cell will contain 0 at that time. If we can show that there is such a time  at which the inner state is also s, we are done, because that would mean that the halting situation at time
at which the inner state is also s, we are done, because that would mean that the halting situation at time  was already given at an earlier time, contradicting the assumption that P halts at time
was already given at an earlier time, contradicting the assumption that P halts at time 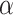 .
.
As  , there must be an ordinal
, there must be an ordinal  such that the head was never on position 0 after time
such that the head was never on position 0 after time 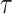 (otherwise, the liminf rule would force the head to be on position 0 at time
(otherwise, the liminf rule would force the head to be on position 0 at time  ). This means that the head was never moved to the left from a limit position after time
). This means that the head was never moved to the left from a limit position after time 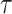 . This further implies that, after time
. This further implies that, after time 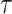 , for any position
, for any position  that the head occupied, all later positions were at most finitely many positions to the left of
that the head occupied, all later positions were at most finitely many positions to the left of  and hence that, if
and hence that, if  is a limit ordinal, then it never occupied a position
is a limit ordinal, then it never occupied a position 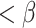 afterwards. In particular, the sequence of limit positions that the head occupied after time
afterwards. In particular, the sequence of limit positions that the head occupied after time 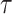 is increasing. Note that the set of head positions occupied before time
is increasing. Note that the set of head positions occupied before time  is bounded in
is bounded in 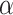 , say by
, say by 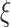 . Let
. Let 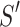 be the set of elements
be the set of elements  of S such that, at time
of S such that, at time 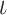 , the head occupied a limit position
, the head occupied a limit position 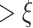 for the first time. Then
for the first time. Then 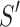 is a closed and unbounded subset of S.
is a closed and unbounded subset of S.
As s is the program state at the limit time  , there must be
, there must be  such that, after time
such that, after time  , the program state was never
, the program state was never  and moreover, the program state s itself must have occured cofinally often in
and moreover, the program state s itself must have occured cofinally often in  after that time.
after that time.
But now, building an increasing 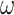 -sequence of times starting with
-sequence of times starting with 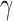 that alternately belong to
that alternately belong to  and have the program state s, we see that its limit
and have the program state s, we see that its limit  is
is 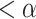 and is a time at which the head was reading z and the state was s, we have the desired contradiction.
and is a time at which the head was reading z and the state was s, we have the desired contradiction.
Since each case leads to a contradiction, our assumption on P must be false; as P was arbitrary,  is not a parameter-free OTM-halting time.
is not a parameter-free OTM-halting time.
To see now that the theorem holds for any finite number of tapes, consider the argument below for each tape separately, note that we showed above that case 2 cannot occur while cases 1 and 3 both imply that, as far as the tape under consideration is concerned, the halting configuration occurred on a closed unbounded set of times before time  . Thus, one can again build an increasing ‘interleaving’ sequence of times at which each head read the same symbol as in the halting configuration and the inner state was the one in the halting configuration. The supremum of this sequence will be
. Thus, one can again build an increasing ‘interleaving’ sequence of times at which each head read the same symbol as in the halting configuration and the inner state was the one in the halting configuration. The supremum of this sequence will be 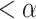 , leading again to the contradiction that the program must have halted before
, leading again to the contradiction that the program must have halted before  .
.
Existence of Admissible OTM-clockable Ordinals
We will now show that at least the first 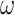 many admissible ordinals are OTM- clockable, thus answering the first question mentioned in the introduction positively. To this end, we need some preliminaries about Infinite Time Register Machines (ITRMs). ITRMs were introduced by Koepke in [11]; we sketch their architecture and refer to [11] for further information. An ITRM has finitely many registers, each of which stores one natural number. ITRM-programs are just programs for (classical) register machines. At successor times, an ITRM proceeds like a classical register machine. At limit levels, the active program line index and the register contents are defined to be the inferior limits of the sequences of earlier program line indices and respective register contents. When that limit is not finite in the case of a register content, the new content is defined to be 0, and one speaks of an ‘overflow’ of the respective register.
many admissible ordinals are OTM- clockable, thus answering the first question mentioned in the introduction positively. To this end, we need some preliminaries about Infinite Time Register Machines (ITRMs). ITRMs were introduced by Koepke in [11]; we sketch their architecture and refer to [11] for further information. An ITRM has finitely many registers, each of which stores one natural number. ITRM-programs are just programs for (classical) register machines. At successor times, an ITRM proceeds like a classical register machine. At limit levels, the active program line index and the register contents are defined to be the inferior limits of the sequences of earlier program line indices and respective register contents. When that limit is not finite in the case of a register content, the new content is defined to be 0, and one speaks of an ‘overflow’ of the respective register.
We recall Lemma 3 from [5]:
Theorem 7
There are no gaps in the ITRM-clockable ordinals. That is, if 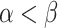 and
and 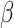 is ITRM-clockable, then
is ITRM-clockable, then 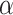 is ITRM-clockable.
is ITRM-clockable.
Combining this result with the main result of [11] on the computational strength of ITRMs, we obtain:
Lemma 3
The ITRM-clockable ordinals are exactly those below  . In particular,
. In particular,  is ITRM-clockable for all
is ITRM-clockable for all 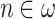 .
.
Lemma 4
Let 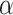 be ITRM-clockable. Then
be ITRM-clockable. Then 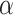 is OTM-clockable.
is OTM-clockable.
Proof
If  , this is straightforward. Now let
, this is straightforward. Now let  .
.
Let P be an ITRM-program that clocks  . We simulate P by an OTM-program that takes the same running time.
. We simulate P by an OTM-program that takes the same running time.
The simulation of ITRMs by OTMs here works like this: Use a tape for each register, have i many 1s, followed by 0s, on a tape to represent that the respective register contains  ; in addition, after a simulation step is finished, the head position on this tape represents the register content, i.e. it is at the first 0 on the tape.
; in addition, after a simulation step is finished, the head position on this tape represents the register content, i.e. it is at the first 0 on the tape.
For an ITTM, the simulation takes an extra 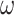 many steps to halt because it takes time to detect an overflow. For an OTM, one can simply use one extra tape for each register, write 1 to their
many steps to halt because it takes time to detect an overflow. For an OTM, one can simply use one extra tape for each register, write 1 to their  th positions at the start of the computation, move their heads along with the heads on the register simulating tapes and know that there is an overflow as soon as one of the heads on the extra tapes reads a 1.9 Since
th positions at the start of the computation, move their heads along with the heads on the register simulating tapes and know that there is an overflow as soon as one of the heads on the extra tapes reads a 1.9 Since 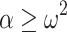 , the initial placement of 1s on the
, the initial placement of 1s on the 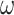 th tape positions does not affect the running time.
th tape positions does not affect the running time.
Corollary 2
For every 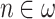 ,
,  is OTM-clockable.
is OTM-clockable.
This answers the first question mentioned above in the positive. By a relativization of the above argument, we can achieve the same for the second (i.e. whether gap starters for OTMs are something “better” than admissible):
Theorem 8
Let 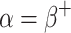 be a successor admissible. Then
be a successor admissible. Then  does not start an OTM-clockable gap.
does not start an OTM-clockable gap.
Proof
Suppose for a contradiction that 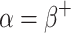 starts an OTM-clockable gap. Then there is an OTM-clockable ordinal
starts an OTM-clockable gap. Then there is an OTM-clockable ordinal  ; pick one. By Lemma 2 above, a real code c for
; pick one. By Lemma 2 above, a real code c for  is OTM-writable in
is OTM-writable in  many steps. Suppose c has been written. Then
many steps. Suppose c has been written. Then  . Thus,
. Thus, 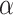 is ITRM-clockable in the oracle c. But now,
is ITRM-clockable in the oracle c. But now,  is OTM-clockable by first writing c and then ITRM-clocking
is OTM-clockable by first writing c and then ITRM-clocking  relative to c, contradicting the assumption that
relative to c, contradicting the assumption that  starts a gap.
starts a gap.
Corollary 3
Every gap-starting ordinal for OTMs is an admissible limit of admissible ordinals.
This allows a considerable strengthening of Corollary 2:
Corollary 4
Every admissible ordinal up to the first admissible limit of admissible ordinals is OTM-clockable.
Conclusion and Further Work
We showed that OTM-gaps are always started by limits of admissible ordinals and that, while admissible ordinals can be OTM-clockable, 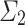 -admissible ordinals cannot. This provokes the following questions:
-admissible ordinals cannot. This provokes the following questions:
Question: Is every gap-starting ordinal for OTMs 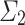 -admissible?
-admissible?
Question: What is the minimal gap-starting ordinal for OTMs? Does it coincide with first 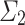 -admissible ordinal?
-admissible ordinal?
Further worthile topics include clockability for OTMs with a fixed ordinal parameter  and for other models of computability, like the “hypermachines” of Friedman and Welch (see [8]),
and for other models of computability, like the “hypermachines” of Friedman and Welch (see [8]), 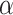 -ITTMs (see [7]) or
-ITTMs (see [7]) or  -ITRMs (see [4]), where the main question left open in [4] is to determine the supremum of the
-ITRMs (see [4]), where the main question left open in [4] is to determine the supremum of the  -ITRM-clockable ordinals.
-ITRM-clockable ordinals.
Footnotes
As one of our referees pointed out, there are earlier considerations of machine models computing along an ordinal time axis; however, none of them was studied in the detail that ITTMs were.
International Conference on Computability Theory and Foundations of Mathematics.
The notion of admissibility will play a prominent role in this paper. Readers unfamiliar with it are referred to Barwise [1].
For example, by simulating multitape machines on a single-type machine in a rather straightforward way, one can see that the following holds: If 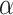 is exponentially closed and clockable by an OTM, then
is exponentially closed and clockable by an OTM, then 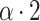 is clockable by an OTM using only one tape.
is clockable by an OTM using only one tape.
The 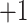 allows limit ordinals to appear as halting times and thus simplifies the theory.
allows limit ordinals to appear as halting times and thus simplifies the theory.
This leaves us with the case that the head occupies one of the first n tape positions at time 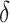 , in which case even a finite delay would increase our running time. However, in this special case, no setback will take place during the last n steps of the computation, so the construction described in this paragraph can simply be skipped.
, in which case even a finite delay would increase our running time. However, in this special case, no setback will take place during the last n steps of the computation, so the construction described in this paragraph can simply be skipped.
It is folklore (and easy to see) that, for any reasonable model of computation, clockable ordinals are closed under ordinal arithmetic, i.e. under addition, multiplication and exponentiation, see e.g. [9] or [5]. This also holds true for OTMs.
If P uses several tapes, the construction below is carried out for each of these.
The fact that more tapes are needed the more registers P uses may be seen as a little defect. (Note that, by the results of [11], the halting times of ITRM-programs using n registers are bounded by 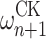 so that indeed arbitrarily large numbers of registers - and thus of tapes - are required to make the above construction work for all
so that indeed arbitrarily large numbers of registers - and thus of tapes - are required to make the above construction work for all  with
with 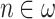 .) It would certainly be nicer to have a uniform bound on the number of required tapes. And indeed, by a slightly refined argument using that only two of the used registers are ultimately relevant for the halting of an ITRM, such a bound can be obtained.
.) It would certainly be nicer to have a uniform bound on the number of required tapes. And indeed, by a slightly refined argument using that only two of the used registers are ultimately relevant for the halting of an ITRM, such a bound can be obtained.
Contributor Information
Marcella Anselmo, Email: manselmo@unisa.it.
Gianluca Della Vedova, Email: gianluca.dellavedova@unimib.it.
Florin Manea, Email: flmanea@gmail.com.
Arno Pauly, Email: arno.m.pauly@gmail.com.
Merlin Carl, Email: merlin.carl@uni-konstanz.de.
References
- 1.Barwise J. Admissible Sets and Structures: An Approach to Definability Theory. Berlin: Springer; 1975. [Google Scholar]
- 2.Boolos G, Putnam H. Degrees of unsolvability of constructible sets of integers. J. Symb. Log. 1968;33:497–513. doi: 10.2307/2271357. [DOI] [Google Scholar]
- 3.Dimitriou, I. (ed.): Bonn International Workshop on Ordinal Computability. Report Hausdorff Centre for Mathematics, Bonn (2007). http://www.math.uni-bonn.de/ag/logik/events/biwoc/index.html
- 4.Carl, M.: Taming Koepkes Zoo II: Register Machines. Preprint (2020). arXiv:1907.09513v4
- 5.Carl M, Fischbach T, Koepke P, Miller R, Nasfi M, Weckbecker G. The basic theory of infinite time register machines. Arch. Math. Logic. 2010;49(2):249–273. doi: 10.1007/s00153-009-0167-x. [DOI] [Google Scholar]
- 6.Carl M, Durand B, Lafitte G, Ouazzani S. Admissibles in gaps. In: Kari J, Manea F, Petre I, editors. Unveiling Dynamics and Complexity; Cham: Springer; 2017. pp. 175–186. [Google Scholar]
- 7.Carl M, Ouazzani S, Welch P. Taming Koepke’s Zoo. In: Manea F, Miller RG, Nowotka D, editors. Sailing Routes in the World of Computation; Cham: Springer; 2018. pp. 126–135. [Google Scholar]
- 8.Friedman S, Welch P. Hypermachines. J. Symb. Log. 2011;76(2):620–636. doi: 10.2178/jsl/1305810767. [DOI] [Google Scholar]
- 9.Hamkins L. Infinite time turing machines. J. Symb. Log. 2000;65(2):567–604. doi: 10.2307/2586556. [DOI] [Google Scholar]
- 10.Koepke P. Turing computations on ordinals. Bull. Symb. Log. 2005;11:377–397. doi: 10.2178/bsl/1122038993. [DOI] [Google Scholar]
- 11.Koepke P. Ordinal computability. In: Ambos-Spies K, Löwe B, Merkle W, editors. Mathematical Theory and Computational Practice; Heidelberg: Springer; 2009. pp. 280–289. [Google Scholar]
- 12.Seyfferth B, Schlicht P. Tree representations via ordinal machines. Computablility. 2012;1(1):45–57. doi: 10.3233/COM-2012-002. [DOI] [Google Scholar]
- 13.Seabold D, Hamkins J. Infinite time turing machines with only one tape. Math. Log. Quart. 1999;47(2):271–287. [Google Scholar]
- 14.Welch P. Characteristics of discrete transfinite time turing machine models: halting times, stabilization times, and normal form theorems. Theor. Comput. Sci. 2009;410:426–442. doi: 10.1016/j.tcs.2008.09.050. [DOI] [Google Scholar]


