Abstract
Computing text-to-pattern distances is a fundamental problem in pattern matching. Given a text of length n and a pattern of length m, we are asked to output the distance between the pattern and every n-substring of the text. A basic variant of this problem is computation of Hamming distances, that is counting the number of mismatches (different characters aligned), for each alignment. Other popular variants include 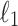 distance (Manhattan distance),
distance (Manhattan distance), 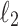 distance (Euclidean distance) and general
distance (Euclidean distance) and general  distance. While each of those problems trivially generalizes classical pattern-matching, the efficient algorithms for them require a broader set of tools, usually involving both algebraic and combinatorial insights. We briefly survey the history of the problems, and then focus on the progress made in the past few years in many specific settings: fine-grained complexity and lower-bounds,
distance. While each of those problems trivially generalizes classical pattern-matching, the efficient algorithms for them require a broader set of tools, usually involving both algebraic and combinatorial insights. We briefly survey the history of the problems, and then focus on the progress made in the past few years in many specific settings: fine-grained complexity and lower-bounds,  multiplicative approximations, k-bounded relaxations, streaming algorithms, purely combinatorial algorithms, and other recently proposed variants.
multiplicative approximations, k-bounded relaxations, streaming algorithms, purely combinatorial algorithms, and other recently proposed variants.
Hamming Distance
A most fundamental problem in stringology is that of pattern matching: given pattern P and text T, find all occurrences of P in T where by occurrence we mean a substring (a consecutive fragment) of T that is identical to P. A huge efforts have been put into advancement of understanding of pattern matching by the community. One particular variant to consider is finding occurrences or almost-occurrences of P in T. For this, we need to specify almost-occurrences: e.g. introduce some form of measure of distance between words, and then look for substrings of T which are close to P. We are interested in measures that are position-based, that is they are defined over strings of equal length, and are based upon distances between letters on corresponding positions (thus e.g. edit distance is out of scope of this survey). Consider for example
Definition 1
(Hamming distance). For strings A, B of equal length, their Hamming distance is defined as
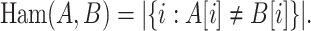 |
Hence, the Hamming distance counts the number of mismatches between two words. This leads us to the core problem considered in this survey.
Definition 2
(Text-to-pattern Hamming distance). For a text T[1, n] and a pattern P[1, m], the text-to-pattern Hamming distance asks for an output array  such that
such that
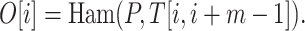 |
Observe that this problem generalizes the detection of almost-occurrences – one can scan the output array and output positions with small distance to the pattern.
Convolution in Text-to-Pattern Distance
Convolution of two vectors (arrays) is defined as follow
Definition 3
(Convolution). For 0-based vectors A and B we define their convolution 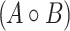 as a vector:
as a vector:
 |
Such a definition has a natural interpretation e.g. in terms of polynomial product: if we interpret a vector as coefficients of a polynomial that is 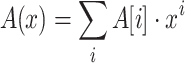 and
and  , then
, then 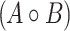 are coefficients of
are coefficients of 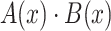 .
.
Convolution over integers is computed by Fast Fourier transform (FFT) in time  . This requires actual embedding of integers into field, e.g.
. This requires actual embedding of integers into field, e.g. 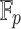 or
or 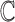 . This comes at a cost, if e.g. we were to consider text-to-pattern distance over (non-integer) alphabets that admit only field operations, e.g. matrices or geometric points. Convolution can be computed using a “simpler” set of operations, that is just with ring operations in e.g.
. This comes at a cost, if e.g. we were to consider text-to-pattern distance over (non-integer) alphabets that admit only field operations, e.g. matrices or geometric points. Convolution can be computed using a “simpler” set of operations, that is just with ring operations in e.g.  using Toom-Cook multiplication [35], which is a generalization of famous divide-and-conquer Karatsuba algorithm [20]. However, not using FFT makes the algorithm slower, with Toom-Cook algorithm taking time
using Toom-Cook multiplication [35], which is a generalization of famous divide-and-conquer Karatsuba algorithm [20]. However, not using FFT makes the algorithm slower, with Toom-Cook algorithm taking time 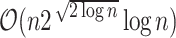 , and increases the complexity of the algorithm.
, and increases the complexity of the algorithm.
Fischer and Paterson in [16] observed that convolution can be used to compute text-to-pattern Hamming distance for small alphabets. Consider the following observation: for binary P and T, denote by  the reversed
P. Then we have the following property:
the reversed
P. Then we have the following property:
 |
where e.g.  denotes negating every entry of T. Thus the whole algorithm is done by computing two convolutions in time
denotes negating every entry of T. Thus the whole algorithm is done by computing two convolutions in time  .1 This approach in fact generalizes to arbitrary size alphabets by following observation: “contribution” of single
.1 This approach in fact generalizes to arbitrary size alphabets by following observation: “contribution” of single  to number of mismatches for all positions can be computed with single convolution. This results in
to number of mismatches for all positions can be computed with single convolution. This results in 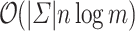 time algorithm.
time algorithm.
The natural question is whether faster (than naive quadratic-time) algorithms for large alphabets exist. The answer is affirmative, by (almost simultaneous) results of Abrahamson [1] and Kosaraju [24]. The insight is that for any letter  , we can compute its “contribution” twofold:
, we can compute its “contribution” twofold:
by FFT in time
 ,
,or in time
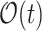 per each of n alignments, where t is the number of occurrences of c in lets say pattern.
per each of n alignments, where t is the number of occurrences of c in lets say pattern.
The insight is that we apply the former for letters that appear often (“dense” case) and latter for sparse letters. Since there can be at most m/T letters that appear at least T times in pattern each, the total running time is  which is minimized when
which is minimized when 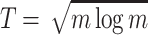 with run-time
with run-time 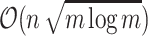 .
.
This form of mixing combinatorial and algebraical insights is typical for the type of problems considered in this paper, and we will see more of it in the following sections. As a side-note, the complexity of 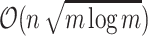 remains state-of-the-art.
remains state-of-the-art.
Relaxation: k-Bounded Distances
The lack of progress in Hamming text-to-pattern distance complexity sparked interest in searching for relaxations of the problem, in hope of reaching linear (or almost linear) run-time. For example if we consider reporting only the values not exceeding a certain threshold value k, then we have the so-called k-approximated distance. The motivation comes from the fact that if we are looking for almost-occurrences, then if the distance is larger than a certain threshold value, the text fragment is too dissimilar to pattern and we are safe to discard it.
The very first solution to this problem was shown by Landau and Vishkin [26] working in time  , using an essentially combinatorial approach of taking
, using an essentially combinatorial approach of taking 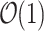 time per mismatch per alignment using LCP queries (Longest Common Prefix queries), where
time per mismatch per alignment using LCP queries (Longest Common Prefix queries), where  returns maximal k such that
returns maximal k such that  . This solution requires preprocessing of T and P with e.g. suffix tree, which is a standard tool-set of stringology. This solution still is slower than naive algorithm for
. This solution requires preprocessing of T and P with e.g. suffix tree, which is a standard tool-set of stringology. This solution still is slower than naive algorithm for  , but has the nice property of using actually
, but has the nice property of using actually  time for constant k. This technique is also known as kangaroo jumps.
time for constant k. This technique is also known as kangaroo jumps.
This initiated a series of improvements to the complexity, with algorithms of complexity  and
and 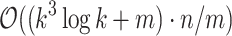 by Amir et al. [4]. First algorithm is an adaptation of general algorithm of Abrahamson with balancing of “sparse” vs. “dense” case done w.r.t. k instead of m (some further combinatorial insights are required to make the cases work with proper run-time). Such trade-off has this nice property that for
by Amir et al. [4]. First algorithm is an adaptation of general algorithm of Abrahamson with balancing of “sparse” vs. “dense” case done w.r.t. k instead of m (some further combinatorial insights are required to make the cases work with proper run-time). Such trade-off has this nice property that for  the complexity matches that of Abrahamson’s algorithm. Second algorithm is more interesting, since it shows that for non-trivial values of k (in this case,
the complexity matches that of Abrahamson’s algorithm. Second algorithm is more interesting, since it shows that for non-trivial values of k (in this case, 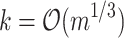 ) near-linear time algorithms are possible.
) near-linear time algorithms are possible.
The later complexity was then improved to  by Clifford et al. [13]. We now discuss the techniques of this algorithm, starting with kernelization technique.
by Clifford et al. [13]. We now discuss the techniques of this algorithm, starting with kernelization technique.
Definition 4
([13]). An integer  is an x-period of a string S[1, m], if
is an x-period of a string S[1, m], if  and
and  is minimal such integer.
is minimal such integer.
Such definition should be compared with regular definition of a period, where  is a period of string S if
is a period of string S if 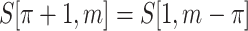 .
.
We then observe the following:
Lemma 1
([13]). If  is a 2x-period of the pattern, then any two occurrences of the pattern in the text with at most x mismatches are at offset distance at least
is a 2x-period of the pattern, then any two occurrences of the pattern in the text with at most x mismatches are at offset distance at least  .
.
The first step of the algorithm is to determine some small 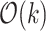 -period of the pattern. This actually does not require any specialized machinery and can be done with a 2-approximate algorithm for text-to-pattern Hamming distance (multiplicative approximations are a topic of the following section). We then distinguish two cases, where small means
-period of the pattern. This actually does not require any specialized machinery and can be done with a 2-approximate algorithm for text-to-pattern Hamming distance (multiplicative approximations are a topic of the following section). We then distinguish two cases, where small means 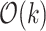 .
.
No small k-period. This is an “easy” case, where a filtering step allows us to keep only
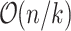 alignments that are candidates for
alignments that are candidates for  -distance matches. A “kangaroo jumps” technique of Landau and Vishkin allows us to verify each one of them in
-distance matches. A “kangaroo jumps” technique of Landau and Vishkin allows us to verify each one of them in 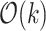 time, resulting in linear time spent in this case.
time, resulting in linear time spent in this case.-
Small 2k-period. This is a case where we can deduce some regularity properties. Denote the 2k-period as
 . First, P can be decomposed into
. First, P can be decomposed into  words from its arithmetic progressions of positions, with step
words from its arithmetic progressions of positions, with step  and every possible offset. From the definition of
and every possible offset. From the definition of  being 2k-period, we know that the total number of runs in those words is small. The more interesting property is that even though the text T can be arbitrary, if T is not regular enough it can be discarded (and this actually concerns any part of the text that is not regular). More precisely, there is a substring of text that is regular enough and contains all the alignments of P that are at Hamming distance at most k (assuming
being 2k-period, we know that the total number of runs in those words is small. The more interesting property is that even though the text T can be arbitrary, if T is not regular enough it can be discarded (and this actually concerns any part of the text that is not regular). More precisely, there is a substring of text that is regular enough and contains all the alignments of P that are at Hamming distance at most k (assuming  , which we can always guarantee).
, which we can always guarantee).What remains is to observe that finding
 , compressing of P into arithmetic progressions and finding compressible region
, compressing of P into arithmetic progressions and finding compressible region  of T all can be done in
of T all can be done in 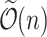 time, and that all of alignments of text to pattern correspond to alignments of those arithmetic progressions, and can be solved in
time, and that all of alignments of text to pattern correspond to alignments of those arithmetic progressions, and can be solved in  time.
time.
Final step in the sequence of improvements to this problem was done by Gawrychowski and Uznański [17]. They observe that the algorithm from [13] can be interpreted in terms of reduction: instance of k-bounded text-to-pattern Hamming distance with T and P is reduced to new  and
and  , where
, where  and
and  are possibly of the same length, but have total number of runs in their Run-length encoding (RLE) representation bounded as
are possibly of the same length, but have total number of runs in their Run-length encoding (RLE) representation bounded as 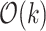 . The algorithm from [13] then falls back to brute force
. The algorithm from [13] then falls back to brute force 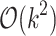 time computation. While
time computation. While 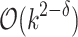 algorithm for RLE-compressed pattern matching would falsify 3-SUM conjecture (c.f. [10]), some structural properties of the instances can be leveraged based on the fact that they are RLE-compressed from inputs of length m. A balancing argument (in style of one from [4] or [1]) follows, allowing to solve this sub-problem in time
algorithm for RLE-compressed pattern matching would falsify 3-SUM conjecture (c.f. [10]), some structural properties of the instances can be leveraged based on the fact that they are RLE-compressed from inputs of length m. A balancing argument (in style of one from [4] or [1]) follows, allowing to solve this sub-problem in time  . The final complexity for the whole algorithm becomes then
. The final complexity for the whole algorithm becomes then  .
.
Relaxation:  Approximation
Approximation
Another way to relax to text-to-pattern distance is to consider multiplicative approximation when reporting number of mismatches. The very elegant argument made by Karloff [21] states the following.
Observation 1
Consider a randomly chosen projection 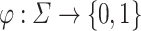 (each letters mapping is chosen independently and uniformly at random) and words A, B. Then
(each letters mapping is chosen independently and uniformly at random) and words A, B. Then
 |
where 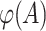 denotes applying
denotes applying  to each letter of A separately.
to each letter of A separately.
Thus the algorithm consists of: (i) choosing independently at random K random projections; (ii) for each projection, computing text-to-pattern Hamming distance over projected input; (iii) averaging answers. A concentration argument then follows, giving standard 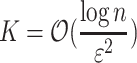 independent repetitions guaranteeing that average recovers actual Hamming distance with
independent repetitions guaranteeing that average recovers actual Hamming distance with  multiplicative guarantee, with high probability. This gives total run-time
multiplicative guarantee, with high probability. This gives total run-time 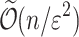 .
.
The 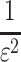 dependency was believed to be inherent, as is the case for e.g. space complexity of sketching of Hamming distance, cf. [8, 19, 38]. However, for approximate pattern matching that was refuted in Kopelowitz and Porat [22, 23], where randomized algorithms were provided with complexity
dependency was believed to be inherent, as is the case for e.g. space complexity of sketching of Hamming distance, cf. [8, 19, 38]. However, for approximate pattern matching that was refuted in Kopelowitz and Porat [22, 23], where randomized algorithms were provided with complexity  and
and  respectively. The second mentioned algorithm is actually surprisingly simple: instead of projecting onto binary alphabet, random projections
respectively. The second mentioned algorithm is actually surprisingly simple: instead of projecting onto binary alphabet, random projections 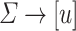 are used, where
are used, where 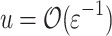 . Such projections collapse in expectation only an
. Such projections collapse in expectation only an  -fraction of mismatches, introducing systematic
-fraction of mismatches, introducing systematic  multiplicative error. A simple Markov bound argument follows, that since expected error is within desired bound, taking few (lets say
multiplicative error. A simple Markov bound argument follows, that since expected error is within desired bound, taking few (lets say 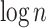 ) repetitions and taking median guarantees recovery of good approximate answer with high probability. What remains to observe is that exact counting of text-to-pattern distance over projected alphabet takes u repetitions of convolution, so the total runtime is
) repetitions and taking median guarantees recovery of good approximate answer with high probability. What remains to observe is that exact counting of text-to-pattern distance over projected alphabet takes u repetitions of convolution, so the total runtime is  . An alternative exposition to this result was provided in [34].
. An alternative exposition to this result was provided in [34].
Other Norms
A natural extension to counting mismatches is to consider other norms (e.g. 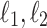 , general
, general 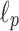 norm or
norm or  norm), or to move beyond norms (so called threshold pattern matching c.f. Atallah and Duket [6] or dominance pattern matching c.f. Amir and Farach [3]).
norm), or to move beyond norms (so called threshold pattern matching c.f. Atallah and Duket [6] or dominance pattern matching c.f. Amir and Farach [3]).
Definition 5
(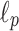 distance). For two strings of equal length over integer alphabet and constant
distance). For two strings of equal length over integer alphabet and constant 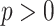 , their
, their 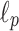 distance is defined as
distance is defined as
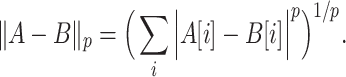 |
Definition 6
( distance). For two strings of equal length over integer alphabet, their
distance). For two strings of equal length over integer alphabet, their  distance is defined as
distance is defined as
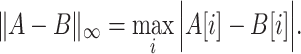 |
Exact Algorithms
To see that the link between convolution and text-to-pattern distance is relevant when considering other norms, consider the case of computing 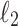 distances. We are computing output array O[] such that
distances. We are computing output array O[] such that 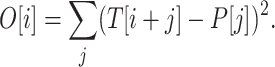 However, this is equivalent to computing, for every i simultaneously, value
However, this is equivalent to computing, for every i simultaneously, value  . While the terms
. While the terms 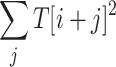 and
and  can be easily precomputed in
can be easily precomputed in 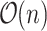 time, we observe (following [29]) that
time, we observe (following [29]) that 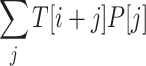 is essentially convolution. Indeed, consider
is essentially convolution. Indeed, consider  such that
such that  , and then what follows.
, and then what follows.
We now consider  distance. Using techniques similar to Hamming distance, the
distance. Using techniques similar to Hamming distance, the 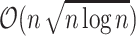 complexity algorithms were developed independently in 2005 by Clifford et al. [11] and Amir et al. [5] for reporting all
complexity algorithms were developed independently in 2005 by Clifford et al. [11] and Amir et al. [5] for reporting all 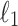 distances. The algorithms use a balancing argument, starting with observation that alphabet can be partitioned into buckets, where each bucket is a consecutive interval of alphabet. The contribution of characters from the same interval is counted in one phase, and contribution of characters from distinct intervals is counted in second phase.
distances. The algorithms use a balancing argument, starting with observation that alphabet can be partitioned into buckets, where each bucket is a consecutive interval of alphabet. The contribution of characters from the same interval is counted in one phase, and contribution of characters from distinct intervals is counted in second phase.
Interestingly, no known algorithm for exact computation of text-to-pattern 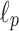 distance for arbitrary value of p is known. By the folklore observation, for any even p we can reduce it to convolution and have
distance for arbitrary value of p is known. By the folklore observation, for any even p we can reduce it to convolution and have  time algorithm (c.f. Lipsky and Porat [29], with
time algorithm (c.f. Lipsky and Porat [29], with  hiding
hiding 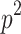 dependency). By the results of Labib et al. [25] any odd-value integer p admits
dependency). By the results of Labib et al. [25] any odd-value integer p admits 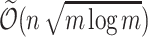 time algorithm (the algorithm is given implicitly, by providing a reduction from
time algorithm (the algorithm is given implicitly, by providing a reduction from  to Hamming distance, with
to Hamming distance, with  hiding
hiding  dependency).
dependency).
Approximate and k-Bounded Algorithms
Once again, the topic spurs interest in approximation algorithm for distance functions. In [29] a deterministic algorithm with a run time of 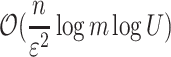 was given, while later in [17] the complexity has been improved to a (randomized)
was given, while later in [17] the complexity has been improved to a (randomized) 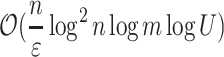 , where U is the maximal integer value on the input. Later [34] it was shown that such complexity is in fact achievable (up to poly-log factors) with a deterministic solution. All those solutions follow similar framework of linearity-preserving reductions, which has actually broader applications. The framework is as follow: imagine we want to approximate some distance function
, where U is the maximal integer value on the input. Later [34] it was shown that such complexity is in fact achievable (up to poly-log factors) with a deterministic solution. All those solutions follow similar framework of linearity-preserving reductions, which has actually broader applications. The framework is as follow: imagine we want to approximate some distance function 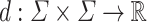 . We build small number of pairs of projections,
. We build small number of pairs of projections, 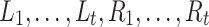 , with the following property:
, with the following property:  .2 Given such formulation, by linearity, text-to-pattern of A and B using distance function d is approximated by a linear combination of convolutions of
.2 Given such formulation, by linearity, text-to-pattern of A and B using distance function d is approximated by a linear combination of convolutions of  and
and 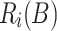 . The complexity of the solutions follows from the number of different projections that need to be used.
. The complexity of the solutions follows from the number of different projections that need to be used.
For  distances, in [29] a
distances, in [29] a  time approximate solution was given, while in Lipsky and Porat [27] a k-bounded
time approximate solution was given, while in Lipsky and Porat [27] a k-bounded  distance algorithm with time
distance algorithm with time  was given. For k-bounded
was given. For k-bounded 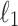 distances, [5] a
distances, [5] a 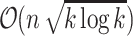 run-time algorithm was given, while in [17] an algorithm with run-time
run-time algorithm was given, while in [17] an algorithm with run-time 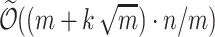 was given. The fact that those run-times are (up to poly-logs) identical to corresponding run-times of k-bounded Hamming distances is not a coincidence, as [17] have shown that k-bounded
was given. The fact that those run-times are (up to poly-logs) identical to corresponding run-times of k-bounded Hamming distances is not a coincidence, as [17] have shown that k-bounded  is at least as easy as k-bounded Hamming distance reporting.
is at least as easy as k-bounded Hamming distance reporting.
A folklore result (c.f. [29]) states that the randomized algorithm with a run time of  is in fact possible for any
is in fact possible for any  distance,
distance, 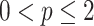 , with use of p-stable distributions and convolution. Such distributions exist only when
, with use of p-stable distributions and convolution. Such distributions exist only when  , which puts a limit on this approach. See [30] for wider discussion on p-stable distributions. Porat and Efremenko [32] has shown how to approximate general distance functions between pattern and text in time
, which puts a limit on this approach. See [30] for wider discussion on p-stable distributions. Porat and Efremenko [32] has shown how to approximate general distance functions between pattern and text in time  . Their solution does not immediately translates to
. Their solution does not immediately translates to  distances, since it allows only for score functions of form
distances, since it allows only for score functions of form 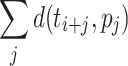 where d is arbitrary metric over
where d is arbitrary metric over 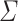 . Authors state that their techniques generalize to computation of
. Authors state that their techniques generalize to computation of  distances, and in fact those generalize further to
distances, and in fact those generalize further to 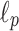 distances as well, but the
distances as well, but the  dependency in their approach is unavoidable. Finally, for any
dependency in their approach is unavoidable. Finally, for any 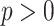 there is
there is 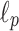 distance
distance 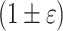 -approximate algorithm running in time
-approximate algorithm running in time  by results shown in [34]. Final result follows the framework of linearity-preserving reductions.
by results shown in [34]. Final result follows the framework of linearity-preserving reductions.
Lower Bounds
It is a major open problem whether near-linear time algorithm, or even  time algorithms, are possible for such problems. A conditional lower bound was shown in [12], via a reduction from matrix multiplication. This means that existence of combinatorial algorithm with run-time
time algorithms, are possible for such problems. A conditional lower bound was shown in [12], via a reduction from matrix multiplication. This means that existence of combinatorial algorithm with run-time 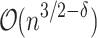 solving the problem for Hamming distances implies combinatorial algorithms for Boolean matrix multiplication with
solving the problem for Hamming distances implies combinatorial algorithms for Boolean matrix multiplication with 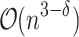 run-time, which existence is unlikely. Looking for unconditional bounds, we can state this as a lower-bound of
run-time, which existence is unlikely. Looking for unconditional bounds, we can state this as a lower-bound of 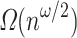 for Hamming distances pattern matching, where
for Hamming distances pattern matching, where 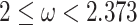 is a matrix multiplication exponent. In fact those techniques can be generalized to take into account k-bounded version of this problem:
is a matrix multiplication exponent. In fact those techniques can be generalized to take into account k-bounded version of this problem:
Theorem 2
([17]). For any positive  such that
such that 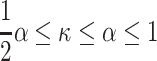 there is no combinatorial algorithm solving pattern matching with
there is no combinatorial algorithm solving pattern matching with 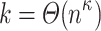 mismatches in time
mismatches in time  for a text of length n and a pattern of length
for a text of length n and a pattern of length 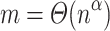 , unless the combinatorial matrix multiplication conjecture fails.
, unless the combinatorial matrix multiplication conjecture fails.
Complexity of pattern matching under Hamming distance and under 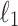 distance was proven to be identical (up to poly-logarithmic terms) in [25]. This equivalence in fact applies to a wider range of distance functions and in general other score functions. The result shows that a wide class of functions are equivalent under linearity-preserving reductions to computation of Hamming distances. The class includes e.g. dominance score,
distance was proven to be identical (up to poly-logarithmic terms) in [25]. This equivalence in fact applies to a wider range of distance functions and in general other score functions. The result shows that a wide class of functions are equivalent under linearity-preserving reductions to computation of Hamming distances. The class includes e.g. dominance score, 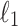 distance, threshold score,
distance, threshold score,  distance, any of above with wildcards, and in fact a wider class called piece-wise polynomial functions.
distance, any of above with wildcards, and in fact a wider class called piece-wise polynomial functions.
Definition 7
For integers A, B, C and polynomial P(x, y) we say that the function  is half-plane polynomial. We call a sum of half-plane polynomial functions a piece-wise polynomial. We say that a function is axis-orthogonal piece-wise polynomial, if it is piece-wise polynomial and for every i,
is half-plane polynomial. We call a sum of half-plane polynomial functions a piece-wise polynomial. We say that a function is axis-orthogonal piece-wise polynomial, if it is piece-wise polynomial and for every i,  or
or 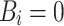 .
.
Observe that  ,
,  ,
,  , and e.g. threshold function can be defined as
, and e.g. threshold function can be defined as  .
.
Theorem 3
Let  be a piece-wise polynomial of constant degree and
be a piece-wise polynomial of constant degree and  number of summands.
number of summands.
If
 is axis orthogonal, then
is axis orthogonal, then  is “easy”:
is “easy”:  convolution takes
convolution takes 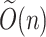 time,
time, 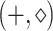 matrix multiplication takes
matrix multiplication takes  time.
time.Otherwise,
 is Hamming distance complete: under one-to-polylog reductions, on inputs bounded in absolute value by
is Hamming distance complete: under one-to-polylog reductions, on inputs bounded in absolute value by 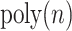 ,
, 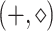 product is equivalent to Hamming distance,
product is equivalent to Hamming distance, 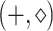 convolution is equivalent to text-to-pattern Hamming distance and
convolution is equivalent to text-to-pattern Hamming distance and  matrix product is equivalent to Hamming-distance matrix product.
matrix product is equivalent to Hamming-distance matrix product.
Some of those reduction (for specific problems) were presented in literature, c.f. [28, 37, 39], but never as a generic class-of-problems equivalence.
This means that the encountered barrier for all of the induced text-to-pattern distance problems is in fact the same barrier, and we should not expect algorithms with dependency 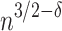 without some major breakthrough. Unfortunately such reductions do not preserve properties of k-bounded instances or
without some major breakthrough. Unfortunately such reductions do not preserve properties of k-bounded instances or  -approximate ones, so this result tells us nothing about relative complexity of relaxed problems, and it is a major open problem to do so.
-approximate ones, so this result tells us nothing about relative complexity of relaxed problems, and it is a major open problem to do so.
Streaming Algorithms
In streaming algorithms, the goal is to process text in a streaming fashion, and answer in a real-time about the distance between last m characters of text and a pattern. The primary measure of efficiency is the memory complexity of the algorithm, that is we assume that the whole input (or even the whole pattern) is too large to fit into the memory and some for of small-space representation is required. The time to process each character is the secondary measure of efficiency, since it usually is linked to memory efficiency. By folklore result, exact reporting of e.g. Hamming distances is impossible in o(m) memory, so the focus of the research has been on relaxed problems, that is k-bounded and 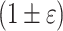 -approximate reporting.
-approximate reporting.
For k-bounded reporting of Hamming distances, in Porat and Porat [31] a  space and
space and 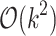 time per character streaming algorithm was presented. It was later improved in [13] to
time per character streaming algorithm was presented. It was later improved in [13] to  space and
space and 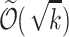 time per character, and then in Clifford et al. [14] to
time per character, and then in Clifford et al. [14] to 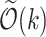 space keeping
space keeping 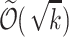 time per character. Many interesting techniques were developed for this problem. As an example, k-mismatch problem can be reduced to (
time per character. Many interesting techniques were developed for this problem. As an example, k-mismatch problem can be reduced to ( many instances of) 1-mismatch problem (c.f. [13]), which in fact reduces to exact pattern matching in streaming model (c.f. [31]). Other approach is to construct efficient rolling sketches for k-mismatch problem, based on Reed-Solomon error correcting codes (c.f. [14]).
many instances of) 1-mismatch problem (c.f. [13]), which in fact reduces to exact pattern matching in streaming model (c.f. [31]). Other approach is to construct efficient rolling sketches for k-mismatch problem, based on Reed-Solomon error correcting codes (c.f. [14]).
For  , two interesting approaches are possible. First approach was presented by Clifford and Starikovskaya [15] and later refined in Svagerka et al. [33]. This approach consists of using rolling sketches of text started every
, two interesting approaches are possible. First approach was presented by Clifford and Starikovskaya [15] and later refined in Svagerka et al. [33]. This approach consists of using rolling sketches of text started every  positions, and additionally
positions, and additionally 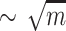 sketches of substrings of length
sketches of substrings of length  of pattern are maintained (guaranteeing that at least one sketch in text is aligned to one sketch of long pattern fragment). One way of building rolling sketches for approximate Hamming distance is to use random projections to binary alphabet and reduce the problem to one for binary alphabet, where binary alphabet uses Johnson-Lindenstrauss type of constructions. This approach results in
of pattern are maintained (guaranteeing that at least one sketch in text is aligned to one sketch of long pattern fragment). One way of building rolling sketches for approximate Hamming distance is to use random projections to binary alphabet and reduce the problem to one for binary alphabet, where binary alphabet uses Johnson-Lindenstrauss type of constructions. This approach results in 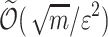 memory and
memory and  time per character.
time per character.
Alternative approach was proposed in recent work of Chan et al. [9]. They start with observation that the Hamming distance can be estimated by checking mismatches at a random subset of positions. Their algorithm uses a random subset as follow: the algorithm picks a random prime p (of an appropriately chosen size) and a random offset b, and considers a subset of positions  . The structured nature of the subset enables more efficient computation. It turns out that even better efficiency is achieved by using multiple (but still relatively few) offsets. When approximating the Hamming distance of the pattern at subsequent text locations, the set of sampled positions in the text changes, and so a straightforward implementation seems too costly. To overcome this challenge, a key idea is to shift the sample a few times in the pattern and a few times in the text (namely, for a trade-off parameter z, our algorithm considers z shifts in the pattern and p/z shifts in the text). Interestingly, the proposed solution is even more efficient when considering a
. The structured nature of the subset enables more efficient computation. It turns out that even better efficiency is achieved by using multiple (but still relatively few) offsets. When approximating the Hamming distance of the pattern at subsequent text locations, the set of sampled positions in the text changes, and so a straightforward implementation seems too costly. To overcome this challenge, a key idea is to shift the sample a few times in the pattern and a few times in the text (namely, for a trade-off parameter z, our algorithm considers z shifts in the pattern and p/z shifts in the text). Interestingly, the proposed solution is even more efficient when considering a  -approximate k-bounded reporting of Hamming distances.
-approximate k-bounded reporting of Hamming distances.
Theorem 4
([9]). There is an algorithm that reports  -approximate k-bounded Hamming distances in a streaming setting that uses
-approximate k-bounded Hamming distances in a streaming setting that uses 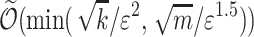 space and takes
space and takes 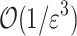 time per character.
time per character.
Focusing on other norms, we note that in [33] a sublinear space algorithms for 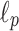 norms for
norms for  was presented. The specific details of construction vary between different values of p, and the techniques include: using p-stable distributions (c.f. [18]), range-summable hash functions (c.f. [7]) and Johnson-Lindenstrauss projections (c.f. [2]).
was presented. The specific details of construction vary between different values of p, and the techniques include: using p-stable distributions (c.f. [18]), range-summable hash functions (c.f. [7]) and Johnson-Lindenstrauss projections (c.f. [2]).
Theorem 5
([33]). Let  denote size of alphabet. There is a streaming algorithm that computes a
denote size of alphabet. There is a streaming algorithm that computes a  -approximation of the
-approximation of the 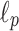 distances. The parameters of the algorithm are
distances. The parameters of the algorithm are
in
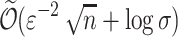 space, and
space, and  time per arrival when
time per arrival when 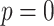 (Hamming distance);
(Hamming distance);in
 space and
space and  time per arrival when
time per arrival when  ;
;in
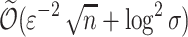 space and
space and  time per arrival when
time per arrival when 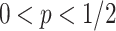 ;
;in
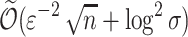 space and
space and  time per arrival when
time per arrival when 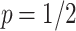 ;
;in
 space and
space and 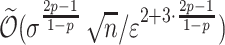 time per arrival when
time per arrival when 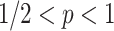 ;
;in
 space and
space and  time per arrival for
time per arrival for  .
.
Open Problems
Below we list several open problems of the area, which we believe are the most promising research directions and/or pressing questions.
Show deterministic algorithm for
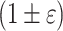 -approximate
-approximate 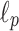 reporting for
reporting for 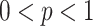 , preferably in time
, preferably in time  .
.What is the time complexity of exact
 reporting for non-integer p?
reporting for non-integer p?Show conditional lower bound for exact Hamming distance reporting from stronger hypotheses, like 3SUM-HARDNESS.
Lower bounds for
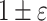 approximations (conditional between problems, or from external problems), for any of the discussed problems.
approximations (conditional between problems, or from external problems), for any of the discussed problems.What is the true space complexity dependency in streaming
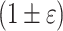 approximate Hamming distance reporting? Is
approximate Hamming distance reporting? Is  complexity optimal?
complexity optimal?Can we close the gap between streaming complexity of approximate
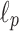 algorithms and streaming complexity of approximate Hamming distance?
algorithms and streaming complexity of approximate Hamming distance?Can we design effective “combinatorial” algorithms for all mentioned problems (e.g. not relying on convolution)? For Hamming,
 and
and 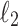 distances answer is at least partially yes (c.f. [9] and [36]).
distances answer is at least partially yes (c.f. [9] and [36]).
Footnotes
Its  not
not 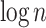 by standard trick of reducing the problem to
by standard trick of reducing the problem to 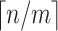 instances with pattern P of length m and text of length 2m.
instances with pattern P of length m and text of length 2m.
Here we used  since its in the context of approximate algorithms. The same framework applies to exact algorithms, then we replace
since its in the context of approximate algorithms. The same framework applies to exact algorithms, then we replace  with
with  .
.
Supported by Polish National Science Centre grant 2019/33/B/ST6/00298.
Contributor Information
Marcella Anselmo, Email: manselmo@unisa.it.
Gianluca Della Vedova, Email: gianluca.dellavedova@unimib.it.
Florin Manea, Email: flmanea@gmail.com.
Arno Pauly, Email: arno.m.pauly@gmail.com.
Przemysław Uznański, Email: puznanski@cs.uni.wroc.pl.
References
- 1.Abrahamson KR. Generalized string matching. SIAM J. Comput. 1987;16(6):1039–1051. doi: 10.1137/0216067. [DOI] [Google Scholar]
- 2.Achlioptas D. Database-friendly random projections: Johnson-Lindenstrauss with binary coins. J. Comput. Syst. Sci. 2003;66(4):671–687. doi: 10.1016/S0022-0000(03)00025-4. [DOI] [Google Scholar]
- 3.Amir A, Farach M. Efficient matching of nonrectangular shapes. Ann. Math. Artif. Intell. 1991;4(3):211–224. doi: 10.1007/BF01531057. [DOI] [Google Scholar]
-
4.Amir A, Lewenstein M, Porat E. Faster algorithms for string matching with
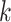 mismatches. J. Algorithms. 2004;50(2):257–275. doi: 10.1016/S0196-6774(03)00097-X. [DOI] [Google Scholar]
mismatches. J. Algorithms. 2004;50(2):257–275. doi: 10.1016/S0196-6774(03)00097-X. [DOI] [Google Scholar] -
5.Amir A, Lipsky O, Porat E, Umanski J. Approximate Matching in the
 Metric. In: Apostolico A, Crochemore M, Park K, editors. Combinatorial Pattern Matching; Heidelberg: Springer; 2005. pp. 91–103. [Google Scholar]
Metric. In: Apostolico A, Crochemore M, Park K, editors. Combinatorial Pattern Matching; Heidelberg: Springer; 2005. pp. 91–103. [Google Scholar] - 6.Atallah MJ, Duket TW. Pattern matching in the hamming distance with thresholds. Inf. Process. Lett. 2011;111(14):674–677. doi: 10.1016/j.ipl.2011.04.004. [DOI] [Google Scholar]
- 7.Calderbank, A.R., Gilbert, A.C., Levchenko, K., Muthukrishnan, S., Strauss, M.: Improved range-summable random variable construction algorithms. In: SODA, pp. 840–849 (2005)
- 8.Chakrabarti A, Regev O. An optimal lower bound on the communication complexity of gap-hamming-distance. SIAM J. Comput. 2012;41(5):1299–1317. doi: 10.1137/120861072. [DOI] [Google Scholar]
- 9.Chan, T.M., Golan, S., Kociumaka, T., Kopelowitz, T., Porat, E.: Approximating text-to-pattern hamming distances. In: STOC 2020 (2020)
- 10.Chen K-Y, Hsu P-H, Chao K-M. Approximate matching for run-length encoded strings is 3sum-hard. In: Kucherov G, Ukkonen E, editors. Combinatorial Pattern Matching; Heidelberg: Springer; 2009. pp. 168–179. [Google Scholar]
-
11.Clifford P, Clifford R, Iliopoulos C. Faster algorithms for
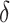 ,
, 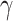 -matching and related problems. In: Apostolico A, Crochemore M, Park K, editors. Combinatorial Pattern Matching; Heidelberg: Springer; 2005. pp. 68–78. [Google Scholar]
-matching and related problems. In: Apostolico A, Crochemore M, Park K, editors. Combinatorial Pattern Matching; Heidelberg: Springer; 2005. pp. 68–78. [Google Scholar] - 12.Clifford, R.: Matrix multiplication and pattern matching under Hamming norm. http://www.cs.bris.ac.uk/Research/Algorithms/events/BAD09/BAD09/Talks/BAD09-Hammingnotes.pdf. Accessed Mar 2017
- 13.Clifford, R., Fontaine, A., Porat, E., Sach, B., Starikovskaya, T.: The k-mismatch problem revisited. In: SODA, pp. 2039–2052 (2016). 10.1137/1.9781611974331.ch142
- 14.Clifford, R., Kociumaka, T., Porat, E.: The streaming k-mismatch problem. In: SODA, pp. 1106–1125 (2019). 10.1137/1.9781611975482.68
- 15.Clifford, R., Starikovskaya, T.: Approximate hamming distance in a stream. In: ICALP, pp. 20:1–20:14 (2016). 10.4230/LIPIcs.ICALP.2016.20
- 16.Fischer, M.J., Paterson, M.S.: String-matching and other products. Technical report (1974)
-
17.Gawrychowski, P., Uznański, P.: Towards unified approximate pattern matching for hamming and
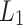 distance. In: ICALP, pp. 62:1–62:13 (2018). 10.4230/LIPIcs.ICALP.2018.62
distance. In: ICALP, pp. 62:1–62:13 (2018). 10.4230/LIPIcs.ICALP.2018.62
- 18.Indyk P. Stable distributions, pseudorandom generators, embeddings, and data stream computation. J. ACM. 2006;53(3):307–323. doi: 10.1145/1147954.1147955. [DOI] [Google Scholar]
- 19.Jayram TS, Kumar R, Sivakumar D. The one-way communication complexity of hamming distance. Theory Comput. 2008;4(1):129–135. doi: 10.4086/toc.2008.v004a006. [DOI] [Google Scholar]
- 20.Karatsuba A. Multiplication of multidigit numbers on automata. Soviet physics doklady. 1963;7:595–596. [Google Scholar]
- 21.Karloff HJ. Fast algorithms for approximately counting mismatches. Inf. Process. Lett. 1993;48(2):53–60. doi: 10.1016/0020-0190(93)90177-B. [DOI] [Google Scholar]
-
22.Kopelowitz, T., Porat, E.: Breaking the variance: approximating the hamming distance in
 time per alignment. In: FOCS, pp. 601–613 (2015). 10.1109/FOCS.2015.43
time per alignment. In: FOCS, pp. 601–613 (2015). 10.1109/FOCS.2015.43
- 23.Kopelowitz, T., Porat, E.: A simple algorithm for approximating the text-to-pattern hamming distance. In: SOSA@SODA, pp. 10:1–10:5 (2018). 10.4230/OASIcs.SOSA.2018.10
- 24.Kosaraju, S.R.: Efficient string matching (1987). Manuscript
- 25.Labib, K., Uznański, P., Wolleb-Graf, D.: Hamming distance completeness. In: CPM, pp. 14:1–14:17 (2019). 10.4230/LIPIcs.CPM.2019.14
-
26.Landau GM, Vishkin U. Efficient string matching with
 mismatches. Theor. Comput. Sci. 1986;43:239–249. doi: 10.1016/0304-3975(86)90178-7. [DOI] [Google Scholar]
mismatches. Theor. Comput. Sci. 1986;43:239–249. doi: 10.1016/0304-3975(86)90178-7. [DOI] [Google Scholar] -
27.Lipsky O, Porat E. Approximate matching in the
 metric. Inf. Process. Lett. 2008;105(4):138–140. doi: 10.1016/j.ipl.2007.08.012. [DOI] [Google Scholar]
metric. Inf. Process. Lett. 2008;105(4):138–140. doi: 10.1016/j.ipl.2007.08.012. [DOI] [Google Scholar] -
28.Lipsky O, Porat E.
 pattern matching lower bound. Inf. Process. Lett. 2008;105(4):141–143. doi: 10.1016/j.ipl.2007.08.011. [DOI] [Google Scholar]
pattern matching lower bound. Inf. Process. Lett. 2008;105(4):141–143. doi: 10.1016/j.ipl.2007.08.011. [DOI] [Google Scholar] -
29.Lipsky O, Porat E. Approximate pattern matching with the
 ,
, 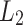 and
and  metrics. Algorithmica. 2011;60(2):335–348. doi: 10.1007/s00453-009-9345-9. [DOI] [Google Scholar]
metrics. Algorithmica. 2011;60(2):335–348. doi: 10.1007/s00453-009-9345-9. [DOI] [Google Scholar] - 30.Nolan J. Stable Distributions: Models for Heavy-Tailed Data. New York: Birkhauser; 2003. [Google Scholar]
- 31.Porat, B., Porat, E.: Exact and approximate pattern matching in the streaming model. In: FOCS, pp. 315–323 (2009). 10.1109/FOCS.2009.11
- 32.Porat, E., Efremenko, K.: Approximating general metric distances between a pattern and a text. In: SODA, pp. 419–427 (2008). http://dl.acm.org/citation.cfm?id=1347082.1347128
-
33.Starikovskaya, T., Svagerka, M., Uznański, P.:
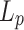 pattern matching in a stream. CoRR abs/1907.04405 (2019)
pattern matching in a stream. CoRR abs/1907.04405 (2019)
- 34.Studený, J., Uznański, P.: Approximating approximate pattern matching. In: CPM, vol. 128, pp. 15:1–15:13 (2019). 10.4230/LIPIcs.CPM.2019.15
- 35.Toom, A.: The complexity of a scheme of functional elements simulating the multiplication of integers. In: Doklady Akademii Nauk, vol. 150, pp. 496–498. Russian Academy of Sciences (1963)
- 36.Uznański, P.: Approximating text-to-pattern distance via dimensionality reduction. CoRR abs/2002.03459 (2020)
- 37.Vassilevska, V.: Efficient algorithms for path problems in weighted graphs. Ph.D. thesis, Carnegie Mellon University (2008)
- 38.Woodruff, D.P.: Optimal space lower bounds for all frequency moments. In: SODA, pp. 167–175 (2004). http://dl.acm.org/citation.cfm?id=982792.982817
- 39.Zhang P, Atallah MJ. On approximate pattern matching with thresholds. Inf. Process. Lett. 2017;123:21–26. doi: 10.1016/j.ipl.2017.03.001. [DOI] [Google Scholar]


